Abstract
In this study, the RHF, B3LYP and wB97XD methods with cc-pVDZ basis set have been used to investigate the influence of carbon atoms substitution with boron atoms on the non-linear optical, electronic, optoelectronic and thermodynamic properties of BEDT-TTF (). The results show that the undoped molecule denoted BEDT-TTF or ET (Eg = 3.88 eV) and its derivatives are semi-conductors materials. However, doping with both 3B and 2B, creating a strong donor-acceptor system and considerably improves its energies gap (Egap). The Eg values of these doped molecules are between 2.2 and 2.39 eV less than 3 eV, which makes more interesting electronic properties. The nonlinear optical parameters such as dipole moment (μ), average polarizability ˂α˃ and first-order hyperpolarizability () have been calculated and compared with the corresponding values of Urea used as prototypical material to study the NLO properties of the compound. These values obtained indicate that these materials exhibit good nonlinear optical properties. Moreover, we have also computed the chemical softness , ionization potential (IP), electron affinity (AE), global hardness (η), refractive index (n), dielectric constant (ε), electric field (E) and electric susceptibility (χ), total electronic energy (Eo), enthalpy H, entropy S. These results indicate that these new materials doped with boron are promising candidates for the construction of optoelectronics and photonic devices.
Keywords: BEDT-TTF, Hyperpolarizability, Nonlinear optical properties, Doping, Optoelectronic, NBO
BEDT-TTF, Hyperpolarizability, Nonlinear optical properties, Doping, Optoelectronic, NBO.
1. Introduction
Organic compounds represent promising materials, certainly, because they could find applications for example in modern communication, optical computing, dynamic image processing, telecommunication, data storage also in light-emitting diode (LED), field-effect transistor (FET) and other laser devices [1]. Organic semiconductors are generally pi-conjugated materials, in which the transport mechanisms are quite different from those conventionally described in solid-state physics with inorganic semiconductors [1]. With the discovery, of bis (ethylenedithio) tetrathiafulvalene abbreviated as BEDT-TTF or simply ET in 1980 [2] (Figure 1). In the literature, others organic conductors have been synthesized and studied previously [3]. Demiralp et al [4], has been reported that, about 30 organic superconductors based on BEDT-TTF have been synthesized with critical temperature up to 12,8K .In the previous study, the infrared and Raman spectra of BEDT-TTF have been reported by Kozlov et al [5], Eldridge et al [6] and Ruifeng et al [7]. Moreover, the works of Flakina et al [8], revealed new molecules from the monosubstituted anion of isocyanuric acid on BEDT-TTF and their crystal structures were determined. The chirality of substituted BEDT-TTF derivatives was in the heart of work of Wallis et al [9]. In addition, gives opportunities for preparing multifunctional materials. Much attention continues to be directed to the development of magnetic molecular conductors taking into account interactions between conductive electrons and localized spins. In this context, a global study of the vibrational dynamics of the bis(ethylenedithio) tetrathiafulvalene has been performed through ab-initio investigations [10, 11, 12, 13, 14]. These studies have contributed much to our knowledge of the vibrational spectra of these molecules. However, the nonlinear optical, electronic, optoelectronic and thermodynamics properties are still not fully understood. In recent years, many works [15, 16, 17, 18] have shown that the ab -initio and the density functional theory methods have become powerful tools in the study of electronic structure, optoelectronic and nonlinear optical properties. The goal of this original research is to propose materials, which find their applications in organic electronic. In this paper, we investigate the semi-conductor nature of the molecule bis (ethylenedithio) tetrathiafulvalene and some of its derivatives by doping it with some atoms, which may have application in quantum dots and other material. Our objectives are: to use ab initio and DFT quantum mechanical calculations to decipher the electronic structure, dipole moments, average polarizability, hyperpolarizabilities, first molecular hyperpolarizabilities, HOMO-LUMO molecular orbital diagram, dielectric constant, refractive index, energy gap, susceptibility, electrical conductivity, Electron affinity, Ionization potential and Molar refractivity of bis(ethylenedithio)tetrathiafulvalene with their doped-molecules. This work present the ab-initio and DFT calculations in the ground state using Hartree-Fock (HF), B3LYP (Becke-3-Lee-Yang-Parr) and wB97XD methods with a cc-pVDZ basis set.
Figure 1.
Molecular structure of BEDT-TTF.
We organized this paper in four sections. We present in section 2, the calculation method. In section 3, the results and discussion are presented. The conclusion is given in section 4.
2. Methods of calculation
The calculations were computed using Gaussian 09 calculation code [19]. To study the electronic structure of bis (ethylenedithio) tetrafulvalene (C10H8S8), and 3B-, 2B-doped BEDT-TTF () and() respectively we first of all constructed these molecules by using Gauss view 6.0.16 modelling software [20]. Initially, pre-optimization was used employing the RHF level of theory with a minimal basis set. Then, the calculations were carried out using the polarized valence double zeta. DFT method was employed with Becke's three parameters non-local exchange functional with the Lee-Yang-Parr correlation function (B3LYP) functional [21, 22]. This functional is used because of their cost-effective method for the inclusion of electron correlations. To take into account the empirical dispersion and long-range correction, wB97XD functional has been used. The geometry optimization has been studied in the ground state.
3. Results and discussion
3.1. Optimized structure and geometric properties
3.1.1. Optimized structure
Figure 2 shows the optimized molecules of bis (ethylenedithio) tetrafulvalene, undoped structure (a) and their derivatives (b) and (c) respectively and , doped molecules. The geometric parameters of the neutral structure of BEDT-TTF are summarized in Table 1.
Figure 2.
Optimized molecules of (a) bis (ethylenedithio) tetrathiafulvalene (ET), (b) 3B-doped (B3ET) and (c) 2B-doped to bromine (B2ET) with B3LYP/cc-pVDZ basis set.
Table 1.
Optimized geometric parameters of bis (ethylenedithio) tetrathiafulvalene (BEDT-TTF), bond lengths (Å) and angles (o) compared with experimentobtained with B3LYP, wB97XD and RHF using cc-pVDZ basis set.
| Bond lengths(Å) | B3LYP | wB97XD | RHF | Exp. [23] |
|---|---|---|---|---|
| R(1,2) | 1.3531 | 1.3467 | 1.3263 | 1.347 |
| R(1,8) | 1.7672 | 1.7596 | 1.772 | 1.745 |
| R(1,12) | 1.7885 | 1.7758 | 1.7816 | 1.768 |
| R(2,7) | 1.7672 | 1.7598 | 1.7706 | 1.746 |
| R(2,11) | 1.7877 | 1.775 | 1.7791 | 1.768 |
| R(3,6) | 1.3542 | 1.3472 | 1.33 | 1.352 |
| R(3,11) | 1.7843 | 1.7736 | 1.7756 | 1.762 |
| R(3,12) | 1.7861 | 1.7751 | 1.7766 | 1.770 |
| R(4,5) | 1.3531 | 1.3467 | 1.3263 | 1.350 |
| R(4,9) | 1.7671 | 1.7596 | 1.772 | 1.755 |
| R(4,13) | 1.7885 | 1.7758 | 1.7815 | 1.778 |
| R(5,10) | 1.7671 | 1.7598 | 1.7706 | 1.757 |
| R(5,14) | 1.7877 | 1.775 | 1.7791 | 1.771 |
| R(6,13) | 1.7861 | 1.7751 | 1.7765 | 1.763 |
| R(6,14) | 1.7843 | 1.7736 | 1.7756 | 1.758 |
| R(7,15) | 1.8477 | 1.8303 | 1.8175 | 1.835 |
| R(8,18) | 1.8672 | 1.8484 | 1.8255 | 1.824 |
| R(9,24) | 1.8674 | 1.8484 | 1.8254 | 1.811 |
| R(10,21) | 1.8478 | 1.8304 | 1.8177 | 1.817 |
| R(15,16) | 1.0996 | 1.0992 | 1.0886 | - |
| R(15,17) | 1.1014 | 1.1 | 1.0903 | - |
| R(15,18) | 1.5196 | 1.5176 | 1.5213 | 1.517 |
| R(18,19) | 1.0991 | 1.0984 | 1.0876 | - |
| R(18,20) | 1.1024 | 1.1009 | 1.0907 | - |
| R(21,22) | 1.0996 | 1.0992 | 1.0886 | - |
| R(21,23) | 1.1014 | 1.1 | 1.0903 | - |
| R(21,24) | 1.5196 | 1.5176 | 1.5213 | 1.518 |
| R(24,25) | 1.0991 | 1.0984 | 1.0876 | - |
| R(24,26) | 1.1024 | 1.1009 | 1.0907 | - |
| Bond angles (°) | ||||
| A (2, 1,8) | 127.4013 | 127.3211 | 129.3176 | 129.74 |
| A (2, 1,12) | 116.8399 | 116.9136 | 116.9503 | 116.91 |
| A (8, 1,12) | 115.7136 | 115.722 | 113.6787 | 113.01 |
| A (1, 2,7) | 123.5173 | 123.4119 | 127.4358 | 127.73 |
| A (1, 2,11) | 117.1404 | 117.2423 | 117.4037 | 116.77 |
| A (7, 2,11) | 118.7068 | 118.7058 | 115.1114 | 115.22 |
| A (6, 3,11) | 123.7415 | 123.5804 | 123.96 | 122.88 |
| A (6, 3,12) | 123.2783 | 123.1584 | 123.5578 | 123.01 |
| A (11, 3,12) | 112.9329 | 113.2254 | 112.4472 | 113.99 |
| A (5, 4,9) | 127.3958 | 127.321 | 129.3183 | 122.49 |
| A (5, 4,13) | 116.8399 | 116.9137 | 116.9533 | 117.49 |
| A (9, 4,13) | 115.7189 | 115.7221 | 113.6748 | 119.64 |
| A (4, 5,10) | 123.5121 | 123.4119 | 127.4371 | 125.08 |
| A (4, 5,14) | 117.139 | 117.2423 | 117.4039 | 117.06 |
| A (10, 5,14) | 118.71 | 118.7059 | 115.1101 | 117.83 |
| A (3, 6,13) | 123.277 | 123.1584 | 123.5563 | 122.88 |
| A (3, 6,14) | 123.7419 | 123.5803 | 123.9582 | 122.65 |
| A(13,6,14) | 112.9347 | 113.2254 | 112.4501 | 114.29 |
| A(2,7,15) | 96.1788 | 95.851 | 99.091 | 99.75 |
| A(1,8,18) | 103.7839 | 103.7149 | 102.5825 | 100.70 |
| A(4,9,24) | 103.7831 | 103.7149 | 102.58 | 96.61 |
| A(5,10,21) | 96.1814 | 95.851 | 99.089 | 103.49 |
| A(2,11,3) | 93.5086 | 93.3924 | 94.2293 | 94.51 |
| A(1,12,3) | 93.621 | 93.525 | 94.2803 | 94.05 |
| A(4,13,6) | 93.6219 | 93.525 | 94.2844 | 93.47 |
| A(5,14,6) | 93.5118 | 93.3924 | 94.2332 | 93.92 |
| A (7,15,16) | 107.5626 | 107.7423 | 109.568 | - |
| A(7,15,17) | 105.823 | 106.2662 | 104.7873 | - |
| A(7,15,18) | 113.0628 | 112.9638 | 112.3925 | 112.34 |
| A(16,15,17) | 108.6664 | 108.5855 | 108.6259 | - |
| A(16,15,18) | 112.0228 | 111.8243 | 111.5666 | - |
| A(17,15,18) | 109.4364 | 109.2284 | 109.6251 | - |
| A(8,18,15) | 115.7202 | 115.6584 | 114.054 | 113.38 |
| A(8,18,19) | 105.6108 | 105.9438 | 109.1802 | - |
| A(8,18,20) | 105.8332 | 106.1314 | 104.0093 | - |
| A(15,18,19) | 110.5685 | 110.2745 | 110.4982 | - |
| A(15,18,20) | 109.9151 | 109.7127 | 110.2224 | - |
| A(19,18,20) | 108.8816 | 108.8445 | 108.5828 | - |
| A(10,21,22) | 107.5579 | 107.7423 | 109.5662 | - |
| A(10,21,23) | 105.8207 | 106.2662 | 104.7844 | - |
| A(10,21,24) | 113.0656 | 112.9638 | 112.3834 | 117.19 |
| A(22,21,23) | 108.666 | 108.5855 | 108.631 | - |
| A(22,21,24) | 112.0235 | 111.8243 | 111.5713 | - |
| A(23,21,24) | 109.4399 | 109.2284- | 109.6291 | - |
| A(9,24,21) | 115.7144 | 115.6584 | 114.0508 | 115.01 |
| A(9,24,25) | 105.6021 | 105.9438 | 109.1854 | - |
| A(9,24,26) | 105.835 | 106.1314 | 104.0089 | - |
| A(21,24,25) | 110.5733 | 110.2745 | 110.4964 | - |
| A(21,24,26) | 109.9181 | 109.7127 | 110.2242 | - |
| A(25,24,26) | 108.8866 | 108.8445 | 108.5813 | - |
3.1.2. Geometric properties
The optimized geometric parameters of bis (ethylenedithio) tetrathiafulvalene undoped molecule (a) such as the bond lengths and bond angles by B3LYP, RHF and wB97XD methods with the same basis set cc-pVDZ are given in Table 1; the experimental results [23] are also in this Table 1 for comparison. Based on our calculations, the results obtained using B3LYP and wB97XD functionals are full agreement with experimental data [23] than the HF method. From this table, some of the calculated bond lengths for BEDT-TTF such as C1–C2, C3–C6 and C4–C5 (double bond length of carbon atom) with both DFT methods are in good agreement with experimental values reported by Guionneau et al [23]. Moreover, the largest difference between experimental and computed bond length is about 0.056 Å for B3LYP, 0.037 Å for wB97XD and 0.042 Å for RHF. On the other hand, the smallest difference is about 0.001 Å for B3LYP, 0.0003 Å for wB97XD and -0.039 Å for RHF. These bond lengths show a slow variation from the uncorrelated level of theory (RHF) to the correlated level (B3LYP and wB97XD). In fact, it is well known that the Hartree-Fock method under-estimates bond lengths and the inclusion of the electron correlation make them longer [24]. This elongation usually makes a better agreement between theory and experiment. The same observation has been done in this work. Most of the bond lengths and angles obtained with B3LYP and wB97XD are very similar to the values reported by Guionneau et al [23], by Imamura et al [3] and by Demiralp et al [4]. However, we observe the large difference between C18–S8 bond length values obtained with the three methods.
The bond angles (o) of the undoped molecule follow the same pattern. The calculated bond angles were slightly equal to the values listed by Guionneau et al [23]. We can conclude that the experimental results and the theoretical calculations have a better agreement.
3.2. Natural bond orbital (NBO) analysis
NBO analysis has been performed on the both doped structures ( and ) in order to explain the intermolecular and intramolecular bonding, transfer of charge, stability and conjugated interactions [25]. The second order perturbation theory of Fock matrix was carried out to estimate the donor-acceptor interactions in NBO studies [26]. For each donor (i) and acceptor (j), the stabilization energy E(2) linked with the delocalization value of i,j is evaluated by these mathematical formulae (see Eq. (1)) [25]:
| (1) |
Where: represent the donor orbital occupancy status
and represent the donor and acceptor orbital energy values respectively;
is Fock matrix elements.
In the present work, the NBO calculations were investigated using B3LYP/cc-pVDZ level of theory and summarized in Tables 2(a) and (b) for both the doped systems. This analysis is carried out in order to examine all interactions between donor (filled) Lewis-type NBOs and acceptor (empty) non-Lewis NBOs and estimate their energetic importance.
Table 2 (a).
Second-order perturbation theory of Fock matrix in NBO basis for .
| Donor (i) | type | occupancy | Acceptor (j) | type | Occupancy | E(2)a kcal/mol | Ei-Ejb a.u | F(i,j)c a.u |
|---|---|---|---|---|---|---|---|---|
| C1–C2 | σ | 1.99034 | C1–S8 | σ∗ | 0.04321 | 1.37 | 1.00 | 0.033 |
| C1–C2 | σ | 1.99034 | C1–S12 | σ∗ | 0.03859 | 0.64 | 0.98 | 0.023 |
| C1–C2 | σ | 1.99034 | C2–S7 | σ∗ | 0.04322 | 1.37 | 1.00 | 0.033 |
| C1–C2 | σ | 1.99034 | C2–S11 | σ∗ | 0.03820 | 0.65 | 0.98 | 0.023 |
| C1–C2 | π | 1.91975 | S7–B18 | π∗ | 0.01181 | 1.85 | 0.32 | 0.022 |
| C1–C2 | π | 1.91975 | S8–B20 | π∗ | 0.01181 | 1.85 | 0.32 | 0.022 |
| C1–S8 | σ | 1.97659 | C1–C2 | σ∗ | 0.03940 | 3.42 | 1.27 | 0.059 |
| C1–S8 | σ | 1.97659 | C2–S11 | σ∗ | 0.03820 | 3.80 | 0.86 | 0.051 |
| C1–S8 | σ | 1.97659 | C 3–S12 | σ∗ | 0.04364 | 0.61 | 0.86 | 0.021 |
| C1–S8 | σ | 1.97659 | B20–H21 | σ∗ | 0.00833 | 0.88 | 1.19 | 0.029 |
| C1–S12 | σ | 1.96758 | C1–C2 | σ∗ | 0.03859 | 2.00 | 1.24 | 0.045 |
| C1–S12 | σ | 1.96758 | C2–S7 | σ∗ | 0.04322 | 6.15 | 0.85 | 0.065 |
| C1–S12 | σ | 1.96758 | C3–C6 | σ∗ | 0.04490 | 2.28 | 1.26 | 0.048 |
| C1–S12 | σ | 1.96758 | C3–C6 | π∗ | 0.37743 | 0.84 | 0.67 | 0.023 |
| C1–S12 | σ | 1.96758 | S 8–B20 | σ∗ | 0.01181 | 1.32 | 0.94 | 0.032 |
| C2–S7 | σ | 1.976559 | C1–C2 | σ∗ | 0.03940 | 3.42 | 1.27 | 0.059 |
| C2–S 7 | σ | 1.976559 | C1–S12 | σ∗ | 0.03859 | 3.80 | 0.86 | 0.051 |
| C2–S7 | σ | 1.976559 | C 3–S11 | σ∗ | 0.04384 | 0.61 | 0.86 | 0.021 |
| C2–S7 | σ | 1.976559 | B18–H19 | σ∗ | 0.00833 | 0.88 | 1.19 | 0.029 |
| C2–S11 | σ | 1.96760 | C1–C2 | σ∗ | 0.03859 | 2.00 | 1.24 | 0.045 |
| C2–S11 | σ | 1.96760 | C1–S 8 | σ∗ | 0.04321 | 6.15 | 0.85 | 0.065 |
| C2–S11 | σ | 1.96760 | C 3–C 6 | σ∗ | 0.04490 | 2.28 | 1.26 | 0.048 |
| C 2–S11 | σ | 1.96760 | C3–C6 | π∗ | 0.37743 | 0.82 | 0.67 | 0.023 |
| C2–S11 | σ | 1.96760 | S7–B18 | σ∗ | 0.07677 | 1.32 | 0.94 | 0.032 |
| C3–C 6 | σ | 1.96257 | C3–S11 | σ∗ | 0.04384 | 0.97 | 0.97 | 0.028 |
| C 3–C6 | σ | 1.99005 | C3–S12 | σ∗ | 0.04364 | 0.98 | 0.97 | 0.028 |
| C3–C6 | σ | 1.99005 | C 6–S13 | σ∗ | 0.04691 | 0.92 | 0.97 | 0.027 |
| C3–C6 | σ | 1.99005 | C6–S14 | σ∗ | 0.04310 | 0.92 | 0.97 | 0.027 |
| C3–C 6 | σ | 1.99005 | C5–S14 | σ∗ | 0.04071 | 0.56 | 0.51 | 0.015 |
| C3–S11 | σ | 1.97010 | C2–S 7 | σ∗ | 0.04322 | 2.79 | 0.85 | 0.044 |
| C3–S11 | σ | 1.97010 | C 3–C 6 | σ∗ | 0.04490 | 2.16 | 1.27 | 0.047 |
| C3–S 11 | σ | 1.97010 | C6–S14 | σ∗ | 0.04310 | 5.52 | 0.84 | 0.061 |
| C3–S 12 | σ | 1.97018 | C1–S8 | σ∗ | 0.04321 | 2.79 | 0.85 | 0.044 |
| C3–S12 | σ | 1.97018 | C 3–C 6 | σ∗ | 0.04490 | 2.17 | 1.27 | 0.047 |
| C3–S 12 | σ | 1.97018 | C6–S 13 | σ∗ | 0.04691 | 5.51 | 0.84 | 0.061 |
| C4–C5 | σ | 1.99008 | C4–S9 | σ∗ | 0.03222 | 1.31 | 0.99 | 0.032 |
| C4–C5 | σ | 1.99008 | C4–S13 | σ∗ | 0.04451 | 0.72 | 0.98 | 0.024 |
| C 4–C5 | σ | 1.99008 | C 5–S 10 | σ∗ | 0.03797 | 1.22 | 0.98 | 0.031 |
| C4–C5 | σ | 1.99008 | C5–S14 | σ∗ | 0.04071 | 0.74 | 0.98 | 0.024 |
| C 4–C5 | π | 1.96426 | S 10–B 22 | π∗ | 0.06517 | 1.37 | 0.31 | 0.019 |
| C 4–S9 | σ | 1.97446 | C 4–C 5 | σ∗ | 0.04081 | 3.24 | 1.27 | 0.058 |
| C 4–S9 | σ | 1.97446 | C 5–S 14 | σ∗ | 0.04071 | 4.26 | 0.85 | 0.054 |
| C 4–S9 | σ | 1.97446 | C 6–S 13 | σ∗ | 0.04691 | 0.63 | 0.84 | 0.021 |
| C 4–S9 | σ | 1.97446 | C 15–H 16 | σ∗ | 0.01198 | 1.08 | 1.11 | 0.031 |
| C 4–S 13 | σ | 1.96734 | C 3–C 6 | σ∗ | 0.04490 | 2.25 | 1.26 | 0.048 |
| C 4–S 13 | σ | 1.96734 | C 4–C 5 | σ∗ | 0.04081 | 2.08 | 1.25 | 0.046 |
| C 4–S 13 | σ | 1.96734 | C 5–S 10 | σ∗ | 0.03797 | 6.03 | 0.84 | 0.063 |
| C 4–S 13 | σ | 1.96734 | S 9–C 15 | σ∗ | 0/01775 | 0.67 | 0.80 | 0.021 |
| C 5–S 10 | σ | 1.97419 | C 4–C 5 | σ∗ | 0.04081 | 3.01 | 1.27 | 0.055 |
| C 5–S 10 | σ | 1.97419 | C 4–S 13 | σ∗ | 0.04451 | 4.23 | 0.85 | 0.054 |
| C 5–S 10 | σ | 1.97419 | C 6–S 14 | σ∗ | 0.04310 | 0.57 | 0.84 | 0.020 |
| C 5–S 10 | σ | 1.97419 | B 22–H 23 | σ∗ | 0.00921 | 1.56 | 1.18 | 0.038 |
| C 5–S 14 | σ | 1.96874 | C 3–C 6 | σ∗ | 0.04490 | 2.27 | 1.26 | 0.048 |
| C 5–S 14 | σ | 1.96874 | C 4–C 5 | σ∗ | 0.04081 | 2.03 | 1.25 | 0.045 |
| C 5–S 14 | σ | 1.96874 | C 4–S 9 | σ∗ | 0.03222 | 5.84 | 0.85 | 0.063 |
| C 5–S 14 | σ | 1.96874 | S 10–B 22 | σ∗ | 0.01511 | 1.09 | 0.92 | 0.028 |
| C 6–S 13 | σ | 1.96925 | C 3–C 6 | σ∗ | 0.04490 | 2.12 | 1.26 | 0.046 |
| C 6–S 13 | σ | 1.96925 | C 3–S 12 | σ∗ | 0.03859 | 5.66 | 0.83 | 0.061 |
| C 6–S 13 | σ | 1.96925 | C 4–S 9 | σ∗ | 0.03222 | 3.08 | 0.85 | 0.046 |
| C 6–S 14 | σ | 1.96919 | C 3–C 6 | σ∗ | 0.04490 | 2.13 | 1.26 | 0.046 |
| C 6–S 14 | σ | 1.96919 | C 3–S 11 | σ∗ | 0.04384 | 5.66 | 0.83 | 0.061 |
| C 6–S 14 | σ | 1.96919 | C 5–S 10 | σ∗ | 0.03797 | 3.13 | 0.84 | 0.046 |
| S 7–B 18 | σ | 1.98201 | C 2–S 11 | σ∗ | 0.03820 | 3.04 | 0.83 | 0.045 |
| S 7–B 18 | σ | 1.98201 | B 20–H 21 | σ∗ | 0.00833 | 1.59 | 1.17 | 0.039 |
| S 7–B 18 | π | 1.87061 | C 1–C 2 | π∗ | 0.36401 | 15.54 | 0.27 | 0.061 |
| S 7–B 18 | π | 1.87061 | S 7–B 18 | π∗ | 0.01181 | 0.60 | 0.29 | 0.012 |
| S 7–B 18 | π | 1.87061 | S 8–B 20 | π∗ | 0.07676 | 4.41 | 0.29 | 0.032 |
| S 8–B 20 | σ | 1.98202 | C 1–S 12 | σ∗ | 0.03859 | 3.04 | 0.83 | 0.045 |
| S 8–B 20 | σ | 1.98202 | B 18–H 19 | σ∗ | 0.00833 | 1.59 | 1.17 | 0.039 |
| S 8–B 20 | π | 1.87055 | C 1–C 2 | π∗ | 0.36401 | 15.55 | 0.27 | 0.061 |
| S 8–B 20 | π | 1.87055 | S 7–B 18 | π∗ | 0.01181 | 4.41 | 0.29 | 0.032 |
| S 8–B 20 | π | 1.87055 | S 8–B 20 | π∗ | 0.07676 | 0.60 | 0.29 | 0.012 |
| S 9–C 15 | σ | 1.97060 | C 4–S 13 | σ∗ | 0.04451 | 2.41 | 0.76 | 0.038 |
| S 9–C 15 | σ | 1.97060 | C 15–B 22 | σ∗ | 0.01724 | 0.70 | 0.97 | 0.023 |
| S 9–C 15 | σ | 1.97060 | B 22–H 23 | σ∗ | 0.00921 | 1.77 | 1.09 | 0.039 |
| S 10–B 22 | σ | 1.97724 | C 5–S 14 | σ∗ | 0.04071 | 3.54 | 0.82 | 0.048 |
| S 10–B 22 | σ | 1.97724 | C 15–H 16 | σ∗ | 0.01198 | 1.55 | 1.08 | 0.037 |
| S 10–B22 | π | 1.92519 | C 4–C 5 | π∗ | 0.35776 | 12.67 | 0.28 | 0.057 |
| C 15–H 16 | σ | 1.97563 | C 4–S 9 | σ∗ | 0.03222 | 1.73 | 0.71 | 0.031 |
| C 15–H16 | σ | 1.97563 | S 10–B 22 | σ∗ | 0.01511 | 2.66 | 0.78 | 0.041 |
| C15–H 16 | σ | 1.97563 | C 15–B 22 | σ∗ | 0.06517 | 0.95 | 0.90 | 0.026 |
| C15–H17 | σ | 1.97498 | C 15–B 22 | σ∗ | 0.06517 | 0.79 | 0.90 | 0.024 |
| C15–H 17 | σ | 1.97498 | B 22–H 23 | σ∗ | 0.00921 | 0.64 | 1.02 | 0.023 |
| C15–B 22 | σ | 1.98864 | C 15–H 16 | σ∗ | 0.01198 | 1.37 | 1.01 | 0.033 |
| C15–B 22 | σ | 1.98864 | C 15–H 17 | σ∗ | 0.01337 | 1.52 | 1.00 | 0.035 |
| B18–H 19 | σ | 1.96952 | C 2–S 7 | σ∗ | 0.04322 | 3.96 | 0.60 | 0.044 |
| B18–H 19 | σ | 1.96952 | S 8–B 20 | σ∗ | 0.07676 | 2.78 | 0.69 | 0.039 |
| B20–H 21 | σ | 1.96952 | C 1–S 8 | σ∗ | 0.04321 | 3.96 | 0.60 | 0.044 |
| B20–H 21 | σ | 1.96952 | S 7–B 18 | σ∗ | 0.07677 | 2.78 | 0.69 | 0.039 |
| B 22–H 23 | σ | 1.97342 | C 5–S 10 | σ∗ | 0.03797 | 2.89 | 0.60 | 0.037 |
| B22–H 23 | σ | 1.97342 | S 9–C 15 | σ∗ | 0.01775 | 2.28 | 0.57 | 0.032 |
| B 22–H 23 | σ | 1.97342 | C 15–H 17 | σ∗ | 0.02153 | 0.70 | 0.85 | 0.022 |
| S 8 | LP (1) | 1.96796 | C 1–C 2 | σ∗ | 0.03859 | 6.93 | 1.17 | 0.080 |
| S 9 | LP (1) | 1.97694 | C 4–C 5 | σ∗ | 0.04081 | 4.80 | 1.24 | 0.069 |
| S 9 | LP (2) | 1.83903 | C 4–C 5 | σ∗ | 0.04081 | 1.36 | 0.84 | 0.031 |
| S 9 | LP (2) | 1.83903 | C 4–C 5 | π∗ | 0.35776 | 16.17 | 0.23 | 0.058 |
| S 9 | LP (2) | 1.83903 | C 4–S 13 | σ∗ | 0.04451 | 2.79 | 0.42 | 0.032 |
| S 10 | LP (1) | 1.96598 | C 4–C 5 | σ∗ | 0.04081 | 5.44 | 1.19 | 0.072 |
| S 11 | LP (2) | 1.78106 | C 1–C 2 | π∗ | 0.36401 | 20.64 | 0.23 | 0.064 |
| S 11 | LP (2) | 1.78106 | C 3–C 6 | π∗ | 0.37743 | 14.96 | 0.26 | 0.058 |
| S 12 | LP (2) | 1.78077 | C 1–C 2 | π∗ | 0.36401 | 20.66 | 0.23 | 0.064 |
| S 12 | LP (2) | 1.78077 | C 3–C 6 | π∗ | 0.37743 | 15.01 | 0.26 | 0.058 |
| S 13 | LP (1) | 1.97254 | C 4–C 5 | σ∗ | 0.04081 | 3.06 | 1.25 | 0.055 |
| S 13 | LP (2) | 1.77831 | C 3–C 6 | π∗ | 0.37743 | 14.28 | 0.26 | 0.056 |
| S 13 | LP (2) | 1.77831 | C4–C5 | π∗ | 0.35776 | 20.41 | 0.24 | 0.064 |
| S 14 | LP (1) | 1.97248 | C 4–C 5 | σ∗ | 0.04081 | 2.98 | 1.25 | 0.055 |
| S 14 | LP (1) | 1.97248 | C 6–S 13 | σ∗ | 0.04691 | 3.36 | 0.83 | 0.047 |
| S14 | LP (2) | 1.78832 | C3–C6 | σ∗ | 0.04490 | 1.36 | 0.85 | 0.032 |
| S14 | LP (2) | 1.78832 | C3–C6 | π∗ | 0.37743 | 14.32 | 0.26 | 0.056 |
| S14 | LP (2) | 1.78832 | C4–C5 | π∗ | 0.35776 | 18.92 | 0.23 | 0.062 |
| S14 | LP (2) | 1.78832 | C6–S13 | σ∗ | 0.04691 | 1.09 | 0.42 | 0.020 |
E(2) means energy of hyper conjugative interaction (stabilization energy).
Energy difference between donor and acceptor i and j NBO orbitals.
F(i,j) is the Fock matrix element between i and j NBO orbitals.
Table 2 (b).
Second-order perturbation theory of Fock matrix in NBO basis for .
| Donor (i) | type | occupancy | Acceptor (j) | type | Occupancy | E(2)a kcal/mol | Ei-Ejb a.u | F(i,j)c a.u |
|---|---|---|---|---|---|---|---|---|
| C 1–C 2 | σ | 1.99035 | C 1–S 8 | σ∗ | 0.04326 | 1.37 | 1.00 | 0.033 |
| C 1–C 2 | σ | 1.99035 | C 1–S 12 | σ∗ | 0.03860 | 0.65 | 0.98 | 0.023 |
| C 1–C 2 | σ | 1.99035 | C 2–S 7 | σ∗ | 0.04323 | 1.37 | 1.00 | 0.033 |
| C 1–C 2 | σ | 1.99035 | C 2–S 11 | σ∗ | 0.03822 | 0.65 | 0.98 | 0.023 |
| C 1–C 2 | π | 1.91921 | S 7–B 18 | π∗ | 0.07744 | 1.86 | 0.32 | 0.022 |
| C 1–C 2 | π | 1.91921 | S 8–B 20 | π∗ | 0.07744 | 1.86 | 0.32 | 0.022 |
| C 1–S 8 | σ | 1.97668 | C 1–C 2 | σ∗ | 0.03939 | 3.41 | 1.27 | 0.059 |
| C 1–S 8 | σ | 1.97668 | C 2–S 11 | σ∗ | 0.03822 | 3.79 | 0.86 | 0.051 |
| C 1–S 8 | σ | 1.97668 | C 3–S 12 | σ∗ | 0.04381 | 0.61 | 0.86 | 0.021 |
| C 1–S 8 | σ | 1.97668 | B 20–H 21 | σ∗ | 0.00834 | 0.88 | 1.19 | 0.029 |
| C 1–S 12 | σ | 1.96758 | C 1–C 2 | σ∗ | 0.03939 | 2.01 | 1.24 | 0.045 |
| C 1–S 12 | σ | 1.96758 | C 2–S 7 | σ∗ | 0.04323 | 6.16 | 0.85 | 0.065 |
| C 1–S 12 | σ | 1.96758 | C 3–C 6 | σ∗ | 0.04510 | 2.27 | 1.26 | 0.048 |
| C 1–S 12 | σ | 1.96758 | C 3–C 6 | π∗ | 0.37850 | 0.84 | 0.67 | 0.023 |
| C 1–S 12 | σ | 1.96758 | S 8–B 20 | σ∗ | 0.01183 | 1.32 | 0.94 | 0.032 |
| C 2–S 7 | σ | 1.97664 | C 1–C 2 | σ∗ | 0.03939 | 3.41 | 1.27 | 0.059 |
| C 2–S 7 | σ | 1.97664 | C 1–S 12 | σ∗ | 0.03860 | 3.79 | 0.86 | 0.051 |
| C 2–S 7 | σ | 1.97664 | C 3–S 11 | σ∗ | 0.04367 | 0.61 | 0.86 | 0.021 |
| C 2–S 7 | σ | 1.97664 | B 18–H 19 | σ∗ | 0.00834 | 0.88 | 1.19 | 0.029 |
| C 2–S 11 | σ | 1.96756 | C 1–C 2 | σ∗ | 0.03939 | 2.01 | 1.24 | 0.045 |
| C 2–S 11 | σ | 1.96756 | C 1–S 8 | σ∗ | 0.04326 | 6.17 | 0.85 | 0.065 |
| C 2–S 11 | σ | 1.96756 | C 3–C 6 | σ∗ | 0.04510 | 2.27 | 1.26 | 0.048 |
| C 2–S 11 | σ | 1.96756 | C 3–C 6 | π∗ | 0.37850 | 0.83 | 0.67 | 0.023 |
| C 2–S 11 | σ | 1.96756 | S 7–B 18 | σ∗ | 0.01182 | 1.32 | 0.94 | 0.032 |
| C 3–C 6 | σ | 1.99004 | C 3–S 11 | σ∗ | 0.04367 | 0.97 | 0.97 | 0.028 |
| C 3–C 6 | σ | 1.99004 | C 3–S 12 | σ∗ | 0.04381 | 0.98 | 0.97 | 0.028 |
| C 3–C 6 | σ | 1.99004 | C 6–S 13 | σ∗ | 0.04607 | 0.92 | 0.97 | 0.027 |
| C 3–C 6 | σ | 1.99004 | C 6–S 14 | σ∗ | 0.04433 | 0.92 | 0.97 | 0.027 |
| C 3–C 6 | π | 1.96263 | C 1–S 12 | σ∗ | 0.03860 | 0.51 | 0.50 | 0.014 |
| C 3–C 6 | π | 1.96263 | C 2–S 11 | σ∗ | 0.03822 | 0.52 | 0.50 | 0.014 |
| C 3–C 6 | π | 1.96263 | C 4–S 13 | σ∗ | 0.04649 | 0.53 | 0.51 | 0.015 |
| C 3–C 6 | π | 1.96263 | C 5–S 14 | σ∗ | 0.03888 | 0.58 | 0.51 | 0.015 |
| C 3–S 12 | σ | 1.97028 | C 1–S 8 | σ∗ | 0.04326 | 2.80 | 0.85 | 0.044 |
| C 3–S 12 | σ | 1.97028 | C 3–C 6 | σ∗ | 0.04510 | 2.15 | 1.27 | 0.047 |
| C 3–S 12 | σ | 1.97028 | C 6–S 13 | σ∗ | 0.04607 | 5.47 | 0.84 | 0.061 |
| C 4–C 5 | σ | 1.99019 | C 4–S 9 | σ∗ | 0.03132 | 1.35 | 1.00 | 0.033 |
| C 4–C 5 | σ | 1.99019 | C 4–S 13 | σ∗ | 0.04649 | 0.74 | 0.98 | 0.024 |
| C 4–C 5 | σ | 1.99019 | C 5––S 10 | σ∗ | 0.03441 | 1.17 | 0.99 | 0.030 |
| C 4–C 5 | σ | 1.99019 | C 5–S 14 | σ∗ | 0.03888 | 0.74 | 0.98 | 0.024 |
| C 4–C 5 | π | 1.96745 | S 9–C 15 | σ∗ | 0.02987 | 0.95 | 0.45 | 0.018 |
| C 4–S 9 | σ | 1.97374 | C 4–C 5 | σ∗ | 0.03994 | 3.29 | 1.27 | 0.058 |
| C 4–S 9 | σ | 1.97374 | C 5–S 14 | σ∗ | 0.03888 | 4.37 | 0.85 | 0.054 |
| C 4–S 9 | σ | 1.97374 | C 6–S 13 | σ∗ | 0.04607 | 0.63 | 0.84 | 0.021 |
| C 4–S 9 | σ | 1.97374 | C 15–H 16 | σ∗ | 0.00924 | 1.15 | 1.10 | 0.032 |
| C 4–S 13 | σ | 1.96798 | C 3–C 6 | σ∗ | 0.04510 | 2.28 | 1.26 | 0.048 |
| C 4–S 13 | σ | 1.96798 | C 3–C 6 | π∗ | 0.37850 | 0.92 | 0.66 | 0.024 |
| C 4–S 13 | σ | 1.96798 | C 4–C 5 | σ∗ | 0.03994 | 2.08 | 1.25 | 0.046 |
| C 4–S 13 | σ | 1.96798 | C 5–S 10 | σ∗ | 0.03441 | 5.97 | 0.84 | 0.063 |
| C 4–S 13 | σ | 1.96798 | S 9–C 15 | σ∗ | 0.02987 | 0.67 | 0.79 | 0.021 |
| C 5–S 10 | σ | 1.97317 | C 4–C 5 | σ∗ | 0.03994 | 3.06 | 1.27 | 0.056 |
| C 5–S 10 | σ | 1.97317 | C 4–S 13 | σ∗ | 0.04649 | 4.42 | 0.85 | 0.055 |
| C 5–S 10 | σ | 1.97317 | C 6–S 14 | σ∗ | 0.04433 | 0.60 | 0.84 | 0.020 |
| C 5–S 10 | σ | 1.97317 | S 10–C 22 | σ∗ | 0.02157 | 0.62 | 0.85 | 0.020 |
| C 5–S 10 | σ | 1.97317 | C 22–H 23 | σ∗ | 0.01928 | 0.72 | 1.14 | 0.026 |
| C 5–S 10 | σ | 1.97317 | C 22–H 24 | σ∗ | 0.01944 | 0.75 | 1.14 | 0.026 |
| C 5–S 14 | σ | 1.96806 | C 3–C 6 | σ∗ | 0.04510 | 2.25 | 1.26 | 0.048 |
| C 5–S 14 | σ | 1.96806 | C 3–C 6 | π∗ | 0.37850 | 0.93 | 0.66 | 0.024 |
| C 5–S 14 | σ | 1.96806 | C 4–C 5 | σ∗ | 0.03994 | 2.04 | 1.26 | 0.045 |
| C 5–S 14 | σ | 1.96806 | C 4–S 9 | σ∗ | 0.03132 | 5.83 | 0.85 | 0.063 |
| C 5–S 14 | σ | 1.96806 | S 10–C 22 | σ∗ | 0.02157 | 0.98 | 0.83 | 0.026 |
| C 6–S 13 | σ | 1.96893 | C 3–C 6 | σ∗ | 0.04510 | 2.14 | 1.26 | 0.046 |
| C 6–S 13 | σ | 1.96893 | C 3–S 12 | σ∗ | 0.04381 | 5.71 | 0.83 | 0.062 |
| C 6–S 13 | σ | 1.96893 | C 4–S 9 | σ∗ | 0.03132 | 3.11 | 0.85 | 0.046 |
| C 6–S 14 | σ | 1.96896 | C 3–C 6 | σ∗ | 0.04510 | 2.10 | 1.26 | 0.046 |
| C 6–S 14 | σ | 1.96896 | C 3–S 11 | σ∗ | 0.04367 | 5.66 | 0.83 | 0.061 |
| C 6–S 14 | σ | 1.96896 | C 5–S 10 | σ∗ | 0.03441 | 3.12 | 0.84 | 0.046 |
| S 7–B 18 | σ | 1.98208 | C 2–S 11 | σ∗ | 0.03822 | 3.03 | 0.83 | 0.045 |
| S 7–B 18 | σ | 1.98208 | B 20–H 21 | σ∗ | 0.00834 | 1.59 | 1.17 | 0.039 |
| S 7–B 18 | π | 1.87086 | C 1–C 2 | π∗ | 0.36429 | 15.50 | 0.27 | 0.061 |
| S 7–B 18 | π | 1.87086 | S 7–B 18 | π∗ | 0.07744 | 0.61 | 0.29 | 0.012 |
| S 7–B 18 | π | 1.87086 | S 8–B 20 | π∗ | 0.07744 | 4.42 | 0.29 | 0.032 |
| S 8–B 20 | σ | 1.98208 | C 1–S 12 | σ∗ | 0.03860 | 3.03 | 0.83 | 0.045 |
| S 8–B 20 | σ | 1.98208 | B 18–H 19 | σ∗ | 0.00834 | 1.59 | 1.17 | 0.039 |
| S 8–B 20 | π | 1.87085 | C 1–C 2 | π∗ | 0.36429 | 15.50 | 0.27 | 0.061 |
| S 8–B 20 | π | 1.87085 | S 7–B 18 | π∗ | 0.07744 | 4.42 | 0.29 | 0.032 |
| S 8–B 20 | π | 1.87085 | S 8–B 20 | π∗ | 0.07744 | 0.61 | 0.29 | 0.012 |
| S 9–C 15 | σ | 1.97492 | C 4–C 5 | π∗ | 0.37201 | 1.43 | 0.58 | 0.028 |
| S 9–C 15 | σ | 1.97492 | C 4–S 13 | σ∗ | 0.04649 | 2.27 | 0.77 | 0.038 |
| S 9–C 15 | σ | 1.97492 | C 22–H 23 | σ∗ | 0.01928 | 1.81 | 1.07 | 0.039 |
| C 15–H 16 | σ | 1.97682 | C 4–S 9 | σ∗ | 0.03132 | 1.61 | 0.73 | 0.031 |
| C 15–H 16 | σ | 1.97682 | S 10–C 22 | σ∗ | 0.02157 | 4.31 | 0.71 | 0.049 |
| C 15–H 17 | σ | 1.99014 | C 22–H 24 | σ∗ | 0.01944 | 1.39 | 1.00 | 0.033 |
| B 18–H 19 | σ | 1.96961 | C 2–S 7 | σ∗ | 0.04323 | 3.95 | 0.60 | 0.044 |
| B 18–H 19 | σ | 1.96961 | S 8–B 20 | σ∗ | 0.01183 | 2.78 | 0.69 | 0.039 |
| B 20–H 21 | σ | 1.96962 | C 1–S 8 | σ∗ | 0.04326 | 3.95 | 0.60 | 0.044 |
| B 20–H 21 | σ | 1.96962 | S 7–B 18 | σ∗ | 0.01182 | 2.78 | 0.69 | 0.039 |
| C 22–H 23 | σ | 1.97504 | C 5–S 10 | σ∗ | 0.03441 | 1.02 | 0.72 | 0.024 |
| C 22–H 23 | σ | 1.97504 | S 9–C 15 | σ∗ | 0.02987 | 4.32 | 0.67 | 0.048 |
| C 22–H 24 | σ | 1.98241 | C 5–S 10 | σ∗ | 0.03441 | 0.68 | 0.71 | 0.020 |
| C 22–H 24 | σ | 1.98241 | C 15–H 17 | σ∗ | 0.02207 | 3.59 | 0.96 | 0.052 |
| S 7 | LP (1) | 1.96802 | C 1–C 2 | σ∗ | 0.03939 | 6.92 | 1.17 | 0.080 |
| S 7 | LP (1) | 1.96802 | B 18–H 19 | σ∗ | 0.00834 | 0.57 | 1.09 | 0.022 |
| S 7 | LP (1) | 1.96802 | B 18–B 20 | σ∗ | 0.01339 | 3.01 | 1.04 | 0.050 |
| S 8 | LP (1) | 1.96802 | C 1–C 2 | σ∗ | 0.03939 | 6.92 | 1.17 | 0.080 |
| S 8 | LP (1) | 1.96802 | B 18–B 20 | σ∗ | 0.01339 | 3.01 | 1.04 | 0.050 |
| S 8 | LP (1) | 1.96802 | B 20–H 21 | σ∗ | 0.00834 | 0.57 | 1.09 | 0.022 |
| S 9 | LP (1) | 1.97732 | C 4–C 5 | σ∗ | 0.03994 | 4.74 | 1.24 | 0.069 |
| S 9 | LP (1) | 1.97732 | C 15–H 17 | σ∗ | 0.02207 | 0.62 | 1.07 | 0.023 |
| S 9 | LP (1) | 1.97732 | C 15–C 22 | σ∗ | 0.02966 | 1.19 | 0.94 | 0.030 |
| S 9 | LP (2) | 1.97732 | C 4–C 5 | σ∗ | 0.03994 | 1.73 | 0.85 | 0.035 |
| S 9 | LP (2) | 1.97732 | C 4–C 5 | π∗ | 0.37201 | 12.98 | 0.23 | 0.052 |
| S 9 | LP (2) | 1.97732 | C 4–S 13 | σ∗ | 0.04649 | 3.25 | 0.43 | 0.034 |
| S 9 | LP (2) | 1.97732 | C 6–S 13 | σ∗ | 0.04607 | 0.52 | 0.42 | 0.013 |
| S 9 | LP (2) | 1.97732 | C 15–H 17 | σ∗ | 0.02207 | 4.03 | 0.68 | 0.048 |
| S 9 | LP (2) | 1.97732 | C 15–C 22 | σ∗ | 0.02966 | 3.16 | 0.55 | 0.038 |
| S 9 | LP (2) | 1.97732 | C 22–H 23 | σ∗ | 0.01928 | 0.82 | 0.72 | 0.022 |
| S 10 | LP (1) | 1.97275 | C 4–C 5 | σ∗ | 0.03994 | 5.00 | 1.22 | 0.070 |
| S 10 | LP (1) | 1.97275 | C 15–C 22 | σ∗ | 0.02966 | 4.23 | 0.92 | 0.056 |
| S 10 | LP (2) | 1.97275 | C 4–C 5 | σ∗ | 0.03994 | 0.58 | 0.85 | 0.020 |
| S 10 | LP (2) | 1.97275 | C 4–C 5 | π∗ | 0.37201 | 18.38 | 0.24 | 0.063 |
| S 10 | LP (2) | 1.97275 | C 5–S 14 | σ∗ | 0.03888 | 1.21 | 0.42 | 0.021 |
| S 10 | LP (2) | 1.97275 | C 22–H 23 | σ∗ | 0.01928 | 3.22 | 0.72 | 0.045 |
| S 10 | LP (2) | 1.97275 | C 22–H 24 | σ∗ | 0.01944 | 4.60 | 0.72 | 0.053 |
| S 11 | LP (1) | 1.97208 | C 1–C 2 | σ∗ | 0.03939 | 3.10 | 1.24 | 0.056 |
| S 11 | LP (1) | 1.97208 | C 3–S 12 | σ∗ | 0.04381 | 3.47 | 0.83 | 0.048 |
| S 11 | LP (2) | 1.78173 | C 1–C 2 | π∗ | 0.36429 | 20.69 | 0.23 | 0.064 |
| S 11 | LP (2) | 1.78173 | C 3–C 6 | σ∗ | 0.04510 | 1.20 | 0.85 | 0.030 |
| S 11 | LP (2) | 1.78173 | C 3–C 6 | π∗ | 0.37850 | 14.76 | 0.26 | 0.058 |
| S 11 | LP (2) | 1.78173 | C 3–S 12 | σ∗ | 0.04381 | 0.82 | 0.42 | 0.017 |
| S 12 | LP (1) | 1.97207 | C 1–C 2 | σ∗ | 0.03939 | 3.10 | 1.24 | 0.056 |
| S 12 | LP (1) | 1.97207 | C 3–S 11 | σ∗ | 0.04367 | 3.48 | 0.83 | 0.048 |
| S 12 | LP (2) | 1.78199 | C 1–C 2 | π∗ | 0.36429 | 20.68 | 0.23 | 0.064 |
| S 12 | LP (2) | 1.78199 | C 3–C 6 | σ∗ | 0.04510 | 1.19 | 0.85 | 0.030 |
| S 12 | LP (2) | 1.78199 | C 3–C 6 | π∗ | 0.37850 | 14.79 | 0.26 | 0.058 |
| S 12 | LP (2) | 1.78199 | C 3–S 11 | σ∗ | 0.04367 | 0.81 | 0.42 | 0.017 |
| S 13 | LP (1) | 1.97220 | C 4–C 5 | σ∗ | 0.03994 | 3.04 | 1.25 | 0.055 |
| S 13 | LP (1) | 1.97220 | C 6–S 14 | σ∗ | 0.04433 | 3.39 | 0.83 | 0.047 |
| S 13 | LP (2) | 1.78677 | C 3–C 6 | σ∗ | 0.04510 | 1.32 | 0.85 | 0.031 |
| S 13 | LP (2) | 1.78677 | C 3–C 6 | π∗ | 0.37850 | 14.53 | 0.25 | 0.057 |
| S 13 | LP (2) | 1.78677 | C 4–C 5 | π∗ | 0.37201 | 19.94 | 0.23 | 0.064 |
| S 13 | LP (2) | 1.78677 | C 6–S 14 | σ∗ | 0.04433 | 1.06 | 0.42 | 0.020 |
| S 14 | LP (1) | 1.97266 | C 4–C 5 | σ∗ | 0.03994 | 3.02 | 1.26 | 0.055 |
| S 14 | LP (1) | 1.97266 | C 6–S 13 | σ∗ | 0.04607 | 3.34 | 0.83 | 0.047 |
| S 14 | LP (2) | 1.78820 | C 3–C 6 | σ∗ | 0.04510 | 1.39 | 0.85 | 0.032 |
| S 14 | LP (2) | 1.78820 | C 3–C 6 | π∗ | 0.37850 | 14.23 | 0.26 | 0.056 |
| S 14 | LP (2) | 1.78820 | C 4–C 5 | π∗ | 0.37201 | 19.44 | 0.24 | 0.063 |
| S 14 | LP (2) | 1.78820 | C 6–S 13 | σ∗ | 0.04607 | 1.08 | 0.42 | 0.020 |
E(2) means energy of hyper conjugative interaction (stabilization energy).
Energy difference between donor and acceptor i and j NBO orbitals.
F(i,j) is the Fock matrix element between i and j NBO orbitals.
In Table 2(a) S8–B20 shows the highest E(2) value of 15.55 kcal/mol in π to π∗ transition. C1–S12 and C2–S11 show the highest E(2) values of 6.15 kcal/mol in σ to σ∗ transition. We also obtained a stabilization energy of 15.54 kcal/mol for S7–B18 (π) to C1–C2 (π∗) transition and 12.67 kcal/mol for S10–B12 (π) to C4–C5 (π∗) transition. Another π to π∗ transition is observed at C1–C2 to S7–B18 with 1.85 kcal/mol. For transition C4–S13 (σ) to C5–S10 (σ∗); C6–S13 (σ) to C3–S12 (σ∗) and C3–S11 (σ) to C6–S14 (σ∗) stabilizations energies are 6.03 kcal/mol; 5.66 kcal/mol and 5.52 kcal/mol respectively. Noted that the lone pairs in the sulfur atoms participate in the stabilization of the molecule by LP(2) to π∗ and LP(2) to σ∗ interactions with considerable stabilization like the highest E(2) value of 20.66 kcal/mol in LP(2) to π∗ transition.
The calculated values E(2) of the second proposed material B2-doped molecule are shown in Table 2(b). S8–B20 and S7–B18 show the highest E(2) value of 15.50 kcal/mol in π to π∗ transition. C2–S11 shows the highest E(2) value of 6.17 kcal/mol inσ to σ∗ transition. A stabilization energy of 4.42 kcal/mol is observed for S8–B20 (π) to S7–B18 (π∗) and 1.86 kcal/mol for C1–C2 (π) to S8–B20 (π∗) transition. For transitions C1–S12 (σ) to C2–S7 (σ∗); C4–S13 (σ) to C5–S10 (σ∗) and C3–S12 (σ) to C6–S13 (σ∗) stabilizations energies are 6.17 kcal/mol, 5.59 kcal/mol and 5.47 kcal/mol respectively. LP(2)→σ∗ and LP(2)→π∗ interactions also participate in the stabilization of the system. The highest E(2) value of 20.69 kcal/mol is shown in LP(2) to π∗ transition.
The π→π∗ transitions in both the doped molecules account for the high polarization and which is further responsible for the NLO activity of the new molecules.
3.3. Nonlinear optical properties of the molecules
The non-linear optical parameters are useful in current technologies such as communication and telecommunication [25, 27, 28]. Nonlinear optical properties are very important for the molecular structure and organic materials [29, 30, 31, 32]. The Parameters, such as first hyperpolarizability (), polarizability (<α>) and the dipole moment (μ) of BEDT-TTF and their derivatives were evaluated using RHF, B3LYP and wB97XD methods with the cc-pVDZ. The anisotropy of the polarizability () and some NLO properties can be calculated using the following Eqs. (2), (3), (4), and (5) [33, 34, 35, 36] and summarized in Table 3.
| (2) |
| (3) |
| (4) |
| (5) |
Table 3.
Calculated values of dipole moment μ (Debye), average polarizability <α> × 10−24(e.s.u), anisotropy (esu)and first order hyperpolarizability of C10H8S8, C7B3H8S8 and C8B2H8S8 obtained employing RHF, B3LYP and Wb97XD with cc-pVDZ basis set.
| Molecules parameters |
|
|
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| B3LYP | wB97XD | RHF | B3LYP | wB97XD | RHF | B3LYP | wB97XD | RHF | |
| μ (Debye) | 1.41 | 1.55 | 0.97 | 2.25 | 1.94 | 1.30 | 3.82 | 3.33 | 2.48 |
| 231.32 | 413.60 | 223.01 | 482.55 | 446.03 | 404.48 | 474.67 | 438.62 | 395.17 | |
| 2.80 | -1.43 | 1.33 | 1.06 | -0.48 | -0.82 | -0.20 | -17 | -0.10 | |
| 393.01 | 226.12 | 335.46 | 239.68 | 234.20 | 225.10 | 238.64 | 233.33 | 226.49 | |
| -1.09 | -0.004 | -0.11 | -14.09 | 12.73 | 10.28 | 16.82 | 14.83 | 8.67 | |
| -113.66 | -0.005 | -93.01 | -0.58 | -0.71 | -0.63 | -1.42 | -1.47 | -1.94 | |
| 172.17 | 122.22 | 156.21 | 120.68 | 119.21 | 112.87 | 121.51 | 120.10 | 114.41 | |
| (esu) | 39.35 | 37.67 | 35.305 | 41.64 | 39.49 | 36.68 | 41.24 | 39.13 | 36.36 |
| Δα(esu) | 41.387 | 26.81 | 33.344 | 33.57 | 30.18 | 26.76 | 32.79 | 29.43 | 25.70 |
| 0.047 | -0.0015 | 0.116 | -2175.57 | 894.52 | 447.04 | 3182.32 | 1382.15 | 65.33 | |
| -9.337 | -0.0007 | -3.892 | 205.86 | 96.93 | 19.41 | 24.71 | -1.43 | 1.03 | |
| -24.498 | 0.0004 | -9.435 | -94.75 | 84.83 | 45.63 | 180.55 | 152.85 | 96.74 | |
| -61.544 | -0.0009 | 45.937 | 54.56 | 45.37 | 20.58 | 5.9 | 1.008 | 1.19 | |
| -22.04 | -31.31 | -9.385 | 770.87 | 388.22 | 197.48 | 651.22 | 319.15 | 202.33 | |
| -23.83 | 35.21 | -8.903 | 37.61 | -22.43 | -7.78 | 19.56 | 17.38 | 6.14 | |
| -34.33 | -18.75 | 26.344 | 52.86 | 45.75 | 27.79 | 21.61 | 19.57 | 11.18 | |
| 24.47 | -0.0007 | 79.041 | -128.38 | 66.05 | 30.71 | 137.32 | 67.32 | 42.29 | |
| 27.681 | -0.0006 | -16.52 | 3.65 | 1.44 | -3.71 | 4.49 | 1.61 | -2.09 | |
| -46.254 | -28.94 | 42.98 | 41.98 | 22.74 | 3.44 | 53.78 | 39.63 | 50.64 | |
| (esu) | 973.45 | 682.51 | 716.07 | 22,149.35 | 9,933.81 | 4,944.48 | 30,885.46 | 14,223.54 | 7,215.52 |
Noted that, α and values of Gaussian output file are reported in atomic units (a.u), the calculated values were converted into electronic units (esu) using:
The μ, α and of the doped molecules, computed using B3LYP/cc-pVDZ basis set, were found to be 2.25D, 41.64 × 10−24esu and 22,149.35 × 10−33esu respectively for C7B3H5S8and 3.82D, 41.24 × 10−24esuand 30,885.46 × 10−33esurespectivelyfor C8B2H6S8, while the obtained by using the wB97XD/cc-pVDZ are1.98D, 39.49 × 10−24esu and 9,933.81 × 10−33esu respectively for C7B3H5S8 and 3.33D, 39.13 × 10−24esuand 14,223.54 × 10−33esu respectively for C8B2H6S8. These values are given in Tables 2(a) and (b) and show that the molecules exhibits nonlinear behavior.
The dipole moment μ of the doped molecules (C8B2H6S8 and C7B3H5S8) are larger than those of the undoped BEDT-TTF molecule (C10H8S8) at all level of study. It is also observed that the of C7B3H5S8 and C8B2H6S8 increase from the RHF level to the electron correlated method. These values are very large compared to those of undoped structure from the three methods. In this Table 3, we noticed that the values of the dipole moment are different from zero, which leads us to believe that these molecules are polar. On the other hand, those dipole moment values increase from the uncorrelated method to the correlated method for doped systems. Moreover, we observed an increase in the anisotropy of those undoped and doped systems in going from RHF to B3LYP and wB97XD.
On comparing the calculated first-order hyperpolarizability values of doped molecules with boron with the corresponding value of Urea (βmol = 928 × 10−33esu) [25]. The molecule of Urea is sometime used as reference molecule to study NLO properties of the compound [37]. The very high value of = 22,149.35 × 10−33esu and = 30,885.46 × 10−33esu using B3LYP/cc-pVDZ indicates that the two doped molecules (C8B2H6S8 and C7B3H5S8) can be a good NLO agent. Furthermore, the values of α and β of the molecules are greater than those reported in literature using other BEDT-TTF derivatives [13, 14].
3.4. Electronic properties
Energy gap is the difference between the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO) [25]. Electronic properties such as ionization potential (IP), electron affinity (AE), electronegativity (χ), global hardness (η), chemical softness (ϛ), chemical potential (μ) and Electrophilicity index (ω) were calculated and summarized in Table 4. The following equations (see Eq. (6)) are used to determine these parameters:
Table 4.
Calculated Energy values of the molecules BEDT-TTF, 3B-, 2B- substituted C10H8S8 employing RHF, B3LYP and wB97XD methods by employing the cc-pVDZ basis set.
| Molecules parameters |
|
|
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| B3LYP | wB97XD | RHF | B3LYP | wB97XD | RHF | B3LYP | wB97XD | RHF | |
| EHOMO (eV) | -4.77 | -6.68 | -7.07 | -5.20 | -1.02 | -7.34 | -5.06 | -6.94 | -7.25 |
| ELUMO (eV) | -0.96 | 0.90 | 2.89 | -2.81 | -7.07 | 0.56 | 2.75 | -0.96 | 0.59 |
| Ionization potential | 4.77 | 6.68 | 7.07 | 5.20 | 1.01 | 7.34 | 5.06 | 6.93 | 7.24 |
| Electron affinity | 0.96 | -0.90 | -2.89 | 2.81 | 7.07 | -0.56 | -2.75 | 0.96 | -0.59 |
| Energy gap (eV) | 3.81 | 7.58 | 9.96 | 2.39 | 6.04 | 7.9 | 2.31 | 5.97 | 7.83 |
| Electronegativity | 2.86 | 2.89 | 2.09 | 4.00 | 4.04 | 3.39 | 1.16 | 3.95 | 3.33 |
| Chemical potential | -2.86 | -2.89 | -2.09 | -4.00 | -4.04 | -3.39 | -1.16 | -3.95 | -3.33 |
| Global hardness | 1.91 | 3.79 | 4.98 | 1.20 | 3.02 | 3.95 | 1.16 | 2.98 | 3.92 |
| Chemical Softness | 0.52 | 0.26 | 0.20 | 0.84 | 0.33 | 0.25 | 0.87 | 0.34 | 0.26 |
| Electrophilicity | 2.14 | 1.10 | 0.44 | 6.70 | 2.69 | 1.46 | 0.58 | 2.61 | 1.41 |
The ionization potential (IP) and electron affinity (EA) can be expressed by HOMO and LUMO orbital energies as [37]:
| (6) |
The electronegativity, based on the average of the electron affinity and ionization potential of molecules, energy gap, Softness, Electrophilicity index and the global hardness are given by the formulas [37, 38, 39, 40] (see Eqs. (7), (8), (9), (10), (11), and (12)):
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
Therefore, Egap is a very important parameter for the explaining stability and reactivity of molecule. A high ionization potential (IP) indicates high stability and hence chemical inertness, while a low ionization energy suggests a propensity of the molecule to reactivity. The electron affinity (AE) is defined as the energy released when an electron is added to a neutral molecule and hence a large (AE) value indicates the trend of the molecule to keep its electrons. A negative chemical potential (μ) indicates molecular stability or the difficulty of the molecule to decompose into its elements. The global electrophilicity index (ω) of a molecule is a measure of its stabilization energy following the addition of an external electronic charge or its resistance to exchange the electron with the system [36].
Based on our calculations, the energy gap changed from the RHF level to the B3LYP and wB97XD electron correlated methods. Our results show that when BEDT-TTF is substituted with boron atom. In this case, three atoms of carbon are replaced with three atoms of boron: C7 B3H5 S8 or with two atoms of carbon with two atoms of boron: C8B2H6 S8. HOMO-LUMO energy gap obtained using B3LYP level of theory with cc-pVDZ are respectively 2.39eV and 2.31eV less than 3eV, which makes them a good semiconductors materials. The Egap of semiconductor is less than 3eV [33], according to the band theory. We can conclude that the appropriate level of theory to study these molecules doped with boron is B3LYP because with RHF and wB97XD, the gap are rather of those of an insulator. We observed the global hardness, the ionization energy and chemical potential are bigger with RHF and smaller with B3LYP. The chemical softness and the electrophilicity index values are higher with the B3LYP and lower by using RHF. It is also mentioned that the high ionization potential (IP) computed with the three levels of theory and chemical potential (μ) indicate the stability and the reactivity, it means that, the undoped and doped molecules will not spontaneously decompose into its elements. Finally, due to the small values of energy gap of 3B- and 2B- doped BEDT-TTF we can conclude that these new materials are a good candidate for electronic applications in the fields of electronic devices.
3.4.1. HOMO and LUMO diagram
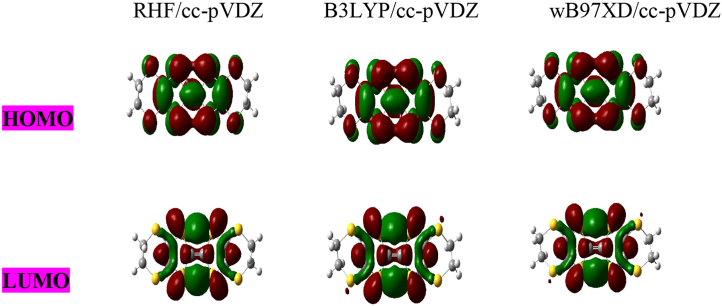
The HOMO and LUMO molecular orbitals of C10H8S8, C7 B3H5 S8andC8B2H6 S8 are shown in Figures 3, 4, and 5 respectively. First, we observed from HOMO, LUMO diagrams of undoped molecule C10H8S8 obtained using the RHF, B3LYP, and wB97XD methods with cc-pVDZ are the same in Figure 3. On the other hand, the HOMO and LUMO diagrams of B-doped molecules Figures 4 and 5 have a good charge distribution within these doped molecules due to their very strong donor-acceptor nature linked to doping with boron. These results make our systems more interesting in electronic devices once more.
Figure 3.
HOMO-LUMO diagram for C10H8S8 obtained at RHF, B3LYP and wB97XD methods using cc-pVDZ basis set.
Figure 4.
HOMO-LUMO diagram for C7 B3H5 S8 obtained at RHF, B3LYP and wB97XD methods using cc-pVDZ basis set.
Figure 5.
HOMO-LUMO diagram for C8B2H6S8.
3.5. Optoelectronic properties
Optoelectronic parameters properties such as the refractive index , electric susceptibility the electric field (E), dielectric constant and polarization density (P) were calculated and listed in Table 5. These parameters values were computed using the formulas given in the literature [41, 42, 43, 44, 45]. We note that our computed results are very different when we move from undoped molecule to doped systems. Moreover, the E, P and increases significantly and this difference is slightly between the uncorrelated to the DFT methods. Therefore, high values of the electric field E, the electric susceptibility χ, refractive index n and low value of dielectric constant Ɛ of doped systems find applications in optoelectronic materials. In fact, in renewable energy, photovoltaic and photonic devices.
Table 5.
Dipole moment μ, average of the polarizability , polarization density(P), the electric field (E), electric susceptibility dielectric constant ( and refractive index of the molecules BEDT-TTF, 3B-, 2B- substituted C10H8S8 by employing the cc-pVDZ basis set.
| Molecules parameters |
|
|
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| B3LYP | wB97XD | RHF | B3LYP | wB97XD | RHF | B3LYP | wB97XD | RHF | |
| μ(Cm) x10−30 | 4.70 | 5.17 | 3.25 | 7.51 | 6.46 | 4.34 | 12.75 | 11.1 | 8.27 |
| α(C2.m2.J−2)x10−41 | 437.75 | 418.76 | 392.79 | 463.26 | 439.36 | 408.04 | 458.80 | 435.3 | 404.53 |
| V(m3) x10−30 | 176.56 | 164.57 | 154.85 | 172.80 | 148.03 | 196.12 | 170.95 | 153.99 | 157.46 |
| E(V.m−1) x109 | 1.07 | 1.23 | 0.83 | 1.62 | 1.47 | 1.06 | 2.77 | 2.54 | 2.04 |
| P(C.m−2) x10−3 | 26.62 | 31.41 | 20.99 | 43.46 | 43.64 | 22.13 | 74.55 | 72.08 | 52.51 |
| χe | 2.81 | 2.88 | 2.86 | 3.03 | 3.35 | 2.36 | 3.04 | 3.2 | 2.9 |
| εr | 3.81 | 3.88 | 3.86 | 4.03 | 4.35 | 3.36 | 4.04 | 4.2 | 3.9 |
| εx10−12 | 33.73 | 34.35 | 34.18 | 35.68 | 38.51 | 29.75 | 35.77 | 37.18 | 34.53 |
| n | 1.95 | 1.97 | 1.96 | 2.01 | 2.09 | 1.83 | 2.01 | 2.05 | 1.70 |
3.6. Thermodynamic properties
The various thermodynamic parameters presented in Table 6 such as Total electronic energy (Eelec), Zero vibrational point energy (ZPVE), Gibbs free energy (G), Thermal energy (E), Entropy (S), Enthalpy (H), constant volume calorific capacity (Cv) were calculated an ambient temperature of 298.15 K and a pressure of 1atm. Our results show that structures doped with boron have a greater total energy than the undoped molecule (C10H8S8). On the other hand, we observe a slight variation of the entropy, enthalpy and specific heat. The same difference is also observed when going from the HF to the two hybrid functional B3LYP and wB97XD. This is explained by the effect of correlation of the electrons taken into account in the both functional. Therefore, we are able to conclude that there is an influence of doping with boron on the entropy of molecular structures, which confirms that the charge dynamics of the doped molecules are higher than its original molecule at the same temperature. This result further demonstrates that these doped materials have a high chemical reactivity and a high thermal resistivity. A better agreement with work reported by Mveme et al [38].
Table 6.
Total electronic energy (Eelec), Zero vibrational point energy (ZPVE), Gibbs free energy (G), Thermal energy (E), Entropy (S), Enthalpy (H), constant volume calorific capacity (Cv), of the molecules C10H8S8 (ET), C7B3H5S8 and C8B2H6S8 obtained using Hartree-Fock, B3LYP and wB97XD with CC-pVDZ basis set at T = 298.15K.
| Molecules parameters |
|
|
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| B3LYP | wB97XD | RHF | B3LYP | wB97XD | RHF | B3LYP | wB97XD | RHF | |
| Eelec(a.u) | -3571.49 | -3571.24 | -3563.51 | -3529.998 | -3529.738 | -3522.28 | -3543.82 | -3543.56 | -3536.01 |
| ZPVE(kcal/mol) | 99.09 | 101.42 | 107.66 | 71.106 | 72.641 | 76.889 | 80.746 | 82.512 | 87.511 |
| Eo(kcal/mol) x103 | -2241.05 | -2240.874 | -2236.03 | -2215.035 | -2214.371 | -2210.19 | -2223.703 | -2223.538 | -2218.798 |
| E(kcal/mol) x103 | -2241.04 | -2240.872 | -2236.02 | -2215.024 | -2214.859 | -2210.17 | -2223.691 | -2223.526 | -2218.787 |
| H(kcal/mol) x103 | -2241.04 | -2240.871 | -2236.02 | -2215.023 | -2214.859 | -2210.178 | -2223.690 | -2223.435 | -2218.789 |
| G(kcal/mol) x103 | -2241.08 | -2240.915 | -2236.06 | -2215.067 | -2214.902 | -2210.22 | -2223.734 | -2223.569 | -2218.829 |
| Ethermal(kcal/mol) | 111.11 | 113.122 | 118.87 | 83.028 | 84.366 | 88.127 | 92.643 | 94.212 | 98.704 |
| Cv(cal/mol.k1) | 69.38 | 67.718 | 64.68 | 69.38 | 68.15 | 65.44 | 69.132 | 67.774 | 64.952 |
| S(cal/mol.k1) | 148.47 | 145.81 | 144.18 | 146.32 | 145.22 | 142.03 | 146.930 | 146.69 | 143.047 |
4. Conclusion
In summary, the nonlinear optical, electronic, optoelectronic and thermodynamic properties of undoped and doped BEDT-TTF have been studied. Our goal was to investigate the effect or influence of doping with boron on the original compound. Our results obtained from the three methods used show that BEDT-TTF has weak NLO properties. However, substituted atom of carbon by boron show more interesting properties such as high first hyperpolarizability makes the molecule to find applications in NLO due to the π-electron conjugation. In fact, we presented for the first time the results on the substitution of C by B in the structure of BEDT-TTF. New systems obtained are good candidate to find application in renewable energy, emerging technologies. The HOMO-LUMO energy gap obtained lead us to believe that BEDT-TTF and its derivatives are good semiconductor materials that can be used in optoelectronic devices of telecommunications, in electronics, in LED, photonic materials and field effect transistor (FET). Finally, we are able to say that, these results reveal original electronic properties for our new materials, which can lead to interesting performances for organic photovoltaic, thus, opening the way to innovative and promising materials.
Declarations
Author contribution statement
G.F. OlingaMbala, M.T.Ottou Abe, Z. Ntieche, G.W.Ejuh, J.M.B.Ndjaka: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This work was supported by Professor Geh Wilson Ejuh and their Mentor Emeritus Professor A.N. Singh through providing the GAUSSIAN code.
Data availability statement
Data will be made available on request.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Shakerzadeh E., Tahmasebi E., Biglari Z. A quantum chemical study on the remarkable nonlinear optical and electronic characteristics of boron nitride nanoclusters by complexation via lithium atom. J. Mol. Liq. 2016;221:443–445. [Google Scholar]
- 2.Demiralp E., Dasgupta S., William A., Goddard Electron-Transfer boat-vibration mechanism for superconductivity in organic molecules based on BEDT-TTF. J. Am. Chem. Soc. 1995;117:8154–8158. [Google Scholar]
- 3.Imamura Y., Ten-no S., Yonemitsu K., Tanimura Y. Structures and electronic phases of the bis(ethylenedithio) tetrathiafulvalene (BEDT-TTF) salts : a theoretical study based on ab initio molecular orbital methods. J. Chem. Phys. 1999;111:5986. [Google Scholar]
- 4.Demiralp E., Dasgupta S., William A., Goddard MSX force field and vibrational frequencies for BEDT-TTF (neutral and cation) J. Phys. Chem. 1997;101:1975–1981. [Google Scholar]
- 5.Kozlov M.E., Pokhodnia K.I., Yurchenko A.A. The assignment of fundamental vibrations of BEDT-TTF and BEDT-TTF- d8. Spectrochim. Acta part A. 1987;43:323–329. [Google Scholar]
- 6.Eldridge J.E., Homes C.C., Williams J.M., Kini A.M., Wang H.H. The assignment of the normal modes of the BEDT-TTF electron-donor molecule using the infrared and Raman spectra of several isotopic analogs. Spectrochim. Acta. 1995;51A(No. 6):947–960. [Google Scholar]
- 7.Liu R., Zhou X., Kasmai H. Toward understanding the vibrational spectra of BEDT-TTF, a scaled density functional force field approach. Spectrochim. Acta, Part A. 1997;53:1241–1256. [Google Scholar]
- 8.Flakina A.M., Chekhlov A.N., Luybovskaya R.N. New organic conductors based on TTF derivatives with polymeric isocyanuric acid anion. J. Phys. IV France. 2004;114:501–503. [Google Scholar]
- 9.Wallis J.D., Griffiths J.P. Substituted BEDT-TTF derivatives: synthesis, chirality, properties and potential applications. J. Mater. Chem. 2005;15:347–365. [Google Scholar]
- 10.Wang Q. A family of unsymmetrical hydroxyl-substituted BEDT-TTF donors: syntheses, structures and preliminary thin film studies. RSC Adv. 2015;5:40205. [Google Scholar]
- 11.Nakazawa Y., Yamashita S. Thermodynamic properties of k-(BEDT-TTF)2X Salts: electron correlations and superconductivity. Crystals. 2012;2:741–761. [Google Scholar]
- 12.Girlando A. Charge sensitive vibrations and electr on-molecular vibration coupling in bis(ethylenedithio)-tetrathiafulvalene (BEDT-TTF) J. Phys. Chem. C. 2011;115:19371–19378. [Google Scholar]
- 13.Pustogow A., Treptow K., Rohwer A., Saito Y., Sanz Alonso M., Löhle A., Schlueter J.A., Dressel M. Charge order in β’’-phase BEDT-TTF salts. Phys. Rev. B. 2019;99:155144. [Google Scholar]
- 14.Midoune A., Messaoudi A. DFT/TDDFT studies of the structural, electronic and NBO properties of some complexes with the tetrathiafulvalene-1,3-benzothiazole ligand. Inorg. Chim. Acta. 2021;516:120151. [Google Scholar]
- 15.Sundaraganesan N., Illakiamani S., Meganathan C., Joshua B.D. Vibrational spectroscopy investigation using ab initio and density functional theory analysis on the structure of 3-aminobenzotrifluoride. Spectrochim. Acta, Part A. 2007;67:214–224. doi: 10.1016/j.saa.2006.07.004. [DOI] [PubMed] [Google Scholar]
- 16.Costa Stefane N., Freire Valder N., Caetano Ewerton W.S., Maia Francisco F., Jr., Barboza Carlos A., Fulco Umberto L., Eudenilson L. DFT calculations with van der Waals interactions of hydrated calcium carbonate crystals CaCO3·(H2O, 6H2O): structural, electronic, optical, and vibrational properties. J. Phys. Chem. 2016;120:5752–5765. doi: 10.1021/acs.jpca.6b05436. [DOI] [PubMed] [Google Scholar]
- 17.Henriques J.M., Barboza C.A., Albuquerque E.L., Fulco U.L., Moreira E. Structural, optoelectronic, infrared and Raman spectra from firstprinciples calculations of γ-Cd(OH)2. J. Phys. Chem. Solid. 2015;76:45–50. [Google Scholar]
- 18.Moreira E., Barboza C.A., Albuquerque E.L., Fulco U.L., Henriques J.M., Araújo A.I. Vibrational and thermodynamic properties of orthorhombic CaSnO3 from DFT and DFPT calculations. J. Phys. Chem. Solid. 2015;77:85–91. [Google Scholar]
- 19.Frisch M.J. Gaussian, Inc.; Wallingford CT: 2009. Gaussian 09, Revision A 1. [Google Scholar]
- 20.Dennington R.T., Keith J.M. 2016. Gauss View, Version 6. SemichemInc, Shawnee Mission KS. [Google Scholar]
- 21.Becke A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A. 1988;38:3098–3101. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 22.Lee Chengteh, Yang Weitao, Parr Robert G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. J. Phys. Rev. B. 1988;37:3098–3101. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 23.Guionneau P., Chasseau D., Judith Howard A.K., Dayc P. Neutral bis(ethylenedithio)tetrathiafulvalene at 100 K. ActaCryst. 2000;C56:453–454. doi: 10.1107/S0108270199016753. [DOI] [PubMed] [Google Scholar]
- 24.Allen F.H. The Cambridge structural database: a quarter of a million crystal structures and rising. Acta Cryst. B. 2002;58:380–388. doi: 10.1107/s0108768102003890. [DOI] [PubMed] [Google Scholar]
- 25.Saji R.S., Prasana J.C., Muthu S., George J. Spectrochim. Acta Part A Mol. Spectrosc. 2020;226:117614. doi: 10.1016/j.saa.2019.117614. [DOI] [PubMed] [Google Scholar]
- 26.Irikura K.K. National Institute of Standards and Technology; Gaithersburg, MD: 2002. THERMO. PL. [Google Scholar]
- 27.Kolinzky P.V. New materials and their characterization for photonic device applications. Opt. Eng. 1992;31:1676–1684. [Google Scholar]
- 28.Eaton D.F. Nonlinear optical materials. Science. 1991;253:281–287. doi: 10.1126/science.253.5017.281. [DOI] [PubMed] [Google Scholar]
- 29.Andraud C., Brotin T., Garcia C., Pelle F., Goldner P., Bigot B., Collet A. Theoretical and experimental investigations of the nonlinear optical properties of vanillin, polyenovanillin, and bisvanillin derivatives. J. Am. Chem. Soc. 1994;116:2094–2102. [Google Scholar]
- 30.Geskin V.M., Lambert C., Bredas J.L. Origin of high second-and third-order nonlinear optical responseinammonio/boratodiphenylpolyenezwitterions: the remarkable role of polarizedaromatic groups. J. Am. Chem. Soc. 2003;125:15651–15658. doi: 10.1021/ja035862p. [DOI] [PubMed] [Google Scholar]
- 31.Nakano M., Fujita H., Takahata M., Yamaguchi K. Theoretical study on second hyperpolarizabilities of phenylacetylenedendrimer: toward an understanding of structure-property relation in nloresponses of fractal antennadendrimers. J. Am. Chem. Soc. 2002;124:9648–9655. doi: 10.1021/ja0115969. [DOI] [PubMed] [Google Scholar]
- 32.Sajan D., Joe H., Jayakumar V.S., Zaleski J. Structural and electronic contributions to hyperpolarizability in methyl phydroxybenzoate. J. Mol. Struct. 2006;785:43–53. [Google Scholar]
- 33.Mveme C.D.D., Tchangnwa Nya F., W Ejuh G., Kamsi R.A.Y., Ndjaka J.M.B. Density functional theory study of optoelectronic, nonlinear optical, piezoelectric and thermodynamic properties of poly (3,4-ethylenedioxythiophene), poly(3,4-ethylenedioxyselenophene) and their derivative. Opt. Quant. Electron. 2020;52:373. [Google Scholar]
- 34.Yossa Kamsi R.A., W Ejuh G., Nkounga P., Ndjaka J.M.B. Study of the molecular structure, electronic and chemical properties of Rubescin D molecule. Chin. J. Phys. 2020;60:104–121. [Google Scholar]
- 35.Yossa Kamsi R.A., Ejuh G.W., Tchoffo F., Mkounga P., Ndjaka J.M.B. Electronic structure, spectroscopic (IR, Raman, UV-vis, NMR), optoelectronic, and NLO properties investigations of rubescin E (C31H36O7) molecule in gas phase and chloroform solution using ab initio and DFT. Methods. 2019;4246810:22. [Google Scholar]
- 36.Midoune A., Messaoudi A. DFT/TD-DFT computational study of the tetrathiafulvalene-1,3-benzothiazole molecule to highlight its structural. electronic, vibrational and non-linear optical properties. 2020;23(issue 2):143–158. [Google Scholar]
- 37.Fonkem C.C., Ejuh G.W., Tchangnwa Nya F., Yossa Kamsi R.A., Tadjouteu Assatse Y., Ndjaka J.M.B. A density functional theory (DFT) study of the doping effect on 2-cyano-3-[4 (diphenylamino) phenyl] acrylic acid. Chin. J. Phys. 2019 [Google Scholar]
- 38.Mveme C.D.D., Nya F.Tchangnwa., Ejuh G.W., Ndjaka J.M.B. A density functional theory (DFT) study of the doping effect on 4-[2-(2-N,N-dihydroxy amino thiophene) vinyl]benzenamine. SN applied Sciences. 2021;3:317. doi: 10.1007/s00894-021-04827-9. [DOI] [PubMed] [Google Scholar]
- 39.G.W Ejuh, M.T.Ottou Abe, T. Ghislain , J.M.B. Ndjaka, Ab initio and DFT studies on the donor–acceptor molecules1,2,3-trihydroxy-9,10-anthraquinone; 1(methylamino)anthraquinone; 2-phenyl quinoxaline and 2-(4-aminophenyl) quinoxaline (2018). Mater Focus 7: 37–44.
- 40.Fankam J.B., Ejuh G.W., Tchangnwa Nya F., Ndjaka J.M.B. Theoretical investigation of the molecular structure, vibrational spectra, thermodynamic and nonlinear optical properties of 4, 5-dibromo-2, 7dinitro- fluorescein. Opt. Quant. Electron. 2020;52:292. [Google Scholar]
- 41.Fankam Fankam J.B., Ejuh G.W., Tchangnwa Nya F., Ndjaka J.M.B. Study of electronic structure, optoelectronics, linear and nonlinear optical properties and chemical descriptors of dibromodinitrofluorescein isomers in gas phase and solvent media using ab initio and DFT methods. Chin. J. Phys. 2020 [Google Scholar]
- 42.Kabé C., Tchangnwa Nya F., Ejuh G.W., Ndjaka J.M. Comparative study of optoelectronic, thermodynamic, linear and nonlinear optical properties of methyl phenalenyl doped to zinc and copper and their applications. J. Mater. Sci. Mater. Electron. 2020;31:7898–7990. [Google Scholar]
- 43.Ejuh G.W., Ottou Abe M.T., Tchangwa Nya F., Ndjaka J.M.B. Prediction of electronic structure, dielectric and thermodynamical properties of flurbiprofen by density functional theory calculation. Karbala J. Mod. Sci. 2018;4:12–20. [Google Scholar]
- 44.Ejuh G.W., Nouemo S., Tchangnwa Nya F., Ndjaka J.M.B. Computational determination of the electronic and nonlinear optical properties of the molecules 2-(4-aminophenyl) quinoline, 4-(4-aminophenyl) quinoline, anthracene, anthraquinone and phenanthrene. Mater. Lett. 2016;178:221–226. [Google Scholar]
- 45.Tchangnwa Nya F., Ejuh G.W., Ndjaka J.M.B. Theoretical study of optoelectronic and thermodynamic properties of molecule 4-[2-(2-N,N-dihydroxy amino thiophene)vinyl] benzanamine: influence of hydroxyl position. Mater. Lett. 2017;202:89–95. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.