Millisecond timescale reactions observed via X-ray spectroscopy in a 3D microfabricated fused silica mixer

Presented is a 3D-microfabricated, 3D hydrodynamic focusing microfluidic mixer to study mixing-triggered reactions via X-ray spectroscopy. The 3D-microfabricated format of the device offers repeatable production. Meanwhile, the mixing scheme enables highly uniform sample residence times on the order of milliseconds.

Abstract

Determination of electronic structures during chemical reactions remains challenging in studies which involve reactions in the millisecond timescale, toxic chemicals, and/or anaerobic conditions. In this study, a three-dimensionally (3D) microfabricated microfluidic mixer platform that is compatible with time-resolved X-ray absorption and emission spectroscopy (XAS and XES, respectively) is presented. This platform, to initiate reactions and study their progression, mixes a high flow rate (0.50–1.5 ml min⁻¹) sheath stream with a low-flow-rate (5–90 µl min⁻¹) sample stream within a monolithic fused silica chip. The chip geometry enables hydro­dynamic focusing of the sample stream in 3D and sample widths as small as 5 µm. The chip is also connected to a polyimide capillary downstream to enable sample stream deceleration, expansion, and X-ray detection. In this capillary, sample widths of 50 µm are demonstrated. Further, convection–diffusion-reaction models of the mixer are presented. The models are experimentally validated using confocal epifluorescence microscopy and XAS/XES measurements of a ferricyanide and ascorbic acid reaction. The models additionally enable prediction of the residence time and residence time uncertainty of reactive species as well as mixing times. Residence times (from initiation of mixing to the point of X-ray detection) during sample stream expansion as small as 2.1 ± 0.3 ms are also demonstrated. Importantly, an exploration of the mixer operational space reveals a theoretical minimum mixing time of 0.91 ms. The proposed platform is applicable to the determination of the electronic structure of conventionally inaccessible reaction intermediates.

1. Introduction  

Fast, 3D hydro­dynamic focusing mixers are critical for many time-resolved studies of structural biology (Wang et al., 2014 ▸; Plumridge et al., 2018 ▸; Calvey et al., 2019 ▸), self-assembly of nano-structures (Othman et al., 2015 ▸; Zhu et al., 2018 ▸), and drug delivery (Vladisavljević et al., 2014 ▸; Borro et al., 2019 ▸). The 3D flow features of these devices are well suited for line-of-sight integrating techniques which cannot discriminate signal from slow-moving (e.g. near wetted surfaces) and fast-moving portions of a liquid stream (Pollack & Doniach, 2009 ▸). Such techniques include X-ray absorption and emission spectroscopy (XAS/XES), which can determine the electronic structure of matter (Bergmann et al., 1998 ▸; Shi et al., 2011 ▸; Kroll et al., 2016 ▸; Mara et al., 2017 ▸). XAS/XES often require large sample volumes and relatively high concentrations to obtain a sufficient signal-to-noise ratio (SNR). The conditions to achieve high SNR, in turn, are typically at odds with those of fast mixing (Huyke et al., 2020 ▸). Recent advances in fused silica subtractive manufacturing, however, provide an opportunity to create repeatable, robust, and complex 3D geometries inside of a monolithic chip (Bellouard et al., 2012 ▸). These advances are here used to fabricate a reproducible, 3D hydro­dynamic focusing device which can mix on the order of milliseconds and provide sufficient SNR for XAS/XES studies.

Various designs and fabrication methods have been used to achieve 3D hydro­dynamic focusing for synchrotron applications (Ghazal et al., 2016 ▸). In one scheme, a 2D hydro­dynamic focusing geometry is laminated with additional bottom and top layers to separate sample from all wetted surfaces (Russell et al., 2002 ▸). A common application for this scheme is the observation of RNA folding processes with mixing timescales as small as 1–2 ms (Das et al., 2003 ▸; Lamb et al., 2008 ▸; Schlatterer et al., 2008 ▸). These devices include microfabricated silicon components, UV-curable adhesives, and/or soft lithography components (Brennich et al., 2011 ▸; Seibt et al., 2018 ▸). As another example, 3D micromachining has been used to create polyimide devices (Vakili et al., 2019 ▸). However, it is difficult to create complex 3D geometries (e.g. concentric or overhanging features) using such fabrication methods. A 3D-printed device recently demonstrated compatibility with serial synchrotron crystallography and reported mixing timescales between 0.18 and 2 s (Monteiro et al., 2020 ▸). A limitation of the 2D hydro­dynamic focusing with additional bottom and top layers scheme is the significant premixing (and reaction completion) which occurs prior to and during sample stream focusing (Hertzog et al., 2006 ▸; Park et al., 2006 ▸).

To this end, manually assembled, telescoping capillary-type assemblies have been developed for greater sample acceleration and reduced premixing (Scampavia et al., 1995 ▸). In this coaxial scheme, a centered capillary directs a sample stream into an annular sheath stream. Plumridge et al. (2018 ▸) reported a coaxial mixer that accelerated flow through a downstream, small inner radius capillary to enhance mixing. They also demonstrated RNA folding via small-angle X-ray scattering (SAXS) and reported data at timescales of 10 ms. Calvey et al. (2016 ▸) used a similar geometry to perform mix-and-inject serial crystallography (MISC) but used a gas dynamic virtual nozzle (GDVN) to further accelerate the mixed stream into a liquid jet.

Fluidic devices in combination with SAXS and MISC can use thin sample streams to quickly mix and determine the geometric structure of reacting molecules. However, these X-ray methods are not able to address the electronic structure, which is also key in chemical bonding and reactivity (Glatzel & Bergmann, 2005 ▸; Schuth et al., 2017 ▸; Yan et al., 2019 ▸). Importantly, 3D hydro­dynamic focusing is yet to be demonstrated in combination with XAS/XES methods. Convection–diffusion-reaction models, furthermore, are not typically implemented in 3D hydro­dynamic focusing mixing devices.

We here present the design, modeling, fabrication, and quantitative experimental validation of a 3D-microfabricated, 3D hydro­dynamic focusing mixer platform. Our platform uses XAS/XES detection, consumes sample at order 10 µl min⁻¹, and demonstrates sample residence times (from mixing initiation to X-ray detection) between 2.1 and 157 ms. The current work first presents the formulation of a convection–diffusion model to predict residence and mixing times within the device. The model is experimentally validated using confocal fluorescence and X-ray detection. Following, the model is extended to include a reaction component which is validated with XAS/XES experiments of a reaction between ferricyanide and ascorbic acid. Lastly, we here report an exploration of the mixer operational parameter space to guide users in selecting appropriate flow rates and initial species concentrations.

2. Hydro­dynamic focusing device geometry and operation  

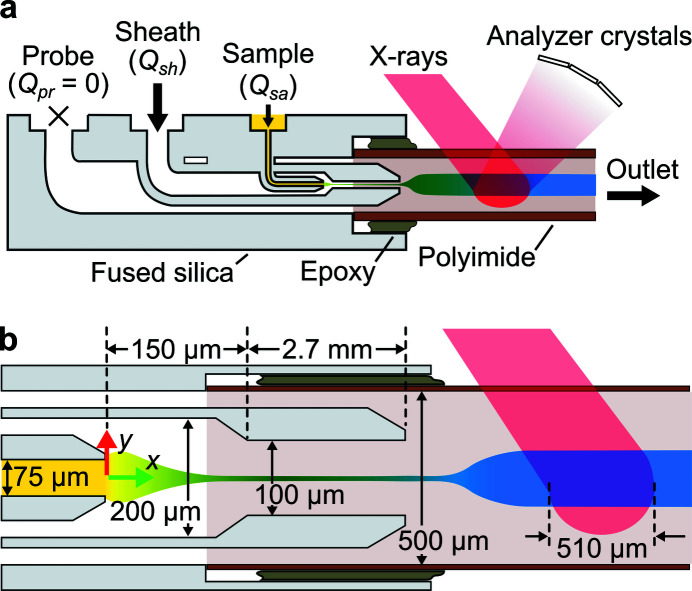
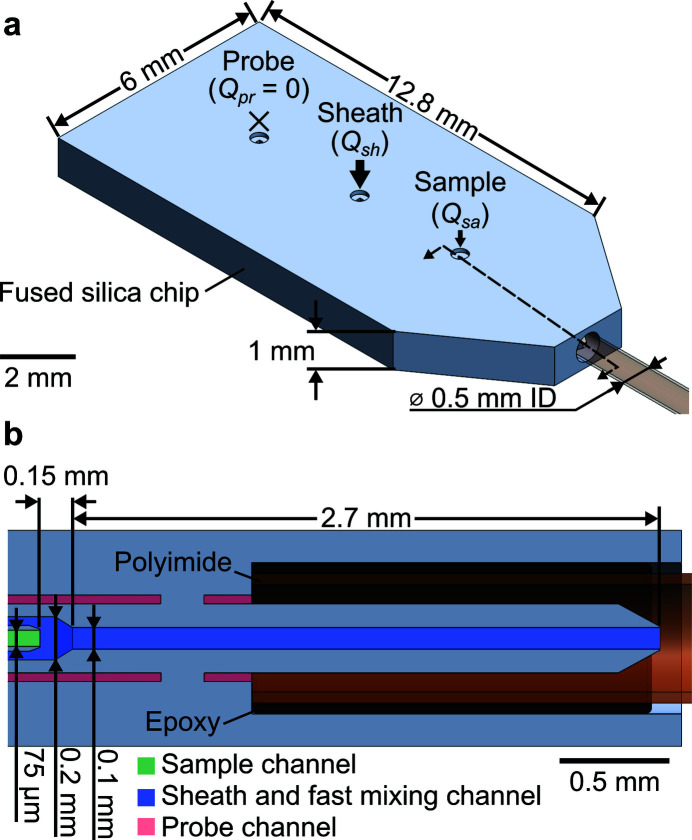
This section provides an overview of the mixer design and operating principles. The mixer comprises a monolithic fused silica chip to initiate mixing and a polyimide (or Kapton) capillary for X-ray detection [Fig. 1 ▸(a)]. The chip itself features three liquid inlets (probe Q _pr, sheath Q _sh, and sample Q _sa) and one liquid outlet connected to the polyimide capillary. A 3D CAD of the chip is available as the Supplementary File 1. Appendix A details the chip fabrication, capillary attachment with ep­oxy, and the connection of the mixer to the holder.

Figure 1.

Overview of the 3D hydro­dynamic focusing microfluidic mixer. (a) Schematic cross-section of the monolithic fused silica chip which shows the three fluid inlets and one main outlet for reactants. The polyimide capillary region of the mixer is compatible with X-ray spectroscopy. Note that the leftmost probe inlet was filled with water and sealed (i.e. permitted no liquid flow) in simulations and experiments for the current work. (b) Schematic view of the mixer and X-ray beam showing critical features and dimensions. The x = 0 position is indicated by the intersection of the red and green arrows. The schematic is topologically accurate but not to scale and aspect ratios have been exaggerated.

Our design achieves 3D hydro­dynamic focusing between a sample and sheath stream [Fig. 1 ▸(b)]. The degree of focusing is governed by the flow conditions, but herein typically results in 5 to 20 µm sample widths. Over this length scale, molecular diffusion acts to quickly mix sheath species (typically, of higher diffusivity) into the sample (typically, of lower diffusivity). The probe stream can be used to independently control the expansion and velocity of the sample stream as it enters the polyimide capillary (Huyke et al., 2020 ▸). The probe inlet can be operated in one of three modes: shut-off (i.e. Q _pr = 0), injection (Q _pr > 0), or withdrawal (Q _pr < 0) mode. In the current work, we studied conditions of moderate sample stream expansion and kept this port in the shut-off mode for all simulations and experiments shown. Note that the probe channel, leading up to the polyimide capillary, was initially filled with water prior to experiments.

3. Mixing and sample delivery  

3.1. Convection–diffusion model and mixing figures of merit  

This section introduces the numerical model and figures of merit to quantify mixing. We here developed a numerical model to solve the steady 3D Navier–Stokes and convection–diffusion equations. The model was implemented in COMSOL Multiphysics 5.5 (COMSOL Inc., Sweden) and is available as the Supplementary File 2. The state equations and boundary conditions are provided in Appendix B . The input values of physical properties, mesh generation procedure, and mesh convergence analyses are provided in the Supplementary Information (Supplementary Table S1, Supplementary Figs. S1 and S2).

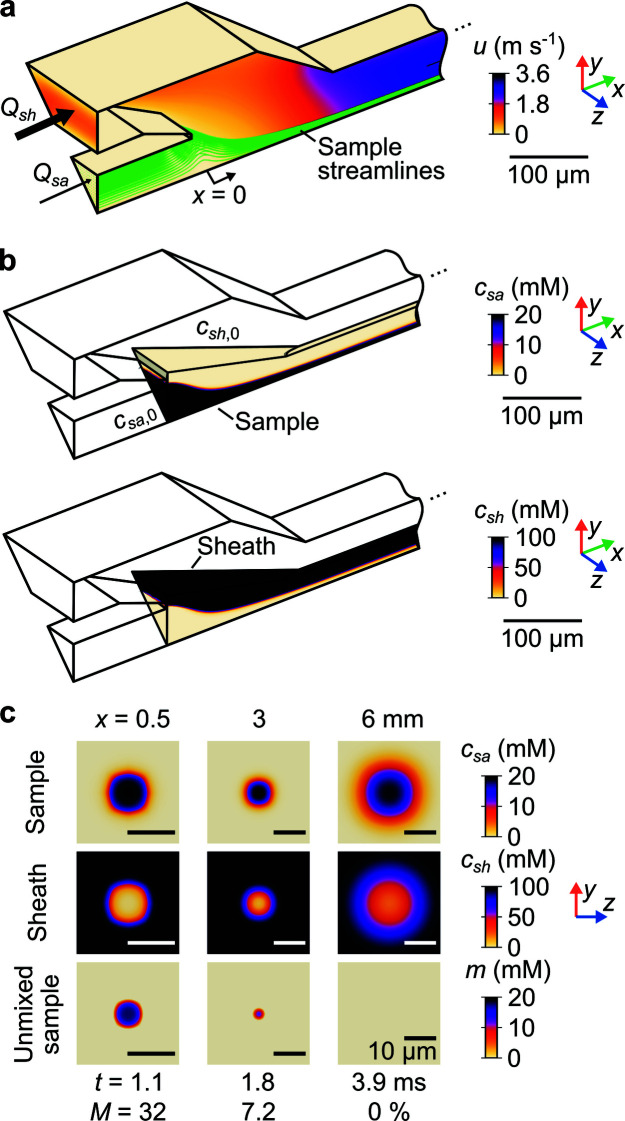
The convection–diffusion model was first used to predict the velocity magnitude field u within the device given sheath Q _sh and sample Q _sa flow rates [Fig. 2 ▸(a)]. Sample streamlines were seeded at the exit of the (center) sample channel, defined as x = 0 [cf. Fig. 1 ▸(b)]. As expected, the streamlines are tightly squeezed as they hydro­dynamically focus in the chip. In the capillary, streamlines expand over an axial distance that we found using simulations to be linearly proportional to a Reynolds number based on the capillary diameter (Supplementary Fig. S3).

Figure 2.

Results of the 3D numerical convection–diffusion model. (a) Velocity magnitude field u in isometric view. Sample streamlines were used to evaluate the sample residence time t. The model has 1/8th symmetry. (b) Sample c _sa (top row) and sheath (bottom row) concentration fields, also in isometric view, for a subdomain of the mixer geometry. (c) Sample (top row) and sheath (middle row) concentration fields in three y–z planes. Also shown is the unmixed sample concentration m (bottom row). Each column of (c) shows an axial position x with corresponding t and depth-averaged, unmixed sample fraction M. Note that flow passages are not circular and the species iso-concentration contours are not circular for x < 3 mm (due to a square cross-sectional geometry within the chip). Downstream into the circular capillary, these contours become approximately circular. Data in all panels are for Q _sa = 10 µl min⁻¹, Q _sh = 1 ml min⁻¹, c _sa, 0 = 20 mM, and c _sh, 0 = 100 mM.

The sample streamlines were used to evaluate the sample residence time since first being exposed to sheath species (at x = 0). We define the Lagrangian residence time t _i for a fluid element which starts at x = 0 and which follows the ith streamline as

where s _i = (x, y, z) _i describes a curve which follows the ith streamline, and u _i is the velocity magnitude along the ith streamline.

We subsequently define the sample residence time t as the molar flux averaged residence time of N streamlines (= 100), uniformly seeded at x = 0. t is given by

where A _i (x) is the cross-sectional area of the streamtube which locally bounds the ith streamline at a position x (Park et al., 2006 ▸). In this way, given flow conditions, axial positions are mapped to a residence time which quantifies the time since the sample species were exposed to sheath species.

Note that t has two main sources of uncertainty (Plumridge et al., 2018 ▸). The first is flow dispersion σ_flow which is primarily due to the nonuniform sample velocity profile. The second is beam smearing σ_X-ray and is due to the finite time that sample species take to cross the X-ray beam L _X-ray (= 510 µm) in the axial direction. We define the residence time uncertainty σ_t as

where

and

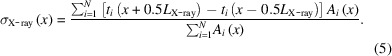This uncertainty estimate provides a characteristic width of the residence time distribution which we report as σ_t (Supplementary Fig. S4).

The convection–diffusion model was also used to predict sheath c _sh and sample c _sa concentration fields within the device given initial concentrations c _sh,0 and c _sa,0 [Fig. 2 ▸(b), top and middle row of Fig. 2 ▸(c)]. Note, for computational efficiency, concentration fields were only predicted in a subdomain of the mixer geometry.

To evaluate mixing, we define a figure of merit that will become relevant for 1:1 reactions (cf. Section 4.1). Specifically, at every position (x, y, z), we quantify the unmixed sample m as

where the 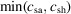operator evaluates to the minimum of either c _sa or c _sh [bottom row of Fig. 2 ▸(c)]. Importantly, our applications of interest do not require an equal sheath concentration across the mixer channel. We require instead that all sample species locally experience a threshold sheath concentration sufficiently high to initiate the reaction. We have here chosen the threshold sheath concentration within the sample region to be equal to the sample concentration, i.e. the stochiometric mixture value for a 1:1 reaction (Calvey et al., 2019 ▸). Note that m should not be negative and this is consistent with subtraction of the minimum of c _sa and c _sh.

Typical XAS/XES experiments involve line-of-sight integrating detectors, which prompt an additional, depth-averaged measure of mixing. We define the depth-averaged, unmixed sample fraction M as

Lastly, t and M enable a definition of the mixing time t _mix based on the time between positions where the sample reaches certain threshold values. t _mix is given by

where x _0.1 and x _0.9 are given by the conditions M(x _0.1) = 0.1 and M(x _0.9) = 0.9. Conceptually, 0.1 and 0.9 have been respectively chosen as representative values of complete and negligible mixing. The condition shown (Fig. 2 ▸) corresponds to a mixing time t _mix of 1.5 ms. Importantly, note that this mixing time (as is the case with most mixing times used in the literature) is a strong function of the flow conditions as well as the diffusivities and concentrations of the sample and sheath species.

3.2. Confocal measurements to validate the convection–diffusion model  

We describe in this section confocal fluorescence experiments to validate the numerical convection–diffusion model within the monolithic chip. Details of the solution preparation, fluid flow setup, image acquisition, and image processing are given in Appendix C .

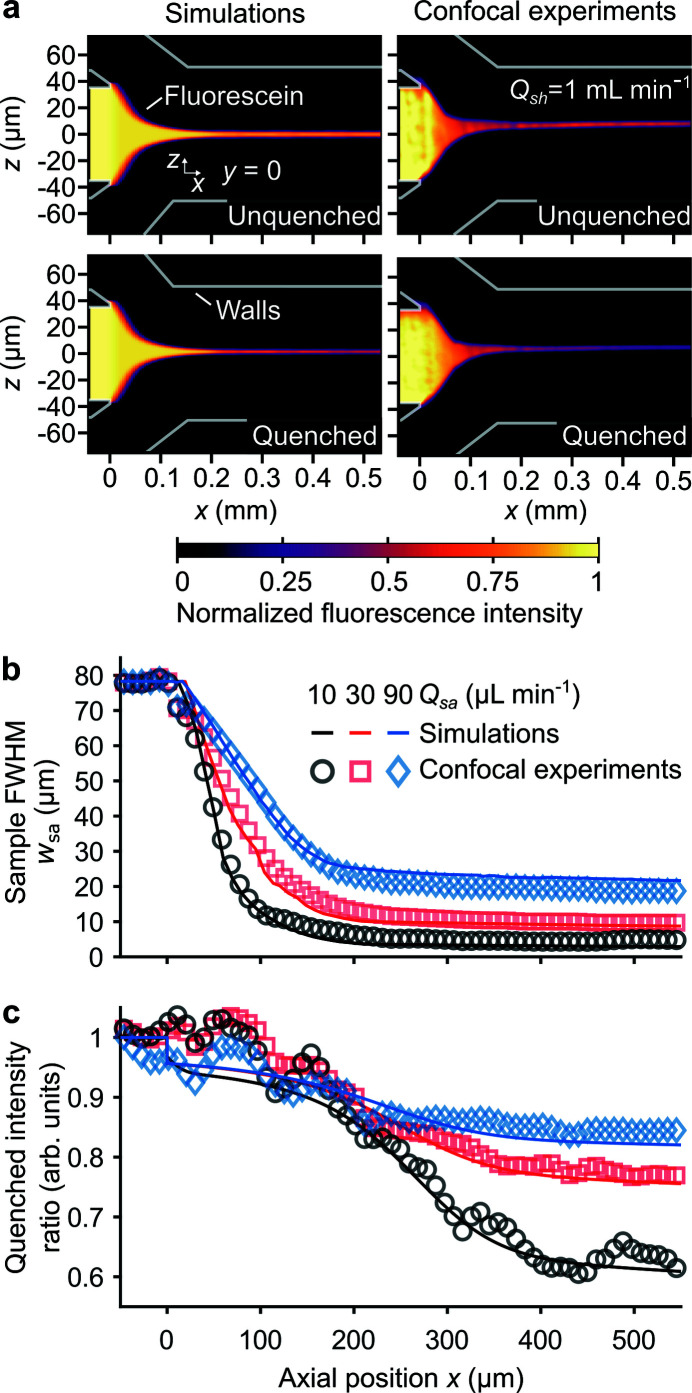
Presented are simulated and experimentally obtained fluorescence intensity fields of 3D hydro­dynamic focusing [top row of Fig. 3 ▸(a)] in the y = 0 plane. We here injected a 50 µM solution of fluorescein into the sample inlet (flow rate Q _sa) and a pure buffer solution into the sheath inlet (flow rate Q _sh). The third inlet of our device (used for Q _pr) was in the shut-off mode. There is good qualitative agreement of the scalar quantities and associated stream surfaces between simulations and experiments. Note that limitations of the imaging technique result in nonuniform illumination, and we addressed this using a flat-field image correction (see Appendix C ).

Figure 3.

Fluorescein focusing and fluorescein–iodide quenching simulations and experiments in the fused silica chip region of the mixer. (a) Normalized fluorescence intensity fields at the y = 0 plane from simulations (left column) and confocal laser scanning experiments (right column). Shown is hydro­dynamic focusing of a fluorescent sample by pure buffer (top row) and buffer with a quencher (bottom row). (b) Sample FWHM w _sa versus axial position x as predicted by simulations and experimentally measured. (c) Quenched intensity ratio versus x predicted by simulations and experimentally measured. We hypothesize the fluctuations in the quenched intensity ratio are due to nonuniform illumination and detection within the focusing region of the chip. Note that those fluctuations appear for all flow conditions and are discussed in Appendix C . Data in (b) and (c) are for varied Q _sa and fixed Q _sh = 1 ml min⁻¹.

Further qualitative validation of 3D hydro­dynamic focusing was performed by injecting a different fluorescent solution into the sheath inlet and imaging both sample and sheath species (Supplementary Fig. S5). We observed that flow rate ratios Q _sh/Q _sa of about 1000 or greater cause secondary, recirculatory flows near the sample channel aperture (Supplementary Fig. S6). To aid in presentation of the volumetric data, 3D fly-through movies of the measured sample and sheath concentration fields are shown (Supplementary Files 3 and 4).

Next, we quantified the agreement between the predicted and experimentally measured width of the sample w _sa [Fig. 3 ▸(b)]. w _sa is here defined as the full width at half-maximum (FWHM) of the sample fluorescence intensity at a given x. There is good quantitative agreement of w _sa predicted by simulations and measured in experiments. Further, note that the lower Q _sa (for fixed Q _sh) resulted in lower w _sa for all x > 0.

We also simulated and measured mixing conditions wherein a 500 mM solution of potassium iodide was injected into the sheath inlet [bottom row of Fig. 3 ▸(a)]. In this scenario, iodide in the sheath diffuses into and quenches the fluorescein sample. Since the quenching interaction timescale [∼0.9 ns (Voss & Watt, 1979 ▸)] is much smaller than the diffusion timescale (order milliseconds), this method provides a way to measure the time for the two fluids to mix.

Lastly, we quantified the simulated and experimentally measured iodide mixing rate [Fig. 3 ▸(c)]. To this end, we calculated the integrated intensity of the quenched and unquenched images at different axial locations. Their ratio is termed the integrated intensity ratio and is related to the average concentration of iodide inside of the fluorescent stream, via the Stern–Volmer relation (see Appendix C ). The integrated intensity ratio predicted by simulations and experimentally measured are in good agreement.

3.3. X-ray measurements to further validate the convection–diffusion model  

This section describes the use of X-ray detection to track Fe species in the polyimide capillary region of the mixer. The measured species intensity fields were compared with those predicted by simulations. The reactant sample was a 40 mM solution of ferricyanide 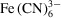and the reactant sheath was a 200 mM solution of ascorbic acid H₂Asc at pH = 10 (the flow setup is shown in Supplementary Fig. S7). Note that the Fe fluorescence measurements presented here are insensitive to reactions between 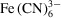and H₂Asc (cf. Section 4.2). Hence, we here detect the concentration field of all Fe species (i.e. both reactants and products) to further validate the convection–diffusion model. Again, the third inlet of our device (used for Q _pr) was in the shut-off mode. Appendix D details the sample preparation, measurement of X-ray interaction locations, data acquisition, and data processing methods.

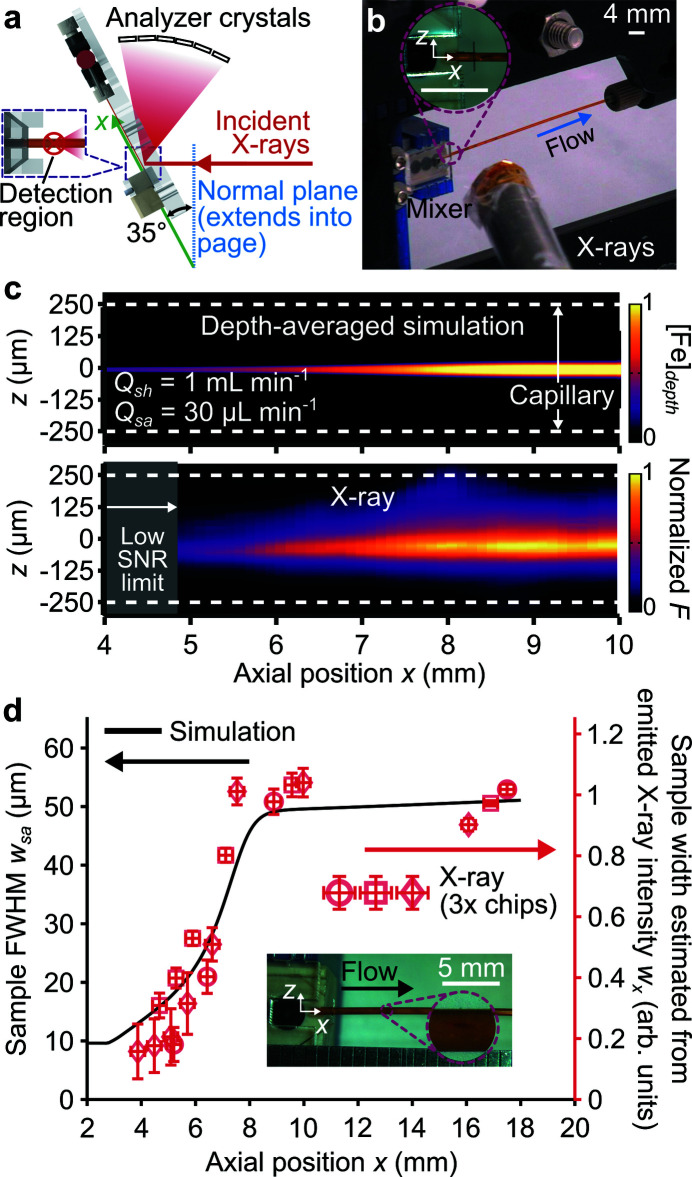
At the beamline, the mixer streamwise direction x was aligned horizontally and rotated along the spanwise direction z (parallel to gravity) by 35° with respect to the normal of the incident beam path [Fig. 4 ▸(a)] to minimize shadowing of the analyzer crystals (Sokaras et al., 2013 ▸). The beam emanating from the X-ray path tube [Fig. 4 ▸(b)] had a FWHM along the horizontal direction of 418 µm, leading to a footprint of 510 µm along the mixer streamwise direction. Meanwhile, the beam FWHM along the spanwise (vertical) direction was 113 µm (Supplementary Fig. S8).

Figure 4.

Experimental setup at the X-ray beamline and comparison with simulations. (a) Schematic of mixer placed at a 35° angle to the incident X-rays. (b) Mixer mounted on the beamline plate during X-ray operation. (c) Line-of-sight integrated profile of predicted axisymmetric concentration fields for all Fe species (top row) and measured Fe X-ray fluorescence (bottom row). The gray area in the X-ray image depicts the region where the sample stream cross-sectional area is too small for X-ray detection. Note that the convolutive effect of the X-ray beam significantly widens the apparent sample. (d) The left ordinate (corresponding to the line) is the predicted sample FWHM w _sa and the right ordinate (corresponding to the symbols) is the sample width associated with the emitted X-ray intensities w _x . Both quantities are plotted versus the axial position x and data are for the same flow conditions as (c). The vertical and horizontal uncertainty bars, respectively, correspond to the standard deviation of w _x among four different methods of measuring the emitted X-ray intensity and the X-ray beam FWHM along x. The inset shows the experimental device and a zoomed-in view of an example X-ray mark on the polyimide capillary.

We here compared the sample expansion predicted by simulations and measured in X-ray experiments [Fig. 4 ▸(c)]. Shown are the depth-integrated sample concentration [Fe]_depth for a simulation (see Appendix B for derivation) and the normalized Fe X-ray fluorescence. Note that the vertical X-ray beam size was almost twice the size of the sample stream and its convolutive effect smears out the Fe fluorescence in the radial direction. As a fair comparison, we compare widefield microscope epifluorescence images to [Fe]_depth and additionally convolve these data with the X-ray beam profile (Supplementary Fig. S9).

The sample FWHM w _sa was calculated from the simulation data [left ordinate of Fig. 4 ▸(d)]. However, the convolutive effect of the X-ray beam precludes an accurate determination of the sample stream width based on the Fe X-ray fluorescence data (Supplementary Fig. S9). Hence, the sample width associated with the emitted X-ray intensity measurements w _x [right ordinate of Fig. 4 ▸(d)] was estimated as

where 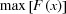is the maximum X-ray fluorescence at x. This formulation assumes that the emitted Fe X-ray fluorescence is proportional to the square of the stream diameter (i.e. F ∝ 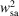). w _x was calculated using the intensity of all X-ray data at each point (XAS edge jump, Kα XES, Kβ XES, and vertical scans) for three mixers that were assembled independently. The vertical range bars are the standard deviation of the estimated w _x among all techniques. The horizontal uncertainty bars show the X-ray beam FWHM along the mixer streamwise direction. The predicted w _sa and experimentally measured w _x are in moderate agreement, which further validates our model in the capillary section.

4. Prediction and XAS/XES measurement of chemical reactions  

4.1. Extension to convection–diffusion-reaction model  

We here describe an extension of our experimentally validated convection–diffusion model to include a reaction component and provide the corresponding simulation results. The full convection–diffusion-reaction model allowed us to predict reactant and product concentration fields within the mixer given initial reactant concentrations and a second-order decay rate. As a model reaction, we here simulated the oxidation of ascorbic acid H₂Asc by ferricyanide 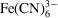to yield de­hydro­ascorbic acid Asc and ferrocyanide 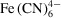products. This model, and associated supplementary files, are detailed in Appendix B .

The model reaction stoichiometry is

and the empirical rate law, at constant pH, was confirmed by stopped-flow measurements to be

where square brackets denote a concentration and k ₂ is the observed (pH-dependent) second-order decay rate. To match the XAS/XES experiments (cf. Section 4.2), we here simulated conditions wherein pH = 10 and k ₂ = 194.07 mM ⁻¹ s⁻¹. k ₂ was experimentally determined for this pH using stopped-flow ultraviolet–visible spectroscopy (UV–Vis) experiments (Supplementary Fig. S10).

To quantitatively compare simulation predictions with X-ray measurements of reaction progression, we here quantify the depth-averaged, unreacted sample fraction M _R as

where S = S(x) is the relative X-ray beam intensity for a beam centered at x (this assumes constant beam intensity in y and z). Note that M _R is analogous to M with only minor differences. First, in the numerator, m is replaced with 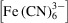since the latter directly quantifies the unreacted sample concentration. Second, both integrals feature a multiplication by S and an additional integration in x to simulate X-ray detection given a beam with a finite length along the streamwise direction.

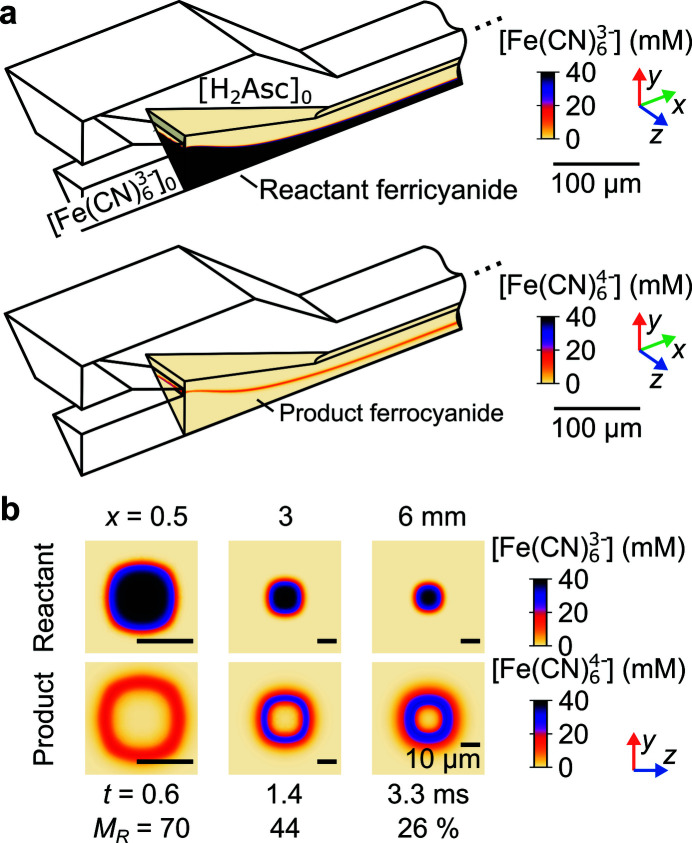
The convection–diffusion-reaction model was used to predict sample reactant ferricyanide 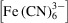and product ferrocyanide 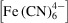concentration fields within the device given flow conditions and initial concentrations 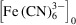and 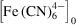[Fig. 5 ▸(a)]. The simulation predicts ferrocyanide first appears in the periphery of the sample stream. Note that mixing continues in the system, even downstream, after the expansion of the sample stream [x > 2.87 mm, see Fig. 5 ▸(b)]. Hence, we expect to see continued mixing of sheath into the sample and simultaneous reactions after sample deceleration and expansion upon entering the polyimide capillary.

Figure 5.

Results of the 3D numerical convection–diffusion-reaction model. The reaction involved ascorbic acid H₂Asc and ferricyanide 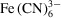reactants and de­hydro­ascorbic acid Asc and ferrocyanide 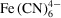products. (a) Concentration fields of 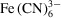(top row) and 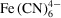(bottom row) in isometric view. (b) 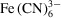(top row) and 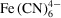(bottom row) concentration fields in three y–z planes. Each column of (b) shows an axial position x with corresponding t and depth-averaged, unreacted sample fraction M _R . Data in both panels are for Q _sa = 30 µl min⁻¹, Q _sh = 1 ml min⁻¹, 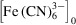= 40 mM, and [H₂Asc]₀ = 200 mM, and pH = 10.

4.2. XAS/XES measurements to validate convection–diffusion-reaction model  

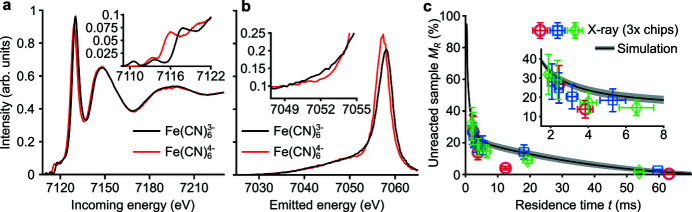
This section presents the results of X-ray measurements of simultaneous mixing and reactions. First, we experimentally obtained the Fe K-edge XAS [Fig. 6 ▸(a)] and Kβ XES [Fig. 6 ▸(b)] reference spectra of low-spin ferricyanide and ferrocyanide in a cubic local environment (O _h symmetry). The spectra were obtained by flowing solutions through the device with water, instead of reactants, in the sheath solution. The spectra of both species matched those reported elsewhere (Lee et al., 2010 ▸). The X-ray experimental methods are detailed in Appendix D .

Figure 6.

Results of X-ray experiments and comparison with predictions from simulations. (a) Reference K-edge XAS spectra of ferricyanide 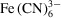reactant and ferrocyanide 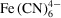product. The inset shows a zoom into the K pre-edge region. (b) Reference Fe Kβ XES spectra for the same species. (c) Predicted (line) and measured (symbols) depth-averaged, unreacted sample fraction M _R versus the sample residence time t. The shaded area near the line shows the range of possible M _R given variations in sample and sheath species diffusivities of 10%. Vertical uncertainty bars denote the standard error of the X-ray measurement and horizontal uncertainty bars denote the sample residence time uncertainty. In this diffusion-limited scenario, mixing and reactions occur simultaneously. We therefore report the average sample residence time since sample species were exposed to sheath species. Data are for Q _sa = 30 µl min⁻¹, Q _sh = 1 ml min⁻¹, 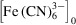= 40 mM, and [H₂Asc]₀ = 200 mM, and pH = 10.

During mixing experiments, we flowed and mixed the reactants sample ferricyanide and sheath ascorbic acid inside our device. The third Q _pr inlet of our device was in the shut-off mode. In these experiments, the relative abundance of sheath species and rapid decay rate of the reaction meant that reactions occurred in tens of microseconds. (Consider that an initial ascorbic acid concentration of 200 mM yields a reaction half-life t _1/2 of 18 µs.) This timescale is much shorter than the shortest accessible sample residence time (about 2 ms) for the flow conditions during X-ray detection. Hence, we here studied a slow mixing scenario to observe the (diffusion-limited) reaction progress in the polyimide capillary region of the mixer with XAS/XES.

The depth-averaged, unreacted sample fraction M _R was experimentally measured for three mixers that were assembled and tested independently [Fig. 6 ▸(c)]. Data were taken at multiple axial positions x along the mixer capillary and the corresponding residence times t were extracted according to equation (2). The ferric and ferrous reference spectra were used to determine M _R at experimentally measured positions by three methods: (i) a linear combination fit of the Kβ spectra, (ii) a linear combination fit of the K pre-edge including π* features (7108–7122 eV), and a peak fit of the low-energy feature of the K pre-edge (∼7110.4 eV). The range bars plotted along with M _R (indicated by the vertical bars) are the standard mean error among the values derived from these three methods. In turn, the temporal uncertainty (indicated by the horizontal bars) is the residence time uncertainty σ_t at the measured location. Kβ XES and Kα XAS/XES measurements at each position took 45 min while the time to collect a dataset for each chip was approximately 6 h. Given the sample flow rate, this corresponds to approximately 10 ml of sample per chip dataset.

M _R predicted by simulations, for the same conditions, are also presented [Fig. 6 ▸(c)]. In this regime of diffusion-limited reactions, M _R is highly sensitive to the species diffusivities input into the model. Note, however, that reported species diffusivities vary based on concentrations, temperature, and measurement technique. For example, the reported values of ferricyanide diffusivity, for a fixed concentration and temperature, vary by 10–20% (Konopka & McDuffie, 1970 ▸). Therefore, to account for this sensitivity, we performed simulations where all species were given 10% higher or lower diffusivity values than nominal.

Note that 70% of the sample has reacted at the shortest accessible residence time t = 2.1 ± 0.3 ms [corresponding to an axial location x = 4.7 mm, see equation (2)], at which point the sample is within the polyimide capillary. Here, the rate of reaction completion decreases rapidly with increasing distance downstream due to sample deceleration and expansion in the capillary. The reaction proceeds slowly for t > 6 ms and the remaining 20% of sample is reacted in ∼60 ms. We attribute the large time delay prior to reaction completion to incomplete mixing within the fused silica chip. Under these experimental conditions, the sample is 90% reacted at t = 27 ms.

The chip 2 and 3 experimental data points (blue and green symbols) are in good agreement with the predictions from simulations. In turn, the chip 1 (red symbols) experimental data points only agree with the predictions for t = 2.4 and 63 ms. We ascribe some disagreement to variations in the chip assembly process which lead to sample stream asymmetries (Supplementary Fig. S9). This variation highlights the importance of testing each device after assembly and prior to each X-ray experiment (see Appendix A ). We additionally hypothesize that X-ray damage to the polyimide capillary creates nucleation sites inside of the capillary. If so, the dissolved gases in the sheath may nucleate and accumulate, forming small gas bubbles. These bubbles can in turn result in flow asymmetries and variability in mixing. The latter observations speak to incorporating optics for visualization of flow between and during X-ray measurements (a capability we hope to add soon).

5. Exploration of operational regimes  

5.1. Complete mixing prior to reactions  

This section describes the use of our validated model to explore a mixer operational regime which achieves complete mixing prior to reactions and provides corresponding mixing time predictions. We are interested in fast and complete mixing since time-resolved studies of chemical reactions, typically, require decoupled mixing and reaction dynamics. This requirement can be formulated explicitly by a Damköhler number Da based on the mixing and reaction times as

where

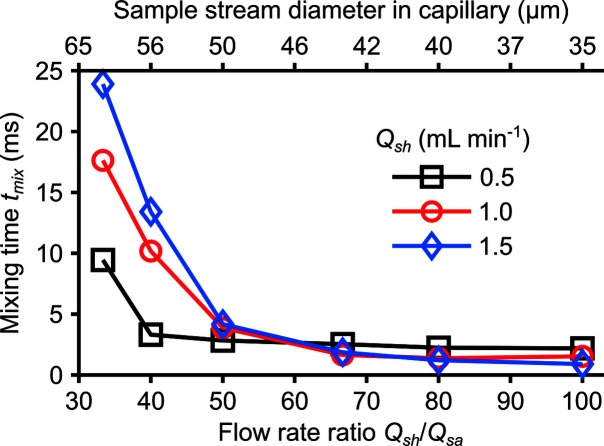
Here, t _mix is the mixing time given by equation (8), k is the second-order decay rate of the relevant reaction (obtained from, for example, UV–Vis experiments), and c _sh,0 is the initial concentration of the sheath. Note that our analysis here assumes a pseudo first-order reaction (i.e. c _sa,0 is much smaller than c _sh,0). Da should be less than 0.1 for complete mixing prior to reaction initiation. The predicted mixing times, therefore, can be used to estimate the addressable timescales of time-resolved studies of chemical reactions.

The operational regime investigated yielded values of t _mix between 0.91 and 24 ms (Fig. 7 ▸). From a mass balance, Q _sh/Q _sa governs the fully developed sample stream diameter in the polyimide capillary. The bottom and top abscissa of the plot therefore have a one-to-one correspondence. We here found that Q _sh/Q _sa < 50 resulted in incomplete mixing upstream of the fused silica chip exit. Hence, in this regime, mixing continues during sample deceleration and so t _mix rapidly increases with decreasing Q _sh/Q _sa. Lower Q _sh (for a fixed Q _sh/Q _sa) aids mixing in this regime because the sample spends more time within the confined channel of the chip. We additionally quantified the depth-averaged, unmixed sample M at a downstream location for the operational regime shown here (Supplementary Fig. S11).

Figure 7.

Predicted mixing time t _mix versus the sheath to sample flow rate ratio Q _sh/Q _sa (bottom abscissa) and expanded sample stream diameter in the polyimide capillary (top abscissa). The sample stream diameter in the polyimide capillary region of the mixer, for a fixed geometry, is governed by Q _sh/Q _sa. The explored operational regime assumed a fixed initial sheath to sample concentration ratio c _sh,0/c _sa,0 of 5. Further, the sample and sheath species have diffusivities, respectively, of 0.425 and 1.05 × 10⁻⁹ m² s⁻¹.

Q _sh and Q _sa, importantly, may be chosen within the studied operational regime as follows. First, t _1/2 should be evaluated given an initial sample concentration c _sa, 0 and k (for example, Fig. 7 ▸ assumes c _sh, 0 = 5c _sa,0). The desired t _mix can be subsequently evaluated as 0.1t _1/2 given our requirement that Da < 0.1. Lastly, we may choose a Q _sh such that the necessary Q _sh/Q _sa provides a sample stream diameter large enough for reasonable detector SNR.

5.2. Incomplete mixing prior to reactions  

This section describes the use of our model to study reactions when the mixing t _mix and reaction t _1/2 timescales are of the same order (i.e. Da is of the order of or greater than 0.1). XAS/XES experiments in such a regime are difficult because the measured spectra would contain mixed and unmixed reactant and product species components. However, the convection–diffusion-reaction model provides the information required to remove the exact weight of the unmixed reactant from the measured spectra. This process requires a simulation performed prior to the X-ray data analysis and input of the appropriate flow rates, species properties, and second-order decay rate. Additionally, the reference spectra of any removed components would have to be known.

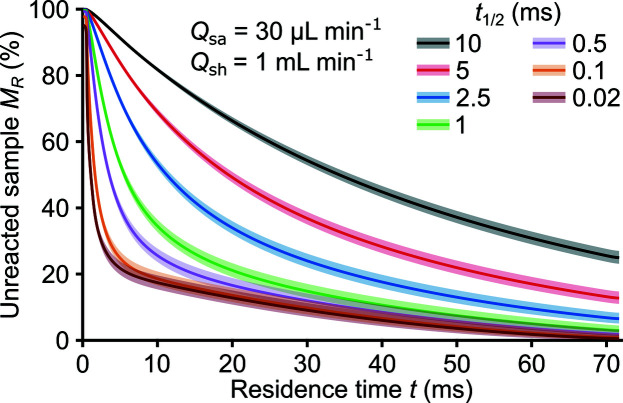
To this end, the unreacted sample fraction M _R was calculated for fixed Q _sa = 30 µl min⁻¹, Q _sh = 1.0 ml min⁻¹, and varied t _1/2 (Fig. 8 ▸). We herein vary t _1/2 to explore the lowest reaction half-lives for which our platform, with these flow rates, is sensitive. Again, the reaction simulated was between ferricyanide and ascorbic acid reactants (cf. Section 4.1). Although t _mix for these flow conditions is 18 ms (see Fig. 7 ▸), M _R is sensitive down to t _1/2 ≥ 0.1 ms.

Figure 8.

Predicted depth-averaged, unreacted sample fraction M _R versus the Lagrangian sample residence time t for varied reaction half-lives t _1/2 and fixed sample Q _sa and sheath Q _sh flow rates. The reaction studied involved ascorbic acid H₂Asc and ferricyanide 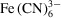reactants and de­hydro­ascorbic acid Asc and ferrocyanide 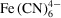products. The shaded area near the lines shows the range of possible M _R given variations in sample and sheath species diffusivities of 10%. The second-order decay rate for these simulations was estimated as k = 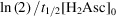. Data are for initial concentrations of 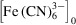= 40 mM and [H₂Asc]₀ = 200 mM.

The ability to predict species concentrations becomes particularly important for reactions with an interesting, short-lived intermediate. At the time of maximal presence of such an intermediate, the sample will be present as a reactant, intermediate, and product. The spectrum of the intermediate can then be obtained from a linear combination of the mixed spectra and the (known) reactant and product spectra. The uncertainty of this method becomes small if the weight of all three configurations is known, for which the theoretical modeling is crucial. Therefore, this methodology enables studies of short-lived intermediates even for timescales below t _mix which corresponds to the mixing conditions.

6. Conclusion and future applications  

In summary, we have developed a novel microfluidic mixer that achieves coaxial, 3D hydro­dynamic focusing and is compatible with XAS/XES methods. The mixer comprises two main components: a fused silica chip to initiate mixing and a polyimide capillary for X-ray detection. The former was microfabricated using a commercially available, highly reproducible subtractive manufacturing technique. This technique further enabled complex 3D geometries in the monolithic chip, such as overhanging and coaxial channels, for greater sample acceleration.

This work used 3D hydro­dynamic focusing to mix and demonstrate reaction kinetics at the millisecond timescale. Specifically, in the monolithic chip, a sample stream was focused by a sheath stream to achieve sample widths as small as 5 µm. Downstream, the sample decelerated and expanded (thereby increasing SNR) upon entering the capillary wherein X-ray detection occurred. Sample widths of 50 µm were demonstrated in this capillary. The studied sheath and sample flow rate ranges were, respectively, 0.50–1.5 ml min⁻¹ and 5–90 µl min⁻¹.

A convection–diffusion-reaction model was developed and used to predict velocity and concentration fields throughout the mixer. The model simulated the reduction of ferricyanide sample by ascorbic acid sheath. The model was also experimentally validated using confocal imaging of fluorescent dye focusing and quenching as well as XAS/XES experiments. Additionally, rational figures of merit (e.g. the sample residence time t, residence time uncertainty σ_t, unmixed sample fraction M, and unreacted sample fraction M _R ) were introduced to quantify mixing performance. This enabled us to demonstrate X-ray data collection for sample residence times (from initiation of reaction to the point of X-ray detection) as small as 2.1 ± 0.3 ms and as large as 157 ± 3 ms. In the slow mixing scenario used for the X-ray experiments, less than 10% of the initial reactant was left after t = 27 ms. However, the theoretical, minimum mixing time that can be achieved by our platform is 0.91 ms. The model also enabled an exploration of the operational regimes of our platform to guide users in selecting flow conditions as well as sample and sheath concentrations.

Our device and experimentally validated model may be used in future XAS/XES experiments to study short-lived reaction intermediates. The combination of this device and model is especially powerful when applied to conditions wherein mixing and reaction timescales are of the same order. Under such conditions, the convection–diffusion-reaction model provides the information required to estimate the exact weight of species present at each time point in the measured XAS/XES spectra. In inorganic chemistry applications, for example, many interesting reactions appear in the millisecond timescale with short-lived intermediates that may be difficult to trap without this mixing scheme. Examples include DNA click-chemistry catalyzed by copper and copper chelating drugs to treat neurodegenerative diseases, or mononuclear and binuclear iron proteins involved in oxidation chemistry. Given the capabilities of the microfabrication technique used here, the current design may be modified to also incorporate a GDVN downstream of the mixing region to enable the creation of free jets compatible with measurements using X-ray free-electron lasers.

7. Related literature  

The following references, not cited in the main body of the paper, have been cited in the supporting information: COMSOL Inc. (2019 ▸); Culbertson et al. (2002 ▸); Darrall & Oldham (1968 ▸); Muller et al. (2012 ▸); Phan et al. (2015 ▸); Shamim & Baki (1980 ▸); Tonomura et al. (1978 ▸).

Appendix A. Chip fabrication, mixer assembly, and preliminary testing

This appendix describes the chip fabrication, chip bonding to a polyimide capillary, and interfacing with the holder and holder plate. The monolithic chip was 3D-microfabricated via a two-photon, fused silica subtractive manufacturing method which was outsourced [FEMTOprint SA, Switzerland (Bellouard et al., 2004 ▸, 2012 ▸)]. A 3D CAD of the chip is provided as part of this work (Fig. 9 ▸ and Supplementary File 1). Hence, the chip is a commercially available device and a user wishing to reproduce these results can purchase a fully fabricated chip from FEMTOprint. A summary of the fabrication is provided as follows. A cuboid block of fused silica is first selectively exposed to a focused femtosecond pulse laser beam. Each exposed voxel of material undergoes a photochemical reaction which increases the local refractive index and imparts a stronger sensitivity to wet chemical etching. Following exposure, the block is treated with an HF wet etching. The modified material regions etch at rates that are roughly six times faster than the untreated material. A monolithic chip with optical access and micrometer-size, highly 3D features was produced.

Figure 9.

CAD renderings of microfluidic mixer. (a) Isometric view of fused silica chip-polyimide capillary subassembly with key dimensions labeled. The three inlets to the chip are labeled. (b) Cross-sectional view at the location of the dashed line in (a). The three channels inside of the fused silica chip are highlighted for clarity.

Mixer assembly commences with ep­oxy bonding of a polyimide capillary (American Durafilm, USA) to the fused silica chip [Fig. 10 ▸(a)]. This process involves dispensing a small volume (∼0.5 µl) of premixed 5 minute ep­oxy onto the capillary tip which is near the chip. The capillary is then fully inserted into the downstream aperture of the chip and gently spun along its axis (two to three turns) so that the ep­oxy wets the inner walls of the chip outlet port. Upon curing, the ep­oxy creates a leak-proof seal at this interface. The capillary was chosen to have an inner diameter (ID) of 500 µm, a length of 40 mm, and a wall thickness of 27 µm.

Figure 10.

CAD-renderings and images of the mixer and assembly process with approximate time estimates for each major step. (a) Assembly commenced with the attachment of a polyamide capillary (500 µm inner diameter, 554 µm outer diameter) to the chip with a ∼0.5 µl drop of 5 minute ep­oxy. (b) After the ep­oxy dried, the chip-capillary subassembly was mounted on the holder including inlet O-rings seals. The chip and O-rings were secured in the holder with a custom acrylic clamp. (c) Next, the holder was secured to the black acrylic holder plate. Shown here are three CAD renderings of the holder plate and associated holder offset and outlet tee components. The top right of (c) shows an image of the assembled device. The bottom right corner of (c) shows the mixer assembly at the X-ray beamline.

To inject liquid into the mixer, the chip was interfaced with a commercially available polyether ether ketone (PEEK) holder (Neptune FFS LLC, USA) [Fig. 10 ▸(b)]. Size 1 O-rings were placed in pockets on the top of the holder to ensure a leak-proof seal to the chip inlets. Each O-ring pocket was connected to a 10–32 coned fitting port on the upstream end of the holder (Flushnut, IDEX Corp, USA). The components of the clamp were laser cut (Fusion M2 Laser, Epilog Corporation, USA) from 1.5 and 3 mm-thick plates of poly(methyl methacrylate) (PMMA, acrylic). The components of the clamp were assembled and bonded irreversibly by dispensing acrylic cement into the interdigitated ends.

A holder plate was used to secure the mixer, holder, and inlet and outlet tubing, during optical and X-ray experiments [Fig. 10 ▸(c)]. The holder plate and associated holder offsets were laser cut out of 6 and 3 mm PMMA, respectively, and bonded as described for the clamp. Lastly, screws were used to secure the holder to the holder offset, and the capillary was secured to a downstream microfluidic tee junction (PEEK tee, IDEX, USA). Microfluidic filters with a 0.5 µm pore size (PEEK Frit 0.5 µm, IDEX, USA) were used immediately upstream of the holder to reduce clogging. Assembled devices typically operate for up to 36 h without clogging.

The assembled devices are tested after assembly and prior to beam time using optical inspection under a widefield fluorescence microscope. Specifically, we flow fluorescein and pure buffer, respectively, into the sample and sheath inlets. These visualizations allow us to observe the degree and symmetry of focusing just downstream of the sample channel outlet (just downstream of x = 0). No new and only some devices operated for more than 24 h fail this evaluation (10–20%). The most common failure mode is partial or complete clogging of a channel within the chip. We hypothesize that most clogs occur due to dust particles which may enter the chip before and during assembly of the device. We also verify the symmetry of the sample stream in the capillary region of the device using fluorescence microscopy (Supplementary Fig. S9). Asymmetries in this region may arise due to improper device-capillary assembly and major asymmetries occur less in less than 10% of assemblies.

Appendix B. Numerical models

This appendix provides the state equations, boundary conditions, and procedure for predicting the quenched intensity ratio for our numerical models. The mixer was simulated using numerical solutions of the steady state, incompressible Navier–Stokes and convection–diffusion-reaction equations. A commercial nonlinear solver (COMSOL Multiphysics 5.5, COMSOL Inc., Sweden) was used to solve for the steady-state Eulerian-frame velocity and concentration fields. The simulations were performed in three dimensions and assumed symmetry along the spanwise-streamwise and the transverse-streamwise planes (resulting in a 1/8th symmetric model). The state equations solved in the simulations are

and

where u is the velocity with components u _x , u _y and u _z , respectively, in the x, y and z directions, ρ is the density, p is the pressure, η is the dynamic viscosity, and D _i , c _i and R _i are, respectively, the concentration, diffusivity, and rate of production of a species i (see Supplementary Table S1 for a summary of the relevant physical parameters). Equations (15)–(17) were subject to the boundary conditions

and

where x _w denotes the location of walls and 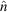is the unit normal vector at the wall. Equations (18) and (19), respectively, represent the no-slip and no-penetration at the wall boundary conditions. Flow rate, pressure and initial sample and sheath concentration boundary conditions were also imposed. The model for the rate of species production R _i is determined by the reaction of interest and the species i. The reaction studied here is shown in equations (10) and (11).

To predict the fluorescence of the quenched sample stream in confocal experiments (Fig. 3 ▸), we here performed simulations of fluorescein hydro­dynamic focusing with an iodide sheath. The quenched fluorescence intensity c _quenched was predicted by the Stern–Volmer relationship as

where c _unquenched and c _I are, respectively, the concentrations of fluorescein and iodide, and K _SV is the quencher rate coefficient. A K _SV value of 7.29 M ⁻¹ was used here (Huyke et al., 2020 ▸).

To simulate the line-of-sight-integrating X-ray detection method [top row of Fig. 4 ▸(c)], we calculated the depth-integrated Fe concentration [Fe]_depth for all axial positions x in the mixer. [Fe]_depth was calculated as

where 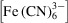and 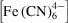are, respectively, the ferricyanide and ferrocyanide concentration fields.

The fluid flow and species transport problems used separate meshes. Specifically, we used an adaptive mesh refinement scheme to reduce numerical error and increase the number of mesh elements in regions of high velocity or concentration gradients. These mesh designs depend on the operating conditions as well as the specified chemistry (Supplementary Fig. S1).

Appendix C. Confocal experimental methods

This appendix describes the solution preparation, flow delivery setup, imaging, and data processing for confocal epifluorescence experiments. For these experiments, we mixed a 50 µM fluorescein (Sigma-Aldrich, USA) sample solution into a pure buffer, 500 mM potassium iodide (Sigma-Aldrich, USA), or 50 µM rhodamine B (Sigma-Aldrich, USA). All solutions were buffered with 20 mM Tris and 10 mM hydro­chloric acid (Sigma-Aldrich, USA) at a measured pH of 8.

Here, sample and sheath solutions were delivered using high-performance liquid chromatography (HPLC) pumps (LC-20AD, Shimadzu Corp., Japan). This pump was chosen because it had an accuracy of 1% at the explored flow rates (0.01–1 ml min⁻¹).

Epifluorescence confocal imaging experiments were performed on an inverted, laser scanning confocal microscope (LSM 880, Carl Zeiss AG, Germany) fitted with a 10× magnification, 0.45 numerical aperture air objective (Plan-Apochromat 10x/0.45 M27, Carl Zeiss AG, Germany). The excitation light for fluorescein was provided by a 488 nm argon laser, while a 561 nm diode-pumped solid-state laser was used for rhodamine B. The emitted light was collected through the objective and passed through a pinhole and a diffraction grating to separate the fluorescein emission (490 to 540 nm) from the rhodamine B emission (600 to 740 nm). The separated light emissions were subsequently detected by two independent photomultiplier tubes. For the fluorescein focusing and fluorescein–iodide quenching experiments shown in this manuscript, 16-bit images and z-stacks were obtained by dwelling 2.6 µs per pixel and rasterizing in x, y and z. The image region of interest was 4000 by 400 by 35 pixels (or 940 by 94 by 120 µm in object space) and the fluorescence SNRs were of the order of 100. The effective depth of field of the confocal images was 3.4 µm.

We note that imaging of scalar fields inside this highly 3D microfluidic chip is challenging and that noise as well as nonuniform illumination in the experimental images is expected. Sources of image noise include the elastic scatter and lensing of excitation and emission light from sharp corners, curved and angled interior walls, as well as rough surfaces (∼80 nm RMS roughness) expected from the manufacturing method. For example, fluorescence emission from the dye within the sample stream passes through at least three sets of wet-etched, curved and angled fused silica–liquid interfaces and one fused silica–air interface. To combat nonuniform illumination, we here applied a flat-field image correction technique (Wheat & Posner, 2009 ▸).

Following flat-field correction, confocal images were processed in MATLAB (R2019b, Mathworks, USA). To reduce light intensity noise due to point-scanning, the images were smoothed with an edge-preserving Gaussian kernel convolution. These were anisotropic diffusion filtering and guided image filtering operations (using, respectively, the ‘imdiffusefilt’ and ‘imguidedfilter’ commands in MATLAB). The Gaussian kernel was square with sides of 4 pixels. The width of the focused stream w _sa was measured by calculating the FWHM of the optical image in the y = 0 plane of the device.

To calculate the experimental integrated intensity ratio, for each quenched and unquenched image stack, we first performed integration of confocal slices along the y direction. This process involved summing corresponding pixel intensity values across six confocal slices. The obtained depth-integrated image was subsequently integrated along the z direction to obtain a single integrated intensity for every axial location x in the image stack. Lastly, the ratio of quenched to unquenched integrated intensity at every x was reported as the integrated intensity ratio.

Appendix D. X-ray experimental methods

This appendix describes the solution preparation, measurement of data collection locations, data collection procedure, and data processing methods for the X-ray experiments. For these experiments, we prepared a 40 mM potassium ferricyanide sample solution and a 200 mM ascorbic acid sheath solution (both Sigma-Aldrich, USA). Solutions were prepared fresh before the measurement and buffered with 500 mM carbonate–bicarbonate buffer (Sigma Aldrich, USA) titrated with hydro­chloric acid to a measured pH of 10.

To determine the locations where X-ray data collection was performed, the chip-capillary subassembly was removed from the mixer holder and imaged in a distance-calibrated stereoscope. Therein, we measured the distance between the chip-capillary junction (x = 2.97 mm) and the X-ray marks on the polyimide capillary. This procedure provided a measurement of x at each location where X-ray data were collected and removed any need to compensate for the 35° offset when calculating distances. However, the 35° angle affects the magnitude of residence time dispersion due to the X-ray beam size. Specifically, because the capillary is not perpendicular to the X-ray beam, the beam becomes larger in the streamwise direction by a factor of .

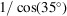The X-ray experiments were performed at beamline 6-2b of the Stanford Synchrotron Radiation Lightsource (SSRL) (Sokaras et al., 2013 ▸) at the SLAC National Accelerator Laboratory under top-up ring operating conditions of 3.0 GeV at 500 mA. Incident radiation from a 56-pole 0.9 T wiggler insertion device was monochromated by a liquid-nitro­gen-cooled Si(111) double-crystal monochromator with an energy resolution of ∼1 eV. Incident energies were calibrated against the first inflection point of a foil standard at 7111.2 eV (Bearden & Burr, 1967 ▸). X-ray emission was detected by a 1 m-radius Johann spectrometer with the Fe Kβ emission resolved by 4 × Ge(620) analyzer crystals and the Fe Kα resolved by 3 × Ge(440) analyzer crystals with detection by an energy-discriminating Hitachi Vortex silicon-drift detector (Hitachi, Japan). The emission spectrometer was calibrated by scanning elastic lines in the Kα and Kβ emission range with a resolution of 1.3 and 1.5 eV at the elastic peak, respectively. X-ray absorption spectra were measured as high-energy-resolution fluorescence detection (HERFD) with the emission spectrometer energy set at the maximum of the Kα₁ emission. The fast-flowing sample and sheath streams prevented X-ray damage to the sample (the sample transit time through the X-ray beam was ∼3 ms). Also, the polyimide capillary was protected from X-ray damage by a fast shutter (Uniblitz, USA). This shutter was closed during motor movements and opened during sample detection. Further, the emitted beam path was enclosed by a He-filled bag to reduce signal attenuation and air scattering.

Fe K-edge XAS data were energy calibrated using a monochromator glitch, background corrected and normalized to one at the edge jump. The Fe Kβ XES energy calibration was determined through a series of elastic scattering peaks. All XES data areas were normalized to unity.

Funding Statement

This work was funded by National Science Foundation; BioX Bowes Fellowship; NIH National Institute of General Medical Sciences grants F32GM122194 and P41GM103393 to Leland B. Gee; National Institute of Health grant GM-40392 to Edward I. Solomon; Beckman Foundation; US Department of Energy, Office of Science, Office of Basic Energy Sciences grant DE-AC02-76SF00515; US Department of Energy, Office of Biological and Environmental Research.