Catecholamines and acetylcholine have dissociable effects on large-scale cortical network activity and behavior.
Abstract
Influential theories postulate distinct roles of catecholamines and acetylcholine in cognition and behavior. However, previous physiological work reported similar effects of these neuromodulators on the response properties (specifically, the gain) of individual cortical neurons. Here, we show a double dissociation between the effects of catecholamines and acetylcholine at the level of large-scale interactions between cortical areas in humans. A pharmacological boost of catecholamine levels increased cortex-wide interactions during a visual task, but not rest. An acetylcholine boost decreased interactions during rest, but not task. Cortical circuit modeling explained this dissociation by differential changes in two circuit properties: the local excitation-inhibition balance (more strongly increased by catecholamines) and intracortical transmission (more strongly reduced by acetylcholine). The inferred catecholaminergic mechanism also predicted noisier decision-making, which we confirmed for both perceptual and value-based choice behavior. Our work highlights specific circuit mechanisms for shaping cortical network interactions and behavioral variability by key neuromodulatory systems.
INTRODUCTION
The catecholaminergic (noradrenergic and dopaminergic) and cholinergic modulatory systems of the brainstem are important regulators of global brain state and cognition (1–3). Their brainstem centers send ascending projections to large parts of the cerebral cortex (1, 4), which is equipped with similarly widely distributed receptors for these neuromodulators (5). Consequently, these systems are in an ideal position to shape cortex-wide network activity in a coordinated fashion. Mounting evidence indicates that neuromodulatory systems have a profound impact on large-scale cortical network activity, as measured by neuroimaging or electrophysiological mass signals (5–9).
Influential theoretical accounts postulate highly specific roles of the catecholaminergic and cholinergic systems in the regulation of cognition and behavior (1, 10, 11). Such specific functional roles imply that these neuromodulators should also have dissociable effects on the cortical micro- and macrocircuit dynamics that implement cognitive computation. One prominent idea holds that catecholamines increase the responsivity (“gain”) of neuronal populations to synaptic input (1, 12, 13). Acetylcholine, on the other hand, has been proposed to reduce the impact of prior knowledge (top-down cortical signaling) relative to new information (bottom-up signaling) (10).
Physiological evidence for such a distinct shaping of cortical network activity through catecholamines and acetylcholine is currently sparse. At the cellular level, catecholamines and acetylcholine, both increase the gain of cortical neurons (14–17). However, the magnitudes of the catecholaminergic versus cholinergic gain modulations have not yet been compared directly. Some studies have shown a suppression of intracortical signaling through acetylcholine (18–20), but it remains unknown whether the same holds for catecholamines. Here, we set out to conduct such a direct comparison between effects of catecholamines and acetylcholine the micro- and macrocircuit levels as well as the behavioral level.
Our approach was inspired by two insights (21). First, just as for single neurons (12), the network effects of gain modulation should depend on the external drive the network receives (22). Second, the large-scale interaction of subtle microcircuit effects can give rise to substantial effects at the level of cortex-wide network activity. Increases in neural gain result from complex microcircuit interactions (23). We hypothesized that one such mechanism may be a change in the ratio between excitation and inhibition (henceforth termed as “E/I”) within cortical microcircuits (17, 24, 25): Noradrenaline suppresses ongoing inhibitory inputs to pyramidal cells across the microcircuit (26), which may translate into a robust increase in the net gain of the complete neural population. We reasoned that an increase in gain yields effects on large-scale network activity that are particularly pronounced during external drive. By contrast, cholinergic increases in gain and E/I seem to only affect a smaller fraction of neurons in the microcircuit (24, 27). This may translate into a smaller impact of acetylcholine on the microcircuit’s (i.e., region’s) net gain. Furthermore, acetylcholine suppresses intracortical (lateral and/or feedback) signaling in sensory cortex (18–20).
We performed placebo-controlled pharmacological manipulations of catecholamine or acetylcholine levels and quantified their effects on cortex-wide functional connectivity assessed with magnetoencephalography (MEG). This was performed in two behavioral contexts: a visual task (i.e., external drive) and rest (absence of drive). We used local and large-scale network models to explore possible circuit mechanisms underlying the pattern of results. We lastly tested predictions derived from the circuit model at the behavioral level.
RESULTS
We increased central catecholamine and acetylcholine levels through the placebo-controlled administration of atomoxetine and donepezil, respectively (Fig. 1A, left; see Methods) [data reanalyzed from a previous report on local cortical variability (28)]. Atomoxetine is a selective noradrenaline reuptake inhibitor. Consequently, atomoxetine increases noradrenaline levels across cortex (3) and dopamine levels in its more restricted cortical projection targets (mainly frontal cortex) (29). Donepezil is a cholinesterase inhibitor (18), which blocks the enzymatic breakdown of synaptic acetylcholine and thus boosts cortical acetylcholine levels.
Fig. 1. Dissociated catecholaminergic and cholinergic effects on cortex-wide activity correlations.
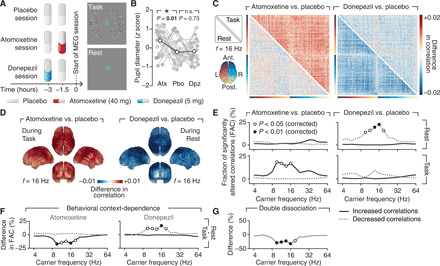
(A) Experimental design. Left: Atomoxetine (40 mg), donepezil (5 mg), or a visually indistinguishable placebo was administered before each session. Right: MEG activity was recorded during a visual task (top) or eyes-open rest (bottom). (B) Drug effect on baseline pupil diameter (rest and task collapsed). Atx, atomoxetine; Pbo, placebo; Dpz, donepezil. *P < 0.05, paired two-sided permutation test. n.s., not significant. (C) Drug effects on cortex-wide activity correlations (at 16 Hz), for task (top triangle) and rest (bottom triangle). Left: Atomoxetine- placebo. Right: Donepezil-placebo. (D) Cortical distribution of drug effects on correlations. Left: Atomoxetine-placebo (during task). Right: Donepezil-placebo (during rest). (E) Frequency spectrum of the drug effects on the fraction of significantly (P < 0.05, paired two-sided t test) altered correlations across brain regions, for atomoxetine (left) and donepezil (left) as well as for rest (top) and task (bottom). Fractions of significantly increased (solid black lines) and decreased (dashed gray lines) correlations are shown separately. (F) Effect of behavioral context on correlations [difference between top and bottom rows in (E)]. (G) Spectrum of double dissociation between atomoxetine and donepezil effects, measured as the difference between (E): solid black line (left) and dashed gray line (right). Open circles, P < 0.05; filled circles, P < 0.01 (paired two-sided single threshold permutation test).
Atomoxetine (catecholamines), but not donepezil (acetylcholine), increased pupil size (Fig. 1B and fig. S1), an established peripheral marker of central arousal state (30–32). Previous analyses of this dataset have shown that atomoxetine also increased heart rate and the so-called Hurst exponent of local fluctuations of MEG power, and both atomoxetine and donepezil altered heart rate variability and local MEG power (28). The current analyses focus on large-scale functional connectivity between cortical regions and on the underlying circuit mechanisms.
The results are organized as follows: We first quantify the effects of the two pharmacological interventions on cortex-wide functional connectivity and behavior. We then present simulations of cortical circuit models that explore specific hypotheses pertaining to the underlying circuit mechanisms. We lastly use an extension of the circuit model to derive a prediction for choice behavior and confirm this prediction for perceptual and value-based decision-making.
Distinct, context-dependent drug effects on large-scale network dynamics
Large-scale functional connectivity was quantified as the frequency-resolved correlations of intrinsic fluctuations of MEG power between all pairs of cortical regions (Fig. 1C) (33). We reasoned that any effect of gain modulation should manifest in changes of functional connectivity that depend on external drive. This intuition was solidified through simulations of a simple version of the circuit model described in the next section (Fig. 2C). Thus, we estimated functional connectivity in two behavioral contexts: a visual task with continuous input and eyes-open “rest” (Fig. 1A, right). The task entailed the continuous presentation of an ambiguous visual stimulus, which, in turn, induced spontaneous and ongoing alternations in perception (Fig. 1A and movie S1) (34). We asked participants to silently count perceived perceptual alternations and report the total count at the end of each MEG run. This allowed us to assess functional connectivity in the absence of transients in visual input and motor movements. In separate blocks, participants reported each perceived alternation with an immediate button press.
Fig. 2. Circuit mechanisms of context-dependent effects on cortex-wide correlations.
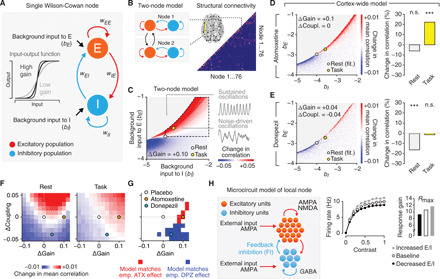
(A) Schematic of a single node (brain region) consisting of an excitatory (E) and an inhibitory population (I), with independent background input to E and I. Inset, input-output function of each population for various gain parameters (slope of the input-output function). (B) Left: Nodes were connected through their excitatory populations. Right: For the cortex-wide model, an estimate of the human structural connectome was used to connect a total of 76 nodes; the model was fitted to the rest-placebo data (Methods). (C) Change in correlation under an increase in gain (+0.1) in the (bE,bI)-plane of the “two-node model.” Inset: Sustained and noise-driven oscillations. The area defined by the dashed black line illustrates the range of the assumed shift in the (bE,bI)-plane from rest to task. (D) Effect of gain increase (+0.1) across all 76 × 76 node pairs (right; white circle, rest; yellow circle, task). (E) As in (D), but for donepezil with gain increase by +0.04 and decrease in global coupling (−0.04). ***P < 0.001; two sided paired permutation test (N = 100,000). (F) Difference in correlation (averaged across all node pairs) for all changes in gain and changes in global coupling, for simulated rest [left; white circle in (D)] and task [right; yellow circle in (D)]. (G) Mask highlighting parameter combinations where the changes in correlation are qualitatively consistent with the observations for atomoxetine (red) or donepezil (blue). (H) Left: Microcircuit consisting of excitatory and inhibitory leaky integrate-and-fire neurons. Middle: Effect of change in E/I on gain for increases (decreased E/I; black line; filled black circles) and decreases in feedback inhibition (increased E/I; gray line; filled gray circles), with respect to baseline (dashed line; open circles). Right: Fitted response gain parameter (Rmax) of the stimulus-response function for three levels of E/I.
We used a previously established approach for the estimation of MEG functional connectivity that attenuates spurious correlations due to signal leakage (33): For any pair of regions, we orthogonalized the regions’ frequency band–limited signals and then computed the correlations between the power envelopes of the residuals (see Methods and fig. S2A). We computed these orthogonalized power envelope correlations for 400 cortical locations and compiled them into a matrix, separately for a range of carrier frequencies. This yielded magnitudes, as well as spatial and spectral structure, of correlations for rest-placebo (fig. S2, B and C) similar to those reported for resting-state measurements in previous work (33).
We then compared the correlation matrices between task and rest (fig. S3, A to C) and between each drug condition and placebo. Neuromodulators may potentially cause correlations between cortical mass signals to shift in a common direction (e.g., toward larger positive correlations), or change in magnitude [e.g., shift toward more negative and more positive correlations (13)], depending on the underlying mechanism (5). To statistically assess the differences between our experimental conditions in an unbiased fashion, we computed the fraction of significantly increased and decreased correlations, separately for each frequency bin. We then tested those fractions for their deviation from the expected chance level while accounting for multiple comparisons across frequencies (Methods).
Atomoxetine increased correlations across most pairs of regions during task (top triangular part in Fig. 1C, left; fig. S4A). This effect was evident in all four cerebral lobes (Fig. 1D, left) and peaked in the “alpha/beta” frequency band (9.51 to 16 Hz; Fig. 1E, left). The effect was absent during rest (Fig. 1E; bottom triangular part in Fig. 1C, left). In contrast, donepezil (acetylcholine) decreased correlations across most region pairs, but only during rest (bottom triangular part in Fig. 1C, right; Fig. 1E, right, and fig. S4B). In other words, both drugs had opposite effects on correlations dependent on behavioral context, an effect that occurred within overlapping frequency bands (Fig. 1F). These opposite effects translated into a frequency-specific and context-dependent double dissociation between the effects of atomoxetine and donepezil on correlations (Fig. 1G; P values 0.0010, 0.0009, 0.0092, 0.0004, and 0.0106 for the frequency bins 9.51, 11.31, 13.45, 16.00, and 19.03 Hz, respectively; paired two-sided permutation test).
The double dissociation was neither present at the level of local activity fluctuations [see (28) and fig. S5A] nor did it depend on specific choices of analysis parameters (fig. S5, B to F). Drug-related differences in correlations, albeit small in absolute terms (|Δr| < 0.02), corresponded to an atomoxetine-induced increase during task of about 16% (collapsed across 9.51- to 16-Hz range and all region pairs) and a donepezil-induced decrease during rest of about 14% (collapsed across 9.51- to 19.0-Hz range and all region pairs). Effect sizes (Cohen’s d) were d = 0.4972 for atomoxetine (task) and d = 0.6135 for donepezil (rest), both corresponding a medium effect size (35).
Catecholamines and acetylcholine both increase the gain of cortical neurons (1, 12, 15, 17). How, then, did the observed dissociation between their effects on large-scale functional connectivity arise? We reasoned that this may result from subtle differences between the catecholaminergic and cholinergic microcircuit effects, amplified through large-scale interactions between the multitude of microcircuits (i.e., regions) across cortex. Specifically, physiological evidence suggests that catecholamines increase net gain of entire cortical regions by tonically increasing E/I across neurons in the circuit and that acetylcholine may have a weaker effect on the regions’ net gain (24). We simulated cortical circuit models at different scales to solidify these hypotheses and assess whether such circuit mechanisms were sufficient to account for the pattern of changes in functional connectivity.
Distinct circuit parameter changes can explain drug effects on large-scale network activity
We first used a large-scale model to simulate the correlations in mass activity (population firing rates) between coupled cortical regions (“nodes”). Each node was composed of an interconnected excitatory and inhibitory neural population (Fig. 2, A and B; see also Methods and Supplementary Discussion) (36). The model had four free parameters: the background inputs to excitatory (bE) and inhibitory (bI) populations, the slope of the input-output function (gain at the neural population level), and a global coupling parameter. The interplay between excitation and inhibition was used to generate oscillatory dynamics within each node, as observed in measurements of cortical population activity (37). Specifically, we simulated a regime in which cortical mass activity exhibits noise-driven (as opposed to sustained) oscillations (fig. S6A) (38): Stochastic fluctuations in activity drive damped oscillations in the local nodes (see also Supplementary Discussion). Superposition of such damped oscillations, triggered at random moments in time, gives rise to ongoing variations in the amplitude of band-limited activity. The power spectrum of the model firing rate time series exhibited a single peak (fig. S6E). The weights of the local nodes were chosen such that the spectral peak was in the range around ~10 Hz, matching the spectral pattern present in the current MEG data during rest and (with smaller amplitude) task (28). The exact peak frequency within this range depended on the background inputs bE and bI (fig. S6F).
Our simulations were further constrained by the assumption of increased background input to excitatory populations (bE) and inhibitory populations (bI) in many cortical regions during task (39). This assumption rests on the notion that our visual task increased the drive of visual and higher-order “task-related” cortical regions and affected both excitatory and inhibitory neural populations in these regions. Sensory input increases not only excitation (i.e., drive of pyramidal cells) but also inhibition (i.e., drive of interneurons) in visual cortex (Supplementary Discussion) (40–42). Correspondingly, in the model, we implemented the task as an increase in the background input to excitatory and inhibitory populations relative to rest. We first used a model made up of only two connected brain regions. The model’s behavior can be studied in the (bE, bI)-plane (Fig. 2C). The increased task-related input resulted in an upward-rightward shift in the (bE,bI)-plane and predicted a shift of the spectral peaks of the local nodes’ power spectra to higher frequencies during task compared to rest (fig. S6, E and F). This was confirmed for the dominant ~10-Hz frequency range (“alpha-band”) in the data (fig. S7B). The model’s task state also captured an overall decrease in correlations (averaged across all region pairs) present in the MEG during task compared to rest (figs. S3, B and C, and S7C). These observations further validated the implementation of task drive as an upward-rightward shift in the (bE, bI)-plane.
An increase in gain in the model was sufficient to explain the context-dependent effect of atomoxetine on cortical correlations we observed in the data (Fig. 2C). Just as observed in the empirical data (Fig. 1E, left), increasing the gain in the “two-node model” produced distinct changes in correlations for different contexts situated in the (bE,bI)-plane (i.e., different levels of background drive; rest, light gray circle; task, yellow circle; Fig. 2C). In a realistic model of the whole cortex (Fig. 2B, right), which was fitted to the measured correlation matrix for rest-placebo (fig. S6G), an increase in gain boosted correlations in the same context-dependent fashion, with no change at rest (Fig. 2D, light gray circle or bar) but a robust increase during task (Fig. 2D, yellow circle or bar). All parameter combinations consistent with the observed pattern of results included an increase in gain combined with a small or no change in the model’s global coupling parameter [Fig. 2, F and G; all red cells to the right of x = 0 in (G); fig. S8 for various levels of task-related input].
We next simulated a cortical microcircuit model (Methods; Fig. 2H, left, and fig. S9) to test the hypothesis that the increase in gain inferred from the large-scale model may be mediated by a global increase (i.e., encompassing most neurons) in E/I of each node. The microcircuit was made up of a population of recurrently connected excitatory and inhibitory conductance-based leaky integrate-and-fire neurons. We increased the circuit’s E/I by decreasing the strength of feedback inhibition and quantified the effect on response gain of the input-output function of the excitatory cells of the circuit (Methods). Increasing E/I translated into a gain increase (Fig. 2H, right).
The large-scale model could also explain the opposite, context-dependent effect of acetylcholine on cortical correlations (Fig. 1E, right). This also entailed a gain increase (smaller or equal to the catecholaminergic one; Fig. 2, E and G). Critically, however, gain change alone was insufficient to account for the results, but it had to be combined with a decrease in global coupling (Fig. 2, E to G): All parameter combinations consistent with the observed results included such a reduction in global coupling [Fig. 2, F and G; all blue cells below of y = 0 in (G); fig. S8 for various levels of task-related input]. This decrease is in line with a reduction of intracortical (lateral and/or feedback) signaling observed in sensory cortex (18–20).
In the simulations shown in Fig. 2, the task-related increase in background input was applied to all nodes of the network. This was based on the observation that task also changed MEG power in the relevant frequency range for most parts of the cortical surface (placebo only; fig. S3D) and statistically significant in about 50% of the regions (in the frequency range from 9.51 to 16 Hz; fig. S3E). We additionally simulated a variant of the large-scale model in which the task-related inputs were only applied to those nodes that also exhibited significant (P < 0.05, two-sided paired t test) task-related decreases in power. This heterogeneous model yielded qualitatively similar results as the homogeneous version (fig. S10).
Circuit mechanism also accounts for catecholaminergic increase in perceptual variability
The above circuit modeling insights, specifically the cortical E/I increase under catecholamines, also accounted for the observed drug effects on visually guided behavior (Fig. 3). Atomoxetine (not donepezil) increased the number of perceptual alternations reported by the participants during MEG (Fig. 3A), which served as a readout of behavioral variability (43). This effect was not due to a change in eye movements or blinks (28), and it was evident both when participants silently counted the perceptual transitions and when they reported each perceptual transition with an immediate button press (fig. S11).
Fig. 3. Catecholamine-induced increase in E/I ratio can increase perceptual variability.
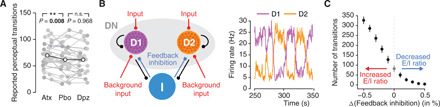
(A) Effect of atomoxetine on rate of transitions in the judgment of continuous input (changes in the apparent direction of rotation of the seemingly rotating sphere). **P < 0.01 (two-sided paired permutation test). (B) Left: Schematic of the decision circuit, endowed with two excitatory decision populations, D1 and D2, and a nonselective population (DN), fully connected to a pool of inhibitory neurons. The two decision populations receive equally strong, noisy Poisson input, reflecting the ambiguous nature of the visual stimulus. Right: The model exhibits spontaneous firing rate fluctuations. Perceptual transitions in the model are defined as changes in the dominance of one population over the other (i.e., one having a higher firing than the other). (C) Effect of E/I increase in circuit model on number of transitions in the judgment of continuous input. E/I increase in the circuit model is implemented via decrease in feedback inhibition (red/blue arrows).
To make the above microcircuit model produce selection behavior, we expanded it to two populations of excitatory neurons, each encoding a specific decision (“D1” and “D2”; corresponding to the two perceptual interpretations of the stimulus), which competed via feedback inhibition (Fig. 3B, left). This architecture matches the one of an established model of perceptual decision-making in two-alternative forced choice (2AFC) tasks with discrete trials (44). In such tasks, increasing E/I in the circuit model amplifies the noise in the transformation from sensory input to choice (45). We adjusted some parameters (see Methods) to simulate the behavior in our current task (i.e., spontaneous perceptual alternations under continuous and ambiguous sensory input). When driving the circuit with sustained and unbiased input (i.e., equally strong input to D1 and D2), it exhibited ongoing transitions in the activity dominance of D1 or D2 (Fig. 3B, right). Critically, we found an increase in the transition rate under increased E/I due to decreased feedback inhibition (Fig. 3C). In other words, increasing E/I in the circuit model rendered the perceptual interpretations of the ambiguous input more volatile, same as atomoxetine did in our participants. This result corroborates our conclusion from the assessment large-scale functional connectivity that catecholamines increased the net E/I in cortical regions.
Analogous catecholaminergic increase in decision noise during foraging
Behavioral variability may be adaptive during foraging in environments with changing reward contingencies (46). Specifically, an influential view holds that catecholamines render choice behavior more variable to facilitate behavioral exploration just when the uncertainty about the environment has increased (1, 47, 48). We performed a second behavioral experiment to probe the effect of atomoxetine (same dose as for the perceptual task; Fig. 4A and fig. S12A) on value-based choice during foraging. Participants performed a modified version of a dynamic foraging task previously used in monkeys (49). On each trial, participants chose between two visual targets presented in the left or right hemifield (horizontal/vertical gratings, randomized by position) through a button press with the corresponding hand. Targets were either associated with a reward or no reward (Fig. 4B). Rewards were assigned to the horizontal and vertical targets at different rates, which underwent hidden changes at random times (Methods and Fig. 4, B and C). Participants attempted to maximize the obtained reward. All but three participants performed the task well, reaching a performance of ~70% (Fig. 4D) and responding to the changes in reward ratios with corresponding changes in their choice behavior (fig. S12B). As in the first dataset, atomoxetine increased baseline pupil diameter (Fig. 4E).
Fig. 4. Catecholamines promote exploratory choice during foraging.
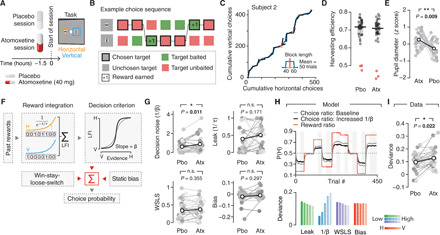
(A and B) Experimental design for value-based choice experiment. (A) Administration protocol for the value-based choice experiment: Atomoxetine or placebo was administered before each session. (B) Reward scheme illustrated for example sequence of rewards and choices across seven trials (see Methods for details). (C) Choice behavior versus reward contingencies for an example participant and session. Continuous blue curve, cumulative choices of horizontal versus vertical targets. Black lines, average ratio of incomes earned from both targets (horizontal:vertical) within each block. (D) Harvesting efficiency (fraction of collected over available rewards) per participant and experimental session. Red circles highlight the excluded participants due to poor performance. (E) Effect of atomoxetine on baseline pupil diameter. **P < 0.01, two-sided paired permutation test (100,000 permutations). (F) Schematic of the algorithmic model for value-based choice task (dynamic foraging). Choice behavior was analyzed with a reward integration model consisting of four parameters: integrator leak, decision noise (1/β of softmax transformation), weight of win-stay, loose-switch (WSLS) heuristic, and overall (static) bias (see Methods). (G) Effect of atomoxetine on model parameters. (H) Top: Example run simulated with the reward integrator model. The model predicts larger deviation of choice fraction from those matching reward ratios (red line) under higher decision noise (black) compared to baseline (gray). Gray shaded areas, temporal intervals used for computing deviance (Methods). Bottom: Deviance as function of all model parameters (see Methods for exact parameter values). (I) Deviance for atomoxetine and placebo. *P < 0.01, two-sided paired permutation test (100,000 permutations).
Previous work on this task has shown that a model entailing leaky integration of the rewards earned from choosing each target yields both successful reward harvesting and fits monkey behavior in this task well (49, 50). Within this reward integration model, decision noise (governing choice variability) refers to the slope of a nonlinear transformation of integrated reward into the probability of choice of a particular target (e.g., horizontal) (50). We fitted a model using the softmax function as choice function in which the parameter 1/β (inverse temperature) quantifies decision noise (Fig. 4F and Methods). The other three parameters were (i) participants’ tendency to use a “win-stay, loose-switch” (WSLS) heuristic; (ii) leak of the reward integrator (inverse of time constant τ); and (iii) overall bias (Fig. 4F). As expected, decision noise was negatively correlated with the duration (i.e., number of trials) of sticking to a given option after harvesting a reward (fig. S12E), whereas stay durations after unrewarded choices were predicted by the WSLS heuristic (fig. S12E). Leak and overall bias were unrelated to stay durations (fig. S12E).
In line with the results from our perceptual task and the circuit model prediction for E/I increase for 2AFC tasks (45), atomoxetine also increased the noise in the decision transformation in the foraging task (Fig. 4G). The increase in decision noise could not be explained by mere differences in the goodness of the integrator model fit, which was about equal for atomoxetine and placebo conditions (fig. S12F). Group mean Bayesian information criterion (BIC) values were 521.29 for placebo and 518.64 for atomoxetine, with 14 of 29 participants showing BIC values smaller by more than 6 (indicating strong evidence for better model fit) for atomoxetine than placebo and 14 of 29 participants showing the opposite pattern (i.e., better fit for placebo than atomoxetine). Furthermore, the increase in decision noise was also supported by analyzing the data with a mechanistically agnostic statistical model (logistic regression, fig. S13): Again, we found a decrease in the slope of the decision transformation (fig. S13A) but no increase in the lapse rate that captured behavioral variability beyond the decision transformation (fig. S13B).
The reward integration model predicted that the increase in decision noise would manifest in participants’ foraging behavior as a larger deviance between their choice fractions and actual reward ratios, reaching an asymptote a few trials after the change points (Methods; Fig. 4H, top). Increases in the other three parameters had no or even opposite effects on the deviance (Fig. 4H, bottom). Participants exhibited an increase in this deviance measure under atomoxetine (Fig. 4I), diagnostic for an increase in decision noise. In summary, our behavioral results show that elevated catecholamine levels increased decision noise in both sensory- and value-guided behavior, likely via increasing E/I in cortical microcircuits.
DISCUSSION
We uncovered a context-dependent double dissociation between catecholaminergic and cholinergic effects on functional connectivity between frequency-specific population activities in different cortical regions. Guided by recent insights into possible differences in catecholaminergic and cholinergic effects at the synaptic level (24), we used a multiscale circuit modeling to develop a mechanistic account of the complete pattern of our large-scale results. This showed that the hypothesized net increase in gain local circuits, through an increase in E/I, was sufficient to account for the catecholaminergic effects; accounting for the cholinergic effects required a reduction in the coupling between cortical regions in addition to an increase in gain. The catecholaminergic E/I increase also predicted an increase in behavioral variability, which we confirmed in two behavioral tasks.
An influential theory postulates that catecholamines and acetylcholine track distinct forms of uncertainty during inference in changing environments (10). Acetylcholine signals so-called “expected uncertainty,” which pertains to uncertainty about the environment in the absence of state change; noradrenaline signals “unexpected uncertainty,” originating from hidden changes in the state of the environment (10). These distinct roles of catecholamines and acetylcholine in cognitive computation imply that they also have separable physiological influences on the cortical networks that implement these computations. Our findings provide strong evidence for this notion and suggest that the physiological distinction may be mediated by the modulators’ distinct effects on local circuit parameters, which translate into pronounced differences at the level of large-scale cortical networks. These insights can serve as constraints for future translations of the above framework from the computational to the implementation level. Our results may also provide new constrains regarding the specific role of acetylcholine. The expected uncertainty in the above account can be decomposed into “irreducible uncertainty,” the inherent noisiness of sensations, and “state uncertainty,” the uncertainty about states in the model. Inference should ignore the former (by weighting priors over sensory input) but try to reduce the latter (by weighting sensory input over priors). The role of acetylcholine in this context has remained unclear. In our data, early visual cortex behaved differently from other regions under donepezil, showing no decrease (some locations even trend toward increase) in functional connectivity with the rest of cortex (Fig. 1, C and D). It is tempting to speculate that this may reflect a weighting of sensory input over priors (the decreased correlations between everywhere else in Fig. 1C). It will be interesting to test in future work how this feature of the data will behave under systematic changes of sensory input and/or prior.
Our behavioral results establish a general catecholaminergic effect on perceptual and value-based decision-making and confirm a key prediction from a prominent account of the noradrenergic modulation of learning and decision-making (1). In this view, the noradrenergic system controls the exploration-exploitation trade-off, whereby high tonic noradrenaline levels boost behavioral variability. While this is detrimental to performance in static environments, it is adaptive in the presence of hidden environmental changes, as were present in our foraging task, by promoting exploration of alternatives (1, 46, 51). Animal behavior becomes more variable during periods of high tonic firing of the locus coeruleus in perceptual tasks in static environments (51, 52) and in value-based choice in changing environments (53, 54). In particular, chemogenetic stimulation of locus coeruleus tonic activity increased decision noise during a foraging task (53), same as in the present Fig. 4. These findings in animals are in line with our current results in humans.
One study reported a decrease in random exploration under atomoxetine during a gambling task (55). This finding appears to be at odds with the above animal work and the increase in decision noise found in the present study. One possibility is that the predominant effect of atomoxetine on tonic versus phasic noradrenaline level differed between our experiments and the one from Warren et al. (55). Such differences may have occurred for several reasons including (i) the different latencies of the behavioral measurements relative to drug intake (1.5 hours in our study versus 3 hours in theirs), (ii) intersession differences in baseline arousal/noradrenaline levels, and/or (iii) interindividual differences in atomoxetine sensitivity between participants. For both our experiments, we found a robust increase of baseline pupil diameter under atomoxetine, consistent with increased tonic noradrenaline levels (30, 31). The decreased exploration reported previously (55) may have resulted from a predominant increase in phasic noradrenaline release (1) or from a (tonic or phasic) increase in dopamine, which other studies have found to reduce decision noise (56). It will be important to differentiate between noradrenergic and dopaminergic effects on choice variability in future work.
In our reward integration model, decision noise affected the reward-dependent component of behavior before its combination with WSLS. This was motivated by model comparisons, indicating that noise should be applied before, not after, the combination of the reward-dependent choice probability with the WSLS heuristic (fig. S12D). This observation is largely consistent with recent evidence pointing to reward integration, rather than response selection, as the dominant source of behavioral variability (57). Separating between noise at each integration step and noise at the transformation from integrated reward [“local fractional income” (LFI)] into choice probability would require a different approach. Future work should further constrain the locus of the catecholaminergic noise boost.
The observed drug effects on functional connectivity may have resulted from interactions between the cholinergic and catecholaminergic systems. For example, activity in these systems’ brainstem centers is correlated (32). Interactions between both systems, however, would not predict the pronounced differences in the physiological and behavioral effects of the catecholaminergic and the cholinergic manipulations we observed here. Our independent pharmacological interventions have likely bypassed the known functional coupling at brainstem level. It is possible that the interactions at the level of the systems’ cortical target networks may be negligible.
Our multiscale circuit modeling shows that subtle differences in the effects of catecholamines and acetylcholine at the cellular level [e.g., gain increases of different magnitude (1, 12, 15)] can combine to yield context-dependent dissociations at the level of large-scale cortical network dynamics. This principle accounts for the context-dependent (task versus rest) double dissociation between the modulatory effects observed here. Our mechanistic insights are consistent with single-cell physiology (1, 15, 24, 26, 39). Specifically, the conclusion that catecholamines and acetylcholine both increase overall gain (and hence E/I) but with different magnitudes is supported by the observation that noradrenaline and acetylcholine differentially modulate E/I in rodent auditory cortex (24). Acetylcholine suppresses stimulus-evoked, inhibitory transients in pyramidal cells (27, 58), while noradrenaline suppresses ongoing inhibition in a more persistent fashion (26). Such synaptic and cellular differences can translate into a differential net gain increase of the whole microcircuit, with a smaller net gain increase under acetylcholine, as described by the nodes of our neural mass model. The idea of a smaller effect of acetylcholine on gain (and hence E/I) is also consistent with the absence of a cholinergic effect on perceptual variability during ambiguous stimulation.
Our second conclusion of reduced intracortical coupling under acetylcholine is also consistent with the reduction of intracortical (lateral and/or feedback) signaling that has been observed in visual and auditory cortex (18–20), possibly mediated by muscarinic receptors (20). At the computational level, this conclusion aligns well with the idea that acetylcholine reduces the impact of prior knowledge (feedback and lateral intracortical signaling) relative to incoming evidence (bottom-up signaling) (10). However, evidence from prefrontal cortex suggests that acetylcholine can also increase synaptic efficacy on recurrent intracortical connections through both nicotinic and muscarinic receptors (59). Further work is needed to elucidate the synaptic basis of the cholinergic effects observed here.
Our insights shed new light on some inconsistencies in the pharmacological effects on functional connectivity as gauged with neuroimaging (5). One positron emission tomography study found an increase in functional connectivity during a task but decrease during rest under clonidine (an α2-adrenergic autoreceptor agonist that reduces noradrenaline release) (9), similar to the context dependence in the present study. A functional magnetic resonance imaging (fMRI) study found a decrease of resting-state functional connectivity under atomoxetine (6), in contrast to the weak effect during rest in our present measurements (Fig. 1C, left). Our modeling demonstrates that subtle differences in the baseline state of the system [i.e., location on the (bE,bI)-plane] can lead to qualitatively different effects of the same gain increase on functional connectivity. Such shifts in baseline state may result from differences in environmental factors, age, or baseline arousal.
Resting-state functional connectivity is widely used in clinical neuroscience, with a focus on the development of biomarkers for neuropsychiatric disorders (60). The behavioral context dependence of the neuromodulatory effects we uncovered here implies that resting-state measurements alone lack a critical dimension: The comparison between rest and task contexts was necessary to uncover the specific impact of neuromodulators on cortical dynamics. It is likely that the same holds for other classes of neurotransmitters and their disturbances in brain disorders.
In summary, we have pinpointed candidate circuit mechanisms for the distinct catecholaminergic and cholinergic shaping of large-scale cortical network activity. Our results can guide future work into the underlying cellular and molecular mechanisms in animals and set the stage for the development of noninvasive biomarkers for the integrity of neuromodulatory systems in humans.
METHODS
Pharmacological MEG experiment (resting-state and continuous perceptual choice task)
Participants
Thirty healthy human participants (16 females, age range of 20 to 36 years, mean of 26.7) participated in the study after informed consent (exclusion criteria in table S1). The study was approved by the ethics committee of the Medical Association Hamburg. Two participants were excluded from the analyses, one due to excessive MEG artifacts and the other due to not completing all three recording sessions. Thus, we report the results from n = 28 participants (15 females).
The present dataset was also used in a previous report (28), which focused on the effects of both drugs (see below) on long-range temporal correlations in local activity fluctuations. The present analyses of the correlations between these fluctuations across different cortical regions are independent from the results presented in this previous work. A different version of the behavioral result shown in Fig. 3A was also shown in the previous paper (28).
Experimental design
General protocol
We manipulated the levels of catecholamines (noradrenaline and dopamine) and acetylcholine through pharmacological intervention (Fig. 1A). Each participant completed three experimental sessions, consisting of drug or placebo intake at two time points; a waiting period of 3 hours; and an MEG recording session. During the recordings, participants were seated on a chair inside a magnetically shielded chamber. Each recording session consisted of six measurement blocks with different behavioral tasks (see below). Each block was 10 min long and followed by a short break of variable duration.
Pharmacological intervention
We tested for the effects of two different drugs in a double-blind, randomized, placebo-controlled, and crossover experimental design. We used the selective noradrenaline transporter inhibitor atomoxetine to boost the levels of catecholamines (noradrenaline and dopamine (3, 29)). We used the cholinesterase inhibitor donepezil to boost acetylcholine levels. A mannitol-aerosil mixture was administered as placebo. The dosages for both drugs were chosen to be below common clinical steady-state dosages and in accord with previous fMRI work, showing clear effects of the same dosages on cortical processing (6, 18): 40 mg for atomoxetine (clinical steady-state dose for adults: 80 mg) and 5 mg for donepezil (common clinical entry dose). All substances were encapsulated identically to render them visually indistinguishable. Peak plasma concentrations are reached ~3 to 4 hours after administration for donepezil (61) and 1 to 2 hours after administration for atomoxetine (62). To maximize plasma drug levels during MEG, participants received two pills in each session, 3 and 1.5 hours before MEG (Fig. 1A): placebo (t = −3 hours) followed by atomoxetine (t = −1.5 hours) in the ATOMOXETINE condition, donepezil (t = −3 hours) followed by placebo (t = −1.5 hours) in the DONEPEZIL condition, and placebo at both times in the PLACEBO condition. The three sessions were scheduled at least 2 weeks apart to allow plasma levels to return to baseline [plasma half-life of atomoxetine: ~5.2 to 21.6 hours (62); half-life of donepezil: ~70 hours].
Behavioral tasks
Within each session (and each of the above-defined pharmacological conditions), participants alternated between three different behavioral conditions, all entailing absent or continuous sensory input (two runs per 10 min per condition), here referred to as REST, TASK, and TASK-PRESSING (Fig. 1A, right; see also movie S1). REST and TASK were steady-state conditions (absent or minimal variations in sensory input or motor output) tailored to quantifying intrinsic correlations between fluctuations in cortical activity. TASK-PRESSING was used to validate the behavioral results from the TASK condition. During REST, participants were instructed to fixate a green fixation disk (radius = 0.45° visual angle) in the center of an otherwise gray screen. During TASK and TASK-PRESSING, participants viewed a perceptually ambiguous three-dimensional structure-from-motion stimulus, which was perceived as a rotating sphere (63). The stimulus subtended 21° of visual angle, consisted of 1000 dots (500 black and 500 white, radius: 0.18° of visual angle) arranged on a circular aperture presented on a mean luminance gray background and a green fixation dot in the center. In TASK, participants were instructed to count the number of changes in the perceived rotation direction and verbally report the total count at the end of the run. In TASK-PRESSING, the participants were instructed to press (and keep pressed) one of two buttons whenever they perceived a change in the rotation direction. The order of the conditions was as follows for 18 of 28 participants: (i) REST, (ii) TASK-PRESSING, (iii) TASK, (iv) REST, (v) TASK-PRESSING, and (vi) TASK. For 10 of 28 participants, the order was reversed: (i) TASK, (ii) TASK-PRESSING, (iii) REST, (iv) TASK, (v) TASK-PRESSING, and (vi) REST. The experiment was programmed in the MATLAB (The MathWorks Inc., Natick, USA) using the Psychophysics Toolbox extensions (PTB-3) (64).
Data acquisition
MEG was recorded using a whole-head CTF 275 MEG system (CTF Systems Inc., Canada) at a sampling rate of 1200 Hz. In addition, eye movements and pupil diameter were recorded with an MEG-compatible EyeLink 1000 Long Range Mount system (SR Research, Osgoode, ON, Canada) and electrooculogram, and vertical, horizontal, and radial electrooculography were acquired using Ag/AgCl electrodes.
Pupil and behavioral data analysis
The pupil diameter recordings were preprocessed as follows: Eye blinks and eye movements were identified using the manufacturer’s default routines, then padded (±200 ms), linearly interpolated, and band-pass filtered using a second-order Butterworth filter with a passband from 0.01 to 10 Hz. Next, the effect of blinks and saccades on pupil diameter was estimated through deconvolution and removed by means of linear regression (65). The mean pupil diameter was computed in a baseline interval from 6 to 3 s before the start of each recording block and for all conditions and averaged across the two corresponding blocks. In some cases, pupil diameter was not recorded, or the signal was too noisy. If this was the case for both blocks of a session, then the corresponding participant was not included in the respective analysis. The following number of participants was excluded/included per combination of conditions: during REST-PLACEBO (N = 0/28), REST-ATOMOXETINE (N = 0/28), and REST-DONEPEZIL (N = 2/26) and during TASK-PLACEBO (N = 0/28), TASK-ATOMOXETINE (N = 0/28), and TASK-DONEPEZIL (N = 1/27). The behavioral data from TASK and TASK-PRESSING were averaged across the two blocks, resulting in N = 28 for all drug conditions for TASK. In the case of TASK-PRESSING, one participant was excluded because of missing triggers in the atomoxetine condition, resulting in N = 27.
MEG signal processing
The MEG signal processing pipeline described below is also illustrated in fig. S2A and entailed the following steps.
Preprocessing
The sensor-level MEG data were first preprocessed: Strong transient muscle artifacts and squid jumps were detected through visual inspection and semiautomatic artifact rejection procedures, as implemented in the FieldTrip toolbox (66) for MATLAB. To this end, data segments contaminated by such artifacts (±500 ms) were removed from the data (across all channels). Subsequently, the data were downsampled to 400 Hz and split into low-frequency [[0.5 to 2] to 40 Hz); the lower cutoff was variable across (but identical within) participants at 0.5, 1, or 2 Hz] and high-frequency (>40 Hz) components using a fourth-order Butterworth filter. Both signal components were separately submitted to independent component analysis using the FastICA algorithm (67). Artifactual components (eye blinks/movements, muscle artifacts, heartbeat, and other extracranial artifacts) were identified on the basis of three criteria: power spectrum, fluctuation in signal variance over time (in bins of 1-s length), and topography. Artifact components were reconstructed and subtracted from the raw signal, and low and high frequencies were combined into a single dataset. On average, 20 (±14) artifact components were identified for the low frequencies and 13 (±7) artifactual components were identified for the high frequencies. There were no statistically significant differences in the number of rejected artifactual components [for the low-frequency data: atomoxetine versus placebo (REST): T = 0.61, P = 0.55; donepezil versus placebo (REST): T = 0.43, P = 0.67; atomoxetine versus placebo (TASK): T = 0.95, P = 0.35; donepezil versus placebo (TASK): T = 0.96, P = 0.18; all two-sided paired t tests). All preprocessing was performed blind with respect to the drug labels.
Spectral analysis
From the cleaned MEG signal, spectral estimates were obtained using Morlet’s wavelets, similar to previous reports (33, 68)
| (1) |
We constructed wavelets for 17 logarithmically spaced (base 2) center frequencies, ranging from 4 to 64 Hz. In keeping with previous works (33, 68), the spectral bandwidth was set to half of an octave (f/σt~5.83). Spectral estimates were obtained for consecutive, half-overlapping segments of length ±3σt. Segments that contained artifactual samples (see the “Preprocessing” section) were omitted from the analysis.
Source analysis
For the main analyses, we projected the sensor-level signal onto 400 vertices located on the cortical surface, resulting in an estimated source level signal Xsrc(r, t, f). To this end, we estimated source-level activity using “linear beamforming” (69), separately for each participant, recording session and block. For each source location r and frequency f, a spatial filter A(r, f) was computed according to
| (2) |
where L was the magnetic lead field, T denoted as matrix transpose, and Creal(f) was the real part of the (complex-valued and regularized) cross-spectral density (CSD) matrix of the sensor-level data for frequency f. A(r, f) contained three orthogonal projections. We used the singular value decomposition of the CSD matrix to determine the direction of the dipole maximizing power (i.e., the first eigenvector) at location r. We then computed the corresponding spatial filter for this direction, henceforth referred to as B(r, f). This filter was used to project the sensor-level data X(t, f) onto that dominant dipole, as follows
| (3) |
where Xsrc(r, t, f) denoted as the complex-valued, source-level spectral estimates for location r. Before computing the spatial filter, the CSD matrix was regularized with the mean of its diagonal multiplied by a scaling parameter α. For the results shown in the main section of this article, this parameter was chosen to be α = 0.3 [see fig. S5 (D to F) for alternative values of α].
Orthogonalized power envelope correlations
Interregional correlations were computed as the correlations of the power estimates at carrier frequency f between two regions i and j, across all non-artifactual segments. To reduce spurious correlations arising from instantaneous signal leakage, we used a procedure established previously (33). Specifically, we orthogonalized each signal Y with respect to signal X according to
| (4) |
where Y⊥X(t, f) was the signal Y(t, f) orthogonalized with respect to signal X(t, f) and * was the complex conjugate. Next, the absolute value was taken, and the resulting signal was squared, yielding source-level power envelopes, and log-transformed to render the distribution more normal. The orthogonalization was performed in two directions, Y⊥X(t, f) and X⊥Y(t, f). Correlation coefficients were computed for both directions, and the resulting (Fisher transformed) values were averaged. Doing this for all pairs of source locations and for each frequency band resulted in a correlation matrix of size 400 × 400 for each of the 17 carrier frequencies. In what follows, we refer to these correlation matrices as “functional connectivity (FC)” matrices.
To compare the empirical results to the results obtained from simulations of a neural mass model (see computational modeling below), we repeated the above-described procedure for computing source-level FC matrices, but now at a coarser granularity. To this end, we selected the 76 cortical regions of the Automated Anatomical Labeling (AAL) atlas (70), excluding the cerebellum and subcortical regions (see table S2 for included regions). Source locations were first arranged on an equally spaced grid (of 4-mm by 4-mm by 4-mm resolution) covering the entire brain, and each grid point was either assigned to 1 of the 76 selected cortical AAL regions or omitted from further analysis. For each of the vertices that were assigned to 1 of the 76 AAL regions, frequency-specific source-level estimates for each time point Xsrc(r, t, f) were computed following the procedure outlined above. Next, for each source location within region i (with i∈ {1,…,76}), we computed its average orthogonalized power envelope correlation to all vertices of region j (after Fisher transformation). This was repeated for all vertices of region i after which the correlation values were again averaged across all vertices within region i. This procedure was repeated for all 76 regions, resulting in a 76 × 76 FC matrix for each of the 17 carrier frequencies.
Quantification of the topology of MEG correlation structure
Degree centrality
We computed frequency-resolved degree centrality k(f) (i.e., collapsed across all nodes) and local degree ki(f) for each of the i = 1…400 source locations (fig. S2, B and C). Degree is defined by the number of edges that connect a given node to all other nodes in the network (71). To this end, the FC matrices of all participants (400 × 400 × 28) were first submitted to a procedure described previously (6, 33). For each connection between nodes i and j, where i = 1…400 and j = 1…400, we assessed whether a connection was present as follows: A connection was determined to be present if the correlation between i and j was significantly larger (P < 0.05, two-sided t test) than the correlations from i to all other nodes or from j to all other nodes. In case of a present connection, the corresponding entry in the adjacency matrix A(i, j) was set to 1. If no connection was present, then A(i, j) was set to 0. This was repeated for all possible pairs of vertices, and the full adjacency matrix was computed. From this, we computed degree by
| (5) |
where N denoted the number of cortical vertices (N = 400).
Statistical tests of MEG effects
Cortex-wide changes in cortical correlations
We adopted a previously described two-stage procedure for an unbiased statistical assessment of cortex-wide changes in power envelope correlations (68). The procedure is illustrated in fig. S3 (A to C). The rationale behind the analysis was as follows: Both neuromodulator classes (catecholamines and acetylcholine) might, in principle, increase correlations between some pairs of areas and, at the same time, suppress correlations between other pairs of areas (13). In this case, drug effects might cancel when averaging correlations indiscriminately across all area pairs and comparing average FC between conditions. Instead, our procedure first identified any pairs exhibiting drug-induced increases or decreases above a certain threshold and then tested whether the fraction of these pairs was significantly different from what would be expected by chance, separately for pairs with increased and decreased correlations. This procedure was repeated across a wide range of frequencies, yielding the spectra of drug effects shown in Fig. 1E.
For each center frequency f, we statistically compared the Fisher-transformed FC matrices, across participants, between the two drug conditions and placebo, using a two-sided paired t test. Then, we counted the number of significantly positively (P < 0.05 and T > 0) and the number of significantly negatively altered correlations (P < 0.05 and T < 0). The resulting value was divided by the number of region pairs M (with M = N × N − N, where N = 400 or 76; see above) to obtain the fraction of significantly altered correlations for both effect directions. This procedure was repeated for all 17 frequencies bands (fig. S3). We used a single threshold permutation procedure to derive P values that accounted for multiple comparisons across frequencies (72). For each of Np = 10,000 permutations, the experimental labels (drug conditions) were randomly reassigned within participants, and the aforementioned procedure was repeated. This resulted in a Np × 17 matrix for both effect directions (significantly increased and significantly decreased correlations). Next, for each permutation, the maximum value across all frequencies (independently for increased and decreased correlations) was determined, yielding a maximum permutation distribution. To derive P values, the empirical results were compared to this maximum permutation distribution. To test the robustness of the obtained results, we repeated the procedure described above using various alpha values for the initial paired t test, ranging from α = 0.01 to α = 0.10, which led to numerically different but qualitatively similar results (fig. S5, B and C).
Significant alterations in the correlations between two regions can be achieved in different ways. A decrease in correlations, for instance, can mean that a positive correlation becomes weaker or that a negative correlation becomes more negative. However, only the former would qualify as a meaningful reduction in correlation, whereas the latter correlation gets numerically smaller (i.e., more negative) but stronger in terms of the linear dependence between two signals. Hence, a “significant decrease/increase” does not always carry the same meaning. In this dataset, the number of positive correlations far outnumbered the number of negative correlations: In the alpha and beta frequency range, where the main effects for atomoxetine and donepezil are observed, more than 90% of all connections were positive (across all blocks and contexts; placebo only). While it is possible that changes in the few negative connections contribute substantially to any observed overall change in correlation, we here interpret an increase (decrease) in correlation in terms of a positive correlation becoming stronger (weaker).
Cortex-wide changes in local cortical variability
Changes in the correlation between two signals can be driven by changes in their covariance (numerator of correlation coefficient) and changes in the variance of one or both of the signals (denominator). To rule out this second possibility, we tested for drug-related changes in the variance of local power envelopes across frequencies (fig. S5A). To this end, we have adopted a procedure similar to the one used to assess changes in cortex-wide activity correlations. First, we computed the variance of the power estimates across half-overlapping temporal segments (see spectral estimation), separately for each of the 17 carrier frequencies. Next, we counted the fraction of nodes that exhibited significantly altered variance, separately for increases and decreases. We used the same permutation procedure described above to derive corresponding permutation distributions from which P values were computed (two-sided single threshold permutation test). Analogous to the “fraction of significantly altered correlations,” this procedure yielded, per frequency band, the fraction of vertices (nodes) with significantly positively or negatively altered variance.
Peak frequency analysis (MEG)
To estimate the peak frequencies of alpha-band activity (~10 Hz) in the MEG data, we first removed the arrhythmic component from the source-level power spectra. To this end, we used the “spectral parametrization” algorithm (73) implemented in the “fooof” toolbox. We modeled each power spectrum (computed via MATLAB’s built-in “pwelch” function with 50% overlap and a frequency resolution of 0.05 Hz) as a combination of periodic components (modeled as Gaussians defined via three parameters: width, height, and center frequency) and an arrhythmic component (modeled as a Lorentzian function with an offset and an exponent; note that we set the knee parameter to 0 for the present analysis). To constrain the fitting algorithm, the maximum number of possible peaks in each spectrum was set to 6, a minimum peak height of 0.05 was assumed, and the minimum and maximum bandwidth of each peak was defined as 1 and 8 Hz, respectively. We fitted the model to the power spectra (from 3 to 40 Hz) of all 76 nodes of the cortical AAL nodes and removed the arrhythmic component. We subsequently identified peaks in the residual fitted power spectra through MATLAB’s built-in “findpeaks” algorithm within the alpha range (6 to 14 Hz). In case only one peak was found within this range, the location of the peak (in hertz) was defined as the peak frequency. In case of two or more peaks, peak frequency was defined as the weighted average of the peak locations (in hertz), with the contribution of each peak being determined by its relative height.
Cortical circuit modeling
Large-scale neural mass model
Single-node dynamics
We simulated neural activity using a population firing rate model based on the Wilson-Cowan (WC) equations (36, 74). Each local WC node consists of an excitatory and an inhibitory neuronal population (Fig. 2A). The dynamics of the E and I populations of each node are governed by the following stochastic differential equations
| (6) |
| (7) |
where E and I represent the firing rates of excitatory and inhibitory populations, respectively. The model parameters were chosen to generate neural dynamics similar to those observed with MEG, with a spectral peak in the alpha range (~7 to 14 Hz; fig. S6E). The local synaptic weights interconnecting the excitatory and inhibitory populations were given as wEE = 12, wIE = 16, wII = 4 , and wEI = 12. bE and bI represent external background inputs to the excitatory and the inhibitory, respectively, ∆bE, I represents task-induced input (∆bE = ∆bI = 0, for resting state), and η was uncorrelated Gaussian noise with amplitude equal to 0.005. Time constants were set to τE = 9 ms and τI = 18 ms for excitatory and inhibitory populations, respectively. The (nonlinear) transfer function converting input currents into output firing rates, σ(u), was chosen to be a sigmoid
| (8) |
where g determined the slope of the input-output function for both excitatory and inhibitory populations (i.e., gain of the node).
The solutions (E*, I*), or fixed points, of the coupled Eqs. 6 and 7, were given by E* = σ(wEEE* − wEII* + bE) and I* = σ(wIEE* − wIII* + bI), yielding solutions depending on the external inputs (bE, bI), which are the bifurcation parameters of the system. In the (bE, bI) parameter space, we observed a region of noise-driven oscillations (i.e., a spiral, damped oscillations that, in the presence of noise, result in noisy oscillations) and a region of sustained oscillations (i.e., a limit cycle) (fig. S6A).
Two coupled nodes
We first studied the effect of gain modulation on correlations during REST and TASK in a minimal network composed of two WC nodes (Fig. 2B, left). This step will provide intuitions before studying the whole-brain network composed of 76 nodes interconnected through a structural connectome. Let the excitatory populations of the nodes be connected through a reciprocal coupling c (in the two-node model, c = 1; see below for cortex-wide model), the firing rates of node 1 evolve as
| (9) |
| (10) |
and analogously for the firing rates, E2 and I2, of node 2.
To study the correlations between nodes in the parameter space, we used a linear noise approximation described in detail in the Supplementary Materials. Using this approximation, we studied how changes in gain, i.e., g → g + ∆g, and inputs, i.e., (bE, bI) → (bE + ∆b, bI + ∆b), change the correlation between the two excitatory populations both during REST (∆b = 0) and TASK (∆b ≠ 0). In this way, we can test hypotheses on the parameter changes induced by ATOMOXETINE and DONEPEZIL, assuming that TASK changed the background inputs bE and bI and the drugs changed g. Note that in the case of the two-node model, the task-related change of the background inputs was equal for E and I, i.e., ∆bE = ∆bI = ∆b.
In summary, the change in correlation between excitatory populations during REST was given as
| (11) |
and the change in correlation between excitatory populations during TASK was given as
| (12) |
Figure 2C maps the change of correlations during REST under gain modulation in the (bE,bI)-plane. The combined effect of the drugs on parameters bE and bI and the effect of TASK were obtained by translating the state of the system in this map.
Cortex-wide model
To directly compare the computational model to the empirical results, we simulated a cortex-wide variant of the model. For each of the 76 cortical AAL nodes, the dynamics were governed by the following differential equations
| (13) |
| (14) |
where i, j ϵ {1,2, …,76}. The long-range cortical connectivity between all possible pairs of regions, Cij, was given by a structural connectivity matrix used in previous studies [e.g., (75)] and was estimated by means of diffusion tensor imaging. Details can be found in the respective publications. The connectivity matrix Cij was scaled by the global coupling parameter c. For the simulation, Eqs. 13 and 14 were integrated using the Euler method with dt = 0.01.
The model was run for a wide range of background inputs to excitatory (bE) and inhibitory populations (bI). To assess activity correlations (functional connectivity) in the model, we computed all-to-all (76 × 76) pairwise correlations between the raw time series of excitatory firing rates Ei. The model was simulated, for a total of 58.5 s for each parameter combination before each run, initial conditions were randomized, and the first 1.8 s were excluded from further analysis to avoid transient effects due to the initial conditions. All simulations and corresponding analyses were carried out in MATLAB 2019b.
Identification of the oscillatory regime in the cortex-wide model
In all model-based analyses, we assume that the (healthy) human brain never resides in a dynamical regime of sustained oscillations (fig. S6A, top; see also the Supplementary Materials). We therefore identified, and excluded, parameter combinations resulting in sustained oscillations in the cortex-wide model (see above). To identify parameter combinations where simulated population activity settled in the oscillatory regime, the cortex-wide model was simulated without noise (i.e., η = 0) for a total of 58.5 s (plus 1.8 s of initialization, as outlined above). Next, for nonoverlapping segments of 27 ms, the maximum and minimum of rE was computed. In a regime of noise-driven (damped) oscillations, the activity relaxes back to a fixed point over time (fig. S6A, middle and bottom). Hence, the computed maximum and minimum should converge on the same value. In a regime of sustained oscillations, on the other hand, the maximum and minimum will remain different throughout the entire simulation (fig. S6A, top). Consequently, the regime was defined as nonoscillatory or noise driven if (i) the maximum and minimum were identical at any point in time or (ii) the difference between maximum and minimum decreased monotonously over time (indicative of a damped oscillation); if none of the two were true, then the signal was defined as a sustained oscillation (see the Supplementary Materials).
Model fitting procedure
We fitted the free parameters of the cortex-wide model through an iterative procedure. The purpose of this procedure was to identify two working points, mimicking the two behavioral conditions (REST and TASK). To this end, we estimated the global coupling parameter α. This end, we simulated the cortex-wide model (76 regions) over a range of 41 different coupling parameters α (with α ϵ {0,0.05, …,2}) and across 61 × 61 combinations of background inputs (with IE ϵ { − 4, − 3.9, …, − 1} and II ϵ { − 5, − 4.9, …, − 2}). We then estimated the similarity of the simulated functional connectivity matrix FCsim and the empirical functional connectivity matrix FCemp (rest and placebo only; averaged across frequencies that showed significant changes for both drugs; see Fig. 1E), separately for each combination of IE and II, by means of a distance metric δ based on Pearson correlation (76)
| (15) |
where ρFCsim,FCi,emp was the correlation (i.e., pattern similarity) between the empirical FC matrix for subject i (averaged across frequencies, with i ϵ {1,2, …,28}) and the simulated FC matrix and 〈 〉 denotes the average across all possible connections. We averaged the resulting distance values δ across all external background inputs (bE and bI) while omitting parameter combinations where the network activity settled into a regime of sustained oscillations (see above). This resulted in a mean distance 〈δ〉 for each level of global coupling α (fig. S6C). In addition, we repeated the procedure but instead computed Pearson correlation between FCsim and FCemp (fig. S6D). We identified the level of α, where the mean distance 〈δ〉 between FCsim and FCemp was minimized (α = 1.15). The parameter with lowest 〈δ〉 also yielded a high correlation between FCsim and FCemp (fig. S6D).
After having fixed the global coupling parameter, we aimed to identify the combination of bE and bI for each individual participant, which resulted in the highest similarity between FCsim and FCemp during REST and PLACEBO (i.e., lowest distance). To this end, we first identified the combinations of bE and bI where the distance between FCsim and FCemp was below the 2.5th percentile. The resulting binary matrix was then submitted to a clustering procedure (using MATLAB’s “bwlabel” function), and the single largest cluster was extracted. This was to reduce the influence of spurious correlations on the fitting procedure. Next, the geometric center of the largest cluster was computed and defined as the best fitting combination of IE and II, yielding a working point for RESTsim. This procedure was repeated separately for each of the 28 participants (fig. S6G). To determine the corresponding TASK parameter TASKsim, we assumed that the constant visual stimulation during TASK increases both excitatory (bE) and inhibitory drive (bI), consistent with electrophysiological recordings in rodent visual cortex V1 (see the Supplementary Materials) (39). Thus, to simulate TASK, we increased the background input to both excitatory and inhibitory populations, i.e., bE and bI. We chose to increase background input to inhibitory populations by ∆bI = 0.475 and to excitatory population by ∆bE = 0.25 (Fig. 2, D and E, cortex-wide model), homogeneously across all nodes.
Parameters yielding qualitative correspondence between model and MEG data
To identify combinations of changes in gain and changes in global coupling where the difference in the model’s activity correlations was consistent with the empirically observed drug effects (Fig. 2, F and G, and fig. S8), we first averaged the simulated functional connectivity matrices across the upper triangular part, for each combination of gain and global coupling, yielding the mean functional connectivity 〈FCsim〉. Next, we searched for combinations of changes in gain (∆g) and global coupling (∆c), where all of three following conditions were satisfied (Fig. 2G, in red; similarly fig. S8, bottom row). For model correspondence with the observed effects of atomoxetine
(1) ∣〈FCSim, ∆g∆c, Rest〉 − 〈FCSim, Pbo, Rest〉∣ < c
(2) 〈FCSim, ∆g∆c, Task〉 − 〈FCSim, Pbo, Task〉 > c
(3) (〈FCSim, ∆g∆c, Rest〉 − 〈FCSim, Pbo, Rest〉) − (〈FCSim, ∆g∆c, Task〉 − 〈FCSim, Pbo, Task〉) < − c
where c was a criterion value and the subscript “Pbo” denotes the placebo state, with ∆g = ∆c = 0. Hence, condition (1) describes the absence of an effect (or only a small effect) on mean FC during REST, (2) the atomoxetine-related increase of FC during TASK, and (3) the corresponding behavioral context-dependence.
For model correspondence with the observed effects of donepezil, we identified the regions of the parameter space where the conditions below were satisfied (Fig. 2G, in blue)
(1) 〈FCSim, ∆g∆c, Rest〉 − 〈FCSim, Pbo, Rest〉 < − c
(2) ∣〈FCSim, ∆g∆c, Task〉 − 〈FCSim, Pbo, Task〉∣ < c
(3) (〈FCSim, ∆g∆c, Rest〉 − 〈FCSim, Pbo, Rest〉) − (〈FCSim, ∆g∆c, Task〉 − 〈FCSim, Pbo, Task〉) < − c
where (1) describes the donepezil-related decrease in correlation during REST, (2) the absence (or weaker) effect during TASK, and (3) the corresponding observed behavioral context dependence. For Fig. 2G and fig. S8, we used a criterion value of c = 0.0015, which corresponds to a 7.6% change in mean correlation relative to the mean correlation of the simulated REST and a 12.1% change relative to the mean correlation of the simulated TASK. For comparison, the average atomoxetine-related increase in the MEG data during TASK was 16.3% (averaged across 9.51 to 16 Hz) and the average donepezil-related decrease was 14.4% (averaged across 9.51 to 19.0 Hz).
Model with heterogeneous task-related inputs
In an additional variant of the neural mass model, we added task-related inputs only to a subset of nodes, rather than to the entire network. To this end, we first identified the AAL nodes that exhibit a significant (P < 0.05, two-sided paired t test) reduction in power during TASK compared to REST (averaged across the frequencies where we observed significant changes in correlations for both drugs; Fig. 1E). Next, for each subject’s combination of bE and bI (obtained from fitting the model to REST), we added an additional task-related input ∆bE and ∆bI to the nodes identified in the previous step. We simulated this version with two different task-related input strengths: (i) ∆bI = 0.475 and ∆bE = 0.25 (fig. S10A; similar to the homogeneous version of the model) and (ii) ∆bI = 0.50 and ∆bE = 0.30 (fig. S10B).
Local microcircuit models
Microcircuit model of local node
To assess how changes in neural gain can be achieved through specific changes in synaptic weights, we simulated a model of a canonical cortical microcircuit, as a conductance-based neural network composed of 400 leaky integrate-and-fire units (20% inhibitory). Model equations and parameters follow (44), with some modifications as mentioned below. The model architecture is depicted in Fig. 2H. The membrane potential dynamics of the excitatory units below threshold were governed by
| ) | (16) |
Here, Isyn(t) denotes the total synaptic current, which was composed of two glutamatergic excitatory currents [with AMPA and NMDA (N-methyl-d-aspartate) components] and GABAergic inhibitory currents. External input and external noise to the network were mediated exclusively via AMPA receptors. Baseline parameters were identical to the original version (44), with the exception of gI → E, GABA = 1.99 nS (conductance of inhibitory to excitatory synapses) and gext → E, AMPA = 2.5 nS (synaptic conductance of external input to excitatory neurons). Moreover, the rate of the external Poisson input to excitatory and inhibitory neurons was changed to vext = 881 Hz (originally vext = 2400 Hz). From these baseline values, we parametrically scaled the conductance parameters gE → E, AMPA and gI → E, GABA [AMPA-mediated recurrent excitation and GABA (γ-aminobutyric acid)–mediated feedback inhibition, respectively] to achieve plausible spontaneous dynamics (see the Supplementary Materials and fig. S9 for details). After simulating the network for 3 s, we selected parameters for gE → E, AMPA (0.1625 nS) and gI → E, GABA (6.97 nS), where the network showed a population firing rate of 4.14 Hz and low spike count correlations of 0.05 (see fig. S9 for alternative values). Next, we presented the network with stimuli in form of external excitatory input (added to the background input) to all excitatory cells, mediated through AMPA receptors, and assessed the effect on resulting excitatory population firing rate (25). In visual cortex, neurons respond to stimuli with increasing contrast with higher firing rates. This relation between a neurons output and the visual input strength is well-described by a hyperbolic ratio function known as the Naka-Rushton function
| (17) |
where R(C) is the firing rate at input contrast C, Rmax is the response gain, S reflects the level of the spontaneous (background) activity, and C50 is the stimulus strength that yields a firing rate at half the maximum. Using this equation, we generated a set of stimuli (with varying “contrast,” i.e., varying levels of C) that were transformed into firing rates of different frequency and were subsequently fed into the network as an AMPA-mediated excitatory Poisson input. The parameters used in the current study were identical to the parameters used in a previous theoretical study on the effects of excitation and inhibition on response gain of single neurons (25): Rmax = 2000 Hz, C = 20.133, n = 1.2, and S = 0. This approach allowed us to measure the response of a neural population to inputs of varying contrast strength, which is typically depicted as a contrast-response curve (Fig. 2H, right). To assess the effect of excitation-inhibition ratio on the shape of the contrast-response curve, we decreased the feedback inhibition in the model by adjusting gI → E, GABA (see the Supplementary Materials for details). Using nonlinear least squares estimation, we fitted the hyperbolic ratio function (Eq. 17), with four free parameters (Rmax, , S, and n), to the resulting contrast-response curves. This yielded, among others, response gain parameters (Rmax) for different levels of feedback inhibition (Fig. 2H, right). The network was simulated for 2.5 s per parameter combination, with continuous external stimulation. All simulations and analyses were carried out in Python 2.7.15 using the Brian spiking neural network simulator (version 1.4.4) (77), the Elephant toolbox for Python, and custom code. The Python code for the model simulations was adapted from publicly available code (78).
Decision circuit
To understand how the increase in reported perceptual transitions during ambiguous visual stimulation under atomoxetine (Fig. 3A and fig. S11) could be related to changes in synaptic activity, we extended the above neural circuit by equipping the model with two excitatory populations, which competed for dominance via common feedback inhibition. The synaptic equations were identical to the homogeneous microcircuit described in the previous section. Unless stated otherwise, the model architecture and parameters were identical to the original description (Fig. 3B, left) (44). The circuit consisted of N = 2000 leaky integrate-and-fire neurons, endowed with full connectivity. One thousand six hundred neurons were excitatory, and 400 neurons were inhibitory. The excitatory cells were assigned to one of the three subpopulations: two decision populations (240 neurons each), D1 and D2, as well as one nonspecific population (DN; 1120 neurons). The two decision populations were assumed to represent the populations that encode the two possible perceived rotation directions of the ambiguous stimulus. All neurons, excitatory and inhibitory, of all populations (D1, D2, DN, and I) received independent AMPA-mediated excitatory background input in the form of a Poisson spike train with a frequency of 2880 Hz. In addition, the neurons of the decision populations D1 and D2 received independent AMPA-mediated excitatory input with a mean firing rate of 55.6 Hz, which was to reflect the stimulus-related sensory input. The identical mean in input to both decision populations was to mimic the ambiguous nature of the structure-from-motion stimulus. Recurrent connections within D1 and D2 were stronger than connections within DN by a factor of w+ = 1.6. The network was simulated for 600 s, and population firing rates were estimated for time bins of 100 ms in length. Perceptual transitions in the model were defined as the time points where the firing rate of one decision population exceeded the firing rate of the other decision population, i.e., at those time points where the difference between firing rates of D1 and D2 changed in sign (Fig. 3B, right). To attenuate the effect of very fast fluctuations on the number of perceptual transitions, we low-pass filtered the firing rates of both decision populations before computing the perceptual transitions (cutoff frequency of 1 Hz). To understand the effect of excitation and inhibition on perceptual transitions, we again modified feedback inhibition by means of adjusting gI → E, GABA and computed the number of perceptual transitions for each level of feedback inhibition. For each level of feedback inhibition, the network was simulated 20 times.
Pharmacological behavioral experiment (value-based choice task)
Participants
We measured 32 participants (21 females, age range of 20 to 36, mean of 27.28) that performed two sessions of a value-based choice task (Fig. 4A and fig. S12A) after informed consent. All included participants were nonsmokers. The study was approved by the ethical committee responsible for the University Medical Center Hamburg-Eppendorf. We excluded three participants from the analysis based on foraging efficiency, which we here defined as the fraction of collected rewards over the total number of available rewards: We excluded participants whose foraging efficiency deviated more than three times the median from the median, scaled by a constant (c ≈ 1.4826, using MATLAB’s “isoutlier” function). On the basis of this criterion, the same three participants were excluded for both experimental sessions (Fig. 4D). This resulted in 29 included participants.
Experimental design
General protocol
We manipulated the levels of catecholamines (noradrenaline and dopamine) in a double-blind, randomized, placebo-controlled pharmacological intervention using atomoxetine (see above the “Pharmacological MEG experiment” section). Each participant completed two experimental sessions, consisting of drug or placebo intake, a waiting period of 1.5 hours, and performance of the behavioral task during MEG recordings. During task performance, participants were seated on a chair inside a magnetically shielded chamber, and the (visual) task stimuli were presented on a screen in front of them (Fig. 4A and fig. S12A). Because this was a standard trial-based task design entailing many sensory and motor transients, the MEG data from this task were not used for the analysis of correlations between intrinsic fluctuations in cortical activity. The MEG data will be reported in a separate paper.
Behavioral task
We used a modified version of a dynamic foraging used in a previous monkey physiology study (49). Participants chose freely between two visual target stimuli (identified by orientation and randomized by position), which were associated with different histories of monetary rewards. The sequence of events during each trial is shown in fig. S12A. Participants were asked to fixate a white box in the center of a uniform gray background. Each trial started with the presentation of the two targets (full-contrast Gabor patches with vertical or horizontal orientations) that were presented on either side of the fixation mark (eccentricity of ~8.5° and diameter of ~4.25° visual angle). The horizontal target’s (left versus right) location was randomly drawn on each trial, under the constraint that it would appear equally frequently on each side within a block of trials with equal “income ratio” (see below). After a 0.5- to 1.5-s delay, the fixation mark changed shape (from box to diamond), prompting the subject’s choice. Participants then pressed a button with their left or right index finger to choose the target at the corresponding location. After another variable delay (2 to 5 s), participants received auditory feedback on the outcome of their choice (reward or no reward) by means of a low- or high-pitched tone (low, 200 Hz; high, 880 Hz; each with duration, 150 ms). The mapping of the tones to “reward” or “no reward” was counterbalanced across participants and instructed before the start of each experimental session. Participants attempted to maximize the number of rewarding feedback tones, which was translated into a corresponding bonus payment at the end of the experiment. Participants were rewarded €0 to €20 bonus based on performance. The lower boundary was chance level performance; the maximum bonus could be earned by performing on par with an ideal observer model, which chose based on full information about the reward ratio at every trial.
If the participant had not yet responded within a deadline of 3 s, then another tone (440 Hz, 50 ms) signaled their missed response (no reward), and the trial was aborted. Targets disappeared after feedback tone so that only the fixation mark remained for an intertrial interval of 2 to 5 s, during which the participants kept fixating. The next trial started upon the new onset of the targets. Trial duration varied between 4.5 and 11.5 s plus reaction time (reaction times could range between 0 and 3 s), respectively, with an average trial duration of 8 s plus reaction time (0 to 3 s). Participants completed 525 trials in each experimental session, taking about 75 min, excluding breaks in between blocks of 100 trials.
Each target was baited with a separate Poisson process for generating rewards, under the following constraints (Fig. 4, B and C): (i) The “income” (i.e., reward) rate averaged across both targets was 0.8 rewards per trial; (ii) the ratios between the reward rates associated with each target for a given block of trials (see below) were drawn from a predefined set {7:1, 5:1, 3:1, 1:1, 1:1, 1:3, 1:5, 1:7}; (iii) a reward assigned to a target (i.e., orientation) remained available there until this target was chosen; and (iv) when a reward was available at a target, no new reward could become available there (i.e., there was never more than one reward available per target). Correspondingly, both or one or none of the targets could carry a reward in a given trial—the rewards associated with both targets were uncoupled.
The ratios between reward rates, called “local income ratios” in accordance with (49), changed between blocks of trials, without this being signaled to the participants. The block duration was sampled from a uniform distribution that ranged between 40 and 60 trials (Fig. 4C). Participants were not informed about these changes. Because of this dynamic nature of the foraging task, a successful policy is to integrate rewards earned from choosing each target, but only locally in time, over the last trials [see (49) and the “Behavioral modeling” section].
Participants were not instructed about the statistics of the process generating the rewards. They were only instructed (i) to try to earn as many reward (i.e., positive feedback tones; see above) as possible and that this would translate to a bonus payment at the end of the session and (ii) to be flexible in their behavior because the relative income of the two targets could change over time.
Pupil analysis
The pupil diameter recordings were preprocessed similar to experiment 1 (see the “Pharmacological MEG experiment” section). Mean pupil diameter was computed in a pretarget baseline interval from 500 to 0 ms before target onset. Pupil recordings were not available for four participants. Hence, the analysis was performed for the remaining 25.
Behavioral modeling
We fitted an algorithmic model of behavior to quantify the effects of atomoxetine on the different computations governing decision-making in the task. Our model, schematically depicted in Fig. 4F, extended a model previously developed to account for monkey choices in the task (49, 50). Model choices were computed as follows: (i) leaky integration of the rewards gathered from choosing each option over the recent trials; (ii) combination of the earned rewards into a relative value signal, the local fractional income (LFI); (iii) nonlinear (softmax) transformation of LFI into a probability of choosing the horizontal option; (iv) a weighted contribution of a ‘win-stay, lose-switch’ (WSLS) heuristic; and (v) a weighted contribution of general bias (preference for the horizontal target) to the final choice probability. Leaky reward integration was applied to account for rapid adaption to the hidden changes in income ratio across blocks [see above the “Experimental design” section and (49, 50)].
Please note that the WSLS heuristic had been suppressed, by design, in the monkey study introducing this task (49) through a so-called “change-over-delay” (i.e., punishment for switching targets after one choice). We did not include this change-over-delay in our task to render the foraging task more ecological. We found that participants’ behavior could be well accounted for by a linear mixture of the leaky reward integration described by steps (i) to (iii) and the heuristic from step (iv) (Fig. 4F). A model containing only the reward integration fits the data far better than a model containing only the WSLS heuristic, indicating that a reward integration mechanism was needed to account for the data (fig. S12C).
We fitted the model by minimizing the negative log likelihood between the model choice probability from step (iv) and the participants’ binary choices, giving the set of parameter values. We first found the minimum in a rough grid search. These parameter values were then used as starting point for a bounded search.
For each trial t, the model computed LIhor(t), the local income earned from choosing the horizontal option, as follows
| (18) |
where were the outcomes of horizontal choices on trials 1 : t and τ was the reward integration time constant (model leak ). Now, rewards earned from choosing the vertical option were coded as 1 and all other outcomes as 0. The same equation was used to update LIver; now, coding rewards were earned from choosing the vertical option as 1 and all other outcomes as 0.
The LFI on trial (t) LFIhor was defined as
| (19) |
LFIhor was transformed into the choice probability p(ct = hor), defined with respect to the horizontal target, through a sigmoidal (softmax) function (50)
| (20) |
where β was the inverse temperature parameter that governed decision noise, i.e., corrupting the mapping from LFI to the behavioral choice. β ranged from 0 to infinity (no noise). Depending on the outcome and the choice on the previous trial, a WSLS value was calculated for the current trial
| (21) |
where ct = 1 for horizontal choices and ct = − 1 for vertical choices at trial t. The probability of choosing horizontal, p(ct = hor), was then combined with the WSLS quantity and a general bias δ, which could range between −1 (all choices to vertical option) and 1 (all choices to horizontal option). The placement of the softmax transformation was motivated by formal comparison between two versions of the models in which the softmax was either applied before or after the integration of the WSLS term. This indicated a better fit of the model with softmax transformation before the combination with WSLS (fig. S12D).
Specifically, the choice probability for horizontal (model quantity fitted to the data) was given by
| (22) |
where p(ct = hor ∣ c1 : t − 1, o1 : t − 1) was the probability of horizontal choice on trial t (constrained between 0 and 1), given the choices made and outcomes (rewards) received from trial 1 to trial t − 1, ωWSLS was a free parameter (ranging from 0 to 1) that controlled the contribution of the WSLS heuristic to the choice probability, and δ was the bias term toward horizontal.
Logistic regression analysis of choice behavior
In a mechanistically agnostic approach complementary to the above reward integration mode, we fitted choice behavior with a logistic regression model with five regressors
| (23) |
where ct was the choice on trial t (1 or −1 for horizontal and vertical, respectively), γ and λ were parameters quantifying the lower and upper lapse rates (e.g., attention lapses or motor errors), g was the logistic function in which α was a “slope” parameter, δhist quantified the impact of previous trial history (see below) on choice, δ0 was a general bias toward horizontal parameter, and ωWSLS was the weight of the WLSLS heuristic, defined as in Eq. 21.
The history term δhist captured the impact of the choice and motor response from the previous trial and the choice outcomes (product of choice and reward) from the past n = 6 trials. Specifically, δhist was calculated as
| (24) |
with the vector ht
| (25) |
ωk was the weight parameter for the kth element of the ht vector (Eq. 25), c coded the choice (horizontal versus vertical), and o coded the choice outcome (horizontal choice rewarded = 1, vertical choice rewarded = −1, and no reward = 0). The term (bt − 1 ∙ bt ∙ ct) was introduced to capture any possible systematic tendency to repeat (or alternate) the left- or right-hand motor response from the preceding trial (1 = left, −1 = right), which was, by design, orthogonal to the vertical/horizontal target choice (see above the “Experimental design” section). The weight for this motor response repetition regressor was slightly negative on average across participants and did not differ between placebo and atomoxetine sessions (P = 0.452, two-sided paired permutation test).
The logistic regression model was fitted by minimizing negative log likelihood using MATLAB’s “fminsearchbnd” with the following bounds: the lapse rates γ and λ [0, 1], general bias δ0 [−1, 1], the weight on the WSLS-heuristic ωWSLS [0, 1], and the slope of the logistic function α [0, 100].
We estimated the time constant of the outcome history impact on current by fitting the six outcome-related weights (ω3 to ω8 , corresponding to the ot−1 to ot−6 elements of vector ht) to the following exponential function
| (26) |
where α was an offset parameter shifting the exponential function horizontally, τ was the time constant, and x was the lag (e.g., x = 1 for ω3).
Deviance between actual and reward-maximizing choice fractions
The deviance between participants’ actual and reward-maximizing choice fractions in a given block served as a model-free behavioral diagnostic of increases in decision noise. The deviance was the difference between the subject’s actual choice fraction and the choice fraction that corresponded to the generative reward ratio for a given block (Fig. 4H). The reward integrator model predicted that actual choice fractions would always deviate from reward-maximizing fractions in the direction toward 0.5. Therefore, the computed deviance needed to take the different directions of the deviance for reward rates symmetric about 0.5 into account. The direction of the deviance was upward for the reward ratio of 1:3 and downward for 3:1. We first computed the differences (D) between actual and reward-maximizing choice fractions for each of these two ratios, inverted the sign of the difference for the ratio of >0.5 (here, 3:1), and then averaged the resulting difference values across the pair. The same computation was done for all pairs of reward ratios symmetric about 0.5 (i.e., excluding the ratio 1:1), and the result was averaged across reward ratios (excluding 1:1) into the final deviance measure.
We computed this deviance measure after excluding the first block of each session reasoning that behavior was likely not yet well accounted for by the integrator model in this early phase of the session. Further, we also excluded the first 23 trials of each block, because simulations of the integrator model showed that differences in deviance between conditions of low and high decision noise were maximized at the asymptotic levels of choice fractions. The cutoff of 23 trials was determined by taking four times the group average time constant (inverse of leak, collapsed across drug and placebo), corresponding to approximately 98% of the asymptotic value of a leaky integrator.
For the simulations of the leaky accumulator model shown in Fig. 4H (bottom), the following parameters were used: leak: 0.1667 to 0.8333, in steps of 0.1667; decision noise (1/β): 0.3333, 0.5, 1, 2, and 3. The decision noise values were multiplied by the average estimated (through fitting) decision noise parameter, averaged across all participants and the two conditions (placebo and atomoxetine). WSLS: 0 to 1, in steps of 0.25; bias: −0.0702, −0.0351, 0, 0.0351, and 0.0702.
Acknowledgments
We thank K. Wimmer for the help with the implementation of the circuit model for decision-making; C. Büchel, S. Nieuwenhuis, and W. Singer for the feedback on an earlier draft of the manuscript; and A. Thiele for the discussion of cholinergic circuit mechanisms. Funding: This work was supported by the Alexander-von-Humboldt Foundation (postdoctoral fellowships to T.P. and R.L.v.d.B.); BMBF 161A130 (to A.K.E.); the Catalan Agencia de Gestión de Ayudas Universitarias Programme 2017 SGR 1545 (to G.D.); the Deutsche Forschungsgemeinschaft (DFG) DO1230/1 and DO1240/1 (to T.H.D.), SFB936/A3 (to A.K.E.), SFB936/A7 (to T.H.D.), and SFB936/Z3 (to G.N. and T.H.D.); the EU Horizon 2020 Research and Innovation Programme under grant agreements 720270 (HBP SGA1) and 785907 (HBP SGA2) (to G.D.); the EU Horizon 2020 Research and Innovation Program, ERC starting grant no. 802905 (to K.T.); the FLAG-ERA JTC (PCI2018-092891) (to A.P.-A.); the International Brain Research Organization (to T.P.); the Netherlands Organization for Scientific Research (NWO, dossiernummer 406-14-016) (to T.H.D.); and the Spanish Research Project PSI2016-75688-P (Agencia Estatal de Investigación/Fondo Europeo de Desarrollo Regional, European Union) (to G.D.); and Deutsche Forschungsgemeinschaft (DFG), TRR169/B4/C1 (to G.N.). Author contributions: T.P.: Conceptualization, methodology, formal analysis, investigation, data curation, writing (original draft), writing (review and editing), visualization, and project administration. A.P.-A.: Methodology, formal analysis, and writing (review and editing). K.T.: Methodology, formal analysis, investigation, and writing (review and editing). T.M.: Formal analysis, investigation, and writing (review and editing). C.J.G.: Investigation and writing (review and editing). R.L.v.d.B.: Conceptualization and writing (review and editing). G.N.: Provided reagents and writing (review and editing). A.K.E.: Resources and writing (review and editing). G.D.: Methodology, writing (review and editing), and supervision. T.H.D.: Conceptualization, methodology, writing (original draft), writing (review and editing), and supervision. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data and code needed to evaluate the conclusions in the paper are available on OSF (https://osf.io/vzswa/). Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/29/eabf5620/DC1
REFERENCES AND NOTES
- 1.Aston-Jones G., Cohen J. D., An integrative theory of locus coeruleus-norepinephrine function: Adaptive gain and optimal performance. Annu. Rev. Neurosci. 28, 403–450 (2005). [DOI] [PubMed] [Google Scholar]
- 2.Harris K. D., Thiele A., Cortical state and attention. Nat. Rev. Neurosci. 12, 509–523 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Robbins T. W., Arnsten A. F. T., The neuropsychopharmacology of fronto-executive function: Monoaminergic modulation. Annu. Rev. Neurosci. 32, 267–287 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Schwarz L. A., Luo L., Organization of the locus coeruleus-norepinephrine system. Curr. Biol. 25, R1051–R1056 (2015). [DOI] [PubMed] [Google Scholar]
- 5.van den Brink R. L., Pfeffer T., Donner T. H., Brainstem modulation of large-scale intrinsic cortical activity correlations. Front. Hum. Neurosci. 13, 340 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.van den Brink R. L., Pfeffer T., Warren C. M., Murphy P. R., Tona K.-D., van der Wee N. J. A., Giltay E., van Noorden M. S., Rombouts S. A. R. B., Donner T. H., Nieuwenhuis S., Catecholaminergic neuromodulation shapes intrinsic MRI functional connectivity in the human brain. J. Neurosci. 36, 7865–7876 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.van den Brink R. L., Nieuwenhuis S., Donner T. H., Amplification and suppression of distinct brainwide activity patterns by catecholamines. J. Neurosci. 38, 7476–7491 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Turchi J., Chang C., Ye F. Q., Russ B. E., Yu D. K., Cortes C. R., Monosov I. E., Duyn J. H., Leopold D. A., The basal forebrain regulates global resting-state fMRI fluctuations. Neuron 97, 940–952.e4 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Coull J. T., Büchel C., Friston K. J., Frith C. D., Noradrenergically mediated plasticity in a human attentional neuronal network. NeuroImage 10, 705–715 (1999). [DOI] [PubMed] [Google Scholar]
- 10.Yu A. J., Dayan P., Uncertainty, neuromodulation, and attention. Neuron 46, 681–692 (2005). [DOI] [PubMed] [Google Scholar]
- 11.Montague P. R., Hyman S. E., Cohen J. D., Computational roles for dopamine in behavioural control. Nature 431, 760–767 (2004). [DOI] [PubMed] [Google Scholar]
- 12.Servan-Schreiber D., Printz H., Cohen J. D., A network model of catecholamine effects: Gain, signal-to-noise ratio, and behavior. Science 249, 892–895 (1990). [DOI] [PubMed] [Google Scholar]
- 13.Eldar E., Cohen J. D., Niv Y., The effects of neural gain on attention and learning. Nat. Neurosci. 16, 1146–1153 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Disney A. A., Aoki C., Hawken M. J., Gain modulation by nicotine in macaque V1. Neuron 56, 701–713 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Herrero J. L., Roberts M. J., Delicato L. S., Gieselmann M. A., Dayan P., Thiele A., Acetylcholine contributes through muscarinic receptors to attentional modulation in V1. Nature 454, 1110–1114 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hurley L. M., Devilbiss D. M., Waterhouse B. D., A matter of focus: Monoaminergic modulation of stimulus coding in mammalian sensory networks. Curr. Opin. Neurobiol. 14, 488–495 (2004). [DOI] [PubMed] [Google Scholar]
- 17.Polack P.-O., Friedman J., Golshani P., Cellular mechanisms of brain state-dependent gain modulation in visual cortex. Nat. Neurosci. 16, 1331–1339 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Silver M. A., Shenhav A., D’Esposito M., Cholinergic enhancement reduces spatial spread of visual responses in human early visual cortex. Neuron 60, 904–914 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Roberts M. J., Zinke W., Guo K., Robertson R., McDonald J. S., Thiele A., Acetylcholine dynamically controls spatial integration in marmoset primary visual cortex. J. Neurophysiol. 93, 2062–2072 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hsieh C. Y., Cruikshank S. J., Metherate R., Differential modulation of auditory thalamocortical and intracortical synaptic transmission by cholinergic agonist. Brain Res. 880, 51–64 (2000). [DOI] [PubMed] [Google Scholar]
- 21.Deco G., Ponce-Alvarez A., Hagmann P., Romani G. L., Mantini D., Corbetta M., How local excitation-inhibition ratio impacts the whole brain dynamics. J. Neurosci. 34, 7886–7898 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shine J. M., van den Brink R. L., Hernaus D., Nieuwenhuis S., Poldrack R. A., Catecholaminergic manipulation alters dynamic network topology across cognitive states. Netw. Neurosci. 2, 381–396 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ferguson K. A., Cardin J. A., Mechanisms underlying gain modulation in the cortex. Nat. Rev. Neurosci. 21, 80–92 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Froemke R. C., Plasticity of cortical excitatory-inhibitory balance. Annu. Rev. Neurosci. 38, 195–219 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Murphy B. K., Miller K. D., Multiplicative gain changes are induced by excitation or inhibition alone. J. Neurosci. 23, 10040–10051 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Martins A. R. O., Froemke R. C., Coordinated forms of noradrenergic plasticity in the locus coeruleus and primary auditory cortex. Nat. Neurosci. 18, 1483–1492 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Froemke R. C., Merzenich M. M., Schreiner C. E., A synaptic memory trace for cortical receptive field plasticity. Nature 450, 425–429 (2007). [DOI] [PubMed] [Google Scholar]
- 28.Pfeffer T., Avramiea A.-E., Nolte G., Engel A. K., Linkenkaer-Hansen K., Donner T. H., Catecholamines alter the intrinsic variability of cortical population activity and perception. PLoS Biol. 16, e2003453 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bymaster F. P., Katner J. S., Nelson D. L., Hemrick-Luecke S. K., Threlkeld P. G., Heiligenstein J. H., Morin S. M., Gehlert D. R., Perry K. W., Atomoxetine increases extracellular levels of norepinephrine and dopamine in prefrontal cortex of rat: A potential mechanism for efficacy in attention deficit/hyperactivity disorder. Neuropsychopharmacology 27, 699–711 (2002). [DOI] [PubMed] [Google Scholar]
- 30.Reimer J., McGinley M. J., Liu Y., Rodenkirch C., Wang Q., McCormick D. A., Tolias A. S., Pupil fluctuations track rapid changes in adrenergic and cholinergic activity in cortex. Nat. Commun. 7, 13289 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Joshi S., Li Y., Kalwani R. M., Gold J. I., Relationships between pupil diameter and neuronal activity in the locus coeruleus, colliculi, and cingulate cortex. Neuron 89, 221–234 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.de Gee J. W., Colizoli O., Kloosterman N. A., Knapen T., Nieuwenhuis S., Donner T. H., Dynamic modulation of decision biases by brainstem arousal systems. eLife 6, e23232 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hipp J. F., Hawellek D. J., Corbetta M., Siegel M., Engel A. K., Large-scale cortical correlation structure of spontaneous oscillatory activity. Nat. Neurosci. 15, 884–890 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Leopold D., Logothetis N., Multistable phenomena: Changing views in perception. Trends Cogn. Sci. 3, 254–264 (1999). [DOI] [PubMed] [Google Scholar]
- 35.J. Cohen, Statistical Power Analysis for the Behavioral Sciences (Routledge, ed. 2, 1988). [Google Scholar]
- 36.Wilson H. R., Cowan J. D., Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 12, 1–24 (1972). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wang X.-J. J., Neurophysiological and computational principles of cortical rhythms in cognition. Physiol. Rev. 90, 1195–1268 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Spyropoulos G., Dowdall J. R., Schölvinck M. L., Bosman C. A., Lima B., Peter A., Onorato I., Klon-Lipok J., Roese R., Neuenschwander S., Singer W., Vinck M., Fries P., Spontaneous variability in gamma dynamics described by a linear harmonic oscillator driven by noise. bioRxiv, 793729 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Haider B., Häusser M., Carandini M., Inhibition dominates sensory responses in the awake cortex. Nature 493, 97–100 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.McCasland J. S., Hibbard L. S., GABAergic neurons in barrel cortex show strong, whisker-dependent metabolic activation during normal behavior. J. Neurosci. 17, 5509–5527 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Swadlow H. A., Thalamocortical control of feed-forward inhibition in awake somatosensory “barrel” cortex. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 357, 1717–1727 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shadlen M. N., Newsome W. T., The variable discharge of cortical neurons: Implications for connectivity, computation, and information coding. J. Neurosci. 18, 3870–3896 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Renart A., Machens C. K., Variability in neural activity and behavior. Curr. Opin. Neurobiol. 25, 211–220 (2014). [DOI] [PubMed] [Google Scholar]
- 44.Wang X.-J., Probabilistic decision making by slow reverberation in cortical circuits. Neuron 36, 955–968 (2002). [DOI] [PubMed] [Google Scholar]
- 45.Lam N. H., Borduqui T., Hallak J., Roque A. C., Anticevic A., Krystal J. H., Wang X.-J., Murray J. D., Effects of altered excitation-inhibition balance on decision making in a cortical circuit model. bioRxiv, 100347 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cohen J. D., McClure S. M., Yu A. J., Should I stay or should I go? How the human brain manages the trade-off between exploitation and exploration. Philos. Trans. R. Soc. B 362, 933–942 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Frank M. J., Doll B. B., Oas-Terpstra J., Moreno F., Prefrontal and striatal dopaminergic genes predict individual differences in exploration and exploitation. Nat. Neurosci. 12, 1062–1068 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Cools R., Chemistry of the adaptive mind: Lessons from dopamine. Neuron 104, 113–131 (2019). [DOI] [PubMed] [Google Scholar]
- 49.Sugrue L. P., Corrado G. S., Newsome W. T., Matching behavior and the representation of value in the parietal cortex. Science 304, 1782–1787 (2004). [DOI] [PubMed] [Google Scholar]
- 50.Corrado G. S., Sugrue L. P., Seung H. S., Newsome W. T., Linear-Nonlinear-Poisson models of primate choice dynamics. J. Exp. Anal. Behav. 84, 581–617 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Usher M., Cohen J. D., Servan-Schreiber D., Rajkowski J., Aston-Jones G., The role of locus coeruleus in the regulation of cognitive performance. Science 283, 549–554 (1999). [DOI] [PubMed] [Google Scholar]
- 52.Aston-Jones G., Rajkowski J., Cohen J., Role of locus coeruleus in attention and behavioral flexibility. Biol. Psychiatry. 46, 1309–1320 (1999). [DOI] [PubMed] [Google Scholar]
- 53.Kane G. A., Vazey E. M., Wilson R. C., Shenhav A., Daw N. D., Aston-Jones G., Cohen J. D., Increased locus coeruleus tonic activity causes disengagement from a patch-foraging task. Cogn. Affect. Behav. Neurosci. 17, 1073–1083 (2017). [DOI] [PubMed] [Google Scholar]
- 54.Tervo D. G. R., Proskurin M., Manakov M., Kabra M., Vollmer A., Branson K., Karpova A. Y., Behavioral variability through stochastic choice and its gating by anterior cingulate cortex. Cell 159, 21–32 (2014). [DOI] [PubMed] [Google Scholar]
- 55.Warren C. M., Wilson R. C., van der Wee N. J., Giltay E. J., van Noorden M. S., Cohen J. D., Nieuwenhuis S., The effect of atomoxetine on random and directed exploration in humans. PLOS ONE 12, e0176034 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Eisenegger C., Naef M., Linssen A., Clark L., Gandamaneni P. K., Müller U., Robbins T. W., Role of dopamine D2 receptors in human reinforcement learning. Neuropsychopharmacology 39, 2366–2375 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Findling C., Skvortsova V., Dromnelle R., Palminteri S., Wyart V., Computational noise in reward-guided learning drives behavioral variability in volatile environments. Nat. Neurosci. 22, 2066–2077 (2019). [DOI] [PubMed] [Google Scholar]
- 58.Letzkus J. J., Wolff S. B. E., Meyer E. M. M., Tovote P., Courtin J., Herry C., Lüthi A., A disinhibitory microcircuit for associative fear learning in the auditory cortex. Nature 480, 331–335 (2011). [DOI] [PubMed] [Google Scholar]
- 59.Arnsten A. F. T., Paspalas C. D., Gamo N. J., Yang Y., Wang M., Dynamic network connectivity: A new form of neuroplasticity. Trends Cogn. Sci. 14, 365–375 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Fox M. D., Greicius M., Clinical applications of resting state functional connectivity. Front. Syst. Neurosci. 4, 19 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tiseo P. J., Rogers S. L., Friedhoff L. T., Pharmacokinetic and pharmacodynamic profile of donepezil HCl following evening administration: Evening administration of donepezil HCl. Br. J. Clin. Pharmacol. 46, 13–18 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Sauer J.-M., Ring B. J., Witcher J. W., Clinical pharmacokinetics of atomoxetine. Clin. Pharmacokinet. 44, 571–590 (2005). [DOI] [PubMed] [Google Scholar]
- 63.Wallach H., O’connell D. N., The kinetic depth effect. J. Exp. Psychol. 45, 205–217 (1953). [DOI] [PubMed] [Google Scholar]
- 64.Brainard D. H., The psychophysics toolbox. Spat. Vis. 10, 433–436 (1997). [PubMed] [Google Scholar]
- 65.Knapen T., de Gee J. W., Brascamp J., Nuiten S., Hoppenbrouwers S., Theeuwes J., Cognitive and ocular factors jointly determine pupil responses under equiluminance. PLOS ONE 11, e0155574 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Oostenveld R., Fries P., Maris E., Schoffelen J.-M., FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011, 156869 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Hyvarinen A., Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 10, 626–634 (1999). [DOI] [PubMed] [Google Scholar]
- 68.Hawellek D. J., Schepers I. M., Roeder B., Engel A. K., Siegel M., Hipp J. F., Altered intrinsic neuronal interactions in the visual cortex of the blind. J. Neurosci. 33, 17072–17080 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Van Veen B. D., van Drongelen W., Yuchtman M., Suzuki A., Localization of brain electrical activity via linearly constrained minimum variance spatial filtering. IEEE Trans. Biomed. Eng. 44, 867–880 (1997). [DOI] [PubMed] [Google Scholar]
- 70.Tzourio-Mazoyer N., Landeau B., Papathanassiou D., Crivello F., Etard O., Delcroix N., Mazoyer B., Joliot M., Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage 15, 273–289 (2002). [DOI] [PubMed] [Google Scholar]
- 71.Rubinov M., Sporns O., Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 52, 1059–1069 (2010). [DOI] [PubMed] [Google Scholar]
- 72.Nichols T. E., Holmes A. P., Nonparametric permutation tests for functional neuroimaging: A primer with examples. Hum. Brain Mapp. 15, 1–25 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Donoghue T., Haller M., Peterson E. J., Varma P., Sebastian P., Gao R., Noto T., Lara A. H., Wallis J. D., Knight R. T., Shestyuk A., Voytek B., Parameterizing neural power spectra into periodic and aperiodic components. Nat. Neurosci. 23, 1655–1665 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Deco G., Jirsa V., McIntosh A. R., Sporns O., Kotter R., Key role of coupling, delay, and noise in resting brain fluctuations. Proc. Natl. Acad. Sci. U.S.A. 106, 10302–10307 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Deco G., Cruzat J., Cabral J., Knudsen G. M., Carhart-Harris R. L., Whybrow P. C., Logothetis N. K., Kringelbach M. L., Whole-brain multimodal neuroimaging model using serotonin receptor maps explains non-linear functional effects of LSD. Curr. Biol. 28, 3065–3074.e6 (2018). [DOI] [PubMed] [Google Scholar]
- 76.Demirtaş M., Burt J. B., Helmer M., Ji J. L., Adkinson B. D., Glasser M. F., Van Essen D. C., Sotiropoulos S. N., Anticevic A., Murray J. D., Hierarchical heterogeneity across human cortex shapes large-scale neural dynamics. Neuron 101, 1181–1194.e13 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Goodman D. F. M., The Brian simulator. Front. Neurosci. 3, 192–197 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Wimmer K., Compte A., Roxin A., Peixoto D., Renart A., de la Rocha J., Sensory integration dynamics in a hierarchical network explains choice probabilities in cortical area MT. Nat. Commun. 6, 6177 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Beggs J. M., Plenz D., Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Leopold D. A., Murayama Y., Logothetis N. K., Very slow activity fluctuations in monkey visual cortex: Implications for functional brain imaging. Cereb. Cortex 13, 422–433 (2003). [DOI] [PubMed] [Google Scholar]
- 81.van Vreeswijk C., Sompolinsky H., Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274, 1724–1726 (1996). [DOI] [PubMed] [Google Scholar]
- 82.Womelsdorf T., Valiante T. A., Sahin N. T., Miller K. J., Tiesinga P., Dynamic circuit motifs underlying rhythmic gain control, gating and integration. Nat. Neurosci. 17, 1031–1039 (2014). [DOI] [PubMed] [Google Scholar]
- 83.Adesnik H., Synaptic mechanisms of feature coding in the visual cortex of awake mice. Neuron 95, 1147–1159.e4 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Renart A., de la Rocha J., Bartho P., Hollender L., Parga N., Reyes A., Harris K. D., The asynchronous state in cortical circuits. Science 327, 587–590 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Moreno-Bote R., Rinzel J., Rubin N., Noise-induced alternations in an attractor network model of perceptual bistability. J. Neurophysiol. 98, 1125–1139 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/29/eabf5620/DC1


