Detection of Meniscal Tear Effects on Tibial Vibration Using Passive Knee Sound Measurements

Abstract

Objective:

To evaluate whether non-invasive knee sound measurements can provide information related to the underlying structural changes in the knee following meniscal tear. These changes are explained using an equivalent vibrational model of the knee-tibia structure.

Methods:

First, we formed an analytical model by modeling the tibia as a cantilever beam with the fixed end being the knee. The knee end was supported by three lumped components with features corresponding with tibial stiffnesses, and meniscal damping effect. Second, we recorded knee sounds from 46 healthy legs and 9 legs with acute meniscal tears (n = 34 subjects). We developed an acoustic event (“click”) detection algorithm to find patterns in the recordings, and used the instrumental variable continuous-time transfer function estimation algorithm to model them.

Results:

The knee sound measurements yielded consistently lower fundamental mode decay rate in legs with meniscal tears (16 ± 13 s⁻¹) compared to healthy legs (182 ± 128 s⁻¹), p<0.05. When we performed an intra-subject analysis of the injured versus contralateral legs for the 9 subjects with meniscus tears, we observed significantly lower natural frequency and damping ratio (first mode results for healthy: f_n1 = 115 ± 44 Hz, ξ₁ = 0.098 ± 0.022, injured: f_n1 = 67 ± 10 Hz, ξ₁ = 0.036 ± 0.029) for the first three vibration modes (p<0.05). These results agreed with the theoretical expectations gleaned from the vibrational model.

Significance:

This combined analytical and experimental method improves our understanding of how vibrations can describe the underlying structural changes in the knee following meniscal tear, and supports their use as a tool for future efforts in non-invasively diagnosing meniscal tear injuries.

I. Introduction

MENISCUS tears are the second most common knee injury in the United States with approximately 850,000 patients afflicted each year [1]. The resulting surgeries account for 10-20% of all orthopedic surgeries [2]. Patients with meniscus tears have a more optimal recovery process if the time between injury and intervention is minimized [3]. Both surgical procedures and non-invasive methods are used to diagnose meniscus injuries. Surgical knee arthroscopy is accepted as the gold standard to diagnose knee injuries [4]; however, it is time consuming, expensive, and requires sedation [5]. Prior to arthroscopy, non-invasive clinical methods including questionnaires [6] and physical exam maneuvers (e.g. McMurray test, Thessaly test and joint line palpation) are used to increase the pre-test probability of imaging-based diagnosis [7]. Commonly used imaging techniques such as magnetic resonance imaging (MRI) are employed following physical exam [8], [9]. However, these non-invasive methods are restricted to clinical settings, and may be cost prohibitive. Point-of-injury diagnosis is particularly important among athletes and military personnel [10], [11]. Therefore, there is a need for an objective, non-invasive and affordable diagnostic method for knee injuries that could be used both inside and outside of the clinic.

Characteristics of the sounds produced by the knee have been proposed as a digital biomarker that could help address this need [12]. These sounds or joint acoustic emissions (JAEs) are thought to arise from joint articulation [13], and the vibrations that are produced by both intra- and extra- articular components [14]. Though machine learning algorithms using acoustic emissions have been described in the literature for diagnostic purposes [15], they are unable to fully explain the underlying structural changes in the knee, and correlate those changes to the sources of the emissions. Recently, our group performed cadaveric studies to investigate the changes in JAEs resulting from tearing the meniscus and meniscectomy. We found differences between intact knees and knees with meniscal tears [16]. Still, the relationship between the structural origin of the changes in JAE is poorly understood. Better understanding of this relationship will allow for JAEs to go beyond primitive diagnosis and enable more precise classification of the knee injury.

Since JAE production is dependent on knee articulation, any variables impacting this movement could confound the signal. Studies in cadaver models have indicated that the laxity, tibial translation and torsional stiffness of the knee are altered with meniscus tear [17]-[20]. Additionally, meniscal tears (particularly of the posterior root or transection) have been shown to decrease the energy absorption capacity of the knee [21]. These studies demonstrated several variables that may confound the JAE signal, but a rigorous analysis of this interaction has not been performed.

The study presented in this work has three objectives: (1) to form a vibrational model of the knee-tibia structure and investigate the changes in the modal characteristics of the tibia following meniscal tear; (2) to detect and model the tibial vibrations from passive knee sound recordings as a damped system response; and (3) to demonstrate the differences in modal parameters between healthy knees and knees with meniscal tears. This approach could help correlate the changes in knee sounds with the structural changes in the knee following meniscal tear, and could readily be adapted for use as a non-invasive and affordable method for monitoring knee stiffness in wearable systems.

II. Methods

A. Analytical Model

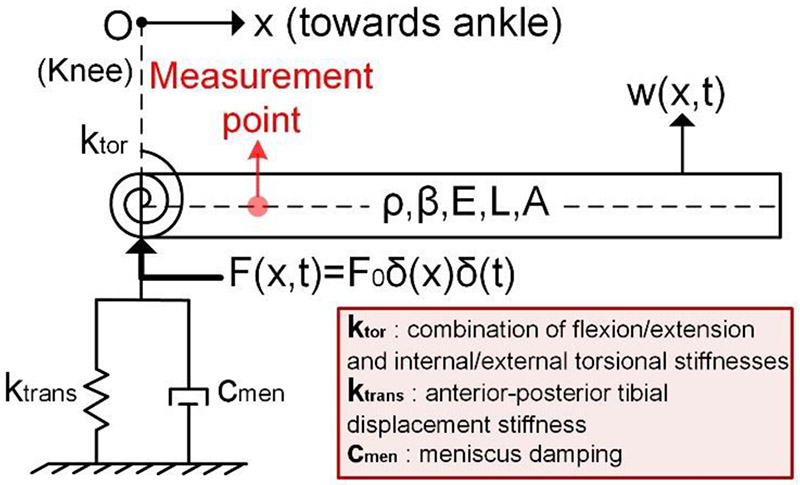
In the literature, a combination of several mass-spring-damper systems was proposed to analytically model the human leg [22]. However, these discrete models are unable to fully explain the tibial vibrations. In prior work, the tibia was modeled as a beam to evaluate its rigidity under various loads [23]. Nonetheless, the modal characteristics of the tibia and injury induced changes on modal parameters have not been studied. To this end, we proposed the vibration model of the knee-tibia structure presented in Fig. 1. In this model, the tibia was modelled as a cantilever beam that was supported by translational and torsional springs, and a damper on the knee end, while the other end of the beam was left free. The knee stiffness related to the anterior-posterior tibial motion was included as the translational spring, k_trans, while the knee stiffness related to both flexion/extension and internal/external rotational motion of the tibia was expressed by the torsional spring, k_tor. The energy absorption property of the meniscus was modelled by the damper, c_men. Note that we only included the tibia in our model since the knee sound measurements were conducted at locations near the tibial bone to minimize the effects of soft tissue.

Fig. 1.

Analytical model of the tibia and the knee.

In this study, we first assumed the leg we are modeling as healthy and with no prior injury, and set the initial parameters accordingly. Then, we changed the parameters according to the manner in which the injury would affect biomechanical properties of the joint. We used the values in Table I to investigate the general response of the model. In addition to these parameters, Rayleigh damping was assumed for the beam in accordance with the reported proportional damping characteristics of the tibia in the literature [27]. We set the critical frequency of Rayleigh damping as 20 Hz in our analysis [27].

Table I.

Parameter Values of the Analytical Model

Parameter	Value
Length of the tibia, L [24]	365 mm
Radius of the tibia, r [25]	17 mm
Young’s modulus of the tibia, E [26]	10 GPa
Mass density of the tibia, ρ [26]	1879 kg/m3
Tibial torsional stiffness, ktor [17]	0.1 Nm/deg
Tibial translational stiffness, ktrans [17]	3*104 N/m

It was reported that partial meniscectomy results in 7.7% and 6.1% increase in trabecular and cortical bone mineral densities, respectively [28]. The increased bone mineral density was reported as a reason for decreased modal damping factor [29]. These observations support the hypothesis that damping ratio decreases with meniscal tear.

After taking the baseline (healthy leg) parameters for stiffnesses, we included their relative changes with meniscal tear. In a previous study, the meniscus injury results in 46.6% decrease in varus-valgus stiffness, and 15.1% decrease in tibial rotational stiffness [30]. In another study, researchers reported that meniscectomy results in on average 30% and 40% decrease in tibial torsional and anterior displacement stiffnesses, respectively [17]. It has also been shown that injuries in the posteromedial corner of the knee, which includes posterior horn of the medial meniscus, result in decrease in tibial posterior displacement and valgus torsional stiffnesses [31].

Though obtaining exact percent changes for all subjects was unattainable due to high variation of physiological parameters among the subjects, we interpreted the decrease in both torsional and translational stiffnesses as 30% for representative purposes. In addition to the changes in stiffnesses, meniscus tear was shown to decrease the energy absorption capacity of the knee by 8% [21]. We took these percent changes as the difference between the healthy and injured legs in our model, and analyzed the resulting changes in the modal parameters of the tibia.

In the proposed analytical model, the equation of motion of the Euler-Bernoulli beam is

$$EI\frac{\partial w^4}{\partial x^4}+\beta \frac{\partial w}{\partial t}+\rho A\frac{\partial w^2}{\partial t^2}=F(x,t)$$ (1)

where E is the Young’s modulus, I is the moment of area, β is the proportional damping constant, ρ is the mass density, and A is the cross-sectional area of the beam. w = w(x, t) is the displacement of the beam, and F(x, t) is the input to the system. By using a separation of variables approach, w can be decomposed as

$$w(x,t)={\sum }_i{q}_i(t){\varphi }_i(x)$$ (2)

where q_i(t), and ϕ_i(x) are the modal coordinates and mode shapes, respectively. By orthogonality of the modes, the zero initial state temporal solution of the equation of motion under forced vibration can be calculated as [32]

$$q_i(t)={\int }_0^t{F}_i(\tau )h_i(t-\tau )d\tau$$ (3)

where $h_i(t)=\frac{1}{{\omega }_{di}}{e}^{-K_{i}t}$ sin(ω_dit), ${\omega }_{di}={\omega }_{ni}\sqrt{1-{\xi }_i^2}$ is the damped natural frequency of the i-th mode where ${\xi }_i=\frac{1}{2}\left(\frac{{\gamma }_1}{{\omega }_{ni}}+{\gamma }_2{\omega }_{ni}\right)$ with ${\gamma }_1,{\gamma }_2\in \mathbb{R}$, K_i = ξ_iω_ni is the decay rate of the i-th mode, and

$$F_i(t)={\int }_0^L{\varphi }_i(x)F(x,t)dx$$ (4)

The solution of the proposed model depends on (1) the input F(x, t), and (2) the four boundary conditions expressed as: (i) ${\varphi }^{″}(0)=\frac{k_{rot}}{EI}{\varphi }^{\prime }(0)$, (ii) ${\varphi }^{″\prime }(0)=-\frac{k_{trans}}{EI}\varphi (0)-\frac{c}{EI}{\varphi }^{\prime }(0)$, (iii) ϕ″(L) = 0, (iv) ϕ″′(L) = 0. Since the experimental part of this study was based on passive knee sound measurements where no controlled excitation was used, defining an input to the analytical model was challenging. Researchers have conducted experiments with cadaver legs by exciting the tibia with a hammer and measuring the modal response [33], [34].The reported measurements yielded high-amplitude and short duration response signals, which are similar to the clicks we observed in knee measurements. These observations suggest an impulsive force as the input to the system. On the other hand, with meniscal tear, there might be a need of additional instantaneous torque to pass through the location of the tear to overcome the additional constraints or friction imposed by the tear. In this case, one can assume an impulsive torque as an input to the system. Though force and torque act on different axes of movement, they would yield the same modal parameters since the modal parameters only depend on the physical parameters and boundary conditions of a given vibration problem. Note that, in both cases, the frequency response functions will have the same poles where the amplitude of the response changes based on the types of the input and mode shapes. Since the proposed analytical model is rather qualitative, and we want to obtain directional changes in modal parameters instead of exact frequency response function, we assumed an impulse force input on the knee end as F(x, t) = F₀δ(x)δ(t) where F₀ ∈ $\mathbb{R}$, and δ(.) is the impulse function. Though such an input is not practical, it still represents the broadband nature of an impact. The actual input should have finite bandwidth and decaying power with frequency that is different from our assumption. However, these differences do not degrade the potential of the model since they only change the response amplitudes, not the natural frequencies or damping ratios of the vibration modes.

The relative changes of the modal parameters with respect to their baseline (healthy leg) were used to understand the effect of the meniscal tear on tibial vibration. By using the definition of proportional damping, it can be shown that

$$\frac{\Delta \xi }{\xi }=(\frac{-\frac{{\gamma }_1}{{\omega }_n}+{\gamma }_2{\omega }_n}{\frac{{\gamma }_1}{{\omega }_n}+{\gamma }_2{\omega }_n})\frac{\Delta {\omega }_n}{{\omega }_n}$$ (5)

Since we assumed the critical frequency at 20 Hz in accordance with the literature [27], and the natural frequency of the fundamental mode of the model was found at 80 Hz from its solution, we found that $\frac{{\gamma }_1}{{\omega }_n}\ll {\gamma }_2{\omega }_n$ which yielded approximately the same relative change in damping ratio as in the natural frequency. For higher order modes, this condition was also satisfied due to larger natural frequencies.

B. Knee Sound Measurement Protocol

This study was approved by the Georgia Institute of Technology Institutional Review Board (IRB) and Emory University IRB (Protocol Number: 00081670, Date of Approval: 10/11/2016), and all subjects provided written consent. In this study, 16 female and 18 male subjects (height = 169.5 ± 9.9 cm, weight = 79.1 ± 16.9 kg, age = 35 ± 14 years) participated. The health conditions of the total of 68 legs are presented in Table II. With this specific study, we compared 46 healthy legs and 9 legs having only meniscal tear. From this point forward, 9 legs with only meniscus tear will be referred to as injured legs.

Table II.

Health Conditions of the Legs

Health Conditions of the Legs	Number of Legs
Healthy*	46
Medial meniscus tear*	7
Anterior Cruciate Ligament (ACL) tear	5
ACL and meniscus tear	4
Posterior Cruciate Ligament (PCL) tear	1
Post ACL surgery	1
Lateral meniscus tear*	1
Medial and lateral meniscus tear*	1
Patellofemoral pain	1
Chondromalacia patella	1

In total, 16 female and 18 male subjects participated.

^*The legs used in this study.

The knee sounds data collection protocol is presented in Fig. 2(a). Each subject was asked to perform 10 unloaded flexion/extension cycles with a period of four seconds with the help of a custom designed video that provided the metronome timing for the subjects. This procedure was used on both legs of the subjects with an accelerometer (3225F7, Dytran Instruments Inc., Chatsworth, CA, USA) attached on the tibia, medial to patella tendon. The medial side was selected due to less impeded route for vibration propagation and minimal attenuation by soft tissue [35]. The accelerometers were sampled by a USB-4431 data acquisition unit (DAQ, National Instruments, Austin, TX, USA) at 100 kHz, and the data were saved on a laptop for post-processing. The recorded signals were analyzed using MATLAB (MathWorks, Natick, MA, USA). Note that, a recording in the context of this paper refers to collected data from each subject during 10 F/E cycles. We took each recording once. To illustrate preparation of an experimental setup and the flow of a measurement, we provided two supplementary videos for representative purposes. We also provided another supplementary visual to help subjects perform the exercises at a consistent pace throughout the measurement.

Fig. 2.

(a) Knee sounds data collection experimental setup, (b) general signal processing steps, and (c) detailed signal processing flow including click detection and transfer function estimation algorithms. x_i[n] represents a detected click, while h_k[n] represent the repeated clicks.

C. Signal Processing and Statistical Analysis

First, the procedure used to find repeated clicks in knee sounds recordings is presented, and the transfer function (TF) estimation algorithms and performance metrics are given. Then, the modal estimation algorithm that was used to estimate modal parameters of both the response of the analytical model and the clicks is discussed. Finally, statistical analysis methods are presented.

C.1. Click Detection and TF Estimation Algorithms

In this study, we were mostly interested in regularly occurring, high-amplitude and short-duration clicks in the recordings. We hypothesized that the clicks occurring at each flexion/extension cycle should be generated by a source that is triggered by the periodic motion of the leg. Therefore, we compared the behavior and the correlation of the clicks with each other by analyzing their frequency spectra and their consistency within each recording.

To this end, a series of signal processing steps were used as shown in Fig. 2 (b). The recorded knee sounds data were first filtered using a finite impulse response (FIR) bandpass filter with 30 Hz – 1 kHz bandwidth. Then, the local maximums of the recording were detected using a simple peak detection algorithm. The algorithm found different peaks some of which were periodic, while some were non-periodic. We used a 20-ms window around each peak which corresponds to one period of a 50 Hz signal. Note that, most of our clicks were found to have a fundamental mode frequency above 50 Hz. Upon finding the peaks, clicks were aligned such that the first zero crossing before the peak was selected as t=0 of that individual click. Note that, this was the instant where the impulse input was assumed to be. Once the clicks were windowed around detected peaks, a cross-correlation matrix was generated where the diagonal elements were corresponding to the autocorrelation of each click, and i-th row, j-th column of the matrix were representing the cross-correlation value between the i-th and j-th clicks, as presented in Fig. 2 (c). Note that, the normalized correlation values were calculated such that the diagonal elements of the matrix were 1. We used the threshold of 0.9 in cross-correlation calculations, which was defined as very high correlation threshold [36], and any value below that was taken as 0. Then, the values in each row were summed and one value was assigned to each row (i.e. each click) to generate the similarity vector. Once the similarity vector was generated, the index of its maximum value was taken as the index of the repeated click. Then, the clicks that are very highly correlated with this click (cross-correlation > 0.9) were selected. For each recording, different numbers of repeated and consistent clicks were found and saved for further processing.

After selecting the repeated clicks, a systematic approach was required to find the best signal that would represent the underlying characteristics of each recording. Note that, the goal was to find a system response that would represent the vibration characteristics of the tibia. This can be achieved by TF estimation algorithms. We preferred time-domain TF estimation rather than frequency-domain, since time-domain estimation guarantees stability of the system [37]. Though a simple non-linear regression method could have been used, we preferred to use direct, iterative instrumental variable (IV) – based continuous-time TF estimation algorithm by a non-linear least squares search method [38], [39]. While some of the time-domain TF estimation methods estimate the discrete-time system response first, and then convert it to continuous-time, several implementation issues arise during discrete – to continuous–time conversion after estimation [38], [40]. Therefore, direct methods have been suggested and are preferred to address such issues [40], [41]. Additionally, IV–based TF estimation method was shown to be the most reliable algorithm among other direct continuous-time approaches [40]. Particularly, the performance of this algorithm on experimental data was shown to be less sensitive to the initialization stage than classic, maximum likelihood based regression models [37], [39]. Note that, the implementation of this method was also simpler compared to other system identification methods, such as state-space estimation [37], [42].

This algorithm uses an input signal, output signal, model order, and input/output delay as its input data and parameters. The input of the system is unknown and in the analytical model, we assumed an impulse force at the knee and as the input. Though the input of the analytical model does not affect the modal parameters of the system, it may affect the performance of the estimation. In fact, we expect that the actual input should have a decaying power characteristic with frequency. To investigate the validity of impulse input, first, we calculated the transfer function of our hypothetical analytical model and obtained the impulse response. Then, we used five exponentially decaying inputs for our simulation as follows:

$$x(t)=C{e}^{-t∕t_{decay}}$$ (6)

where C ∈ $\mathbb{R}$, and five different values of t_decay were taken as 0.4, 0.8, 1.2 ,1.6 and 2 ms. The simulation input signals were presented in Supplementary Fig. 1 (a). We also calculated the power spectrum of each signal and presented in Supplementary Fig. 1 (b). It was shown that all simulation inputs have decaying power with frequency which are more realistic representations of the actual input. Then, we used these inputs and calculated the exact responses based on the analytical model (solid lines) as presented in Supplementary Fig. 2. After that, for each exact response, we ran TF and modal estimation (Section II.C.2.) algorithms with an impulse input assumption. We used the optimal model order of 10 as discussed in Section III.B, and we did not assume any delay between the input and output. We presented the estimated responses for each case (dashed lines) in Supplementary Fig. 2. The estimation yielded 99 ± 0.5 % (μ ± σ) fit percentage (Equation 11). This result shows that even the actual input has a decaying power with frequency, the impulse assumption is valid for the estimation given it does not have any resonances/antiresonances in 30 Hz – 1 kHz frequency band. Therefore, an impulse at t = 0 was assumed as the input of the system. As the output of the system, we used the repeated clicks that we found in the previous steps. The speed of vibration propagation in the tibia was reported as 4000 m/s [43], thus, indicating an elapsed time of 6.25 μs for the excitation to reach the measurement location on the knee that is 2.5 cm away from the source during measurements. Since the time resolution of our system is 10 μs, we did not assume any delay between the input and the output. To determine the model order, we used the corrected Akaike Information Criterion (AICc) which was the modified version of AIC for small sample sizes [44], [45]. AICc was calculated as

$$AICc=Nlog(MSE)+2n_p+N(log(2\pi )+1)+\frac{2n_p(n_P+1)}{N-n_p-1}$$ (7)

where N is the number of training datapoints, MSE is the in-sample mean-square error, and n_p is the number of parameters to estimate. MSE error was calculated as the weighted average of the MSEs between the clicks and the prediction.

After the model order was selected, the estimation algorithm was used to estimate the TF of the system that is given in the general form by

$$H(s,\theta )=\frac{Y(s)}{X(s)}=\frac{b_0+b_{1}s+\cdots +b_{n-1}{s}^{n-1}}{a_0+a_{1}s+\cdots +a_n{s}^n}$$ (8)

where a_n = 1, θ = [a_n–1 … a₀ b_n–1 … b₀]^T, X(s) is the Laplace transform of the input, Y(s) is the Laplace transform of the output, n is the model order, and s is the complex variable in Laplace domain. Note that, when the TF was converted in time domain by replacing the complex variable s by the time derivative operator, calculations of time derivatives were required. However, it was impractical to calculate time derivatives of the sampled data due to (1) the absence of the numerical values of the derivative functions, and (2) the presence of measurement noise [38]. To address these problems, different pre-filtering methods have been proposed which yielded the estimation of the TF without the need of calculating time derivatives [46]-[48].

The main idea of pre-filtering is to handle the measurement noise by assuming parametric or non-parametric noise characteristics. However, the conventional least-squares methods, such as Basic State Variable Filter or Generalized Poisson Moment Function, provide biased initialization in the presence of the measurement noise since they only assume Gaussian (parametric) noise in the measurements [38], [49]. In contrast, the IV method does not assume any parametric distribution of the noise in measurements. Therefore, IV method was used to obtain the initial guess on θ [50]. In this method, first, the input was projected onto a subspace where the real, noise-free, input was believed to reside. Then, the projected input was used to estimate the input/output mapping. Note that, this projected input is the IV in the algorithm. Then, the optimization was performed to find the optimal input subspace that minimizes the MSE between the predicted output and the measured output. After finding the initial guess of the mapping, which yielded the initial guess on θ, the optimal parameters were searched by steepest gradient descent least squares search method which updates the step sizes at each iteration, unlike standard gradient descent where the step sizes are fixed [51]. Updating the step sizes helped preventing local minimums and decreasing the computation time.

The loss function of the algorithm was defined as

$$\mathcal{L}=\frac{1}{N_c}{\sum }_{i=1}^{N_c}{\mid y_{predicted}-y_i\mid }_2^2$$ (9)

where N_c is the number of clicks used for estimation, y_predicted is the predicted system response, and y_i is the i-th click. To validate the performance of the algorithm, we used leave-one-click-out cross-validation for each recording. This decision was based on the average number of repeated clicks per recording (4.01 clicks/recording).

C.2. Modal Estimation Algorithm

After estimating the system response extracted from each recording by using the repeated clicks, the least-squares complex exponential modal estimation method was used to obtain natural frequencies and damping ratios of different modes of a given response [52]. Note that, we used the response that is estimated by the TF estimation algorithm as the input of the modal estimation algorithm. The number of modes were selected according to the model order optimized by AICc: the number of modes is half of the model order since each mode has one pair of complex conjugate eigenvalues for an underdamped system. The algorithm assumes the signal is the superposition of underdamped system responses in the form

$$s(t)={\sum }_{i=1}^{N_o}{A}_i{e}^{-{\xi }_i{\omega }_{ni}t}\sin (w_{di}t+{\varphi }_i)$$ (10)

where N_o is the number of modes, A_i is the amplitude, ξ_i the damping ratio, ω_ni is the natural frequency, ω_di is the damped natural frequency, and ϕ_i is the phase of the i-th mode. The loss function of the algorithm was defined as the MSE between the estimated signal by the TF estimation algorithm, y_predicted(t). and the modal prediction, s(t). Note that the algorithm assumes damped system response and it is only valid for such signals. Nevertheless, since the clicks are the results of experimental measurements with finite energy, they all should be damped signals, and we can use this algorithm for modal parameter estimation in this study.

To obtain the overall performance of the algorithm from measurement to the end of modal estimation, in each cross-validation iteration, the fit percentage was calculated as:

$$Fit(\%)=\frac{1}{N_c-1}{\sum }_{i=1}^{N_c-1}\left(1-\frac{\mid s-y_i{\mid }_2}{\mid y_i-{\mu }_i{\mid }_2}\right)x100$$ (11)

where μ_i is the mean value of the i-th click [37]. Note that, we used N_c − 1 in the calculations since one click was left out at each iteration. The average of the fit percentages over all CV iterations was calculated, and one fit percentage value was assigned to each estimation problem. Fit percentage is the quantity that explains the RMSE in the context of the standard deviation in the data, and it is a commonly used parameter in dynamic modeling to quantify the performance of the algorithm [53], [54]. We also reported coefficient of determination which is another commonly used performance metric in regression analysis defined as follows [55]:

$$R^2=\frac{1}{N_c-1}{\sum }_{i=1}^{N_c-1}\left(1-{\left(\frac{\mid s-y_i{\mid }_2}{\mid y_i-{\mu }_i{\mid }_2}\right)}^2\right)$$ (12)

C.3. Statistical Analysis

For the statistical analysis of the results, first, we used Shapiro-Wilks tests for a normality check [56]. For the data that rejects the hypothesis that the distribution is normal, the Wilcoxon signed rank test was used, while for the data that does not reject the hypothesis that the distribution is normal, a pairwise t-test was used [56]. A confidence interval of 95% was used in all calculations. A p-value less than 0.05 was considered statistically significant for this work.

III. Results and Discussion

A. Analytical Model

The first three modes of vibration were present within the frequency range previously considered in the experimentation (i.e. 30 Hz to 1 kHz). Note that we normalized the natural frequencies of each mode with respect to its baseline since the relative changes as a result of simulated injury were targeted in this study. The percentage changes in natural frequencies of the first three modes with the changes in lumped component values (30% decrease in k_tor, k_trans, and 8% decrease in c_men) are shown in Fig. 3.

Fig. 3. Percentage changes in first three natural frequencies of the analytical model with the changes in lumped component values.

* Each mode was normalized to its baseline

We observed that the percent change in the first mode natural frequency was higher than the other modes, in other words, the structural changes (i.e. changes in the boundary condition of the beam) after injury had affected the fundamental mode of the beam the most. It is known that some modes of vibration in a beam are more controlled by the boundary conditions and others by the changes in the beam dimensional and material parameters [57]. In this case, the fundamental mode was the one which was more affected by the boundary conditions.

The percent change in the damping ratio as a result of alterations in boundary had similar characteristics as in natural frequency since proportional damping was utilized in the analytical model (not shown in the figure due to similar behavior). A decrease in the natural frequency of the beam results in a proportional decline in the damping. Additionally, the reduction in the boundary damping, c_men, decreases the overall modal damping of the system.

Note that the percent changes predicted by the hypothetical analytical modal is qualitative since the changes in lumped parameters with simulated meniscus injury varies among different subjects. Therefore, the analytical model solution in this study suggests directional changes in the modal parameters rather than the exact percentage change values.

B. Knee Sound Measurements

The peak detection algorithm found 4.01 ± 0.88 (μ ± σ) repeated clicks per recording from 10 flexion/extension cycles per recording. Next, the model order decision was made using AICc. Among 55 recordings, the optimum model order was found as 9.81 ± 0.12 (μ ± σ). To obtain a generalized structure in TF estimation with a common model order, we decided to take the model order as 10 for all recordings.

The fit percentage and coefficient of determination of the algorithm were found to be 71 ± 12 % (μ ± σ) and 0.90 ± 0.06 (μ ± σ), respectively. A 71 % fit percentage indicates that prediction RMSE was approximately 30% of the standard deviation in the data. Prior work reported that the performance of any TF estimation algorithm highly depends on the inherent variation in the signal, and the noise [53]. The knee sound recordings included different noise components, such as accelerometer noise, rubbing noise [58] and motion artifacts [59]. In addition, researchers in different areas have reported wide range of successive fit percentage values, 11 - 80 %, with different modeling approaches [53], [60]-[62]. Note, the fit percentage that IV method yielded was shown to be the highest among other direct continuous-time transfer estimation methods [49]. Additionally, the mean coefficient of determination value of 0.9 is accepted as very high correlation [36]. We presented examples of peaks, similarity vector and repeated clicks together with the estimated response s(t) for a sample recording in Supplementary Fig. 3.

The fundamental mode natural frequency versus damping ratio characteristics of 46 healthy and 9 injured legs were presented in Fig. 4 (a). Both the natural frequency and the damping ratio had decreased with injury (meniscal tear). Since the damping ratio and the natural frequency present similar behavior, the decay rate parameter, K, was used to achieve a higher statistical significance. We performed Wilcoxon signed-rank test to check the significance level since the groups are not balanced. Fundamental mode decay rates of healthy and injured legs were separated with p<0.05 as shown in Fig. 4 (b). Note that the decay rate is a quantity that can readily be measured experimentally where an impulse excitation is used, and the vibrational response is measured in real-time. The decrease in the fundamental mode natural frequency and damping ratio agreed with the analytical model results (Fig. 3), which suggested this behavior with simulated meniscal tear owing to the decrease in torsional and translational stiffnesses, meniscus damping and the proportional damping.

Fig. 4.

First mode (a) natural frequency versus damping ratio characteristics and (b) decay rate, and (c) damping ratios of first three modes of 46 healthy and 9 injured legs. Error bars represent mean in the middle and ± one standard deviation. (* stands for p<0.05)

The damping ratios of the first three modes were presented in Fig 4 (c). All legs (n=55) were included in this analysis. We performed t-tests to check the significance levels. The damping ratio was increasing with the increasing modes, i.e. increasing frequencies, which also agreed with the proportional damping hypothesis which was based on the observations in the literature [27].

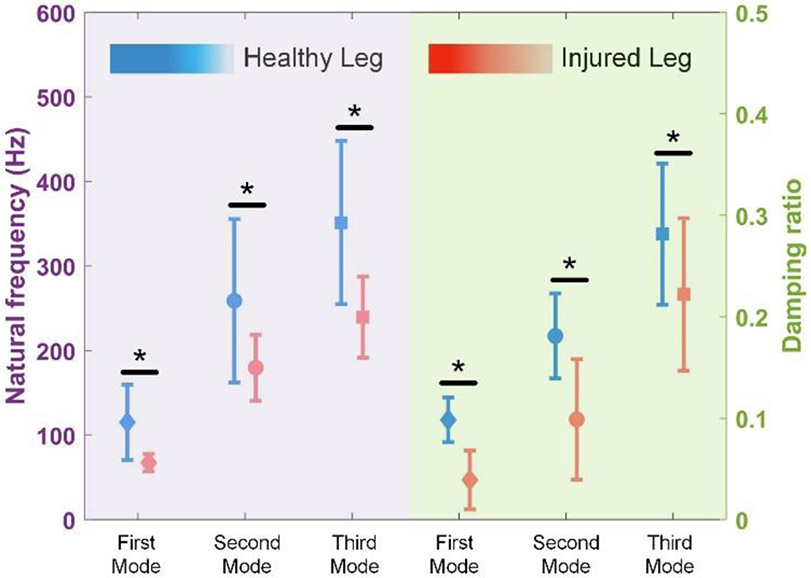
Though a statistically significant change in decay rate was obtained for the fundamental mode, we did not observe the same behavior at higher order modes when all 55 legs were used. This observation was attributed to: (1) the high variation in physiological parameters of different legs making it hard to obtain consistent and statistically significant trends with lower signal-to-noise ratios at higher frequencies, (2) the low-pass characteristics of the skin, resulting in less power at higher order modes (i.e. higher frequencies) which makes it more difficult to detect relevant information with high accuracy [63], [64], and (3) the increasing damping ratio of the tibia with increasing frequency owing to its proportional damping characteristics that results in less power at higher order modes [27]. Accordingly, we reduced our data set such that only injured subjects were included. We thus reduced the high inter-subject variability. We compared the healthy and injured legs of injured subjects (N=9), and the results were presented in Fig. 5. We performed t-tests to check the significance levels.

Fig. 5.

The comparison of the modal parameters of healthy and injured legs of the injured subjects (n=9). Error bars represent mean in the middle and ± one standard deviation. (* stands for p<0.05)

The natural frequencies of first three modes decreased with injury in agreement with the analytical model. As before, this behavior was attributed to the decreased stiffnesses and meniscus damping following meniscal tear. In addition, as suggested by the proportional damping and the change in the boundary damping (meniscus), damping ratio followed the same trend as the natural frequency and resulted in consistent decrease at first three modes. This observation can particularly be useful in cases where low frequency information (fundamental mode) is corrupted by motion artifacts and noise, such as vibration analysis during walking and running [65], [66]. In such cases, even second and third order mode parameters can provide relevant information regarding the knee health.

Additionally, though statistically significant changes were obtained at the second and third order modes, the significance level decreased as presented in Fig. 5. Finally, we compared the right and left legs of 12 healthy subjects to observe any difference in modal parameters, but no statistically significant change was observed in any of the modal parameters.

C. Limitations and Future Work

There are some limitations of this work that should be noted. First, our work is limited by the perfect impulse input assumption in both theoretical and experimental parts. A practical impulse has a decaying frequency response rather than a flat response assumption made here. While such an assumption is imperfect, it should not substantially affect the results unless the actual input includes any resonances. We would expect changes in the magnitude of the TF, not the modal frequencies and damping ratios. A better understanding of the input can be built by experiments with cadaver legs where the tibia is directly excited by an impact source such as a hammer, and the response is measured from the skin. Second, the experimental data was collected only during flexion/extension motion. The performance of the click detection algorithm should be evaluated for more challenging exercises with great number of motion artifacts, such as walking and running.

In future work, the analytical model and the algorithm will be tested to diagnose other knee injuries such as ACL and PCL injuries. Since both injuries were shown to affect the knee stiffnesses in the similar way as a meniscal tear [17], [31], [67], the model has the potential to predict the presence of such injuries. It will also be aimed to differentiate the injuries by decomposing the changes in modal parameters to the changes in analytical model parameters. We will also explore the ways to develop further understanding of the tibial vibration by designing non-invasive experiments with controlled inputs, such as vibration motors with different source frequencies. Such experiments may include locating the input at the one end of the tibia and using an array of accelerometers along the tibia which may also provide mode shapes of the vibrational modes and the dispersion information. Furthermore, the dynamics of muscles, tendons, and ligaments during various activities can also be explored by improving the analytical model by including the other joint components alongside a biomechanical analysis of the lower-limb movement.

By taking calibration measurements, the subject specific values of the proposed lumped components can be found. Specifically, the ability to measure the knee stiffness can provide valuable information. For example, lower-limb amputees can be prescribed by the proper prosthetic devices such that they can adapt to unimpaired gait [68], [69]. This information can also be used when designing a knee brace for amputees, especially to decide the brace material [70].

Finally, by continuously acquiring knee sound measurements with today’s wearable devices [71], gradual changes in knee health can be detected and correlated to the parameters of the analytical model to better understand the mechanism of injury and/or the success of the post-surgery rehabilitation period. The proposed analytical model can also be used to develop improved understanding of whole-body vibrations, and it can assist in developing analytical models for other parts of the body, such as femur.

IV. Conclusion

We demonstrated that the vibrational behavior of the knee-tibia structure can be analytically modelled using an Euler-Bernoulli beam model. The model was utilized to analyze the vibrations of the knee and to investigate the effects of structural changes within the joint following meniscal injury. Experimental verification was conducted on 46 healthy legs and 9 legs with meniscal tear. The findings suggest that the meniscal tear results in decrease in natural frequencies and damping ratios of the knee observed in the acoustic emission signals collected from articulating joints during flexion/extension. As there is a paucity of information in the literature regarding the correlation between the injury related changes in the knee sounds and the structural changes in the knee – the proposed combined analytical and experimental method can serve as a framework to address this knowledge gap, and to improve our understanding of the underlying physiological changes in the knee using acoustic emission and vibration analysis.

The agreement between the analytical model and the experimental data is an important finding of this study. To the best of our knowledge, this is the first time that such an analytical model for tibial vibration was proposed and validated. The model offers improved understanding of the tibial vibration and the resultant changes in modal characteristics with meniscus injury. It can be further developed by including soft tissues around the tibia to understand the effect of muscle contractility on tibial vibration. Lastly, since measuring and calculating the decay rate is computationally inexpensive, and it was shown to be a successful predictor of the knee health, it can be used as a knee health classifier through implementation in firmware on board an embedded system.