Abstract
Purpose.
To investigate the impact of 4D-CBCT image quality on radiomic analysis and the efficacy of using deep learning based image enhancement to improve the accuracy of radiomic features of 4D-CBCT.
Material and Methods.
In this study, 4D-CT data from 16 lung cancer patients were obtained. Digitally reconstructed radiographs (DRRs) were simulated from the 4D-CT, and then used to reconstruct 4D CBCT using the conventional FDK (Feldkamp et al 1984 J. Opt. Soc. Am. A 1 612–9) algorithm. Different projection numbers (i.e. 72, 120, 144, 180) and projection angle distributions (i.e. evenly distributed and unevenly distributed using angles from real 4D-CBCT scans) were simulated to generate the corresponding 4D-CBCT. A deep learning model (TecoGAN) was trained on 10 patients and validated on 3 patients to enhance the 4D-CBCT image quality to match with the corresponding ground-truth 4D-CT. The remaining 3 patients with different tumor sizes were used for testing. The radiomic features in 6 different categories, including histogram, GLCM, GLRLM, GLSZM, NGTDM, and wavelet, were extracted from the gross tumor volumes of each phase of original 4D-CBCT, enhanced 4D-CBCT, and 4D-CT. The radiomic features in 4D-CT were used as the ground-truth to evaluate the errors of the radiomic features in the original 4D-CBCT and enhanced 4D-CBCT. Errors in the original 4D-CBCT demonstrated the impact of image quality on radiomic features. Comparison between errors in the original 4D-CBCT and enhanced 4D-CBCT demonstrated the efficacy of using deep learning to improve the radiomic feature accuracy.
Results.
4D-CBCT image quality can substantially affect the accuracy of the radiomic features, and the degree of impact is feature-dependent. The deep learning model was able to enhance the anatomical details and edge information in the 4D-CBCT as well as removing other image artifacts. This enhancement of image quality resulted in reduced errors for most radiomic features. The average reduction of radiomics errors for 3 patients are 20.0%, 31.4%, 36.7%, 50.0%, 33.6% and 11.3% for histogram, GLCM, GLRLM, GLSZM, NGTDM and Wavelet features. And the error reduction was more significant for patients with larger tumors. The findings were consistent across different respiratory phases, projection numbers, and angle distributions.
Conclusions.
The study demonstrated that 4D-CBCT image quality has a significant impact on the radiomic analysis. The deep learning-based augmentation technique proved to be an effective approach to enhance 4D-CBCT image quality to improve the accuracy of radiomic analysis.
Keywords: deep learning, radiomics, generative adversarial networks, under-sampled projections, 4D-CBCT
1. Introduction
In the past several years, radiomics has been studied to extract information from image data for outcome prediction and treatment assessment (Nie et al 2019). Specifically, radiomic analysis extracts high dimensional quantitative features from images (Gillies et al 2016) to uncover characteristics that are hard to be distinguished by eyes. In recent publications, radiomics has proven its clinical values when extracting features from computed tomography (CT) (Ganeshan et al 2012, Lin et al 2020), magnetic resonance imaging (Chang et al 2019, Xu et al 2019), positron emission tomography (Bogowicz et al 2017) and cone-beam CT (CBCT) (van Timmeren et al 2019).
Several publications have shown that image quality can have a significant impact on radiomic analysis. The effects from acquisition methods, noise, and resolution have been studied. Firstly, different reconstruction kernels will cause variations of radiomic features, which may negatively impact the reproducibility of radiomic features. A convolutional neural network (CNN) was designed to standardize CT images between two different reconstruction kernels, B30f and B50f (Choe et al 2019). The results have shown that radiomic features were more reproducible after the standardization. Similarly, a generative adversarial network (GAN) has been used to normalize CT images of different imaging protocols, and the model successfully reduces the variability of radiomic features (Li et al 2020). In addition, the effect of CT image slice thickness on the reproducibility of radiomic features has been studied (Park et al 2019). In the study, a CNN- based super-resolution algorithm was developed to convert the CT images with slice thickness of 3 mm and 5 mm, to that of 1 mm. Results of concordance correlation coefficients evaluation showed that the robustness of radiomic features was significantly improved after the super-resolution enhancement. These publications have shown the efficacy of using deep learning methods to improve the robustness and accuracy of radiomic features by enhancing the CT image quality.
However, similar studies for CBCT images are lacking. CBCT images are scanned from patients for positioning guidance before the fractional treatment. Throughout the treatment courses, CBCT images can provide valuable information for treatment assessment, response prediction, or adaptive planning. For anatomical sites affected by respiratory motions, traditional 3D-CBCT only provides an average image from different respiratory phases, which would inevitably suffer from motion artifacts around the tumor and consequently degraded accuracy of radiomic analysis. Thus, four-dimensional CBCT (4D-CBCT) has been developed to minimize the motion artifacts by reconstructing respiratory phase-resolved images, providing benefits over 3D average CBCT images. However, due to the acquisition time and dose constraints, the projections acquired for each respiratory phase in a 4D-CBCT scan are always under-sampled, leading to severe noise and streak artifacts. Although the degraded image quality of 4D-CBCT will likely affect the accuracy of the radiomic analysis, no such studies have been carried out to investigate the effects.
Several methods were proposed to improve the image quality of 4D-CBCT: for example, motion compensation and prior knowledge-based estimation (Rit et al 2009, Ren et al 2014), iterative reconstruction (IR) algorithms based on the compressed sensing theory (Li et al 2002) and deep learning-based augmentation (Jiang et al 2019). The motion compensation method merges 10 phases of 4D-CBCT into a single phase with deformable registration. Although the image quality is improved, the reconstruction is time-consuming, and the motion blurriness would occur (Jiang et al 2019). IR methods, such as total variation, over smooth the anatomical structures and make images lack of high-frequency information. Besides traditional methods, deep learning has demonstrated its efficacy and efficiency for medical imaging augmentation. For example, SR-CNN (Jiang et al 2019) enhances the anatomical details and edge information of 4D-CBCT images in nearly real-time. Low-dose CT reconstruction CNN (Kang et al 2017) shows a greater power for denoising than traditional MBIR methods. However, most of the previous deep learning studies for image enhancement only augment 2D axial plane images for a single respiratory phase. For 4D-CBCT, it is valuable to make use of the inter-phase information for image enhancement. Temporally coherent GAN (TecoGAN) (Chu et al 2018) is a state-of-the-art model developed to generate super-resolution video sequences from low-resolution videos. In this study, we employed TecoGAN to generate high-quality 4D-CBCT from 10 phase low-quality 4D-CBCT by exploring the inter-phase information.
To our knowledge, there has not been any study to investigate the accuracy and robustness of radiomic analysis against 4D-CBCT image quality and the feasibility to use state-of-the-art image enhancement methods to improve the accuracy of radiomic analysis. In this study, we aim to investigate the accuracy and robustness of radiomic features against the under-sampling artifacts in 4D-CBCT reconstructed by the FDK method used in the clinics. Furthermore, we explored the efficacy of using a deep learning model, TecoGAN, to substantially enhance the image quality of 4D-CBCT, and hence, to improve the accuracy of radiomic features. The robustness of radiomic features over respiratory phases and the effects of projection number and angle distributions were also investigated. Overall, the study provides valuable insight into building a robust and accurate 4D-CBCT based radiomic analysis, which is crucial for its clinical applications in outcome prediction or treatment assessment.
2. Materials and methods
2.1. Overall workflow
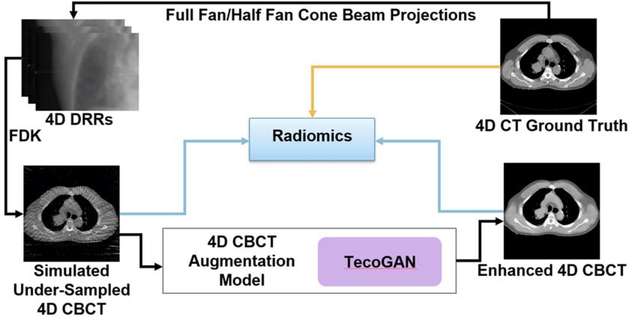
Figure 1 is a schematic illustration of the overall workflow of this study. In general, there are 4 steps for the workflow: (1) Generation of under-sampled 4D-CBCT images: 4D-CBCT were simulated from 4D-CT using DRRs and FDK reconstruction. (2) Enhancement of 4D-CBCT images using TecoGAN: 4D-CT were served as the ground truth, and the corresponding 4D-CBCT simulated in step 1 were served as the input. 4D-CBCT images from 10 patients were used for training, another 4D-CBCT images from 3 patients were used for validation, and the remaining 4D-CBCT from 3 patients were used for testing. (3) Radiomics extraction: 540 radiomic features are extracted from the gross tumor volume (GTV) of each of the 3 patients. (4) Evaluation: Intensity histograms, difference image, and radiomic features extracted from original 4D-CBCT and enhanced 4D-CBCT are compared to those extracted from the ground truth 4D-CT.
Figure 1.
Workflow of the study.
2.2. DRRs and FDK reconstruction
4D-CT volumes are served as the ground truth for original 4D-CBCT simulation. 4D-CBCT images with different projection numbers: 72, 120, 144, and 180 projections per phase were simulated. These projection angles are evenly distributed through 360°. However, in real CBCT machines from Varian or Elekta, the angles are not evenly distributed. Thus, projection angle distribution information from Varian and Elekta machine was obtained and it has been used to generate more realistic 4D-CBCT images. The Varian system contains ~300 half-fan projections per phase and the Elekta has ~100 full-fan projections per phase. The projections were simulated using a ray-tracing algorithm from the CT images without scatter and used an in-house FDK reconstruction software for 4D-CBCT reconstruction. The software is MATLAB based and it has also been used for a few published papers from our group (Chen et al 2018, 2019, Jiang et al 2020). The reconstruction geometry was set up based on the real on-board imaging system. Specially, the projection matrix size is 512 × 384 with a pixel size of 0.776 mm × 0.776 mm. The source-to-isocenter distance is 100 cm, and the source-to-detector distance is 150 cm. The detector was shifted 16 cm for half-fan projection acquisition. Projections were processed with spectral-domain Hamming filter and then back-projected to generate the 3D images. The simulated 4D-CBCT has 512 × 512 size and [0.9766 mm, 0.9766 mm, 3 mm] resolution.
2.3. TecoGAN deep learning network (Chu et al 2018)
2.3.1. The architecture of TecoGAN model
TecoGAN architectures consist of three components: a recurrent generator G, a flow estimation network F, and a discriminator D. Instead of learning the frames directly, TecoGAN learns the motion compensation to reduce the model complexity and improve the speed of training. The generator is used to generate high-resolution video frames recurrently by concatenating the last generated frame with the motion estimation. The motion compensation learns the differences between frames and helps to provide a motion prediction of the next frame. The discriminator used warping to deform the previous frame forward, later frame backward, and recognize the temporal correctness of the image frames. Appendix A shows the detailed architectures of the generator, discriminator, and flow estimator.
2.3.2. Loss functions of TecoGAN
Both the loss function of generator G and flow estimation network F are defined as the sum of 6 different losses LMSE,–Ladversarial, Lfeature space, LVGG, Lpp, and Lwarp:
| (1) |
where λi is the weighting parameter for losses.
Equations (2)–(7) represent a detailed explanation of 6 losses. In the equations, g denotes the generated image. yt represents the real images. D is the discriminator function, and Ig represents a sequence of generated images: [gt−1, gt, gt+1]. Φ denotes the feature map from the pretrained VGG-19 network (Simonyan and Zisserman 2014), and W means warping that corrects the image distortion.
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
The mean squared error loss LMSE is the difference between the ground truth 4D-CT image and the enhanced 4D-CBCT image. The adversarial loss, Ladversarial represents the evaluation ability of the discriminator. If the generated image looks like a 4D-CT image, Ladversarial is small. On the contrary, large Ladversarial means the generated image does not look like a 4D-CT image. LVGG is the perceptual loss (Simonyan and Zisserman 2014). It improves the high-level perceptual similarity between the generated image and ground truth. The ping pong loss, LPP, is the difference between the two generated images in different ordering. Specifically, gk is the image generated from the standard ordering of input, and g′k denotes the image generated from the reversed ordering of the input. The loss has demonstrated the capability to remove the drifting artifacts and improve temporal coherence. The warping loss Lwarp is used to improve the flow estimation network F by calculating the difference between the real image and F estimated image. The total loss LG,F combines all the 6 losses above.
2.3.3. Configuration of TecoGAN
During the training process, the learning rate has been set to 1.2e-5 and decay rate = 0.8 to reduce the possibility of overfitting and stabilize the output images at the end. The Adam optimizer with beta1 = 0.9 and beta2 = 0.999 is used. Batch size has been set to be 4 to reduce memory usage.
2.4. Experiment design
2.4.1. Dataset
The training dataset of the study was obtained from the SPARE Challenge dataset (Shieh et al 2019). It is a dataset used for sparse-view reconstruction challenge for 4D-CBCT. In this study, prior 4D-CT images from 13 lung patients, each patient with one scan, were obtained from the SPARE challenge dataset. These 4D-CT scans served as the ground truth of the TecoGAN model. Specifically, 10 scans were used as training, and 3 scans were used for validation. For the testing dataset, 4D-CT images with different GTV tumor sizes from 3 lung cancer patients treated in our clinic were obtained. Patient GTV size information is shown in table 1.
Table 1.
Patient GTV size information.
| Patient # | GTV diameter | GTV volume |
|---|---|---|
| 1 | 2.7 cm | 9.8 cm3 |
| 2 | 4.8 cm | 57.2 cm3 |
| 3 | 8.9 cm | 369 cm3 |
To reduce the impact of couch and artifacts outside the body, we generated body contour masks for each image. A threshold of −800 HU was set to remove the intensity values outside of the body. The background intensity was set at −1000 HU. Furthermore, the flood fill algorithm has been implemented to fill the holes inside the lung after thresholding. In this case, the model training will focus on the body without affecting by the noise and artifacts outside the body.
After the data preparation step, the 4D-CBCT dataset were generated with the image dimension of 512 × 512. Due to the FDK reconstruction algorithm, the intensity distribution of 4D-CBCT is intrinsically different from that of the CT. So, images of 4D-CBCT were scaled to [−1000, 3000] to match the intensity of 4D-CT. These images have been cropped to 256 × 256 by excluding outside of the body to reduce the training time and memory usage. Each of the original 4D-CBCT data has a paired ground truth 4D-CT data. All the 4D-CT data are bicubically resized from 256 × 256 to 1024 × 1024 since the TecoGAN model requires x4 resolution of input. After the training and testing, the output images, which has size of 1024 × 1024, were resized back to 256 × 256 to match with the resolution of the input 4D-CBCT.
2.4.2. Radiomics extraction
In this study, radiomics extraction requires 4 steps (Gillies et al 2016): (1) acquiring the images (2) identify and segment the GTV (3) preprocessing (4) feature extraction.
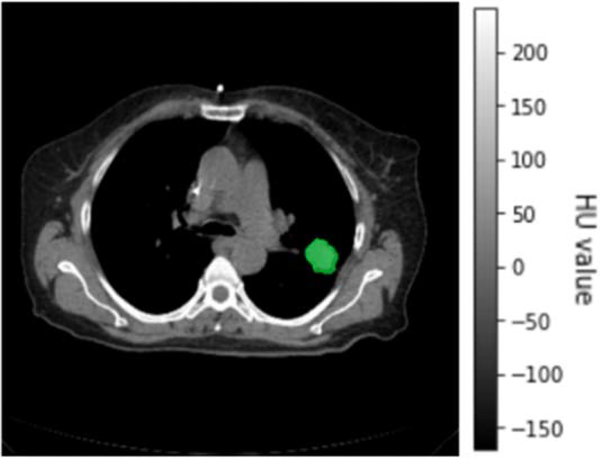
For the first step, the images for radiomic analysis were obtained from testing data. For each patient, the original 4D-CBCT, enhanced 4D-CBCT, and the ground truth 4D-CT were acquired. Then, in each phase, the GTV, was identified and segmented manually by the physician. The GTV information of the testing group is shown in table 1. Figure 2 has shown a slice of 4D-CT image with GTV of patient 1, phase 5.
Figure 2.
GTV of patient 1 in phase 5.
Next, z-score normalization has been performed on the GTVs of each 4D-CBCT so that the intensities of GTVs of different patients are on a standardized scale before feature extraction. Radiomic features were extracted with [1, 1, 3] mm voxel size and 256 bins. For each patient, radiomic features from the original 4D-CBCT, enhanced 4D-CBCT, and the ground-truth 4D-CT were calculated. For each 4D image, radiomic features from 10 different phases were obtained to evaluate the robustness of radiomic features against phases. In total, 540 radiomic features were extracted from the GTV of images based on the MATLAB based radiomics toolbox (Vallières et al 2015). These features include 7 histograms features: variance, skewness, kurtosis, mean, energy, entropy and uniformity; 53 texture features: 22 gray level co-occurrence matrix (GLCM) (Haralick et al 1973), 13 gray-level run-length matrix (GLRLM) (Galloway 1974), 13 gray level size-zone matrix (GLSZM) (Thibault et al 2014), 5 neighborhood gray-tone difference matrix (NGTDM) (Amadasun and King 1989); 480 wavelet features which are obtained based on the 60 features mentioned above by performing wavelet band-pass filtering to the images in eight different octants (Xu et al 2019). In this study, the shape features were excluded in the analysis since the same GTV contour was used for CT and CBCT images for the same patient.
2.4.3. Investigate the impact of projection numbers and angle distributions on 4D-CBCT radiomic analysis
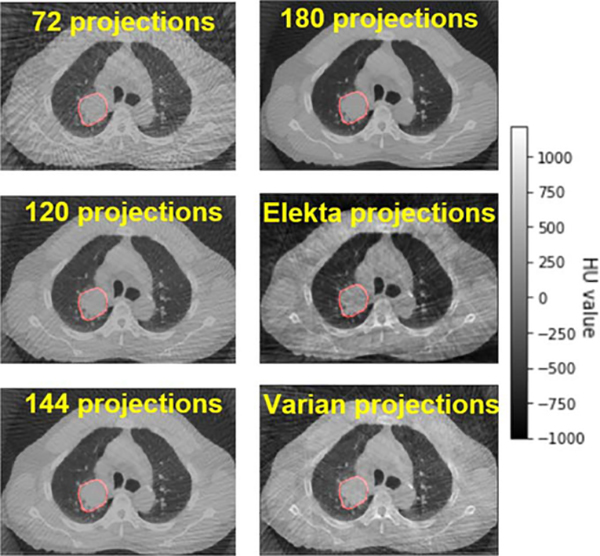
For original 4D-CBCT, under-sampled projections were simulated from the 4D-CT ground truth based on the full fan or half fan cone beam. To investigate the impact of projection angles on radiomic analysis, we simulated the 4D-CBCT with the different numbers of half fan cone-beam projections: 72, 120, 144, 180 for each phase. These projections are evenly distributed over a 360° scan angle. Real unevenly distributed projection angles extracted from Elekta and Varian patient scans were also used to simulate the 4D-CBCT. In total, 6 scenarios for different projection numbers and angle distributions were simulated in the study, as listed in table 2. The FDK reconstruction method was used to generate 6 groups of 4D-CBCT images. Figure 3 is an example of the simulated 4D-CBCT images for different scenarios.
Table 2.
Different cone-beam projections used for FDK reconstruction to simulate 4D-CBCT from 4D-CT images.
| # of projections per phase | Angle distributions | Geometry |
|---|---|---|
| 72 | Evenly | Half fan |
| 120 | Evenly | Half fan |
| 144 | Evenly | Half fan |
| 180 | Evenly | Half fan |
| ~100 (Real elekta projections) | Unevenly | Full fan |
| ~300 (Real varian projections) | Unevenly | Half fan |
Figure 3.
Simulated 4D-CBCT images from the different number of projections.
2.4.4. Investigate radiomic features robustness against phases
For our dataset, each 4D-CT or 4D-CBCT consists of 10 phases of the breathing cycle. The radiomic features of the tumor can change with the respiratory phases due to the deformations and variations of the artifacts. In this study, radiomic features were extracted from all the 10 phases of original 4D-CBCT, enhanced 4D-CBCT, and ground truth 4D-CT. The robustness of radiomic features across 10 phases before and after deep learning enhancement was studied.
2.4.5. Evaluation
To evaluate the performance of TecoGAN models, we compared the results of the original 4D-CBCT and the enhanced 4D-CBCT with the ground truth 4D-CT. The intensity histogram from the whole body and GTV of original 4D-CBCT, enhanced 4D-CBCT, and 4D-CT were compared. The image differences between the original 4D-CBCT and 4D-CT, enhanced 4D-CBCT and 4D-CT were evaluated.
To evaluate the accuracy of radiomic features extracted from 4D-CBCT, the error of each feature was defined based on the following formula:
| (8) |
In the formula, the 4D-CT features served as the ground truth. Both the original 4D-CBCT feature and enhanced 4D-CBCT feature were compared with the ground truth by calculating the relative difference of the features. This feature error was calculated for each phase of the original 4D-CBCT and the enhanced 4D-CBCT.
3. Results
3.1. Image evaluation
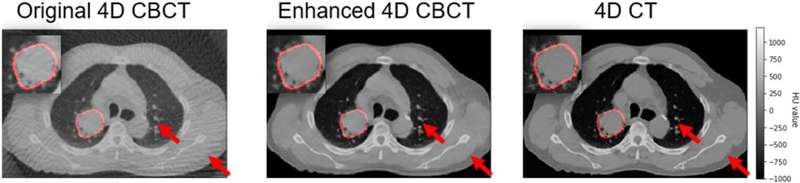
Figure 4 demonstrated examples of the under-sampled 4D-CBCT (original 4D-CBCT) simulated from evenly distributed 120 half-fan cone-beam projections, enhanced 4D-CBCT, and the ground truth 4D-CT. The enhanced result proves that TecoGAN model is able to remove noise and streaks without compromising the high-frequency anatomical details. In addition, the general intensities and contrast of the enhanced 4D-CBCT images are much closer to the ground truth 4D-CT than the original 4D-CBCT. The regions circled by red color represent GTV of each image, and these GTVs were magnified at the upper left corner of each image. In each image, the red arrows are two random picked locations for the convenience of image comparison. The locations of arrows are same in each image.
Figure 4.
Simulated 4D-CBCT, enhanced 4D-CBCT with corresponding real 4D-CT images of patient 2.
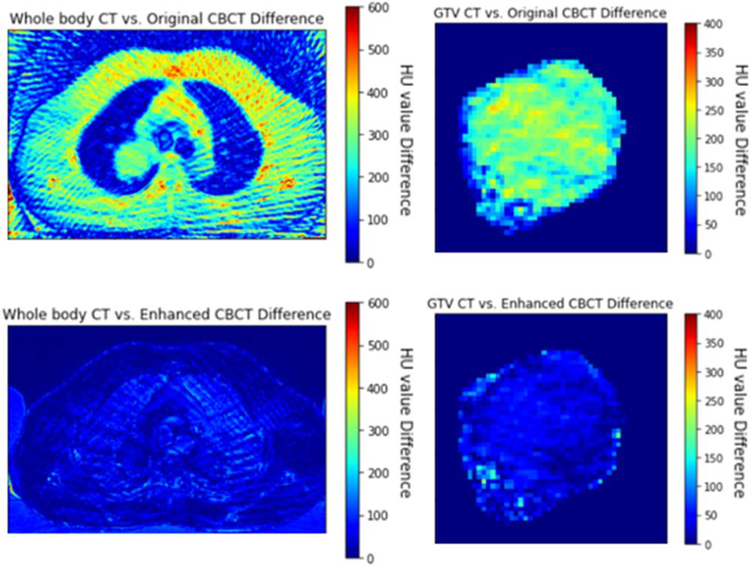
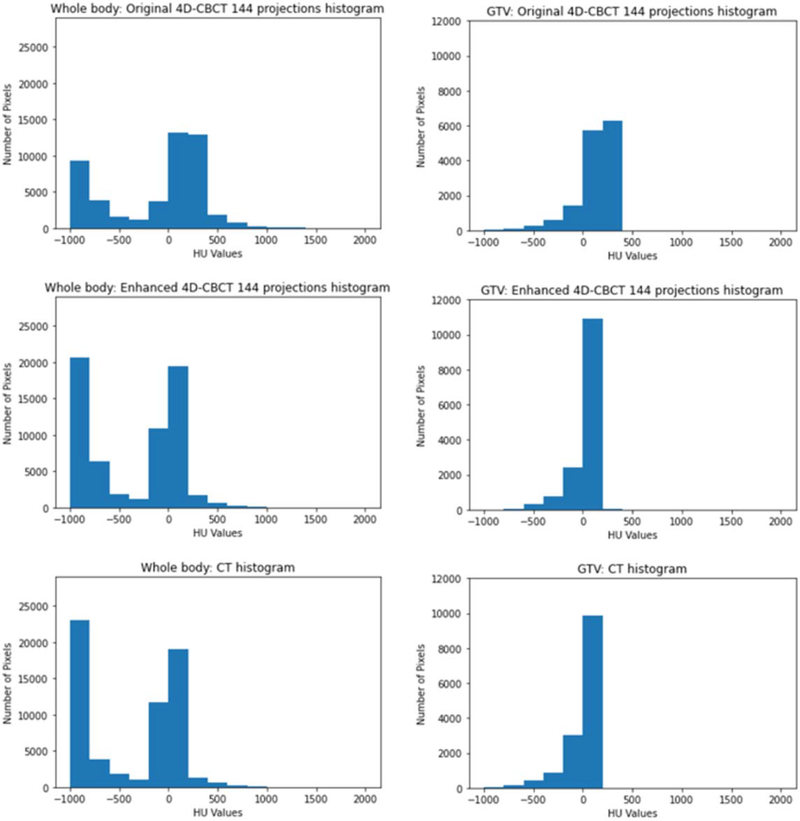
Figure 5 Shows the image intensity difference of original 4D-CBCT versus 4D-CT, enhanced 4D-CBCT versus 4D-CT. These images indicate that TecoGAN model has the capability to correct the original 4D-CBCT pixel values to match with the ground-truth 4D-CT pixel values in both GTV and whole body. Figure 6 shows the pixel value histogram comparisons. These plots indicate that TecoGAN can effectively correct the distribution of HU values in the original 4D-CBCT to match with 4D-CT.
Figure 5.
GTV and whole body intensity difference of patient 2, the spectrums represent the value difference of images.
Figure 6.
GTV and whole body intensity histogram of patient 2.
3.2. Radiomics evaluations
3.2.1. Radiomic features of a single phase
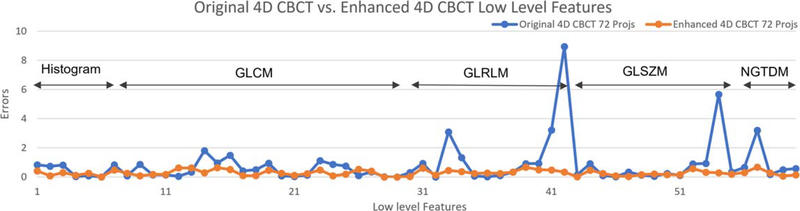
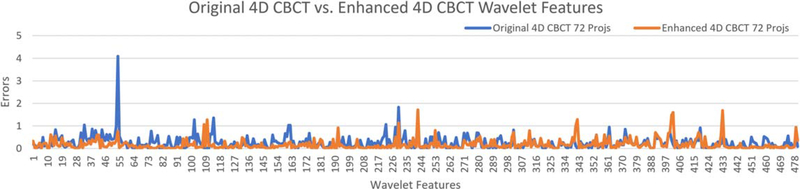
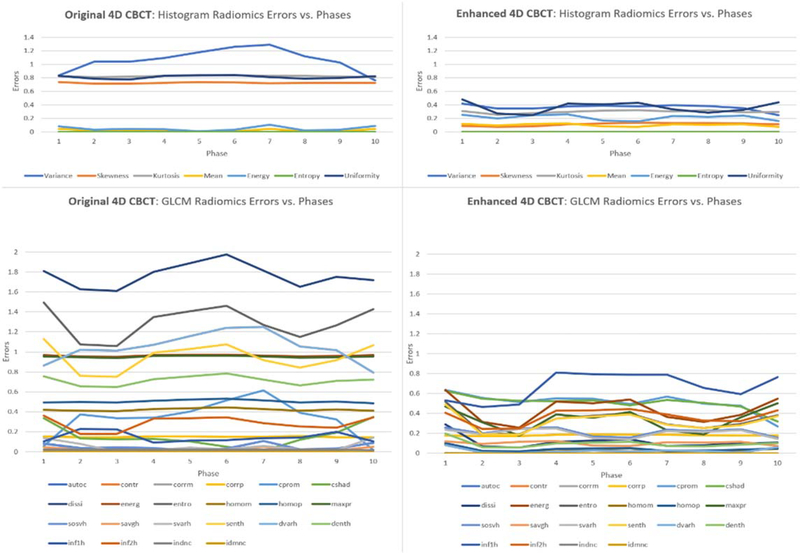
Figures 7 and 8 show the errors of different radiomic features for the original 4D-CBCT and enhanced 4D-CBCT for patient 3. The plots are based on the results of phase 1 of 4D-CBCT reconstructed from 72 projections. Figure 7 shows the low-level feature (Histogram, GLCM, GLRLM, GLSZM, NGTDM) errors of original 4D-CBCT and enhanced 4D-CBCT. Figure 8 plots the higher order wavelet feature errors. In each of the plots, the blue line represents the original 4D-CBCT radiomics errors, and the orange line shows the errors of enhanced 4D-CBCT. In general, the magnitude of the errors is highly feature-dependent. The enhanced 4D-CBCT has less errors for most of low-level features. Among all the features, run-length variance feature had the most significant improvement among all low-level features. The gray level intensity variance feature in low-frequency sub-bands had the most improvement in all wavelet features.
Figure 7.
Intensity and texture features of patient 3, phase 1, 72 projections.
Figure 8.
Wavelet features errors of patient 3, phase 1, 72 projections.
3.2.2. Radiomic features across 10 phases
Radiomics errors across 10 phases are shown in figure 9. In this figure, histogram features and GLCM results of patient 3 with a tumor diameter of 8.9 cm was used. The left column includes the errors of the histogram and GLCM features in all 10 phases of the original 4D-CBCT. The right column includes the errors of the histogram and GLCM features in all 10 phases of the enhanced 4D-CBCT. Each line in the figure represents a feature over 10 phases. From the overall view of the figure, the radiomic feature errors were substantially reduced after the image enhancement, and the error reduction was consistent across all phases.
Figure 9.
Histogram and GLCM radiomics errors across 10 phases of patient 3.
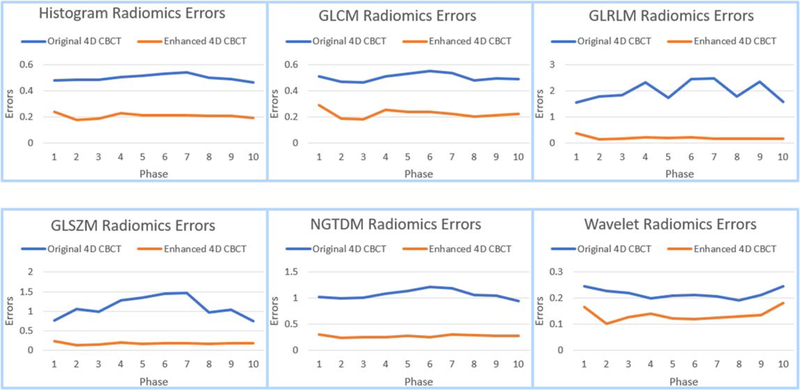
Figure 10 shows the average errors of different categories of radiomic features of patient 3. It contains 6 different categories (Histogram, GLCM, GLRLM, GLSZM, NGTDM, Wavelet) across 10 phases of 4D-CBCT reconstructed using 72 projections. The blue lines represent errors of original 4D-CBCT across 10 phases, and the orange lines are the radiomics errors of enhanced 4D-CBCT. In general, the errors have been reduced and are more consistent across phases after enhancement.
Figure 10.
Average radiomics features of the histogram, GLCM, GLRLM, GLSZM, NGTDM and wavelet of patient 3.
3.2.3. Radiomics errors for different acquisition scenarios
Table 3 includes results from 3 patients of different GTV diameters: 2.7, 4.8 and 8.9 cm. For every patient, 4D-CBCT images for 6 different acquisition scenarios were compared in different categories: histogram, GLCM, GLRLM, GLSZM, NGTDM, wavelet. The mean and standard deviation of feature errors are listed for each category. Green color indicates the enhanced CBCT has smaller errors than the original CBCT, while red color indicates the opposite. Results showed that the enhanced CBCT has less error than the original CBCT for the majority of radiomic features. The improvement by the enhanced CBCT is more overwhelming for larger tumors. Based on the table, the average reduction of radiomics errors among 3 patients were calculated: 20.0%, 31.4%, 36.7%, 50.0%, 33.6% and 11.3% for histogram, GLCM, GLRLM, GLSZM, NGTDM and Wavelet features.
Table 3.
Radiomics errors of all three testing patients with different training data and different projection numbers.
| 2.7cm GTV Error | Histogram | GLCM | GLRLM | GLSZM | NGTDM | Wavelet |
| Original_CBCT_72 | 0.41±0.48 | 0.26±0.24 | 0.26±0.26 | 0.64±1.08 | 0.37±0.27 | 0.20±0.45 |
| Enhanced_CBCT_72 | 0.26±0.37 | 0.16±0.18 | 0.15±0.11 | 0.37±0.46 | 0.26±0.19 | 0.17±0.42 |
| Original_CBCT_120 | 0.31±0.44 | 0.18±0.2 | 0.2±0.2 | 0.54±0.95 | 0.26±0.2 | 0.15±0.29 |
| Enhanced_CBCT_120 | 0.37±0.71 | 0.13±0.15 | 0.18±0.14 | 0.27±0.33 | 0.19±0.16 | 0.12±0.17 |
| Original_CBCT_144 | 0.31±0.47 | 0.15±0.18 | 0.2±0.19 | 0.43±0.62 | 0.21±0.15 | 0.14±0.28 |
| Enhanced_CBCT_144 | 0.11±0.15 | 0.1±0.1 | 0.18±0.19 | 0.19±0.16 | 0.17±0.11 | 0.14±0.26 |
| Original_CBCT_180 | 0.22±0.35 | 0.1±0.14 | 0.14±0.16 | 0.28±0.34 | 0.14±0.1 | 0.119±0.22 |
| Enhanced_CBCT_180 | 0.2±0.37 | 0.09±0.1 | 0.17±0.17 | 0.14±0.11 | 0.12±0.07 | 0.120±0.21 |
| Original_CBCT_Elekta | 0.22±0.17 | 0.21±0.21 | 0.2±0.14 | 0.42±0.54 | 0.32±0.22 | 0.18±0.39 |
| Enhanced_CBCT_Elekta | 0.7±1.61 | 0.12±0.11 | 0.24±0.24 | 0.21±0.19 | 0.13±0.1 | 0.17±0.37 |
| Original_CBCT_Varian | 0.28±0.31 | 0.19±0.2 | 0.22±0.19 | 0.45±0.67 | 0.27±0.19 | 0.15±0.25 |
| Enhanced_CBCT_Varian | 0.38±0.78 | 0.1±0.09 | 0.18±0.17 | 0.18±0.15 | 0.18±0.1 | 0.14±0.24 |
| 4.8cm GTV Error | Histogram | GLCM | GLRLM | GLSZM | NGTDM | Wavelet |
| Original_CBCT_72 | 0.30±0.20 | 0.29±0.26 | 0.58±0.99 | 0.45±0.50 | 0.37±0.22 | 0.14±0.23 |
| Enhanced_CBCT_72 | 0.11±0.10 | 0.21±0.17 | 0.35±0.25 | 0.24±0.16 | 0.35±0.20 | 0.13±0.24 |
| Original_CBCT_120 | 0.23±0.19 | 0.24±0.23 | 0.37±0.57 | 0.29±0.29 | 0.38±0.29 | 0.12±0.26 |
| Enhanced_CBCT_120 | 0.18±0.14 | 0.23±0.20 | 0.21±0.16 | 0.19±0.11 | 0.43±0.27 | 0.12±0.20 |
| Original_CBCT_144 | 0.20±0.17 | 0.23±0.21 | 0.26±0.35 | 0.27±0.25 | 0.36±0.30 | 0.11±0.26 |
| Enhanced_CBCT_144 | 0.13±0.09 | 0.17±0.14 | 0.18±0.13 | 0.15±0.08 | 0.31±0.18 | 0.10±0.20 |
| Original_CBCT_180 | 0.18±0.17 | 0.20±0.19 | 0.16±0.14 | 0.23±0.21 | 0.36±0.30 | 0.11±0.26 |
| Enhanced_CBCT_180 | 0.11±0.07 | 0.14±0.12 | 0.22±0.15 | 0.13±0.07 | 0.28±0.16 | 0.10±0.15 |
| Original_CBCT_Elekta | 0.34±0.26 | 0.30±0.24 | 0.44±0.52 | 0.50±0.61 | 0.46±0.42 | 0.16±0.41 |
| Enhanced_CBCT_Elekta | 0.18±0.16 | 0.15±0.14 | 0.14±0.11 | 0.19±0.13 | 0.32±0.30 | 0.14±0.37 |
| Original_CBCT_Varian | 0.24±0.20 | 0.25±0.23 | 0.37±0.53 | 0.32±0.31 | 0.40±0.34 | 0.116±0.22 |
| Enhanced_CBCT_Varian | 0.08±0.05 | 0.10±0.08 | 0.11±0.08 | 0.11±0.05 | 0.25±0.13 | 0.121±0.29 |
| 8.9cm GTV Error | Histogram | GLCM | GLRLM | GLSZM | NGTDM | Wavelet |
| Original_CBCT_72 | 0.5±0.46 | 0.5±0.51 | 1.99±3.89 | 1.11±2.49 | 1.07±1.14 | 0.22±0.23 |
| Enhanced_CBCT_72 | 0.21±0.14 | 0.22±0.19 | 0.19±0.08 | 0.18±0.12 | 0.27±0.2 | 0.14±0.16 |
| Original_CBCT_120 | 0.39±0.29 | 0.41±0.34 | 1.7±2.9 | 0.61±1 | 0.69±0.51 | 0.18±0.19 |
| Enhanced_CBCT_ 120 | 0.21±0.22 | 0.23±0.23 | 0.47±0.35 | 0.3±0.29 | 0.29±0.19 | 0.13±0.14 |
| Original_CBCT_144 | 0.34±0.29 | 0.35±0.3 | 1.13±1.63 | 0.45±0.68 | 0.58±0.37 | 0.16±0.18 |
| Enhanced_CBCT 144 | 0.21±0.19 | 0.25±0.22 | 0.44±0.37 | 0.28±0.32 | 0.33±0.18 | 0.13±0.14 |
| Original_CBCT_180 | 0.3±0.24 | 0.33±0.26 | 0.8±0.94 | 0.41±0.55 | 0.47±0.29 | 0.14±0.14 |
| Enhanced_CBCT_180 | 0.2±0.17 | 0.23±0.2 | 0.35±0.21 | 0.28±0.26 | 0.29±0.17 | 0.13±0.16 |
| Original_CBCT_Elekta | 0.73±0.78 | 0.64±0.53 | 1.44±2.35 | 0.99±2.18 | 1.49±1.72 | 0.22±0.21 |
| Enhanced_CBCT_Elekta | 0.44±0.4 | 0.62±0.61 | 0.66±0.41 | 0.57±0.74 | 0.67±0.71 | 0.20±0.24 |
| Original_CBCT_Varian | 0.4±0.31 | 0.41±0.34 | 1.57±2.64 | 0.59±0.97 | 0.72±0.53 | 0.18±0.19 |
| Enhanced_CBCT_Varian | 0.26±0.21 | 0.33±0.31 | 0.42±0.24 | 0.31±0.26 | 0.31±0.3 | 0.14±0.16 |
3.3. Runtime
The network was implemented in Python 3 and Tensorflow 1.14 framework. Models were trained separately for different acquisition scenarios. For each model, the training took 72 h on an NVIDIA Tesla P100 GPU with 100000 iterations. The enhancement step for each 4D-CBCT takes 0.75 s per slice.
4. Discussion
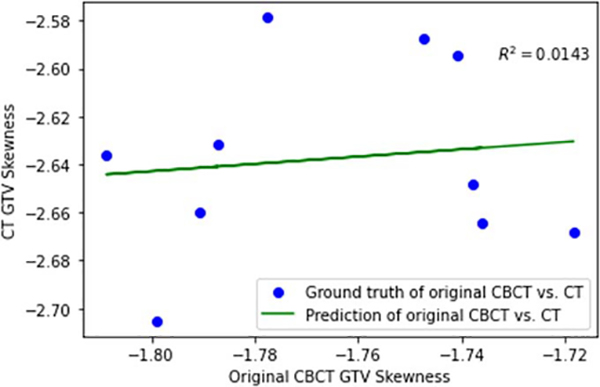
Radiomic features have been widely investigated for diagnosis and outcome prediction for lung cancer. However, there have been growing concerns about the robustness and reproducibility of radiomic features in recent years. Investigating this issue is especially crucial for CBCT based radiomic analysis considering the limited image quality of CBCT. A previous study showed that the CBCT images were affected by the scanner, scatter, and motion artifacts (Fave et al 2015). As a result, the image quality degradation is different for different scenarios. Furthermore, the impact of image quality degradation on radiomic features is dependent on the specific calculation of each feature, which is often nonlinear, especially for higher-order features. Thus, a simple scaling or offset would not be enough to correct the errors. Instead, we need an advanced technique, such as deep learning, to first address the image quality before deriving radiomic features, which is the rationale of this study. To validate this claim further, we implemented a linear regression algorithm to correct the radiomics features of 4D CBCT. As an example, we calculated the skewness feature from both the original 4D-CBCT and 4D-CT for linear regression. Figure 11 below shows the regression results between features extracted from 10 phases of 4D-CBCT and 4D-CT. From the results, the coefficient of determination after regression is R2 = 0.0143, which means the CBCT and ground-truth CT features are not linearly correlated. We further compared the radiomics errors after the two correction methods: linear regression and deep learning. The mean square error of linear regression corrected radiomics is 0.4314, while the mean square error of deep learning corrected radiomics is 0.1299. These results justify the need to use the deep learning GAN model to improve the image quality first before radiomics calculation. In summary, both logical analysis and experimental results demonstrated that the radiomic features in CBCT are not a simple systematic scaling or offset of ground-truth feature values in CT, but rather a complex nonlinear degradation of the CT features. Therefore, when CBCT radiomic features are used for outcome prediction, its prediction inevitably deviates from the prediction using the ground-truth CT, leading to degraded prediction accuracy.
Figure 11.
Linear Regression of skewness features from 4D-CBCT to 4D-CT.
Another aim of this project is to enhance the 4D-CBCT images for better radiomics results by deep learning-based image enhancement. As discussed above, 4D-CBCT images are suffer from noise, artifacts, and HU inaccuracy. As shown in figure 6, the histogram of original 4D-CBCT HU values is different from that of the CT. The difference is mainly due to two factors: (1) Undersampling in data acquisition: Projections are always undersampled in 4D-CBCT acquisition, violating the Nyquist-Shannon sampling theorem. This lack of complete information in the acquired data leads to ill-conditioning of the reconstruction problem itself, which inevitably causes inaccuracy of pixel values in the reconstructed images. (2) Limitation of the FDK reconstruction algorithm: FDK reconstruction basically preprocesses projection images with a spectral-domain Hamming filter and then back-project them to generate the 3D images. FDK is a fast approximate reconstruction algorithm that is widely used due to its speed. However, FDK does not maintain good data fidelity like IR does. In other words, the DRRs of the FDK reconstructed images do not match well with the pixel values in the acquired projections used for reconstruction. This lack of data fidelity in FDK reconstruction leads to deviations in the pixel values of the reconstructed image. The two factors above combined led to differences CBCT and CT histograms, even without scatter or beam hardening. The model effectively reduced the noise, streaks artifacts as well as corrected the HU values in 4D-CBCT.
For radiomic analysis, 540 features were extracted from GTV of patients, and the robustness and accuracy of features before and after enhancement were studied in three aspects: (1) accuracy of radiomic features within one phase (2) robustness of radiomic features across 10 phases (3) accuracy of radiomic features across different acquisition scenarios. Results showed an overall improvement of all feature categories after the enhancement of 4D-CBCT. This improvement was consistent across all 10 phases of 4D-CBCT. The improvement of radiomic feature accuracy was also observed for the majority of features for different acquisition scenarios. Original 4D-CBCT reconstructed from fewer projections with worse qualities had more significant improvement after the enhancement compared to 4D-CBCT with better qualities to start with. Results also showed that the improvement of radiomic feature accuracy was more overwhelming for large tumors.
There are several limitations of this study. Firstly, the efficacy of CBCT enhancement to improve radiomic feature accuracy is affected by two factors: (1) Tumor size. The deep learning model was trained to enhance the general quality of the entire body, not just the tumor region, in CBCT images. The larger the tumor is, the more weight it has in the deep learning enhancement, and consequently, the more accurate its radiomic feature will be. As shown in table 3, the accuracy of radiomic features after deep learning enhancement improved as tumor size increased. In the future, we will explore the feasibility of training a deep learning model to enhance a specific region of interest in the CBCT images, such as the tumor region. (2) Loss function of the deep learning training. The TecoGAN model was trained to improve the image quality by minimizing a loss function, which is the L1 loss between pixel values in CBCT and CT. On the other hand, the radiomic features used to evaluate the enhanced images include not just first-order metrics, such as histogram, but also many higher-order features. The discrepancy between training loss function and evaluation metrics, i.e. radiomic features, can affect the efficacy of correcting radiomic errors. As shown in table 3, for large tumors, the limited number of features that shows slightly larger errors after image improvement are mostly higher-order features. In the future, we will explore other loss functions that incorporate the information for higher-order features to improve the accuracy of these features after enhancement.
Secondly, simulated projections, instead of real projections, were used to reconstruct 4D-CBCT in this study. The advantage of using simulated projections is that the 4D-CT images used to generate the projections can be employed as the ground truth to evaluate the radiomic feature accuracy of the 4D-CBCT. The limitation is that noise and artifacts from a real projection acquisition were not considered in the study. In the future, we would like to carry out similar studies using real projections. However, one major challenge of using 4D-CBCT reconstructed from real projections is the lack of ground truth images to evaluate its radiomic feature accuracy. 4D-CT cannot be reliably used as the ground truth images due to the following reasons: (1) Deformations from 4D-CT to 4D-CBCT scans. Daily deformations caused by patient positioning or breathing changes can lead to changes in the radiomic feature values, especially for small tumors. Although deformable registration can be used to correct for the deformation, residual deformations always exist after the registration. (2) As 4D-CT and 4D-CBCT are always acquired on different days, there can be potential anatomical or texture changes of the tumor from the day of the CT scan to the day of the CBCT scan. Consequently, the textures extracted from 4D-CT may not reflect the true textures for the CBCT scan. One possible solution to address this challenge is to use Monte Carlo to simulate real projections from 4D-CT to generate 4D-CBCT. This way, there will be no daily deformation or texture changes, and the 4D-CT can be used as the ground truth to evaluate the 4D-CBCT. We will carry out this investigation in future studies.
Additionally, we think the uniqueness of our study is to look at the impact of 4D-CBCT image quality on radiomic analysis, which, to our knowledge, has not been investigated in the past. This is an important question that needs to be addressed to establish a robust radiomic analysis, and this new and important perspective sets our study apart from all previous publications. The observer variability due to tumor segmentation is a factor that has been investigated before, and it is not a focus of the current study. However, in the future, we do plan to incorporate contouring uncertainty into the study to investigate the combined effects from different aspects.
Furthermore, we used the SPARE dataset for training and dataset from our own institution for testing because its image quality and artifacts are similar to our own dataset. This method can also validate the robustness of the model across different datasets, which is also important for its clinical application. In the future, we plan to accrue more data from our own institution to investigate the potential to further improve the results. Moreover, we used TecoGAN for image enhancement and have not compared it with any other models. We would like to compare different deep learning methods in future studies.
Our current studies evaluated the accuracy of only handcrafted radiomic features. In the future, we can also investigate the accuracy of deep learning features, which are features extracted by a deep learning model. A study has developed deep learning features and demonstrated their potential applications for the prediction of overall survival. Lao et al (2017) Investigating the robustness and accuracy of these features in CBCT will be crucial for their clinical implementations.
5. Conclusion
In this study, we investigated the impact of 4D-CBCT image quality on the radiomic features and the efficacy of using a deep learning based method for 4D-CBCT image enhancement to improve the radiomic analysis. Results showed that radiomic features were affected by the under-sampling and reconstruction algorithm in 4D-CBCT. The degree of impact was feature-dependent. Furthermore, using deep learning for 4D-CBCT image enhancement showed the potential for improving the accuracy and robustness of radiomic feature analysis across different respiratory phases and image acquisition scenarios.
Acknowledgments
This work was supported by the National Institutes of Health under Grant No. R01-CA184173 and R01-EB028324.
Appendix A
In the following, details of TecoGAN architectures are listed (Chu et al 2018). Table A1 shows the architecture of the generator G, table A2 illustrated the architecture of the discriminator D and table A3 demo nstrated the architecture of the flow estimator F.
Table A2.
Architecture of the discriminator D.
| Layer | Input | Kernel size | Activation function | Output channel | Stride size | Output |
|---|---|---|---|---|---|---|
| Convolution | lin | 3 | LeakyReLU | 64 | 1 | l0 |
| Convolution | l0 | 4 | LeakyReLU | 64 | 2 | l1 |
| Convolution | l1 | 4 | LeakyReLU | 64 | 2 | l2 |
| Convolution | l2 | 4 | LeakyReLU | 128 | 2 | l3 |
| Convolution | l3 | 4 | LeakyReLU | 256 | 2 | l4 |
| Dense | l4 | / | Sigmoid | / | / | lout |
Table A3.
Architecture of the flow estimator F.
| Layer | Input | Kernel size | Activation function | Output channel | Stride size | Output |
|---|---|---|---|---|---|---|
| Convolution | lin | 3 | LeakyReLU | 32 | 1 | l0 |
| Convolution+MaxPooling | l0 | 3 | LeakyReLU | 32 | 1 | l1 |
| Convolution | l1 | 3 | LeakyReLU | 64 | 1 | l2 |
| Convolution+MaxPooling | l2 | 3 | LeakyReLU | 64 | 1 | l3 |
| Convolution | l3 | 3 | LeakyReLU | 128 | 1 | l4 |
| Convolution+MaxPooling | l4 | 3 | LeakyReLU | 128 | 1 | l5 |
| Convolution | l5 | 3 | LeakyReLU | 256 | 1 | l6 |
| Convolution+BilinearUp2 | l6 | 3 | LeakyReLU | 256 | 1 | l7 |
| Convolution | l7 | 3 | LeakyReLU | 128 | 1 | l8 |
| Convolution+BilinearUp2 | l8 | 3 | LeakyReLU | 128 | 1 | l9 |
| Convolution | l9 | 3 | LeakyReLU | 64 | 1 | l10 |
| Convolution+BilinearUp2 | l10 | 3 | LeakyReLU | 64 | 1 | lll |
| Convolution | l11 | 3 | LeakyReLU | 32 | 1 | l12 |
| Convolution | l12 | 3 | tanh | 2 | 1 | lout |
Table A1.
Architecture of the generator G.
| Layer | Input | Kernel size | Activation function | Output channel | Stride size | Output |
|---|---|---|---|---|---|---|
| Convolution | lin | 3 | ReLU | 64 | 1 | l0 |
| Residual block | li, i = 0,...,n − 1 | / | / | / | / | li+1 |
| Transposed convolution | ln | 3 | ReLU | 64 | 2 | lup2 |
| Transposed convolution | lup2 | 3 | ReLU | 64 | 2 | lup4 |
| Convolution | lup4 | 3 | ReLU | 3 | 1 | lres |
| Summation | Resize4 (xt), lres | / | / | / | / | gt |
Footnotes
Ethical statements
All patient data included in this study are anonymized. Patient data are acquired from SPARE Challenge data (https://image-x.sydney.edu.au/spare-challenge), and from Duke University Medical Center under an IRB-approved protocol.
References
- Amadasun M and King R 1989. Textural features corresponding to textural properties IEEE Trans. Syst. Man Cybern. 19 1264–74 [Google Scholar]
- Bogowicz M, Riesterer O, Stark LS, Studer G, Unkelbach J, Guckenberger M and Tanadini-Lang S 2017. Comparison of PET and CT radiomics for prediction of local tumor control in head and neck squamous cell carcinoma Acta Oncol 56 1531–6 [DOI] [PubMed] [Google Scholar]
- Chang Y, Lafata K, Sun W, Wang C, Chang Z, Kirkpatrick JP and Yin F-F 2019. An investigation of machine learning methods in delta-radiomics feature analysis PLoS One 14 e0226348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Yin FF, Zhang Y, Zhang Y and Ren L 2018. Low dose CBCT reconstruction via prior contour based total variation (PCTV) regularization: a feasibility study Phys. Med. Biol. 63 085014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Yin FF, Zhang Y, Zhang Y and Ren L 2019. Low dose cone-beam computed tomography reconstruction via hybrid prior contour based total variation regularization (hybrid-PCTV) Quantum Imaging Med. Surg. 9 1214–28 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choe J, Lee SM, Do K-H, Lee G, Lee J-G, Lee SM and Seo JB 2019. Deep learning–based image conversion of CT reconstruction kernels improves radiomics reproducibility for pulmonary nodules or masses Radiology 292 365–73 [DOI] [PubMed] [Google Scholar]
- Chu M, Xie Y, Leal-Taixé L and Thuerey N 2020. Learning temporal coherence via self-supervision for GAN-based video generation ACM Trans. Graphics 39 75 [Google Scholar]
- Fave X, Mackin D, Yang J, Zhang J, Fried D, Balter P, Followill D, Gomez D, Kyle Jones A and Stingo F 2015. Can radiomics features be reproducibly measured from CBCT images for patients with non-small cell lung cancer? Med. Phys. 42 6784–97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldkamp LA, Davis LC and Kress JW 1984. Practical cone-beam algorithm J. Opt. Soc. Am. A1 612–9 [Google Scholar]
- Galloway MM. Texture analysis using grey level run lengths. STIN. 1974;75:18555. [Google Scholar]
- Ganeshan B, Panayiotou E, Burnand K, Dizdarevic S and Miles K 2012. Tumour heterogeneity in non-small cell lung carcinoma assessed by CT texture analysis: a potential marker of survival Eur. Radiol. 22 796–802 [DOI] [PubMed] [Google Scholar]
- Gillies RJ, Kinahan PE and Hricak H 2016. Radiomics: images are more than pictures, theyare data Radiology 278 563–77 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haralick RM Shanmugam K and Dinstein I 1973. Textural features for image classification IEEE Trans. Syst. Man Cybern. SMC-3 610–21 [Google Scholar]
- Jiang Z, Chen Y, Zhang Y, Ge Y, Yin F and Ren L 2019. Augmentation of CBCT reconstructed from under-sampled projections using deep learning IEEE Trans. Med. Imaging 38 2705–15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Z, Yin F-F, Ge Y and Ren L 2020. Enhancing digital tomosynthesis (DTS) for lung radiotherapy guidance using patient-specific deep learningmodel Phys. Med. Biol. ( 10.1088/1361-6560/abcde8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang E, Min J and Ye JC 2017. A deep convolutional neural network using directional wavelets for low-dose x-ray CT reconstruction Med. Phys. 44 e360–75 [DOI] [PubMed] [Google Scholar]
- Lao J, Chen Y, Li Z-C, Li Q, Zhang J, Liu J and Zhai G 2017. A deep learning-based radiomics model for prediction of survival in glioblastoma multiforme Sci. Rep. 7 1–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, Yang H and Kudo H 2002. An accurate iterative reconstruction algorithm for sparse objects: application to 3D blood vessel reconstruction from a limited number ofprojections Phys. Med. Biol. 47 2599. [DOI] [PubMed] [Google Scholar]
- Li Y, Han G, Wu X, Li Z, Zhao K, Zhang Z, Liu Z and Liang C 2020. Normalization of multicenter CT radiomics by a generative adversarial network method Phys. Med. Biol. ( 10.1088/1361-6560/ab8319) [DOI] [PubMed] [Google Scholar]
- Lin P, Yang P-F, Chen S, Shao Y-Y, Xu L,Wu Y, Teng W, Zhou X-Z, Li B-H and Luo C 2020. A delta-radiomics model for preoperative evaluation of Neoadjuvant chemotherapy response in high-grade osteosarcoma CancerImaging 20 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nie K, Al-Hallaq H, Li XA, Benedict SH, Sohn JW, Moran JM, Fan Y, Huang M, Knopp MV and Michalski JM 2019. NCTN assessment on current applications of Radiomics in oncology Int. J. Radiat. Oncol Biol. Phys. 104 302–15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S, Lee SM, Do K-H, Lee J-G, Bae W, Park H, Jung K-H and Seo JB 2019. Deep learning algorithm for reducing CT slice thickness: effect on reproducibility of radiomic features in lung cancer Korean J. Radiol. 20 1431–40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren L, Zhang Y and Yin FF 2014. A limited-angle intrafraction verification (LIVE) system for radiation therapy Med. Phys. 41 020701. [DOI] [PubMed] [Google Scholar]
- Rit S, Wolthaus JW, van Herk M and Sonke JJ 2009. On-the-fly motion-compensated cone-beam CT using an a priori model of the respiratorymotion Med. Phys. 36 2283–96 [DOI] [PubMed] [Google Scholar]
- Shieh CC, Gonzalez Y, Li B, Jia X, Rit S, Mory C, Riblett M, Hugo G, Zhang Y and Jiang Z 2019. SPARE: sparse-view reconstruction challenge for 4D cone-beam CT from a 1-min scan Med. Phys. 46 3799–811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simonyan K and Zisserman A 2014. Very deep convolutional networks for large-scale image recognition arXiv preprint: [Google Scholar]
- Thibault G, Angulo J and Meyer F 2014. Advanced statistical matrices for texture characterization: application to cell classification IEEE Trans. Biomed. Eng. 61 630–7 [DOI] [PubMed] [Google Scholar]
- van Timmeren JE, van Elmpt W, Leijenaar RT, Reymen B, Monshouwer R, Bussink J, Paelinck L, Bogaert E, De Wagter C and Elhaseen E 2019. Longitudinal radiomics of cone-beam CT images from non-small cell lung cancer patients: evaluation of the added prognostic value for overall survival and locoregional recurrence Radiother. Oncol. 136 78–85 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallières M, Freeman CR, Skamene SR and El Naqa I 2015. A radiomics model from joint FDG-PET and MRI texture features for the prediction oflung metastases in soft-tissue sarcomas of the extremities Phys. Med. Biol. 60 5471. [DOI] [PubMed] [Google Scholar]
- Xu L, Yang P, Liang W, Liu W, Wang W, Luo C, Wang J, Peng Z, Xing L and Huang M 2019. A radiomics approach based on support vector machine using MR images for preoperative lymph node status evaluation in intrahepatic cholangiocarcinoma Theranostics 9 5374. [DOI] [PMC free article] [PubMed] [Google Scholar]