Gamma rhythm communication between entorhinal cortex and dentate gyrus neuronal assemblies

Abstract

INTRODUCTION:

Learning induces a dynamic reorganization of brain circuits but the neuronal mechanisms underlying this process are not well understood. Interregional gamma-frequency oscillations (~30 to 130 Hz) have been postulated as a mechanism to precisely coordinate upstream and downstream neuronal ensembles, for example, in the hippocampal system. The lateral (LEC) and medial (MEC) entorhinal cortex receive inputs from two distinct streams of cortical hierarchy (the “what” and the “where” paths) and convey these neuronal messages to the hippocampus. However, the mechanisms by which such messages are packaged and integrated or segregated by hippocampal circuits had yet to be explored.

RATIONALE:

Neuronal assemblies firing within gamma time frames in an upstream region can most effectively discharge their downstream partners. This gamma-time-scale organization appears essential for physiological functions because manipulations that impair precision timing of spikes in the hippocampus often affect behavior. However, direct support for distinct gamma-frequency communication in appropriate behavioral situations is missing. To bring physiological operations closer to behavior, we designed “spatial” and “object” learning tasks and examined the selective engagement of gamma-frequency communication between the MEC and LEC inputs and their target neuronal assemblies in the hippocampal dentate gyrus. We combined these correlational observations with optogenetic perturbation of gamma oscillations in LEC and MEC, respectively, to test their roles in pathway-specific neuronal communication and learning.

RESULTS:

During spatial learning, fast gamma (100 to 150 Hz) oscillations synchronized MEC and dentate gyrus and entrained predominantly granule cells. During object learning, slow gamma (30 to 50 Hz) oscillations synchronized LEC and dentate gyrus and preferentially recruited mossy cells and CA3 pyramidal neurons, suggesting task-specific routing of MEC and LEC messages in the form of gamma-cycle-spike packets of selected cell types. The low- and high-frequency gamma sub-bands were dominant in the outer and middle third of the dentate molecular layer, respectively, and their amplitude maxima were locked to different phases of theta oscillation.

Gamma frequency optogenenetic perturbation of MEC and LEC led to learning impairments in a spatial and object learning task, respectively. In the same animals, the dentate layer–specific low- and high-frequency gamma sub-bands and spike-gamma LFP coupling were selectively reduced, coupled with deterioration of spatial and object-related parameters of dentate neurons.

CONCLUSION:

These findings demonstrate that distinct gamma-frequency-specific communication between MEC and LEC and the hippocampal cell assemblies are critical for routing task-relevant information, and our selective gamma-band perturbation experiments suggest that they support specific aspects of learning. We hypothesize that sending neuronal messages by segregated gamma-frequency carriers allows a target “reader” area to disambiguate convergent inputs. In general, these results demonstrate that specific projected gamma patterns dynamically engage functionally related cell assemblies across brain regions in a task-specific manner.

Graphical Abstract

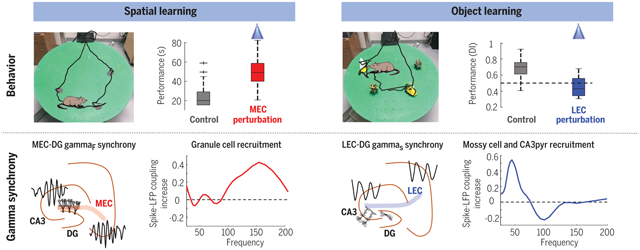
Task-specific engagement and gamma-frequency coupling of distinct neuronal populations. First row: Impairment of spatial (left) and object (right) learning during gamma-frequency perturbation of MEC (left) and LEC (right). Second row: MEC and LEC project high-frequency (gamma_F) and low-frequency (gamma_S) gamma oscillations to DG, respectively, and entrain granule cells, mossy cells, and CA3 pyramidal neurons in a task-specific manner.

Gamma oscillations are thought to coordinate the spike timing of functionally specialized neuronal ensembles across brain regions. To test this hypothesis, we optogenetically perturbed gamma spike timing in the rat medial (MEC) and lateral (LEC) entorhinal cortices and found impairments in spatial and object learning tasks, respectively. MEC and LEC were synchronized with the hippocampal dentate gyrus through high- and low-gamma-frequency rhythms, respectively, and engaged either granule cells or mossy cells and CA3 pyramidal cells in a task-dependent manner. Gamma perturbation disrupted the learning-induced assembly organization of target neurons. Our findings imply that pathway-specific gamma oscillations route task-relevant information between distinct neuronal subpopulations in the entorhinal-hippocampal circuit. We hypothesize that interregional gamma-time-scale spike coordination is a mechanism of neuronal communication.

Learning induces a dynamic reorganization in a brain circuit’s functional connectivity, but the cellular mechanisms underlying this process are not well understood. Interregional gamma synchrony has been proposed as a mechanism to precisely coordinate upstream and downstream neuronal assemblies (1–5). However, the supporting data to date are mostly correlational (6–14). The hippocampo-entorhinal network is an optimal candidate for the investigation of the functional role of gamma-frequency communication because of the behavioral dependence of oscillatory synchrony, its regular cytoarchitectural organization, and the laminar stratification of their synaptic inputs (15, 16). The hippocampus receives multimodal and higher-order inputs from the neocortex through its parahippocampal interface structures, most prominently the entorhinal cortex (17), and constructs temporally organized relationships among them [“maps” (18, 19)]. The major divisions of the entorhinal cortex, the lateral (LEC) and medial (MEC) areas, receive inputs from two relatively distinct streams of cortical hierarchy, the object processing ventral (“what”) and space-related dorsal (“where” or “how”) pathways (20, 21) through the perirhinal and postrhinal cortices, respectively (22). The physiological relevance of this anatomical segregation received a boost from the discovery of grid cells and other spatially modulated neurons, such as border cell and head direction cells, in MEC and their absence in LEC (23–25), as well as from object-encoding neurons in LEC (26, 27). Furthermore, lesions in or inactivation of MEC or LEC has resulted in largely distinct impairment in spatial navigation and object recognition, respectively (28–30). However, it has been emphasized that the two pathways are intertwined at multiple stages, and the spatial versus object “processing” distinction is a strong simplification (22, 31, 32). Experiments demonstrate that neurons in the LEC display spatial properties, defined by object locations or remembered object locations (26, 27, 33). LEC lesions affect aspects of spatial navigation (30, 34). As a result, alternative formulations have recently been introduced, equating the function of MEC as supporting navigation based on global cues and an allocentric reference framework, whereas LEC would support local landmark-based navigation using an egocentric framework (31–33).

Irrespective of the designation of the functions of the two streams, how their final convergence is integrated by hippocampal circuits is not well understood. In the CA1 region, layer 3 MEC and LEC projections target different cell populations at the subicular and CA3-neighboring parts, and this connectivity shift is mirrored by the varying properties of place cells along the CA1 transverse axis (35, 36). By contrast, layer 2 neurons of MEC and LEC converge on the same dentate granule cells (GCs) and CA3 pyramidal (CA3pyr) cells (16, 37), and it has been postulated that the dentate gyrus (DG)–CA3 region is the critical location where inputs from MEC and LEC are integrated (38–43).

A key missing element in the above general framework is the physiological mechanisms by which neuronal information is conveyed from MEC and LEC to DG and/or CA3 neurons. A postulated mesoscopic mechanism of interregional communication are gamma-frequency oscillations (1–14). Neurons communicate most effectively as assemblies, and assemblies of neurons that fire within gamma time frames in an upstream region can most effectively discharge their downstream partners (44). However, direct support for the functional role of gamma-time-scale synchrony of neuronal spiking between the entorhinal cortices and DG-CA3 cell ensembles is missing.

To bring physiological operations closer to behavior, we present a set of experiments that allowed us to probe gamma-frequency communication between MEC and LEC and their target DG-CA3 regions during specific behaviors. We hypothesized that in situations when the DG-CA3 is more tuned to inputs from the LEC (such as object learning) or from the MEC (spatial learning), different gamma-oscillatory patterns synchronize specific neuronal populations in these circuits, and that the precisely timed firing of these neurons is critical for learning. To test this hypothesis, we leveraged several technical innovations that allowed us to identify the distinct gamma oscillations that synchronize MEC and LEC with their postsynaptic targets and to specifically perturb them to probe their role during learning. In spatial navigation and object recognition tasks, gamma-frequency coupling of neurons was selectively increased between the MEC-DG and LEC-DG areas, respectively. To support the validity of these correlations, we selectively perturbed gamma-cycle organization in MEC and LEC and examined the effect on the physiological activity in their target DG-CA3 neurons and learning of spatial and object memory tasks. Optogenetically induced gamma-frequency perturbation of MEC and LEC resulted in selective learning deficits in the spatial and object variants of the task, respectively, and differentially affected the MEC- and LEC-projected gamma rhythms in their target dentate dendritic layers.

RESULTS

Optogenetic perturbation of MEC and LEC circuits selectively impairs learning

We designed three learning tasks to examine the selective engagement of gamma-frequency communication between the hippocampus and two processing streams involved in spatial navigation (MEC) and object recognition (LEC) (Fig. 1, A to E, and materials and methods). In the “spatial learning task,” rats learned to find three hidden water rewards that had a fixed position on a “cheeseboard” maze within the same day but varied from day to day (Fig. 2A) (45). After collecting the three rewards, the rat was required to return to the home base, where it was confined for 10 s between trials. In the “object learning task,” a new pair of identical objects indicated reward location, and two other objects acted as distractors (Fig. 2B). The objects varied from day to day and required new object learning daily. In the “object-in-place” task, the maze was partitioned into left and right halves by a wall. In the left half of the platform, one of two objects cued the location of the water well and the other served as the distractor (Fig. 2C). In the right half of the platform, the significance of the objects was reversed so that the distractor object in the left half served as the reward cue in the right half. To succeed in this task, the rat had to both to correctly locate itself and learn to associate the platform side–specific object with reward location. This third task thus simultaneously probed the contribution of MEC and LEC.

Fig. 1. Experimental paradigm and optogenetic perturbation.

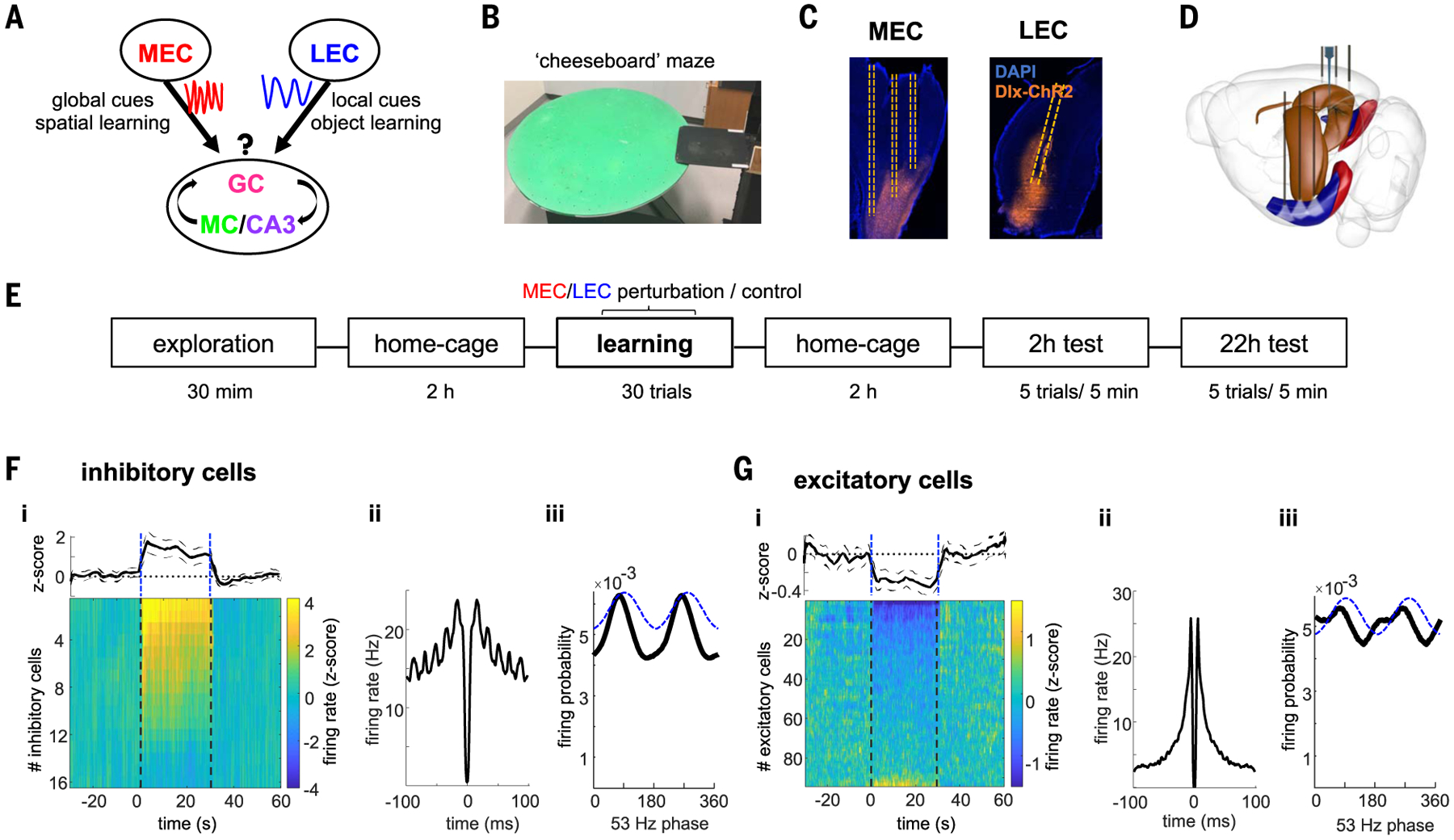
(A) Framework of MEC and LEC to DG communication conveying information about environmental global cues for spatial learning and object identity, respectively. We hypothesize that different gamma oscillations route these messages to specific hippocampal targets. (B) Photograph of the cheeseboard maze. (C) Histological section showing expression of Dlx-ChR2-mCherry in interneurons (orange) in MEC (sagittal slice) or LEC (coronal slice) and location of optic fibers (dashed lines). Blue is DAPI staining. (D) Schematic of the surgical implants. Three optic fibers in MEC or LEC bilaterally and silicon probe recordings in dorsal hippocampus. (E) Schema with timeline of the experiment. F) Entorhinal local perturbation and recording experiment. (F) (i) Average firing response across all entorhinal inhibitory cells showing a significant increase in their mean firing rates during 30 s of 53-Hz stimulation (1.6 ± 0.3 z-scored firing rate compared with baseline, n = 16 units from 2 rats, P < 0.001 sign-rank test). Each line is the average response of a single unit across 20 stimulation trials. Dashed lines indicate stimulation onset and offset. (ii) Average autocorrelogram for all inhibitory cells during stimulation show strong ~53-Hz modulation. (iii) Distribution of firing probability of all inhibitory units as a function of the phase of light stimulation (dashed blue line). (G) Same as (F) but for excitatory neurons (n = 86 units from 2 rats). On average, excitatory cells decreased their firing rates during stimulation (− 0.27 ± 0.06, P < 0.001, sign-rank test), although a minority of them increased their firing. Note that suppression of pyramidal cells is sixfold smaller than the magnitude of firing rate increase of interneurons.

Fig. 2. Optogenetic perturbation of MEC or LEC selectively affects learning.

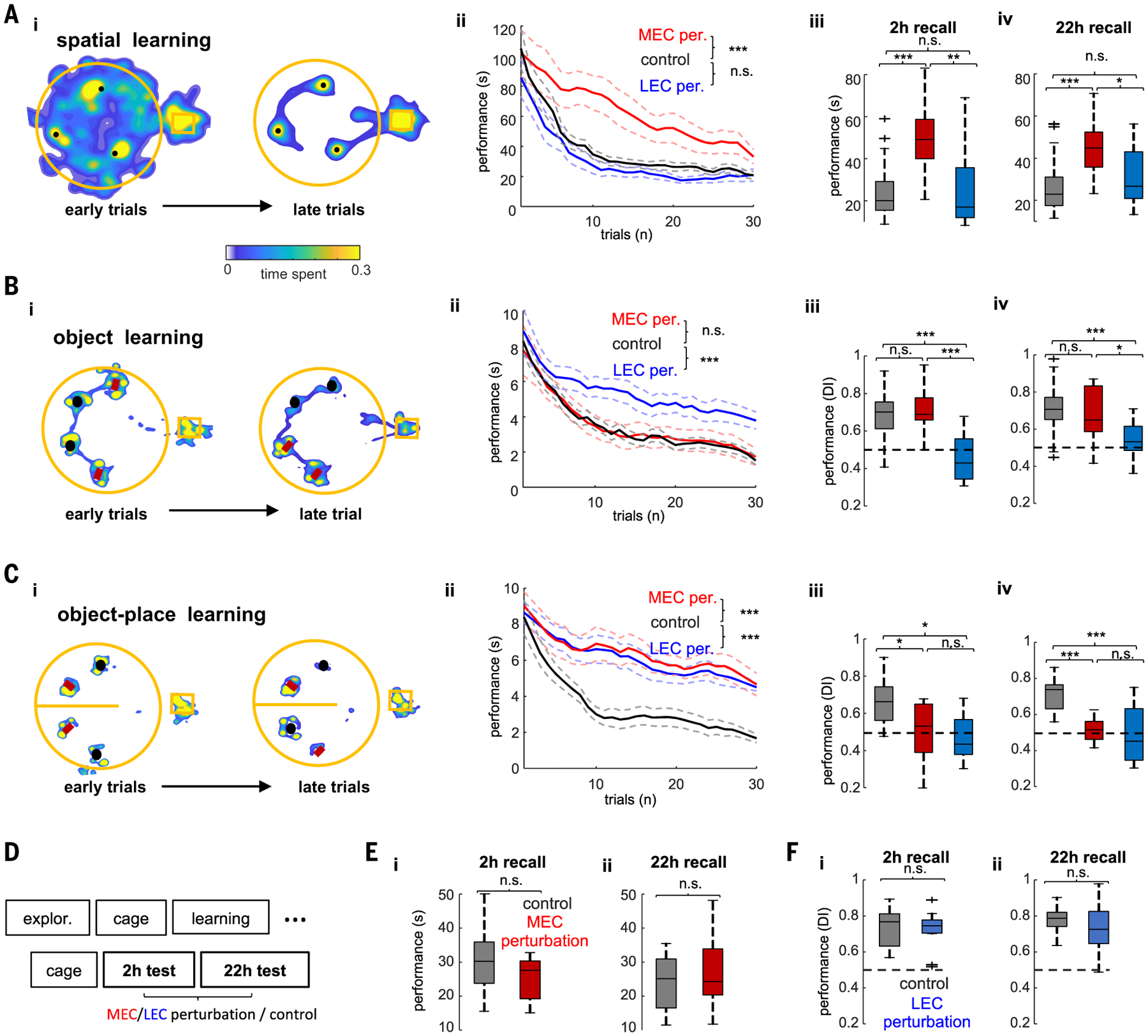
(A) Spatial learning task. (i) Example occupancy maps of the first three (left) and last three (right) learning trials. Black dots indicate locations of hidden water rewards. (ii) Learning performance quantified as time spent to find the three rewards during control (no stimulation) and MEC and LEC perturbation sessions (n = 6/6 rats in MEC and LEC tests, respectively). ANOVA with repeated measures showed a significant main effect of group (F_(2,60) = 93.96, P < 10⁻¹⁰). (iii and iv) Memory performance during recall test 2 hours after learning (F_(2,60)= 16.7, P = 1.4 × 10⁻⁶, one-way ANOVA) (iii) and 22 hours after learning (F_(2,60) = 10.62, P = 1 × 10⁻⁴, one-way ANOVA) (iv). (B) Same layout as in (A) but in the object learning task. Objects marked with red rectangles cued the location of reward. Black circles indicate distractor objects. (ii) Learning performance was quantified as time spent exploring around distractor objects [same 6/6 rats as in (F); F_(2,57) = 51.61, P < 10⁻¹⁰, repeated-measures ANOVA for group effect]. (iii and iv) Memory recall at 2 hours (iii) or 22 hours (iv) after learning was quantified with a DI (see the materials and methods; F_(2,57) = 21.55, P = 7.8 × 10⁻⁸ and F_(2,57) = 9.12, P = 4 × 10⁻⁴, for the 2-hour and 22-hour tests, respectively). (C) Object-in-place learning task. Same layout as in (A). In the right side of the maze (top part in the figure), the red object was rewarded and the black one served as a distractor. In the left side (bottom part in the figure), the black object was rewarded and the red one served as a distractor. Learning performance was quantified as in the object learning task (n = 4/4 rats in MEC and LEC tests). ANOVA with repeated measures showed a significant main effect of group during learning trials (F_(2,44) = 136.87, P < 10⁻¹⁰). Memory performance was also disrupted 2 hours after learning (F_(2,44)= 5.7, P = 7.6 × 10⁻³) and 22 hours after learning (F_(2,44)= 13.39, P = 6.9 × 10⁻⁵). *P < 0.05, **P < 0.01, ***P < 0.001, Tukey’s post hoc test. (E) Timeline of the experiment for testing the effect of MEC and/or LEC perturbation during postlearning test sessions. (F) Memory performance in the spatial memory task for control and MEC perturbation sessions during recall test 2 hours after learning (P = 0.35, rank-sum test) (i) and 22 hours after learning (P = 0.78) (ii). (G) Memory performance in the object memory task for control and LEC perturbation sessions during recall test 2 hours (P = 0.83) (i) and 22 (ii) hours after learning (P = 0.26, rank-sum test).

To manipulate gamma-frequency timing of neuronal firing in MEC or LEC, we virally expressed ChR2 in GABAergic cells in the superficial layers of each region [Fig. 1C and fig. S1; AAV5/2-Dlx-ChR2-mCherry (46)] and activated them optogenetically at 53 Hz (n = 6 rats for MEC perturbation and n = 6 rats for LEC perturbation). Gamma-frequency optogenetic stimulation perturbed the spike timing in EC circuits by phase locking the majority of interneurons (72% with P < 0.05, Rayleigh test; Fig. 1F) and a considerable fraction of excitatory neurons (26%; Fig. 1G) to the stimulation phase, coupled with reduced firing of entorhinal excitatory cells (Fig. 1G and fig. S1). This artificial gamma oscillation was transmitted to the target dendritic layers in the hippocampus (fig. S2).

This 53-Hz frequency was chosen to affect gamma-time-scale timing of entorhinal neurons without compromising hippocampal theta oscillations (figs. S1 and S2). By contrast, continuous stimulation silenced principal neurons in the EC and strongly reduced theta power in the hippocampus (fig. S1). In addition, sinusoidal 53-Hz light stimulation achieved a more stable modulation of entorhinal spiking over several seconds-long trials compared with continuous stimulation (fig. S1).

Optogenetic perturbation of native gamma patterns in MEC or LEC, applied during learning trials, resulted in a large and selective impairment in the spatial and object tasks, respectively, which persisted during memory recall tests at 2 and 22 hours after learning (Fig. 2, A and B and fig. S3). Learning in the object-in-place task was impaired by both MEC and LEC perturbations (Fig. 2C and fig. S3). Other behavioral parameters, such as running speed and time spent exploring the maze or the objects, were unaffected by the manipulations (fig. S4). In a subgroup of eight rats, we also examined the effect of MEC (n = 4) and LEC (n = 4) perturbation during the postlearning sessions (Fig. 2E). The same optogenetic stimulation that brought about profound deterioration of learning had no discernable effect when applied during the probe trials at either 2 or 22 hours after learning (Fig. 2, F and G). Thus, after learning was established, neither MEC nor LEC was critical to recalling an already learned task.

Layer- and frequency-specific separation of MEC and LEC gamma inputs in DG

During locomotion, theta oscillations displayed a characteristic phase shift along the dorsoventral axes of the hippocampus, MEC, and LEC, which allowed us to identify the location of cellular layers (Fig. 3A) (9, 47). The power and frequency of theta-modulated gamma oscillations also displayed characteristic laminar profiles across the dorsoventral hippocampal and entorhinal axes (Fig. 3B) (8, 9, 47–50). We used high-spatial-resolution laminar recordings (20 or 50 mm), combined with local field potential (LFP) blind source separation by independent component analysis (ICA) (51, 52) to quantify layer- and frequency-specific gamma oscillations (Figs. 3, C to E, and figs. S5 and S6; n = 12 rats). We identified three main sources of gamma LFPs in the outer, middle, and inner third of the DG molecular layer (Fig. 3C). Based on the main anatomical afferents that target each of these dendritic domains, we refer to these “projected” oscillations as MEC gamma (100 to 150 Hz, gamma_F), LEC gamma (30 to 50 Hz, gamma_S), and commissural gamma (60 to 80 Hz, gamma_M). This result did not depend on the selection of the theta reference signal (fig. S6). In six rats, an eight-shank, 256-site probe was implanted in the hippocampus, which allowed us to compute the two-dimensional (2D) distribution of gamma components in DG. In these IC maps, the gamma_S, gamma_F, and gamma_M LFP patterns consistently occupied the outer, middle, and inner third of the molecular layers, respectively, the targets of LEC, MEC, and commissural inputs (Fig. 3D and fig. S5).

Fig. 3. MEC and LEC inputs project distinct gamma oscillations to the DG.

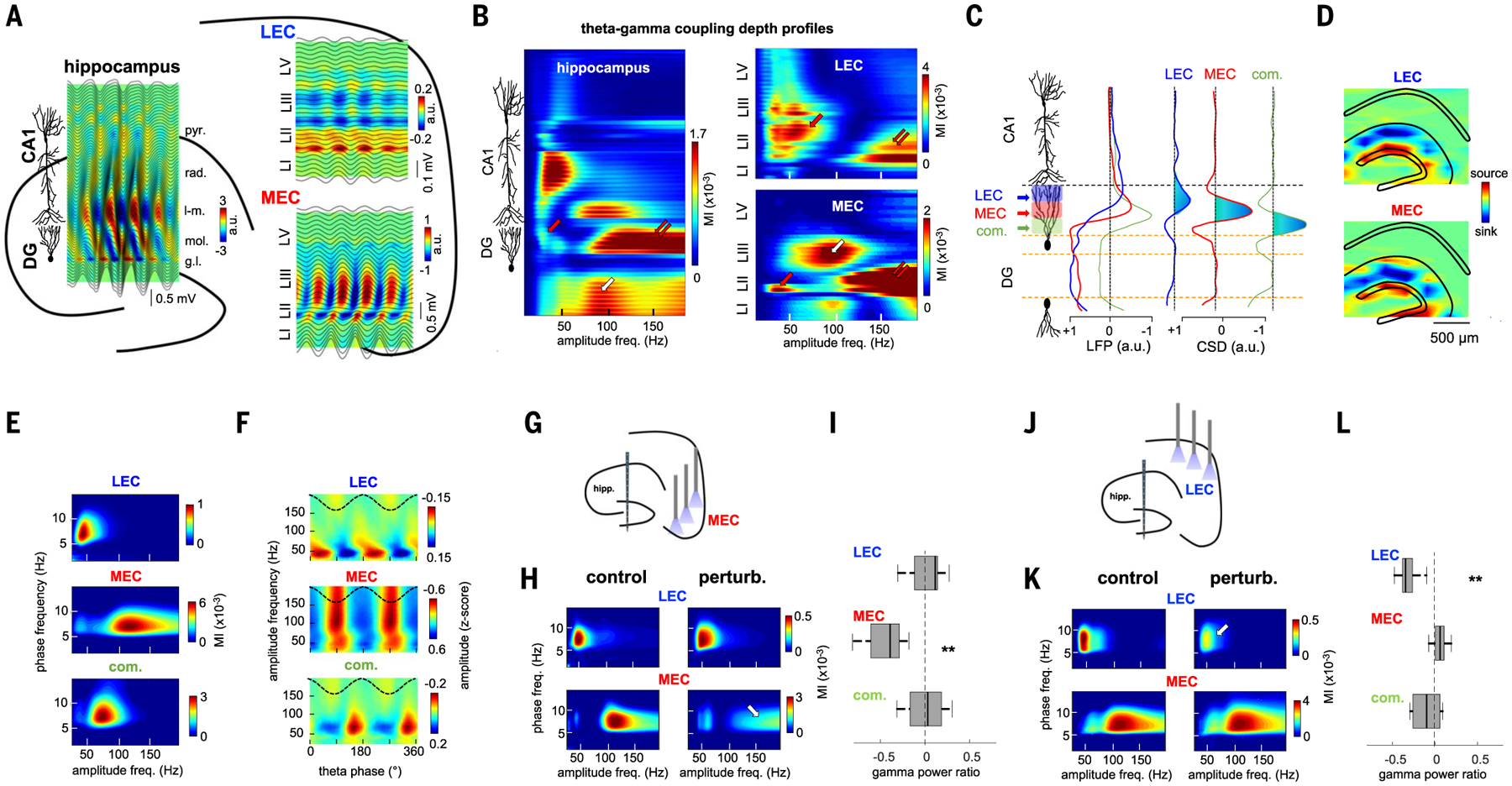
(A and B) Example laminar recordings across hippocampal, MEC, and LEC layers in the same animal. (A) Plots are depth profiles of averaged theta LFPs in each structure (black lines) superimposed on CSD color maps. Note the characteristic phase shift of theta oscillations across CA1pyr cell layer and EC layer 2. rad, stratum radiatum; l-m, stratum lacunosum-moleculare; mol, molecular layer; gl, GC layer; LI/II/III/V, entorhinal layers. (B) Gamma amplitude- theta frequency comodulograms (GA-TF) for each recording site (LFP) were concatenated into a single matrix. DG gamma_S, gamma_M, and gamma_F are marked by red, white, and double arrows, respectively. (C) ICA decomposition of LFPs along the dorsoventral hippocampal axis resulted in three main ICs with currents restricted to the DG. Left: IC depth voltage profiles. Right: IC second spatial derivative (CSD). Current sinks are indicated in blue. (D) 2D CSD maps of LEC and MEC were back-projected to the anatomical electrode space (eight shanks paced 300 μm, each with 32 recording sites). (E) GA-TF comodulograms for each IC displayed modulation in a specific gamma sub-band (group data from n = 12 rats): LEC in gamma_S (45 ± 2 Hz), MEC in gamma_F (115 ±3 Hz), and commissural in gamma_M (63 ± 3 Hz). (F) LEC, MEC, and commissural-projected gamma oscillations occur on the descending phase (47 ± 9°), trough (168 ± 3°), and ascending theta phase (284 ± 8°), respectively. Reference theta phase (black dashed line) from CA1pyr cell layer is also shown. (G) Schematic of MEC perturbation experiment. (H) GA-TF comodulograms for the LEC and MEC gamma components in an example animal without (left) and with MEC optogenetic perturbation (right). Note the strong decrease in power in MEC gamma_F (arrow). (I) Group results of the effect of MEC perturbation on the power (control − perturbation/control + perturbation) of the different gamma oscillations (ICs) in the DG (**P = 3.9 × 10⁻³, signed-rank test; n = 6 rats). (J to L) Same as (D) to (F) but during LEC perturbation (**P = 0.002; n = 6 rats). MEC perturbation had stronger effect on MEC gamma_M than did LEC perturbation (P = 4.1 × 10⁻⁵, rank-sum test), whereas the opposite was true for LEC gamma_S (P = 6.3 × 10⁻⁴).

The power of the identified gamma sub-bands covaried with the phase of theta oscillations (Fig. 3E). In addition, theta-phase gamma-amplitude coupling analysis revealed that LEC gamma_S, MEC gamma_F, and commissural gamma_M were phase locked to the descending phase, trough phase, and ascending phase of the (CA1-referenced) theta cycle, respectively (Fig. 3F). The entorhinal origin of these gamma oscillations was further supported by experiments in which linear probes were implanted in the MEC or LEC. In layer 2 of LEC, the dominant gamma pattern was of low frequency (gamma_S), whereas in layer 2 of MEC, the most prominent pattern was gamma_F (Fig. 3B and figs. S7 and S8).

To gain more direct support for the origin of the layer-specific gamma sub-bands, we examined the effects of optogenetic and pharmacological perturbation of MEC and LEC on DG LFPs. MEC gamma_F power, but not LEC gamma_S power, strongly decreased during optogenetic perturbation of MEC (Fig. 3, G to I). Conversely, LEC gamma_S power, but not MEC gamma_F power, strongly decreased during LEC perturbation (Fig. 3, J to L). A similar effect was observed with pharmacological inactivation of MEC and LEC (fig. S9). Perturbation of LEC, but not of MEC, reduced DG-CA3 unit spike-gamma_S phase coupling, whereas perturbation of MEC, but not of LEC, reduced spike-gamma_F coupling (fig. S9).

Learning-type specificity of MEC-DG and LEC-DG gamma-frequency communication

To bring gamma-band communication between EC and DG closer to its hypothesized role in spatial and object learning, we examined LFP-LFP and LFP-spike coupling between DG gamma LFP and spikes of putative layer 2 MEC and LEC neurons (Fig. 4; n = 8 rats). The change of LFP-LFP synchrony [measured by their weighted phase-lag index (53) in the 25- to 200-Hz band; see fig. S10 for additional metrics] between the prelearning maze exploration session and the learning session was used as a behaviorally relevant physiological measure. During spatial learning, both MEC-DG LFP-LFP synchrony (Fig. 4A) and MEC spiking–DG gamma LFP phase coupling [measured as the pairwise-phase consistency (PPC) (54) between entorhinal spikes and gamma-filtered DG LFPs; Fig. 4B], but not DG-LEC coupling, increased in the gamma_F band compared with the prelearning baseline. Conversely, during object learning, LEC-DG LFP-LFP synchrony and LEC spiking–DG gamma LFP coupling increased in the gamma_S band, but not MEC-DG synchrony (Fig. 4, A and B). In addition, the power of MEC gamma_F and LEC gamma_S in the DG increased during spatial and object learning, respectively (Fig. 4C), supporting the hypothesis that different behavioral demands select distinct gamma-frequency communication channels (Fig. 4D).

Fig. 4. Task-specific gamma synchrony between entorhinal cortex and hippocampus.

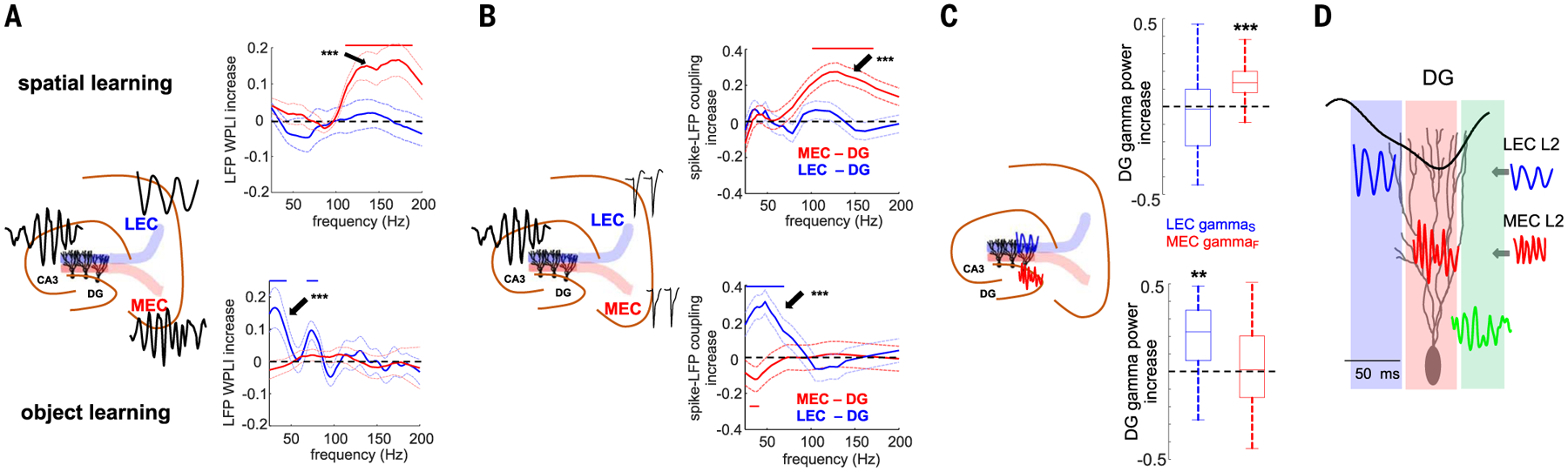
(A) Learning-induced changes for MEC-DG and LEC-DG LFP-LFP gamma WPLI in the spatial and object learning tasks, respectively. Mean ± SEM WPLI (learning − baseline)/(learning + baseline) (n = 12/12 sessions in 4/4 rats for MEC and LEC, respectively). LFP traces were taken from the DG molecular layer and EC layer 2. Red and blue lines indicate frequencies with a significant effect (P < 0.05 with Bonferroni correction for multiple comparisons). In the spatial task, DG WPLI increased more with MEC than with LEC in the gamma_F band (P = 4.8 × 10⁻⁶, rank-sum test), whereas in the object task it increased more with LEC than MEC in the gamma_S band (P = 9.0 × 10⁻⁵). (B) Spike-LFP coupling (PPC) between spikes of layer II MEC and DG gamma LFP and LEC LII excitatory neurons and DG gamma LFP during spatial or object learning, respectively (n = 192/95 MEC cells in the spatial and object tasks and n = 72/128 LEC cells, from four rats in each case). In the spatial task, DG spikes’ PPC increased more with MEC gamm_F LFP than with LEC (P = 3.8 × 10⁻³, rank-sum test), whereas in the object task, it increased more with gamma_S LEC LFPs than with MEC (P = 1.4 × 10⁻⁴). (C) Learning-induced power change for DG LEC gamma_S and MEC gamma_F oscillations in the two tasks (P = 6.3 × 10⁻⁷/0.0033 gamma_S versus gamma_F, signed-rank test, n = 36/24 sessions in the spatial and objects tasks from 12 rats). In (A) to (C), **P < 0.01, ***P < 0.001, signed-rank test for learning versus baseline effect in the gamma_S or gamma_F bands. (D) Schema summarizing the spatiotemporal organization of LEC and MEC gamma inputs to the DG.

Learning-type-specific recruitment of CA3-DG neurons

Because MEC and LEC axons converge onto downstream DG and CA3 neurons, we examined their gamma-oscillation-related firing during learning. DG-CA3 cells spike-LFP coupling exhibited three distinct peaks in the gamma_S, gamma_M, and gamma_F bands (Fig. 5A). Excitatory target neurons were classified as GCs, mossy cells (MCs), and CA3pyr cells on the basis of electrophysiological criteria (Fig. 5, B and C, and fig. S11) (40). Cluster isolation quality was similar for the three groups (fig. S11). A larger portion of GCs were phase locked to MEC gamma_F, and their coupling was stronger than that to LEC-gamma_S (Fig. 5, D and E, and fig. S12). Conversely, a higher fraction of MCs and CA3pyr cells were phase locked to LEC gamma_S, and their phase modulation was stronger than that to MEC gamma_F (Fig. 5, D and E, and fig. S12).

Fig. 5. Entorhinal gamma inputs differentially engage hippocampal neuronal populations during learning.

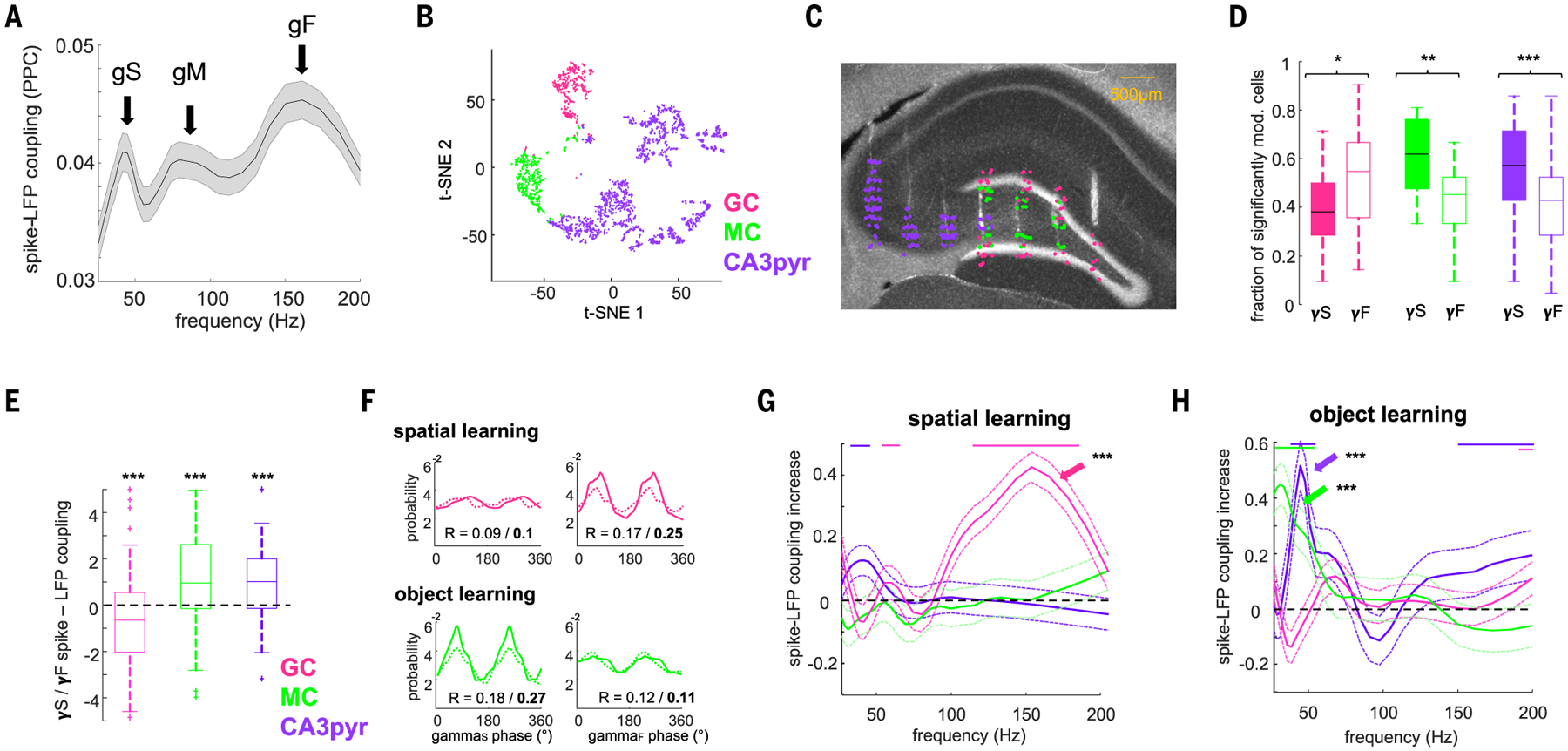
(A) Distribution of spike-gamma LFP coupling (PPC) of all neurons in the DG/CA3 with DG molecular layer LFPs yielded three distinct peaks in the gamma_S (gS), gamma_M (gM), and gamma_F (gF) sub-bands (arrows). (B) t-distributed stochastic neighbor embedding (t-SNE) plot illustrating the separation of putative CA3pyr cells (n = 1554), GCs (n = 377), and MCs (n = 323) on the basis of physiological criteria (see the materials and methods; n = 20 rats). (C) Anatomical location of GCs, MCs, and CA3pyr cells in an example animal. Histological section shows tracks of silicon-probe array shanks across the transversal axis of CA3-DG (DAPI staining). (D) Fraction of neurons significantly modulated (P < 0.05, Rayleigh test) by gamma_S (γS) and gamma_F (γF) (GCs, P = 0.01; MCs, P = 0.0012; CA3pyr cells, P = 5.7 × 10⁻⁵, rank-sum test). (E) Ratio of spike-gamma LFP coupling [PPC (gamma_S − gamma_F)/(gamma_S + gamma_F)] for each cell type (GCs, P = 1.4 × 10⁻³; MCs, P = 1.5 × 10⁻⁴; CA3pyr cells, P = 9.9 × 10⁻⁵, signed-rank test). (F) (Top) Example GC firing modulation by gamma_S phase (left) and gamma_F (right) during baseline (dashed) and spatial learning (solid) sessions. (Bottom) Example MC firing modulation by gamma_S (left) and gamma_F (right) during baseline and object learning. (G) During spatial learning spike-gamma_F coupling (PPC) selectively increased for GCs (arrow) (P = 3.6 × 10⁻³, signed-rank test, n = 201) but not for MCs (P > 0.05, n = 145) or CA3pyr cells (P > 0.05, n = 704). y axis shows the difference between learning session and prelearning exploration session spike-DG molecular layer LFP PPC. Color lines indicate frequencies with a significant effect for the respective cell types (P < 0.05, with Bonferroni correction for multiple comparisons). (H) Same as (G) but during object learning. Spike-gamma_S coupling increased for MCs (P = 1.1 × 10⁻⁴, n = 111) and CA3pyr cells (P = 2.1 × 10⁻⁵, n = 548) but not GCs (P > 0.05, n = 130).

We next examined the temporal dynamics of these neuron types during learning. In the spatial learning task, spike-LFP coupling of GCs, but not that of MCs and CA3pyr cells, increased in the gamma_F band relative to the prelearning baseline (Fig. 5, F and G, and fig. S12). During object learning, GCs were not affected, whereas both MCs and CA3pyr cell spikes significantly increased their phase coupling to the gamma_S band (Fig. 5, F and H, and fig. S12). To examine their ensemble activity (55, 56), we detected assemblies of coactive neurons in gamma-time-scale windows during both tasks (Fig. 6A and fig. S13). Most assemblies (~50%) were composed of cells of the same type, whereas other assemblies consisted of combinations of GCs, MCs, and CA3pyr cells (Fig. 6B). GCs contributed more strongly to assembly activation during spatial learning compared with object learning, whereas CA3pyr cells contributed more during object than spatial learning (Fig. 6C). The overall contribution of GCs to assembly activation increased when time windows corresponding to gamma_F were used (10 ms), whereas the contribution of MCs and CA3pyr cells increased for windows corresponding to gamma_S (20 to 25 ms; fig. S13). These results imply that projected gamma oscillation in a target region can support learning by synchronizing specific cell populations in a task-dependent manner.

Fig. 6. Neuronal assembly composition is task specific.

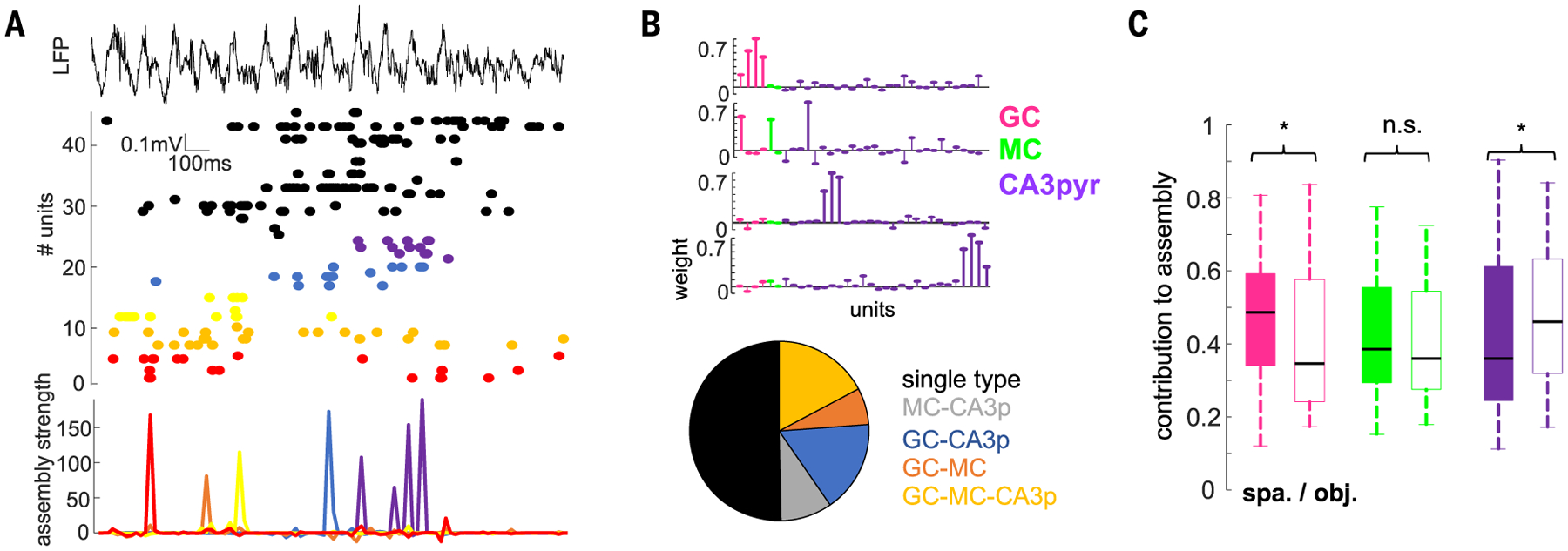
(A) Activation of cell assemblies during an example learning trial. Shown is a LFP and raster plot of spiking of simultaneously recorded neurons (top, middle; color-coded) and activation of individual assemblies (bottom). For this figure, a 20-ms time window was used for assembly detection (see the materials and methods). (B) Weight vectors of three representative assemblies in one session (top) and proportion of assemblies (bottom) with GCs, MCs, or CA3pyr cell members or their combinations (n = 182 assemblies from 20 rats). (C) Cell-type contribution to assemblies in the spatial and object learning tasks (n = 77/83 GCs 36/44 MCs, and 237/186 CA3pyr cell assembly members in spatial and object tasks; F_(647,2) = 5.37, P = 4.8 × 10⁻³, two-way ANOVA). *P < 0.05, rank-sum test.

Impact of MEC and LEC perturbation on behaviorally relevant features of DG-CA3 neurons

DG-CA3 neurons continued to express place fields during both MEC and LEC optogenetic perturbation, albeit several aspects of place field features were altered (Fig. 7 and fig. S14), similar to previous inactivation experiments (29, 57–60). Although MEC and LEC perturbation had a minor effect on the overall firing rates of DG-CA3 neurons (fig. S14), MEC, but not LEC, perturbation during spatial learning significantly reduced peak firing rates of place cells within their place fields (Fig. 7D), increased place field size (fig. S14), and decreased spatial information (Fig. 7E). MEC perturbation altered the stability of the spatial map, as illustrated by the remapping of place fields of individual neurons and average lower spatial correlations during learning compared with baseline (Fig. 7, B and F). In control sessions, spike trains of place cells oscillated ~1 Hz faster than the theta rhythm, and this difference was reduced during MEC perturbation, indicating an impaired temporal coding [“phase precession” (61); Fig. 6G].

Fig. 7. Effect of entorhinal circuit perturbation on place cell coding properties.

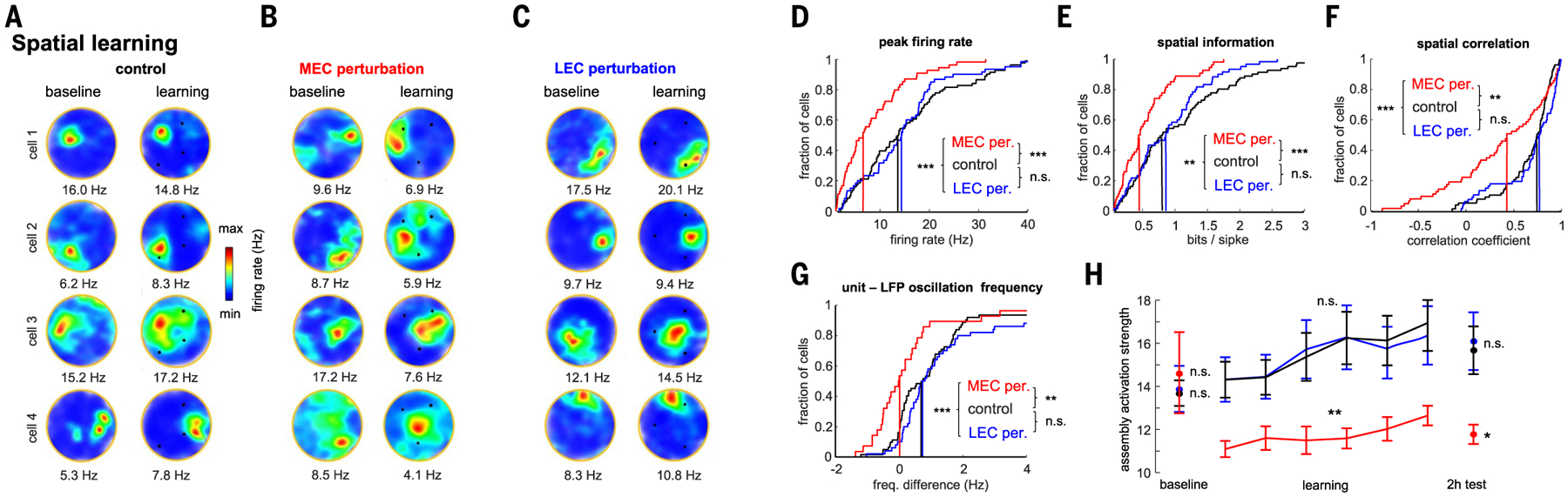
(A to C) Example CA3-DG firing rate maps during baseline (left column) and spatial learning (right column) during control and MEC (B) or LEC (C) perturbation sessions. (D to G) Spatial coding metrics for control (n = 81 place cells), MEC (n = 54), and LEC (n = 60) perturbation sessions (during learning trials, n = 36 sessions from 10 rats). Vertical lines indicate median of the distributions. ***P < 0.001, rank-sum test MEC and LEC perturbation versus control. (H) Activation strength of CA3-DG assemblies for control learning trials (n = 93 assemblies from 10 rats) and for MEC (n = 44) and LEC (n = 58) perturbation sessions during baseline, learning (each point is a five-trial block), and 2-hour postlearning recall. *P < 0.05, **P < 0.01, ***P < 0.001, rank-sum test.

We also quantified the strength of DG-CA3 assembly activation during learning and recall (supplementary materials and methods; fig. S13). Assembly strength gradually increased during learning compared with their baseline activation (Fig. 7H), whereas firing rates of member units remained stable (F_(128,7) = 1.2, P = 0.29). MEC, but not LEC, perturbation significantly decreased assembly activation strength during learning, which persisted during the 2-hour recall session in the absence of optogenetic perturbation (Fig. 7H), suggesting a lasting effect of learning-induced assembly strengthening that depends on MEC inputs. Place field similarity of assembly members was stronger than that of nonmember cells (fig. S13), suggesting a link between the single-cell and population effects.

During object learning, several DG-CA3 neurons developed object-selective firing, as reflected by their increased or decreased firing rates during the exploration of one versus the other object (Fig. 8, A and D). This increase in firing selectivity was abolished by LEC, but not MEC, perturbation (Fig. 8, B, C, E, and F), suggesting that LEC input is critical for the object learning–induced plasticity in DG-CA3 neurons.

Fig. 8. Effect of entorhinal circuit perturbation on object-related firing.

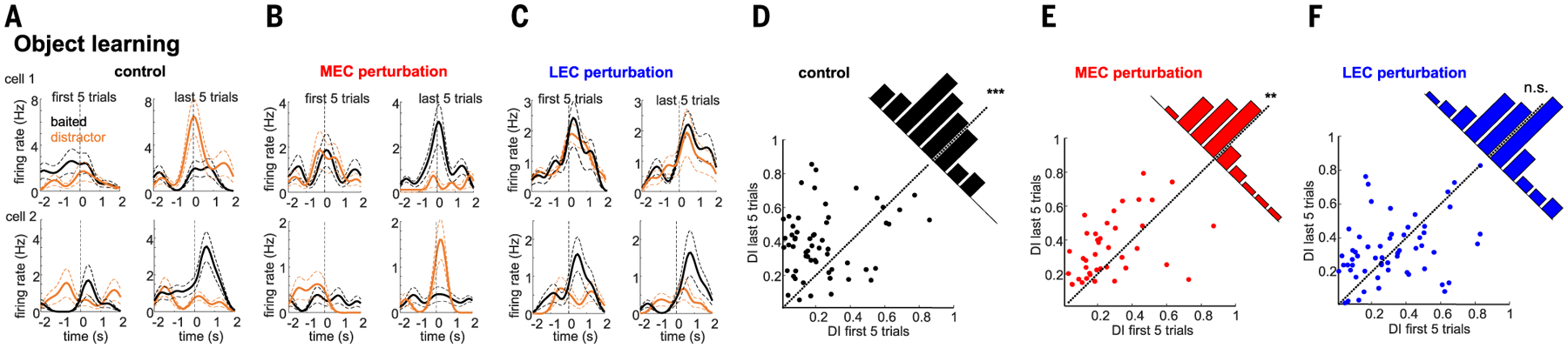
(A to C) Two example single-cell responses each to cue and distractor objects for the first and last five trials of a control (A), MEC (B), and LEC (C) perturbation session. (D to F) Object DIs (see the materials and methods) were higher in the last five learning trials compared with the first five trials in control sessions [(D); P = 7.4 × 10⁻⁶, signed-rank test, n = 64 CA3-DG cells from 10 rats] and MEC perturbation sessions [(E); P = 2.1 × 10⁻³, n = 42 cells] but did not change during LEC perturbation [(F); P = 0.47, n = 47 cells]. MEC versus sham: P = 0.08, rank-sum test; LEC versus sham: P = 0.0014.

DISCUSSION

We used a combination of behavioral testing, physiological recordings, source separation analyses, and optogenetic perturbation to examine learning-specific communication between MEC and LEC and their target DG-CA3 region. We identified three distinct gamma-frequency patterns in the outer (slow gamma_S, 30 to 50 Hz), middle (fast gamma_F, 100 to 150 Hz), and inner (intermediate gamma_M, 60 to 80 Hz) molecular layer of the DG, corresponding to projected gamma rhythms from LEC, MEC, and the associational and/or commissural inputs, respectively (Fig. 3). When rats were engaged in a spatial learning task, gamma_F power in DG, synchrony between MEC and DG gamma_F, and coupling between unit firing in layer 2 of MEC and DG gamma_F selectively increased (Fig. 4). Conversely, in an object discrimination task, gamma_S power, synchrony between LEC and DG gamma_S, and coupling between unit firing in layer 2 of LEC and DG gamma_S increased, suggesting task-dependent routing of MEC and LEC messages in the form of gamma-cycle-packaged spikes to the DG-CA3 region. To support this hypothesis, we optogenetically perturbed gamma-frequency oscillations in MEC or LEC, which induced selective learning deficits in the spatial and object variants of the task (Fig. 2), differentially affected the projected gamma rhythms in the DG (Fig. 3), and perturbed assembly organization of neurons (Fig. 7).

A larger fraction of GCs was entrained to MEC gamma_F than to LEC gamma_S, and their spike coupling to gamma_F selectively increased during spatial learning (Fig. 5). By contrast, MCs and CA3pyr neurons were more strongly entrained to gamma_S than to gamma_F, and their spike coupling to LEC gamma_S increased during object learning. Optogenetic perturbation of MEC, but not LEC, reduced peak firing rates of DG-CA3 place cells and induced remapping of their place fields (Fig. 7). Conversely, perturbation of LEC, but not MEC, abolished differential firing responses of DG-CA3 principal neurons to cue versus distractor objects (Fig. 8). Our findings demonstrate that gamma-frequency communication between medial and lateral EC and hippocampal neuronal assemblies is critical for routing task-relevant neuronal messages, and we hypothesize that their perturbation explains the selective learning impairments that we observed.

Physiological mechanisms of entorhinal cortex-DG and CA3-supported behaviors

Our findings provide support for the dominant view that the main function of the entorhinal-hippocampal system is to support episodic memory. Under this general hypothesis, LEC conveys information about the “content” of experience, whereas MEC provides spatial context in which those events take place, and both MEC and LEC add a timeline to the events (31, 62–66). Our experiments demonstrate that selective gamma-time-scale spike synchrony between MEC and LEC and their target DG-CA3 is fundamental to accomplish these functions.

We found that the superficial layer circuits of LEC and MEC generate spectrally separable gamma-band oscillations (gamma_S and gamma_F, respectively), which are projected to different layers of the DG molecular layer at different theta phases. Conveying the slower signal to the distal dendrites and the faster gamma bursts to the more proximal segments of the same GCs may serve to reduce the dendritic filtering properties of the electronically compact GCs and facilitate integration of these inputs (67–70). In addition to entorhinal inputs, the associational and/or commissural afferents from MCs provide yet another gamma-frequency input (gamma_M). Segregation and integration of these frequency-specific inputs may be assisted by layer-specific inhibition (9, 71–76).

The relevance of MEC and LEC gamma communication with the hippocampus was demonstrated in the learning tasks. Engagement in the spatial learning task increased gamma_F synchrony and spike-LFP coupling between MEC and DG, associated with increased power of projected gamma_F in DG, whereas no such changes were observed between LEC and DG. In a complementary task, object discrimination learning, we observed a pathway-specific increase of gamma_S synchrony and spike-LFP coupling between LEC and DG and increased power of gamma_S in DG, suggesting that task demands select the anatomical conduit and determine the communication frequency between EC and DG-CA3. It is important to emphasize that spike-LFP coupling, interregional phase coupling, and gamma-band power in the target area are interdependent measures. Although correlations among these measures are expected, they capture different aspects of the same neural mechanism(s).

MEC gamma_F input engaged GCs more effectively, and this entrainment was specifically enhanced during spatial learning. Conversely, LEC gamma_S input engaged MCs and CA3pyr neurons more strongly, and this coupling increased during object learning. These results suggest that GCs are mainly part of the head direction–governed MEC spatial system, which is sensitive to distant cues, whereas MCs and CA3c-pyr neurons are more strongly controlled by LEC-mediated local cues. The preferential control of GCs by MEC inputs and that of MCs and CA3pyr cells by LEC inputs can explain previous observations in which changes of global cues induced place field remapping of GCs, whereas changes in local cues induced remapping of MCs and CA3pyr cells (38–41, 77, 78).

Optogenetic perturbation of MEC selectively disrupted spatial learning and place cell properties of DG neurons, whereas perturbation of LEC impaired object learning and object discrimination–related firing. These results extend previous observations using lesions or inactivation of MEC and LEC (28–30, 57–60). However, the key element of our study was the perturbation of gamma spike timing with only moderately effects on DG-CA3 firing rates and theta power. These findings highlight the importance of sub-theta-cycle spike timing for leaning (9, 79–82). In support of this interpretation, gamma-time-scale assemblies of GCs, MCs, and CA3pyr cells were strengthened during learning and reactivated during subsequent recall but were disrupted by optogenetic manipulations of their EC inputs. We hypothesize that precise spike coordination of functional cell assemblies in the hippocampo-entorhinal circuits is necessary for learning.

In the interpretation of the behavioral effects, we also need to consider the role of layer 3 projections from MEC and LEC, which also transmit pathway-specific gamma messages to the CA1 region (6–10, 83–88). In contrast to the hypothesized ability of GCs to combine gamma inputs by dendritic integration, CA1pyr neurons may not use such a mechanism because both LEC and MEC afferents from layer 3 terminate on distal apical dendrites, carry similar frequency inputs (8, 9), and engage different populations of CA1pyr neurons in the transversal axis of the CA1 region (15, 17).

In summary, although the exchange of information between the dorsal (“where” or “how”) and ventral (“what”) systems (20, 21) may occur at many levels (22, 31), the connectivity and physiological operation of the DG-CA3 system are poised to both segregate and integrate messages conveyed by the “what” and “where/how” streams and forward them to CA1. We hypothesize that sending neuronal messages by segregated gamma-frequency carriers allows a target “reader” area to disambiguate convergent inputs. Our findings demonstrate that distinct gamma-frequency-specific communication between MEC and LEC and hippocampal cell assemblies are critical for routing task-relevant information. Our selective perturbation experiments suggest that they support specific learning tasks. In general, these results demonstrate that specific gamma patterns dynamically engage functionally related cell assemblies across brain regions in a task-specific manner.

MATERIALS AND METHODS

Surgical procedures

Rats (adult male Long-Evans, 300 to 500 g, 3 to 6 months old) were kept in the vivarium on a 12-hour light/dark cycle and were housed two to three animals per cage before surgery and individually after surgery. All experiments were approved by the institutional Animal Care and Use Committee at New York University Langone Medical Center.

Silicon probe and optic fiber implantation were performed as described previously (9, 89, 90). Animals were anesthetized with isoflurane anesthesia, and craniotomies were performed under stereotaxic guidance. Silicon probes (NeuroNexus or Cambridge Neurotech) were mounted on custom-made 3D-printed micro-drives to allow precise adjustment of vertical position of sites after implantation. The probes were inserted above the target region. Craniotomies were sealed with sterile wax. Two stainless steel screws were placed bilaterally over the cerebellum to serve as ground and reference electrodes. Several additional screws were driven into the skull and covered with dental cement to strengthen the implant. Finally, a copper mesh mounted on a 3D-printed resin base was attached to the skull with dental cement and connected to the ground screw to act as a Faraday cage, attenuating the contamination of the recordings by environmental electric noise and protecting the headgear. After postsurgery recovery, probes were moved gradually in 50- to 150-μm steps per day until the desired position was reached. Hippocampal and entorhinal cellular layers were identified physiologically by unit activity and characteristic LFP patterns (9, 91). The identification of dendritic sublayers was achieved by the application of current source density (CSD) and ICA analysis to the LFPs (8, 51, 52).

For optogenetic experiments, rats (n = 12) were implanted with a single silicon probe (64 recording sites, aligned on the linear edge of the probe, with 20-μm vertical separation; Cambridge Neurotech) over the right dorsal hippocampus [4.0 anteroposterior (AP) from bregma and 2.6 mm from the midline (ML)]. In addition, custom-made optic fiber arrays (three 200-μm core multimode fiber each, ~500 um apart, connected to a single 2.5-mm steel ferrule; Doric Lenses) were implanted in both hemispheres over the medial (−7.7/−8.4/−9.1 AP; ± 4.6 ML; and 4.7/ 4.3/3.2 mm from the surface of the brain, for each fiber, respectively) or lateral (−6.1/−7.1/−8.0 AP; ± 6.0 and 6.8/5.0/4.0 mm depth) entorhinal cortex.

In animals without optogenetic manipulations, a variety of different silicon probes were implanted in the dorsal hippocampus and the medial and lateral entorhinal cortex. Data from these animals have also been included in previous studies, and surgical procedures were described previously in more detail (9, 89, 91). Briefly, eight-shank silicon probes (300-μm separation; 32 electrodes per shank with 50-μm spacing) were implanted parallel to the transverse axis of the dorsal hippocampus (Fig. 3D and fig. S5). The coordinates of the craniotomy (45° respect to the midline) were the following: −2.5 mm AP and 2.6 mm ML from bregma for the outer side and −4 mm AP and 0.8 mm lateral for the inner side. Single-shank probes (32 recording sites with 50-μm spacing) were implanted along the rostrocaudal axis of the MEC approximately perpendicular to the cellular layers (− 6.0 mm AP, 4.5 mm ML, with a 25° angle in the sagittal plane pointing caudally) or along the dorsoventral axis of the LEC (8 mm AP, 5 mm ML, 15° angle in the coronal plane pointing laterally). In three rats, a four-shank probe (200-μm shank separation; 64 sites in two rows per shank with 25-μm spacing) was implanted along the dorsoventral axis of MEC (n = 2) or LEC (n = 1, same coordinates as above). The MEC probe was inserted 4.5 mm lateral, parallel to the midline with 25° pointing anterior and the most caudal shank was inserted just rostral to the transverse sinus. In this configuration, each shank recorded activity from a different entorhinal layer. Calbindin immunostaining was used to identify entorhinal layer II.

In a few experiments (n = 4 rats), bipolar tungsten stimulating electrodes were implanted in the ipsilateral fornix (−1.4 mm posterior to bregma, 1.4 lateral and 4.5 depth) and/or the lateral olfactory tract (5.0 mm anterior to bregma, 2.0 lateral and 7.0 depth). Evoked potentials elicited by brief current pulses (100 μs, 100–500 μA) delivered to the fimbria and/or the lateral olfactory track were used to further guide the identification of entorhinal layers (fig. S7).

Optogenetic experiments

For optogenetic experiments, rats were injected with custom-prepared AAV5-mDlx-hChR2 (H134R)-mCherry from AddGene (plasmids were a gift from Dr. Gord Fishell) (46).

Three injections per hemisphere were performed along the dorsoventral MEC or LEC entorhinal axes as follows. MEC: (i) −7.7 AP, ±4.6 ML, 4.7 mm depth, 200 nl; (ii) −8.4 AP, ±4.6 ML, 4.3 mm depth, 400 nl; and (iii) −9.1 AP, ±4.6 ML, 3.2 depth, 700 nl. LEC: (i) −6.1 AP, ±6.0 ML, 6.8 mm depth, 400 nl; (ii) −7.1 AP, ±6.0 ML, 5.0 mm depth, 400 nl; and (iii) −8.0 AP, ±6.0 ML, 4.0 depth, 400 nl; with 10° mediolateral in the three cases. After injection, craniotomies were sealed, and animals recovered in the vivarium for 3 weeks. After this period, a second surgical procedure for implanting optic fibers and electrodes was performed, as described above. Optic fiber arrays were implanted in the same craniotomies performed previously for virus injection. For optogenetic stimulation, fiber array ferrules were connected with mating sleeves to 450-nm blue light-emitting laser diodes coupled to 2.5-mm steel ferrules (PL-450, Osram).

Optogenetic perturbations were performed by delivering blue light, modulated with a positive 53-Hz current sinusoid using an isolated current driver (Thorlabs). Light intensity was calibrated for each animal during home cage recordings by analyzing the suppression of LFP gamma power in the DG during stimulation. A minimum power of 3 mW and a maximum of 6 mW was used. Optogenetic stimulation in the home cage did not induce any overt behavioral responses. During the task, light stimulation automatically started once the animal entered the maze and stopped when it returned to the start box (the duration of a trial).

Local entorhinal optogenetic manipulation and recordings

To assess the effect of optogenetic perturbation on the firing of entorhinal cells, two rats were injected with virus in the MEC as described above and a silicon probe with a 200-μm core fiber glued to it was implanted to target layer 2 (−8.4 AP, 4.6 ML, 5.0 mm depth). Animals were recorded in their home cages, and the same pattern and intensity of simulation as in the behavioral experiments were used while local units were recorded (fig. S1).

Experiments under anesthesia

Four rats were anesthetized with urethane (1.2 mg/kg intraperitoneally) and implanted with a single linear probe (32 sites with 50 μm spacing; NeuroNexus) in the right dorsal hippocampus (4.0 AP, 2.6 ML, and 3.5 mm depth). Custom-made concentric stimulation electrodes were implanted in the lateral olfactory tract (5.0 AP, 2.0 ML, and 7.0 mm depth), medial (−8.0 AP, 4.0 ML, and 4 mm depth) and lateral (−8.0 AP, 5.5 ML, and 3.5 mm depth) perforant path. Stimulating electrodes were also used for local injection of the Na⁺ channel blocker lidocaine, allowing the chemical blockade and electrical activation of the presynaptic region to be tested simultaneously (fig. S9) (51, 91). Brief current pulses (100 μs, 200 to 500 μA) were delivered through the concentric electrodes to evoke field excitatory postsynaptic potentials in the DG. Under urethane anesthesia, hippocampal LFPs alternated between epochs of delta waves and low-frequency theta oscillations (51, 52, 91). To test the effect or MEC or LEC inactivation, first a baseline epoch was recorded (2 to 3 hours), followed by injections of a small volume of lidocaine (~50 to 100 nl) every 5 min for ~30 min. The effect of the lidocaine was tested by the hippocampal evoked potentials in response to stimulating the MEC or LEC electrode every 10 s (fig. S9). Evoked potentials elicited with the other electrode served to verify the specificity of the injections.

Behavioral tasks

After surgery, animals were handled daily and accommodated to the experimenter, recording room, and cables for 1 week before the start of the experiments. Before the start of the behavioral experiment, animals were water restricted.

The position of the animal was tracked with an OptiTrack camera system (Natural Point Corp.) (50, 89). Infrared reflective markers were mounted on the animal’s head stage and imaged simultaneously by six cameras (Flex 3). Calibration across cameras allowed for a 3D reconstruction of the animal’s head position and orientation (120-Hz sampling).

Apparatus

Behavior was conducted on a cheeseboard maze (45). The maze was made of painted wood 150 cm in diameter and located on a platform 1 m above the floor (Fig. 1B). A total of 177 water wells (7 mm in diameter and 3 mm in depth) were drilled 8 cm apart in the maze surface, forming evenly distributed, parallel columns and rows. The room around the maze was rich with distal visual cues to facilitate the animal’s orientation. These included a black curtain on one side and walls on the others, one with shelves and one with a hanger and an instrumentation rack. A walled starting box (20 × 30 cm with 30-cm walls) was attached to one of the sides of the maze and connected to it with a movable bridge.

Pretraining

Water-deprived rats were first familiarized with exploration of the maze to collect water. Initially, animals were placed in the center of the maze and allowed to explore and retrieve multiple (~15) randomly placed hidden water rewards. Depending on which task was tested first (semirandomly chosen by the experimenter in a balanced manner), objects were or were not introduced at this stage. Over the next 3 to 4 days, the number of available water rewards in the maze was gradually reduced, and a trial structure was introduced such that the rat received a food reward (Froot Loops, Kellogg’s) after successful retrieval of all water rewards. The rat was then trained to return to the starting box to obtain its food reward. After 2 to 3 days of this repeated procedure, the rat would consistently explore the maze to obtain the three or four hidden water rewards, and then return to the starting box to obtain its food reward. To prevent the use of an odor-mediated search strategy, the maze was wiped with a towel soaked in 70% ethanol and rotated by random degrees relative to the starting box between all trials. This phase of general training ended when the rat completed 30 trials per session.

General behavioral protocol

A given recording day started with a probe session in which the reward configuration of the previous day was tested (22 hours after the end of the previous learning session). The rat was then returned to its home cage for ~10 min, after which time it was placed on the maze for a 20-min baseline exploration session (Fig. 1E). During this baseline session, it freely explored the maze and collected food rewards (Froot Loop crumples) randomly scattered by the experimenter. The configuration of the maze was the same as in the subsequent learning session (presence or absence of objects or a wall) but without any water reward. After a 2-hour rest period in the home cage, the learning session started. This stage consisted of 30 trials in which the animal was allowed to leave the start box, entered the maze to collect water rewards, and returned to the start box for a food reward. If the rat could not find all three rewards in 2 min, the trial was ended and the animal was placed back in the start box. Control (no stimulation) and optogenetic perturbation sessions were conducted on interleaved days. During perturbation sessions, 53 Hz of sinusoidal light stimulation was delivered during the entire duration of the learning (or probe) trials. The learning session was followed by a 2-hour rest period in the home cage, followed by second probe session to test whether the animal remembered the reward configuration learned on that day. All rats were tested in both the spatial and object tasks, and eight of them (four with MEC perturbation and four with LEC perturbation) were also tested in the object-in-place task after they completed the first two tasks. The initial task (either spatial of object learning) was decided semirandomly in a balanced manner by the experimenter. Once the animal learned the task, an average of three sessions of each type (control, perturbation, etc.) were conducted in interleaved days. After this stage, the animal was allowed to rest for 2 to 3 days before the training in the new task started. Because all animals performed at least two tasks (spatial and object learning), the entire experiment lasted 4 to 6 weeks per animal.

Spatial learning task

In this task, rats had to retrieve three hidden water rewards on the maze before returning to the start box in each trial. The location of the rewards was constant with respect to the distal cues of the room and the start box during all trials, but changed every day, allowing for new learning to be tested. Rats typically learned to navigate directly to rewards, taking the shortest route in ~10 trials. Learning performance was evaluated as time spent to collect the three rewards after entering the maze. Probe sessions consisted in five trials with the same reward configuration of the learning session.

Object learning task

In this version of the task, two sets of identical objects were placed on the maze, each in one of four possible locations and fixed in place with Velcro strips at their bases. Two of the objects cued the location of two water rewards hidden in adjacent wells. The two other objects served as distractors. The position of some or all the objects changed semirandomly from trial to trial. Each day, two new sets of objects were introduced. During the pretraining phase, animals were introduced to all of the objects that would appear later and learned that rewards were located near to objects. All rats quickly learned to navigate directly to the objects and searched around them until finding the two rewards. During leaning sessions, animals learned to ignore or only briefly examine distractor objects and focus their search around baited objects. Learning performance was evaluated by the time spent exploring distractor objects. In probe sessions, the same two sets of objects were present in the maze but without any reward. Memory performance was evaluated with a discrimination index (DI), determined as follows: DI = (time exploring previous baited objects − time spent exploring distractor objects)/total object exploration time.

Object-in-place learning task

This task was similar to the object learning task, but in this case the maze was divided into two halves by a thin cardboard wall and the objects were placed on each side. As in the previous case, two new sets of identical objects were introduced every day. In the left half of the platform, one of two objects cued the location of the water wells and the other served as the distractor. In the right half of the platform, the significance of the objects was reversed so that the distractor object in the left half served as the reward cue in the right half. To succeed in this task, the rat had to both correctly locate itself and learn to associate the platform half-specific object with reward location. The position of some or all the objects changed semirandomly trial by trial but there were always two different objects in each half of the maze. During probe sessions, the same four objects were placed on the maze without any rewards. Memory performance was evaluated by the same measure as in the object learning task.

Tissue processing and immunohistochemistry

After the termination of the experiments, animals were deeply anesthetized and perfused transcardially, first with a 0.9% saline solution then with a 4% paraformaldehyde solution. Brains were sectioned in 70-μm-thick slices (Leica Vibratome). Sections were finally washed and mounted on glass slides with fluorescence medium [Fluoroshield with 4′,6-diamidino-2-phenylindole (DAPI) F6057, Sigma, USA]. An epifluorescence microscope (Bx61VS, Olympus) was used to obtain high-quality photos and verify virus expression and the tracks of both optical fibers and silicon probe shanks.

Quantification and statistical analysis

Electrophysiological recordings were conducted using an Intan RHD2000 interface board and 64-channel digital head stages with sampling at 30 kHz (IntanTech). Signals were recorded in a unipolar manner against a reference and common ground (cerebellar screws) and digitized by the head-mounted preamplifier.

Spike sorting and unit classification

Spike sorting was performed semiautomatically with KiloSort (93) (https://github.com/cortex-lab/KiloSort), followed by a manual curation using Phy software (https://github.com/kwikteam/phy) and custom-designed plugins (https://github.com/petersenpeter/phy-plugins) to obtain well-isolated single units. Cluster quality was assessed by manual inspection of waveforms and autocorrelograms and by the isolation distance metric (fig. S11). Multiunit, noise clusters, or poorly isolated units were discarded for the analysis.

Putative excitatory and inhibitory neurons were separated on the basis of their autocorrelograms and waveform characteristics (fig. S11) (9, 91, 94), assisted by monosynaptic excitatory and inhibitory interactions between simultaneously recorded, well-isolated units (9, 91, 94). Two key metrics used for this separation were burst index and trough-to-peak latency (fig. S11). Burst index was determined by calculating the average number of spikes in the 3- to 5-ms bins of the spike autocorrelogram divided by the average number of spikes in the 200- to 300-ms bins. To calculate the trough-to-peak latency, the average waveforms were taken from the recording site with the maximum amplitude for the averaged waveforms of a given unit.

Excitatory units in the hippocampus were first tentatively classified as CA3 or DG neurons on the basis of their anatomical position with respect to CA3pyr cell and GC layers. The location of these layers was estimated using electrophysiological markers (phase-shift of theta oscillation and LFP dentate spikes, power of ripple and gamma oscillations) and ICA (Fig. 3 and fig. S5) (8, 9, 91), and verified histologically postmortem. Excitatory dentate units were further divided into putative GCs and MCs following the procedure described and validated by Senzai and Buzsaki (40). First, a principal component analysis (PCA) was performed on the average waveforms. Average waveforms were normalized by the peak amplitude and up-sampled to 100 kHz with a spline interpolation method. Waveform PCA was performed using the time between 0 and 0.8 ms of the second derivative of the up-sampled average waveform. As a result of the waveform PCA, w-PC1 and w-PC2 were obtained. The amplitude of the LFP type 2 dentate spike at the recording site where the units’ maximum waveform amplitude was observed was used to estimate the unit’s anatomical location relative to the maximum amplitude of the type 2 dentate spike. Third, we calculated the firing rate ratios for each unit between non–rapid eye movement (NREM) sleep and waking. We separated GCs and MCs into two clusters using the k-means method based on w-PC1, w-PC2, DS2 amplitude, and the ratio of the firing rate during NREM and waking (Fig. 5 and fig. S11).

ICA and CSD analysis of LFPs

To separate the different sources that contribute to the LFP mixed signal, we used an approach based on ICA that has been described and validated previously for hippocampal recordings (8, 9, 51, 52, 85, 92). ICA is a blind-source-separation technique that can isolate spatially segregated stable patterns of activity in a mixed signal recorded with an array of sensors. Applied to linear profiles of LFPs, it can separate physiologically meaningful sources that can be attributed to known anatomical pathways, as has been demonstrated for the rat hippocampus (8, 9, 51, 52, 85, 92), mice visual cortex (95), and rat motor cortex (96).

Here, we applied ICA to spatially contiguous LFP channels after filtering in the gamma band (25 to 200 Hz). This filtering step is needed to reduce the strong contribution of lower frequencies to the LFP. If low frequencies are included, then their orders-of-magnitude higher power dominate the mixing matrix and reduce the effectiveness of the ICA algorithm for higher frequencies (8, 9, 95). To increase the contribution of the signals from the target region (i.e., DG), LFP channels outside of the structure of interest were removed before running ICA. The ICA algorithm [runinca (97)] takes a time series of data with dimension equal to the number of recording sites and returns a time series of the same dimensionality but rotated so that each dimension represents a different IC. The inverse of the mixing matrix that transforms the LFP data into the ICs gives the channel weight of each component that is captured for each recording site. When projected back to the anatomical location of the recording site, this corresponds to the spatial voltage loadings of each IC (51, 52, 92). In most cases, we computed ICA on the LFP profiles recorded with a single shank. In a few cases (such as for Fig. 3D or fig. S5), we computed ICA on the LFP signals recorded simultaneously at all sites of multiple shank probes (2D electrode matrix). We ranked the components by the amount of variance that they explain in the original data (relative power). Once ICs have been extracted from the raw LFP traces, they can be analyzed as if they were active independently from activities at other locations. We reconstructed the virtual LFP produced by a single IC by multiplying the IC time course by its corresponding voltage loading. CSDs for each IC were calculated from their voltage loadings after application of ICA, calculating the second spatial derivative of the LFP profile (51, 52, 92).

Spectral analysis, cross-frequency coupling, and spike-LFP coupling

All spike and LFP spectral analyses were restricted to periods of behavior in the maze when animal’ speed exceeded 5 cm/s unless specified otherwise. The LFP signal was down-sampled to 1250 Hz for all analyses.

To obtain of phase of the theta rhythm, one channel (typically in the middle of the CA1pyr cell layer from the same shank from which gamma LFP signals or ICs were computed) was chosen as global reference theta. LFP was bandpass filtered in the range of 5 to 15 Hz. Theta phase was then computed using the Hilbert transform of the filtered LFP. Theta peaks correspond to 0° and 360° and troughs at 180° and 540° of theta waves recorded in the CA1pyr cell layer herein. In a subset of sessions, this method was compared with an alternative one that consisted of estimating theta phase by the linearly interpolated phase between maxima and minima in each theta cycle of the 1- to 60-Hz bandpass-filtered LFP, but theta-gamma coupling and spike-phase coupling analysis results did not differ significantly.

The first step for all spectral analyses and ICA was to filter LFP signal in the 25- to 200-Hz band using a type 1 linear phase fast infrared filter with a Hanning window.

Cross-frequency coupling

To perform spectral analysis at a high resolution in time and frequency, the complex wavelet transform of the LFP (or ICs) was calculated using complex Morlet wavelets. Wavelets were calculated using a logarithmically spaced frequency vector in the band of interest (25 to 200 Hz). Phase-amplitude cross-frequency coupling for a given LFP recording was assessed using the modulation index (MI) measure (98). Phase time series were binned into phase intervals, and the mean wavelet amplitude was calculated for each. The MI was obtained by measuring the divergence of the observed amplitude distribution from the uniform distribution. The statistical significance of the MI values (P value) was assessed by a surrogate analysis (n = 1000 surrogates) with random shifts between the phase and amplitude time series. For the presented plots, grand averages were calculated as the mean across all animals unless otherwise indicated, and the MI values reported were significant (P < 0.01 compared with surrogate distribution).

LFP-LFP synchrony

Different metrics of LFP synchrony were calculated using the FieldTrip toolbox (99). For each session, LFP signals were selected from the middle of the anatomical layer of interest (e.g., the DG molecular layer). LFP epochs recorded during the same type of behavior were concatenated and divided into 5-s non-overlapping epochs. Epochs that contained artifacts were rejected. Spectra were estimated by multitaper Fourier transform, using a discrete prolate spheroidal sequence. Coherence was calculated as the magnitude of the summed cross-spectral density between two LFP time series, normalized by respective power spectra. Because coherence is affected by both power and phase synchrony, we assessed specifically LFP phase-phase coupling using two complementary metrics: PPC (54) and the weighted phase-lag index (WPLI) (53). These metrics are based only on the imaginary component of the LFP cross-spectrum. WPLI has the advantage that is not spuriously affected by volume conduction or a common reference and it is more robust to noise contamination, so it was used for the analyses in the main figures.

Spike-LFP coupling

The phase locking of spikes to LFP features at each frequency was measured for individual units using the wavelet phase from 25 to 200 Hz (30 logarithmically spaced wavelet scales) at the time of each spike (8). Only neurons that fired at least 100 spikes during the selected task intervals were included in the analysis. Reference LFP was taken 200 to 400 μm away from the electrode where the unit was recorded to minimize spike energy leakage into the LFP. MIs were calculated using either the mean resultant length of the phases or its PPC, and significance was estimated using the Rayleigh test for nonuniformity (P < 0.05) using circular statistics. PPC was quantified on the basis of the concentration of pairwise differences between spike phases, and has the advantage that is not biased by the number of spikes (54). Preferred frequency of modulation was determined as the largest mean vector length or PPC of each significantly modulated neuron. The mean angle of the phases for a given neuron’s spikes was taken as the preferred phase.

Place cell analysis

Spiking data were binned into 1-cm-wide segments of the camera field projected onto the maze floor, generating raw maps of spike counts and occupancy probability. A Gaussian kernel (SD = 5 cm) was applied to both raw maps of spike and occupancy, and a smoothed rate map was constructed by dividing the spike map by the occupancy map. Only periods in which animal velocity was above 5 cm/s were included. A place field was defined as a continuous region of at least 15 cm², where the mean firing rate was >10% of the peak rate in the maze, the peak firing rate was >2 Hz, and the spatial coherence was >0.7 (9, 36, 83, 89). Spatial correlation between blocks of trials was calculated as the average pixel-by-pixel correlation of the smoothed-averaged firing rate maps.

Spatial information and spatial sparsity

We calculated the spatial information encoded in place cell firing rates (or spike phases) using two complementary approaches. We used the method of Skaggs et al., 1993 to calculate spatial information in bits per spike as follows:

$$\text{SPI}=\sum _i{p}_i\frac{{\lambda }_i}{\lambda }\text{log}2\frac{{\lambda }_i}{\lambda }$$

where λ_i is the mean firing rate of a unit in the i^th bin, λ_i is overall mean firing rate, and p_i is the probability that animal being in the i^th bin (occupancy in the i^th bin/total recording time). The sparsity index (36, 83) was defined as follows:

$$\text{Sparsity}=\frac{{\left(\sum _i{p}_i{\lambda }_i\right)}^2}{\sum _i{p}_i{\lambda }_i^2}$$

Cell assembly analyses

For detecting cell assembly patterns, we used an unsupervised statistical framework based on a hybrid PCA followed by ICA as previously reported (55, 56, 100). In brief, spike trains of each neuron were binned in 20-ms intervals for the whole session (including only task periods) and z-scored firing rates were calculated for each bin. Spike trains were convolved with a Gaussian kernel (SD = 10 ms), and the matrix of firing correlation coefficients for all pairs of neurons was constructed. Next, we calculated the number of assemblies based on those principal components with eigenvalues that exceeded the threshold for random firing correlations (using the Marčenko-Pastur law). This method provides a number of significant patterns smaller than the number of neurons. Each of these patterns explained more variance of the spike train correlation matrix than other patterns that would result from independently firing neurons (55, 56, 100). The fast-ICA algorithm (62) was then used to determine for each assembly (component) the vector of weights with which each neuron’s firing contributes to that assembly. To measure the strength of each assembly’s activation as a function of time in a given episode, we multiplied the convolved z-scored firing rate of a given neuron at a given time by the weight of that neuron’s contribution to a given assembly. We then summed the product of these weighted spike counts for all nonidentical pairs of neurons to provide the assembly activation strength at the given time point. Assembly activity was considered when its expression strength exceeded a threshold of 5 (55, 56, 100).

Most of the detected assembly patterns consisted of a few neurons with high weights and a large group of neurons with weights around zero (Fig. 3K and fig. S10). Assembly members were thus considered those cells with weight that exceeded the mean weight of the assembly by 2 SDs (55, 56, 100). Conversely, the contribution of a cell to an assembly (Fig. 3L) was its weight.

Analysis of object-related responses of single neurons

First, periods of active object exploration were identified as those when the head of the animal was within 3 cm of the object perimeter and its nose was pointing to it, excluding grooming or reward-consuming periods. To analyze single-neuron responses to objects on a given trial (or set of trials), all periods of exploration of one particular pair of identical objects were pooled together and aligned by the start of the object engagement. Firing rates during each of these periods were calculated, smoothed using a Gaussian kernel (SD = 10 ms), and averaged to obtain a firing rate response to that type of object (100). Object discrimination was computed as follows: absolute (firing rate during interaction with object type A − firing rate during interaction with object type B)/(firing rate during interaction with object type A + firing rate during interaction with object type B). Values closer to 0 indicated that a given cell had a similar firing response to both types of objects, and values closer to 1 reflected that it fired preferentially while exploring one of the two types (either target or distractor object; “high discrimination”).

Statistical analyses

Statistical analyses were performed with MATLAB functions or custom-made scripts. No specific analysis was used to estimate minimal population sample or group size, but the numbers of animals, sessions, and recorded cells were larger or similar to those used in previous related work (8–10, 83–90). The unit of analysis was typically identified as single neurons or assemblies. In a few cases, the unit of analysis was sessions or animals, and this is stated in the text. Unless otherwise noted, non-parametric two-tailed Wilcoxon rank-sum (equivalent to Mann-Whitney U test) or Wilcoxon signed-rank test was used. For multiple comparisons after ANOVA, Tukey’s honesty post hoc test was used.

For statistical analysis of spike-LFP and LFP-LFP coupling, a two-step testing was conducted (14). First, statistical significance at P < 0.05 level was tested for each frequency step while correcting for multiple comparisons across frequencies (Bonferroni correction). Second, for the band of interest (e.g., gamma_F), all significant frequencies were averaged, and a second test was performed to estimate precise significance level within that frequency band.

On box plots, the central mark indicates the median and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively; whiskers extend to the most extreme data points not considered outliers. Outliers are not displayed in some plots but were included in statistical analysis. Because of experimental design constraints, the experimenter was not blinded to the manipulation performed during the experiment (i.e., optogenetic manipulation).