Abstract
The human cardiovascular (CV) system elicits a physiological response to gravitational environments, with significant variation between different individuals. Computational modeling can predict CV response, however model complexity and variation of physiological parameters in a normal population makes it challenging to capture individual responses. We conducted a sensitivity analysis on an existing 21-compartment lumped-parameter hemodynamic model in a range of gravitational conditions to 1) investigate the influence of model parameters on a tilt test CV response and 2) to determine the subset of those parameters with the most influence on systemic physiological outcomes. A supine virtual subject was tilted to upright under the influence of a constant gravitational field ranging from 0 g to 1 g. The sensitivity analysis was conducted using a Latin hypercube sampling/partial rank correlation coefficient methodology with subsets of model parameters varied across a normal physiological range. Sensitivity was determined by variation in outcome measures including heart rate, stroke volume, central venous pressure, systemic blood pressures, and cardiac output. Results showed that model parameters related to the length, resistance, and compliance of the large veins and parameters related to right ventricular function have the most influence on model outcomes. For most outcome measures considered, parameters related to the heart are dominant. Results highlight which model parameters to accurately value in simulations of individual subjects’ CV response to gravitational stress, improving the accuracy of predictions. Influential parameters remain largely similar across gravity levels, highlighting that accurate model fitting in 1 g can increase the accuracy of predictive responses in reduced gravity.
NEW & NOTEWORTHY Computational modeling is used to predict cardiovascular responses to altered gravitational environments. However, considerable variation between subjects and model complexity makes accurate parameter assignment for individuals challenging. This computational effort studies sensitivity in cardiovascular model outcomes due to varying parameters across a normal physiological range. This allows determination of which parameters have the largest influence on outcomes, i.e., which parameters must be most carefully selected to give accurate predictions of individual responses.
Keywords: cardiovascular physiology, gravitational effects, individual differences, Latin hypercube sampling, sensitivity analysis
INTRODUCTION
Humans experience strong physiological responses to gravitational changes. For example, effects of exposure to microgravity on the cardiovascular (CV) system include a cephalad fluid shift, a decrease in circulating blood volume, cardiac atrophy, and a redistribution of blood and extravascular fluids that can lead to orthostatic intolerance (1, 2). There is also considerable variation in individual responses to altered gravity levels. For example, this is seen in both spaceflight studies (3–7) and in Earth-based research analogs, including long-duration studies such as –6° head-down tilt bedrest (8–10) and dry immersion (11, 12), as well as short-duration interventions such as parabolic flights (13–15), tilt platform tests (16, 17), and centrifugation (18–20). Aside from normal variation between individuals, multiple studies have also found significant differences in response associated to gender (21–24).
To further understand the human CV response to altered gravity environments, we can use computational approaches to simulate a variety of environmental conditions and scenarios. Since Guyton et al.’s early models (25, 26), a variety of modeling techniques have been used to investigate various aspects of the cardiovascular system. These techniques cover a range of functions, including investigating the effects of exercise (27), microgravity (28), head-up tilt (29–31), lower-body negative pressure (29, 32, 33), and postural changes (34–36). Thus, modeling techniques allow us to expand beyond the limits imposed by human experimentation and therefore, to make predictions on the risk of orthostatic intolerance, the efficacy of countermeasures, and the variation in responses elicited by different individuals.
One of the challenges of computational approaches is linking the models with experimental data. This includes both the process of assigning values to simulated physiological parameters, and also the validation of the model (37). Often, fitting experimental data requires a significant degree of processing, estimating values from related physiological measurements, or scaling from nonhuman studies (38). When using a model to predict individual responses, rather than general trends, this challenge is compounded by the necessity to know the specific measurements for that specific individual.
Complex systemic models can have hundreds of parameters (27, 29), and it would be too resource-intensive, and in many cases impossible, to determine every single parameter for an individual. However, we can overcome this limitation by performing sensitivity analyses (39). Thus, once an appropriate and reasonable range of variation for all parameters has been determined, sensitivity analysis techniques identify the most important parameters that dominate the physiological response in the specific context being modeled, i.e., parameters that we need to determine accurately for the individual in order to get accurate results (as opposed to parameters where using a population mean will not adversely affect the predictive power of the model).
We conducted a comprehensive Latin hypercube sampling/partial rank correlation coefficient (LHS/PRCC) sensitivity analysis on an existing 21-compartment lumped-parameter CV model (27, 29, 38, 40–42) to determine the sensitivity of various physiological model parameters to variation within their normal nonpathological range. Simulations capture short-term cardiovascular responses of healthy subjects during an acute (600 s) tilt test (from supine to upright posture) at various constant gravitational conditions. Similar to Monte Carlo analysis, the proposed technique involves a large number of simulations in which model parameters are selected randomly (within the appropriate constraints). Therefore, each one of the simulations includes a different combination of parameters, thus representing a different individual subject. Moreover, we used a range of gravitational conditions (from 0 g to 1 g, in 0.25 g increments) to further determine whether the most relevant physiological features differ with the strength of the gravitational field.
METHODS
Description of the Cardiovascular Model
We used a lumped-parameter model to represent the CV system (27, 29) as shown in Fig. 1. This model has been implemented and validated in multiple physiological conditions including tilt (29, 38), centrifugation (41), and exercise (27). The model consists of 21 compartments: 15 compartments represent the systemic circulation, 4 compartments represent the cardiac chambers (which include variable capacitors representing contractions and diodes representing the mitral, tricuspid, pulmonary, and aortic nonreturn valves), 2 two compartments represent the pulmonary circulation. Parameters associated with each compartment include the anatomical vertical length (superior-to-inferior extension of the vascular segment), a resistance, and a vascular compliance, and they were estimated from the literature (38). Three venous compartments (legs, splanchnic, and abdominal veins) are modeled with a nonlinear pressure-volume relationship. The model also incorporates the two-major reflex mechanism concerning the short-term hemodynamic regulation response: the arterial baroreflex and the cardiopulmonary reflex. These are represented as feedback loop mechanisms using set-point controllers and reference pressures. A detailed description of this model has been previously published elsewhere (27), and it is also included in appendix c for completeness.
Figure 1.
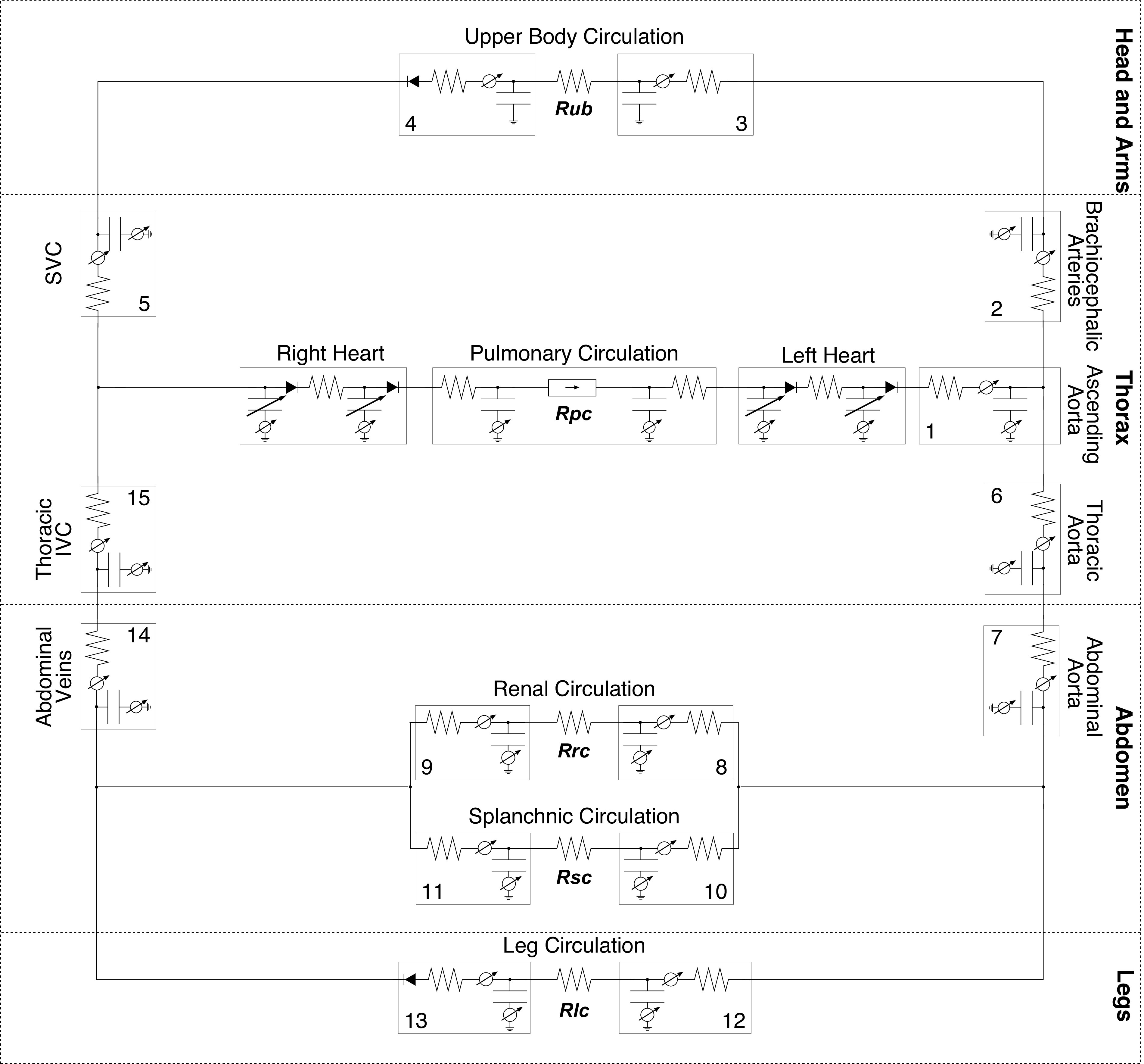
Circuit representation of the 21-compartment cardiovascular model, composed of 4 sections: head and arms, thorax, abdomen, and legs. The 15 systemic compartments are numbered as follows: 1, proximal aorta; 2, brachiocephalic arteries; 3, upper body arteries and 4, veins; 5, superior vena cava; 6, thoracic aorta; 7, abdominal aorta; 8, renal arteries and 9, veins; 10, splanchnic arteries and 11, veins; 12, leg arteries and 13, veins; 14, abdominal veins; and 15, inferior vena cava. Capillary beds are represented by four microvascular resistances: upper body Rub, kidneys Rrc, splanchnic Rsc, and legs Rlc. Pulmonary circulation is represented by Rpc.
Modeling Orthostatic Stress
The effects of gravitational stress are particularly important in this study. These are represented using three mechanisms: 1) changes in hydrostatic pressure, a term included in all systemic compartments; 2) changes in intrathoracic pressure due to the weight of the liver being pulled down in the thoracic compartment (41, 43, 44); and 3) changes in total blood volume due to the increase in transcapillary fluid flow from the intravascular volume into the dependent vasculature (27, 45). Gravitational stress expressions are summarized in Table 1.
Table 1.
Mathematical expressions used to simulate constant gravitational stress
| Gravitational Effect | Expression |
|---|---|
| Hydrostatic pressure, mmHg | Ph,n = ρgchn |
| Intrathoracic pressure, mmHg | |
| Maximal blood volume lost from intravascular volume, mL |
Ph,n, hydrostatic pressure in compartment n; ρ, density of blood (7.95 mmHg/s2/m2); gc, gravitational acceleration in constant gravity field; hn, effective vertical length of compartment n (defined as half of the anatomical vertical length, except of the leg compartments where the effective length is assumed to be one third of the anatomical vertical length); Pth, intrathoracic pressure; , nominal intrathoracic pressure (−4 mmHg); gE, gravitational acceleration on Earth (9.81 m/s2); Vmax, maximal blood volume lost from intravascular volume into the interstitial space.
Parameter Groups
The cardiovascular system and thus, our model, have a small number of global key parameters which, based on previous simulations (38) and a preliminary analysis, cause larger variation in the outcome measures than the rest of the parameters. Examples of these are total blood volume or resting arterial pressure set-point. It was assumed that any future model simulations to determine differences between individuals would by necessity involve the accurate measurement or determination of these parameters using allometric scaling laws (46–48) and data given from reference sources such as Leggett and Williams (49). As such, they were not included in the detailed LHS/PRCC sensitivity analysis presented herein, which aimed to determine the most important of the remaining limited (i.e., non-global) parameters. A discussion of these global parameters is given in appendix a. In all our simulations presented in the rest of this paper, the subject was modeled with a height of 169.3 cm, a weight of 70 kg, a total blood volume of 5,625 mL (29, 50, 51), a nominal heart rate of 70 beats/min, a resting arterial set point of 91 mmHg, and a resting cardiopulmonary reflex set point of 8 mmHg.
We divided the cardiovascular parameters of interest into three groups: compartments (includes parameters related to the systemic circulation: resistances, compliances, and anatomical lengths), controls (includes parameters related to the baroreceptors and the cardiopulmonary reflex: gains for resistances, volumes, and ventricular contractility), and heart and lungs (includes parameters related to the cardiac and pulmonary systems: resistances and compliances).
Table B1 in appendix b shows the 45 parameters of the compartments group, comprising 15 resistances, 15 compliances, and 15 anatomical lengths. Anatomical length was defined as the vertical distance from the superior to the inferior end of the vascular segment. The control parameters, shown in Table B2 in appendix b, corresponded to the gains of the control system feedback signals in the baroreflex and cardiopulmonary reflex. Finally, Table B3 in appendix b shows the heart and lungs group parameters. These were the compliances and resistances corresponding to the pulmonary arteries and veins, and the compliances and resistances corresponding to the four cardiac chambers.
As the exact distributions of many physiological parameters are relatively unknown, we assumed that they are represented by truncated Gaussian distributions (i.e., they follow a standard normal distribution where the two ends are modified to include lower and upper bounds. Thus, values outside the defined range are not included in the simulations) (39, 52, 53). The ranges were chosen based on extensive literature reviews (38) to capture the total variation in a normal, nonpathological population. The LHS was set up to capture 90% of this population (i.e., means ± 1.64 standard deviations).
Simulation Profile and Gravity Levels Investigated
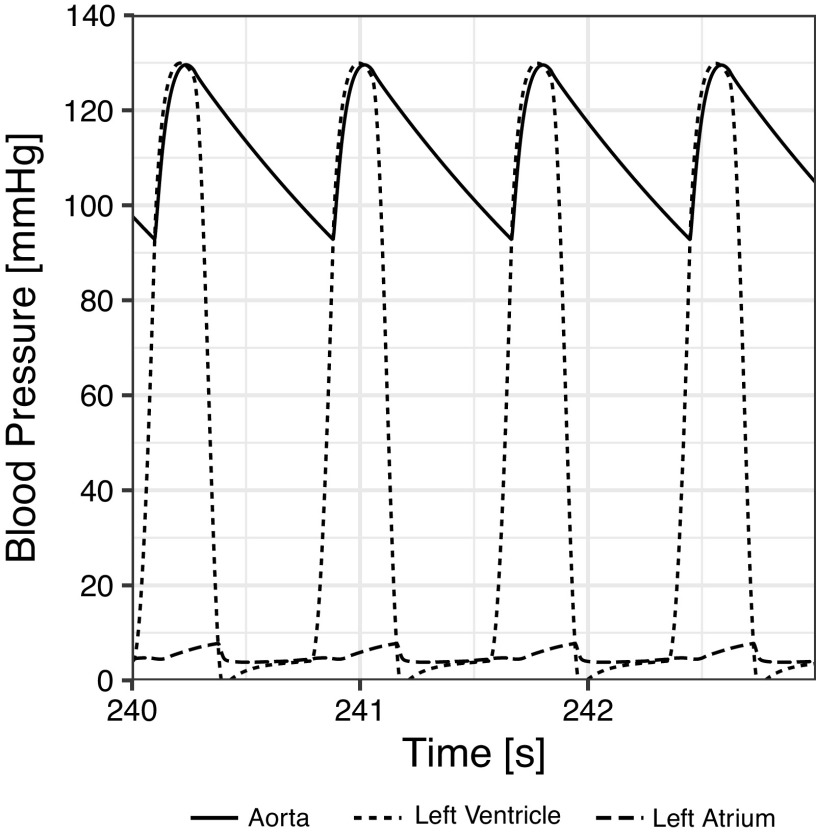
We simulated cardiovascular responses when subjected to a constant gravitational field. During simulations, the subject model was initially in a supine position during 60 s before being tilted to an upright position. Five levels of constant gravity were used: 0 g, 0.25 g, 0.5 g, 0.75 g, and 1 g. Since we are concerned with steady-state outcomes, the simulations were run until all transients had vanished and the model had reached stability. In all cases this occurred within 300 s of tilt. All outcomes were averaged across the final 60 s of the simulation, with stability assured by comparing means and variances with the preceding 240 s (giving a total 660 s runtime for each simulation). In each of the three groups (compartments, controls, and heart and lungs) and at each of the five gravitational conditions, we conducted a separate sensitivity analysis using LHS/PRCC techniques. When analyzing one of the groups, the other two were held constant, generating 15 independent sensitivity analysis datasets. Figure 2 shows examples of our tilt test simulations, including blood pressure (at 1 g), and heart rate (at multiple gram levels: 0 g, 0.25 g, 0.5 g, 0.75 g, and 1 g).
Figure 2.
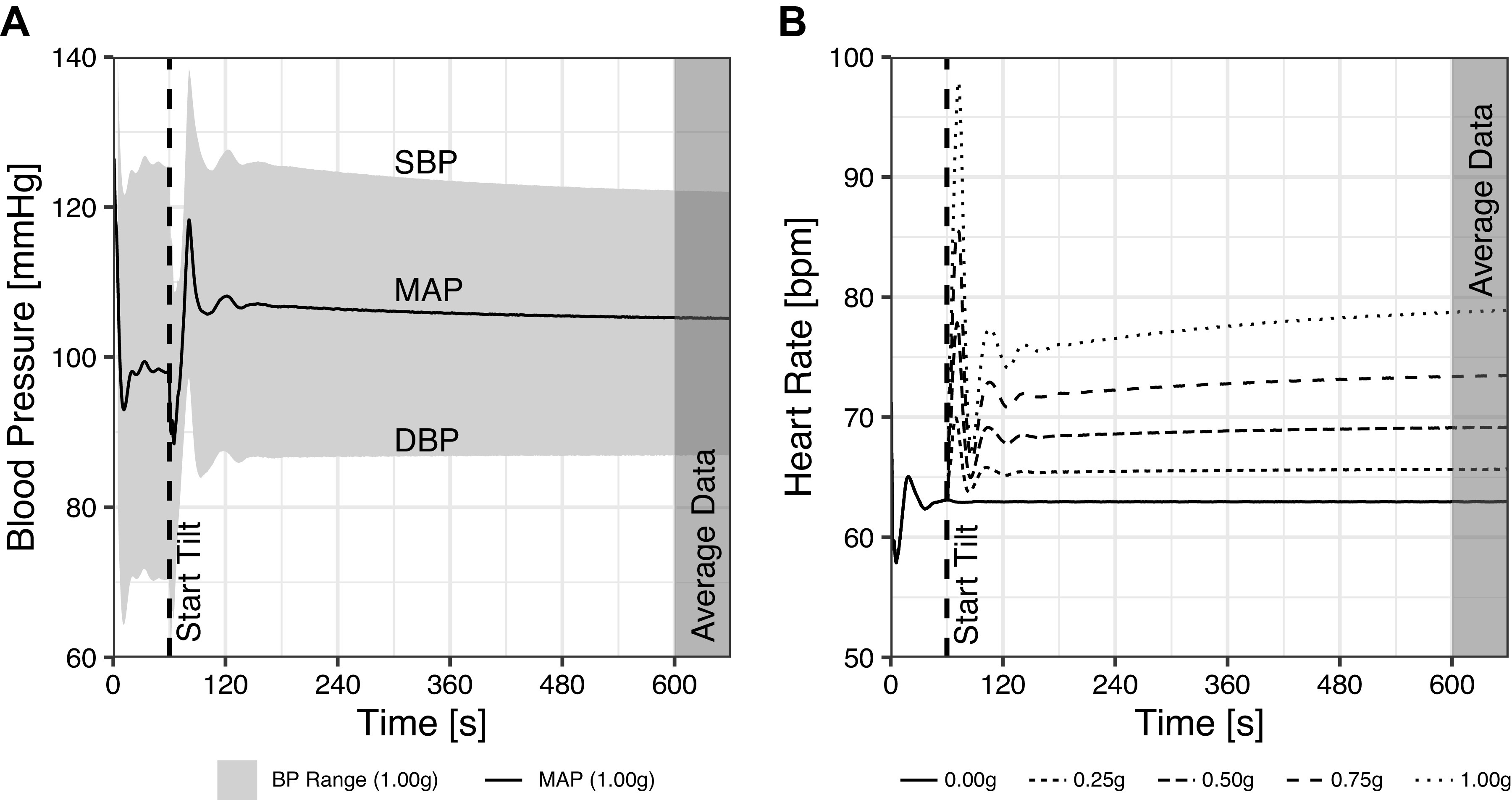
Examples of model outcome responses during the tilt test simulations. A: blood pressure evolution over time for a single simulation run at 1 g. The gray ribbon shows the blood pressure range (with systolic, mean, and diastolic blood pressures labeled). The tilt maneuver from 0° to 90° occurs at 60 s (dashed line), and model outcomes were averaged during the final 60 s of the simulation (shaded area starting at 600 s). B: heart rate evolution over time for five simulations at the five levels of constant gravity used (0 g, 0.25 g, 0.5 g, 0.75 g, and 1 g).
Outcome Measures
The primary outcome measures considered were the following CV variables: heart rate, stroke volume, central venous pressure, mean arterial pressure, systolic blood pressure, and diastolic blood pressure. We further considered two secondary outcome measures calculated from the primary measures: cardiac output and pulse pressure.
Latin Hypercube Sampling/Partial Rank Correlation Coefficient
We adopted a Latin hypercube sampling/partial rank correlation coefficient (LHS/PRCC) approach to examine the effects of varying model parameters on the outputs (i.e., heart rate, stroke volume, central venous pressure, mean arterial pressure, systolic blood pressure, and diastolic blood pressure). This method is a combination of an ordered sampling method (i.e., Latin hypercube sampling) (54) followed by a correlation method (partial rank correlation coefficient) (55, 56).
Latin hypercube sampling.
LHS was introduced by McKay et al. (57) and developed by W. J. Conover (58), and was initially created to characterize the uncertainty in inputs to computer models (52). It is a stratified Monte Carlo sampling scheme to achieve maximal coverage of an input space. The “stratified sampling” scheme divides the distribution of a random variable Xj into n nonoverlapping intervals of equal-probability. Then, a random sample is selected from each of the n intervals. This is repeated for each of k variables of interest (53, 54, 59–61). This method has two main advantages: first, it ensures that samples are taken from the entire distribution, with more samples taken from closer to the probability peak of the distribution; and second, it is more computationally efficient than Monte Carlo methods, while ensuring that every interval in the n × k space is included in the experiment.
The LHS method ensured that we sampled over the entire distribution of each parameter. However, it is important to generate a sufficient number of intervals, since too few divisions could lead to an erroneous representation of the parameter space. According to Khan et al. (52), the recommended number of divisions when the number of variables is large falls between 4 N/3 and 5 N for N total parameters. Our three groups (compartments, controls, and heart and lungs) had 45, 20, and 15 parameters, respectively. To be consistent, we took the same number of divisions, 100, for each of the three groups. This number of divisions lies on Khan’s range for the compartments and controls groups (52), but is higher for the heart and lungs group, leading to a longer computational time but ensuring a large enough sampling size.
Furthermore, within each group and gravity condition, the entire LHS method described earlier was applied three times, resulting in 300 simulations per group and per gravity condition. Thus, the total experiment space was given by:
100 simulations × 3 trials × 3 variable groups × 5 gravity conditions
resulting in a total of 4,500 runtimes of the model. Each runtime of the model could be considered as representing a separate subject with a unique combination of individual physiological parameters (all within a normal physiological range).
Partial rank correlation coefficient.
PRCC is a nonlinear correlation method used to interpret the association between a parameter and an outcome measure after removing the effects of all other parameters on that outcome (39). This method allows quantification of the relationship between each pairing of a parameter and an outcome measure by a rank correlation coefficient between –1 (perfect inverse relationship) and +1 (perfect direct relationship), with 0 indicating no relationship (55, 62–64). Since this is a rank methodology, the linearity of the relationship is not determined or quantified.
Data Analysis
Cumulative influence factor.
Every parameter was related to each of the six primary outcome measures by a PRCC coefficient, generating six PRCCs for each parameter, at each gravity condition. After those coefficients were calculated, they were normalized to obtain, for every parameter, a single value (the cumulative influence factor) that quantifies its overall influence on the outcome measures. Thus, the “cumulative influence factor” is calculated as follows:
| (1) |
where |rjkl| is the absolute value of the PRCC between parameter j and outcome measure k at gravity level l, which is then averaged across all six outcome measures and all five gravity levels to calculate CIFj. Each CIF has a value between 0 and 1, where 0 indicates no influence of the parameter on the outcome measures, and 1 indicates a very strong influence. For the compartments group, we further grouped and normalized the influence of the three parameter types (resistance, compliance, and anatomical length) that represent a systemic compartment, giving a single numerical value representing the overall influence of each compartment on the outcome measures (53).
Cumulative distribution function and coefficient of variation.
To quantitatively compare the variation of the outcome measures as a function of the gravity condition, and to compare between groups of parameters (i.e., compartments vs. controls vs. heart and lungs), we generated cumulative distribution functions (CDFs) for each of the three groups of parameters at each of the five gravity conditions (53, 65, 66). To quantify these differences, we used the coefficient of variation (COV) to describe the spread of each CDF. Coefficient of variation is defined by:
| (2) |
where σk,lm and μk,lm represent the standard deviation and mean, respectively, of the outcome measure k, from group m (compartments, controls, or heart and lungs) at gravity level l. We further calculated the CDF and COV of the two secondary outcome measures (cardiac output and pulse pressure).
RESULTS
Figure 3 shows the CIF of the compartments (Fig. 3A), controls (Fig. 3B), and heart and lungs (Fig. 3C) groups.
Figure 3.
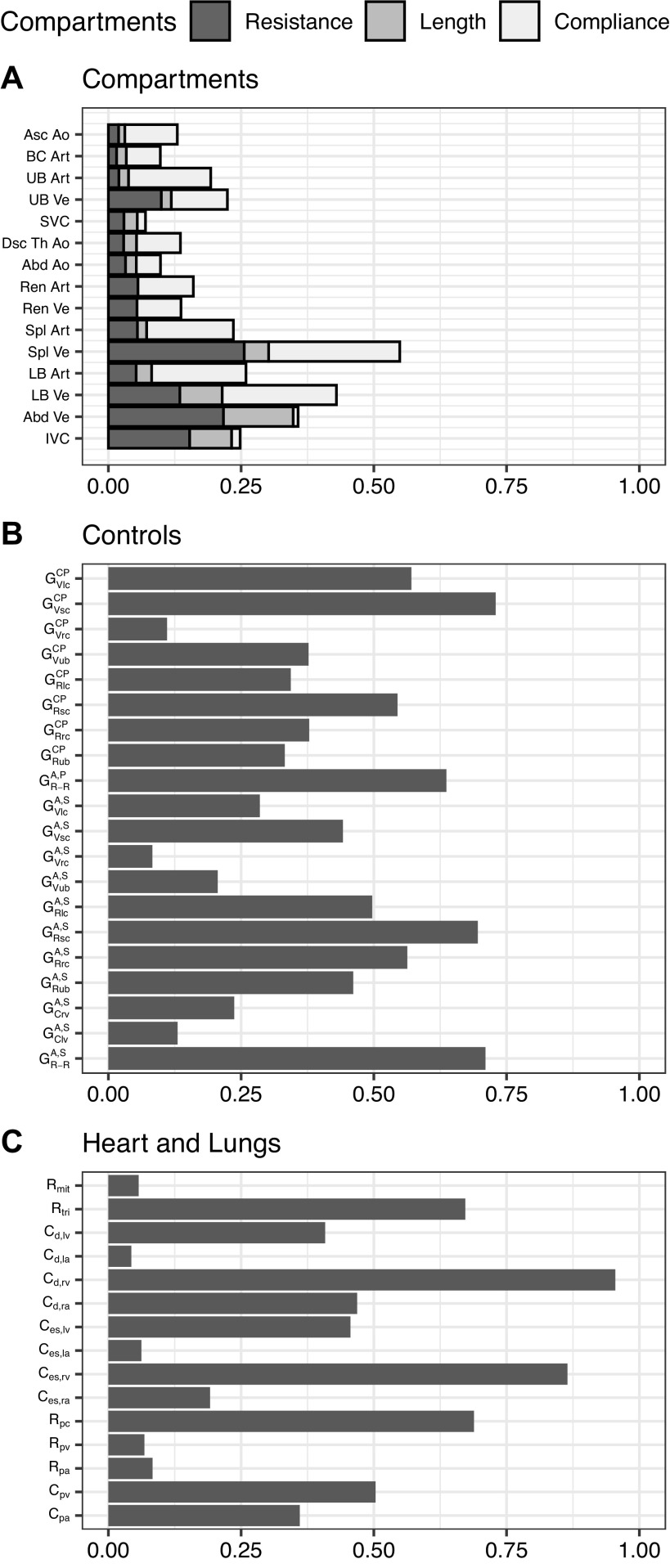
Cumulative influence factor (CIF) for compartments (A), controls (B), and heart and lungs (C) groups. In the compartment group (A), the CIF is further divided to show the individual contributions of the different parameters forming a compartment (resistance, length, and compliance). CIF takes a value between 0 and 1 where a higher value represents greater influence on the outcome measures. A, arterial baroreflex; Abd, abdominal; Ao, aorta; Art, arteries; Asc, ascending; BC, brachiocephalic; C, compliance; CP, cardiopulmonary reflex; d, diastolic; Dsc, descending; es, end-systolic; G, gain; IVC, inferior vena cava; la, left atrium; LB, lower body; lc, lower body microcirculation; lv, left ventricle; mit, mitral valve; P, parasympathetic; pa, pulmonary arteries; pc, pulmonary microcirculation; pv, pulmonary veins; R, resistance; ra, right atrium; rc, renal microcirculation; Ren, renal; R-R, R-R interval; rv, right ventricle; S, sympathetic; sc, splanchnic microcirculation; Spl, splanchnic; SVC, superior vena cava; Th, thoracic; tri, tricuspid valve; UB, upper body; ub, upper body microcirculation; V, unstressed volume; Ve, veins.
Figure 3 shows that within the compartments group, most influence comes from varying parameters in the splanchnic (Spl), lower body (LB), and abdominal (Abd) veins (Ve). Within each compartment, in the majority of cases the compliance is the dominant parameter, although toward the end of the venous segment (i.e., the abdominal vein and inferior and superior venae cavae), the resistance exerts the most influence. Within the controls group, the arterial baroreflex sympathetic arc resistance gains to the lower systemic circulation (, , ), along with the cardiopulmonary reflex volume gains to the splanchnic () and lower body () circulations, show the largest CIF. Both arcs of the arterial baroreflex (sympathetic and parasympathetic) related to R-R interval (, ), also have a high (>0.6) CIF. Finally, within the heart and lungs group, parameters related to the right ventricle have the largest CIF. These include end-systolic and diastolic compliances (Ces,rv, Cd,rv) and the tricuspid valve resistance (Rtri).
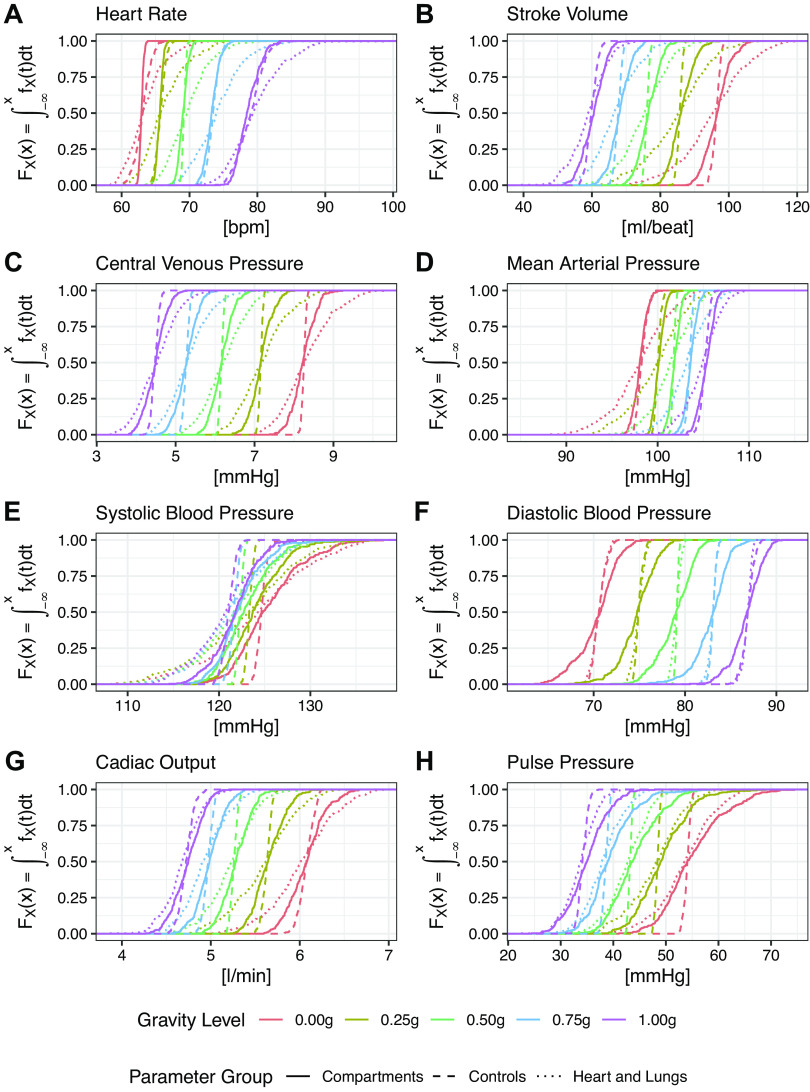
Figure 4 shows the cumulative distribution functions for all six primary outcome measures (heart rate, stroke volume, central venous pressure, mean arterial pressure, systolic blood pressure, and diastolic blood pressure) and the two secondary outcome measures (cardiac output and pulse pressure). Each plot shows the CDF for all five gravity levels (0 g, 0.25 g, 0.50 g, 0.75 g, 1 g) and all three parameter groups (compartments, controls, and heart and lungs). These plots allow for comparison between the three groups showing the overall variation of the outcome measures as a function of the variation of the model parameters.
Figure 4.
Cumulative distribution function (CDF) of all outcome measures under multiple gravity conditions. Each plot shows the total variation of the outcome measure across the entire range of model parameters in each one of the five gravity conditions (0 g, 0.25 g, 0.5 g, 0.75 g, and 1 g). A: heart rate (HR); B: stroke volume (SV); C: central venous pressure (CVP); D: mean arterial pressure (MAP); E: systolic blood pressure (SBP); F: diastolic blood pressure (DBP); G: cardiac output (CO); and H: pulse pressure (PP).
Figure 4 shows a decrease in stroke volume and central venous pressure, along with an increase in heart rate and diastolic blood pressure with increasing gravity level. There is also a small increase in mean arterial pressure. Systolic blood pressure is largely held constant. Both cardiac output and pulse pressure decrease with increasing gravity level. All parameters stay within a normal physiological range. For most of the outcome measures, the largest variation (i.e., largest spread of the CDFs) occurs in the heart and lungs group except for diastolic blood pressure and pulse pressure, where the largest variation occurs in the compartments group.
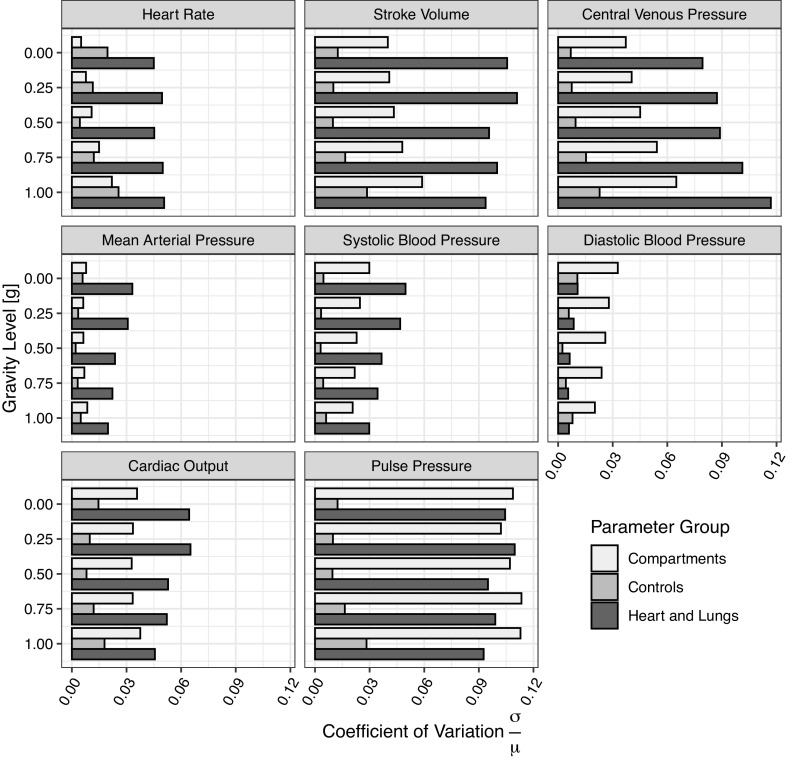
Figure 5 shows the coefficient of variation (COV) for each of the three parameter groups (compartments, controls, and heart and lungs) and each outcome measure, at each gravity level simulated. These figures highlight the change in the relative influence of each group as the gravity level changes from 0 g to 1 g.
Figure 5.
Coefficient of variation (COV) for each outcome measure and parameter group at each gravity level simulated. Each plot shows a single outcome measure, the gravity levels are on the y-axis and COV on the x-axis. All plots have the same scale.
Overall, the largest COVs (∼0.1) are found in the heart and lungs group for stroke volume, central venous pressure, and pulse pressure, and in the compartments group for pulse pressure. The remaining COVs are 0.05 or lower. For heart rate, stroke volume, central venous pressure, and mean arterial pressure, the heart and lungs group has the largest COV at all gravity levels and it is significantly higher (around twice the value) than the COV of the other two groups. These results suggest that variation of the heart and lungs parameters has significantly more effect on heart rate, stroke volume, central venous pressure, and mean arterial pressure than variation of either the compartments or controls parameters. For systolic blood pressure, the heart and lungs group still has the largest COV, but with increasing gravity the difference between COVs from heart and lungs and compartments groups decreases. In relation to diastolic blood pressure, the compartments group has the largest COV. In regards to the secondary outcome measures, cardiac output follows a similar trend to systolic blood pressure: the heart and lungs group has the largest COV but the COV of the compartment group is also high, particularly at higher gravity levels. The COV of pulse pressure is equally high in both the compartments and heart and lungs groups.
DISCUSSION
By varying parameter values across a normal physiological range and considering changes in systemic outcomes, we have identified a subset of parameters that have most influence on cardiovascular response to orthostatic stress in a number of gravitational conditions. We have also identified the parameters within our three chosen parameter groups with the most cumulative influence in constant gravitational fields. We have further compared these groups to one another, identifying the extent to which parameter variation within the group affects the overall systemic outcomes. Finally, we have quantified changes in the influence of each group with increasing gravity level.
Within-Group Influence
Figure 3A shows that the largest influence in the compartments group comes from the splanchnic, abdominal, and lower body venous compartments. From a systemic perspective this is unsurprising, since at rest, 70% of blood is contained in the venous system at any instant, and these three compartments account for 47% of all circulating blood (38). Together, this represents the total venous outflow from the gastrointestinal tract, all of the pelvic organs, two thirds of the skin, one half of the skeleton, 90% of the skeletal muscle, and nearly all of the adipose tissue (27, 38, 40).
Based on physiological principles, total venous return is expected to match cardiac output, both at rest and during exercise. The lower body venous compartment must be responsible for returning any blood from the legs back to the heart primarily through a combination of muscle pump and sympathetic nervous system stimulated venoconstriction (67, 68). The lower body microcirculation is predominantly supplying oxygen to skeletal muscle. Hyperemia to skeletal muscle can be up to 100-fold (69), particularly during high-intensity exercise. Hence, the resistance of the lower body veins must ordinarily swing through a large range to promote effective venous return. It is therefore unsurprising that varying the resistance of the lower limb veins compartment in the absence of exercise causes large changes in hemodynamic parameters. As an example, Skoog et al. (70) found reduced venous compliance to be an important determinant of orthostatic intolerance in some populations.
Within the majority of the compartments, compliance is the dominant influencing factor, with resistance being the second most influential parameter, particularly in the venous system. These findings confirm the decision to model the higher fidelity nonlinear relationship between pressure and volume in the large veins (details can be found in appendix c). In addition, the majority of the total blood volume at any instant resides in relatively compliant venous compartments and therefore, it is reasonable that the pressure-volume relationship of these compartments exerts the most influence on model outcomes. Some alternative models (for review, see Refs. 71, 72) choose to control compliance directly rather than controlling unstressed venous volume. Our results show that compliance is a key parameter for global outcomes and therefore the set points for these control systems should be carefully selected. Finally, the importance of accurate measures of compliance is underscored. This is particularly relevant when applying the model to simulate individual subjects, since studies have shown trends in compliance varying with age (73) and also deconditioning [for example time in bed rest (74) or microgravity (75)].
With respect to the abdominal and splanchnic venous compartments, these are the large venous compartments directly before the right atrium—excluding the thoracic inferior vena cava. The role of the venous components of circulation is to return blood to the heart. Hence, the large venous compartments are naturally compliant in order to accommodate a large variation in cardiac output while protecting systemic mean arterial pressure. As indicated in Table B1 in appendix b, these compliance values also present a fairly wide range (e.g., 47.7–72.3 mL/mmHg for the splanchnic veins compared with 0.04–0.36 mL/mmHg for the splanchnic arteries). Our modeling exercise demonstrates that varying the large range of compliance parameters in compartments associated with a high percentage of blood flow accounts for the largest changes to the systemic outcomes that the large venous compartments are partially responsible for regulating.
Finally, when considering the heart and lungs group, Fig. 3C shows that the right ventricular compliance, both end-systolic and diastolic (along with the tricuspid valve resistance), exerts the most influence on systemic outcome measures out of all the parameters studied. This may seem counterintuitive, since we usually associate left ventricular function or degradation with many cardiovascular adaptation and pathologies [for example, left ventricular hypertrophy is associated with both the physiological response to training and as a marker for cardiovascular disease associated with hypertrophic cardiomyopathy (76)]. The left ventricle pumps blood around the entire system accommodating a wide range of preloads (determined principally by cardiac output matched to venous return) and afterloads (determined principally by peripheral resistance and the range of normal mean arterial pressures throughout the systemic system). From a resting baseline, mean arterial pressure rises only moderately in dynamic exercise scenarios, primarily due to significant vasodilation as a result of functional sympatholysis (77). However, the same mean arterial pressure increases dramatically during isometric exercise as a result of the pressor response (78). As a consequence, in a model simulation that involves no exercise response, the left ventricle is overdesigned and underutilized, and therefore adjusting its parameters will not greatly affect the systemic response. By contrast, the right ventricle must only accommodate a narrower range of afterloads, determined by the limits of systolic pressure in the lower pressure pulmonary circulation. As such, the right ventricle becomes a systemic bottleneck, and varying these parameters can dramatically affect the flow of blood arriving at the left chambers, amplifying the impact of the right heart parameters in the system response.
Between-Group Influence
The CIFs displayed in Fig. 3 show the relative influence of each parameter within each group, but do not provide any information about the relative importance of one group with respect to the others. To investigate this relative importance, we must also consider the CDFs and COV (Figs. 4 and 5) Qualitatively, the CDFs follow the expected acute physiological response to changing the gravity level: when gravity level decreases there is an increase in cardiac output primarily due to an increased stroke volume as a result of increased preload (79), blunted by increased vagal modulation (seen as a fall in heart rate) (80). The expected increase in pulse pressure (80) as a result of increased stroke volume is also well simulated.
Quantitatively, our models show a 1.34 L/min (Welch two sample t test, t(1,537) = 128.8, P < 0.0005, 95% CI 1.32–1.36 L/min) increase in cardiac output between 1 g and 0 g, from 4.71 ± 0.17 L/min to 6.05 ± 0.26 L/min. This is closely matched to the 1.6 L/min acute increase found on entering microgravity reported by Norsk et al. (81), although their absolute cardiac output values are higher (6.6 ± 0.7 in 1 g to 8.4 ± 0.9 L/min in 0 g). The same study found no change in mean arterial pressure or heart rate. Our model shows a small decrease in mean arterial pressure of 6.98 mmHg (Welch two sample t test, t(1598) = –87.9, P < 0.0005, 95% CI 6.83–7.14 mmHg), and a decrease in heart rate of 15.98 beats/min (Welch two sample t test, t(1532) = –142.2, P < 0.0005, 95% CI 15.76–16.20 beats/min). It should be noted that Norsk’s experimental values are taken after a week in space, when adaptation has already begun. Also, we note that we expect to see less variation in our population at a given condition since we are not varying parameters such as height, weight, and total blood volume that grossly impact our systemic CV outcomes (appendix a). Varying these parameters would lead to larger standard deviations such that, for example, our decrease in mean arterial pressure may not be significant in a global population. By comparison, Mukai et al. (82) found a decrease in heart rate of 22 ± 7 beats/min in microgravity induced by parabolic flight, which is entirely consistent with our acute simulations.
Finally, visual inspection of the CDFs shows that for the majority of the parameters, the spread of the CDFs (which is a measure of the absolute variance) in the heart and lungs group (dotted lines) is often larger than the other two groups. This is most noticeable in mean arterial pressure, heart rate, and stroke volume. Based on these results, we preliminarily conclude that the heart and lungs group exerts the major influence on the outcome measures. In certain parameters (most noticeably stroke volume, central venous pressure, cardiac output, and pulse pressure), we further note that the absolute variation in the heart and lungs group appears to increase with decreasing gravity. We hypothesize that this model effect is related to decreased regulatory control in lower gravity, a finding supported by tilt studies showing reduced baroreflex sensitivity when decreasing orthostatic stress (83, 84).
Further insight into the relative influence of the groups can be seen through the coefficient of variation shown in Fig. 5. In all outcome measures at all gravity levels, the controls group of parameters exert the least variation on outcome measures. In five of the outcome measures, the heart and lung parameters provided the most variation, whereas in diastolic blood pressure it was the compartments parameters. Taking into context our understanding of the relative influence of the parameters within the groups, our results suggest that the right ventricular elastances are the key parameters that must be accurately determined for accurate system response, due to the systemic bottleneck.
Interestingly, with increasing gravity levels, the influence of both the compartments group and the controls group slightly increase. However, the COV of the controls group never matches the COV of the heart and lungs group, and only in heart rate does it present a higher COV than the compartments group. We hypothesize that the increased influence of the controls group is due to the fact that, as the primary regulator of blood pressure, the arterial baroreflex is increasingly stressed at higher gravity levels. We further posit that the increased influence of the compartments stems from increased blood pooling in the large veins at higher gravity levels, leading to greater importance of their parameters in promoting effective venous return in order to allow regulated circulation; a change in these parameters will cause large-scale changes in blood flow, which the already stressed control system is attempting to regulate. Aside from the aforementioned trends, it is important to note that in general, the COV of the different groups is similar across gravity levels. First, this underscores that our cardiovascular model (and more generally the cardiovascular system) behaves similarly across the 0 g to 1 g gravitational range. From the modeling perspective, these results specifically mean that the important set of parameters that must be accurately selected to simulate the behavior of a subject on Earth remain constant across reduced gravity conditions. This in itself is an important finding, stated simply that “if you can select precisely the necessary parameters to accurately model a subject on Earth, you can also accurately model the same subject in reduced gravity.”
Summary
Our simulations suggest that a small subset of parameters exert a large influence on CV regulation. Thus, more effort should go into determining the specific value of these parameters for individuals whose physiological responses we intend to simulate. Specifically, we have determined that the most important physiological characteristics to be described are those related to the large veins (lower body, splanchnic, and abdominal), and the right ventricle. To give examples of how these could be measured, right ventricular function can be accurately estimated noninvasively using biplanar contrast cineangiography (85), and venous characteristics (at least in the lower body) can be readily determined using a combination of allometric scaling and water-displacement plethysmography (86) to determine the appropriate pressure-volume relationships.
To highlight the potential impact of these findings with a short case study, numerous studies (21–24, 87) have found significant differences in CV responses to orthostatic stress based on gender. Aside from the global key parameters, many of which will be different between men and women (most notable those, such as total blood volume (TB5), linked to allometric scaling), there have also been studies noting gender differences in many of our important parameters. Maffessanti et al. (88) found that gender was highly significant (P < 0.01) in studies of right ventricular parameters. Similarly, it is expected that vascular length will be different in men and women based on allometry, but Monahan and Ray (89) also found gender differences in venous compliance (specifically in the leg, one of our influential compartments). All in all, our sensitivity analysis results suggest that accurately valuing differences in this subset of parameters, along with the global key parameters, could provide more accurate predictions of the CV responses of men and women, and more broadly, of specific individuals, to gravitational stress.
Limitations
Diaz-Artiles et al. (27) examined in detail some of the physiological limitations in the model in a previous publication. This included limitations of lumped-parameter modeling to determine pulse wave propagation, and intra-beat changes, along with assumed linearities in the systolic and diastolic pressure-volume relationships, and lack of viscoelastic stress-relaxation effects of the systemic veins. Inertial effects are also not included, since this model was primarily designed to analyze cycle-to-cycle cardiovascular changes in blood flow and pressure when exposed to orthostatic stress. In our case, we are primarily concerned with steady-state outcomes, and the contribution of inertial effects to pressure and flow is largest within the cardiac cycle (i.e., intra-beat changes) rather than on a beat-to-beat scale. Defares et al. (90) estimated that less than 1% of stroke volume and mean arterial pressure are due to inertial effects. Thus, their inclusion would only serve as a slight refinement of the arterial waveform at a higher computational cost. Diaz-Artiles et al. further commented on the difficulty of assigning numerical values to model parameters, and how a sensitivity analysis could help determine the subset of important parameters—this study intends to answer that limitation.
Similarly, the decision not to include compliances for the microvasculature, which are modeled as pure lumped resistances, was a modeling choice designed to limit the number of systemic compartments for computational efficiency. Literature on compliance of capillary beds, or their natural variation is scarce. Gallo et al. (91) modeled all capillary compliances in the order of 0.03 mL/mmHg in a similar 0-D lumped-parameter model. This is at least an order of magnitude smaller than our arterial compliances, and two to three orders of magnitude smaller than our venous compliances. As such, any minute variation in distension in the microvasculature is unlikely to have a significant impact on outcome measures.
Other models found in the literature incorporate additional features not included in our model, but we expect to find our results applicable. For example, both Blanco et al. (72) and Coats and Keith Sharp (71) developed models using arterial baroreflex control systems involving varying compliance, as opposed to the varying unstressed volume found in our model. In both of these models, we expect that the parameters with the highest sensitivity (aside from the heart and lung parameters, which are modeled similarly) are the ones related to the large venous compartments (for example venous resistance in the Coats and Sharp model), the compliance set points in these compartments, and the gains from the sympathetic arc of the arterial baroreflex.
With regard to the design of the sensitivity analysis, the full model contains in excess of 150 parameters. We selected a subset of parameters that we considered most likely to have large influence on the model outcomes, however there are others (such as time constants for the reflex arcs) that were not varied. The model outcomes only measured the average steady-state response after acute transients had settled, such that the impact of variation on the time response of the system was untested. Since we are considering steady-state cardiovascular responses to resting conditions, we also neglected the impact of exercise on the system. This adds an entirely new set of variables that could be separately analyzed using the same methodology as an additional group.
The simulations varied the chosen model parameters within predefined ranges. These ranges were chosen based on an extensive literature review as detailed by Heldt (38), and were designed to capture the majority of individual variation within a nonpathological population. The influence of each parameter is valid only within the ranges given, and caution should be taken extrapolating the results outside of these ranges. In particular, extrapolation to populations with pathological indications, such as acute ventricular hypertrophy, should be avoided. In addition, since the exact distribution of the selected parameters is largely unknown, we assumed that they followed truncated normal distributions. However, these underlying distributions could be slightly different for certain parameters and reflect, for example, lognormal distributions, or have a bimodal behavior driven by gender differences. By dividing the subset of varied parameters into three separate groups, we are potentially losing some influence due to a potential complex interaction of parameters from different groups. We have considered the relative importance of the groups using CDFs and COVs, but we recognize there could be a certain amount of information lost. In addition, our methodology assumes that all parameters are independently sampled. This was a choice to capture the largest range of possible variation. In reality, some parameters are certainly correlated, and this additional correlation could influence the PRCC used in the sensitivity analysis. A refined analysis using, for example, Copula models (92), could allow for more realistic selection of parameter combinations. The associated correlations and allometric scaling could be applied to both the local and global parameters together, as there is a relationship between body type/size and the homeostatic set point of an individual. This approach is dependent on identifying the potential correlations between parameter variables, and while the results may vary slightly in the details, due to the underlying physiological reasoning we anticipate the same underlying findings, namely high sensitivity from the large venous compartments and right ventricular parameters.
The parameter ranges chosen represent the individual variation found within healthy subjects in terrestrial conditions during a tilt test. As such, the model represents the acute response to changing gravitational conditions in the head-to-toe direction, as opposed to the response after deconditioning caused by a period spent in reduced gravity. It should be noted that this deconditioning causes a very specific trend in a subset or parameters, as opposed to the random variation assigned by the LHS/PRCC methodology. There are recently published models (91) that investigate long duration deconditioning due to microgravity, and combining the sensitivity analysis described in this paper with long duration trends could provide further insight into individual deconditioning responses.
Our model demonstrates an acute increase in central venous pressure with reducing gravity. This is in agreement with terrestrial studies in which an acute increase in gravity in the head-to-toe direction through tilt causes a decrease in central venous pressure (93, 94). However, these trends contrast with spaceflight and parabolic flight evidence (95–98). Buckey et al. (99, 100) suggest that this unexpected decrease in central venous pressure occurs as a result of the loss of tissue compressive forces produced by tissue weight. Our model does not capture changes in tissue weight, and therefore, our simulations on reduced gravity could also be interpreted as a partial tilt on Earth (including supine position representing 0 g, and upright position representing 1 g) that generates the appropriate head-to-toe orthostatic stress at each one of the gravitational conditions tested. The consequences are that we do not find similar reductions in central venous pressure evidenced in spaceflight but instead, our results are supported by findings from tilt maneuvers on Earth. Although this is an inherent limitation of our model, our findings related to the sensitivity of physiological parameters with respect to general hemodynamic response to orthostatic stress are not invalidated by this limitation.
Conclusion
We have conducted a thorough sensitivity analysis of a lumped-parameter model of the cardiovascular system in a range of constant gravity conditions. Model simulations compared well qualitatively and quantitatively to expected changes based on physiological principles. We have determined a subset of model parameters, including those related to the large venous compartments and the right ventricle, that have the largest influence on model outcomes. The purpose of this sensitivity analysis was to determine the most important model parameters that must be accurately valued in order to model and predict the responses of individuals to gravitational environments. By effectively measuring those influential parameters (i.e., characteristics of the leg, abdominal, and splanchnic veins, and the right ventricle) in addition to the important global parameters, we can more accurately simulate and predict acute response to changing gravitational conditions. This allows for the design of more effective countermeasures and protocols.
ACKNOWLEDGMENTS
The authors thank D. A. Alonso of the Sibley School of Mechanical and Aerospace Engineering at Cornell University for preliminary contributions to model simulations.
APPENDIX
APPENDIX A: GLOBAL PARAMETERS
Our model includes a small number of “global” parameters that cause larger variation in the outcome measures than the rest of the parameters. In particular, the four parameters that have the largest effect on one or more outcomes measures are total blood volume (Vtot), the arterial baroreflex and cardiopulmonary reflex set points (Paspa, Paspc), and nominal heart rate (HRnom). The aim of this study was to determine other influential parameters besides these four, so they were not included in the main sensitivity analysis. However, we did conduct a simple sensitivity analysis varying each of these four parameters in turn uniformly ±2SD from the mean [ranges taken from Heldt (38)], in order to capture their influence on systemic outcomes. More detail on how these global parameters fit into the model can be found in appendix c.
Figure A1 shows the result of varying each of these four parameters (one at a time) on the six primary and two secondary outcome measures at each one of the five gravity levels simulated. The simulations had the same profile as described in the main text. All other parameters were held constant at their mean value.
Figure A1.
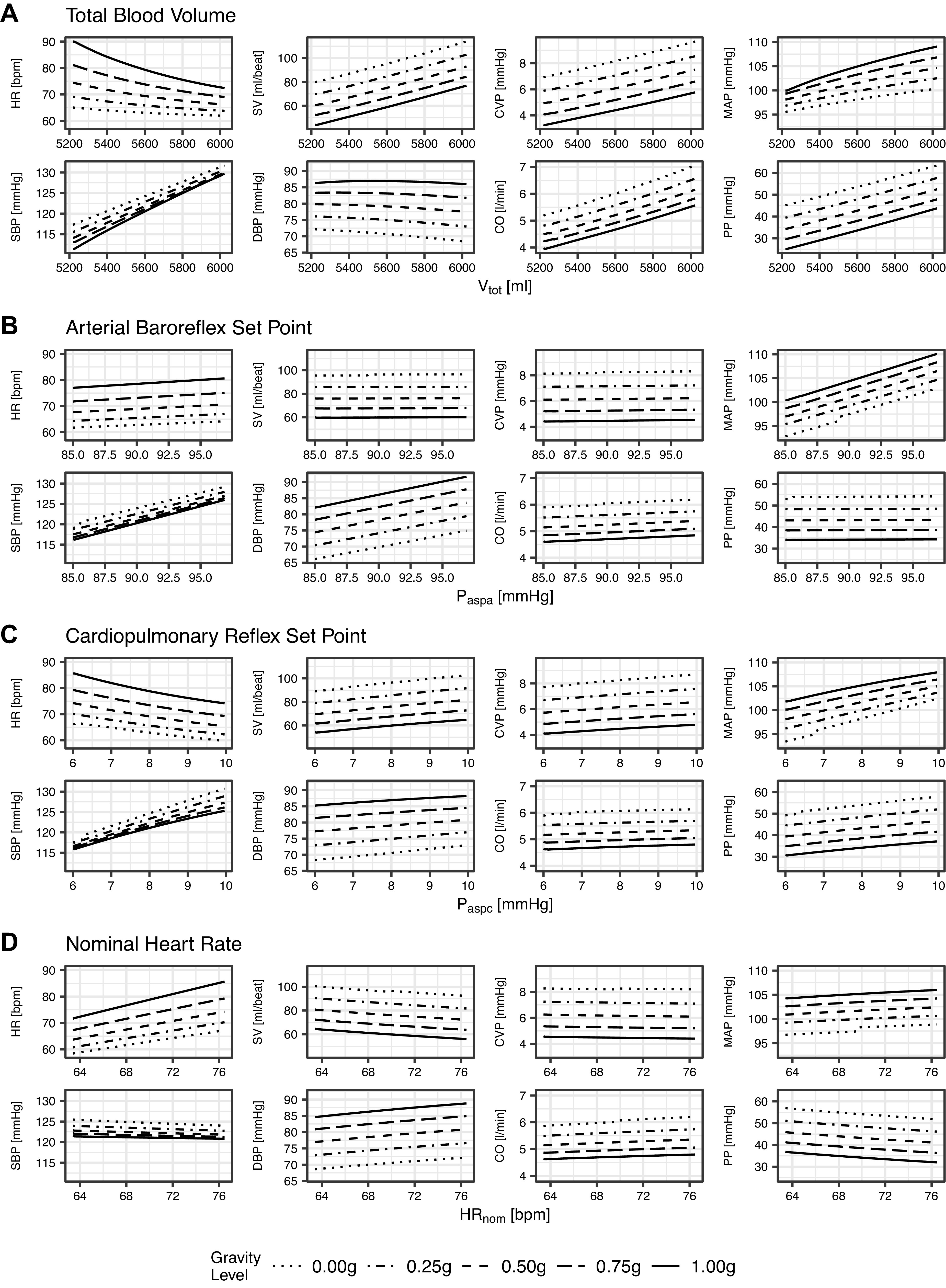
Change in outcome measures as a result of varying each of four key global parameters by ±2SD with respect to baseline. Total blood volume (Vtot), mean = 5625.0 mL, SD = 203.0 Ml (A); arterial baroreflex set point (Paspa), mean = 91.0 mmHg, SD = 3.0 mmHg (B); cardiopulmonary reflex set point (Paspc), mean = 8.0 mmHg, SD = 1.0 mmHg (C); and nominal heart rate (HRnom), mean = 70.0 beats/min, SD = 3.3 beats/min (D). Graphs showing the same outcome measure have the same y-axis scale.
Figure A1A shows that total blood volume has a large effect on all outcome measures except diastolic blood pressure. In particular, at 1.0 g, a 203 mL increase in Vtot (1 SD from the mean of 5,625 mL) leads to a 4.4 beats/min drop in heart rate, an 8.4 mL increase in stroke volume, a 0.6 mmHg increase in central venous pressure, a 2.3 mmHg increase in central venous pressure, a 4.6 mmHg increase in systolic blood pressure, a 0.1 mmHg drop in diastolic blood pressure, a 0.4 L/min increase in cardiac output, and a 4.7 mmHg increase in pulse pressure. Figure A1B shows that the arterial baroreflex set point has an effect on blood pressure. In particular, at 1.0 g, a 3.0 mmHg increase of Paspa (1 SD) leads to a 2.5 mmHg increase in mean arterial pressure, systolic blood pressure, and diastolic blood pressure, but does not significantly change other outcomes. In contrast, the cardiopulmonary reflex set point (Fig. A1C) also has an influence on heart rate. A 1.0 mmHg (1 SD) increase in Paspc at 1.0 g leads to a 2.9 beats/min decrease in heart rate, a 1.5 mmHg increase in mean arterial pressure, and a 2.4 mmHg increase in systolic blood pressure. Finally, nominal heart rate (HRnom) obviously has a significant influence on heart rate (Fig. A1D) with a 3.3 beats/min increase (1 SD) leading to a 3.5 beats/min increase in outcome heart rate.
It is unsurprising that the amount of blood circulating in the body has a large influence on all hemodynamic outcome measures. Similarly, the primary function of the arterial baroreflex and cardiopulmonary reflex is to provide blood pressure regulation, so changing the set point has a direct influence on blood pressure. All of these parameters can be easily measured in an individual. As discussed in the main text, the aim of this study was to determine the other model parameters with large influence. As such, these four global parameters were excluded from the sensitivity analysis, but must be considered when applying the model to an individual.
APPENDIX B: CARDIOVASCULAR MODEL PARAMETERS AND ASSOCIATED RANGES
Model parameters were chosen based on sizeable clinical studies of normal male subjects with no known cardiovascular pathology (27, 29, 38). The target anthropometry aims to capture a subject population with the following baseline characteristics, given as means ± SE (5–95th percentile range): height 169.3 ± 1.5 (161.5–186.8) cm; weight 70.3 ± 2.1 (59.8–98.5) kg; and body surface area 1.83 ± 0.02 (1.51–2.10) m2. Tables B1, B2, and B3 show the parameters and values for the compartments, controls, and heart and lungs groups, respectively.
Table B1.
Compartment parameters and their associated values (range for the sensitivity analysis: means ± 1.64 standard deviations)
| Compartments | |||
|---|---|---|---|
| Name | Symbol | Means | SD |
| Anatomical length 1 (Ascending aorta) | lv1, cm | 10.0 | 0.5 |
| Anatomical length 2 (Brachiocephalic arteries) | lv2, cm | 4.5 | 0.5 |
| Anatomical length 3 (Upper body arteries) | lv3, cm | 20.0 | 1.0 |
| Anatomical length 4 (Upper body veins) | lv4, cm | 20.0 | 1.0 |
| Anatomical length 5 (Superior vena cava) | lv5, cm | 14.5 | 0.5 |
| Anatomical length 6 (Thoracic aorta) | lv6, cm | 16.0 | 0.8 |
| Anatomical length 7 (Abdominal aorta) | lv7, cm | 14.5 | 0.5 |
| Anatomical length 8 (Renal arteries) | lv8, cm | 0.0 | 0.0 |
| Anatomical length 9 (Renal veins) | lv9, cm | 0.0 | 0.0 |
| Anatomical length 10 (Splanchnic arteries) | lv10, cm | 5.0 | 0.5 |
| Anatomical length 11 (Splanchnic veins) | lv11, cm | 5.0 | 0.5 |
| Anatomical length 12 (Leg arteries) | lv12, cm | 106.0 | 6.0 |
| Anatomical length 13 (Leg veins) | lv13, cm | 106.0 | 6.0 |
| Anatomical length 14 (Abdominal veins) | lv14, cm | 14.5 | 1.5 |
| Anatomical length 15 (Thoracic IVC) | lv15, cm | 6.0 | 0.5 |
| Compliance 1 (Ascending aorta) | C1, mL/mmHg | 0.28 | 0.04 |
| Compliance 2 (Brachiocephalic arteries) | C2, mL/mmHg | 0.13 | 0.02 |
| Compliance 3 (Upper body arteries) | C3, mL/mmHg | 0.20 | 0.10 |
| Compliance 4 (Upper body veins) | C4, mL/mmHg | 7.00 | 2.00 |
| Compliance 5 (Superior vena cava) | C5, mL/mmHg | 1.30 | 0.10 |
| Compliance 6 (Thoracic aorta) | C6, mL/mmHg | 0.10 | 0.03 |
| Compliance 7 (Abdominal aorta) | C7, mL/mmHg | 0.10 | 0.01 |
| Compliance 8 (Renal arteries) | C8, mL/mmHg | 0.21 | 0.05 |
| Compliance 9 (Renal veins) | C9, mL/mmHg | 5.00 | 1.00 |
| Compliance 10 (Splanchnic arteries) | C10, mL/mmHg | 0.20 | 0.10 |
| Compliance 11 (Splanchnic veins) | C11, mL/mmHg | 60.00 | 7.50 |
| Compliance 12 (Leg arteries) | C12, mL/mmHg | 0.20 | 0.10 |
| Compliance 13 (Leg veins) | C13, mL/mmHg | 20.00 | 3.00 |
| Compliance 14 (Abdominal veins) | C14, mL/mmHg | 1.30 | 0.10 |
| Capacitance 15 (Thoracic IVC) | C15, mL/mmHg | 0.50 | 0.10 |
| Resistance 1 (Ascending aorta) | R1, PRU | 0.007 | 0.002 |
| Resistance 2 (Brachiocephalic arteries) | R2, PRU | 0.003 | 0.001 |
| Resistance 3 (Upper body arteries) | R3, PRU | 0.014 | 0.004 |
| Resistance 4 (Upper body veins) | R4, PRU | 0.110 | 0.050 |
| Resistance 5 (Superior vena cava) | R5, PRU | 0.028 | 0.014 |
| Resistance 6 (Thoracic aorta) | R6, PRU | 0.011 | 0.002 |
| Resistance 7 (Abdominal aorta) | R7, PRU | 0.010 | 0.003 |
| Resistance 8 (Renal arteries) | R8, PRU | 0.100 | 0.050 |
| Resistance 9 (Renal veins) | R9, PRU | 0.110 | 0.050 |
| Resistance 10 (Splanchnic arteries) | R10, PRU | 0.070 | 0.040 |
| Resistance 11 (Splanchnic veins) | R11, PRU | 0.070 | 0.040 |
| Resistance 12 (Leg Arteries) | R12, PRU | 0.090 | 0.050 |
| Resistance 13 (Leg veins) | R13, PRU | 0.100 | 0.050 |
| Resistance 14 (Abdominal veins) | R14, PRU | 0.019 | 0.007 |
| Resistance 15 (Thoracic IVC) | R15, PRU | 0.008 | 0.003 |
Table B2.
Control parameters and their associated values (range for the sensitivity analysis: means ± 1.64 standard deviations)
| Controls | |||
|---|---|---|---|
| Name | Symbol | Means | SD |
| ABR R-R interval sympathetic gain | 0.012 | 0.004 | |
| ABR left ventricular contractility gain | 0.014 | 0.001 | |
| ABR right ventricular contractility gain | 0.021 | 0.003 | |
| ABR upper body arterial resistance gain | −0.13 | 0.05 | |
| ABR renal circulation arterial resistance gain | −0.13 | 0.05 | |
| ABR splanchnic circulation arterial resistance gain | −0.13 | 0.05 | |
| ABR leg circulation arterial resistance gain | −0.13 | 0.05 | |
| ABR upper body venous unstressed volume gain | 5.30 | 0.85 | |
| ABR renal venous unstressed volume gain | 1.30 | 0.20 | |
| ABR splanchnic venous unstressed volume gain | 13.30 | 2.10 | |
| ABR leg venous unstressed volume gain | 6.70 | 1.10 | |
| ABR R-R interval parasympathetic gain | 0.009 | 0.004 | |
| CPR upper body arterial resistance gain | −0.30 | 0.05 | |
| CPR renal circulation arterial resistance gain | −0.30 | 0.05 | |
| CPR splanchnic circulation arterial resistance gain | −0.30 | 0.05 | |
| CPR leg circulation arterial resistance gain | −0.30 | 0.05 | |
| CPR upper body venous unstressed volume gain | 13.5 | 2.7 | |
| CPR renal venous unstressed volume gain | 2.7 | 0.5 | |
| CPR splanchnic venous unstressed volume gain | 64.0 | 12.8 | |
| CPR leg venous unstressed volume gain | 30.0 | 6.0 | |
Table B3.
Heart and lungs parameters and their associated values (range for the sensitivity analysis: means ± 1.64 SD)
| Heart and Lungs | |||
|---|---|---|---|
| Name | Symbol | Means | SD |
| Pulmonary arterial compliance | Cpa, mL/mmHg | 3.4 | 1.8 |
| Pulmonary venous compliance | Cpv, mL/mmHg | 9.0 | 3.7 |
| Right ventricular outflow resistance | Rpa, PRU | 0.006 | 0.003 |
| Pulmonary venous outflow resistance | Rpv, PRU | 0.006 | 0.003 |
| Pulmonary microvascular resistance | Rpc, PRU | 0.070 | 0.040 |
| Right atrial end-systolic compliance | Ces,ra, mL/mmHg | 1.35 | 0.18 |
| Right ventricular end-systolic compliance | Ces,rv, mL/mmHg | 1.30 | 0.47 |
| Left atrial end-systolic compliance | Ces,la, mL/mmHg | 1.64 | 0.19 |
| Left ventricular end-systolic compliance | Ces,lv, mL/mmHg | 0.40 | 0.10 |
| Right atrial diastolic compliance | Cd,ra, mL/mmHg | 3.33 | 0.56 |
| Right ventricular diastolic compliance | Cd,rv, mL/mmHg | 19.29 | 5.00 |
| Left atrial diastolic compliance | Cd,la, mL/mmHg | 2.00 | 0.40 |
| Left ventricular diastolic compliance | Cd,lv, mL/mmHg | 9.69 | 1.18 |
| Tricuspid valve resistance | Rtri, PRU | 0.006 | 0.003 |
| Mitral valve resistance | Rmit, PRU | 0.010 | 0.001 |
APPENDIX C: DESCRIPTION OF THE CARDIOVASCULAR MODEL
Figure 1 in the main text shows a circuit representation of the 21-compartment cardiovascular model. This model has been described in previous publications (27, 29, 38, 40–42); however, a brief overview is provided here for completeness. The model is a 0-D lumped-parameter model with 15 compartments representing the systemic circulation, two compartments representing the pulmonary circulation, and four compartments representing the cardiac chambers. The arterial baroreflex and cardiopulmonary reflex are also captured in the model (not shown in the figure).
Systemic and Pulmonary Compartments
The physical properties of each compartment are characterized by an inflow resistance Rn, an outflow resistance Rn+ 1, a capacitive element representing the pressure-volume relationship Vn (Pn – Pe), and two pressure sources: Ph represents the hydrostatic pressure associated with the compartment, whereas Pe represents the external pressure acting on the compartment. The flows assigned to the nth compartment, qn, the n + 1th compartment, qn+ 1, and the capacitive element, qc, are defined as follows:
| (C1) |
| (C2) |
| (C3) |
Combining the constitutive relationships for the flow in the compartment gives an expression for the rate of change of luminal pressure:
| (C4) |
| (C5) |
with Cn = dVn/d(Pn – Pe) representing the incremental vascular compliance (capacitance). The entire system is thus defined by a set of coupled first-order differential equations with pressure as the principal variable of interest. These equations are solved iteratively by a 4th-order Runge-Kutta algorithm. The primary outcome measures detailed in the main text (heart rate, stroke volume, central venous pressure, mean arterial pressure, systolic blood pressure, and diastolic blood pressure) are thus derived each beat using the above equations (along with the equations of the cardiac chambers and cardiac pacemaker).
In three of the venous compartments (11—splanchnic, 13—legs, and 14—abdominal), a nonlinear pressure volume relationship is implemented as follows (29, 38):
| (C6) |
where Vt,n denotes the total volume in compartment n, V0,n denotes the zero-pressure filling volume, Vmax,n denotes the distending volume limit (1,500 mL, 1,000 mL, and 650 mL for compartments 11, 13, and 14 respectively), C0,n denotes the vascular compliance at zero transmural pressure, and ΔPn denotes the transmural pressure. Total blood volume (shown in Fig. A1A) is the sum of the volumes in all compartments and is modified to account for transcapillary flow as shown in Table 1 (29, 41, 101). The pulmonary circulation is represented by two compartments (pulmonary arteries and veins, respectively) and a resistor representing the pulmonary capillaries.
Microvascular Resistances
Capillary flow is modeled by four resistors representing flow in the upper body, renal, splanchnic, and lower body circulations, respectively. As such, the capillary flows are modeled as nondistending volumes with no associated compliance.
Cardiac Chambers
Each of the four cardiac chambers is simulated using a time-varying elastance model (29, 101). The elastance E(t) is defined by a piecewise function of the diastolic and end-systolic elastances (Ed and Ees respectively) such that the time of diastolic relaxation is half of the systolic time interval Ts:
| (C7) |
Note that in the sensitivity analysis, we vary the compliance (i.e., the inverse of the elastance) of the cardiac chambers in the heart and lungs group. Relative timing between the chambers is characterized by the atrial and ventricular systole durations ( and ), and the PR interval represents the delay between the onset of atrial and ventricular depolarizations (29, 101), Ta-v. These are all assumed to be proportional to the square root of the RR interval with:
| (C8) |
The cardiac pacemaker is represented by an Integral Pulse Frequency Modulation (IPFM) model (29, 41, 101, 102):
| (C9) |
where M(t) represents the behavior of the sino-atrial node transmembrane potential as a function of a constant cumulative automaticity, m0, and the combination of neural control input from either sympathetic or parasympathetic activity since the end of the last heartbeat, mr(t). A new heartbeat occurs at time tk when both M(t) reaches a predefined threshold potential, Γ = 1, and the time since the previous heartbeat is at least one fifth of the preceding cycle length:
| (C10) |
After this time, M(t) is reset and the integration process repeats. We define m(t) as the inverse of the instantaneous RR interval, I(t), which is the sum of the nominal RR interval, I0 (the inverse of I0 is the nominal heart rate, shown in Fig. A1D in appendix a), and the control input from the arterial baroreflex control system, ΔIAB(t):
| (C11) |
Figure C1 shows the beat-to-beat response of the blood pressure waveform during a four-beat simulation cycle. This figure shows the pressure waveform in the descending aorta, the left ventricle, and the left atrium over a period of four heartbeats.
Figure C1.
Pressure waveform of the descending aorta (solid), left ventricle (short dashes), and left atrium (long dashes) over a four-beat simulation cycle.
Control Systems
Two control systems, the arterial baroreflex and cardiopulmonary reflex, are modeled using negative feedback loops. The feedback error signals are described by:
| (C12) |
where δPAB[n] and δPCP[n] represent the error signals to the arterial baroreflex and cardiopulmonary reflex loops, respectively; and are the respective pressure set-points (Fig. A1, B and C, in appendix a); ΔPCS is the carotid sinus pressure defined as located 25 cm superior to the heart; ΔPAA is the aortic arch pressure; and ΔPRA is the transmural pressure in the right atrium. The transfer functions ΔX[n] for the sympathetic and parasympathetic arcs are modeled as static gains and multiplied by impulse response functions s[n] and p[n] with associated delays, peaks, and ends:
| (C13) |
where in the transfer functions superscript A refers to the arterial baroreflex, superscript CP refers to the cardiopulmonary reflex, superscript S refers to the sympathetic arc, superscript P refers to the parasympathetic arc, and subscript Y refers to the effector.
The model includes separate impulse responses to represent the parasympathetic, β-sympathetic, and α-sympathetic response for each reflex, and static gains (subscript Y) associated with loops to each effector separately. The effectors for the arterial baroreflex are RR interval (sympathetic and parasympathetic), left and right ventricular contractility (sympathetic only), systemic microvascular resistances (sympathetic only), and venous unstressed volume (sympathetic only). The effectors for the cardiopulmonary reflex are systemic microvascular resistances and venous unstressed volume (both sympathetic only). These static gains are the parameters that form the controls group in the sensitivity analysis, and their mean and standard deviation are shown in Table B2 in appendix b.
Transcapillary Flow and the Interstitial Fluid Volume
Orthostatic stress causes an increase in transcapillary flow to the dependent vasculature leading to a decrease in intravascular volume (29, 41, 101). In the model this is represented using additional RC compartments. The transcapillary flow is computed analytically and subtracted from the venous return in the splanchnic, leg, and abdominal venous compartments (compartments 11, 13, and 14). The total intercapillary flow (q(t)) and interstitial volume change (V(t)) is characterized by three parameters: the time constant τ = RC = 4.6 min (29, 101), the maximum interstitial volume change Vmax (given in Table 1 in the main text—dependent on the gravity level), and the time of completing the tilt maneuver Δt (fixed at 2 s for all simulations). In the simulation, the subject is initially in supine position before being tilted to 90° upright. Thus, two regions (while tilting and after tilt in upright position) defining q(t) and V(t) are characterized by the following analytic equations:
Region I: Gradual increase in orthostatic stress over a period of length Δt:
| (C14) |
| (C15) |
Region II: Full gravitational stress:
| (C16) |
| (C17) |
DATA AVAILABILITY
The data that support the findings of this study are openly available in GitHub at https://github.com/rswhittle/CVModel-Sensitivity.
GRANTS
This work was supported by the National Aeronautics and Space Administration (NASA) Human Research Program (HRP), Grant 80NSSC20K1521.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
R.S.W. and A.D-A. conceived and designed research; R.S.W. and A.D-A. performed experiments; R.S.W. and A.D-A. analyzed data; R.S.W. and A.D-A. interpreted results of experiments; R.S.W. and A.D-A. prepared figures; R.S.W. and A.D-A. drafted manuscript; R.S.W. and A.D-A. edited and revised manuscript; R.S.W. and A.D-A. approved final version of manuscript.
REFERENCES
- 1.Charles JB, Fritsch-Yelle JM, Whitson PA, Wood ML, Brown TE, Fortner GW. Cardiovascular deconditioning. In: Extended Duration Orbiter Medical Project, Final Report: 1989–1995, edited by Sawin CF, Taylor GR, Smith WL.. Houston, TX: NASA JSC, 1999, p. 1.1–1.19. [Google Scholar]
- 2.Charles JB, Lathers CM. Cardiovascular adaptation to spaceflight. J Clin Pharmacol 31: 1010–1023, 1991. doi: 10.1002/j.1552-4604.1991.tb03665.x. [DOI] [PubMed] [Google Scholar]
- 3.Baisch F, Beck L, Blomqvist G, Wolfram G, Drescher J, Rome J-L, Drummer C. Cardiovascular response to lower body negative pressure stimulation before, during, and after space flight. Eur J Clin Invest 30: 1055–1065, 2000. doi: 10.1046/j.1365-2362.2000.00750.x. [DOI] [PubMed] [Google Scholar]
- 4.Buckey JC, Lane LD, Levine BD, Watenpaugh DE, Wright SJ, Moore WE, Gaffney FA, Blomqvist CG. Orthostatic intolerance after spaceflight. J Appl Physiol 81: 7–18, 1996. doi: 10.1152/jappl.1996.81.1.7. [DOI] [PubMed] [Google Scholar]
- 5.Baevsky RM, Baranov VM, Funtova II, Diedrich A, Pashenko AV, Chernikova AG, Drescher J, Jordan J, Tank J. Autonomic cardiovascular and respiratory control during prolonged spaceflights aboard the International Space Station. J Appl Physiol 103: 156–161, 2007. doi: 10.1152/japplphysiol.00137.2007. [DOI] [PubMed] [Google Scholar]
- 6.Hughson RL, Shoemaker JK, Blaber AP, Arbeille P, Greaves DK, Pereira-Junior PP, Xu D. Cardiovascular regulation during long-duration spaceflights to the International Space Station. J Appl Physiol 112: 719–727, 2012. doi: 10.1152/japplphysiol.01196.2011. [DOI] [PubMed] [Google Scholar]
- 7.Eckberg DL, Halliwill JR, Beightol LA, Brown TE, Taylor JA, Goble R. Human vagal baroreflex mechanisms in space. J Physiol 588: 1129–1138, 2010. doi: 10.1113/jphysiol.2009.186650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Macaulay TR, Macias BR, Lee SMC, Boda WL, Watenpaugh DE, Hargens AR. Treadmill exercise within lower-body negative pressure attenuates simulated spaceflight-induced reductions of balance abilities in men but not women. NPJ Microgravity 2: 16022, 2016. doi: 10.1038/npjmgrav.2016.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Maggioni MA, Castiglioni P, Merati G, Brauns K, Gunga HC, Mendt S, Opatz OS, Rundfeldt LC, Steinach M, Werner A, Stahn AC. High-intensity exercise mitigates cardiovascular deconditioning during long-duration bed rest. Front Physiol 9: 1–14, 2018. doi: 10.3389/fphys.2018.01553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Westby CM, Martin DS, Lee SMC, Stenger MB, Platts SH. Left ventricular remodeling during and after 60 days of sedentary head-down bed rest. J Appl Physiol 120: 956–964, 2016. doi: 10.1152/japplphysiol.00676.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Larina IM, Baevsky RM, Pastushkova LK, Navasiolava NM, Custaud MA, Eshmanova AK, Luchitskaya ES. Seven-day dry immersion: interrelationship between the changes in the water-electrolyte balance and cardiovascular responses. Hum Physiol 37: 602–609, 2011. doi: 10.1134/S0362119711050124. [DOI] [Google Scholar]
- 12.Tomilovskaya E, Shigueva T, Sayenko D, Rukavishnikov I, Kozlovskaya I. Dry immersion as a ground-based model of microgravity physiological effects. Front Physiol 10: 284, 2019. doi: 10.3389/fphys.2019.00284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Deliere Q, Migeotte PF, Neyt X, Funtova I, Baevsky RM, Tank J, Pattyn N. Cardiovascular changes in parabolic flights assessed by ballistocardiography. Proc Annu Int Conf IEEE Eng Med Biol Soc EMBS 2013: 3801–3804, 2013. doi: 10.1109/EMBC.2013.6610372. [DOI] [PubMed] [Google Scholar]
- 14.Schlegel TT, Benavides EW, Barker DC, Brown TE, Harm DL, DeSilva SJ, Low PA. Cardiovascular and valsalva responses during parabolic flight. J Appl Physiol 85: 1957–1965, 1998. doi: 10.1152/jappl.1998.85.5.1957. [DOI] [PubMed] [Google Scholar]
- 15.Limper U, Gauger P, Beck P, Krainski F, May F, Beck LEJ. Interactions of the human cardiopulmonary, hormonal and body fluid systems in parabolic flight. Eur J Appl Physiol 114: 1281–1295, 2014. doi: 10.1007/s00421-014-2856-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Diaz-Artiles A, Navarro TP, Perez F. Cardiopulmonary responses to sub-maximal ergometer exercise in a hypo-gravity analog using head-down tilt and head-up tilt. Front Physiol 10: 720, 2019.doi: 10.3389/fphys.2019.00720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Alessandro C, Sarabadani Tafreshi A, Riener R. Cardiovascular responses to leg muscle loading during head-down tilt at rest and after dynamic exercises. Sci Rep 9: 2804, 2019. doi: 10.1038/s41598-019-39360-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Diaz-Artiles A, Heldt T, Young LR. Short-term cardiovascular response to short-radius centrifugation with and without ergometer exercise. Front Physiol 9: 1492, 2018. doi: 10.3389/fphys.2018.01492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Diaz A, Heldt T, Young LR. Cardiovascular responses to artificial gravity combined with exercise. IEEE Aerosp Conf Proc 2015, Big Sky, Montana, June, 2015. doi: 10.1109/AERO.2015.7118969. [DOI]
- 20.Diaz A, Trigg C, Young LR. Combining ergometer exercise and artificial gravity in a compact-radius centrifuge. Acta Astronaut 113: 80–88, 2015. doi: 10.1016/j.actaastro.2015.03.034. [DOI] [Google Scholar]
- 21.Gotshall RW, Tsai PF, Frey MA. Gender-based differences in the cardiovascular response to standing. Aviat Space Environ Med 62: 855–859, 1991. [PubMed] [Google Scholar]
- 22.Siamwala JH, Macias BR, Lee PC, Hargens AR. Gender differences in tibial microvascular flow responses to head down tilt and lower body negative pressure. Physiol Rep 5: e13143, 2017. doi: 10.14814/phy2.13143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Evans JM, Knapp CF, Goswami N. Artificial gravity as a countermeasure to the cardiovascular deconditioning of spaceflight: gender perspectives. Front Physiol 9: 716, 2018. doi: 10.3389/fphys.2018.00716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fong KJ, Arya M, Paloski WH. Gender differences in cardiovascular tolerance to short radius centrifugation. J Gravit Physiol 14: P15–9, 2007. [PubMed] [Google Scholar]
- 25.Guyton AC, Coleman TG, Granger HJ. Circulation: overall regulation. Annu Rev Physiol 34: 13–44, 1972. doi: 10.1146/annurev.ph.34.030172.000305. [DOI] [PubMed] [Google Scholar]
- 26.Guyton AC, Lindsey AW, Kaufmann BN. Effect of mean circulatory filling pressure and other peripheral circulatory factors on cardiac output. Am J Physiol 180: 463–468, 1955. doi: 10.1152/ajplegacy.1955.180.3.463. [DOI] [PubMed] [Google Scholar]
- 27.Diaz-Artiles A, Heldt T, Young LR. Computational model of cardiovascular response to centrifugation and lower-body cycling exercise. J Appl Physiol 127: 1453–1468, 2019. doi: 10.1152/japplphysiol.00314.2019. [DOI] [PubMed] [Google Scholar]
- 28.Summers R, Coleman T, Meck J. Development of the Digital Astronaut Project for the analysis of the mechanisms of physiologic adaptation to microgravity: validation of the cardiovascular system module. Acta Astronaut 63: 758–762, 2008. doi: 10.1016/j.actaastro.2007.12.054. [DOI] [Google Scholar]
- 29.Heldt T, Shim EB, Kamm RD, Mark RG. Computational modeling of cardiovascular response to orthostatic stress. J Appl Physiol (1985) 92: 1239–1254, 2002. doi: 10.1152/japplphysiol.00241.2001. [DOI] [PubMed] [Google Scholar]
- 30.Van Heusden K, Gisolf J, Stok WJ, Dijkstra S, Karemaker JM. Mathematical modeling of gravitational effects on the circulation: importance of the time course of venous pooling and blood volume changes in the lungs. Am J Physiol Hear Circ Physiol 291: H2152–H2165, 2006. doi: 10.1152/ajpheart.01268.2004. [DOI] [PubMed] [Google Scholar]
- 31.Lim E, Chan GSH, Dokos S, Ng SC, Latif LA, Vandenberghe S, Karunanithi M, Lovell NH. A cardiovascular mathematical model of graded head-up tilt. PLoS One 8: e77357, 2013. doi: 10.1371/journal.pone.0077357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Melchior FM, Srinivasan RS, Thullier PH, Clere JM. Simulation of cardiovascular response to lower body negative pressure from 0 to −40 mmHg. J Appl Physiol 77: 630–640, 1994. doi: 10.1152/jappl.1994.77.2.630. [DOI] [PubMed] [Google Scholar]
- 33.Hao WY, Bai J, Wu XY, Zhang LF. Simulation study of the effects of hypovolaemia on cardiovascular response to orthostatic stress. Med Biol Eng Comput 41: 44–51, 2003. doi: 10.1007/BF02343538. [DOI] [PubMed] [Google Scholar]
- 34.Olufsen M, Tran H, Ottesen J. Modeling cerebral blood flow control during posture change from sitting to standing. Cardiovasc Eng 4: 47–58, 2004. doi: 10.1023/B:CARE.0000025122.46013.1a. [DOI] [Google Scholar]
- 35.Olufsen MS, Ottesen JT, Tran HT, Ellwein LM, Lipsitz LA, Novak V. Blood pressure and blood flow variation during postural change from sitting to standing: model development and validation. J Appl Physiol 99: 1523–1537, 2005. doi: 10.1152/japplphysiol.00177.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ellwein LM, Tran HT, Zapata C, Novak V, Olufsen MS. Sensitivity analysis and model assessment: mathematical models for arterial blood flow and blood pressure. Cardiovasc Eng 8: 94–108, 2008. doi: 10.1007/s10558-007-9047-3. [DOI] [PubMed] [Google Scholar]
- 37.Niederer SA, Smith NP. At the heart of computational modelling. J Physiol 590: 1331–1338, 2012. doi: 10.1113/jphysiol.2011.225045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Heldt T. Computational Models of Cardiovascular Response to Orthostatic Stress (PhD Thesis). Massachusetts: Massachusetts Institute of Technology, 2004. [Google Scholar]
- 39.Marino S, Hogue IB, Ray CJ, Kirschner DE. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol 254: 178–196, 2008. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Diaz Artiles A, Heldt T, Young LR. Effects of artificial gravity on the cardiovascular system: computational approach. Acta Astronaut 126: 395–410, 2016. doi: 10.1016/j.actaastro.2016.05.005. [DOI] [Google Scholar]
- 41.Zamanian S. Modeling and Simulating Human Cardiovascular Response to Acceleration (SM Diss). Massachusetts: Massachusetts Institute of Technology, 2007. [Google Scholar]
- 42.Diaz-Artiles A. Exercise under Artificial Gravity—Experimental and Computational Approaches (PhD Thesis). Massachusetts: Massachusetts Institute of Technology, 2015. [Google Scholar]
- 43.Mead J, Gaensler EA. Esophageal and pleural pressures in man, upright and supine. J Appl Physiol 14: 81–83, 1959. doi: 10.1152/jappl.1959.14.1.81. [DOI] [PubMed] [Google Scholar]
- 44.Ferris BG, Mead J, Frank NR. Effect of body position on esophageal pressure and measurement of pulmonary compliance. J Appl Physiol 14: 521–524, 1959. doi: 10.1152/jappl.1959.14.4.521. [DOI] [Google Scholar]
- 45.Smit AAJ, Halliwill JR, Low PA, Wieling W. Pathophysiological basis of orthostatic hypotension in autonomic failure. J Physiol 519: 1–10, 1999. doi: 10.1111/j.1469-7793.1999.0001o.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kleiber M. Body size and metabolism. Hilgardia 6: 315–353, 1932. doi: 10.3733/hilg.v06n11p315. [DOI] [Google Scholar]
- 47.McMahon TA. Size and shape in biology. Science (80) 179: 1201–1204, 1973. doi: 10.1126/science.179.4079.1201. [DOI] [PubMed] [Google Scholar]
- 48.McMahon TA. Scaling physiological time. In: Some Mathematical Questions in Biology—Lectures on Mathematics in the Life Sciences, edited by Oster GF. Providence, RI: American Mathematical Society, 1980, vol. 13, p. 131–163. [Google Scholar]
- 49.Leggett RW, Williams LR. A proposed blood circulation model for reference man. Health Phys 69: 187–201, 1995. doi: 10.1097/00004032-199508000-00003. [DOI] [PubMed] [Google Scholar]
- 50.Gibson BYJG, Evans WA. Clinical studies of the blood volume. II. The relation of plasma and total blood volume to venous pressure, blood velocity rate, physical measurements, age and sex in ninety normal humans. J Clin Invest 16: 317–328, 1937. doi: 10.1172/JCI100860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sjöstrand T. Volume and distribution of blood and their significance in regulating the circulation. Physiol Rev 33: 202–228, 1953. doi: 10.1152/physrev.1953.33.2.202. [DOI] [PubMed] [Google Scholar]
- 52.Khan AA, Lye L, Husain T. Latin hypercube sampling for uncertainty analysis in multiphase modelling. J Environ Eng Sci 7: 617–626, 2008. doi: 10.1139/S08-031. [DOI] [Google Scholar]
- 53.Feola AJ, Myers JG, Raykin J, Mulugeta L, Nelson ES, Samuels BC, Ethier CR. Finite element modeling of factors influencing optic nerve head deformation due to intracranial pressure. Invest Ophthalmol Vis Sci 57: 1901–1911, 2016. doi: 10.1167/iovs.15-17573. [DOI] [PubMed] [Google Scholar]
- 54.Helton JC, Davis FJ. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab Eng Syst Saf 81: 23–69, 2003. doi: 10.1016/S0951-8320(03)00058-9. [DOI] [Google Scholar]
- 55.Gomero B. Latin Hypercube Sampling and Partial Rank Correlation Coefficient Analysis Applied to an Optimal Control Problem (MS Diss). Tennessee: The University of Tennessee Knoxville, 2012. [Google Scholar]
- 56.Yu H, Chung CY, Wong KP, Lee HW, Zhang JH. Probabilistic load flow evaluation with hybrid Latin hypercube sampling and cholesky decomposition. IEEE Trans Power Syst 24: 661–667, 2009. doi: 10.1109/TPWRS.2009.2016589. [DOI] [Google Scholar]
- 57.McKay MD, Beckman RJ, Conover WJ. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 21: 239–245, 1979. doi: 10.2307/1268522. [DOI] [Google Scholar]
- 58.Iman RL. Latin hypercube sampling. In: Encyclopedia of Quantitative Risk Analysis and Assessment, edited by Melnick EL, Everitt BS.. Hoboken, NJ, USA: Wiley, 2008. [Google Scholar]
- 59.Stein M. Large sample properties of simulations using latin hypercube sampling. Technometrics 29: 143–151, 1987. doi: 10.1080/00401706.1987.10488205. [DOI] [Google Scholar]
- 60.Viana FAC, Venter G, Balabanov V. An algorithm for fast optimal Latin hypercube design of experiments. Int J Numer Methods Eng 82: 135–156, 2010. doi: 10.1002/nme.2750. [DOI] [Google Scholar]
- 61.Minasny B, McBratney AB. A conditioned Latin hypercube method for sampling in the presence of ancillary information. Comput Geosci 32: 1378–1388, 2006. doi: 10.1016/j.cageo.2005.12.009. [DOI] [Google Scholar]
- 62.Taylor R. Interpretation of the correlation coefficient: a basic review. J Diagn Med Sonogr 6: 35–39, 1990. doi: 10.1177/875647939000600106. [DOI] [Google Scholar]
- 63.Hauke J, Kossowski T. Comparison of valuess of Pearson’s and Spearman’s correlation coefficients of the same sets of data. Quaestiones Geogr 30: 87–93, 2011. doi: 10.2478/v10117-011-0021-1. [DOI] [Google Scholar]
- 64.Kendall MG. Rank Correlation Methods (5th ed). Oxford, UK: Oxford University Press, 1990. [Google Scholar]
- 65.Nelder JA, Baker RJ. Generalized linear models. In: Encyclopedia of Statistical Sciences, edited by Kotz S, Read CB, Balakrishnan N, Vidakovic B, Johnson NL.. Hoboken, NJ, USA: Wiley, 2006. [Google Scholar]
- 66.Gallego G, Moon I. The distribution free newsboy problem: review and extensions. J Oper Res Soc 44: 825–834, 1993. doi: 10.2307/2583894. [DOI] [Google Scholar]
- 67.Recek C. Calf pump activity influencing venous hemodynamics in the lower extremity. Int J Angiol 22: 23–30, 2013. doi: 10.1055/s-0033-1334092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Greenway CV, Lautt WW. Blood volume, the venous system, preload, and cardiac output. Can J Physiol Pharmacol 64: 383–387, 1986. doi: 10.1139/y86-062. [DOI] [PubMed] [Google Scholar]
- 69.Joyner MJ, Wilkins BW. Exercise hyperaemia: is anything obligatory but the hyperaemia? J Physiol 583: 855–860, 2007. doi: 10.1113/jphysiol.2007.135889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Skoog J, Lindenberger M, Ekman M, Holmberg B, Zachrisson H, Länne T. Reduced venous compliance: An important determinant for orthostatic intolerance in women with vasovagal syncope. Am J Physiol Regul Integr Comp Physiol 310: R253–R261, 2016. doi: 10.1152/ajpregu.00362.2015. [DOI] [PubMed] [Google Scholar]
- 71.Coats BW, Keith Sharp M. Simulated stand tests and centrifuge training to prevent orthostatic intolerance on earth, moon, and mars. Ann Biomed Eng 38: 1119–1131, 2010. doi: 10.1007/s10439-010-9943-3. [DOI] [PubMed] [Google Scholar]
- 72.Blanco PJ, Trenhago PR, Fernandes LG, Feijóo RA. On the integration of the baroreflex control mechanism in a heterogeneous model of the cardiovascular system. Int J Numer Method Biomed Eng 28: 412–433, 2012. doi: 10.1002/cnm.1474. [DOI] [PubMed] [Google Scholar]
- 73.Bulpitt CJ, Cameron JD, Rajkumar C, Armstrong S, Connor M, Joshi J, Lyons D, Moioli O, Nihoyannopoulos P. The effect of age on vascular compliance in man: which are the appropriate measures? J Hum Hypertens 13: 753–758, 1999. doi: 10.1038/sj.jhh.1000879. [DOI] [PubMed] [Google Scholar]
- 74.van Duijnhoven NTL, Bleeker MWP, Groot PCE, Thijssen DHJ, Felsenberg D, Rittweger J, Hopman MTE. The effect of bed rest and an exercise countermeasure on leg venous function. Eur J Appl Physiol 104: 991–998, 2008. doi: 10.1007/s00421-008-0854-z. [DOI] [PubMed] [Google Scholar]
- 75.Iwase S, Nishimura N, Tanaka K, Mano T. Effects of microgravity on human physiology. In: Beyond LEO—Human Health Issues for Deep Space Exploration [Working Title]. London, UK: IntechOpen, 2020. [Google Scholar]
- 76.Maron BJ, Pelliccia A, Spirito P. Cardiac disease in young trained athletes: insights into methods for distinguishing athlete’s heart from structural heart disease, with particular emphasis on hypertrophic cardiomyopathy. Circulation 91: 1596–1601, 1995. doi: 10.1161/01.CIR.91.5.1596. [DOI] [PubMed] [Google Scholar]
- 77.MacDonald JR. Potential causes, mechanisms, and implications of post exercise hypotension. J Hum Hypertens 16: 225–236, 2002. doi: 10.1038/sj.jhh.1001377. [DOI] [PubMed] [Google Scholar]
- 78.Bull RK, Davies CT, Lind AR, White MJ. The human pressor response during and following voluntary and evoked isometric contraction with occluded local blood supply. J Physiol 411: 63–70, 1989. doi: 10.1113/jphysiol.1989.sp017560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Norsk P, Asmar A, Damgaard M, Christensen NJ. Fluid shifts, vasodilatation and ambulatory blood pressure reduction during long duration spaceflight. J Physiol 593: 573–584, 2015. doi: 10.1113/jphysiol.2014.284869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Aubert AE, Beckers F, Verheyden B, Pletser V. What happens to the human heart in space?-Parabolic flights provide some answers parabolic flights. ESA Bull 119: 31–38, 2004. http://www.esa.int/esapub/bulletin/bulletin119/bul119_chap4.pdf [Google Scholar]
- 81.Norsk P, Damgaard M, Petersen L, Gybel M, Pump B, Gabrielsen A, Christensen NJ. Vasorelaxation in space. Hypertension 47: 69–73, 2006. doi: 10.1161/01.HYP.0000194332.98674.57. [DOI] [PubMed] [Google Scholar]
- 82.Mukai CN, Lathers CM, Charles JB, Bennett BS, Igarashi M, Patel S. Acute hemodynamic responses to weightlessness during parabolic flight. J Clin Pharmacol 31: 993–1000, 1991. doi: 10.1002/j.1552-4604.1991.tb03662.x. [DOI] [PubMed] [Google Scholar]
- 83.Cooper VL, Hainsworth R. Effects of head-up tilting on baroreceptor control in subjects with different tolerances to orthostatic stress. Clin Sci 103: 221–226, 2002. doi: 10.1042/cs1030221. [DOI] [PubMed] [Google Scholar]
- 84.Iwasaki K-I, Zhang R, Zuckerman JH, Pawelczyk JA, Levine BD. Effect of head-down-tilt bed rest and hypovolemia on dynamic regulation of heart rate and blood pressure. Am J Physiol Integr Comp Physiol 279: R2189–R2199, 2000. doi: 10.1152/ajpregu.2000.279.6.R2189. [DOI] [PubMed] [Google Scholar]
- 85.Dell'Italia LJ, Walsh RA. Application of a time varying elastance model to right ventricular performance in man. Cardiovasc Res 22: 864–874, 1988. doi: 10.1093/cvr/22.12.864. [DOI] [PubMed] [Google Scholar]
- 86.Henry JP. The significance of the loss of blood volume into the limbs during pressure breathing. J Aviat Med 22: 31–38, 1951. [PubMed] [Google Scholar]
- 87.Platts SH, Bairey MC, Barr Y, Fu Q, Gulati M, Hughson R, Levine BD, Mehran R, Stachenfeld N, Wenger NK. Effects of sex and gender on adaptation to space: cardiovascular alterations. J Women’s Heal 23: 950–955, 2014. doi: 10.1089/jwh.2014.4912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Maffessanti F, Muraru D, Esposito R, Gripari P, Ermacora D, Santoro C, Tamborini G, Galderisi M, Pepi M, Badano LP. Age-, body size-, and sex-specific reference values for right ventricular volumes and ejection fraction by three-dimensional echocardiography: a multicenter echocardiographic study in 507 healthy volunteers. Circ Cardiovasc Imaging 6: 700–710, 2013. doi: 10.1161/CIRCIMAGING.113.000706. [DOI] [PubMed] [Google Scholar]
- 89.Monahan KD, Ray CA. Gender affects calf venous compliance at rest and during baroreceptor unloading in humans. Am J Physiol Hear Circ Physiol 286: H895–H901, 2004. doi: 10.1152/ajpheart.00719.2003. [DOI] [PubMed] [Google Scholar]
- 90.Defares JG, Osborn JJ, Hara HH. Theoretical synthesis of the cardiovascular system. Study I: the controlled system. Acta Physiol Pharmacol Neerl 12: 189–265, 1963. [PubMed] [Google Scholar]
- 91.Gallo C, Ridolfi L, Scarsoglio S. Cardiovascular deconditioning during long-term spaceflight through multiscale modeling. NPJ Microgravity 6: 1–14, 2020. doi: 10.1038/s41526-020-00117-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Berkes P, Wood F, Pillow J. Characterizing neural dependencies with copula models. Adv Neural Inf Process Syst 21: 1–8, 2008. doi: 10.5555/2981780.2981797.26215079 [DOI] [Google Scholar]
- 93.Bie P, Secher NH, Astrup A, Warberg J. Cardiovascular and endocrine response to head-up tilt and vasopressin infusion in humans. Am J Physiol Regul Integr Comp Physiol 251: R735–R741, 1986. doi: 10.1152/ajpregu.1986.251.4.R735. [DOI] [PubMed] [Google Scholar]
- 94.Minson CT, Wladkowski SL, Pawelczyk JA, Kenney WL. Age, splanchnic vasoconstriction, and heat stress during tilting. Am J Physiol Regul Integr Comp Physiol 276: R203–R212, 1999. doi: 10.1152/ajpregu.1999.276.1.r203. [DOI] [PubMed] [Google Scholar]
- 95.Lawley JS, Petersen LG, Howden EJ, Sarma S, Cornwell WK, Zhang R, Whitworth LA, Williams MA, Levine BD. Effect of gravity and microgravity on intracranial pressure. J Physiol 595: 2115–2127, 2017. doi: 10.1113/JP273557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Videbaek R, Norsk P. Atrial distension in humans during microgravity induced by parabolic flights. J Appl Physiol 83: 1862–1866, 1997. doi: 10.1152/jappl.1997.83.6.1862. [DOI] [PubMed] [Google Scholar]
- 97.Foldager N, Andersen TA, Jessen FB, Ellegaard P, Stadeager C, Videbaek R, Norsk P. Central venous pressure in humans during microgravity. J Appl Physiol 81: 408–412, 1996. doi: 10.1152/jappl.1996.81.1.408. [DOI] [PubMed] [Google Scholar]
- 98.Buckey JC, Gaffney FA, Lane LD, Levine BD, Watenpaugh DE, Wright SJ, Yancy CW, Meyer DM, Blomqvist CG. Central venous pressure in space. J Appl Physiol 81: 19–25, 1996. doi: 10.1152/jappl.1996.81.1.19. [DOI] [PubMed] [Google Scholar]
- 99.Buckey JC, Anderson A, Archambault-Leger V, Phillips SD, Anderson AP, Chepko AB, Masterova KS, Fellows AM, Cowan DR. The importance of tissue weight and tissue compressive forces in human spaceflight. 68th International Astronautical Congress (IAC), Adelaide, Australia 2017.
- 100.Buckey JC, Phillips SD, Anderson AP, Chepko AB, Archambault-Leger V, Gui J, Fellows AM. Microgravity-induced ocular changes are related to body weight. Am J Physiol Regul Integr Comp Physiol 315: R496–R499, 2018. doi: 10.1152/ajpregu.00086.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Heldt T, Mukkamala R, Moody GB, Mark RG. CVSim: an open-source cardiovascular simulator for teaching and research. Open Pacing Electrophysiol Ther J 3: 45–54, 2010. [PMC free article] [PubMed] [Google Scholar]
- 102.Boer RW, Karemaker JM, Strackee J. Description of the heart rate variability data in accordance with a physiological model for the genesis of heartbeats. Phychophysiology 22: 147–155, 1985. doi: 10.1111/j.1469-8986.1985.tb01577.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are openly available in GitHub at https://github.com/rswhittle/CVModel-Sensitivity.