Keywords: ammoniagenesis, net acid excretion, renal cortex, renal medulla, renal microcirculation
Abstract
Ammonia generated within the kidney is partitioned into a urinary fraction (the key buffer for net acid excretion) and an aliquot delivered to the systemic circulation. The physiology of this partitioning has yet to be examined in a kidney model, and that was undertaken in this work. This involves explicit representation of the cortical labyrinth, so that cortical interstitial solute concentrations are computed rather than assigned. A detailed representation of cortical vasculature has been avoided by making the assumption that solute concentrations within the interstitium and peritubular capillaries are likely to be identical and that there is little to no modification of venous composition as blood flows to the renal vein. The model medullary ray has also been revised to include a segment of proximal straight tubule, which supplies ammonia to this region. The principal finding of this work is that cortical labyrinth interstitial ammonia concentration is likely to be several fold higher than systemic arterial ammonia. This elevation of interstitial ammonia enhances ammonia secretion in both the proximal convoluted tubule and distal convoluted tubule, with uptake by Na+-K+-ATPases of both segments. Model prediction of urinary ammonia excretion was concordant with measured values, but at the expense of greater ammoniagenesis, with high rates of renal venous ammonia flux. This derives from a limited capability of the model medulla to replicate the high interstitial ammonia concentrations that are required to drive collecting duct ammonia secretion. Thus, renal medullary ammonia trapping appears key to diverting ammonia from the renal vein to urine, but capturing the underlying physiology remains a challenge.
NEW & NOTEWORTHY This is the first mathematical model to estimate solute concentrations within the kidney cortex. The model predicts cortical ammonia to be several fold greater than in the systemic circulation. This higher concentration drives ammonia secretion in proximal and distal tubules. The model reveals a gap in our understanding of how ammonia generated within the cortex is channeled efficiently into the final urine
INTRODUCTION
The kidney is a source of ammonia, with net ammonia production demonstrated by comparing renal venous outflow plus urinary excretion to renal arterial ammonia delivery (1, 2).1 Both total ammoniageneis and the fraction diverted to the urine (fractional excretion) can vary in disease states. In both acidosis and hypokalemia, ammoniagenesis is enhanced. With acidosis in dogs, an increase in the fractional excretion of ammonia was observed (3); with potassium depletion in humans, ammoniagenesis increased with little impact on fractional excretion (4). In experimental liver disease and in humans, there may be little change in renal ammoniagenesis, but the kidney can alter fractional excretion, so that renal venous ammonia is less than the delivered load, and the kidney becomes an organ for negative ammonia balance (5). In view of the implication of ammonia in the pathogenesis of hepatic encephalopathy, physicians have identified control of renal ammonia transport as a possible therapeutic strategy in reducing the morbidity of advanced liver disease (6).
Within the kidney, renal ammonia transport shows large reabsorptive and secretory fluxes, proximally and distally (7). The source of ammonia within the kidney is the proximal tubule (8–12). Proximal tubule ammonia addition occurs early in the segment, with net reabsorption in late proximal tubule, as backleak overtakes secretory flux at high luminal NH4+ concentrations (13, 14); ammonia secretion shows flow dependence (15). The renal medulla is a region of high interstitial ammonia concentrations, sustained by vigorous NH4+ reabsorption by the ascending Henle limb (AHL). There is ammonia secretion within the distal tubule (16, 17). Ammonia secretion into the medullary collecting duct (CD) has been documented by both micropunture (8) and microcatheterization (18–20).
Mathematical models have been developed, which represent ammonia transport along the ensemble of superficial (SF) and juxtamedullary (JM) nephrons (21, 22). There have been only two models, however, that have addressed the balance of tubule transport and blood flow of ammonia to predict medullary interstitial ammonia concentrations: that of Noiret et al. (23) and models from this laboratory (24, 25). Although Noiret et al. calculated medullary ammonia concentrations, medullary pH and K+ and HCO3− concentrations were fixed a priori and renal medullary ammonia delivery from the cortex was specified but not computed. This last condition, cortical ammonia handling, has emerged as a stumbling block for the kidney model of this laboratory. Specifically, the difficulties encountered here were as follows: limited medullary ammonia delivery from the proximal tubule, due to late tubule ammonia backflux; substantial reduction of tubular ammonia due to reabsorption within the cortical AHL; and limited ammonia secretion by the distal convoluted tubule (DCT). In those models, the workaround for unrealistically low urine and interstitial ammonia was to specify a generous systemic blood ammonia concentration (0.2 mM) and an even higher ammonia concentration in the vasa recta and in capillary flow to the medullary ray (MR) [2.0 mM (24)].
In this work, patchwork fixes to ammonia transport have been replaced with a more realistic representation of the kidney cortex: specifying cortical blood flow and computing cortical interstitial solute concentrations that provide balance between capillary uptake and tubular reabsorption. In addition, the architecture of the MR has been modified so that it now contains a proximal straight tubule (PST) segment, which acts to blunt ammonia depletion from the cortical AHL. What will be shown is that with this architecture, the model predicts a cortical ammonia concentration that is several-fold higher than in arterial blood; it also predicts an elevated cortical Pco2 that is comparable to measured values. The high cortical ammonia enhances both proximal delivery to the medulla and DCT ammonia secretion, so that both are of similar magnitude. What will also be found is that a considerable portion of renal ammoniagenesis is returned to the systemic circulation. From the perspective of this model, a mechanism to increase this fractional excretion of ammonia is not readily apparent.2
MODEL DEVELOPMENT
A natural approach to representing the cortical vasculature would be to start with the large vessels and capture their branching into the tissue. This had been the path taken by Atherton et al. (26) in their calculations of diffusive CO2 transport, from which they concluded that interlobular arteries and veins, running in apposition, could act as a countercurrent exchanger for CO2. This protected an elevated cortical Pco2, generated from tubule oxidative metabolism. Perhaps the observation of that paper most relevant to the concerns here is their estimate that countercurrent amplification of metabolic ammonia would be negligible, in view of the fact that the more permeable ammonia species, NH3, is a tiny fraction of total ammonia. In more sophisticated models of the renal arterial network, Gardiner et al. (27) focused on the question of whether countercurrent exchange of arterial O2 could limit delivery to deep cortical tissues. In that calculation, however, O2 shunting was estimated to be ∼10% of the delivered load; in their subsequent work (28, 29) and in models of others (30), the estimate was reduced to 1%. In their consideration of the implications of these calculations for cortical ammonia transport, this group estimated that the arteriovenous shunting of ammonia was likely to be trivial (31). In short, cortical ammonia uptake happened in the peritubular capillaries and, from there, returned to the systemic circulation with little venous loss.
With respect to the microvascular anatomy of the kidney, Beeuwkes (32) made foundational observations with his application of a cardiac vascular filling method to the study of dog kidneys. What he observed was that except in the subcapsular region, there is no congruence of the efferent arteriole and its capillaries with the proximal tubule of the originating glomerulus. The capillaries are true to their region of origin, but not to their nephron. With respect to the nephron, there is proximity of proximal and distal tubules at each level, so that each sees the same cortical interstitial conditions (33, 34). In that work, it was also documented that blood supply to the MRs derives from midcortical efferent arterioles. These vessels either go into the depth of the cortex or into the rays. Within the MRs, there are PSTs that derive from SF nephrons, which run in parallel with cortical AHLs and cortical CDs (CCDs) (35, 36). In the rat, when cortical thickness was measured at 2.5 mm, the total PST length was ∼5 mm (37).
With respect to representing kidney cortical perfusion (in contrast to medullary flows), the prospect of specifying local capillary anatomy is not feasible. This problem has been acknowledged in models of muscle perfusion, and one resolution has been a continuum approach put forward by Salathé (38). With this, the tissue is treated as a porous medium in which O2 is consumed and in which O2 flows are described by convection-diffusion equations that ignore capillary walls and depend on bulk fluid movement and O2 gradients. This approach has been advanced in subsequent models of muscle oxygenation (30, 39). The present model adopts this perspective with the coarsest approximation that the cortical labyrinth is a well-stirred compartment, with uniform solute concentrations determined by plasma perfusion and tubular reabsorption [from proximal convoluted tubules (PCTs), distal tubules, and connecting segments]. The venous effluent from the cortical labyrinth has solute concentrations identical to their interstitial values. With respect to the MRs, axial geometry is preserved, but at each level from the cortex to the outer medulla (OM), there are uniform local concentrations. Thus, within the rays, there is local blood perfusion at systemic concentrations and venous effluent at the tissue concentrations of that position along the ray.
Schematics for the structural components within the cortical labyrinth, MR, and medulla are shown in Fig. 1. With respect to solute concentrations, the subscripts M, C, and S designate tubule, capillary, and interstitial values, respectively. By virtue of the compartment assumption, for each solute (i) the labyrinth interstitium has a single concentration CS(i), whereas the ray has axial variability, CS(i,x). With respect to capillary perfusion of the labyrinth and ray, entering flows are denoted as FC(i) and FC(i,x) and exiting flows are denoted as FS(i) and FS(i,x); there are analogous notations for volume flows. For the MR, entering capillary solute concentrations are uniform at each level, x, and equal to the systemic values that perfuse the labyrinth; volume flows are also uniform and equal to total MR blood flow divided by spatial discretization. This is a change from the prior scheme (24, 25), in which MR vessels had entered at the top level, descending and returning to that position in a hairpin configuration. For the labyrinth and ray, total reabsorptive transport from each tubule segment to its interstitium is denoted as TMS(i). Specifically, for distance, x, along tubule segment, k, of length, L(k),
Figure 1.
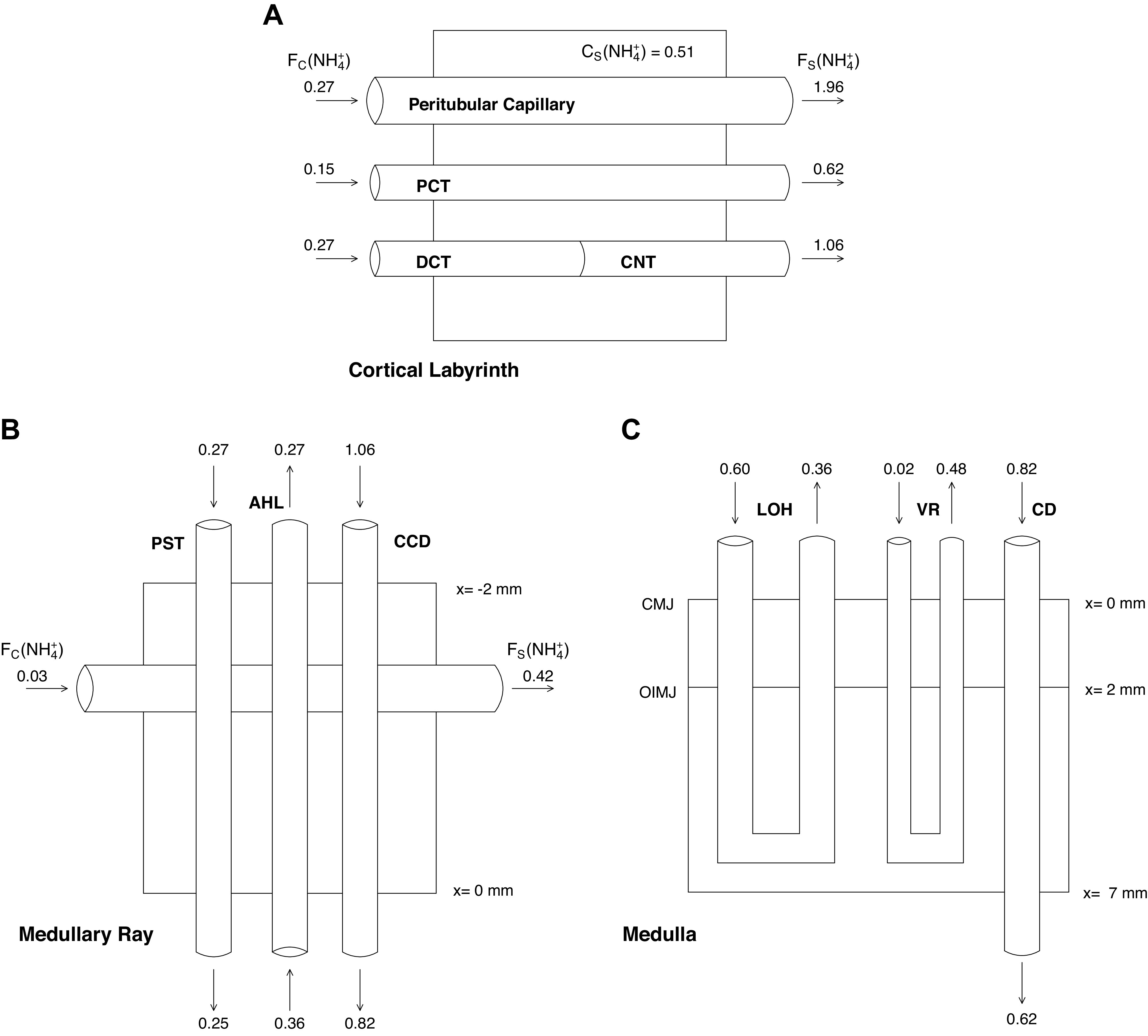
Schematics of the three model regions. A: the cortical labyrinth containing superficial and juxtamedullary proximal convoluted tubules, distal tubules, and connecting segments. Peritubular capillaries drain a well-mixed interstitial compartment, with exiting blood solute concentrations, CS, equal to those of the labyrinth interstitium. Ammonia flows (µmol/min) are shown for tubules and vessels; FC and FS denote vascular entry and exit. B: the medullary ray, containing proximal straight tubules (PST) from superficial nephrons, cortical ascending Henle limbs (AHL), and cortical collecting ducts (CCD). Blood vessels enter and leave across the lateral boundary, supplying the interstitium at their axial level, denoted by x. Venous blood solute concentrations, CS(x), are equal to those of the interstitium at that level. C: the kidney medulla with the loop of Henle (LOH), medullary collecting duct (CD), and vasa recta (VR). Vasa recta solute transport occurs according to vascular permeabilities, so that no equilibration assumptions are made.
| (1) |
| (2) |
in which BM is tubule circumference and JES and JIS are reabsorptive fluxes across the lateral interspace basement membrane and basal cell membrane, respectively. For volume and nonreacting solutes, these are identical to flux sums across the tight junction plus luminal cell membrane; for reacting species, or for those with cytosolic generation or consumption, luminal exit and interstitial uptake will be different.
For both the cortical labyrinth and MR, vascular input is specified, and vascular exit is convective. The model unknowns are all 15 tubule solutes and 14 hemoglobin species, along with a specification of interstitial hydrostatic pressure. Set solute exit as:
| (3) |
Define the combined vascular and interstitial mass generation:
| (4) |
| (5) |
Using these generation expressions, conservation of nonreactive species is expressed as:
| (6) |
| (7) |
for i = Na+, K+, Cl−, urea, glucose, and protein. For binary plasma buffers (phosphate, ammonia, and formate), conservation of total buffer has two terms:
| (8) |
| (9) |
| (10) |
Conservation of total CO2 contains three terms:
| (11) |
Strictly speaking, generation of CO2 is provided by the kinetics of hydration:
| (12) |
in which VS is interstitial and vascular volume. However, we obviate the need to estimate this parameter (as was done for the medullary interstitium) by assuming hydration equilibrium:
| (13) |
For the four plasma buffers, the four additional equations are their pH equilibrium relations.
The 14 hemoglobin buffering species are divided among X, Y, and amino or carbamino buffer groups, and each exists as oxy- and deoxy-forms, with total concentrations defined as:
| (14) |
| (15) |
| (16) |
Thus, for each of these three buffer groups, conservation equations may be written as:
| (17) |
| (18) |
| (19) |
in which [following Atherton et al. (40)] the relevant flow, FC(b), denotes vessel blood flow rather than plasma flow, FC(v). For each group, the sum of the concentrations of oxygenated species, relative to total buffer, is provided by the oxygen saturation, σ:
| (20) |
| (21) |
| (22) |
Hemoglobin oxygen saturation depends on the Po2 (Hill equation) and pH (Bohr effect). An equation for σ was developed by Weinstein (24). In model calculations, cortical Po2 is taken from the model of Lee et al. [see Fig. 9 in Ref. (29)]. The hemoglobin oxygen saturation is then computed according to cortical pH. The remaining eight equations are the equilibrium relations for these hemoglobin species.
Atherton et al. (40) provided the initial conditions for the conservation equations as dependent on total hemoglobin concentration and oxygen saturation. These buffer totals (mM) are then proportional to hematocrit:
| (23) |
| (24) |
| (25) |
The eight equilibrium relations, using initial pH, allow calculation of all entering hemoglobin species. In these vessels, blood flow satisfies:
| (26) |
with HC denoting the entering hematocrit. With conservation of erythrocyte volume, we identify the hematocrit of the capillary plexus, HS, as that of the exiting blood:
| (27) |
Interconversion of the amino and carbamino species provides an additional source of CO2 within the vessels, which needs to be included in the conservation equations. Corresponding to the equilibria:
The equation for total CO2 conservation is:
| (28) |
The last of the conservation equations is that for protons, which can react with plasma buffers and the hemoglobin species. Those reactions must result in no net charge generation, so that one may write an electroneutrality condition as:
| (29) |
in which the index, i, runs over all solutes; Z(i) are their valences. Applying the conservation condition for nonreacting species, and the equation for phosphate, this proton conservation equation simplifies to:
| (30) |
Finally, interstitial hydrostatic pressures for the cortical labyrinth and MR, PS and PS(x) will be specified as model parameters, as there is no reliable way to calculate them. Together, these pressures along with the interstitial solute concentrations determine water reabsorption from the nephron segments. These volumes are added to the initial capillary plasma flows, to yield the exiting volume flows from the cortical labyrinth and MR.
Ammonia transport pathways within the nephron have been examined over years of model development. Within the proximal tubule, ammoniagenesis was introduced by Weinstein (41), and the important ammonia fluxes appear in Fig. 9 of that work. Peritubular uptake of ammonia is as NH4+ via Na+-K+-ATPase and as NH3 diffusion from the peritubular space to the cell. That peritubular flux, augmented by ammoniagenesis, is secreted into the lumen via Na+/H+ exchanger isoform 3 (NHE3). AHL ammonia flux is complex, as there are important secretory and reabsorptive fluxes (see Fig. 2 in Ref. 42). At the peritubular membrane, there is uptake of NH4+ via Na+-K+-ATPase and reabsorption via the K+-Cl− cotransporter; at the luminal membrane, the important reabsorptive fluxes are via Na+-K+-2Cl− cotransporter (NKCC2) and renal outer medullary K+ channels (ROMK), whereas secretion is as NH4+ on NHE3 and as NH3 diffusion from the cell to the lumen. Overall, the secretory and reabsorptive fluxes are balanced (with modest net AHL ammonia reabsorption), providing a catalytic role for ammonia in facilitating Na+ reabsorption via NKCC2 (augmenting the effect of luminal K+). When the DCT model was formulated, it was examined in a setting in which the peritubular NH4+ concentration was only 0.2 mM and net flux was reabsorptive (see Table 3 in Ref. 43). In that simulation, there was peritubular uptake of NH4+ via Na+-K+-ATPase and luminal uptake via NHE; ammonia exit from the cell was as reabsorptive NH3 flux across the peritubular membrane. Within the principal cells of the connecting tubule (CNT), the dominant ammonia flux is diffusive NH3 reabsorption across luminal and peritubular membranes, with peritubular efflux augmented by NH4+ entry via Na+-K+-ATPase; intercalated ammonia fluxes were modest in comparison (see Table 2 in Ref. 44). This principal cell route for epithelial ammonia transport persisted along the CCD and OMCD. Within the inner medullary (IM) CD, the importance of peritubular NH4+ uptake was emphasized, as it provided the proton source for a carbonic anhydrase-insensitive component of luminal acidification, occurring in parallel with secretory NH3 flux across the luminal cell membrane (see Table 2 in Ref. 45). All of these component transport pathways have been synthesized into the full kidney model of this work.
Compared with the prior version of this model (25), the major change in nephrons has been addition of a 2-mm segment of the SFPST within the MR. The transport parameters for this segment are identical to those that have been in place for its continuation as the OMPST. To accommodate the additional Na+ reabsorption provided the MR PST, the SFPCT has been shortened from 9 to 8 mm. JM proximal tubules are unchanged. The presence of a PST segment within the MR provides an ammonia source, acting to increase interstitial ammonia there. Nevertheless, there was still ammonia depletion within cortical AHLs, due to brisk NH4+ transport via luminal membrane NKCC2. This was addressed by reducing the ammonia affinity of the B-isoform (in both SF and JM nephron segments) from equality with the K+ affinity to 20% of that value (see Table 2a in Ref. 46). In parameter selection for that NKCC2 model, there had been no experimental information on the Km for NH4+ for the B-isoform, so it had been taken equal to that for K+.
MODEL RESULTS
With expansion of the model to include the cortical interstitium, specification of entering vessel composition has simplified. Rather than separate assignment of plasma concentrations for the cortex, MR, and vasa recta, there is now a single set of values for arterial composition. Those values are shown in Table 1, which includes parameters for the baseline calculation and for the condition of metabolic acidosis. For the two conditions glomerular filtration rate (GFR) values differ slightly, due to the activity of tubuloglomerular feedback, but approximate total kidney GFR is 1.5 mL/min, evenly split between SF and JM nephrons. With that as a starting point, plasma flow to the cortical labyrinth was set at 2.7 mL/min. Plasma flow to the MR is unknown, but since ∼10% of tubular Na+ reabsorption occurs in the nephron segments of this region (vide infra), plasma flow to this region was set at 0.31 mL/min (∼10% of cortical plasma flow). Medullary perfusion (short- and long ascending vasa recta) has been carried forward from the original version of this model (see Table 4 in Ref. 24) and had been taken to be low (0.23 mL/min) compared with cortical flow in order to minimize medullary solute washout. Thus, total regional plasma flow is 3.2 mL/min, and with GFR of 1.5 mL/min, total renal plasma flow is 4.7 mL/min; the filtration fraction is 32%. This filtration fraction is concordant with measurements in normal and cirrhotic rats (47, 48). As in the prior models, Po2 is 65 mmHg in the cortex, 35 mmHg in the OM, and varying from 35 to 7 mmHg as one descends into the inner medulla (IM). In the baseline case, entering vessel Pco2 has been set to 40 mmHg (1.2 mM), and cortical interstitial Pco2 is now computed. In the prior versions of this model, cortical Pco2 had been specified at 50 mmHg (1.5 mM), and only medullary Pco2 was computed. Similarly, entering vessel ammonia has been set at 0.1 mM, for consistency with measurements of arterial ammonia, and cortical ammonia is now computed. In the prior versions of this model, cortical ammonia had been specified at 0.2 mM. Rates of proximal tubule ammoniagenesis are 75% of those used previously in this model (24, 25), taken to achieve baseline NH4+ excretion of 0.6 µmol/min.
Table 1.
Boundary conditions and model parameters
| Baseline | Acidosis | |
|---|---|---|
| Plasma flow, µL/min | ||
| Cortical labyrinth | 2,700.0 | 2,700.0 |
| Medullary ray | 311.0 | 311.0 |
| Short ascending vasa recta | 192.0 | 192.0 |
| Long ascending vasa recta | 37.2 | 37.2 |
| Hematocrit, % | 45 | 45 |
| Po2, mmHg | ||
| Cortical labyrinth | 65 | 65 |
| Medullary ray | 65 | 65 |
| Outer medulla | 35 | 35 |
| Inner medulla | 35 → 7 | 35 → 7 |
| Interstitial pressure, mmHg | ||
| Cortical labrynth | 10.0 | 10.0 |
| Medullary ray | 10.0 | 10.0 |
| Glomerular filtration rate, µL/min | ||
| SF | 749.0 | 737.0 |
| JM | 774.1 | 705.7 |
| Filtration fraction, % | 32 | 31 |
| Plasma concentrations | ||
| Na+, mM | 144.00 | 144.00 |
| K+, mM | 5.00 | 5.00 |
| Cl−, mM | 118.40 | 125.46 |
| HCO3−, mM | 25.0 | 18.0 |
| H2CO3, µM | 3.53 | 2.94 |
| CO2, mM | 1.20 | 1.00 |
| HPO42−, mM | 2.10 | 2.04 |
| H2PO4−, mM | 0.50 | 0.56 |
| Urea, mM | 5.00 | 5.00 |
| NH3, µM | 1.83 | 1.58 |
| NH4+, mM | 0.10 | 0.10 |
| HCO2−, mM | 1.00 | 1.00 |
| H2CO2, µM | 0.22 | 0.25 |
| Glucose, mM | 5.00 | 5.00 |
| Protein, g/dL | 8.00 | 8.00 |
| Ammoniagenesis, nmol/s/cm2 | ||
| SFPCT | 0.150 | 0.300 |
| SFPST | 0.015 | 0.030 |
| JMPCT | 0.300 | 0.600 |
| JMPST | 0.030 | 0.060 |
SF, superficial; JM, juxtameullary; PCT, proximal convoluted tubule; PST, proximal straight tubule.
Baseline Calculations
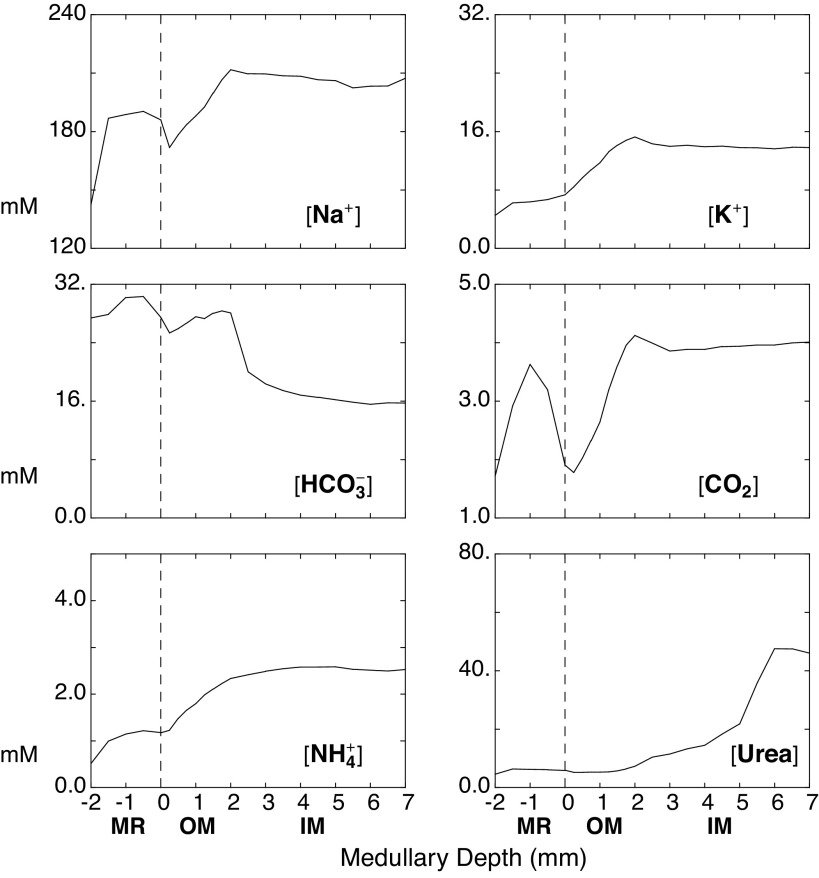
Solution of the model provides cortical and medullary interstitial solute concentrations along with tubular and vascular fluxes and flows. Table 2 shows predicted cortical capillary concentrations, in which end-capillary solute values are identical with those of the interstitium. Depression of capillary protein by 28% is due to dilution by nephron volume reabsorption. Concentration changes in nonreactive cortical solutes are small and reflect the various reabsorptive and secretory fluxes within PCT, DCT, and CNT. In this work, attention will focus on the impact of cortical solute generation, specifically the increase of cortical CO2 from 1.2 to 1.7 mM (40–57 mmHg) and the increase of cortical ammonia from 0.10 to 0.51 mM. The predicted cortical CO2 is identical to measurements by Maddox et al. (48), and this higher CO2 acidifies capillary blood, titrates hemoglobin buffers, and thus augments the increase in cortical HCO3−. By virtue of the Bohr effect, cortical acidification reduces hemoglobin oxygen saturation (see Appendix in Ref. 24). Of note, this calculated cortical CO2 is slightly higher than the estimate that had been used in the prior versions of this model (1.5 mM), and the calculated cortical ammonia is substantially greater than its prior estimate (0.2 mM). The important medullary and MR concentration profiles are shown in Fig. 2. The abscissa on these curves is corticomedullary distance, with −2.0 to 0.0 mm denoting the MR, 0.0–2.0 mm denoting the OM, and 2.0–7.0 mm denoting the IM. These can be compared with the profiles in Fig. 5 in Ref. 24, and the medullary concentrations are similar. What is notable here is that MR ammonia is ∼1.0 mM, and medullary ammonia ∼2.5 mM. To achieve such medullary ammonia concentrations in the prior model, descending vasa recta ammonia had been set to 2.0 mM.
Table 2.
Cortical blood concentrations
| Baseline |
Acidosis |
Low TJ P(NH4) |
||||
|---|---|---|---|---|---|---|
| Entry | Exit | Entry | Exit | Entry | Exit | |
| Na+, mM | 144.00 | 142.42 | 144.00 | 141.80 | 144.00 | 141.72 |
| K+, mM | 5.00 | 4.52 | 5.00 | 4.65 | 5.00 | 4.54 |
| Cl−, mM | 118.40 | 114.87 | 125.46 | 121.58 | 118.40 | 114.33 |
| HCO3−, mM | 25.00 | 27.39 | 18.00 | 20.66 | 25.00 | 27.10 |
| CO2, mM | 1.20 | 1.72 | 1.00 | 1.28 | 1.20 | 1.70 |
| HPO42−, mM | 2.10 | 1.93 | 2.04 | 1.95 | 2.10 | 1.93 |
| H2PO4−, mM | 0.50 | 0.60 | 0.57 | 0.60 | 0.50 | 0.60 |
| Urea, mM | 5.00 | 4.60 | 5.00 | 4.61 | 5.00 | 4.61 |
| NH4+, mM | 0.10 | 0.51 | 0.10 | 1.01 | 0.10 | 0.35 |
| HCO2−, mM | 1.00 | 0.72 | 1.00 | 0.73 | 1.00 | 0.71 |
| Glucose, mM | 5.00 | 3.59 | 5.00 | 3.65 | 5.00 | 3.57 |
| Protein, mg/dL | 8.00 | 5.74 | 8.00 | 5.85 | 8.00 | 5.71 |
| pH | 7.420 | 7.308 | 7.357 | 7.311 | 7.420 | 7.308 |
| Hematocrit, % | 45.0 | 37.0 | 45.0 | 37.4 | 45.0 | 36.9 |
| Hgb buffers | ||||||
| O2 saturation, % | 83.3 | 76.9 | 79.9 | 77.1 | 83.3 | 76.8 |
| ONH2, mM | 1.94 | 1.24 | 1.74 | 1.29 | 1.94 | 1.23 |
| NH2, mM | 0.51 | 0.51 | 0.63 | 0.55 | 0.51 | 0.52 |
| ONH3+, mM | 4.12 | 3.40 | 4.28 | 3.52 | 4.12 | 3.39 |
| NH3+, mM | 0.49 | 0.64 | 0.69 | 0.68 | 0.49 | 0.64 |
| ONHCO2−, mM | 0.69 | 0.49 | 0.45 | 0.38 | 0.69 | 0.48 |
| NHCO2−, mM | 0.35 | 0.39 | 0.31 | 0.31 | 0.35 | 0.38 |
| OXH, mM | 3.86 | 3.63 | 4.18 | 3.66 | 3.86 | 3.63 |
| XH, mM | 1.41 | 1.92 | 1.88 | 1.92 | 1.41 | 1.93 |
| OX−, mM | 21.73 | 15.77 | 20.35 | 16.03 | 21.73 | 15.69 |
| X−, mM | 3.71 | 3.90 | 4.28 | 3.92 | 3.71 | 3.90 |
| OYH, mM | 27.32 | 22.12 | 27.23 | 22.41 | 27.32 | 22.04 |
| YH, mM | 6.22 | 7.37 | 7.68 | 7.39 | 6.22 | 7.39 |
| OY−, mM | 10.43 | 6.51 | 8.98 | 6.65 | 10.43 | 6.46 |
| Y−, mM | 1.33 | 1.22 | 1.42 | 1.23 | 1.33 | 1.22 |
TJ P(NH4), tight junction NH4+ permability.
Figure 2.
Interstitial solute concentration profiles of selected species from the medullary ray (−2 < x < 0 mm) through the outer medulla (OM) (0 < x < 2 mm) and inner medulla (IM) (2 < x < 7 mm). Within the OM, there is mixing of flows from the proximal straight tubules arising from the cortex (juxtamedullary nephrons) and from the medullary ray (superficial nephrons).
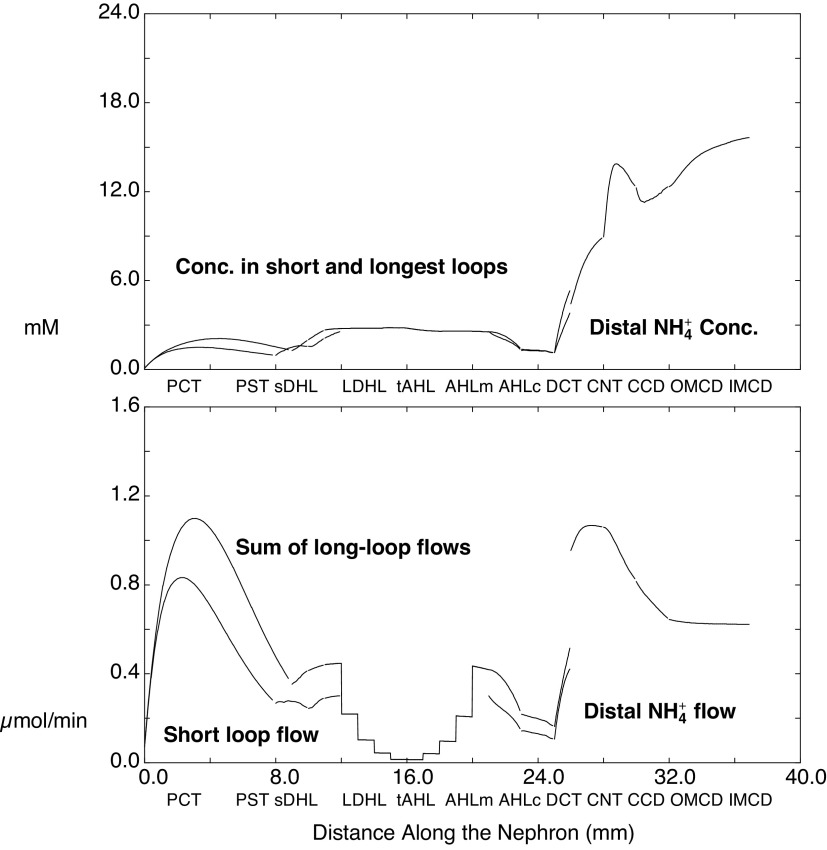
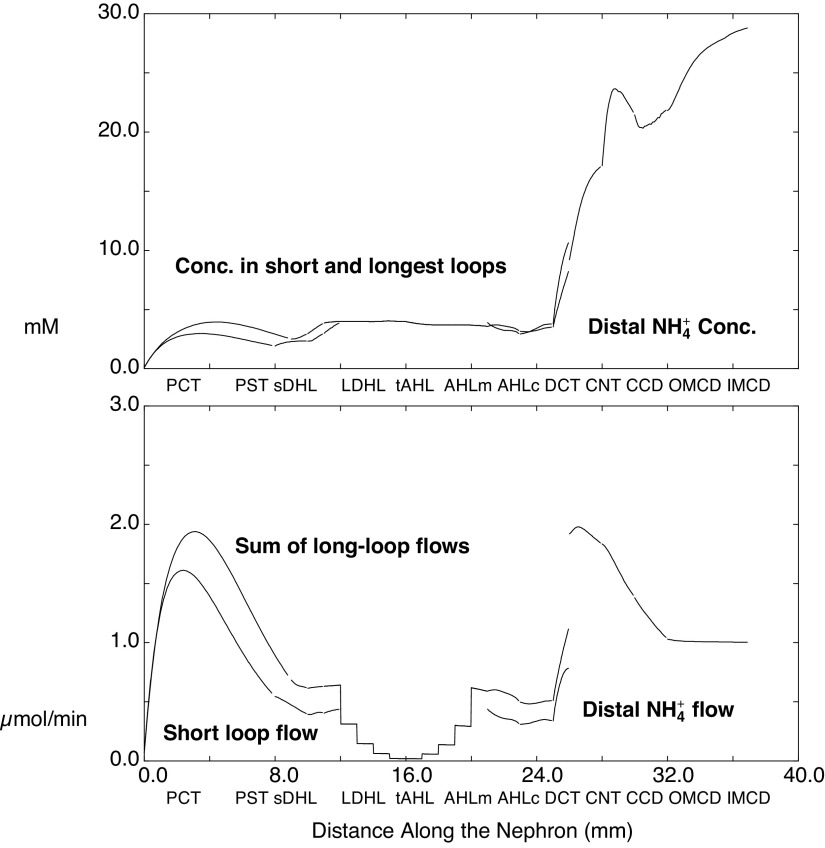
Luminal ammonia within kidney tubules is shown in Fig. 3, in which the abscissa is distance along the nephron. The top panel shows ammonia concentrations in SF nephrons and in the longest of the JM nephrons and in their common distal nephron; the bottom panel shows ammonia flows. These concentrations and flows provide for direct comparison with micropuncture data. For both nephrons, the ammonia concentration at the end-PCT is ∼1 mM, with slightly higher values in JM nephrons attributable to the twofold greater rate of ammoniagenesis in this population. Ammonia increases to 2.5 mM within the loop of Henle (LOH) and then drops to 1 mM by the end of cortical AHL. Within the LOH, the aggregate of long-loop flows appears as a staircase pattern, reflecting the five populations of JM nephrons that turn at each millimeter of IM depth. Tubule ammonia bumps up to 5 mM within the DCT, to 9 mM in the CNT, and then is further concentrated within the CD. The flows show vigorous ammonia addition in the early PCT, with substantial backflux as additional fluid reabsorption proceeds. In the descending portions of the LOH, there is modest additional ammonia uptake as the tubule encounters higher OM interstitial ammonia; the bulk of tubular ammonia is then reabsorbed within medullary and cortical AHL segments. The DCT increases ammonia flow several-fold, and the discontinuity in the curve occurs at the DCT-CNT junction, at which SF and JM nephrons combine. The discontinuity reflects coalescing of short- and long-loop flows at this point in the nephron and the summation of their flows. Thereafter, about half of the flowing ammonia is reabsorbed in the CCD and OMCD.
Figure 3.
Ammonia concentrations and flows within the nephron, as a function of distance along the tubules. The top shows the concentrations within superficial nephrons and within the longest of the juxtamedullary nephrons, through the distal convoluted tubules; from the connecting segment onward, there is a common distal nephron population. The bottom displays aggregate ammonia flow within superficial nephrons and for all juxtamedullary nephrons. The staircase pattern for juxtamedullary flow reflects nephrons turning at steps within the inner medulla. The discontinuity at the connecting segment is due to the confluence of superficial and juxtamedullary flows at that point. See text for abbreviations.
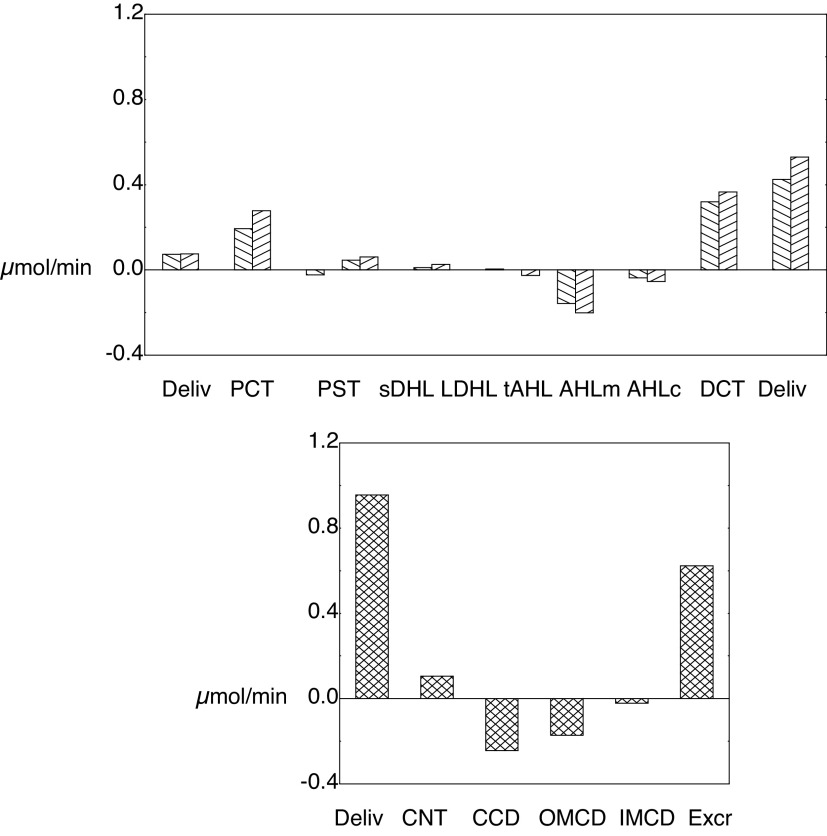
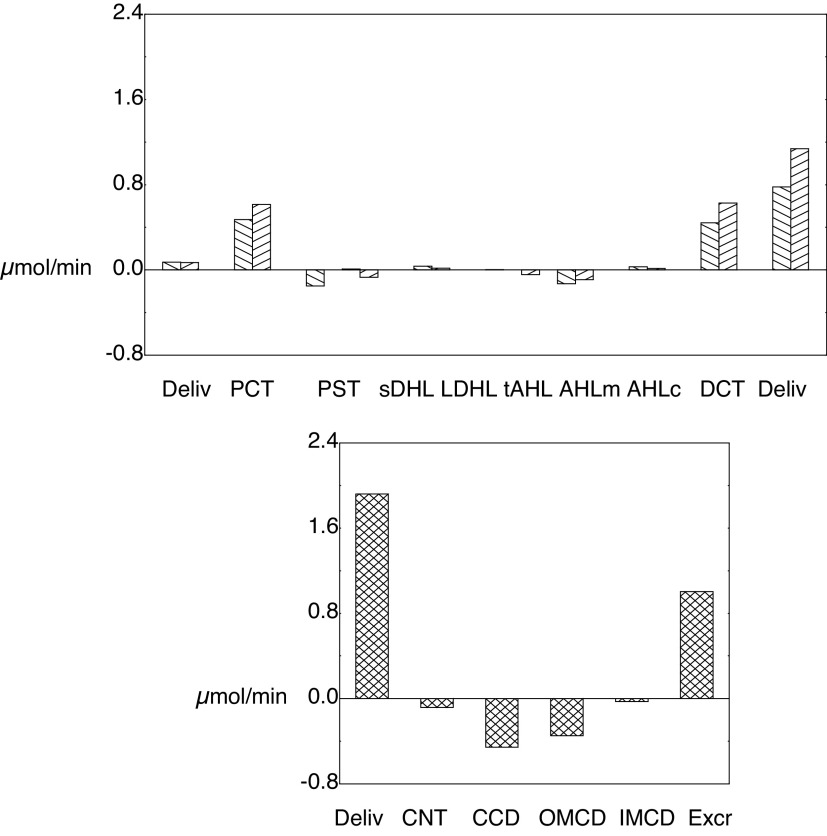
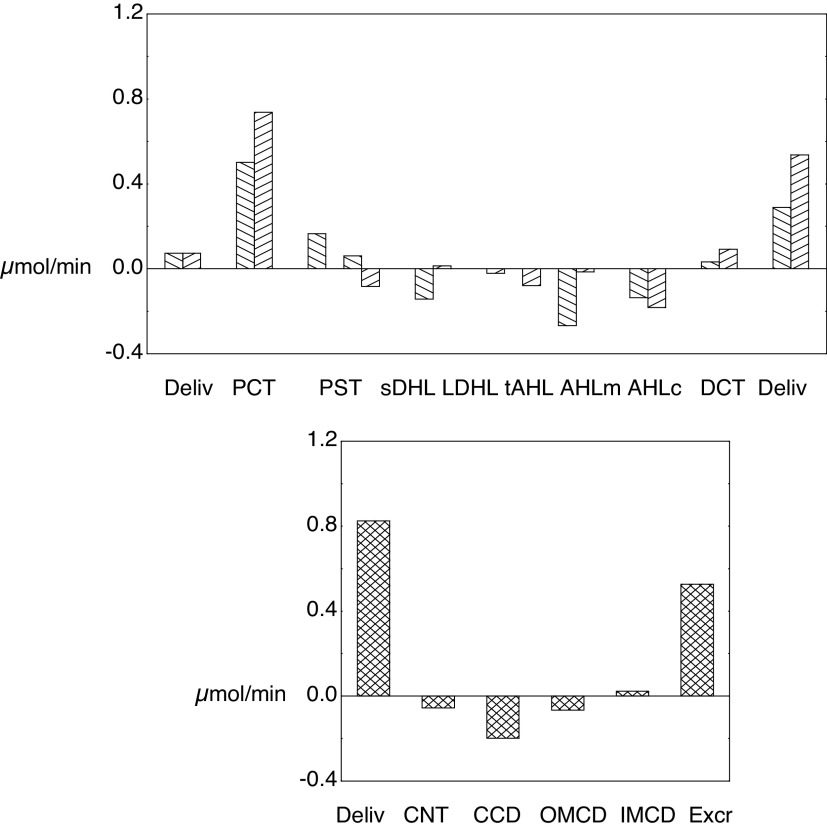
For these baseline calculations, Tables 3 and 4 show a detailed summary of segmental delivery and transport, in which contributions of the five classes of JM nephrons have been summed. With the reconfiguration of the SF proximal tubule to include a MR segment, the SFPCT fractional Na+ reabsorption is 62% in the cortical labyrinth and 10% in the MR, so that delivery to the OM-SFPST is 27% of the filtered load. For JM nephrons, the JMPST receives 32% of filtered Na+. In both nephron classes, the AHL reabsorbs ∼17% (6% from the cortical AHL) and the DCT resorbs ∼3% of filtered Na+. In the common distal nephron, the CNT and full CD each transport ∼1.5% of the filtered Na+. In summary, the final urine contains ∼3% of filtered Na+, 10% of filtered K+, and 25% of filtered urea. Net acid excretion is 1.2 µmol/min, and of this the NH4+ contribution is 0.6 µmol/min. Figure 4 shows ammonia accounting along both SF and JM nephrons (top) and in the common distal nephron (bottom). The first pair of bars in the top panel shows PCT ammonia delivery, and then each pair of bars beyond that the segmental ammonia fluxes, for which deflections upward are secretion and downward are reabsorption. The secretory fluxes within the PCT are both substantial, whereas the MR component of the SFPST shows a small reabsorptive flux. PST fluxes within the OM are secretory and constitute a small countercurrent ammonia flux from the medullary AHL. The final pair of bars of the top panel marks ammonia delivery out of the SFDCT and JMDCT. Within the common distal nephron, there is a modest ammonia secretion from the CNT and reabsorption along the CD. With respect to the ammonia profile shown in Fig. 3, Tables 3 and 4 and Fig. 4 show that the increase in luminal ammonia concentration within the CNT is the result of water reabsorption in concert with ammonia secretion. Within the CD, variations in the pace of water reabsorption and ammonia reabsorption produce a more complex concentration profile. The message from this figure is that while the PCT is the site of renal ammoniagenesis, the secretory contribution within the PCT is modest, and a major addition comes from the DCT. The DCT contribution derives from the relatively high ammonia concentration within the cortical labyrinth and cellular uptake by Na+-K+-ATPase.
Table 3.
Segmental flows and fluxes: baseline conditions
| SF | PCT | PST-MR | PST | sDHL | AHLm | AHLc | DCT |
|---|---|---|---|---|---|---|---|
| Absolute delivery (μmol/min) | |||||||
| Na+ | 106.5 | 40.0 | 29.3 | 25.5 | 25.1 | 13.8 | 6.9 |
| K+ | 3.70 | 1.42 | 1.15 | 1.45 | 1.55 | 0.52 | 0.22 |
| NH4+ | 0.073 | 0.267 | 0.244 | 0.290 | 0.301 | 0.143 | 0.106 |
| Fv | 0.740 | 0.281 | 0.156 | 0.137 | 0.117 | 0.111 | 0.093 |
| Delivery relative to PCT delivery | |||||||
| Na+ | 100.0% | 37.5% | 27.5% | 24.0% | 23.5% | 13.0% | 6.5% |
| K+ | 100.0% | 38.5% | 31.0% | 39.2% | 42.0% | 14.1% | 6.1% |
| NH4+ | 100.0% | 367.8% | 336.4% | 399.2% | 414.4% | 196.7% | 146.1% |
| Fv | 100.0% | 38.0% | 21.1% | 18.5% | 15.9% | 15.0% | 12.6% |
| Absolute resorption (μmol/min) | |||||||
| Na+ | 66.6 | 10.7 | 3.8 | 0.5 | 11.3 | 6.9 | 3.8 |
| K+ | 2.28 | 0.28 | −0.31 | −0.10 | 1.03 | 0.30 | −0.18 |
| NH4+ | −0.194 | 0.023 | −0.046 | −0.011 | 0.158 | 0.037 | −0.319 |
| Fv | 0.459 | 0.125 | 0.019 | 0.020 | 0.006 | 0.018 | 0.015 |
| Reabsorption relative to PCT delivery | |||||||
| Na+ | 62.5% | 10.0% | 3.5% | 0.4% | 10.6% | 6.5% | 3.5% |
| K+ | 61.5% | 7.5% | −8.3% | −2.8% | 27.9% | 8.1% | −4.9% |
| NH4+ | −267.8% | 31.4% | −62.8% | −15.2% | 217.7% | 50.6% | −439.7% |
| Fv | 62.0% | 16.9% | 2.6% | 2.6% | 0.8% | 2.5% | 2.0% |
| All JM | PCT | PST | lDHLu | lDHLl | tAHL | AHLm | AHLc | DCT |
|---|---|---|---|---|---|---|---|---|
| Absolute delivery (μmol/min) | ||||||||
| Na+ | 110.5 | 40.2 | 35.6 | 34.4 | 34.0 | 33.7 | 19.8 | 13.1 |
| K+ | 3.84 | 1.53 | 1.87 | 2.10 | 2.13 | 2.29 | 0.57 | 0.30 |
| NH4+ | 0.075 | 0.354 | 0.415 | 0.441 | 0.445 | 0.419 | 0.218 | 0.163 |
| Fv | 0.768 | 0.284 | 0.206 | 0.165 | 0.161 | 0.161 | 0.157 | 0.144 |
| Delivery relative to PCT delivery | ||||||||
| Na+ | 100.0% | 36.4% | 32.2% | 31.1% | 30.8% | 30.5% | 17.9% | 11.9% |
| K+ | 100.0% | 39.8% | 48.6% | 54.6% | 55.5% | 59.6% | 14.9% | 7.9% |
| NH4+ | 100.0% | 469.0% | 550.2% | 585.3% | 590.4% | 555.8% | 288.7% | 216.6% |
| Fv | 100.0% | 37.0% | 26.8% | 21.5% | 20.9% | 20.9% | 20.4% | 18.8% |
| Absolute resorption (μmol/min) | ||||||||
| Na+ | 70.3 | 4.6 | 1.2 | 0.3 | 0.4 | 13.9 | 6.7 | 3.3 |
| K+ | 2.31 | −0.34 | −0.23 | −0.03 | −0.16 | 1.71 | 0.27 | −0.20 |
| NH4+ | −0.278 | −0.061 | −0.026 | −0.004 | 0.026 | 0.201 | 0.054 | −0.367 |
| Fv | 0.484 | 0.078 | 0.041 | 0.004 | 0.000 | 0.004 | 0.012 | 0.008 |
| Reabsorption relative to PCT delivery | ||||||||
| Na+ | 63.6% | 4.2% | 1.1% | 0.3% | 0.3% | 12.6% | 6.0% | 2.9% |
| K+ | 60.2% | −8.9% | −6.0% | −0.9% | −4.1% | 44.6% | 7.0% | −5.3% |
| NH4+ | −369.0% | −81.2% | −35.0% | −5.1% | 34.6% | 267.1% | 72.1% | −486.3% |
| Fv | 63.0% | 10.2% | 5.3% | 0.6% | 0.0% | 0.5% | 1.6% | 1.0% |
SF, superficial; PCT, proximal convoluted tubule; PST, proximal straight tubule; MR, medullary ray; PST, proximal straight tubule; DHL, descending Henle's limb; AHL, ascending Henle's limb; DCT, distal convoluted tubule; JM, juxtamedullary; lDHL, long descending Henle's limb; Fv, volume flow (mL/min).
Table 4.
Distal nephron flows and fluxes: baseline conditions
| CNT | CCD | OMCD | IMCD | Total* | |
|---|---|---|---|---|---|
| Absolute delivery (μmol/min) | |||||
| Na+ | 13.0 | 10.1 | 9.6 | 9.1 | 6.4 |
| K+ | 0.91 | 1.54 | 1.50 | 1.15 | 0.76 |
| NH4+ | 0.955 | 1.060 | 0.816 | 0.644 | 0.623 |
| NAE | 0.83 | 0.74 | 0.56 | 0.80 | 1.18 |
| Fv | 0.215 | 0.118 | 0.067 | 0.052 | 0.040 |
| Delivery relative to PCT delivery | |||||
| Na+ | 6.0% | 4.6% | 4.4% | 4.2% | 3.0% |
| K+ | 12.1% | 20.4% | 19.9% | 15.3% | 10.1% |
| NH4+ | 645.4% | 716.2% | 551.3% | 435.3% | 420.8% |
| Fv | 14.3% | 7.9% | 4.4% | 3.5% | 2.6% |
| Absolute resorption (μmol/min) | |||||
| Na+ | 2.9 | 0.5 | 0.5 | 2.7 | 210.7 |
| K+ | -0.63 | 0.04 | 0.34 | 0.39 | 6.78 |
| NH4+ | -0.105 | 0.244 | 0.172 | 0.022 | -0.475 |
| Fv | 0.097 | 0.052 | 0.014 | 0.013 | 1.468 |
| Reabsorption relative to PCT delivery | |||||
| Na+ | 1.4% | 0.2% | 0.2% | 1.3% | 97.1% |
| K+ | -8.4% | 0.6% | 4.6% | 5.2% | 89.9% |
| NH4+ | -70.8% | 164.9% | 115.9% | 14.6% | -320.8% |
| Fv | 6.4% | 3.4% | 1.0% | 0.8% | 97.4% |
CNT, connecting tubule; CCD, cortical collecting duct; OMCD, outer medullary collecting duct; IMCD, inner medullary collecting duct; PCT, proximal convoluted tubule; Fv, volume flow (mL/min).
Under “total kidney,” “delivery” refers to urine flows and “reabsorption” includes fluxes from all segments of all nephrons.
Figure 4.
Segmental accounting of whole kidney flows and fluxes of ammonia. The top distinguishes superficial (\) and juxtamedullary (/) transport. The initial pair of bars shows ammonia delivery to proximal tubules (via glomerular filtration). Subsequent pairs display ammonia secretion (positive deflection) or reabsorption (negative deflection) in the respective segments. There are three bars for the PST (medullary ray PST from superficial nephrons and OM segments from superficial and juxtamedullary nephrons); The sDHL contains two bars, one from short nephrons and one from the upper segment of the long DHL; only juxtamedullary nephrons provide bars for the long DHL and thin AHL. The final pair of bars in the top shows distal ammonia delivery from each nephron population, and the sum of these two flows appears as the first bar in the bottom. Segmental fluxes from the common distal nephron are displayed in the bottom, with the final bar being urinary ammonia flow (IMCD exit). AHL, ascending Henle limb; CCD, cortical collecting duct; CNT, connecting tubule; DCT, distal convoluted tubule; DHL, descending Henle's limb; IM, inner medulla; IMCD, inner medullary collecting duct; OM, outer medulla; OMCD, outer medullary collecting duct.
Tables 5–7 show mass transfer within the kidney regions defined in Fig. 1. For each panel, the top section displays cortical labyrinth entering flows into the PCT, DCT, and peritubular capillaries, fluxes from each structure, and exiting flows from the PCT, CNT, and capillaries. Reabsorptive fluxes are positive; secretory are negative. For the volume fluxes shown in Table 5, the sum of nephron fluxes matches vascular uptake, as was a condition of the model equations. The middle section summarizes MR flows and fluxes for its three nephron segments (MR-PST, cortical AHL, and CCD) and for the peritubular capillaries. The volume fluxes in this region are much smaller, but again the balance between tubular reabsorption and vascular uptake is confirmed. In the bottom section of the panel, the LOH contribution comprises all of the LOH segments for both the OM and IM, from SF nephrons and all five of the long nephron classes. The medullary CD (MCD) is composed of the OMCD (entering flow) and IMCD (exit flow). The vasa recta contribution includes all classes of short- and long vasa recta. In this more complex geometry with its relatively coarse medullary sectioning, mass balance accuracy is confirmed to within 0.5%. Table 6 shows regional fluxes of total ammonia and has the same format as that for volume; these fluxes are those shown in Fig. 1, A–C. With respect to the nephron segments, the fluxes are the sum of NH3 and NH4+ across the basal surface of cells and lateral interspaces, as these are different from the luminal surface fluxes, due to ammoniagenesis. Again within the cortex, there is a balance of tubular flux and vascular uptake, but in this region the exiting ammonia (vascular plus tubular flow) exceeds the entering flow by 3.0 µmol/min. The contributions of ammoniagenesis within the MR and medulla are two orders of magnitude smaller (0.03 µmol/min) and derive from the PST. The discrepancy between tubular and capillary ammonia fluxes within the medulla may reflect the relatively coarse spatial segmentation (500 µm between medullary grid points). The important observation from this table is that overall ammoniagenesis is fivefold greater than renal ammonia delivery (capillaries plus the PCT = 0.6 µmol/min). However, final urine ammonia flow (MCD exit) is ∼0.5 µmol/min greater than PCT ammonia delivery, so that 16% of new ammonia is excreted and 84% is delivered into the systemic circulation.
Table 5.
Regional volume flows and fluxes (µL/min): baseline parameters
| Entry | Flux | Exit | |
|---|---|---|---|
| Labyrinth | |||
| Capillaries | 2.700 | −1.066 | 3.766 |
| PCT | 1.507 | 0.945 | 0.565 |
| DCT | 0.237 | 0.022 | 0.215 |
| CNT | 0.215 | 0.098 | 0.117 |
| Nephrons | 1.745 | 1.066 | 0.682 |
| Medullary ray | |||
| Capillaries | 0.311 | −0.209 | 0.520 |
| MR-PST | 0.281 | 0.125 | 0.156 |
| AHLc | 0.268 | 0.030 | 0.237 |
| CCD | 0.118 | 0.054 | 0.067 |
| Nephrons | 0.667 | 0.209 | 0.460 |
| Medulla | |||
| Vasa recta | 0.229 | −0.198 | 0.427 |
| Loop of Henle | 0.440 | 0.173 | 0.267 |
| OMCD-IMCD | 0.067 | 0.027 | 0.040 |
| Nephrons | 0.507 | 0.199 | 0.307 |
| All vessels | 3.240 | −1.473 | 4.713 |
PCT, proximal convoluted tubule; DCT, distal convoluted tubule; CNT, connecting tubule; MR, medullary ray; PST, proximal straight tubule; AHL, ascending Henle's limb; CCD, cortical collecting duct; OMCD, outer medullary collecting duct; IMCD, inner medullary collecting duct.
Table 7.
Regional total CO2 flows and fluxes (µmol/min): baseline parameters
| Entry | Flux | Exit | Generation | |
|---|---|---|---|---|
| Labyrinth | ||||
| Capillaries | 75.86 | −38.88 | 114.84 | |
| PCT | 39.50 | 33.52 | 7.66 | |
| DCT | 1.98 | 4.80 | 1.09 | |
| CNT | 1.09 | 0.57 | 1.21 | |
| Nephrons | 41.48 | 38.88 | 8.87 | 6.37 |
| Medullary ray | ||||
| Capillaries | 8.74 | −3.67 | 12.41 | |
| MR-PST | 4.83 | 1.32 | 3.50 | |
| AHLc | 3.15 | 1.99 | 1.98 | |
| CCD | 1.21 | 0.36 | 0.87 | |
| Nephrons | 9.19 | 3.67 | 6.35 | 0.84 |
| Medulla | ||||
| Vasa recta | 6.61 | −5.55 | 12.16 | |
| Loop of Henle | 6.33 | 4.60 | 3.15 | |
| OMCD-IMCD | 0.87 | 0.95 | 0.26 | |
| Nephrons | 7.20 | 5.55 | 3.41 | 1.75 |
| All vessels | 91.21 | −48.10 | 139.40 | |
PCT, proximal convoluted tubule; DCT, distal convoluted tubule; CNT, connecting tubule; MR, medullary ray; PST, proximal straight tubule; AHL, ascending Henle's limb; CCD, cortical collecting duct; OMCD, outer medullary collecting duct; IMCD, inner medullary collecting duct.
Table 6.
Regional ammonia flows and fluxes (µmol/min): baseline parameters
| Entry | Flux | Exit | Generation | |
|---|---|---|---|---|
| Labyrinth | ||||
| Capillaries | 0.270 | −1.686 | 1.956 | |
| PCT | 0.151 | 2.482 | 0.624 | |
| DCT | 0.270 | −0.690 | 0.956 | |
| CNT | 0.956 | −0.105 | 1.060 | |
| Nephrons | 0.421 | 1.686 | 1.684 | 2.950 |
| Medullary ray | ||||
| Capillaries | 0.031 | −0.391 | 0.422 | |
| MR-PST | 0.269 | 0.058 | 0.246 | |
| AHLc | 0.362 | 0.092 | 0.270 | |
| CCD | 1.060 | 0.242 | 0.817 | |
| Nephrons | 1.691 | 0.391 | 1.333 | 0.033 |
| Medulla | ||||
| Vasa recta | 0.023 | −0.458 | 0.481 | |
| Loop of Henle | 0.601 | 0.270 | 0.362 | |
| OMCD-IMCD | 0.817 | 0.196 | 0.623 | |
| Nephrons | 1.419 | 0.466 | 0.985 | 0.025 |
| All vessels | 0.324 | −2.536 | 2.860 | |
PCT, proximal convoluted tubule; DCT, distal convoluted tubule; CNT, connecting tubule; MR, medullary ray; PST, proximal straight tubule; AHL, ascending Henle's limb; CCD, cortical collecting duct; OMCD, outer medullary collecting duct; IMCD, inner medullary collecting duct.
The same regional description of ammonia may be applied to CO2, which is generated in all nephron segments containing an ATPase, and this is shown in Table 7. In this model (24), cellular CO2 generation appears as an increase in total CO2:
| (31) |
in which sI is cytosolic generation of the indicated species and MI is metabolic CO2 production. In turn, MI(CO2,x) is the sum of three terms, each proportional to active transport by Na+-K+-ATPase, H+-K+-ATPase, and H+-ATPase in any cell. Those proportionality constants reflect the generation of 5 ATP per O2, and a stoichiometry of 3 Na+ per ATP for Na+-K+-ATPase and 2 H+ per ATP for both of the proton ATPases. Assuming a respiratory quotient of CO2 to O2 equal to 1.0, there is 1 CO2 generated for active transport of 15 Na+ or 10 H+. In the prior model, the estimate of medullary metabolism was modified, with the assumption that one-third of active transport within the medulla (AHL, OMCD, and IMCD) was anaerobic (25), in order to mitigate what seemed unrealistically high medullary Pco2 predictions. With regard to Tables 5–7, total vascular CO2 entry for all regions is 91.2 µmol/min (including a relatively small contribution from carbamino hemoglobin species) and total filtered CO2 is 39.5 µmol/min, so that total CO2 delivery is 130.7 µmol/min. Vascular CO2 exit is 139.4 µmol/min, and there is little CO2 within the final urine. Thus, renal CO2 generation by this kidney is 8.7 µmol/min, and this is the model estimate of renal O2 consumption.
Metabolic Acidosis
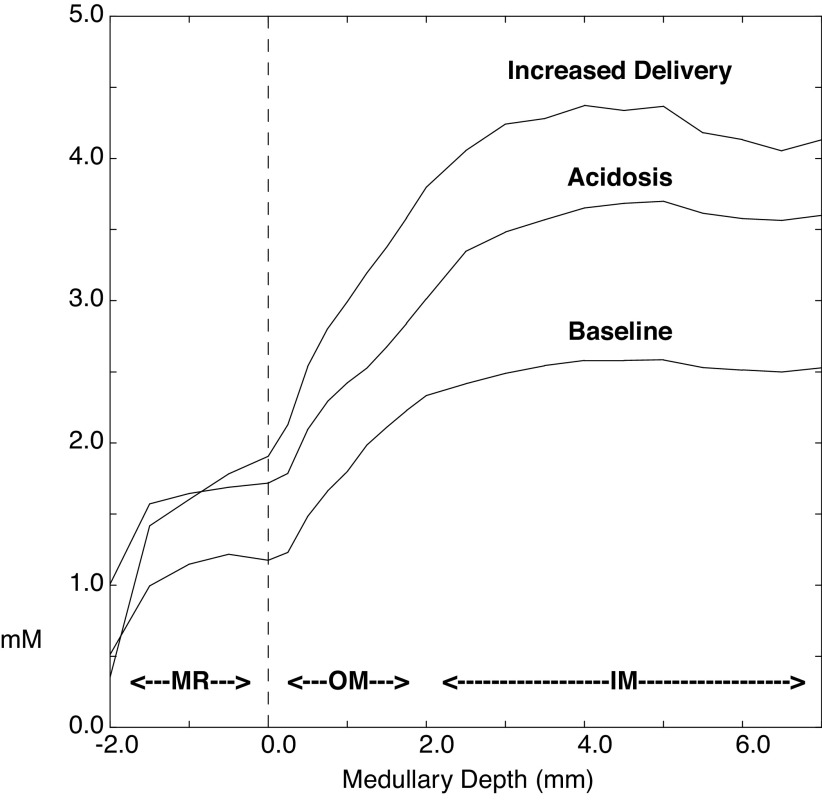
In the simulation of metabolic acidosis, HCO3− is reduced from 25 to 18 meq/L, and entering CO2 has been reduced from 1.2 to 1.0 mM, to reflect ventilatory compensation (Table 1). With respect to the other buffer pairs, their total concentrations are unchanged, while the distribution between acid and basic forms is adjusted according to the pH. In the model proximal tubules, there is ammoniagenesis within the PCT and PST, and within the PCT ammonia generation is flow dependent (49). For this acidosis simulation, ammoniagenesis has been assumed to have doubled in all proximal tubule segments. The second pair of columns in Table 2 shows peritubular capillary concentrations within the cortical labyrinth during acidosis. Exit solute concentrations are those of the cortical interstitium and show a near doubling of interstitial ammonia, from 0.5 to 1.0 mM. Tubular transport also increases ambient HCO3−, although the higher cortical Pco2 still acidifies exiting blood. Figure 5 shows interstitial ammonia concentrations along the corticomedullary axis; baseline concentrations from Fig. 2 are included for comparison. Within the medulla, acidosis has increased ammonia from ∼2.5 to 3.7 mM, so that compared with the increase within the cortical labyrinth, the fractional increase in medullary interstitial ammonia has been attenuated.
Figure 5.
Interstitial ammonia concentrations from the medullary ray (MR) through the medulla. The values are displayed as in Fig. 2 with baseline NH4+ concentrations from Fig. 2 included here for comparison. The two additional curves correspond to values obtained in metabolic acidosis and with increased medullary ammonia delivery (obtained by reducing proximal tubule tight junction ammonia permeability along with raising the proximal straight tubule ammoniagenesis rate to that of the proximal convoluted tubule). IM, inner medulla; OM, outer medulla.
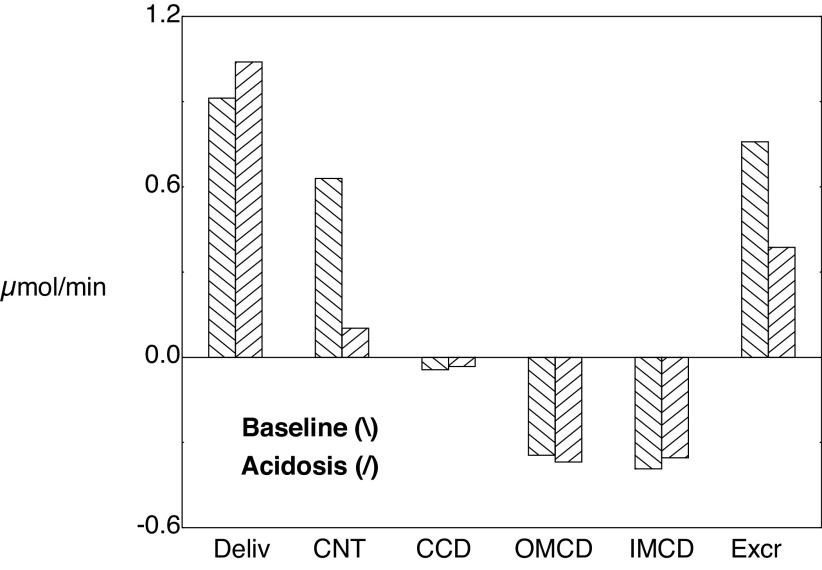
Figure 6 shows luminal ammonia, concentrations, and flows for SF and JM nephrons. Compared with Fig. 3, the curves of this simulation appear as simply scaled up by a factor of 2, with secretion in both the early PCT and DCT and enhanced reabsorption in the late PCT and both the CCD and OMCD. Table 8 shows delivery and reabsorption to the distal nephron segments, along with final urinary excretion. Compared with the baseline values shown in Table 4, acidosis has decreased Na+ excretion only slightly, and this is still a natriuretic kidney. Despite ample Na+ delivery to the CNT (10 compared with 13 µmol/min), CNT Na+ reabsorption has been halved from 2.9 to 1.5 µmol/min, largely through the epithelial Na+ channel (ENaC). With acidosis, there is acidification of the principal cells, from pH 7.23 to 7.13, which derives from increased interstitial ammonia promoting uptake into principal cells via Na+-K+-ATPase. In all segments of the model, ENaC has a cytosolic pH-dependence, in which acidification reduces its activity (44). This pH modulation of ENaC function had been incorporated into model principal cells with the work of Strieter et al. (50), which followed observations of Palmer and Frindt (51). Consequent to reduced ENaC activity, CNT K+ secretion decreases from 0.6 to 0.1 µmol/min. The impact of acidosis on distal K+ transport is shown in Fig. 7, in which comparable CNT K+ delivery and CD K+ reabsorption contrast with the impact on CNT secretion. Table 8 also shows that in acidosis net acid excretion increases from 1.2 to 1.7 µmol/min, due primarily to increased urinary NH4+ (0.6 to 1.0 µmol/min). Segmental ammonia transport is shown in Fig. 8, formatted as for the baseline transport of Fig. 4. Compared with baseline, there are prominent increases in ammonia secretion by the PCT and DCT during acidosis, with little change elsewhere along the nephron. The regional ammonia fluxes are shown in Table 9, which is of the form of Table 6. With acidosis, ammonia generation within the cortical labyrinth (total exit less entry, from the capillary and nephron) has nearly doubled from 3.0 to 5.6 µmol/min, as has PST delivery (PCT exit, from 0.6 to 1.2 µmol/min), with a smaller fractional increase CNT ammonia exit (1.1 to 1.8 µmol/min). Of the 5.7 µmol/min ammoniagenesis, 0.9 has been added to entering PCT flow and appears in the final urine; 4.9 will appear in renal venous blood. As in the baseline case, ∼85% of renal ammoniagenesis is delivered into the systemic circulation.
Figure 6.
Ammonia concentrations and flows within the nephron, as a function of distance along the tubules. Values are displayed as in Fig. 3, but from the simulation of metabolic acidosis, in which systemic blood composition shows reductions in HCO3− and CO2, and in which rates of proximal tubule ammoniagenesis have been doubled. Compared with Fig. 3 (baseline), the scale of values for the ordinate has been increased to accommodate the larger concentrations and fluxes of this simulation. See text for abbreviations.
Table 8.
Distal nephron flows and fluxes: acidosis
| CNT | CCD | OMCD | IMCD | Total* | |
|---|---|---|---|---|---|
| Absolute delivery (μmol/min) | |||||
| Na+ | 10.1 | 8.6 | 8.3 | 8.1 | 5.4 |
| K+ | 1.04 | 1.14 | 1.11 | 0.74 | 0.39 |
| NH4+ | 1.919 | 1.835 | 1.379 | 1.030 | 1.004 |
| NAE | 2.05 | 1.56 | 1.29 | 1.39 | 1.71 |
| Fv | 0.209 | 0.107 | 0.064 | 0.047 | 0.035 |
| Delivery relative to PCT delivery | |||||
| Na+ | 4.9% | 4.2% | 4.0% | 3.9% | 2.6% |
| K+ | 14.5% | 16.0% | 15.5% | 10.3% | 5.4% |
| NH4+ | 1361.3% | 1301.7% | 978.5% | 731.0% | 712.2% |
| Fv | 14.6% | 7.5% | 4.5% | 3.3% | 2.4% |
| Absolute resorption (μmol/min) | |||||
| Na+ | 1.5 | 0.3 | 0.2 | 2.7 | 200.9 |
| K+ | −0.10 | 0.03 | 0.37 | 0.35 | 6.78 |
| NH4+ | 0.084 | 0.455 | 0.349 | 0.027 | −0.863 |
| Fv | 0.102 | 0.043 | 0.017 | 0.012 | 1.398 |
| Reabsorption relative to PCT delivery | |||||
| Na+ | 0.7% | 0.1% | 0.1% | 1.3% | 97.4% |
| K+ | −1.4% | 0.5% | 5.2% | 4.9% | 94.6% |
| NH4+ | 59.6% | 323.1% | 247.5% | 18.9% | −612.2% |
| Fv | 7.1% | 3.0% | 1.2% | 0.9% | 97.6% |
CNT, connecting tubule; CCD, cortical collecting duct; OMCD, outer medullary collecting duct; IMCD, inner medullary collecting duct; PCT, proximal convoluted tubule; Fv, volume flow (mL/min).
Under “total kidney,” “delivery” refers to urine flows and “reabsorption” includes fluxes from all segments of all nephrons.
Figure 7.
Segmental accounting of common distal nephron flows and fluxes of K+. The bar pairs indicate values obtained using baseline parameters (\) and those for acidosis (/). The first pair shows K+ delivery to the connecting tubule (CNT); middle pairs are segmental addition (K+ secretion) or subtraction (K+ reabsorption); the rightmost pair indicates renal K+ excretion. The salient difference is within the CNT, in which acidosis inhibits epithelial Na+ channel Na+ permeability, and thus blunts K+ secretion by that segment. CCD, cortical collecting duct; OMCD, outer medullary collecting duct; IMCD, inner medullary collecting duct.
Figure 8.
Segmental accounting of whole kidney flows and fluxes of ammonia, from the simulation of metabolic acidosis. The display is of the form of Fig. 4 with the ordinate flux values increased twofold. Doubling of flux magnitudes reflects the approximate doubling of ammoniagenesis. See text for abbreviations.
Table 9.
Regional ammonia flows and fluxes (µmol/min): acidosis
| Entry | Flux | Exit | Generation | |
|---|---|---|---|---|
| Labyrinth | ||||
| Capillaries | 0.270 | −3.510 | 3.780 | |
| PCT | 0.143 | 4.508 | 1.233 | |
| DCT | 0.849 | −1.082 | 1.921 | |
| CNT | 1.921 | 0.084 | 1.836 | |
| Nephrons | 0.992 | 3.510 | 3.069 | 5.587 |
| Medullary ray | ||||
| Capillaries | 0.031 | −0.632 | 0.664 | |
| MR-PST | 0.547 | 0.221 | 0.396 | |
| AHLc | 0.807 | −0.042 | 0.849 | |
| CCD | 1.836 | 0.453 | 1.381 | |
| Nephrons | 3.190 | 0.632 | 2.627 | 0.069 |
| Medulla | ||||
| Vasa recta | 0.023 | −0.713 | 0.736 | |
| Loop of Henle | 1.082 | 0.342 | 0.807 | |
| OMCD-IMCD | 1.381 | 0.379 | 1.004 | |
| Nephrons | 2.464 | 0.721 | 1.811 | 0.061 |
| All vessels | 0.324 | −4.856 | 5.180 | |
PCT, proximal convoluted tubule; DCT, distal convoluted tubule; CNT, connecting tubule; MR, medullary ray; PST, proximal straight tubule; AHL, ascending Henle's limb; CCD, cortical collecting duct; OMCD, outer medullary collecting duct; IMCD, inner medullary collecting duct.
Increasing Medullary Ammonia Delivery
Measurements of ammonia partitioning between blood and urine in the dog (3), human (52), and rat (5) all indicate a larger urinary component than is predicted by this model. Accordingly, it is important to consider what aspect of the model might be adjusted to control this partitioning. One obvious consideration is the magnitude of ammonia reabsorption within the latter portion of the PCT. In these model segments, the preponderance of ammonia backflux is due to electrodiffusive reabsorption across tight junctions, for which NH4+ permeability is 60% greater than that for K+. Accordingly, in the calculations that follow, tight junction NH4+ permeabilities have been reduced by 80% in all proximal tubules (PCT and PST). A second parameter adjustment has been to increase the rate of PST ammoniagenesis (within the MR and OM) to values equal to rates in their respective PCT. Experimental support for this change comes from the study of Good and Burg (53), who measured ammonia production by rat nephron segments in suspension, and by Nagami (54), who found ammonia production by isolated perfused mouse S3 proximal tubules to be about half that from mouse S2 segments (12). The only other change in model parameters was a 20% reduction in ammoniagenesis for all PT segments, as this adjustment provides renal excretion of net acid and ammonia that is approximately equal to that at baseline. The calculations assume baseline blood composition, and the last two columns in Table 2 show predicted cortical solute concentrations. The salient finding is that with reduced PCT tight junction permeability, peritubular NH4+ has decreased from 0.51 to 0.35 mM. Figure 5, which contains predicted MR and medullary interstitial NH4+ profiles, shows the increase from 2.5 to 4.4 mM within the IM, due to the increase in medullary delivery.
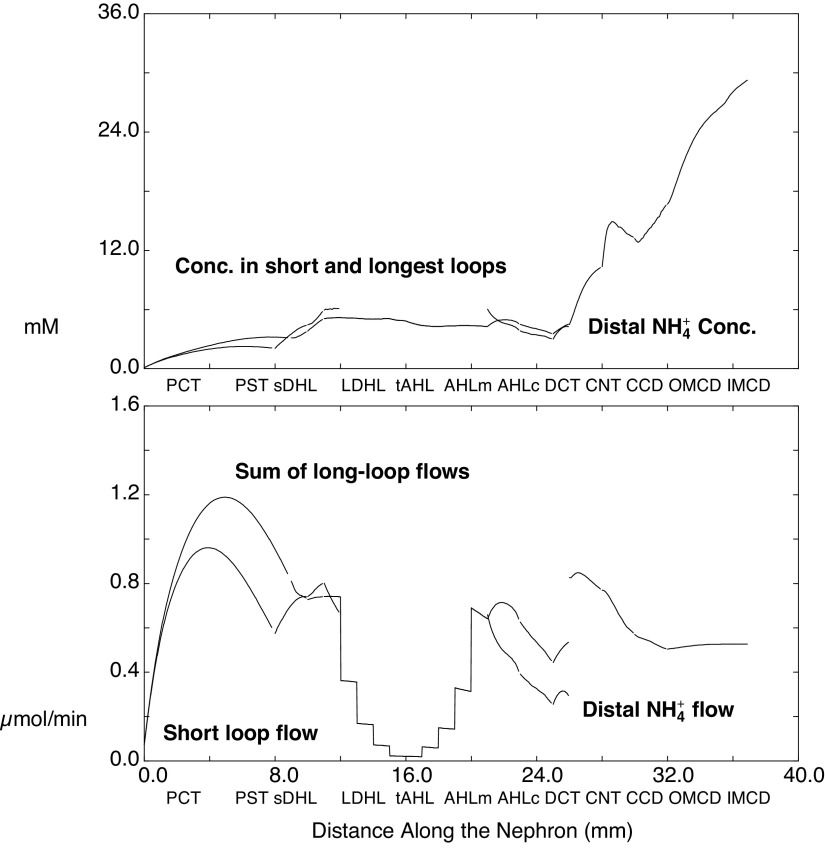
Tubular NH4+ concentrations and flows are shown in Fig. 9, which is comparable with Fig. 3. Here, the decrease in proximal tubule tight junction NH4+ permeability has blunted reabsorptive flux, such that end-tubule flow is ∼60% of the midtubule maximum, rather than one-third maximum obtained using the baseline parameters. Segmental accounting of NH4+ delivery and reabsorption is shown in Tables 10 and 11 and Fig. 10. With regard to Fig. 10, the impact of decreasing proximal tubule tight junction permeability is a doubling of net PCT ammonia secretion. One downstream effect of increasing medullary ammonia delivery is that within JM nephrons, the OM portion of thin descending Henle limbs now shows a small reabsorptive ammonia flux (rather than the small baseline secretory flux). More important, however, is that for all nephrons, DCT secretory ammonia flux has been reduced by 80%. This is due to a 25% reduction in DCT Na+ reabsorption (compare Tables 10 and 3), in conjunction with the reduction in cortical labyrinth NH4+ concentration, which decreases NH4+ uptake on DCT peritubular Na+-K+-ATPase. As a consequence, NH4+ delivery to the CNT is now less than what it had been at baseline, although within the CD, NH4+ reabsorption is about half the baseline value, due to higher interstitial NH4+ concentrations (compare Tables 11 and 4). The final urine composition, with respect to net acid and NH4+, is approximately that of baseline.
Figure 9.
Ammonia concentrations and flows within the nephron, as a function of distance along the tubules. Values are displayed as in Fig. 3 for this simulation in which medullary ammonia delivery is increased by 80% reduction of tight junction ammonia permeabilities (for all proximal convoluted and straight tubules) and an increase of proximal straight tubule ammoniagenesis rates to those of the proximal convoluted tubule. The ordinate values of the bottom panel (flows) are as in Fig. 3 to facilitate comparison. See text for abbreviations.
Table 10.
Segmental flows and fluxes: increased medullary delivery
| SF | PCT | PST-MR | PST | sDHL | AHLm | AHLc | DCT |
|---|---|---|---|---|---|---|---|
| Absolute delivery (μmol/min) | |||||||
| Na+ | 107.6 | 39.2 | 29.2 | 25.1 | 24.5 | 11.6 | 5.0 |
| K+ | 3.74 | 1.42 | 1.25 | 1.25 | 1.24 | 0.64 | 0.28 |
| NH4+ | 0.073 | 0.574 | 0.740 | 0.801 | 0.659 | 0.391 | 0.255 |
| Fv | 0.747 | 0.280 | 0.166 | 0.135 | 0.110 | 0.103 | 0.085 |
| Delivery relative to PCT delivery | |||||||
| Na+ | 100.0% | 36.5% | 27.1% | 23.3% | 22.7% | 10.8% | 4.7% |
| K+ | 100.0% | 37.9% | 33.5% | 33.4% | 33.3% | 17.1% | 7.5% |
| NH4+ | 100.0% | 783.5% | 1009.0% | 1092.2% | 898.9% | 533.7% | 348.3% |
| Fv | 100.0% | 37.4% | 22.2% | 18.0% | 14.7% | 13.7% | 11.4% |
| Absolute resorption (μmol/min) | |||||||
| Na+ | 68.3 | 10.1 | 4.1 | 0.6 | 12.8 | 6.6 | 3.2 |
| K+ | 2.32 | 0.16 | 0.00 | 0.00 | 0.60 | 0.36 | −0.13 |
| NH4+ | −0.501 | −0.165 | −0.061 | 0.142 | 0.268 | 0.136 | −0.033 |
| Fv | 0.468 | 0.114 | 0.031 | 0.025 | 0.007 | 0.018 | 0.017 |
| Reabsorption relative to PCT delivery | |||||||
| Na+ | 63.5% | 9.4% | 3.8% | 0.6% | 11.9% | 6.1% | 3.0% |
| K+ | 62.1% | 4.4% | 0.1% | 0.1% | 16.2% | 9.7% | −3.4% |
| NH4+ | −683.5% | −225.5% | −83.2% | 193.3% | 365.2% | 185.4% | −45.3% |
| Fv | 62.6% | 15.2% | 4.2% | 3.3% | 0.9% | 2.3% | 2.2% |
| All JM | PCT | PST | lDHLu | lDHLl | tAHL | AHLm | AHLc | DCT |
|---|---|---|---|---|---|---|---|---|
| Absolute delivery (μmol/min) | ||||||||
| Na+ | 107.8 | 38.0 | 33.5 | 32.3 | 31.7 | 31.2 | 15.0 | 8.7 |
| K+ | 3.75 | 1.44 | 1.57 | 1.61 | 1.65 | 1.83 | 0.88 | 0.44 |
| NH4+ | 0.074 | 0.810 | 0.727 | 0.741 | 0.720 | 0.641 | 0.626 | 0.444 |
| Fv | 0.749 | 0.273 | 0.192 | 0.147 | 0.143 | 0.143 | 0.138 | 0.126 |
| Delivery relative to PCT delivery | ||||||||
| Na+ | 100.0% | 35.2% | 31.0% | 29.9% | 29.4% | 28.9% | 13.9% | 8.1% |
| K+ | 100.0% | 38.4% | 41.9% | 42.9% | 43.9% | 49.0% | 23.4% | 11.7% |
| NH4+ | 100.0% | 1102.5% | 989.1% | 1008.2% | 979.4% | 872.1% | 851.4% | 603.7% |
| Fv | 100.0% | 36.4% | 25.6% | 19.6% | 19.0% | 19.0% | 18.4% | 16.8% |
| Absolute resorption (μmol/min) | ||||||||
| Na+ | 69.9 | 4.5 | 1.2 | 0.5 | 0.5 | 16.2 | 6.3 | 2.9 |
| K+ | 2.31 | −0.13 | −0.04 | −0.04 | −0.19 | 0.96 | 0.44 | −0.15 |
| NH4+ | −0.737 | 0.083 | −0.014 | 0.021 | 0.079 | 0.015 | 0.182 | −0.093 |
| Fv | 0.476 | 0.081 | 0.045 | 0.004 | 0.000 | 0.004 | 0.012 | 0.009 |
| Reabsorption relative to PCT delivery | ||||||||
| Na+ | 64.8% | 4.2% | 1.1% | 0.5% | 0.5% | 15.0% | 5.8% | 2.7% |
| K+ | 61.6% | −3.5% | −1.0% | −1.0% | −5.1% | 25.6% | 11.8% | −4.0% |
| NH4+ | −1002.5% | 113.4% | −19.1% | 28.7% | 107.4% | 20.7% | 247.8% | −126.8% |
| Fv | 63.6% | 10.8% | 6.0% | 0.6% | 0.0% | 0.6% | 1.7% | 1.3% |
SF, superficial; PCT, proximal convoluted tubule; PST, proximal straight tubule; MR, medullary ray; PST, proximal straight tubule; DHL, descending Henle's limb; AHL, ascending Henle's limb; DCT, distal convoluted tubule; JM, juxtamedullary; lDHL, long descending Henle's limb; Fv, volume flow (mL/min).
Table 11.
Distal nephron flows and fluxes: increased medullary delivery
| CNT | CCD | OMCD | IMCD | Total* | |
|---|---|---|---|---|---|
| Absolute delivery (μmol/min) | |||||
| Na+ | 7.7 | 5.1 | 4.9 | 4.7 | 2.4 |
| K+ | 0.99 | 1.59 | 1.46 | 0.94 | 0.46 |
| NH4+ | 0.826 | 0.770 | 0.570 | 0.504 | 0.527 |
| NAE | 0.87 | 0.77 | 0.60 | 0.85 | 1.20 |
| Fv | 0.185 | 0.074 | 0.043 | 0.030 | 0.018 |
| Delivery relative to PCT delivery | |||||
| Na+ | 3.6% | 2.4% | 2.3% | 2.2% | 1.1% |
| K+ | 13.3% | 21.2% | 19.5% | 12.6% | 6.1% |
| NH4+ | 562.2% | 524.2% | 388.4% | 343.2% | 358.7% |
| Fv | 12.4% | 5.0% | 2.9% | 2.0% | 1.2% |
| Absolute resorption (μmol/min) | |||||
| Na+ | 2.5 | 0.3 | 0.1 | 2.3 | 213.0 |
| K+ | −0.59 | 0.12 | 0.52 | 0.48 | 7.02 |
| NH4+ | 0.056 | 0.199 | 0.066 | −0.023 | −0.380 |
| Fv | 0.110 | 0.031 | 0.013 | 0.012 | 1.478 |
| Reabsorption relative to PCT delivery | |||||
| Na+ | 1.2% | 0.1% | 0.1% | 1.1% | 98.9% |
| K+ | −7.9% | 1.7% | 7.0% | 6.5% | 93.9% |
| NH4+ | 38.1% | 135.8% | 45.2% | −15.5% | −258.7% |
| Fv | 7.4% | 2.1% | 0.9% | 0.8% | 98.8% |
CNT, connecting tubule; CCD, cortical collecting duct; OMCD, outer medullary collecting duct; IMCD, inner medullary collecting duct; PCT, proximal convoluted tubule; Fv, volume flow (mL/min).
Under “total kidney,” “delivery” refers to urine flows and “reabsorption” includes fluxes from all segments of all nephrons.
Figure 10.
Segmental accounting of whole kidney flows and fluxes of ammonia, for the simulation in which medullary ammonia delivery is increased by reducing proximal tubule tight junction ammonia permeabilities and increasing proximal straight tubule ammoniagenesis. The ordinate values are as in Fig. 4 to facilitate comparison. See text for abbreviations.
Regional ammonia accounting is shown in Table 12, and these regional fluxes are quite different from baseline (Table 6). Using baseline parameters, ammonia addition to the PCT and DCT are 0.5 and 0.7 µmol/min, whereas ammonia reabsorption from the LOH and the CCD plus MCD are 0.3 and 0.4 µmol/min. When tight junction ammonia permeabilities are reduced, ammonia addition to the PCT and DCT are 1.2 and 0.1 µmol/min, whereas loss from the LOH and CD are 0.5 and 0.2 µmol/min. Thus, as more ammonia is delivered to the medulla from the proximal tubule and additional ammonia is generated in the OMPST, there is little change in aggregate reabsorptive loss to the vasa recta. The dominant change is the reduction of the DCT contribution to tubular NH4+ flow. In aggregate, of the 2.9 µmol/min ammoniagenesis, 2.6 µmol/min (87%) is added to the renal vein, and 0.4 µmol/min (13%) appears in the urine. These proportions are identical to those of the baseline case and in acidosis.
Table 12.
Regional ammonia flows and fluxes (µmol/min): increased medullary delivery
| Entry | Flux | Exit | Generation | |
|---|---|---|---|---|
| Labyrinth | ||||
| Capillaries | 0.270 | −1.086 | 1.356 | |
| PCT | 0.150 | 1.157 | 1.392 | |
| DCT | 0.700 | −0.129 | 0.826 | |
| CNT | 0.826 | 0.058 | 0.770 | |
| Nephrons | 0.849 | 1.086 | 2.162 | 2.399 |
| Medullary ray | ||||
| Capillaries | 0.031 | −0.624 | 0.655 | |
| MR-PST | 0.579 | 0.105 | 0.746 | |
| AHLc | 1.020 | 0.321 | 0.700 | |
| CCD | 0.770 | 0.198 | 0.571 | |
| Nephrons | 2.369 | 0.624 | 2.017 | 0.272 |
| Medulla | ||||
| Vasa recta | 0.023 | −0.855 | 0.878 | |
| Loop of Henle | 1.559 | 0.815 | 1.020 | |
| OMCD-IMCD | 0.571 | 0.045 | 0.527 | |
| Nephrons | 2.131 | 0.860 | 1.547 | 0.271 |
| All vessels | 0.324 | −2.566 | 2.890 | |
PCT, proximal convoluted tubule; DCT, distal convoluted tubule; CNT, connecting tubule; MR, medullary ray; PST, proximal straight tubule; AHL, ascending Henle's limb; CCD, cortical collecting duct; OMCD, outer medullary collecting duct; IMCD, inner medullary collecting duct.
DISCUSSION
The model of this paper advances the effort to simulate kidney function by explicitly representing renal cortical blood flow and computing interstitial solute concentrations. This extension is a necessity for representation of renal ammonia transport. The model recognizes two cortical regions: the labyrinth, which contains the PCT, DCT, and CNT, and the MR, which contains a straight segment of the SFPST, along with the cortical AHL and CCD. The approach is rooted in anatomical observations from Beeuwkes and coworkers (32, 34), who demonstrated disengagement of efferent arterioles and downstream peritubular capillaries from their nephron of origin. These capillaries provide regional drainage from one or more nephrons, in a plexus so complex that any attempt to represent individual blood vessel flows would be fanciful at best. What has been done here is to consider the capillary uptake, presumably some mix of convective and diffusive fluxes, to yield vascular solute concentrations that are approximately those of the interstitium. It further assumes that there is no further solute flux into or out of renal veins as blood exits the kidney. This approach, which treats the interstitium and capillaries as a continuum, follows vascular models, which have been applied to muscle O2 delivery (38, 39). In this kidney model, there is the additional simplification that the cortical labyrinth is a single uniform compartment. This may be viewed as a model limitation, in view of cortical regional differences among nephrons, and along the CNT arcades (37). Nevertheless, if it is assumed that there is glomerulotubular balance of PCT ammoniagenesis, in parallel with transport, then there is reason to expect some uniformity of cortical interstitial ammonia concentration. Beyond that, there are no data that would guide more refined regionalization within the labyrinth.
The possibility of additional solute exchange within the renal venous system, especially within smaller veins, has been given substantial attention, with respect to both CO2 transport and O2 delivery. Regarding CO2, Atherton et al. (26) considered the alignment of small interlobular arteries and veins and calculated that diffusive exchange between small veins and arteries could render this a countercurrent system for CO2, which could sustain a hypercapneic cortex. Although the local CO2 increase is driven by oxidative metabolism, the prerequisites for countercurrent transfer (and preservation of the local increase) are high vessel CO2 permeabilities plus near millimolar concentration gradients of this diffusing species. The situation is different for O2, whose local concentration is an order of magnitude less than that of CO2, and estimates of vascular shunting have been only ∼1% of the delivered load (28–30). For NH3, whose concentration is micromolar, there is no potential for substantial arteriovenous countercurrent exchange (26, 31). Thus, cortical ammonia uptake happens within peritubular capillaries and, from there, returns to the systemic circulation with little venous loss. In this model, diffusive exchange of CO2 between cortical veins and arteries has not been represented, although the model predicts that local CO2 generation is sufficient to sustain cortical hypercapnia.
In the model presented here, the MR has been reconfigured from prior versions (24, 25). Previously, the MR consisted of the cortical AHL and CCD, along with an axial blood flow in a countercurrent configuration. That representation was intended to examine the possibility that AHL solute reabsorption would promote CCD water reabsorption, reduce water entry into the OM, and thus enhance urine osmolality. This did not prove to be quantitatively important in the effort to simulate antidiuresis. One problem with that MR configuration (and all prior models that included the cortical AHL) was that the cortical AHL would deplete itself of luminal ammonia such that ammonia delivery to the DCT was unrealistically low (compared with micropuncture measurements). The remedy for those models was to provide ample AHL peritubular ammonia, by setting a high-ammonia concentration (2 mM) within blood vessels supplying the MR. In the current work, all arteriolar blood of all kidney regions have the same composition. However, an additional change with this model has been the inclusion of a straight segment of the SF proximal tubule within the MR. This conforms to anatomic studies (35, 36), and this PST segment serves as an ample ammonia source for AHL function. One further modification is that MR blood vessels no longer course axially but rather enter laterally along the MR bringing blood of arterial composition to each level. The local solute concentrations at each axial point are determined by the mixing of tubular transport and arterial supply. As with the cortical labyrinth, the venous effluent at each level has a solute composition identical to that of the interstitium. One notable omission in this and prior nephron models has been the Rhbg and Rhcg ammonia transport proteins within the distal nephron (55, 56). This derives in part from the fact that the model segments were formulated according to tubule measurements made before identification of these transporters, but more importantly to the uncertainties that still remain in assigning fluxes of NH3 and NH4+ quantitatively to each transporter.
The principal finding of this model is that cortical labyrinth ammonia concentration is predicted to be several-fold greater than in arterial blood (Table 2). This concentration increases proportionally with higher rates of ammoniagenesis (acidosis). It decreases with greater renal blood flow (calculations not shown) and when PCT NH4+ backflux is reduced, by lowering tight junction NH4+ permeability. The impact of this elevation of peritubular NH4+ within the cortical labyrinth is greater medullary delivery of ammonia to the PST and also increased ammonia secretion by the DCT. It must be noted that there is a degree of freedom in model parameter selection, specifically in assigning the rate of proximal tubule ammoniagenesis. In formulating this model, the ammoniagenesis rate is specified by a single parameter assigned to SFPCT cells. This value is doubled for the JMPCT, and both PST segments are assigned ammoniagenesis rates that are 10% of their respective PCT values. All transport parameters of the MR SFPST are identical to those of its OM-SFPST. Within the PCT, the actual rate of ammoniageneis varies along the tubule, in proportion to tubule flow velocity (57). In formulating this model, the SFPCT ammoniagenesis rate was selected to achieve final urine net acid excretion and ammonia excretion that would be generally concordant with measured values under control conditions. This value was 75% of that used in the prior models, reflecting the fact that the PCT of this model was now working in an interstitial environment with higher ambient NH4+.
Concordance of model predictions and experimental observation can be considered with reference to Table 13, which displays data from rat micropuncture and microcatheterization. Notably, there have never been measurements of cortical blood vessel ammonia concentrations, so there is no comparing the predictions of Table 2; what is available are tubular concentrations and flows. All of the rat studies have reported similar arterial NH4+ concentration, so that filtered loads depend on the kidney size and GFR (animal weight). Within the SFPCT, the ammonia concentration is quite variable, starting out near arterial values and then achieving a maximum concentration at some point along the tubule. Thus, the measured PCT concentration will depend on the sampling point. The predictions from this model, for filtered load, and maximum SFPCT NH4+ concentration and flow fall closest to the data from Simon et al. (58), under both control conditions and in acidosis. In distal tubules (the accessible DCT and CNT), Wilcox et al. (17) and Simon et al. (58) sampled both early and late tubule fluid and demonstrated a step up in ammonia flow, i.e., DCT ammonia secretion. Although Jaeger et al. (16) found an axial increase in NH4+ concentration, this was attributed to water reabsorption, and no increase in flow was discernible. Again, the predictions from this model for DCT concentration and flow are close to those found by Simon et al. (58), both in control conditions and in acidosis. This speaks to the adequacy of the model MR to sustain adequate interstitial NH4+ concentrations to support AHL transport and deliver realistic concentrations of NH4+ to the DCT. (In Fig. 5, MR NH4+ concentrations are ∼1 mM under baseline conditions and 1.5 mM in acidosis.) One notable difference between this model and the data of Simon et al. is that despite agreement of late distal ammonia flows, the model predicts a 70% increase in urinary ammonia excretion with acidosis, whereas Simon et al. found a 130% increase. Indeed, in the other two studies in which distal ammonia flows were measured, acidosis increased distal ammonia flow by less than twofold, whereas increased ammonia excretion by 140% (8, 17). This suggests that the model may not be capturing some aspect of CD ammonia transport. Finally, it must be acknowledged that all of the micropuncture data shown in Table 13 have been accrued from studies of male rats, and indeed the model of this work has been based on rat micropuncture data. Recent observations in mice demonstrate that despite the smaller proximal tubule volume of females, their baseline ammonia excretion is greater than that of males (59). With acidosis, and increased ammonia excretion, the sex difference disappears (60). That physiology falls outside the scope of what can be addressed in the present model.
Table 13.
Renal ammonia handling
| Rat | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Art. | Filtered | PCT | PCT Flow | DCT | DCT Flow | Excr. Flow | Renal V. Flux | Generation | FEAmm* | Reference |
| mM | µmol/min | mM | pmol/min | mM | pmol/min | µmol/min | µmol/min | µmol/min | ||
| 0.46 | (18)-Base | |||||||||
| 1.40 | (18)-Acidosis | |||||||||
| 0.13 | 0.07 | 2.31 | 12.3 | 4.17 | 5.9 | 0.39 | (8)-Base | |||
| 0.19 | 0.09 | 4.06 | 21.5 | 8.17 | 9.4 | 0.94 | (8)-Acidosis | |||
| 2.77 | 38.0 | 1.2→9.1 | 18 | 1.07 | (16) | |||||
| 1.99 | 45.0 | 1.51→3.91 | 15.1→28.9 | 0.65 | (17)-Base | |||||
| 2.46 | 50.4 | 1.34→4.26 | 13.4→34.1 | 1.61 | (17)-Acidosis | |||||
| 0.11 | 0.14 | 1.74 | 19.4 | 1.19→4.04 | 5.3→7.4 | 1.05 | (58)-Base | |||
| 0.14 | 0.16 | 3.31 | 34.0 | 2.04→4.97 | 9.9→12.3 | 2.39 | (58)-Acidosis | |||
| 0.08 | 0.12 | 0.40→0.45 | 8.1→5.7 | 0.18 | (13)-Base | |||||
| 0.11 | 0.17 | 0.8→1.3 | 16.0→18.1 | 0.97 | (13)-Acidosis | |||||
| 0.06 | 0.05 | 0.06 | 0.18 | 0.19 | 5.6% | (20)-Base | ||||
| 0.09 | 0.08 | 0.34 | 0.49 | 0.75 | 34.8% | (20)-Acidosis | ||||
| 0.06 | 0.72 | 0.54 | 1.26 | 57% | (5) | |||||
| Model | max→end | max→end | Init→end | Init→end | ||||||
| 0.10 | 0.15 | 1.50→0.95 | 13.1→4.45 | 1.14→4.88 | 3.7→7.1 | 0.62 | 2.54 | 2.95 | 13.9% | Base |
| 0.10 | 0.14 | 2.97→1.91 | 26.9→9.1 | 3.31→10.7 | 5.6→13.0 | 1.00 | 4.86 | 5.59 | 13.1% | Acidosis |
| 0.10 | 0.15 | 2.25→2.06 | 16.0→9.6 | 3.00→4.22 | 4.3→4.8 | 0.53 | 2.57 | 2.94 | 12.6% | Increased OM delivery |
| Dog | (3) | |||||||||
| 6.5 | 10.9 | 17.4 | 37% | Expt 18 | ||||||
| 18.9 | 6.3 | 25.2 | 75% | Expt 24 | ||||||
| Human | ||||||||||
| 22.5 | 18.2 | 40.6 | 55% | (52)-Base | ||||||
| 51.5 | 14.6 | 66.1 | 76% | (52)-Acidosis |
PCT, proximal convoluted tubule; DCT, distal convoluted tubule; OM, outer medulla.
FEAmm = 1− (renal vein flux/generation).
The kidney as an ammonia source becomes especially important in patients with advanced liver disease, so that our understanding of mechanism, and perhaps control of fractional ammonia excretion, takes on translational significance. When renal venous blood is sampled and ammonia outflow is determined, then subtracting renal arterial ammonia delivery provides the ammonia “flux” into the systemic circulation. The sum of ammonia flux plus excreted ammonia is renal ammoniagenesis. In Table 13, “generation” denotes ammoniagenesis and “FEAmm” refers to urinary ammonia addition (excreted ammonia, less filtered ammonia), relative to generation, i.e., what fraction of new ammonia shows up in the urine. There appear to have been few determinations of flux and generation in the rat. Stern et al. (20) examined 100-g rats and found that under control conditions, both generation and fractional excretion were low (0.19 µmol/min and 5.6%), whereas in acidosis, they increased substantially (0.75 µmol/min and 35%). Subsequent studies by DeJong et al. (5) using 300-g rats reported baseline ammoniagenesis of 1.26 µmol/min with FEAmm = 57%. In humans, Tizianello et al. (52) found that fractional ammonia excretion was 55% at baseline, increasing to 76% with acidosis. In two early dog experiments, Denis et al. (3) calculated fractional excretion of ammonia at 37% and 75%. In summary, the kidney model achieves agreement with experimental values of ammonia excretion by presuming a rate of ammoniagenesis greater than has been measured; the model’s ability to capture this new ammonia and divert it to the urine appears to fall short.
There have been three microcatherization studies of the rat kidney, in which IM fluid was assayed for ammonia, and all documented ammonia secretion into the IMCD (18–20). This secretory flux was augmented in metabolic acidosis (18, 20). Stern et al. (20) also sampled blood from the IM vasa recta and found a baseline concentration of 9.2 mM, which increased to 22.5 mM during acidosis. These observations were given foundational support from the isolated tubule studies of Wall and coworkers (61, 62), who demonstrated that Na+-K+-ATPase was responsible for this secretory flux, with NH4+ competing with K+ for peritubular uptake. This scheme was captured in the initial IMCD model (that has been incorporated in this work), which showed that when IM interstitial ammonia was set to 9 mM, axial IMCD ammonia flow increased by 50% from outer-inner medullary junction to papillary tip (Fig. 3 in Ref. 45). In the current work, the model predicted NH4+ reabsorption along the MCD; only by limiting tight junction NH4+ permeability could the net flux be reduced toward zero, but not transformed into secretion. With reference to Tables 6 and 12, a reduction of PCT NH4+ backflux produced an approximate doubling of LOH NH4+ delivery, and this increase appeared evenly divided between the outflows of the AHL and vasa recta. The doubling of medullary NH4+ delivery produced a bump in IM interstitial NH4+ concentration from 2.5 to 3.0 mM (Fig. 5). In short, the model fails to capture sufficient medullary ammonia trapping, necessary to sustain CD NH4+ secretion.
Noiret et al. (23) provided a careful examination of medullary ammonia fluxes in their extension of a mathematical model of the antidiuretic rat kidney. In that work, the salient observation was that ammonia excretion was largely a product of OM reabsorption from the AHL and secretion into the OMCD. Points of congruence of their model with the model of this work are the magnitudes of ammonia entry into the LOH and descending vasa recta [0.41 and 0.05 compared with 0.60 and 0.02 µmol/min (Table 6)]. Nevertheless, their predicted ammonia excretion is smaller (0.24 compared with 0.62 µmol/min here). In this regard, an important difference between the models is that ammonia entry into their OMCD was ∼0.12 µmol/min, whereas here it is much larger (0.82 µmol/min), as a consequence of DCT ammonia secretion. Beyond that, their model has medullary ammonia concentrations that are several-fold higher than in this model and sufficient to drive ammonia secretion into the OMCD. Notably, the magnitude of OM ammoniagenesis in the study by Noiret et al. was 0.24 µmol/min, just about their rate of ammonia excretion; here, the baseline value for medullary ammoniagenesis is 0.03 µmol/min. Their assignment of the rate of OM ammoniagenesis was supported by findings by Good and Burg (53) in rat S3 segments in suspension and has additional support from Nagami, who compared ammonia production in perfused mouse proximal tubules (12, 54). This motivated the third set of calculations of this paper, in which medullary ammonia delivery was increased both by increasing NH4+ entry from the proximal tubule and by increasing PST ammoniagenesis rates to those of the PCT. With both of those changes, medullary ammonia concentrations approximately doubled but were still only a third of the value calculated by Noiret et al. Beyond that, the fractional ammonia excretion remained only 13% of total ammoniagenesis. In other calculations not shown, the impact of medullary ammoniagenesis in isolation was examined by assigning to the SFPST (in the MR and OM) and to the JMPST the ammoniagenesis rates of their respective PCT (Table 1). With only those changes (and keeping all other baseline parameters), both MR and OM ammonia generation increase by an order of magnitude of 0.3 µmol/min (comparable to their values in Table 12). In that simulation, IM interstitial NH4+ concentration increased from 2.5 to 3.2 mM, but IMCD ammonia flux was still reabsorptive (0.19 compared with 0.20 µmol/min), and excretion was unchanged (0.60 from 0.62 µmol/min). In short, the impact of this increase in PST ammoniagenesis was small. Perhaps the most important difference between the model by Noiret et al. and the model here is that their medullary osmotic gradients were supported by generation of “external osmolytes.” It seems likely that these additional osmolytes, by extracting water, may also serve to sustain a steeper medullary ammonia gradient and thus support CD ammonia secretion.
In summary, this kidney model has been extended in a manner in which the salient aspects of renal ammonia transport can be represented. This involves explicit representation of the cortical labyrinth and revision of the MR. In so doing, cortical interstitial solute concentrations are computed, rather than assigned, and a single-arterial composition can be specified for perfusion of all kidney regions (the labyrinth, MR, and medulla). A detailed representation of the cortical vasculature has been avoided by taking advantage of the assumption that solute concentrations within the interstitium and peritubular capillaries are likely to be identical and that there is little to no modification of venous composition as it flows to the renal veins. The principal finding of this work is that cortical labyrinth interstitial ammonia concentration is likely to be three- to fivefold higher than systemic arterial ammonia. This elevation of interstitial ammonia enhances ammonia secretion in both the PCT and DCT. Overall ammonia excretion is captured by this kidney model, but at the expense of high rates of ammoniagenesis, with high rates of renal venous ammonia flux. Specifically, the model does not capture the high fractional excretion rates for renal ammonia, which have been observed experimentally and clinically. This derives, in part, from a limited capability of the model medulla to replicate the high-interstitial ammonia concentrations needed for CD ammonia secretion. This model shortcoming is consistent with its difficulty in capturing medullary gradients of Na+ and urea (25) and identifies a gap in our understanding of renal ammonia transport.
SUPPLEMENTAL DATA
All of the model computer codes, and reference to model publications, may be found on the github website, https://github.com/amweins/kidney-models-amw.
GRANTS
This work was supported by National Institute of Diabetes and Digestive and Kidney Diseases Grant R01DK29857.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author.
AUTHOR CONTRIBUTIONS
A.M.W. conceived and designed research; performed experiments; analyzed data; interpreted results of experiments; prepared figures; drafted manuscript; edited and revised manuscript; and approved final version of manuscript.
Footnotes
Throughout this work, “ammonia” and “ammoniagenesis” refer to total ammonia. When NH3 and NH4+ need to be specified, those symbols will be used.
Throughout this work, “fractional excretion” of ammonia will denote the fraction of ammoniagenesis that appears in the urine. Specifically, this is ammonia excretion minus filtered ammonia, relative to total ammoniagenesis.
REFERENCES
- 1.Pitts RF. Production and excretion of ammonia in relation to acid-base regulation. Chapter XX. In: Handbook of Physiology. Section 8: Renal Physiology, edited by Orloff J, Berliner RW.. Washington, DC: American Physiological Society, 1973, p. 455–496. [Google Scholar]
- 2.Tannen RL. Chapter 23: Renal ammonia production and excretion. In: Handbook of Physiology. Section 8: Renal Physiology, edited by Windhager EE. New York: Oxford University Press, 1992, p. 1017–1059. [Google Scholar]
- 3.Denis G, Preuss H, Pitts R. The pNH3 of renal tubular cells. J Clin Invest 43: 571–582, 1964. doi: 10.1172/JCI104942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tizianello A, Garibotto G, Robaudo C, Saffioti S, Pontremoli R, Bruzzone M, Deferrari G. Renal ammoniagenesis in humans with chronic potassium depletion. Kidney Int 40: 772–778, 1991. doi: 10.1038/ki.1991.274. [DOI] [PubMed] [Google Scholar]
- 5.Dejong CHC, Deutz NEP, Soeters PB. Metabolic adaptation of the kidney to hyperammonemia during chronic liver insufficiency in the rat. Hepatology 18: 890–902, 1993. doi: 10.1002/hep.1840180422. [DOI] [PubMed] [Google Scholar]
- 6.Wright G, Noiret L, Olde Damink SWM, Jalan R. Interorgan ammonia metabolism in liver failure: the basis of current and future therapies. Liver Int 31: 163–175, 2011. doi: 10.1111/j.1478-3231.2010.02302.x. [DOI] [PubMed] [Google Scholar]
- 7.Knepper MA, Packer R, Good DW. Ammonium transport in the kidney. Physiol Rev 69: 179–249, 1989. doi: 10.1152/physrev.1989.69.1.179. [DOI] [PubMed] [Google Scholar]
- 8.Buerkert J, Martin D, Trigg D. Ammonium handling by superficial and juxtamedullary nephrons in the rat. Evidence for an ammonia shunt between the loop of Henle and the collecting duct. J Clin Invest 70: 1–12, 1982. doi: 10.1172/JCI110581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Buerkert J, Martin D, Trigg D. Segmental analysis of the renal tubule in buffer production and net acid formation. Am J Physiol Renal Physiol 244: F442–F454, 1983.doi: 10.1152/ajprenal.1983.244.4.F442. [DOI] [PubMed] [Google Scholar]
- 10.Glabman S, Klose RM, Giebisch G. Micropuncture study of ammonia extraction in the rat. Am J Physiol 205: 127–132, 1963. doi: 10.1152/ajplegacy.1963.205.1.127. [DOI] [PubMed] [Google Scholar]
- 11.Nagami GT. Luminal secretion of ammonia in the mouse proximal tubule perfused in vitro. J Clin Invest 81: 159–164, 1988. doi: 10.1172/JCI113287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nagami GT. Enhanced ammonia secretion by proximal tubules from mice receiving NH(4)Cl: role of angiotensin II. Am J Physiol Renal Physiol 282: F472–F477, 2002. doi: 10.1152/ajprenal.00249.2001. [DOI] [PubMed] [Google Scholar]
- 13.Good DW, DuBose TD Jr.. Ammonia transport by early and late proximal convoluted tubule of the rat. J Clin Invest 79: 684–691, 1987. doi: 10.1172/JCI112871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Simon EE, Fry B, Hering-Smith K, Hamm LL. Ammonia loss from rat proximal tubule in vivo: effects of luminal pH and flow rate. Am J Physiol Renal Physiol 255: F861–F867, 1988. [DOI] [PubMed] [Google Scholar]
- 15.Simon EE, Hamm LL. Ammonia entry along rat proximal tubule in vivo: effects of luminal pH and flow rate. Am J Physiol Renal Physiol 253: F760–F766, 1987. [DOI] [PubMed] [Google Scholar]
- 16.Jaeger P, Karlmark B, Giebisch G. Ammonium transport in rat cortical tubule: relationship to potassium metabolism. Am J Physiol Renal Physiol 245: F593–F660, 1983. [DOI] [PubMed] [Google Scholar]
- 17.Wilcox CS, Granges F, Kirk G, Gordon D, Giebisch G. Effects of saline infusion on titratable acid generation and ammonia secretion. Am J Physiol Renal Physiol 247: F506–F519, 1984. doi: 10.1152/ajprenal.1984.247.3.F506. [DOI] [PubMed] [Google Scholar]
- 18.Graber ML, Bengele HH, Mroz E, Lechene C, Alexander EA. Acute metabolic acidosis augments collecting duct acidification rate in the rat. Am J Physiol Renal Physiol 241: F669–F676, 1981. doi: 10.1152/ajprenal.1981.241.6.F669. [DOI] [PubMed] [Google Scholar]
- 19.Sonnenberg H, Cheema-Dhadli S, Goldstein MB, Stinebaugh BJ, Wilson DR, Halperin ML. Ammonia addition into the medullary collecting duct of the rat. Kidney Int 19: 281–287, 1981. doi: 10.1038/ki.1981.18. [DOI] [PubMed] [Google Scholar]
- 20.Stern L, Backman KA, Hayslett JP. Effect of cortical-medullary gradient for ammonia on urinary excretion of ammonia. Kidney Int 27: 652–661, 1985. doi: 10.1038/ki.1985.60. [DOI] [PubMed] [Google Scholar]
- 21.Layton AT, Vallon V, Edwards A. A computational model for simulating solute transport and oxygen consumption along the nephrons. Am J Physiol Renal Physiol 311: F1378–F1390, 2016. doi: 10.1152/ajprenal.00293.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Weinstein AM. A mathematical model of the rat nephron: glucose transport. Am J Physiol Renal Physiol 308: F1098–F1118, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Noiret L, Baigent S, Jalan R, Thomas SR. Mathematical model of ammonia handling in the rat renal medulla. PLoS One 10: e0134477, 2015. doi: 10.1371/journal.pone.0134477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Weinstein AM. A mathematical model of the rat kidney: K+-induced natriuresis. Am J Physiol Renal Physiol 312: F925–F950, 2017. doi: 10.1152/ajprenal.00536.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Weinstein AM. A mathematical model of the rat kidney. II. Antidiuresis. Am J Physiol Renal Physiol 318: F936–F955, 2020.doi: 10.1152/ajprenal.00046.2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Atherton LJ, Maddox DA, Gennari FJ, Deen WM. Analysis of pCO2 variations in the renal cortex. II. Countercurrent exchange. Am J Physiol Renal Physiol 255: F361–F371, 1988. doi: 10.1152/ajprenal.1988.255.2.F361. [DOI] [PubMed] [Google Scholar]
- 27.Gardiner BS, Smith DW, O'Connor PM, Evans RG. A mathematical model of diffusional shunting of oxygen from arteries to veins in the kidney. Am J Physiol Renal Physiol 300: F1339–F1352, 2011. doi: 10.1152/ajprenal.00544.2010. [DOI] [PubMed] [Google Scholar]
- 28.Lee CJ, Gardiner BS, Ngo JP, Kar S, Evans RG, Smith DW. Accounting for oxygen in the renal cortex: a computational study of factors that predispose the cortex to hypoxia. Am J Physiol Renal Physiol 313: F218–F236, 2017. doi: 10.1152/ajprenal.00657.2016. [DOI] [PubMed] [Google Scholar]
- 29.Lee CJ, Ngo JP, Kar S, Gardiner BS, Evans RG, Smith DW. A pseudo-three-dimensional model for quantification of oxygen diffusion from preglomerular arteries to renal tissue and renal venous blood. Am J Physiol Renal Physiol 313: F237–F253, 2017. doi: 10.1152/ajprenal.00659.2016. [DOI] [PubMed] [Google Scholar]
- 30.Olgac U, Kurtcuoglu V. Renal oxygenation: preglomerular vasculature is an unlikely contributor to renal oxygen shunting. Am J Physiol Renal Physiol 308: F671–F688, 2015. doi: 10.1152/ajprenal.00551.2014. [DOI] [PubMed] [Google Scholar]
- 31.Ngo JP, Ow CP, Gardiner BS, Kar S, Pearson JT, Smith DW, Evans RG. Diffusive shunting of gases and other molecules in the renal vasculature: physiological and evolutionary significance. Am J Physiol Regul Integr Comp Physiol 311: R797–R810, 2016. doi: 10.1152/ajpregu.00246.2016. [DOI] [PubMed] [Google Scholar]
- 32.Beeuwkes R III. Efferent vascular patterns and early vascular-tubular relations in the dog kidney. Am J Physiol 221: 1361–1374, 1971. doi: 10.1152/ajplegacy.1971.221.5.1361. [DOI] [PubMed] [Google Scholar]
- 33.Beeuwkes R III. The vascular organization of the kidney. Annu Rev Physiol 42: 531–542, 1980. doi: 10.1146/annurev.ph.42.030180.002531. [DOI] [PubMed] [Google Scholar]
- 34.Beeuwkes R III, Bonventre JV. Tubular organization and vascular-tubular relations in the dog kidney. Am J Physiol 229: 695–713, 1975. doi: 10.1152/ajplegacy.1975.229.3.695. [DOI] [PubMed] [Google Scholar]
- 35.Bankir L, Figueres L, Prot-Bertoye C, Bouby N, Crambert G, Pratt JH, Houillier P. Medullary and cortical thick ascending limb: similarities and differences. Am J Physiol Renal Physiol 318: F422–F442, 2020. doi: 10.1152/ajprenal.00261.2019. [DOI] [PubMed] [Google Scholar]
- 36.Pfaller W. Structure Function Correlation on Rat Kidney: Quantitative Correlation of Structure and Function in the Normal and Injured Rat Kidney. Heidelberg, Berlin: Springer-Verlag, 1982, p. 1–116. [PubMed] [Google Scholar]
- 37.Christensen EI, Grann B, Kristoffersen IB, Skriver E, Thomsen JS, Andreasen A. Three-dimensional reconstruction of the rat nephron. Am J Physiol Renal Physiol 306: F664–F671, 2014. doi: 10.1152/ajprenal.00522.2013. [DOI] [PubMed] [Google Scholar]
- 38.Salathé EP. Mathematical modeling of oxygen transport in skeletal muscle. Math Biosci 58: 171–184, 1982. doi: 10.1016/0025-5564(82)90071-2. [DOI] [Google Scholar]
- 39.Secomb TW, Hsu R. Simulation of O2 transport in skeletal muscle: diffusive exchange between arterioles and capillaries. Am J Physiol Heart Circ Physiol 267: H1214–H1221, 1994. [DOI] [PubMed] [Google Scholar]
- 40.Atherton LJ, Deen WM, Maddox DA, Gennari FJ. Analysis of the factors influencing peritubular pCO2 in the rat. Am J Physiol Renal Physiol 247: F61–F72, 1984. doi: 10.1152/ajprenal.1984.247.1.F61. [DOI] [PubMed] [Google Scholar]
- 41.Weinstein AM. Ammonia transport in a mathematical model of the rat proximal tubule. Am J Physiol Renal Physiol 267: F237–F248, 1994. doi: 10.1152/ajprenal.1994.267.2.F237. [DOI] [PubMed] [Google Scholar]
- 42.Weinstein AM, Krahn TA. A mathematical model of rat ascending Henle limb. II. Epithelial function. Am J Physiol Renal Physiol 298: F525–F542, 2010. doi: 10.1152/ajprenal.00231.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Weinstein AM. A mathematical model of rat distal convoluted tubule (I): cotransporter function in early DCT. Am J Physiol Renal Physiol 289: F699–F720, 2005. doi: 10.1152/ajprenal.00043.2005. [DOI] [PubMed] [Google Scholar]
- 44.Weinstein AM. A mathematical model of rat distal convoluted tubule (II): potassium secretion along the connecting segment. Am J Physiol Renal Physiol 289: F721–F741, 2005. doi: 10.1152/ajprenal.00044.2005. [DOI] [PubMed] [Google Scholar]
- 45.Weinstein AM. A mathematical model of the inner medullary collecting duct of the rat: pathways for Na and K transport. Am J Physiol Renal Physiol 274: F841–F855, 1998. doi: 10.1152/ajprenal.1998.274.5.F841. [DOI] [PubMed] [Google Scholar]
- 46.Weinstein AM. A mathematical model of rat ascending Henle limb. I. Cotransporter function. Am J Physiol Renal Physiol 298: F512–F524, 2010. doi: 10.1152/ajprenal.00230.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lopez-Novoa JM, Rengel MA, Rodicio JL, Hernando L. A micropuncture study of salt and water retention in chronic experimental cirrhosis. Am J Physiol Renal Physiol 232: F315–F318, 1977. doi: 10.1152/ajprenal.1977.232.4.F315. [DOI] [PubMed] [Google Scholar]
- 48.Maddox DA, Atherton LJ, Deen WM, Gennari FJ. Proximal HCO3− reabsorption and the determinants of tubular and capillary pCO2 in the rat. Am J Physiol Renal Physiol 247: F73–F81, 1984. doi: 10.1152/ajprenal.1984.247.1.F73. [DOI] [PubMed] [Google Scholar]
- 49.Weinstein AM. A mathematical model of rat proximal tubule and loop of Henle. Am J Physiol Renal Physiol 308: F1076–F1097, 2015. doi: 10.1152/ajprenal.00504.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Strieter J, Weinstein AM, Giebisch GH, Stephenson JL. Regulation of potassium transport in a mathematical model of the cortical collecting tubule. Am J Physiol Renal Physiol 263: F1076–F1086, 1992. doi: 10.1152/ajprenal.1992.263.6.F1076. [DOI] [PubMed] [Google Scholar]
- 51.Palmer LG, Frindt G. Effects of cell Ca and pH on Na channels from rat cortical collecting tubule. Am J Physiol Renal Physiol 253: F333–F339, 1987. [DOI] [PubMed] [Google Scholar]
- 52.Tizianello A, Deferrari G, Garibotto G, Robaudo C, Acquarone N, Ghiggeri GM. Renal ammoniagenesis in an early stage of metabolic acidosis in man. J Clin Invest 69: 240–250, 1982. doi: 10.1172/jci110436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Good DW, Burg MB. Ammonia production by individual segments of the rat nephron. J Clin Invest 73: 602–610, 1984. doi: 10.1172/JCI111250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Nagami GT. Ammonia production and secretion by S3 proximal tubule segments from acidotic mice: role of ANG II. Am J Physiol Renal Physiol 287: F707–F712, 2004. doi: 10.1152/ajprenal.00189.2003. [DOI] [PubMed] [Google Scholar]
- 55.Weiner ID, Verlander JW. Ammonia transport in the kidney by Rhesus glycoproteins. Am J Physiol Renal Physiol 306: F1107–F1120, 2014. doi: 10.1152/ajprenal.00013.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Weiner ID, Verlander JW. Ammonia transporters and their role in acid-base balance. Physiol Rev 97: 465–494, 2017. doi: 10.1152/physrev.00011.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Weinstein AM, Weinbaum S, Duan Y, Du Z, Yan Q, Wang T. Flow-dependent transport in a mathematical model of rat proximal tubule. Am J Physiol Renal Physiol 292: F1164–F1181, 2007. doi: 10.1152/ajprenal.00392.2006. [DOI] [PubMed] [Google Scholar]
- 58.Simon E, Martin D, Buerkert J. Contribution of individual superficial nephron segments to ammonium handling in chronic metabolic acidosis in the rat. Evidence for ammonia disequilibrium in the renal cortex. J Clin Invest 76: 855–864, 1985. doi: 10.1172/JCI112043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Harris AN, Lee HW, Osis G, Fang L, Webster KL, Verlander JW, Weiner ID. Differences in renal ammonia metabolism in male and female kidney. Am J Physiol Renal Physiol 315: F211–F222, 2018. doi: 10.1152/ajprenal.00084.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Harris AN, Lee HW, Fang L, Verlander JW, Weiner ID. Differences in acidosis-stimulated renal ammonia metabolism in the male and female kidney. Am J Physiol Renal Physiol 317: F890–F905, 2019. doi: 10.1152/ajprenal.00244.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wall SM. NH4 augments net acid secretion by a ouabain-sensitive mechanism in isolated perfused inner medullary collecting ducts. Am J Physiol Renal Physiol 270: F432–F439, 1996. doi: 10.1152/ajprenal.1996.270.3.F432. [DOI] [PubMed] [Google Scholar]
- 62.Wall SM, Koger LM. NH4 transport mediated by Na-K-ATPase in rat inner medullary collecting duct. Am J Physiol Renal Physiol 267: F660–F670, 1994. doi: 10.1152/ajprenal.1994.267.4.F660. [DOI] [PubMed] [Google Scholar]