Resolution of subcomponents of synaptic release from postsynaptic currents in rat hair-cell/auditory-nerve fiber synapses

Eric D Young; Jingjing Sherry Wu (武靜靜); Mamiko Niwa; Elisabeth Glowatzki

doi:10.1152/jn.00450.2020

. 2021 May 5;125(6):2444–2460. doi: 10.1152/jn.00450.2020

Resolution of subcomponents of synaptic release from postsynaptic currents in rat hair-cell/auditory-nerve fiber synapses

Eric D Young ^1,^2,^3,^4,^✉, Jingjing Sherry Wu (武靜靜) ^1,⁴, Mamiko Niwa ^1,³, Elisabeth Glowatzki ^1,^3,^4,^✉

PMCID: PMC8285654 PMID: 33949889

graphic file with name jn-00450-2020r01.jpg

Keywords: EPSC, hair cell, synapse

Abstract

The synapse between inner hair cells and auditory nerve fiber dendrites shows large excitatory postsynaptic currents (EPSCs), which are either monophasic or multiphasic. Multiquantal or uniquantal (flickering) release of neurotransmitter has been proposed to underlie the unusual multiphasic waveforms. Here the nature of multiphasic waveforms is analyzed using EPSCs recorded in vitro in rat afferent dendrites. Spontaneous EPSCs were deconvolved into a sum of presumed release events having monophasic EPSC waveforms. Results include, first, the charge of EPSCs is about the same for multiphasic versus monophasic EPSCs. Second, EPSC amplitudes decline with the number of release events per EPSC. Third, there is no evidence of a mini-EPSC. Most results can be accounted for by versions of either uniquantal or multiquantal release. However, serial neurotransmitter release in multiphasic EPSCs shows properties that are not fully explained by either model, especially that the amplitudes of individual release events are established at the beginning of a multiphasic EPSC, constraining possible models of vesicle release.

NEW & NOTEWORTHY How do monophasic and multiphasic waveshapes arise in auditory-nerve dendrites; mainly are they uniquantal, arising from release of a single vesicle, or multiquantal, requiring several vesicles? The charge injected by excitatory postsynaptic currents (EPSCs) is the same for monophasic or multiphasic EPSCs, supporting uniquantal release. Serial adaptation of responses to sequential EPSCs favors a multiquantal model. Finally, neurotransmitter partitioning into similar sized release boluses occurs at the first bolus in the EPSC, not easily explained with either model.

INTRODUCTION

The synapse between an inner hair cell (IHC) and the dendrite of an auditory-nerve fiber (ANF) is specialized to serve the needs of auditory encoding, which require high rates of discharge and precise timing of neural spikes evoked by acoustic signals (1, 2). In the mature mammalian cochlea, spike timing in ANFs is determined by the timing of single excitatory postsynaptic currents (EPSCs) and thus by the temporal properties of neurotransmitter release from the IHC (3–6). An understanding of the physiology of this synapse is an essential part of a comprehensive description of auditory encoding.

An IHC has several synaptic ribbons that are thought to organize glutamatergic vesicles for high-rate release (7–10). In electron-microscopic examinations, there are multiple vesicles that are apparently in position for immediate release under the ribbon (1, 7, 11) and others associated with the ribbon away from the membrane. Examination of postsynaptic EPSCs in mammalian ANF dendrites has revealed a range of waveforms. EPSCs are either monophasic, with a smooth rise to a single peak followed by a near-exponential decay, or multiphasic, with multiple peaks (12). The latter likely are responses to multiple rapid sequential releases of neurotransmitter (13–15). This range of EPSC waveforms raises the question of the nature of vesicle release, in particular whether it is uniquantal (one synaptic vesicle per EPSC) or multiquantal (12, 15–17). Clearly release is multiquantal in some hair-cell preparations (e.g., frog, Refs. 18, 19; turtle, Ref. 20) and in similar ribbon synapses in rat retinal bipolar cells (21), but the extent of multiquantal release in mammalian cochlear hair cells is still undetermined. Mechanisms by which multiphasic EPSCs could arise from either the release of a single vesicle or the asynchronous release of several vesicles have been proposed (1, 13, 15, 22).

Chapochnikov and colleagues (15) argued for uniquantal release in which the multiphasic EPSCs are produced by “flickering,” rapid opening and closing, of the fusion pore during the release of one vesicle. Their conclusion was based on theoretical arguments supporting the adequacy of uniquantal release to produce the observed EPSCs and on data consistent with univesicular release. These data include capacitance recordings in IHCs (17) and measurement of the charge injected by EPSCs that showed that multiphasic EPSCs inject the same charge into the postsynaptic terminal as monophasic ones (12, 15). While this evidence is compelling, it is based on a relatively small number of recordings.

Here we further analyze the question of the nature of EPSCs using a large database of recordings of spontaneous EPSCs in afferent dendrites of hearing rats. Deconvolution is used to separate the EPSCs into a sum of elementary monophasic events that are assumed to correspond to successive releases of neurotransmitter. From 50% to 79% of EPSCs are monophasic with symmetrical, single-mode amplitude and charge distributions, and the rest are multiphasic. The charge injected by monophasic and multiphasic EPSCs is roughly the same, consistent with previous findings (12, 15), showing that vesicle release is from pools of neurotransmitter of fixed size, implying that a constant number of vesicles (one or more) is released for each EPSC. The properties of EPSC amplitudes are also consistent with the fixed-pool model. However, analysis of the details of serial neurotransmitter release in multiphasic EPSCs show that the neurotransmitter pool is divided into multiple subunits at the beginning of the EPSC, a property that is not fully explained by either uniquantal or multiquantal models.

MATERIALS AND METHODS

Experimental Methods

All aspects of the animal preparation were approved by the Johns Hopkins Animal Care and Use Committee. The data used here overlap with data previously reported (Refs. 6, 12; Table 1). Experimental methods are detailed in the original papers (4, 12). Briefly, Sprague-Dawley rats of either sex and ages between postnatal day (P) 17 to 31 were deeply anesthetized with isoflurane and decapitated. The cochleae were removed, and the apical cochlear coil was placed in a recording chamber in extracellular solution (in mM: 5.8 KCl, 144 NaCl, 0.9 MgCl₂, 1.3 CaCl₂, 0.7 NaH₂PO₄, 5.6 glucose, 10 HEPES, pH 7.4, adjusted with NaOH, and 300 mosmol/H₂O). The bath temperature was 22–25ºC. The preparation was viewed using differential interference contrast optics, which allowed ANF dendritic terminals on IHCs to be visualized. Intracellular recordings from single dendritic terminals were obtained in whole cell patch-clamp configuration using Sylgard (Dow-Corning)-coated pipettes of resistance 11–15 MΩ. The series resistance was not compensated and was estimated post hoc as described (4). In brief, the capacitance current in response to a 10-mV voltage step is fitted with a sum of two exponential equations. The series resistance is calculated by back extrapolating of the exponential fit to the beginning of the current step. The estimated series resistance ranged from 30 to 65 MΩ in six experiments and was ∼200 MΩ in two others (experiments E and F in Table 1). The decay times were not different in the experiments with high series resistances (Fig. 3; experiments E and F in Table 1), although the amplitudes and areas of EPSCs were smaller by ∼30% compared with the median of the six low-series resistance experiments. Other than that, the properties of the recordings were not correlated with series resistance.

Table 1.

Summary of the 8 experiments

Experiment	Age, days	[K⁺]	TTX	EPSC Rate, /s	#EPSCs	Monos	Multis	Fraction Monos	Decay Time, ms
A	17	5.8		11	1,840	1,141	699	0.62	1.3
B	20	15	TTX	2.1	1,384	1,100	284	0.79	1.3
H	31	5.8		58	19,362	14,605	4,757	0.75	1.0
C	29	5.8		15	5,132	3,441	1,691	0.67	0.8
D	30	15	TTX	45	12,305	6,212	6,093	0.50	1.0
T	28	15	TTX	18	11,849	6,056	5,793	0.51	1.0
E	26	15	TTX	4.5	3,024	1,791	1,233	0.59	1.2
F	26	15	TTX	9.4	6,334	3,290	3,044	0.52	1.1

Open in a new tab

The experiments are identified in the column 1 and match Figs. 5 and 7, A, B, C, D, E, and F, along with H and T, which match Figs. 4 and 6. Total numbers of excitatory postsynaptic currents (EPSCs) are given, as well as the number of monophasic and multiphasic EPSCs. Kernel decay time is time from 90% to 10% of maximum value, as in Fig. 3. The K⁺ concentration in the bath solution is in column 3. Tetrodotoxin (TTX) was present in 5 experiments in column 4. Experiments B and H were used in previous publications (6, 12).

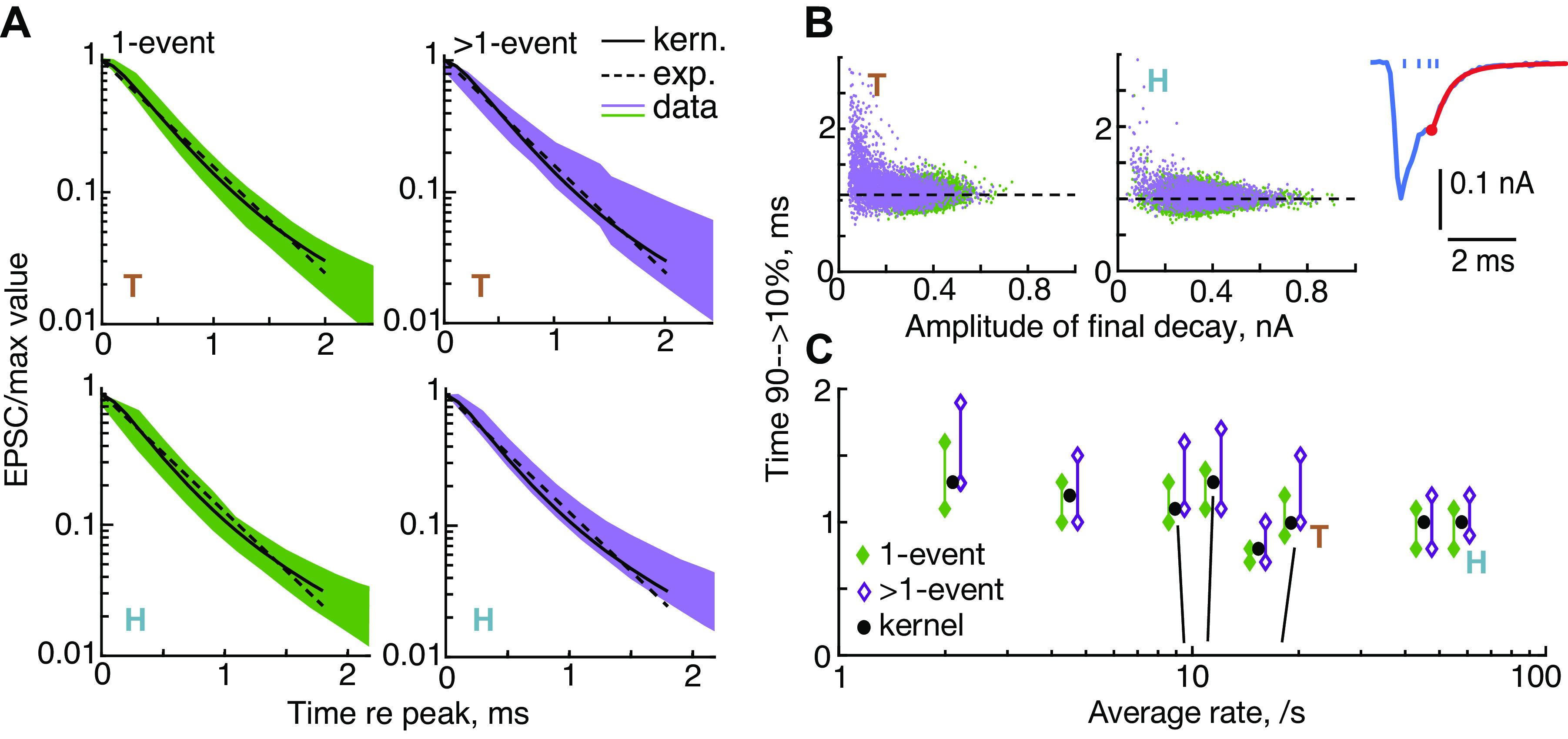
Figure 3. — Evidence for linearity: the decay times of excitatory postsynaptic currents (EPSCs) vary little across EPSCs. Times for the EPSC to decay from 90% to 10% of its peak value were estimated from the final decay in the EPSC (the red portion of the EPSC in *B, inset*, starting at the red circle; the ticks show the calculated event times). A: final decays are plotted from *experiments T* (*top row*) and H (*bottom row*), separately for monophasic (1-event) EPSCs (*left column*, green) and multiphasic (>1-event) EPSCs (*right column*, purple). The waveforms are normalized to the beginning of the final decay and inverted for plotting. Solid black lines show the decay of the kernel and the green and purple bands show the 10th to 90th percentiles of the population. The dashed lines show the best single-exponential fits to the kernel. B: final decay times vs. event amplitudes for all EPSCs in *experiments T* and H; 1 event (green) and >1 event (purple). Dashed lines are the decay times of the kernels (1.08 and 0.97 ms). C: mean decay times for 8 experiments, plotted against the average rate of EPSCs. Each pair of points shows the 10th and 90th percentiles of the values for individual EPSCs. For clarity, the data for experiments with rates between 8 and 20/s are separated slightly along the x-axis. The correct rates are indicated by the black near-vertical lines. A best fit of decay time vs. log rate (slope –0.101, R² = 0.32, P = 0.08). exp., Exponential; kern., kernel.

The electrophysiological properties of afferent boutons were similar to those described previously (12): capacitance: ∼1 pF; membrane time constant: ∼0.5 s; and membrane resistance: ∼400 MΩ. The pipette solution contained the following (in mM): 20 KCl, 110 K-methanesulfonate, 5 MgCl₂, 0.1 CaCl₂, 5 EGTA, 5 HEPES, 5 Na₂ATP, 0.3 Na₂GTP, 5 Na₂ phosphocreatine, pH 7.2, adjusted with KOH, and 290 mosmol/H₂O, except for two experiments (experiments A and B in Table 1), which used 135 KCl, 3.5 MgCl₂, 0.1 CaCl₂, 5 EGTA, 5 HEPES, 0–4 Na₂ATP, and 0–0.2 Na₂GTP, pH 7.2, adjusted with KOH, 290 mosmol/H₂O. In five out of eight recordings, EPSCs were recorded in the presence of tetrodotoxin (1–2 µM; R&D Systems, 1069/1); see Table 1. The cells were voltage clamped (pCLAMP 9.2 or 10.2 software and a Multiclamp 700 A or 700B amplifier, Molecular Devices) at holding potentials between −99 and −84 mV. Membrane current was digitized at 50 kHz sampling rate (Digidata 1322 A; Molecular Devices), low-pass filtered at 10 kHz, and recorded for further analysis. The data consist of long runs (up to 600 s) of EPSCs recorded in 8 experiments (Table 1).

There was no explicit stimulation of the hair cells, except that in some experiments the extracellular solution contained an elevated potassium concentration (15 mM in 5 cases; 3 others had the normal 5.8 mM; Ref. 23), with a corresponding decrease in sodium concentration. This was done to guarantee that the hair cells in these preparations had resting membrane potentials near in vivo values, necessary to produce spontaneous neurotransmitter release (12, 24, 25). To check the IHC potentials, intracellular recordings were performed from 10 IHCs in a P24 preparation. The pipette solution for the IHC recordings contained the following (in mM): 145 KCl, 0.1 CaCl₂, 5 HEPES, 1 EGTA, 1 MgCl₂, 2.5 Na₂ATP, pH 7.41, adjusted with KOH, and 300 mosmol/H₂O. In 5.8 mM K⁺, the IHC membrane potential was −60.4 (SD 7.4) mV, and in 15 mM K⁺ it was −40.5 (SD 12.0) mV; this range covers the likely in vivo values (25). The average rate of EPSCs varied from 2 to 58/s in different experiments (Table 1). There was no systematic difference between the EPSC rates at the two potassium concentrations [see also Grant and Glowatzki (12)]; across the experiments, the median steady-state rates were 15.3/s (5.8 mM) and 10.2/s (15 mM), respectively (NS, rank sum).

The data analyzed in this paper come from the eight experiments summarized in Table 1. Each experiment consists of the recording from a single auditory-nerve dendrite, and each was done in a different preparation. These were cases in which the experimental preparation and the properties of the EPSCs were stable through the entire recording period. Holding currents (between 0 and −150 pA) were often constant, although sometimes they slowly drifted up or down by up to 50 pA. Sudden jumps in holding current were not seen, except in one experiment (B in Table 1) where a –65-pA jump occurred. This experiment was included, as no changes in the properties of EPSCs were observed near the jump. The properties reported here were similar across all experiments, except as noted in results. There were fluctuations in rate during each recording, like those described previously in loose-patch recordings (Ref. 6; Fig. 2) and in vivo extracellular recordings in the auditory nerve (e.g., Ref. 26). These were not accompanied by changes in EPSC amplitude or other characteristics. In particular, the EPSC properties derived by deconvolution did not show long-term trends in any experiment. All experiments were evaluated for stability by plotting the variables studied (rate, number of events/EPSC, amplitude and area of EPSCs, decay time constants, and fraction of monophasic EPSCs) versus time in a diary style plot. These varied by <15%. Note that rate was not systematically controlled or evaluated, e.g., with a time-varying stimulus.

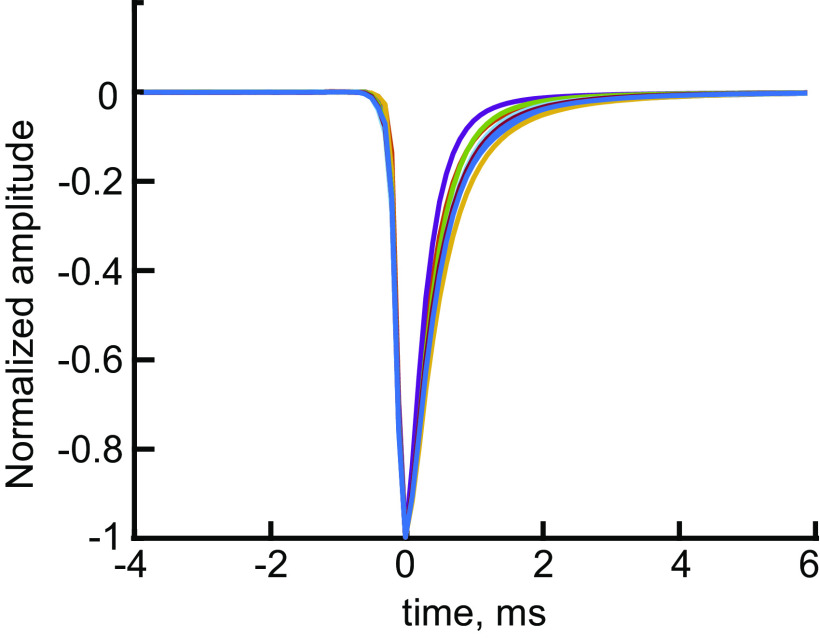
Figure 2. — Kernel waveforms for the 8 experiments show similar shapes, with slightly different decay times. Kernels derived by averaging monophasic excitatory postsynaptic currents (EPSCs). These are k(t) in *Eq. 1*. The kernels rise rapidly to a peak over a fraction of a ms (0.2–0.26 ms, median 0.24 ms) and have similar decay times (Table 1 and Fig. 3C).

Data from five additional experiments were analyzed but not included here. In three of these experiments, substantial changes (>40 pA) and sudden jumps in holding current and the properties of EPSCs occurred during the recording time, suggesting damage to the preparation. The data in two other experiments showed unusually high numbers of multiphasic EPSCs (>50%), and they had properties that were similar to the three damaged preparations mentioned above. All five excluded data sets also showed substantial differences between the time constants of monophasic and multiphasic EPSCs in terms of decay time constant (as explained in Fig. 3), not typical of the eight included experiments. This behavior suggests substantial nonlinearity in the EPSCs, which means that the assumptions necessary for the analysis do not hold for these experiments.

Analysis

EPSC recordings were downsampled from 50 kHz to 10 kHz using the Matlab resample() function. This function first low-pass filters the data with an antialiasing filter (cutoff frequency 5 kHz) and then resamples. The filtering and resampling reduce noise in the data (∼10 dB), by eliminating high-frequency noise components. Resampling does not change the wave shapes or amplitudes of the EPSCs, which have low-pass spectra with cutoff frequencies ≈2.5 kHz. Reducing the sampling rate is also convenient because it reduces the time required for the model-fitting calculations described below. Two experiments were reanalyzed using 20-kHz resampling, with no change in the qualitative results.

EPSCs occur as isolated signals separated by periods of baseline (examples in Fig. 1A). EPSCs were delimited by setting a threshold (typically −15 to −30 pA relative to the baseline), estimated by manually scrolling through the data, looking for a threshold that did not exclude the smallest EPSCs. These thresholds are not limited by the baseline noise; the ratio of the EPSC threshold to the root mean squares value of the baseline noise is 9.3 to 15.7 in eight experiments, median 13.6. EPSCs were then defined as compact regions where current was more negative than the threshold. EPSC definition was done once crudely to allow baseline zeroing and then again after baseline correction. The black bars in Fig. 1A show the EPSC extents resulting from thresholding. To ensure that small EPSCs were not missed, the waveforms of the largest currents remaining in the data record after EPSC detection and removal were displayed; if these waveforms seemed to be EPSCs based on their waveforms and durations, the threshold for EPSC detection was adjusted. The number of such waveforms was small (<100 in data sets with thousands of EPSCs).

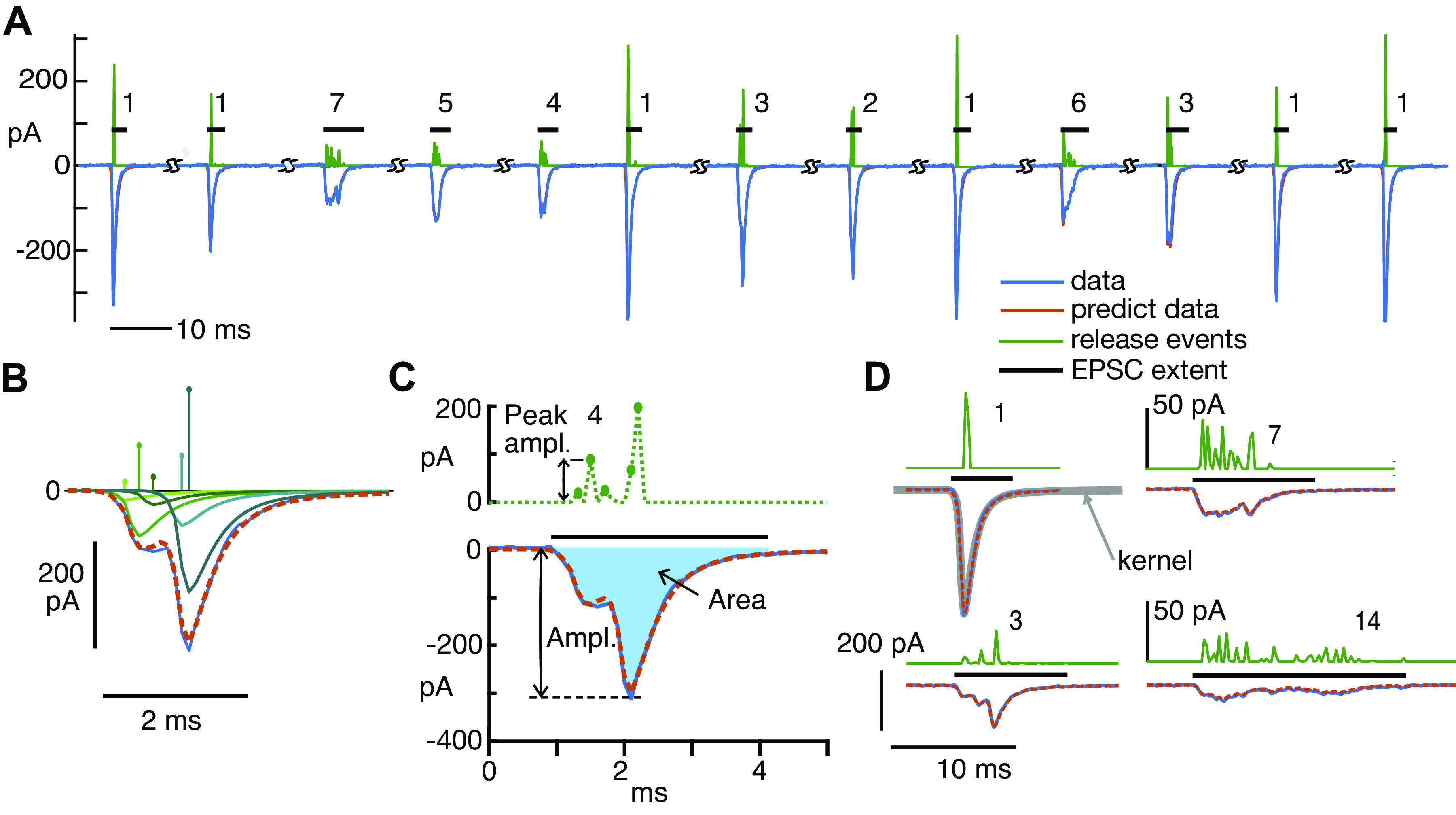
Figure 1. — Deconvolution analysis of monophasic and multiphasic excitatory postsynaptic currents (EPSCs) provides an estimate of the number of release events in each. A: 13 examples of EPSCs (blue negative waveforms), the sequence of kernels producing the best fitting event sequences (whose amplitudes and times are shown by the green positive waveforms), and the fits calculated from the event sequences (red, mostly hidden behind blue). The EPSCs are shown in the order in which they occurred in 1 experiment, except that segments of baseline have been removed, where marked (SS). The numbers are the numbers of events (defined in the text) in the fit of the EPSC. The horizontal black bars show the nonzero extent of each EPSC. B: detailed view of 1 EPSC (blue negative trace) and the calculated fit (overlying dashed red trace), with the 5 kernels in the fit waveform plotted separately below to show how they sum to approximate the EPSC. The kernel amplitudes (*a_j* in *Eq. 1*) and times of occurrence (*t_j*) are plotted as impulses above. The kernels are greenish in color, with hues coded to match the amplitudes. C: the same EPSC as in B. The peak amplitude of the EPSC (“Ampl.”) and the area (“Area,” filled with blue) are marked. The dashed green waveform at *top* is the event sequence as in B, except plotted as dots connected with dashed lines to emphasize that there are zero values in between most of the events. Immediately adjacent events are gathered together in classifying EPSCs, as described in the text. Thus there are 4 events in this fit, and the last 2 nonzero kernels are combined into 1 event. D: expanded view of four EPSCs with calculated event sequences and fits, labeled by the number of events in the fit. The event sequences (but not the waveforms) for the examples at *right* (7 and 14 events) are expanded vertically by a factor of 4 for clarity, note the different scale bars. The kernel used for all parts of D is shown by the gray line overlying the monophasic EPSC (labeled “1,” *top left*). Note that the kernel closely overlies the waveform of this monophasic EPSC. In fact, the variance of the monophasic waveforms was very small; they generally varied only in amplitude.

In the raw data, the baseline between EPSCs was equal to the holding current and showed slow variations through a recording. To set the baseline to zero, the portions of the data record remaining after excluding EPSCs were fit with a smooth function computed by averaging non-EPSC points in overlapping 10-ms windows and interpolating (linearly) to the sampling rate. The resulting interpolated function was an estimate of the baseline and was subtracted from the data record, including during the EPSCs, to set the baseline to zero. Note that this method does not modify the EPSC waveforms.

To analyze the EPSCs, each was approximated as a sum of elementary waveforms, called the kernel below. The majority of EPSCs are monophasic (Table 1), and these monophasic EPSCs have very similar waveforms, with different amplitudes. We assumed that the waveform of monophasic EPSCs is the kernel, which was estimated by averaging monophasic EPSCs, after normalizing them to an amplitude of −1. EPSCs were included in the average only if they were preceded and followed for 10 ms by baseline, i.e., no nearby EPSCs, and not part of an overlapping pair of EPSCs. Multiphasic waveforms were manually edited out of the average by superimposing all apparently monophasic waveforms (normalized to the same maximum amplitude and aligned on their peaks) in an interactive display and then setting limits on the waveforms included. Most (median 89%) of the waveforms ultimately determined to be monophasic in the data were included in the averages, which were only slightly different in different experiments, mainly in the decay time (Table 1, column 10; Fig. 2).

In terms of this averaged kernel waveform, k(t), an EPSC can be approximated by the following:

\hat{e} (t) = \sum_{j = 1}^{J} a_{j} k (t - t_{j}) .

(1)

The estimated EPSC ê(t) is the sum of J kernels with amplitudes a_j and occurrence times t_j (actually the time of the minimum of the kernel, time 0 in Fig. 2). An example of such a sum is shown in Fig. 1B where the EPSC (negative blue trace) is fit by the red dashed waveform, which is the sum of the green kernels. The lines in Fig. 1B, top, show the amplitude a_j of each kernel; they are located at the kernel’s time delay t_j. Each EPSC e(t) was fit individually by such a sum by choosing J and the amplitudes {a_j} and times {t_j} so as to minimize the squared error between the EPSC waveform and ê(t). The error is given by

E = \sum_{t = t_{o}}^{t_{1}} {(\hat{e} (t) - e (t))}^{2} + λ \sum_{j = 1}^{J} | a_{j} | .

(2)

The first term in E is the squared difference between the EPSC e(t) and the fit function ê(t) from Eq. 1. The difference is computed over a time range [t₀, t₁] which is the extent of the EPSC determined by thresholding (the black bars in Fig. 1A), extended by 2 ms in both directions. The baseline extension is done to include baseline adjacent to the EPSC, which provides a zero reference that forces the DC term in the fit to 0, consistent with Eq. 1, which does not have a constant term. Because the data are noisy, the squared difference component of E can always be minimized by increasing J, the number of kernels, up to the limit of one kernel in each sampling time increment. However, as more small kernels are added, they are likely fitting noise in the data. The second term in the error is designed to avoid this by penalizing the addition of more kernels. This method, called lasso (27), allows the addition of another kernel to the sum (increasing J and adding another a_j-sized kernel at time t_j) only if it reduces the squared error (first term in Eq. 2) more than it increases the penalty, equal to the sum of the kernel amplitudes multiplied by λ (second term in Eq. 2). The penalty term increases as more kernels are added.

The parameter λ sets the relative importance of the squared-difference and the penalty. Increasing λ reduces the number of kernels at the cost of an increase in squared error. The Matlab function lasso() was used to fit each EPSC individually. λ was set to the value at which the squared error exceeds its minimum by 1 SE (estimated by 5-fold cross-validation). As shown by the examples in Fig. 1, the errors in the fits are small (but not as small as they could be with no penalty). The accuracy of the fit can be measured by the relative root-mean-square error, equal to the root-mean-square error divided by the root-mean-square EPSC value. The relative error was 0.0087 (median across experiments) for monophasic EPSCs (J = 1) and 0.0034, 00033, and 0.0028 for EPSCs with J = 2, 3, and >3. The fact that the error for multicomponent fits (J > 1) is small supports the validity of the assumptions in Eq. 1.

This calculation is a form of deconvolution; different approaches to this problem for the hair-cell/auditory-dendrite synapse are described by Andor-Ardó et al. (28) and Chapochnikov et al. (15) and for cerebellar synapses by Malagon et al. (29). Andor-Ardó and colleagues (28) use a blind method in which the kernel is inferred from the data with minimal assumptions. The other papers use a kernel equal to monophasic EPSCs, as was done here. This requires the assumption of linear summation of a fixed kernel, but has the advantage of resembling the actual physiology of the recordings. The lasso method was used here instead of standard Wiener deconvolution to provide a principled way to minimize small noise components in the results. Previous approaches have done the same de-noising using template matching on the final result (29). Ultimately all these methods give the same result, which is finding a sum of kernels that closely matches the EPSC waveform.

In the body of the paper, the kernels making up a fit are called events. These events are assumed to correspond to releases of boluses of neurotransmitter. To classify EPSCs according to the number of presumed neurotransmitter releases they contain, events were counted, except that kernels located in adjacent time samples were combined into one event (as in Fig. 1C), under the assumption that they represent a release event spanning the two bins. Usually, events contain one kernel except when combined in this way. Thus the EPSC in Fig. 1C is classified as having four events, even though it contains five kernels. The event counts shown in Fig. 1, A and D, are calculated in this way.

In many cases, there are one or more very small events. An example is the sixth EPSC in Fig. 1A, in which there is one very small event evident in the green trace. Because such small events may represent noise, the small events are not counted in classifying the EPSC, in cases where the areas of small events are less than 0.03 times the area of the event sequence. Thus in the example in Fig. 1A, the sixth EPSC is labeled as having one event. The results seem reasonable in terms of the shapes of the EPSCs; for example, EPSCs with J = 2 kernels in the fit, with one very small one, usually have waveforms that are essentially the same as monophasic EPSCs. None of the results described here are dependent on this reclassification, except in minor quantitative details. To check its effect, the threshold was raised to 0.1. At this threshold the median fraction of EPSCs modified by removing a small event was 0.07 (range 0.03 to 0.12 in 8 experiments).

Figure 1D shows two EPSCs that were fit with very large numbers of events (7 and 14). It is not possible to estimate the number of events just by looking at the waveform of either EPSC (negative blue traces). The green event traces show the events clearly, including their locations. Both illustrate the results of applying the classification rules discussed in the previous paragraph; note that there are more than 7 and 14 bumps in the 2 event traces.

EPSC Overlap

Because spontaneous EPSCs occur randomly in time, on some occasions EPSCs overlap partially (discussed further in Figs. 4–7). The degree of overlap was checked by simulating EPSC trains with the same rates as these data sets. The simulations generated EPSCs at random interevent intervals (a Poisson process with the same rate as the data provided exponentially distributed interevent intervals) and random EPSC areas drawn from the same distribution as monosynaptic EPSCs in the data. The waveform for EPSCs was the kernel for that experiment. The resulting trains of EPSCs were analyzed with the same algorithms used for the data giving the area histograms shown in black in Fig. 6, A and B, and Fig. 7C. At the rates observed here, overlap in the simulation was infrequent (13% of EPSCs for the highest EPSC rate, 58/s, less for the others).

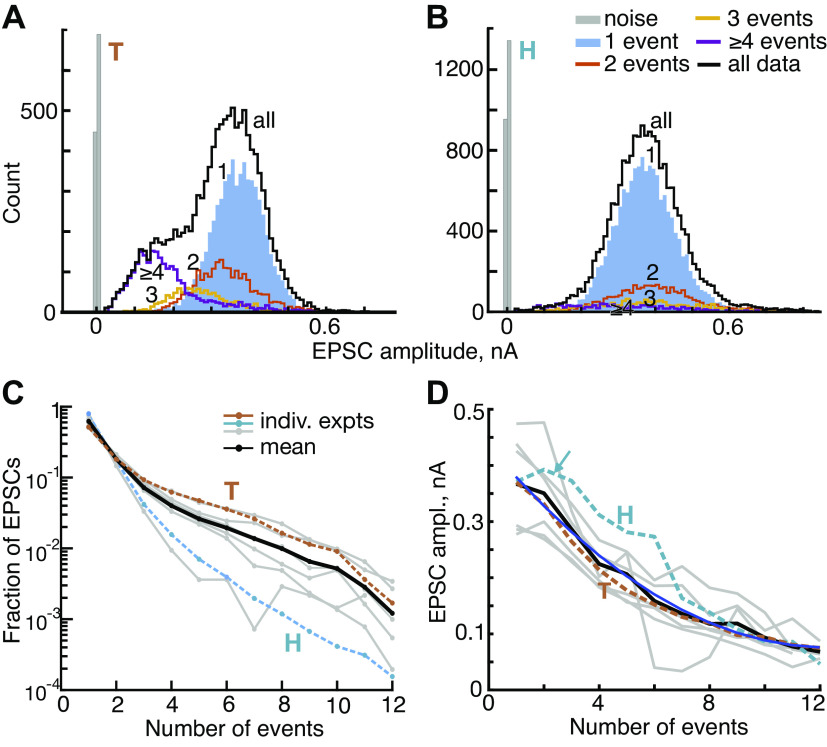
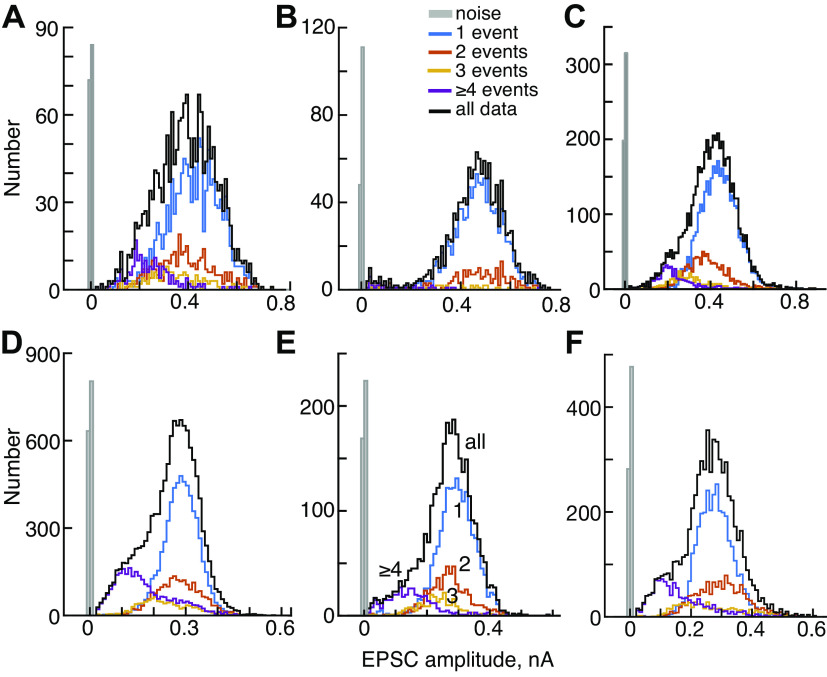
Figure 4. — Amplitudes of excitatory postsynaptic current (EPSC) decrease with the number of events in the EPSC waveform. A and B: histograms of EPSC amplitudes for *experiments T* and H. EPSCs with 1, 2, 3, and ≥4 events are plotted separately (legend in B). The black histograms show all the data and the gray histograms show noise. In the data for H, the 3 and ≥4 histograms are scaled up by 2 times to make them visible. The amplitudes were measured at the largest negative value of the EPSC. C: the fraction of EPSCs with various numbers of events for 8 experiments (gray and colored lines) and the mean (black). EPSCs with 1 event (monophasic) are most numerous, and the number decreases rapidly and monotonically as the number of events increases. Note that the ordinate is logarithmic. D: mean values of EPSC amplitude vs. the number of events in the EPSC for 8 experiments and the overall mean. The decrease is clear (blue quadratic line, R² = 0.99, P << 0.001). The arrow points out an exception to the monotonic decrease for *experiment H*. ampl., Amplitude; indiv. expts, individual experiments.

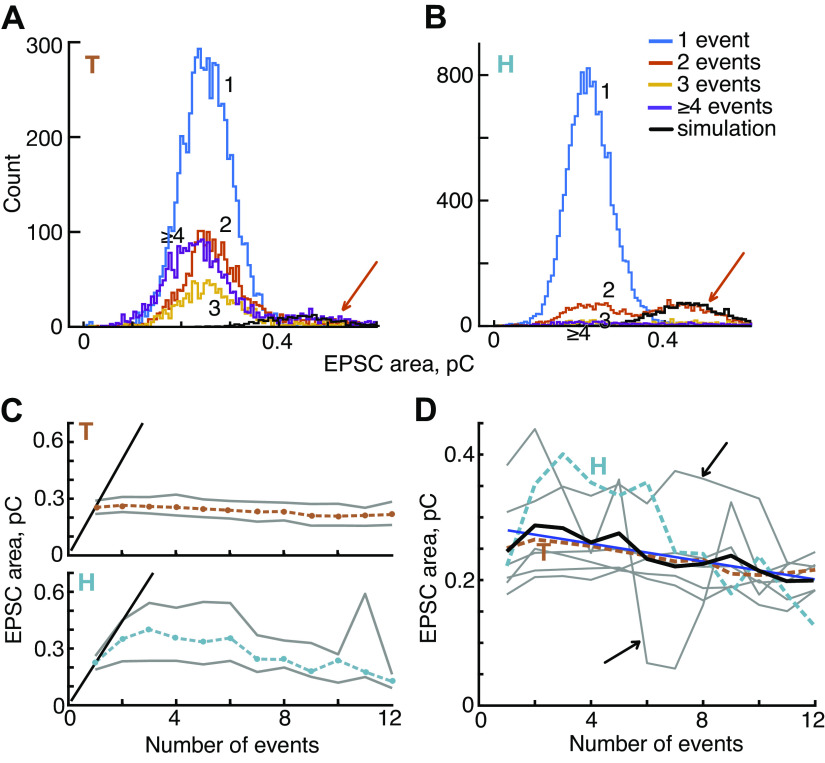
Figure 6. — Excitatory postsynaptic currents (EPSC) area declines slightly as the number of events in the EPSC increases. A and B: histograms of EPSC areas for 2 example experiments. Most experiments are similar to T in that areas show a roughly normal distribution which is similar for different numbers of events. In both figures, the histogram for 2-event EPSCs (orange) shows a noticeable second peak (orange arrow) at the expected place if these EPSCs represent overlap of EPSCs from 2 releases of neurotransmitter occurring close together (see text). The black lines show the tail distributions computed using this assumption. C: plots of the mean area (dashed colored lines) plus and minus 1 SD (gray lines) vs. the number of events in the EPSC for T and H. The diagonal black lines at *left* are the expected behavior if multiple-event EPSCs result entirely from overlapping 1-event EPSCs, so that area increases linearly with the number of events. D: mean EPSC area vs. event number, for 8 experiments (gray and colored lines, as in Fig. 4D); the mean of the 8 experiments is the black line. The data show small but significant declines in area as event count increases (blue line, R² = 0.68, P = 0.004). Two experiments (black arrows) have few EPSCs for 5 and more events, so are noisy.

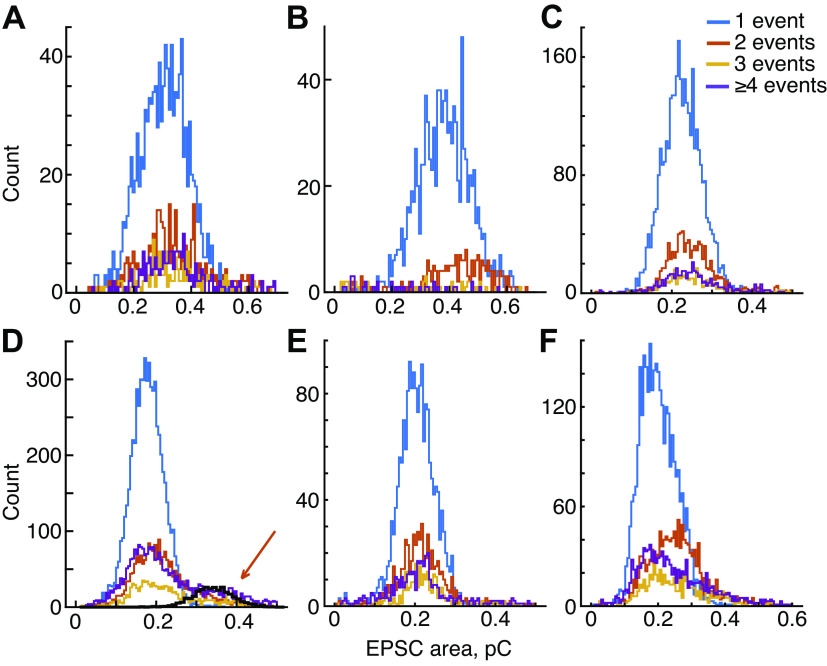
Figure 7. — A–F: distributions of excitatory postsynaptic current (EPSC) area for s6 additional experiments (arranged in the same order as Fig. 5). The distributions for multievent EPSCs usually center around a mean similar to the 1-event histogram, except for B and F. D: data from an experiment with high EPSC rate (45/s); as for *experiment H*, there is a secondary peak in the 2-event distribution at the place predicted by the simulation of overlapping EPSCs (heavy black plot, orange arrow).

EPSCs with overlaps have larger areas than nonoverlapped EPSCs (discussed in Figs. 6 and 7), so that area can be used to detect overlapped EPSCs for elimination. When this is done, it does not change the results reported here, except that it eliminates the effects of overlaps, described in Figs. 4D, 6, and 7, on the data from experiments H, T, and D. Because the error rate of the area-doubling detector is relatively large (theoretically 5–17% of EPSCs misclassified) and to provide an accurate description of the actual data, overlap elimination was not done for any of the data shown.

Amplitude, Area, and Statistics

The amplitudes of kernels a_j have units pA. The kernel itself is always normalized to have maximum amplitude −1, so is dimensionless. The areas of EPSCs and events are expressed as charge. For EPSCs, this is computed straightforwardly as the sum of the EPSC currents (the blue area in Fig. 1C) multiplied by the sampling time increment (0.1 ms) yielding units of coulombs. For events, the kernel amplitude (a_j) is multiplied by the sampling time increment and by the area of the dimensionless kernel (mean 7.10, SD 0.89, for 8 experiments). The result is the charge (C) delivered by that kernel. The charge of an event is the sum of its kernel charges. The sum of the event charges is approximately the same as the overall EPSC charge, as it must be from Eq. 1.

Statistical tests on the data are described as they are used. Usually nonparametric methods were used (ranksum); trends in the data were evaluated with least-squares line-fitting and cross correlation. Statistics were calculated with routines in the Matlab statistics toolbox: ranksum(), corr(); models were fit using fitnlm() and evaluated with the coefficient of determination R², i.e., the fraction of variance predicted by the model. R² was adjusted for the number of coefficients in the fit.

Linearity in the Deconvolution of EPSCs

The analytical approach used here assumes that an EPSC is a linear sum of currents (Eq. 1) produced by releases of boluses of neurotransmitter (the kernels). Because neurotransmitter receptor kinetics contain nonlinearities and nonstationarities in that rate constants depend on the concentration of neurotransmitter and the state of the receptor molecule (e.g., Refs. 30, 31), there is reason to question whether EPSC generation is as linear as assumed.

A necessary condition for nonstationarity, which may also detect nonlinearity, is based on the decay time of the EPSCs. This time is sensitive to changes in the open-state rate constants of the receptor molecules. The simplest time constant to measure is that associated with the final decay of the EPSC, after the last release event. In the linear summation model, that decay should be the same as the decay of the kernel, because the EPSC decay is the sum of one or more decaying kernels (Fig. 1B). An example of the final decay is shown by the red tail on the EPSC inset in Fig. 3, top right. Final decay is defined here as the decay of the EPSC after the last event.

The EPSC decays are remarkably similar. Figure 3A shows decay waveforms from two example experiments (called experiment T and H in all subsequent figures). The waveforms are inverted and normalized by the current at the beginning of the final decay (i.e., the current at the red dot in the inset of Fig. 3). The colored bands show the region occupied by all the waveforms between the 10th and the 90th percentiles of the population at each time point. The solid black lines show the decay of the kernel waveforms from these two experiments. The decays are plotted on a log ordinate, so a single exponential decay is a straight line. The dashed black lines show the exponential that fits best the decay of the kernel. Both the kernels and the individual EPSCs (colored bands) are seen to be multiexponential, because their waveforms are not straight lines in this plot. For eight experiments the median values of the first two decay time constants of the kernel are 0.50 ms and 1.47 ms. Because they are multiexponential [see also Häusser and Roth (31)], the decays are quantified in the rest of the figure and in Table 1 as the time required to decay from 90% to 10% of the peak amplitudes (median value 1.0 ms across 8 experiments). Using the kernel decays as a reference for comparison, it is clear that the decay times are very similar for monophasic EPSCs (left column of Fig. 3A, left, green) and multiphasic EPSCs (Fig. 3A, right, purple) for both experiments T and H.

The effect of current amplitude is shown in Fig. 3B where 90-10 decay time is plotted against the amplitude of the EPSC at the final event (the current at the red dot in the inset). There is no effect of amplitude, except for very small amplitudes, where the decay times cover a broad range. However, at small amplitudes, the decay waveforms are strongly affected by baseline noise currents and it seems likely that the broadening of the time constant range represents noise in the measurement rather than a systematic effect.

The results for experiments T and H are typical of all eight experiments (Fig. 3C) in that the kernel decay time is similar to the decay times from both monophasic and multiphasic EPSCs. There is a weak dependence of decay time on average EPSC rate, (for decay time versus log rate, R² = 0.32 P = 0.08). This marginal effect may reflect variability of experimental conditions from experiment to experiment, such as temperature (Ref. 6; Fig. 5C).

Figure 5. — A–F: amplitudes of excitatory postsynaptic currents (EPSCs) of 6 additional experiments. Histograms of EPSC amplitudes, plotted as in Fig. 4, A and B. These are mostly similar to Fig. 4A in that distributions move toward lower amplitudes for larger number of events. In all cases, the low-amplitude EPSCs are mostly or entirely multiphasic waveforms (event numbers ≥4).

The behavior shown in Fig. 3 is a necessary condition for the linearity assumption to be valid. In the five experiments not included in this analysis, the decay times were different for monophasic and multiphasic EPSCs, suggesting the existence of nonlinearities in those experiments.

Despite the result in Fig. 3B, there was a small tendency for the halfwidth of monophasic EPSCs to increase as the amplitude of the EPSCs increases (0.02–0.1 ms in 8 data sets). This broadening of EPSCs might reflect a small nonlinearity in the receptor kinetics or an effect of series resistance in the electrode. However, given the constancy of the decay time constant in Fig. 3B, it seems more likely that this effect is due to a slight asynchrony of the neurotransmitter boluses as the amount of transmitter increases. Consistent with asynchrony, the rise time of EPSCs also becomes longer at larger EPSC amplitudes, by roughly the same amount and rise time is correlated with halfwidth (median correlation: r = 0.29, interquartile range: 0.25–0.33, in 8 experiments). Because these changes are quite variable and small (less than the sampling interval 0.1 ms), they are not considered further.

RESULTS

EPSCs were recorded in the apical turn of isolated rat (P17 to P31) cochleas, in vitro. We used data from patch voltage-clamp recordings on the dendritic terminals of ANFs contacting IHCs. EPSCs occurred without explicit stimulation, except for depolarizing the IHC membrane potential with 15 mM potassium in the extracellular solution in five out of eight experiments. In the preparations analyzed here, EPSCs were adult-like in their properties, meaning the range of spontaneous rates and the interevent-interval properties are as described by Wu et al. (6) in the oldest preparations (approximately P20 and older). Data from eight experiments (Table 1) containing between 1,384 and 19,362 EPSCs are included; the average rates of EPSCs ranged between 2 and 58/s (see Ref. 6, Fig. 3).

Measuring EPSC Waveforms

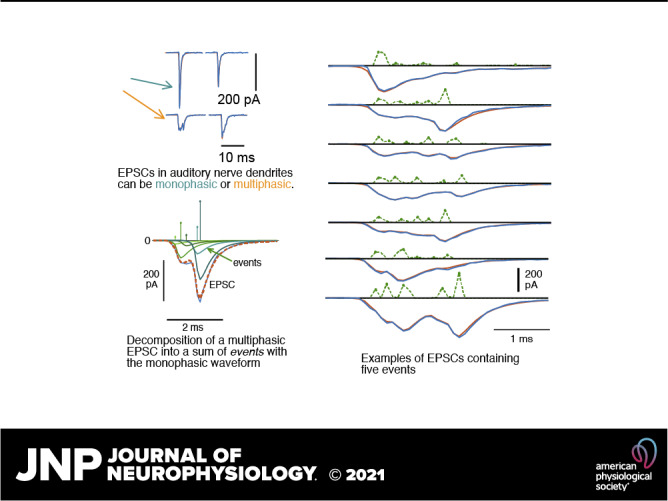
Examples of EPSCs are shown by the negative-going blue waveforms in Fig. 1A. EPSCs in this preparation show a variety of amplitudes and shapes, as illustrated here (12, 13). These range from “monophasic” waveforms with a single peak (the examples labeled “1”) to complex “multiphasic” ones (multipeak waveforms labeled with numbers >1). The shapes of the multiphasic EPSCs suggest that they might represent a summation of monophasic waveforms occurring asynchronously over the duration of the EPSC. Under this hypothesis, the monophasic waveform represents the release of a single bolus of neurotransmitter. The bolus could be from all or part of one synaptic vesicle or from the simultaneous release of several vesicles. The analysis makes no a-priori assumptions about which.

The shape of the monophasic EPSC (here called the kernel, Fig. 2) reflects all the dynamics of generating the EPSC, including neurotransmitter release, diffusion to the postsynaptic membrane, binding to the receptors, and channel gating. We assume that multiphasic EPSCs are the result of asynchronous release of differently sized packets of neurotransmitter, each of which is subject to the same dynamics, producing the same monophasic waveform; these monophasic waveforms summate linearly to produce the multiphasic waveforms (Eq. 1, Fig. 1B). To analyze these waveforms, deconvolution was used to estimate the set of monophasic waveforms (kernels) making up a multiphasic EPSC (Fig. 1B; see materials and methods for details). The computation finds the set of kernels, in terms of their amplitudes and times of occurrence, that provides the best fit to the EPSC waveform, subject to the constraint that the smallest possible number of kernels should be used (lasso method, Ref. 27). The deconvolution results in a series of impulses (the green positive signals in Fig. 1) located at the times of kernel occurrences (releases of boluses of neurotransmitter) with amplitudes equal to the amplitudes of the kernels (Figs. 1, C and D; see also Refs. 15, 32). The kernel waveforms are computed by averaging monophasic EPSCs in the data record, as described in Methods. The kernels are slightly different in different datasets (Fig. 2).

Figure 1B illustrates the deconvolution of an EPSC into five kernels (called “events”). The events are shown as impulses, vertical lines whose time and height are the kernel time and amplitude. The corresponding kernel waveforms are plotted below, with the EPSC waveform (blue) and the sum of the kernels (red dashed). Figure 1C shows the deconvolution result for the same EPSC as in Fig. 1B, now with dashed lines connecting the kernel amplitudes and the sample points with no kernel in between. Generally, the kernels are isolated with zeros in between, as in the first three in this example. However, there are often nonzero values at successive (adjacent) sample times (spaced by 0.1 ms here); in the analysis below, these are assumed to form a single event for the sake of classifying EPSCs (as in the 4th and 5th kernels in Figs. 1C). Of course, how the events are parsed makes no difference to the calculation of the fit or its accuracy. The amplitude of an event is the sum of the kernel amplitudes contained within it.

The measures used to characterize EPSCs are shown in Fig. 1C, bottom. EPSCs are characterized by: 1) the number of events in the EPSC, determined as described in the previous paragraph; 2) the EPSC amplitude (the current at the negative minimum of the EPSC); and 3) the area of the EPSC (the region shaded blue) multiplied by the sampling increment. This product is the total charge delivered to the terminal by the EPSC. The use of charge is supported by data from dual recordings showing that postsynaptic EPSC charge is proportional to the presynaptic capacitance change in a prolonged depolarization of the hair cell, a direct measure of the amount of neurotransmitter released (18). Moreover, charge is a measure of the postsynaptic excitation that will be produced by the EPSC, because for brief currents, the EPSC charge flows mainly into the membrane capacitance, which has the effect of depolarizing the membrane by an amount proportional to the charge.

Across the range of EPSC rates (Table 1 and Fig. 3C), most EPSC properties are similar. This includes their amplitudes and areas, the fraction of monophasic versus multiphasic EPSCs, and the number of release events within multiphasic EPSCs. One property of EPSCs, the decay time, is weakly correlated with rate, shown in Fig. 3C.

EPSCs Are Mostly Monophasic; Multiphasic EPSCs Are Smaller in Amplitude

The number of events in the best fit to an EPSC provides a way to characterize its qualitative nature (monophasic versus multiphasic for example). In Fig. 1, A and D, the green positive waveforms show the event sequence calculated as described above for that EPSC. The numbers next to each EPSC give the number of events in the signal. Note in Fig. 1A that the largest-amplitude EPSCs are monophasic and the multiphasic EPSCs are smaller in amplitude, especially those with more than four events. This is expected, for example, if each EPSC represents the release of a fixed (except for random variation) total amount of neurotransmitter, so that the amplitude of a multiphasic EPSC is reduced by desynchronization in the release process.

EPSCs most commonly show monophasic waveforms, 50–79% in the eight experiments analyzed here (Table 1). In Fig. 4C, the fraction of monophasic EPSCs is shown separately (gray and dashed colored plots) for each experiment and as an average across all experiments (black). Note that the ordinate of this plot is scaled logarithmically to show the small numbers of EPSCs containing larger numbers of events. Although monophasic waveforms predominate, there is a surprisingly large number of multiphasic EPSCs, different from most synapses.

In this and subsequent figures, data from two experiments are identified with brown (experiment T) and cyan (experiment H) dashed lines. These two experiments were chosen because T is typical of the population in all measures, whereas H is an outlier in some measures. These data sets have large numbers of EPSCs (11,849 and 19,364, respectively) and derive from very stable recordings. Experiment H has the highest EPSC rate (58/s) and also contains the second largest fraction of monophasic waveforms (75%), whereas T has a medium EPSC rate (18/s) and contains 51% monophasic waveforms.

The distributions of EPSC amplitudes are shown for the two example experiments in Fig. 4, A and B, for all EPSCs and EPSCs having one, two, three, and at-least four events (see legend). The mean EPSC amplitude decreases with the number of events in the EPSC, seen clearly by the leftward shift of the distributions of experiment T. The same trend holds in the data from experiment H but is less apparent because of the small number of multievent EPSCs. Nevertheless, the mean amplitudes decline, usually monotonically, with the number of events in the EPSCs in all experiments (Figs. 4D and 5).

Note that the mean amplitudes of EPSCs having two and three events are larger than the amplitudes of monophasic EPSCs for experiment H (cyan arrow). The reason for this is discussed in the next section.

The amplitude distributions in Fig. 4, A and B, and Fig. 5 do not show evidence of mini-EPSCs, meaning a peak in the monophasic distribution at small amplitudes. The traditional analyses of the amplitudes of multiquantal EPSCs or EPSPs is based on summation of various numbers of simultaneously released vesicles, and this model assumes a monophasic waveform shape for a single-vesicle release (the mini-EPSC). However, the monophasic EPSCs (blue histograms labeled “1”) have a symmetric Gaussian-like distribution of amplitudes with no small-amplitude peak. The overall amplitude distributions (black lines labeled “all”) may have a tail that extends toward zero amplitude (7/8 experiments, H being the exception). However, these low-side tails are always multiphasic EPSCs, clearly shown by the experiment T in Fig. 4A and five others (Fig. 5). A multiphasic mini-EPSC is inconsistent with the usual models of synapse function.

EPSC Area Declines Only Slightly as Event Number Increases

To test the hypothesis that EPSCs containing different numbers of events result from asynchronous release of neurotransmitter from a pool of fixed size (e.g., a single vesicle or a fixed number of vesicles), and not recruitment of different sized release pools (e.g., different numbers of vesicles), we examined the areas of EPSCs. The area is equal to the charge delivered by an EPSC and is a measure of the total neurotransmitter received by the synapse, assuming that no nonlinear effects occur. Thus, under the assumption of a fixed pool of transmitter, the area should be constant regardless of the number of events in an EPSC (12, 15). This expectation is approximately realized in the data. Distributions of the EPSC area are shown in Fig. 6, A and B, for the two example experiments. The areas are shown separately according to the number of events per EPSC (1, 2, 3, and ≥4, see the legend). In all eight experiments (Fig. 6, A and B, and Fig. 7), the areas of monophasic EPSCs (the blue histograms labeled “1”) are symmetrically distributed with a single mode. The coefficient of variation (SD divided by the mean) of these histograms varies between 0.21 and 0.27 (median 0.24) for the eight experiments, a finding similar to those obtained in other synapses (1).

Experiment T is typical of most of the data in that the distributions of areas are similar for various numbers of events, with roughly the same mean values. However, on close inspection, the mean values usually decline slightly when plotted against the number of events, as for experiment T in Fig. 6C, top.

If multiphasic EPSCs result from multiquantal release, and each event corresponds to a vesicle, then the corresponding area histograms should have mean values that increase with the number of events in the EPSC. This should give the multiphasic-EPSC area histogram a right-side tail. Such a tail is clearly shown in Fig. 6B by the two-event histogram (orange) (for experiment H, at areas > 0.35, orange arrow); another example is shown in Fig. 7D. Such tails are largest in experiments, like these two, with high rates of EPSC production. They occur when two EPSCs occur closely enough together to overlap; if two EPSCs are sufficiently close, then the waveforms will partially merge and the algorithm for defining EPSCs will classify them as part of the same EPSC, with two or more events. The resulting composite EPSC has an area twice as large as isolated EPSCs; it may also have a larger amplitude, depending on the degree of overlap (e.g., the cyan arrow in Fig. 4D for experiment H). To test this idea, the two-event area histogram expected from such overlaps was calculated from the one-event histogram and an exponential interevent (time) interval histogram (6); the result corresponds well to the upper tail of the observed two-event histogram (the black lines in Fig. 6B and Fig. 7D, see also Refs. 15, 33). A small upper tail is also seen in experiment T (Fig. 6A).

The plot of mean area for experiment H in Fig. 6C, bottom, shows clearly this effect of waveform overlap in that the mean area for two- through six-event EPSCs exceeds the mean for one-event EPSCs substantially (by up to 1.8). The black diagonal lines in Fig. 6C, left, show the location of the data predicted if the area of EPSCs is proportional to the number of events in the waveform, which is the expected behavior if the larger areas reflect release from a larger neurotransmitter pool (e.g., as many vesicles as there are events in the EPSC). The data from experiment H lie well below the black diagonal line, consistent with the generation of such EPSCs from a mixture of mostly true two-event releases and a few that are the overlap of adjacent one-event EPSCs. The decrease of the area for larger numbers of events is expected because of the low likelihood of many EPSCs occurring close enough in time to overlap. Consistent with this interpretation of the right-side tails, elimination of overlapping EPSCs, as described in materials and methods, abolishes the elevated areas of experiment H in Fig. 6, C and D, (not shown). Because the algorithm for elimination of overlaps has a high error rate and distorts the properties of EPSCs, we have not eliminated overlapping EPSCs in any of the data shown in this paper.

The difference in behavior between experiments H and T for two- and three-event EPSCs is striking. The T experiment also shows right-side tail distributions, but the number of EPSCs in those tails is small and has little effect on the mean areas. The mean area curves computed from eight experiments (Fig. 6D) are mostly similar to the result for experiment T: there is a small but steady decline of area with event count. Two experiments had few EPSCs at larger numbers of events, and their plots are quite variable (black arrows), but still show a general decrease with event number. The overall mean across all eight experiments (black line) shows the same trend, a small decrease of area with event number (but still significant R² = 0.68, P = 0.004). Thus the data support previous results suggesting that each EPSC, whether mono- or multiphasic, has a similar net charge, consistent with the presynaptic release of about the same amount of neurotransmitter. The small decrease in area for multiphasic EPSCs still needs explanation.

Lack of Serial Dependence of the Event Numbers

Figure 1 shows an apparently random ordering of the numbers of events in subsequent EPSCs. However, serial order effects are often observed in hair-cell and ANF activity (6, 34, 35), and it is worthwhile to look for similar effects on the synchrony of release. There is not a serial dependence of the number of events in an EPSC, as measured by the conditional mean event-number in the nth EPSC, given the event-number in the (n-1)^th EPSC (Fig. 8A, R² = −0.09, NS, line-fit not shown). The conditional mean event count (ordinate) is normalized by the overall mean count in the same experiment, to deemphasize differences in mean count among experiments. This lack of dependence was confirmed by computing the mutual information between the event numbers for successive pairs and triples of EPSCs; this measure is very small (median 0.02 bits, NS) meaning that there is no information in the previous one or two EPSCs about the number of events in an EPSC. There is also no effect of the amplitude or area of an EPSC on the event number in the following EPSC (not shown).

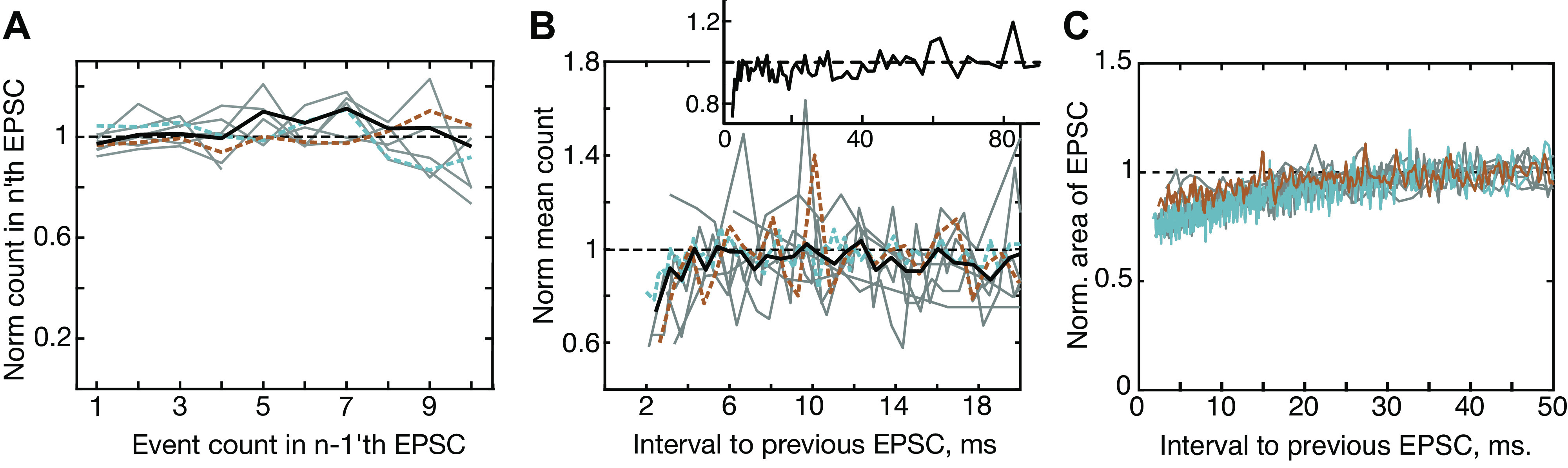
Figure 8. — Serial dependence between event counts in successive excitatory postsynaptic currents (EPSCs) is not seen, but event count and EPSC area decrease slightly for closely spaced EPSCs. A: conditional mean counts in an EPSC plotted against the event count in the previous EPSC. Plots are shown for 8 experiments (gray or colored, as in Figs. 4D and 6D) and the overall mean (heavy black line, slope not significant, R² = –0.09, line fit not shown); the counts are normalized (Norm.) by the overall mean count in the same experiment. B: normalized mean event count plotted against the interval to the previous EPSC, for pairs with the first EPSC having only 1 event. The count is reduced slightly for EPSCs that follow a previous EPSC closely (< 6 ms). The normalization is done by dividing by the mean count of the pairs with inter-EPSC intervals >40 ms in the same experiment. The heavy black line is the mean across experiments and the *inset* shows the mean on a longer time axis. The mean at intervals <10 ms is well fit by an exponential with time constant 0.57 ms (SE ± 0.28 ms). C: the area of EPSCs also decreases at short inter-EPSC interval. Area is normalized by dividing by the mean area for pairs with inter-EPSC intervals >30 ms. The data are well fit by an exponential with time constant 15.3 ms (SE ± 0.5 ms). For amplitude, the result is similar, with time constant 12 ms (SE ± 0.4 ms).

Two rather weak serial dependence phenomena are observed in these data. First, the number of events per EPSC is smaller for EPSCs occurring at short intervals (less than ∼6 ms) following a previous EPSC (Fig. 8B). The decrease in event count occurs through an increase in the fraction of monophasic EPSCs (from 68% to 88%, averaged across 8 experiments) and also a decrease in the mean event counts of multiphasic EPSCs (from 3.3 to 2.7). EPSCs are longer in duration for larger event numbers, because of the asynchronous occurrence of neurotransmitter releases. Because this lengthening constrains the possible interevent intervals, the analysis in Fig. 8B was done using only pairs of EPSCs in which the first EPSC has one event, so is as short as possible. Repeating the analysis with all pairs gave the same result as in Fig. 8B. The count is again normalized across experiments by dividing by the mean event counts for intervals >40 ms from the same experiment. The dip in event number at short intervals amounts to ∼0.5 event on an absolute scale (without normalization). The recovery of event count appears to show two phases, a fast phase that lasts around 6 ms, shown in the main part of Fig. 8B, and a slower phase that is not fully recovered until ∼40–50 ms, shown by the inset, which is the same mean data on a longer time scale.

The second serial-dependence phenomenon is that the area and amplitude of EPSCs decreases slightly for EPSCs spaced closer than 20 ms (shown for area in Fig. 8C).

Event Organization within EPSCs

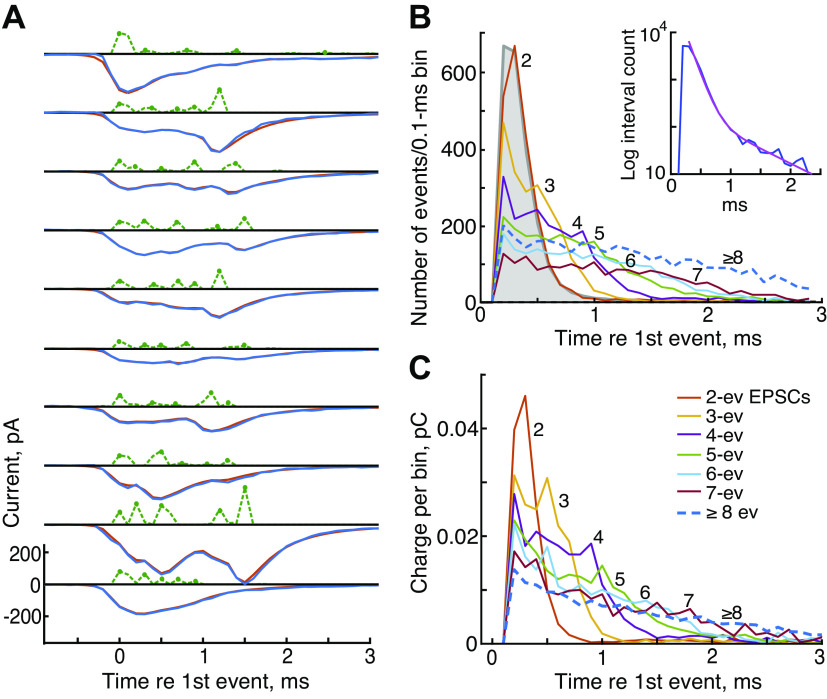
If EPSCs containing different numbers of events draw from roughly constant-sized pools of neurotransmitter, it is interesting to ask how that pool is divided up among the events in the EPSC. This includes both the timing and the charge-contents of the events. Figure 9A shows 10 examples of EPSCs (blue negative signals from experiment T) containing five events (green positive signals) and the calculated best-fitting model EPSCs (red, mostly occluded by the blue plots), plotted as in Fig. 1C. There is a diversity of patterns of events, both in terms of amplitudes and occurrence times, which is typical of the data.

As expected, the events are spread out over the duration of the EPSC. Figure 9B shows histograms of the event times averaged across all the EPSCs in experiment T containing two or more events. Time zero is the time of the first event in the EPSC, but the numbers of first events are not shown because they are perfectly aligned and so off-scale. In two-event EPSCs (red-orange histogram labeled “2”), the second events occur centered around a single discrete maximum near 0.35 ms. In EPSCs with more events, indicated by the color code (legend in Fig. 9C and numbers next to the curves), the events are spaced out over longer times; the total duration of the EPSC grows with the number of events. This result is complementary to that shown in Fig. 4D: as the number of events increases, they spread out in time, leading to less summation of events and smaller EPSC amplitudes.

A histogram of all the interevent intervals (regardless of event number) from experiment T is shown by the gray histogram in Fig. 9B. The histogram rises rapidly from zero to a mode near 0.3 ms and then decays with time, from 90% to 10%, over 0.34 ms (median 0.34 ms across 8 experiments). The decay is multiexponential, shown on a logarithmic ordinate in the Fig. 9B, inset. A two-exponential fit to the decay (the magenta line) has time constants 0.13 and 0.74 ms. The exponential decay shown in Fig. 9B, inset, is consistent with a random occurrence of events and not with a regular, clock-like occurrence. There is an apparent refractory period following the first event, in that the gray histogram has zero events in the bin at 0.1 ms, but any refractory period is very short in duration, one time bin or a fraction of a bin, and is too short to be measured at the time resolution used here, especially with the rule for combining adjacent kernels into one event.

Figure 9B shows only the times of occurrence of events, not the amplitudes. A more useful measure of EPSCs is the amount of charge injected into the postsynapse at various times. This is shown in Fig. 9C, which plots the average profile of charge injection in experiment T obtained by summing the event waveforms (like the green plots in Fig. 9A), across all EPSCs with a given number of events, and converting the result to charge in the 0.1-ms bins of this histogram. The charge delivered by individual events is computed as the product of the event amplitude (current), the sampling increment, and the dimensionless area of the kernel (see materials and methods). Again, time zero is the time of the first event. The summed currents in the first events are again off-scale and not plotted. The charge curves decrease significantly as the number of events in the EPSC increases, as they must, given the constant area result of Fig. 6.

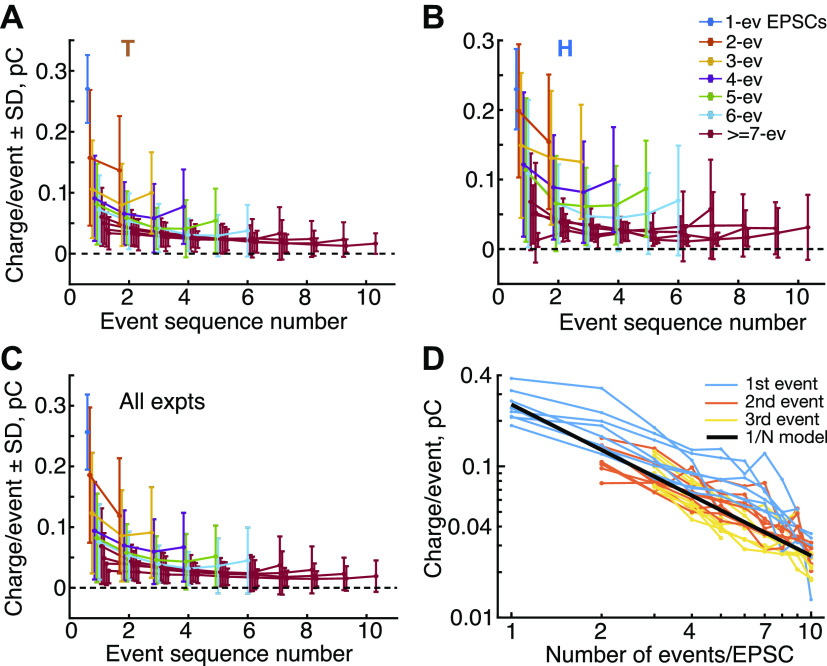
The charges delivered by events in EPSCs with different event counts are shown in Fig. 10; this figure shows averages (with SDs) of the charge injected by each event plotted against the sequence number of the event. Estimates are shown for experiments T (Fig. 10A) and H (Fig. 10B) along with the average across all eight experiments (Fig. 10C). Each plot shows data from EPSCs with different numbers of events (legend in Fig. 10B). Consistent with the variability illustrated in Fig. 9A, the SDs of each point are large, generally about equal to the mean. The variability is partially produced by the variation in EPSC amplitude (Fig. 4, A and B), which amounts to ∼40% of the SD, based on the reduced error-bars after normalization of each EPSC’s data by its area, Additional variability derives from variation in the event size within an EPSC (Fig. 9A).

The average charge shows a shallow U shape through the EPSC, declining for early events and increasing for events near the end of the EPSC. That is, the first and last events tend to be larger than the events in between. More important, the charges get smaller as the number of events in the EPSC increases. Note that as the number of events increases, the decrease in charge is already apparent on the first event, on the first data point at left in each plot. This suggests that the amplitude of the boluses of neurotransmitter released in an EPSC is somehow determined at the beginning of the EPSC, as if the neurotransmitter is divided into smaller packets, which are then released in sequence.

The size of the smaller packets is hard to see in Fig. 10, A, B, and C. Figure 10D shows (blue lines) the charges of the first events in EPSCs plotted against the number of events in the EPSC; each line is from one of the eight experiments. These are like the first data points in Fig. 10, A, B, and C. A simple behavior would be for the neurotransmitter to be divided into equal packets, so that the charges in the first events would decrease as 1/N, for EPSCs with N events. This idealized behavior is shown by the heavy black line which is (total charge)/N. For this line the “total charge” is the mean charge injected by monophasic (1-event) EPSCs. The blue lines are above the black line for EPSCs with two or more events. This means that a larger amount of neurotransmitter is released in the first event of a multiphasic EPSC than is predicted by equipartition of the monophasic EPSC

For comparison, the orange and yellow lines show the same analysis for the second and third events in the EPSC. These are close to the inverse-N model, suggesting that equipartition holds for these events. As can be inferred from Fig. 10, A and B, later events are smaller than the heavy black line, until the last one or two events in each sequence are larger again (not shown in Fig. 10D).

DISCUSSION

The Analysis

The results show that EPSCs in rat ANF dendrites can be resolved into a sum of individual release events consisting of current waveforms (kernels) having the same wave-shape as monophasic EPSCs. We assume that the release events correspond to pulsatile releases of boluses of neurotransmitter. The waveform of the kernel is determined by the cumulative transformation between the release of a pulse of neurotransmitter and the current in the afferent dendrite. It includes the diffusion of transmitter in the cleft, receptor binding, and receptor gating kinetics. This decomposition allows EPSCs to be classified by the number and asynchrony of the presumed release events making them up and thereby provides a quantitative measure of monophasic and multiphasic EPSCs. The data show that multiphasic EPSCs are a minority fraction of the total but may account for as many as 50% of the EPSCs in some preparations (Fig. 4 and Table 1). This is generally consistent with previous results in the same preparation (12), where the classification of mono- versus multiphasic was done by eye.

The analysis assumes that the kernels summate linearly to produce an EPSC, requiring the assumption that the receptors are not saturated. Evidence of saturation was not observed, although direct tests of saturation were not done. However, the model fits uniformly well across the range of EPSC amplitudes; moreover the time constant of EPSC decay does not change with amplitude (see materials and methods and Fig. 3B). Thus the changes in waveform expected with saturation of responses to large neurotransmitter release were not observed. In principle, saturation can occur also for small events (Ref. 24; Fig. 3). Low-level saturation was not seen, although this conclusion is less certain because of noise in small EPSCs.

Are the EPSCs Multiquantal?

In this analysis, multiphasic EPSCs result from the rapid sequential occurrence of individual smaller release events, whereas monophasic EPSCs result from a single synchronous release. This behavior raises the question of whether the release is multiquantal, representing synchronous (monophasic) or asynchronous (multiphasic) release of multiple vesicles (13, 14, 18) or uniquantal, resulting from a single vesicle. With uniquantal release, multiphasic EPSCs would result from flickering of the fusion pore, producing multiple partial releases of the vesicle’s contents (15, 17).

In the present data, the most important observation is that the releases generating an EPSC are made from a constant (except for random variation) pool of neurotransmitter. This conclusion is suggested by two features of the data: First, multiphasic EPSCs are smaller in amplitude than monophasic EPSCs, both individual events (Fig. 10, A, B, and C) and the overall EPSCs (Fig. 4, A and D). This behavior is consistent with sharing a fixed pool of neurotransmitter by dividing it into smaller aliquots. Second, the total charge delivered by an EPSC, as measured by its area, is roughly constant, decreasing slightly as the number of events increases (Fig. 6D; see also Refs. 12, 15). The area (charge) of an EPSC is linearly related to the amount of neurotransmitter released, as judged by presynaptic capacitance measurements (18). Thus, within a single recording, EPSCs of all types seem to result, on average, from the same total amount of neurotransmitter release; by this is meant that the amount of neurotransmitter is, on average, the same and does not increase as the number of events in the EPSC increases. A constant neurotransmitter release could come about either from uniquantal release or from multiquantal release in which the average number of quanta released per EPSC is fixed.

Uniquantal release as proposed by Chapochnikov et al. (15) seems consistent with most of the data in this paper. This mechanism assumes some variability in the fusion pore to explain the occurrence of mono- and multiphasic EPSCs. The randomness of the presumed flickers (Fig. 9, A and B) suggests a process in which open fusion pores are unstable, so that multiphasic EPSCs are produced by a variable and random sequence of openings. Recently the stability of fusion pores in CNS synapses has been shown to depend on the number of SNARE proteins recruited for the pore (36, 37); a similar mechanism might apply to the IHC pore. Flickering might also result from a negative feedback interaction in the presynaptic release, such as inactivation of the presynaptic Ca channels when a fusion pore opens (22).

Whatever the mechanism of flickering, it must be flexible enough to account for the range of partitions of the vesicle contents observed in the data (Fig. 10), from the entire vesicle for a monophasic EPSC, to a number of partitions ranging up to a value of 10 or more in these data. An important property of that partition is that it occurs on the first opening and is maintained (except for random fluctuation) throughout the EPSC (see also Ref. 15; Fig. 8E). It is not clear, for example, whether a mechanism like variability in the SNAREs recruited to form the fusion pore could produce the multiple possible partition sizes.

An additional question about uniquantal release is how the serial-dependence properties of EPSCs (Fig. 8) arise. The phenomena in Fig. 8, B and C, have time constants similar to those of synaptic depression (24, 38–40), and the effect shown in Fig. 8C represents a weakening of synaptic transmission, similar to synaptic depression. Depression seems to be mainly due to synaptic-vesicle depletion in this synapse, although there may be a small contribution of receptor desensitization (39, 41). Anatomical studies show the presence of ≈10 vesicles docked at the membrane under the synaptic bar (11, 42), apparently in position for release. Assuming that these represent independent release sites with a low enough probability of release that usually only one site releases at a time (for a uniquantal EPSC), then the serial dependence of release asynchrony (Fig. 8B) and the adaptation of EPSC charge (Fig. 8C) are hard to explain. Presumably, parallel release sites should release independently and thus should not show serial dependence. That is, the only release site that should show the effects in Fig. 8, B and C, is the one site that released on the previous EPSC. Given that there are multiple apparent release sites in a synaptic bar, it is not clear that the same site would release again and again, which seems to be necessary for uniquantal release and the effects in Fig. 8, B and C.

Multiquantal release is also consistent with much of the data, as long as the release is highly coordinated across release sites, so that the number of sites releasing is constant from EPSC to EPSC. Then small asynchrony in release times could produce multiphasic EPSCs with roughly constant area. Such a release model requires some mechanism, like cooperativity among release sites, to synchronize the releases and generate the constant release number. However, there must be enough randomness in the release times that multiphasic EPSCs are possible, i.e., there must be enough randomness to account for patterns like those in Fig. 9A These ideas were explored in a preliminary way with a hair cell synaptic model similar to those used by Peterson et al (35) and Andor-Ardó et al. (32). The model contains multiple parallel release sites driven by a common signal, presumably calcium. The synchronization of release across sites was produced by adding to the model strong cooperativity, in which release from one site increases the probability of release at other sites. With a delicate adjustment in the cooperativity strength, it is possible to achieve enough randomness in the release to produce results similar to Figs. 9 and 10 but not so much that the number of sites releasing varies from EPSC to EPSC, in which case the constant-EPSC-area constraint is violated. This fussiness of the model makes its results unconvincing.

It is useful to compare the present data on the rat hair-cell synapse with the properties of EPSCs in other ribbon synapses where the transmitter release is clearly multiquantal, e.g., ANF dendrites in the turtle (20) and frog (14, 18, 19, 28) and the retinal bipolar cell (21). The present data differ from these in two important ways. First, multiquantal-release synapses have mini-EPSCs that correspond to uniquantal release events. These are monophasic and are uniform in size and shape. In the usual theory used to describe EPSPs, mini-EPSCs serve the role of the kernel in the present analysis: larger EPSCs are constructed by increasing the number of vesicles released, thereby summing the mini-EPSCs. However there is no convincing evidence for mini-EPSCs in the present data set. In particular, there are very few monophasic EPSCs with small amplitudes (Figs. 4, A and B, and Fig. 5, blue histograms) or areas (Fig. 6, A and B, and Fig. 7) that would be suitable candidates for uniquantal mini-EPSCs. Indeed, the smallest amplitude EPSCs are mostly multiphasic in the data analyzed here (e.g., the histogram for ≥4 event EPSCs in Figs. 4 and 5), clearly inappropriate for a mini-EPSC.

The conclusion in the previous paragraph is tentative, because it may be necessary to reduce probability of release by a manipulation that lowers the calcium flux into IHCs to isolate mini-EPSCs (18, 43). That manipulation was not done in these experiments, in which the hair cells’ resting potentials were near the values seen in vivo (see materials and methods). If recordings are performed in IHCs at fairly negative membrane potentials (approximately equal to −70 mV; Ref. 33), spontaneous EPSC rate is near zero, presumably because of a lack of calcium flux into IHCs (12, 25, 43). In this condition, compared with recordings with more depolarized IHCs, EPSCs tend to have smaller amplitudes and area as well as a low number of events per EPSC, and some of these small and fast events have the expected shape of mini-EPSCs.

The second difference between the present data and the multiquantal EPSCs of Li et al. (18) is in the histograms of EPSC amplitudes (Fig. 4) or areas (Fig. 6). Multiquantal amplitude histograms have a substantial tail on the large-amplitude side of both distributions (18, 21, 28). This large-amplitude multiquantal tail, of course results from the mixture of EPSCs containing different numbers of quanta. Similar tails are observed here in EPSC area distributions, but only with overlapping of EPSCs in high-rate data sets like experiment H (Fig. 6B), as discussed previously.

There is a small decline in the area of EPSCs with larger numbers of release events (Fig. 6D); this is a robust phenomenon, observed in all experiments. It seems to reflect some loss of neurotransmitter through a multievent release. Chapochnikov and colleagues (15) argued against receptor desensitization as a mechanism for these declines, using modeling. Receptor desensitization also seems inconsistent with 1) the randomness of event sizes and the occurrence of larger release events near the end of multiphasic EPSCs as in some of the examples in Fig. 9A; and 2) the upturn in average release event size near the end of multiphasic EPSCs in Fig. 10, A, B, and C; that is, there is no evidence of a monotonic decline of event size during the EPSC, as would be produced by desensitization. Instead one is led to consider mechanisms like failure to release some fraction of the neurotransmitter during an extended release (as occurs in the “kiss-and-run” phenomenon in other synapses; Ref. 44), loss of neurotransmitter through an extended release sequence, a predilection for smaller pools of neurotransmitter to be released asynchronously, or restricted permeation through a uniquantal release pore in multiphasic releases.

Quantal Sizes

The presynaptic quantal size of an EPSC can be estimated with simultaneous presynaptic capacitance recording and postsynaptic EPSC recording. With this method, Li and collaborators (18) estimated the postsynaptic EPSC charge injection from a single presynaptic vesicle to be ∼45 fC, as in mini-EPSCs in the frog hair-cell synapse. This corresponds reasonably well to the charge injected by the smallest events in the data of Fig. 10, roughly 10–30 fC. It is much smaller than the charge required to produce monophasic EPSC in Fig. 6, which is 200–300 fC.

The data in the previous paragraph argue for a multiquantal mechanism in the rat hair cell. The experiment of Li and collaborators has not been done in a mammal; however, capacitance recordings in hair cells have been done (e.g., Refs. 16, 17), in which it was possible to resolve single steps in the capacitance data that seem to correspond to single vesicle releases. These capacitance steps had the amplitudes expected for one or two single synaptic vesicles, based on synaptic vesicle surface area. However, postsynaptic recordings were not made in those experiments so the amount of charge injected by the resulting EPSCs was not determined. Thus the question of quantal size requires further research.

Final Comments

In our opinion, the question of multiquantal versus uniquantal release remains open. The uniquantal flickering-release model is supported by the near constancy of EPSC charge and the lack of a convincing mini-EPSC in the present data. However experimental verification that a single vesicle can produce the large charge injections required for the postsynaptic EPSCs in these datasets is missing. Multiquantal release is also consistent with much of the data, however, one has to assume that release is highly coordinated across release sites, to support near-constancy of release charge, with enough variability to produce both monophasic and multiphasic EPSCs.

The flickering model is similar to the “kiss-and-run” phenomenon which has been proposed for CNS synapses (44, 45). In both, the fusion pore closes after a partial release of the vesicle contents. In the case of kiss-and-run, there is only a single opening of the pore, after which the vesicle is recycled in a way that speeds its availability for another release. The evidence presented here and by Chapochnikov et al (15) for uniquantal flickering suggests a different process in which the pore repeatedly opens and closes until the vesicle contents are released. These differences in function could derive from the different molecular constitution of the vesicle fusion pore in hair cells versus CNS synapses (46).

SUPPLEMENTAL DATA

All Supplemental material is available at https://doi.org/10.12751/g-node.ylt20r.

DATA AVAILABILITY

Raw and processed data from one experiment (T) have been posted on the GIN website (https://doi.org/10.12751/g-node.ylt20r) and can be accessed anonymously. Included is a Matlab program that reproduces most figures in the paper and provides examples of how the data can be accessed. The program can be used to produce many examples in the form of Fig. 9A for excitatory postsynaptic currents with various numbers of events.

GRANTS

This work was supported by National Institute on Deafness and Other Communication Disorders (NIDCD) Grants R01-DC-006476 and R01-DC-012957 (to E.G.) and P30-DC-005211 to the Center for Hearing and Balance at Johns Hopkins, the David M. Rubenstein Fund for Hearing Research, and the John Mitchell Jr. Trust. M.N. was partially supported by NIDCD R0-DC-1009913 (to A. J. Ricci, Stanford Univ.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

E.D.Y. and E.G. conceived and designed research; J.S.W. performed experiments; E.D.Y. and M.N. analyzed data; E.D.Y. interpreted results of experiments; E.D.Y. prepared figures; E.D.Y. drafted manuscript; E.D.Y., J.S.W., M.N., and E.G. edited and revised manuscript; E.D.Y., J.S.W., M.N., and E.G. approved final version of manuscript.

ENDNOTE

At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at https://doi.org/10.12751/g-node.ylt20r. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.

ACKNOWLEDGMENTS

We thank Eunyoung Yi and Lisa Grant for recordings that were included in the analysis of excitatory postsynaptic currents and Philippe Vincent for measurements of hair-cell membrane potential.

Present addresses: J. S. Wu, Dept. of Neurobiology, Harvard Medical School, Boston, MA; M. Niwa, Kresge Hearing Research Institute, University of Michigan, Ann Arbor, MI.

REFERENCES

1.Matthews G, Fuchs P. The diverse roles of ribbon synapses in sensory neurotransmission. Nat Rev Neurosci 11: 812–822, 2010. dois: 10.1038/nrn2924. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Rutherford MA, Moser T. The ribbon synapse between type I spiral ganglion neurons and inner hair cells. The Primary Auditory Neurons of the Mammalian Cochlea, edited by Dabdoub A, Fritzsch B, Popper AN, Fay RR.. New York: Springer, 2016, p. 117–156. doi: 10.1007/978-1-4939-3031-9_5. [DOI] [Google Scholar]
3.Siegel JH. Spontaneous synaptic potentials from afferent terminals in the guinea pig cochlea. Hearing Res 59: 85–92, 1992. doi: 10.1016/0378-5955(92)90105-V. [DOI] [PubMed] [Google Scholar]
4.Yi E, Roux I, Glowatzki E. Dendritic HCN channels shape excitatory postsynaptic potentials at the inner hair cell afferent synapse in the mammalian cochlea. J Neurophysiol 103: 2532–2543, 2010. doi: 10.1152/jn.00506.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Rutherford MA, Chapochnikov NM, Moser T. Spike encoding of neurotransmitter release timing by spiral ganglion neurons of the cochlea. J Neurosci 32: 4773–4789, 2012. doi: 10.1523/JNEUROSCI.4511-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Wu JS, Young ED, Glowatzki E. Maturation of spontaneous firing properties after hearing onset in rat auditory nerve fibers: spontaneous rates, refractoriness, and interfiber correlations. J Neurosci 36: 10584–10597, 2016. doi: 10.1523/JNeurosci.1187-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Frank T, Rucherford MA, Strenzke N, Neef A, Pangršič T, Khimich D, Fejtova A, Gundelfinger ED, Liberman MC, Harke B, Bryan KE, Lee A, Egner A, Riedel D, Moser T. Basoon and the synaptic ribbon organize Ca²⁺ channels and vesicles to add release sites and promote refilling. Neuron 68: 724–738, 2010. doi: 10.1016/j.neuron.2010.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Buran BN, Strenzke N, Neef A, Gundelfinger ED, Moser T, Liberman MC. Onset coding is degraded in auditory nerve fibers from mutant mice lacking synaptic ribbons. J Neurosci 30: 7587–972010, 2010. doi: 10.1523/JNEUROSCI.0389-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Becker L, Schnee ME, Niwa M, Sun W, Maxeiner S, Talaei S, Kachar B, Rutherford MA, Ricci AJ. The presynaptic ribbon maintains vesicle populations at the hair cell afferent fiber synapse. eLife 7: e30241, 2018. doi: 10.7554/eLife.30241. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Jean P, Lopez de la Morena D, Michanski S, Tobón LM, Chakrabarti R, Picher MM, Neef J, Jung SY, Gültas M, Maxeiner S, Neef A, Wichmann C, Strenzke N, Grabner CP, Moser T. The synaptic ribbon is critical for sound encoding at high rates and with temporal precision. eLife 7: e29275, 2018. doi: 10.7554/eLife.29275. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Chakrabarti R, Michanski S, Wichmann C. Vesicle sub-pool organization at inner hair cell ribbon synapses. EMBO Reports 19: e44937, 2018. doi: 10.15252/embr.201744937. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Grant L, Yi E, Glowatzki E. Two modes of release shape the postsynaptic response at the inner hair cell ribbon synapse. J Neurosci 30: 4210–4220, 2010. doi: 10.1523/JNEUROSCI.4439-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Glowatzki E, Fuchs PA. Transmitter release at the hair cell ribbon synapse. Nature Neuroscience 5: 147–154, 2002. doi: 10.1038/nn796. [DOI] [PubMed] [Google Scholar]
14.Keen EC, Hudspeth AJ. Transfer characteristics of the hair cell’s afferent synapse. PNAS 103: 5537–5542, 2006. doi: 10.1073/pnas.0601103103. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Chapochnikov NM, Takago H, Huang CH, Pangrsic T, Khimich D, Neef J, Auge E, Göttfert F, Hell SW, Wichmann C, Wolf F, Moser T. Uniquantal release through a dynamic fusion pore is a candidate mechanism of hair cell exocytosis. Neuron 83: 1389–1403, 2014. doi: 10.1016/j.neuron.2014.08.003. [DOI] [PubMed] [Google Scholar]
16.Neef A, Khimich D, Pirih P, Riedel D, Wolf F, Moser T. Probing the mechanism of exocytosis at the hair cell ribbon synapse. J Neurosci 27: 12933–12944, 2007. doi: 10.1523/JNEUROSCI.1996-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Grabner CP, Moser T. Individual synaptic vesicles mediate stimulated exocytosis from cochlear inner hair cells. PNAS 115: 12811–12816, 2018. doi: 10.1073/pnas.1811814115. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Li GL, E Keen EC, Andor-Ardó D, Hudspeth AJ, von Gersdorff H. The unitary event underlying multiquantal EPSCs at a hair cell’s ribbon synapse. J Neurosci 29: 7558–7568, 2009. doi: 10.1523/JNEUROSCI.0514-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Li GL, Cho S, von Gersdorff H. Phase-locking precision Is enhanced by multiquantal release at an auditory hair cell ribbon synapse. Neuron 83: 1404–1417, 2014. doi: 10.1016/j.neuron.2014.08.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Schnee ME, Castellano-Muñoz M, Ricci AJ. Response properties from turtle auditory hair cell afferent fibers suggest spike generation is driven by synchronized release both between and within synapses. J Neurophysiol 110: 204–220, 2013. doi: 10.1152/jn.00121.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Singer JH, Lassová L, Vardi N, Diamond JS. Coordinated multivesicular release at a mammalian ribbon synapse. Nature Neurosci 7: 826–833, 2004. doi: 10.1038/nn1280. [DOI] [PubMed] [Google Scholar]
22.Vincent PF, Cho S, Tertrais M, Bouleau Y, von Gersdorff H, Dulon D. Clustered Ca²⁺ channels are blocked by synaptic vesicle proton release at mammalian auditory ribbon synapses. Cell Reports 25: 3451–3464, 2018. doi: 10.1016/j.celrep.2018.11.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Bosher SK, Warren RL. A study of the electrochemistry and osmotic relationships of the cochlear fluids in the neonatal rat at the time of the development of the endocochlear potential. J Physiol 212: 739–761, 1971. doi: 10.1113/jphysiol.1971.sp009354. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Goutman JD, Glowatzki E. Time course and calcium dependence of transmitter release at a single ribbon synapse. PNAS 104: 16341–16346, 2007. doi: 10.1073/pnas.0705756104. [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Johnson SL. The resting transducer current drives spontaneous activity in prehearing mammalian cochlear inner hair cells. J Neurosci 32: 10479–10483, 2012., doi: 10.1523/JNEUROSCI.0803-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Teich MC, Johnson DH, Kumar AR, Turcott RG. Rate fluctuations and fractional power-law noise recorded from cells in the lower auditory pathway of the cat. Hear Res 46: 41–52, 1990. doi: 10.1016/0378-5955(90)90138-F. [DOI] [PubMed] [Google Scholar]
27.Tibshirani R. Regression shrinkage and selection via the lasso. J Royal Stat Soc Series B 58: 267–288, 1996. [Google Scholar]
28.Andor-Ardó D, Keen EC, Hudspeth AJ, Magnasco MO. Fast, automated implementation of temporally precise blind deconvolution of multiphasic excitatory postsynaptic currents. PLoS One 7: e38198, 2012. doi: 10.1371/journal.pone.0038198. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Malagon G, Miki T, Llano I, Neher E, Marty A. Counting vesicular release events reveals binomial release statistics at single glutamatergic synapses. J Neurosci 36: 4010–4025, 2016. doi: 10.1523/JNEUROSCI.4352-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Destexhe A, Mainen ZF, Sejnowski TJ. Fast kinetic models for simulating AMPA, NMDA, GABAA, and GABAB receptors. In: The Neurobiology of Computation, edited by Bower J. Norwell, MA: Kluwer Academic Press, 1995, p. 9–14. [Google Scholar]
31.Häausser M, Roth A. Dendritic and somatic glutamate receptor channels in rat cerebellar Purkinje cells. J Physiol 501: 77–95, 1997. doi: 10.1111/j.1469-7793.1997.077bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Andor-Ardó D, Hudspeth AJ, Magnasco MO, Piro O. Modeling the resonant release of synaptic transmitter by hair cells as an example of biological oscillators with cooperative steps. PNAS 107: 2019–2024, 2010. doi: 10.1073/pnas.0914372107. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Niwa M, Young ED, Glowatzki E, Ricci AJ. Functional subgroups of cochlear inner hair cell ribbon synapses differently modulate their EPSC properties in response to stimulation. J Neurophys (in press)., 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Lowen SB, Teich MC. Auditory-nerve action potentials form a nonrenewal point process over short as well as long time scales. J Acoust Soc Am 92: 803–806, 1992. doi: 10.1121/1.403950. [DOI] [PubMed] [Google Scholar]
35.Peterson AJ, Irvine DR, Heil P. A model of synaptic vesicle-pool depletion and replenishment can account for the interspike interval distributions and nonrenewal properties of spontaneous spike trains of auditory-nerve fibers. J Neurosci 34: 15097–15109, 2014. doi: 10.1523/JNEUROSCI.0903-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Shi L, Shen QT, Kiel A, Wang J, Wang W-W, Melia TJ, Rothman JE, Pincet F. SNARE proteins: one to fuse and three to keep the nascent fusion pore open. Science 355: 1355–1359, 2012. doi: 10.1126/science.1214984. [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Wu Z, Bello OK, Thiyagarajan S, Auclair SM, Vennekate W, Krishnakumar SS, O’Shaughnessy B, Karatekin E. Dilation of fusion pores by crowding of SNARE proteins. eLife 6: e22964, 2017. doi: 10.7554/eLife.22964. [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Goutman JD, Glowatzki E. Short-term facilitation modulates size and timing of the synaptic response at the inner hair cell ribbon synapse. J Neurosci 31: 7974–7981, 2011. doi: 10.1523/JNEUROSCI.0604-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Goutman JD. Transmitter release from cochlear hair cells is phase locked to cyclic stimuli of different intensities and frequencies. J Neurosci 32: 17025–17036, 2012. doi: 10.1523/JNEUROSCI.0457-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
40.Cho S, Li GL, von Gersdorff H. Recovery from short-term depression and facilitation is ultrafast and Ca²⁺ dependent at auditory hair cell synapses. J Neurosci 31: 5682–5692, 2011. doi: 10.1523/JNEUROSCI.5453-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Goutman JD. Mechanisms of synaptic depression at the hair cell ribbon synapse that support auditory nerve function. PNAS 114: 9719–9724, 2017. doi: 10.1073/pnas.1706160114. [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Khimich D, Nouvian R, Pujol R, Tom Dieck S, Egner A, Gundelfinger ED, Moser T. Hair cell synaptic ribbons are essential for synchronous auditory signalling. Nature 434: 889–894, 2005. doi: 10.1038/nature03418. [DOI] [PubMed] [Google Scholar]
43.Huang H, Moser T. Ca²⁺ regulates the kinetics of synaptic vesicle fusion at the afferent inner hair cell synapse. Front Cell Neurosci 12: 364, 2018. doi: 10.3389/fncel.2018.00364. [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Alabi AA, Tsien RW. Perspectives on kiss-and-run: role in exocytosis, endocytosis, and neurotransmission. Annu Rev Physiol 75: 393–422, 2013. doi: 10.1146/annurev-physiol-020911-153305. [DOI] [PubMed] [Google Scholar]
45.He L, Wu XS, Mohan R, Wu LG. Two modes of fusion pore opening revealed by cell-attached recordings at a synapse. Nature 444: 102–105, 2006. doi: 10.1038/nature05250. [DOI] [PubMed] [Google Scholar]
46.Nouvian R, Neef J, Bulankina AV, Reisinger E, Pangršič T, Frank T, Sikorra S, Brose N, Binz T, Moser T. Exocytosis at the hair cell ribbon synapse apparently operates without neuronal SNARE proteins. Nature Neurosci 14: 411–413, 2011. doi: 10.1038/nn.2774. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

[B1] 1.Matthews G, Fuchs P. The diverse roles of ribbon synapses in sensory neurotransmission. Nat Rev Neurosci 11: 812–822, 2010. dois: 10.1038/nrn2924. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B2] 2.Rutherford MA, Moser T. The ribbon synapse between type I spiral ganglion neurons and inner hair cells. The Primary Auditory Neurons of the Mammalian Cochlea, edited by Dabdoub A, Fritzsch B, Popper AN, Fay RR.. New York: Springer, 2016, p. 117–156. doi: 10.1007/978-1-4939-3031-9_5. [DOI] [Google Scholar]

[B3] 3.Siegel JH. Spontaneous synaptic potentials from afferent terminals in the guinea pig cochlea. Hearing Res 59: 85–92, 1992. doi: 10.1016/0378-5955(92)90105-V. [DOI] [PubMed] [Google Scholar]

[B4] 4.Yi E, Roux I, Glowatzki E. Dendritic HCN channels shape excitatory postsynaptic potentials at the inner hair cell afferent synapse in the mammalian cochlea. J Neurophysiol 103: 2532–2543, 2010. doi: 10.1152/jn.00506.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B5] 5.Rutherford MA, Chapochnikov NM, Moser T. Spike encoding of neurotransmitter release timing by spiral ganglion neurons of the cochlea. J Neurosci 32: 4773–4789, 2012. doi: 10.1523/JNEUROSCI.4511-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B6] 6.Wu JS, Young ED, Glowatzki E. Maturation of spontaneous firing properties after hearing onset in rat auditory nerve fibers: spontaneous rates, refractoriness, and interfiber correlations. J Neurosci 36: 10584–10597, 2016. doi: 10.1523/JNeurosci.1187-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B7] 7.Frank T, Rucherford MA, Strenzke N, Neef A, Pangršič T, Khimich D, Fejtova A, Gundelfinger ED, Liberman MC, Harke B, Bryan KE, Lee A, Egner A, Riedel D, Moser T. Basoon and the synaptic ribbon organize Ca²⁺ channels and vesicles to add release sites and promote refilling. Neuron 68: 724–738, 2010. doi: 10.1016/j.neuron.2010.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B8] 8.Buran BN, Strenzke N, Neef A, Gundelfinger ED, Moser T, Liberman MC. Onset coding is degraded in auditory nerve fibers from mutant mice lacking synaptic ribbons. J Neurosci 30: 7587–972010, 2010. doi: 10.1523/JNEUROSCI.0389-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B9] 9.Becker L, Schnee ME, Niwa M, Sun W, Maxeiner S, Talaei S, Kachar B, Rutherford MA, Ricci AJ. The presynaptic ribbon maintains vesicle populations at the hair cell afferent fiber synapse. eLife 7: e30241, 2018. doi: 10.7554/eLife.30241. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B10] 10.Jean P, Lopez de la Morena D, Michanski S, Tobón LM, Chakrabarti R, Picher MM, Neef J, Jung SY, Gültas M, Maxeiner S, Neef A, Wichmann C, Strenzke N, Grabner CP, Moser T. The synaptic ribbon is critical for sound encoding at high rates and with temporal precision. eLife 7: e29275, 2018. doi: 10.7554/eLife.29275. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B11] 11.Chakrabarti R, Michanski S, Wichmann C. Vesicle sub-pool organization at inner hair cell ribbon synapses. EMBO Reports 19: e44937, 2018. doi: 10.15252/embr.201744937. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B12] 12.Grant L, Yi E, Glowatzki E. Two modes of release shape the postsynaptic response at the inner hair cell ribbon synapse. J Neurosci 30: 4210–4220, 2010. doi: 10.1523/JNEUROSCI.4439-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B13] 13.Glowatzki E, Fuchs PA. Transmitter release at the hair cell ribbon synapse. Nature Neuroscience 5: 147–154, 2002. doi: 10.1038/nn796. [DOI] [PubMed] [Google Scholar]

[B14] 14.Keen EC, Hudspeth AJ. Transfer characteristics of the hair cell’s afferent synapse. PNAS 103: 5537–5542, 2006. doi: 10.1073/pnas.0601103103. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B15] 15.Chapochnikov NM, Takago H, Huang CH, Pangrsic T, Khimich D, Neef J, Auge E, Göttfert F, Hell SW, Wichmann C, Wolf F, Moser T. Uniquantal release through a dynamic fusion pore is a candidate mechanism of hair cell exocytosis. Neuron 83: 1389–1403, 2014. doi: 10.1016/j.neuron.2014.08.003. [DOI] [PubMed] [Google Scholar]

[B16] 16.Neef A, Khimich D, Pirih P, Riedel D, Wolf F, Moser T. Probing the mechanism of exocytosis at the hair cell ribbon synapse. J Neurosci 27: 12933–12944, 2007. doi: 10.1523/JNEUROSCI.1996-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B17] 17.Grabner CP, Moser T. Individual synaptic vesicles mediate stimulated exocytosis from cochlear inner hair cells. PNAS 115: 12811–12816, 2018. doi: 10.1073/pnas.1811814115. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B18] 18.Li GL, E Keen EC, Andor-Ardó D, Hudspeth AJ, von Gersdorff H. The unitary event underlying multiquantal EPSCs at a hair cell’s ribbon synapse. J Neurosci 29: 7558–7568, 2009. doi: 10.1523/JNEUROSCI.0514-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B19] 19.Li GL, Cho S, von Gersdorff H. Phase-locking precision Is enhanced by multiquantal release at an auditory hair cell ribbon synapse. Neuron 83: 1404–1417, 2014. doi: 10.1016/j.neuron.2014.08.027. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B20] 20.Schnee ME, Castellano-Muñoz M, Ricci AJ. Response properties from turtle auditory hair cell afferent fibers suggest spike generation is driven by synchronized release both between and within synapses. J Neurophysiol 110: 204–220, 2013. doi: 10.1152/jn.00121.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B21] 21.Singer JH, Lassová L, Vardi N, Diamond JS. Coordinated multivesicular release at a mammalian ribbon synapse. Nature Neurosci 7: 826–833, 2004. doi: 10.1038/nn1280. [DOI] [PubMed] [Google Scholar]

[B22] 22.Vincent PF, Cho S, Tertrais M, Bouleau Y, von Gersdorff H, Dulon D. Clustered Ca²⁺ channels are blocked by synaptic vesicle proton release at mammalian auditory ribbon synapses. Cell Reports 25: 3451–3464, 2018. doi: 10.1016/j.celrep.2018.11.072. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B23] 23.Bosher SK, Warren RL. A study of the electrochemistry and osmotic relationships of the cochlear fluids in the neonatal rat at the time of the development of the endocochlear potential. J Physiol 212: 739–761, 1971. doi: 10.1113/jphysiol.1971.sp009354. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B24] 24.Goutman JD, Glowatzki E. Time course and calcium dependence of transmitter release at a single ribbon synapse. PNAS 104: 16341–16346, 2007. doi: 10.1073/pnas.0705756104. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B25] 25.Johnson SL. The resting transducer current drives spontaneous activity in prehearing mammalian cochlear inner hair cells. J Neurosci 32: 10479–10483, 2012., doi: 10.1523/JNEUROSCI.0803-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B26] 26.Teich MC, Johnson DH, Kumar AR, Turcott RG. Rate fluctuations and fractional power-law noise recorded from cells in the lower auditory pathway of the cat. Hear Res 46: 41–52, 1990. doi: 10.1016/0378-5955(90)90138-F. [DOI] [PubMed] [Google Scholar]

[B27] 27.Tibshirani R. Regression shrinkage and selection via the lasso. J Royal Stat Soc Series B 58: 267–288, 1996. [Google Scholar]

[B28] 28.Andor-Ardó D, Keen EC, Hudspeth AJ, Magnasco MO. Fast, automated implementation of temporally precise blind deconvolution of multiphasic excitatory postsynaptic currents. PLoS One 7: e38198, 2012. doi: 10.1371/journal.pone.0038198. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B29] 29.Malagon G, Miki T, Llano I, Neher E, Marty A. Counting vesicular release events reveals binomial release statistics at single glutamatergic synapses. J Neurosci 36: 4010–4025, 2016. doi: 10.1523/JNEUROSCI.4352-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B30] 30.Destexhe A, Mainen ZF, Sejnowski TJ. Fast kinetic models for simulating AMPA, NMDA, GABAA, and GABAB receptors. In: The Neurobiology of Computation, edited by Bower J. Norwell, MA: Kluwer Academic Press, 1995, p. 9–14. [Google Scholar]

[B31] 31.Häausser M, Roth A. Dendritic and somatic glutamate receptor channels in rat cerebellar Purkinje cells. J Physiol 501: 77–95, 1997. doi: 10.1111/j.1469-7793.1997.077bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B32] 32.Andor-Ardó D, Hudspeth AJ, Magnasco MO, Piro O. Modeling the resonant release of synaptic transmitter by hair cells as an example of biological oscillators with cooperative steps. PNAS 107: 2019–2024, 2010. doi: 10.1073/pnas.0914372107. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B33] 33.Niwa M, Young ED, Glowatzki E, Ricci AJ. Functional subgroups of cochlear inner hair cell ribbon synapses differently modulate their EPSC properties in response to stimulation. J Neurophys (in press)., 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B34] 34.Lowen SB, Teich MC. Auditory-nerve action potentials form a nonrenewal point process over short as well as long time scales. J Acoust Soc Am 92: 803–806, 1992. doi: 10.1121/1.403950. [DOI] [PubMed] [Google Scholar]

[B35] 35.Peterson AJ, Irvine DR, Heil P. A model of synaptic vesicle-pool depletion and replenishment can account for the interspike interval distributions and nonrenewal properties of spontaneous spike trains of auditory-nerve fibers. J Neurosci 34: 15097–15109, 2014. doi: 10.1523/JNEUROSCI.0903-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B36] 36.Shi L, Shen QT, Kiel A, Wang J, Wang W-W, Melia TJ, Rothman JE, Pincet F. SNARE proteins: one to fuse and three to keep the nascent fusion pore open. Science 355: 1355–1359, 2012. doi: 10.1126/science.1214984. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B37] 37.Wu Z, Bello OK, Thiyagarajan S, Auclair SM, Vennekate W, Krishnakumar SS, O’Shaughnessy B, Karatekin E. Dilation of fusion pores by crowding of SNARE proteins. eLife 6: e22964, 2017. doi: 10.7554/eLife.22964. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B38] 38.Goutman JD, Glowatzki E. Short-term facilitation modulates size and timing of the synaptic response at the inner hair cell ribbon synapse. J Neurosci 31: 7974–7981, 2011. doi: 10.1523/JNEUROSCI.0604-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B39] 39.Goutman JD. Transmitter release from cochlear hair cells is phase locked to cyclic stimuli of different intensities and frequencies. J Neurosci 32: 17025–17036, 2012. doi: 10.1523/JNEUROSCI.0457-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B40] 40.Cho S, Li GL, von Gersdorff H. Recovery from short-term depression and facilitation is ultrafast and Ca²⁺ dependent at auditory hair cell synapses. J Neurosci 31: 5682–5692, 2011. doi: 10.1523/JNEUROSCI.5453-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B41] 41.Goutman JD. Mechanisms of synaptic depression at the hair cell ribbon synapse that support auditory nerve function. PNAS 114: 9719–9724, 2017. doi: 10.1073/pnas.1706160114. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B42] 42.Khimich D, Nouvian R, Pujol R, Tom Dieck S, Egner A, Gundelfinger ED, Moser T. Hair cell synaptic ribbons are essential for synchronous auditory signalling. Nature 434: 889–894, 2005. doi: 10.1038/nature03418. [DOI] [PubMed] [Google Scholar]

[B43] 43.Huang H, Moser T. Ca²⁺ regulates the kinetics of synaptic vesicle fusion at the afferent inner hair cell synapse. Front Cell Neurosci 12: 364, 2018. doi: 10.3389/fncel.2018.00364. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B44] 44.Alabi AA, Tsien RW. Perspectives on kiss-and-run: role in exocytosis, endocytosis, and neurotransmission. Annu Rev Physiol 75: 393–422, 2013. doi: 10.1146/annurev-physiol-020911-153305. [DOI] [PubMed] [Google Scholar]

[B45] 45.He L, Wu XS, Mohan R, Wu LG. Two modes of fusion pore opening revealed by cell-attached recordings at a synapse. Nature 444: 102–105, 2006. doi: 10.1038/nature05250. [DOI] [PubMed] [Google Scholar]

[B46] 46.Nouvian R, Neef J, Bulankina AV, Reisinger E, Pangršič T, Frank T, Sikorra S, Brose N, Binz T, Moser T. Exocytosis at the hair cell ribbon synapse apparently operates without neuronal SNARE proteins. Nature Neurosci 14: 411–413, 2011. doi: 10.1038/nn.2774. [DOI] [PubMed] [Google Scholar]

PERMALINK

Resolution of subcomponents of synaptic release from postsynaptic currents in rat hair-cell/auditory-nerve fiber synapses

Eric D Young

Jingjing Sherry Wu (武靜靜)

Mamiko Niwa

Elisabeth Glowatzki

Series information

Abstract

INTRODUCTION

MATERIALS AND METHODS

Experimental Methods

Table 1.

Figure 3.

Figure 2.

Analysis

Figure 1.

EPSC Overlap

Figure 4.

Figure 6.

Figure 7.

Amplitude, Area, and Statistics

Linearity in the Deconvolution of EPSCs

Figure 5.

RESULTS

Measuring EPSC Waveforms

EPSCs Are Mostly Monophasic; Multiphasic EPSCs Are Smaller in Amplitude

EPSC Area Declines Only Slightly as Event Number Increases

Lack of Serial Dependence of the Event Numbers

Figure 8.

Event Organization within EPSCs

Figure 9.

Figure 10.

DISCUSSION

The Analysis

Are the EPSCs Multiquantal?

Quantal Sizes

Final Comments

SUPPLEMENTAL DATA

DATA AVAILABILITY

GRANTS

DISCLOSURES

AUTHOR CONTRIBUTIONS

ENDNOTE

ACKNOWLEDGMENTS

REFERENCES

Associated Data

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases