Towards a deeper understanding of microbial communities: integrating experimental data with dynamic models

Abstract

Microbial communities and their functions are shaped by complex networks of interactions among microbes and with their environment. While the critical roles microbial communities play in numerous environments have become increasingly appreciated, we have a very limited understanding of their interactions and how these interactions combine to generate community-level behaviors. This knowledge gap hinders our ability to predict community responses to perturbations and to design interventions that manipulate these communities to our benefit. Dynamic models are promising tools to address these questions. We review existing modeling techniques to construct dynamic models of microbial communities at different scales and suggest ways to leverage multiple types of models and data to facilitate our understanding and engineering of microbial communities.

1. Introduction and motivating example

Microbial communities are ubiquitous on Earth and perform important functions in diverse environments spanning oceans and soils to multi-cellular host organisms. The functions of these communities are often defined by chemical (e.g. metabolite degradation or release) or physical transformations (e.g. biofilm formation) that shape the environment they reside in. A prime example is the microbial community that inhabits the human gut, which is highly dense and diverse. It has become increasingly evident that the functional activities performed by gut microbiota are linked to a wide range of health outcomes including obesity, behavior, and response to cancer treatments [1]–[3]. While the ecological and molecular mechanisms underlying the majority of these links are not yet known, certain metabolic transformations and fermentation end products of gut microbiota have been shown to impact host biology [4]–[6].

Consider Clostridiodes difficile, an enteric pathogen that can cause recurrent disease in the human gut leading to 400,000 hospitalizations every year in the United States [7]. Normally, the native gut microbiota protects from C. difficile infection. However, use of antibiotics disrupts the native gut microbiota, providing an opportunity for C. difficile to establish an ecological niche [8]. Importantly, fecal microbiota transplantation (FMT), where the native microbial community from healthy donor fecal samples is transplanted into a recipient, and a related treatment whereby spores of natural fecal microbiota are used instead of unmodified fecal samples, have been highly effective in treating recurrent C. difficile infection (CDI), whereas well-defined bacterial cocktails consisting of tens of species have been absent in successful large clinical trials [9]–[11]. The success of FMT and spore therapies suggests that the complex network of microbial interactions between the introduced healthy microbiota, disrupted native microbiota, and C. difficile is a key determinant of the efficacy of the treatment. However, the lack of widely used and effective synthetically designed bacterial treatments indicates the need for a better understanding of the mechanisms that protect against CDI.

To better design effective and safe microbial interventions to modify complex microbial communities, we need to transition beyond correlational studies, such as associating cross-sectional community composition to host phenotype [12], to studies that can establish mechanistic understandings and/or generate quantitative and reliable predictions. These tasks include, for example, mapping ecological interactions [13], molecular mediators [14], and metabolic pathways linking members in a community to time-dependent community behaviors in a fluctuating environment. Correlational studies fall short of these tasks in several ways. First, they have difficulty in accounting for the directionality of interactions and causality. Second, they are incapable of predicting time-dependent properties of the community, such as long-term stability [15] and transient dynamics [16]. Finally, a community’s abiotic environment is often changing over multiple timescales. Dynamic modelling is a powerful tool capable of bridging these gaps, allowing for inference of directionality and causality [17], [18], prediction of time-dependent properties [15], [16], and capturing the dynamic behaviors of a microbiome in fluctuating environments [19], [20]. Hence, dynamic models can be used to identify key microbes, molecules, and genetic determinants that have large causal effects on microbial community behaviors, predict their response to perturbations, and guide the design of precise interventions to modify community functions.

Here, we review promising approaches to model the dynamics of microbial communities. We pay particular attention to the integration of experimental techniques with mechanistic and empirical dynamic models to describe the community at ecological and molecular effector scales. We define a model as mechanistic if its mathematical structure is based on biologically relevant hypotheses. For example, the generalized Lotka-Volterra model (see the next section for details) is considered a mechanistic dynamical model at the ecological scale, because its mathematical structure is based on the assumption that the growth of a microbial community depends on each member’s intrinsic growth rate and all pairwise interactions with other community members. Given such a hypothesis-driven model structure, the parameters within can then be inferred/constrained or directly measured from experimental data. In contrast, the mathematical structures of empirical models are data-driven and often do not have a direct interpretation in the physical world. For example, recurrent neural networks [21] are popular empirical dynamic models that are often chosen because they are flexible enough to describe temporal data with highly nonlinear behaviors. The examples drawn in this paper are mainly from the human gut microbiome literature, but the experimental and modeling techniques described here are applicable to microbial communities in other environments. While we show successes in developing predictive and/or interpretable models using different modeling frameworks, our ability to mechanistically understand community functions is still largely limited to either small communities with 2–3 members [22]–[26] or specific molecular mechanisms in isolation, such as pH [27], [28] or hydrogen sulfide [28], in larger communities. This is due to (i) the inherent complexity of interactions among microbes and with their environment, and (ii) the difficulty in obtaining large amounts of high quality temporally resolved data. On the other hand, there exists a wide range of modeling frameworks and experimental methods to investigate microbial communities at varying degrees of detail to deepen our understanding of their dynamic behaviors.

2. Ecological models

A microbial community can be described as the collection of distinct and interacting microbial populations that inhabit a shared environment. The focus of ecological models is to predict and analyze population dynamics, including temporal changes in abundance of each constituent member and how each population influences each other without regard to the molecular basis of the interactions. When used properly, ecological models can recapitulate and predict community compositional dynamics in both biotic and abiotic environments. For example, ecological models can effectively capture changes in community composition during antibiotic treatment and subsequent C. difficile infection in defined microbial communities introduced into gnotobiotic mice [30], [31]. These models are then used to design microbial communities that are robust to C. difficile colonization [30]. We briefly introduce common ecological models and the relevant data required to train them.

Generalized Lotka-Volterra models

Ecological models can take a number of mathematical forms. The most widely used class of models are a set of coupled ordinary differential equations (ODEs) called generalized Lotka-Volterra (gLV) models. As shown in Figure 1a, these models can describe the absolute abundance of each community member as a function of time due to its intrinsic growth rate, pairwise interactions with each community member, as well as external inputs representing a dietary shift or antibiotics treatment for example [30]. The unknown parameters of a gLV model can be inferred by fitting the model to absolute abundance measurements of each species.

Figure 1. Modeling frameworks available at various scales to develop dynamic models for microbial communities.

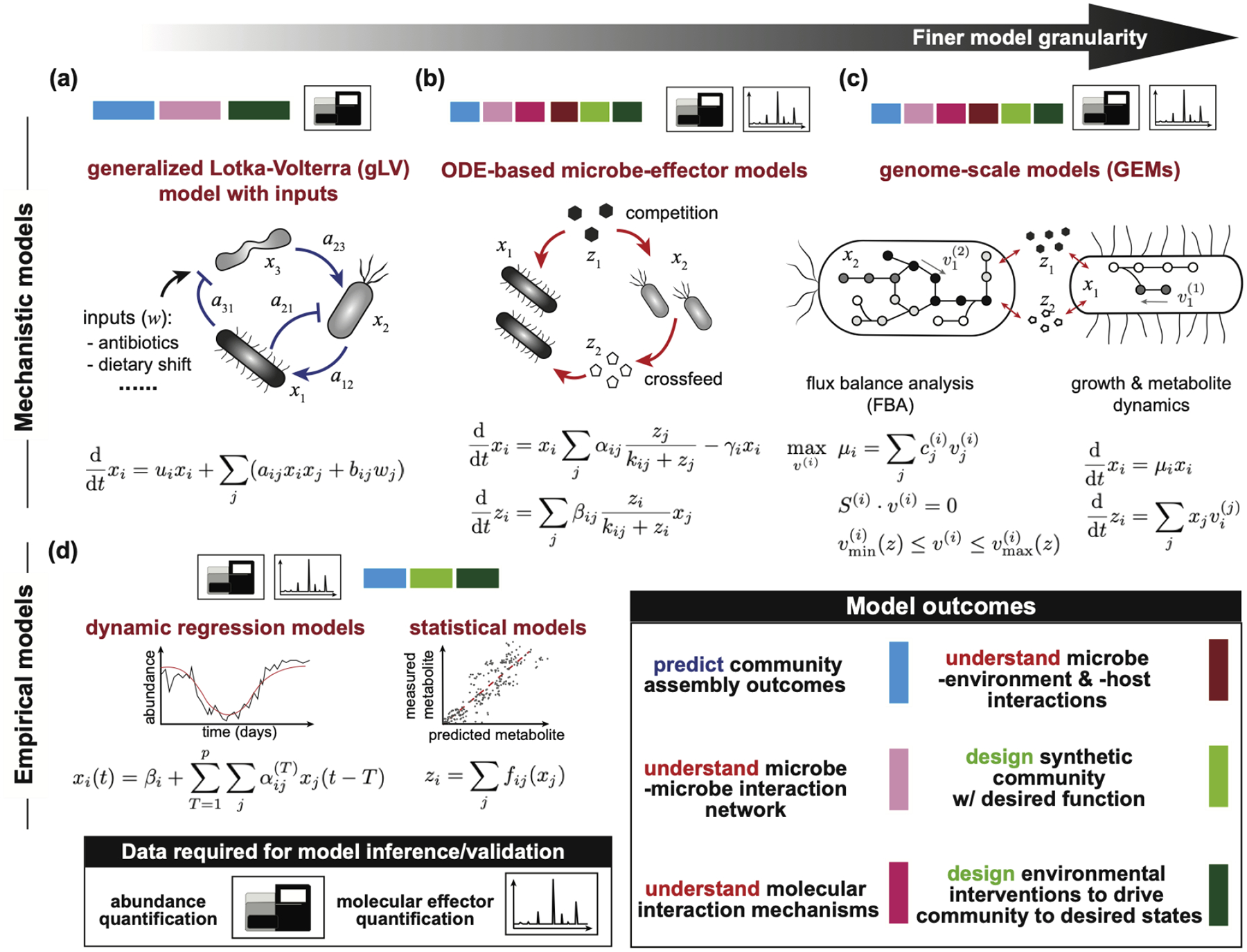
(a) Generalized Lotka-Volterra (gLV) models with an input can describe how the absolute abundance of community member i (x_i) changes with the abundance of other community members and with external inputs w. Parameter b_ij describes the effect of the j-th input on member i. Effect of member j on the growth of member i is represented by a constant interaction coefficient a_ij, and u_i is the basal growth rate of member i. (b) Ordinary differential equation (ODE) based microbe-effector models describe how species abundance (x) variation depends on metabolite concentration (z), and how, in turn, metabolite concentration changes dynamically with species abundance through uptake and release. Parameter α_ij describes the maximum growth rate of member i using resource j, γ_i is the death rate of member i, and β_ij is the uptake/release rate of metabolite i by member j. (c) Genome scale models can be used to simulate community dynamics. The equations show dynamic multispecies metabolic modeling framework as described in [26]. At each time interval, the metabolic fluxes (v⁽ⁱ⁾) and growth rate (μ_i) of each community member i is determined using FBA and the species’ genome-scale model (GEM). The fluxes of metabolite exchange reactions are then used to update the metabolite concentration in the environment. The uptake rates of metabolites from the environment depend on extracellular metabolite concentrations. Hence, the bounds of exchange fluxes (v⁽ⁱ⁾_min and v⁽ⁱ⁾_max) are generally functions of extracellular metabolite concentration, which often take Michaelis-Menten form. (d) Dynamic regression models assume that species abundance at time t can be written as a combination of previous p abundance measurements x(t-1)…x(t-p). The equation shows an example of the vector autoregression framework in [29]. Previous external inputs can also be included in these models to predict community member abundances in the presence of inputs (not shown in the figure). Static regression models have been used to map species abundance to molecule concentrations [28]. Model outcomes: Each colored square indicates a modeling framework’s ability to solve a class of scientific or engineering problems in microbial communities as shown in the legend. The required types of data to infer and validate each model are indicated by schematics for abundance and molecular effector quantification.

Absolute abundance can be determined by combining relative compositional data, available most commonly through marker gene (e.g. 16S rRNA gene) amplicon sequencing or metagenomic sequencing, with total bacterial load measurements [13], [30]. While these experimental techniques are relatively easy and inexpensive to access, there are inherent biases associated with each method, thus motivating the need for method standardization across different studies [32]–[35]. In addition, it is important to carefully design the sampling schemes (e.g. time intervals between data collections) and, if applicable, the temporal profile of the external input [36]. For instance, if all taxonomic data are collected after the community composition dynamics have reached a steady state, then data collected after this time point do not provide additional information. In general, parameter inference benefits from high-resolution temporal data and sufficiently “rich” external inputs that can excite all dynamic modes in a community [36]. This requirement, as well as accurate determination of total bacteria abundance, is sometimes difficult for in vivo studies where sampling is not always easy and straightforward. However, in in vitro studies, if the constituent species are labeled with fluorescent reporters [37], the efforts required to obtain high-resolution temporal taxonomic data could be significantly reduced.

A major limitation of gLV models is that they rely on constant parameters to describe microbe-microbe interactions, which are determined by the temporally changing biotic and abiotic environment. This rigid mathematical structure may thus sacrifice their predictive power across different environmental contexts. In fact, Lotka-Volterra models are historically considered as a first-order Taylor expansion of ecological interactions near equilibrium [38], and hence they fail to capture higher-order interactions [39]. Furthermore, a microbial community may dynamically change its environment through, for example, metabolite release. Changes in the abiotic environment shift the metabolic activities and ecological niches of community members over time, creating an environment-mediated feedback loop that in turn alters their growth dynamics as well as the interaction strengths and directions. Therefore, despite their success in describing context-specific interactions, gLV models alone may not be able to capture community-level behaviors when the environment changes significantly over time, such as during an active C. difficile infection in the human gut.

Data-driven dynamic regression models

In contrast to the predetermined mathematical structure of a gLV model, ecological models based on data-driven dynamic regression techniques can take more flexible mathematical forms [15], [29], [40]. These models assume that the community composition at the current time depends on previously measured community compositions (see Figure 1d). Due to their flexible structures, training these models often require more data compared to gLV models. While extracting biological information from these regression models is often not straightforward, they can be effective in predicting how community composition changes in response to an external input. This is especially the case when the model is trained on a large volume of longitudinal data, which was collected for the same community perturbed persistently by the same type of input [41]. In this sense, the model is predictive but not mechanistic. Other types of data-driven, time-series prediction techniques that have been used in other engineering domains, such as auto-regressive neural networks and recurrent neural networks [21], may also be suitable to capture more complicated nonlinear dynamics in microbial communities. The lack of interpretability, which is traditionally a drawback of these types of complex black box models, could potentially be alleviated using newly developed mathematical tools for model interpretation [42]. While this mathematical interpretability can guide biological hypotheses and new experimental designs, it may not lead directly to mechanistic understandings of interactions at either ecological or molecular effector scales. Furthermore, when applied to microbial communities, training data availability continues to be a major bottleneck.

Ecological models can be extended to account for the temporal variation of each member’s population density at different spatial locations. These spatiotemporal ecological dynamics are often captured by a class of partial differential equation (PDE) models called reaction-diffusion models. They have been frequently used to study range expansion of microbial communities [43], [44]. Experimental methods for obtaining high quality spatial taxonomic data for complex microbial communities are still in its infancy. To collect the needed experimental data, measurements are typically based on fluorescent reporters to track community members, limiting the experimental setup to genetically tractable species [45], [46]. Fluorescent in-situ hybridization is a promising approach to obtaining spatial taxonomic data for complex communities, but requires fixing and permeabilizing the cells and thus limits our ability to temporally characterize the system [47].

In summary, ecological models are typically coarse-grained models for capturing microbe-microbe interactions at a high level of abstraction, without accounting for any underlying molecular mechanisms. Usually, ecological interaction parameters are represented by fixed values, and due to the context dependence of most microbial interactions, these models have limited ability to extrapolate to different environmental contexts. While identifying the molecular basis of interaction is often not straightforward using ecological models, they can be used to identify significant interactions or sub-communities for further detailed experimental characterization. For example, these models alone would not be able to identify key microbial metabolic pathways mediating C. difficile colonization of the gut environment but could point towards key species responsible for C. difficile inhibition. This limitation can be addressed, to some extent, by microbe-effector models, which we discuss next.

3. Microbe-effector models

The interactions among community members often occur through molecular effectors such as metabolites and toxins that microbes release and take up from their shared environment, which generates a bipartite network linking community members and molecular effectors [48]. Microbe-effector models aim to explicitly capture the dynamics of these effectors in mediating microbial growth, community assembly, and functions.

ODE-based microbe-effector models

ODE models can be used to describe how microbial growth varies dynamically with the extracellular concentrations of key effectors, and how, in turn, these effectors change the shared environment to influence growth of community members (Figure 1b). The MacArthur consumer resource model is a popular example of such a modeling framework [49]. This type of model helps to establish a mechanistic understanding of how ecological interactions arise from biochemical processes including metabolite cross-feeding and competition [23], [24], [49]–[53], while maintaining a manageable model complexity and interpretability. For example, microbe-effector ODE models can capture the changes in ecological interactions between E. coli amino acid auxotrophs in response to supplementation of amino acids [23], describe antibiotics-induced multi-stability [52], and the effects of dietary changes on microbiome composition and function [53]. Similar to ecological models, ODE-based microbe-effector models can be extended to account for spatial gradients of biomass and substrates using reaction-diffusion dynamics. The resultant PDE-based microbe-effector models have been used, for example, to study spatial heterogeneity in biofilm formation [54].

A major challenge when constructing an ODE or PDE-based microbe-effector model is to wisely determine model complexity given data availability. While increasing the number of effectors in the model provides greater flexibility in capturing complex behaviors, it also quickly increases the number of unknown kinetic parameters that need to be identified from longitudinal effector data, which is often challenging to collect. For simple and well-defined communities, the list of metabolites to include in the model is often decided based on expert knowledge. Targeted metabolite measurements can then be used to obtain high-resolution and high-quality data for parameter inference. For complex communities, low temporal resolution ‘omics data and genome-scale metabolic models (see next section) may serve as initial screening tools to help identify metabolites mediating inter-species interactions for targeted analysis. Furthermore, for PDE-based microbe-effector models, spatially-resolved measurements of substrate gradients represents a significant challenge.

The parameters in an ODE or PDE-based microbe-effector model have defined physical roles, such as the rates of metabolite uptake and release. Hence, in principle, these parameters can be determined directly from simpler experimental systems (i.e. monoculture) and then applied to the community model [45]. Compared to fitting parameters directly from community data, this parameter inference approach helps to validate the model structure and reduces the risk of overfitting [36]. However, experiments must be carefully designed for the individually quantified parameters to be applicable in the community setting, as some physical parameters can change as a function of environmental conditions or may even change due to evolutionary adaptation of the community members [45].

Dynamic flux balance analysis based on genome-scale models

Microbial genome-scale models (GEMs) have recently emerged as a powerful knowledge-driven tool to analyze and design communities. GEMs describe all metabolic reactions that are predicted to occur within a microbe based on genomic information and experimental evidence. In theory, GEM-based microbial community models can predict community composition and metabolism without any experimental data. Thus, GEMs can be exploited to develop hypotheses a priori or to augment any available experimental data. For instance, they can transform taxonomic measurements into difficult to measure metabolite data to generate predictions for the molecular basis of ecological interactions [55], generate an unprecedented volume of simulated data to reveal community assembly rules and design principles [56]–[59], and identify potential metabolic conditions giving rise to hysteresis in co-culture experiments [25]. By combining GEMs of the host and the microbe, they can also help understand microbe-host interactions [60], [61], where data-driven approaches are often limited by the availability of ex vivo or in vivo measurements.

Simulation of GEMs is enabled through flux balance analysis (FBA), which determines the fluxes through all reactions in a metabolic network (Figure 1c) [62]. In its simplest and most commonly used form, FBA finds fluxes that optimize a microbe’s growth rate given the metabolic reactions’ stoichiometric constraints and the bounds for reaction fluxes. Compared to microbe-effector ODE models, this optimality assumption relaxes the need to identify thousands of kinetic parameters for all metabolic reactions. Dynamic flux balance analysis (dFBA) solves this optimization problem at every time step to determine the rate of metabolite uptake and release. This is then used to determine dynamic variations of the extracellular metabolite concentrations and cell growth [63] (Figure 1c). Changes in extracellular metabolite concentrations, in turn, affect the uptake reaction fluxes to impact growth of community members [26].

This bottom-up dynamic modeling framework has been extended to the community setting to account for the microbes’ growth in a shared environment and their ability to shape the environment through metabolic exchanges. A number of computational tools [26], [64], [65] have emerged in recent years to implement this modeling framework. Some of these tools can further account for spatial heterogeneity in the community [65]. This is accomplished by first discretizing space into small, homogeneous compartments and then carrying out dFBA for microbial communities in each compartment. Diffusion models are used to characterize biomass and metabolite flow across compartment boundaries. This type of spatially structured, GEM-based community models has been used, for example, to study how colony spatial arrangements affect interactions between two mutualistic strains [65].

Integrating experimental data to validate and improve GEMs in a specific context is not straightforward. This is because the main outcomes of (d)FBA are reaction fluxes, which are difficult to directly measure. Nevertheless, ‘omics data, especially transcriptomics data, can be integrated with GEMs to tighten the constraints in (d)FBA to improve their predictive power [66], [67]. For example, transcriptomics data have been used to determine that certain reactions never occur under certain experimental contexts, and their upper flux bound (v_max in Figure 1c) can be set to 0. Experimentally measured taxonomic abundance and metabolite concentration time series have also been used to calibrate a subset of parameters in GEM-based community models [68].

The predictive power of most FBA-based modeling approaches hinges on the assumption that all microbes regulate metabolic fluxes to maximize their biomass objective functions at all times. While such objective functions can be refined by experimental data [69], this assumption may not be appropriate in all growth conditions [70]. Alternative mathematical formulations of FBA may alleviate the impact of objective function choices on simulation outcomes but are also significantly more computationally intensive [71]. Another limitation of GEM-based community model is that they do not account for interactions mediated through pathways beyond central metabolism, such as the effects of antimicrobial compounds or quorum-sensing molecules. Finally, GEMs require accurate genome annotation, including transporters that play a critical role in metabolite uptake and release and are difficult to accurately identify in microbial genomes [72]. As such, high quality GEMs are still limited to model organisms such as E. coli. Hence, GEMs alone are usually unable to accurately predict the metabolic activities of microbes within a microbial community, but could be used to generate potential hypotheses for experimental testing or to qualitatively test hypotheses in conjunction with other models and experimental data.

Individual-based models

Another type of microbe-effector model is the individual-based model (IbM). Whereas ODE, PDE- and GEM-based community models describe microbial behavior and interactions at the population level, IbMs describe microbial behaviors and interactions at the individual cell level. Hence, this modeling framework is especially suitable to characterize communities with significant cell-cell heterogeneity [73]–[75]. In an IbM, microbial growth and metabolite-mediated cell-cell interactions can be accounted for using GEM [73] or ODE-based microbe-effector models [74], [75] for each individual cell. In addition, IbMs can also include mechanical interactions (e.g. cell-cell contact) as well as advection, convection, and diffusion of nutrients [75]. IbMs can encompass enormous mechanistic details and are typically associated with a large number of parameters that are often difficult to measure or constrain. Therefore, IbMs are more suitable as a tool to summarize current knowledge about a system and explain experimental observations, rather than directly incorporate experimental observations and make quantitative predictions about system behaviors.

In summary, unlike ecological models, microbe-effector models based on ODEs, PDEs, GEMs, and IbMs can directly provide molecular-level mechanistic insights into microbe-microbe and microbe-environment/host interactions, which may enable the design of precise molecular interventions. GEMs and IbMs are more suitable to make qualitative predictions given limited experimental data, while ODE and PDE models are more appropriate to solve context-specific problems given sufficient experimental data to infer model parameters. Therefore, these methods are complementary to each other to solve different problems with varying degrees of data availability.

4. Emerging trend: Integrating mechanistic and data-driven models

Describing microbial communities under a single, comprehensive, fine-grained mechanistic model, such as a high dimensional ODE or PDE-based microbe-effector model, is usually not practical due to our lack of expert knowledge to determine model structure and the difficulty in obtaining the large amount of data required to constrain model parameters. Mechanistic and data-driven models describing separate parts of a system can be combined to obtain a more comprehensive integrative model with an expanded scope. This modeling approach has a long history in engineering domains, where a complex system model is often built from both data-driven components and mechanistic components. For instance, to simulate a vehicle’s response to driver input, a lookup table is first used to relate instantaneous fuel injection rate, which is determined by the driver’s accelerator pedal position, to engine torque output. This lookup table is generated from large amounts of engine testing data in various operating conditions and hence is a data-driven modeling component. The effect of engine torque output on vehicle acceleration is then computed using Newtonian mechanics (i.e. mechanistic modeling components) [76]. Similar strategies have started to emerge in modeling microbial communities. For example, empirical models have been used to relate pH [27] and temperature [77] to growth rates of community members in monoculture. These empirical models are then combined with mechanistic models by replacing constant growth parameters with mathematical functions of the environmental parameters. This enables the resultant model to describe community dynamics under a range of pH and temperature conditions. Regression models combined with gLV models have also been used to link synthetic human gut community composition to butyrate production [28], a health-relevant microbial fermentation end product, and T-cell activity [78]. These integrative models hold promise to expand the applicability of traditional mechanistic microbial community models to broader contexts.

Establishing mechanistic connections between high-dimensional outcomes from mechanistic models (e.g. metabolic fluxes of thousands of reactions) to biological outcomes not directly quantified in the mechanistic models (e.g. antibiotics susceptibility) is challenging. This gap could be filled by first performing high throughput experiments and simulations of mechanistic models under a large number of conditions, and then use a statistical model to connect model outcomes to a biological property under investigation. For example, Yang et al. combined GEMs with a regression model that maps metabolic fluxes in E. coli to antibiotics susceptibility in a large number of growth conditions, thus revealing how metabolic networks impact antibiotic responses [79]. In a similar vein, by fitting microbe-effector ODE models to denitrification dynamics of many microbes, Gowda et al. [80] uses a regression model to link the presence/absence of relevant genes in the organism to the inferred kinetic parameters of the microbe-effector model. These approaches could be used to predict the complex mapping between genomic information, intracellular networks, and community dynamics that are too complicated to decipher directly from experimental data or mechanistic simulations.

5. Opportunities and challenges ahead.

Microbial communities are highly dynamic systems that respond to environmental stimuli. Dynamic models of microbial community composition and function can represent system behaviors at the ecological and/or molecular effector scales. Hence, they are promising tools to guide engineering of microbial communities for our benefit. Yet we face many obstacles including the inherent complexity of microbial communities and the highly varied types and qualities of data. For complex communities especially in natural settings, data collection remains the largest bottleneck. Hence, dynamic modeling of microbial communities requires careful consideration of the specific scientific question or engineering goal and the limitations of each modeling framework, including the ability to collect the types and quantities of data needed to sufficiently constrain the model to make meaningful predictions. As data collection and dynamic modeling techniques improve, we will be able to better understand the complex functions of microbial communities and leverage that knowledge to harness microbial communities to benefit our health and the environment. In the near future, we can already expect many advances will be made by integrating multiple types of models to exploit the wide range of data types available.

Highlights.

• Dynamic models are powerful tools to understand and engineer microbial communities.

• Model frameworks vary across scales and require different types of experimental data.

• Careful considerations should be given to model limitations and experimental designs.

• Integrating multiple types of models and data expedites understanding and design.