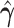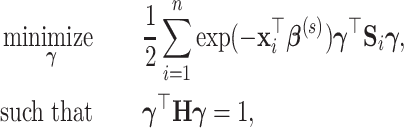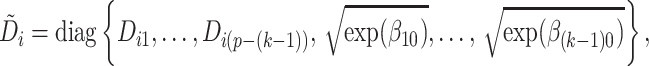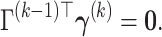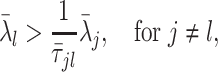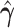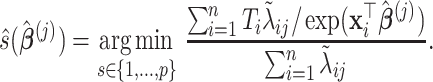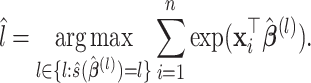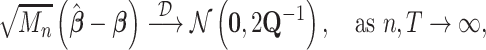Summary
In this study, we consider the problem of regressing covariance matrices on associated covariates. Our goal is to use covariates to explain variation in covariance matrices across units. As such, we introduce Covariate Assisted Principal (CAP) regression, an optimization-based method for identifying components associated with the covariates using a generalized linear model approach. We develop computationally efficient algorithms to jointly search for common linear projections of the covariance matrices, as well as the regression coefficients. Under the assumption that all the covariance matrices share identical eigencomponents, we establish the asymptotic properties. In simulation studies, our CAP method shows higher accuracy and robustness in coefficient estimation over competing methods. In an example resting-state functional magnetic resonance imaging study of healthy adults, CAP identifies human brain network changes associated with subject demographics.
Keywords: Common diagonalization, Heteroscedasticity, Linear projection
1. Introduction
Modeling variances is an important topic in the statistics and finance literature. In linear regression with heterogeneous errors, various generalized linear models have been proposed to model error variances using covariates directly or indirectly as functions of the means (e.g., Box and Cox, 1964; Carroll and others, 1982; Smyth, 1989; Cohen and others, 1993). These models use separate regression models of the covariates to predict the scalar error variance, as well as the mean of the response. This article aims to generalize such models from scalar variances to covariance matrices. Briefly, we aim to link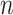 
sample covariance matrices 
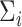to the corresponding covariate vectors 
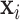, for 
. Our generalization is not straightforward, because the response variable is here multidimensional and must be positive (semi-) definite. To overcome these challenges, we borrow the principal idea behind principal component analysis (PCA) on covariance matrices, and propose to seek a covariate-dependent rotation vector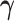 
, such that the scalar product 
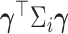is the response in a generalized linear model of 
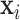. In the following, we will review two broadly relevant areas—covariance matrix modeling and PCA on multiple covariance matrices, as well as the motivation for our model from the analysis of multi-subject functional magnetic resonance imaging (fMRI) connectivity matrices.
Regression models for covariance matrix outcomes have been studied before. Anderson (1973) proposed an asymptotically efficient estimator for a class of covariance matrices, where the covariance matrix is modeled as a linear combination of symmetric matrices. Chiu and others (1996) proposed to model the elements of the logarithm of the covariance matrix as a linear function of the covariates, which requires a large number of parameters to be estimated. These approaches have been further extended to high dimensions. Hoff and Niu (2012) introduced a regression model where the covariance matrix is a quadratic function of the explanatory variables. Applying low-rank approximation techniques, Fox and Dunson (2015) generalized the framework to a scalable nonparametric covariance regression model. Zou and others (2017) linked the matrix outcome to a linear combination of similarity matrices of covariates and studied the asymptotic properties of various estimators under this model. A common thread among these approaches is that they model the whole covariance matrix as outcomes, and thus the interpretation can be challenging for large matrices.
PCA and related methods are also widely used to model multiple covariance matrices. Flury (1984, 1986) introduced a class of models, called common principal components analysis (CPCA), to uncover the shared covariance structures. Boik (2002) generalized these models using spectral decompositions. Hoff (2009) developed a Bayesian hierarchical model and estimation procedure to study the heterogeneity in both the eigenvectors and eigenvalues of the covariance matrices. Assuming that the eigenvectors span the same subspace, Franks and Hoff (2016) extended this to high dimensional settings with large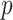 
and small 
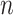. For longitudinal data, Pourahmadi and others (2007) employed the Cholesky decomposition and Gaussian maximum likelihood to estimate various models for multiple covariance matrices, including CPCA. It is unclear, however, how these methods can be extended to incorporate multiple continuous and categorical covariates.
In the application area of neuroimaging analysis, PCA-type methods are becoming increasingly popular for modeling covariance matrices, partly because of their computational capability for analyzing large and multilevel observations. Covariance matrices (or correlation matrices after standardization) of multiple brain regions are also commonly known as functional connectivity matrices (Friston, 2011). Decomposing the covariance matrices into separate components enables explaining the variation in neuroimaging data using only a few components (Friston and others, 1993), and such components when visualized as image patterns are interpreted as brain subnetworks (Poldrack and others, 2011). As before, it is unclear how these methods can be extended to include multiple covariates for explaining the variation.
Indeed, modeling the covariate-related alterations in covariance matrices is an important topic in neuroimaging analysis, because changes in functional connectivity have been found to be associated with various demographic and clinical factors, such as age, sex, and cognitive behavioral function including developmental and mental health capacities (Just and others, 2006; Wang and others, 2007; Luo and others, 2011; Mennes and others, 2012; Hafkemeijer and others, 2015; Park and others, 2016). A commonly implemented method to analyze the covariance changes is to regress one matrix entry on the covariates, and this model is repeatedly fitted for each matrix element (e.g., Wang and others, 2007; Lewis and others, 2009). Though this approach has good interpretability and is scalable, it suffers from multiplicity issues, because of the large number of regressions involved: 
regressions for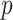 
brain regions. Building on Hoff and Niu (2012), Seiler and Holmes (2017) simplified the method by assuming the covariance matrix to be diagonal with independent variances, and they also included a random effects term to analyze multilevel neuroimaging data.
In this article, we propose a Covariate Assisted Principal (CAP) regression model for several covariance matrix outcomes. This model integrates the PCA principle with a generalized linear model of multiple covariates. Analogous to PCA, our model aims to identify linear projections of the covariance matrices, while being computationally feasible for large data. Unlike PCA, our method targets those projections that are associated with the covariates. This enables us to study changes in covariance matrices that are associated with subject-specific factors.
This article is organized as follows. In Section 2, we introduce the CAP regression model. Section 3 presents the estimation and computation algorithms for identifying covariate-related principal projection directions. Under the assumption that multiple covariance matrices share identical eigencomponents, we establish the asymptotic properties of our method. We compare the performance of our proposed methods with competing approaches through simulation studies in Section 4. We then apply our methods to an fMRI data set in Section 5. Section 6 summarizes the article and discusses potential future directions of research.
2. Model
For each subject/uni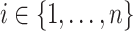t 
, let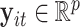 
, 
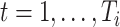, be independent and identically distributed random samples from a multivariate normal distribution with mean zero and covariance matrix 
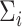, where 
may depend on explanatory variables, denoted by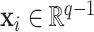 
. The variable 
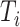is the number of observations from subject 
, 
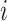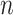is the number of subjects, and 
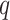is the number of predictors including the intercept. In our application, 
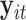is a sample of fMRI measurements of 
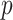brain regions, and 
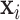is a vector of covariates, both collected from subject 
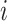. We assume that there exists a vector 
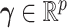such that 
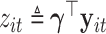satisfies the following multiplicative heteroscedasticity model:
 |
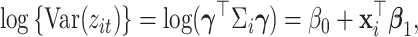(2.1) |
where 
and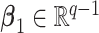 
are model coefficients. The logarithmic linear model above generalizes the variance regression model (Harvey, 1976) in which 
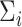is a scalar. Similar to the goal of Harvey (1976), this article focuses on studying the variation in covariance matrices. Without loss of generality, we assume 
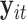has mean zero for each coordinate. In practice, before applying our method, one can subtract from 
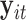the sample average across 
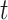on each coordinate, for each subject 
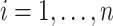. This study also requires the normality assumption, as in the previous literature (Flury, 1984, 1986; Pourahmadi and others, 2007). If the distribution significantly departures from normal, our method may introduce estimation bias and the asymptotic confidence intervals may also yield poor coverage probability, as we investigate later in Section 4 using simulations.
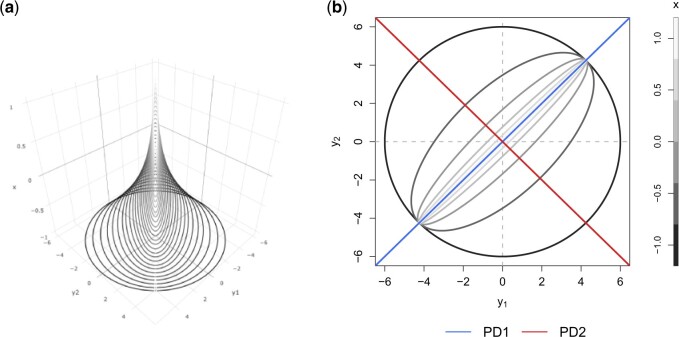
A toy example of this model (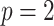
and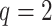 
with one continuous covariate 
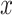and an intercept) is shown in Figure 1. The covariance matrices, represented by the contour plot ellipses, vary as the covariate 
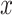varies. On the first projection direction (PD1), with the larger variability, there is no variation under different 
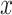values. Only the variance in the second direction (PD2) decreases as 
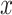increases. Our proposed model (2.1) identifies PD2 (through 
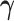) first, whereas PCA recovers PD1 first even though the variability along PD1 is not associated with 
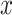. In other words, our objective is to discover the rotation such that the data variation in the new space is associated with the explanatory variables.
Fig. 1.
Covariance matrices, shown as contour plot ellipses (
), vary as a continuous 
varies (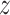
-axis in (a) and gray/color scales in (b)). A fixed intercept (not shown) is also included in this example, and thus 
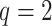. (a) 3D contour plot and (b) 2D contour plot.
Compared with existing methods, our proposed model has three main advantages. Firstly, different from the models proposed by Hoff and Niu (2012) and Zou and others (2017), which directly model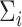 
by linear combinations of symmetric matrices in quadratic forms of 
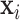, we assume a log-linear model for the variance component after rotation. The linear form in 
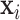allows for an easy interpretation of the regression coefficient and provides the modeling flexibility of generalized linear models, such as interactions. The projection enables computational scalability, similar to PCA. Secondly, various CPCA methods, studied in Flury (1984) and others, only allow the eigenvalues to vary across a subject or group indicator. These methods do not consider covariates; CAP bridges this gap. Thirdly, instead of restricting to the eigenvector projections in CPCA methods, we assume that there exists at least one linear projection, not necessarily an eigenvector projection, such that model (2.1) is satisfied. In this sense, CPCA methods are special cases of CAP.
3. Method
Under model (2.1), we propose to estimate the parameters by maximizing the likelihood function of the data in the projection space:
 |
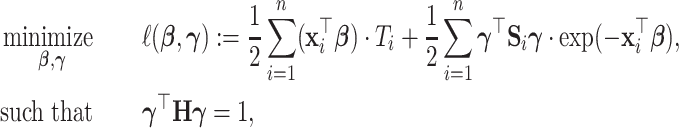(3.2) |
where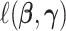 
is the negative log-likelihood function (ignoring constants) for data 
(
, 
), 
, 
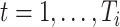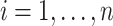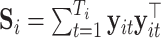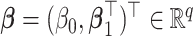, and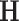 
is a positive definite matrix in 
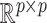. The constraint is critical, since without it 
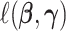is minimized by 
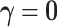for fixed 
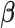. We set 
to be the average sample covariance matrix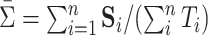 
. This choice is similar in spirit to the choice of common PCA in Krzanowski (1984). Another possibility is to set 
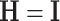, where 
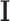is the identity matrix. However, this choice leads to less desirable estimates related to small eigenvalues, as shown in Section A.1 of the supplementary material available at Biostatistics online.
In the following sections, we will introduce three algorithms for estimation under different scenarios. Section 3.1 first introduces the algorithm for computing the first pair of 
and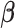 
by solving (3.1), and this algorithm also illustrates the key ideas used by all other proposed algorithms. In Section 3.2, we apply the first algorithm sequentially to compute multiple pairs, and this algorithmic approach is named as CAP. Here, one can also choose a variant (CAP-OC) of this algorithm to include an optional constraint. Section 3.3 presents an modified algorithm (CAP-C) for computing multiple pairs under a more restrictive assumption that all the covariance matrices share the same eigenstructure. In most applications, we recommend the CAP algorithm in Section 3.2, because it does not require the same eigenstructure assumption which can be sometimes unrealistic in certain cases, especially for large 
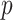. In addition, our simulation studies (Section 4 and Section E of the supplementary material available at Biostatistics online) demonstrate that this algorithm performs well under most scenarios and its variant (CAP-OC) has similar performance though is computationally slower. The CAP-C algorithm should be used if one wishes to impose the same eigenstructure assumption. However, in this case, we recommend that users should examine the validity of this assumption using the diagonality metric defined in Section 3.2.1 or visual inspection of the off-diagnonal elements (e.g., Figure F8 in the Section F.6 of the supplementary material available at Biostatistics online).
3.1. An algorithm of identifying the first projection direction
The optimization problem (3.2) is biconvex. We propose a block coordinate descent algorithm for fitting the first pair of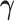 
and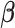 
. Given 
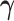, the update of 
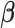is obtained by Newton–Raphson. Given 
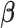, solving for 
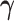requires quadratic programming. We derive explicit updates in Proposition A.1 of the supplementary material available at Biostatistics online. The algorithm is summarized in Algorithm 1. This algorithm applies for any positive definite 
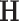. To mitigate the possibility of converging to a local minimum, we suggest randomly choosing a series of initial values and taking the estimate with the lowest objective function value (i.e., the largest likelihood).
Algorithm 1
A block coordinate descent algorithm of computing the first pair of projection direction and regression coefficients by solving the optimization problem (3.1).
Input:
: a list of data where the
th element is a
data matrix
: an
matrix of covariate variables with the first column of ones
,
: initial values
Output:
,
Given
from the
th step, for the
th step:
by
where
(3.2) ;
by solving
using Proposition A.1 in the supplementary material available at Biostatistics online.
Repeat steps (i)–(ii) until convergence.
3.2. Algorithmic extension for finding multiple projection directions
It is possible that more than one projection direction is associated with the covariates. We propose to find these directions sequentially. This is analogous to the strategy of finding principal components sequentially.
Suppose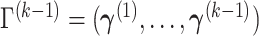 
contains the first 
components (for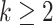 
), and let 
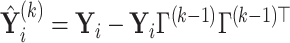, where 
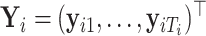for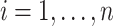 
. One cannot directly apply Algorithm 1 to 
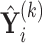as in PCA algorithms, since 
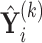is not of full rank. Thus, we introduce a rank-completion step. The algorithm is summarized in Algorithm 2. Step (iii) completes the data to full rank by adding nonzero positive eigenvalues to the zero eigencomponents, considering the exponential of the intercept as a baseline level of data variation in the corresponding components. This step also guarantees that there are no identical eigenvalues in the covariance matrix of 
.
Analogous to the PCA approach, step (iv) includes an optional orthogonal constraint to ensure that the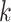 
th direction is orthogonal to the previous ones, which is equivalent to the following optimization problem, for 
,
 |
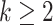(3.3) |
For any fixed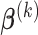 
, we derive an explicit formula for solving 
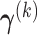in Section A.2 of the supplementary material available at Biostatistics online. The proof is related to solving the generalized eigenvalue problem studied in Rao (1964, 1973). We later compare the numeric performance of our algorithms with or without this constraint in Section 4.
Algorithm 2
Algorithms for computing the
th (
) projection direction: the Covariate Assisted Principal (CAP) regression algorithm, and a variant of CAP with an Orthogonality Constraint (CAP-OC).
Input:
: a list of data where the
th element is a
data matrix
: an
matrix of covariate variables with the first column of ones
: a
matrix contains the first
directions
: a
matrix contains the model coefficients of the first
directions
Output:
,
(1) For
, let
.
(2) Apply singular value decomposition (SVD) on
, such that
.
with
where
are the first
diagonal elements of matrix
, and
are the intercept of the first
directions (first row of
).
(
) as the new data, and apply Algorithm 1 directly or with an (optional) orthogonal constraint
3.2.1. Choosing the number of projection directions
We propose a data-driven approach to choose the number of projection directions. Extending the common principal component model, Flury and Gautschi (1986) introduced a metric to quantify the “deviation from diagonality.” Suppose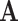 
is a positive definite symmetric matrix, the deviation from diagonality is defined as
 |
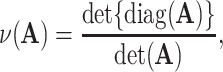(3.4) |
where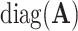 
is a diagonal matrix of the diagonal elements from 
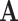, and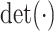 
is the determinant. From Hadamard’s inequality, we have that 
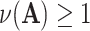, where equality is achieved if and only if 
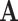is a diagonal matrix.
To adapt this metric in our model, we let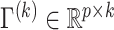 
denote the matrix containing the first 
projection directions. We define the average deviation from diagonality as
 |
(3.5) |
which is the weighted geometric mean of each subject’s deviation from diagonality. As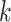 
increases, the requirement for 
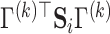to be a diagonal matrix, as in Flury and Gautschi (1986), may become more stringent. In practice, we can plot the average deviation from diagonality and choose the first few projection directions with 
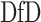value close to one, or choose a suitable number right before a sudden jump in the plot. Section E of the supplementary material available at Biostatistics online demonstrates this with an example. In Section 4, we use simulation studies to evaluate the performance.
3.3. Method and algorithm under the common principal component condition
In this section, we derive a special case of our method under the common principal component condition (Flury, 1984, 1986) when the eigenspace of the covariance matrices is assumed to be identical. Suppose there exist eigencomponents that satisfy the following eigenvalue condition.
Condition 1
(Eigenvalue condition) Assume
is the eigendecomposition of
with
an orthogonal matrix and
a diagonal matrix, for
. The eigenvectors are ordered based on the average of the eigenvalues such that
, where
(for
) and
is the eigenvalue of
corresponding to eigenvector
. Suppose
is the component satisfying
. Then, the eigenvalues are assumed to have the following relationship,
(3.6) where
, and
.
This condition requires that the eigenvalues are well separated from each other such that it is not ambiguous to analyze specific linear combinations of eigenvectors. Further, let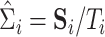 
denote the sample covariance matrix of unit 
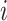. Suppose 
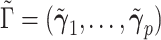and 
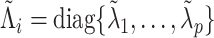are the maximum likelihood estimator of 
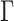and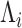 
(
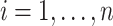) (e.g., as in Flury, 1984), respectively. We replace 
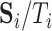by the consistent estimator, 
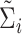, in our optimization problem (3.1). Since 
is an orthonormal basis, 
can be represented by a linear combination of its columns,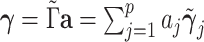 
, where 
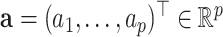. The optimization problem (3.1) is reformulated as:
 |
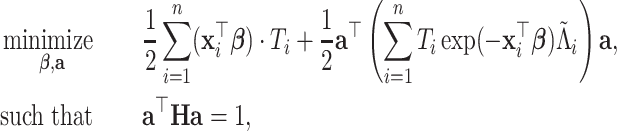(3.8) |
where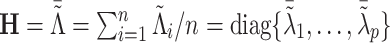 
, 
(j=1,…,p). With appropriate change of variables (see details in Section A.3 of the supplementary material available at Biostatistics online), minimizing the objective function in (3.7) is equivalent to solving the following problem,
 |
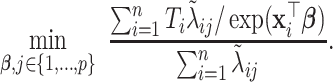(3.8) |
Let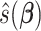 
denote the minimizer given 
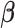of the above optimization problem. Suppose 
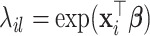is the eigencomponent whose eigenvalue satisfies the log-linear model specification, with 
, the minimizer 
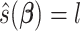is achieved under condition that
 |
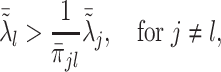(3.9) |
where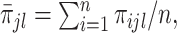 
and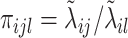 
, 
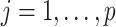. Under the common eigenstructure assumption, we can first estimate the common eigenvectors and the corresponding 
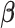coefficients denoted by 
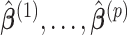. The covariate-related components are those satisfy that 
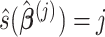. This algorithm is summarized in Algorithm 3. If one only needs to estimate the first 
(
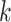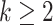) directions, we propose to order those 
components, where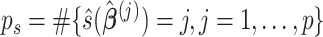 
, by the average eigenvalues and return the first 
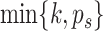components.
Algorithm 3
Covariate Assisted Principal regression under the Common principal components assumption (CAP-C).
Input:
: a list of data where the
th element is a
data matrix
: an
matrix of covariate variables with the first column of ones
Output:
,
(1) Under the assumption that
(
) have the same eigencomponents, estimate
and
by maximizing the likelihood function, denoted by
and
, respectively.
(2) For
, estimate
with
, denoted by
.
, minimize the objective function with
, maximize the variance with
(5) Estimate
and
.
3.4. Asymptotic properties under the common principal component condition
In this section, we establish the asymptotic properties of our proposed maximum likelihood estimator under the common principal component condition (Algorithm 3 or CAP-C). Though the asymptotic theory for common PCA under the same condition was studied in Flury (1986) among others, the existing results do not consider estimating regression coefficients as in our method. The proof of the theorems are presented in Sections B and C of the supplementary material available at Biostatistics online.
We first discuss the asymptotic property of our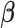 
estimator given the true 
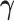. As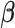 
is estimated by maximizing the log-likelihood function, we have the following theorem.
Theorem 1
Assume
as
. Let
,
, with known
, we have
(3.10) where
is the maximum likelihood estimator when
is known.
When 
and 
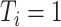(for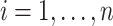 
), our proposed model (2.1) degenerates to a multiplicative heteroscedastic regression model. The asymptotic distribution of 
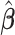in Theorem 1 is the same as in Harvey (1976). We now establish the asymptotic theory when 
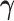is estimated under the assumption that all the covariance matrices have identical eigencomponents.
Theorem 2
Assume
, where
is an orthogonal matrix and
with
(
), for at least one
. There exists
such that for
,
. Let
be the maximum likelihood estimator of
. Assuming that the assumptions in Theorem 1 are satisfied,
from Algorithm 3 is a
-consistent estimator of
.
4. Simulation study
In this section, we focus on comparing the performance of our CAP algorithms and other competing methods using one simulation scenario. Results from additional simulation scenarios, including the assessment of robustness, will be summarized at the end.
In one simulation scenario, we generate data from a multivariate normal distribution with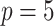 
and covariance 
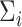for unit 
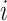. We assume the covariance matrices have identical eigencomponents, but distinct eigenvalues, i.e., 
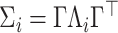, where 
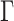is an orthonormal matrix and 
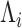is a diagonal matrix with diagonal elements 
, for 
. In the log-linear model,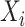 
(
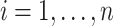) is generated from a Bernoulli distribution with probability 0.5 to be one. Thus, 
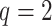because of the intercept column. Two cases are tested: (i) the null case with 
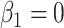(the results are presented in Section E of the supplementary material available at Biostatistics online) and (ii) the alternative case with the second and third eigenvalues satisfying the regression model. For the first case, 
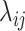is generated from a log-normal distribution with mean 
and variance 
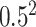. For the second case, 
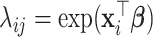with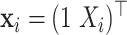 
. The simulation is repeated 200 times.
In Algorithm 2, for higher-order directions, enforcing the orthogonality constraint reduces the parameter search space but increases computation complexity. In this simulation study, we implement both cases with and without the orthogonality constraint. We compare the following methods: (i) our algorithm (Algorithm 2) without the orthogonality constraint, denoted as CAP; (ii)our algorithm with the orthogonality constraint, denoted as CAP-OC; (iii) our modified algorithm assuming that all covariance matrices have identical eigencomponents (Algorithm 3), denoted as CAP-C; (iv) a PCA-based method, where we apply PCA on each unit and regress the first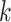 
eigenvalues separately on the covariates, denoted as PCA
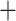Reg; and (v) a common principal component method, where we apply common PCA on all units using the method in Flury (1984) and again regress the first 
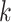eigenvalues separately on the covariates, denoted as CPCA
Reg.
Under the alternative hypothesis setup, we set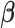 
as
 |
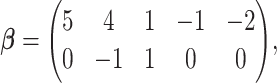where the first row is for the intercept term (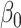
’s). Under this setting, the second and third eigencomponents of the covariance matrices follow the log-linear model (2.1) and the eigencondition (Condition 1) is satisfied. Table 1 presents the estimate of 
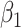and Table 2 the estimate of 
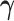over 200 simulations with 
and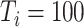 
, where the number of components is determined by the average DfD value using the threshold of two (the validity of this choice is studied using simulations in Section E of the supplementary material available at Biostatistics online). Since the intercept term is not of our study interest, we will not report the results here. For our proposed methods, the coverage probability is obtained by both the asymptotic variance in Theorem 1 and 500 bootstrap samples; while for the two (common) PCA-based methods, only coverage probability from bootstrap is reported. As the data are generated with identical eigencomponents, CAP-C yields the 
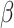estimate with the lowest bias because its assumption is satisfied here. Overall, the estimated 
’s from all our methods are very close, and the coverage probability from either the asymptotic variance or bootstrap achieves the designated level (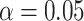
). For the second direction, our first two algorithms (CAP and CAP-OC) have slightly higher bias and their coverage probabilities is smaller than 0.95. The two (common) PCA-based methods do not take into account the covariate information and thus the first two 
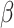estimates are associated with the largest two eigenvalues, even though the first estimated 
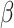component is practically zero. For the estimate of 
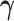, all of our proposed methods yield good estimation of the two true principal directions.
Table 1.
Comparison of estimated (Est.) 
, standard error (SE), and coverage probability of confidence intervals by different methods. Confidence intervals are constructed from 500 bootstrap samples (CP-B) for all methods, and from our normal asymptotic theory (Theorem 1, CP-A) for three CAP algorithms. All values are averaged over 200 simulations
| Method | First direction | Second direction | |||||
|---|---|---|---|---|---|---|---|
| Est. (SE) | CP-A | CP-B | Est. (SE) | CP-A | CP-B | ||
| Truth | −1.00 | — | — | 1.00 | — | — | |
| CAP | −1.00 (0.03) | 0.950 | 0.950 | 0.81 (0.58) | 0.885 | 0.870 | |
| CAP-OC | −1.00 (0.03) | 0.950 | 0.950 | 0.52 (0.84) | 0.730 | 0.715 | |
| CAP-C | −1.00 (0.03) | 0.950 | 0.955 | 1.00 (0.03) | 0.975 | 0.960 | |
PCA Reg |
−0.02 (0.10) | — | 0.940 | −0.98 (0.03) | — | 0.910 | |
CPCA Reg |
−0.01 (0.11) | — | 0.935 | −1.00 (0.03) | — | 0.960 | |
Table 2.
Comparison of estimated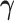 
(standard error) by three CAP algorithms. All values are averaged over 200 simulations
|
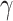
Truth | CAP | CAP-OC | CAP-C | |
|---|---|---|---|---|---|
| First direction |
|
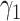
0.45 | 0.42 (0.125) | 0.42 (0.125) | 0.45 (0.002) |
|
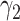
−0.86 | −0.82 (0.057) | −0.82 (0.057) | −0.86 (0.002) | |
|
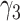
0.14 | 0.13 (0.050) | 0.13 (0.050) | 0.14 (0.004) | |
|
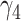
0.14 | 0.13 (0.161) | 0.13 (0.161) | 0.14 (0.002) | |
|
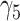
0.14 | 0.14 (0.210) | 0.14 (0.210) | 0.14 (0.002) | |
| Second direction |
|
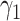
0.45 | 0.43 (0.085) | 0.43 (0.111) | 0.45 (0.002) |
|
0.14 | 0.15 (0.110) | 0.13 (0.157) | 0.14 (0.003) | |
|
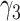
−0.86 | −0.76 (0.282) | −0.61 (0.423) | −0.86 (0.001) | |
|
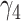
0.14 | 0.13 (0.087) | 0.11 (0.171) | 0.14 (0.003) | |
|
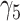
0.14 | 0.06 (0.288) | −0.06 (0.408) | 0.14 (0.002) |
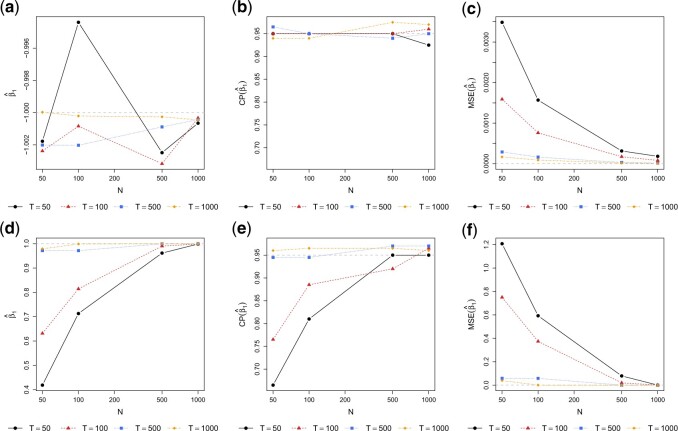
To further assess the finite sample performance of our proposed methods, we vary the number of units with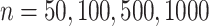 
and the number of observations with 
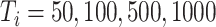. Figure 2 shows the estimate, coverage probability from the asymptotic variance, and the mean squared error (MSE) of model coefficients of the first two directions. From the figure, as both 
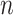and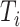 
increase, the estimates of 
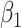in both the first and second estimated direction converge to the true values. The coverage probability of the first direction is close to the designated level of 0.95, and the coverage probability of the second direction converges to 0.95 as both 
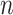and 
increase. The MSEs of both directions converge to zero. Similar results from CAP-C are shown in Figure E.4 of Section E of the supplementary material available at Biostatistics online. To assess the performance of estimating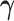 
, we use 
to measure the estimation error due to different scaling factors and sign flipping, where 
is the inner product of two vectors. Figure E.5 in Section E of the supplementary material available at Biostatistics online demonstrates that the error goes to zero as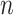 
and 
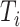increase. The error also goes to zero with increased 
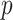and/or 
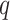as long as 
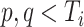and 
.
Fig. 2.
Performance of estimating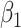 
by CAP as 
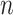and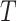 
varies in simulations. Coverage probability (CP) is calculated based on confidence intervals constructed from our normal asymptotic theory (Theorem 1). The gray dashed lines are the true parameters in (a) and (d), the designated level 0.95 in (b) and (e), and zero in (c) and (f). (a) D1: Estimate of 
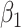, (b) D1: CP of 
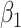, (c) D1: MSE of 
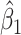, (d) D2: Estimate of 
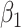, (e) D2: CP of 
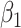, and (f) D2: MSE of 
.
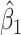To summarize, all our algorithms achieve good performance and the CPA-C algorithm performs slightly better when its complete common diagonalization assumption is satisfied. Without utilizing this assumption, CAP and CAP-OC sacrifice a bit in performance, and the performance differences become negligible as the sample sizes (the number of observations within each subject and the number of subjects) increase.
In the Supplementary material available at Biostatistics online, we present the results from several other simulation scenarios. Tables E.2 and E.3 of the supplementary material available at Biostatistics online present the performance of estimating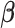 
and 
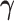, respectively when the data are generated from three non-Gaussian distributions. Our method with bootstrap-based confidence intervals is robust against multivariate 
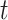with heavy tails (degrees of freedom = 5) but can introduce estimation bias and yield poor probability coverage if the data distribution exhibits extremely heavy tails or skewness. Section E.6 of the supplementary material available at Biostatistics online shows that our method is also relatively robust for estimating the projection parameters, even when some other eigenvectors vary across units.
5. Resting-state fmri data example
We apply our proposed method to the Human Connectome Project resting-state fMRI data, which are publicly available at http://www.humanconnectomeproject.org/. The overarching aim of this project is to characterize human brain structure, function, connectivity, and the associated variability in healthy adults. In this study, we apply our method to study the variation of brain functional connectivity in sex and/or age. Our data set includes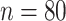 
healthy young adults (aged 22–35; 22 female and 58 male) from the most recent 1200 subjects release. The sample size selected here is typical for fMRI studies. The blood-oxygen-level dependent signals are extracted from 
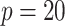functional brain regions in the default mode network (DMN) (Power and others, 2011). The data preprocessing procedure is described in the Supplementary material available at Biostatistics online.
It has been shown that there exists sex and/or age differences in various functional connectivity metrics in the DMN (Gong and others, 2011). In a previous study (Zhang and others, 2016), the sex and age interaction effects were detected in several covariance entries using element-wise regression, but none survived Bonferroni or false discovery rate (FDR) correction. In this study, our covariates include the individual demographic information, i.e., age (continuous) and sex (categorical), together with their interaction. For sex,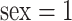 
is for male and 0 for female.
Three methods are compared in this section, including (i) element-wise correlation regression (Wang and others, 2007); (ii) common principal component, i.e., the CPCA
Reg method in Section 4; (iii) our CAP algorithm. In this analysis, we also include a post hoc procedure to examine the orthogonality among the identified projection directions. The 
-values in the element-wise regression are adjusted by FDR correction (Benjamini and Hochberg, 1995), and those in all other models are adjusted by Bonferroni correction.
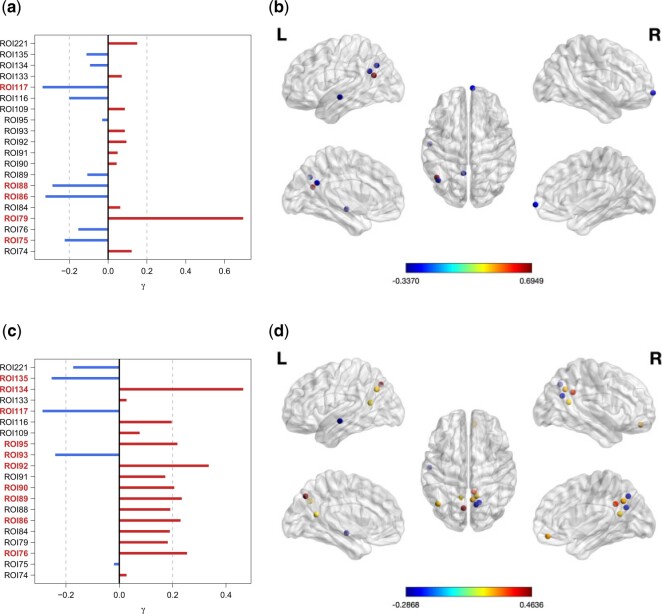
Our CAP method recovers two projection directions, where the number two is chosen based on the average DfD (Figure F.6 of the supplementary material available at Biostatistics online). Table 3 presents the model coefficients (and 95% confidence intervals from 500 bootstrap samples) of the two projection directions. Both directions yield significant regression coefficients associated with sex, age, or interaction. Our result especially discovers the opposite linear trends between male and female young adults with age (Figure F.9 of the supplementary material available at Biostatistics online). This complements a previous finding (Zuo and others, 2010) that the developmental trajectories show sex-related differences based on a much larger age range and a different fMRI metric. Finding a statistically significant interaction by our method improves the inconclusive result on the interaction effect in a previous analysis (Zhang and others, 2016). Figure 3 plots the loading profiles and brain regions with at least moderate loadings. The image patterns show greater local connectivity clustering (Figure 3d) associated with male age trajectories, compared to females (Figure 3b). These patterns are consistent with previous findings.
Table 3.
Estimated regression coefficients (standard errors) and 95% confidence intervals (CI) of the two CAP components estimated from the fMRI data set. Standard errors and confidence intervals are computed using 500 bootstrap samples
| D1 | D2 | |||
|---|---|---|---|---|
| Estimate (SE) | 95% CI | Estimate (SE) | 95% CI | |
| Male–female | −2.068 (0.468) | (−2.985, −1.151) | 0.804 (0.456) | (−0.090, 1.699) |
| Age (female) | −0.051 (0.013) | (−0.077, −0.025) | −0.008 (0.012) | (−0.033, 0.016) |
| Age (male) | 0.013 (0.008) | (−0.002, 0.028) | −0.036 (0.008) | (−0.052, −0.020) |
|
0.064 (0.015) | (0.035, 0.094) | −0.028 (0.015) | (−0.059, 0.002) |
Fig. 3.
Visualizations of the CAP loading values (a and c) and the brain regions (b and d) with absolute loading values greater than 0.2, in the two projection directions (D1–D2) estimated from the fMRI data set. (a) D1: loadings, (b) D1: regions with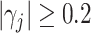 
in brain map, (c) D2: loadings, and (d) D2: regions with 
in brain map.
Table 4 presents the number of significant components in each method at two significance levels after multiple testing corrections. None of the coefficients in the other two competing methods, element-wise regression and CPCA
Reg, are significant at level 0.1. This is because these approaches do not employ the covariates to find covariance patterns and thus perform tests on many irrelevant connections.
Table 4.
Comparison of the number of statistically significant components (and the total number of components) found by different methods on the fMRI data set. Statistical significance is assessed at two significance levels (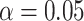
and 
) after multiple testing corrections
Significance level ( ) |
Covariate | CAP | CPCA Reg |
Element-wise regression |
|---|---|---|---|---|
| 0.05 | Age | 1 (2) | 0 (10) | 0 (190) |
| Sex | 1 (2) | 0 (10) | 0 (190) | |
Age sex |
1 (2) | 0 (10) | 0 (190) | |
| 0.10 | Age | 1 (2) | 0 (10) | 0 (190) |
| Sex | 2 (2) | 0 (10) | 0 (190) | |
Age sex |
2 (2) | 0 (10) | 0 (190) |
In summary, our method attains higher statistical power by directly targeting the brain subnetworks that are associated with the covariates of interest and we also demonstrate its robustness and reproducibility across fMRI data sets. Other competing methods may lose power because they do not utilize the covariate information when fitting these subnetworks of interest.
In Section F of the supplementary material available at Biostatistics online, we present comparisons with our other proposed algorithms, detailed analysis results from different methods, validation of our modeling assumptions, and assessment of the reliability of our results using additional fMRI data from the same subjects.
6. Discussion
In this study, we introduced a CAP regression model for multiple covariance matrix outcomes. The approach targets projection directions that are associated with the explanatory variables or covariates, rather than those that explain large variations. Under regularity conditions, our proposed estimators are asymptotically consistent. Extensive simulation studies showed CAP and the variations studied have good finite sample estimation accuracy. Notably, our method avoids the massive number of hypothesis testing in the element-wise regression approaches, which are particularly prevalent in resting-state fMRI analyses. We demonstrate sex- and age-related findings in a sample of healthy adults that are indicated, but not significant, with standard approaches.
One challenge in modeling covariance matrices directly is forcing positive definiteness of model parameters and outcome predictions. Via projections, the study of a positive definite matrix is reduced into modeling the eigenvalues in orthogonal spaces. This preserves the geometric interpretation while working in a space where adhering to the constraint is simple. Existing spectral decomposition-based methods rely on the assumption that the eigencomponents of the covariance matrices are identical. In practice, this is typically unrealistic, especially when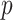 
is large or there are covariates that impact common rotations as well as eigenvalues. Researchers are often more interested in studying a subset of the components related to the covariates. Though our proposed CAP method enables identification of a small set of components, the theoretical analysis is challenging without the common diagonalization regularity condition as in CPCA. For example, in fMRI, some diseases, such as Alzheimer’s, are hypothesized to impact both network architecture (common eigencomponents) and engagement (eigenvalues). One future direction will consider relaxing these assumptions.
Our simulations also assess the robustness and performance of our method for: (i) varying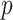 
and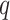 
, (ii) noncommon eigenvectors, and (iii) non-Gaussian distributions. Our method is relatively robust under the first two cases but may introduce estimation bias under some extreme settings in the last case. Our bootstrap confidence intervals can partially mitigate the poor coverage probability issue of the Gaussian theory-based intervals.
The current framework assumes the dimension of the data 
, as well as the dimension of the covariates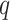 
, is fixed and less than both the number of observations within a subject and the number of subjects. Another future direction is to extend the method to settings of large 
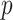and/or large 
.
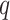7. Software
Software in the form of R package cap, together with a sample input data set and complete documentation is available on CRAN https://cran.r-project.org/web/packages/cap/.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Funding
National Institutes of Health (R01EB022911, P41EB015909, R01NS060910, R01EB026549, R01MH085328, and R01MH085328-S1).
References
- Anderson, T. W. (1973). Asymptotically efficient estimation of covariance matrices with linear structure. The Annals of Statistics 1, 135–141. [Google Scholar]
- Benjamini, Y. and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 57, 289–300. [Google Scholar]
- Boik, R. J. (2002). Spectral models for covariance matrices. Biometrika 89, 159–182. [Google Scholar]
- Box, G. E. P. and Cox, D. R. (1964). An analysis of transformations. Journal of the Royal Statistical Society. Series B (Methodological) 26, 211–252. [Google Scholar]
- Carroll, R. J., Ruppert, D. and Holt R. N. Jr, (1982). Some aspects of estimation in heteroscedastic linear models. Statistical Decision Theory and Related Topics, III 1, 231–241. [Google Scholar]
- Chiu, T. Y. M., Leonard, T. and Tsui, K.-W. (1996). The matrix-logarithmic covariance model. Journal of the American Statistical Association 91, 198–210. [Google Scholar]
- Cohen, M., Dalal, S. R. and Tukey, J. W. (1993). Robust, smoothly heterogeneous variance regression. Applied Statistics 42, 339–353. [Google Scholar]
- Flury, B. N. (1984). Common principal components in k groups. Journal of the American Statistical Association 79, 892–898. [Google Scholar]
- Flury, B. N. (1986). Asymptotic theory for common principal component analysis. The Annals of Statistics 14, 418–430. [Google Scholar]
- Flury, B. N. and Gautschi, W. (1986). An algorithm for simultaneous orthogonal transformation of several positive definite symmetric matrices to nearly diagonal form. SIAM Journal on Scientific and Statistical Computing 7, 169–184. [Google Scholar]
- Fox, E. B. and Dunson, D. B. (2015). Bayesian nonparametric covariance regression. Journal of Machine Learning Research 16, 2501–2542. [Google Scholar]
- Franks, A. and Hoff, P. (2016). Shared subspace models for multi-group covariance estimation. arXiv preprint arXiv:1607.03045. Available at: http://arxiv.org/abs/1607.03045. [Google Scholar]
- Friston, K. J., Frith, C. D., Liddle, P. F. and Frackowiak, R. S. J. (1993). Functional connectivity: the principal-component analysis of large PET data sets. Journal of Cerebral Blood Flow & Metabolism 13, 5–14. [DOI] [PubMed] [Google Scholar]
- Friston, K. J. (2011). Functional and effective connectivity: a review. Brain Connectivity 1, 13–36. [DOI] [PubMed] [Google Scholar]
- Gong, G., He, Y. and Evans, A. C. (2011). Brain connectivity: gender makes a difference. The Neuroscientist 17, 575–591. [DOI] [PubMed] [Google Scholar]
- Hafkemeijer, A., Möller, C., Dopper, E. G. P., Jiskoot, L. C., Schouten, T. M., van Swieten, J. C., van der Flier, W. M., Vrenken, H., Pijnenburg, Y. A. L. and Barkhof, F. (2015). Resting state functional connectivity differences between behavioral variant frontotemporal dementia and Alzheimer’s disease. Frontiers in Human Neuroscience 9: 474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey, A. C. (1976). Estimating regression models with multiplicative heteroscedasticity. Econometrica: Journal of the Econometric Society 44, 461–465. [Google Scholar]
- Hoff, P. D. (2009). A hierarchical eigenmodel for pooled covariance estimation. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 71, 971–992. [Google Scholar]
- Hoff, P. D. and Niu, X. (2012). A covariance regression model. Statistica Sinica 22, 729–753. [Google Scholar]
- Just, M. A., Cherkassky, V. L., Keller, T. A., Kana, R. K. and Minshew, N. J. (2006). Functional and anatomical cortical underconnectivity in autism: evidence from an fMRI study of an executive function task and corpus callosum morphometry. Cerebral Cortex 17, 951–961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krzanowski, W. J. (1984). Principal component analysis in the presence of group structure. Journal of the Royal Statistical Society: Series C (Applied Statistics) 33, 164–168. [Google Scholar]
- Lewis, C. M., Baldassarre, A., Committeri, G., Romani, G. L. and Corbetta, M. (2009). Learning sculpts the spontaneous activity of the resting human brain. Proceedings of the National Academy of Sciences United States of America 106, 17558–17563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo, C., Li, Q., Lai, Y., Xia, Y., Qin, Y., Liao, W., Li, S., Zhou, D., Yao, D. and Gong, Q. (2011). Altered functional connectivity in default mode network in absence epilepsy: a resting-state fMRI study. Human Brain Mapping 32, 438–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mennes, M., Vega Potler, N., Kelly, C., Di Martino, A., Castellanos, F. X. and Milham, M. P. (2012). Resting state functional connectivity correlates of inhibitory control in children with attention-deficit/hyperactivity disorder. Frontiers in Psychiatry 2, 83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park, B., Kim, J. and Park, H. (2016). Differences in connectivity patterns between child and adolescent attention deficit hyperactivity disorder patients. In: 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). Orlando, FL, USA: IEEE, pp. 1127–1130. [DOI] [PubMed] [Google Scholar]
- Poldrack, R. A., Mumford, J. A. and Nichols, T. E. (2011). Handbook of Functional MRI Data Analysis. New York, NY: Cambridge University Press. [Google Scholar]
- Pourahmadi, M., Daniels, M. J. and Park, T. (2007). Simultaneous modelling of the Cholesky decomposition of several covariance matrices. Journal of Multivariate Analysis 98, 568–587. [Google Scholar]
- Power, J. D., Cohen, A. L., Nelson, S. M., Wig, G. S., Barnes, K. A., Church, J. A., Vogel, A. C., Laumann, T. O., Miezin, F. M. and Schlaggar, B. L. (2011). Functional network organization of the human brain. Neuron 72, 665–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao, C. R. (1964). The use and interpretation of principal component analysis in applied research. Sankhyā: The Indian Journal of Statistics, Series A, 329–358. [Google Scholar]
- Rao, C. R. (1973). Algebra of vectors and matrices. Linear Statistical Inference and its Applications, 2nd edition. New York: Wiley, pp. 1–78. [Google Scholar]
- Seiler, C. and Holmes, S. (2017). Multivariate heteroscedasticity models for functional brain connectivity. Frontiers in Neuroscience 11: 696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyth, G. K. (1989). Generalized linear models with varying dispersion. Journal of the Royal Statistical Society. Series B (Methodological) 51, 47–60. [Google Scholar]
- Wang, K., Liang, M., Wang, L., Tian, L., Zhang, X., Li, K. and Jiang, T. (2007). Altered functional connectivity in early Alzheimer’s disease: a resting-state fMRI study. Human Brain Mapping 28, 967–978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, C., Cahill, N. D., Arbabshirani, M. R., White, T., Baum, S. A. and Michael, A. M. (2016). Sex and age effects of functional connectivity in early adulthood. Brain Connectivity 6, 700–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou, T., Lan, W., Wang, H. and Tsai, C.-L. (2017). Covariance regression analysis. Journal of the American Statistical Association 112, 266–281. [Google Scholar]
- Zuo, X.-N., Kelly, C., Di Martino, A., Mennes, M., Margulies, D. S., Bangaru, S., Grzadzinski, R., Evans, A. C., Zang, Y.-F. and Castellanos, F. X. (2010). Growing together and growing apart: regional and sex differences in the lifespan developmental trajectories of functional homotopy. Journal of Neuroscience 30, 15034–15043. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.