Modeling the selective advantage of new amino acids on the hemagglutinin of H1N1 influenza viruses using their patient age distributions

Abstract

In 2009, a new strain of H1N1 influenza A virus caused a pandemic, and its descendant strains are causing seasonal epidemics worldwide. Given the high mutation rate of influenza viruses, variant strains having different amino acids on hemagglutinin (HA) continuously emerge. To prepare vaccine strains for the next influenza seasons, it is an urgent task to predict which variants will be selected in the viral population. An analysis of 24,681 pairs of an amino acid sequence of HA of H1N1pdm2009 viruses and its patient age showed that the empirical fixation probability of new amino acids on HA significantly differed depending on their frequencies in the population, patient age distributions, and epitope flags. The selective advantage of a variant strain having a new amino acid was modeled by linear combinations of patients age distributions and epitope flags, and then the fixation probability of the new amino acid was modeled using Kimura’s formula for advantageous selection. The parameters of models were estimated from the sequence data and models were tested with four-fold cross validations. The frequency of new amino acids alone can achieve high sensitivity, specificity, and precision in predicting the fixation of a new amino acid of which frequency is more than 0.11. The estimated parameter suggested that viruses with a new amino acid having a frequency in the population higher than 0.11 have a significantly higher selective advantage compared to viruses with the old amino acid at the same position. The model considering the Z-value of patient age rank-sums of new amino acids predicted amino acid substitutions on HA with a sensitivity of 0.78, specificity of 0.86, and precision of 0.83, showing significant improvement compared to the constant selective advantage model, which used only the frequency of the amino acid. These results suggested that H1N1 viruses tend to be selected in the adult population, and frequency of viruses having new amino acids and their patient ages are useful to predict amino acid substitutions on HA.

1. Introduction

There are one billion seasonal influenza cases, with three to five million severe cases and around 409 thousand influenza-related deaths annually (World Health Organization 2019). The seasonal influenza is caused by two subtypes of influenza A viruses, H1N1 and H3N2, and two strains of influenza B viruses circulating in the human population. Quadrivalent vaccines, containing two strains from type A viruses and two strains from type B, or trivalent vaccines, containing two from type A viruses and one type B strain, are used to reduce the risk of severe symptoms caused by seasonal influenza (World Health Organization 2020).

The hemagglutinin (HA), the major antigen of influenza A viruses, undergoes adaptive evolution that alters their antigenicity in human population. This antigenic evolution is caused by a process where human immunity selects variant strains antigenically different from strains that have been circulating in the past (Smith et al. 2004). Amino acid substitutions on epitope regions on HA are responsible for the difference in antigenicity (Koel et al. 2013). HA of subtype H3N2 has five epitope regions (Wilson and Cox 1990), while H1N1 HA has four epitope regions (Igarashi et al. 2010). It is known that epitope regions on HA show positive selection, under which non-synonymous mutations occurred more frequently than synonymous mutations (Bush et al. 1999a; Suzuki 2008). The adaptive evolution of circulating influenza strains can be observed using genomic sequences stored in public databases in real time (Neher and Bedford 2015).

Different age groups have different adaptive immune profiles against influenza viruses. An individual’s immunity is known to be mostly affected by the first infection in life, and this phenomenon is called the original antigenic sin (Francis et al. 1947; Davenport et al. 1955; Francis, 1960; Lessler et al. 2012; Nachbagauer et al. 2017). Using a mathematical model, Kucharski and Gog (2012) demonstrated that the more influence the original antigenic sin has on current immunity against seasonal influenza, the more it alters the age distribution of immunity. Gostic et al. (2016) showed that the subtype with which an individual was infected first in life affected the severity of infections with H5N1 and H7N9. Using data on vaccine efficacy, Arevalo et al. (2020) showed that severity of H1N1 and H3N2 influenza infections was reduced depending on the subtype that the individual was first infected with.

The driving force of the adaptive evolution of seasonal influenza viruses is immunity in the human population, which are different depending on age groups. Several studies have developed computational models to predict influenza strains that would become dominant in subsequent seasons. Bush et al. (1999b) predicted strains that became dominant in next seasons by using positively selected codons. Ito et al. (2011) used statistics on the number of different amino acids from past strains to predict future dominant strains of H3N2 viruses. Physicochemical properties of amino acids on HA have also been used to predict the antigenic variations of H3N2 (Du et al. 2012; Suzuki 2013; Cui et al. 2014; Suzuki 2015). (Steinbrück et al. 2014) combined serological data with the phylogenetic tree of HA to predict suitable vaccine strains. (Łuksza and Lässig 2014) developed a model to estimate the fitness of H3N2 strains using adaptive mutations on epitopes and deleterious mutations outside the epitopes on HA. Neher et al. (2014) used the shape of genealogical tree to predict progenitor lineage of the upcoming season. Huddleston et al. (2020) developed a model to predict the frequency of an H3N2 strain in the future using its current frequency and fitness, determined by the antigenic novelty of epitopes and the mutational load in non-epitopes of HA. See a review paper by Morris et al. (2018) for a comprehensive list of previous models attempting to predict the evolution of influenza viruses. However, none of these previous studies considered the age distribution of patients to predict the evolution of influenza viruses.

Given the high mutation rate of influenza viruses, variant strains having different amino acids on HA continuously emerge during seasonal epidemics (Fitch et al. 1991). However, only a limited number of new amino acids become fixed in the viral population and most of them become extinct. The probability that a new allele becomes fixed is called fixation probability. The relationship between allele frequency and fixation probability was investigated in conditions under neutral evolution (Kimura 1955), adaptive evolution (Kimura 1962), nearly neutral evolution (Ohta 1992), and various relaxed assumptions (Gerrish and Lenski 1998; Gavrilets and Gibson 2002; Wilke 2003; Lambert 2006; Patwa and Wahl, 2008). There are a few previous works studying the fixation probability of variant strains of influenza viruses. (Steinbrück and McHardy 2011) analyzed the allele frequency of H3N2 viruses over time and showed that alleles that increases in frequency more rapidly were more likely to become fixed, and this phenomenon was later confirmed by computer simulations (Castro et al. 2020). (Strelkowa and Lässig 2012) found that non-synonymous mutations on non-epitope regions of HA reduced the fixation probability of strains. Illingworth and Mustonen (2012) modeled the effect of linkage disequilibrium on the selection of alleles in adaptive evolution, and they estimated the influence of interference by other alleles in the evolution of H3N2 strains.

In this article, we investigate the relationships between fixation probabilities of new amino acids on HA and their frequencies, patient age distributions, and epitope flags. We construct mathematical models of the selective advantage of a new amino acid using patient age distributions and the epitope flags, then calculate the fixation probability using Kimura’s formula for advantageous selection. The model parameters are estimated by maximizing the likelihood of fixation and extinction events observed in the HA sequence data of H1N1 influenza viruses circulating from 2009 to 2020. We evaluate the predictability of models using training-test cross-validations. Based on the results, we discuss the importance of the distribution of patient ages in predicting adaptive evolution of seasonal influenza viruses.

2. Materials and methods

2.1 Sequence data

We downloaded complete HA sequences of influenza A H1N1 pandemic 2009 viruses isolated from humans during March 2009 to May 2020 from the Global Initiative on Sharing All Influenza Data (GISAID) (Shu and McCauley 2017). The HA sequences that had metadata about ages of patients were selected and used for subsequent analyses. As a result, we obtained a total of 24,681 unique pairs of an amino acid sequence and the age of its patient. To investigate temporal change in the frequency of amino acids on HA, the sequences were grouped into four-month sliding windows. A total of 130 four-month sliding windows were obtained. The first sliding window contains HA sequences from March to June 2009, the second contains those from April to July 2009, and the last contains those from February to May 2020. The four-month sliding windows contain an average of 741,58 sequences with a minimum of 47 and a maximum of 4,347 sequences. The temporal change in the number of sequences in each four-month window is shown in Supplementary Fig. S1A. The patient age distribution for each year from March 2009 to May 2020 is shown in Supplementary Fig. S1B.

2.2 Tracking frequencies of newly emerged amino acids

Amino acid substitution is a process where an allele having a new amino acid at a residue position on a protein becomes fixed and those having the other amino acids at the position become extinct. To track the transition from an old amino acid to a new amino acid at a position on HA, we calculated frequencies of amino acids on each position for each sliding window. Historically, an allele is called fixed when its frequency becomes 1.0, and extinct when it becomes 0.0. In this study, however, we relax the condition of fixation and consider an amino acid as fixed when its frequency exceeds 0.95 in a sliding window. The reason for this relaxation is that variant strains with other amino acids than the new amino acid emerge from time to time, and there is almost no chance for the frequency to become 1.0. The condition for extinction remains the same as the historical definition, where an allele becomes extinct at a frequency of 0.0. For each residue position on HA, an amino acid in a window is called old if the amino acid has just become fixed in the current window or it has been old in its preceding windows. After a fixation event, the other amino acids found at this position are considered as new amino acids. An old amino acid remains old, even though its frequency drops below 0.95, until another amino acid becomes fixed at its position. When an old amino acid has been substituted by another amino acid and appears after the substitution, it is considered as a new amino acid. In the first window, the old amino acid at each position is defined by its consensus amino acid.

2.3 Months from emergence and frequency of amino acids

For each new amino acid, a set of consecutive four-month sliding windows from its emergence to its fixation or extinction was identified. Frequencies of the new amino acid in these windows were recorded with its evolutionary outcome, that is, fixation or extinction. We stratified amino acids in the identified four-month sliding windows into strata of frequency ranges with a width of 0.1 starting with (0.0, 0.1] and ending with (0.9, 1.0] according to their frequencies. For each frequency range, the evolutionary outcomes of new amino acids of which frequencies at a time point were within the range were collected and used to calculate the empirical fixation probabilities. The empirical fixation probability of new amino acids within each frequency range was calculated as the number of new amino acids that later became fixed divided by the total number of new amino acids. Amino acids in which their outcomes have not yet been determined were excluded from the calculation. Amino acids with frequencies higher than 95% were excluded from the analysis because they were considered to have already been fixed. The 95 per cent binomial confidence intervals of fixation probabilities were calculated by the method of Clopper and Pearson (1934).

2.4 Comparison of patient age distributions between new and old amino acids

We define the transition phase of an amino acid substitution as the period from its emergence to its fixation. For each new amino acid at a position on HA that later became fixed, sequences in each four-month sliding window during its transition phase were divided into three groups: those having the new amino acid that later became fixed at the position, those having new amino acids which later became extinct, and those having the old amino acid. The age of patients of sequences in each group was collected. Patient ages of sequences with the new amino acids that later became fixed and those with old amino acids at the position were compared using the two-tailed Wilcoxon rank-sum test, with a null hypothesis that the distribution of patient ages of sequences with the new amino acid that later became fixed are the same as those of the old amino acid. The resulting P-values from the two-tailed Wilcoxon rank-sum test were adjusted by Bonferroni’s correction. Cohen’s $d$ (Cohen 1992) was used to estimate the effect size of having a new amino acid on median patient ages for fixed amino acid substitution.

2.5 Relationship between empirical fixation probability and patient ages and epitope flags

For each four-month sliding window that contains at least one new amino acid, the evolutionary outcomes of all new amino acids were collected. To exclude four-month sliding windows that had extremely small numbers of sequences, four-month sliding windows containing less than sixty sequences, the first percentile of numbers of sequences of all windows, were excluded from the analyses. We set a threshold on the minimum frequency of a new amino acid in a four-month sliding window to be included in the calculation of the empirical fixation probability. The threshold was set to 0.11 in order to have a total empirical fixation probability of 0.5 (Supplementary Fig. S2A). This ensures that the number of four-month sliding windows consisting of new amino acids which became fixed is almost equal to the number of those which became extinct. However, new amino acids that became extinct would naturally appear in less numbers of windows compared to those that became fixed. Thus, the number of unique new amino acids may not be equal. See Section 4 for the reason for setting a threshold.

For each new amino acid of which frequency among all sequences at its position is more than 0.11 in a four-month sliding window, the profile of the new amino acid was defined as follows. The profile of new amino acid $i$ in a four-month sliding window is represented by a combination of three variables $(f_i,\mathrm{ }{a}_i,\mathrm{ }{\mathrm{e}}_i)$, where $f_i$ is the frequency of $i$ in the four-month sliding window, $a_i$ is its patient age statistic, and $e_i$ is its epitope flag. We used the epitope information of HA of H1N1 viruses according to Igarashi et al. (2010). Epitope flag $e_i=1$ if $i$ is a new amino acid in an epitope region on HA and $e_i=0$ otherwise.

We stratified profiles of new amino acids in all four-month sliding windows according to patient age statistic $a_i$ and epitope flag $e_i$. The patient age statistics involved the median patient age of the new amino acids, median patient ages of old amino acids, differences of median patient ages between new and old amino acids and differences of distribution of patient ages between new and old amino acids, which are defined as follows.

Let X and Y be sets of patient ages of amino acid sequences with a new amino acid and an old amino acid at a position, respectively. The median age difference, $a.\mathit{diff}$, is defined by

$$a.\mathit{diff}\mathrm{ }=\mathrm{ }\mathrm{median}\left(X\right)\mathrm{ }–\mathrm{ }\mathrm{median}\left(Y\right).$$

As another statistic for the difference in distributions of patient ages between a new amino acid and an old amino acid at the same position, we considered the z-value of the W statistic under its normal approximation, which is used in the Wilcoxon rank-sum test with continuity correction (Hollander et al. 2014). The z-value of rank-sum of a new amino acid, $a.\mathit{wilcox}$, is defined by

$$a.\mathit{wilcox}\mathrm{ }=\mathrm{ }\frac{{\sum }_{i=0}^{|X|}\mathit{rank}\left(x_i\right)-{\mu }_X}{{\sigma }_X}$$

Here, $x_i$ represents an element of X and $\mathit{rank}\left(x\right)$ represents the rank of $x$ in $X\cup Y$, and $|X|$ and $|Y|$ represent sizes of X and Y, respectively. The ${\mu }_X$ and ${\sigma }_X$ are the expected mean and the standard deviation of the sum of ranks of $x$ in X, which are obtained by

$${\mu }_X=\frac{|X|(|X|+|Y|+1)}{2},\mathit{and}$$

$${\sigma }_X=\sqrt{\frac{|X||Y|(|X|+|Y|+1)}{12}}.$$

The empirical fixation probability for each stratum was calculated from the number of profiles of new amino acids that later became fixed and those that later became extinct.

2.6 Model of fixation probability

We use Kimura’s formula for advantageous selection (Kimura 1962) to represent the fixation probability of a new amino acid. Thus, the fixation probability of a new amino acid at a residue position on HA, $P_{\mathit{fix}}(f,\mathrm{ }Ns)$, is given by

$$P_{\mathit{f}\mathit{i}\mathit{x}}\left(f,\mathrm{ }Ns\right)=\frac{1-e^{–4Nsf}}{1-e^{–4Ns}}\mathrm{ },$$ (1)

where N is the effective population size, s is the selective advantage of the amino acid, and $f\mathrm{ }(0\le f\le 1)$ is the frequency of viruses having the new amino acid at the position on HA in the viral population. We assume that $N$ is constant over time to use formula (1) as the first approximation for its simplicity. This constant assumption of viral population is discussed in detail in the Section 4.

Let $s_i$ be the selective advantage of viruses that have new amino acid $i$ at a position on HA over those having the other amino acids at the same position. In this study, we hypothesized that $s_i$ can be represented as a linear combination of factors associated with survival in the human population. By assuming a constant effective population $N$, the product of $N$ and selective advantage $s_i$ are expressed as

$$N{s}_i=C_a{a}_i\mathrm{ }+\mathrm{ }{C}_e{e}_i\mathrm{ }+\mathrm{ }{C}_0\mathrm{ },$$ (2)

where $a_i$ is an age statistic representing how effectively the viruses with new amino acid $i$ can infect adults compared to those with the old amino acid at the same position, $e_i$ is the epitope flag of the position expressing whether or not the position is epitope of HA. $C_a$, $C_e$, and $C_0$ represent coefficients for the age statistic, the epitope flag, and the intercept, respectively.

Combinations of age statistics $a.\mathit{dif}{f}_i$, $a.\mathit{wilco}{x}_i$, and epitope flag $e_i$ for a new amino acid $i$ yield a total of six models.

(M1)$N{s}_i=C_0$,

(M2)$N{s}_i=C_{a}a.\mathit{dif}{f}_i+C_0$,

(M3)$N{s}_i=C_{a}a.\mathit{wilco}{x}_i+C_0$,

(M4)$N{s}_i=C_e{e}_i+C_0$,

(M5)$N{s}_i=C_{a}a.\mathit{dif}{f}_i+C_e{e}_i+C_0$,

(M6)$N{s}_i=C_{a}a.\mathit{wilco}{x}_i+C_e{e}_i+C_0$

Suppose $F=\left\{\right(f_1^F,\mathrm{ }{a}_1^F,\mathrm{ }{e}_1^F),\mathrm{ }(f_2^F,\mathrm{ }{a}_2^F,\mathrm{ }{e}_2^F),\mathrm{ }\dots ,\mathrm{ }(f_n^F,\mathrm{ }{a}_n^F,\mathrm{ }{e}_n^F\left)\right\}$ is a set of profiles of new amino acids that later became fixed and $E=\left\{\right(f_1^E,\mathrm{ }{a}_1^E,\mathrm{ }{e}_1^E),\mathrm{ }(f_2^E,\mathrm{ }{a}_2^E,\mathrm{ }{e}_2^E),\mathrm{ }\dots ,\mathrm{ }(f_m^E,\mathrm{ }{a}_m^E,\mathrm{ }{e}_m^E\left)\right\}$ is a set of those that later became extinct. The likelihood of coefficients $\theta =(C_a,\mathrm{ }{C}_e,\mathrm{ }{C}_0)$ is given by

$$={\prod }_{i=1}^n\frac{1-\text{exp}(-4N{s^F}_i{f^F}_i)}{1-\text{exp}(-4N{s^F}_i)}{\prod }_{j=1}^m(1-\frac{(1-\text{exp}(-4N{s^E}_j{f^E}_j\left)\right)}{1-\text{exp}(-4N{s^E}_j)})$$

$$={\prod }_{i=1}^n\frac{1-\exp \left(-4\left(C_a{a^F}_i\mathrm{ }+\mathrm{ }{C}_e{e^F}_i\mathrm{ }+\mathrm{ }{C}_0\right){f^F}_i\right)}{1-\exp \left(-4\left(C_a{a^F}_i\mathrm{ }+\mathrm{ }{C}_e{e^F}_i\mathrm{ }+\mathrm{ }{C}_0\right)\right)}$$

$${\prod }_{j=1}^m(1-\frac{(1-\text{exp}(-4(C_a{a^E}_j\mathrm{ }+\mathrm{ }{C}_e{e^E}_j\mathrm{ }+\mathrm{ }{C}_0){f^E}_j\left)\right)}{1-\text{exp}(-4(C_a{a^E}_j\mathrm{ }+\mathrm{ }{C}_e{e^E}_j\mathrm{ }+\mathrm{ }{C}_0\left)\right)})$$

• $L\left(\theta \right)={\prod }_{i=1}^n\left(P_{\mathit{fix}}\left(f_i^F,{Ns}_i^F\right)\right){\prod }_{j=1}^m\left(1-P_{\mathit{fix}}\left(f_j^E,{Ns}_j^E\right)\right)$

The maximum likelihood estimation of $\theta =(C_a,\mathrm{ }{C}_e,\mathrm{ }{C}_0)$ was performed by maximizing the logarithm of $L(\theta )$. The optim function in R software was used for the maximization of log likelihood (Bélisle 1992). The 95 per cent confidence intervals for each parameter were obtained by the profile likelihood methods (Pawitan 2001).

2.7 Evaluation of models

The models of fixation probability were evaluated by four-fold cross-validation prediction tests. From March 2009 to May 2020, there were sixty-two new amino acids exceeding a frequency of 0.11, of which nineteen resulted in fixation and forty-three resulted in extinction (Supplementary File 1). The nineteen fixed amino acids were considered as positive samples, $F=\mathrm{ }{D}_1^{+}\cup D_2^{+}\cup \cdots \cup D_{19}^{+}$, consisting of 304 profiles in total. The forty-three extinct amino acids were considered as negative samples, $E=D_1^{–}\cup D_2^{–}\cup \cdots \cup D_{43}^{–}$, consisting of 286 profiles in total. Because it can take longer than four months for an amino acid to reach fixation or extinction, the same new amino acid appears in multiple profiles from different four-month windows during the course of its evolutionary trajectory. For this reason, the number of profiles exceeds the number of fixed amino acids and extinct amino acids.

New amino acids at different positions may evolve in an almost perfect linkage disequilibrium. If profiles of an amino acid substitution in a test set is linked to another amino acid substitution in training set, the result of the cross-validation test may be affected by the shared information of a single evolutionary event. To avoid sharing information of the linked amino acid substitution between the training set and the test set in cross-validation tests, groups of amino acid substitutions that are almost in perfect linkage disequilibrium were identified using correlation coefficient squared $r^2$ based on linkage disequilibrium coefficient (Sved and Hill 2018).

Suppose we have a new amino acid, $A$, at a position of HA and a new amino acid, $B$, at another position. Let $p\left(A\right)$ and $p\left(B\right)$ denote the frequency of allele $A$ and $B$ in the population, respectively.

The square of correlation coefficient between two alleles, $r^2$, which is commonly used to measure linkage disequilibrium of a pair of alleles at two loci, is defined by

$$r^2\left(AB\right)=\frac{{\left(p\left(AB\right)-p\left(A\right)p\left(B\right)\right)}^2}{p\left(A\right)\left(1-p\left(A\right)\right)p\left(B\right)(1-p\left(B\right))}$$

$r^2$ of one means that the pair are in perfect linkage disequilibrium. To identify groups of linked new amino acids, pairwise $r^2$ between all new amino acids occurring during overlapping periods were calculated. Highly linked new amino acids, defined by having pairwise $r^2$ of more than 0.75 are grouped together using DBSCAN algorithm (Sander et al. 1998). The cutoff value for $r^2$ of 0.75 was selected so that all synchronized pairs of fixed new amino acids, visually identified from Supplementary Fig. S11, were grouped together and that the total number of groups remained as large as possible (Supplementary Fig. S3). Using the cutoff value, a total of forty-nine groups of amino acid substitutions, each of which consists of new amino acids that are almost in perfect linkage disequilibrium with another amino acid in the group, were identified.

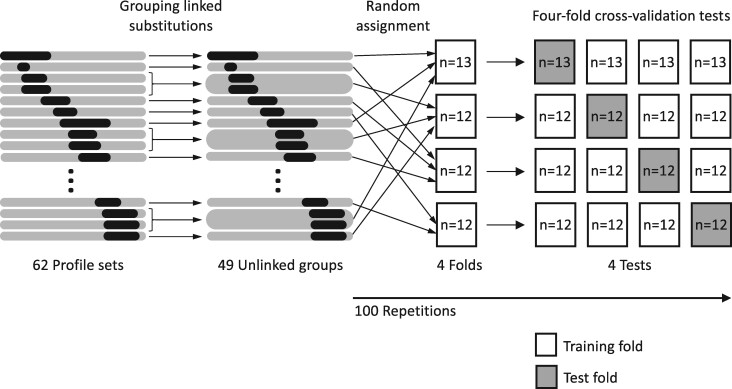
Finally, in order to perform cross-validation, the forty-nine groups were randomly assigned to four datasets, three of which consisting of twelve groups and the other consisting of thirteen groups (Fig. 1). For each random assignment, profiles in three of the datasets were used as training set to estimate parameters of each model by maximizing log likelihood to the observed evolutionary outcomes. The other dataset was used as test set to evaluate the predictability of the model. Four cross-validation tests were conducted in each random assignment and this process was repeated 100 times. The cross-validation was performed 400 times in total. The grouping of profiles prior to cross-validation ensured that no fixation or extinction events of the same amino acids or amino acids in linkage disequilibrium were shared between the training and test data during cross-validation. Akaike information criterion (AIC) values of models were calculated from the log likelihood estimation of the training set. Figure 1 shows the schematic diagram of cross-validation tests.

Figure 1.

Schematic diagram of cross-validation tests.

In each prediction test, the model predicts a new amino acid to become fixed if $P_{\mathit{fix}}$ for its profile in its four-month sliding window is greater than 0.5, and extinct if otherwise. Sensitivity, specificity, precision, and Youden’s index of each model were calculated from the number of true-positive predictions ($tp$), true-negative predictions ($tn$), false-positive predictions ($fp$), and false-negative predictions ($fn$) as follows:

$\text{Sensitivity}=\frac{tp}{tp+fn},$ $\text{Specificity}=\frac{tn}{tn+fp},$ $\text{Precision}=\frac{tp}{tp+fp},$

Youden’s index = Sensitivity + Specificity – 1

2.8 Timing of amino acid substitutions in different birth-year groups

The timing of amino acid substitutions in different birth-year groups was visualized as follows. For each new amino acid that later become fixed, amino acid sequences during its transition phases were divided into ten-year bins according to the year when patients were born. The frequency of sequences having the new amino acid at the position among those having new and old amino acids was calculated for each birth-year group in each four-month sliding window. The frequency of a new amino acid for a birth-year group equals zero when the new amino acid has not yet been found at its position on HA of viruses isolated from patients in the birth-year group. The frequency becomes one when viruses having the old amino acid at the position on HA was completely replaced by those having new amino acid in patients of the birth-year group.

The dominant amino acids on HA of the H1N1 strains circulating before the 2009 pandemic were determined from amino acid sequences obtained from GISAID database.

3. Results

3.1 Empirical fixation probability of new amino acids on HA

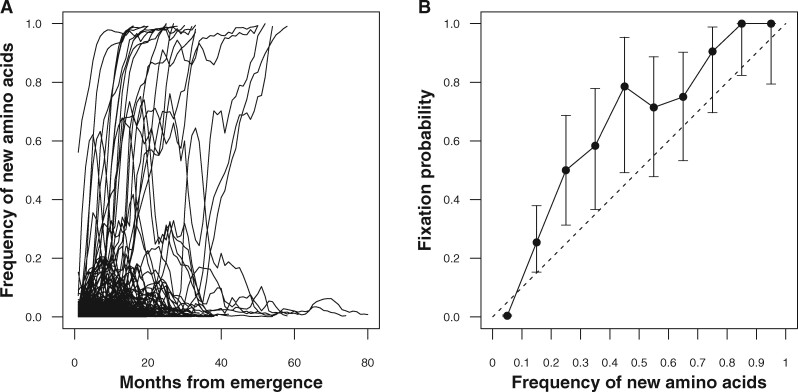
From March 2009 to May 2020, HA had a total of 4,580 new amino acids at 491 amino acid positions, which cover 89 per cent of residues of the molecule. Figure 2A shows trajectories of frequencies in four-month sliding windows of all these amino acids. For some amino acids, it took twelve months to become fixed while some took fifty-four months. Most of the new amino acids became extinct shortly after their emergence, while a few of them remained for more than seventy months. Of 4,580 new amino acids, nineteen resulted in fixation (solid lines) while the others became extinct (dotted lines). The empirical fixation probability of all new amino acids was 0.004. However, the empirical fixation probability increased as the frequency of new amino acids increased (Fig. 2B). Supplementary Table S1 shows the number of fixed and extinct amino acid trajectories that reached a frequency of 0.10 and those that did not reach the frequency. The number of fixed and extinct amino acid trajectories is dependent on whether the frequency of viruses having new amino acids have exceeded 0.10 or not ($p<{10}^{-16}$ with ${\chi }^2$ test). The fixation probabilities exceeded the mid-point value of each frequency range of the new amino acids when the frequency is above 0.10. The lower 95 per cent confidence intervals of fixation probabilities for the frequency ranges within 0.20 to 0.55 exceeded the mid-point values of those frequency ranges.

Figure 2.

The frequency of new amino acids on HA and their empirical fixation probability. (A) Trajectories of the frequency of new amino acids in the population from their emergence to fixation or extinction. Solid lines represent the frequency of new amino acids that later became fixed, while dotted lines represent those that later became extinct. (B) Empirical fixation probabilities of new amino acids stratified by their frequencies. X-axis represents the frequency of new amino acids at a position in the population. Y-axis represents the empirical fixation probability of new amino acid trajectories that reached the frequency on the X-axis. Error bars are the 95% binomial confidence intervals of the fixation probability.

Neutral evolution is an evolutionary process where every new allele becomes fixed with an equal chance. It is known that the fixation probability of a strain would be equal to its frequency under neutral evolution (Kimura 1955). If the fixation of amino acid substitutions occurs under neutral evolution, the fixation probability will fall upon the neutral line (dashed line in Fig. 2B). The excess of the empirical fixation probability indicates that the fixation of new amino acids on HA is under adaptive evolution where viral or environmental factors increase their chance of becoming fixed.

3.2 Fixation of new amino acids on HA

As of December 2020, nineteen new amino acids on HA have become fixed since the beginning of the pandemic in 2009 (Table 1). Of nineteen fixations, two occurred at position 185 on HA. These eighteen fixed positions spread across the HA1 domain with three exceptions occurring on HA2 (positions 374, 451, and 499). Seven (36.84%) out of nineteen substitutions occurred on one of the four distinct antigenic sites, Sa, Sb, Ca, and Cb (Igarashi et al. 2010).

Table 1.

Amino acid substitutions on HA and median patient ages during their transition phases.

Position	Epitope	Transition phase	Duration (month)	Old amino acids		New amino acids		Difference between median patient agesb (year)	P-value
				Amino acid (n)	Median patient age (Q1, Q3)a (year)	Amino acid (n)	Median patient age (Q1, Q3)a (year)
203	Ca	2009.03–2009.09	6	S (211)	18 (9, 31)	T (632)	20 (11, 33)	2	$\approx$ 1
374	–	2009.03–2011.04	25	E (1747)	19 (10, 31)	K (984)	21 (8, 36.25)	2	0.6538
451	–	2009.04–2012.08	40	S (2468)	19 (9, 31)	N (691)	23 (10, 41)	4	0.0002***
185	Sb	2009.10–2012.08	34	S (1647)	19 (9, 31)	T (669)	23 (9, 41)	4	0.0004***
97	–	2009.04–2013.05	49	D (2654)	19 (9, 32)	N (1056)	24 (8, 41)	5	0.0002***
499	–	2011.07–2013.05	22	E (482)	22 (8, 37)	K (437)	28 (9, 43)	6	0.0262*
283	–	2012.03–2013.06	15	K (345)	21 (7, 37)	E (453)	28 (10, 44)	7	0.0141*
163	Sa	2012.07–2013.11	16	K (464)	26 (6, 40.25)	Q (303)	30 (16.5, 44)	4	0.0208*
256	–	2012.07–2013.11	16	A (588)	25 (6, 41)	T (308)	29 (16, 44)	4	0.0231*
84	–	2014.08–2016.06	22	S (1176)	23 (5, 47)	N (3900)	31 (7, 51)	8	5.13 × 10-6***
216	–	2014.10–2016.06	20	I (1467)	23 (5, 47)	T (3579)	32 (7, 52)	9	6.33 × 10-9***
162	Sa	2015.05–2016.06	13	S (852)	20 (4, 43)	N (3568)	32 (7, 52)	12	8.81 × 10-14***
295	–	2016.09–2017.09	12	I (958)	25 (5, 47)	V (399)	29 (5, 51)	4	$\approx$ 1
74	Cb	2016.09–2017.10	13	S (971)	24 (5, 47)	R (583)	24 (4, 48)	0	$\approx$ 1
164	Sa	2016.10–2017.10	12	S (1082)	27 (5, 48)	T (385)	19 (3, 47)	–8	0.1883
183	–	2014.08–2019.02	54	S (8713)	27 (5, 49)	P (6392)	28 (6, 52)	1	4.51 × 10-5***
260	–	2017.06–2020.01	31	N (7413)	22 (5, 48)	D (6020)	33 (8, 55)	11	6.50 × 10-48***
185	Sb	2015.09–2020.02	53	T (13718)	28 (5, 51)	I (5088)	30 (6, 53)	2	0.0072**
129	–	2017.06–2020.02	32	N (8764)	26 (5, 50)	D (4718)	32 (7, 54)	6	1.58 × 10-18***

^aQ₁ and Q₃ represent the first and third quartiles of patient ages, respectively.

^bThe difference in median patient age is calculated by subtracting the median patient age of old amino acid from the median patient age of new amino acid.

^* $P<0.05$ by two-sided Wilcoxon rank-sum test adjusted by Bonferroni’s correction with $n=19$.

^** $P<0.01$ as above.

^*** $P<0.001$ as above.

Of nineteen fixed new amino acids, seventeen had higher median patient ages than old amino acids during their transition phases (Table 1). Exceptions were amino acid substitutions at positions 74 and 164. Arginine (R) at position 74 had the same median age as Serine (S). Threonine (T) at position 164 had lower median patient age than S. The median patient ages of viruses having the fixed new amino acids was higher than those of the old amino acids by an average of 4.4 years. Viruses having fourteen fixed new amino acids (73.68%) had significantly higher patient ages than those having the old amino acids at the same position during their transition phases. Cohen’s $d$ effect size based on the nineteen pairs of median patient ages of new amino acid and old amino acid in Table 1 was estimated to be 1.11, with 95 per cent CI from 0.45 to 1.77. The effect sizes are considered as negligible, small, medium, and large when $\left|d\right|<0.2$, $\left|d\right|<0.5$, $\left|d\right|<0.8$, and $\left|d\right|\ge 0.8$, respectively (Cohen 1992). Thus, we can reject a null hypothesis that the effect of having a new amino acid on median patient age is negligible in fixed amino acid substitutions. This result indicated that viruses that had been selected by human immunity had non-negligible excess infectivity to the adult population. The patient ages of viruses having new amino acids may be used as an indicator for viral fitness driving the amino acid substitutions.

3.3 Factors associated with fixation probability

Figure 3 shows empirical fixation probabilities of new amino acids stratified by attributes in their profiles. Empirical fixation probabilities of new amino acids varied with median patient ages (Fig. 3A and 3B). Supplementary Table S2 shows the number of fixed and extinct new amino acid profiles having median patient ages between 25 and 35 and those of the others. The number of fixed and extinct new amino acid profiles is dependent on whether their median patient ages are between 25 and 35 or not ($P<{10}^{-15}$ with ${\chi }^2$ test). Supplementary Table S3 shows the number of fixed and extinct new amino acid profiles in which median patient ages of old amino acids are less than or equal to 15 and those of the others. The number of fixed and extinct new amino acid profiles is dependent on whether the old amino acids have a median patient age less than or equal to 15 or not ($P<{10}^{-9}$ with ${\chi }^2$ test). These results indicated that new amino acids tended to become fixed when the viruses with the new amino acids infected the population with a median age between 25 and 35 or when the viruses having the old amino acids at the corresponding positions infected the population with a median age from 0 to 15.

Figure 3.

Empirical fixation probabilities of new amino acids stratified with (A) the median patient ages of sequences having new amino acids, (B) median patient ages of sequences having old amino acids, (C) excesses of median patient age of sequences having new amino acids with respect to old ones, (D) z-values of rank-sum of patient ages of sequences having new amino acid, (E) epitope flags at the position of amino acids. The error bars indicate the 95% binomial confidence intervals of fixation probabilities.

We further investigated the correlation between empirical fixation probabilities and the excess infectivity of strains with new amino acids to the adult population over strains with old amino acids (Fig. 3C and 3D). The excess infectivity of the new strains to the adult population was measured by comparing patient age distributions of amino acid sequences with new amino acids and old amino acids at the same positions on HA.

Empirical fixation probabilities of new amino acids were positively correlated with the excess of median patient ages of new amino acids with respect to those of old amino acids (Fig. 3C). Pearson’s correlation coefficient between fixation probability and excess in median patient ages was 0.94 ($P<{10}^{-3}$). The empirical fixation probability was also positively correlated with the z-value of rank-sums of the patient ages of new amino acids (Fig. 3D), with a correlation coefficient of 0.95 ($P<{10}^{-2}$). Supplementary Fig. S5A shows a scatterplot of fixation probability versus excess in median patient ages with its regression line. Supplementary Fig. S5B shows a scatterplot of fixation probability versus z-value of rank-sums of the patient ages of new amino acids with its regression line. Supplementary Fig. S5A and 5B correspond to Fig. 3C and D, respectively. Both results indicated that fixation probabilities of new amino acids increased when viruses having the new amino acids on HA infected the population with a higher age than those infected with viruses with old amino acids at the corresponding positions.

Figure 3E shows empirical fixation probabilities of new amino acids stratified with epitope flags of their positions. The empirical fixation probability of new amino acids at epitope positions was 0.66 with a 95 per cent binomial confidence interval of 0.57 to 0.74. On the other hand, the empirical fixation probability of new amino acids at non-epitope positions was 0.48 with a 95 per cent binomial confidence interval of 0.43 to 0.52. The fixation probability of new amino acids at epitope positions was significantly higher than that of new amino acids at non-epitope positions ($P<{10}^{-3}$ with χ² test).

3.4 Models of fixation probability

Table 2 shows results of the maximum likelihood estimation of parameters of models using profiles having frequencies more than 0.11 in the dataset (see Section 4 for details). Model M1, which assumes $Ns$ is constant, has a maximum log likelihood of –260.441 and an AIC of 522.882. The maximum likelihood increased when we included age statistics, $a.\mathit{diff}$ (M2) or $a.\mathit{wilcox}$ (M3), and the AIC decreased to 503.345 and 505.310, respectively. When we added the epitope flag $e$ (M4), the maximum likelihood also increased, and the model’s AIC decreased to 512.886. The increase in maximum likelihood from the constant advantage model (M1) when modeled with epitope flags (M4) was smaller than the increases when modeled with patient age statistics (M2 and M3).

Table 2.

Maximum likelihood estimation of parameters of six models.

Model	$C_a\mathrm{ }$ (95% CI)	$C_e$ (95% CI)	$C_0\mathrm{ }$ (95% CI)	Maximum log likelihood	AIC	$\Delta$ AICa
(M6) $Ns=C_{a}a.\mathit{wilcox}+C_{e}e+C_0$	0.126 (0.073, 0.185)	0.572 (0.265, 0.922)	0.115 (-0.012, 0.243)	–243.881	493.761	0
(M5) $Ns=C_{a}a.\mathit{diff}+C_{e}e+C_0$	0.032 (0.018, 0.047)	0.521 (0.206, 0.870)	0.141 (0.016, 0.265)	–244.149	494.298	0.537
(M2) $Ns=C_{a}a.\mathit{diff}+C_0$	0.031 (0.018, 0.045)	−b	0.228 (0.115, 0.329)	–249.672	503.345	9.584
(M3) $Ns=C_{a}a.\mathit{wilcox}+C_0$	0.119 (0.065, 0.175)	–	0.217 (0.102, 0.333)	–250.655	505.310	11.549
(M4) $Ns=C_{e}e+C_0$	–	0.526 (0.219, 0.867)	0.225 (0.109, 0.343)	–254.443	512.886	19.125
(M1) $Ns=C_0$	–	–	0.313 (0.207, 0.421)	–260.441	522.882	29.121

^a $\Delta$ AIC is calculated by subtracting AIC of M6 from the AIC of the model.

^bThe hyphens indicate the model does not use that parameter.

When $Ns$ was modeled using a combination of a patient age statistic and the epitope flag (M5 and M6), we observed further increases in the maximum likelihood and decreases in AIC. The AIC of M5 was 494.298, which is lower than those of its simpler models M2 and M4. Similarly, the AIC of M6 was 493.761, which is lower than those of its simpler models M3 and M4. Models using a combination of a patient age statistic and epitope flag seemed to be better to represent the selective advantage of viruses than those using either parameter alone.

In the maximum likelihood estimation of M6 in Table 2, the 95 per cent CI for $C_0$ contains zero, which means that the intercept may not necessarily be positive in M6. The epitope flag in our model takes the value of zero or one. The term $C_{e}e$ always takes a non-negative value if $C_e$ is positive. The average of $Ns$ can become positive even if $C_0$ takes a negative value. The lower bound of 95 per cent CI for $C_0$ for M6 would be positive if we used epitope flags of –1 and +1. The small positive value of the lower bound of 95 per cent CI for M5 can be explained by the same reason.

3.5 Linkage disequilibrium among amino acids

Table 3 shows groups of new amino acids that are almost in perfect linkage disequilibrium. Groups of linked amino acids were identified using correlation coefficient squared $r^2$ based on the frequency of the amino acids. Using a cutoff value of $r^2$ at 0.75, a total of forty-nine groups of amino acid substitutions, each of which consists of new amino acids that are almost in perfect linkage disequilibrium with another amino acid in the group, were identified in the sixty-two sets of new amino acid profiles. The grouping information of amino acid profiles were provided in Supplementary File S1 with profiles of all new amino acids.

Table 3.

New amino acids identified as being almost in perfect linkage disequilibrium.

Group no.	Profile set	Substitution	Outcome	Emergence month	Outcome month	$r^2$
3	${\mathrm{D}}_3^{+}$	S185T	Fixed	2009–10	2012–08	0.9592
	${\mathrm{D}}_4^{+}$	S451N	Fixed	2009–04	2012–08
5	${\mathrm{D}}_6^{+}$	E499K	Fixed	2011–07	2013–05	0.7943
	${\mathrm{D}}_7^{+}$	K283E	Fixed	2012–03	2013–06
6	${\mathrm{D}}_8^{+}$	K163Q	Fixed	2012–07	2013–11	0.9797
	${\mathrm{D}}_9^{+}$	A256T	Fixed	2012–07	2013–11
8	${\mathrm{D}}_{11}^{+}$	S162N	Fixed	2015–05	2016–06	0.9689
	${\mathrm{D}}_{12}^{+}$	I216T	Fixed	2014–10	2016–06
9	${\mathrm{D}}_{13}^{+}$	I295V	Fixed	2016–09	2017–09	0.9893
	${\mathrm{D}}_{14}^{+}$	S74R	Fixed	2016–09	2017–10
13	${\mathrm{D}}_{18}^{+}$	N129D	Fixed	2017–06	2020–02	0.7528
	${\mathrm{D}}_{19}^{+}$	T185I	Fixed	2015–09	2020–02
24	${\mathrm{D}}_{11}^{-}$	I216V	Extinct	2010–08	2012–08	0.8785
	${\mathrm{D}}_{27}^{-}$	R205K	Extinct	2009–03	2014–04
25	${\mathrm{D}}_{12}^{-}$	E356A	Extinct	2010–10	2012–08	0.7829
	${\mathrm{D}}_{21}^{-}$	H138Q	Extinct	2010–10	2013–06
27	${\mathrm{D}}_{14}^{-}$	S69T	Extinct	2011–09	2013–01	0.9506
	${\mathrm{D}}_{15}^{-}$	N260D	Extinct	2011–07	2013–01
34	${\mathrm{D}}_{23}^{-}$	A197T	Extinct	2010–07	2013–07	0.9247
	${\mathrm{D}}_{25}^{-}$	S143G	Extinct	2010–08	2013–11
45	${\mathrm{D}}_{36}^{-}$	R45G	Extinct	2017–06	2019–05	0.9504 with ${\mathrm{D}}_{37}^{-}$
	${\mathrm{D}}_{37}^{-}$	P282A	Extinct	2017–07	2019–05	0.9558 with ${\mathrm{D}}_{39}^{-}$
	${\mathrm{D}}_{39}^{-}$	I298V	Extinct	2017–07	2019–08	0.936 with ${\mathrm{D}}_{36}^{-}$
47	${\mathrm{D}}_{40}^{-}$	E68D	Extinct	2018–07	2020–02	0.9175
	${\mathrm{D}}_{41}^{-}$	S121N	Extinct	2017–08	2020–02

3.6 Evaluation by cross-validation

We evaluated the predictability of models using four-fold cross-validation tests. Table 4 shows the means and the standard deviations of AIC and maximum log likelihood for training sets and the means and the standard deviations of sensitivity, specificity, precision, and Youden’s index for test sets in the cross-validations. The models were sorted in the descending order of Youden’s indices, which is the sum of sensitivity and specificity minus one. The confusion matrices for each cross-validation test in Table 4 is provided in Supplementary File S2.

Table 4.

Results of cross-validation tests.

	Training		Test
Model	AIC	Maximum log likelihood	Sensitivity	Specificity	Precision	Youden’s index	P-value ($n=400$)
(M3) $Ns=C_{a}a.\mathit{wilcox}+C_0$	374.27 ± 45.02	–185.13 ± 22.51	0.78 ± 0.09	0.86 ± 0.11	0.83 ± 0.17	0.64 ± 0.11	5.76 × 10-20***
(M2) $Ns=C_{a}a.\mathit{diff}+C_0$	373.00 ± 44.65	–184.50 ± 22.33	0.79 ± 0.10	0.84 ± 0.11	0.81 ± 0.17	0.63 ± 0.12	0.003**
(M1) $Ns=C_0$	388.27 ± 42.33	–193.13 ± 21.17	0.76 ± 0.08	0.86 ± 0.11	0.83 ± 0.18	0.62 ± 0.11	–
(M6) $Ns=C_{a}a.\mathit{wilcox}+C_{e}e+C_0$	366.35 ± 43.52	–179.17 ± 21.76	0.77 ± 0.11	0.84 ± 0.11	0.80 ± 0.18	0.61 ± 0.14	$\approx$ 1.000
(M4) $Ns=C_{e}e+C_0$	381.72 ± 40.84	–187.86 ± 20.42	0.75 ± 0.10	0.85 ± 0.11	0.81 ± 0.18	0.6 ± 0.13	0.218
(M5) $Ns=C_{a}a.\mathit{diff}+C_{e}e+C_0$	366.92 ± 43.41	–179.46 ± 21.71	0.77 ± 0.11	0.82 ± 0.11	0.79 ± 0.18	0.59 ± 0.14	4.01 × 10-5***

All values, except P values, are presented as mean ± standard deviation in 400 cross-validation tests.

^* $P<0.05$ by two-sided paired Wilcoxon rank-sum test adjusted by Bonferroni’s correction with $n=5$ with a null hypothesis that the model’s Youden’s indices are the same as those of M1.

^** $P<0.01$ as above.

^*** $P<0.001$ as above.

Consistent with Table 2, model M6 had the best AIC for training sets, followed by M5. However, model M3 had the highest mean Youden’s index of 0.64 with a mean sensitivity of 0.78 and a mean specificity of 0.86. The model M2 had the second highest Youden’s index of 0.63 with a mean sensitivity of 0.79 and a specificity of 0.84. The model M1, in which we assume $Ns$ is constant, had the third highest Youden’s index of 0.62 with a mean sensitivity of 0.76 and mean specificity of 0.86. Models M6, M4, and M5 had lower Youden’s indices than M1.

Youden’s indices of M3 and M2 have a mean of 0.64 with a standard deviation of 0.11 and a mean of 0.63 with a standard deviation of 0.12, respectively. The difference between the Youden’s indices of the models becomes clear when a result using a model for each test is compared to the result using M1 in a pair-wise manner. Supplementary Fig. S6 shows the distribution of excess Youden’s indices of M2, M3, M4, M5, and M6 over M1 in 400 cross-validation tests. Panel A in Supplementary Fig. S6 clearly shows that the excess Youden’s index of M3 over M1 was distributed more in the positive side than the negative side. Paired two-sided Wilcoxon rank-sum test adjusted by Bonferroni’s correction shows that the Youden’s indices of M3 and M2 is significantly larger than that of M1 with P-values of 5.76_×${10}_{\mathbf{\text{−}}}^{20}$ and 0.003, respectively. There is no significant difference between the Youden’s indices of M6 and M4, compared to M1 ($P\approx 1.000$ and $P=0.218$, respectively). The Youden’s indices of M5 is significantly lower than that of M1 ($P=4.01\times {10}^{-5}$). These results indicate that the predictability of the fixation of new amino acids is significantly improved compared to the constant advantage model, M1, when $Ns$ is modeled using $a.\mathit{wilcox}$ or $a.\mathit{diff}$ with an intercept.

In Table 4, a new amino acid was predicted to become fixed when $P_{\mathit{fix}}$ is higher than a threshold of 0.5. We further investigated the effect of the threshold of $P_{\mathit{fix}}$, $\tau$, on the prediction of the fixation of new amino acids. For each model, sensitivity and specificity for predicting the fixation of new amino acids were obtained by using different thresholds $\tau$ from zero to one in cross-validation tests. The sensitivities and specificities were averaged over 400 cross-validation tests for each threshold for each model. Supplementary Fig. S4 shows the receiver operating characteristic (ROC) curve created from the resulting sensitivities and specificities. Points around the lower left corner correspond to cross-validation tests using $\tau \cong 1$ and points around the upper right correspond to cross-validation tests using $\tau \cong 0$. The cross on the curve of M3 represents the sensitivity and specificity of M3 when $\tau$ equals 0.5, which is shown in Table 4. The ROC curve of M3 reached the maximum distance from the diagonal line when $\tau$ equals 0.43 (circle). This threshold increased Youden’s index of M3 to 0.656 from 0.646 which is obtained when $\tau$ equals 0.5. The order of the furthest distances from the diagonal line was the same as the order of Youden’s indices in Table 4. These results indicated that M3 had the highest predictive power when using a threshold of 0.43. The choice of threshold for $P_{\mathit{fix}}$ faces the trade-off between the sensitivity and specificity, and the value should be determined by considering the purpose of prediction.

3.7 The fixation probability of a new amino acid on HA

Figure 4A shows the three-dimensional surface plot of the fixation probability of a new amino acid on HA based on model M3 with its parameters in Table 2. The fixation probability of a new amino acid increases as its frequency increases, as expected from the property of formula (1). The fixation probability starts from zero when the frequency equals zero, as shown in green, and it approaches one when the frequency approaches one, shown in blue. The fixation probability also increases as the z-value of the rank-sum of patient ages of the new amino acid becomes larger, as one can observe an increase in height when looking at a band of the same color in the increasing direction of the z-value of the age rank-sum. This result indicates that viruses with a new amino acid on HA obtain additional chance to become fixed, when they can infect elderly patients more effectively than the viruses with the old amino acid at the same position. In other words, new strains’ excess infectivity to adult population over old strains increases their chances to become fixed in addition to its chance of fixation gained from how large a fraction of the population they are currently infecting. Figure 4B shows the same information as Fig. 4A in a two-dimensional figure. The lines in Fig. 4B represent the fixation probabilities at values of $a.\mathit{wilcox}$ from –5 to 5 with a step of 1.

Figure 4.

The fixation probability of viruses with a new amino acid on HA. (A) Three-dimensional surface plot of the fixation probability of viruses with a new amino acid on HA. X-axis and color represent the frequency of virus having the new amino acid in the viral population. Green represents frequencies close to zero, blue nearly reaching one, yellow and orange in-between. Y-axis represents the fixation probability of the new amino acid. Z-axis represents its $a.\mathit{wilcox}$, calculated by z-value of its patient age rank-sum compared to the old amino acid, representing the excess infectivity to adult population of viruses having the new amino acid compared to viruses with the old amino acid at the same position on HA. (B) The relationship between the frequency of a new amino acid on HA and fixation probability when the new virus infects different age groups compared to the old virus. X-axis represents the frequency of virus having the new amino acid in the viral population. Y-axis represents the fixation probability of the new amino acid. Color represents its $a.\mathit{wilcox}$, calculated by z-value of its patient age rank-sum compared to the old amino acid, representing the excess infectivity to adult population of viruses having the new amino acid compared to viruses with the old amino acid at the same position on HA.

3.8 Timing of selection of new amino acids in different birth-year groups

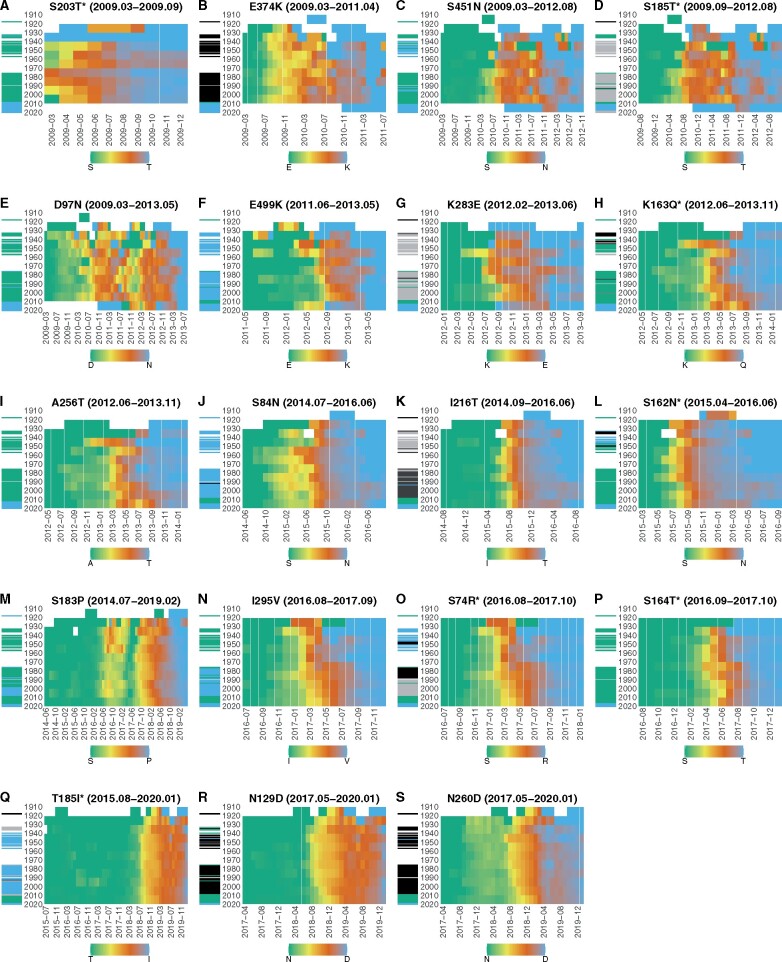
Figure 5 shows the time evolution of frequencies of amino acid sequences having the nineteen fixed new amino acids on HA in different birth-year groups during their transition phases. Panels A–S in the figure correspond to amino acid substitutions shown in Table 1 in the same order. We assume that the patients were first exposed to the dominant strain of the H1N1 viruses circulating in the year when they were born.

Figure 5.

Timing of amino acid substitutions in different birth-year groups. Panels A–S in the figure correspond to amino acid substitutions shown in Table 1 in the same order. In each panel, X-axis represents the first month of a four-month sliding window, and Y-axis represents the birth-year of patients. The population of patients were grouped into ten-year birth-year groups. Each cell in a heatmap is color-coded according to the frequency of viruses having the fixed new amino acid in the population of a birth-year group at Y-axis in a four-month sliding window starting at the month on the X-axis. A cell is green if the frequency of new amino acid in the birth-year group is zero, and it is blue if the frequency in the birth-year group is one, as shown in the color key in the legend. Cells with no data are represented in white. The horizontal bars on the left of each heatmap represent the dominant amino acid at the corresponding position on HA of viruses circulating in the year on the Y-axis. The color of a bar on the left of each heatmap represents the dominant amino acid at the same position on HA of viruses circulating in the year when patients were born. A green bar indicates the circulation of viruses having the old amino acid at the substituted position on HA in the year when patients were born, and a blue bar indicates the circulation of viruses having the new amino acid at the same position. A bar with grey or black color indicates the circulation of viruses having a dominant amino acid different from both the old and new amino acids at the substituted position in the year when the patients were born. Amino acid substitutions with an asterisk represent substitutions which occurred at an epitope position.

The transitions from old amino acids to new amino acids showed different timings of emergence and fixation depending on birth-year groups (Fig. 5). Amino acid T at position 203 on HA has had frequencies of more than 0.30 in all birth-year groups since the first four-month sliding window starting from March 2009 (Supplementary Fig. S8A). The next three fixed new amino acids, lysine (K) at position 374, asparagine (N) at position 451, and T at position 185 exceeded a frequency of 0.10 first in the youngest birth-year groups followed by others (Supplementary Fig. S7B, S7C, and S7D). Amino acid N at position 97 exceeded a frequency of 0.10 and 0.30 first in the second oldest birth-year groups (Supplementary Figs. S7E and S8E). However, the tendency is not clear because of the drop in the frequency of new amino acid in the middle of its transition phase (Fig. 5E).

After 2011, we observed a general tendency that new amino acids exceeded a frequency of 0.30 earliest in the old and middle-aged birth-year groups (Supplementary Fig. S8). These are K at position 499 (Supplementary Fig. S8F), glutamic acid (E) at position 283 (Supplementary Fig. S8G), glutamine (Q) at position 163 (Supplementary Fig. S8H), T at position 256 (Supplementary Fig. S8I), N at position 84 (Supplementary Fig. S8J), T at position 216 (Supplementary Fig. S8K), N at position 162 (Supplementary Fig. S8L), V at position 295 (Supplementary Fig. S8M), R at position 74 (Supplementary Fig. S8N), T at position 164 (Supplementary Fig. S8O), proline (P) at position 183 (Supplementary Fig. 8P), aspartic acid (D) at position 260 (Supplementary Fig. S8Q), isoleucine (I) at position 185 (Supplementary Fig. S8R), and D at position 129 (Supplementary Fig. S8S).

Supplementary Fig S10 shows a clear trend that the fixation starts from old birth-year groups, followed by the middle-aged birth-year groups and ended with the young birth-year groups for all the nineteen fixed amino acids (see Section 2 for the definition of fixation in this study). Despite this general tendency, three new amino acids became fixed quite early in the youngest birth-year group (Supplementary Fig. S10B, S10C, S10D). However, the timing of overturn, when the frequency of a new amino acid exceeds 0.50 in a birth-year group did not show a clear tendency (Supplementary Fig. S9).

Some amino acid substitutions were associated with the dominant amino acids of the viruses circulating in the year when patients were born. For example, the transition from K to Q at position 163 on HA appeared earlier in patients born in 1940–50 than those born in 1930–40 (Fig. 5H). Precisely, the timings when Q at position 163 on HA first exceeded a frequency of 0.30 in patients born in 1940–50 preceded those born in 1930–40 by seven months (Supplementary Fig. S8H). The dominant amino acid at position 163 on HA of viruses circulating during 1940–50 was K (Fig. 5H). In contrast, as shown in the black bars in Fig. 5H, the dominant amino acid at position 163 on HA of viruses circulating during 1930–40 was neither K nor Q. Patients born in 1940–50 may be first exposed to viruses having K at position 163. The substitution from K to Q at position 163 may have selective advantage in patients born in 1940–50. On the other hand, the birth-year group in 1930–40 may be first exposed by viruses having a different amino acid other than Q or K at position 163. The viruses having Q at position 163 may not have large advantage compared to viruses having K at this position in the birth-year group of 1930–40. The difference in the timings of amino acid substitutions between the two birth-year groups may be attributed to the different amino acids at this position on HA of viruses that first infected to patients of the two birth-year groups.

Some amino acid substitutions may be associated with the disappearance of H1N1 viruses in the human population during 1957 to 1977, which is the period between the year of the Asian flu pandemic in 1957 and the year of the Russian flu pandemic in 1977. For example, the transition from S to N at position 84 on HA appeared earlier in patients born in 1950–60 than those born in 1940–50 (Fig. 5J). Precisely, the first sliding window in which N at position 84 on HA exceeded a frequency of 0.30 in patients born in 1950–60 was five months earlier than that in patients born in 1940–50 (Supplementary Fig. S8J). The same tendency can be found for frequencies of 0.10 and 0.50 (Supplementary Figs. S7J and S9J). The amino acid substitution from S to N at position 84 may have immunological disadvantage because most population have firstly exposed to viruses having N at position 84, as shown in the blue bars in Fig. 5J. Due to the absence of H1N1 during 1957–77, a considerable number of patients of birth-year groups 1950–60 and 1960–70 are likely to be first infected with H2N2 influenza viruses. Viruses having N at position 84 on HA may have less immunological disadvantage in these birth-year groups, resulting in an earlier transition from S to N at this position than the birth-year group of 1940–1950. We can also explain the delay in transition from K to Q in 163 in patients of the birth-year group 1950–60 by the absence of H1N1 strain during 1957–77.

When we considered the whole period of transition, the age distributions of patients infected with viruses having the new amino acids were not significantly different from those of old amino acids at positions 203, 374, 295, 74, and 164 on HA (Table 1). However, when observing the timing of amino acid substitutions in different birth-year groups, amino acid substitutions at positions 295, 74, and 164 still followed a general tendency of beginning in the old and middle-aged birth-year groups and ending in the youngest birth-year groups (Fig. 5N, 5O, and 5P). This suggests that, even though age distributions of patients may not significantly differ between viruses having new and old amino acids when considering the whole transition period, the new amino acid’s distributions of patient ages in each window still tend to be skewed towards people in older birth-year groups for these amino acid substitutions.

4. Discussion

In this study, we investigated the patient age distributions and fixation probabilities of new amino acids on HA of 2009 pandemic strains of H1N1 influenza viruses. The empirical probability that a new amino acid on HA later became fixed in the viral population was only 0.004. The empirical fixation probability significantly increased when the frequency of viruses having new amino acids exceeded 0.1. The empirical fixation probability also significantly increased when the viruses having the new amino acids more effectively infected the adult age population from twenty-five to thirty-five years old than the viruses with old amino acids at the same position. Based on these observations, we modeled fixation probability of a new amino acid using Kimura’s formula of advantageous selection. The selective advantage of a new amino acid was modeled by a linear combination of patient age distributions and epitope flags. The parameters of models were estimated by maximizing the likelihood of parameters from profiles of fixed and extinct new amino acids from 2009 to 2020. Four-fold cross-validation tests revealed that the model using the difference in patient age distribution and frequency of new amino acid predicted amino acid substitutions on HA with a sensitivity of 0.78, specificity of 0.86, and precision of 0.83.

When we looked at trajectories of new amino acids that emerged on HA of H1N1 viruses from March 2009 to May 2020, the empirical fixation probability of a new amino acid was only 0.004 (Fig. 2). It means that a frequency of 0.996 of the new amino acids that appeared on HA went extinct. If we look at relationship between the frequency of a new amino acid and its empirical fixation probability in a four-month sliding window, the empirical fixation probability became different, because the fixed new amino acids can be counted multiple times in different four-month sliding windows. A new amino acid having a frequency no more than 0.11 in a four-month sliding window had an empirical fixation probability of 0.02 (Supplementary Fig. S2B). This means that a new amino acid having a frequency below 0.11 in a four-month sliding window had almost no chance to becoming fixed later. In contrast, a new amino acid having frequencies more than 0.11 in a four-month sliding window had an empirical fixation probability close to 0.50 (Supplementary Fig. S2A). It means that a new amino acid having a frequency more than 0.11 in a four-month sliding window would have equal chance of becoming either fixed or extinct. Thus, the prediction of fixation of a new amino acid having a frequency more than 0.11 in a four-month sliding window, which have an empirical probability close to 0.50, is the most difficult setting to predict the fixation of new amino acids. For this reason, we focused on the prediction of the fixation of new amino acids which exceeded a frequency of 0.11 in a four-month sliding window.

Our study found that the frequency of new amino acids alone can achieve high sensitivity, specificity, and precision in predicting the fixation of a new amino acid of which frequency is more than 0.11 in a four-month sliding window. Model M1, which modeled the fixation probability of a new amino acid using its current frequency under the assumption of a constant selective advantage, predicted the fixation of a new amino acid with an average sensitivity of 0.76, specificity of 0.86, and precision of 0.83 in four-fold cross-validations (Table 4). This result suggested that the fixation probability of a new amino acid is largely attributed to its frequency. The constant for the selective advantage, $C_0$, was estimated to be 0.313 with its confidence intervals of from 0.207 to 0.421 by the maximum likelihood method (Table 2). Since positive coefficient for Kimura’s formula indicates advantageous selection, we can conclude that viruses with a new amino acid having a frequency higher than 0.11 in a four-month sliding window has a significantly higher selective advantage compared to viruses with the old amino acid at the same position.

The predictability of the fixation of a new amino acid was significantly improved by considering the Z-value of patient age rank-sums of new amino acids compared to the constant selective advantage model in cross-validation tests. Youden’s index, which is the sum of sensitivity and specificity minus one, was significantly improved in model M3 from model M1 (Table 4). The coefficient for $a.\mathit{wilcox}$, $C_a$, was estimated to be 0.119 with its confidence intervals of from 0.065 to 0.175 by the maximum likelihood method (Table 2). Since $a.\mathit{wilcox}$ represents the excess infectivity to the adult population of viruses having new amino acids compared to those having old amino acids, this result suggests that inclusion of age statistics of viruses significantly improved the prediction of the fixation of a new amino acid. This result is consistent with the current understanding of the mechanism of evolution of influenza viruses, in which new strains are selected by the immunity of people who were infected with and recovered from strains circulating previously (Ferguson et al. 2003).

The proportion of adults who have been infected with influenza viruses is higher than that of children, because adults have more chance of being exposed to the viruses due to their longer time since birth compared to children. Therefore, viruses having different antigenicity from viruses that have been circulating before can have a higher advantage in adult population than in child population. In other words, the advantage of a new amino acid that alter the antigenicity of HA over its old amino acid in the child population can be lower compared with the advantage in adult population. We think that this is the main reason why a statistic of patient age distributions improved the accuracy of the prediction of amino acid substitutions. In addition to this straightforward interpretation, we can consider another explanation. Viruses infecting adults are more likely to be spread globally than children as adults are more likely to travel long distances (Bedford et al. 2015). This is an alternative explanation of the phenomena, but a clear trend that the fixation starts from old birth-year groups, followed by the middle-aged birth-year groups and ended with the young birth year groups (Supplementary Fig. S10) supports the first interpretation that the higher selective advantage in adult population is attributed to the immunity from previous infections.

Since influenza viruses are transmitted among individuals of different age groups, the difference in the age distributions between new amino acids and old amino acids were not supposed to differ largely. As shown in Supplementary Fig S1B, the distributions of patient ages of GISAID sequences are bimodal, with one mode in the child population younger than ffiteen years old, and another mode in the adult population older than 15, especially after 2012. The number of fixed and extinct new amino acid profiles in Supplementary Table S2 is dependent on whether their median patient ages are between 25 and 35 or not ($P<{10}^{-15}$ with ${\chi }^2$ test). Furthermore, the number of fixed and extinct new amino acid profiles in Supplementary Table S3 is dependent on whether the old amino acids have a median patient age less than or equal to 15 or not ($P<{10}^{-9}$ with ${\chi }^2$ test). The most probable hypothesis we have for the bimodal distribution is as the following. In the younger population who have not experienced influenza infections, the viruses with old amino acids can infect as effectively as viruses with new amino acids. The number of infections in the younger population decreases as patient age increases because of acquisition of immunity by the first exposure to influenza viruses. In the adult population who has experienced previous exposures, on the other hand, viruses having new amino acids is more infectious than those having old amino acids because of the original antigenic sin. The first mode in the patient age distribution is formed by the first influenza infection in life and the second mode was formed from the second or subsequent influenza infections. This is our best explanation for the results obtained in this study.

It is known that the 2009 pandemic strain shows cross-reactivity with the Spanish flu and Russian flu strains (Garten et al. 2009; Itoh et al. 2009). An individual’s immunity profile against influenza is highly affected by their first infection in their childhood (Francis et al. 1947). Some strains having a new amino acid on HA seemed to have an advantage in infecting patients who were infected with the viruses having the old amino acid in their first infection. Examples of these amino acid substitutions include K163Q (Fig. 5H). Some amino acid substitutions may be associated with the disappearance of H1N1 viruses in the human population during 1957 to 1977, which is the period between the year of the Asian flu pandemic in 1957, caused by a strain of H2N2 viruses, and the year of the Russian flu pandemic in 1977, caused by a strain of H1N1 viruses. A considerable number of patients of birth-year groups 1950–60 and 1960–70 are likely to be first infected with H2N2 influenza viruses. Viruses having the S84N substitution have less immunological disadvantage in these birth-year groups compared with the birth-year group of 1940–50, resulting in the different timings of transition from S to N (Fig. 5J). Selections of these strains can be explained as an effect of the original antigenic sin.

We found that epitope flags of substituted positions did not largely contribute to the prediction of amino acid substitutions in cross-validation tests. From nineteen fixed amino substitutions on HA observed in this study, only seven (36.84%) occurred on its epitope regions (Table 1). It has been suggested that amino acid substitutions on nonepitope regions compensate the fitness cost of substitutions on epitope regions (Kryazhimskiy et al. 2011; Koel et al. 2013; Yokoyama et al. 2017). However, 90.5 per cent of amino acid substitutions on the HA1 domain of H3N2 viruses were known to have occurred at its epitope region (Shih et al. 2007). A possible reason for the small contribution of epitope flags in prediction is that the positions of epitopes we used in this study have been determined from H1N1 viruses before the 2009 pandemic (Igarashi et al. 2010). The epitope for the 2009 pandemic strain may differ from the epitope for previous seasonal strains circulating before 2009 pandemic. In fact, Ren et al. (2015) showed that antigenic regions cover a larger area than regions previously defined as the epitope. The same was true for H3N2 (Lees et al. 2010). Further studies are required for a wider characterization of epitope sites on HA of influenza viruses.

The human influenza shows seasonality, and the population of the viruses fluctuates depending on the time of year. Although the assumption of constant effective population size may not be valid for the population genetics of seasonal influenza viruses, we use this Kimura’s formula under the assumption of constant effective population size for its simplicity. It is suggested that the fixation probability increases when the effective population size is growing (Fisher 1930). This means the fixation probability predicted from our model would be underestimated during influenza seasons when the number of new cases is growing. Even so, the model has achieved high predictability in cross-validation tests, indicating that the error may be marginal and an acceptable trade-off for the model’s simplicity. However, for more precise predictions, the method may adopt fixation probability models that take into account changing population sizes (Lambert 2006).

Synchronized substitutions were observed at positions 451 and 185, positions 499 and 283, positions 163 and 256, positions 84, 216, and 162, positions 295 and 74, and positions 185 and 129 (Supplementary Fig. S11). Fixations of the synchronized amino acids may be hitchhiking substitutions, which do not contribute to the increase in viral fitness but became fixed due to the selective advantage gained from another substitution on HA of the same strain (Barton 2000; Smith et al. 2004). For example, transitions from S to N at position 84, I to T at position 216, and S to N at position 162 occurred simultaneously (Supplementary Fig. S11). H1N1 strains circulating before the 2009 pandemic had S at position 162 on their HA (Fig. 5L). Since position 162 is located in the epitope region Sa (Table 1), viruses having N at this position may have had selective advantage over viruses having S at this position. In contrast, S at position 84 and I at position 216 of the 2009 pandemic strain were different from amino acids at these positions on HA of H1N1 strain circulating before the 2009 pandemic (Fig. 5J and 5K). These two substitutions may not have a selective advantage in terms of antigenicity, and there is a possibility of hitchhiking substitutions of S162N. Another explanation of the synchronized transitions of amino acids is that the fixations can occur through synergistic epistasis between several mutations (Neverov et al. 2015). Viruses with a new amino acid with slow transition may initially lack large advantage over viruses with an old amino acid at the same position. These viruses became fixed when they gained a synergistic advantage from another new amino acid on HA. For example, the slow transition from D to N at position 97 have become fixed when viruses have additional new amino acids at positions 499 and 283.

One of the limitations of our method is that the model can only predict the evolutionary outcome of new amino acids. Thus, the model cannot predict the time it takes before they became fixed in viral population. Each year, WHO makes recommendations for vaccine strains by reviewing the circulation and spread of new strains through their global influenza surveillance network (Russell et al. 2008). The recommendation of vaccine strains must be decided eight months before the season starts for the vaccine development and production process (World Health Organization 2007). Our method can predict the fixation of a new amino acid accurately once its frequency exceeds 0.11. The time for a new amino acid to become fixed or extinct after exceeding a frequency of 0.11 had a mean of 18.8 months with a standard deviation of 13.6 months (Supplementary File 3). Assuming that the time to fixation or extinction after exceeding a frequency of 0.11 follows a normal distribution with a mean of 18.8 months and a standard deviation of 13.6 months, we can get the prediction by our model eight months earlier than its fixation or extinction for 79% of new amino acids that exceed a frequency of 0.11 in a four- month sliding window. Thus, the applicability of our method to the actual vaccine selection process is not largely restricted by the limitation due to the lack of a mechanism for predicting the timing of fixation.

The applicability of our method to H3N2 viruses should be tested in the future. Most studies to predict amino acid substitutions have targeted H3N2 viruses as sequence data are available from its emergence in 1968 (Agor and Ozaltin 2018; Klingen et al. 2018). H1N1 viruses emerged in the Spanish flu pandemic in 1918 (Cohen 2010), disappeared in 1957, and re-emerged in the Russian flu in 1977, and were replaced with a swine flu strain in the 2009 pandemic (Girard et al. 2010). In contrast, H3N2 viruses have been circulating in the human population since its pandemic in 1968. The structure of the population having immunity against H3N2 viruses may be simpler than that of H1N1 viruses. However, due to the limitation of patient age information of amino acid sequences of past H3N2 viruses, our method can be applicable only to the fixation of new amino acids that have been observed recently.