Power-saving design opportunities for wireless intracortical brain computer interfaces

Abstract

The efficacy of wireless intracortical brain–computer interfaces (iBCIs) is partly limited by the number of recording channels, which is constrained by the power budget of the implantable system. Designing wireless iBCIs that provide the high-quality recordings of today’s wired neural interfaces may lead to inadvertent over-design at the expense of power consumption and scalability. Here we analysed neural signals collected from experimental iBCI measurements in rhesus macaques and from a clinical-trial participant with implanted 96-channel Utah multi-electrode arrays to understand the trade-offs between signal quality and decoder performance. We propose an efficient hardware design for clinically viable iBCIs, and suggest that the circuit design parameters of current recording iBCIs can be relaxed considerably without loss of performance. The proposed design may allow for an order of magnitude power savings and lead to clinically viable iBCIs with a higher channel count.

1. Introduction

Electrophysiological devices are widely used in basic neuroscience research to measure the activity of a population of neurons (e.g., electroencephalography - EEG, and electrocorticography - ECoG) or individual neurons (e.g., using intracortical electrodes) to understand the function of the nervous system. Decades of electrophysiological research initially aimed at understanding the brain gave rise to the field of brain-computer interfaces (BCIs), also referred to as brain-machine interfaces (BMIs) or neural prostheses. In this paper, we collectively refer to these systems as BCIs. BCIs provide a direct communication path between the brain and an external device. While they can be used in research to better understand the brain, they are increasingly intended for clinical applications [1].

BCIs can help restore lost sensory capabilities through stimulation (e.g., vision and hearing), or restore lost motor capabilities of people with motor impairments (e.g., due to amyotrophic lateral sclerosis - ALS, brainstem stroke, or spinal cord injury). In clinical motor prosthesis applications, BCIs estimate the user’s intention from brain activity and use this ‘decoded’ intention to guide the person’s own limb [2, 3] or an assistive device, such as a prosthetic arm [4–6] or a computer cursor [7–9] (Fig. 1). Different neural sensors (e.g., EEG, ECoG and intracortical electrodes) can be used as part of BCIs for clinical applications. Recent intracortical BCI (iBCI) studies have shown promising results in pilot clinical trials by enabling high-performance computer cursor control, making them prime candidates for contributing to an assistive technology for people with paralysis [3,5,8,10,11]. Although these results are encouraging, for most applications, iBCIs would benefit from further improvements to be suitable for widespread, standard-of-care human clinical use.

Figure 1:

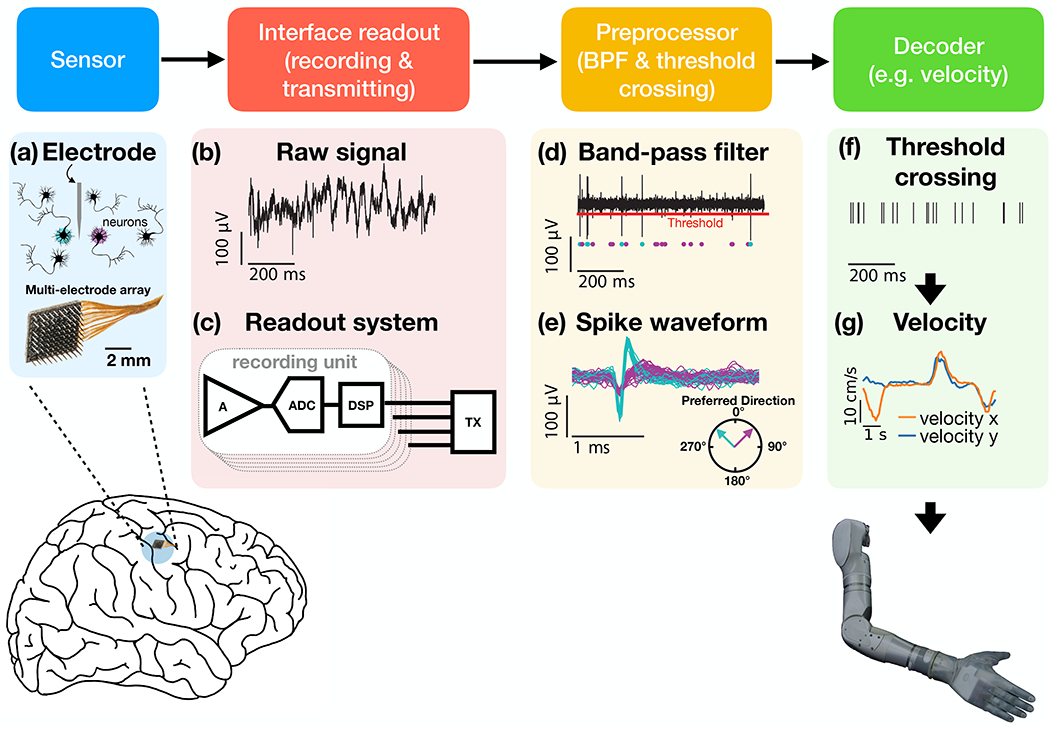
iBCI schematic signal flow. Neural activity is recorded using an electrode array (e.g., (a) Utah array), with each electrode measuring the neural activity in its vicinity. (b) The raw analog signal (c) is amplified in the frequency band of interest (by a neural amplifier - A), digitized (by an analog-to-digital converter - ADC), and then transmitted (by a transmitter - TX) to a computer for further processing. In some cases, some preprocessing (e.g., spike detection) happens before the transmitter by digital signal processing (DSP). Most iBCI neuroprosthetic studies process the signal by applying a further band-pass filter (in addition to that implemented in the neural amplifier) and (d) a simple threshold crossing for spike detection (red line). The threshold crossings are evaluated for each electrode, although an electrode might record from multiple neurons simultaneously (e.g., cyan and magenta dots marks in (d) spikes of different neurons), (e) which can mix correlations with behavior (e.g., movement preferred direction). Lastly, a decoder (e.g., Kalman filter) estimates the user’s intention (e.g., robotic arm velocity) from the binary threshold-crossing signal (f), and sends the control signals (g) to the prosthetic controller.

There is considerable industrial and academic interest in continuing to advance all aspects of iBCI design. Two major requirements for improving iBCIs are increasing the number of recording electrodes, and implementing wireless transcutaneous implants [12–14]. Increasing the number of recorded neurons and the variety of recorded cortical areas is predicted to lead to iBCI performance improvements (see e.g., [13, 15]) and might also enable control of more sophisticated prosthetic devices (e.g., with higher degrees of freedom) [14,16,17]. In addition, wireless links will enable the development of transcutaneous systems that minimize the risk of infection and improve aesthetic appearance, user’s mobility and independence [12, 13]. Existing chronic systems for non-human primates (NHPs) that record from hundreds to thousands of electrodes are power-hungry, and are usually based on wired communication which will not translate well to people [14, 18, 19]. While substantial progress has been made in developing fully implantable, wireless technologies that can support ~100 electrodes, the field (including future clinical use) will benefit from smaller devices with larger number of electrodes (channels) [20–23].

Current systems were designed for basic neuroscience research to record and transmit wide-bandwidth signals with high resolution, thus requiring relatively high power consumption. This “leave nothing behind” approach enables the extraction of a variety of signals including action potentials (spikes) and local field potentials (LFPs), and permits “spike sorting” to attribute action potentials to putative individual neurons [24].

As custom signal specifications for iBCI applications are now crystallizing and diverging from those needed for basic neuroscience, efforts from the neuroscience community have investigated the required signal characteristics for iBCI decoders [25–29]. At the same time, the engineering community focused on designing more efficient neural interfaces. Recent designs, aimed at reducing the quantity of raw data generated by conventional neural interfaces, use a wide range of techniques such as on-chip thresholding [30–32], on-chip spike sorting [33], on-chip compression [34–37] and compressive sensing [38,39]. Despite these engineering-led forays into compression, there is not yet consensus on the required specifications for iBCI oriented neural interfaces. As a result, current in-vivo systems still typically record the neural signal with unnecessarily high fidelity [20, 22, 23, 40–46]. Here, we will present a holistic analysis validating how neural interface specifications for iBCIs can be relaxed with respect to basic neuroscience systems. Results are obtained using data collected from experimental iBCI measurements in rhesus macaques and a BrainGate2 clinical trial human participant. We suggest a considerably more power-efficient approach designed around the anticipated needs and constraints of clinical use. Our estimates indicate that this can reduce power consumption by an order of magnitude while maintaining high decoding performance. We focus on three main questions: 1) what type of signal should be recorded from the brain, 2) how reliable should this signal be, and 3) how will the resulting new specifications affect the iBCI neural interface design, with particular emphasis on its power consumption?

In the first section, we discuss which type of neural signal is needed for iBCIs and how robust the system must be against noise. Next, we assess which design specifications can be relaxed without substantially sacrificing iBCI performance. This informs a possible customized recording strategy for implantable clinical iBCIs. Finally, we describe how the new specifications affect the overall power consumption of the system and highlight the potential for substantial power savings.

2. Neural signal requirements for iBCI decoders

2.1. Binary threshold-crossing signals sampled at low rates

Current neural interfaces record and transmit wideband signals (e.g., 0.1-10,000 Hz) at high resolution (10 - 16 bits), see Fig. 1(b). The low-frequency spectrum contains the LFP, which reflects a spatial averaging of the neural population activity in the electrode’s surroundings [47–49]. The high-frequency spectrum enables capturing delicate features in the recorded signal, which can help in investigating spike waveforms, spike sorting, and differentiating between neuron classes on the basis of their spike waveform. While these properties are of interest for basic neuroscience research, they are not necessarily essential for estimating the user’s neural state or intention for iBCIs applications (e.g., arm movement direction and speed intention) [27, 29, 50, 51].

Most high-performing motor iBCIs use only a simple binary signal encoding of threshold crossing events (’1’ if a spike is detected; ’0’ otherwise) in a short time bin (see Fig. 1(f)) to decode the user’s intention [8, 11, 12, 25, 52–59]. The LFPs contain less information about the intended movement (e.g., movement velocity) compared to spikes; they are beneficial for continuous iBCI control mostly when the spike signals have degraded severely [8, 12, 26, 60, 61] or to classify between a small set of discrete states [62]. A few studies, in addition to threshold-crossing events, also used high-frequency band power (250 Hz to 3kHz or 5kHz) for iBCIs [3, 9, 63]. However, the importance of these additional signals might diminish as the number of electrodes in iBCI systems increases and as neural interfaces improve their ability to record thresholded spikes [64, 65]. Although recording and transmitting only LFPs can also potentially reduce power consumption and should be further investigated, here we focus only on spike signals as they currently achieve the highest iBCI performance.

Sorting spikes by individual neurons detected on a given electrode (Fig. 1(e)) can be of interest when investigating single neuron modulation. In some cases, it can potentially improve iBCI performance by distinguishing spikes from neural population that are tuned differently (e.g., have different preferred directions) or by separating neurons from high-amplitude noise or high-frequency LFP. However, this might be unnecessary for decoding purposes when the activity of the entire neuron population is summarized to evaluate the desired user intention (e.g., by linear combination). Accumulating evidence in NHPs suggests that the benefit of spike sorting on iBCI performance is minimal compared to simple threshold crossing (~5% performance difference) [25–29]. Taken together, these developments suggest that iBCIs may benefit most from larger electrode counts, and can compromise on signal fidelity by transmitting only binary threshold-crossing events. In addition, sorting spikes on the device will increase the complexity of the circuit design as it might need to adaptively track moving signals due to slight array movement and other non-stationary properties of the signal. Even efficient spike sorting techniques [33,66] increase power consumption significantly when compared to threshold-crossing architectures. Because of the minimal benefits in terms of decoding performance and the high costs of integrating spike sorting into the device, we have decided to focus on neural interface designs that record, transmit, and decode threshold crossing events.

One can imagine transmitting even more abstract signal representations such as binned spike counts (the number of spikes in a defined time window, e.g. 20 ms window), dimensionality-reduced signals (i.e., compressed signals with fewer channels. e.g., [67]), or just the output control signals for the prosthesis (e.g., velocity). While it is common in the iBCI field to use threshold crossings for decoding [8,11,52–54,57,68], the optimal bin size, dimensionality reduction technique, and the decoding and control algorithms are still under active investigation (e.g., [52,53,67,69,70]). There is evidence that small bin sizes (e.g., 1 ms) can improve performance; however, the effect of bin size on performance is still unclear and likely depends on the decoding algorithm [8,53,71]. Additional work is required before determining the trade-off between bin size, dimensionality reduction technique, decoder algorithm and system performance. Intensive processing before transmitting the signal may therefore limit the compatibility of the device with future algorithms. Given all this, we have chosen to follow a conservative approach and recommend requirements that are commonly used practice in the iBCI field. Thus, at the present time, we believe that transmitting the presence or absence of unsorted spikes in 1 ms bins is a well-balanced level of simplification that fits current iBCI best practices, while still leaving the door open to future research and development.

2.2. Tolerance to high recording and transmission error rates

Wired iBCIs being used in clinical research, like many other medical and research devices, are currently designed to have minimal recording and transmission errors. This guarantees minimal spike misdetection. However, this high reliability of the recorded and transmitted brain activity comes with a high cost in terms of integrated circuit power consumption. The empirical observation that there is a high degree of redundancy in the neural population spiking activity suggests that high signal fidelity might not be required for iBCIs. The aim in motor iBCI applications is to estimate the user’s intention from the ensemble of all recorded neurons. Correlations across electrodes and the temporal smoothness of the underlying intention (e.g., hand velocity) mitigate the effect of noise on each electrode. Therefore, it may be possible to reduce the recording and transmission reliability of each electrode as long as the final decoding accuracy does not degrade. To demonstrate this, we investigated the tolerance of iBCI decoders to noise and quantified how much we could distort the spiking activity while keeping comparable decoding quality.

Specifically, we tested an iBCI system’s robustness to spike errors. Digital communication fidelity is traditionally described by the bit error rate (BER), which is the rate of flipped bits from 0 to 1 and vice versa. For our purpose, to measure the accuracy of the recording and transmission of spikes, which are binary threshold crossing events, we introduce the notion of spike error rate (SER). SER is the rate at which a spike event was falsely transmitted or missed, i.e. a bit in the binary spike train was flipped. The iBCI decoder is agnostic to the source of the error. Spike errors (i.e., spike error rate, SER) can result from the noise added to the analog signal or digital signal processing throughout the recording and transmitting system. For example, electrode or amplifier noise can be incorrectly detected as a spike. Also, the low resolution of the analog-to-digital converter can lead to erroneously detected spikes. Moreover, bit errors in the transmission system (BER) can also translate to spike errors, depending on the communication protocol (as will be discussed later). Hence, we distinguish between BER and SER because SER represents the error rate of the entire neural interface system, both in recording and in transmission.

To evaluate the robustness of the iBCI decoder to SER, we post hoc measured NHP and human movement behavior predictability using an intentionally distorted neural signal, i.e. we randomly flipped bits in the binary threshold spikes (Fig. 1(f)) and then tried to decode this distorted signal. We note that this noise injection is different from the common practice in the field as we flip spikes in 1 ms resolution and we do not add Gaussian noise to the spike rate in a longer time window (e.g., 20-100 ms [63,69,72]). The original neural signals were recorded with Blackrock Microsystems recording systems [73] from able-bodied monkeys and a person with paralysis while they performed a computer cursor movement task. The monkeys moved the cursor to cued targets using their hand, whereas BrainGate2 clinical trial participant ’T5’ controlled it with an iBCI system (see Methods: Neural and hand position recording for more details). As a decoding performance metric, we use the coefficient of determination (R²), which describes how much of the variability of the cursor velocity can be predicted from the neural activity. First, we generated synthetically distorted neural signals by injecting errors in the recorded data at different SERs (10⁻⁶ to 10^−0.5). This was done by flipping the binary spiking signal bits with an independent Bernoulli distribution with the probability of the SER (see Methods from more information). Then, we estimated how well the distorted neural signal could predict the cursor velocity using a Kalman filter (KF), a widely used decoder for iBCIs [8, 11, 57] (Fig. 2(a), see Methods from more information).

Figure 2:

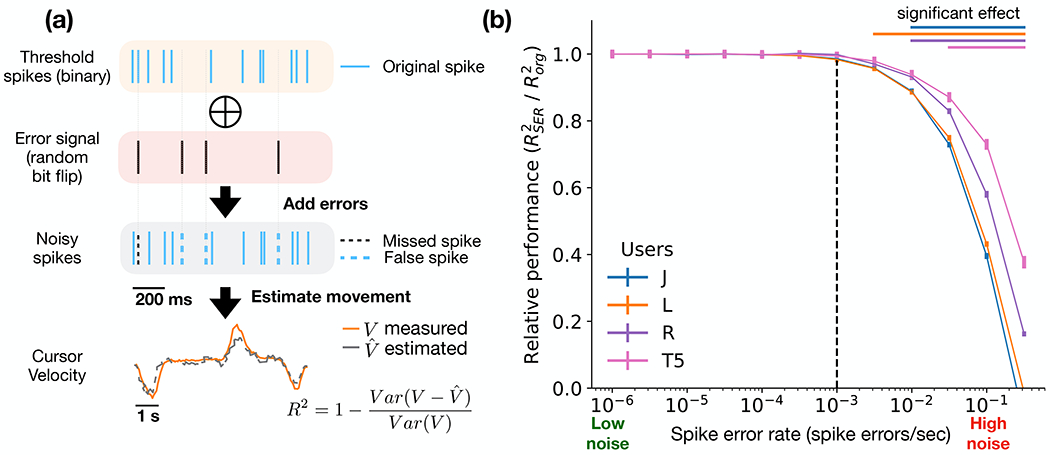
iBCI robustness to spike error. Data recorded during centre-out-and-back cursor trials of the three monkeys (J, L, and R) and the human participant (T5). (a) SER (spike errors/sec) simulation process. First, binary threshold neural signal bits (’1’ - spike , ’0’ - otherwise) were flipped at different rates (10⁻⁶ to 10^−0.5). Second, cursor velocity was predicted from the noisy signal. (b) Decoder performance (velocity coefficient of determination, R²) as a function of added SER (ranges from 0 to 1). Values are normalized to performance when decoding an undistorted signal (i.e., $\frac{R_{SER}}{R_{original}}$). Vertical bars along the lines represent the standard error of 10-fold cross validation across 10 days (total of 100 R² estimates). Horizontal bars in the right top corner indicate significant change in performance compared to the undistorted signal (two-sided Wilcoxon rank-sum test, p<0.05). Vertical dashed line indicates the SER in which performance starts to degrade. Bar colors correspond to the user.

Surprisingly, across the three monkeys and the human participant, SER only had a statistically significant effect on performance at a rate higher than 10⁻³ (see horizontal bars Fig. 2(b) in the right top corner, two-sided Wilcoxon rank-sum test, p<0.05), when compared to an undistorted signal ($R_{org}^2$). In other words, the neural interface recording and transmission system can tolerate a SER of up to 10⁻³ while maintaining comparable decoding performance. Intuitively, if the SER is much smaller than the rate of spikes, it should not have a significant effect on the decoder; but if the SER is of the order of magnitude of the action potential emission rate (firing rate), then the movement intention information will become highly corrupted. Indeed, our results on SER robustness correspond to the recorded firing rate (~10 spikes/sec, see Sup. Fig. S5) at the sample rate of 1,000 samples/sec (1 kSps). We extended the same analysis to three additional methods: a linear regression decoder to predict cursor velocity (as done with KF) and two types of discrete iBCI classifiers using a naive Bayes method and a support vector machine (SVM) to predict the location of the cued target. Similar to the findings for the KF, the performance of these decoders started to degrade when the SER approached 10⁻³ (see Sup. Methods - Offline decoders, and Sup. Fig. S3). For the rest of the manuscript, we will focus our analysis on the KF decoder, given its ubiquity in iBCI systems and the comparable results obtained by the other methods.

The proposed metric for spike distortion (i.e., SER) and the upper limit for the allowed error can be a guiding tool for iBCI neural interface designs, both in terms of recording and transmitting architecture, as well as specifications for the individual blocks in the system. Our results suggest that a neural interface (from electrode to transmitter in Fig. 2(a,c)) can distort the transmitted spike signal by a rate of up to 10⁻³, which is several orders of magnitude higher than the BER traditionally targeted by telecommunication systems [74, 75]. Here, we propose a neural interface that transmits a binary threshold-crossing spike signal at 1 kSps with an error rate of up to 10⁻³. This allows new trade-offs that could lower the device power requirements, and could give rise to novel neural interface designs that are custom-optimized for iBCIs.

3. Custom neural interfaces for iBCIs

Recording and transmitting binary threshold-crossing signals while tolerating high spike error rates opens an avenue for new recording system architectures that are customized for the needs of clinical iBCIs. These devices can be more efficient in power compared to current neural interfaces (Fig. 1(c)). To estimate the potential power savings of this approach, we investigated the benefits of using conventional architectures with distinct parameter choices informed by anticipated clinical iBCI needs. We intend for these conventional architecture estimates to be a starting point and an upper bound for more drastically different future designs and architectures. In this section, we describe the key parameters of conventional systems, and perform analyses similar to the previous section to examine how these parameters can be relaxed while still maintaining sufficient decoding accuracy.

3.1. Neural interface circuit design parameters

Figure 1(c) shows a conventional wireless implantable neural interface system similar to what is currently used in animal studies [14,20] and is being developed for human use [22,76]. The system consists of a sensor (such as a penetrating electrode array) connected to multiple recording units and a wireless transmitter (TX). Each recording unit contains a neural amplifier (A), an analog-to-digital converter (ADC), and digital signal processing (DSP, e.g., spike detector). The amplifier amplifies the neural signal in the frequency band of interest (f₀, f₁ - e.g. 0.3-7.5 kHz for action potentials). The noise introduced by this stage is defined as the input-referred noise level $\left(\overline{v_{in}^2}\right)$ of the neural amplifier (see Sup. Methods - Neural interface parameter simulation). The output signal is then converted into a digital signal by the ADC. The ADC is defined by the sampling frequency (f_s) and the resolution (B, number of bits). Due to circuit nonidealities (thermal noise and nonlinearities), the achieved effective resolution is usually 0.5-1.5 less than the number of bits, and it is defined by the signal-to-noise-ratio-based number of bits (SNR-bits) when nonlinearities are not taken into account [77]. Threshold crossing detection is implemented in post-processing and adds negligible power consumption as discussed in [78]. Hence, it will not be part of our analysis here. The transmitter data rate is usually defined as ${\text{R=f}=\text{f}}_s\text{BN}$, where N is the number of channels, if no DSP is applied and raw data is transmitted directly. The main factors that guarantee fidelity of this process are a wide filter frequency band, low noise, high quantizer sampling frequency, high quantizer resolution, and low data link bit error rate (BER). Unfortunately, these capabilities contribute to the power budget and total size of the system. In the next subsection, we focus on the recording unit’s design parameters, which also affect the transmitter power consumption. The transmitter-specific design parameters will be discussed later.

3.2. Custom circuit parameters for a movement iBCI

To investigate the range of circuit parameters that do not compromise performance in the iBCI application domain, we estimated the velocity prediction quality from a neural signal degraded by relaxing the specifications of several specific circuit components (see Fig. 3(a–c) and Method: Neural interface parameter simulation section for more details).

Figure 3:

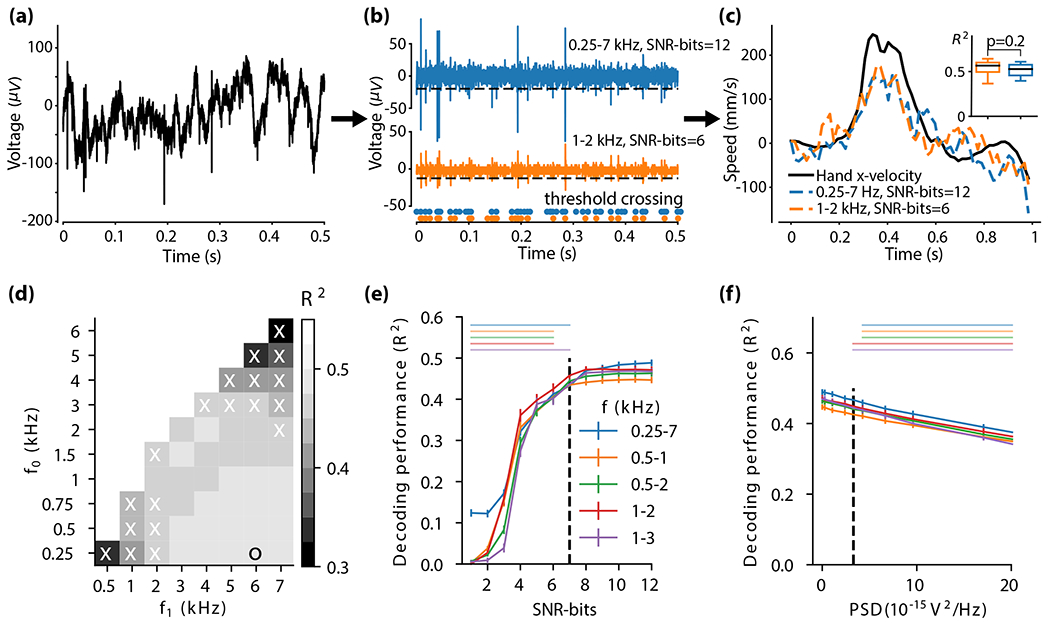
Study of iBCI performance as a function of the neural interface parameters (monkey J, for the other monkeys and the human participant see Sup. Fig. S6). (a-c) parameter simulation pipeline and examples for the simulation done in (d-f). (a) raw data was (b) filtered, re-quantized (with SNR-bits, signal-to-noise-ratio-based number of bits) or corrupted with noise, and then thresholded. The simulation pipeline corresponds to the raw signal pipeline of a conventional system, where filtering occurs only in the analog domain: Amplifier → analog-to-digital converter → digital signal processing (for spike detection). For more details see Methods: Neural interface parameter simulation. The threshold was set proportionally to each electrode’s root mean square voltage $\left(Threshol{d}_{electrode}=n\times RM{S}_{electrode}\right)$, where n was optimized for each set of parameters (e.g., number of bits). Orange and blue dots are the corresponding binary spike signals after thresholding for distorted and undistorted signals, respectively. (c) Hand velocity was then predicted with a Kalman filter (10-fold cross validated across 10 days with 100 trials in each day) from the preprocessed spike signal. Decoding performance was evaluated with velocity coefficient of determination (n=100 R² estimates, see insert). Significance was tested with two-sided Wilcoxon rank-sum test (p<0.05) (d) R² as a function of f₀ and f₁ (the cut-off frequencies for the bandpass filter). The threshold was optimized for each frequency band separately. The ’o’ marks the frequency band with maximum performance, and ’x’s mark frequency bands that resulted in significantly lower performance than the best frequency band. (e-f) R² (mean ± s.e.) as a function of (e) SNR-bits, and (f) power spectral density of added noise. Horizontal bars above the plots show significant differences compared to best R² (two-sided Wilcoxon rank-sum test, p<0.05) - bar colors correspond to the respective frequency bands (see legend). Vertical dashed lines indicate the minimum SNR-bits and maximum PSD values in which performance starts to degrade.

First, we varied the observation frequency band, f₀ and f₁, by sweeping the lower and upper cut-off frequencies of a second-order Butterworth bandpass filter used to filter the raw signal (see Methods). To relax the filter roll-off requirements and avoid aliasing issues, the sampling rate was set to f_s = 3f₁, allocating a slight oversampling above the Nyquist limit. Fig. 3(d) shows that decoding performance is kept consistent in a wide range of frequency bands, and that competitive decoding accuracy is also achieved at lower and narrower frequency bands, e.g. 0.5 kHz - 3 kHz. These results are consistent with previous studies examining finger position decoding [31].

Second, we investigated the effect of the quantizer resolution on performance. Fig. 3(e) shows that the decoder performance is fairly independent of ADC resolution for SNR-bits ≥ 7 (see horizontal bars in the top left corner). This minimum resolution is limited by the precision requirements on the threshold values used for spike detection, rather than by the signal resolution. Here, a threshold was set proportionally to each electrode’s (el) root mean square signal $\left(T{h}_{el}=n\times RM{S}_{el}\right)$, where n was optimized for each set of parameters (e.g., number of bits) by sweeping the range of −6≤n≤−1 (see Methods section for more details). Thresholding in the analog domain would allow for 1-bit quantization; however, Gibson and colleagues [78, 79] showed that low-resolution digital spike detection is more efficient than the analog counterpart.

Third, we investigated the effect of raw signal noise on decoding performance. In a neural interface, there are four main sources of noise: tissue thermal noise; electrode impedance thermal noise; noise from the interface electronics; and neuronal background electrical activity that might carry information from the surrounding neurons, but which for the purpose of spike detection we also consider as noise (Fig. 1(a)). Very low-noise interfaces (e.g.,$\sqrt{\overline{{\upsilon }_{in}^2}}=1-5\mu {\text{V}}_{rms}$ [20, 23, 31]) are usually designed to avoid being the main source of noise and to provide measurements limited only by the biological system [80]. However, Fig. 3(f) shows that decoder performance is robust (across all users) to a larger added Gaussian noise with a power spectral density ($\text{PSD=}\overline{{\upsilon }_{in}^2}/\Delta f$) of up to ~3.5×10⁻¹⁵V²/Hz. The PSD of an amplifier scales inversely with its power consumption. Hence, the extra noise budget can be utilized to reduce the power consumption of the amplifier. Alternatively, larger noise contributions from variations in the electrode impedance in chronic implants can be accommodated. Other noise sources, like motion artifacts and electromagnetic interference (EMI), usually appear to the recording system as common-mode signals. Hence, the differential structure of the system is able to reject them quite efficiently.

These results suggest that neural interface designs can be relaxed substantially and that there is a wide space of parameters (e.g., f₀, f₁, B, and $\overline{{\upsilon }_{in}^2}$) that can achieve comparable iBCI performance. Design decisions should be based on the neural interface architecture and the trade-offs between power consumption and complexity. For example, as we will present in the next section, in a conventional design, the ADC power consumption is negligible compared to that of the amplifier. Thus, the amplifier parameters should be optimized first (e.g., f = 0.5-3 kHz and PSD = 3.3×10⁻¹⁵V²/Hz) and the minimal number of bits that maintain performance with such an amplifier (e.g., SNR-bits = 7) should then be determined. An ongoing research effort to reduce power consumption already exists, with groups trying to create custom neural interfaces (academic prototype systems) [20, 22, 23, 40–46, 81, 82] for a wide range of applications. Table 1 summarizes the system specifications for a conventional system (commercialized [73]), selected academic prototypes [20, 22, 23, 41–45], and a minimalistic iBCI-focused design based on our results. Here we compare against systems designed for in-vivo (fully implanted) neural interfaces like the one we characterized in this study, [20, 22, 23, 41–45, 73]. It can be noted from Table 1 how neural interfaces have been evolving towards more efficient designs with respect to commercially available systems (i.e. amplification and quantization are optimized for maximizing signal-to-noise ratio at the output of the interface without compromising power efficiency). However, if specifications were derived based on iBCI decoding performance, further optimization could be achieved. This presents an opportunity to design custom neural interfaces for iBCI applications based on existing architectures that are power efficient and still support high channel count and wireless communication. Next, we will give an intuition as to the power savings that could be achieved by such specification relaxation as compared to designs intended for neuroscientific measurements.

Table 1:

Neural interface specifications for a conventional system (commercialized [73]), academic prototypes [20,22,23,41–45] and the suggested minimalistic design. The parameters are the total integrated noise power $\left(\overline{{\upsilon }_{in}^2}\right)$, the power spectral density (PSD), the lower and upper frequency corners of the bandpass analog filter (f₀ and f₁), the sampling frequency (f_s), the number of bits of the analog-to-digital converter (B), the data-rate of the ADC (R_ADC), and the data-rate of the transmitter (R_TX). We propose in the column Minimalistic Design that parameters can be relaxed up to 2-4 times with respect to the state-of-the-art (R_TX can be further reduced thanks to on-chip thresholding).

Parameters	Blackrock [73]	Yin et al. [23]	NeuroPixel [41]	Borton et al. [22]	HermesE [20]	Lopez et al. [42]	SiNAPS [45]	De Dorigo et al. [43]	WINeRS-8 [44]	Minimalistic Design
$\overline{{\upsilon }_{in}^2}$a (10−12V2) PSDb	9.0	7.8	25.0	74.0	4.8	41.0	56.3	110.3	9.0	–
(10−15V2/Hz)	0.8c	0.6c	1.6c	6.0c	0.3c	2.7c	5.0c	7.2c	0.4c	4.0d
f0 [Hz]	0.3	1	300	0.1	280	300	300	300	400	250
f1 [kHz]	7.5	7.8	10	7.8	10	10	7.5	10	15	3
fs [kS/s]	30	20	30	20	31.25	30	25	20	50	9
B [bits]	16	12	10	12	10	10	12	10	10	8e
${\text{R}}_{ADC}^f$ [kbit/s] f	480	240	300	240	312.5	300	300	200	500	72
${\text{R}}_{TX}^f$ [kbit/s]	480	240	300	240	312.5	300	300	200	500	1g

^aReported total integrated noise referred to the input of the interface.

^bThermal power spectral density referred to the input of the interface.

^cPSD was calculated from the reported total integrated noise, assuming a first-order filter roll-off and a thermal spectrum. $PSD=\overline{{\upsilon }_{in}^2}/\left(\Delta f\pi /2\right)$, where $\Delta f=f_1-f_0$.

^dTotal PSD is the original PSD in our recording system [73] plus the added PSD in our analysis.

^eSNR-bits = 7

^fData-rate is calculated per channel.

^gTransmitter data-rate assumes on-chip thresholding for the minimalistic design.

4. Neural interface power consumption

The previous results present a wide range of acceptable neural interface designs for use as part of an iBCI. In this section, we analyze how much power could be saved in each system component by allowing more noise over a reduced bandwidth of interest. The following analysis is based on theoretical limits and/or extrapolations from published work. An important next step for future work is to build a hardware proof of concept of the proposed system.

4.1. Neural amplifier

To estimate the amplifier power consumption we used the power efficiency factor (PEF) metric (Muller [83] extension to Steyaert [84] noise efficiency factor NEF):

$$PEF=NE{F}^2{V}_{DD}=\frac{\overline{{\upsilon }_{in}^2}}{\Delta f}\frac{I_{tot}}{2\pi U_{T}kT}{V}_{DD}$$ (1)

where V_DD is the supply voltage, $\overline{{\upsilon }_{in}^2}$ is the total integrated noise contributed by the recording electronics (referred to the input of the amplifier), $\Delta \text{f=}\left({\text{f}}_1-{\text{f}}_0\right)$ is the bandpass filter bandwidth, I_tot is the total bias current, $U_T=\frac{kT}{q}$ is the thermal voltage, k is the Boltzmann constant, T is the temperature and q is the charge of an electron. The NEF describes how many times the noise of an amplifier is higher compared to the ideal case of a bipolar junction transistor, operating with the same bias current, and the PEF is used to compare solutions working at different supply voltages. State-of-the-art neural amplifiers [30, 81, 85–87] usually result in a power budget ($P_A=I_{tot}{V}_{DD}$) in the 0.5-10 μW range per channel, and a PEF in the 1-30 V range. For more details on the amplifier power consumption, see Methods.

Fig. 4(a) shows the power consumption of an amplifier as a function of the input-referred power spectral density. PEF = 1.12 V from [30] was used here to calculate the power consumption. Given a required PSD, circuit topologies and supply voltage are the only degrees of freedom to reduce power consumption, as the bias current is set by the noise requirements.

Figure 4:

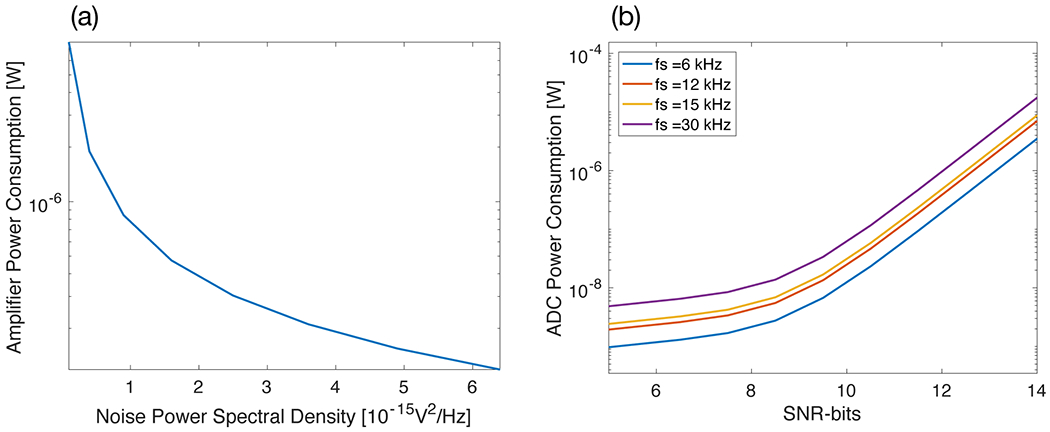
Power consumption trends in neural amplifiers and analog-to-digital converters. (a) Power consumption as a function of input-referred noise power spectral density (PSD) for a neural amplifier - equation (1) and PEF = 1.12 V used for this plot [30]. (b) Power consumption as a function of SNR-bits for an analog-to-digital converter for different sampling frequency (f_s)- see Methods for the model used for this plot.

4.2. Analog-to-digital converter

The conversion power for ADCs scales linearly with the sampling rate in designs that are not limited by the transit frequency of the technology. Estimating the conversion energy as a function of SNR-bits, however, is a more complex task. A model for the conversion energy is used here and described in the Methods section. This model considers the minimum power consumption of a proxy successive approximation register ADC [88], and it provides a realistic estimate of the power savings as a function of SNR-bits. The model does not take nonlinearities into account, as they do not noticeably affect the performance of the spike detector.

Fig. 4(b) shows the power consumption of an ADC as a function of the SNR-bits, for different sampling frequencies, f_s. Reducing the number of SNR-bits gives a large benefit in power consumption for medium to high resolutions (SNR-bits > 8). However, for low-resolution ADCs, this benefit becomes less dominant and power consumption is dominated by secondary effects (see Methods section).

4.3. Wireless transmitter

The design suggested here would take advantage of the reduced requirements, both in terms of single channel data rate and bit error rate, to allow for a larger number of channels transmitting simultaneously. Current systems implement simple modulation schemes such as On-Off Keying (OOK) or Frequency-Shift Keying (FSK) to reduce the complexity at the transmitter [89, 90], while still achieving BER lower than 10⁻⁴. The efficiency of the transmitter, E_b, is defined in terms of energy per bit and accounts for both the dynamic and static power consumption needed to transmit a single bit of information. At high data rates, the static power consumption is negligible compared to the dynamic power consumption and the overall efficiency ranges from a few pJ/bit to a few tens of pJ/bit [75,91]. For our analysis, we used the achieved 8.5 pJ/bit in [91]. Given the data rate, R, the total power consumption becomes

$$P_{TX}=E_{b}R$$ (2)

Transmitting threshold-crossing spike events instead of wide-band high-resolution signals will reduce the power consumption of the transmitter as long as the transmission efficiency is kept constant. The power saved can be allocated for integrating more channels (electrodes) into the device and maintaining the same data rate, which would yield the same efficiency (given the same design parameters such as coil size, transmission protocol, receiver distance, output power, etc.). Compared to a conventional system for basic neuroscience (e.g., 16 bits at 30 kS/s per channel) or academic prototype solutions (e.g., 10 bits at 20 kS/s per channel), the proposed solution tailored for iBCIs transmitting only binary events (e.g., 1 kbit/s per channel) could enable an increase in the number of channels (electrodes) by 480x and 200x, respectively. Designing for a lower BER (e.g., 10⁻³ and higher) could further improve the power consumption.

4.4. Low total power consumption for an iBCI

Fig. 5 summarizes the results presented in this section. Power consumption is plotted for each component (amplifier (A), analog-to-digital converter (ADC) and transmitter (TX)) of the systems in Table 1. The minimalistic design suggested here is analyzed for two cases: if raw data is transmitted (“Minimalistic Design”) and if only threshold-crossing events are transmitted (“Minimalistic Design with Thresholding (TH)”). The transmitter assumes an efficiency E_b = 8.5 pJ/b, and the amplifier assumes a power efficiency factor PEF = 1.12 V. The reader should note that the results presented here are obtained under the assumptions described above for power efficiency in each component and could vary significantly for different implementations and assumptions. The objective of Fig. 5 is to illustrate the relationship between system specifications and power consumption under reasonable assumptions.

Figure 5:

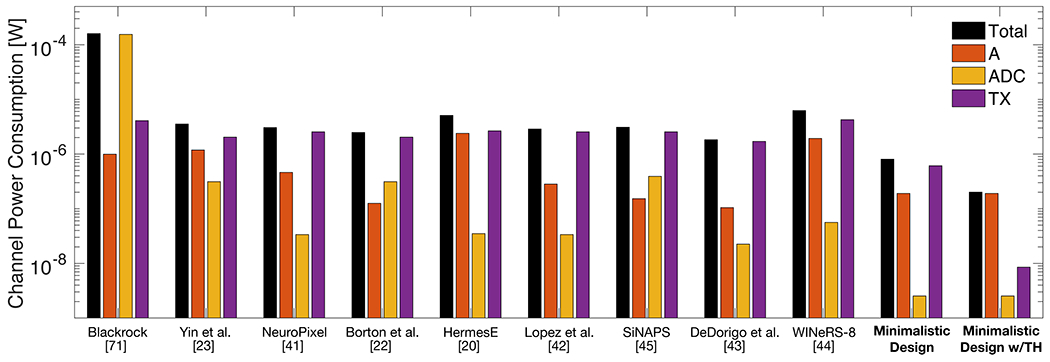
Power consumption estimates per channel (log-scale) for systems described in Table 1 [20,22,23,41–45,73]. A minimalistic design implementing on-chip thresholding (TH) could reduce the total power consumption by at least one order of magnitude.

Fig. 5 shows how more recent academic systems [20, 22, 23, 41–45] have lowered power consumption because they use more relaxed quantization strategies than commercialized systems [73] and optimize noise specifications for the neural amplifier [80]. Importantly, however, further power savings could be achieved when adopting the relaxed specifications we are proposing (‘Minimalistic Design’). If on-chip thresholding is performed (‘Minimalistic design with thresholding (TH)’) and only the presence or absence of a threshold crossing event is transmitted, the power consumption of the transmitter (which is the dominant power draw in most systems) can be drastically lowered with negligible extra cost in power and complexity. Such a system could reduce the total power consumption by two orders of magnitude compared to a commercialized system designed for basic neuroscience, or one order of magnitude compared to emerging research-tailored academic prototypes. These power savings come from loosening the parameters of all three components together. For example, transmitting spike events detected on chip with wide bandwidth (like in [32]) would have reduced the power by only about two fold. In contrast to the conventional system, whose power consumption would be limited by the transmitter (50-93%), the proposed design’s power consumption is limited by the neural amplifier (92%).

5. Outlook

Our results suggest that iBCIs with dedicated circuits designed for clinical use could consume an order of magnitude less power than an iBCI built with basic neuroscience-motivated specifications. The suggested minimalistic specifications are significantly relaxed without compromising decoding accuracy. This can give rise to new high-electrode count wireless iBCIs by reducing power and space requirements to the point that these circuits can support thousands of channels. In this section we identify areas where future research efforts in circuit-level and system-level solutions can further push an exponential increase in the number of wirelessly transmitted recording channels.

5.1. Circuit-level opportunities

5.1.1. Recording unit and transmitter

Transmitting only threshold crossing events does more than just relax the system specifications. It also opens an avenue for new recording system architectures for clinical iBCIs. For example, different spike detectors can be implemented, such as the nonlinear energy operator (NEO) that looks at the energy of the signal instead of the absolute value of the voltage trace, [92, 93]. Such detectors might provide more robust protection against thermal noise and could further relax the amplifier and ADC specifications.

In our approach, the neural amplifier is the main power consumer. It therefore should be the focus of future studies of new circuit topologies and tests of the robustness of iBCIs to noise. While we found that an iBCI decoder can be robust to added Gaussian noise of up to 3.5×10⁻¹⁵V²/Hz, we were not able to isolate the different noise sources and calculate the amplifier input referred noise. This is because noise from different sources (biology, electrodes, electronics) are indivisible in the recordings. Future work should aim to isolate these sources and better characterize the iBCI decoder robustness specifically to noise from the neural amplifier. Also, continuous improvement in electrode design and manufacturing is likely to lead to better SNR and larger signals. This trend will likely increase the robustness to added electronic noise in the system.

The total SER is related to the transmitter BER through the communication protocol. If the raw output of the threshold detector is transmitted (‘1’ for a spike, ‘0’ otherwise - transmitted per channel at bin rate), then the BER is equal to the SER, and an error in the transmitted data will result in either a false spike or a missed spike. More elaborate protocols that take into consideration the sparsity of the signal can reduce the transmitter data rate and obtain a different relationship between SER and the transmitter BER. For example, since the average rate at which action potentials arise is typically on the order of 10 action potentials per second, only 1% of the bits will be 1 at 1 kS/s (e.g., N/100, where N is the number of electrodes). Transmitting only the index of the electrodes that have an action potential, which requires log(N) bits per index, will result in an average data rate of $log\left(N\right)\times N\times 1\%$. In this protocol, a bit error will create an erroneous spike at an incorrect electrode index number, and a missed spike at the actual electrode index number, thereby doubling the SER. On the other hand, error detection and correction techniques at the receiver end could help alleviate the requirements on the BER, at the cost of minimal increase in the data rate requirements.

5.1.2. Device area

Another limited resource for an implantable neural interface is the chip area, but quantitative estimates for this area are difficult to obtain. Area depends on many factors, such as technology and architecture. However, reducing the noise requirements of an integrated circuit usually results in a smaller footprint. Smaller transconductance results in smaller active devices, and smaller sampling capacitors result in smaller passive devices. Increasing the high-pass pole of the filter might also reduce the neural amplifier total area. Future work should investigate the limitations of area consumption and find trade-offs that balance reduced area with acceptable performance.

5.2. System-level opportunities

5.2.1. Dimensionality reduction on-chip

As we mentioned earlier, dimensionality reduction techniques are still under active investigation and consensus on a single reduction strategy has not been reached. Nevertheless, to further reduce the system’s data rate, one could implement dimensionality reduction directly on-chip. A common approach is to implement principal component analysis (PCA) before the decoder. However, it is not immediately clear how on-chip PCA would help reduce the overall system power consumption. The data rate reduction is not massive and the power overhead of the hardware implementation for PCA might actually result in an increase in power consumption. For example, for 1000 channels the original data rate would be, after the threshold detector, f_TX,1 = 1 Mbps (assuming 1b at 1 kHz output). If 20 PCs with 8 bit resolution are transmitted after PCA analysis, the new data rate would be f_TX,₁ = 0.16 Mbps. The gains in reducing the data rate from 1 Mbps to 0.16 Mbps might not be enough to justify the computational cost of PCA and the storage cost of a projection matrix. This conclusion differs from previous work done on on-chip compression of neural signals, [89], since the raw data here is a binary threshold-crossing signal and not a high-resolution signal used for spike sorting.

Currently, PCA is computed using floating-point resolution. To properly estimate the benefit of on-chip PCA, future work should study the resolution requirements on the PCs for iBCI decoders, i.e. how many components to use and at what bit resolution to represent each component. This will allow a numerical analysis of the computation and storage cost of on-chip PCA, as well as the data reduction factor.

5.2.2. Real-time iBCI

Here, we estimated the effects of system parameters on iBCI performance using offline decoding analyses based on real movement and iBCI data. However, during real-time iBCI control, the user has continuous feedback about the decoder’s performance (for example, by seeing how the cursor or robotic arm is moving). This allows the user to compensate for errors [60, 69, 94]. Thus, the robustness to SER in real-time is probably higher than in the offline analysis we presented here. This can be verified by future closed-loop studies in which various types of signal processing alterations (such as spike errors or different filtering or bit resolution) are made to the neural data during real-time iBCI control.

5.2.3. Number of required recording channels

A natural question is how many channels are needed for an iBCI? Until high electrode count devices exist (e.g., »1000 channels), it will be difficult to determine how many electrodes suffice for each iBCI application. There have been a few attempts to extrapolate the performance of iBCIs with increasing numbers of electrodes (e.g. [14,15,95]). However, extrapolations are challenging because they do not reliably predict how neural activity will change in more complex tasks [96] and how more advanced decoders might make use of this data. Schwarz and colleagues [14] postulated that recording 5,000 to 10,000 neurons is necessary for an iBCI to restore limb movement, and that 100,000 neurons will be required to control whole body movement. Once a high electrode count device exists, it might reveal that it is advantageous to have more electrodes even at the expense of the reliability and accuracy of each electrode signal; this would provide opportunities to reduce per-channel power even more by further relaxing the specifications.

5.3. Implications beyond movement iBCIs

5.3.1. Other types of BCIs

Here we evaluated circuit specifications for neural interfaces for decoding movement intentions. Our results – that design specifications can be dramatically relaxed – may well apply to other types of neural interfaces, such as those used in retinal prostheses, peripheral nervous system interfaces, etc. Our prediction is that neural interfaces that rely mainly on decoding spike activity will have similar recording system requirements (e.g., f₀, f₁ and B), though the SER might change based on the redundancy of the signal and the robustness of the decoders. Applications where spike sorting is required, e.g. artificial retinas, can also benefit from a design that uses a holistic approach to reduce power consumption at the interface, like the work in [34]. Similar power calculation and parameter analyses might also be beneficial for wireless miniature microscopes to enable longer recording times (e.g., [97]).

5.3.2. Implications for basic neuroscience research

While this work focuses on neural interface design for a clinical iBCI application, basic neuroscience research might also benefit from low-resolution, high channel count devices. Although research-based studies traditionally require accurate single neuron recording, in some scenarios they can benefit from trading off recording from more neurons for better per-neuron signal fidelity. For example, this may be the case when when looking for population-level phenomena for which spike sorting is not necessary [29], or in studies where wireless recording is essential [14, 23, 98]. In particular, this approach can enable longer duration and/or wireless recording from model organisms that are too small to carry the bulky electronics needed for high-bandwidth recording and data transmission/storage.

6. Conclusion

When developing a new device, an iterative process of design and user testing is essential. In multidisciplinary research, such as neuroscience, this process may take years or even decades since the design and the testing are sometimes done by separate entities (e.g., different research labs). A large body of neuroscience research gave rise to the iBCI field, which since its inception used similar methods and tools as neuroscience. Decades of iBCI research with monkeys and recent clinical trials with human participants have now brought the field to a new level of maturity and confidence about its neural interface requirements. While future iterations (e.g., further on-chip processing) are inevitable, our study can be viewed as central feedback on current neural interface designs and a guidance for dedicated designs for the next generation of iBCIs. We believe that this study, which arose from a collaborative effort between electrical engineers, neural engineers, clinicians, and neuroscientists, is a path forward towards the next generation of clinically viable iBCIs.

7. Methods

7.1. Monkeys hand movement data

All monkeys’ procedures and experiments were approved by the Stanford University Institutional Animal Care and Use Committee. Three male rhesus macaques (monkeys J, R and L) were trained to perform point-to-point movements of a 6 mm radius virtual cursor in a 2D plane, while their other arm was gently restrained. The monkey performed center-out-and-back task to 8 targets uniformly distributed on a 8 cm radius circle (Sup. Fig. S1). Two mirrors, setup as a Wheatstone stereo-graph, visually fused the monitors into a single 3-D percept for the monkeys, although all task relevant motion was limited to two dimensions [99]. In this work, about 100 continuous successful trials (about 2 min) from 10 experiment session days (about 1000 total trials) were recorded from each monkey and analyzed.

Monkeys were implanted with two (monkeys ’J’ and ’R’) or one (monkey ’L’) 96-electrode Utah arrays (Blackrock Microsystems, Inc.), using standard neurosurgical techniques 95 (J), 75 (R) and 91 (L) months prior to the recorded sessions. The arrays contained a 10 × 10 grid of 1 mm microelectrodes with 400 μm center-to-center spacing between adjacent electrodes. J’s and R’s arrays were implanted into the left cortical hemisphere; one array went into the primary motor cortex (M1) and the other into the dorsal premotor cortex (PMd). In this study we used only the PMd array of monkey R, since his M1 array was severely degraded and recorded almost no large waveform action potentials. L’s single array was implanted into the right hemisphere boundary between M1 and PMd.

7.2. Human participant iBCI cursor movement data

Permission for these studies was granted by the US Food and Drug Administration (Investigational Device Exemption) and Institutional Review Boards of Stanford University (protocol #20804), Partners Healthcare / Massachusetts General Hospital (2011P001036), Providence VA Medical Center (2011-009), and Brown University (0809992560). The participant in this study, ’T5’, was enrolled in a pilot clinical trial of the BrainGate2 Neural Interface System (http://www.clinicaltrials.gov/ct2/show/NCT00912041). Informed consent, including consent to publish, was obtained from the participant prior to his enrollment in the study.

Participant T5 is a right-handed man, 63 years old at the time of the study, whose iBCI cursor control research sessions were previously described in [8,62]. T5 was diagnosed with a C4 AIS-C spinal cord injury approximately nine years prior to study enrollment. In August 2016, participant T5 had two 96-channel intracortical silicon microelectrode arrays (1.5 mm electrode length, Blackrock Microsystems, Salt Lake City, UT) implanted in the arm-hand area of dominant (left) motor cortex.

T5 also performed 10 research sessions from which we analyzed 2 min durations of a cursor movement task. In his task, a grid spanning 1000 × 1000 pixels on the computer monitor was divided into a 6 × 6 or 9 × 9 grid of equally-sized gray squares. Each square was a selectable target, and on each trial, one square would randomly be prompted as the correct target by changing its color to green. The participant had to select the correct target (which resulted in a trial success) while avoiding selecting any of the other (incorrect) targets, which resulted in a trial failure.

T5 controlled the computer cursor using an iBCI. In his sessions, neural control and task cuing were controlled by custom software running on the Simulink/xPC real-time platform (The Math-works, Natick, MA), enabling millisecond-timing precision for all computations. Neural data were collected by the NeuroPort System (Blackrock Microsystems, Salt Lake City, UT) and available to the real-time system with 5 ms latency.

Two-dimensional continuous control of the cursor was enabled by the ReFIT Kalman Filter detailed in [8, 11]. T5 could select a target by dwelling on it for 1 s or by a discrete “click” signal. Discrete selection (“click”) was achieved using a Hidden Markov Model (HMM)-based state classifier. The user commanded a “click” by attempting to squeeze his left hand (i.e., the hand ipsilateral to the array(s)). For both the continuous cursor-positioning ReFIT-KF decoder and the discrete click-state HMM decoder, spiking activity was binned every 15 ms and sent through the decoders. Since the executed kinematics were an output of a Kalman filter based decoder, they were more temporally structured compared to the monkeys’ hand kinematics.

7.3. Neural and hand position recording

We used Blackrock Microsystems neural acquisition systems during both monkey (Cerebus system) and human (NeuroPort system) research sessions. Both data acquisition systems achieve 3 μV_rms of input-referred noise over a bandwidth of [0.3 - 7500] Hz, and sample each electrode with 16 bits at 30 kSps. We refer to the system output signal as our raw signal. Nonactive electrodes with zero firing rates were removed from the analysis. During the session, the monkey’s contralateral hand position was measured for decoder training and hand kinematics were analyzed using an infrared reflective bead tracking system (Polaris, Northern Digital) polling at 60 Hz. Hand velocity was computed from the recorded position of the bead, which was taped to the monkey’s reaching hand.

7.4. Offline decoders

We used a Kalman filter to estimate the 2D hand velocity $\left({\upsilon }_t\in R^2\right)$ from the spike events ($y_t\in {\left\{0,1\right\}}^N$, N is number of electrodes), ${\upsilon }_t=f\left(y_t\right)$. In all analyses, decoders were 10-fold cross validated on each day (total of 100 decoders per user) and their quality was measured with R² (r-squared) compared to the true hand (monkeys) or cursor (human) velocity. With the monkey datasets, we estimated the velocity of their native hand while they conducted a center-out reaching task. As T5 could not move his hands, we offline estimated the cursor velocity. During T5’s sessions, the cursor was controlled by the iBCI system, which used a ReFIT-KF algorithm to decode his intention in real-time. We note that for both the monkey and human movements, the key question was the same: did decoding these same neural data, subject to varying additional spike errors, output similar decoded kinematics?

The same analysis performed for the KF decoder was extended here to a linear regression decoder to estimate cursor velocity, and its performance was similarly measured using R². Also, two different discrete iBCI decoders were analyzed using a naive Bayes and a support vector machine (SVM) classifier. Each iBCI discrete decoder’s task was to detect the intended target the user was aiming to based on the neural activity at the beginning of each trial. Similar to the optimal parameters found in [100], we used 64 ms of neural activity starting from 160 ms after target-onset. We used classification accuracy to measure the classifiers’ performance. For all decoders and classifiers, we used 10-fold cross validation for each day, as described above. Sup. Fig. S3 summarizes the results for different decoders. Conclusions based on discrete decoding regarding SER robustness are consistent with those drawn for the KF decoder.

7.5. Spike error rate (SER) simulation

To extract neural spiking activity using the Blackrock system, a 250 Hz high-pass filter was applied to the raw signal. Then, a spike was detected whenever the voltage crossed below a threshold set at −4.5 × rms voltage. This threshold value was updated every session. The spike detector used a window of 1 millisecond, and multiple spikes were accumulated in non-overlapping 60 Hz bins in order to align to hand velocity recordings. Spike errors were simulated by independently, randomly flipping the binary signal samples y_t ($y_t\in 0,1^N$, where y is the spike events, t is time and N is the number of electrodes) with a Bernoulli distribution with probability equal to the tested SER (Fig. 2(a)). For example, if the error rate was 10⁻², each sample (bits) of the signal was independently, randomly flipped with a Bernoulli distribution with a probability of p = 10⁻².

7.6. Neural interface parameter simulation

To simulate a neural interface with a set of new parameters, we degraded the raw signals (recording system output signal - 16 bits at 30kSps) with a series of manipulations, as described in the main text and elaborated below. Then, we detected the spikes from this manipulated raw signal and estimated the hand velocity using the decoders as described earlier (Sup. Fig. S2). We note that the spikes were detected with a threshold (as described below - Threshold crossing detection section) and no spike sorting was performed. Future work could explore the effect of spike sorting on what region of the parameter space would still result in comparable performance. Here, the raw signal emulates a continuous time (CT) signal to be processed by our recording system. This is equivalent to a real CT analysis, since the sampling rate of our recording system is well below the sampling rate of the raw signal.

Input-referred noise:

the input-referred noise represents the total noise introduced by the circuit via a fictitious input source that captures all circuit-internal noise sources. Noise is usually referred (scaled) to the input so it can be readily compared to the input signal level. To simulate higher input-referred noise $\left({\overline{{\upsilon }_{in}}}_{,rms}\right)$, we added Gaussian noise with variance of ${\sigma }_{noise}^2$ to the raw signal.

Bandpass:

to simulate the amplifier filtering function, we filtered the signal between f₀ and f₁ (the cutoff frequencies of the filter) with a 2^nd order Butterworth filter.

Sampling:

the output of the bandpass filter was sampled at f_s = 3f₁, for allocating some oversampling above the Nyquist limit and relaxing the bandpass filter performances. This choice is commonly adopted to relax the filter roll-off requirements and avoid aliasing issues. Optimizing the ratio $\frac{f_s}{f_1}$ can be investigated in future work.

Quantization:

the sampled signal was re-quantized at B bits.

Threshold crossing detection:

threshold detection was applied every millisecond (in a causal 30 samples window) to detect the presence of a putative neural spike. The threshold was set to be proportional to the estimated raw signal rms (root mean square) for each electrode

$$V_{threshold}^e=n\times V_{rms}^e$$

where e is the electrode’s number. The number of rms (n) was optimized by sweeping the range of −6 to −1 using increments of 0.5 for all of the electrodes, for each set of parameters; see Sup. Fig. S7 for best nRMS distribution across parameters sets. The Blackrock system’s built-in function was used for calculating the rms voltage of the noise, which is slightly different than the standard rms calculation [27]. Specifically, the BlackRock algorithm calculates a biased estimate of the rms with an aim to exclude spikes and artifacts that inflate the rms. First, the algorithm computes mean squares of each of 100 non-overlapping bins (x_j) of 600 continuous samples (20 ms) of the raw data (s_i), with total of 60,000 samples (2 sec):

$$x_j=\frac{1}{600}\sum _{i=1}^{600}{s}_i^2,1\le j\le 100$$

Then, the rms is calculated by averaging the 6^th until the 25^th lowest x_j values (20 out 100 values):

$$rms=\sqrt{\frac{1}{20}\sum _{i=6}^{25}mi{n}_{i}x}$$

min_ix is the ith minimum value of x.

Spike binning:

the resulted binary signal was binned in 60 Hz non-overlapping bins aligned to velocity recordings.

7.7. Statistical Testing

When comparing two different distributions of R², we used a two-sided Wilcoxon rank-sum test with a confidence level of p = 0.05 unless stated otherwise.

7.8. Neural amplifier noise and power

In order to gain insight into the amplifier power consumption and its lower limits, let us consider the input-referred thermal noise contribution of a single MOS transistor

$$\overline{{\upsilon }_{in}^2}=\frac{4kT\gamma }{g_m}$$ (3)

where γ is a technology dependent noise factor here approximated to 0.8, [101, 102], and g_m is the device transconductance. g_m can be linked to the power consumption through the device transconductance efficiency, g_m/I_D, where I_D is the transistor bias current. For a device working 1 in the sub-threshold region, g_m/I_D can be as large as $30\frac{S}{A}$ (upper limit is $q/\text{kT}\sim 38\text{S}/\text{A}$ for bipolar transistors). In these conditions, the power consumed (P_D) to obtain an input referred noise of 5 μV_rms over a bandwidth ∆f = 10 kHz (assuming a supply voltage of 1 V) is

$$P_D=\frac{1}{{\left(5\mu V_{rms}\right)}^2}\frac{4kT\gamma }{g_m/I_D}\Delta f{V}_{DD}=177nW$$ (4)

Although this result might look promising, this refers to a lower limit for biasing a single device that ensures enough thermal noise margin for a complete system. In reality, a differential readout s is usually implemented to deal with common-mode noise injections, chopping or correlated double sampling is used to attenuate flicker noise, and multiple gain stages are used for better conditioning of the signal before the ADC. As a result, practical implementations will consume more power than) that described in Eq. (4).

Steyaert et al. [84] proposed a metric for comparing the noise performance of amplifiers called 1 the Noise Efficiency Factor (NEF).

$$NEF={\upsilon }_{in,rms}\sqrt{\frac{2I_{tot}}{\Delta f\pi U_{T}4kT}}$$ (5)

where I_tot is the total bias current, $U_T=\frac{kT}{q}$ is the thermal voltage, k is the Boltzmann constant, T is the temperature and q is the charge of an electron. The NEF describes how many times the noise of an amplifier is higher compared to the ideal case of a bipolar junction transistor, operating with the same bias current¹. However, the NEF lacks the ability to compare solutions operating at different supply voltages. To overcome this problem, Muller [83] introduced the power efficiency factor (${\text{PEF=NEF}}^2{\text{V}}_{DD}$), which takes into account both the operating current and the supply voltage.

$$PEF=\overline{{\upsilon }_{in}^2}\frac{2P_A}{\Delta f\pi U_{T}4kT}$$ (6)

where P_A is the total power consumption of the amplifier. State-of-the-art neural amplifiers [81, 85–87] usually result in a power budget (P_A = I_totV_DD) in the 0.5-10 μW range, and PEF in the 1-30 V range.

7.9. ADC Power Model

To study the effect of resolution on the ADC energy, we considered a model of a successive approximation register (SAR) ADC, [88], shown in Sup. Fig. S4. The model assumes that the three main sources of power consumption are the capacitive DAC, the comparator and the logic. Also, it assumes that the comparator, the sampling capacitor and the quantization process, each contribute a third of the total noise. From these assumptions, we can derive the minimum energy required to resepect the SNR specifications for each component.

Capacitive DAC:

the input is sampled by the capacitive DAC, hence the minimum capacitance must satisfy:

$$SNR=\frac{\frac{1}{2}\left(\frac{V_{inpp}^2}{2}\right)}{3\frac{kT}{C_{DAC}}}$$ (7)

where V_inpp is the peak-to-peak input voltage, k is the Boltzmann constant, T is the temperature, $C_{DAC}=2^B{C}_U$ is the total DAC capacitance, and C_U is the unit capacitance. As a result, the minimum unit capacitance becomes:

$$C_U=-\frac{24kTSNR}{2^B{V}_{inpp}^2}+C_{U,\min }$$ (8)

where C_U,min is the minimum realizable capacitance allowed by the technology (usually [0.1 - 1] fF). The total energy depends on the switching activity of the DAC. The solution in [103] grants:

$$E_{DAC}=\sum _{i=1}^{B-1}{2}^{B-3-2i}\left(2^i-1\right)C_U{V}_{REF}^2$$ (9)

where B is the number of bits of the ADC, and V_REF is the reference voltage.

Comparator:

here, a simple latch model is used for the comparator and the noise is simplified to $\frac{kT}{C_C}$, where C_C is the load capacitance of the latch. For a more complete analysis, the reader can refer to [104]. Similar to the capacitive DAC, the minimum load capacitance for the latch can be derived as:

$$C_C=\frac{24kTSNR}{V_{inpp}^2}+C_{C,\min }$$ (10)

where C_C,min is the minimum load capacitance available (usually [1 - 10] fF). The total energy then becomes

$$E_{comp}=\left(C_C{V}_{DD}^2\right)B$$ (11)

where V_DD is the supply voltage of the comparator.

Logic:

for simplicity, we assume that the logic complexity depends linearly on the number of bits. The total energy then becomes:

$$E_{logic}=N_B{E}_{G}B$$ (12)

where N_B is the number of gates required per bit, and E_G is the energy per gate.

The total energy, and contributions from each block are plotted in Sup. Fig. S4 as a function of SNR. Reference points from literature are also plotted in figure, [20,82,105,106]. For low SNR, the conversion energy is dominated by the logic. For high SNR, the conversion energy is dominated by the comparator and increases 4x per bit, [107].

Here, we assume that power is a linear function of the sampling frequency, f_s, which is a realistic assumption for sampling frequencies well below the transit frequency of the technology. Hence,

$$P_{ADC}=f_s\left(E_{DAC}+E_{comp}+E_{logic}\right)$$ (13)

7.10. Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Data availability

The sharing of the raw human neural data is restricted due to the potential sensitivity of this data. These data are available upon request to the senior authors (KVS or JMH). To respect the participants’ expectation of privacy, a legal agreement between the researcher’s institution and the BrainGate consortium would need to be set up to facilitate the sharing of these datasets. Processed data is provided as source data, and is available at https://shenoy.people.stanford.edu/data.