Abstract
Cantor coding provides an information coding scheme for temporal sequences of events. In the hippocampal CA3–CA1 network, Cantor coding-like mechanism was observed in pyramidal neurons and the relationship between input pattern and recorded responses could be described as an iterated function system. However, detailed physiological properties of the system in CA1 remain unclear. Here, we performed a detailed analysis of the properties of the system related to the physiological basis of learning and memory. First, we investigated whether the system could be simply based on a series of on–off responses of excitatory postsynaptic potential (EPSP) amplitudes. We applied a series of three spatially distinct input patterns with similar EPSP peak amplitudes. The membrane responses showed significant differences in spatial clustering properties related to the iterated function system. These results suggest that existence of some factors, which do not simply depend on a series of on–off responses but on spatial patterns in the system. Second, to confirm whether the system is dependent on the interval of sequential input, we applied spatiotemporal sequential inputs at several intervals. The optimal interval was 30 ms, similar to the physiological input from CA3 to CA1. Third, we analyzed the inhibitory network dependency of the system. After GABAA receptor blocker (gabazine) application, quality of code discrimination in the system was lower under subthreshold conditions and higher under suprathreshold conditions. These results suggest that the inhibitory network increase the difference between the responses under sub- and suprathreshold conditions. In summary, Cantor coding-like iterated function system appears to be suitable for information expression in relation to learning and memory in CA1 network.
Keywords: Spatiotemporal coding, Iterated function system, Single neuron, Hippocampus, Patch-clamp recording
Introduction
Contextual information, used by the brain for immediate response to the stimuli, is believed to be stored in the hippocampus structure in form of short-term-memory (Ekstorm and Ranganath 2018). In the hippocampus, it is possible to identify 3 different structures connected in a circuit system where the information flow from the Dentate Gyrus, to the CA3 and the CA1 region. Moreover, CA3 is characterized by a recurrent (feedback) subcircuit. Tsuda (2001) and Tsuda and Kuroda (2001) reported the possibility of Cantor coding in the CA3–CA1 network. Cantor coding is an information coding scheme for temporal sequences of events (Tsuda 1992, 1996). It forms a hierarchical structure in the state space of neural dynamics. In the model, it is assumed that the CA3 state revolves around quasi-attractors, each of which represents a single episodic event, and that CA3 outputs a temporal sequence of events, which should be encoded in CA1, particularly in temporal dimensions. The input-dependent distribution of the CA1 state is hierarchically clustered in the vector space.
A physiological basis has been observed for Cantor coding-like system in hippocampal CA1 neurons, with the property dependent on the magnitude of the excitatory postsynaptic potential (EPSP) (Fukushima et al. 2007), and the stored information also reflects to frequency of action potentials as output (Kuroda et al. 2009). Furthermore, the relationship between the input pattern and the recorded responses could be described as an iterated function system. A newly invented virtual reconstruction of neurons, whose data was obtained individually by patch-clamp recording, improved the quality of code discrimination in CA1 model. These results support the idea of existence of the Cantor coding-like iterated function system in CA3-CA1. However, the detailed physiological properties of the system in the CA1 are still unclear.
In this study, to clarify whether Cantor coding-like iterated function system is physiologically suitable for neural networks in CA3–CA1, we did 3 experiments. First, generally, neural processing related to learning and memory in CA1 pyramidal neurons is not simply dependent on only mean firing rate of input from CA3, but also on the sequential and spatial effects of input patterns (Tsukada et al. 1996, 2007). However, spatial effect of input pattern in the system is unclear. We applied series of 3 spatially distinct input patterns with similar EPSP peak amplitudes (Experiment I). Second, Yamaguti et. al (2011) used two-compartment modeled neurons to show that the theoretical performance of the quality code discrimination in the Cantor coding-like iterated function system is dependent on both the interval of the input sequence and main neuron types. However, the interval dependency of input sequence was not physiologically recorded, so we applied sequential inputs at several intervals (Experiment II). Third, there are many kinds of inhibitory neurons in the hippocampus, and previous work showed the importance of inhibitory networks for learning and memory in CA1 (Freund and Buzsáki 1996). However, the inhibitory network dependency of the Cantor coding-like iterated function system was not clear. We recorded neural response with/without GABAa receptor blocker and analyzed the system (Experiment III).
Materials and methods
Preparations and patch-clamp recording
All procedures were approved by Animal Care and Use Committee of the Tamagawa University and Kawasaki University of Medical Welfare. The brain of Wister rats (4–5 weeks old) was sliced at an angle of 30–45° along the long axis of the hippocampus at a thickness of 300 μm. Before recording was begun, the slices were kept in bath solutions (142 NaCl/2 MgSO4/5 KCl/2.6 NaH2PO4/2 CaCl2/26 NaHCO3/10 glucose [all mM], bubbled with 95% O2/5% CO2) at room temperature for at least 60 min. A slice was placed in the recording chamber. Neurons were visualized with an IR-DIC camera (C2741-79H; Hamamatsu, Japan). Recording electrodes were pulled from borosilicate glass and had resistances of 5–8 MΩ. Recordings were obtained at 28–30 °C. The internal solution of the recording electrode was contained (in mM) 120 KMeSO4/20 KCl/10 HEPES/10 EGTA/4 Mg2ATP/0.3 Tris-GTP/14 Tris2phosphocreatine/4 NaCl (pH 7.25 with KOH). The starting voltages of the recorded neurons were between − 55 and − 62 mV, and the membrane potential was kept at − 68 mV by current injection to the soma. Whole-cell patch-clamp recording was performed from the soma using an electrical amplifier (CEZ-3100; Nihonkoden, Japan). Signals were filtered at 10 kHz, sampled at 20 kHz, and stored (micro1401; CED, England). When needed, 10 μM gabazine (Sigma), which is a one of the major GABAA receptor antagonists, was applied to the bath solutions.
Electrical stimulation
EPSPs were induced by extracellular electrical stimulation using 3 (Experiment I) or 2 (Experiments II and III) theta glass electrodes (TST-150–6; WPI, FL, USA). The tips of the electrodes were set to the Schaffer collaterals in positions that divides the area into 4 (Experiment I) or 3 (Experiment II and III) approximately equal parts from proximal to distal. The overlap of the stimulating pathway between the electrodes was checked by paired-pulse facilitation (at a 50 ms interval). The duration of the electrical stimulation was 200 µs.
In Experiment I, one set of stimuli was as follows: electrical stimulation through one of 3 stimulating electrodes (proximal “100”, middle “010”, or distal “001”), was randomly repeated 10 times (at 30 ms intervals). A set of stimuli at 10 s intervals was applied for 20 min. There were 2 experimental conditions dependent on the variety of the 3 peak EPSP amplitudes induced by each electrode: “different responses” and “similar responses” conditions. The ratio of maximum/minimum peak EPSP amplitudes was high (2.23 ± 0.37, mean ± SEM) under “different responses” condition, and was low (1.36 ± 0.11) under “similar responses” condition. The peak amplitudes of the EPSPs under “different responses” and “similar responses” were 2.91 ± 0.37 mV and 3.85 ± 0.64 mV, respectively.
In Experiments II and III, the 4 input spatial patterns were as follows: (1) electrical stimulation through both electrodes (“11”), (2) electrical stimulation through one electrode (“10”), (3) electrical stimulation through the other electrode (“01”), and (4) no electrical stimulation (“00”). One set of stimuli was as follows: one of the four spatial patterns ("11", "10", "01", and "00") was randomly repeated 10 times (at a 20–720 ms interval). The set of stimuli at 10 s intervals was applied for 20 min. The strength of the stimulating current was adjusted to the amplitude of the elicited EPSP (1–6 mV). To clarify the effect of action potentials, neural responses were classified into 2 groups, subthreshold and suprathreshold conditions. This classification was defined by whether the stimulus induced any action potentials or not.
Data analysis
To evaluate how spatiotemporal information from CA3 affects the membrane potentials of CA1 neurons, the following two measures were used: (1) a spatial clustering index, which comprises a pattern classification measure for the spatial input pattern [("100", "010","001") or (“11”, “10”, “01”, “00”)] at each time-history, and (2) a self-similarity index, which comprises a measure of hierarchical self-similarity in the time-history. Both spatial clustering and self-similarity indices were calculated as in previous paper (Fukushima et al. 2007). In both indices, the amplitude 20 ms after each pattern of electrical stimulation was used as a representative value of the responses. The spatial clustering index indicates how well the distribution of responses is clustered by the patterns of electrical stimulation. Each response was categorized into 3 (or 4) groups by the current pattern (the first time-history step), one preceding pattern (the second time-history step), 2 preceding patterns (the third time-history step), or more of electrical stimulation. The spatial clustering index indicates the probability that the distance between “the value concerned and the weighted center of its own group” is not the shortest of the 3 (or 4) distances between “the value concerned and the weighted center of all 3 (or 4) groups”. The self-similarity index indicates a measure of hierarchical self-similarity. The 3 (or 4) weighted centers for each time-history step of the spatial input pattern forms an observed pattern in amplitudes. The self-similarity measure is given by the number of neighboring permutations to get a target-ordered pattern corresponding to the standard pattern (the corresponding pattern to the first time-history step). The spatial clustering and self-similarity indices were normalized according to the chance level. That is, 0 indicates completely distinguishable and 1 indicates completely indistinguishable. For both indices, the smaller their values, the higher quality of code discrimination. Two-way ANOVAs and Fisher’s LSD were used for statistical analysis.
Results
Spatial effect of input pattern in the Cantor coding-like system (Experiment I)
Self-similarity and spatial clustering indices were estimated for two conditions, “different responses” (n = 10) and “similar responses” (n = 5). In neither condition, action potentials were induced. The self-similarity index under the “different responses” condition was significantly lower than chance at the time-history pairs of “one and two” and “one and three” steps in the sequences (Fig. 1a). In contrast, the self-similarity index under “similar responses” condition did not show a significant difference from chance for any pair. The spatial clustering index under “different responses” condition was significantly lower than chance at the first and second time-history step (Fig. 1b). The spatial clustering index under “similar responses” conditions was also significantly lower than chance level. The spatial clustering index was higher under “similar responses” conditions than under “different responses” conditions at the first and second history steps. Our results under “similar responses” conditions show statistically significant spatial clustering index, and suggest that the iterated function system was not only using a series of on/off input signals but using some spatial factors in input signals.
Fig. 1.
Self-similarity and spatial clustering indices with “similar” or “different” responses. a The self-similarity index at "one and two", "one and three", and "one and four" pairs by electrical stimulation with “similar (red line)” and “different (blue line)” responses. The X- and Y-axes indicate the time-history step pairs and the self-similarity index, respectively. Error bars indicate the standard error of the mean. * indicates significant difference vs chance level: p < 0.05. b The spatial clustering index of the neurons. In the X-axis, #1, #2, #3, and #4 are defined as the spatial clustering index classified by the first, second, third, and fourth time-history steps, respectively. The X- and Y-axes indicate the time-history step and the spatial clustering index, respectively. Error bars indicate the standard error of the mean. * indicates significant difference vs chance level: p < 0.05. Figure created using Microsoft PowerPoint and Excel. (Color figure online)
Effect of the input intervals in Cantor coding-like system (Experiment II)
The intervals of sequential input under subthreshold conditions were 20 ms (n = 7), 30 ms (n = 12), 60 ms (n = 8), 90 ms (n = 5), 180 ms (n = 7), 360 ms (n = 8), and 720 ms (n = 5). The stimulus intervals under suprathreshold conditions were 20 ms (n = 10), 30 ms (n = 10), 60 ms (n = 10), 90 ms (n = 9), 180 ms (n = 6), and 360 ms (n = 6). Under subthreshold conditions, the spatial clustering index was larger with an older time-history step (Fig. 2a). However, the indices differed according to input interval. The spatial clustering index was smaller at the first time-history step when the interval of sequential input was longer. The spatial clustering index was larger at the second time-history step when the interval was longer, and a significant difference vs chance was not observed at a 360 ms and 720 ms intervals. The spatial clustering index was larger at the third time-history step, when the interval was longer, and a significant difference vs chance was not observed at over 180 ms interval. Under suprathreshold conditions, the spatial clustering index was also higher with a higher time-history step (Fig. 2b). The spatial clustering index was smaller at the first time-history step when the interval was longer. At the second time-history step, the spatial clustering index was smallest when the interval was 30 ms, and was larger when the interval was lomger or shorter than 30 ms. The spatial clustering index was larger at the third time-history step, when the interval was longer. At the first time-history step, the spatial clustering index was smaller under subthreshold than suprathreshold conditions. In contrast, at the third time-history steps, the spatial clustering index was larger under subthreshold than under suprathreshold conditions.
Fig. 2.
Spatial clustering index patterns of the first, second, and third time-history steps by electrical stimulation at several intervals under a subthreshold and b suprathreshold conditions. In each graph, the X-axis and Y-axis indicates the interval of series of the electrical stimulation and spatial clustering index, respectively. The spatial clustering indices of the neurons were plotted at the first (#1, blue line), second (#2, red line), and third (#3, green line) time-history steps. Error bars indicate the standard error of the mean. *: p < 0.05. Asterisks is not shown in the pair when the interval is longer and the spatial clustering index is smaller (#1), and when the interval is longer and spatial clustering index is larger (#2, #3). Figure created using Microsoft PowerPoint and Excel. (Color figure online)
Effect of the inhibitory network in Cantor coding-like system (Experiment III)
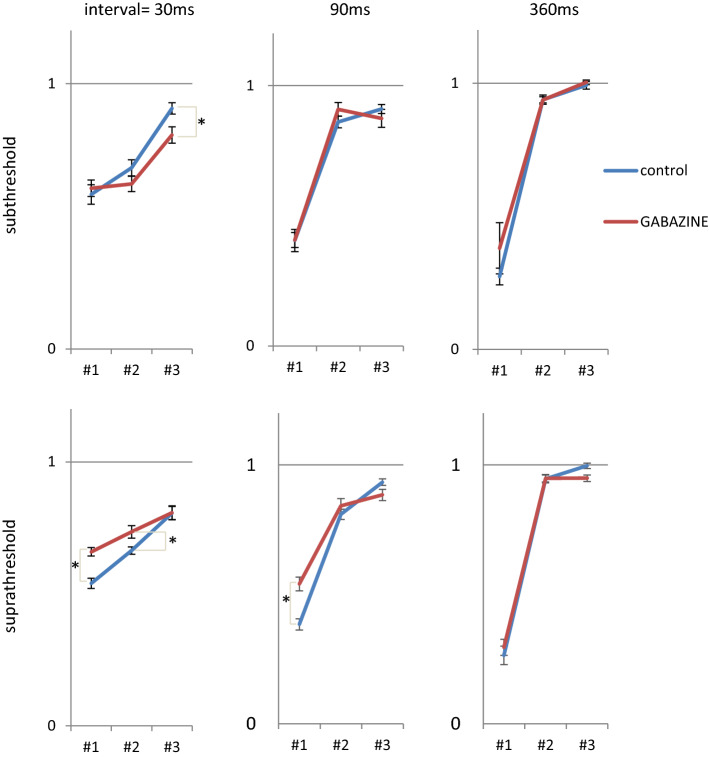
Neural responses before/after gabazine application were recorded at 30 ms (n = 5), 90 ms (n = 5), and 360 ms (n = 6) intervals under subthreshold conditions, and at 30 ms (n = 8), 90 ms (n = 13), and 360 ms (n = 6) intervals under suprathreshold conditions. Under subthreshold conditions at a 30 ms interval, the spatial clustering index was smaller after gabazine application than before at the third time-history step and did not show significant differences at the first and second time-history steps (Fig. 3, upper left). Under suprathreshold conditions at a 30 ms interval, the spatial clustering index was larger than before at the first and second time-history steps and did not show a significant difference at the third time-history step (Fig. 3, lower left). Under subthreshold condition at a 90 ms interval, the significant differences were not found (Fig. 3, upper middle). Under suprathreshold conditions at a 90 ms interval, the spatial clustering index was larger than before at the first time-history step and did not show significant differences at the second and third time-history steps (Fig. 3, lower middle). No significant differences were found at a 360 ms interval (Fig. 3, upper and lower right). In the self-similarity index, gabazine dependency was not observed under either sub- or suprathreshold conditions (data not shown). In summary, the quality of code discrimination in the system was decreased under subthreshold conditions, and improved under suprathreshold conditions.
Fig. 3.
Spatial clustering index patterns of the first, second, and third time-history steps by series of electrical stimulation before (blue line)/after (red line) gabazine application. The 3 upper and lower graphs indicate the spatial clustering index under subthreshold and suprathreshold conditions, respectively. The 2 left, middle, and right graphs show spatial clustering index at 30 ms, 90 ms, and 360 ms interval, respectively. In each graph, the X-axis indicates the time-history steps, whereas the Y-axis indicates the spatial clustering index. Error bars indicate the standard error of the mean. *: p < 0.05. Figure created using Microsoft PowerPoint and Excel. (Color figure online)
Discussion
Cantor coding-like iterated function system is not simply dependent on a series of on/off responses of EPSPs
To expand the Cantor coding-like iterated function system concept to learning and memory in CA1, it is important to consider its consistency to the conventional learning rule. One of the important learning rules for CA1 is the spatiotemporal learning rule (STLR) by Tsukada (Tsukada and Fukushima 2011). In STLR, it can be hypothesized that the hippocampal CA3 network establishes the time sequence context while CA1 maps the spatiotemporal context to its synaptic weight space. In the STLR, the learning process of pyramidal neurons is dependent not only on the strength (i.e. mean firing rate) of input signals, but also on both the spatial input pattern and the coincident timing of inputs from several synapses on dendrites (Tsukada et al. 1996; Aihara et al. 1997). Before the ideas of STLR and Cantor coding-like iterated function system are combined, the spatial input pattern dependency of the system should be examined, because previous study of the iterated function system showed input strength dependency alone, without spatial input dependency (Fukushima et al. 2007). In this study, the iterated function system was shown by not only using series of on/off input signals but using series of spatial input pattern with similar EPSP peak amplitudes. These results suggest that Cantor coding-like iterated function system and STLR show a common property, which contains spatial input dependency.
One of the reasons why pyramidal neurons can distinguish spatial input patterns with similar EPSP peak amplitude is the electrical properties of neural dendrites. Theoretically, dendrites show the cable theory property, and the input site dependency of dendrites was observed by attenuation of the EPSP shape (Komendantov and Ascoli 2009). Physiologically, EPSP shape is dependent on the input site on dendrites in CA1 pyramidal neurons (Williams and Stuart 2003). Synaptic input to apical sites on dendrites induces EPSPs with a short time constant decay, whereas that to distal sites induces EPSP with a longtime constant decay. In addition, the summation rule of EPSPs is dependent on spatial input sites and input order on dendrites (Spruston 2008; Yoneyama et al. 2011). Furthermore, the distributions of AMPA receptors (Andrasfalvy and Magee 2001) and GABAergic inputs (Freund and Buzsáki 1996; Megías et al. 2001) differ between apical and distal dendrites.
The frequency of physiological input from CA3 shows best quality in the code discrimination
In our results, the interval showing the best quality of code discrimination was 30 ms (i.e., 33 Hz), which is consistent with frequency band of input from CA3 to CA1 (30–50 Hz, Colgin et al. 2009). A beta to gamma bandwidth around 30 Hz induces specific responses in CA1. For example, long-lasting electrical stimulation around at 30 Hz decreases the effect of GABAergic input in CA1 (Bracci et al. 2001). Our results suggest that neurons in CA1 may play a role in optimizing the response of information processing by physiological input from CA3 at a 30-Hz frequency.
Yamaguti (2011) calculated the input interval dependency of quality of code discrimination in theoretical model of the system by changing the induction property of action potentials (“Bursting” or “Spiking”) and main glutamate receptor type (“AMPA” or “NMDA”) of neurons. The physiological property of action potential induction in CA1 pyramidal neurons is “Spiking”, according to the results using an acute slice preparation with normal external solutions (Staff et al. 2000). NMDA-type glutamate receptor is only activated when the neuron receives strong inputs. For these reasons, it is assumed that the input interval dependency is similar under suprathreshold conditions to that of the “Spiking NMDA” in Yamaguti's data (2011) and is similar under subthreshold conditions to that of "Spiking AMPA". From the theoretical data, the discrimination quality of the iterated function system is higher when the input interval to “Spiking AMPA” is short. In contrast, for “Spiking NMDA”, the highest discrimination quality was seen at a 100 ms interval, and the quality was low when the input interval was 30 ms. There is thus a clear gap between the theoretical and physiological results. One reason for this gap may be that actual neurons under suprathreshold conditions exhibit an intermediate property between theoretical “Spiking NMDA” and “Spiking AMPA”, shortening the interval of the peak.
Inhibitory network dependency of Cantor coding-like system
In CA1, there are many kinds of interneurons, divided into 2 groups, feedforward and feedback types. First, we considered the effect of feedforward interneurons under subthreshold conditions because feedback type interneuron does not work without action potential induction. The time decay constant of inhibitory post synaptic potentials (IPSPs) via GABAA receptor is longer than that of EPSPs via AMPA receptor (Buhl et al. 1996). Therefore, GABAergic input affects the membrane potential up to 100 ms after electrical stimulation, which includes three successive time-history steps of membrane responses by electrical stimulation with a 30 ms interval. In the iterated function system using the fractal property of the EPSP responses, the difference from the resting membrane potential in reference to the EPSP response becomes smaller and more sensitive to noise, as the time-history steps becomes older. Our results under subthreshold conditions suggest that feedforward interneurons simply decrease the amplitude of EPSP and reduce the quality of the discrimination. When the interval is 90 ms, the GABAergic input weakly affects responses of only one time-history step, and does not affect responses by the two and three time-history steps.
Feedforward- and feedback-type interneurons in CA1 are activated under suprathreshold conditions. Under suprathreshold conditions, significant degradation of the discrimination quality due to gabazine application was observed at the first and second time-history step with a 30 ms interval and at the first step with a 90 ms interval. One of the major reasons is thought to be the difference between after-effects with and without action potential induction. When an action potential was not induced, the membrane response was shown as the sum of EPSPs and IPSPs, and was smaller than the membrane response by EPSP alone like under subthreshold conditions. On the other hand, when an action potential was induced, the membrane potential was kept at a high level even though the existence of IPSPs. Our results under suprathreshold conditions suggest that feedforward and feedback interneurons increased the quality of the discrimination. In addition, increase of inward currents of cations are induced by hyperpolarization under specific conditions (Maccaferri et al. 1993) and action potentials are more actively generated in the presence of GABAergic input (Staff and Spruston 2003). These results suggest that inhibitory neurons in the CA1 increase the difference in the discrimination quality between under subthreshold and suprathreshold conditions, which plays an active role in improving the quality of code discrimination. The network including both types of interneurons, which is based on specific anatomical structure in CA1, plays a key role in spatiotemporal learning. Feedforward-type interneurons could play a role in lateral inhibition of spatiotemporal input sequence (Dupret et al. 2013, Müller and Remy 2014). Feedback inhibition in this system sometimes induces disinhibition of pyramidal neurons, enhances their activity, and mediates a form of LTP.in CA1 (Ormond and Woodin 2009; Letzkus et al. 2015). It is considered that the inhibitory network property is closely related to spatiotemporal learning with high pattern separability and influences the quality of code discrimination in Cantor coding-like iterated function system in CA1.
Conclusion
This study obtained the following results: (1) Cantor coding-like iterated function system have common property with STLR in spatial input dependency, which is a characteristic of learning and memory in the hippocampal CA1; (2) input interval at 30 ms shows high quality of code discrimination in the system and is consistent with physiological input from CA3 to CA1; and (3) the inhibitory network distinguishes the difference in spatial clustering properties between sub- and suprathreshold conditions clearly and increases quality of code discrimination in the system under suprathreshold conditions. These findings suggest that Cantor coding-like iterated function system is suitable for information expression in CA1. Furthermore, these results suggest that the system is involved in STLR via spatial input and inhibitory neurons dependency, suggesting that it may interact with short-term memory writing and erasure in the hippocampal CA1 system. Our next study is to investigate how learning changes the property of the iterated function system.
Author contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Yasuhiro Fukushima, Yutaka Yamaguti and Shigeru Kuroda. The first draft of the manuscript was written by Yasuhiro Fukushima and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Funding
This study was supported by KAKENHI (Grant-in-Aid for Scientific Research (C), JP15K00325).
Availability of data and material
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
All procedures were approved by Animal Care and Use Committee of Tamagawa University and Kawasaki University of Medical Welfare.
Consent for publication
Not applicable.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Aihara T, Tsukada M, Crair MC, Sinomoto S. Stimulus-dependent induction of long-term potentiation in CA1 area of the hippocampus: experiment and model. Hippocampus. 1997;7:416–426. doi: 10.1002/(SICI)1098-1063(1997)7:4<416::AID-HIPO7>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- Andrasfalvy BK, Magee JC. Distance dependent increase in AMPA receptor number in the dendrites of adult hippocampal CA1 pyramidal neurons. J Neurosci. 2001;21:9151–9159. doi: 10.1523/JNEUROSCI.21-23-09151.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bracci E, Vreugdenhil M, Hack SP, Jefferys JG. Dynamic modulation of excitation and inhibition during stimulation at gamma and beta frequencies in the CA1 hippocampal region. J Neurophysiol. 2001;85:2412–2422. doi: 10.1152/jn.2001.85.6.2412. [DOI] [PubMed] [Google Scholar]
- Buhl EH, Szilágyi T, Halasy K, Somogyi P. Physiological properties of anatomically identified basket and bistratified cells in the CA1 area of the rat hippocampus in vitro. Hippocampus. 1996;6:294–305. doi: 10.1002/(SICI)1098-1063(1996)6:3<294::AID-HIPO7>3.0.CO;2-N. [DOI] [PubMed] [Google Scholar]
- Colgin LL, Denninger T, Fyhn M, Hafting T, Bonnevie T, Jensen O, Moser MB, Moser EI. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature. 2009;462:353–357. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
- Dupret D, O'Neill J, Csicsvari J. Dynamic reconfiguration of hippocampal interneuron circuits during spatial learning. Neuron. 2013;78(1):166–180. doi: 10.1016/j.neuron.2013.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Exstorm AD, Ranganath C. Space, time, and episodic memory: the hippocampus is all over the cognitive map. Hippocampus. 2018;28(9):680–687. doi: 10.1002/hipo.22750. [DOI] [PubMed] [Google Scholar]
- Freund TF, Buzsáki G. Interneurons of the hippocampus. Hippocampus. 1996;6:347–470. doi: 10.1002/(SICI)1098-1063(1996)6:4<347::AID-HIPO1>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
- Fukushima Y, Tsukada M, Tsuda I, Yamaguti Y, Kuroda S. Spatial clustering property and its self-similarity in membrane potentials of hippocampal CA1 pyramidal neurons for a spatio-temporal input sequence. Cognitiv Neurodyn. 2007;1:305–316. doi: 10.1007/s11571-007-9026-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komendantov AO, Ascoli GA. Dendritic excitability and neuronal morphology as determinants of synaptic efficacy. J Neurophysiol. 2009;101:1847–1866. doi: 10.1152/jn.01235.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuroda S, Fukushima Y, Yamaguti Y, Tsukada M, Tsuda I. Iterated function systems in the hippocampal CA1. Cogn Neurodyn. 2009;3:205–222. doi: 10.1007/s11571-009-9086-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Letzkus JJ, Wolff SBE, Lüthi A. Disinhibition, a circuit mechanism for associative learning and memory. Neuron. 2015;88(2):264–276. doi: 10.1016/j.neuron.2015.09.024. [DOI] [PubMed] [Google Scholar]
- Maccaferri G, Mangoni M, Lazzari A, DiFrancesco D. Properties of the hyperpolarization-activated current in rat hippocampal CA1 pyramidal cells. J Neurophysiol. 1993;69:2129–2136. doi: 10.1152/jn.1993.69.6.2129. [DOI] [PubMed] [Google Scholar]
- Megías M, Emri Z, Freund TF, Gulyás AI. Total number and distribution of inhibitory and excitatory synapses on hippocampal CA1 pyramidal cells. Neuroscience. 2001;102:527–540. doi: 10.1016/s0306-4522(00)00496-6. [DOI] [PubMed] [Google Scholar]
- Müller C, Remy C. Dendritic inhibition mediated by O-LM and bistratified interneurons in the hippocampus. Front Synaptic Neurosci. 2014;6:1–15. doi: 10.3389/fnsyn.2014.00023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ormond J, Woodin MA. Disinhibition mediates a form of hippocampal long-term potentiation in area CA1. PLoS ONE. 2009;4(9):e7224. doi: 10.1371/journal.pone.0007224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston N. Pyramidal neurons: dendritic structure and synaptic integration. Nat Rev Neurosci. 2008;9:206–221. doi: 10.1038/nrn2286. [DOI] [PubMed] [Google Scholar]
- Staff NP, Spruston N. Intracellular correlate of EPSP-spike potentiation in CA1 pyramidal neurons is controlled by GABAergic modulation. Hippocampus. 2003;13:801–805. doi: 10.1002/hipo.10129. [DOI] [PubMed] [Google Scholar]
- Staff NP, Jung HY, Thiagarajan T, Yao M, Spruston N. Resting and active properties of pyramidal neurons in subiculum and CA1 of rat hippocampus. J Neurophysiol. 2000;84:2398–2408. doi: 10.1152/jn.2000.84.5.2398. [DOI] [PubMed] [Google Scholar]
- Tsuda I. Dynamic link of memory—chaotic memory map in nonequilibrium neural networks. Neural Netw. 1992;5(5):857. doi: 10.1016/S0893-6080(05)80146-7. [DOI] [Google Scholar]
- Tsuda I. A new type of self-organization associated with chaotic dynamics in neural networks. Int J Neural Syst. 1996;7:451–459. doi: 10.1142/s0129065796000439. [DOI] [PubMed] [Google Scholar]
- Tsuda I. Toward an interpretation of dynamic neural activity in terms of chaotic dynamical systems. Behav Brain Sci. 2001;24(5):793–847. doi: 10.1017/S0140525X01000097. [DOI] [PubMed] [Google Scholar]
- Tsuda I, Kuroda S. Cantor coding in the hippocampus. Japan J Indust Appl Math. 2001;18:249–258. doi: 10.1007/BF03168573. [DOI] [Google Scholar]
- Tsukada M, Fukushima Y. A context-sensitive mechanism in hippocampal CA1 networks. Bull Math Biol. 2011;73:417–435. doi: 10.1007/s11538-010-9566-8. [DOI] [PubMed] [Google Scholar]
- Tsukada M, Saito HA, Aihara T, Kato H. Hippocampal LTP depends on spatial and temporal correlation of inputs. Neural Netw. 1996;9:1357–1365. doi: 10.1016/S0893-6080(96)00047-0. [DOI] [PubMed] [Google Scholar]
- Tsukada M, Yamazaki Y, Kojima H. Interaction between the spatiotemporal learning rule (STLR) and hebb type (HEBB) in single pyramidal cells in the hippocampal CA1 area. Cogn Neurodyn. 2007;1:157–167. doi: 10.1007/s11571-006-9014-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams SR, Stuart GJ. Role of dendritic synapse location in the control of action potential output. Trends Neurosci. 2003;26:147–154. doi: 10.1016/S0166-2236(03)00035-3. [DOI] [PubMed] [Google Scholar]
- Yamaguti Y, Kuroda S, Fukushima Y, Tsukada M, Tsuda I. A mathematical model for Cantor coding in the hippocampus. Neural Netw. 2011;24:43–53. doi: 10.1016/j.neunet.2010.08.006. [DOI] [PubMed] [Google Scholar]
- Yoneyama M, Fukushima Y, Tsukada M, Aihara T. Spatiotemporal characteristics of synaptic EPSP summation on the dendritic trees of hippocampal CA1 pyramidal neurons as revealed by laser uncaging stimulation. Cogn Neurodyn. 2011;5:333–342. doi: 10.1007/s11571-011-9158-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.