Memory retention in pyramidal neurons: a unified model of energy-based homo and heterosynaptic plasticity with homeostasis

Abstract

The brain can learn new tasks without forgetting old ones. This memory retention is closely associated with the long-term stability of synaptic strength. To understand the capacity of pyramidal neurons to preserve memory under different tasks, we established a plasticity model based on the postsynaptic membrane energy state, in which the change in synaptic strength depends on the difference between the energy state after stimulation and the resting energy state. If the post-stimulation energy state is higher than the resting energy state, then synaptic depression occurs. On the contrary, the synapse is strengthened. Our model unifies homo- and heterosynaptic plasticity and can reproduce synaptic plasticity observed in multiple experiments, such as spike-timing-dependent plasticity, and cooperative plasticity with few and common parameters. Based on the proposed plasticity model, we conducted a simulation study on how the activation patterns of dendritic branches by different tasks affect the synaptic connection strength of pyramidal neurons. We further investigate the formation mechanism by which different tasks activate different dendritic branches. Simulation results show that compare to the classic plasticity model, the plasticity model we proposed can achieve a better spatial separation of different branches activated by different tasks in pyramidal neurons, which deepens our insight into the memory retention mechanism of brains.

Introduction

The human and most animal brains are constantly acquiring new information without destroying previous memories, an ability known as memory retention (Abraham and Robins 2005). A large number of pyramidal neurons exist in the central nervous system of the brain. How well each pyramidal neuron maintains its memory in a multi-task, multi-synaptic connection pattern and the key factors that influence its memory retention remain unclear. Considering that activity-dependent synaptic plasticity is thought to be the principal neuronal mechanism underlying memory storage (Morris et al. 2003; Neves et al. 2008), we create a model of synaptic plasticity to explain the memory retention of pyramidal neurons. Based on the local metabolic energy of the postsynaptic membrane, this model can perform homo- and heterosynaptic plasticity calculation and can effectively analyze the synaptic plasticity of pyramidal neurons in multi-synaptic connection mode.

In vivo experiments on individual layer 5 pyramidal neurons in the mouse motor cortex showed that different motor learning tasks trigger dendritic Ca²⁺ spikes on different apical tuft branches; this spatial separation is crucial to the induction and maintenance of synaptic plasticity (Cichon and Gan 2015). However, unlike the motor cortex, tuft plateau potentials induced by active sensory task occur in all apical tufts of single L5 pyramidal neurons in the barreled cortex of mice (Xu et al. 2012). The synaptic connections of the former are completely separated according to different tasks, while the synaptic connections of the latter are not spatially separated. This phenomenon raises an interesting question: How do the activation patterns of dendritic branches by different tasks affect the synaptic connection strength in pyramidal neurons? Here we consider two activation patterns: temporal and spatial. The temporal activation pattern involves the start and duration of different tasks, while spatial activation pattern involves whether different tasks activate the same or different dendrites. The spatial overlap refers to the ratio of the number of branches activated by two tasks to the total number of branches. Thus, the spatial overlap is 0 when each branch is activated by a corresponding task, and it is 1 when each branch is activated by both tasks. The time overlap refers to the ratio of the time taken for two tasks performing simultaneously to the maximum duration (i.e. performing period). Thus, when two tasks start at the same time with the same duration, the temporal overlap is 1, and it is 0 when two tasks are executed in sequence.

Pyramidal neurons have complex dendritic branches that accept functionally different task inputs, each targeted to spatially separate regions (Spruston 2008; Petreanu et al. 2009). The activation of synapses in a certain region will lead to changes in synaptic plasticity in the inactivated region (Chistiakova et al. 2015; Zenke et al. 2017; Lynch et al. 1977; Royer and Paré 2003; Lee et al. 2012), which will inevitably lead to changes in task-dependent memory retention in the inactivated region. The following questions remain elusive: how does the time difference between task-dependent synaptic inputs in each dendritic region affect memory retention; and to what extent is it strong or weak compared with the spatial characteristics mentioned earlier? Previous homosynaptic plasticity models cannot be directly used to calculate heterosynaptic plasticity due to the need of presynaptic spikes; and recently developed heterosynaptic plasticity models are virtually a mixture of multiple existing plasticity models (Chen et al. 2013; Jedlicka et al. 2015; Zenke et al. 2015). In the present work, we propose a novel unified model based on postsynaptic metabolic energy to calculate homo- and heterosynaptic plasticity.

Is there any theoretical or computational basis for building a plasticity model based on the local metabolic energy of the postsynaptic membrane? First, an increasing number of studies show that metabolic energy is related to the dynamics of ion channels, firing rate, and other various mechanisms and characteristics of neurons. The neuron activity model based on metabolic energy displayed an equivalent relationship with the classical HH model (Wang et al. 2015; Wang and Wang 2018; Zhu et al. 2018). Metabolic energy can be used as a common basis for controlling neuron biophysical mechanism and nerve activity (Laughlin 2001; Hasenstaub et al. 2010). Therefore, our model can give an explicit biophysical interpretation for diverse plasticity according to the principle of metabolic energy. Second, theoretical calculation methods of experimental-based metabolic energy have been proposed in recent years (Attwell and Laughlin 2001; Howarth et al. 2012; Wang et al. 2017; Zhu and Wang 2019) and provide theoretical and experimental bases for calculating the metabolic energy of pyramidal neurons. Finally, the detailed compartmentalized biophysical model of pyramidal neurons (Bono and Clopath 2017) can be used as a basis for further development. Here, we compared the experimental results under multiple induction protocols with the simulation results of our model and systematically studied the memory retention ability of L5 pyramidal neurons. The spatial overlap has a greater impact on the memory retention of pyramidal neurons than the temporal overlap. This result enhances our insight of pyramidal neuronal memory retention.

Methods

All simulations in this paper were carried out on the Brian2 neuron simulator in Python (Goodman and Brette 2009). We used the model of the biophysical neurons and synapses developed by Bono and Clopath (2017) based on Brian2. Given that L5 and L2/3 pyramidal neuron models have been found to have similar results (Bono and Clopath 2017), we only conducted simulation studies on synaptic plasticity and memory retention in L5 pyramidal neurons.

Synaptic plasticity model

Maintaining a constant transmembrane ion gradient is essential for neurons to function normally and even survive. Neurons have potential energy similar to batteries due to the existence of transmembrane ion gradient (Hasenstaub et al. 2010). We call the potential energy of neurons in resting state as the resting energy state.. Activities, such as action potential, input integration, and synaptic transmission, will change the potential energy of the neuron, leading to a new energy state, which is referred to as firing energy state. To maintain normal information processing ability, neurons can restore the firing energy state to the resting energy state through active transport by expending metabolic energy. We assumed that synaptic plasticity might function similarly to, or be a manifestation of, active transport and be closely related to changes in the energy state of neurons. To restore the resting energy state, when the firing energy state is larger than the resting energy state, the synaptic strength weakens, thus presenting as LTD. When the firing energy state is less than the resting energy state, the synaptic strength is enhanced, thus presenting as LTP. When the firing energy state is close to the resting energy state, the synaptic weight remains unchanged. The idea can be described by the following equation

$$W_j=A\left(E_j^r-E_j\right)$$ 1

where $W_j$ is the weight of synapse $j$, $A$ is a scaling factor, $E_j^r$ and $E_j$ are the resting and firing energy states at unit membrane of post-synapse $j$, respectively. $E_j^r$ and $E_j$ are all dimensionless variables. $E_j$ represents the accumulated energy required when the membrane voltage is not below the firing threshold voltage, while $E_j^r$ represents the accumulated energy when the membrane voltage is lower than the firing threshold voltage, so the two energy states can not be changed at the same time. When the membrane voltage is lower than the firing threshold voltage, $E_j$ remains unchanged, while when the membrane voltage is higher than the firing threshold voltage, $E_j^r$ remains unchanged.

The differential expression of Eq. (1) is

$$\frac{d{W}_j}{\mathit{dt}}=A\left(\frac{d{E}_j^r}{\mathit{dt}}-\frac{d{E}_j}{\mathit{dt}}\right)$$ 2

When the membrane voltage is lower than the firing threshold voltage, $\frac{d{E}_j}{\mathit{dt}}=0$ because $E_j$ remains unchanged. Similarly, when the membrane voltage is above the firing threshold voltage, $\frac{d{E}_j^r}{\mathit{dt}}=0$ because $E_j^r$ remains unchanged.

Previous variables in the homosynaptic plasticity model generally include pre and post synaptic spike frequency (Bienenstock et al. 1982), pre and post synaptic spike timing (Pfister and Gerstner 2006), presynaptic spike and postsynaptic membrane potential (Clopath et al. 2010), and Ca²⁺ concentration (Shouval et al. 2002; Graupner and Brunel 2012). These models require presynaptic spike data directly or indirectly. The existing heterosynaptic plasticity model directly adjusts the synaptic weight according to probability (Chen et al. 2013). To study memory retention, we need a unified model suitable for homo- and heterosynaptic plasticity. Therefore, in contrast to previous synaptic plasticity models, the proposed model represents the energy state with postsynaptic local membrane voltage and membrane current density as variables.

To calculate the energy states $E_j^r$ and $E_j$ in Eqs. (1) and (2), one of the simplest and most straightforward methods is to describe the energy states by the product of postsynaptic membrane voltage $v_m$ and postsynaptic membrane current density $I_m$. If the energy state need to be restored to resting state, the postsynaptic membrane voltage should reflect the difference between the intracellular potential and resting potential rather than the difference between the intracellular potential and extracellular potential expressed by ${\text{v}}_{\text{m}}$. Therefore, we defined a driving voltage $f_j\left(v_m\right)$ (Fig. 1a) to replace $v_m$.

$$f_j\left(v_m\right)=sign\left(v_m\right)\left|v_m-{\theta }_l\right|$$ 3

where variable $v_m$ is the postsynaptic voltage, ${\theta }_l$ is a parameter called the resting threshold voltage, $v_m$ and ${\theta }_l$ are dimensionless with mV. In general, ${\theta }_l$ is less than the resting potential and larger than or equal to the minimum potential in pyramidal neurons. The direction of driving voltage $f_j\left(v_m\right)$ is the same as that of $v_m$, and the amplitude is the absolute value of the difference between $v_m$ and ${\theta }_l$.

Fig. 1.

Illustration of the model. a Relationship between postsynaptic membrane potential $v_m$ and driving potential $f_j\left(v_m\right)$. The farther $v_m$ was from the driving threshold potential ${\theta }_l$, the larger the amplitude of the driving voltage (black solid line) would be, but $f_j\left(v_m\right)$ had the same sign as $v_m$. A transformation of the driving voltage (the dashed red line) stayed the same for $v_m<{\theta }_h$ and opposite sign occurred for $v_m\ge {\theta }_h$, reminiscent of the scalar function ϕ in the BCM model (Bienenstock et al. 1982). b Relationship between postsynaptic membrane current density $I_m$ and driving current $g_j\left(I_m\right)$. The amplitude of $g_j\left(I_m\right)$ decreased exponentially if the amplitude of $I_m$ was larger than the allowable maximum current density $I_{\mathit{max}}$. c The instantaneous change in the synaptic strength under different postsynaptic membrane potential and membrane current density. The synaptic strength increased in D, E, and F but decreased in R, S, and T. d, e Postsynaptic membrane potential, membrane current density, energy state, and weight change with time for the classical STDP protocol. Red traces: $v_m\ge {\theta }_h$; insets: zoom in on the red curve. The synaptic strength potentiated for a pre–post spike pair d and depressed for a post–pre spike pair e mainly due to the difference in the current density of the postsynaptic membrane. The electric power represent the curves of $\frac{d{E}_j^r}{\mathit{dt}}$ and $\frac{d{E}_j}{\mathit{dt}}$ with time, respectively. Because $\frac{d{E}_j}{\mathit{dt}}=0$ at $v_m<{\theta }_h$ and $\frac{d{E}_j^r}{\mathit{dt}}=0$ at $v_m\ge {\theta }_h$, the overall effect is equivalent to $\frac{d{E}_j^r}{\mathit{dt}}+\frac{d{E}_j}{\mathit{dt}}$. The last line (weight) represents $\frac{d{E}_j^r}{\mathit{dt}}-\frac{d{E}_j}{\mathit{dt}}$. The integral (shaded part) of the red curve in the third line (electrical power) should be negative in the weight representation

We also defined the driving current $g_j\left(I_m\right)$: when the postsynaptic membrane current density $I_m$ does not exceed a certain threshold $I_{\mathit{max}}$, the driving current is equal to $I_m$, but when it exceeds $I_{\mathit{max}}$, the driving current decreases exponentially (Fig. 1b). To confer homeostatic feature to our plasticity model (Turrigiano 2012; Turrigiano and Nelson 2004), we adopt the research results of intrinsic homeostatic plasticity for the design of the driving current (Debanne et al. 2019; Gasselin et al. 2017; Campanac et al. 2008). The idea of constructing driving current is to make the functional relationship between $g_j\left(I_m\right)$ and $I_m$ similar to Fig. 3c in Debane et al. 2019. Electric power represents the change in energy per unit time; as such, the instantaneous change in the resting energy state and firing energy state in Eq. (2) $\left(\frac{d{E}_j^r}{\mathit{dt}}\text{and}\frac{d{E}_j}{\mathit{dt}}\right)$ can be expressed by the product of driving voltage and driving current.

Fig. 3.

Verifying our model with the triplet and quadruplet experimental data. Each protocol was repeated 60 times with a frequency of 1 Hz for apical compartments (Fig. 2a). Black bars and dots represented the experimental data from Wang et al. (2005) and Table 2 in Pfister and Gerstner (2006). a, b Synaptic weight changes under triplet protocol. Magenta bars: average synaptic weights for proximal compartments, cyan bars: average synaptic weights for distal compartments. a Synaptic strength changes corresponding to different time intervals under the four pre–post–pre protocols. Each protocol consisted of two presynaptic spikes and one postsynaptic spike characterized by $\mathrm{\Delta }{\text{t}}_1={\text{t}}^{\text{post}}-{\text{t}}_1^{\text{pre}}$ and $\mathrm{\Delta }{\text{t}}_2={\text{t}}^{\text{post}}-{\text{t}}_2^{\text{pre}}$ where ${\text{t}}_1^{\text{pre}}$ and ${\text{t}}_2^{\text{pre}}$ were the first and second presynaptic spikes of the triplet. b Synaptic strength changes corresponding to different time intervals under the four post–pre–post protocols. Each protocol consisted of one presynaptic spike and two postsynaptic spikes. In this case, $\mathrm{\Delta }{\text{t}}_1={\text{t}}_1^{\text{post}}-{\text{t}}^{\text{pre}}$ and $\mathrm{\Delta }{\text{t}}_2={\text{t}}_2^{\text{post}}-{\text{t}}^{\text{pre}}$ where ${\text{t}}_1^{\text{post}}$ and ${\text{t}}_2^{\text{post}}$ were the first and second postsynaptic spikes of the triplet. c Synaptic weight change as a function of a delayed time $T$ under the quadruplet protocol. Magenta line corresponded to the average synaptic weights of proximal compartments, cyan line corresponded to the average synaptic weights of distal compartments, and black line corresponded to the average synaptic weights of all compartments. The gray shaded regions represented the standard deviation of synaptic strength for all compartments

To make our model homeostatic, we constructed the following driving current (Fig. 1b)

$$g_j\left(I_m\right)=\left\{\begin{array}{c}{I}_m,\left|I_m\right|<I_{\mathit{max}}\hfill \\ I_{\mathit{max}}sign\left(I_m\right)exp\left[D\left(I_{\mathit{max}}-\left|I_m\right|\right)\right],\left|I_m\right|\ge I_{\mathit{max}}\hfill \end{array}\right)$$ 4

where $I_m$ is the current density at the postsynaptic membrane, $I_{\mathit{max}}$ represents maximum current density of the postsynaptic membrane, $I_m$ and $I_{\mathit{max}}$ are dimensionless with $pA/\mu m^2$. Parameter $D$ denotes damping factor with $0\le D\le 1$. If $\left|I_m\right|<I_{\mathit{max}}$, then the driving current $g_j\left(I_m\right)$ is equal to $I_m$; if $\left|I_m\right|<I_{\mathit{max}}$, then the amplitude of $g_j\left(I_m\right)$ decreases exponentially, consistent with the recent opinions (Debanne et al. 2019; Gasselin et al. 2017; Campanac et al. 2008). Equation (2) representing the change in synaptic strength over time with the driving voltage and driving current described above is as follows

$$\frac{d{W}_j}{\mathit{dt}}=A\left[\Theta \left({\theta }_h-v_m\right)f_j\left(v_m\right)g_j\left(I_m\right)-\Theta \left(v_m-{\theta }_h\right)f_j\left(v_m\right)g_j\left(I_m\right)\right]$$ 5

combined with the hard bounds $0.0002\le W_j/W_{\mathit{ini}}\le 4$. Here $W_{\mathit{ini}}$ is initial weight. $\Theta \left(x\right)$ represents Heaviside function, $\Theta \left(x\right)=1$ for $x\ge 0$ and $\Theta \left(x\right)=0$ for $x<0$. ${\theta }_h$ is called firing threshold voltage, which is a dimensionless parameter with the unit of mV. $\Theta \left({\theta }_h-v_m\right)f_j\left(v_m\right)g_j\left(I_m\right)$ is the time derivative term of the resting energy state, namely $\frac{d{E}_j^r}{\mathit{dt}}$ in Eq. (2). $\Theta \left(v_m-{\theta }_h\right)f_j\left(v_m\right)g_j\left(I_m\right)$ denotes the derivative of the firing energy state, that is $\frac{d{E}_j}{\mathit{dt}}$.

Equation (5) can now be used to more explicitly analyze the instantaneous synaptic strength change under different postsynaptic membrane voltage and membrane current density (Fig. 1c). $\Theta \left(v_m-{\theta }_h\right)=0$ and $\Theta \left(v_m-{\theta }_h\right)=1$ for $v_m\ge {\theta }_h$, thus Eq. (5) is reduced to $\frac{d{W}_j}{\mathit{dt}}$$=-A{f}_j\left(v_m\right)g_j\left(I_m\right)$. In this case, if the membrane voltage is in the same direction as the membrane current density, then the synaptic strength will decrease (S,T); otherwise, the synaptic strength will increase (E,F). On the other hand, if $v_m<{\theta }_h$, $\Theta \left({\theta }_h-v_m\right)=1$ and $\Theta \left(v_m-{\theta }_h\right)=0,$ then Eq. (5) evolves into $\frac{d{W}_j}{\mathit{dt}}=A{f}_j\left(v_m\right)g_j\left(I_m\right)$. At this point, if the membrane voltage and membrane current density are in the same direction, then the synaptic strength increases (D); if they are in the opposite direction, then the synaptic strength decreases (R).

Our model has similarities and differences with the classical BCM model (Bienenstock et al. 1982) (Fig. 1a). Without considering the scaling factor $A$, the right term of Eq. (5) can be rewritten as $\Theta \left[\left({\theta }_h-v_m\right)-\Theta \left(v_m-{\theta }_h\right)\right]f_j\left(v_m\right)g_j\left(I_m\right)$. Where $\left[\Theta \left({\theta }_h-v_m\right)-\Theta \left(v_m-{\theta }_h\right)\right]f_j\left(v_m\right)<0$ for $v_m<{\theta }_h$, and $\Theta \left[\left({\theta }_h-v_m\right)-\Theta \left(v_m-{\theta }_h\right)\right]f_j\left(v_m\right)>0$ for ${\theta }_h\le v_m<0$. If $v_m$ is taken as the output $c$ in the BCM model and ${\theta }_h$ as the modification threshold ${\theta }_M$ in the BCM model, $\left[\Theta \left({\theta }_h-v_m\right)-\Theta \left(v_m-{\theta }_h\right)\right]f_j\left(v_m\right)$ (the dashed red line in Fig. 1a) is equivalent to the scalar function ϕ in the BCM model for $v_m<0$. $\left[\Theta \left({\theta }_h-v_m\right)-\Theta \left(v_m-{\theta }_h\right)\right]f_j\left(v_m\right)<0$ for $v_m\ge 0$ in our model. However, scalar function ϕ in the BCM model does not possess such a feature. The postsynaptic driving current $g_j\left(I_m\right)$ in Eq. (5) of our model corresponds to the presynaptic firing frequency $d_j$ in the BCM model, although the two variables are correlated, they are different obviously. This feature is another distinction between the two models.

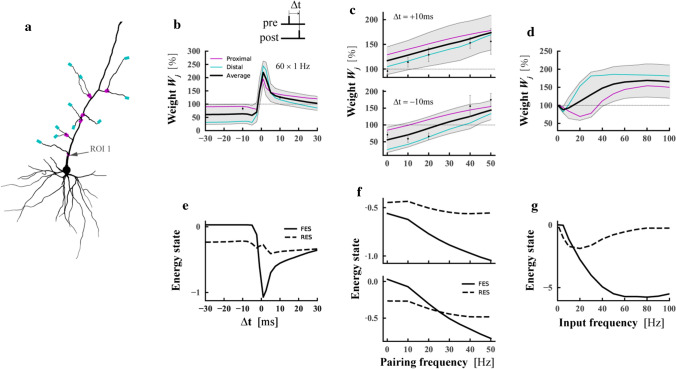
We illustrate some characteristics of postsynaptic membrane voltage, membrane current density, resting and firing energy states, and synaptic weight changes over time through an example (Fig. 1d, e). An STDP protocol was performed at ROI1 in the layer 5 pyramidal neurons (Fig. 2a), in which the presynaptic spike preceded the postsynaptic spike (pre-post) by 10 ms (Fig. 1d) or the presynaptic spike followed by the postsynaptic spike (post–pre) by 10 ms (Fig. 1e). If the postsynaptic membrane voltage $v_m$ is lower than the spike threshold voltage ${\theta }_h$, then the driving voltage is negative and the driving current is positive, so the resting energy state $E_j^r$ accumulated in one period is negative. If $v_m$ is above ${\theta }_h$, due to the different membrane current density $I_m$, although the change of driving voltage and current with time may be positive or negative, as the cumulative result of the product of the driving voltage and current, then the firing energy state $E_j$ in the pre-post case is more negative than the resting energy state $E_j^r$, thus the final result during a period is synaptic enhancement. However, in the post–pre case, the firing energy state is negative but larger than the resting energy state, so the final result in one period is the decrease in the synaptic weight. Comparison of the results of the two stimulation protocols shows that the postsynaptic membrane current density is a variable that can better reflect the synaptic plasticity than the postsynaptic membrane voltage.

Fig. 2.

Verifying our model with classical plasticity experimental data. a Proximal (magenta) and distal (cyan) locations on a thin apical branch of the detailed neuron model. b, c, d Changes in the mean synaptic strength of the distal compartments of dendrites (cyan curve), proximal compartments (magenta curve), and all compartments (black curve) under different induction protocols. The gray shaded regions represented the standard deviation of synaptic strength for all compartments. b Synaptic weight change for different time intervals $\mathrm{\Delta }\text{t}$ between pre- and postsynaptic firing by using 60 pre–post pairs at 1 Hz. Dots indicated data from Wang et al. (2005). c Weight change as a function of pairing repetition frequency using pairings with a time delay of +10 ms (pre-post, top) and –10 ms (post–pre, bottom). Dots were data from Sjöström et al. (2001) d Weight change as a function of afferent frequency. A group of synapses on a proximal compartment or distal compartment were activated by a Poisson process. e, f, g Dynamics of the mean firing energy state (FES, solid line) and the mean resting energy state (RES, dashed line). The stimulation protocols used by e, f, and g were the same as b, c, and d respectively

Various stimulations alter the local resting energy state and firing energy state in postsynaptic neurons simultaneously. Synapses are depressed when the firing energy state is above the resting energy state and strengthened when the firing energy state is below the resting energy state to make neurons return to the resting state.

Parameters in synaptic model

In addition to the two variables of postsynaptic membrane voltage and postsynaptic membrane current density, our model includes five parameters: resting threshold voltage ${\theta }_l$, maximum membrane current density $I_{\mathit{max}}$ and damping factor $D$, scaling factor $A$ and firing threshold voltage ${\theta }_h$. In the choice of model parameters, our goal is to make a set of parameters suitable for as many stimulation protocols as possible. The five model parameters are all determined by trial and error methods. The first is to estimate the range of parameters according to their physical meaning, such as ${\theta }_l$ should be below - 60 mV, ${\theta }_h$ should be between - 60 and - 50 mV, and so on. Then fine tuning is done manually to make the simulation results match the experimental results as well as possible. We therefore simulated different parameters and determined four general model parameters by comparing the simulation results with the experimental data, that is, $A=0.0625$, ${\theta }_l=-68.5\text{mV}$, ${\theta }_h=-55\text{mV}$, and $D=0.05$. The maximum membrane current density may vary with different pyramidal neurons. We therefore set two different values, namely, $I_{\mathit{max}}=4\text{pA}/\mathrm{\mu }{\text{m}}^2$ for pyramidal neurons in visual cortex and $I_{\mathit{max}}=3\text{pA}/\mathrm{\mu }{\text{m}}^2$ for pyramidal neurons in hippocampal cultures. After comparing the simulation results of synaptic strength changing with spike frequency (Fig. 2c,f) with the corresponding experimental data of cortical pyramidal neurons (Sjöström et al. 2001), $I_{\mathit{max}}=4\text{pA}/\mathrm{\mu }{\text{m}}^2$ was chosen; meanwhile, $I_{\mathit{max}}=3\text{pA}/\mathrm{\mu }{\text{m}}^2$ was selected for all other simulations.

Pairing protocol

Ten distal and proximal compartments (Fig. 2a) are found in the apical dendrites of the L5 pyramidal neuron model. Each distal and proximal compartment is connected to a synapse. Postsynaptic spikes were induced by the injection of 1 nA and 3 ms current pulses into the soma of postsynaptic neurons. The initial synaptic weights were set to 0.5. The weight change was multiplied by a factor of 12 (60/5) to mimic the experimental protocols in the research of Wang et al. (2005) and Sjöström et al. (2001). In the protocol of spike timing dependence (Fig. 2b), pairs of pre–post or post–pre spikes at 1 Hz were repeated five times for different interspike intervals (1, 2.5, 5, 7.5, 10, 12.5, 15, 17.5, 20, 25, and 30 ms). For the study of spike rate dependence (Fig. 2c), pairs of pre–post or post–pre spikes separated by 10 ms were repeated five times at different frequencies of 5 Hz up to 50 Hz with steps of 5 Hz, and for 0.1 Hz.

Cooperative Poisson afferent protocol

Each compartment shown in Fig. 2a was connected to 10 synapses, each with an initial weight of 0.5. The 10 synapses were activated using Poisson process with the same average rate, lasting 200 ms. This protocol was repeated with different firing rates ranging from 1 Hz to 100 Hz (Fig. 2d).

Triplet protocol

Similar to the paired protocol, each distal and proximal compartment was connected to a synapse in the apical dendrite of the L5 pyramidal neuron (Fig. 2a). A current pulse of 1 na lasting 3 ms was injected into the soma of postsynaptic neurons to induce postsynaptic spike. The initial weight of all synapses was 0.5. To simulate the experimental protocol of Wang et al. (2005), the weight change was also multiplied by 12. The first triplet protocol (Fig. 3a) consisted of five sets of three spikes that repeated at a given frequency of 1 Hz. Each triplet consisted of two presynaptic spikes and one postsynaptic spike. The time differences $\left(\mathrm{\Delta }{t}_1,\mathrm{\Delta }{t}_2\right)$ were (5,-5), (10,-10), (15,-5), and (5,-15) respectively. The second triplet protocol (Fig. 3b) also included five sets of three spikes that repeated with frequency of 1 Hz. The only difference from the first protocol was that each triplet consisted of a presynaptic spike and two postsynaptic spikes. The time differences of the two pairs $\left(\mathrm{\Delta }{t}_1,\mathrm{\Delta }{t}_2\right)$ were set as (− 5,5), (− 10,10), (− 5,15), and (− 15,5).

Quadruplet protocol

This protocol consisted of five quadruplets at frequency of 1 Hz (Fig. 3c). A post–pre pair with a time difference of $\mathrm{\Delta }{\text{t}}_1=-5\text{ms}$ was followed by a pre–post pair with a time difference of $\mathrm{\Delta }{\text{t}}_2=5\text{ms}$ after time $T$. In this case, $T$ was set to positive. When $T$ is negative, a pre–post pair with a time difference of $\mathrm{\Delta }{\text{t}}_1=5\text{ms}$ was followed by a post–post pair with a time difference of $\mathrm{\Delta }{\text{t}}_2=-5\text{ms}$ after time $T$. Formally, $T$ was defined by $T=\frac{\left(t_2^{\mathit{pre}}+t_2^{\mathit{post}}\right)}{2}-\frac{\left(t_1^{\mathit{pre}}+t_1^{\mathit{post}}\right)}{2}$. This protocol was repeated with various $T$ (− 100, − 80, − 60, − 50, − 40, − 30, − 25, − 20, − 15, − 10, 10, 15, 20, 25, 30, 40, 50, 60, 80, 100).

Relation between memory retention and spatial overlaps

0–13 overlapping branches (i.e. branches activated by both tasks) were randomly selected among the 13 branches in the apical tuft dendrites (Fig. 4a). In the remaining branches, all the compartments of one half of the branches were assigned to task 1, and all the compartments of the other half are allocated to task 2, but the synaptic connections in each compartment were random. For each overlapping branch, half of the compartments were randomly selected for task 1 and the other half for task 2. The above random selection process was carried out 10 times, so a total of 140 connection patterns for the two tasks were randomly generated, and then each connection pattern was simulated once. Each compartment connected five synapses, each with an initial weight of 0.5. The five synapses connected to each compartment were activated by Possion process, with an average frequency of 40 Hz. The execution period of each task was 200 ms. The synapses of the first task were activated for 50 ms and then ceased to be activated for 150 ms. The synapses of the second task were activated for 50 ms and then also stopped to be activated for 150 ms.

Fig. 4.

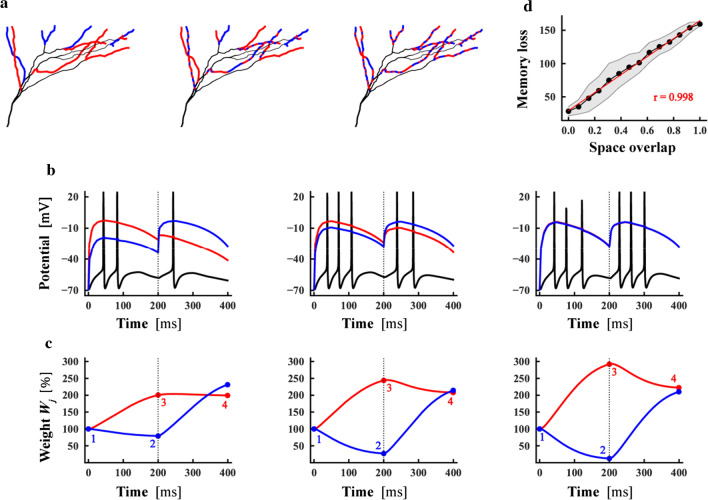
Effect of spatial overlap on memory retention of apical tuft dendrites in L5 pyramidal neurons. The activation time for each task was 50 ms. a Synaptic connection patterns for different spatial overlaps. Seven of the 13 thin branches were connected to task 1, and the six other ones were connected to task 2 with the spatial overlap of 0 (left). When the spatial overlap was close to 0.5 (middle), each of the six branches was connected to different tasks, and four of the remaining 7 branches were connected to tasks 1 and 3 were connected to task 2. Each of the 13 thin branches connected the two different tasks with the spatial overlap of 1 (right). b The change in the postsynaptic potential with time under the connection patterns of (a). The black curve represented the membrane potential of the postsynaptic cell body, the red curve indicated the mean value of the postsynaptic local membrane potential corresponding to task 1, and the blue curve represented the mean value of the postsynaptic local membrane potential corresponding to task 2. The left, middle, and right corresponded to the left, middle, and right of (a), respectively. c Evolution of synaptic weight. The execution of task 1 before the start of task 2 (vertical dot line) not only caused a change in its own synaptic strength (red) but also caused a change in the average synaptic strength of task 2 (blue, 1 to 2). The execution of task 2 changed its own synaptic strength (blue), and at the same time changed the average synaptic strength corresponding to task 1 (red, 3 to 4). The left, middle, and right corresponded to the left, middle, and right of (a) respectively. d Memory loss as a function of the spatial overlap. The black dots and shadow represented the mean and variance of memory loss of each spatial overlap under 10 different connection patterns. r: Pearson correlation. The red line was a linear fitting of average memory loss

Relation between memory retention and temporal overlaps

The spatial overlap was set to zero in this protocol. The protocol (Fig. 5) randomly selected seven dendritic branches for task 1 and 6 branches for task 2 from 13 branches in the apical tuft dendrites. Each compartment was connected to five synapses. The above random selection process was performed 10 times. Therefore, 10 different synaptic connection patterns were generated. The initial weight of each synapse is 0.5. Each synaptic connection pattern was simulated at different overlap time ranging from 0 to 200 ms, with the steps of 20 ms. The five synapses connected to each compartment are activated by Possion process, with an average frequency of 40 Hz. The execution period of each task is 200 ms. The synapse of the first task was activated for 50 ms and then ceased to be activated for 150 ms. The synapse of the second task was activated for 50 ms and then also stopped to be activated for 150 ms.

Fig. 5.

Effect of temporal overlap on memory retention of apical tuft dendrites in L5 pyramidal neurons. The activation time for each task was 50 ms. Space overlap was zero. a Connection pattern of different tasks to the apical tuft dendrites. Seven of the 13 thin branches were connected to task 1, and the six other ones were connected to task 2. b Evolution of postsynaptic potential. Black, red, and blue lines indicated the average postsynaptic potentials for soma, task 1, and task 2, respectively. The start time of the second task (vertical dotted line) was 200 ms with the temporal overlap of 0 (left), the start time of the second task was 100 ms with the temporal overlap of 0.5 (middle), and the second task and the first task started simultaneously with the temporal overlap of 1 (right). c Evolution of synaptic weight. The execution of task 1 before the start of task 2 (vertical dot line) changed not only its own synaptic strength (red) but also the average synaptic strength of task 2 (blue, 1 to 2). The execution of task 2 changed its own synaptic strength (blue), and at the same time changed the average synaptic strength corresponding to task 1 (red, 3 to 4). ${\text{t}}_1$, ${\text{t}}_2$: the start time of task 1 and task2, respectively, $T$: the period of each task, $\mathrm{\Delta }\text{t}$: the delay between two tasks activated, and $\mathrm{\Delta }{\text{t}}_{\text{o}}$: the overlapping time between two tasks. The temporal overlap was 0 with ${\text{t}}_2=200\text{ms}$ (left), the temporal overlap was 0.5 with ${\text{t}}_2=100\text{ms}$ (middle), and the temporal overlap was 1 with ${\text{t}}_2=0\text{ms}$ and overlap of point 1 and 2 (right). d Memory lost as a function of the temporal overlap. The black dots and shadow represented the mean and variance of memory loss of each spatial overlap under 10 different connection patterns respectively. The red line was a linear fitting of average memory loss. r: Pearson correlation

Results

Fitting the plasticity model to experimental data

We first examined the influence of presynaptic and postsynaptic spike time differences on synaptic plasticity at a given spike frequency (Fig. 2b). Under the stimulation of 60 pairs with a frequency of 1 Hz, the synapse was strengthened for pre–post pairing and depressed for post–pre procedure, consistent with the experimental data (Wang et al. 2005). The analysis on the postsynaptic energy states (Fig. 2e) shows that the firing energy state is lower than the resting energy state when the time intervals between the pre and post synaptic spike are very small, which is manifested as a significant increase in synaptic strength. At the time of pre–post pairing, the firing energy state is gradually close to but always lower than the resting energy state with increasing time difference; as such, the increase in the synaptic strength gradually decreases to 0. However, in the post–pre condition, the firing energy state increases rapidly and quickly exceeds the resting energy state, and they slowly approach each other with increasing time difference after the resting energy state is exceeded, leading to broader depression window than the potentiation window.

We then studied the influence of different spike frequencies on synaptic plasticity with presynaptic and postsynaptic spike time intervals determined (Fig. 2c). Under the stimulation of 60 pairs of pre–post spikes with a timing difference of 10 ms, if the spike frequency is greater than 10 Hz, then LTP is induced; if the frequency is less than 10 Hz, then the increase in the synaptic strength is very small or does not change. The general trend is that the higher the frequency, the greater the LTP is. For the post–pre pair with a spike time difference of 10 ms for 60 repetitions, if the spike frequency is less than 30 Hz, then it will induce LTD; however, LTP will be generated when the frequency is above 30 Hz. Our simulation and experimental data (Sjöström et al. 2001) are consistent with each other. The resting and firing energy states decrease gradually with increasing frequency under the two stimulus protocols. The amplitude of the energy state caused by the two protocols is different (Fig. 2f). In the case of pre–post pairing, the firing energy state is always lower than the resting energy state and the distance between the two states gradually increases with increasing pairing frequency; as such, the synaptic strength also gradually potentiates. At very low frequencies (such as 0.1 Hz), the firing energy state is close to the resting energy state, indicating minimal change in the synaptic strength. In the case of post–pre pairing, if the frequency is below 30 Hz, the firing energy state is greater than the resting energy state, resulting in synaptic depression; if the frequency is greater than 30 Hz, the firing energy state is less than the resting energy state, resulting in synaptic enhancement.

In summary, our simulation results show that no matter the change of frequency or the change of time difference is, the firing energy state is always lower than the resting energy state under the pre–post protocol. No intersection exists between the two energy states. However, in the post–pre protocol, an intersection exists between them.

The computational results (Fig. 2d) of our model for classical afferent stimulation experiments show that LTP is induced when the stimulation frequency is low (usually less than 10 Hz) with only presynaptic stimulation; if the frequency is higher (usually greater than 10 Hz), LTP occurred, consistent with earlier electrophysiological experiment results (Bliss and Lømo 1973; Dudek and Bear 1992). We also found that if the frequency is very high (above 80 Hz), the amplitude of synaptic enhancement begins to decline, which is qualitatively consistent with the theoretical and experimental results of synaptic homeostatic plasticity (Turrigiano 2012). The curve of firing and resting energy state changing with frequency (Fig. 2g) indicates that at a lower frequency, the firing energy state is greater than the resting energy state. When the stimulation frequency is about 10 Hz, the two curves cross, and then the resting energy state gradually increases and tends to saturation and then gradually decreases. Meanwhile, the firing energy state rapidly decreases and gradually increases after reaching saturation. The difference between the resting and firing energy states reflects the computational results of synaptic plasticity.

Our model also shows the dependence of synaptic plasticity on dendritic location. The LTP of the proximal synapse is greater than that of the distal synapse in the STDP protocol (Fig. 2b, c). In the case of cooperative afferent protocol (Fig. 2d), the LTP of the distal synapse is larger than that of the proximal synapse. These calculated results are consistent with the experimental results (Froemke et al. 2005; Sjöström and Häusser 2006; Letzkus et al. 2006; Golding et al. 2002).

Finally, to further prove the effectiveness of our model, we considered a hippocampal culture data set, which consists of triplet and quadruplet protocols (Fig. 3a,b). The mean weight of the proximal synapses in our model reproduce the triplet experimental results (Fig. 6c in Wang et al. 2005,Table 2 in Pfister and Gerstner 2006), whereas the mean weight of the distal synapses is significantly different from the experimental results. In the triplet experiment of Wang et al. 2005, the location of the stimulus in the dendritic branch was not shown, while the simulation results of the proximal stimulation are quite consistent with the experimental results (Fig. 6c in Wang et al. 2005,Table 2 in Pfister and Gerstner 2006), so we judge that the stimulus location in the triplet experiment of Wang et al. 2005 is at the proximal site. In the quadruplet simulations (Fig. 3c), the average weight of all synapses at the proximal and distal ends of the dendritic branches can well fit the experimental results (Fig. 5 in Wang et al. 2005,Table 2 in Pfister and Gerstner 2006).

Fig. 6.

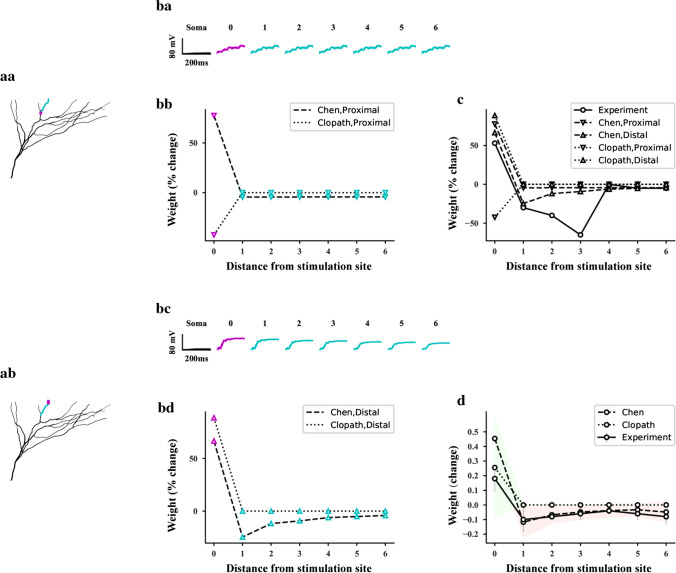
Comparison between model simulation and experiment in the basal region of pyramidal neurons. a Stimulation on a branch of pyramidal neurons. 0-6 represent the numbers of the compartments and the distance between the compartments and the stimulated site. magenta: stimulated site, cyan: unstimulated site. (aa) proximal stimulated site. (ab) distal stimulated site. (ba) The somatic action potential and the postsynaptic depolarization potential of each compartment during proximal stimulation. (bb) Changes of synaptic strength in each compartment after the proximal stimulation. (bc, bd) Same as (ba) and (bb) respectively, but for the distal stimulation. (c) The change of synaptic strength in each compartment shown in (aa) and (ab). (d) Changes of mean synaptic connection strength after stimulation for all branches in the basal region. The data in 0, 1 and 2 sites in the experiment (Fig. 3Ab, Ac in Royer and Paré 2003) were averaged as the experimental data of compartment 0. In the model simulation, the compartments in each branch were divided into 7 groups corresponding to the site distance of 0-6, and then the data of synaptic strength of each group were averaged. The gray error bar represents the experimental standard deviation, the red shaded area represents the standard deviation of our model simulation, and the green shaded area represents the standard deviation of Clopath’s model simulation

Effects of spatial overlap of synaptic connections on memory retention in pyramidal neurons

To study the memory retention ability, we present a calculation method on memory retention (Fig. 4c). The synaptic weights corresponding to task 2 at the beginning and end of task 1 are expressed as ${\text{W}}_1$ and ${\text{W}}_2$, respectively, and the synaptic weights corresponding to task 1 at the beginning and end of task 2 are expressed as ${\text{W}}_3$ and ${\text{W}}_4$, respectively. The first task before the second task causes the synaptic weight of the second task to change to $\left|{\text{W}}_2-{\text{W}}_1\right|$; the second task then causes the synaptic weight of the first task to change to $\left|W_4-W_3\right|$. The influence of the two tasks on each other’s synaptic weight is called memory loss and quantitatively calculated as $\left|W_2-W_1\right|+\left|W_4-W_3\right|$. Obviously, memory loss is the opposite of memory retention, that is, the smaller the memory loss is, the stronger the memory retention will be, and vice versa.

To investigate the effect of spatial overlap on memory retention, we applied two tasks with temporal overlap of 0 and set the execution period of each task as 200 ms. We conducted stimulation process using a Possion distribution with an average rate of 40 Hz (Relation between memory retention and spatial overlaps in Methods). First, we simulated the synaptic input with activation time of 50 ms in apical tuft dendrites (Fig. 4a). The average postsynaptic potential of the two tasks gradually approaches almost the same (Fig. 4b) with increasing spatial overlap of synaptic connections. When the spatial overlap is 0 (Fig. 4c, left), the change in the average synaptic strength corresponding to the second task after the execution period of the first task is $\left|W_2-W_1\right|=21.1$; and the average synaptic strength of the first task change to $\left|W_4-W_3\right|=1.1$ after the second task, thus the total memory loss is 22.2. When the spatial overlap is close to 0.5(6/13) (Fig. 4c, middle), the average synaptic strength corresponding to the second task changes to $\left|W_2-W_1\right|=72.9$ after the completion of the first task; and the average synaptic strength change corresponding to the first task is $\left|W_4-W_3\right|=35.9$ after the completion of the second task, so the memory loss is 108.8. When the spatial overlap is 1 (Fig. 4c, right), the average synaptic strength corresponding to the second task changes to $\left|W_2-W_1\right|=72.9$ after the completion of the first task; and the average synaptic strength change corresponding to the first task is $\left|W_4-W_3\right|=35.9$ after the completion of the second task, so the memory loss is 108.8. The statistical results of 10 random simulations on the connection mode indicate that memory loss has a significant positive linear correlation with the spatial overlap of synaptic connections (Fig. 4d). The larger the spatial overlap of synaptic connections is, the weaker the memory retention ability will be and a perfect linear relationship between them, consistent with the experimental results (Cichon and Gan 2015).

Influence of temporal overlap of synaptic connections on memory retention in pyramidal neurons

To explore the effect of temporal overlap on memory retention ability, we observed the simulation results of different temporal overlaps under the condition that the space overlap was set as 0. Similar to the protocols with spatial overlap, we first selected the protocol with synapse activation time of 50 ms to calculate the synaptic strength in the apical tuft dendrites of pyramidal neurons (Fig. 5). With increasing temporal overlap, the postsynaptic membrane potential corresponding to the two tasks are gradually close to each other. When the temporal overlap is 1, they almost overlapped, which is the same as the result of space overlap (Fig. 5b). If the temporal overlap is 0 (Fig. 5c, left), the execution time of the first task is $\mathrm{\Delta }\text{t}=200\text{ms}$ before the start of the second task. At this time, the average synaptic strength change of the second task caused by the first task is $\left|{\text{W}}_2-{\text{W}}_1\right|=21.1$, and the average synaptic strength change corresponding to the first task is $\left|W_4-W_3\right|=0.3$ after the second task execution period, so the total memory loss is 21.4. When the temporal overlap is 0.5 (Fig. 5c, middle), the execution time of the first task is $\mathrm{\Delta }\text{t}=100\text{ms}$ before the start of the second task. At this time, the average synaptic strength change of the second task caused by the first task is $\left|W_2-W_1\right|=13.4$, and the average synaptic strength change corresponding to the first task is $\left|W_4-W_3\right|=33.8$ at the end of the second task, so the total memory loss is 47.2. When the temporal overlap is 1, the two tasks are synchronized (Fig. 5c, right), and the execution time of the first task before the second task is 0 ($\mathrm{\Delta }\text{t}=0\text{ms}$), showing the overlap of the two points 1 and 2. Therefore, the average synaptic strength change corresponding to the second task is $\left|W_2-W_1\right|=0$. After the completion of the second task, and the average synaptic strength change corresponding to the first task was $\left|W_4-W_3\right|=87.7$; thus, the memory loss is 87.7. The statistical results of 10 simulations (Fig. 5d, synaptic connections generated randomly) indicate that the memory loss decreases slightly with increasing temporal overlap at low levels; then the memory loss increases linearly with increasing temporal overlap.

How does spatial overlap compare with temporal overlap in terms of memory retention? We performed analysis on memory retention data at activation time of 50 ms with spatial overlap (Fig. 4) and temporal overlap (Fig. 5). For spatial overlap, the average value of the maximum value minus the minimum value of memory loss is 116.6, but the average value is 78.7 for temporal overlap, indicating that the effect of spatial overlap on memory retention is larger than that of temporal overlap.

Automatic transformation from spatially separated (overlap 1) to not separated (Overlap 0)

Different motor learning tasks activate different branches in apical tuft dendrites (Cichon and Gan 2015), indicating that the synaptic input of different tasks is projected to different branches of the dendrites in a non-overlapping manner or in a spatial overlap of 0. This non-overlapping projection is conducive to memory retention or overcoming catastrophic forgetting (Masse et al. 2018). However, it is not clear how such non-overlapping synaptic inputs are formed and whether they can be generated automatically from random synaptic inputs.

Royer and Paré (2003) reported that, in intercalated neurons of the amygdala, activity dependent potentiation or depression of particular glutamatergic inputs leads to opposite changes in the strength of inputs that end at other dendritic sites. High frequency afferent tetanization induces a Mexican hat like profile of response amplitude changes: Homosynaptic LTP at stimulated inputs, surrounded by heterosynaptic LTD (Fig. 3 in Royer and Paré, 2003). This pattern of amplitude changes may provide a kind of lateral inhibition in plasticity space, serving to accentuate the impact of plastic change at a local population of synapses. It also results in synaptic survival of the fittest and task-dependent non-overlapping synaptic connections.

To understand the mechanism of non-overlapping synaptic connections, we first compared our plasticity model with Clopath’s plasticity model (Clopath et al. 2010; Bono and Clopath 2017) based on the observations of high frequency stimulation by Royer and Paré (2003). We only focused on high frequency stimulation because the logic of the induction of heterosynaptic LTP by homosynaptic LTD under low frequency stimulation (Fig. 2 in Royer and Paré 2003) is different from the logics of strong calcium signals leading to LTP and weak calcium signals to the LTD (Chistiakova and Volgushev 2009). The proximal and distal compartments of each thin branch in the basal region of the pyramidal neurons were subjected to 200 ms and 100 Hz tetanic stimulation respectively. Each compartment on the thin basal branch of the L5 pyramidal neuron model is connected to 3 synapses. The proximal (Fig. 6aa) or distal (Fig. 6ab) stimulation induced the postsynaptic dendritic spikes of each compartment in the thin branch and the somatic action potential (Fig. 6ba, bc). In our model, the regulation of synaptic strength depends on postsynaptic membrane potential and membrane current density (Eq. 5) rather than presynaptic activity. Different from our model, the modification of synaptic strength in the Clopath model depends on both the postsynaptic membrane potential (Fig. 6ba, bc) and presynaptic spike (the same for BCM model). Because both presynaptic spikes (200 ms, 100 Hz tetonic stimulation) and postsynaptic dendritic spikes were generated at the stimulus site (compartment 0), both models generated homosynaptic LTP. However, at the non stimulation sites (compartment 1–6), because there were no presynaptic stimulations, our model generated heterosynaptic LTD, while Clopath’s model did not (Fig. 6bb, bd). In the case of proximal stimulation, the postsynaptic plateau potential of each compartment decreased slightly with the increase of the distance between the compartment and the stimulation site (Fig. 6ba), and the corresponding heterosynaptic LTD also changed slightly (Fig. 6bb). In the case of distal stimulation, the postsynaptic plateau potential of each compartment decreased with the increase of the distance between the compartment and the stimulation site (Fig. 6bc), and the corresponding heterosynaptic LTD also showed similar changes (Fig. 6bd). The comparison between the profile of synaptic plasticity in above branch and the experimental results (Fig. 3Ab in Royer and Pare 2003) showed that our model can reflect the experimental results of all homo and hetero synaptic plasticity, while the Clopath model can only reflect the experimental results of homoplasticity (Fig. 6c). To further clarify the differences between our model and Clopath’s model, we averaged the computational results of synaptic plasticity in all branches and compared them with the corresponding experimental results (Fig. 3Ac in Royer and Paré 2003). The results of our model was consistent with the experimental observations, while the Clopath’s model could not reflect the experimental heterosynaptic plasticity (Fig. 6d).

To clarify the relationship between synaptic plasticity and dendritic spikes, we used the same stimulation protocol to the tuft region of pyramidal neurons as in the previous section (Fig. 7). Different from the basal region, in the tuft region, both proximal and distal stimuli failed to induce soma action potential. Although the soma potentials and dendrite spikes in the basal and tuft regions are different, the postsynaptic plateau potentials in the two regions follow the same rule: the postsynaptic plateau potential is the highest at the stimulation site, and it lowers as it is farther away from the stimulation site (Fig. 6ba, 7ba; Fig. 6bc, 7bc). The simulations of our model yield consistent results with previous evidences, indicate that synaptic plasticity is a reflection of the postsynaptic plateau potential: for homosynaptic plasticity, the larger the postsynaptic plateau potential, the larger the amplitude of synaptic enhancement; for heterosynaptic plasticity, the greater the postsynaptic plateau potential, the greater the amplitude of synaptic depression. In the Clopath model, although it has the same postsynaptic dendritic spikes like us, their synaptic weight does not change due to the absence of presynaptic spikes in the calculation of heterosynaptic plasticity, which is inconsistent with the former experimental results.

Fig. 7.

Comparison between model simulation and experiment in the tuft region of pyramidal neurons. a Stimulation on a branch of pyramidal neurons. 0–6 represent the numbers of the compartments and the distance between the compartments and the stimulated site. magenta: stimulated site, cyan: unstimulated site. aa proximal stimulated site. ab distal stimulated site. ba The somatic action potential and the postsynaptic depolarization potential of each compartment during proximal stimulation. bb Changes of synaptic strength in each compartment after the proximal stimulation. bc, bd Same as ba and bb respectively, but for the distal stimulation. c The change of synaptic strength in each compartment shown in aa and ab. d Changes of mean synaptic connection strength after stimulation for all branches in the tuft region. The data in 0, 1 and 2 sites in the experiment (Fig. 3Ab, Ac in Royer and Paré 2003) were averaged as the experimental data of compartment 0. In the model simulation, the compartments in each branch were divided into 7 groups corresponding to the site distance of 0-6, and then the data of synaptic strength of each group were averaged. The gray error bar represents the experimental standard deviation, the red shaded area represents the standard deviation of our model simulation, and the green shaded area represents the standard deviation of Clopath’s model simulation

We then proposed a stimulus protocol for synaptic input from random connection (spatial overlap is about 1) to non-overlapping connection (spatial overlap degree is 0) based on the above results. The synaptic inputs corresponding to the two tasks were randomly connected to the branches in the basal (Fig. 8a) or apical tuft (Fig. 8d). For each randomly selected branch, the synapse corresponding to task 1 (task 2) received 200 ms, 100 Hz tetanic stimulation, and then the synapse corresponding to task 2 (task 1) received the same stimulation. The performing order of task 1 and task 2 alternated randomly with branches. The initial strength of all synapses was set to 0.5. When all the branches had been stimulated, synapses whose strength was less than a certain threshold (a tenth of the initial strength here) were clipped. According to this stimulus protocol, our model can significantly reduce the number of synaptic connections and cluster the synaptic connections of each task to different dendrite branches (Fig. 8ba, ea). It can be seen from the distribution of synaptic weights that, due to the competition among synapses, the average weights of the remaining synaptic connections eventually reach the maximum value, while the average weights of the clipped synaptic connections reach the minimum value (Fig. 8b, eb). The competition among synapses is caused by the coexistence of homosynaptic LTP and heterosynaptic LTD. Because there is more than one synapse connection in each task, the heterosynaptic LTD induced by the homosynaptic LTP in each task is stronger than that of the single synapse connection in the previous section. The homosynaptic LTP generated by the execution of one task in each branch induces the heterosynaptic synaptic LTD of other tasks in the same branch and all tasks in other branches. For different regions (basal and tuft) of pyramidal neurons and different initial connections of each region, this stimulation protocol can automatically transform the spatial overlap from 1 to 0 based on our model, indicating that the stimulation protocol based on our model is robust and effective. Under the same stimulation protocol, the Clopath’s model fails to change the initial random synaptic connections and achieve the automatic transformation of spatial overlap from 1 to 0 (Fig. 8ca, fa). Clopath’s model only changes the synaptic connection strength from the initial value to the maximum value (Fig. 8cb, fb). In summary, the above results indicate that homosynaptic LTP and simultaneous induction of heterosynaptic LTD are critical for pyramidal neurons to achieve task-dependent synaptic connections that automatically convert spatial overlap from 1 to 0, or synaptic connections from random to clustering.

Fig. 8.

Automatic transformation of spatial overlap from 1 to 0. a Random synaptic connections in the basal region of pyramidal neurons of the two corresponding tasks before our stimulation protocol. magenta: synaptic connections for task 1, cyan: synaptic connections for task 2. nCon is the compartment number of the synaptic connections after learning, and nDiscon is the compartment number of the clipped synaptic connections. wCon is the average connection strength (weight) of the unclipped synapses, while wDiscon is the average connection strength (weight) of the clipped synapses. Top and bottom panels: two different initial synaptic connections that were randomly generated. ba Based on our model, the distribution of synaptic connections in the basal regions after our stimulation protocol was implemented. bb Based on our model, the distribution of synaptic weights in the basal regions after our stimulation protocol was implemented. c Same as b, but based on the Clopath’s model. d, e, f Same as a, b, c, but for the apical tuft region in pyramidal neurons

Discussion and conclusion

We proposed a synaptic plasticity model based on the metabolic energy of postsynaptic neurons. The model suggests that to ensure the survival and normal physiological function of neurons, their energy state should be maintained at a normal resting energy state level. Neurons recover to the resting state by active transport mechanism. The active transport mechanism moves ions back across the neuronal membrane against their electrochemical gradients through ion pumps (e.g., sodium–potassium pump) distributed on the cell membrane, which needs to be driven directly by metabolic energy (e.g., by the hydrolysis of ATP). Synaptic plasticity is associated with the degree of deviation of energy states. If the firing energy state is larger than the resting energy state, then the synaptic strength weakens; if the firing energy state is less than the resting energy state, then the synaptic strength strengthens; and if the firing energy state is relatively close to the resting energy state, then the synaptic weight remains unchanged. The model is a unified one of homo- and heterosynaptic plasticity, in which the metabolic energy is calculated based on the postsynaptic membrane potential and membrane current density.

To date, studies on neuron energy expenditure and synaptic plasticity have developed independently, and our model links synaptic plasticity with neuron energy expenditure. For synaptic plasticity, a large number of experiments have shown that activated and inactivated synapses have plasticity; the former is called homosynaptic plasticity, and the latter is heterosynaptic plasticity (Chistiakova et al. 2015; Zenke et al. 2017). Many models of synaptic plasticity have been established according to different factors affecting synaptic plasticity. Typical homosynaptic plasticity models include spike-rate-dependent (Bienenstock et al. 1982) spike-timing-dependent (Pfister and Gerstner 2006), and voltage-dependent (Clopath et al. 2010). These models cannot be used directly for heterosynaptic plasticity because the synaptic strength does not change without presynaptic activity. Some heterosynaptic plasticity models established in recent years are mainly based on the following two ideas: one is to directly adjust the synaptic weight in a short timescale according to homeostatic plasticity (Chen et al. 2013; Zenke et al. 2015). Given that plasticity is achieved through direct adjustment of weights, such models must be combined with existing homosynaptic plasticity models to play a role (Turrigiano 2012; Turrigiano and Nelson 2004). Another idea considers that heterosynaptic plasticity is caused by spontaneous activity of neurons in the input fibers (Jedlicka et al. 2015). Although this idea has been consolidated in the experiment in vivo (Abraham et al. 2007; Abraham and Goddard 1983), many experiments in vitro without spontaneous presynaptic activity have also observed the phenomenon of heterosynaptic plasticity (Volgushev et al. 2016; Lynch et al. 1977; Royer and Paré 2003), suggesting that this idea is still questionable. All of the above models are phenomenological models with neuron activity patterns as variables, and the causes of synaptic plasticity induced by various activity patterns are generally explained by biophysical models based on Ca²⁺ dynamics (Shouval et al. 2002; Graupner and Brunel 2012). Given that Ca²⁺ dynamics is affected by many complex and unknown factors and severely restricted by testing methods, these models are often difficult to obtain practical applications. Although increasing lines of theoretical and experimental evidence show that metabolic energy can be used as a unified theoretical basis for controlling neural activity (Laughlin 2001; Hasenstaub et al. 2010; Wang et al. 2015; Wang and Wang 2018; Zhu et al. 2018), the focus is still on the utilization efficiency of energy and the amount of ATP consumed during synaptic transmission and synaptic integration (Attwell and Laughlin 2001; Howarth et al. 2012; Wang et al. 2017; Zhu and Wang 2019), rather than on how energy cost affects synaptic plasticity. The synaptic strength of mature brains can be increased or decreased through the plasticity process, which simultaneously changes the metabolic energy consumption of synapses (Harris et al. 2012). The synaptic strength needs to be readjusted by homeostatic mechanisms to avoid the increase in the synaptic strength and thus increase the energy consumption (Turrigiano 2012). However, these results only indicate the influence of synaptic plasticity on metabolic energy, rather than the influence of metabolic energy on synaptic plasticity. As such, the mechanism of synaptic plasticity cannot be illuminated from the perspective of metabolic energy.

Our model provides a link between stimulation protocols and evoked synaptic changes, which accounts for diverse existing synaptic plasticity phenomena from the perspective of neuron metabolic energy and can also allow us to predict the plasticity induced by new stimulation protocols. For example, when the spatial and temporal overlaps are between 0 and 1, we predict the changes of postsynaptic potential and synaptic plasticity with time (Figs. 4, 5). Neurons are stimulated in a variety of ways; as long as the stimulus-induced firing energy state and resting energy state can be determined, the corresponding synaptic strength changes can be obtained (Figs. 1, 2). Experiments and modeling calculations in layer five pyramidal neurons have shown that the efficiency of action potential and metabolic energy consumption are specific to time and space, and they change according to the morphology of neurons (Hallermann et al. 2012). The electrical properties of pyramidal neurons are not invariable but generate different electrical behavior gradients due to the position dependence of input resistance (Fletcher and Williams 2019). These results indicate that, regardless of whether the synapse is active or not, the energy state at different locations in pyramidal neurons is different, and the firing and resting energy states are also location dependent. These factors lead to the occurrence of heterosynaptic plasticity. Since the metabolic energy cost varies with different synaptic strength (Harris et al. 2012), the heterosynaptic plasticity is closely related to the initial strength of synapses (Volgushev et al. 2016). The temporal and locational dependence of the energy state has revealed that the initial strength of the synapse is not a key factor in the heterosynaptic plasticity. Our simulation results (Figs. 4, 5) have shown the occurrence of heterosynaptic plasticity even if the initial strength of the synapses at different locations in pyramidal neurons is the same.

The simulation results of our model show that task-dependent, dendritic branch-specific synaptic connections are most conducive to memory retention in pyramidal neurons, consistent with corresponding experimental results (Cichon and Gan 2015). Compared with the Clopath model, our model can automatically convert synaptic connections with spatial overlap of 1 to synaptic connections with spatial overlap of 0 through tetonic stimulation, providing a new approach for effective memory retention. The spatial and temporal separation is also crucial to the memory retention in the neural network (Benna and Fusi 2016; Masse et al. 2018). Our study on a single pyramidal neuron is similar to this, indicating that the memory retention is stronger at the lower spatial and temporal overlap. The reason for the similarity between a single pyramidal neuron and neural network is that a pyramidal neuron has been shown to function as a two-layer neural network (Poirazi et al. 2003; Polsky et al. 2004; Eberhardt et al. 2019). We found that pyramidal neurons’ memory retention capacity decreased linearly with increasing spatial and temporal overlap of synaptic connections, which needs further experimental verification. Unlike the motor cortex, however, spatial overlap in the barrel cortex occurs in all apical tuft branches of an individual L5 pyramidal neuron (Xu et al. 2012). In this regard, for such perceptual tasks, the recognition and positioning functions of the target are far more important than the memory retention functions, thus the spatial separation of synaptic connections may be unnecessary.

Our synaptic plasticity model can be improved and extended in the following aspects. First, our model considers the energy state as the potential energy of the postsynaptic membrane. The activity of neurons deviates from the original resting energy state to the firing energy state, while the active transport is responsible for restoring the energy state to the resting state. We used the postsynaptic driving potential and current instead of the original postsynaptic membrane potential and current density to calculate the energy state because only in this way can the model be consistent with the experimental results. This finding indicates that the dynamic process of active transport to restore the resting level of the energy state is complex. The energy state changes continuously with time in the process of energy state deviation and recovery. The dynamics of energy state with time should be further investigated by experiment. Along this line of thought, a relationship possibly exists between the kinetic process of energy state recovery and the metabolic energy consumption. Further exploration is necessary to understand this relationship. Second, our model introduced the Hebbian homeostatic plasticity rule (Debanne et al. 2019; Gasselin et al. 2017; Campanac et al. 2008) into the design of the driving current to avoid setting the hard boundary of synaptic weight by such means. A hard boundary of synaptic weight was not required in most cases for the stimulation protocols adopted. However, in some special cases (for example, Fig. 3a, the distal synapses at $\mathrm{\Delta }{\text{t}}_1=15,\mathrm{\Delta }{\text{t}}_2=-5$), the synaptic weight was below zero, while the synaptic weight would increase continuously under the induction with the postsynaptic membrane current density less than the maximum membrane current density for a long time. For this reason, we force the synaptic weight to be 0 when it is negative in the simulation of memory retention. Synaptic plasticity can change the consumption of metabolic energy, while the homeostatic synaptic plasticity indicates that the energy consumption needs to be limited to a reasonable range. In the future, this principle can also be applied to make our model have better homeostatic plasticity, so that the hard boundary of synaptic weight is unnecessary. Third, increasing theories and experiments show that learning and memory are not only related to synaptic plasticity but also related to the intrinsic plasticity of neurons (Debanne et al. 2019; Lisman et al. 2018; Goodman and Brette 2009). We have studied the impact of temporal and spatial overlap on memory retention based on synaptic plasticity. Further research should focus on determining how the overlap affect the intrinsic plasticity (such as spike threshold and resting membrane potential) in pyramidal neurons and memory retention. Fourth, it has been challenged with recent experimental results (O’Donnell et al. 2011; Humble et al. 2019) that the memory retention is closely associated with the long-term stability of synaptic strength. It is necessary to combine these research results to further improve our model in the future.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.