Abstract
Proper assessment of reference evapotranspiration (ET0) is necessary for pastoral activity and water management. The Penman-Monteith FAO56 (ETpmf) method has been recommended as the identical ET0 estimation model; nonetheless, it belongs to a vast climatic data requirement. There is an urgent need to discover an ideal alternate model for evaluating ET0 in particular places where all climatic data is insufficient. The performances of 15 empirical models were assessed to get the best alternative model by comparing it with the PMF-56 model. These 15 models were evaluated by employing a daily scatter plot and three well known numerical approaches: relative root-mean-square error, mean absolute error and Nash–Sutcliffe coefficient in this study. Furthermore, a linear regression model was implemented to calibrate and validate the empirical models' performances throughout the 1981–2005 and 2006–2018 time intervals, separately. The outcomes displayed that the ETpmf rose primarily and declined later on a monthly period with the topmost amount in April and the lowermost amount in January. Overall, the Abtew model was the best alternate method showing the highest determination coefficient values more than 0.85 from January to December. In contrast, the Penman, WMO, Trabert, Valiantzas1, Valiantzas2, Valiantzas3 and Jensen-Haise models presented moderate performances with fewer inaccuracies. Afterwards, modification, the version of the above-described models every month has been upgraded deliberately related to actual. The Abtew model had simplicity in the computation process, only used maximum temperature and solar radiation data and linearly well connected to the PMF-56 model.
Keywords: Reference evapotranspiration, Penman-Monteith, Empirical models, Performance evaluation, Model modification
reference evapotranspiration; Penman-Monteith; empirical models; performance evaluation, model modification
1. Introduction
Reference evapotranspiration (ET0) is the amount of evapotranspiration through a theoretical grass reference crop with an elevation of 0.12 m, a settled and immovable plane resistance of 70 sec m−1 and an albedo of 0.23, vigorously rising, effectively watered, and entirely covering the land (Allen et al., 1998). ET0 integrates different climatic influences and demonstrates the evaporative necessity of the atmosphere free of crop variety, crop growth and managing exercises (Alexander and Simon Bindoff, 2013). ET0 has been a crucial factor in climate, agriculture and water sector, and irrigation scheduling and development in the universally acknowledged global warming issue (Smith et al., 1991; Li et al., 2010; Sentelhas et al., 2010). Recently, investigation of ET0 using the FAO56-PM model has been broadly studied as the FAO56-PM was suggested as a qualified ET0 calculation procedure by the Food and Agricultural Organization (FAO) (Traore et al., 2010; McVicar et al., 2007; Temesgen et al., 2005; Sumner and Jacobs, 2005; Garcia, 2004). The critical lacking of the PMF-56 method is the prerequisite of large datasets containing the air mean, maximum and minimum temperature, relative humidity, wind speed, and solar radiation. In the areas where the historic long-term climatological data are tough to manage, the FAO56-PM model will not be the most incredible option (Chu et al., 2017). So, the ET0 calculation method with a lower data necessity and a simple calculation procedure is better to execute. There are four vital empirical models: mass transfer-based, temperature-based, radiation-based, and combined models. The temperature-based Thornthwaite (1948), Blaney and Criddle (1950), and Hargreaves and Samani (1985, 1982) equations had been broadly implemented since they mostly use simply-attained temperature data. The radiation-based had been employed too (Slatyer and Mgilroy, 1961). The physically-based combination model was chosen as the qualified ET0 calculation model by FAO since it nearly estimates ET0 at the sites assessed (Allen et al., 1998; López-Urrea et al., 2006; Stöckle et al., 2004).
Although sufficient research on evapotranspiration in different states has been performed by applying model data, it is very scarce for Bangladesh (Ayub and Miah, 2011; Shahid, 2011; Karim et al., 2008; Mojid et al., 2015). For example, Ayub and Miah (2011) investigated ET0 in the northwest part (Bogra, Rangpur, Dinajpur, Rajshahi, and Ishwardi) by experimental and PRECIS model's data. Shahid (2011) performed climate data for the timescale of 1961–1990 and MAGICC/SCENGEN output in the identical area to evaluate the necessity of irrigation water. Like Ayub and Miah (2011), Mojid et al. (2015) also researched ET0 in the same place, but for only two observatories (Bogra and Dinajpur) by applying 21 years (1990–2010) of climatic data.
Bangladesh has been facing the consequence of climate variation (Ali, 1996; Mirza, 2002; Karim and Mimura, 2008; Climate Change Cell, 2008). The fundamental causes of climate change are an unbalanced farming-dependent economy, specific physiographical positions, growing densely populated conditions, and lesser ability of adjustment for its weak infrastructural setup (IPCC, 2007). Dry season (from December to April) rice (Boro) is the chief provider of food kernels for the densely populated nation like Bangladesh and needs an enormous irrigation water volume, provided from groundwater. There is slight or no precipitation in the dry season in the country. So, problems arise from the excess withdrawal of groundwater. Therefore, water level decreasing, rising irrigation and crop manufacture price, raising the magnitude of salinity in nearshore regions, increasing the current arsenic trouble in groundwater, etc. (Rahman et al., 2018). So, the main problem will be the job of intensifying food manufacture in scarcity of water because of change of climate soon. Research on the proper and precise estimation of ET0 and its shift in Bangladesh trend is needed as ET0 is a crucial component for evaluating the necessity of irrigation water and therefore can perform an essential act to identify the issue of controlling cultivated water to ensure food safety of Bangladesh. Since the long-term climatological data are tough to manage from Bangladesh's actual perspective, the ETpmf model will not be the most acceptable option. Consequently, it is urgent to discover an appropriate, precise, and more straightforward substitute empirical method for calculating the ET0 instead of the ETpmf way when the climatological data are absent or incomplete.
As far we know, any inclusive research work was not accepted for analyzing the spatiotemporal trends of monthly ET0 and assessing the acts of other alternative methods for Bangladesh, specifically on a monthly period, which will be the innovation of the present study. For covering the emptiness of knowledge, in current work, 15 broadly used empirical models were selected—including two temperature-based models (Hargreaves–Samani and Berti et al.), three mass transfer-based models (Penman, WMO, and Trabert), six radiation-based models (Makkink, Priestly–Taylor, Jensen–Haise, Abtew, Irmak, and Tabari), and four combined models (Doorenbos-Pruitt, Valiantzas1, Valiantzas2, and Valiantzas3)—based on their climatological involved elements and appropriateness globally. Eventually, two theories were anticipated for the present research work. Firstly, the individual empirical models will provide notably different outcomes to calculate the reference evapotranspiration monthly. Secondly, the linear regression technique will effectually modify the 15 ETemp models versus the ETpmf model in the study area. Based on the hypotheses above, the essential purposes of the present research work are (1) evaluation of the spatiotemporal variations and trends of the ETpmf applying climatic data from the sort outed 25 stations in Bangladesh during 1981–2018 on a monthly timescale; (2) to relate the performance of the 15 selected ETemp models with the standard ETpmf model to calculate ET0 on a daily period in Bangladesh; (3) to discover a best alternate model against the PMF-56 model, which will be easier in ET0 calculation and use a fewer climatic parameter; and (4) to modify the ET0 using the alternate model with the ETpmf model by adopting linear regression model. The results of the research work will produce significant direction for farming manufacture and hydrological development in Bangladesh.
2. Material and methods
2.1. Study area
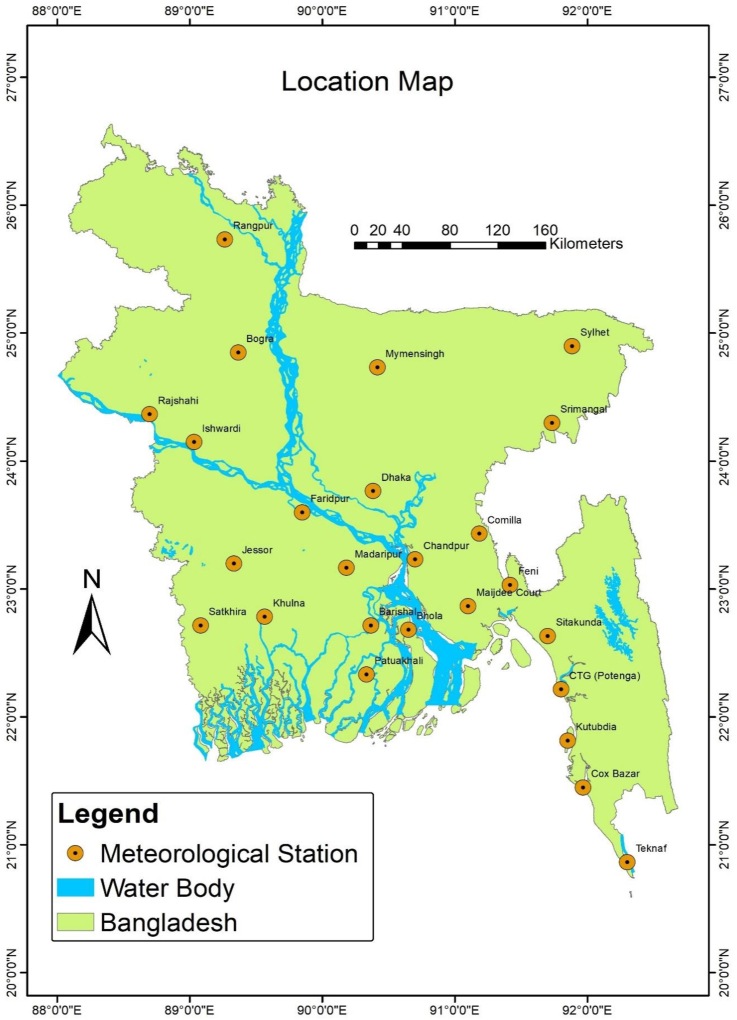
Bangladesh, placed in semi-tropics of southeast Asia located among latitude 20°34′N and 26°38′N, and longitude of 88°01′E to 92°41′E (Figure 1). Total entire land belongs to 147,570 km2 and maximum portions are alluvial plain exclude a small number of southeastern and eastern hilly regions of the kingdom. By Köppen's categorization of climate, the total land is occupied by four subgroups: monsoon climate, tropical savanna climate, humid subtropical climate, and humid subtropical or subtropical oceanic highland climate (Rashid, 1991). The Winter (December–February), Pre-Monsoon (March–May), Monsoon (June–September) and Post-Monsoon (October–November) are four primary seasons (Khatun et al., 2016). The mean lowest and highest temperatures are 21.18 and 30.33 °C, separately. Mean smallest temperature differs from 12.5 to 25.7 °C, while the topmost temperature is 25.2–33.2 °C in a monthly period. Bangladesh experienced the most incredible cold condition in January while the most heated situation in April and May month (Rahman and Lateh, 2015). The average annual precipitation belongs to 2488 mm (Rahman et al., 2017) as well as overall precipitation's approximate eighty percent happens in June, July, and August month (Das et al., 2005). Changes in cloudage, air moisture with air velocity have been detected at different periods of various state.
Figure 1.
Location of the study area and the distribution of weather stations used in this study.
2.2. Data sources
Historic daily minimum temperature (Tmin) and maximum temperature (Tmax) (°C), relative humidity (RH) (%), wind speed (W.S.) (m sec−1), and sunshine hour (SH) (h day−1) data had been obtained from 35 weather observatories of Bangladesh Meteorological Department. But long-term climate documentations are not entirely found in each observatory since some observatories are recently launched, and some observatories belong to missing data for prolonged intervals. In the present research work, climatic data from 25 observatories were chosen (Figure 1) to estimate ET0; the selected observatories got 38 years (1981–2018) daily climatic information. Annual means of the sunshine hour (SH), maximum temperature (Tmax), minimum temperature (Tmin), average temperature (Tavg), relative humidity (R.H.), wind speed (W.S.) and evapotranspiration (ETo) are found 6.19 h, 30.66 °C, 21.32 °C, 25.99 °C, 79.79%, 3.24 m/s and 3.81 mm/day, respectively for Bangladesh during 1981–2018 in present study (Table 1). The absence of extensive volume data of various climatic parameters for a long time in historical records was critical. Most of the observatories get the well standard of temperature and relative humidity data. Still, at the same time sunshine hour and wind speed data were absent for a remarkable quantity of years. The closest adjacent stations' data had been taken to fulfil the missing data for solving this problem.
Table 1.
Annual means of the main climatic factors in Bangladesh during 1981–2018.
| Total BD | SH | Max T | Min T | Avg T | RH | WS | ET0 |
|---|---|---|---|---|---|---|---|
| 1981–2018 | 6.19 | 30.66 | 21.32 | 25.99 | 79.79 | 3.24 | 3.81 |
2.3. Estimation of ET0 using the Penman-Monteith FAO-56 model
Allen et al. suggested the Penman-Monteith FAO-56 model in 1998. This model was then acknowledged as the best model to calculate reference evapotranspiration considering the absence of monitoring of lysimeters. It was also approved as supreme qualified universally (Chu et al., 2017; Estévez et al., 2009; Dinpashoh et al., 2011; Jhajharia et al., 2012). The Penman-Monteith FAO-56 model (ETpmf) is presented by the below Eq. (1):
| (1) |
where, ETpmf = reference evapotranspiration [mm day−1], Rn = net radiation at the crop surface [MJ m−2 day−1], G = soil heat flux density [MJ m−2 day−1], T = mean daily air temperature at 2 m height [°C], u2 = wind speed at 2 m height [m s−1], es = saturation vapour pressure [kPa], ea = actual vapour pressure [kPa], es-ea = saturation vapour pressure deficit [kPa], Δ = slope vapour pressure curve [kPa °C−1], γ = psychrometric constant [kPa °C−1].
2.4. Estimation of ET0 using fifteen (15) empirical models
The fifteen (15) empirical ET0 models, those usually performed fine in different areas of the earth, were chosen to relate with the PMF-56 model in the present research work. These models were Hargreaves-Samani and Berti et al. (based on temperature); Penman, WMO, and Trabert (based on mass transfer); Makkink, Priestly–Taylor, Jensen–Haise, Abtew, Irmak and Tabari (based on radiation); and Doorenbos-Pruitt, Valiantzas1, Valiantzas2, and Valiantzas3 (combined). The particular calculations, key involved inconstant, and citations have been displayed by Table 2.
Table 2.
The original form of the 15 empirical models (abbreviated as ETemp models).
| No | Models | Models Input | Equations | References |
|---|---|---|---|---|
| Temperature-based | ||||
| 1 | Hargreaves–Samani | Ra, Tave, Tmax, Tmin | EThs = [0.0023 Ra (Tave +17.8) (Tmax − Tmin)0.517]/λ | (Hargreaves and Samani, 1985) |
| 2 | Berti et al. | Ra, Tave, Tmax, Tmin | ETber = [0.00193 Ra (Tave +17.8) (Tmax − Tmin)0.5]/λ | (Berti et al., 2014) |
| Radiation-based | ||||
| 3 | Makkink | Rs, T | ETmak = 0.61 | Makkink, 1957 |
| 4 | Jensen–Haise | Rs, T | ETjh =(0.025T + 0.08) | Jensen and Haise, 1963 |
| 5 | Irmak | Rs, T | ETirm = 0.149Rs + 0.079T - 0.611 | Irmak et al., 2003 |
| 6 | Tabari | Rs, Tmax, Tmin | ETtab = 0.156Rs - 0.0112Tmax +0.0733Tmin - 0.478 | Tabari et al., 2013 |
| 7 | Priestley–Taylor | Rn, T | ETpt = 1.26 | Priestley and Taylor, 1972 |
| 8 | Abtew | Rs, Tmax | ETabt = | Abtew, 1996 |
| Mass transfer-based | ||||
| 9 | Penman | u2, es-ea | ETpen = 0.35 (1 + 0.98/100u2) (es-ea) | Penman, 1948 |
| 10 | WMO | u2, es-ea | ETwmo = (0.1298 + 0.0934u2) (es-ea) | WMO, 1996 |
| 11 | Trabert | u2, es-ea | ETtra = 3.075u20.5 (es-ea) | Trabert, 1896 |
| Combined | ||||
| 12 | Doorenbos-Pruitt | Rn, u2, es-ea | ETdp | Doorenbos and Pruitt, 1977 |
| 13 | Valianlzas1 | Rn, T, RH | ETva1 = 0.0393 Rs–0.19 Rs0.6 Φ0.15 + 0.078 (T+20) (1 - ) | Valiantzas, 2013; 2013a |
| 14 | Valianlzas2 | Rn, T, Tmin | ETva2 = 0.0393 Rs–0.19 Rs0.6 Φ0.15 + 0.0061 (T+20) (1.12T - Tmin -2)0.7 | Valiantzas, 2013; 2013a |
| 15 | Valianlzas3 | Rn, T, RH, u2 | ETva3 = 0.0393 Rs–0.19 Rs0.6 Φ0.15 + 0.078 (T+20) (1 - ) u20.7 | Valiantzas, 2013; 2013a |
Note: Ra is the extraterrestrial radiation (MJ·m−2·d−1), Rs is the solar radiation (MJ·m−2·d−1), Rn is the net solar radiation (MJ·m−2·d−1), Tave, Tmax, and Tmin are mean, maximum, and minimum temperature (◦C), respectively, u2 is the wind speed at 2 m height (The unit of u2 is in m·s−1 in all equations except the Penman model, where u2 is in miles·d−1), es and ea are saturation and actual vapor pressure, respectively (The units of es and ea are in hPa in all equations except the Penman model, where es and ea are in mmHg.), RH is the relative humidity (%), Δ is the slope of the vapor pressure curve (kPa·◦C−1), γ is the psychrometric constant (kPa·◦C−1), λ is the latent heat of vaporization (≈2.45 MJ·kg−1), G is the soil heat flux density (MJ·m−2·d−1), and ϕ is the latitude (rad). The abbreviations of the 15 empirical models are arranged in order that the models appear in Table 2: hs, berti, pen, wmo, tra, mak, pt, jh, abt, irm, tab, dp, va1, va2, and va3.
2.5. Performance assessment of fifteen (15) empirical models
Three statistical methods: relative root-mean-square error (RRMSE), mean absolute error (MAE), and the Nash–Sutcliffe coefficient (NS) (Feng et al., 2017; Samaras et al., 2014) were adopted for assessing the performance of the 15 empirical models in this research work. The Eqs. (2), (3), and (4) (mentioned below) were accomplished for this purpose:
| (2) |
| (3) |
| (4) |
ETipmf and ETiemp are daily reference evapotranspiration calculated by the ETpmf model and the 15 ETemp models; correspondingly, n is the number of the test measurements and ETpmf, mean is the mean value of ETpmf. The RRMSE is limitless, with the value varying from 0 to ∞. The MAE is in mm/day. The closer the value of the RRMSE or the MAE to 0, the stronger the empirical equations' performance. The NS is endless, by the values ranged from −∞ to 1. While NS is near 1, the model's standard to calculate ETemp will be fine, having good dependability. Whenever NS is near to 0, ETemp belongs to a nearby mean value to ETpmf possessing a complete authenticated calculation; nevertheless, the inaccuracies of the calculation procedures are considerable; while NS is considerably below 0, the measure is unauthenticated.
2.6. Calibration and validation of empirical models
In this study, the performance of the 15 methods to estimate ET0 is chosen here to be calibrated. The calibration comprises converting the coefficient values of the methods to enhance their performance and decrease errors. In keeping with performance evaluation results, linear regression analysis was utilized to modify the empirical models' performance for further improvement (Allen et al., 1998). This linear regression analysis can model the correlation among the diurnal ET0 gained from ETemp models obtained from the ETpmf model. The correlation receipts the succeeding Eq. (5) (Li et al., 2018a):
| ETpmf = a ETemp + b | (5) |
where a and b are fitted regression coefficients. The objective is to improve the efficiency of the N.S. and reduce the errors obtained from RRMSE and MAE during the evaluation. For this, the total period (1981–2018, 38 years) is separated into two portions as suggested by Xu and Singh (1998): two-third of the serials (1981–2005) for calibration one-third (2006–2018) for validation. The fifteen models were calibrated and validated separately for these two parts. The values obtained from the calibration on the first 25 years (1981–2005) were used to validate evapotranspiration for the last 13 years (2006–2018) of the available climate data.
2.7. Trend test
The universal suggested nonparametric Mann–Kendall (M.K.) statistical test (Mann, 1945; Kendall, 1975) was utilized for classifying the implication of trend of the ET0. The M.K. test statistic (Z) follows the standard normal distribution with a mean of 0 and variance of 1 under the null hypothesis of no trend in the ET0. A statistic S is calculated by Eqs. (6) and (7) as follows:
| (6) |
where n is the number of the observations, the xj is the jth observation in the data set, and
| (7) |
Under the postulation that the data are self-determining and equitably disseminated, the mean and the variance of the S statistic and standardized test statistic Z are determined by Eqs. (8), (9), and (10) in this way (Mann 1945; Kendall 1975):
| E (S) = 0 | (8) |
| (9) |
where ti is the number of ties of extent m. The standardized test statistic Z is determined by Eq. (10):
| (10) |
The null hypothesis is disapproved if |Z|≥ Z1−β/2 at a significance level of β, where Z1−β/2 is the (1 − β/2)–quantile. If the Z value is positive (or negative), then the ET0 has an increasing (or decreasing) trend. As β = 0.05 and 0.01, if |Z| > 1.96 and 2.56, respectively demonstrating ET0 has a significant change trend at the 95% and 99% confidence level, respectively. Moreover, Theil–Sen's slope estimator (β) (Sen, 1968; Theil, 1950) was implemented for directing the range of a trend. The Theil–Sen's estimator, β, is determined as follows by Eq. (11):
| (11) |
where xj and xi are the time-series data. A positive β indicates an increasing trend, while a negative β indicates a decreasing trend. This method was generally adopted for detecting the slope of a trend in hydrometeorological time series data, which is available in many related types of research (Chu et al., 2017; Li et al., 2018b, 2018c).
2.8. Spatial interpolation method for ET0
The Inverse Distance Weighted (IDW) interpolation model, an easy arithmetical technique, was employed to explore the spatial distribution of ET0 for ETpmf and ETemp model in the study area. The key reason to apply the IDW was its swiftly and precisely calculation ability of the spatially-interpolated values than other techniques, for example, kriging. Chen and Liu (2012) stated Inverse Distance Weighted (IDW) equations by the Eqs. (12) and (13):
| (12) |
| (13) |
here Rp represents the unknown depth data (cm); Ri represents the depth data measured by MBES (cm); N is the number of points (in the search radius area); Wi means the weighting of each depth. di is the distance from each penetration to the calculated grid node, and α is the power and is also a control parameter, generally assumed to be two. Application of ArcGIS (version 9.3) software (Environmental Systems Research Institute, USA) was accomplished to create all spatial distribution maps.
3. Results and discussion
3.1. Monthly variations of the ETpmf
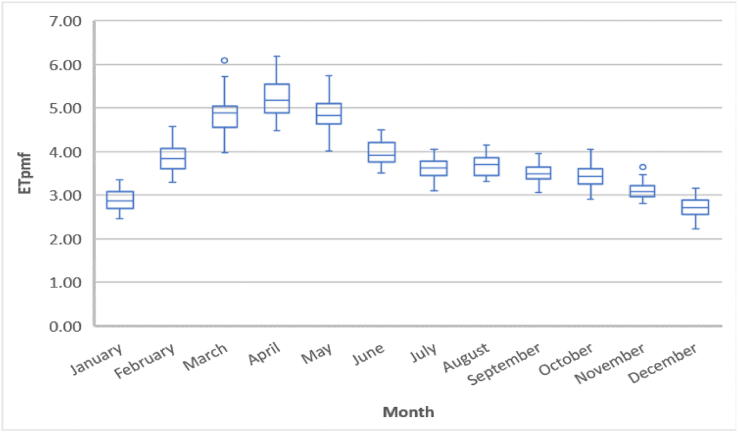
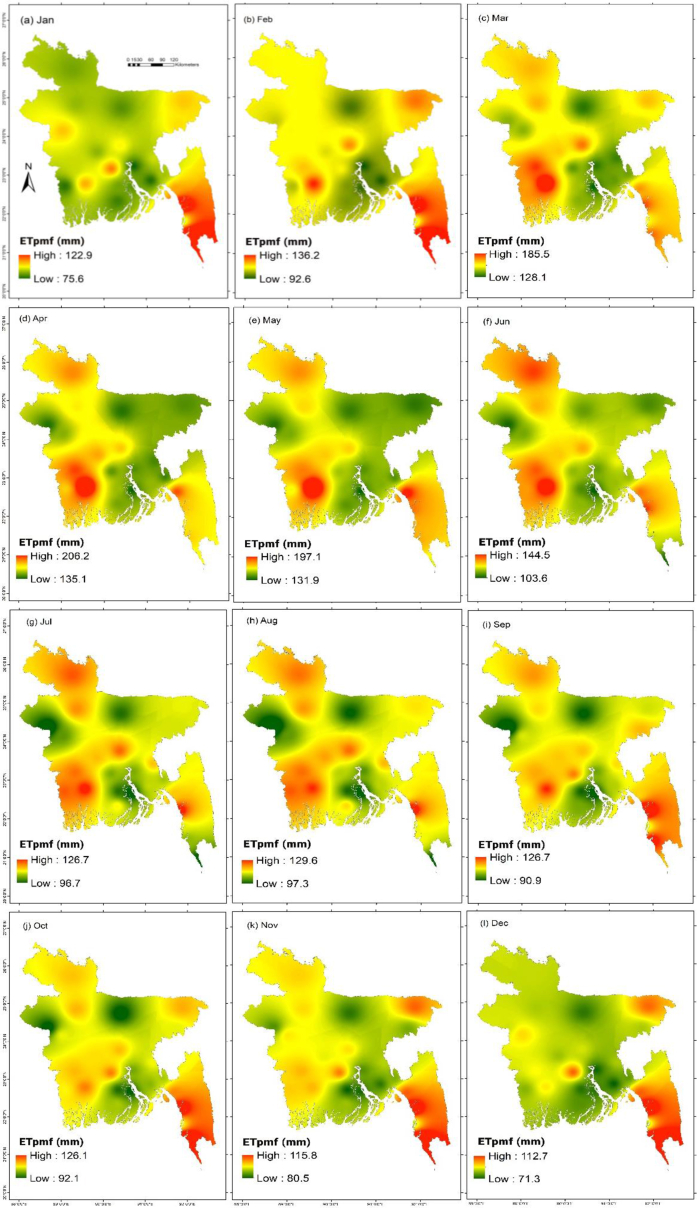
According to the boxplot result, the ETpmf rose primarily and reduced later on a monthly period, by the uppermost value in April and the lowermost value in December (Figure 2). In the meantime, the ETpmf also discovered significant variances in March, April, and May, which were particularly apparent in May, when the span of ETpmf was 4.0–5.8 mm. The spatial distribution of the ETpmf exhibited a parallel inclination of temporal distribution in Bangladesh (Figure 3). In the first six months (January–June), the peak-value province of the ETpmf moved from southeast to northwest and southwest portions of Bangladesh, mostly indicating a progressively growing trend from south to north and south to west. On the other hand, the lowest value region of ETpmf shifted from northwest and middle to northeast and southeast regions. However, more down to middle range value of ETpmf existed maximum period in the central and northern parts, particularly the northeastern part of Bangladesh. From July to December, the highest value of ETpmf shifted back from the northwestern and southwestern parts to the southeastern part and northeastern part, in particular the Sylhet region. Sylhet region belongs to the middle to high range value of ETpmf in November and December. The highest and lowest difference value of ETpmf happened in April (71.1 mm) and July (30 mm), respectively.
Figure 2.
Box plot of the monthly ETpmf in the Bangladesh.
Figure 3.
Spatial distribution of monthly ETpmf in the Bangladesh during 1981–2018. Note: Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, and Dec are the abbreviations of January, February, March, May, June, July, August, September, October, November, and December, respectively. (a–l) represent the ETpmf from January to December respectively.
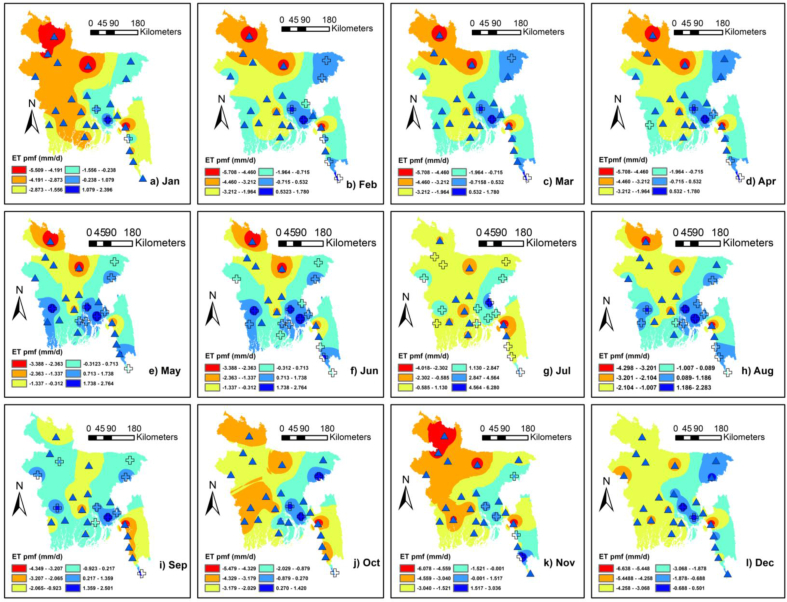
The M.K. test and Sen's slope estimator had been adopted for getting a better realization of the monthly basis of ETpmf trends in Bangladesh. On a sequential scale, January, February, March, April, May, August, September, October, November, and December months presented decreasing trends of ETpmf having the values of -0.013, -0.008, -0.018, -0.020, -0.009, -0.017, -0.003, -0.013, -0.012 and -0.016, respectively (Table 3 and Figure 4). Nevertheless, ETpmf displayed increasing trends in June and July month. The values of June and July were 0.014 and 0.013, respectively. The magnitude of directions of the ETpmf was higher in April based on spatial scale, and this result was similar to the outcomes of Figure 2. In the first six months duration (from January to June), the highest decreasing trend of ETpmf existed in the northwestern part, north-middle part (specifically Dhaka division), and a small part of Chittagong hilly region (mainly from January to April). Simultaneously, the slightly growing trend of ETpmf (from February to May) has existed in the southwestern part of the country, more specifically the Sylhet division (Figure 4). Like the first six months duration, northwestern part (except August and November) and middle part, i.e., Dhaka division (except November) of the country, did not show the highest decreasing trend of ETpmf in last six months duration (from July to December). A small part of the Chittagong hilly area showed the highest decreasing trend over the previous six months (July–December). For the last six months, some parts of the Comilla division (July–December) and Sylhet division showed a slightly increasing trend of ETpmf (July–November) in Bangladesh. Besides, Coxsbazar station also showed a slightly increasing trend of ETpmf in the last six months. Here it is mentionable that for the first six months (from January to June) duration, a majority decreasing trend is being shown in the first five months. Out of 25 stations, 22 stations in January, 17 stations in February, 21 stations in March, 19 stations in April, and 16 stations in May showed a decreasing trend of ETPMF. Still, the exception is happened not only in June but also sequentially in July month. Among 25 observatories, 15 observatories exposed a rising trend of ETpmf in both June and July month. August month showed almost neutral conditions, i.e., 13 (52%) stations and 12 stations (48%) showed a decreasing and increasing trend. For the case of the last four months, September (15 stations, 60%), October (21 stations, 84%), November (20 stations, 80%), and December (23 stations, 92%) presented the prevalence of decreasing trend of ETpmf.
Table 3.
Temporal trends of the ETpmf on a monthly time scale during 1981–2018 in Bangladesh.
| Parameters | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β | -0.013∗ | -0.008 | -0.018 | -0.020 | -0.009 | 0.014 | 0.013 | -0.017 | -0.003 | -0.013∗ | -0.012∗ | -0.016∗∗ |
| Z | -2.520 | -1.198 | -1.735 | -1.751 | -0.891 | 0.193 | 0.589 | -0.562 | -0.657 | -2.393 | -2.304 | -3.054 |
Note: ∗ and ∗∗ denote the significance levels of 0.05 and 0.01, respectively. β is the estimated slope trend of the ETpmf, and β > 0 and β < 0 signify an upward and a downward trend, respectively. Z is the Mann–Kendall test statistic. Note: Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, and Dec are the abbreviations of January, February, March, May, June, July, August, September, October, November, and December, respectively.
Figure 4.
Spatial distribution of monthly ETpmf trends in Bangladesh during 1981–2018. Note: Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, and Dec are the abbreviations of January, February, March, May, June, July, August, September, October, November, and December, respectively. The solid rhombus and cross-shaped signs represent the decreasing and increasing trends. (a–l) represent the trends of ETpmf from January to December, respectively.
3.2. Performance evaluation of the 15 empirical models in Bangladesh
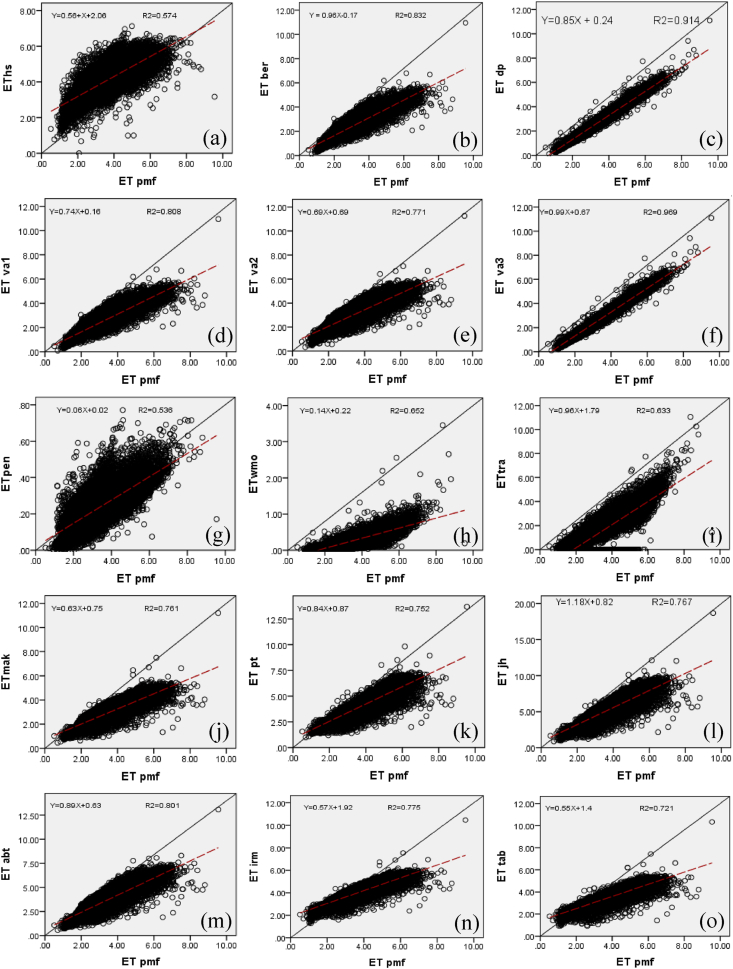
The scatter plots of ET0 valued by the ETpmf model and 15 ETemp models for the research area are delineated in Figure 5. Six radiation-based (mak, pt, jh, abt, irm, and tab), four combined (dp, va1, va2, and va3), and one temperature-based model (ber) have better performances with all the scatter of the ETemp dispersed the 1:1 line laterally and having the values of determination coefficients (R2) at more than 0.7 (Figure 5). So, these models have a strong linear relationship with the ETpmf model. The rest of the other models, i.e., the hs (temperature-based) and pen, wmo, and tra (mass transferred-based), has the value of R2 less than 0.7, i.e., 0.574, 0.536, 0.652, and 0.633, respectively. For that, they have a moderate linear relationship with the ETpmf model (Rumsey, 2016). Thus, the performance of these four models was not so acceptable.
Figure 5.
Comparisons of monthly ETpmf and ETemp by scatter plots. The red dashed line indicates the linear fit of the scatters. Here (a), (b), (c), (d), (e), (f), (g), (h), (i), (j), (k), (l), (m), (n) and (o) represent the comparison of EThs, ETber, ETdp, ETva1, ETva2, ETva3,ETpen, ETwmo, ETtra, ETmak, ETpt, ETjh, ETabt, ETirm and ETtab model, respectively with ETpmf model.
The numerical analysis of RRMSE, MAE, and NS is shown in Table 4 to improve every empirical model. The temperature-based hs and ber model showed moderate performance by the RRMSE, MAE, and N.S. values of 0.577 and 0.611, 0.474 and 0.489, and 0.655 and 0.623, respectively. The performance of three mass transfer-based models was in the following order: tra > wmo > pen. According to the values of RRMSE, MAE, and NS, these three models were not matched to be appropriate substitutes. Specifically, the pen model displayed bad performances with huge inaccuracies (as it belonged the RRMSE, MAE, and NS values of 1.142, 1.035, and -1.041, respectively), and things finding was supported by Li et al. (2018b). In Iran Tabari et al. (2013) assessed ten mass transfer-based models and concluded that some of them exhibited unsatisfactory performance underestimating the results. Among the combined models, the sequence of the performances was as follows: dp > va3 > va1 > va2. Valiantzas (2013a, 2013b) suggested the va1, va2, and va3 models, which were comparatively not old, but they presented the poorest performance (underestimated ETpmf with huge errors) than the other methods in Bangladesh. Consider the performance of va2 model as an example, the RRMSE, MAE, and NS values were 1.484, 1.472, and -3.109, respectively. The worst performances of these combined models have similarities to the results of Peng et al. (2017) and dissimilarities to Li et al. (2018b) in China. Between the radiation-based models, the two models abt and irm have good performance, by showing the values of the RRMSE, MAE, and NS of 0.298 and 0.469, 0.184 and 0.347, and 0.903 and 0.701, respectively. The total performances were in following sequences: abt > irm > mak > tab > pt > jh. The unsatisfied performance of model jh has matched the findings of Ahooghalandari et al. (2016) in Australia, Trajkovic and Kolakovic (2009) in Serbia, and Irmark et al., (2003) in Florida, USA. Based on the abovementioned findings, the temperature-based ETabt model will be the greatest alternate model in the absence of the ETpmf model to evaluate the ET0 properly on a diurnal period in Bangladesh. Irmak et al. (2006) showed that the radiation-based models' performances in humid conditions were better because of the solar radiation's crucial activity (Rs) in ET0 calculation.
Table 4.
Numerical analysis of the 15 empirical models against the PMF-56 model for assessing daily reference evapotranspiration in the Bangladesh from 1981 to 2018.
| EThs | ETber | ETpen | ETwmo | ETtra | ETmak | ETpt | ETjh | ETabt | ETirm | ETtab | ETdp | ETva1 | ETva2 | ETva3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RRMSE | 0.577 | 0.611 | 1.142 | 1.115 | 0.942 | 0.652 | 0.881 | 0.924 | 0.298 | 0.469 | 0.714 | 0.901 | 1.355 | 1.484 | 0.951 |
| MAE | 0.474 | 0.489 | 1.035 | 1.020 | 0.847 | 0.452 | 0.758 | 0.808 | 0.184 | 0.347 | 0.580 | 0.803 | 1.350 | 1.472 | 0.914 |
| NS | 0.655 | 0.623 | -1.041 | -1.012 | -0.976 | 0.040 | -0.797 | -0.938 | 0.903 | 0.701 | -0.151 | 0.114 | -9.765 | -3.109 | -0.991 |
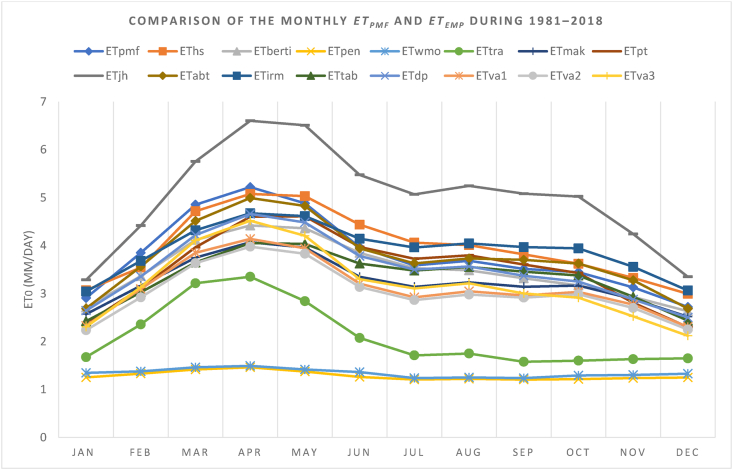
3.3. Comparability between the monthly status of ETemp and ETpmf
In this study, the estimated monthly values of 15 ETemp models are compared against the estimated monthly values of the ETpmf model (Figure 6). Overall, the performances of radiation-based models (particularly abt, irm, and pt) and temperature-based models (hs and ber) were better than the other models. Among these five models, best performances followed the order of abt > irm > hs > pt > ber. According to presentations of 15 ETemp models, it is remarkable that these best three abt, irm, and hs models individually were all-time in the first three positions (whether first/second/third position) for twelve months (from January to December). The performance of the rest of the three radiation-based models (sequentially tab>mak>jh) was not so satisfactory but even then, better than the performance of three mass transfer-based models (pen, wmo, and tra) and three combined models va1, va2 and va3 (except model dp). Among three models (tab, mak and jh), considering jh model as for instances, it overrated the ET0 in 12 months, but it vastly overestimated the ET0 from April to October. Similarly, Jensen et al. (1990), Tabari et al. (2013), and Tegos et al. (2015) published that the jh model inclines for overrating ET0 in moist weather states. Again, three mass transfer-based models (pen, wmo, and tra) exhibited poor performance by underestimating the ET0 notably in 12 months. This finding was supported by the outcomes of Tabari et al. (2013) in Iran. Combined models va1, va2, and va3 (except dp) also exhibited their average performance by undervaluing the ET0 significantly in 12 months.
Figure 6.
Comparison of the monthly ETpmf and ETemp in Bangladesh during 1981–2018.
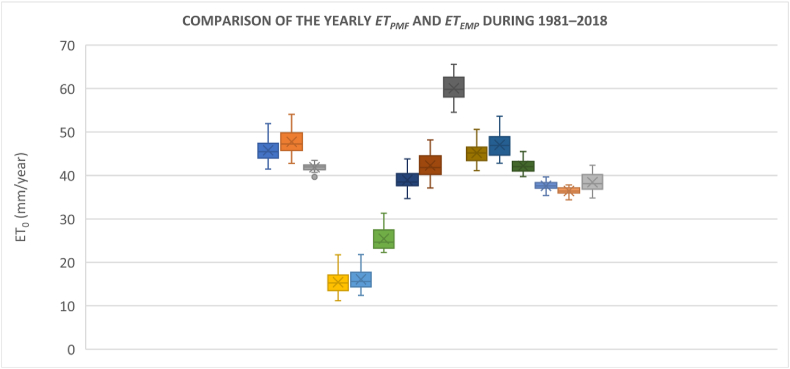
3.4. Annual status of the yearly ETpmf and ETemp
In this study, a comparison between 15 ETemp and ETpmf models with their maximum, median and minimum values on annual scales is exhibited in Figure 7. For example, the average highest, median, and lowest annual values of ETpmf are 51.94 mm, 45.77 mm, and 41.49 mm, respectively. Like monthly scale (Figure 6), the performances of three radiation-based models (abt, irm, and pt) and two temperature-based models (hs and ber) were also better than the other models on annual scales. Their performance sequences were also the same: abt > irm > hs > pt > ber (Figure 7). Besides, three mass transfer-based models, pen, wmo, and tra, and three combined models va1, va2, and va3 (except model dp), exhibited their comparatively weak performances than radiation-based and temperature-based models by underestimating the ETpmf on annual scales.
Figure 7.
Box plot of annual ETpmf and ETemp models in Bangladesh over 1981–2018.
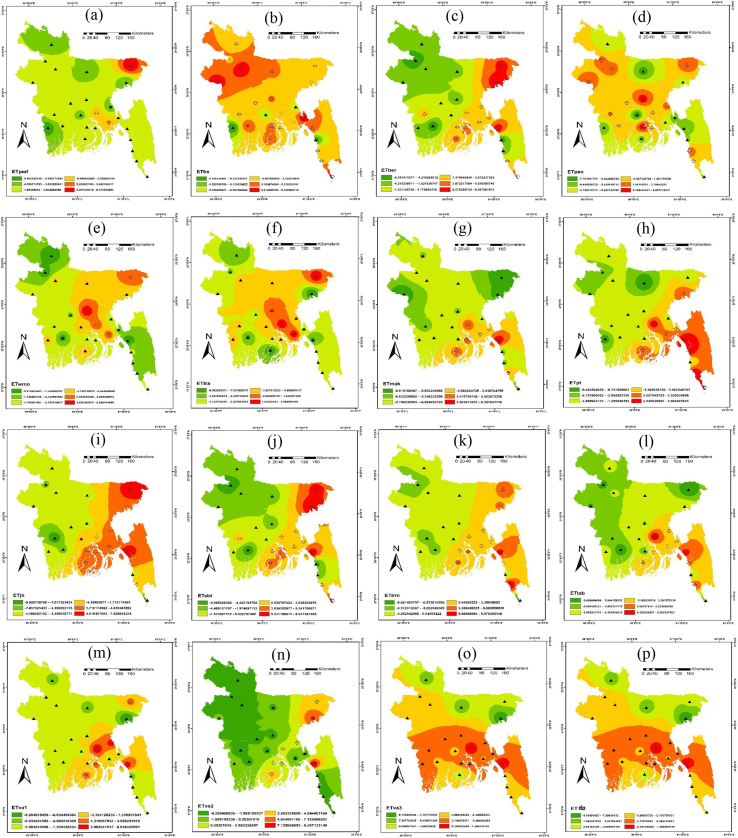
3.5. Spatial distribution of ETpmf and ETemp trends
The spatial distribution of ETpmf and ETemp trends were showed in Figure 8. Among fifteen ETemp models, eleven models (except hs, ber, jh, and pen) with ETpmf displayed the negative trend (Table 5). The hs, ber, jh, and pen models presented the positive direction of ET0 in Bangladesh. In the case of the overall distribution of the ETpmf model, opposing trends were exhibited in most parts (22 stations) except in Sylhet and some parts of the Comilla division, i.e., Chandpur Noakhali, as these three stations exhibited the positive trend of ET0. Besides, consider model H.S. for example, most parts of the country (21 stations) revealed the positive trends of ET0 except Comilla, Chittagong, Madaripur, and Satkhira; these four stations showed the negative direction of ET0.
Figure 8.
Spatial distribution of ETpmf and ETemp with their trends in Bangladesh over 1981–2018. Here (a), (b), (c), (d), (e), (f), (g), (h), (i), (j), (k), (l), (m), (n), (o) and (p) represent the models of ETpmf, EThs, ETber, ETpen, ETwmo, ETtra, ETmak, ETpt, ETjh, ETabt, ETirm, ETtab, ETva1, ETva2, ETva3 and ETdp, respectively.
Table 5.
β and Z values for Spatial distribution of ETpmf and ETemp with their trends in Bangladesh over 1981–2018.
| Parameters | ETpmf | EThs | ETber | ETpen | ETwmo | ETtra | ETmak | ETpt | ETjh | ETabt | ETirm | ETtab | ETdp | ETva1 | ETva2 | ETva3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β | -3.7052∗∗ | 3.1224∗ | 0.9132 | 1.148 | -1.8832∗∗∗ | -2.5172∗∗∗ | -2.462∗ | -1.2648 | 0.1488 | -0.1 | -0.1968 | -0.8584 | -3.866∗∗ | -2.7228 | -2.3532 | -4.1548∗∗ |
| Z | -2.6824 | 2.368 | 0.6208 | -0.522 | -3.2432 | -3.318 | -2.1568 | -0.5172 | -0.2504 | 0.1512 | -0.0004 | -1.3744 | -2.7156 | -1.5 | -0.4904 | -2.7164 |
Note: ∗, ∗∗, and ∗∗∗ denote the significance levels of 0.05, 0.01, and 0.001, respectively. β is the estimated slope trend of the ETpmf and ETemp, and β > 0 and β < 0 signify an upward and a downward trend, respectively. Z is the Mann–Kendall test statistic.
3.6. Calibration of empirical models
The 15 empirical models were justified (calibrated) by the climatic parameters from 1981 to 2005 using the linear regression method among the ETpmf and the ETemp in this research work. According to Table 6, we can observe that the determination coefficient (R2) of all the empirical models increased firstly for the first four months (January–April) of the year and then decreased from May to July. Remarkably all the models increased in August comparing to July. Then the values of R2 reduced sequentially from September to December for temperature and radiation-based models and increased sequentially (opposite of temperature and radiation-based models) from September to December for mass transfer-based models. The combined models exhibited the values of R2 in the following order: August > September < October < November > December. Eight ETemp models, i.e., six Radiation-based (mak, pt, jh, abt, irm, and tab) and one temperature-based (ber) and one combined (dp) model, displayed better performances than other models for twelve months (January–December). They have the highest values of the determination coefficient (R2 > 0.8). The radiation-based ETabt model showed the most nuanced performance, and the highest and lowest R2 value for ETabt was 0.913 and 0.856 in April and December, respectively. The highest and lowest R2 values for the temperature-based (ber) model and combined (dp) models were 0.890 and 0.912 and 0.805 and 0.855 in April and December. The rest three combined models va1, va2, and va3 presented comparatively below standard performances. ETva2 showed the worst performance with the values of R2 at less than 0.7 in all the months except in April (R2 = 0.701). Among the three mass transfer-based models, top performances were shown in the following orders: ETtra > ETwmo > ETpen. The highest and lowest value of R2 for ETtra was 0.827 and 0.741 in April and September, respectively. Remarkably, one mass transferred based model (tra) and one temperature-based model (hs) have up to the mark values of the determination coefficients (R2 > 0.75) for eight months (January–August) and Six months (January–June), respectively. Besides the eight models mentioned above (which are best for twelve months), these tra and hs models could be acknowledged as replacements to calculate the ET0 during these respective months. However, the performances of the other models in other months were not so satisfactory. Climatic parameters have significant influences on ET0 formation. According to Khan et al. (2019), the monthly average wind speed (W.S.) and temperature (T) (with maximum temperature, Tmax) showed their highest dominancy from March to October, i.e., in pre-monsoon and monsoon time. The average monthly minimum temperature (Tmin) was dominant in monsoon time (June–September) in Bangladesh. T, Tmax, and Tmin showed their lowest amount in December and January, whereas the lowest W.S. was estimated from November to January. Like precipitation, relative humidity (R.H.) showed its peak amount from June to September, and the smallest amount of R.H. existed in February, March, and April month. Similar findings are supported by Banglapedia (2014), Das et al. (2005), Shahid (2010), and Rahman and Lateh (2015). Day length variation regulates the arriving solar radiation (Rs), which plays an active part in ET0 development. The maximum amount of Rs was considered from April to August and a minimum from December to January (Rahman, 2013; Turzo et al., 2015). T, Rs and W.S., and R.H. are strong positively and negatively correlated with ET0, respectively, Rahman and Lateh (2015). Interestingly the discoveries from our study support the abovementioned findings from different related tasks from Bangladesh's perspective. For example, the highest amount of ET0 for all temperature-based and radiation-based models existed from March to June. The lowest ET0 occurred in December and January since temperature and solar radiation are positively correlated with ET0. So, Temperature and Rs performed as one of the most influencing factors for the above-described models. Combined model dp exceptionally got the same performance type like temperature and radiation-based models. The combined model dp is correlated with Rs. In contrast, the three mass transfer-based models (pen, wmo, and tra) got the maximum and minimum amount of ET0 in March, April, May and June, and in July, August and September, respectively compared to other empirical models since W.S. (positively), and R.H. (negatively) are dominantly associated with the three mass transfer-based models in these respective months.
Table 6.
The fitted a, b and R2 values for correlating ETemp with ETpmf in monthly time scale over 1981–2005.
| Month | Parameters | ETmak | ETpt | ETjh | ETabt | ETirm | ETtab | ETber | EThs | ETpen | ETwmo | ETtra | ETva1 | ETva2 | ETva3 | ETdp |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| January | a b R2 |
-2.37 2.31 .818 |
-2.06 2.12 .831 |
-.213 .960 .836 |
.086 1.07 .871 |
-1.65 1.52 .853 |
-1.61 1.89 .815 |
-1.47 1.63 .838 |
-1.7 1.52 .751 |
2.16 3.37 .706 |
2.03 5.39 .714 |
1.91 .821 .762 |
.056 1.19 .656 |
-.107 1.32 .651 |
.328 1.07 .659 |
-1.04 1.48 .870 |
| February | a b R2 |
.023 1.36 .823 |
.172 1.22 .842 |
.868 .703 .847 |
1.00 .827 .877 |
-1.05 1.36 .874 |
-.640 1.52 .826 |
-1.67 1.61 .851 |
-.60 1.19 .760 |
1.62 6.94 .706 |
2.00 5.46 .723 |
1.88 .834 .776 |
-.271 1.32 .667 |
.687 1.08 .657 |
-.060 1.21 .672 |
-1.27 1.52 .882 |
| March | a b R2 |
-2.63 2.18 .836 |
-2.54 1.90 .853 |
-1.09 1.08 .860 |
-.564 1.23 .889 |
-4.66 2.23 .880 |
-4.10 2.49 .849 |
-1.92 1.67 .865 |
-1.6 1.4 .769 |
2.11 6.87 .712 |
2.69 4.67 .738 |
2.45 .751 .801 |
-1.28 1.59 .680 |
-1.01 .1.61 .671 |
-.327 1.23 .688 |
-1.92 1.60 .899 |
| April | a b R2 |
-1.20 1.71 .851 |
.194 1.12 .884 |
.250 .779 .875 |
.013 1.06 .913 |
-3.38 1.86 .901 |
-2.63 1.97 .879 |
-1.77 1.60 .890 |
-2.0 1.46 .778 |
2.39 7.39 .719 |
3.50 3.53 .750 |
3.11 .635 .827 |
-1.47 1.61 .709 |
-.348 1.40 .701 |
.026 1.11 .716 |
-2.09 1.56 .912 |
| May | a b R2 |
-.293 1.41 .850 |
-1.13 1.31 .849 |
-.057 .773 .873 |
.486 .945 .895 |
-2.77 1.67 .877 |
-2.44 1.82 .873 |
-1.80 1.55 .868 |
-1.9 1.36 .763 |
2.21 8.00 .714 |
3.05 3.33 .721 |
2.42 .859 .804 |
.461 1.11 .706 |
.169 1.22 .696 |
.256 1.05 .712 |
-1.23 1.35 .887 |
| June | a b R2 |
-.390 1.43 .847 |
-.915 1.24 .848 |
-.541 .834 .868 |
-.109 1.06 .876 |
-2.90 1.67 .875 |
-2.68 1.85 .869 |
-.550 1.19 .854 |
-.68 1.06 .752 |
1.61 9.55 .701 |
2.24 5.52 .712 |
1.83 1.00 .782 |
.091 1.19 .692 |
113 1.21 .683 |
.406 .983 .700 |
-.553 1.19 .876 |
| July | a b R2 |
-.032 1.25 .842 |
-.563 1.12 .837 |
-.071 .733 .861 |
.185 .957 .869 |
-2.38 1.52 868 |
-1.82 1.57 .860 |
-.938 1.29 .821 |
-1.38 1.23 .721 |
1.20 11.67 .681 |
2.13 5.60 .702 |
1.63 1.11 .758 |
.329 1.10 .662 |
.143 1.19 .654 |
.507 .933 .671 |
-.474 1.16 .867 |
| August | a b R2 |
.217 1.18 .858 |
-.414 1.08 .865 |
-.296 .105 .879 |
.342 .906 .886 |
-2.05 1.42 .879 |
-1.49 1.46 .872 |
-.087 1.10 .837 |
-.43 .104 .743 |
1.22 11.35 .689 |
2.14 5.97 .716 |
1.62 1.15 .761 |
.383 1.07 .671 |
.357 1.10 .662 |
.514 .947 .679 |
-.352 1.13 .885 |
| September | a b R2 |
.141 1.16 .848 |
-.479 1.10 .862 |
.070 .676 .871 |
.465 .832 .879 |
-1.85 1.35 .868 |
-1.49 1.44 .862 |
-.202 1.12 .829 |
.390 1.03 .737 |
1.44 .918 .685 |
2.06 6.07 .688 |
1.73 1.06 .737 |
.502 .984 .679 |
.409 1.03 .668 |
.623 .911 .684 |
-.237 1.10 .861 |
| October | a b R2 |
-.072 1.22 .838 |
-.925 1.23 .843 |
-.327 .761 .863 |
.098 .911 .871 |
-2.44 1.50 .869 |
-2.16 1.66 .852 |
-1.55 1.60 .821 |
-1.7 1.44 .732 |
1.78 6.88 .691 |
2.02 6.26 .701 |
1.85 1.00 .741 |
.436 .971 .685 |
.080 .1.10 .678 |
.341 1.02 .691 |
-.669 1.26 .868 |
| November | a b R2 |
1.28 .727 .828 |
1.92 .452 .823 |
1.59 .393 .850 |
1.62 .480 .864 |
.459 .767 .855 |
1.07 .722 .818 |
-.403 1.23 .816 |
-.08 .992 .728 |
1.28 6.97 .700 |
2.12 4.27 .706 |
2.14 .605 .745 |
.381 .974 .691 |
1.28 .686 .682 |
.167 1.09 .698 |
-.995 1.43 .874 |
| December | a b R2 |
1.84 .431 .813 |
2.31 .226 .814 |
2.29 .161 .829 |
2.22 .223 .856 |
1.65 .381 .846 |
2.05 .319 .810 |
-.447 .895 .805 |
-.66 .724 .723 |
1.20 6.30 .704 |
1.78 4.52 .712 |
1.77 .656 .749 |
.831 .810 .687 |
1.87 .405 .667 |
.329 1.05 .691 |
-.997 1.47 .855 |
3.7. Validation of empirical models
In the present research work, to validate the calibrated empirical models, the meteorological datasets from 2006 to 2018 were applied. The radar charts of Figures 9, 10, and 11 show the RRMSE, MAE and NS values among the original and the calibrated reference evapotranspiration employing 15 empirical models in the study area. Subsequently, the modification, the RRMSE, and MAE values are closer to 0 and the NS values are nearer to 1. Additionally, the RRMSE, MAE, and NS values became smaller and inclined to be steady. After the calibration, every model's performance every month has been upgraded deliberately related to actual performance. In RRMSE, combined models' overall performance (especially va1, va2, and va3) is relatively finer aside from other models (Figure 9). After that, the mass transfer-based ETpen model and temperature-based ETber model showed better results. From December to May, among the combined models except for ETdp, top performances were shown in the following orders: ETva2 > ETva1 > ETva3. Then from June to November, combined models showed the values of RRMSE in the following order: ETva2 > ETva3 > ETva1. The performance of next best ETpen model were as follows: ETva3 < ETpen < ETva1< ETva2 for four months (February to May) and ETva1 < ETpen < ETva3 < ETva2 for four months (June to September) and ETpen < ETva3 < ETva1 < ETva2 for rest four months (October to January). The next best temperature-based ETber model followed by the radiation-based ETabt model showed improved results after the above described four models for twelve months. In MAE, mass transfer-based models' total performance is comparatively better than other models for the entire year (Figure 10). The highest performances were displayed in the following orders: ETpen > ETwmo > ETtra. The combined models presented better performances after mass transfer-based models. Unlike RRMESE, combined models dp was ahead of va1, va2, and va3. These combined models showed the consequences in following order: ETdp > ETva2 > ETva1 > ETva3. The temperature-based ETber model and afterwards radiation-based ETabt model was just behind these four combined performance models from January to December. Parallel to MAE, the overall performance of mass transfer-based models (except ETtra) is comparatively better than other models for NS from January to December (Figure 11). Equivalent to MAE, combined models (excluding dp) were succeeding finest having performances in following order: ETva2 > ETva1 > ETva3. After these three combined models, the mass transfer-based ETtra model's performance and the radiation-based ETabt model were moderately better than the rest other models. Dissimilarly to RRMSE and MAE, the radiation-based ETjh model, presented few remarkable results in the case of NS. Though the performance of the ETjh model was minor than the performance of mass transfer-based models (va1, va2, and va3) during the first six months (January to June) but the performance was healthier than these models for the last six months (July to December) of the year. It is mentionable that the temperature-based EThs model accomplishes quite less perfection than other models in the case of RRMSE, MAE, and NS. As stated in Table 6, three combined models (va1, va2, and va3) displayed comparatively lowermost performances than other models. Significant improvement was usually carried out during the validation period by these three models since they could improve their performance. Like combined models, three mass transfer-based models (pen, wmo and tra) attained good improvement in the validation period. The overall perfection carried out by the previously best-performed ETabt model throughout the validation period was not so unsatisfying. It already achieved fewer error results and better sufficiency compared to other models.
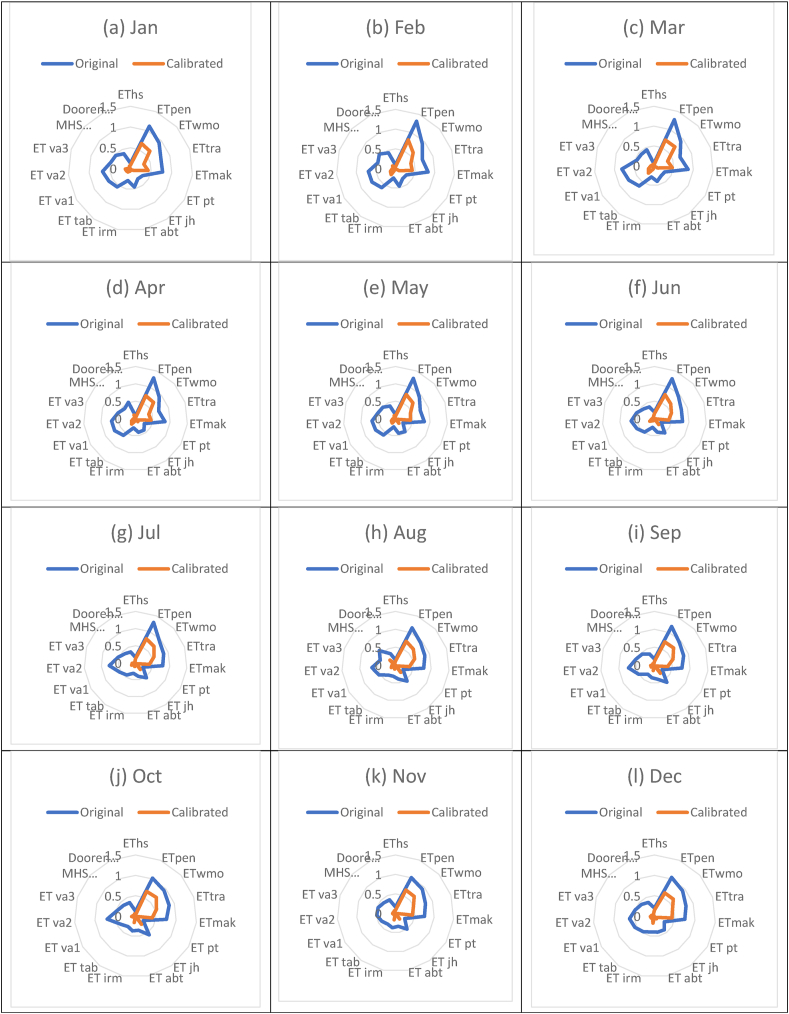
Figure 9.
Radar charts showing the comparison of the RRMSE values between the original reference evapotranspiration and the calibrated reference evapotranspiration using the 15 empirical models in Bangladesh from 2006 to 2018. (a–l) represent the months from Jan to Dec, respectively. Note: Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, and Dec are the abbreviations of January, February, March, May, June, July, August, September, October, November, and December, respectively.
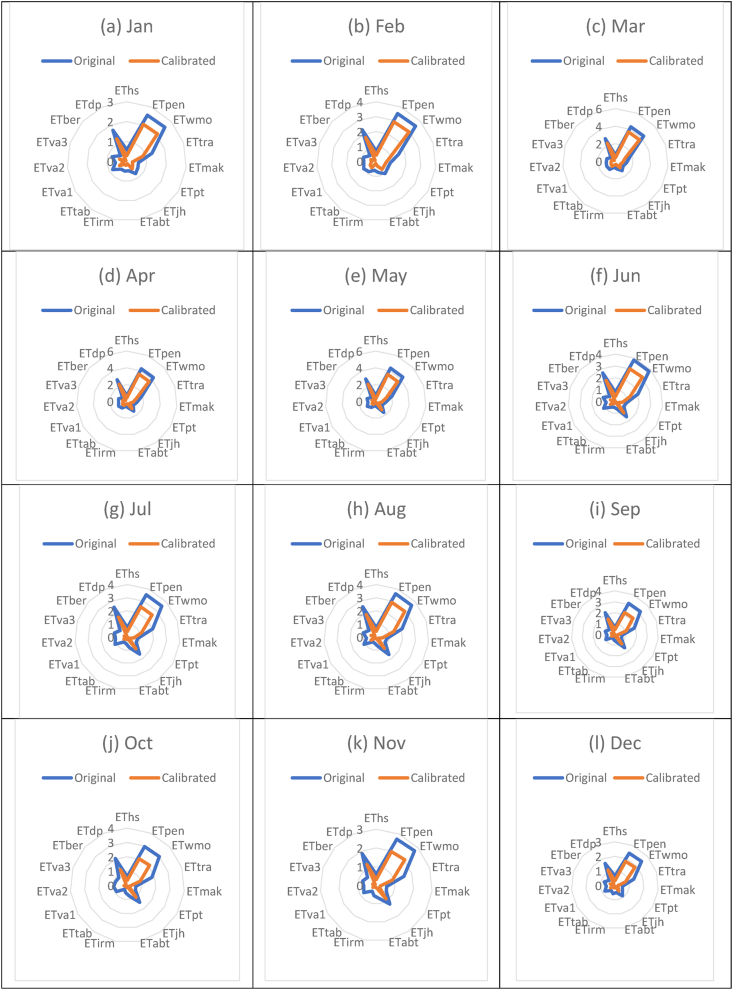
Figure 10.
Radar charts showing the comparison of the MAE values between the original reference evapotranspiration and the calibrated reference evapotranspiration using the 15 empirical models in Bangladesh from 2006 to 2018. (a–l) represent the months from Jan to Dec, respectively. Note: Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, and Dec are the abbreviations of January, February, March, May, June, July, August, September, October, November, and December, respectively.
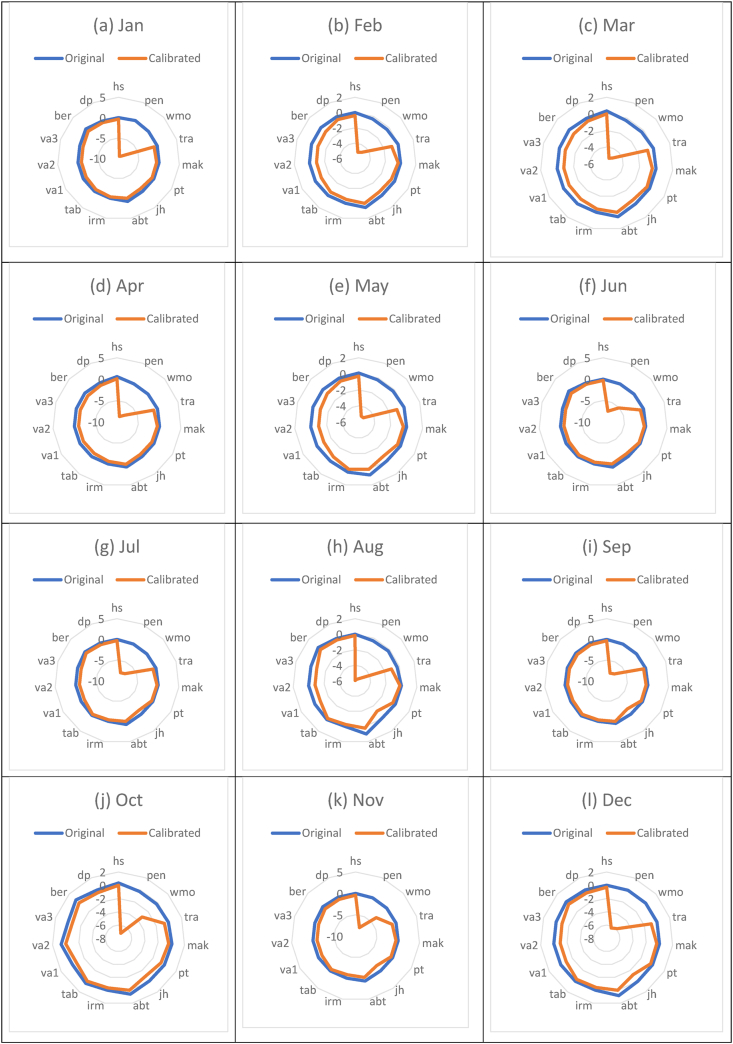
Figure 11.
Radar charts showing the comparison of the NS values between the original reference evapotranspiration and the calibrated reference evapotranspiration using the 15 empirical models in Bangladesh from 2006 to 2018. (a–l) represent the months from Jan to Dec, respectively. Note: Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, and Dec are the abbreviations of January, February, March, May, June, July, August, September, October, November, and December, respectively.
Based on the above discussion, it can be concluded after all performances (including calibration and validation) that the most pleasing performance belongs to the radiation-based ETabt model. It could be the best alternative model instead of ETpmf over the other empirical models. Moreover, the abt model had a satisfactory accuracy. Complete meteorological datasets are not compulsory for abt model's simple estimation formula since only Rs and Tmax data are needed to compute this abt model. However, except ETabt model, the radiation-based ETirm model and temperature-based ETber model can be suggested as alternatives to the ETpmf model to calculate ET0 in Bangladesh.
4. Conclusions
Based on the complete set of quotidian climatic information throughout 1981–2018 gathered from 25 weather observatories of Bangladesh, the present research work's goals are to recognize the spatiotemporal trends of the ETpmf on a monthly period and associating the performances of 15 ETemp models with the ETpmf model. The key findings are compiled below:
The ETpmf increased primarily and declined later on a monthly period having the topmost amount in April and the lowermost amount in January. The ETpmf displayed increasing tendencies in June and July but demonstrated decreasing trends in the rest of ten months. Before the modification, on a daily timescale in the scatter plot, the three combined (dp, va3, and va1), one radiation-based (abt), and one temperature-based (ber) models had been a better performer as alternative model comparing to the other models for ET0 estimation. The pen, wmo, tra and hs models became unworthy for being proper substitutes, as their poor performances were shown by daily scatter plot. After that, the three combined models va1, va2, and va3 (except dp) had worse performance than other models according to the values of RRMSE, MAE, and NS. RRMSE, MAE, and NS values for va3 (better than va1 and va2) were 0.942, 0.914, and -0.976, respectively. Consistent with performance, three mass transfer-based models (sequentially tra > wmo > pen) had not been suited to be proper substitutes, in particular the pen model (the values of the RRMSE, MAE, and NS for pen were 1.142, 1.035, and -1.041, respectively). The temperature-based hs and ber model exhibited moderate performance, with the RRMSE, MAE and NS were 0.577 and 0.611, 0.474 and 0.489, and 0.655 and 0.623, respectively. The sequence of comprehensive performances of the radiation-based models was as follows: abt > irm > mak > tab > pt > jh. Eventually, the best performance was exhibited by abt followed by IRM since their RRMSE, MAE, and NS results were satisfactory, having the values of 0.298 and 0.469, 0.184 and 0.347, and 0.903 and 0.701, respectively.
According to the comparison of the monthly ETemp and ETpmf on a monthly time scale, comparatively, the performances of radiation-based models (particularly abt, irm, and pt) and temperature-based models (hs and ber) were better than the other models. Among these five models, best performances followed the order of abt > irm > hs > pt > ber. According to the results of 15 ETemp models, it is remarkable that these best three abt, irm, and hs models individually were all-time in the first three positions (whether first/second/third position) for twelve months (from January to December). Similar to the monthly scale, the performances of three radiation-based (abt, irm, and pt) and two temperature-based (hs and ber) models were also better than the other models with the same sequence of abt > irm > hs > pt > ber on annual scales. Three mass transfer-based (pen, wmo, and tra) and combined (va1, va2 and va3) models (except dp) exhibited their poor and average performances, respectively, by underestimating the ETpmf on annual scales. From the figure of the spatial distribution of the ETpmf and ETemp with their trends in Bangladesh, it was observed that the negative trends had been displayed by the ETpmf model and eleven ETemp models (except hs, ber, jh, and pen). Since the hs, ber, jh and pen models presented the positive trend of ET0 in Bangladesh.
After calibration, the values of R2 of all models displayed variation of trends that raised firstly from January to April and then decreased from May to July month. Remarkably all models increased in August comparing to July. Then for September to December, the values of R2 were reduced sequentially from September to December for all temperature and radiation-based models and increased sequentially from September to December for all mass transferred based models and combined va1, va2 and va3 models (September–November). The high R2 values (approximately) of all the models mainly existed between March and August except va1, va2 and va3 combined models. Combined models (except dp) presented the relatedly subpar performances according to the values of R2. For example, the highest and lowest value of R2 for ETva2 is 0.701 and 0.651 in April and January, respectively. Radiation-based six methods (mak, pt, jh, abt, irm, and tab) showed best performances by delivering the highest points of determination coefficient (R2), i.e., the values of R2 at more than 0.8 in all the months (January–December) than other models of the year. For instance, among these six models, the most acceptable performance is shown by the ETabt model, which belongs to the highest and lowest R2 values of .913 and .856 in April and December, respectively. Remarkably, one mass transferred-based (tra) and temperature-based (hs) model have the accepted values of the determination coefficients (R2 > 0.7) for Six months (January–June) and eight months (January–August), respectively. Remarkably, one mass transferred based model (tra) and one temperature-based model (hs) have up to the mark values of the determination coefficients (R2 > 0.75) for eight months (January–August) and Six months (January–June), respectively. However, the performances of the other models in other months were not so magnificent.
After validation, the RRMSE and MAE values are nearer to 0 and the NS values are closer to 1. Furthermore, the RRMSE, MAE, and NS values became lesser and inclined to be steady. After validation, every model's performance every month has been upgraded deliberately related to that of actual. The overall results in the case RRMSE, MAE, and NS, three mass transfer-based models (pen, wmo, and tra) and four combined models (particularly va1, va2, and va3) achieved more remarkable improvement apart from the rest other models. As stated in Table 6, three combined models (va1, va2, and va3) displayed comparatively lowermost performances than other models. Significant improvement was usually carried out during the validation period by these three models since they could improve their performance. Similar to combined models, three mass transfer-based models (pen, wmo and tra) attained good improvement in the validation period. It is mentionable that the temperature-based ETjh model accomplishes relatively more minor perfection than other models in the case of RRMSE, MAE, and NS. The overall embodiment carried out by the previously best-performed ETabt model throughout the validation period was not so unsatisfying. It already achieved fewer error results and better sufficiency compared to other models.
Finally, consistent with the 15 empirical models' overall judgment, the radiation-based abt model displayed the optimum performance than others even after calibration and validation. Notably, abt model had a satisfactory accuracy, and only solar radiation and highest temperature data are needed to compute this model. When the ETpmf method is not available, then the ETabt model will be the best substitute in Bangladesh. However, except ETabt model, the radiation-based ETirm and temperature-based ETber models can be suggested as alternate in the absence of the ETpmf model to calculate ET0 in Bangladesh. This research work's findings are vital contributors for the approximation of ETo in Bangladesh when huge necessities of data of climatic parameters might not be fulfilled completely. Attained results of this research work will direct the responsible authorities of water, agriculture, and other related sectors in Bangladesh and other provinces with the same climates. This research will help them make the agriculture and irrigation calendar strategy. The precise alternative model will give an exact and consistent evaluation of the ET0 when the complete climatic information will be inaccessible.
Declarations
Author contribution statement
Shakibul Islam: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
A.K.M. Rashidul Alam: Conceived and designed the experiments.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
The data that has been used is confidential.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- Abtew W. Evapotranspiration measurements and modeling for three wetland systems in South Florida. J. Am. Water Resour. Assoc. 1996;32:465–473. [Google Scholar]
- Ahooghalandari M., Khiadani M., Jahromi M.E. Developing equations for estimating reference evapotranspiration in Australia. Water Resour. Manag. 2016;30:3815–3828. [Google Scholar]
- Alexander L., Simon Bindoff N.L. Working group I contribution to the IPCC fifth assessment report climate change. Phys. Sci. Basis Summ. Policymak. 2013 [Google Scholar]
- Ali A. Vulnerability of Bangladesh to climate change and sea level rise through tropical cyclones and storm surges. Water Air Soil Pollut. 1996:92,171–179. [Google Scholar]
- Allen R.G., Pereira L.S., Raes D., Smith M. FAO; Rome: 1998. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; p. D05109. 300. [Google Scholar]
- Ayub R., Miah M.M. The Fourth Annual Paper Meet and 1st Civil Engineering congress, December, 2011, Dhaka. 2011. Effects of change in temperature on reference crop evapotranspiration (ETo) in the northwest region of Bangladesh; pp. 978–984. [Google Scholar]
- Banglapedia . 2014. National Encyclopedia of Bangladesh Climate. http://en.banglapedia.org/index.php?title¼Climate. [Google Scholar]
- Berti A., Tardivo G., Chiaudani A., Rech F., Borin M. Assessing reference evapotranspiration by the Hargreaves method in northeastern Italy. Agric. Water Manag. 2014;140:20–25. [Google Scholar]
- Blaney H., Criddle W. 1950. Determining Water Needs from Climatological Data. USDA Soil Conservation Service. SOS–T.P., USA; pp. 8–9. [Google Scholar]
- Chen F.W., Liu C.W. Estimation of the spatial rainfall distribution using inverse distance weighting (IDW) in the middle of Taiwan. Paddy Water Environ. 2012;10(3):209–222. [Google Scholar]
- Chu R., Li M., Shen S., Islam A.R.M.T., Cao W., Tao S., Gao P. Changes in reference evapotranspiration and its contributing factors in Jiangsu, a major economic and agricultural province of eastern China. Water. 2017;9:486. [Google Scholar]
- Climate Change Cell . 2008. Economic Modeling of Climate Change Adaptation Needs for Physical Infrastructures in Bangladesh Department of Environment, Ministry of Environment and Forests, Component 4b. Comprehensive Disaster Management Programme, Ministry of Food and Disaster Management, Bangladesh. [Google Scholar]
- Das G.A., Singh B.M., Albert X., Mark O. Water sector of Bangladesh in the context of integrated water resources management: a review. Int. J. Water Resour. Dev. 2005;21:385–398. [Google Scholar]
- Dinpashoh Y., Jhajharia D., FakheriFard A., Singh V.P., Kahya E. Trends in reference crop evapotranspiration over Iran. J. Hydrol. 2011;399:422–433. [Google Scholar]
- Doorenbos J., Pruitt W. 1977. Crop Water Requirements. FAO Irrig. Drain. Paper No. 24, Food and Agric. Organization, United Nations, Rome, Italy. [Google Scholar]
- Estévez J., Gavilán P., Berengena J. Sensitivity analysis of a Penman-Monteith type equation to estimate reference evapotranspiration in southern Spain. Hydrol. 2009;23:3342–3353. [Google Scholar]
- Feng Y., Jia Y., Cui N., Zhao L., Li C., Gong D. Calibration of Hargreaves model for reference evapotranspiration estimation in Sichuan basin of southwest China. Agric. Water Manag. 2017;181:1–9. [Google Scholar]
- Garcia M. Dynamics of reference evapotranspiration in the Bolivian highlands (Altiplano) Agric. For. Meteorol. 2004;125:67–82. [Google Scholar]
- Hargreaves G.H., Samani Z.A. Estimating potential evapotranspiration. J. Irrigat. Drain. Div. 1982;108:225–230. [Google Scholar]
- Hargreaves G.H., Samani Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985;1:96–99. [Google Scholar]
- IPCC . Climate change 2007: impacts, adaptation and vulnerability. In: Parry M.L., Canziani O.F., Palutikof J.P., van der Linden P.J., Hanson C.E., editors. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press; Cambridge: 2007. p. 976. [Google Scholar]
- Irmak S., Irmak A., Allen R.G., Jones J.W. Solar and net radiation-based equations to estimate reference evapotranspiration in humid climates. J. Irrigat. Drain. Eng. 2003;129:336–347. [Google Scholar]
- Irmak S., Payero J.O., Martin D.L., Irmak A., Howell T.A. Sensitivity analyses and sensitivity coefficients of standardized daily ASCE-Penman-Monteith Equation. J. Irrigat. Drain. Eng. 2006;132:564–578. [Google Scholar]
- Jensen M.E., Burman R.D., Allen R.G. 1990. Evapotranspiration and Irrigation Water Requirements: A Manual; ASCE Manuals and Reports on Engineering Practice, No. 70; ASCE: New York, NY, USA. [Google Scholar]
- Jensen M.E., Haise H.R. Estimating evapotranspiration from solar radiation. J.Irrig. Drain. Div. 1963;89:15–41. [Google Scholar]
- Jhajharia D., Dinpashoh Y., Kahya E., Singh V.P., Fakheri-Fard A. Trends in reference evapotranspiration in the humid region of northeast India. J. Hydrol. 2012;26:421–435. [Google Scholar]
- Karim M.F., Mimura N. Impacts of climate change and sea level rise on cyclonic storm surge floods in Bangladesh. Glob. Environ. Chang. 2008;18:490–500. [Google Scholar]
- Karim N.N., Talukder M.S.U., Hassan A.A., Khair M.A. Temporal trend of reference crop evapotranspiration due to changes of climate in North Central hydrological region of Bangladesh. J. Agric. Eng. 2008;34/A.E:91–100. [Google Scholar]
- Kendall M.G. 1975. Rank Correlation Methods; Griffin: London, UK. [Google Scholar]
- Khan M.H.R., Rahman A., Luo C., Kumar S., Islam G.M.A., Hossain M.A. Detection of changes and trends in climatic variables in Bangladesh during 1988-2017. Heliyon. 2019;5:e01268. doi: 10.1016/j.heliyon.2019.e01268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khatun M.A., Rashid M.B., Hygen H.O. 2016. Climate of Bangladesh. MET Report. Norwegian Meteorological Institute and Bangladesh Meteorological Department. ISSN: 2387–4201. [Google Scholar]
- Li M., Chu R., Islam A.R.M.T., Shen S. Reference evapotranspiration variation analysis and its approaches evaluation of 13 empirical models in sub-humid and humid regions: a case study of the huai river basin, eastern China. Water. 2018;10:493. [Google Scholar]
- Li M., Chu R., Shen S., Islam A.R.M.T. Dynamic analysis of pan evaporation variations in the Huai River Basin, a climate transition zone in eastern China. Sci. Tot. Cal. Environ. 2018;625:496–509. doi: 10.1016/j.scitotenv.2017.12.317. [DOI] [PubMed] [Google Scholar]
- Li M., Chu R., Shen S., Islam A.R.M.T. Quantifying climatic impact on reference evapotranspiration trends in the Huai River Basin of eastern China. Water. 2018;10:144. [Google Scholar]
- Li Y., Horton R., Ren T., Chen C. Prediction of annual reference evapotranspiration using climatic data. Agric. Water Manag. 2010;97:300–308. [Google Scholar]
- López-Urrea R., de Santa Olalla F.M., Fabeiro C., Moratalla A. Testing evapotranspiration equations using lysimeter observations in a semiarid climate. Agr. Water Manage. 2006;85:15–26. [Google Scholar]
- Makkink G.F. Testing the Penman formula by means of lysimeters. J. Inst. Water Eng. 1957;11:277–288. [Google Scholar]
- Mann H.B. Nonparametric test against trend. Econometrica. 1945;13:245–259. [Google Scholar]
- McVicar T.R., Van Niel T.G., Li L., Hutchinson M.F., Mu X., Liu Z. Spatially distributing monthly reference evapotranspiration and pan evaporation considering topographic influences. J. Hydrol. 2007;338:196–220. [Google Scholar]
- Mirza M.M.Q. Global warming and changes in the probability of occurrence of floods in Bangladesh and implications. Glob. Environ. Chang. 2002;12:127–138. [Google Scholar]
- Mojid M.A., Rannu R.P., Karim N.N. Climate change impacts on reference crop evapotranspiration in northwest hydrological region of Bangladesh. Int. J. Climatol. 2015;35:4041–4046. [Google Scholar]
- Peng L., Li Y., Feng H. The best alternative for estimating reference crop evapotranspiration in different sub-regions of mainland China. Sci. Rep. 2017;7:5458. doi: 10.1038/s41598-017-05660-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penman H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. A Math. Phys. 1948;193:120–145. doi: 10.1098/rspa.1948.0037. [DOI] [PubMed] [Google Scholar]
- Priestley C.H.B., Taylor R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972;100:81–92. [Google Scholar]
- Rahman M.A., Yunsheng L., Sultana N. Analysis and prediction of rainfall trends over Bangladesh using Mann-Kendall, Spearman's rho tests and ARIMA model. Meteorol. Atmos. Phys. 2017;129:409–424. [Google Scholar]
- Rahman M.A., Yunsheng L., Sultana N., Ongoma V. Analysis of reference evapotranspiration (ET0) trends under climate change in Bangladesh using observed and CMIP5 data sets. Meteorol. Atmos. Phys. 2018;131:639–655. [Google Scholar]
- Rahman M.M. Renewable energy system for sustainable future of Bangladesh. Int. J. Renew. Energy Resour. 2013 [Google Scholar]
- Rahman M.R., Lateh H. Climate change in Bangladesh: a spatiotemporal analysis and simulation of recent temperature and rainfall data using GIS and time series analysis model. Theor. Appl. Climatol. 2015 [Google Scholar]
- Rashid H.E. University Press Ltd; Dhaka: 1991. Geography of Bangladesh. [Google Scholar]
- Rumsey D.J. second ed. 2016. Statistics for Dummies. [Google Scholar]
- Samaras D.A., Reif A., Theodoropoulos K. Evaluation of Radiation-Based reference evapotranspiration models under different Mediterranean climates in central Greece. Water Resour. Manag. 2014;28:207–225. [Google Scholar]
- Sen P.K. Estimates of the regression coefficient based on kendall's tau. J. Am. Stat. Assoc. 1968;63:1379–1389. [Google Scholar]
- Sentelhas P.C., Gillespie T.J., Santos E.A. Evaluation of FAO Penman–Monteith and alternative methods for estimating reference evapotranspiration with missing data in Southern Ontario, Canada. Agric. Water Manag. 2010;97:635–644. [Google Scholar]
- Shahid S. Rainfall variability and the trends of wet and dry periods in Bangladesh. Int. J. Climatol. 2010;30(15):2299–2313. [Google Scholar]
- Shahid S. Impact of climate change on irrigation water demand of dry season Boro rice in northwest Bangladesh. Clim. Change. 2011:105,433–453. [Google Scholar]
- Slatyer R.O., Mgilroy I. Practical microclimatology, with special reference to the water factor in soil-plant-atmosphere relationships. 1961. Practical microclimatology, with special reference to the water factor in soil-plant-atmosphere relationships. [Google Scholar]
- Smith M., Allen R.G., Pereira L.S. 1991. Revised FAO Methodology for Crop Water Requirements. Land and Water Dev. Division, FAO, Rome.http://www.fao.org/WAICENT/FaoInfo/Agricult/agl/aglw/webpub/REVPUB.htm [Google Scholar]
- Stöckle C.O., Kjelgaard J., Bellocchi G. Evaluation of estimated weather data for calculating Penman-Monteith reference crop evapotranspiration. Irr. Sci. 2004;23:39–46. [Google Scholar]
- Sumner D.M., Jacobs J.M. Utility of Penman–Monteith, Priestley–Taylor, reference evapotranspiration, and pan evaporation methods to estimate pasture evapotranspiration. J. Hydrol. 2005;308:81–104. [Google Scholar]
- Tabari H., Grismer M.E., Trajkovic S. Comparative analysis of 31 reference evapotranspiration methods under humid conditions. Irrig. Sci. 2013;31:107–117. [Google Scholar]
- Tegos A., Malamos N., Koutsoyiannis D. A parsimonious regional parametric evapotranspiration model based on a simplification of the Penman-Monteith formula. J. Hydrol. 2015;524:708–717. [Google Scholar]
- Temesgen B., Eching S., Davidoff B., Frame K. Comparison of some reference evapotranspiration equations for California. J. Irrig Drain E-ASCE. 2005;131:73–84. [Google Scholar]
- Theil H. North-Holland Publishing Co.; Amsterdam, The Netherlands: 1950. A Rank Invariant Method of Linear and Polynomial Regression Analysis. [Google Scholar]
- Thornthwaite C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948;38:55–94. [Google Scholar]
- Trabert W. Neue beobachtungen uber Verdampfungsgeschwindigkeiten. Meteorol. Z. 1896;13:261–263. [Google Scholar]
- Trajkovic S., Kolakovic S. Wind-adjusted Turc equation for estimating reference evapotranspiration at humid European locations. Hydrol. Res. 2009;40:45–52. [Google Scholar]
- Traore S., Wang Y.M., Kerh T. Artificial neural network for modeling reference evapotranspiration complex process in Sudano-Sahelian zone. Agr. Water Manage. 2010;97:707–714. [Google Scholar]
- Turzo M.I.A., Islam S., Das R.S. International Conference on Mechanical Engineering and Renewable Energy (ICMERE2015) 2015. Prospects of solar power and its applications in Bangladesh. [Google Scholar]
- Valiantzas J.D. Simple ET0 forms of Penman's Equation without wind and/or humidity data. I: theoretical development. J. Irrigat. Drain. Eng. 2013;139:1–8. [Google Scholar]
- Valiantzas J.D. Simple ET0 forms of Penman's Equation without wind and/or humidity data. II: Comparisons with reduced set-FAO and other methodologies. J. Irrigat. Drain. Eng. 2013;139:9–19. [Google Scholar]
- World Meteorological Organization WMO . ume 83. WMO; Geneva, Switzerland: 1966. (Measurement and Estimation of Evaporation and Evapotranspiration). Technical Paper (CIMO-Rep) [Google Scholar]
- Xu C.-Y., Singh V.P. Dependence of evaporation on meteorological variables at different timescales and intercomparison of estimation methods. Hydrol. Process. 1998;12:429–442. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that has been used is confidential.