Abstract
Current fixation plates for bone fracture treatments are built with biocompatible metallic materials such as stainless steel, titanium, and its alloys (e.g., Ti6Al4V). The stiffness mismatch between the metallic material of the plate and the host bone leads to stress shielding phenomena, bone loss, and healing deficiency. This paper explores the use of three dimensional topology-optimization, based on compliance (i.e., strain energy) minimization, reshaping the design domain of three locking compression plates (four-screw holes, six-screw holes, and eight-screw holes), considering different volume reductions (25, 45, and 75%) and loading conditions (bending, compression, torsion, and combined loads). A finite-element study was also conducted to measure the stiffness of each optimized plate. Thirty-six designs were obtained. Results showed that for a critical value of volume reductions, which depend on the load condition and number of screws, it is possible to obtain designs with lower stiffness, thereby reducing the risk of stress shielding.
Keywords: Bone plates, Finite element analysis, Mesh dependency, Stress shielding, Topology optimization
1. Introduction
Bone fractures represent a critical healthcare problem. In USA, number of fracture cases is predicted to increase from 2.1 million in 2005 to around three million in 2025[1]. Bone fixation implants are considered one of the riskiest implants[2], as the UK’s National Health Service (NHS) reported over 11,000 revision operations for failed implants in 2016[3].
Fractures are often surgically treated with bone fixation devices such as internal fixators, external fixators, and intramedullary pins[4]. Internal fixations, the focus of this research, are usually applied to fixate the fractured bone through restoring the bone segments into its original functionality and anatomy. Since the introduction of the first metallic internal fixations in 1895 by Lane, different designs were developed and introduced in the market[5]. At present, the Locking Compression Plate (LCP) is the most commonly used fixation plate due to its hybrid design consisting of a conventional screwing system and a Locking Head Screw system[6]. LCP allows a gap between the bone and the implant to achieve callus formation and is more suitable for osteoporotic fractures[6].
Internal fixations (e.g., plates and screws) are built using biocompatible metallic materials such as stainless steel (i.e., 316L) and titanium-based alloys (e.g., Ti-6Al-4V). Such metallic materials present Young’s modulus of around 120 GPa for Ti-6Al-4V and 190 GPa for 316L stainless steel, significantly higher than that for cortical bone (around 20 GPa)[7-9]. This large difference is one of the main causes of the stress shielding phenomenon characterized by the lack of mechanical stimulation of the bone through disruption of load distribution across in the bone-plate construct. This phenomenon affects the bone remodeling process, causing implant loosening and bone loss.
Different methods have been explored to reduce the stress shielding effect through the change of built material (e.g., functionally graded materials) and/or design modifications (e.g. lattice structure, internal hollow, or porous structures)[10,11]. However, the fabrication of functionally graded structures is complex and expensive, while design modifications usually require laborious and costly iterative steps performed by expert technicians. Recently, we proposed a novel design method to minimize stress shielding using topology optimization (TO)[12]. Results-focused on two-dimensional (2D) topologies, considering tensile loads on the plates, loads on the holes simulating the screw and combination of both, and a maximum volume reduction of 75%. The approach allowed to obtain designs of lightweight plates with reduced equivalent stiffness compared to the proposed original design domains. In this paper, we extended the study to three-dimensional (3D) topologies, investigating the use of 3D TO to redesign novel LCPs to minimize the stress shielding phenomenon. Three initial plate designs with different screw hole numbers (four-, six-, and eight-hole plates) were redesigned considering different loading conditions (compression, bending, torsion, and a combination of these loads) imposing different volume reductions to the initial designs (25, 45, and 75%). The effect of mesh density on the TO is also investigated and discussed. Topology-optimized plate design considering bending load presented bending elastic modulus equivalent to native bone.
2. TO
TO is an automatic iterative design technique to obtain optimal structural topologies based on the user-defined loading and boundary conditions. The goal is to achieve a design with an optimal material distribution (Ω*) from an initially given design domain (Ω), which is discretized into number of finite elements (N). The aim was to redesign the domain by minimizing compliance (maximizing stiffness):

where u is the displacement vectors and f is load vectors governed by:
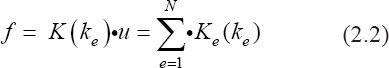
where K is the global stiffness matrix, Ke is the matrices of the element stiffness, and ke is the stiffness of each element.
The density (ρ) is considered as a function to modify the design’s stiffness matrix and treated as a design variable. Therefore, the density imposed on each element (ρe) of the design domain follows a binary variation resulting in either ρe=1 (i.e., keeping the element) or ρe=0 (i.e., removing the element) values. Solving this problem through mathematical programming algorithms require the rewriting of optimization problem (2.1) as follows:
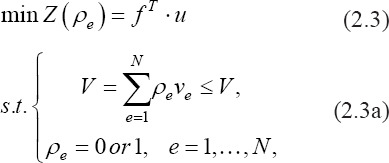
where V is the initial volume and ve is volume of each element.
The Solid Isotropic Microstructure with Penalization (SIMP), a gradient-based TO approach, was considered to solve the TO problem[13,14]. SIMP forces the design variable, to have a penalized continuous convergence as follows:
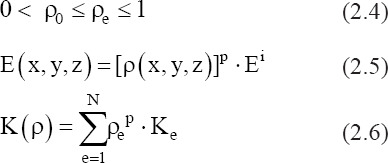
where ρ0 is the non-zero minimum density, p is the penalization factor (recommended to have a value of three for a better convergence), and Ei is the initial Elastic modulus at r=1 of the material.
Therefore, SIMP solves equation (2.3) as follows:
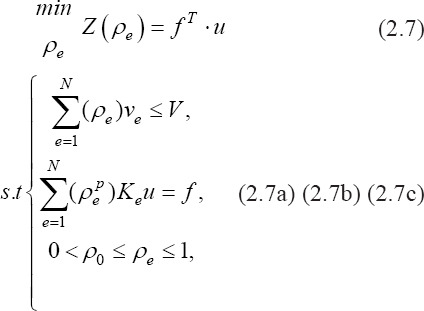
The iterative steps to achieve optimality through TO are shown in Figure 1. The solution starts with the given design domain, Ω, comprising the user-defined material being discretized into a set of finite elements, with each element consisting of a density value contributing to the overall design density. Then, sensitivity breakdown is defined across the displacement field according to the loading and boundary conditions, which means that the density is updated toward optimality, satisfying the objective function and constraints in each iteration.
Figure 1.
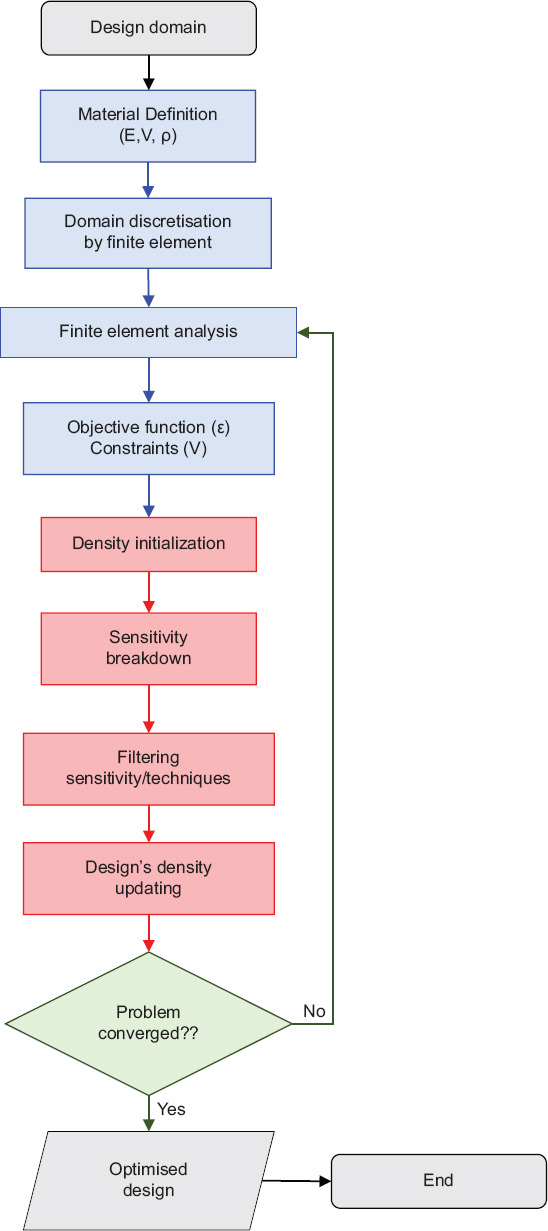
Workflow of SIMP optimisation.
The first step in each computational iteration corresponds to the calculation of element sensitivity based on deriving Eq. 2.7 in respect to the density:
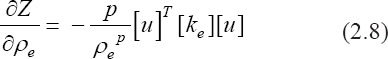
Sensitivity filtering determines the element distribution passing through filtering formulas (e.g., mesh-independent filtering and sensitivity filtering to prevent checkerboarding) along the design domain.
3. Simulation and optimization
3.1. Initial design domains
The DePuy Synthes narrow LCP, commonly used for the treatment of long bones such as humerus, femur, and tibia, was considered as a reference design. Three plates (four-screw holes, six-screw holes, and eight-screw holes) were designed using Solidworks (Dassault Systèmes, France) with a length of 180 mm, width of 14 mm, and thickness of 5 mm (Table 1). Abaqus (Dassault Systèmes, France) was used to perform the TO and finite element analysis. Plates were considered to be made with Ti-6Al-4V (120 GPa of Elastic Modulus and 0.3 of Poisson’s ratio). Finite element meshes were created using eight-node linear hexahedral elements and approximately 400,000 elements were considered. Different mesh densities were also considered for the mesh dependency study.
Table 1.
The initial designs considered for the bone plates
| Plate reference | Number of holes | |
|---|---|---|
| ID4 | 4 |  |
| ID6 | 6 |  |
| ID8 | 8 |  |
3.2. Loading and boundary conditions
Considering possible physiological events, the plate was subjected to four types of loadings: compression, bending, torsion, and a combination of these loads that mainly occur on the screw holes and the mid-plate (Table 2). Compression corresponded to a static compressing force along the X-axis (the axis along the length of the plate) applied on both far-end sides of the plate and constraining the six nodes on the two opposite middle faces of the plate in all directions and rotations (dx=dy=dz=rx=ry=rz=0), symbolized by an encastre constraint. Bending corresponded to a static four-point bending test applied on the plate according to the bone fixation plate testing standards (ISO 9585:1990)[15]. The two loading points were separated with a distance of two screw holes and at least one screw hole between the load and support point. The support points constrained the bone plate from moving across the Z-axis (dx=dy=0, dz≠0) (the axis crossing the thickness of the plate), symbolized by a red-colored pin constraint. An additional two constraints were used to ensure stability in the X and Y axis (dx=dy≠0, dz=0) (the axis along the width of the plate) during loading, symbolized by an orange color pin constraint. Torsion corresponded to static moment acting along the X-axis on one end and constrained (i.e. pinned) on the other end of the plate (dx=dy=dz=0), symbolized by an orange color pin constraint. Combined load was the combination of compression, bending, and torsion, considering the constraints of the compression test. It is important to note that SIMP method was not sensitive to the load magnitude when the compliance for a given load was minimized.
Table 2.
Loading and boundary conditions considered for topology optimization
| Loading type | Description |
|---|---|
| Compression load | 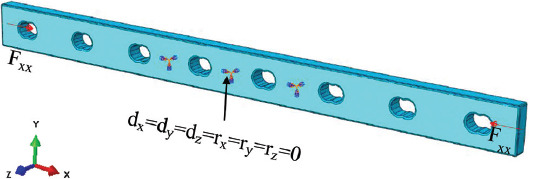 |
| Bending load | 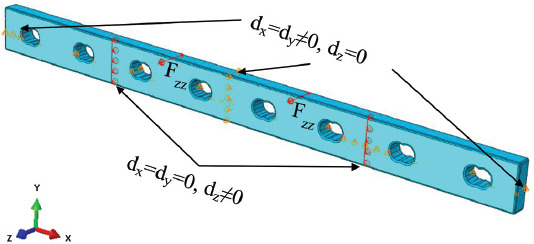 |
| Torsion load |  |
| Combined load | 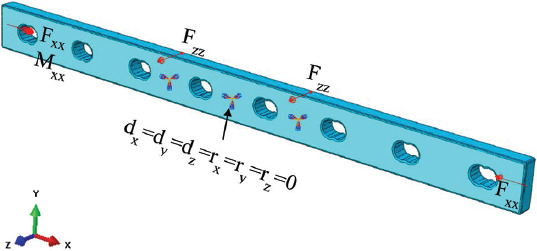 |
SIMP optimization was used to minimize the strain energy of the plate designs shown in Table 1, considering different volume reductions (25, 45, and 75%) of the initial design volume. To guarantee the integrity of the screw holes to preserve their shape during TO, the holes were considered frozen regions, as shown in Figure 2.
Figure 2.
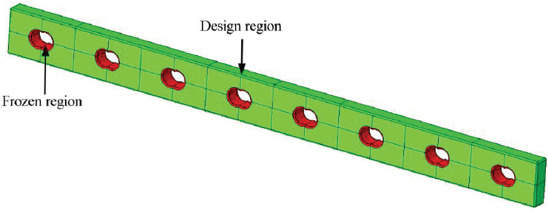
Design (green) and frozen (red) regions of the bone plates.
3.3. Mesh dependency
Similar to any numerical approximation method, TO results are dependent on the meshing quality[16]. Therefore, a preliminary study was conducted considering an eight screw holes plate under compression loading and a volume reduction of 45%, discretized with eight-node linear hexahedral elements and meshed with different number of elements (5000 elements, 10,000 elements, 25,000 elements, 50,000 elements, 75,000 elements, 100,000 elements, 250,000 elements, 350,000 elements, and 400,000 elements).
3.4. Stress shielding analysis
The stiffness of each plate, for different loading conditions, is the main criteria to determine possible stress shielding problems. In all cases, the optimized plates were considered homogeneous and isotropic. Based on the numerical finite element analyses and their loading and boundary conditions in Table 2, the corresponding equivalent stiffness of each plate was determined[12]. For the compression case (similar to combined load case), the equivalent stiffness was calculated considering the longitudinal reaction uniaxial force (RFxx) in kilonewton (kN) along the X-axis applied on one end of the bone plate and constraining the opposite side, as follows:

where KTe is the equivalent stiffness in kN/mm and Dxx is the resulted displacement in mm. In the bending case, the equivalent bending stiffness was calculated according to the following equation (British Standard 1991)[15]:
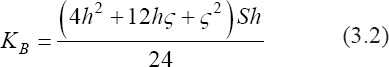
where KB is the equivalent bending stiffness in N.m2, h is the distance between the load and support points, is the distance between the load points, and S is the slope of the load-deflection curve.
The equivalent elastic bending modulus was measured as follows (ASTM Standard 2017)[17]:
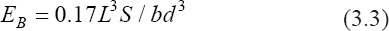
where EB is the equivalent bending elastic modulus in GPa, L is the support span, b is the plate’s width, and d is the plate’s thickness.
For the torsion case, the equivalent stiffness was determined considering the reaction moment across the X-axis (Txx) applied on one end of the plate, constraining the other end. The resulted angle of twist along the X-axis direction (Φxx) was recorded and the torsional stiffness was determined as follows:

where KTr is the torsional stiffness in Nmm/Rad.
4. Results and discussion
Despite utilizing mesh-dependency filtering techniques, TO in commercial software appears to be affected by the mesh density[16,18]. The effect of mesh size on the optimization process is shown in Figure 3 and the corresponding equivalent stiffness is presented in Figure 4. Coarse mesh results in less material removal and lower computational time, while finer mesh increases the volume reduction and the computational time. As observed, no significant difference in equivalent stiffness values will be obtained if elements were to be increased more than 400,000 elements and the computational cost will significantly increase.
Figure 3.

Mesh dependency - plate redesigns for different number of elements.
Figure 4.
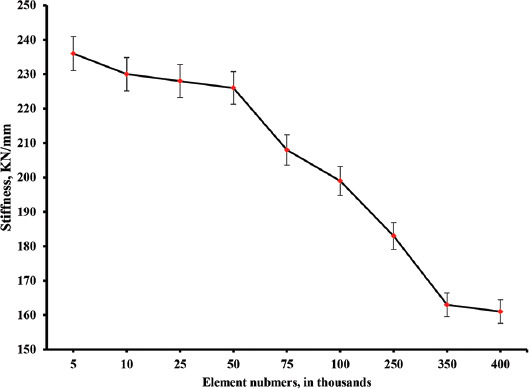
Equivalent stiffness values as a function of mesh size.
Figures 5-8 present the optimized designs for all plates (eight-, six-, and four- screw holes), different loading conditions, and volume reduction. Imposed volume reductions vary between 25% and 75% as values higher than 75% can jeopardize the design’s structural integrity, while values lower than 25% have no significant effect on the stiffness reduction. The corresponding equivalent stiffness values are presented in Tables 3-6. In all cases, the equivalent stiffness decreases by increasing the volume reductions, confirming previously reported observations for TO of 2D plates[12]. Several authors observed similar results using TO to address stress shielding by redesigning orthopedic implants in the case of pelvic prosthetics[19], hip prosthetics,[20] and spine implants[21]. The results also indicate that the mechanical properties are directly related to the material volume as it is clear that for all the loading cases with the same volume reduction, plates containing four holes are stiffer than plates containing six holes, which are also stiffer than plates containing eight holes. These results present significant findings of the possibility of optimizing the bone plate’s stiffness considering physiological loads by reducing the design’s material volume. In addition, a significant reduction of the stiffness is a major indication of reduced risk of the stress shielding (i.e., bone loss), thus promoting callus formation and bone formation[22-24]. Considering that the bone elastic bending modulus ranges between 9 to 15 GPa, the bending optimized plate with eight holes and 75% of volume reduction showed an equivalent elastic bending modulus (11 GPa) within this region[25]. This proves that using topology optimization is possible to obtain designs that are able to match the mechanical properties of native bone and thus, and eliminate the main cause to stress shielding. In addition, previous studies reported that using TO in designing generic fixation plates[26] and mandible fixation plates[27], which depends on the volume reduction and loading condition, is possible to reduce the plate’s stiffness while maintaining its mechanical stability to withstand stresses.
Figure 5.

Topology-optimized plates under compression conditions.
Figure 8.

Topology-optimised plates under combined loading conditions.
Table 3.
Equivalent stiffness of optimized plate designs considering compression loading conditions
| Volume reduction % | Equivalent stiffness (kN/mm) | ||
|---|---|---|---|
| Plate with 4 holes | Plate with 6 holes | Plate with 8 holes | |
| Initial design | 306±6.46 | 247±12.65 | 237±5.38 |
| 25 | 252±5.32 | 203±10.39 | 196±4.45 |
| 45 | 167±3.52 | 135±6.91 | 161±3.65 |
| 75 | 23±0.48 | 21±1.07 | 28±0.63 |
Table 6.
Equivalent stiffness of optimized plate designs considering combined loading conditions
| Volume reduction % | Equivalent stiffness (kN/mm) | ||
|---|---|---|---|
| Plate with 4 holes | Plate with 6 holes | Plate with 8 holes | |
| Initial design | 306±6.45 | 247±12.65 | 237±5.38 |
| 25 | 237±5.00 | 214±10.96 | 145±3.29 |
| 45 | 158±3.33 | 101±5.17 | 123±2.79 |
| 75 | 22±0.46 | 20±1.02 | 28±0.63 |
Figure 6.

Topology-optimized plates under bending loading conditions.
Figure 7.

Topology-optimised plates under torsion loading conditions.
Table 4.
Equivalent stiffness of optimized plate designs considering bending loading conditions
| Volume reduction % | Equivalent stiffness (N.m2) | ||
|---|---|---|---|
| Plate with 4 holes | Plate with 6 holes | Plate with 8 holes | |
| Initial design | 19.27±0.41 | 18.68±0.96 | 16.22±0.39 |
| 25 | 16.32±0.34 | 15.41±0.79 | 13.38±0.3 |
| 45 | 13.23±0.28 | 11.34±0.58 | 4.81±0.11 |
| 75 | 9.26±0.19 | 4.14±0.21 | 2.34±0.05 |
Table 5.
Equivalent stiffness of optimized plate designs considering torsion loading conditions.
| Volume reduction % | Equivalent stiffness (Nmm/Rad) | ||
|---|---|---|---|
| Plate with 4 holes | Plate with 6 holes | Plate with 8 holes | |
| Initial design | 28550±602 | 26170±1336 | 24792±562 |
| 25 | 23550±496 | 24574±1258 | 15737±357 |
| 45 | 15767±333 | 17539±898 | 13348±302 |
| 75 | 3653±77 | 6932±355 | 7304±166 |
Design symmetry is important when considering design to manufacture and to eliminate the design complexity for the surgeons during surgery. Symmetrical designs were observed in the case of compression and torsion due to the considered symmetrical loading and boundary conditions. Bending optimized designs were symmetrical in YZ plane but not in the XY plane due to the bending load which compresses one side of the plate and tensions the other. In the combined load case, the designs were freely designed regardless of the symmetry as the combination of compression, bending, and torsion loads result in asymmetric stress and strain distributions.
In addition, the optimized bone plates produced using TO present complex features which are impossible to manufacture using conventional manufacturing but possible through additive manufacturing[28]. Researchers previously reported the successful combination of TO, electron beam melting, and selective laser melting, considering different conditions (i.e. low mesh density)[29], and similar conclusions were also obtained by other researchers[19].
5. Conclusion
Stress shielding is a common problem in standard bone fixation plates, requiring new tools to redesign them and new fabrication methods to produce them. This paper, extending previously reported results considering 3D plates, shows that TO is a suitable tool to redesign bone fixation plates with different geometries, considering different loading conditions and volume reduction, allowing to obtain plates with reduced equivalent stiffness that matches the mechanical properties of native bone in case of eight-hole plate, and considering bending load and 75% volume reduction. A trend between volume reduction and equivalent stiffness was observed. A significant stiffness reduction was achieved for high volume reductions, preventing stress shielding and potentially avoiding bone resorption and eventual plate failure.
Previously reported results showed the ability of topology-optimized fixation plates, obtained by different conditions (i.e., low mesh density), to withstand stresses in a biomechanical setting. This study did not investigate the potential stress concentration regions resulting from the TO and the mechanical strength (yield stress) of the optimized plates with high mesh density. Future studies must address this limitation by computationally assessing the optimized bone plate designs with high mesh density designs from a biomechanical perspective in a fractured bone configuration.
Acknowledgments
Researchers Supporting Project number (RSP-2021/299), King Saud University, Riyadh, Saudi Arabia.
Conflicts of interest
The author declare no conflicts of interest.
References
- 1.Amin S, Achenback S, Atkinson E, et al. Trends in Fracture Incidence:A Population-based Study Over 20 Years. J Bone Miner Res. 2014;29:581–9. doi: 10.1002/jbmr.2072. https://doi.org/10.1002/jbmr.2072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kramer D, Xu S, Kesselheim A. Regulation of Medical Devices in the United States and European Union. N Engl J Med. 2012;366:848–55. doi: 10.1056/NEJMhle1113918. https://doi.org/10.1056/nejmhle1113918. [DOI] [PubMed] [Google Scholar]
- 3.Green M, Wishart N, Young E. NJR 14th Annual Report. National Joint Registry; England: 2016. [Google Scholar]
- 4.Alsop H. Tidy's Physiotherapy. 15th ed. Vol. 22. Churchill Livingstone; United Kingdom: 2013. An introduction to fractures'in porter. [Google Scholar]
- 5.Uhthoff HK, Poitras P, Backman DS. Internal Plate Fixation of Fractures:Short History and Recent Developments. J Orthop Sci. 2006;11:118–26. doi: 10.1007/s00776-005-0984-7. https://doi.org/10.1007/s00776-005-0984-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Szypryt P, Forward D. The Use and Abuse of Locking Plates. Orthop Trauma. 2009;23:281–90. https://doi.org/10.1016/j.mporth.2009.07.002. [Google Scholar]
- 7.Elias CN, Lima JHC, Valiev R, et al. Biomedical Applications of Titanium and its Alloys. JOM. 2008;60:46–9. https://doi.org/10.1007/s11837-008-0031-1. [Google Scholar]
- 8.McNamara L. Comprehensive Biomaterials. Elsevier; Oxford: 2011. Bone as a Material in Ducheyne. [Google Scholar]
- 9.Prasad K, Bazaka O, Chua M, et al. Metallic Biomaterials:Current Challenges and Opportunities. Materials. 2017;10:884. doi: 10.3390/ma10080884. https://doi.org/10.3390/ma10080884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mahmoud D, Elbestawi MA. Lattice Structures and Functionally Graded Materials Applications in Additive Manufacturing of Orthopedic Implants:A Review. J Manufact Mater Proc. 2017;1:13. https://doi.org/10.3390/jmmp1020013. [Google Scholar]
- 11.Pałka K, Pokrowiecki R. Porous Titanium Implants:A Review. Adv Eng Mater. 2018;20:1700648. https://doi.org/10.1002/adem.201700648. [Google Scholar]
- 12.Al-Tamimi A, Fernandes PRA, Peach C, et al. Metallic Bone Fixation Implants:A Novel Design Approach for Reducing the Stress Shielding Phenomenon. Virtual Phys Prototy. 2017;12:141–51. https://doi.org/10.1080/17452759.2017.1307769. [Google Scholar]
- 13.Bendsøe MP. Optimal Shape Design as a Material Distribution Problem. Struct Optim. 1989;1:193–202. https://doi.org/10.1007/bf01650949. [Google Scholar]
- 14.Bendsøe MP, Sigmund O. Topology Optimization by Distribution of Isotropic Material in Topology Optimization:Theory, Methods, and Applications. Springer Berlin Heidelberg; Berlin, Heidelberg: 2004. https://doi.org/10.1007/978-3-662-05086-6_1. [Google Scholar]
- 15.British Standard. Implants for Osteosynthesis-Part 23:Bone Plates-Section 23.1 Method for Determination of Bending Strength and Stiffness. British Standard; United Kingdom: 1991. https://doi.org/10.3403/00189873u. [Google Scholar]
- 16.Sigmund O, Petersson J. Numerical Instabilities in Topology Optimization:A Survey on Procedures Dealing with Checkerboards, Mesh-dependencies and Local Minima. Struct Optim. 1998;16:68–75. https://doi.org/10.1007/bf01214002. [Google Scholar]
- 17.ASTM Standard. Standard Test Method for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials by Four-point Bending. ASTM Standard; United States: 2017. pp. D6272–17. https://doi.org/10.1520/d6272-02r08e01. [Google Scholar]
- 18.Buhl T, Pedersen C, Sigmund O. Stiffness Design of Geometrically Nonlinear Structures Using Topology Optimization. Struct Multidisc Optim. 2000;19:93–104. https://doi.org/10.1007/s001580050089. [Google Scholar]
- 19.Iqbal T, Wang L, Li D, et al. A General Multi-objective Topology Optimization Methodology Developed for Customized Design of Pelvic Prostheses. Med Eng Phys. 2019;69:8–16. doi: 10.1016/j.medengphy.2019.06.008. https://doi.org/10.1016/j.medengphy.2019.06.008. [DOI] [PubMed] [Google Scholar]
- 20.Saravana KG, George S. Optimization of Custom Cementless Stem Using Finite Element Analysis and Elastic Modulus Distribution for Reducing Stress-shielding Effect. Proc Inst Mech Eng H. 2017;231:149–59. doi: 10.1177/0954411916686125. https://doi.org/10.1177/09544119166↤5. [DOI] [PubMed] [Google Scholar]
- 21.Chuah HG, Rahim IA, Yusof MI. Topology Optimisation of Spinal Interbody Cage for Reducing Stress Shielding Effect. Comput Methods Biomech Biomed Eng. 2010;13:319–26. doi: 10.1080/10255840903208189. https://doi.org/10.1080/10255840903208189. [DOI] [PubMed] [Google Scholar]
- 22.Woo S, Simon B, Akeson W, et al. An Interdisciplinary Approach to Evaluate the Effect of Internal Fixation Plate on Long Bone Remodeling. J Biomech. 1977;10:87–95. doi: 10.1016/0021-9290(77)90072-0. https://doi.org/10.1016/0021-9290(77)90072-0. [DOI] [PubMed] [Google Scholar]
- 23.Goodship A, Kenwright J. The Influence of Induced Micromovement Upon the Healing of Experimental Tibial Fractures. J Bone Joint Surg Br. 1985;67:650–5. doi: 10.1302/0301-620X.67B4.4030869. https://doi.org/10.1302/0301-620x.67b4.4030869. [DOI] [PubMed] [Google Scholar]
- 24.Claes L, Augat P, Suger G, et al. Influence of Size and Stability of the Osteotomy Gap on the Success of Fracture Healing. J Orthop Res. 1997;15:577–84. doi: 10.1002/jor.1100150414. https://doi.org/10.1002/jor.1100150414. [DOI] [PubMed] [Google Scholar]
- 25.Keller TS, Mao Z, Spengler DM. Young's Modulus, Bending Strength, and Tissue Physical Properties of Human Compact Bone. J Orthop Res. 1990;8:592–603. doi: 10.1002/jor.1100080416. https://doi.org/10.1002/jor.1100080416. [DOI] [PubMed] [Google Scholar]
- 26.Al-Tamimi AA, Quental C, Folgado J, et al. Stress Analysis in a Bone Fracture Fixed with Topology-optimised Plates. Biomech Model Mechanobiol. 2020;19:693–9. doi: 10.1007/s10237-019-01240-3. https://doi.org/10.1007/s10237-019-01240-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liu Y, Fan Y, Jiang X, et al. A Customized Fixation Plate with Novel Structure Designed by Topological Optimization for Mandibular Angle Fracture Based on Finite Element Analysis. BioMedical Eng Online. 2017;16:1–17. doi: 10.1186/s12938-017-0422-z. https://doi.org/10.1186/s12938-017-0422-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zegard T, Paulino GH. Bridging Topology Optimization and Additive Manufacturing. Struct Multidiscip Optim. 2016;53:175–92. https://doi.org/10.1007/s00158-015-1274-4. [Google Scholar]
- 29.Al-Tamimi AA, Hernandez MA, Omar A, et al. Mechanical, Biological and Tribological Behaviour of Fixation Plates 3D Printed by Electron Beam and Selective Laser Melting. Int J Adv Manufact Technol. 2020;109:673–88. https://doi.org/10.1007/s00170-020-05676-1. [Google Scholar]


