Practical high-performance lead-free piezoelectrics: structural flexibility beyond utilizing multiphase coexistence

Abstract

Due to growing concern for the environment and human health, searching for high-performance lead-free piezoceramics has been a hot topic of scientific and industrial research. Despite the significant progress achieved toward enhancing piezoelectricity, further efforts should be devoted to the synergistic improvement of piezoelectricity and its thermal stability. This study provides new insight into these topics. A new KNN-based lead-free ceramic material is presented, which features a large piezoelectric coefficient (d₃₃) exceeding 500 pC/N and a high Curie temperature (T_c) of  ∼200°C. The superior piezoelectric response strongly relies on the increased composition-induced structural flexibility due to lattice softening and decreased unit cell distortion. In contrast to piezoelectricity anomalies induced via polymorphic transition, this piezoelectricity enhancement is effective within a broad temperature range rather than a specific small range. In particular, a hierarchical domain architecture composed of nano-sized domains along the submicron domains was detected in this material system, which further contributes to the high piezoelectricity.

INTRODUCTION

Piezoelectric materials are a unique medium for the conversion between mechanical and electrical energy and play a vital role in a variety of applications such as sensors, transducers, and actuators [1,2]. For decades, the global piezoelectric materials market was monopolized by lead zirconium titanate (PZT) based materials. However, a strong increase in environmental concerns has driven tremendous efforts toward lead-free substitutes [2–4]. Among the various types of lead-free substitutes, their overall excellent performance highlights (Na,K)NbO₃ (KNN)-based ceramics as one of the most promising candidates [3,5–7]. The breakthrough by Saito et al. has manifested the promising potential of KNN-based ceramics [5]. Over the last decade, developing KNN-based ceramics with large piezoelectricity has become a hot research topic in both academic and industrial fields. Extensive studies have concentrated on constructing phase transitions near room temperature [5,8–11]. Forming a rhombohedral–tetragonal R-T (or rhombohedral–orthorhombic–tetragonal, R-O-T) phase boundary has been considered to be an effective strategy to achieve an ultrahigh d₃₃ value in KNN-based ceramics [4,9–12]. However, not all KNN-based piezoceramics with the R-T (or R-O-T) phase boundary exhibit such a large d₃₃ [13–16]. Although constructing a R-T (or R-O-T) phase boundary is not difficult as long as appropriate dopants are utilized, obtaining high piezoelectricity via this method still remains very challenging [4,9–11]. Furthermore, the origins of superior piezoelectricity in lead-free ceramics remain controversial, thus obstructing the further development of lead-free ceramics.

Sufficient temperature stability of the piezoelectricity is another essential requirement for practical applications. Several novel approaches, such as inducing electrically enhanced diffused polymorphic phase transition (EED-PPT) and introducing diffused R-O-T phase transition, have been proposed to develop temperature-insensitive lead-free piezoelectric materials [14,17–19]. However, it should be noted that the temperature-insensitive piezoelectricity originating from the diffused polymorphic phase transition is essentially induced by the degraded singularity of polymorphic phase transition (PPT) effects, which comes at the expense of high piezoelectricity [19]. An ideal scenario to achieve high and thermally stable piezoelectricity would be that the property enhancement is only related to the composition-induced free-energy instability [20]. Recent studies have provided evidence that the ultrahigh piezoelectricity of relaxor systems could be the result of structural instability associated with an interaction competition between the static structure of bulk and composition-induced local heterogeneities, i.e. local polar clusters known as polar nanoregions (PNRs) [20–25]. A further typical example of practical interest is the morphotropic phase boundary (MPB), in the vicinity of which high piezoelectric performance might arise from the anomalous softening of dielectric susceptibility and elastic moduli, resulting from composition-induced structural instability [20,26–29]. Therefore, both local structural instability and structure softening by chemical modification could contribute to temperature-independent property enhancement. This should be further emphasized to achieve high and thermally stable piezoelectricity. Consequently, the current study has developed a new lead-free ceramic composition: 0.93(Li_xNa_0.52K_0.48-x)(Nb_1-y,Sb_y)O₃-0.05BaZrO₃-0.02(Bi_0.5,Na_0.5)HfO₃ with 1 wt% MnO₂ as a sintering aid (abbreviated as L_xKNNS_y-5BZ-2BNH-1Mn). The impacts of Li and Sb contents on the piezoelectric response and its thermal stability were investigated, the results of which clarified the piezoelectricity enhancement mechanisms. Enhanced thermal stability of piezoelectricity was observed in the optimum compositions with a large d₃₃ exceeding 500 pC/N and a high T_c of  ∼200°C. This is strongly associated with the increased composition-induced structural flexibility, which benefits from reduced unit cell distortion and lattice softening.

RESULTS AND DISCUSSION

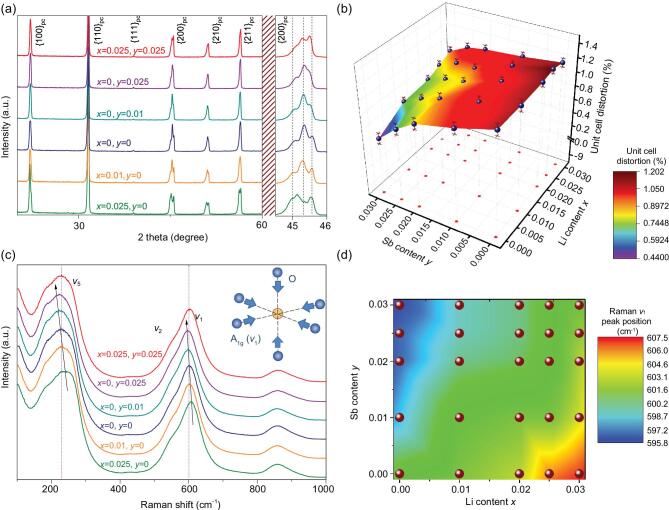
The L_xKNNS_y-5BZ-2BNZ-1Mn ceramics exhibited a pure perovskite structure, and no evidence of macroscopic impurity could be found. This indicates that BZ and BNH had diffused into the L_xKNNS_y lattices to form a stable solid solution (see Fig. S1, Supporting Information). As shown in Fig. 1a, these ceramics all featured multiphase coexistence according to the apparent splitting of 002_pc reflection peaks around 2θ ≈ 45° [3,4,10,11,13–15,19,30–32]. With increasing Sb content, the feature of the R phase became more prominent in the 002_pc reflection peaks. With increasing Li content, the 002_pc reflection peaks of the ceramics exhibited more characteristics of the T and O coexistent phases. Based on the 2θ interval between the leftmost 002_pc peak and the rightmost 002_pc peak, as a function of compositional change, the unit cell distortion (calculated by (c/a – 1) × 100%) of the global lattice decreased with increasing Sb content. Furthermore, it showed a mild increasing trend with increasing concentration of Li as shown in Fig. 1b. The increased lattice distortion can be interpreted as a lowering of symmetry, which is believed to be associated with octahedral tilting [33,34]. The need for this octahedral tilting is determined by the volume matching degree between the BO₆ octahedron and the AO₁₂ polyhedron. This can be evaluated according to the tolerance factor t (determined by (R_A + R_O)/[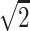(R_B + R_O)], where R_A, R_B, and R_O are the radii of A, B, and O ions, respectively) [33]. The increased tolerance factor from a value below 1 indicates a better matching between the BO₆ octahedron and the AO₁₂ polyhedron as well as the reduced potential of octahedral tilting to accommodate cations. The tolerance factor increases with the B-site cation substitution by Sb⁵⁺ but decreases with the A-site substitution by Li⁺ due to the smaller radii of Sb⁵⁺ and Li⁺ compared with those of Nb⁵⁺ and K⁺, respectively [35]. Thus, Li doping can increase the potential of octahedral tilting while the opposite effects are expected in Sb doping, which might account for the changing trend of the lattice distortion.

Figure 1.

(a) XRD patterns for representative L_xKNNS_y-5BZ-2BNZ-1Mn samples. (b) Unit cell distortion (calculated by (c/a – 1) × 100%) of the global lattice for L_xKNNS_y-5BZ-2BNZ-1Mn samples. (c) Room-temperature Raman spectra of representative L_xKNNS_y-5BZ-2BNH-1Mn samples. The inset shows a schematic illustration of the breath-type stretching A_1g mode. (d) Raman v₁ peak position of the L_xKNNS_y-5BZ-2BNH-1Mn samples.

Changes of short-range structures can be revealed by the collected Raman spectra (see Fig. S2). As shown in Fig. 1c, three broad bands were identified in all these ceramics, indicating the highly disordered lattice matrix [19]. As indicated in the inset of Fig. 1c, the A_1g mode denotes the breath-type stretching of the oxygen octahedron, which is naturally influenced by A–O or B–O bonds. Thus, the influence of Li and Sb contents on the perovskite structure can be indirectly detected by investigating the change of the A_1g mode. The A_1g mode wavenumber showed a decreasing trend with increasing Sb content but an increasing trend with increasing Li content, as shown in Fig. 1d. The reduced wavenumber could be attributed to the weakening of the bonding strength, which in turn is associated with the lower force constant [19,36]. The above changing trend is expected since the Sb–O bond energy is much lower than the Nb–O bond energy, while the Li–O bond energy is higher than the K–O bond energy [37,38]. Given the lower force constant and the less tight octahedral environment due to the smaller radius of Sb⁵⁺ compared with Nb⁵⁺, the matrix was considered to be softened by the introduction of Sb. More covalent KNN-based perovskite also occurred due to the much higher electronegativity of the Sb⁵⁺ compared with Nb⁵⁺. Collectively, these factors make it easier for ferroelectric active B-site cations to move between equivalent off-centering positions in the oxygen octahedral. This can result in a lower energy barrier between ferroelectric states [34].

When investigating the temperature dependences of the permittivity for the L_xKNNS_y-5BZ-2BNZ-Mn unpoled samples (see Fig. S3), a relaxed bump situated near room temperature signifying a PPT was observed in the ϵ_r–T curves of all samples.

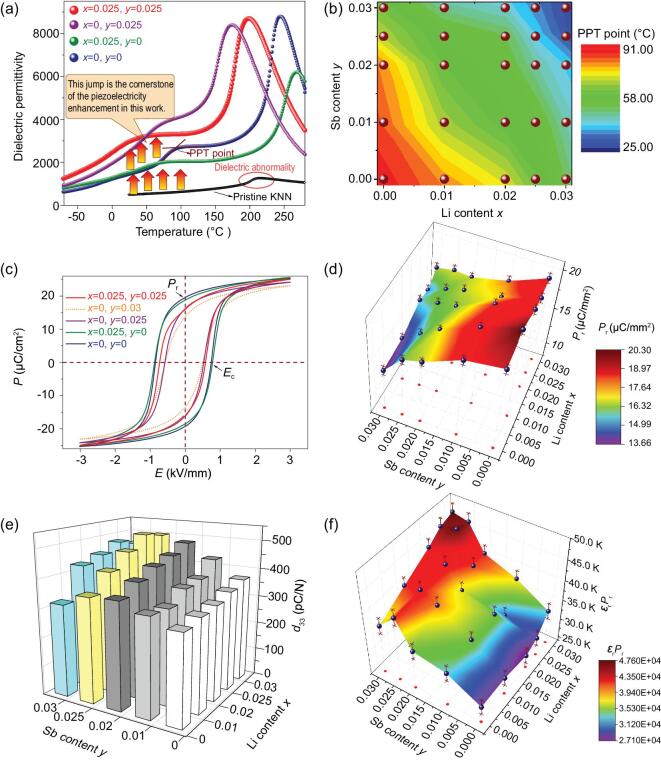
As shown in Fig. 2a, the ϵ_r level in the temperature range above the PPT point showed an increasing tendency as Sb content increased, while the opposite effects were observed for Li. Figure 2b shows the PPT points of the L_xKNNS_y-5BZ-2BNZ-Mn samples, which were extracted according to the method illustrated in Fig. 2a. The PPT point showed a decreasing trend with increasing Li or Sb contents. Similar phase transition points were observed in the samples incorporated with a similar sum of Li and Sb contents.

Figure 2.

(a) Temperature dependence of the dielectric permittivity for representative L_xKNNS_y-5BZ-2BNZ-1Mn samples. (b) The compositional dependence of the PPT point for L_xKNNS_y-5BZ-2BNH-1Mn samples. (c) Room-temperature P–E loops of the representative L_xKNNS_y-5BZ-2BNZ-1Mn samples. (d) P_r extracted from the room-temperature P–E loops of the L_xKNNS_y-5BZ-2BNZ-1Mn samples. (e) The room-temperature piezoelectric coefficient d₃₃ of the L_xKNNS_y-BZ-BNH-1Mn samples. (f) ϵ_r·P_r of the L_xKNNS_y-5BZ-2BNZ-1Mn samples.

Piezoelectricity is closely related to not only ferroelectricity but also dielectricity. P–E loops were measured to investigate the impacts of Li and Sb contents on the ferroelectricity of the L_xKNNS_y-5BZ-2BNZ-1Mn samples (see Fig. S4). As shown in Fig. 2c, the P–E loop changed to be slimmer as Sb content increased, while the opposite trend occurred as Li content increased. Clearly, increasing the Sb content induced a lower E_c while increasing Li content resulted in a higher E_c. The compositional dependence of the remanent polarization P_r extracted from the P–E loops is summarized in Fig. 2d. Significant reduction of P_r was observed when the Sb content was increased. The decreased unit cell distortion can degrade the spontaneous polarization, which then leads to a reduction of the macroscopic remanent polarization. It should be noted that increasing the Li content was found to help maintain a relatively larger remanent polarization in the ceramic samples modified with high Sb content.

Figure 2e shows the room-temperature piezoelectric coefficient d₃₃ of L_xKNNS_y-BZ-BNH-1Mn ceramics. In general, Sb-modified samples exhibited a larger d₃₃ than Li-modified samples. d₃₃ increased as Li or Sb contents increased but extensive addition of Sb or Li deteriorated d₃₃. A similar trend could also be observed with regard to the planar electromechanical coupling factor k_p (see Fig. S5). A peak d₃₃ value ∼510 pC/N was attained in the x = 0.025, y = 0.025 composition. This d₃₃ ranks among the largest d₃₃ values reported in current KNN-based ceramics [4,9–11]. The relationship among the piezoelectric coefficient d₃₃, dielectric permittivity ϵ_r, and remanent polarization P_r has been roughly described as d₃₃ ∝ ϵ_r·P_r in the literature [4,9–11,19]. The relationship d₃₃ ∝ ϵ_r·P_r was also validated in this work, as shown in Fig. 2f. The optimal ϵ_r·P_r was achieved in the composition around x = 0.025, y = 0.025, consistent with the largest d₃₃. As mentioned above, introducing Li and Sb into the KNN matrix did not enhance P_r. The enhancement of ϵ_r·P_r was mainly due to the significant enhancement of ϵ_r, the origin of which could be attributed to the following two mechanisms. One is the dielectric abnormality adjusted by shifting the PPT point close to room temperature by further introducing both Li and Sb. The other is the dielectricity enhancement in the wide temperature range (referred to as dielectricity ‘jumping’), which can be clearly observed when increasing the Sb content (see Fig. S5). The dielectricity ‘jumping’, induced by the various dopants, such as BZ-BNH and Sb, constitutes the main source of the dielectricity enhancement when compared with that of the pristine KNN. This is deemed the cornerstone of the piezoelectricity enhancement in this work.

Investigating the thermal stability of the piezoelectric performance can help to unravel the origin of the property enhancement and also provides valuable information for practical applications. Our previous work showed that the thermal stability of the piezoelectric response could be estimated by measuring field-dependent piezoelectric coefficient d₃₃(E) curves at different temperatures [10,39]. According to this method, the in situ thermal stability of the d₃₃ of the representative compositions was evaluated, and the results are shown in Figs 3a and S6. As expected, all compositions exhibited the highest d₃₃ around their phase transition temperatures, and a monotonically decreasing trend was observed when the temperature deviated from the phase transition point. These results were consistent with the temperature dependence of the ϵ_r·P_r–T curves (see Fig. S7). It is worth noting that the present optimal materials in this study demonstrate higher d₃₃ values and better temperature stability when compared with recently reported KNN-based ceramics, as shown in Fig. 3a [10,13,14,18,19,40–44]. Piezoelectricity enhancement can be witnessed in a broad temperature range (also see Fig. S8). Since piezoelectric abnormality induced by PPT is naturally limited to a specific and small temperature range, the PPT effect is not considered as the main piezoelectricity enhancement mechanism in this study. Instead, we propose that composition-induced structural flexibility, the features of which will be described below, is the main contributing factor for the high piezoelectricity and the dielectricity ‘jumping’. Comparing the results of the temperature dependence of d₃₃, composition-induced structural flexibility accounts for a more than 300% piezoelectricity increase in contrast to that of pristine KNN.

Figure 3.

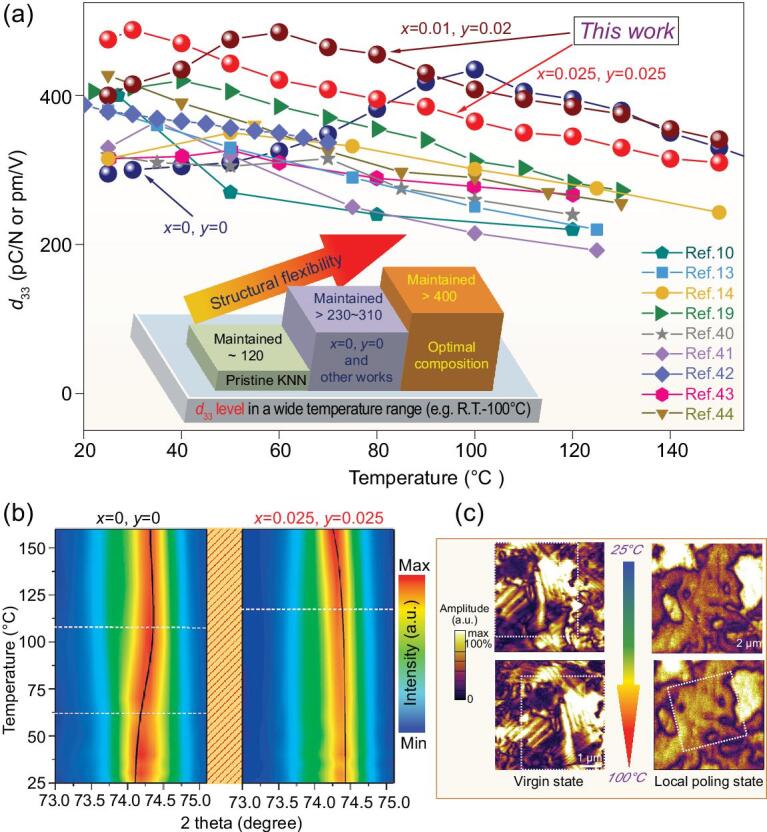
(a) Comparison of the temperature dependences of d₃₃ for various representative KNN-based ceramics. (b) Temperature-dependent neutron diffraction intensity mapping of the 002_pc reflection of the x = 0, y = 0 and x = 0.025, y = 0.025 samples. (c) Out-of-plane PFM amplitudes of the x = 0.025, y = 0.025 sample in the virgin state and local poling state at 25°C and 100°C.

Thermal stability is significantly influenced by the phase structure evolution; thus, temperature-dependent neutron diffraction (ND) measurements on two selected samples, x = y = 0 and x = y = 0.025, were conducted. Figure 3b shows the 002_pc reflection of the ND patterns at a temperature range of 20–160°C. The evolution of the 002_pc reflections with temperature increasing for the x = y = 0 sample was more obvious than that of the x = y = 0.025 sample. The latter almost stood still in the temperature range between approximately 20°C and 100°C. The divided three different parts of the temperature-dependent 002_pc reflections for the x = y = 0 corresponded to the temperature dependence of the d₃₃ (E = 0) and ϵ_r. These were associated with two sudden temperature-induced structural changes. In contrast, the phase structure of the x = y = 0.025 sample experienced a gradual change over a broad temperature range. The diffused thermally stable structure might be partially responsible for the high thermal stability of the piezoelectric performance.

The piezoelectric property is also intimately associated with the domain morphology. The micro-scale domain morphology was investigated via piezoresponse force microscopy (PFM). In situ observations of the domain morphologies of the virgin state and the local poling state for the x = y = 0.025 sample were investigated at different temperatures. Figure 3c shows the amplified domain morphologies, where no significant change was observed as the temperature increased from 25°C to 100°C (full data can be found in Fig. S9). The thermally stable micro-scale domain structure might also contribute to the noteworthy thermal stability of d₃₃.

The underlying mechanisms of high piezoelectricity of the x = y = 0.025 ceramics were further explored via transmission electron microscopy (TEM). Substructural twinning was observed at the nanoscale, as shown in Fig. 4a, c, d. Stripe sub-micron domains were well arranged and composed by lamellar nanodomains, and both domains exhibited strict alternation. The average width of the lamellar nanodomains was approximately 5–10 nm, which is much smaller than nanotwinned structures that have been extensively reported in other lead-based and lead-free materials [4,10,11,14,19,45–51]. As shown in Fig. 4b, the corresponding electron diffraction pattern demonstrated streaking and elongating of the reflection spots, which was attributed to the slim nanodomains [46]. Clearly, the current material possessed a hierarchical nanodomain architecture as outlined in Fig. 4e [49]. It is worth noting that the domain configuration is a 3D architecture; however, the domain morphology observed using TEM only shows a 2D projection. This can be influenced by various factors such as the viewing direction, the thickness of the specimen, and boundary conditions [47,48,51]. It is common to observe utterly different morphologies in the TEM investigations; however, useful structural information can still be verified. Domain patterns featured with irregular fringe contrast or fibrous structures were observed as illustrated in Figs 4f–h and S10. Interestingly, traces of numerous nanodomains within sub-micron domains could be found in these domain patterns, which also possess a hierarchical characteristic. Recently, it has been reported that the fragmentation of local structure can contribute to the enhancement of the piezoelectric response [24,25]. An in situ TEM investigation of the electric-field-driven evolution of the domain structure showed that the existence of nanodomains is closely related to the extrinsic piezoelectric effect. This is because the real-time response occurred in nanodomains rather than the visibly unchanged micro-domain structures [47]. The facilitation of polarization reorientation under external stimulation enabled the miniaturization of the domain structure due to the drastic decrease of the domain wall energy [20,46,50]. The transformation stress between two polarization states of different phases can also be alleviated by the nanotwinned structure, which induces lattice softening [46,47,52]. Consequently, a hierarchical domain configuration that consists of nanodomains and nanotwins can lead to both a nearly vanishing polarization anisotropy and elastic softening. This ultimately results in the enhancement of the piezoelectric response [53].

Figure 4.

(a, c, d) Bright-field TEM images of the x = 0.025, y = 0.025 sample, showing hierarchical domain configuration and the corresponding selected area electron diffraction (SAED) pattern (b). (e) Schematic diagram of the hierarchical nanodomain architecture. (f–h) Bright-field TEM images of the x = 0.025, y = 0.025 sample showing strip-like and fibrous nanodomain patterns.

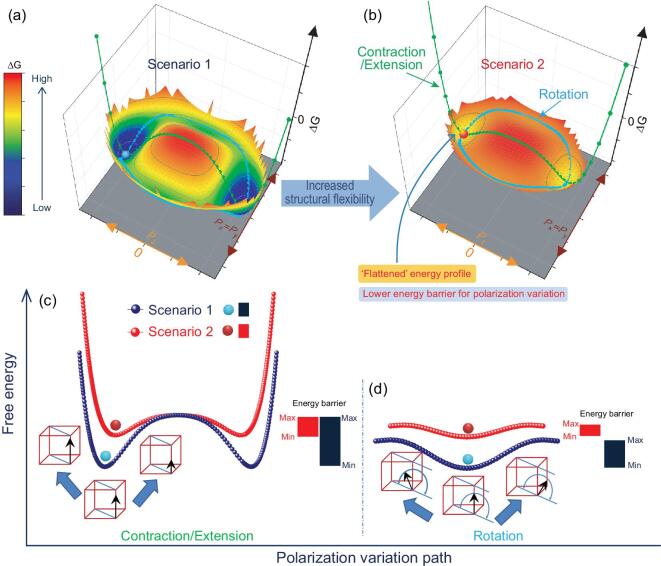
Based on these investigations, a phenomenological analysis of the piezoelectricity enhancement mechanism was conducted. In this study, the unit cell distortion of the global lattice decreased with increasing Sb content and increased with increasing Li content. The reduction of the unit cell distortion indicates a decrease in crystalline anisotropy, which can result in a smaller free energy barrier among the ferroelectric/paraelectric phases. Furthermore, the presence of lattice softening can alleviate transformation stress during lattice deformation. This favors a lower energy barrier during the polarization variation between ferroelectric states. Structural flexibility can arise from all these factors, leading to an ease of polarization variation and thus ‘soft’ behavior, expressed as low E_c and high dielectricity (see Fig. S4). However, the decreased unit cell distortion can also exert negative effects. It can decrease the spontaneous polarization, which then leads to the reduction of the macroscopic remanent polarization. The lowered polarization value might counteract the positive effect of the easier polarization variation when the unit cell distortion becomes too small. Thus, the lower unit cell distortion ratio might contribute to the piezoelectric response; however, an optimum value exists. The obtained experimental results indicate that introducing both Sb and Li elements into the ceramics was verified to be an effective way to achieve both the ‘soft’ behavior and maintaining the macroscopic remanent polarization. Possible energy landscapes can be generated by the suitable arrangement of parameters, while fully considering the above factors in the framework of the Landau–Ginzburg–Devonshire model [20,54]. This might help to understand the property enhancement due to increased structural flexibility. Figure 5 depicts the dissimilarity of energy landscapes for one polarization variation path between the following two scenarios: with and without increased structural flexibility. For the consistence of experimental results in this study, the tetragonal phase is considered as the initial and most stable phase in both cases. To aid an intuitive understanding, the energy landscapes are presented in a colorful 3D surface, as shown in Fig. 5a and b. This exhibits the change of free energy via the polarization variation path under the condition of polarization components P_x = P_y. Moreover, the energy landscapes of two typical polarization variation paths, namely, constriction/extension and rotation [55,56], are extracted from the 3D surfaces and compared, as shown in Fig. 5c and d, respectively. Decreased anisotropy of the free energy with polarization can be perceived when the energy barrier between various ferroelectric/paraelectric states decreases. A more ‘flattened’ energy profile can be established by cautiously increasing the composition-induced structural flexibility, which can result from lattice softening [46,53] and reduced unit cell distortion. The induced ‘flattened’ energy profile contributes to the facilitation of the polarization variation, thus accounting for the piezoelectricity enhancement of Li and Sb co-modified ceramics.

Figure 5.

Phenomenological illustration of the piezoelectricity enhancement associated with increased structural flexibility. (a, b) Comparison of the energy landscape with polarization variation under the condition of P_x = P_y between two ferroelectric systems before and after additional structural flexibility is introduced. (c) Comparison of the energy landscapes for the polarization contraction/extension paths of scenario 1 and scenario 2 according to the 3D surfaces in (a) and (b), respectively. (d) Comparison of the energy landscapes for the polarization rotation paths of scenario 1 and scenario 2 according to the 3D surface in (a) and (b), respectively.

CONCLUSION

In summary, enhanced piezoelectricity with improved thermal stability was achieved in L_xKNNS_y-BZ-BNH-1Mn ceramics, and its physical origins were systematically studied via comparative analyses. The softening effect and the optimum unit cell distortion are indispensable for large d₃₃ exceeding 500 pC/N, achieved in this work. The presence of a hierarchical domain structure played a vital role in synergistically achieving reduced polarization anisotropy and elastic softening. This results in enhancements in the piezoelectric properties and thermal stability. We believe that this work can pave the way for the exploration of high-performance piezoceramics with excellent thermal reliability.

METHODS

Sample preparation

Lead-free ceramic samples of the nominal composition 0.93(Li_xNa_0.52K_0.48-x)(Nb_1-y,Sb_y)O₃-0.05BaZrO₃-0.02(Bi_0.5,Na_0.5)HfO₃ with 1 wt% MnO₂ as a sintering aid [39] (abbreviated as L_xKNNS_y-5BZ-2BNH-1Mn, 0 ≤ x ≤ 0.03, 0 ≤ y ≤ 0.03) were synthesized via conventional ceramic processing. Firstly, the precursor oxides powders, including Li₂CO₃ (99%), Na₂CO₃ (99.8%), K₂CO₃ (99%), Nb₂O₅ (99.99%), Sb₂O₃ (99.99%), BaCO₃ (99.95%), ZrO₂ (99.9%), HfO₂ (99.99%), and Bi₂O₃ (99.99%), were weighed according to their stoichiometric ratio and were then homogeneously mixed in ethanol using a planetary ball mill for 24 h. Calcination of the dried mixture was performed at 950°C for 4 h, and then the resultant powders were subjected to ball milling again with 1.0 wt% MnO₂ as a sintering aid for 24 h. After drying, the powder mixtures were pressed into compacted disks of 10 mm in diameter, which was followed by cold isostatic pressing at 200 MPa for 2 min. The green pellets were sintered in the temperature range between 1080°C and 1180°C for 6 h.

Crystal structure and microstructure analysis

The crystal structure was determined by an X-ray diffractometer (XRD, D/Max 2500; Rigaku, Tokyo, Japan) with a Cu K_α1 (λ = 1.5405 Å) monochromator. The Raman spectra were collected by a Raman spectrophotometer (LabRAM HR, HoRIBA Jobin Yvon, France) with a 633 nm laser. Piezoresponse force microscope (PFM) observations were conducted using a commercial atomic force microscope (MFP-3D, Asylum Research, USA) with the functionality of a PFM. Additionally, to obtain TEM specimen, the as-sintered disks were first mechanically polished to around 20 μm in thickness. Lamellar samples were further reduced to reach electron transparency by using argon-ion beam milling (Gatan PIPS 695, Gatan Inc., USA) with an acceleration voltage of 0.1–6 kV. A high-resolution TEM (JEOL 2100, JEOL, Japan), which operated at 200 kV, was used to conduct TEM investigations. Neutron diffraction measurements were conducted using a high-intensity powder diffractometer (Wombat) at the Australian Nuclear Science and Technology Organisation (ANSTO). A CaAlNaF₃ standard sample was used to determine the wavelength of the neutron beam, which was refined to 2.41962(6) Å. The dimension of the samples was 3.5 × 3.5 ×30 mm [3].

Electrical property measurements

The as-sintered pellets were first ground to 1 mm thickness. Two surfaces of the samples, which were polished by using silicon carbide papers, were painted with silver pastes burnt in afterwards at 600°C for 30 min. The measurement of the temperature dependence of permittivity was conducted under 1 kHz during the heating process (2°C/min) using a precision LCR meter (TH2827C, Changzhou Tonghui Electronic Co., China) with a temperature-regulated chamber. The quasistatic piezoelectric coefficient d₃₃ was measured by a Berlincourt meter (ZJ-3A, Institute of Acoustics, Chinese Academy of Sciences, China). Other ferroelectric and piezoelectric parameters including the piezoelectric coefficient d₃₃(E), the unipolar strain S(E), and polarization P(E) hysteresis loops were measured by the same apparatus and method used previously [19,57].

FUNDING

This work was supported by the Basic Science Center Project of the National Natural Science Foundation of China (51788104 and 51761135118), the Ministry of Science and Technology of China (2015CB654605), the German Research Society (DFG) (HI1867/1–1), and the China Postdoctoral Science Foundation (2017 M620042).

AUTHOR CONTRIBUTIONS

Q.L. synthesized the samples, conducted the experiments, and analyzed the results with J.F.L. and Y.C.Z. All authors discussed the results. Q.L. wrote the manuscript, and Y.C.Z. and J.F.L. revised the manuscript.

Conflict of interest statement. None declared.