Superconductivity in chromium nitrides Pr₃Cr_10-xN₁₁ with strong electron correlations

Abstract

Exploration of superconductivity in Cr-based compounds has attracted considerable interest because only a few Cr-based superconductors (CrAs, A₂Cr₃As₃ and ACr₃As₃ (A = K, Rb, Cs, Na)) have been discovered so far and they show an unconventional pairing mechanism. We report the discovery of bulk superconductivity at 5.25 K in chromium nitride in Pr₃Cr_10-xN₁₁ with a cubic lattice structure. A relatively large upper critical field of H_c2(0) ∼ 12.6 T is determined, which is larger than the estimated Pauli-paramagnetic pair-breaking magnetic field. The material has a large electronic specific-heat coefficient of 170 mJ K⁻² mol⁻¹—about 10 times larger than that estimated by the electronic structure calculation, which suggests that correlations between 3d electrons are very strong in Pr₃Cr_10-xN₁₁, and thus quantum fluctuations might be involved. Electronic structure calculations show that the density of states at the Fermi energy are contributed predominantly by Cr 3d electrons, implying that the superconductivity results mainly from the condensation of Cr 3d electrons. Pr₃Cr_10-xN₁₁ represents a rare example of possible unconventional superconductivity emerging in a 3D system with strong electron correlations. Nevertheless, clarification of the specific pairing symmetry needs more investigation.

INTRODUCTION

The 3d transition-metal oxides or pnictides exhibit rich quantum phases with novel quantum states, such as long-range magnetic orders, charge or spin density waves, metal-insulator transitions, high-T_c superconductivity and colossal magnetoresistance. In particular, unconventional high-T_c superconductivity has been discovered in cuprates as well as in iron-based superconductors [1,2]. Many compounds with 3d transition-metal elements can become superconducting at low temperatures. However, it is relatively difficult to find a superconducting material in chromium-based compounds because most Cr-based compounds have strong magnetism, which generally is not in favor of superconductivity. In fact, CrAs, A₂Cr₃As₃ and ACr₃As₃ (A = Na, K, Rb, Cs) are the only Cr-based superconductors so far [3–6].

Superconductivity in CrAs was discovered in 2014 [3,4]. CrAs undergoes a first-order antiferromagnetic transition with a double helical spin structure at T_N ≈ 265 K [3,7,8]. A bulk superconductivity with T_c ≈ 2 K emerges above a pressure P_c ≈ 8 kbar, where the antiferromagnetic order is completely suppressed. Both the NMR and neutron-scattering measurements for CrAs under high pressure revealed that there are strong magnetic fluctuations and line nodes may exist in the superconducting gap function [9–13], as in Sr₂RuO₄ or some heavy fermion superconductors [14,15]. After the discovery of superconductivity in CrAs, superconductivity has also been found in the quasi-1D compounds A₂Cr₃As₃ (A = K, Rb, Cs) [3,4]. The upper critical field H_c2 of K₂Cr₃As₃ is about three times larger than the Pauli-paramagnetic limit.

In this paper, we report a novel Cr-based nitride superconductor with a cubic structure, Pr₃Cr_10-xN₁₁, which was first synthesized and characterized by Broil et al. in 1995 [16]. The compound crystallizes in space group Fm-3m (No. 225) with lattice constant a = 12.891 Å. It contains 192 atoms in a face-centered cubic (FCC) cell with three kinds of building blocks, as illustrated in Fig. 1a. The building blocks are Pr₆N₉, Cr₈N₁₃ and Cr₆. Previous studies showed that there are Cr vacancies in the lattice structure. However, no low-temperature physical properties were reported [16,17]. Our key finding of this study is the observation of superconductivity in Pr₃Cr_10-xN₁₁ with T_c ∼ 5.25 K. The high-quality samples have a shielding fraction of 85% at 2 K from zero-field-cooled (ZFC) magnetic susceptibility and a prominent superconducting peak in the specific-heat measurement. A relatively large upper critical field is found at the zero-temperature limit, H_c2(0) ∼ 12.6 T, which is larger than the Pauli-paramagnetic pair-breaking field. From electronic structure calculations, we find that the density of states (DOS) at the Fermi energy are predominately contributed by Cr 3d electrons. The present results demonstrate that Pr₃Cr_10-xN₁₁ is the first Cr-based superconductor discovered in chromium nitrides and it represents a rare example that possibly unconventional superconductivity emerges in a 3D system with strong electron correlations.

Figure 1.

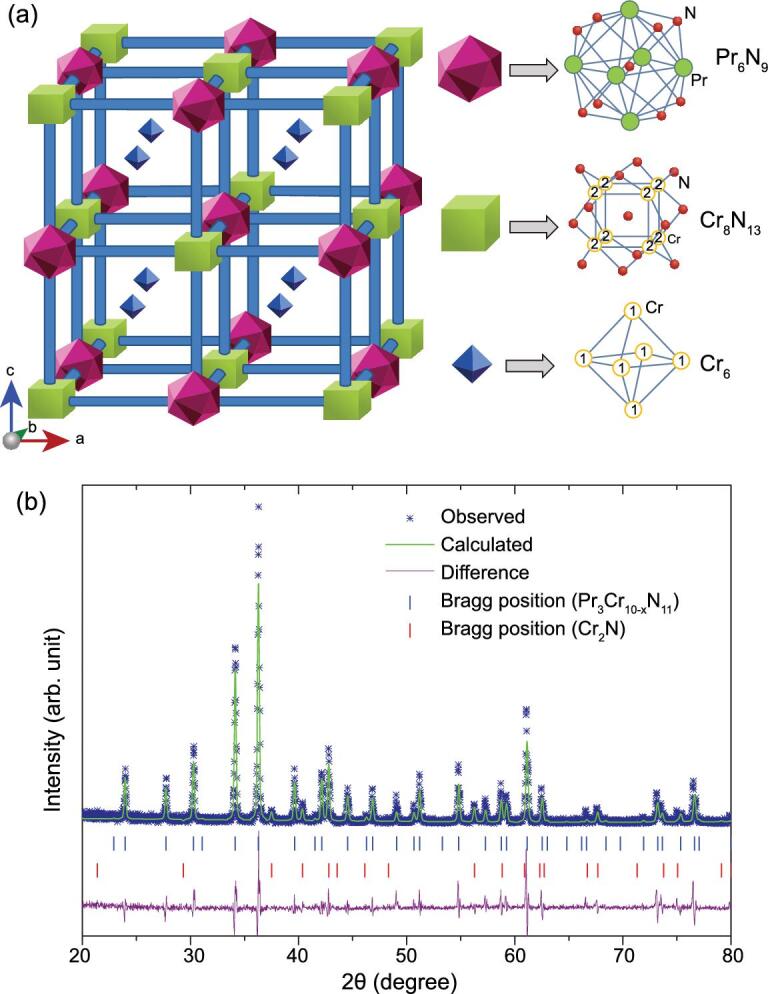
(a) The face-centered cubic cell of Pr₃Cr_10-xN₁₁ with three kinds of building blocks: Pr₆N₉, Cr₈N₁₃ and Cr₆, respectively. The blocks are shown in a shrunken form. There are two Cr positions: Cr1 and Cr2. (b) Typical Rietveld refinement of Pr₃Cr_10-xN₁₁ under ambient conditions. The vertical bars represent the calculated Bragg reflection positions of the diffraction peaks for Pr₃Cr_10-xN₁₁. The difference between the observed (scatters) and the fitted patterns (line) is shown at the bottom of the diffraction peaks.

RESULTS AND DISCUSSION

Sample and characterization

Polycrystalline samples of Pr₃Cr_10-xN₁₁ were prepared by direct reactions of the corresponding binary nitrides with solid reaction. Synthesized powder shows a dark-brown color and is air-sensitive, as it is easily oxidized to Pr₂O₃ within a few hours. Figure 1b shows the General Structure Analysis System (GSAS) refinement of Pr₃Cr_10-xN₁₁ under ambient conditions, which indicates that Pr₃Cr_10-xN₁₁ crystallized in an FCC structure with space group Fm-3m. All the Pr₃Cr_10-xN₁₁ reflections can be well indexed based on a cubic cell with lattice parameter a = 12.8521 Å, which is consistent with those reported in the literature (a = 12.891 Å) [16], indicating their ideal composition. A small amount of raw reactant Cr₂N was marked with a red vertical bar.

Temperature-dependent resistivity in Pr₃Cr_10-xN₁₁

Figure 2a shows the temperature-dependent resistivity for Pr₃Cr_10-xN₁₁ from 1.8 to 300 K at zero field. The normal-state resistivity is metallic, with no phase transition observed. At low temperatures, a sharp superconducting transition is observed with onset T_c of about 5.25 K, as shown in the inset of Fig. 2a. The T_c of Pr₃Cr_10-xN₁₁ is higher than that of CrAs with T_max ∼ 2 K under pressure and is close to K₂Cr₃As₃ with T_c ∼ 6.1 K [12].

Figure 2.

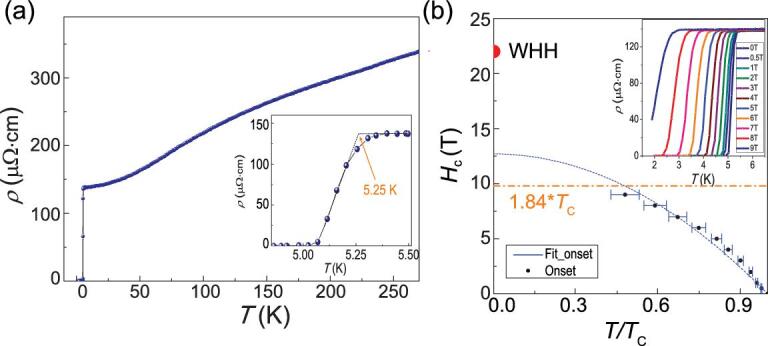
(a) Temperature dependence of the resistivity for Pr₃Cr_10-xN₁₁ from 1.8 to 300 K at the zero field. The inset shows the resistivity near superconducting transition. (b) The temperature dependence of the upper critical magnetic field. The solid circle shows the upper critical field obtained from WHH fitting. The inset shows the temperature dependence of the resistivity at different fields.

The new superconductor Pr₃Cr_10-xN₁₁ shows a relatively large upper critical field. Figure 2b shows resistivity data in magnetic fields up to 9 T. As the field increases, the transition temperature T_c shifts to a lower temperature and the transition width is gradually broadened, similar to the iron-based superconductors [18,19]. The upper critical field H_c2 (T) curve obtained from the field-dependent transition temperatures shows a remarkably high critical field of 12.6 T using the formula H_c2(T) = H_c2(0)(1 − t²), where t is the reduced temperature t = T/T_c and of 22 T using the Werthamer−Helfand−Hohenberg (WHH) theory [20]. On the other hand, the Pauli-paramagnetic limit for the upper critical field is H_P = 1.84T_c ≈ 9.6 T in the case of an isotropic full superconducting gap without considering spin–orbit coupling [21,22]. The H_c2 (0) in Pr₃Cr_10-xN₁₁ is 130% as large as H_P. Usually, the high superconducting upper critical field can be originated from multi-band effects, the strong-coupling effect, the spin-triplet pairing and the strong spin–orbit coupling effect in a low-dimensional system [23–25]. The origin of large H_c2(0) in Pr₃Cr_10-xN₁₁ needs to be further studied. The obtained 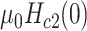allows us to estimate the Ginzburg–Landau coherence length 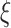= 51 Å according to the relationship: 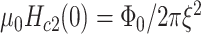, where 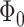=2.067 × 10⁻¹⁵ Wb is the magnetic flux quantum.

Magnetic-susceptibility measurements in Pr₃Cr_10-xN₁₁

The bulk superconductivity in Pr₃Cr_10-xN₁₁ was confirmed by magnetic-susceptibility measurements. Figure 3a shows susceptibility χ at low temperatures with ZFC and field cool (FC) under a magnetic field of 30 Oe. χ starts to drop below T_c and the diamagnetic signal tends to saturate at low temperatures. The shielding fraction estimated from the ZFC magnetic susceptibility at 2 K is 85%, confirming bulk superconductivity in the sample. The normal-state susceptibility χ increases with decreasing temperature in Pr₃Cr_10-xN₁₁, showing a Curie–Weiss behavior as shown in the inset of Fig. 3a. Such behavior is different from that of isostructural material La₃Cr_10-xN₁₁, which shows a Pauli paramagnetism with a nearly temperature-independent susceptibility [16]. Since La³⁺ ion has no occupied 4f electrons while each Pr³⁺ ion has two occupied 4f electrons, it is natural to attribute the Curie–Weiss behavior of χ(T) in Pr₃Cr_10-xN₁₁ to the magnetic moments of Pr³⁺ 4f electrons. Using a Curie–Weiss fit with formula χ(T) = χ₀ + C/(T-θ), we obtained the effective moment of each Pr ion at about 3.6 μ_B, which is very close to the calculated moment of 3.5 μ_B for Pr³⁺ by Hund’s rule. The negative value of θ indicates the correlations between Pr ions are antiferromagnetic.

Figure 3.

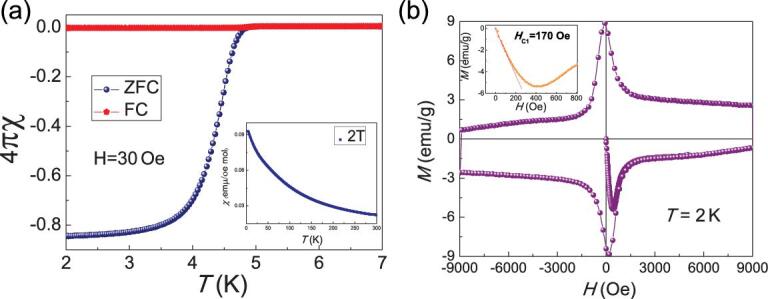
(a) Temperature dependence of the dc magnetic susceptibility with zero field cool (ZFC) and field cool (FC) measured in a field of 30 Oe. The inset of Fig. 3a is the normal-state susceptibility measured in a field of 2 T. (b) The magnetic hysteresis of the sample measured at 2 K. The left inset shows the lower critical magnetic field.

Further confirmation of superconductivity is shown by the magnetic hysteresis of the sample measured at 2 K in Fig. 3b, which displays the typical magnetic hysteresis curve for a type-II superconductor. From the inset of Fig. 3b, the lower critical magnetic fields H_c1 of 170 Oe can be obtained.

Specific-heat measurements

Figure 4a shows the specific-heat coefficient C/T as a function of T² from 2 to 10 K at the zero field. The bulk nature of superconductivity is confirmed by a pronounced anomaly around T_c = 5.25 K, consistently with the resistivity and susceptibility measurements. Extrapolating C/T to zero temperature gives a residual value of γ₀ = 0.061 mJ g⁻¹ K⁻². As indicated previously, there is raw reactant phase Cr₂N in the sample. We measured the specific heat of Cr₂N and found that it can be well fitted by C = γT + βT³ below 10 K with γ = 22 mJ mol⁻¹ K² and β = 0.0373 mJ mol⁻¹ K⁴. Given the residual specific-heat γ₀ origin from the Cr₂N phase, we can then obtain the specific heat of pure Pr₃Cr_10-xN₁₁ by subtracting that of Cr₂N from the total specific heat, as shown in the inset of Fig. 4a.

Figure 4.

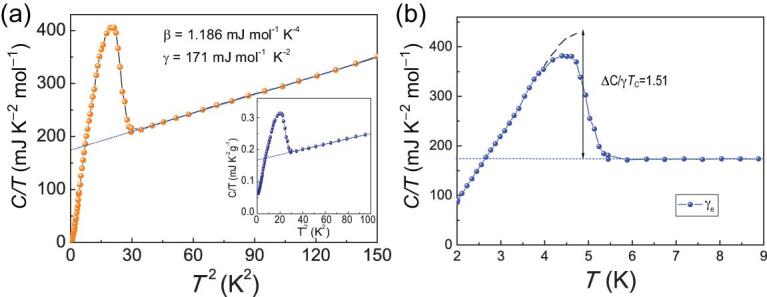
(a) The specific-heat coefficient C/T of Pr₃Cr_10-xN₁₁ as a function of T ². The inset shows C/T versus T ² for a sample with Cr₂N_. (b) Temperature dependence of normalized electronic specific-heat C_e/ T.

Above T_c, the good linear T ² dependence of C/T indicates that the normal-state specific heat consists of two parts of contributions: the electronic part, which is proportional to T, and the phonon part, which is proportional to T³ at low temperatures. By fitting the normal-state specific heat C with the formula C = γ_nT + βT³, we find that γ_n = 173 mJ K⁻² mol⁻¹ and β = 1.186 mJ K⁻⁴ mol⁻¹. The normal-state electronic coefficient γ_n is proportional to the DOS at the Fermi level. Assuming that most of the DOS comes from the Cr 3d electrons, the value of γ_n per mole Cr is γ_n = 17.3 mJ K⁻² mol Cr⁻¹ for Pr₃Cr_10-xN₁₁, which is much larger than the corresponding value for CrAs (∼7 mJ K⁻² mol⁻¹) and MnP (∼8.3 mJ K⁻² mol⁻¹) at ambient pressure [11,26] and it is slightly less than that for K₂Cr₃As₃ (∼23.3 mJ K⁻² mol Cr⁻¹) and KCr₃As₃(∼27.1 mJ K⁻² mol Cr⁻¹) [14,27,28]. The relatively large γ_n for Pr₃Cr_10-xN₁₁ indicates strong correlations of Cr 3d electrons. The Debye temperature θ_D obtained from β is 339 K.

In Fig. 4b, the normalized specific-heat jump at T_c is found to be ΔC/γ_nT_c = 1.51. This value is much smaller than those of K₂Cr₃As₃ (∼2.5) and LaNiAsO (∼1.9), which are regarded as strong-coupling superconductivity [14,27,29]. The normalized ΔC/γ_nT_c reflects the coupling strength between the conducting electrons and the pairing glue. We can then estimate the electron–phonon coupling constant λ = 0.6 from the modified McMillian formula [25,30,31]:

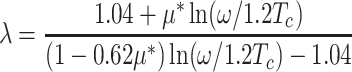where μ^∗ is a Coulomb pseudopotential and ω is a logarithmic averaged phonon frequency. ω can be determined from the specific-heat jump at T_c using the formula: ΔC/γ_nT_c = 1.43[1 + 53(T_c/ω)2ln(ω/3T_c)]. Taking μ^∗ = 0.10 and T_c = 5.25 K, we obtained ω = 320 K and λ = 0.6. For such a small electron–phonon coupling constant, the large H_c2(0) value is not likely due to the strong-coupling effect.

Theoretical calculations

In order to examine which atomic species contribute most around the Fermi level (E_F), we have plotted the local density of states (LDOS) for Pr₃Cr_9.5N₁₁ as shown in Fig. 5. Electronic structure calculations show that the DOS at the Fermi energy are contributed predominantly by Cr 3d electrons, implying that the superconductivity results mainly from the condensation of Cr 3d electrons similar to that in CrAs [32]. The primitive cell of Pr₃Cr_10-xN₁₁ is shown in the inset of Fig. 5, in which there are two types of nonequivalent Cr atoms, labeled as Cr1 and Cr2, respectively. Both the Cr1 and Cr2 atoms have large contributions around E_F, mainly originating from the 3d orbitals of Cr atoms. In contrast, the vast majority of states for Pr and N atoms are far from the Fermi level. A higher density of Cr2 vacancies, such as in Pr₃Cr₉N₁₁, does not change the results very much. According to our calculations, the total DOS of Pr₃Cr_9.5N₁₁ at the Fermi level N(E_F) is 7.37 states/(eV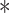f.u.). As a result, the corresponding calculated electronic specific-heat coefficient γ_e is 17.4 mJ K⁻² mol⁻¹. Experimentally, the measured γ_e for Pr₃Cr_10-xN₁₁ is about 173 mJ K⁻² mol⁻¹—about 10 times more than the band calculations, which indicates the strong mass-enhancement effect.

Figure 5.

Local density of states (LDOS) for Pr, Cr1, Cr2 and N atoms in Pr₃Cr_9.5N₁₁. Inset shows a primitive cell with the yellow, blue, maroon and gray balls representing Pr, Cr1, Cr2 and N atoms, respectively. The atomic vacancy at the Cr2 site is highlighted by a red dashed circle.

CONCLUSION

Superconductivity in Pr₃Cr_10-xN₁₁ shows several novel characters. First, electronic structure calculations show that most of DOS at Fermi energy is contributed by Cr 3d electrons, suggesting that the superconductivity is originated from the condensation of Cr 3d electrons. So Pr₃Cr_10-xN₁₁ is the first Cr-based superconductor discovered in nitrides. A few other known Cr-based superconductors (CrAs, A₂Cr₃As₃ and ACr₃As₃ (A = K, Rb, Cs, Na)) are arsenide. Superconductivity in CrAs emerges in the vicinity of a quantum critical point and antiferromagnetic spin fluctuations associated with the quantum criticality could act as an important glue medium for Cooper pairing. Superconductivity in the quasi-1D compounds A₂Cr₃As₃ (A = K, Rb, Cs) shows non-s-wave pairing. Both of them show an unconventional pairing mechanism. So the Cr d-electrons play an important role in electron correlations and possibly unconventional superconductivity in Pr₃Cr_10-xN₁₁ with Cr d-electrons.

Second, Pr₃Cr_10-xN₁₁ has a relatively large upper critical field H_c2(0) ∼ 12.6 T, exceeding the Pauli limit of the paramagnetic pair-breaking field; this is rare in 3D-structure superconductors. The upper critical field provides very important information on the superconducting pairing. This behavior resembles that unconventional superconducting in K₂Cr₃As₃ in which H_c2 is three times the Pauli-paramagnetic limit that is regarded as evidence of spin-triplet superconductivity.

Last but not least, the measured γ_e for Pr₃Cr_10-xN₁₁ is about 173 mJ mol⁻¹ K⁻², equivalent to 17.3 mJ K⁻² mol Cr⁻¹. This γ value is close to that of K₂Cr₃As₃ (mJ K⁻² mol Cr⁻¹), indicating enhanced electron correlations in Pr₃Cr_10-xN_11. The experimental value of γ_e is about 10 times higher than the electronic calculations. This large renormalization factor cannot be explained by electron–phonon interactions and thus quantum fluctuations might be involved.

In conclusion, we report the experimental result for a novel Cr-based superconductor nitrides Pr₃Cr_10-xN₁₁ with a cubic lattice structure. Bulk superconductivity with T_c ∼ 5.25 K is observed from the resistivity, susceptibility and specific-heat measurements. Further theoretical and experimental studies are needed to determine the pairing symmetry and the corresponding mechanism, especially the role of Cr 3d electrons, for the observed superconductivity in Pr₃Cr_10-xN₁₁.

METHODS

Sample preparation

Polycrystalline samples of Pr₃Cr_10-xN₁₁ were prepared by direct reactions of the corresponding binary nitrides, staring with PrN (99%) and a mixture of the chromium nitrides (CrN and Cr₂N) in a mass ratio of 4:6. The operations were all performed in an Ar-filled glovebox. Cold-pressed pellets of the mixtures were sealed in an evacuated quartz tube (<10⁻⁴ Pa). The pellets were gradually heated in 1 day to 1000°C, held at that temperature for 50 hours, then cooled to the room temperature in the furnace. The products were again ground in a glovebox, pressed into pellets, wrapped in Ta foil and heated in an evacuated quartz tube at 1165°C for 120 hours. It is worth noting that, after this treatment, the samples were usually still contaminated by the binary nitrides. The treatment of these samples with diluted hydrochloric acid only dissolved the rare-earth nitrides. In between these treatments, the pellets were ground to a fine powder, the decomposed rare-earth nitride was dissolved in hydrochloric acid and fresh rare -earth nitride was added again to the mixture to maintain the proper composition. The reaction temperature was carefully selected to avoid decomposition of the products, meanwhile obtaining a good crystallization. In our study, we found that Pr₃Cr_10-xN₁₁ partially decomposed above 1200°C. Synthesized powder shows a dark-brown color and is air-sensitive, as it is easily oxidized to Pr₂O₃ within a few hours.

Measurements

The electrical transport measurement was carried out on a physical-property measurement system (PPMS-9, Quantum Design). The resistivity was measured by a standard four-probe method, employing silver-paste contacts cured at room temperature, used for resistivity measurements, with the electric current applied in an arbitrary direction. The magnetic susceptibility was measured in a Quantum Design SQUID VSM. The specific-heat measurements were performed up to 9 T in a PPMS.

Theoretical modeling

We carried out first-principles electronic structure calculations on Pr₃Cr_10-xN₁₁. The first-principles calculations were performed using the projector augmented-wave method [33], as implemented in the VASP package [34]. The generalized gradient approximation of the Perdew–Burke–Ernzerhof type [35] was adopted for the exchange-correlation function.

FUNDING

This work was supported by the National Basic Research Program of China (2017YFA0302901, 2014CB921500), the National Natural Science Foundation of China (11674375, 11634015) and the Strategic Priority Research Program and Key Research Program of Frontier Sciences of the Chinese Academy of Sciences (XDB07020200).

Conflict of interest statement. None declared.