Abstract
Ever since its first proposal in 1976, Jackiw-Rebbi zero-mode has been drawing extensive attention for its charming properties including charge fractionalization, topologically protected zero-energy and possible non-Abelian statistics. We investigate these properties through the Jackiw-Rebbi zero-modes in quantum spin Hall insulators. Though charge fractionalization is not manifested, Jackiw-Rebbi zero-mode's zero-energy nature leads to a double-frequency Aharonov-Bohm effect, implying that it can be viewed as a special case of Majorana zero-mode without particle-hole symmetry. Such relation is strengthened for Jackiw-Rebbi zero-modes also exhibiting non-Abelian properties in the absence of superconductivity. Furthermore, in the condition that the degeneracy of Jackiw-Rebbi zero-modes is lifted, we demonstrate a novel non-Abelian braiding with continuously tunable fusion rule, which is a generalization of Majorana zero-modes’ braiding properties.
Keywords: Jackiw-Rebbi zero-mode, Aharanov-Bohm effect, non-Abelian statistics, Majorana zero-mode
INTRODUCTION
Jackiw-Rebbi zero-mode was first raised as the zero-energy soliton solution of Dirac equation in one spatial dimension [1]. In the presence of such a zero-mode, the total charge of the ‘Dirac sea’ is half-integer [2–6] due to charge-conjugation symmetry, which is regarded as another mechanism of charge fractionalization, in addition to the prestigious fractional quantum Hall (FQH) effect [7–10]. In condensed matter physics, Jackiw-Rebbi zero-mode is closely related to the band topology [11,12]. The first famous example is the Su-Schrieffer-Heeger (SSH) model [13] whose low-energy effective Hamiltonian is equivalent to a 1D topological insulator (TI), and Jackiw-Rebbi zero-mode resides in the domain wall separating topologically distinct phases. Another celebrated example is the Kitaev's chain [14] whose effective Hamiltonian is again equivalent to a 1D TI. The difference is that the zero-mode here is self-conjugate due to the superconductivity and therefore a Majorana one. In this vein, Jackiw-Rebbi zero-mode can be regarded as a special case of Majorana zero-mode (MZM) in the absence of particle-hole (PH) symmetry [10,15].
In the last decade, Jackiw-Rebbi zero-mode was proposed in topological systems including spin ladders [16,17], Rashba nanowires [18–21], and quantum spin Hall insulator (QSHI) with constriction [22,23] or external magnetic field [24]. These zero-modes are created or annihilated pairwisely, hence the braiding processes are non-commutative [8] due to the fermion parity conservation [16,25]. However, on the contrary of its Majorana cousin [26], Jackiw-Rebbi zero-mode's non-Abelian nature has not yet been demonstrated in a practical device such as trijunction [17,27–30] or cross-shaped junction [31,32] as has been done for MZMs.
Another peculiar property of the Jackiw-Rebbi zero-mode is the 1/2 charge fractionalization, which has been claimed [24] to be detectable in a pumping process [33] or by Coulomb blockade. Recently, a novel 3/2 FQH plateau is observed in single layer 2D electron gas with confined geometry [34]. Jackiw-Rebbi zero-mode induced by the confined geometry could be a tentative explanation [34] that similar mechanism has been proposed in QSHI [22].
In this article, we first construct a QSHI heterostructure supporting Jackiw-Rebbi zero-mode. Then we investigate the Aharonov-Bohm (AB) effect where a single Jackiw-Rebbi zero-mode is embedded in an AB ring, showing a double-frequency AB oscillation at zero-energy. A comparison with MZM’s AB effect supports the aforementioned relation between Jackiw-Rebbi zero-mode and MZM. We also set up a cross-shaped QSHI junction and numerically confirm the non-Abelian braiding properties of Jackiw-Rebbi zero-modes to be in analogy with MZMs. Importantly, Jackiw-Rebbi zero-modes represent a novel non-Abelian braiding corresponding to a generalized fusion rule when the zero-modes’ degeneracy is lifted by chiral-symmetry-breaking disorder or by tuning gate voltages. Such generalized and continuously tunable non-Abelian braiding can also be realized for MZMs if ‘fictitious’ disorder breaking PH-symmetry is presented.
LATTICE REALIZATION OF JACKIW-REBBI ZERO-MODE
The 1D effective Hamiltonian describing four edge channels of QSHI constriction can be constructed [22] as 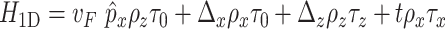 , where the four terms represent the kinetic energy, the spin-orbit interaction (SOI), the Zeeman term, and a spin-conserved inter-edge tunneling term, respectively (
, where the four terms represent the kinetic energy, the spin-orbit interaction (SOI), the Zeeman term, and a spin-conserved inter-edge tunneling term, respectively (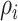 ,
,  are Pauli matrices working in right-/left-moving spinor and chirality spinor, respectively). The competition between the Zeeman term
are Pauli matrices working in right-/left-moving spinor and chirality spinor, respectively). The competition between the Zeeman term 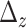 and the tunneling strength t induces two distinct topological phases and the Jackiw-Rebbi zero-mode resides in the domain wall. The effective Hamiltonian
and the tunneling strength t induces two distinct topological phases and the Jackiw-Rebbi zero-mode resides in the domain wall. The effective Hamiltonian 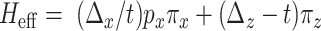 describing topological phase transition has the form of 1D TI (
describing topological phase transition has the form of 1D TI (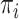 are Pauli matrices for real spin). It is worth noting that quantum Hall insulator with two pairs of edge channels [34] possesses similar Hamiltonian.
are Pauli matrices for real spin). It is worth noting that quantum Hall insulator with two pairs of edge channels [34] possesses similar Hamiltonian.
The 2D Hamiltonian of QSHI constriction supporting Jackiw-Rebbi zero-modes is obtained by adding the Zeeman term  and the SOI term
and the SOI term  into the Bernevig-Hughes-Zhang (BHZ) model [35,36] as:
into the Bernevig-Hughes-Zhang (BHZ) model [35,36] as:
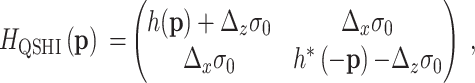 |
(1) |
where 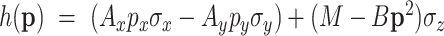 (
(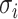 for Pauli matrices). The discretized version of Equation (1) in a 2D lattice with finite width
for Pauli matrices). The discretized version of Equation (1) in a 2D lattice with finite width 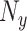 generally possesses four edge states. However, a strong inter-edge tunneling will destroy these edge states and bring about a topologically trivial phase. The strength of such tunneling depends on the overlap between opposite edge states, therefore it can be modulated through the Hamiltonian parameters [e.g.,
generally possesses four edge states. However, a strong inter-edge tunneling will destroy these edge states and bring about a topologically trivial phase. The strength of such tunneling depends on the overlap between opposite edge states, therefore it can be modulated through the Hamiltonian parameters [e.g., 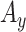 , see Fig. 1(b, c)] or lattice width
, see Fig. 1(b, c)] or lattice width 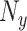 (i.e., QSHI constrictions [22,23]). Based on the method of Green's function, the density of states (DOS) [Fig. 1(d, e)] of a QSHI heterostructure [Fig. 1(a)] composed of two topologically distinct halves demonstrates the subgap zero-energy Jackiw-Rebbi state localized at its interface. It is worth noting that the Jackiw-Rebbi zero-mode's energy may deviate from zero [e.g. if kinetic term (
(i.e., QSHI constrictions [22,23]). Based on the method of Green's function, the density of states (DOS) [Fig. 1(d, e)] of a QSHI heterostructure [Fig. 1(a)] composed of two topologically distinct halves demonstrates the subgap zero-energy Jackiw-Rebbi state localized at its interface. It is worth noting that the Jackiw-Rebbi zero-mode's energy may deviate from zero [e.g. if kinetic term ( ) is presented in the BHZ model]. However, both the transport and the braiding properties of the Jackiw-Rebbi zero-modes remain unchanged in the presence of such a constant shift of energy.
) is presented in the BHZ model]. However, both the transport and the braiding properties of the Jackiw-Rebbi zero-modes remain unchanged in the presence of such a constant shift of energy.
Figure 1.

(a) Schematic diagram of the QSHI heterostructure lattice [with finite width 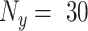 through (a-e)] which is composed of two semi-infinite QSHI halves (yellow and blue, respectively) whose energy spectrums are shown as (b) and (c), respectively. Hamiltonian parameter
through (a-e)] which is composed of two semi-infinite QSHI halves (yellow and blue, respectively) whose energy spectrums are shown as (b) and (c), respectively. Hamiltonian parameter 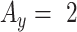 in (b) and there are four edge channels;
in (b) and there are four edge channels;  in (c) and the edge channels here are destroyed. (d) The DOS inside the shaded region (
in (c) and the edge channels here are destroyed. (d) The DOS inside the shaded region (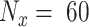 ) of (a). (e) The local density of states distribution inside the shaded region of (a) at energy
) of (a). (e) The local density of states distribution inside the shaded region of (a) at energy 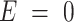 . Other parameters are
. Other parameters are 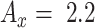 ,
,  ,
, 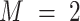 ,
,  , and
, and 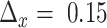 .
.
THE AHARONOV-BOHM EFFECT OF JACKIW-REBBI ZERO-MODE AND A COMPARISON WITH MZM
Apart from pumping of the domain wall [24,33], transport signature of Jackiw-Rebbi zero-mode is also shown in the Jackiw-Rebbi zero-mode intermediated electron transmission [18,37], whose peculiarities may be revealed by a two-path interference with a normal electron transmission, i.e., AB effect with a Jackiw-Rebbi zero-mode embedded [Fig. 2(a)]. The direct hopping strength between the two leads is 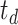 , and the hopping strength between the leads and the QSHI heterostructure supporting Jackiw-Rebbi zero-mode is
, and the hopping strength between the leads and the QSHI heterostructure supporting Jackiw-Rebbi zero-mode is 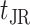 . The transmission coefficient between the two leads
. The transmission coefficient between the two leads 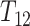 depending on the incident electron's energy E as well as the magnetic flux
depending on the incident electron's energy E as well as the magnetic flux 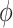 inclosed [
inclosed [ is in the unit of
is in the unit of 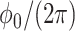 ,
,  is the flux quantum] can be numerically investigated by the Green's function. For weak
is the flux quantum] can be numerically investigated by the Green's function. For weak 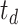 [Fig. 2(b-d)], the AB effect shows an unexpected
[Fig. 2(b-d)], the AB effect shows an unexpected 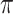 -period sinusoidal oscillation in the zero-energy case that the incident electron's energy E matches the zero-mode's energy level. As E slightly deviates from zero,
-period sinusoidal oscillation in the zero-energy case that the incident electron's energy E matches the zero-mode's energy level. As E slightly deviates from zero, 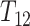 becomes the superposition of a
becomes the superposition of a 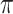 -period and a
-period and a 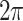 -period sinusoidal functions. The AB effect comes back to the normal
-period sinusoidal functions. The AB effect comes back to the normal 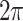 -period sinusoidal oscillation for significant non-zero E. For strong
-period sinusoidal oscillation for significant non-zero E. For strong 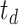 [Fig. 2(e-g)], though no longer in the simple sinusoidal form, the AB effect still exhibits a
[Fig. 2(e-g)], though no longer in the simple sinusoidal form, the AB effect still exhibits a  -period oscillation for
-period oscillation for 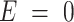 , while a
, while a 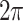 -period oscillation for
-period oscillation for 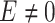 .
.
Figure 2.

(a) Sketch of the AB ring in a lattice model. An AB ring enclosing a magnetic flux 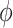 is sandwiched between two identical 2D metal leads (green lattice). The upper arm of the ring is the direct hopping with strength
is sandwiched between two identical 2D metal leads (green lattice). The upper arm of the ring is the direct hopping with strength 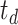 between the two leads (black arrows), and the lower arm contains a Jackiw-Rebbi zero-mode in a QSHI heterostructure (yellow and blue lattice) which is equally coupled to the two leads with hopping strength
between the two leads (black arrows), and the lower arm contains a Jackiw-Rebbi zero-mode in a QSHI heterostructure (yellow and blue lattice) which is equally coupled to the two leads with hopping strength 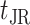 (orange arrows). (b-d) [(e-g)] In the condition of weak (strong)
(orange arrows). (b-d) [(e-g)] In the condition of weak (strong) 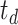 , numerical results of
, numerical results of  at fixed energies as (b) [(e)]
at fixed energies as (b) [(e)] 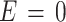 , (c) [(f)]
, (c) [(f)] 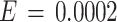 , and (d) [(g)]
, and (d) [(g)] 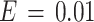 , respectively. For simplicity, in (b-g), conductance constants irrelevant to the oscillations have been subtracted. (h)
, respectively. For simplicity, in (b-g), conductance constants irrelevant to the oscillations have been subtracted. (h) 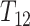 solely induced by the Jackiw-Rebbi zero-mode, where numerical results (orange) can be perfectly fitted by the analytic formula (green) with
solely induced by the Jackiw-Rebbi zero-mode, where numerical results (orange) can be perfectly fitted by the analytic formula (green) with 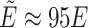 .
.
The S-matrix theory [38,39] shows that 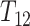 has the analytical form as:
has the analytical form as:
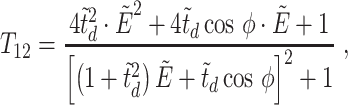 |
(2) |
where 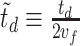 , and
, and 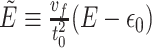 (see Supplementary Material). In the resonant tunneling condition
(see Supplementary Material). In the resonant tunneling condition  ,
, 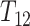 reduces to
reduces to 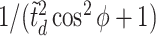 thus verifies the
thus verifies the 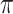 -period AB oscillation. Furthermore, the numerical results can be well fitted by Equation (2) (see Supplementary Material). In the limit of
-period AB oscillation. Furthermore, the numerical results can be well fitted by Equation (2) (see Supplementary Material). In the limit of 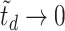 ,
, 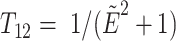 indicates the transmission solely induced by the Jackiw-Rebbi zero-mode has a peak value of 1, other than the naively expected
indicates the transmission solely induced by the Jackiw-Rebbi zero-mode has a peak value of 1, other than the naively expected 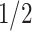 . Such analytic result drawn from S-matrix is numerically verified [Fig. 2(h)] and consistent with previous research [18].
. Such analytic result drawn from S-matrix is numerically verified [Fig. 2(h)] and consistent with previous research [18].
For comparison, if the Jackiw-Rebbi zero-mode in the AB ring is replaced by a MZM [40,41], then the transmission conductance  between the two leads is related to the S-matrix in the Bogoliubov-de Gennes basis [38,42] as
between the two leads is related to the S-matrix in the Bogoliubov-de Gennes basis [38,42] as
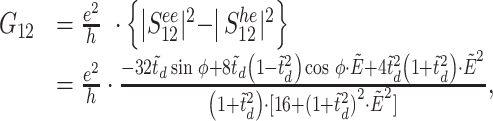 |
(3) |
where 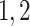 for lead indices,
for lead indices,  for electron and hole, respectively,
for electron and hole, respectively, 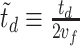 , and
, and 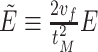 (see Supplementary Material). In contrast to the Jackiw-Rebbi zero-mode, Equation (3) indicates that MZM’s AB effect oscillates in a
(see Supplementary Material). In contrast to the Jackiw-Rebbi zero-mode, Equation (3) indicates that MZM’s AB effect oscillates in a 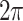 -period at both zero-bias (
-period at both zero-bias ( ) and finite-bias (
) and finite-bias (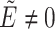 ) [40]. However, as discussed above, Jackiw-Rebbi zero-mode can be viewed as a special case of MZM where PH symmetry is absent. The electron and hole indices in Equation (3) are replaced by two electron subband indices (denoted by
) [40]. However, as discussed above, Jackiw-Rebbi zero-mode can be viewed as a special case of MZM where PH symmetry is absent. The electron and hole indices in Equation (3) are replaced by two electron subband indices (denoted by 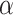 and
and 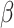 ) if the Majorana condition is not imposed. Hence the sign difference between electron and hole is absent, and Equation (3) is modified as
) if the Majorana condition is not imposed. Hence the sign difference between electron and hole is absent, and Equation (3) is modified as  , which qualitatively retrieve the consequence that the Jackiw-Rebbi zero-mode exhibits
, which qualitatively retrieve the consequence that the Jackiw-Rebbi zero-mode exhibits  -period (
-period (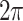 -period) AB effect at zero-bias (finite-bias).
-period) AB effect at zero-bias (finite-bias).
NON-ABELIAN BRAIDING PROPERTIES
The similarities between Jackiw-Rebbi and MZM revealed by the AB effect inspire us to investigate the possible non-Abelian statistics of Jackiw-Rebbi zero-modes through cross-shaped junction [Fig. 3(a)]. Each of the four arms of the junction is a topologically nontrivial QSHI supporting Jackiw-Rebbi zero-modes, and three gates (G1, G2, and G3) are located near the crossing. If the gate voltage is turned on (off), then the corresponding arm is separated (connected) due to the presence (absence) of the gating potential barrier. Initially, G1 and G3 are turned on while G2 is turned off, hence three pairs of Jackiw-Rebbi zero-modes (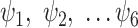 ) are localized at the ends of the three divided parts [Fig. 3(a)]. The braiding protocol [31] takes three steps (time cost for each step is T) to swap
) are localized at the ends of the three divided parts [Fig. 3(a)]. The braiding protocol [31] takes three steps (time cost for each step is T) to swap 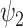 and
and 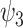 spatially. Firstly, G1 is turned off and then G2 is turned on, hence
spatially. Firstly, G1 is turned off and then G2 is turned on, hence 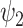 is moved to the top of G2. Secondly, G3 is turned off and then G1 is turned on, so now
is moved to the top of G2. Secondly, G3 is turned off and then G1 is turned on, so now 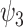 is at the left of G1. Thirdly, turning off G2 is followed by turning on G3, as a result
is at the left of G1. Thirdly, turning off G2 is followed by turning on G3, as a result 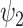 and
and 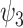 are swapped. In the whole braiding process taking time of
are swapped. In the whole braiding process taking time of 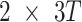 ,
, 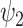 and
and 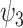 are swapped twice in succession.
are swapped twice in succession.
Figure 3.

(a) Sketch of the cross-shaped QSHI junction. Distributions of the three pairs of Jackiw-Rebbi zero-modes ( ) before braiding are shown. (b-d) Evolution of an eigenstate
) before braiding are shown. (b-d) Evolution of an eigenstate  as
as 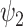 and
and 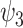 are swapped twice in succession with
are swapped twice in succession with 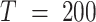 (b) in the clean limit; (c) in the presence of chiral-symmetry-breaking disorder
(b) in the clean limit; (c) in the presence of chiral-symmetry-breaking disorder 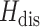 with
with 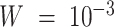 ; (d) in the presence of chiral-symmetry-conserved disorder
; (d) in the presence of chiral-symmetry-conserved disorder 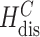 with
with 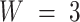 .
. 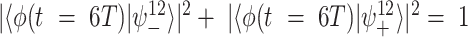 is valid in (b) and (c), while invalid in (d) for strong disorder destructing topological gap. (e)
is valid in (b) and (c), while invalid in (d) for strong disorder destructing topological gap. (e) 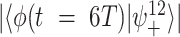 in a fixed chiral-symmetry-breaking disorder profile with different disorder strength W and braiding time T. Numerical results can be well fitted (black curve) by Equation (5) as
in a fixed chiral-symmetry-breaking disorder profile with different disorder strength W and braiding time T. Numerical results can be well fitted (black curve) by Equation (5) as 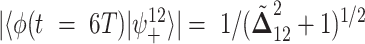 for intermediate T satisfying adiabatic condition
for intermediate T satisfying adiabatic condition  . Topological gap
. Topological gap 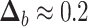 , the coupling energy
, the coupling energy 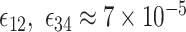 .
.
In the following, we verify that swapping 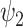 and
and 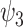 once lead to
once lead to 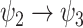 and
and 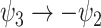 , which is identical to the MZM [26,43]. In the clean limit, finite-size induced coupling betweem paired Jackiw-Rebbi zero-modes
, which is identical to the MZM [26,43]. In the clean limit, finite-size induced coupling betweem paired Jackiw-Rebbi zero-modes 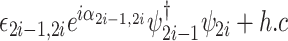 . (
. (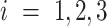 , and
, and  for arbitrary phase) leads to symmetric and antisymmetric eigenstates
for arbitrary phase) leads to symmetric and antisymmetric eigenstates 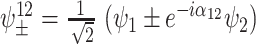 [16]. Numerical simulation of the adiabatical time-evolution (see Supplementary Material) shows that an eigenstate
[16]. Numerical simulation of the adiabatical time-evolution (see Supplementary Material) shows that an eigenstate 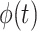 evolving from
evolving from 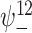 to
to 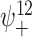 after
after 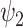 and
and 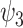 are swapped twice in succession [Fig. 3(b)], which indicates
are swapped twice in succession [Fig. 3(b)], which indicates 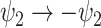 . Similarly,
. Similarly, 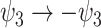 is confirmed for another eigenstate evolving from
is confirmed for another eigenstate evolving from 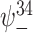 to
to 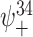 simultaneously. Consequently, braiding properties
simultaneously. Consequently, braiding properties 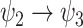 and
and 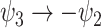 (after swapping
(after swapping 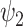 and
and 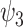 once) can be drawn from the above results up to a gauge transformation. It is worth noting that the basis of the wavefunction we adopted here is
once) can be drawn from the above results up to a gauge transformation. It is worth noting that the basis of the wavefunction we adopted here is 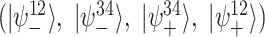 [Fig. 3(b)], while the basis usually chosen for MZMs’ braiding is
[Fig. 3(b)], while the basis usually chosen for MZMs’ braiding is 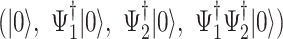 [26,31,32] instead.
[26,31,32] instead.
GENERALIZED NON-ABELIAN BRAIDING IN SYSTEMS WITH DEGENERACY LIFTING
The QSHI constriction [Equation (1)] is in the AIII symmetry class possessing chiral symmetry 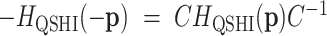 [44,45], which protects the degeneracy of Jackiw-Rebbi zero-modes (
[44,45], which protects the degeneracy of Jackiw-Rebbi zero-modes (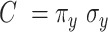 ,
,  is Pauli matrix for real spin). Strikingly, the eigenstate
is Pauli matrix for real spin). Strikingly, the eigenstate 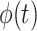 evolves from
evolves from 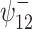 to a superposition of
to a superposition of 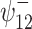 and
and  [Fig. 3(c)] in the presence of tiny chiral-symmetry-breaking disorder
[Fig. 3(c)] in the presence of tiny chiral-symmetry-breaking disorder 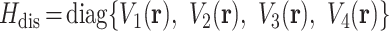 (
( uniformly distributed within
uniformly distributed within  ) where disorder strength W comparable with
) where disorder strength W comparable with 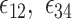 but much smaller than the topological gap
but much smaller than the topological gap 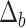 . On the contrary, the non-Abelian braiding remains integrity until the disorder is strong enough to destruct the topological gap [Fig. 3(d)], if the disorder has a chiral-symmetry-conserved form as
. On the contrary, the non-Abelian braiding remains integrity until the disorder is strong enough to destruct the topological gap [Fig. 3(d)], if the disorder has a chiral-symmetry-conserved form as 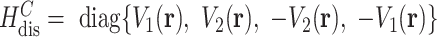 (see Supplementary Material).
(see Supplementary Material).
Due to the self-conjugation condition 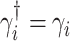 , MZM’s occupation energy term
, MZM’s occupation energy term 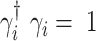 is a trivial constant. For Jackiw-Rebbi zero-mode, however,
is a trivial constant. For Jackiw-Rebbi zero-mode, however, 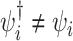 and the energy deviation
and the energy deviation  (e.g., originated from disorder effect or gate voltages tuning local chemical potential) can be introduced into the Hamiltonian as:
(e.g., originated from disorder effect or gate voltages tuning local chemical potential) can be introduced into the Hamiltonian as:
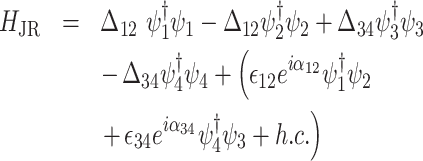 |
(4) |
(widely separated zero-modes 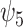 and
and  with negligible coupling are dropped). The eigenstates of Equation (4) spanned by
with negligible coupling are dropped). The eigenstates of Equation (4) spanned by  and
and 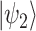 are
are  (
(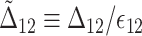 , and
, and 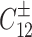 are normalization constants). In case of non-zero
are normalization constants). In case of non-zero 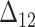 , numerical simulation confirms that the exchange properties
, numerical simulation confirms that the exchange properties 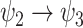 and
and  are still valid (see Supplementary Material). However, due to the new form of eigenstates
are still valid (see Supplementary Material). However, due to the new form of eigenstates  with different weights of
with different weights of  and
and 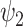 (in other words,
(in other words, 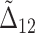 induces a ‘rotation’ of the eigenstates
induces a ‘rotation’ of the eigenstates 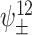 ), a novel non-Abelian braiding is obtained:
), a novel non-Abelian braiding is obtained:
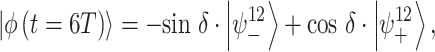 |
(5) |
where 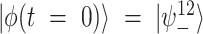 , and
, and 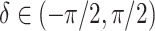 is defined as
is defined as 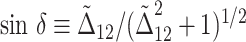 and
and  . With the increase of
. With the increase of 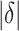 describing the degeneracy lifting, the
describing the degeneracy lifting, the 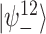 component in
component in  increases from 0 to 1, while the weight of
increases from 0 to 1, while the weight of 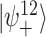 decreases from 1 to 0. In the adiabatic condition
decreases from 1 to 0. In the adiabatic condition 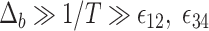 [31], numerical simulation results are T-independent and well fitted by Equation (5) [Fig. 3(e)]. According to the model described above, if moderate coupling strength
[31], numerical simulation results are T-independent and well fitted by Equation (5) [Fig. 3(e)]. According to the model described above, if moderate coupling strength 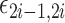 between Jackiw-Rebbi zero-modes is provided,
between Jackiw-Rebbi zero-modes is provided, 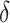 will be relatively small for weak disorder and therefore the non-Abelian braiding properties identical to the MZMs can be retrieved. Furthermore, by exerting additional gate voltages modulating the local chemical potentials of
will be relatively small for weak disorder and therefore the non-Abelian braiding properties identical to the MZMs can be retrieved. Furthermore, by exerting additional gate voltages modulating the local chemical potentials of  and
and 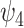 ,
, 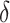 and then the non-Abelian braiding properties can be modulated in a controlled manner. For chiral-symmetry-conserved disorder
and then the non-Abelian braiding properties can be modulated in a controlled manner. For chiral-symmetry-conserved disorder 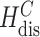 , in contrast, disorders in opposite signs are imposed on edge states with opposite chirality, hence the energy deviation
, in contrast, disorders in opposite signs are imposed on edge states with opposite chirality, hence the energy deviation 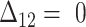 and the corresponding non-Abelian properties remain the same as the MZM.
and the corresponding non-Abelian properties remain the same as the MZM.
Mathematically, in the basis of  (where
(where 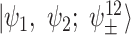 indicating
indicating  and
and  fusing into
fusing into 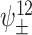 ), as shown in Table 1, such novel braiding can be expressed in the form of braiding operator B [46,47]. Besides, the fusion operator F and the exchange operator R can also be extracted from
), as shown in Table 1, such novel braiding can be expressed in the form of braiding operator B [46,47]. Besides, the fusion operator F and the exchange operator R can also be extracted from  (see Supplementary Material). The fusion rule of Jackiw-Rebbi zero-mode can be tuned by
(see Supplementary Material). The fusion rule of Jackiw-Rebbi zero-mode can be tuned by 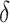 and is a generalization of MZM (Table 1). In the limit of
and is a generalization of MZM (Table 1). In the limit of 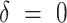 , as expected, it retrieves MZM’s fusion rule up to a phase
, as expected, it retrieves MZM’s fusion rule up to a phase  . Such generalized and tunable fusion rule implies potential application in topological quantum computation.
. Such generalized and tunable fusion rule implies potential application in topological quantum computation.
Table 1.
Braiding operator 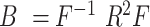 , fusion operator F, and the square of exchange operator R for both Jackiw-Rebbi zero-mode and MZM.
, fusion operator F, and the square of exchange operator R for both Jackiw-Rebbi zero-mode and MZM. 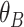 is an overall phase factor.
is an overall phase factor.
| Operator | Jackiw-Rebbi zero-mode | MZM |
|---|---|---|
| B |
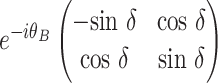
|
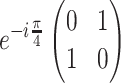
|
| F |
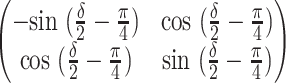
|

|

|
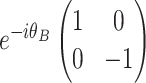
|
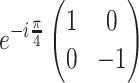
|
Finally, if ‘fictitious’ PH-symmetry-breaking disorder is introduced into a 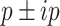 -wave superconductor (D symmetry class [48,49]), then similar
-wave superconductor (D symmetry class [48,49]), then similar  -dependent braidings are also observed for MZM (see Supplementary Material). The only difference is that the important role preserving MZMs’ degeneracy is played by PH symmetry instead of chiral symmetry.
-dependent braidings are also observed for MZM (see Supplementary Material). The only difference is that the important role preserving MZMs’ degeneracy is played by PH symmetry instead of chiral symmetry.
DISCUSSIONS
The relation and similarity between Jackiw-Rebbi and MZM are uncovered by both AB effect and non-Abelian braiding properties. Though the double-frequency AB oscillation of the Jackiw-Rebbi zero-mode is irrelevant to the charge fractionalization, such effect relies on the resonant condition 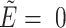 in which Jackiw-Rebbi zero-mode's zero-energy nature is topologically protected, while such peculiarity can be easily removed for an ordinary zero-mode such as a localized state in a quantum dot. As for the non-Abelian properties, the symmetry-protected degeneracy for MZM is robust since PH symmetry is always presented provided that the superconductivity is not destroyed, therefore the fusion rule of MZM has a fixed form while the Jackiw-Rebbi one is tunable. Furthermore, for MZM-based braiding, considering the adiabatic condition
in which Jackiw-Rebbi zero-mode's zero-energy nature is topologically protected, while such peculiarity can be easily removed for an ordinary zero-mode such as a localized state in a quantum dot. As for the non-Abelian properties, the symmetry-protected degeneracy for MZM is robust since PH symmetry is always presented provided that the superconductivity is not destroyed, therefore the fusion rule of MZM has a fixed form while the Jackiw-Rebbi one is tunable. Furthermore, for MZM-based braiding, considering the adiabatic condition 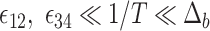 [31] where the SC gap
[31] where the SC gap 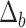 is in the order of 1 meV, it requires relative low braiding frequency
is in the order of 1 meV, it requires relative low braiding frequency 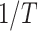 and larger device scale to reduce the finite-size-induced coupling
and larger device scale to reduce the finite-size-induced coupling 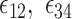 . These restrictions could be relaxed for Jackiw-Rebbi zero-modes since superconductivity is no longer required and the topological gap
. These restrictions could be relaxed for Jackiw-Rebbi zero-modes since superconductivity is no longer required and the topological gap 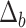 could be generally larger. These comparisons show the possibility of quantum computation device with higher integration level and higher braiding frequency.
could be generally larger. These comparisons show the possibility of quantum computation device with higher integration level and higher braiding frequency.
Supplementary Material
Acknowledgements
We thank Chui-Zhen Chen, Qing-Feng Sun, and Xin Wan for fruitful discussion.
FUNDING
This work was supported by the National Basic Research Program of China (2015CB921102, 2017YFA0303301 and 2017YFA0304600) and the National Natural Science Foundation of China (11534001, 11504008, 11674028, 11574245 and 11822407).
Conflict of interest statement. None declared.
REFERENCES
- 1. Jackiw R, Rebbi C. Solitons with fermion number 1/2. Phys Rev D 1976; 13: 3398–409. [Google Scholar]
- 2. Goldstone J, Wilczek F. Fractional quantum numbers on solitons. Phys Rev Lett 1981; 47: 986–9. [Google Scholar]
- 3. Kivelson S, Schrieffer JR. Fractional charge, a sharp quantum observable. Phys Rev B 1982; 25: 6447–51. [Google Scholar]
- 4. Rajaraman R, Bell JS. On solitons with half integral charge. Phys Lett B 1982; 116: 151–4. [Google Scholar]
- 5. Rajaraman R. Fractional charge. arXiv:cond-mat/0103366. [Google Scholar]
- 6. Jackiw R. Fractional and Majorana fermions: the physics of zero-energy modes. Phys Scr 2012; T146: 014005. [Google Scholar]
- 7. Laughlin RB. Nobel lecture: fractional quantization. Rev Mod Phys 1999; 71: 863–74. [Google Scholar]
- 8. Seidel A, Lee D-H. Abelian and non-abelian Hall liquids and charge-density wave: quantum number fractionalization in one and two dimensions. Phys Rev Lett 2006; 97: 056804. [DOI] [PubMed] [Google Scholar]
- 9. Arovas D, Schrieffer JR, Wilczek F. Fractional statistics and the quantum Hall effect. Phys Rev Lett 1984; 53: 722–3. [Google Scholar]
- 10. Lee D-H, Zhang G-M, Xiang T. Edge solitons of topological insulators and fractionalized quasiparticles in two dimensions. Phys Rev Lett 2007; 99: 196805. [DOI] [PubMed] [Google Scholar]
- 11. Ruostekoski J, Dunne GV, Javanainen J. Particle number fractionalization of an atomic Fermi-Dirac gas in an optical lattice. Phys Rev Lett 2002; 88: 180401. [DOI] [PubMed] [Google Scholar]
- 12. Shen S-Q. Topological Insulators. Berlin: Springer, 2012. [Google Scholar]
- 13. Su WP, Schrieffer JR, Heeger AJ. Solitons in polyacetylene. Phys Rev Lett 1979; 42: 1698–701. [Google Scholar]
- 14. Kitaev AY. Unpaired Majorana fermions in quantum wires. Phys-Usp 2001; 44: 131–6. [Google Scholar]
- 15. Tewari S, Das Sarma S, Lee D-H. Index theorem for the zero modes of Majorana fermion vortices in chiral p-Wave superconductors. Phys Rev Lett 2007; 99: 037001. [DOI] [PubMed] [Google Scholar]
- 16. Klinovaja J, Loss D. Fractional fermions with non-Abelian statistics. Phys Rev Lett 2013; 110: 126402. [DOI] [PubMed] [Google Scholar]
- 17. Pedrocchi FL, Chesi S, Gangadharaiah Set al. Majorana states in inhomogeneous spin ladders. Phys Rev B 2012; 86: 205412. [Google Scholar]
- 18. Rainis D, Saha A, Klinovaja Jet al. Transport signatures of fractional fermions in Rashba nanowires. Phys Rev Lett 2014; 112: 196803. [DOI] [PubMed] [Google Scholar]
- 19. Klinovaja J, Stano P, Loss D. Transition from fractional to Majorana fermions in Rashba nanowires. Phys Rev Lett 2012; 109: 236801. [DOI] [PubMed] [Google Scholar]
- 20. Klinovaja J, Loss D. Fermionic and Majorana bound states in hybrid nanowires with non-uniform spin-orbit interaction. Eur Phys J B 2015; 88: 62. [Google Scholar]
- 21. Gangadharaiah S, Trifunovic L, Loss D. Localized end states in density modulated quantum wires and rings. Phys Rev Lett 2012; 108: 136803. [DOI] [PubMed] [Google Scholar]
- 22. Klinovaja J, Loss D. Fractional charge and spin states in topological insulator constrictions. Phys Rev B 2015; 92: 121410. [Google Scholar]
- 23. Väyrynen JI, Ojanen T. Chiral topological phases and fractional domain wall excitations in one-dimensional chains and wires. Phys Rev Lett 2011; 107: 166804. [DOI] [PubMed] [Google Scholar]
- 24. Qi X-L, Hughes TL, Zhang S-C. Fractional charge and quantized current in the quantum spin Hall state. Nat Phys 2008; 4: 273–6. [Google Scholar]
- 25. Halperin BI, Oreg Y, Stern Aet al. Adiabatic manipulations of Majorana fermions in a three-dimensional network of quantum wires. Phys Rev B 2012; 85: 144501. [Google Scholar]
- 26. Ivanov DA. Non-Abelian statistics of half-quantum vortices in p-wave superconductors. Phys Rev Lett 2001; 86: 268–71. [DOI] [PubMed] [Google Scholar]
- 27. Alicea J, Oreg Y, Refael Get al. Non-Abelian statistics and topological quantum information processing in 1D wire networks. Nat Phys 2011; 7: 412–7. [Google Scholar]
- 28. Sau JD, Clarke DJ, Tewari S. Controlling non-Abelian statistics of Majorana fermions in semiconductor nanowires. Phys Rev B 2011; 84: 094505. [Google Scholar]
- 29. Gao P, He Y-P, Liu X-J. Symmetry-protected non-Abelian braiding of Majorana Kramers pairs. Phys Rev B 2016; 94: 224509. [Google Scholar]
- 30. Sekania M, Plugge S, Greiter Met al. Braiding errors in interacting Majorana quantum wires. Phys Rev B 2017; 96: 094307. [Google Scholar]
- 31. Amorim CS, Ebihara K, Yamakage Aet al. Majorana braiding dynamics in nanowires. Phys Rev B 2015; 91: 174305. [Google Scholar]
- 32. Chen C-Z, Xie Y-M, Liu Jet al. Quasi-one-dimensional quantum anomalous Hall systems as new platforms for scalable topological quantum computation. Phys Rev B 2018; 97: 104504. [Google Scholar]
- 33. Saha A, Rainis D, Tiwari RPet al. Quantum charge pumping through fractional fermions in charge density modulated quantum wires and Rashba nanowires. Phys Rev B 2014; 90: 035422. [Google Scholar]
- 34. Fu H, Wu Y, Zhang Ret al. 3/2 fractional quantum Hall plateau in confined two-dimensional electron gas. Nat Commun 2019; 10: 4351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Bernevig BA, Hughes TL, Zhang S-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 2006; 314: 1757–61. [DOI] [PubMed] [Google Scholar]
- 36. Qi X-L, Zhang S-C. Topological insulators and superconductors. Rev Mod Phys 2011; 83: 1057–110. [Google Scholar]
- 37. Heeger AJ, Kivelson S, Schrieffer JRet al. Solitons in conducting polymers. Rev Mod Phys 1988; 60: 781–850. [Google Scholar]
- 38. Law KT, Lee PA, Ng TK. Majorana fermion induced resonant andreev reflection. Phys Rev Lett 2009; 103: 237001. [DOI] [PubMed] [Google Scholar]
- 39. Datta S. Electronic Transport in Mesoscopic Systems. Cambridge: Cambridge University Press, 1997. [Google Scholar]
- 40. Tripathi KM, Das S, Rao S. Fingerprints of Majorana bound states in Aharonov-Bohm geometry. Phys Rev Lett 2016; 116: 166401. [DOI] [PubMed] [Google Scholar]
- 41. Benjamin C, Pachos JK. Detecting Majorana bound states. Phys Rev B 2010; 81: 085101. [Google Scholar]
- 42. Nilsson J, Akhmerov AR, Beenakker CWJ. Splitting of a cooper pair by a pair of Majorana bound states. Phys Rev Lett 2008; 101: 120403. [DOI] [PubMed] [Google Scholar]
- 43. von Oppen F, Peng Y, Pientka F. Topological superconducting phases in one dimension. Oxford: Oxford University Press, 2015. [Google Scholar]
- 44. Altland A, Zirnbauer MR. Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures. Phys Rev B 1997; 55: 1142–61. [Google Scholar]
- 45. Schnyder AP, Ryu S, Furusaki Aet al. Classification of topological insulators and superconductors in three spatial dimensions. Phys Rev B 2008; 78: 195125. [Google Scholar]
- 46. Lahtinen V, Pachos JK. A short introduction to topological quantum computation. SciPost Phys 2017; 3: 021. [Google Scholar]
- 47. Pachos JK. Introduction to Topological Quantum Computation. Cambridge: Cambridge University Press, 2012. [Google Scholar]
- 48. Lin Y, Hao W, Wang Met al. Topological superconductors from one-dimensional periodically modulated Majorana chains. Sci Rep 2017; 7: 9210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Bernevig BA, Hughes TL. Topological Insulators and Topological Superconductors. Princeton: Princeton University Press, 2013. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


