Abstract

The understanding of materials requires access to the dynamics over many orders of magnitude in time; however, single analytical techniques are restricted in their respective time ranges. Assuming a functional relationship between time and temperature is one viable tool to overcome these limits. Despite its frequent usage, a breakdown of this assertion at the glass-transition temperature is common. Here, we take advantage of time- and length-scale information in neutron spectroscopy to show that the separation of different processes is the minimum requirement toward a more universal picture at, and even below, the glass transition for our systems. This is illustrated by constructing the full proton mean-square displacement for three bottlebrush polymers from femto- to nanoseconds, with simultaneous information on the partial contributions from segmental relaxation, methyl group rotation, and vibrations. The information can be used for a better analysis of results from numerous techniques and samples, improving the overall understanding of materials properties.
Keywords: Time−Temperature Superposition, Quasi-Elastic Neutron Scattering, Bottlebrush Polymer, Polydimethylsiloxane
In polymer science and other material-specific disciplines, e.g., medicine1 or construction chemistry,2−4 dynamical processes occur over a wide time range.5 Because analytical instruments have finite time/frequency windows, only a fraction of the existing processes is accessible at a given temperature.6−10 A common approach to overcome this limitation is the empirical time–temperature superposition principle.1,3,11,12 In this technique, the analyzed quantity is measured at different temperatures and then shifted to one reference temperature, yielding a significantly extended time/frequency range. However, a breakdown of the time–temperature superposition principle seems to be very common, significantly impeding fundamental understanding of materials, especially polymer melts.
Samples are either classified as thermorheologically simple or complex.13,14 While in the first case the characteristic times scale with the temperature, heterogeneities and phase transitions, including the glass transition, are expected to cause a breakdown of thermorheological simplicity. Structural inhomogeneities seem to be a natural cause of this breakdown; however, dynamic heterogeneities may also have substantial impact. Both the influence on time–temperature scaling and the origin of the dynamic heterogeneities are still under debate and may be linked to structural heterogeneities, different chemical surroundings, and could also be caused by a superposition of different relaxation processes.15,16 Below we report the apparent breakdown of the universal time–temperature scaling approach and illustrate a more generic principle, which specifies the minimum requirement to compare experimental results from different techniques, related to contributions of different relaxation processes.
We take advantage of length- and time-scale information in quasi-elastic
neutron scattering (QENS) experiments to examine the influence of
superpositioned processes on the violation of the time–temperature
superposition principle. The process focuses on the glassy dynamics
or  -process captured at
small length scales
corresponding to dimensions smaller than the size of Gaussian blobs.5 In the related momentum transfer range,
-process captured at
small length scales
corresponding to dimensions smaller than the size of Gaussian blobs.5 In the related momentum transfer range, 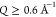 , the dynamic correlation function probes
the heterogeneous relaxation associated with the segmental relaxation.
Thus, the selection of the length-scale range excludes contributions
of the homogeneous large-scale polymer dynamics typically associated
with Rouse relaxation and also the transition region between Rouse
and the more local segmental relaxation, facilitating focus on the
various local heterogeneities,
, the dynamic correlation function probes
the heterogeneous relaxation associated with the segmental relaxation.
Thus, the selection of the length-scale range excludes contributions
of the homogeneous large-scale polymer dynamics typically associated
with Rouse relaxation and also the transition region between Rouse
and the more local segmental relaxation, facilitating focus on the
various local heterogeneities, 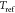 .
.
The dynamical heterogeneities of two different origins are introduced
to study the influence on the time–temperature superposition
via the mean-square displacement (MSD) obtained from quasi-elastic
neutron scattering (QENS). The systems of study are poly(dimethylsiloxane)-based
homopolymer bottlebrushes, PDMS-g-PDMS, with varying
side chain and similar backbone molecular weights of  g/mol and
g/mol and 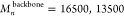 g/mol, synthesized
by anionic polymerization
and investigated by dielectric spectroscopy and QENS.17,18 Despite
being a structurally very complex polymer, there seems to be no indication
of any thermorheologically complex behavior.17 As illustrated below, this unexpected observation is a consequence
of the experimental technique’s specific sensitivity and reflects
a different superposition that is method specific of the underlying
molecular processes. The presented analysis is exemplified using one
bottlebrush polymer,
g/mol, synthesized
by anionic polymerization
and investigated by dielectric spectroscopy and QENS.17,18 Despite
being a structurally very complex polymer, there seems to be no indication
of any thermorheologically complex behavior.17 As illustrated below, this unexpected observation is a consequence
of the experimental technique’s specific sensitivity and reflects
a different superposition that is method specific of the underlying
molecular processes. The presented analysis is exemplified using one
bottlebrush polymer, 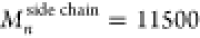 g/mol, followed by a comparison of all
three samples.
g/mol, followed by a comparison of all
three samples.
The first dynamical heterogeneity is a consequence
of the three
different relaxation processes in PDMS, visible at 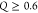 Å–1.19 At high
temperatures, the dynamics accessible
for PDMS-based polymers in the QENS time window are governed by segmental
relaxation, whereas at lower temperatures, rotational jump motions
of the methyl groups are captured, as shown in Figure 1a.18 Additional
fast motions, like vibrations, can be well separated, but give a noticeable
contribution to the mean-square displacement. Changing the temperature
shifts the dynamical processes through the accessible time window
and allows to either capture the pure relaxation phenomena or a mixture
of them. Measurements in this study are carried out at temperatures
at which our experimental data reflect only individual processes because
of separated processes. Knowing the individual processes and their
characteristic behavior provides the opportunity to calculate experimental
data in the intermediate temperature range in which more than one
process contributes.
Å–1.19 At high
temperatures, the dynamics accessible
for PDMS-based polymers in the QENS time window are governed by segmental
relaxation, whereas at lower temperatures, rotational jump motions
of the methyl groups are captured, as shown in Figure 1a.18 Additional
fast motions, like vibrations, can be well separated, but give a noticeable
contribution to the mean-square displacement. Changing the temperature
shifts the dynamical processes through the accessible time window
and allows to either capture the pure relaxation phenomena or a mixture
of them. Measurements in this study are carried out at temperatures
at which our experimental data reflect only individual processes because
of separated processes. Knowing the individual processes and their
characteristic behavior provides the opportunity to calculate experimental
data in the intermediate temperature range in which more than one
process contributes.
Figure 1.
Dynamical heterogeneity of the example PDMS-g-PDMS
bottlebrush polymer with  g/mol. (a) Relaxation
times,
g/mol. (a) Relaxation
times,  , vs
, vs  for the different dynamical processes occurring
in PDMS. The solid purple line is the best description with the Vogel–Fulcher–Tammann
equation for the segmental relaxation times, obtained by dielectric
spectroscopy.17 The solid green line is
the best description with the Arrhenius equation for the relaxation
times of the methyl group rotations, obtained by QENS.18 The solid blue symbols are the segmental relaxation
times for different momentum transfers,
for the different dynamical processes occurring
in PDMS. The solid purple line is the best description with the Vogel–Fulcher–Tammann
equation for the segmental relaxation times, obtained by dielectric
spectroscopy.17 The solid green line is
the best description with the Arrhenius equation for the relaxation
times of the methyl group rotations, obtained by QENS.18 The solid blue symbols are the segmental relaxation
times for different momentum transfers, 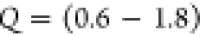 Å–1 from top to
bottom, obtained by QENS.18 Inset: Chemical
structure of PDMS-g-PDMS. (b) Non-Gaussian parameter,
Å–1 from top to
bottom, obtained by QENS.18 Inset: Chemical
structure of PDMS-g-PDMS. (b) Non-Gaussian parameter, 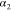 , vs time,
, vs time,  , for the PDMS-g-PDMS bottlebrush
polymer for three selected temperatures,
, for the PDMS-g-PDMS bottlebrush
polymer for three selected temperatures, 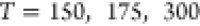 K. Inset: Pictorial representation
of the
morphology of PDMS-g-PDMS.
K. Inset: Pictorial representation
of the
morphology of PDMS-g-PDMS.
The second dynamical heterogeneity in our sample is associated with the intrinsic heterogeneity of the segmental relaxation and is magnified because of the branched nature of the bottlebrush architecture.20 The grafting of side chains onto a polymer backbone results in a broader distribution of relaxation times.17
Dynamic heterogeneity is specified by
the non-Gaussian parameter, 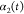 , which is theoretically defined as
, which is theoretically defined as  . It is represented
by the ratio of the
fourth moment,
. It is represented
by the ratio of the
fourth moment, 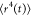 , and the second moment squared,
, and the second moment squared, 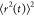 , of
a distribution function. Distinct nonzero
values of
, of
a distribution function. Distinct nonzero
values of 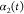 indicate deviations from a Gaussian distribution
of relaxation times, i.e., deviations from homogeneous dynamics.16 As seen in Figure 1b,
indicate deviations from a Gaussian distribution
of relaxation times, i.e., deviations from homogeneous dynamics.16 As seen in Figure 1b, 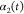 displays values well above zero. For all
temperatures it shows a time dependence, indicating an increase in
homogeneity at longer times.21
displays values well above zero. For all
temperatures it shows a time dependence, indicating an increase in
homogeneity at longer times.21
We
use the mean-square displacement representation of the time–temperature
scaling of the incoherent intermediate scattering function,  , resulting from the combination
of three
different QENS instruments capturing three orders of magnitude in
the time scale, ranging from pico- to nanoseconds.18
, resulting from the combination
of three
different QENS instruments capturing three orders of magnitude in
the time scale, ranging from pico- to nanoseconds.18
| 1 |
The different temperature data sets are converted
into the mean-square
displacement,  , of all protons in the system by using
the cumulant series expansion which has been shown to produce highly
reliable information by plotting data in the Guinier representation,
i.e.,
, of all protons in the system by using
the cumulant series expansion which has been shown to produce highly
reliable information by plotting data in the Guinier representation,
i.e., 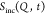 vs
vs 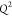 (Figure S1).15,16,22−24
(Figure S1).15,16,22−24
This model-independent analysis allows the identification of distinct processes apparently separated in temperature. At high temperatures the segmental relaxation, at intermediate-to-low temperatures the methyl group rotations, and at low temperatures the Debye–Waller factor contribute to the mean-square displacement and the resulting power laws (Figure 2a). The mean-square displacement of the methyl group rotation is found to show a pronounced plateau expected for the constrained nature of the motion, whereas the segmental dynamics show a continuous increase.25,26
Figure 2.
Mean-square
displacement of the example PDMS-g-PDMS with 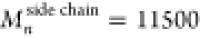 g/mol, obtained
from QENS. (a) Mean-square
displacement,
g/mol, obtained
from QENS. (a) Mean-square
displacement,  ,
vs time,
,
vs time,  , as obtained from the intermediate scattering
function,
, as obtained from the intermediate scattering
function, 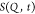 , by using the cumulant series expansion, eq 1. (b) Mean-square displacement,
, by using the cumulant series expansion, eq 1. (b) Mean-square displacement, 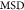 ,
vs time,
,
vs time,  , for the low temperatures, showing contributions
from methyl group rotations and fast vibrations at the reference temperature,
, for the low temperatures, showing contributions
from methyl group rotations and fast vibrations at the reference temperature,  K, not fulfilling the time–temperature
superposition principle. Insets: Pictorial representation of vibrations
and methyl group rotations. (c) Mean-square displacement,
K, not fulfilling the time–temperature
superposition principle. Insets: Pictorial representation of vibrations
and methyl group rotations. (c) Mean-square displacement,  ,
vs time,
,
vs time,  , for the high temperatures, showing contributions
from segmental dynamics, methyl group rotation, and fast vibrations
at the reference temperature,
, for the high temperatures, showing contributions
from segmental dynamics, methyl group rotation, and fast vibrations
at the reference temperature, 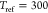 K, not fulfilling the time–temperature
superposition principle. Inset: Pictorial representation of vibrations,
methyl group rotations, and segmental dynamics.
K, not fulfilling the time–temperature
superposition principle. Inset: Pictorial representation of vibrations,
methyl group rotations, and segmental dynamics.
The set of mean-square displacement graphs show strong similarities, thus hinting at the possibility of a valid time–temperature scaling. Yet, a test of the classic time–temperature superposition principle by introducing shift factors in horizontal and vertical directions reveals strong disparities (Figure 2b for methyl group dynamics and Figure 2c for segmental dynamics). In particular, the breakdown of the time–temperature superposition at high temperatures is striking, though one would expect that it should work best at high temperatures. A closer look at both failed attempts of constructing a master curve shows that the discrepancies are most pronounced on short scales and in the region of relatively small displacements. At longer times and relatively high displacements, in contrast, a good overlap is reached.
Considering the possible
sources of heterogeneity (Figure 1), the coexistence of two or
more processes in the momentum transfer region 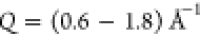 for which the MSD has been calculated could
already be responsible for at least a part of the mismatch of our
data illustrated in Figure 2b and Figure 2c. Therefore, consider the influence of the coexistence of two or
more processes by taking advantage of the strongest individual contribution
on different time scales, i.e., vibrations at short times, methyl
group rotations at intermediate times, and segmental relaxation at
long times. Hence, using the occurrence of the processes on very different
time scales and the additivity of the mean-square displacement allows
for the examination of how much of the mismatch can be related to
the existence of multiple processes in polymers. This essentially
reflects the time–temperature superposition principle at the
single molecular process level and identifies the individual contributions
as the major source of the breakdown of the time–temperature
scaling applied to the directly measured data.
for which the MSD has been calculated could
already be responsible for at least a part of the mismatch of our
data illustrated in Figure 2b and Figure 2c. Therefore, consider the influence of the coexistence of two or
more processes by taking advantage of the strongest individual contribution
on different time scales, i.e., vibrations at short times, methyl
group rotations at intermediate times, and segmental relaxation at
long times. Hence, using the occurrence of the processes on very different
time scales and the additivity of the mean-square displacement allows
for the examination of how much of the mismatch can be related to
the existence of multiple processes in polymers. This essentially
reflects the time–temperature superposition principle at the
single molecular process level and identifies the individual contributions
as the major source of the breakdown of the time–temperature
scaling applied to the directly measured data.
The vibrations
governing short times are typically considered via
the atomistic mean-square displacement,  , included in the Debye–Waller
factor,
, included in the Debye–Waller
factor, 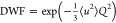 (Figure S2a).5,27 Access to
(Figure S2a).5,27 Access to 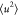 is provided by the description
of the intermediate
scattering function,
is provided by the description
of the intermediate
scattering function, 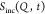 .18 The atomistic
mean-square displacement has a pronounced temperature dependence but
is time independent within our time and
.18 The atomistic
mean-square displacement has a pronounced temperature dependence but
is time independent within our time and 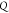 -window, giving a constant contribution
to the respective mean-square displacement as shown in Figure S2b. The values of
-window, giving a constant contribution
to the respective mean-square displacement as shown in Figure S2b. The values of 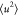 are comparatively small (Figure S2), thus subtraction in the temperature
range of
are comparatively small (Figure S2), thus subtraction in the temperature
range of  K results in the pure methyl group
motion.
Applying the Arrhenius type temperature scaling for methyl group rotation
(Figure S3) leads to temperature superposition
as illustrated in Figure 3a. Within the experimental accuracy, excellent agreement is
found up to
K results in the pure methyl group
motion.
Applying the Arrhenius type temperature scaling for methyl group rotation
(Figure S3) leads to temperature superposition
as illustrated in Figure 3a. Within the experimental accuracy, excellent agreement is
found up to 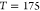 K,
i.e., for the entire temperature range
for which the motion is visible. Thus, time–temperature scaling
seems to be applicable to methyl group rotation.
K,
i.e., for the entire temperature range
for which the motion is visible. Thus, time–temperature scaling
seems to be applicable to methyl group rotation.
Figure 3.
Partial mean-square displacements relating to single processes,
specifically methyl group rotation and segmental dynamics for the
example PDMS-g-PDMS bottlebrush polymer with 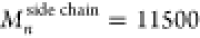 g/mol. Partial
mean-square displacement,
g/mol. Partial
mean-square displacement, 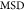 ,
vs time,
,
vs time,  of (a) the methyl
group rotation at the
reference temperature,
of (a) the methyl
group rotation at the
reference temperature, 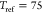 K, and (b) of the segmental dynamics at
K, and (b) of the segmental dynamics at  K. Insets: Pictorial representations of
the methyl group rotation and segmental dynamics, respectively. With
the partial mean-square displacements in hand, the temperature-dependent
full mean-square displacement can be reconstructed.
K. Insets: Pictorial representations of
the methyl group rotation and segmental dynamics, respectively. With
the partial mean-square displacements in hand, the temperature-dependent
full mean-square displacement can be reconstructed.
At higher temperatures, the mean-square displacement of the
segmental
relaxation contains contributions from all three motions, including
vibrations and methyl group rotations. A shifting of the master curve
of the mean-square displacement of the pure methyl group dynamics
by extrapolating the gained shift factors to the data at the two high
temperatures (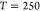 K
and
K
and  K) allows the calculation of the mean-square
displacement of the segmental dynamics alone, resulting in the single
mean-square displacement of the pure segmental dynamics.
K) allows the calculation of the mean-square
displacement of the segmental dynamics alone, resulting in the single
mean-square displacement of the pure segmental dynamics.
Similar to the methyl group rotation, the segmental mean-square displacement can also be combined into a single master curve avoiding artificial scaling on the time axis by using shift factors obtained by dielectric spectroscopy. The superpositioned data point to a well-working time–temperature superposition for the segmental relaxation. Analysis of the QENS data in this way shows that in fact the time–temperature superposition principle is valid over the whole time and temperature range, including at temperatures well below the glass-transition temperature, if the data are carefully analyzed to reflect only one single dynamical process, even if heterogeneous processes are studied. Therefore, this method enables to increase the experimental window from three orders of magnitude up to five and four for the methyl group and segmental relaxation, respectively, on a single process level.
| 2 |
In the full mean-square
displacement, the
time scale is expanded to seven orders of magnitude as shown in Figure 4. A self-consistent
verification for the approach used is achieved by comparing the created
full mean-square displacement with the original mean-square displacement
data of the reference temperature, 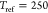 K. In the restricted time range of the
original mean-square displacement (
K. In the restricted time range of the
original mean-square displacement ( ps
ps 
 ns)
from Figure 2a, both
data sets, i.e., the constructed
full mean-square displacement and the original mean-square displacement
at
ns)
from Figure 2a, both
data sets, i.e., the constructed
full mean-square displacement and the original mean-square displacement
at 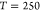 K, agree very well (Figure S5).
K, agree very well (Figure S5).
Figure 4.

Full proton mean-square displacement of the example PDMS-g-PDMS bottlebrush polymer with 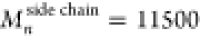 g/mol. Mean-square
displacement,
g/mol. Mean-square
displacement, 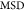 ,
vs time,
,
vs time,  , for all contributing motions, segmental
dynamics, methyl group rotations, and fast vibrations, obtained by
the combination of the single processes at the reference temperature,
, for all contributing motions, segmental
dynamics, methyl group rotations, and fast vibrations, obtained by
the combination of the single processes at the reference temperature, 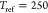 K. Dashed lines indicate the resulting
power laws for the respective time scale. Insets: Pictorial representation
of vibrations, methyl group rotations, and segmental dynamics.
K. Dashed lines indicate the resulting
power laws for the respective time scale. Insets: Pictorial representation
of vibrations, methyl group rotations, and segmental dynamics.
This result has a remarkable consequence, as it
reflects the strong
influence of the individual process contributions to the full mean-square
displacement. The absence of strong deviations points to a lesser
importance of the heterogeneities of the individual processes to the
breakdown of the known time–temperature superposition principle.
Thus, the importance of the individual contributions of different
processes explains why the validity of time–temperature superposition
seems to have different temperature ranges when it comes to different
techniques. For example, dielectric spectroscopy does not detect the
methyl group rotation, and therefore, the frequency scaling of the
segmental relaxation can be observed at least down to temperatures  . Though dielectric spectroscopy has an
extremely broad frequency window, below this temperature the experimental
signal leaves the finite frequency range.17 Hence, lower temperatures have not been accessed. The current QENS
results suggest that the observation continues to much lower temperatures.
. Though dielectric spectroscopy has an
extremely broad frequency window, below this temperature the experimental
signal leaves the finite frequency range.17 Hence, lower temperatures have not been accessed. The current QENS
results suggest that the observation continues to much lower temperatures.
The last point to discuss in more detail is the mean-square displacement.
Based on the separate constituting processes, three regions can be
identified (Figure 4), each dominated by different relaxations. At short times, a mixture
of vibrations and methyl group rotations cause a power law of  . This is followed by
. This is followed by 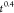 in the intermediate time
scale, which is
seen as an interplay of methyl group rotations and segmental relaxation.
In the long-time limit the segmental relaxation dominates the mean-square
displacement, showing a pronounced power law of
in the intermediate time
scale, which is
seen as an interplay of methyl group rotations and segmental relaxation.
In the long-time limit the segmental relaxation dominates the mean-square
displacement, showing a pronounced power law of 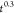 .
.
Using the same
ansatz for the other two samples, i.e., PDMS-g-PDMS
with  g/mol and
g/mol and  g/mol, results in the full proton mean-square
displacement of the PDMS-g-PDMS bottlebrush polymer
having elongated shapes17 (Figure 5). While the three different
dynamical regions are visible in all three samples, the power law
dependence of the mean-square displacement changes depending on the
side chain length. The short time region, vibrational motions and
methyl group rotations, shows the same power law of
g/mol, results in the full proton mean-square
displacement of the PDMS-g-PDMS bottlebrush polymer
having elongated shapes17 (Figure 5). While the three different
dynamical regions are visible in all three samples, the power law
dependence of the mean-square displacement changes depending on the
side chain length. The short time region, vibrational motions and
methyl group rotations, shows the same power law of 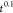 independent of the side
chain length. Continuing
to the intermediate time region, the interplay of methyl group rotations
and segmental relaxation, an increasing power law from
independent of the side
chain length. Continuing
to the intermediate time region, the interplay of methyl group rotations
and segmental relaxation, an increasing power law from 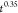 to
to 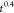 is observable. The same
effect is visible
for the long-time region, where the dynamics are dominated by the
segmental relaxation. Here, the power law increases from
is observable. The same
effect is visible
for the long-time region, where the dynamics are dominated by the
segmental relaxation. Here, the power law increases from  to
to 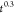 with increasing the side
chain length.
This allows the assumption that with increasing molecular weight of
the side chains, i.e., with increasing distance from the backbone,
the segmental dynamics is less confined, resulting in steeper power
laws, eventually approaching the behavior of linear polymers at sufficiently
long side chain lengths.
with increasing the side
chain length.
This allows the assumption that with increasing molecular weight of
the side chains, i.e., with increasing distance from the backbone,
the segmental dynamics is less confined, resulting in steeper power
laws, eventually approaching the behavior of linear polymers at sufficiently
long side chain lengths.
Figure 5.

Full proton mean-square displacement of the
three different PDMS-g-PDMS bottlebrush polymers.
Mean-square displacement,  ,
vs time,
,
vs time,  , for all contributing motions, segmental
dynamics, methyl group rotations, and fast vibrations, obtained by
the combination of the single processes at the reference temperature,
, for all contributing motions, segmental
dynamics, methyl group rotations, and fast vibrations, obtained by
the combination of the single processes at the reference temperature, 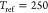 K. Dashed lines indicate the resulting
power laws for the respective time scale. The MSD for the
K. Dashed lines indicate the resulting
power laws for the respective time scale. The MSD for the  and
and 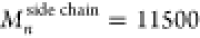 are shifted vertically by factors of
are shifted vertically by factors of  and
and 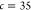 ,
respectively, for clarity.
,
respectively, for clarity.
However, these results deviate from power laws expected for polymers, including Rouse dynamics and reptation.5,28 The previous paragraph explains that a part of these deviations comes from the experimental observation of the entire proton motion reflecting multiple processes as mirrored by the full mean-square displacement, while typical theoretical equations usually pick a certain process such as segmental relaxation. However, the closer inspection of the partial mean-square displacements, Figure 3, shows a behavior that does not reflect the relaxation of an ideal polymer chain, which may be attributed to the bottlebrush polymer itself. To date, there is no theory available that would explain the mean-square displacement of this branched polymer with complex architecture.
In conclusion, the approach presented here shows how the time–temperature superposition principle can successfully be used for dynamically heterogeneous samples, as long as the dynamics can be split into single processes based on their respective time and temperature dependences. It is not limited to a bottlebrush shape; it could also be applied to any material as long as the length and time scales can be separated. This enables a significant extension of the available time/frequency range, typically limited for experimental methods commonly used to study polymer dynamics, e.g., QENS, rheology, or NMR, etc. and for a multitude of possible samples. We anticipate that this analysis will have a notable impact on the data analysis and understanding of resulting master curves, enhancing the data interpretation based on a single-process approach.
Acknowledgments
We gratefully acknowledge funding by the U.S. Department of Energy (DoE) under grant DE-SC0019050. We also would like to acknowledge ACNS (P7387 and P7389), Sydney, Australia, and the ISIS Neutron and Muon Facility (DOI: 10.5286/ISIS.E.RB1910220), Didcot, United Kingdom, for access to the quasi-elastic neutron scattering instruments. We thank Prof. David Spivak (Department of Chemistry, Louisiana State University) for carefully proofreading the manuscript.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.1c01379.
Description of the used method, supporting analysis steps for the example PDMS-g-PDMS with
 g/mol, supporting data for PDMS-g-PDMS bottlebrush polymers with
g/mol, supporting data for PDMS-g-PDMS bottlebrush polymers with  g/mol, and supporting data for PDMS-g-PDMS bottlebrush polymers with
g/mol, and supporting data for PDMS-g-PDMS bottlebrush polymers with  g/mol (PDF)
g/mol (PDF)
Author Present Address
⊥ K.J.B.: Department of Chemistry, Louisiana State University, Baton Rouge, Louisiana 70803, United States.
The authors declare no competing financial interest.
Supplementary Material
References
- Peters G. W. M.; Meulman J. H.; Sauren A. A. H. J. The Applicability of the Time/Temperature Superposition Principle to Brain Tissue. Biorheology 1997, 34, 127–138. 10.1016/S0006-355X(97)00009-7. [DOI] [PubMed] [Google Scholar]
- Chen Z.; Zhang H.; Duan H.; Wu C. Determination of time-temperature superposition relationship of SBS modified asphalt based on special rheological phenomenon caused by SBS-formed structure in asphalt matrix. Constr. Build. Mater. 2020, 260, 119835. 10.1016/j.conbuildmat.2020.119835. [DOI] [Google Scholar]
- Chehab G.; Kim Y.; Schapery R.; Witczak M.; Bonaquist R.. Time-temperature superposition principle for asphalt concrete with growing damage in tension state. In Proceedings of the Asphalt Paving Technologists 2002, Journal of the Association of Asphalt Paving Technologists, March 18–20, 2002, Colorado Springs, Colorado; Transportation Research Board: 2002; pp 71.
- Lai J.-C.; Liu J.; Huang C.-W. The Application of Frequency-Temperature Superposition Principle for Back-Calculation of Falling Weight Deflectometer. Appl. Sci. 2020, 10 (1), 132. 10.3390/app10010132. [DOI] [Google Scholar]
- Richter D.; Monkenbusch M.; Arbe A.; Colmenero J.. Neutron Spin Echo in Polymer Systems; Springer-Verlag: Berlin, 2005. [Google Scholar]
- de Souza N. R.; Klapproth A.; Iles G. N. EMU: High-Resolution Backscattering Spectrometer at ANSTO. Neutron News 2016, 27 (2), 20–21. 10.1080/10448632.2016.1163985. [DOI] [Google Scholar]
- Yu D.; Mole R.; Noakes T.; Kennedy S.; Robinson R. Pelican - a Time of Flight Cold Neutron Polarization Analysis Spectrometer at OPAL. J. Phys. Soc. Jpn. 2013, 82, SA027. 10.7566/JPSJS.82SA.SA027. [DOI] [Google Scholar]
- Demmel F.; McPhail D.; French C.; Maxwell D.; Harrison S.; Boxall J.; Rhodes N.; Mukhopadhyay S.; Silverwood I.; Sakai V. G.; Fernandez-Alonso F. ToF-Backscattering spectroscopy at the ISIS Facility: Status and Perspectives. J. Phys.: Conf. Ser. 2018, 1021, 012027. 10.1088/1742-6596/1021/1/012027. [DOI] [Google Scholar]
- Mezger T.The Rheology Handbook: For users of rotational and oscillatory rheometers; Vincentz Network: 2020; pp 153–247. [Google Scholar]
- Kremer F.; Schönhals A.. Broadband Dielectric Spectroscopy; Springer: 2012; pp 99–130. [Google Scholar]
- Arrighi V.; Ganazzoli F.; Zhang C.; Gagliardi S. New interpretation of local dynamics of poly (dimethyl siloxane) observed by quasielastic neutron scattering. Phys. Rev. Lett. 2003, 90 (5), 058301. 10.1103/PhysRevLett.90.058301. [DOI] [PubMed] [Google Scholar]
- Arrighi V.; Gagliardi S.; Zhang C.; Ganazzoli F.; Higgins J. S.; Ocone R.; Telling M. T. F. A Unified Picture of the Local Dynamics of Poly(dimethylsiloxane) across the Melting Point. Macromolecules 2003, 36 (23), 8738–8748. 10.1021/ma034843x. [DOI] [Google Scholar]
- Dealy J.; Plazek D. Time-temperature superposition-a users guide. Rheol. Bull. 2009, 78, 16–31. [Google Scholar]
- Harper B.; Weitsman Y. Characterization method for a class of thermorheologically complex materials. J. Rheol. 1985, 29 (1), 49–66. 10.1122/1.549786. [DOI] [Google Scholar]
- Zorn R. Deviation from Gaussian behavior in the self-correlation function of the proton motion in polybutadiene. Phys. Rev. B: Condens. Matter Mater. Phys. 1997, 55 (10), 6249–6259. 10.1103/PhysRevB.55.6249. [DOI] [Google Scholar]
- Kanaya T.; Tsukushi I.; Kaji K. Non-Gaussian parameter and heterogeneity of amorphous polymers. Prog. Theor. Phys., Suppl. 1997, 126, 133–140. 10.1143/PTPS.126.133. [DOI] [Google Scholar]
- Jakobi B.; Bichler K. J.; Sokolova A.; Schneider G. J. Dynamics of PDMS-g-PDMS Bottlebrush Polymers by Broadband Dielectric Spectroscopy. Macromolecules 2020, 53 (19), 8450–8458. 10.1021/acs.macromol.0c01277. [DOI] [Google Scholar]
- Bichler K. J.; Jakobi B.; Sakai V. G.; Klapproth A.; Mole R. A.; Schneider G. J. Short-Time Dynamics of PDMS-g-PDMS Bottlebrush Polymer Melts Investigated by Quasi-Elastic Neutron Scattering. Macromolecules 2020, 53 (21), 9553–9562. 10.1021/acs.macromol.0c01846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borah R.; Ahamad N.; Debnath P. Investigation of dynamical heterogeneities in polymer melts. Curr. Sci. 2017, 113 (10), 1974. 10.18520/cs/v113/i10/1974-1985. [DOI] [Google Scholar]
- Chremos A.; Glynos E.; Green P. F. Structure and dynamical intra-molecular heterogeneity of star polymer melts above glass transition temperature. J. Chem. Phys. 2015, 142 (4), 044901. 10.1063/1.4906085. [DOI] [PubMed] [Google Scholar]
- Bedrov D.; Smith G.; Douglas J. F. Structural and dynamic heterogeneity in a telechelic polymer solution. Polymer 2004, 45 (11), 3961–3966. 10.1016/j.polymer.2004.01.082. [DOI] [Google Scholar]
- Gerstl C.; Schneider G. J.; Fuxman A.; Zamponi M.; Frick B.; Seydel T.; Koza M.; Genix A. C.; Allgaier J.; Richter D.; Colmenero J.; Arbe A. Quasielastic Neutron Scattering Study on the Dynamics of Poly(alkylene oxide)s. Macromolecules 2012, 45 (10), 4394–4405. 10.1021/ma3003399. [DOI] [Google Scholar]
- Rahman A.; Singwi K.; Sjölander A. Theory of slow neutron scattering by liquids. I. Phys. Rev. 1962, 126 (3), 986. 10.1103/PhysRev.126.986. [DOI] [Google Scholar]
- Becker T.; Smith J. C. Energy resolution and dynamical heterogeneity effects on elastic incoherent neutron scattering from molecular systems. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2003, 67 (2), 021904. 10.1103/PhysRevE.67.021904. [DOI] [PubMed] [Google Scholar]
- Engelke S.; Marbella L. E.; Trease N. M.; De Volder M.; Grey C. P. Three-dimensional pulsed field gradient NMR measurements of self-diffusion in anisotropic materials for energy storage applications. Phys. Chem. Chem. Phys. 2019, 21 (8), 4538–4546. 10.1039/C8CP07776B. [DOI] [PubMed] [Google Scholar]
- Dopico A.Methods in Membrane Lipids; Humana Press: 2007; pp 295–321. [Google Scholar]
- Higgins J. S.; Benoit H. C.; Benoît H.. Polymers and Neutron Scattering; Clarendon Press: 1996; pp 81–115. [Google Scholar]
- Boyd R.; Smith G.. Polymer Dynamics and Relaxation; Cambridge University Press: 2007; pp 244–247. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.





