Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2022 Oct 1.
Published in final edited form as: Magn Reson Imaging. 2021 Jun 24;82:104–110. doi: 10.1016/j.mri.2021.06.012

On the down-sampling of diffusion MRI data along the angular dimension

Nan-kuei Chen 1,*, Ryan P Bell 2, Christina S Meade 2
PMCID: PMC8289744  NIHMSID: NIHMS1718007  PMID: 34174330

Abstract

Background:

It has been established that the diffusion gradient directions in diffusion MRI should be uniformly distributed in 3D spherical space, so that orientation-dependent diffusion properties (e.g., fractional anisotropy or FA) can be properly quantified. Sometimes the acquired data need to be down-sampled along the angular dimension before computing diffusion properties (e.g., to exclude data points corrupted by motion artifact; to harmonize data obtained with different protocols). It is important to quantitatively assess the impact of data down-sampling on measurement of diffusion properties.

Materials and methods:

Here we report 1) a numerical procedure for down-sampling diffusion MRI (e.g., for data harmonization), and 2) a spatial uniformity index of diffusion directions, aiming to predict the quality of the chosen down-sampling schemes (e.g., from data harmonization; or rejection of motion corrupted data points). We quantitatively evaluated human diffusion MRI data, which were down-sampled from 64 or 60 diffusion gradient directions to 30 directions, in terms of their 1) FA value accuracy (using fully-sampled data as the ground truth), 2) FA fitting residuals, and 3) spatial uniformity indices.

Results:

Our experimental data show that the proposed spatial uniformity index is correlated with errors in FA obtained from down-sampled diffusion MRI data. The FA fitting residuals that are typically used to assess diffusion MRI quality are not correlated with either FA errors or spatial uniformity index.

Conclusions:

These results suggest that the spatial uniformity index could be more valuable in assessing quality of down-sampled diffusion MRI data, as compared with FA fitting residual measures. We expect that our implemented software procedure should prove valuable for 1) guiding data harmonization for multi-site diffusion MRI studies, and 2) assessing the impact of rejecting motion corrupted data points on the accuracy of diffusion measures.

Keywords: Diffusion MRI, down-sampling, spatial uniformity index, data harmonization

1. Introduction

Diffusion MRI data are typically acquired with a series of diffusion gradient directions and b values that are suitable for the targeted analyses [1–3]. It has been established that the optimal gradient direction schemes for quantifying orientation-dependent diffusion properties (e.g., fractional anisotropy or FA values [4]) are the ones that uniformly sample in 3D spherical space [5,6], such as the regular polyhedra scheme [7]. For example, MRI protocols with 30 uniformly distributed diffusion-encoding directions at b=1000 s/mm2 have been used in many diffusion-tensor imaging (DTI) studies [8]; and imaging protocols with higher angular-resolution (i.e., more diffusion-encoding directions uniformly distributed in 3D spherical space) at multiple b values are recommended for estimating higher-order information [9–13].

Usually all the acquired diffusion MRI data corresponding to different diffusion encoding directions are used in analyses. In some cases, the acquired diffusion MRI data might need to be down-sampled along the angular dimension (i.e., excluding a subset of diffusion encoding directions) before computing the diffusion properties. For example, 1) when subsets of diffusion MRI data are corrupted by motion related artifact, they should be excluded from analyses; 2) for research studies that jointly analyze data obtained with different protocols, one might need to down-sample higher angular-resolution diffusion MRI data (with more diffusion encoding directions) to lower angular-resolution (with fewer directions), as part of data harmonization procedures [14].

Since the diffusion gradient directions of down-sampled diffusion MRI data may not necessarily be uniformly distributed in space, it is expected that the derived orientation-dependent diffusion properties (e.g., FA) would be less accurate. However, to our knowledge, a procedure for guiding and quantitatively assessing diffusion MRI down-sampling schemes remains to be established. Although the FA fitting residual (i.e., sum of squared errors) has been used in multiple studies to assess the quality of diffusion MRI data [15,16], its association with the FA deviation from the ground truth remains to be investigated. To address this need, here we report 1) a post-processing software procedure for down-sampling diffusion MRI (e.g., for data harmonization), 2) a spatial uniformity index of diffusion encoding directions, aiming to predict the quality of a chosen down-sampling scheme (e.g., for either data harmonization; or exclusion of motion corrupted data points), and 3) comparison of our proposed spatial uniformity index and FA fitting residual, in terms of their association with FA deviation from the ground truth.

2. Material and Methods

2.1. Down-sampling of diffusion MRI

We have implemented a simple matlab script that down-samples a higher angular-resolution sampling scheme (e.g., protocol P64 with 64 gradient-encoding directions in our matlab example) to a lower angular-resolution scheme (e.g., 30 directions down-sampled from protocol P64) in order to match data to another imaging protocol (e.g., protocol P30 with 30 gradient-encoding directions in our matlab example), which could be used as a part of data harmonization (e.g., for harmonizing data obtained with scan protocols P64 and P30). Specifically, for each of the 30 diffusion-encoding gradient directions of scan protocol P30 in our matlab example, we use the absolute value of inner product (matlab functions: abs and dot) to identify the most similar direction among the 64 diffusion-encoding directions of protocol P64. Note that two diffusion encoding directions are considered the same, when the inner product is either n or -n (ignoring eddy current [17,18] and assuming that, for example, diffusion encoding schemes [1,0,0] and [−1,0,0] have the same effect on diffusion signals). The matlab code is available at: https://github.com/nankueichen/DWI_downsampling

Figure 1A shows the Delaunay triangulation representation of 30 gradient directions for protocol P30. It can be seen that, since those 30 diffusion gradient directions are uniformly distributed in 3D spherical space, the Delaunay triangles formed by 3 nearest neighboring vertices have similar areas. Note that there are 60 vertices for 30 gradient directions (e.g., the gradient scheme [1,0,0] corresponds to two vertices [1,0,0] and [−1,0,0]). Figure 1B shows the Delaunay triangulation representation of 30 gradient directions that are down-sampled from protocol P64 (using the inner product approach described above), and as expected the areas of those triangles are less similar as compared with Figure 1A. The areas of triangles shown in Figures 1A and B are plotted in the left and right panels of Figure 1C, respectively, in ascending order. The standard deviation of triangle areas in Figure 1B is 3.37 times greater than that in Figure 1A.

Figure 1.

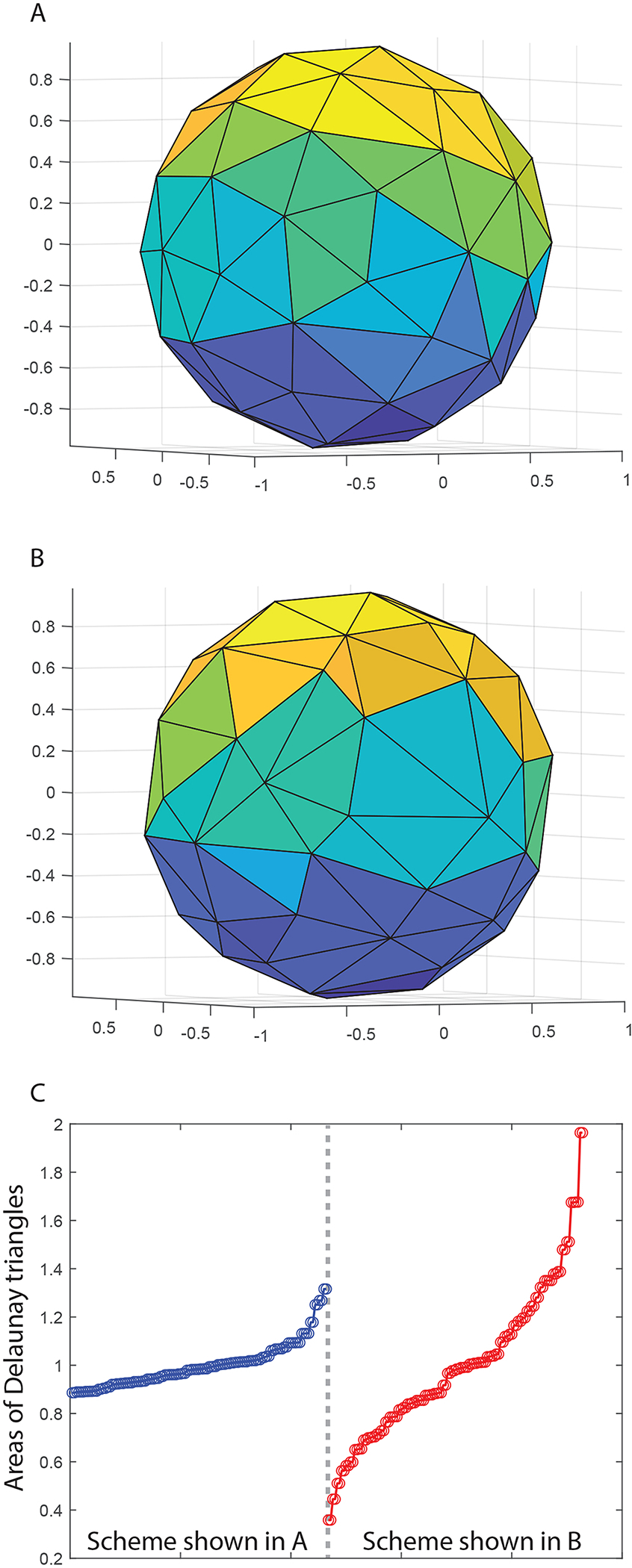
Figure 1

Open in a new tab

Figure 1A shows the Delaunay triangulation representation of 30 gradient directions that are uniformly distributed in space. Figure 1B shows the Delaunay triangulation representation of 30 gradient directions that are down-sampled from a protocol with 64 gradient directions (using the inner product approach described in the section 2.1). The areas of triangles shown in Figures 1A and B are plotted in the left and right panels of Figure 1C, respectively, in ascending order.

When the diffusion sampling vectors are uniformly distributed in 3D space, it is expected that 1) the corresponding points on a spherical surface are equally spaced [6], 2) the inner product for any pair of vectors is minimal, and 3) the Delaunay triangles formed by points on a spherical surface have the same area (as suggested by Figure 1). In this paper, the spatial uniformity index for a chosen diffusion-encoding down-sampling scheme is defined as the ratio of the standard deviation across Delaunay triangle areas for that chosen scheme (e.g., Figure 1B) to the standard deviation for an optimal sampling scheme (e.g., Figure 1A), which equals to 3.37 for the sampling-scheme shown in Figure 1B. Note that a smaller spatial uniformity index means that the spatial distribution of diffusion gradient is more uniform.

2.2. Numerical computation for assessing the distribution of spatial uniformity index

We first assessed the distribution of our proposed spatial uniformity index when 64 gradient-encoding directions (for protocol P64 in our matlab code) were randomly down-sampled to 30 directions (instead of using the inner-product based approach described in section 2.1). The down-sampling was repeated 1000 times with randomly generated orders (using matlab function: randperm), and the spatial uniformity indices were computed from the corresponding Delaunay triangulation representations.

The spatial uniformity indices computed from 1000 randomly generated down-sampling schemes were then sorted (in ascending order), and 10 of them (100th, 200th, … 1000th) were used to process human MRI data described in section 2.3.

2.3. Human MRI study 1: assessing diffusion property measures corresponding to different sub-sampling schemes

Here we quantitatively evaluated human diffusion MRI data, which were down-sampled from data with 64 diffusion gradient directions (protocol P64 in our matlab code) to 30 directions, in terms of their 1) FA value accuracy (using fully-sampled data as the ground truth), 2) FA fitting residual, and 3) spatial uniformity index (defined in section 2.1).

Diffusion MRI data were obtained from 12 adult volunteers using a 3 Tesla GE scanner equipped with an 8-channel head coil. Informed consent was obtained from our participants for this MRI study according to the protocols approved by the Institutional Review Board of Duke University. Scan parameters of diffusion-weighted single-shot echo-planar imaging included: flip angle = 90°, FOV = 25.6 × 25.6 cm2, in-plane matrix size = 128 × 128, slice thickness = 2 mm, TR = 8 sec, TE = 77.9 msec, and in-plane acceleration factor = 2. Each acquired data set included 11 b0 (i.e., minimally diffusion-weighted) images, 64 diffusion-weighted images with b=800 s/mm2, 6 images with b=266.7 s/mm2, and 7 images with b=533.3 s/mm2. Only b0 images and 64 diffusion-weighted images with b=800 s/mm2 were included in our analyses.

The acquired data (b0 and b=800 s/mm2) for each subject first underwent FSL’s motion and eddy current correction procedure to minimize image misalignment, and then were processed with FSL’s DTIFIT program to compute the FA values, which were considered the ground truth in subsequent analyses for assessing down-sampled diffusion MRI data.

Eddy-current corrected diffusion MRI data for each subject were then down-sampled from 64 to 30 directions using 11 different down-sampling schemes, including the inner-product based approach described in the section 2.1 (i.e., as shown in Figure 1B) and 10 randomly generated down-sampling schemes (as described in section 3.1). Afterward, the down-sampled diffusion MRI data were processed with FSL’s DTIFIT program to compute FA maps. The differences between FA maps derived from down-sampled and fully-sampled diffusion MRI data were then quantified with the following steps. First, the absolute values of the difference FA maps (between down-sampled and fully-sampled data) were computed on a voxel-by-voxel basis. Second, voxels with FA values greater than 0.25 in the fully-sampled diffusion MRI data were identified and used to create white-matter masks (for each subject). Third, the difference maps obtained from the first step were multiplied with the white-matter masks obtained from the second step, and the L1 norm of the masked map was computed for each subject. In addition, the FA fitting residuals (obtained from running FSL’s DTIFIT program with -sse option) were also multiplied with the white-matter masks obtained from the second step, and the L1 norm of the masked fitting residuals was computed for each subject.

2.4. Human MRI study 2: assessing diffusion property measures corresponding to different sub-sampling schemes

In order to assess the generalizability of our findings from human MRI study 1, we further evaluated the association of FA errors (i.e., deviation from the ground truth) with 1) FA fitting residual and 2) the spatial uniformity index in another set of human MRI data, shared by Cardiff University (see https://www.cardiff.ac.uk/cardiff-university-brain-research-imaging-centre/research/projects/cross-scanner-and-cross-protocol-diffusion-MRI-data-harmonisation) [14]. These human MRI data were originally acquired for evaluating the harmonization algorithms to match diffusion MRI data obtained with 3 different scanners (3T GE Signa Excite HDx; 3T Siemens Prisma; 3T Siemens Connectom) and 2 protocols (standard; state-of-the-art). Here we only used data of 10 subjects obtained from 3T Siemens Prisma with the state-of-theart protocol as the ground truth, to evaluate the quality of down-sampled data. Specifically, the ground truth data comprised 4 non-diffusion (b0) images and 60 diffusion-weighted images at b = 1200 s/mm2 with diffusion gradient directions specified in the state-of-the-art protocol. Diffusion MRI at higher b values (3000 and 5000 s/mm2) were excluded in our analysis. These data were down-sampled to 30 directions, using the procedures described in section 2.1, to best match the 30 directions specified in the standard protocol. Similar to human MRI study 1, 10 additional diffusion MRI data sets of 30 diffusion gradient directions were generated, for each of the 10 subjects, using randomly sampled patterns. The FA deviation from the ground truth and FA fitting residual, for each of the 11 down-sampled data sets, were computed with the procedures shown in section 2.3.

3. Results

3.1. Numerical computation for assessing the distribution of spatial uniformity index

The spatial uniformity indices range between 4.22 and 9.01, when randomly down-sampling 64 gradient-encoding directions to 30 directions. As expected, the randomly chosen down-sampled scheme is not as uniform as the one obtained with the inner-product based approach described in section 2.1 (with a spatial uniformity index = 3.37).

3.2. Human MRI studies: assessing diffusion property measures corresponding to different sub-sampling schemes

The left and right panels of Figure 2A show the errors of FA values derived from down-sampled diffusion MRI data, corresponding to 11 levels of gradient-direction spatial uniformity in two human MRI studies, using the fully-sampled data as the ground truth. It can be seen that the FA errors increase with the spatial uniformity index (with a smaller value indicating a more uniform gradient-direction distribution in space), at a nonlinear rate. The solid dots indicate the mean value across subjects (12 subjects in study 1; 10 subjects in study 2), and the error bars indicate the standard deviations. Figure 2B shows that the FA fitting residuals do not differ much across data obtained from 11 different down-sampling schemes, in both human MRI studies. These results illustrate that the errors in FA values derived from down-sampled diffusion MRI data (as compared with fully-sampled data) are more strongly associated with the spatial uniformity index derived from our implementation, as compared with the sum of squared errors in voxel-wise tensor fitting (which has been typically used to assess the quality in fitting FA and other diffusion properties).

Figure 2.

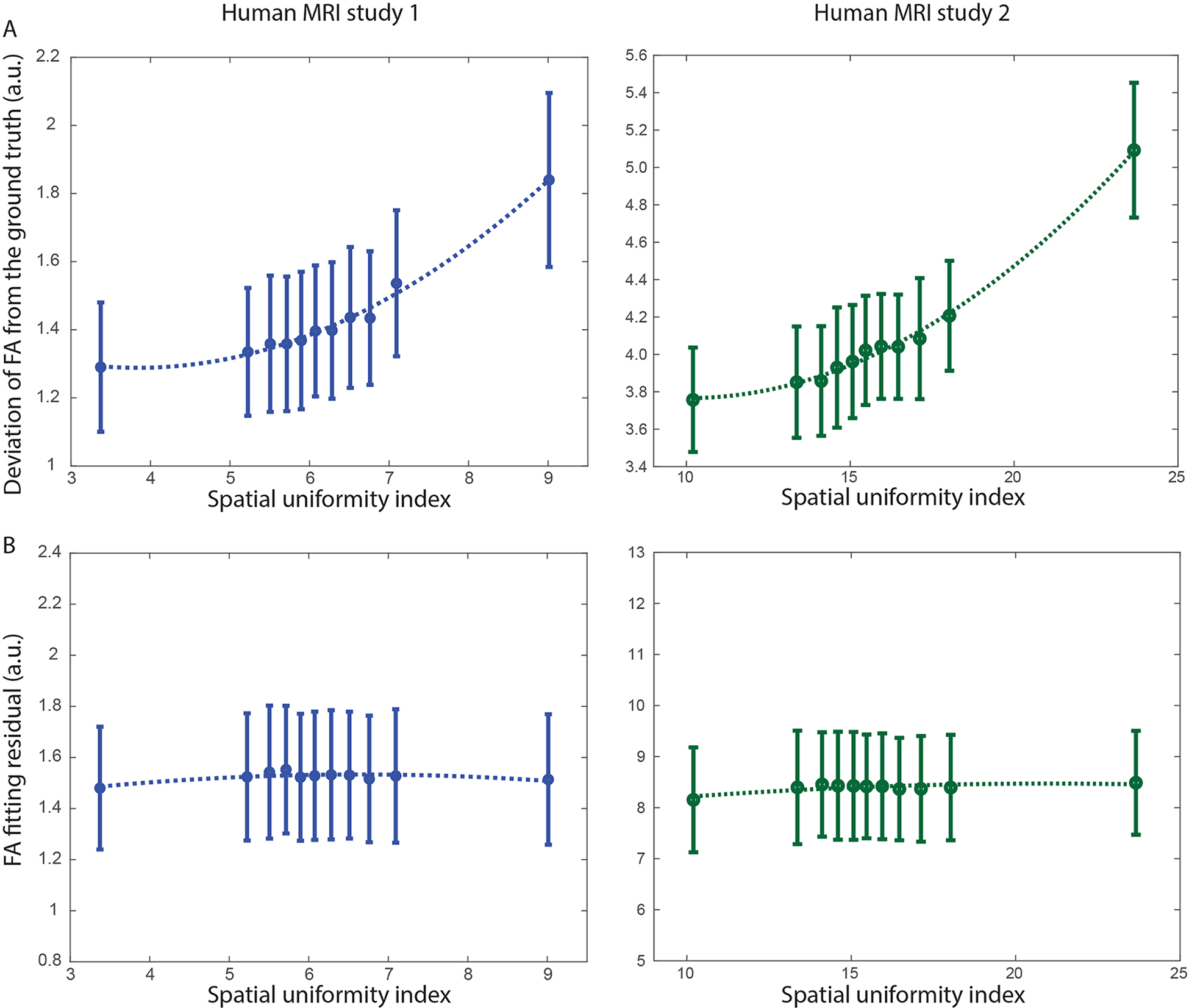
Figure 2

Open in a new tab

Figure 2A shows the errors of FA values derived from down-sampled diffusion MRI data, corresponding to 11 levels of gradient-direction spatial uniformity, using the fully-sampled data as the ground truth. The solid dots indicate the mean value across subjects, and the error bars indicate the standard deviations. Figure 2B shows that the FA fitting residuals do not differ much across data obtained from 11 different down-sampling schemes.

Figure 3 compares the FA maps in human MRI study 1, derived from A) fully-sampled diffusion MRI (64 directions), B) down-sampled MRI (30 directions) with spatial uniformity index = 3.37, and C) down-sampled MRI (30 directions) with spatial uniformity index = 9.01, for 4 of the subjects. Images in the zoomed-in panels show that the down-sampled MRI with a worse spatial uniformity index are more susceptible to artificially increased or decreased FA values (indicated by arrows).

Figure 3.

Figure 3

Open in a new tab

Figure 3 compares the FA maps in human MRI study 1 derived from A) fully-sampled diffusion MRI (64 directions), B) down-sampled MRI (30 directions) with spatial uniformity index = 3.37, and C) down-sampled MRI (30 directions) with spatial uniformity index = 9.01, for 4 of the subjects.

Figure 4 show FA maps in human MRI study 2, derived from A) fully-sampled diffusion MRI (60 directions), B) down-sampled MRI (30 directions) with spatial uniformity index = 10.05, and C) down-sampled MRI (30 directions) with spatial uniformity index = 23.65, for 4 of the subjects. Images in the zoomed-in panels illustrate that 1) the difference between FA maps derived from data with different down-sampling procedures is not obvious in most brain regions, and 2) down-sampled MRI with a worse spatial uniformity index have a slightly higher noise level only in a few areas for this data set.

Figure 4.

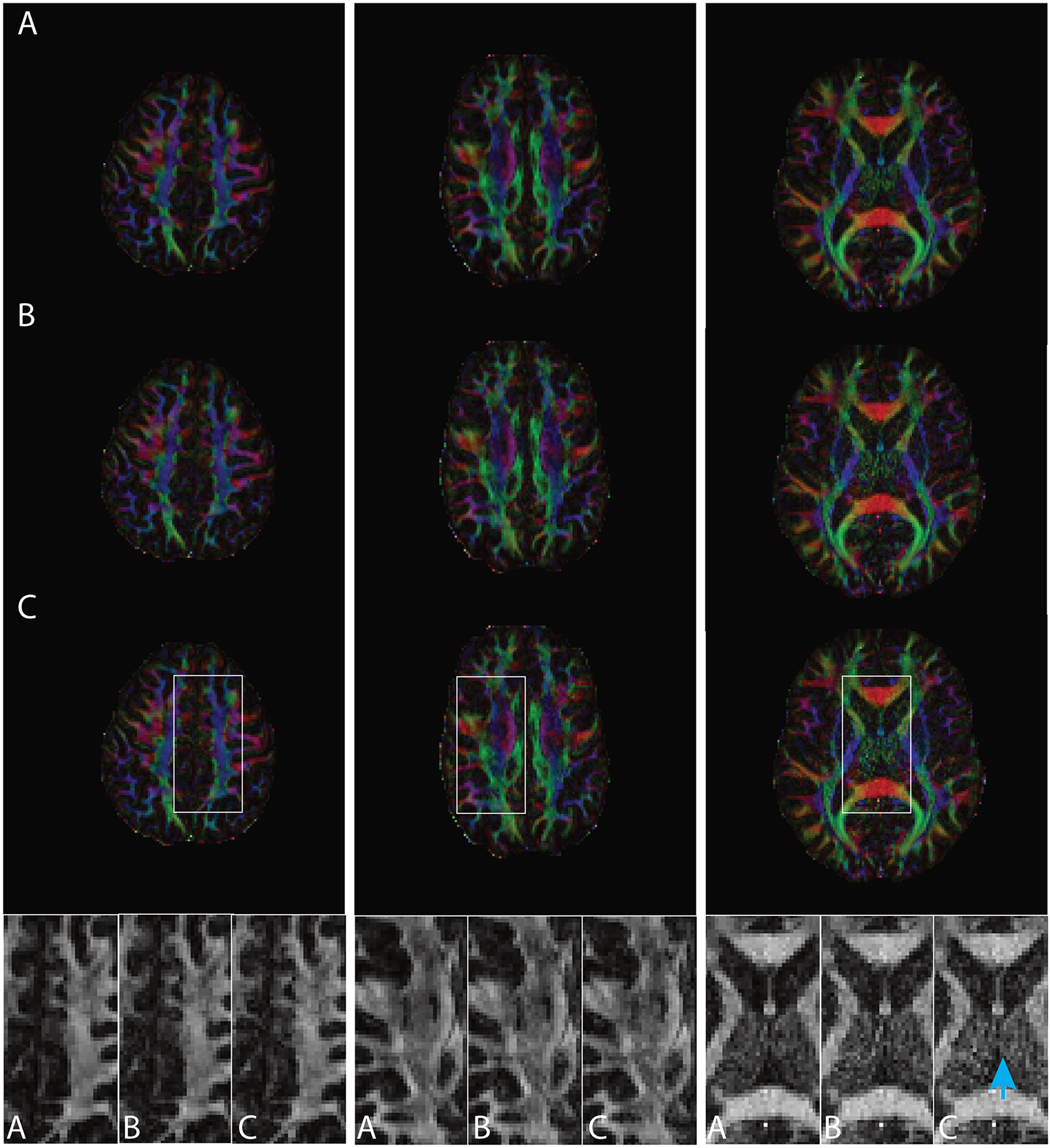
Figure 4

Open in a new tab

Figure 4 compares the FA maps in human MRI study 2 derived from A) fully-sampled diffusion MRI (60 directions), B) down-sampled MRI (30 directions) with spatial uniformity index = 10.05, and C) down-sampled MRI (30 directions) with spatial uniformity index = 23.65, for 4 of the subjects.

4. Discussion

In this paper a spatial uniformity index, which measures the spatial uniformity of diffusion encoding gradients based on areas of Delaunay triangles, is used to assess the quality of down-sampled diffusion MRI data. As shown in Figure 2A, the proposed spatial uniformity index is correlated with errors in FA values obtained from down-sampled diffusion MRI data. On the other hand, the FA fitting residuals that are typically used to assess diffusion MRI quality are not correlated with either FA errors or spatial uniformity index. These data suggest that the spatial uniformity index could be more valuable in assessing quality of down-sampled diffusion MRI data (e.g., as a part of data harmonization; or exclusion of motion corrupted data points), as compared with FA fitting residual measures.

We would like to point out that the standard deviation of Delaunay triangle areas is not the only spatial uniformity measure for diffusion encoding schemes. As reported by Jones et al. [6], the spatial uniformity of diffusion encoding can also be measured by the distance between diffusion vector points on a spherical surface. Specifically, based on electrostatic model, uniformly distributed charged points in 3D space are expected to have a lower total repulsive force (that is inversely proportional to the square of the distance between charged points). We have implemented the electrostatic model based spatial uniformity assessment, and compared it with our Delaunay triangle based approach in a numerical study, where 64 diffusion encoding directions (from the scheme shown in Figure 1) were randomly down-sampled to 30 directions. As shown in Supplemental Figure 1, the spatial uniformity measured by standard deviation of Delaunay triangle areas is linearly correlated with the spatial uniformity measured by total repulsive force in the electrostatic model, across 5000 randomly chosen down-sampling schemes. We therefore expect that both spatial uniformity measures should equally benefit diffusion MRI studies that require protocol harmonization.

In this study we used the inner-product based algorithm (as described in section 2.1) to identify a suitable set of down-sampling scheme, aiming to harmonize data obtained from two protocols with different numbers of diffusion gradient directions. We would like to point out that the inner-product based method is only one of the several possible ways of down-sampling diffusion gradient directions. Future studies should be carried out to quantitatively compare different down-sampling schemes.

A strength of this study is that we used human MRI data (from two studies) of high angular resolution as the ground truth to quantitatively evaluate down-sampled data, instead of using pure numerical simulation. However, our study has a few limitations. First, we only evaluated the quality of down-sampled diffusion MRI data in terms of the FA accuracy. The dependence of other orientation-dependent diffusion measures (e.g., from higher-order diffusion models beyond the tensor) on down-sampling schemes remains to be evaluated in future studies. Second, the sample sizes of two human MRI studies are 12 and 10, and the value of the proposed spatial uniformity index in assessing data quality for large-scale multi-site diffusion MRI studies remains to be established. Third, our procedure has only been evaluated with diffusion MRI data corresponding to a single b value, and its performance for harmonizing protocols with multiple b values remains to be assessed. To harmonize two sets of diffusion MRI protocols comprising multiple b values, one may use the inner-product method to match diffusion encoding schemes for each of the matching b values. However, if two sets of MRI protocols to be harmonized do not have matching b values, then our reported inner-product method might not be readily used for protocol harmonization.

In conclusion, here we report a software procedure for 1) down-sampling and harmonizing diffusion MRI data (through an inner-product based algorithm) and 2) evaluating diffusion MRI down-sampling schemes (through a spatial uniformity index). Experimental results suggest that the proposed spatial uniformity index is correlated with errors in FA values obtained from down-sampled diffusion MRI data. We expect that our implemented software procedure should prove valuable for 1) guiding data harmonization for multi-site diffusion MRI studies, and 2) assessing the impact of rejecting motion corrupted data points on the accuracy of diffusion measures.

Supplementary Material

1

Highlights.

  • The proposed spatial uniformity index can assess quality of a down-sampling scheme

  • The spatial uniformity index is associated with fractional anisotropy (FA) errors in down-sampled data

  • Our software procedure can down-sample diffusion MRI data for data harmonization

Acknowledgments

This research is supported by NIH grants R01-DA045565, R03-DA035670, and R01-NS102220.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Declarations of interest

Dr. Nan-kuei Chen has a disclosed financial interest in Duke University that had no involvement in the work reported here. Specifically, the MUSE algorithm (PCT/US2013/048252; US Patent Application No. 13/928,757) invented by Dr. Nan-kuei Chen and owned by Duke University was licensed by Magtron Inc. (Jiangyin, China) and GE Healthcare (Waukesha, USA). The terms of this arrangement have been properly disclosed to the University of Arizona and reviewed by the Institutional Review Committee in accordance with its conflict of interest policies.

References

  • [1].Basser PJ, Jones DK. Diffusion-tensor MRI: theory, experimental design and data analysis - a technical review. NMR Biomed 2002;15:456–67. 10.1002/nbm.783. [DOI] [PubMed] [Google Scholar]
  • [2].Kiselev VG. Fundamentals of diffusion MRI physics. NMR Biomed 2017;30. 10.1002/nbm.3602. [DOI] [PubMed] [Google Scholar]
  • [3].Le Bihan D, Johansen-Berg H. Diffusion MRI at 25: exploring brain tissue structure and function. Neuroimage 2012;61:324–41. 10.1016/j.neuroimage.2011.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [4].Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson - Ser B 1996;111:209–19. 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
  • [5].Mori S Introduction to Diffusion Tensor Imaging. Elsevier; 2007. 10.1016/B978-0-444-52828-5.X5014-5. [DOI] [Google Scholar]
  • [6].Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med 1999;42:515–25. . [DOI] [PubMed] [Google Scholar]
  • [7].Hasan KM, Parker DL, Alexander AL. Comparison of gradient encoding schemes for diffusion-tensor MRI. J Magn Reson Imaging 2001;13:769–80. 10.1002/jmri.1107. [DOI] [PubMed] [Google Scholar]
  • [8].Jones DK. The Effect of Gradient Sampling Schemes on Measures Derived from Diffusion Tensor MRI: A Monte Carlo Study. Magn Reson Med 2004;51:807–15. 10.1002/mrm.20033. [DOI] [PubMed] [Google Scholar]
  • [9].Mang SC, Gembris D, Grodd W, Klose U. Comparison of gradient encoding directions for higher order tensor diffusion data. Magn Reson Med 2009;61:335–43. 10.1002/mrm.21797. [DOI] [PubMed] [Google Scholar]
  • [10].Wedeen VJ, Hagmann P, Tseng WYI, Reese TG, Weisskoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med 2005;54:1377–86. 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]
  • [11].De Santis S, Gabrielli A, Palombo M, Maraviglia B, Capuani S. Non-Gaussian diffusion imaging: A brief practical review. Magn Reson Imaging 2011. 10.1016/j.mri.2011.04.006. [DOI] [PubMed] [Google Scholar]
  • [12].Tuch D, Reese T, Wiegell M, Neuron VW-, 2003. undefined. Diffusion MRI of complex neural architecture. Elsevier; n.d. [DOI] [PubMed] [Google Scholar]
  • [13].Tournier JD, Mori S, Leemans A. Diffusion tensor imaging and beyond. Magn Reson Med 2011;65:1532–56. 10.1002/mrm.22924. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [14].Tax CM, Grussu F, Kaden E, Ning L, Rudrapatna U, John Evans C, et al. Cross-scanner and cross-protocol diffusion MRI data harmonisation: A benchmark database and evaluation of algorithms. Neuroimage 2019;195:285–99. 10.1016/j.neuroimage.2019.01.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [15].Andersson JLR, Skare S. A model-based method for retrospective correction of geometric distortions in diffusion-weighted EPI. Neuroimage 2002. 10.1006/nimg.2001.1039. [DOI] [PubMed] [Google Scholar]
  • [16].Mohammadi S, Möller HE, Kugel H, Müller DK, Deppe M. Correcting eddy current and motion effects by affine whole-brain registrations: Evaluation of three-dimensional distortions and comparison with slicewise correction. Magn Reson Med 2010. 10.1002/mrm.22501. [DOI] [PubMed] [Google Scholar]
  • [17].Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn Reson Med 2003;49:177–82. 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]
  • [18].Truong T-K, Song AW, Chen N. Correction for Eddy Current-Induced Echo-Shifting Effect in Partial-Fourier Diffusion Tensor Imaging. Biomed Res Int 2015. 10.1155/2015/185026. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS1718007-supplement-1.pdf (663KB, pdf)

RESOURCES