Abstract
Breast cancer is one of the leading causes of mortality in the world and it occurs in high frequency among women that carries away many lives. To detect cancer, extraction or segmentation of lesions/tumors is required. Segmentation process is very crucial if the mammogram images are blurred or low contrast. This paper suggests a novel clustering approach for segmenting lesions/tumors in the mammogram images using Atanassov’s intuitionistic fuzzy set theory. The algorithm initially converts an image to an intuitionistic fuzzy image using a novel intuitionistic fuzzy generator. From the intuitionistic fuzzy image, two membership intervals are computed. Then, using Zadeh’s min t-conorm, a new membership function is computed. Using the new membership function, an interval type 2 fuzzy image is constructed. Two types of distance functions are used in clustering—intuitionistic fuzzy divergence and a fuzzy exponential type distance function. Further, in each iteration, membership matrix is updated using a hesitation degree and a clustered image is obtained. Tumors/lesions are then segmented from the clustered image. The proposed method is compared with existing methods both quantitatively and qualitatively and it is observed that the proposed method performs better than the existing methods.
Keywords: Intuitionistic fuzzy set, Clustering, Zadeh’s t-conorm, Intuitionistic fuzzy divergence, Fuzzy exponential distance function
Introduction
Today globally, breast cancer is a commonly occurring cancer among women. Occurrence of breast mass is the main cause of developing breast cancer among women and early detection of breast mass may increase the survival rate. One common approach for detecting abnormalities in mammograms is isolation or segmentation of masses/lesions from the breast. Tumors/lesions and calcification are the common abnormalities for breast cancer. Segmentation plays an important role in deciding whether the mammogram image is benign or malignant. Blurry boundaries and low contrast of ultrasound images make automatic segmentation a difficult task. In order to extract any lesion/mass from the mammograms, image segmentation is done. There are many fuzzy and non-fuzzy methods in literature that segment breast tumor, lesion, or mass. But medical images are mostly non-uniformly illuminated and have vague regions/boundaries, so fuzzy methods normally perform better.
Clustering is an important method that segments tumors/lesions in the breast. It partitions the image into homogeneous regions in such a way that the pixels in a group are more similar than the pixels in different groups. Though there are many clustering algorithms in literature that clusters real-time images accurately, the accuracy of clustering algorithm is still a debatable topic. Fuzzy c means clustering (FCM), suggested by Bezdek [1], is the first and most widely used clustering algorithm. It allows each data to belong in ‘c’ number of clusters and each data has a membership degree. The membership degree of each data point in each cluster depends on the distance between the cluster centre and data point. Later, many researchers modified the FCM algorithm by incorporating spatial terms, using different types of kernel functions that may be Gaussian, radial basis, or hypertangent kernels [2–6]. But the accuracy in the segmentation is not better. Later with the introduction of intuitionistic fuzzy set theory by Atanassov [7], intuitionistic fuzzy c means clustering (IFCM) is introduced [8–10]. Intuitionistic fuzzy set takes into account a hesitation degree while defining the membership function. So, the non-membership degree is not the complement of the membership degree rather less than or equal to the complement of the membership degree.
With the introduction of IFCM algorithm, many modified intuitionistic fuzzy clustering algorithms are suggested. Verma et al. [11] suggested an intuitionistic fuzzy clustering algorithm with the introduction of hesitation degree. They used membership, non-membership, and hesitation degree while computing cluster centroids. The distance function, they used, is the Euclidean distance that considers all the three terms—membership, non-membership, and hesitation degrees. Xu and Wu [12] suggested an intuitionistic fuzzy clustering method, where they used an intuitionistic fuzzy distance measure and extended the algorithm to an interval-valued intuitionistic fuzzy sets. Kumar and Harish [13] used Hausdorff distance measure in place of Euclidean distance and used Bustince intuitionistic fuzzy generator to compute the non-membership degree. Dubey [14] suggested a rough set-based intuitionistic fuzzy clustering algorithm. They initialized cluster centroids from the location of peak points, obtained from intuitionistic fuzzy roughness measure. Roughness measure is computed by considering intuitionistic fuzzy histon as an upper approximation of rough set and fuzzy histogram as a lower approximation of rough set. A new fuzzy complement is used to compute the non-membership degree and then performed clustering.
The methods that use intuitionistic fuzzy set work better than fuzzy set as intuitionistic fuzzy set considers two uncertainties—membership and non-membership degrees. The reason is that medical images contain uncertainties that are present in the form of vague boundaries or non-uniform illumination. Fuzzy set considers only one uncertainty, which is the membership function whereas the intuitionistic fuzzy set considers two uncertainties, so better results may be expected.
In this paper, we propose a novel intuitionistic fuzzy clustering approach to segment breast mass/tumor. Initially, the image is converted to an intuitionistic fuzzy image using a novel intuitionistic fuzzy generator for computing the non-membership degree. Then, using hesitation degree, two levels are computed. Using Zadeh’s min t-norm, a new membership function is computed that is used to create an interval type 2 fuzzy image. In the clustering algorithm, four features—pixel energy, mean, standard deviation, gradient features—are used. Two types of distance functions—fuzzy divergence and an exponential distance measure—are used. Further, in each membership iteration, the membership matrix is updated using hesitation degree. The algorithm is compared with existing methods quantitatively and qualitatively.
The paper is organized as follows. “Intuitionistic Fuzzy Set” outlines the preliminaries of an intuitionistic fuzzy set. “Conversion of the Image to an Intuitionistic Fuzzy Image” presents the concept of converting the image to an intuitionistic fuzzy image. “Conversion of Intuitionistic Fuzzy Image to an Interval Type 2 Fuzzy Image” details the conversion of intuitionistic fuzzy image to an interval type 2 fuzzy image. “Clustering” describes the novel intuitionistic fuzzy clustering algorithm. Results and discussion are detailed in “Results and Discussion”. “Conclusion” concludes the paper.
Highlights of the Paper
The given image is initially converted to an intuitionistic fuzzy image using a novel intuitionistic fuzzy generator.
The intuitionistic fuzzy image is then converted to an interval type 2 fuzzy image, where the membership level lies in an interval range. Then, intuitionistic fuzzy c means clustering algorithm is applied, where the constant term in the hesitation degree in the intuitionistic fuzzy set is selected from a graphical approach. Two types of distance functions—intuitionistic fuzzy divergence and an exponential distance functions—are used in the clustering process. Four features are considered in the clustering algorithm—mean, pixel energy, gradient, standard deviation.
Lesion/tumor region is then isolated from other regions using histogram thresholding.
Morphological operators such as opening operation are applied to remove any unwanted spots to obtain a final segmented image.
Intuitionistic Fuzzy Set
Fuzzy set theory, proposed by Zadeh [16], was designed to mathematically represent uncertainty and vagueness in a set. This uncertainty is represented in terms of membership function. But in real-time images, fuzzy techniques sometimes face difficulty in case when there are more uncertainties. To overcome this drawback, Atanassov in 1985 proposed an intuitionistic fuzzy set (IFS) theory where two uncertainties—membership degree and non-membership degree—are considered. In fuzzy set, non-membership degree is the complement of the membership degree, but in IFS, non-membership degree is less than or equal to the complement of the membership degree. This ‘less than’ is due to the hesitation while defining the membership function.
For a finite set X, , an IFS may be mathematically represented as:
, where are the membership and non-membership degrees, respectively, with the condition
| 1 |
is the membership function that may be Gaussian, Gamma, triangular, S-membership function, or any other type of membership function. Non-membership function, , is computed from intuitionistic fuzzy generator that may be Sugeno, Yager, or any other generator.
In Eq. (1), the condition, “, is due to the hesitation that arises while defining the membership function. Hesitation degree is denoted by with . So, considering all the three degrees, we get
Intuitionistic fuzzy generator is almost similar to fuzzy negation or complement. The difference between fuzzy complement and intuitionistic fuzzy generator is explained as follows:
A function is called intuitionistic fuzzy generator if , ‘’ is due to the consideration of hesitation degree while defining the membership function. When there is no hesitation, it becomes a standard fuzzy set, i.e., .
Sugeno class of fuzzy complement [17] is given as
, where is the constant.
If the value of is taken as, then or and . Then, the set is not an intuitionistic fuzzy set. So, Sugeno’s intuitionistic fuzzy generator is written as with the condition .
Conversion of the Image to an Intuitionistic Fuzzy Image
In this paper, a new type of intuitionistic fuzzy generator is used. Many authors suggested different types of intuitionistic fuzzy generators [15, 17–19]. An intuitionistic fuzzy generator recently used by Chaira in [15], where the author used an increasing function, and the fuzzy complement was obtained as . But in this work, a different type of increasing function is used, where the constant term is different. If the increasing function in [15] is used, then the misclassification error will be more and better result will not be obtained. A sample result is shown in Fig. 1 below.
Fig. 1.
(a) Original image. (b) Segmentation result using increasing generator by [15]; (c) proposed segmented image—method 1; (d) proposed segmented image—method 2; (e) ground truth image
To create an intuitionistic fuzzy generator, characterization of fuzzy complement is required. Characterization of fuzzy complemental function is given as follows [17]:
If is a function, , then is an involutive fuzzy complement if and only if there exists a continuous function such that and is an increasing function. It is represented as
| 2 |
where is an increasing function.
Klir and Yuan [18] showed that involutive fuzzy complement function can be generated using a dual of Eq. (2). It is written as:
| 3 |
where is a decreasing function. This is called dual generator.
In this work, let us consider an increasing function:
| 4 |
Considering for simplicity, we may write
| 5 |
with , is a constant term.
Inverse function of Eq. (5) is written as
So,
After solving, we get
| 6 |
In terms of membership function,, the non-membership function is written as
| 7 |
where in Eq. (7) is constant and it determines the non-membership function.
It is observed that with any value of ,. This implies that the condition of intuitionistic fuzzy generator holds.
In the case of images, initially, the image is converted to a fuzzy image, and the membership function is computed using normalization, which is given as follows:
| 8 |
is the pixel gray level, and are the minimum and maximum gray levels of the image, respectively.
Intuitionistic fuzzy membership function of the image, with membership function, at position, is now written as
| 9 |
is obtained from Eq. (3).
Non-membership function is computed using Eq. (2) as
| 10 |
Hesitation degree is obtained as
| 11 |
As is not fixed for all the images, optimum value of is obtained using an intuitionistic fuzzy entropy.
Zadeh [20] first introduced the idea of fuzzy entropy in 1969. It is a measure of fuzziness in a fuzzy set or amount of uncertainty present in a set. From the concept of De Luca and Termini [21] for non-probabilistic entropy, fuzzy exponential entropy is also defined accordingly [22]. If the membership degree is 0.5, then there is maximum fuzziness or uncertainty, which implies maximum entropy. If the membership degree is 0 or 1, then the fuzziness is less, which implies that entropy is minimum. Just like conventional entropy, if the probability is 0.5, then the entropy, i.e., uncertainty, is maximum and likewise, if the probability is 0 or 1, the entropy is minimum. Intuitionistic fuzzy entropy is similar to fuzzy entropy where non-membership degree is also taken into account.
A real function is called intuitionistic fuzzy entropy (IFE) on [23] if:
(1) if A is non-fuzzy,
(2) cardinal if
(3) if is less fuzzy than , i.e.,
and for or
and for
(4), where , implies
and
In this paper, an intuitionistic fuzzy entropy is used, which is given as [9]
| 12 |
is the hesitation degree at position, which is computed using Eq. (11).
Optimum value of is computed by maximizing in , which is written as
| 13 |
For each value of , intuitionistic fuzzy entropy () is computed and the maximum value of is chosen. Substituting the value of in Eq. (9), an intuitionistic fuzzy image is created.
Conversion of Intuitionistic Fuzzy Image to an Interval Type 2 Fuzzy Image
A preliminary on type 2 fuzzy set is discussed.
(a) Type 2 fuzzy set
Type 2 fuzzy set is an extension of fuzzy set, where the membership function of the fuzzy set is considered to be fuzzy. It is also called as a blurred type 1 fuzzy set. If a type 1 fuzzy membership function (primary membership) is blurred, then all of its points shift either left or right of the membership function. The value of the shift or amplitudes at all points may not be equal. That means, corresponding to each primary membership, there is a secondary membership that also lies in the range [0, 1], which defines the possibilities for the primary membership. If the amplitude is the same and equal to 1, then it is called interval type 2 fuzzy set [23]. Thus, interval type 2 fuzzy set consists of two membership levels—lower membership level and upper membership level. A type 2 fuzzy set is written as
where is the secondary membership function and is the primary membership of .
From the intuitionistic fuzzy image, two levels are constructed—upper and lower membership levels. The upper and lower membership functions are defined as:
| 14 |
where .
Using hesitation degree from Eq. (11), two levels are modified and computed as follows [24]:
| 15 |
where is the fuzzy hedge. Fuzzy hedge is an important feature in a fuzzy system that modifies the membership values. These are also called ‘modifiers’.
The two membership functions are then combined using Zadeh’s fuzzy t-conorm as follows [25]:
| 16 |
Though there are different types of t-conorm in literature, in this paper, the simplest form of fuzzy t-conorm, which is Zadeh’s t-conorm, is used.
In this method, after thorough working on images on trial basis, the value of is found suitable and is used in this work.
Clustering
The type 2 fuzzy image is then clustered to obtain a segmented image. In this paper, an intuitionistic fuzzy clustering algorithm [9] is used. A brief idea on fuzzy clustering is described.
Initially, a number of clusters are chosen. Then, membership values are randomly (initial guess) assigned to each pixel for being in the clusters. As we do not know the belongingness of each pixel in different clusters, initialization is required and this is done randomly [1]. Then, cluster centers are computed. To each pixel corresponding to each cluster center, distance between the cluster center and the pixel is computed and the membership matrix is updated. At each iteration, distance between the cluster center and the pixel is computed and membership matrix is updated and this is repeated until the difference between the updated membership matrix and previous matrix is less than . Here, is taken. When the difference is , then the last updated membership matrix is the final matrix and the cluster centers are the final cluster centers.
In this work, four fuzzy features are computed—pixel energy, mean, standard deviation, and gradient. These features are considered for obtaining clustered image almost accurately.
Pixel energy is computed as square of pixel intensity. It is also called uniformity. On squaring the pixel intensity, lesser pixel intensity values become less and the brighter pixel intensity values also become slightly less. In doing so, the darker region becomes uniformly darker, and brighter region also becomes uniformly brighter.
Gradient feature takes into account the Sobel operator [26]. It consists of two spatial masks that are convolved with the original image to calculate gradient magnitude.
Two Sobel convolution kernels in x and y directions are as follows:
Kernels are applied separately on the image and are combined together to compute the absolute magnitude of the gradient at each point. The gradient magnitude is given by
, and are the gradients in x and y directions.
In our work, gradient feature at position is computed as
| 17 |
where is the local mean value of the neighborhood of the pixel at position . is the image gradient value using the Sobel operator at the position .
Final gradient feature is computed by normalizing Eq. (17) with the maximum value of which is written as
| 18 |
where is the maximum value of . Multiplying the gradient value with the mean value of the window makes the high gradient values slightly less that implies that the brightness is also less. Likewise, unwanted small gradient values also become less that implies that the brightness is also less. In doing so, the outline of the clustered region is clear and the clustered image looks better. If the edge brightness is more, then the image regions are not properly clustered.
Standard deviation is computed as , where is the mean of the image.
Intuitionistic fuzzy C means algorithm cluster the feature vectors by searching for local minima using the following objective function:
| 19 |
where is any distance measure between (cluster center) of each region and (points in the pattern), and is the membership value of data () in cluster. is the number of clusters and is the number of data points.
is the intuitionistic fuzzy entropy, where , is the hesitation degree of the element in cluster ‘’.
In this paper, we have used two distance functions separately instead of Euclidean distance—(i) a fuzzy exponential type distance function and (ii) an intuitionistic fuzzy divergence [27], in Eq. (14).
(i) Fuzzy exponential type distance function: We have used a fuzzy exponential distance function as
| 20 |
If is a universal set and is the class of all fuzzy sets in and is the class of all crisp set of , then the following criteria holds [28]:
(a)
(b) ,
(c) , , is the complement of
(d) If
(ii) Intuitionistic fuzzy divergence:
| 21 |
Now, minimization of is based on suitable selection of U (membership matrix) and using an iterative process through the following equations:
| 22 |
At each iteration, the membership function, is updated considering hesitation degree as follows:
| 23 |
where
denotes the intuitionistic fuzzy membership of the data in class.
The modified cluster center is written as
| 24 |
Using Eq. (24), the cluster center is updated, and simultaneously, the membership matrix is also updated.
It is to be noted that while updating the membership degree at each iteration, the hesitation degree is also considered.
Hes_degree = 1-membership degree − non-membership degree.
| 25 |
In the membership matrix computation, the value of in Eq. (25) takes a different value rather than the value computed using Eq. (13) for obtaining an intuitionistic fuzzy image.
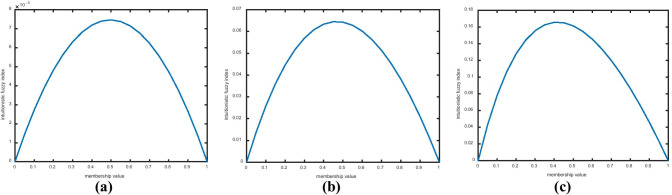
The choice of here is crucial. The plot of membership degree versus hesitation degree with different values of is shown in Fig. 2. It is observed from the figure that the plot is symmetric at , but at , the plot is not symmetric. In the algorithm, is selected. This is due to the fact that the hesitation degree or intuitionistic fuzzy index is very less, i.e., 0.0075 at whereas with , the hesitation degree is 0.065.
Fig. 2.
Plot of membership function against hesitation degree: (a) λ = 1.1, (b) λ = 1.3, (c) λ = 1.5
At each iteration, the cluster center and the membership matrix are updated and the algorithm stops when the updated membership matrix and the previous matrix, i.e.,
, is a user defined, and in this algorithm, is selected as .
Clustered image, showing different types of regions including the region of interest, is obtained. Then, lesion/tumor/mass is segmented from the clustered image by removing the unwanted regions from the clustered image and a binary image is formed. As the ground truth image is a binary image, so we segmented the required region of interest and displayed it in binary form.
After segmentation, using morphological operator, i.e., an opening operation is done to remove unwanted small spots in the segmented image. The opening operation removes unwanted small objects (ones in binary images) in the foreground region.
It is to be noted that for comparing our proposed method with the existing methods, opening operation is also applied on all the existing methods to remove unwanted small spots in the segmented image to maintain uniformity (Fig. 3).
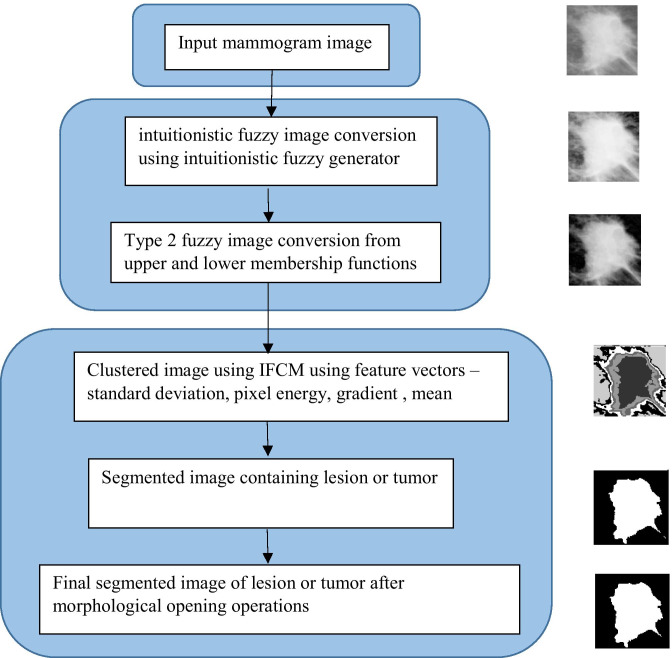
Fig. 3.
Model of the proposed method along with images
Algorithm:
Select an image.
Convert the image into an intuitionistic fuzzy image using a novel intuitionistic fuzzy generator.
Compute two levels using hesitation degree from Eq. (15).
Using Zadeh’s t-conorm, compute a modified membership function and create a new image using the modified membership function.
Compute four features of the new image.
Cluster the image using 4 fuzzy features and distance functions.
Modify the membership function in each iteration using hesitation degree, computed from the novel intuitionistic fuzzy generator.
Stop the clustering algorithm when the difference between the updated membership matrix and the previous matrix is less than ,
Segment the lesion/tumor from the clustered image by removing the unwanted regions from the clusters.
Apply morphological opening operation to remove any unwanted small spots in the segmented image.
Results and Discussion
The test is performed on 25 images and these images are downloaded from the website. Results on 20 images are shown. The proposed method is compared with four methods—fuzzy clustering method (FCM) [1], intuitionistic fuzzy method IFCM-1 [11], a method by IFCM-2 [14], and Kernel fuzzy clustering by KFCM [2]. Image results on 4 images are shown.
It is observed that in Fig. 4, the proposed method shows the tumor region without any unwanted region and is almost similar to that of ground truth image. FCM can also segment the tumor without noise, but the segmented region is less when compared with the ground truth image.
Fig. 4.
(a) Original image, (b) proposed clustered image, (c) segmented image using IFCM-1, (d) segmented image using FCM, (e) segmented image using IFCM-2, (f) segmented image using KFCM, (g) proposed segmented image-exponential distance, (h) proposed segmented image-divergence, (i) ground truth image
Figure 5 shows a mammogram image with lesion. It is observed that as compared with the other existing methods, the tumor/lesion in the proposed methods is almost similar to that of ground truth image.
Fig. 5.
(a) Original image, (b) proposed clustered image, (c) segmented image using IFCM-1, (d) segmented image using FCM, (e) segmented image using IFCM-2, (f) segmented image using KFCM, (g) proposed segmented image-exponential distance, (h) proposed segmented image-divergence, (i) ground truth image
Figure 6 shows a breast tumor where the proposed two methods perform better than the other methods. FCM can also segment the tumor without noise and the segmented region is slightly less than the proposed method. The other methods contain unwanted regions.
Fig. 6.
(a) Original image, (b) proposed clustered image, (c) segmented image using IFCM-1, (d) segmented image using FCM, (e) segmented image using IFCM-2, (f) segmented image using KFCM, (g) proposed segmented image-exponential distance, (h) proposed segmented image-divergence, (i) ground truth image
Figure 7 shows that the proposed method using both the distance functions performs better than all the methods. IFCM-2 method does not contain any unwanted region but the segmented tumor region is less than that of the ground truth image. In other methods, there are many unwanted regions.
Fig. 7.
(a) Original image. (b) Proposed clustered image, (c) segmented image using IFCM-1, (d) segmented image using FCM, (e) segmented image using IFCM-2, (f) segmented image using KFCM, (g) proposed segmented image-exponential distance, (h) proposed segmented image-divergence, (i) ground truth image
Tables 1 and 2 show the misclassification error of the 20 images of the proposed method using two distance measures separately and the other methods.
Table 1.
Percentage misclassification error of the proposed method using exponential distance function 1 with 4 existing methods
| IMAGE | Prop method (exponential distance) | IFCM-1 | FCM | IFCM-2 | KFCM |
|---|---|---|---|---|---|
| Mam-1 | 0.22 | 0.27 | 1.3 | 0.53 | 1.30 |
| Mam-2 | 0.27 | 0.49 | 0.41 | 0.98 | 1.26 |
| Mam-3 | 0.18 | 0.99 | 0.95 | 0.96 | 2.58 |
| Mam-4 | 1.35 | 1.64 | 1.69 | 2.49 | 1.58 |
| Mam-5 | 2.10 | 3.69 | 3.69 | 3.69 | 4.71 |
| Mam-6 | 3.28 | 3.99 | 6.18 | 6.59 | 9.48 |
| Mam_7 | 0.25 | 0.27 | 0.20 | 0.20 | 0.19 |
| Mam_8 | 0.47 | 1.12 | 1.35 | 1.22 | 1.30 |
| Mam-9 | 0.12 | 0.75 | 1.2 | 1.16 | 2.06 |
| Mam-10 | 3.86 | 4.27 | 9.13 | 8.07 | 4.82 |
| Mam-11 | 3.01 | 5.61 | 5.63 | 5.63 | 6.53 |
| Mam-12 | 1.93 | 5.03 | 4.8 | 3.31 | 4.9 |
| Mam-13 | 0.11 | 0.40 | 0.40 | 0.40 | 0.40 |
| Mam-14 | 0.30 | 0.71 | 1.6 | 0.74 | 1.50 |
| Mam-15 | 0.95 | 4.02 | 3.01 | 4.02 | 2.08 |
| Mam-16 | 1.48 | 3.37 | 2.76 | 2.16 | 3.79 |
| Mam-17 | 1.11 | 4.31 | 1.92 | 3.70 | 2.17 |
| Mam-18 | 0.79 | 2.98 | 4.74 | 0.92 | 3.62 |
| Mam-19 | 2.30 | 4.99 | 2.37 | 2.69 | 5.62 |
| Mam-20 | 1.07 | 4.12 | 2.38 | 2.96 | 5.53 |
| TOTAL | 1.26 | 2.65 | 2.77 | 2.62 | 3.28 |
Table 2.
Percentage misclassification error of the proposed method using divergence as distance function with 4 existing methods
| Image | Prop. method (divergence) | IFCM-1 | FCM | IFCM-2 | KFCM |
|---|---|---|---|---|---|
| Mam-1 | 0.05 | 0.27 | 1.3 | 0.53 | 1.30 |
| Mam-2 | 0.25 | 0.49 | 0.41 | 0.98 | 1.26 |
| Mam-3 | 0.18 | 0.99 | 0.95 | 0.98 | 2.58 |
| Mam-4 | 0.68 | 1.64 | 1.69 | 2.49 | 1.58 |
| Mam-5 | 2.89 | 3.69 | 3.69 | 3.69 | 4.71 |
| Mam-6 | 2.45 | 3.99 | 6.18 | 6.59 | 9.48 |
| Mam_7 | 0.21 | 0.27 | 0.20 | 0.20 | 0.19 |
| Mam_8 | 0.57 | 1.12 | 1.35 | 1.22 | 1.30 |
| Mam-9 | 0.16 | 0.75 | 1.2 | 1.16 | 2.06 |
| Mam-10 | 3.96 | 4.27 | 9.13 | 8.07 | 4.82 |
| Mam-11 | 4.42 | 5.61 | 5.63 | 5.63 | 6.53 |
| Mam-12 | 2.79 | 5.03 | 4.8 | 3.31 | 4.90 |
| Mam-13 | 0.38 | 0.40 | 0.40 | 0.40 | 0.40 |
| Mam_14 | 0.48 | 0.71 | 1.6 | 0.74 | 1.50 |
| Mam-15 | 0.91 | 4.02 | 3.01 | 4.02 | 2.08 |
| Mam-16 | 1.73 | 3.37 | 2.76 | 2.16 | 3.79 |
| Mam-17 | 0.79 | 4.31 | 1.92 | 3.70 | 2.17 |
| Mam-18 | 4.78 | 2.98 | 4.74 | 0.92 | 3.62 |
| Mam-19 | 2.27 | 4.99 | 2.2 | 2.69 | 5.98 |
| Mam-20 | 1.59 | 4.12 | 2.38 | 2.96 | 5.53 |
| TOTAL | 1.58 | 2.65 | 2.77 | 2.62 | 3.28 |
Performance evaluation: In order to verify the performance of the segmented region of the proposed method and all other methods with respect to the ground-truth images, misclassification error is calculated. It is defined as [29]
where and denote the foreground and background area pixels of the ground truth image. and are the foreground and background area pixels of the segmented test image.
From Table 1, it is observed that in the proposed method using exponential distance function, the average misclassification error of 1.26%, i.e., percentage classification is 98.74%. Result of IFCM-1 shows an average misclassification error of 2.65%, i.e., percentage classification is 97.35%. FCM shows an average misclassification error of 2.77%, i.e., percentage classification is 97.33%. IFCM-2 shows an average misclassification error of 2.62%, i.e., percentage classification is 97.38%. KFCM shows an average misclassification error of 3.28%, i.e., percentage classification is 96.72%.
From Table 2, it is observed that the proposed method using divergence-based distance function also performs better but fails to perform better on one image, i.e., ‘mam-18’. It shows an average misclassification error of 1.58%, i.e., percentage classification is 98.42%. IFCM-1 and IFCM-2 show an average misclassification error of 2.65% and 2.62%, i.e., percentage classifications are 97.35% and 97.38%, respectively. So, the proposed method using divergence-based distance function also performs better than the 4 methods.
It is observed that on average, the proposed method using two types of distance function performs almost similar and better than the existing methods.
Conclusion
The paper suggests a modified intuitionistic fuzzy clustering approach for segmenting lesion/tumor in mammogram images. A novel intuitionistic fuzzy generator is used to compute the non-membership degree of the fuzzy image and an intuitionistic fuzzy image is created. From intuitionistic fuzzy membership function, two membership levels are computed using fuzzy hedge. These two membership levels are combined using Zadeh’s t norm and an interval type 2 fuzzy image is obtained. The image is then clustered in different regions where four fuzzy features are used. Two types of distance functions—fuzzy divergence and fuzzy exponential type distance functions—are used in the clustering algorithm. Further, in the membership matrix iteration, hesitation degree is taken into account that is computed from the novel intuitionistic fuzzy generator. The clustered image is then segmented to obtain lesion/tumor in the image. The proposed method is compared with the existing algorithms both quantitatively and qualitatively. It is observed that the proposed method can segment the tumor/lesions with better accuracy as compared with the existing methods.
Acknowledgements
The author would like to acknowledge the editor and anonymous reviewers for their valuable comments in improving the quality of the manuscript.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Bezdek JC, Hall LO, Clark LP. Review of MR segmentation technique in pattern recognition. Medical Physics. 1993;10(20):33–48. doi: 10.1118/1.597000. [DOI] [PubMed] [Google Scholar]
- 2.Kannan SR, et al. Effective fuzzy c-means based kernel function for efficient segmenting medical images. Computer in Biology and Medicine. 2010;40:572–579. doi: 10.1016/j.compbiomed.2010.04.001. [DOI] [PubMed] [Google Scholar]
- 3.Kannan SR et al.: Robust kernel FCM in segmentation of breast medical images. Expert Systems with Applications 38 : 4382–4389,2011.
- 4.Das A, Sabut SK. Kernelized fuzzy C-means clustering with adaptive thresholding for segmenting liver tumors. Procedia Computer Science. 2016;92:389–395. doi: 10.1016/j.procs.2016.07.395. [DOI] [Google Scholar]
- 5.Yang MS. Tsai, HS : A Gaussian kernel-based fuzzy c-means algorithm with a spatial bias correction. Pattern Recognition Letters. 2008;29:1713–1725. doi: 10.1016/j.patrec.2008.04.016. [DOI] [Google Scholar]
- 6.Chen S Zhang D: Robust image segmentation using FCM with spatial constraint based on new kernel induced distance measure. IEEE Transaction on Sytems, Man and Cybernetics B 34(4): 1906–1917, 2004. [DOI] [PubMed]
- 7.Atanassov KT: Atanassov's, Intuitionistic fuzzy sets, VII ITKR’s Session, Sofia, 983 (Deposed in Central Science - Technology Library of Bulgaria Academy of Science- 1697/84).
- 8.Chaira T. Intuitionistic fuzzy color clustering of human cell images on different color models. International Journal of intelligent and fuzzy systems Journal of Intelligent & Fuzzy Systems. 2012;23:43–51. doi: 10.3233/IFS-2012-0494. [DOI] [Google Scholar]
- 9.Chaira T. A novel intuitionistic fuzzy c means clustering algorithm and its application to medical images. Applied Soft Computing. 2011;11(2):1711–1717. doi: 10.1016/j.asoc.2010.05.005. [DOI] [Google Scholar]
- 10.Chaira T, Panwar A: An Atanassov's intuitionistic Fuzzy Kernel Clustering for Medical Image segmentation. International Journal of Computational Intelligence Systems : 1–11, 2013.
- 11.Verma H, et al. Modified intuitionistic fuzzy c means algorithm incorporating hesitation degree. Pattern Recognition Letters. 2019;122:45–52. doi: 10.1016/j.patrec.2019.02.017. [DOI] [Google Scholar]
- 12.Xu Z. Wu, J : Intuitionistic fuzzy C-means clustering algorithms. Journal of Systems Engineering and Electronics. 2010;42(4):580–590. doi: 10.3969/j.issn.1004-4132.2010.04.009. [DOI] [Google Scholar]
- 13.Kumar SA, Harish BS: A modified intuitionistic fuzzy clustering algorithm for medical image segmentation, Journal of Intelligent Systems 27(4), 2017.
- 14.Dubey YK, Mushriff MM. Mitra K : Segmentation of MR brain images using rough set based intuitionistic fuzzy clustering. Biocybernetics and Biomedical Engineering. 2016;36:413–426. doi: 10.1016/j.bbe.2016.01.001. [DOI] [Google Scholar]
- 15.Chaira, T: Intuitionistic fuzzy approach for enhancement of low contrast mammogram images. Internation Journal of Imaging Systems and Technology, 1–11, 2020.
- 16.Zadeh LA: Fuzzy sets, Information Control 8: 338–35, 1965.
- 17.M. Sugeno Fuzzy measures and fuzzy integrals: A survey, in:476 M. Gupta, G.N. Saridis, B.R. Gaines (eds) Fuzzy Automata and Decision Process; North Holland Amsterdam, New York, 47, 89–102,1997.
- 18.Klir GJ, Yuan B. Fuzzy sets and fuzzy logic. Upper Saddle River, NJ: Prentice Hall PTR; 1995. [Google Scholar]
- 19.Yager RR. On the measures of fuzziness and negation. Part II: lattices. Information and Control. 1980;44:236–260. [Google Scholar]
- 20.Zadeh LA: The Concept of a linguistic variable and its application to approximate reasoning-I. Information Sciences 8: 199–249, 1975.
- 21.De Luca A, Termini S. A definition of a non-probabilistic entropy in the setting of fuzzy sets theory. Inform. and Control. 1972;20:301–312. doi: 10.1016/S0019-9958(72)90199-4. [DOI] [Google Scholar]
- 22.Some properties of exponential entropy [Pal NR, Pal SK. Information Sciences. 1992;66:119–137. doi: 10.1016/0020-0255(92)90090-U. [DOI] [Google Scholar]
- 23.Entropy for intuitionistic fuzzy set Szmidt E, Kacpryzk. J Fuzzy sets and systems. 2001;118:467–477. doi: 10.1016/S0165-0114(98)00402-3. [DOI] [Google Scholar]
- 24.Mendel JM: General Type-2 Fuzzy Logic Systems Made Simple: A Tutorial. IEEE Transactions on Fuzzy Systems 22: 1162–1182, 2014.
- 25.Deng He, Duan C, Zhou X: A novel fuzzy enhancement of mammograms. Proc. of IET International Conference on Biomedical Image and Signal Processing, Beijing, China, 2015.
- 26.Gonzalez RC, Woods RE: Digital Image Processing, Pearson Education 2009; New Delhi, India,
- 27.Chaira T, Ray AK: Segmentation using fuzzy divergence, Pattern Recognition Letters 24(12): 1837–1844, 2003.
- 28.Fan J. Xie W : Distance measure and induced fuzzy entropy. Fuzzy Sets and Systems. 1999;104(2):305–314. doi: 10.1016/S0165-0114(99)80011-6. [DOI] [Google Scholar]
- 29.Yasnoff LA et al.: Error measures for scene segmentation, Pattern Recognition 9: 217–231, 1077.