Chemical Gradients in Human Enamel Crystallites.

Abstract

Dental enamel is a principal component of teeth.^[1] It has evolved to bear large masticatory forces, resist mechanical fatigue, and withstand wear over decades of use.^[2] Functional impairment or loss, as a consequence of developmental defects or tooth decay (caries), has a dramatic impact on health and quality of life, with significant costs to society.^[3] While the last decade has seen great progress in our understanding of enamel formation (amelogenesis) and the functional properties of mature enamel, attempts to repair enamel lesions or synthesize enamel in vitro have had limited success.^[4–6] This is partly due to the highly hierarchical structure of enamel and the additional complexities arising from chemical gradients that we are only beginning to understand.^[7–9] Herein, we show, using atomic-scale quantitative imaging and correlative spectroscopies, that the nanoscale crystallites of hydroxylapatite (OHAp; Ca₅(PO₄)₃(OH)) that are the fundamental building blocks of enamel are comprised of two nanometric layers enriched in magnesium flanking a core rich in sodium, fluoride, and carbonate ions; this sandwich core is surrounded by a shell with lower concentration of substitutional defects. A mechanical model based on DFT calculations and X-ray diffraction data predicts that significant residual stresses arise as a consequence of the chemical gradients, in agreement with preferential dissolution of the crystallite core. Further, stresses may impact the mechanical resilience of enamel. Finally, the two additional layers of hierarchy suggest a new model for biological control over crystal growth during amelogenesis and have implications for the preservation of biomarkers during tooth development.

Enamel covers the entire crown of human teeth (Fig. 1a), reaching thicknesses of several millimeters (Fig. 1b). A characteristic microstructural element, the enamel rod, (Fig. 1c) is comprised of thousands of lath-like crystallites aligned with their crystallographic c-direction approximately parallel to the long axes of the rods (Fig. 1d). Crystallites sectioned normal to their long axis appear as oblong polygons with an edge length of 20-50 nm in the short and 70-170 nm in the long direction (Fig. 1e,f). Characteristic length scales of the periodic hydroxylapatite lattice are in the sub-nanometer regime (Fig. 1g–i).

Figure 1: The hierarchical architecture of human enamel.

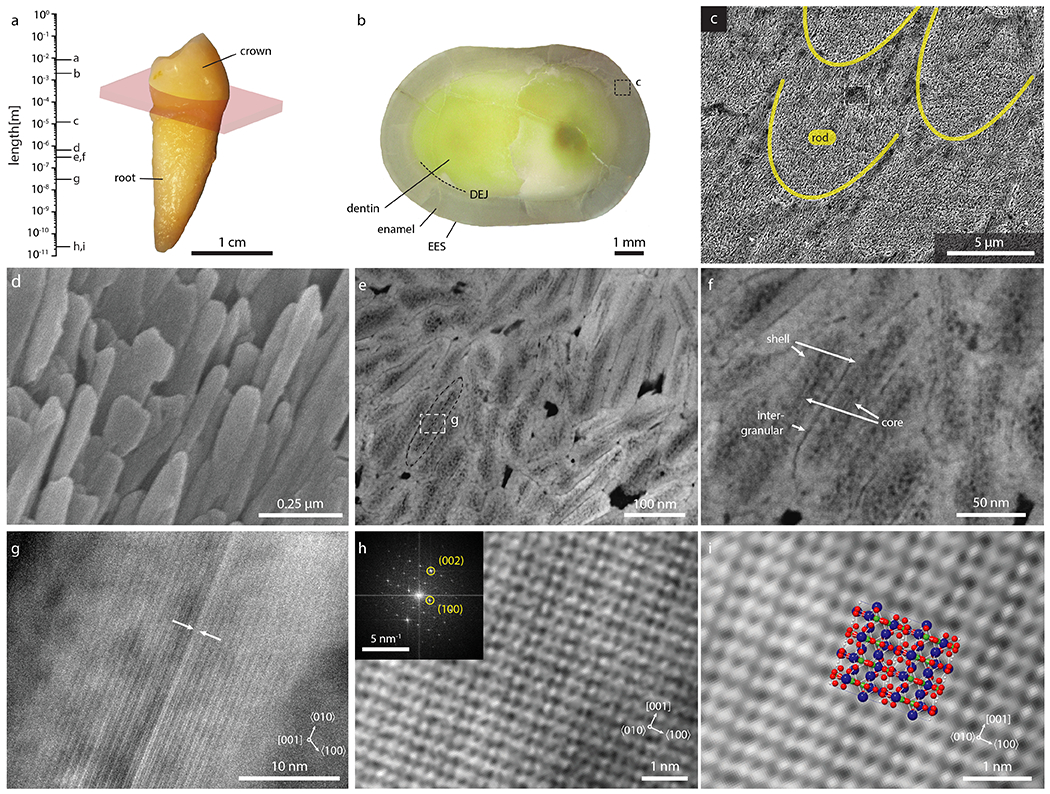
a. Length scales of enamel in a human premolar. b. Section parallel to the mid-coronal cervical plane (indicated in pink in a). c. SEM image of keyhole-shaped cross-sections of enamel rods in lactic acid-etched outer enamel. d. SEM image of OHAp crystallites. e-g. STEM-ADF images of enamel crystallites in cross section, oriented approximately parallel to the [001] zone axis. The CDL (arrows) appears bright in ADF. h. Cryo-STEM-ADF lattice image of a crystallite oriented parallel to the [010] zone axis (inset: FFT). i. Close up of (h) with rendering of 2×2×2 OHAp supercell (Ca, blue; O, red; P, green; H, white).

Enamel owes its hardness (~5 GPa) to its high mineral content (~96wt%).^[10] Nominally comprised of OHAp, magnesium (0.2–0.6wt%), sodium (0.2–0.9wt%), carbonate (2.7–5wt%), and fluoride (~0.01wt%) are also present.^[11] While the distribution of the minor constituents is known to vary over tens to hundreds of μm,^[11] gradients over much shorter distances have only recently been discovered. Specifically, in rodent incisor enamel, most Mg is confined between crystallites as Mg-substituted amorphous calcium phosphate (Mg-ACP), controlling enamel dissolution and mechanical properties.^[7] Segregation of Mg and Na ions to a 2-10 nm thick layer in between human enamel crystallites was confirmed.^[8] However, it has not yet been shown that this layer is identical to the Mg-substituted amorphous calcium phosphate found in rodent enamel.

Perhaps uniquely to human enamel, the center of the crystallite seems to be more soluble, is more prone to electron beam-induced damage, and displays a poorly understood contrast feature that is known as the central dark line (CDL).^[12–13] All three have generally been assumed to be related to the presence of defects in the crystallite lattice, but the exact nature of these defects is not known.^[13] We therefore set out to test whether there are compositional gradients of minor enamel constitutents across single crystallites.

In annular dark field scanning transmission electron microscopy (STEM-ADF) images of human outer enamel, crystallites are separated by narrow regions that appear darker than the crystallite (Fig. 1e,f), consistent with expectations for a Mg-rich amorphous intergranular phase. Additionally, they exhibit a shell that appears brighter than the core (Fig. 1e). The sensitivity of enamel to radiation limits the tolerable electron dose and hampers high-resolution analysis of enamel crystallites (SI section 1.3). Here, sample cooling and low-dose imaging conditions in cryogenic STEM (cryo-STEM) enable atomic-resolution imaging of ultrathin sections (20-30 nm, Fig. S1, Table S1), revealing a continuous atomic lattice across the entire crystallite (Figs. 1h,i; 2A; S2; S3). Unlike the shell, the core appears as a patchwork of lighter and darker areas on either side of the CDL, and seems more prone to beam damage.^[13]

Figure 2: Atomic scale structure and composition of human enamel crystallites.

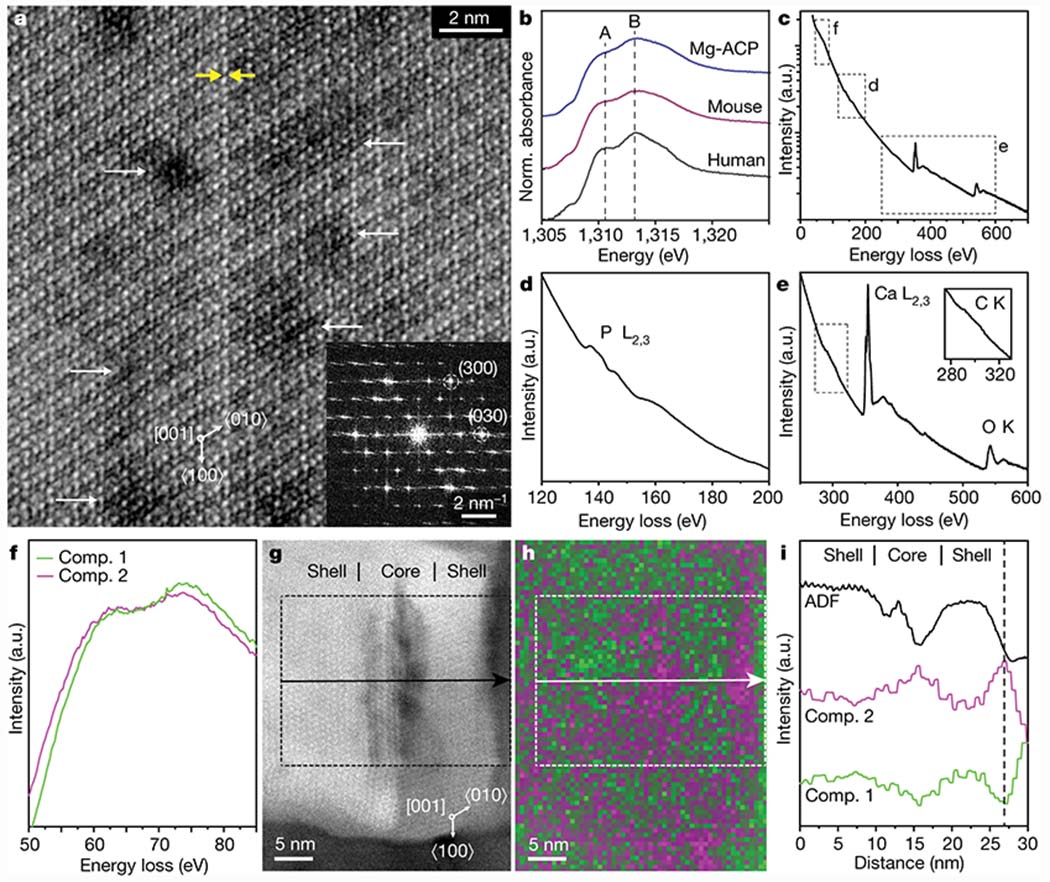
a. Cs-corrected cryo-STEM ADF lattice image of the core of a single enamel crystallite oriented to the [001] zone axis, close to the CDL (yellow arrows). Inset: FFT. b. Mg-K edge XANES of human enamel and reference materials. Fit parameters are reported in Table S3. c-e. Cryo-STEM EEL spectra obtained from a region containing several enamel crystallites, with closeups of the P-L_2,3 edge (d) and the Ca-L_2,3, O-K, and C-K edges (e). f. MCR components contributing to feature near the Mg-L_2,3 edge. g. Cryo-STEM ADF image of an enamel crystallite. h. Spatial intensity map of MCR components 1 (green) and 2 (magenta) in (g). i. Average intensity profile for the region of interest indicated in (g) and (h), in the direction of the arrow.

While STEM in conjunction with energy-dispersive X-ray spectroscopy (STEM-EDS) reported ~0.4at% Mg, 0.7at% Na, and 0.6at% F in crystallites (Fig. S4, Table S2), elemental maps were largely featureless (not shown). The presence of at least some Mg on apatite sites in addition to Mg-ACP was confirmed by bulk X-ray absorption spectroscopy (XAS) at the Mg-K edge (Figs. 2b, S7). Major components are well represented in cryo-STEM electron energy loss spectra (EELS) (Fig. 2c–e). Unfortunately, Na and F were not detected, the C-K edge is rather weak (Fig. 2e inset), and spectral component maps did not show gradients within crystallites (Fig. S5), despite the use of a sensitive direct electron detector for EELS.^[14]

However, a feature near the expected onset of the Mg-L_2,3 edge at 51 eV decomposes into two statistically significant components by multivariate curve resolution (MCR, Fig. 2f, Fig. S6).^[15] One of these is predominant in the shell, the other in the intergranular Mg-ACP and in the core (cf. Fig. 2g,h, Fig. S6). While other elements may also have minor edges in this spectral area, STEM-EDS and bulk XAS do support the presence of Mg. The two components suggest distinct local environments in the core and shell, and even gradients within the core (Fig. 2i). As susceptibility to beam damage limited our ability to further explore such gradients by cryo-STEM methods, we turned to atom probe tomography (APT, Fig. S8^[16–17]) to provide additional insights.

APT spectra of untreated human enamel resemble those of rodent enamel (Fig. S9, Table S4).^[7,16] In 3D reconstructions of APT data, it takes some practice to recognize the faceted cross sections of enamel crystallites (Figs. S10, S11). Treatment of samples with 250 mM NaF at pH 8.4 (37°C, 24h), however, resulted in a dramatic increase of CaF⁺ ions (Table S5). These ions clearly outline individual crystallites (cf. Fig. S10a–c and d–e) and thus greatly facilitate the analysis of reconstructions (Fig. 3). Fluoride treatment further results in an increase in sodium content (+0.39at%, +71% relative) with moderate statistical significance (p < 0.1) that also seems to be limited to the intergranular phase (see below), but has a negligible overall impact on composition of the samples otherwise (Tables S5, S6). These observations confirm that Na⁺ and F⁻ rapidly diffuse in between, but do not appreciably penetrate into crystallites under the treatment conditions. Similar to rodent enamel, Mg is enriched in this intergranular space (mean 0.35at%; range 0.15-0.51at%); in fluoridated samples levels of Na (1.27at%, 0.69-1.76at%) and F (1.36at%, 1.10-1.59at%) are also elevated there (Fig. 3e vs. f; Fig. S12, S13). In combination with the disordered local structure around Mg observed by Mg-K edge XAS, this is robust evidence for the presence of Mg-ACP in the intergranular phase; the thickness of this region is consistent with previous observations in human enamel.^[8]

Figure 3: Chemical gradients in human enamel crystallites and the amorphous intergranular phase.

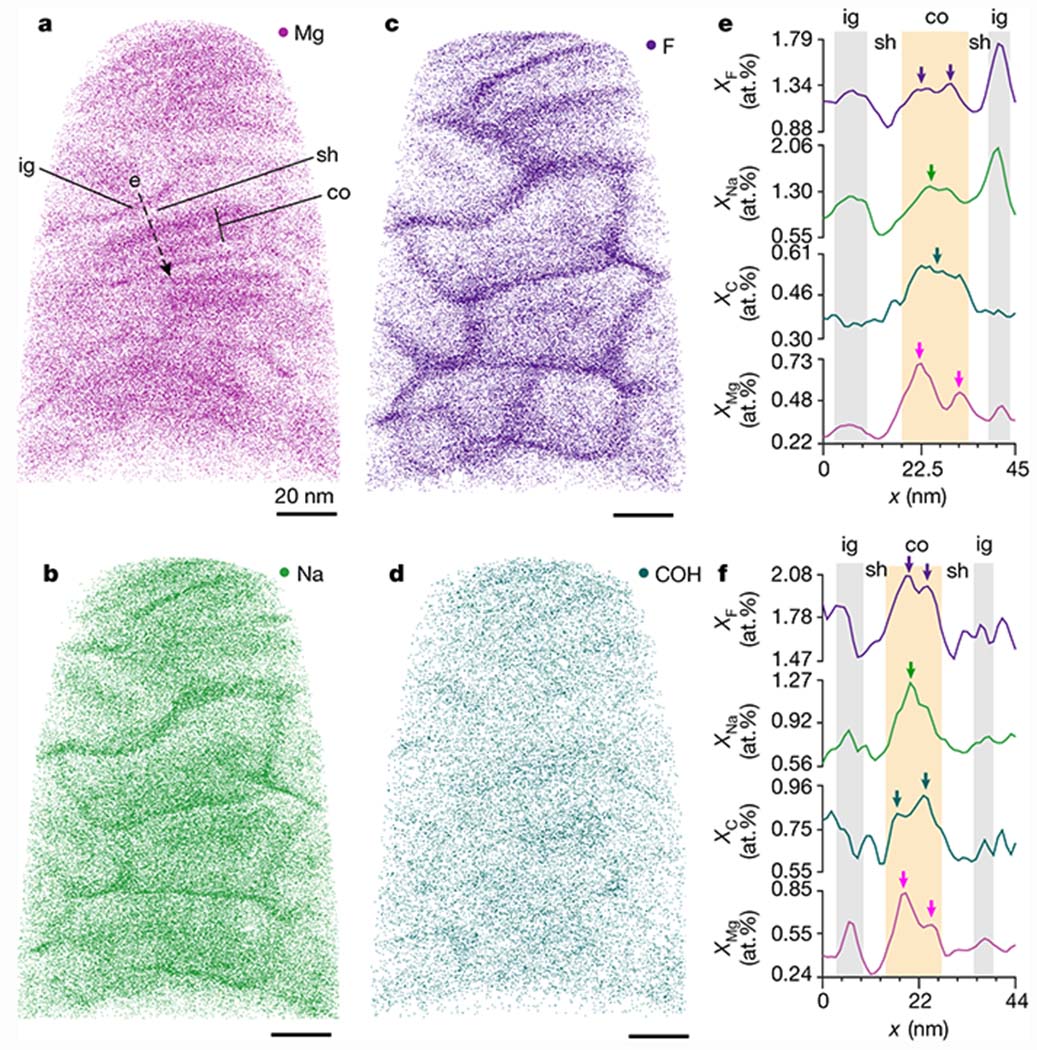
Rendering of Mg (a), Na (b), F (c), and COH (d) positions in a 3D reconstruction of fluoridated human enamel, viewed along the long axis of crystallites. Scale bars represent 20 nm. e. Concentration profiles of F (purple), Na (green), C (teal), and Mg (magenta) along the dashed line in (a). Profiles for n = 15 crystallites across 3 technical replicates are shown in Fig. S13a–o. f. Concentration profiles in a crystallite from a sample that had not been fluoridated. Profiles for n = 5 crystallites across 2 biological replicates are shown in Fig. S13p–t. Note that fluoridation increases the concentration of Na and F in the intergranular phase (ig, gray highlights) vs. the core (co, orange highlight), due to short circuit diffusion, whereas the concentration in the shell (sh) is not affected.^[7]

In striking difference to rodent enamel, however, Mg levels are elevated not only in the intergranular Mg-ACP, but also in two distinct layers in the core (Figs. 3a, S10, S11, Videos S1, S2). The core is further enriched in sodium, likely as Na⁺, and fluorine, likely as F⁻ (Fig. 3b,c). In addition, the carbon concentration is elevated (Fig. 3d), most likely due to the presence of carbonate (CO₃²⁻). APT data thus proves true the hypothesis that there exist a Mg- and CO₃²⁻-rich core in human enamel crystallites.^[18–19]

Line profiles taken approximately normal to the midplane in 20 crystallites identified in 5 reconstructions (3 NaF-treated, 2 untreated, Figs. 3e,f, S12, S13) reveal that, on average, the two Mg-rich layers (mean 0.5at%; range 0.33-0.72at%) are also enriched in Na. However, Na levels usually peak closer to the midplane (1.2at%; 0.87-1.55at%), where F (1.4at%; 1.13-2.44at%) and C (~0.6at%; 0.45-1.01at%) are also elevated, and Mg goes through a minimum (0.4at%). We note that the distributions of Na, F and C are more variable than that of Mg and can be asymmetric or show additional local maxima. While a form of shot noise may responsible for the latter effect, we note that contrast in STEM-ADF shows similar variation. It is therefore possible that there is some clustering of substituents. Regardless, mole fractions are always significantly lower in the shell (on average, 0.22at% Mg, 0.81at% F, 0.52at% Na, and 0.32at% C). APT therefore not only confirms the core-shell structure observed in many crystallites and over large areas by STEM, but clearly indicates that the core itself has a sandwich structure.

Driven by the significant size mismatch between Ca²⁺ and Mg²⁺, we expect a substantial contraction of the apatite lattice in the Mg-rich layers.^[20–23] Lattice parameters determined by DFT calculations and X-ray diffraction experiments, after correction for thermal expansion, agree within 1%, and indicate a contraction in both the a- and c-directions with increasing level of Mg substitution (Tables S7, S8, Figs. S14–16).^[24] Carbonate substitution also results in a contraction of the lattice in the a-directions.^[25] However, there is a mild expansion of the lattice in the c-direction that partially offsets the effect of Mg (Fig. S17).

Because enamel crystallites are coherent, lattice parameter changes that result from Mg²⁺- and CO₃^2—gradients are in effect residual (eigen) strains and may therefore cause a net residual stress. Residual stresses in turn can affect the overall mechanical performance of a material, but also impact the local chemical potential and therefore the solubility. To explore these possibilities, we predicted residual stresses in an idealized crystallite (Fig. S18) using finite element (FE) modeling. In mechanical equilibrium, the core experiences a net tensile stress, with distinct maxima in the Mg-rich layers (Fig. 4a–c). The highest compressive stress (−46.4 MPa) is found on the free surface parallel to the (001) plane (Fig. 4b), again in the Mg-rich layers. The shell of the crystallite experiences compressive residual stresses (Fig. 4c). On the majority of the surface, these stresses are near −39 MPa. While absolute values of the stresses reported here will vary as real crystallites differ in shape and composition from the highly idealized model we employ here, there is every reason to believe that the model captures trends quite well and provides insights on how we can expect crystallites to behave on average.

Figure 4. Impact of substitution on mechanical and chemical properties of human enamel crystallites.

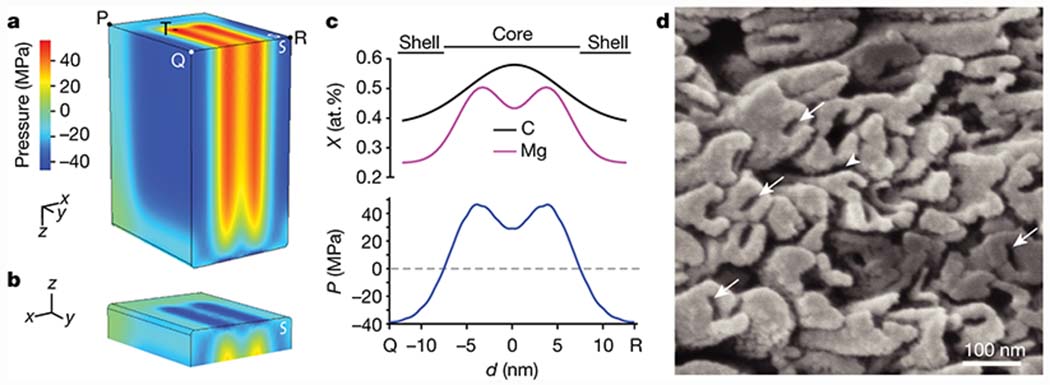
a. Rendering of the scalar pressure, calculated as one third of the trace of the stress tensor, as a measure of residual stress in an FE model of an enamel crystallite. Note that symmetric boundary conditions were applied to two faces (white “S”); values on these represent internal rather than surface stresses. b. View of (a) showing the free surface parallel to the (001) plane. c. Plot of the mole fractions of C (black) and Mg (magenta), and of the residual pressure (blue), against the distance from Q to R. d. SEM image of an acid-etched enamel section in which crystallites emerge end-on, displaying intergranular corrosion (arrowhead) and preferential dissolution of the core (white arrows).

For instance, at the water-accessible endcap (Fig. 4b), stresses in the core are between 4 and 40 times higher in the core than in the shell. This is expected to increase the solubility of the core compared to the shell. Indeed, the core of outer enamel crystallites is preferentially etched, similar to the intergranular Mg-ACP (Fig. 4d, Fig. S19), and consistent with reports for crystallites extracted from in human caries lesions.^[26–27] The core shell-architecture and associated residual stresses are thus an important aspect of disease progression and may be used for the modeling of dissolution and re-precipitation during the progression of caries lesions. Compressive stresses in the shell may further impede crack initiation, extend the size range at which crystallites perform at their theoretical strength,^[28] and deflect cracks, thereby increasing the tolerance of enamel.^[29–30] On a different note, the strong modulation of stresses and the resulting strain just beneath the surface of the endcaps may be responsible for the CDL feature observed in electron microscopy. We note that while the Mg-rich layers do appear to be parallel to the CDL, proof that the CDL runs in in between the layers would require correlative imaging of the same crystallite by STEM and APT. While correlative imaging of this kind is not unprecedented, it is a very significant challenge, especially for beam sensitive materials such as enamel.^[31–32] It would, however, be particularly rewarding, as one could also address the spatial correlation between contrast in STEM-ADF and local concentration maxima reported by APT.

Taken together, we find strong evidence that the core-shell architecture and resulting residual stresses impact the dissolution behavior of human enamel crystallites and provide a plausible avenue for extrinsic toughening of enamel. This leads us to the question of how the gradients are created in the first place. During amelogenesis, mineral first precipitates in the organic enamel matrix as ribbons of amorphous calcium phosphate (ACP).^[33–35] ACP is tolerant of impurities, and it is conceivable that the ribbons retain Na⁺ and CO₃²⁻ as they crystallize by an unknown mechanism. Crystallites initially grow much slower in thickness than in width. In human primary teeth for instance, ribbons are 3 nm thick and 29 nm wide at a distance of 25 μm from the ameloblasts, and grow to 10-by-58 nm by the time the ameloblasts have moved to 200 μm (Fig. S20).^[33] In this first phase, the fast growth direction is thus parallel to the Mg rich layers (Fig. 5, for relative growth velocities, see Table S9), suggesting that Mg substitution breaks the crystal symmetry. Presumably, Mg acts on its own, or in concert with organic matrix molecules, by blocking active sites for growth in the direction normal to the layer direction, through anisotropic stresses generated as it incorporates into the crystal, or a combination of these effects. This would require that Mg is deliberately introduced into the system after the ribbon has formed, and indeed the Mg concentration in porcine enamel is known to reach a maximum in the late secretory stage.^[36] Consistent with a regulatory role, perturbation of putative Mg transporters is known to impact amelogenesis, even though the impact on crystallite shape is not known.^[37–39]

Figure 5. A model for human enamel crystallite growth during amelogenesis.

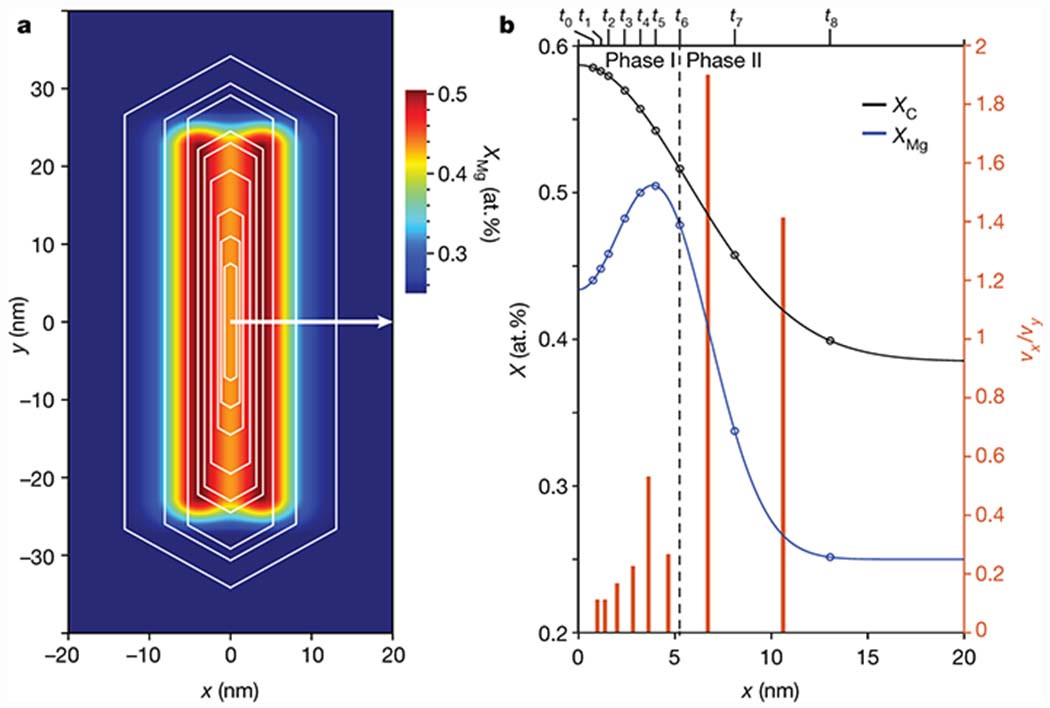
a. Schematic drawing of growth stages (timepoints t₀-t₈) of human primary enamel crystallites (white hexagons, after Daculsi and Kerebel, Ref. ^[33]) superimposed on an idealized map of the Mg concentration based on observation of human permanent enamel crystallites reported herein. b. On the left y-axis, plot of the mole fraction of Mg (blue) and carbon(ate) (black, see Fig. S21 for map) against distance along the white arrow in (a). The open circles indicate the mole fractions at the interface of the growing crystallite at t₀-t₈. On the right y-axis, plot of the ratio of the average growth velocities in the x- and y-directions in successive time intervals (Table S9). Note that scaling of the time axis is unknown, and likely non-linear. As a consequence, absolute speeds cannot be determined and may vary.

In the second phase that is likely identical to the maturation stage of amelogenesis, growth slows down significantly. At the same time, the ratio of the growth velocities changes, with crystals growing thicker rather than wider. In human primary enamel, this results in mature crystallites with a thickness of 26 nm and a width of 80 nm.^[33] The Mg-poor shell is likely formed during this period. Slow growth at low supersaturation, which may be combined with a significant drop in Mg and Na concentration in the enamel matrix,^[36,40] is indeed expected to result in low rates of incorporation of impurities on the apatite lattice. Any Mg still present would accumulate ahead of the interface of the growing crystallite. In the final stage of maturation, as crystals start to impinge on each other, the Mg/Ca ratio in the matrix would rise rapidly, and exceeding the threshold for Mg-ACP,^[23] trigger precipitation of the amorphous intergranular phase. While this mechanism is consistent with and provides an explanation for a number of independent observations, we note that the data we draw on comes from both primary and permanent human enamel and includes observation in other species. Clearly, a thorough compositional analysis of immature enamel ribbons and crystallites in one species would greatly aid in confirming the proposed sequence of events.

Independent of whether this mechanistic proposal is accurate, what emerges is that the concentration of Mg and other minor ions at the surface of the crystallite, and therefore also the medium in its immediate proximity, varies systematically during amelogenesis of human permanent teeth. This may impact how enamel matrix proteins and their degradation products, thought to be involved in controlling enamel crystallite formation, interact with the mineral phase and each other.

That ions that are not essential for amelogenesis, such as fluoride, are incorporated into the crystallite core has an important corollary. Enamel forms over very specific times during the development of different teeth (in humans starting as early as second trimester in utero until the late teens), is not significantly remodeled, and is very well preserved in remains and fossils. Crystallite cores might thus encapsulate spatially resolved biomarkers for environmental exposure, disease, or medical intervention, over an extended period of time. With APT and correlative imaging and spectroscopy, this record is now accessible and might help decipher for instance genetic pre-disposition to caries or the mechanism behind molar-incisor hypomineralization (MIH), a dental developmental defect of unclear etiology that affects as many as 20% of all school children.^[2,41]

Methods:

Consumables

Unless otherwise specified, all solutions were prepared using ultra-pure water (18.2 MΩ∙cm) dispensed from a Barnstead Nanopure UF+UV unit (Thermo-Fisher Scientific, Waltham, MA). Lactic acid (C₃H₆O₃) (Mallinckrodt Chemicals, Center Valley, PA); propionamide (98%), NaF (Sigma-Aldrich, St. Louis, MO); NaH₂PO₄, Na₂HPO₄, HNO₃ (65wt%), Mg(NO₃)₂×6 H₂O (99%), Ca(NO₃)₂×4 H₂O (99%, Lot No. 86432), ethanol (VWR, Radnor, PA); Ca(NO₃)₂×4 H₂O (99.98%, Lot No. 61600281), formaldehyde (CH₂O) (Alfa Aesar, Tewksbury, MA); (NH₄)₂HPO₄ (99%, Lot A0059707, Merck KGaA, Darmstadt, Germany); PELCO® liquid silver paint, graphite tape (Ted Pella, Redding, CA); EPO-TEK 301 (Epoxy Technology, Billerica, MA); CarbiMet SiC grinding paper, Metadi supreme polycrystalline aqueous diamond polishing suspension, Microcloth polishing cloth (Buehler, Lake Bluff, IL). MM22 microtip coupons for FIB liftout (CAMECA Instruments, Madison, WI).

Preparation of enamel sections

Deidentified human premolars extracted for orthodontic reasons were kept in 10% buffered formalin at room temperature for 10 days, and at 4°C thereafter. Before use, samples were rinsed with water and dried under a gentle stream of nitrogen gas (“rinsed and dried”). Samples were embedded in Epo-Tek 301 epoxy, sectioned along the buccal-lingual line, ground with SiC paper (600, 800, 1200 grit), and polished on a Buehler Trident polishing cloth with polycrystalline diamond suspensions (3 μm, 1 μm), rinsed and dried. Some sections were treated with fluoride by immersion in 50 mL of aqueous NaF (250 mM, pH 8.4) under gentle agitation using an orbital shaker, at 37°C for 24 hours, then rinsed and dried. Some sections were exposed to lactic acid (250 mM, pH 4, for ~20 seconds), and subsequently rinsed and dried. Some sections, oriented such that rods (and crystallites) emerge approximately perpendicular to the surface, were positioned under an angle of roughly 45 degrees with respect to the underlying lab bench surface. The sample was etched using a steady stream of droplets of lactic acid (250 mM, pH 4) flown across the surface for a total of 30 seconds. Thereafter, the tooth sections were quenched immediately in ethanol, rinsed and dried.

Unless otherwise noted, samples were affixed to an aluminum stub using carbon tape, coated with AuPd (~25 nm) using a Denton Desk IV sputter coating system (Denton Vacuum, Moorestown, NJ). The surface of the sample was then grounded to the stub using colloidal silver paint.

Scanning Electron Microscopy (SEM)

SEM was performed using a Hitachi S4800-II or a Hitachi SU8030 (Hitachi High-Tech, Schaumburg, IL), both equipped with a cold cathode field emission electron gun, operated at an accelerating voltage of 5kV and an emission current of 8600 nA. Images were acquired using secondary electron contrast.

(Scanning) Transmission Electron Microscopy (TEM, STEM)

Lamellae were prepared from ground and polished, transverse sections of outer, buccal human enamel. A dual-beam FIB/SEM (FEI Helios NanoLab or FEI Strata 400) with a gallium liquid metal ion source (LMIS) operating at an accelerating voltage of 2–30 kV was used to prepare FIB samples for TEM. A ~200 nm thick layer of protective carbon was deposited on a 2 μm x 15 μm area of interest, either by using the electron beam (5 kV, 1.4 nA) through decomposition of a phenanthrene precursor gas (FEI Helios Nanolab), or by selecting a similar area of interest using a permanent marker deposition method ^[42] (FEI Strata 400). On top of the carbon, a ~1 μm thick protective platinum layer was deposited using the ion beam (30 kV, 93 pA) through decomposition of a (methylcyclopentadienyl)-trimethyl platinum precursor gas. Subsequently, two trenches were cut to allow for a roughly 2 μm thick lamella of enamel. Next, the micromanipulator was welded onto the lamellae, and the sample was cut loose from the bulk material. An in situ liftout of the sample was performed, and the lamellae was welded onto a TEM half-grid. After thinning to about 80 nm in a sub-region of the lamellae (5 kV, 81 pA), the thin section was cleaned at low voltage and current (2 kV, 28 pA).

STEM images were acquired on a JEOL JEM-2100F (JEOL USA, Peabody, MA), a JEOL GrandARM 300F, or an aberration-corrected FEI Titan Themis (FEI Company) equipped with a monochromator, a side-entry double tilt liquid nitrogen-cooled sample holder (Gatan 636; Gatan, Pleasanton, CA), and a cryogenically cooled anti-contamination device (for typical conditions please see Table S1). Image post-processing was performed as described in the Supplemental Information.

STEM-EDS

EDS spectrum images of regions of interest chosen in STEM HAADF images were acquired on a windowless 100 mm² XMax^N 100TLE Silicon Drift Detector (SDD) with a solid angle of ~0.98 sr (Oxford Instruments NanoAnalysis, Concord, MA) with a dwell time of 5 μs/pixel.

Cryo-STEM-EELS

EELS 2D spectrum images were acquired on a Titan Themis (FEI Company) using a K2 Summit direct electron detector in counting mode (Gatan Inc, Pleasanton, CA). This direct electron detector with high quantum efficiency (DQE up to 80%) allowed simultaneous acquisition of all relevant inner shell ionization (core loss) edges at high energy resolution and low background levels despite the low dose required to minimize beam damage.^[43] The entrance aperture was 5 mm, the energy dispersion 0.5 eV/channel. The beam current was 4.0-8.5 pA, the dwell time 2.5 μs/pixel. STEM-ADF images were recorded in parallel. Concentration maps were extracted by fitting and subtracting the pre-edge background with a linear combination of power laws and integrating the intensity under the EELS edge of interest. MCR analysis of the Mg-L₂,₃ edge region (Fig. S6) was performed as described previously.^[44]

X-ray Absorption Spectroscopy (XAS)

XAS measurements were performed at the Spherical Grating Monochromator (SGM, 11ID-1) at the Canadian Light Source (Saskatoon, SK), following a literature protocol.^[45] Briefly, enamel from de-identified human third molars was ground into a powder using an agate mortar pestle and spread on graphite tape. Samples were scanned relative to the edge Mg K-edge (1303 eV) from −60 to −12 eV in steps of 2 eV, −12 to −8 eV in steps of 0.5 eV, −8 to 30 eV in steps of 0.1 eV, 30 to 190 eV in steps of 0.2 eV, 190 to 300 eV in steps of 0.3 eV and 300 to 400 eV in steps of 0.5 eV, with a constant dwell time of 2 seconds/step. Monochromator energy calibration was performed by setting the first absorbance maxima of the MgO reference sample spectra to 1309.5 eV. X-ray fluorescence intensity was measured simultaneously with four solid state silicon drift energy dispersive X-ray detectors (Amptek, Bedford, MA). Incident flux was measured by recording the current from a gold mesh upstream. The exit slit was adjusted and the undulator detuned to reduce flux to prevent saturation of X-ray fluorescence detectors when measuring concentrated reference samples. Between 1 and 7 scans were collected for each sample and averaged. No beam-induced changes were observed when comparing sequential spectra. The Mg X-ray fluorescence intensity was isolated from the total fluorescence intensity containing contributions from X-ray fluorescence from other elements and the scattered incident beam using custom written code in Mathematica (Wolfram Research, Champaign, IL). For XANES spectra, please see Fig. S7.

Absorption data were normalized, background subtracted using AUTOBK, and converted to k-space using Athena.^[46] Edge energy (E₀) was set to the maximum of the first derivative of the absorption spectra. χ(k) data were weighted by k² and Fourier transformed over a k-range of 2-9.5 Å⁻¹, applying a Hanning window with a sill width of 1 Å⁻¹. Theoretical photoelectron scattering amplitudes and phase shifts based on the crystal structures of dolomite^[47], huntite^[48], whitlockite^[49], and hydroxyapatite^[22] were calculated using FEFF6^[50]. Shell-by-shell fitting of the EXAFS data was performed in R-space using Artemis^[46]. An energy shift parameter (E₀) was maintained constant for the scattering paths but allowed to vary between samples. The amplitude reduction factor (S₀² = 0.8) was determined based on a fit to the dolomite, huntite and whitlockite spectra with coordination numbers constrained based on their respective crystal structures. Multiple scattering in the carbonate reference samples was accounted for following Reeder and coworkers.^[51] Enamel and ACP EXAFS spectra were fit using a model based on the Ca[II] site of OHAp, consisting of a single Mg-O and two Mg-P scattering paths.^[52–53] To minimize the number of fitting parameters, the coordination number and σ² for the two Mg-P paths were constrained for each sample but allowed to vary between samples. For EXAFS spectra, please see Fig. S7. For fitted parameters, see Table S3.

Atom Probe Tomography (APT)

Samples for APT were extracted ca. 10 μm below the external enamel surface on mid-coronal cervical sections of human premolars, using a Dual Beam SEM/FIB (Helios NanoLab; FEI Company), and following standard protocols ^[54–55]. Briefly, a 200 nm thick layer of protective platinum was deposited using the electron beam (5 kV, 1.4 nA) on a 2 μm x 25 μm area of interest through decomposition of a (methylcyclopentadienyl) trimethyl platinum precursor gas. A thicker coating of FIB platinum (~400 nm) was then deposited using the ion beam (30 kV, 93 pA). An angled cut was then made on either side of the Pt strap, and one end was cut free and attached to an in-situ manipulator (Omniprobe, Dallas, TX) using FIB-Pt. After cutting the final side free, 1-2 μm segments were attached to the top of silicon posts on the APT array with FIB-Pt. Tips were sharpened in the ion beam using annular mill patters with progressively smaller inner and outer diameters (16-30kV, 0.28–0.47 nA). The majority of contamination/gallium implantation was removed by a final cleaning step (2 kV, 0.25 nA).

APT analysis was performed using a LEAP 5000 XS (CAMECA Instruments) with a laser operating at a wavelength of 355 nm and a pulse frequency of 250 kHz, at a power of 40 pJ. The temperature in the analysis chamber was kept 25 K, the pressure <10⁻⁸ Pa. The DC potential on the microtip was adjusted to maintain an evaporation rate of 0.005 ions per laser pulse. 3D reconstructions of the sample tips were made using the IVAS software package (CAMECA Instruments). Standard parameters were used for all reconstructions.

For representative APT spectra, please see Fig. S9. For peak identities and integration limits, see Table S4, and for a comparison of the composition of human and rodent samples see Table S6. In this manuscript, we analyze data from three reconstructions of fluoridated enamel, and two reconstructions of enamel that were not fluoridated by us. Inspection revealed that the cross sections of 8 crystallites (8 fluoridated, 0 non-fluoridated) were fully contained in the reconstructions, and that of 14 crystallites (7/5) were partially contained. For 20 crystallites (15/5) we were able to extract 1D concentration profiles approximately normal to the midplane of the crystallite, using ROIs that were defined manually in IVAS (CAMECA Instruments; Figure S12). For the remaining, too little of the crystallite was contained in the reconstruction, or it was not possible to deduce the orientation. As a consequence, 1D profiles could not be extracted. 1D profiles were corrected for homogeneous background. Please find additional reconstructions in Fig. S10 and S11. As a visual aide, the reconstruction of a 30 nm thick slice through one enamel crystallite showing individual ion positions in 3D space (Video S1) and iso-concentration surfaces (Video S2) was animated using the Matlab platform (The Mathworks, Natick, MA).

Hydrothermal synthesis of OHAp and Mg-substituted OHAp samples

Hydroxylapatite (OHAp, 0 at% Mg) was synthesized following a literature protocol.^[16] Briefly, 5 mL of an aq. solution of 99.98% Ca(NO₃)₂ × 4 H₂O (0.1M, 0.5 mmol) was mixed with 5 mL aq. solution of (NH₄)₂HPO₄ (0.06M, 0.3 mmol). To the resulting suspension, 5 mL of an aqueous solution of propionamide (1M, 5 mmol) was added. The pH was adjusted to 3 by addition of approx. 45 μL aq. HNO₃ (5 M), to give a clear, transparent solution. The solution was transferred to a PTFE-lined microwave digestion vessel and treated hydrothermally (heating ramp: 30°C/min, final temperature 180°C for 30 min), using a Milestone EthosEZ Microwave Digestion System (Milestone, Shelton, CT). The resulting precipitate was centrifuged and washed with deionized water (3 × 15mL) and ethanol (3 × 15mL), and dried in vacuo.

OHAp (0.22 at% Mg) was synthesized as described above, but using 99% Ca(NO₃)₂ × 4 H₂O instead of 99.98% Ca(NO₃)₂ × 4 H₂O.

OHAp (1.15 at% Mg): To 475 μL of an aq. solution of 99.98% Ca(NO₃)₂ × 4 H₂O (1M, 0.475 mmol, was added 25 μL of an aq. solution of Mg(NO₃)₂ × 6 H₂O (1M, 0.025mmol). The solution was diluted to 5 mL overall volume with DI water. A 5 mL aq. solution of (NH₄)₂HPO₄ (0.06M, 0.3 mmol) solution and 5 mL of an aqueous solution of propionamide (1M, 5 mmol) were added to give a suspension. The pH was adjusted to 3 by addition of approx. 45 μL aq. HNO₃ (5 M) to give a clear, transparent solution. The solution was transferred to a PTFE-lined microwave digestion vessel and treated hydrothermally as described above. The resulting precipitate was centrifuged and washed with deionized water (3 × 15mL) and ethanol (3 × 15mL), and dried in vacuo to give OHAp (approx. 20 wt% by PXRD) and whitlockite (approx. 80 wt% by PXRD). Needle-shaped OHAp crystals could easily be differentiated from whitlockite platelets.

Phase identify and purity for all samples was confirmed by PXRD. The magnesium mole fraction was determined using ICP-MS.

Powder X-ray diffraction (PXRD)

PXRD patterns of OHAp were collected at 100 K on a STOE-STADI-P powder diffractometer (STOE Corporation, Chicago, IL) equipped with an asymmetric curved Germanium monochromator (CuKα1 radiation, λ = 1.54056 Å) and one-dimensional silicon strip detector (MYTHEN2 1K, DECTRIS Ltd., Philadelphia, PA). The line-focused Cu X-ray tube was operated at 40 kV and 40 mA. Powder was packed in a polyimide capillary (0.5 mm inner diameter) and intensity data were collected over an angular range of 2θ = 10 – 70°, over a period of 10 mins. Instrument was calibrated against a NIST Silicon standard (640d). Data was processed and Rietveld refinement was performed using MDI Jade 2010 (Materials Data, Inc., Livermore, CA). Lattice parameters are reported in Table S7.

Single Crystal X-ray diffraction

Diffraction data for OHAp (0.22 at% Mg) and OHAp (1.15 at% Mg) were collected at a set temperature of 100 K using a Bruker Kappa APEX2 diffractometer (Bruker AXS, Madison, WI) equipped with a Mo Kα (λ = 0.71073 Å) source. Single crystals (50 μm×5 μm×5 μm) were picked from powders and mounted with Paratone N on a cryo-loop. Diffraction patterns were indexed, refined, and integrated using SAINT of the APEX2 package (Bruker AXS). Using Olex2,^[17] the structure was solved with XT and refined with the ShelXL package using least squares minimization (Fig. S14).^[18] Lattice parameters are reported in Table S7 and Fig. S15.

Inductively coupled plasma mass spectrometry (ICP-MS)

ICP-MS was carried out on a Thermo iCAP Q ICP-MS (Thermo Fisher Scientific, Inc.; Waltham, MA). For phase-pure samples, powders were used as is. For the sample containing whitlockite, the single crystal that was analyzed by X-ray diffraction was used. Samples were dissolved in trace metal-grade HNO₃ solution (0.1 M) in a metal-free tube. Trace metal-grade HCl solution was used as a blank.

Density Functional Theory (DFT) Calculations

DFT calculations were performed within the generalized gradient approximation using the Perdew-Burke-Ernzerhof revised for solids (GGA-PBEsol) exchange-correlation functional^[59] with the planewave pseudopotential code, Quantum ESPRESSO^[60]. We used the ultrasoft pseudopotentials^[61] taken from the PSLibrary^[62]. A plane-wave cutoff of 60 Rydberg was used during the ionic and electronic relaxation steps. For the simulation of Mg-doped OHAp solid solutions, we employed a 2×2×1 supercell (with 352 atoms) in the monoclinic crystal structure (P2₁/c symmetry). Our initial simulation performed on a pristine Ca₁₀(PO₄)₆(OH)₂ supercell serves as the reference. Additional simulations were performed, whereby 1, 2, 3, and 4 Ca atoms were substituted with Mg atoms. The atomic positions and the cell volume were relaxed until the Hellmann-Feynman forces were less than 2 meV Å⁻¹ and components of the stress tensor were less than 0.1 kbar. The Brillouin zone integration was performed using a 1×1×1 Monkhorst-Pack k-point mesh (Γ-point calculation). Lattice parameters as calculated (at 0 K) and corrected to 298 K using the coefficient of thermal expansion reported by Babushkin and coworkers^[63] are reported in Fig. S15.

Lattice Strain as a Function of Composition

Lattice parameters as a function of magnesium mole fraction were determined by XRD and DFT as outlined above (Fig. S15). Lattice parameters as a function of carbonate weight fraction were obtained from Demier and coworkers.^[25] using WebPlotDigitizer.^[64] Carbonate weight fractions were converted to mole fractions (X_C) using the stoichiometric models postulated by Deymier and coworkers.^[25] The concentration dependent lattice strain in the a- and c-direction was calculated from the lattice parameters and fitted with a linear model,

$${\epsilon }_i{}^j=n_i{}^j{X}_j+b_i{}^j$$

, where ε_i^j denotes the strain in the i-direction due to substitution with species j, X_j is the mole fraction of species j, n_i^j is the slope, and b_i^j is the intercept (Figs. S16 and S17). Fit parameters are reported in Table S8.

Finite Element Modelling

Enamel crystallites were idealized as slabs with rectangular cross section, oriented with the [001] direction parallel to the z-axis and the [100] parallel to the x-axis. Mg and carbonate concentrations were modeled as continuous, 2-dimensional distributions (Fig. S18), chosen to represent experimental 1D concentrations profiles in the x-direction (Fig. S13). For simplicity, the contributions of fluoride and of sodium ions in excess of those needed to charge balance carbonate ions were ignored, as were contributions from surface free energies. All modelling was performed using COMSOL Multiphysics® (COMSOL, Burlington, MA).

Data availability:

The data that support the findings of this study are available from the corresponding author upon reasonable request. Source data for Figures 2 [b,c,d,e,f,i], 3 [e,f], 4c, S4 [b,c], S5f, S6a, S7 [a,b,c], S13, S14, S15, S16, and S17 are provided with the paper.