Mechanical Forces Have a Range of Effects on the Rate of Ribosome Catalyzed Peptidyl Transfer Depending on Direction

Abstract

Mechanical forces acting on the nascent chain residue located at the P-site of the ribosome can influence codon translation rates. Most observations to date involve force vectors aligned collinear with the long axis of the ribosome exit tunnel. What is poorly understood is how force applied in other directions will impact the rate of peptide bond formation catalyzed by the ribosome. Here, we utilize quantum mechanical/molecular mechanics simulations to estimate the changes in the activation free energy as a consequence of applying a constant force in various directions on the C-terminal residue at the P-site. Qualitatively consistent with the Bell model, we find this force can either accelerate, decelerate, or not alter the reaction rate depending on the force direction. A force in the average direction between the P-site 3′ O–C ester bond that breaks and the peptide bond that forms accelerates the reaction. A force in the opposite direction slows down the reaction as it opposes these bonds breaking and forming, but surprisingly it does not do so to the maximum extent possible. In this case, there is a counterbalancing trend; the force in this direction brings the A-site amino nitrogen and the P-site tRNA A76 3′ oxygen groups closer together, which promotes one of the proton shuttling steps of the reaction. We find the maximum force-induced slowdown occurs 37° off this axis. If force is applied in orthogonal directions to the reaction coordinates, there is no significant change in the reaction speed. These results indicate that there is a richer set of scenarios of force effects on translation speed that have yet to be experimentally explored and raise the possibility that cells could use these mechanochemical effects to modulate and regulate protein synthesis.

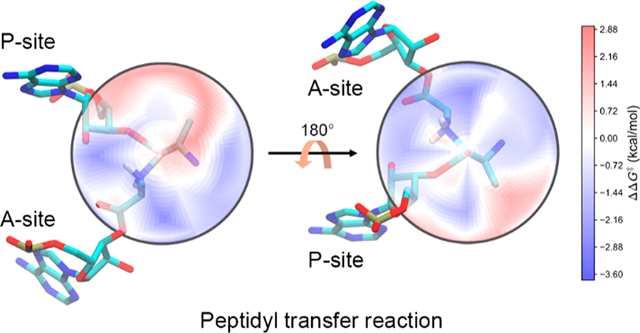
Graphical Abstract

INTRODUCTION

Mechanical forces play an essential role in guiding and modulating many molecular and cellular processes: from the differentiation of stem cells,¹ to the movement of vesicles or organelles by kinesin,² to the contraction of muscles by myosin.³ Recently, it was found that mechanical forces can be generated during the process of translation,^4,5 in which a protein molecule is synthesized through the action of the ribosome reading an mRNA molecule. Pulling forces have been observed with magnitudes ranging from unity to hundreds of piconewtons by various cotranslational processes, such as unfolded nascent chains exiting the ribosome tunnel,⁶ cotranslational protein folding,⁷ membrane insertion,⁸ and translocation.⁹ These forces arise from the hydrophobic and electrostatic interactions within the nascent chain or between the nascent chain and other ribosomal or cellular components. The forces are transmitted to the peptidyl transfer center (PTC) of the ribosome, where peptide bond formation is catalyzed and the nascent chain elongated. To date, only a few biological consequences of these mechanical forces have been identified including facilitation of programmed ribosomal frameshifting¹⁰ and relief of ribosomal stalling, allowing proteins to fold and interact with the translocon at the proper time and chain length before continuing synthesis.^{6–9,11–14}

One plausible hypothesis of how mechanical forces modulate the multistep process of translation is that these forces alter the transition state barrier of the peptidyl transfer reaction catalyzed by the ribosome. This hypothesis has been computationally tested in our previous work⁶ based on entropic pulling forces generated by the unstructured nascent chain. In that study, quantum mechanics/molecular mechanics (QM/MM) calculations were utilized to estimate the change in transition state barrier due to piconewtons of force applied along one specific direction (the long axis of the ribosome exit tunnel). However, force is a vector quantity, where both direction and magnitude are important. Thus, there may be a range of scenarios of the impact of force on peptidyl transfer beyond what has been reported to date.

Here, using QM/MM umbrella sampling simulations, we systematically investigate the changes in the activation free energy barrier for the peptidyl transfer reaction of two alanine (Ala) residues in the PTC as a function of the direction of the force applied to the P-site residue. We find that for the same force magnitude different directions of the force can result in the rate of reaction either not changing, accelerating, or decelerating relative to a zero-force reference condition.

METHODS

Simulation System Setup.

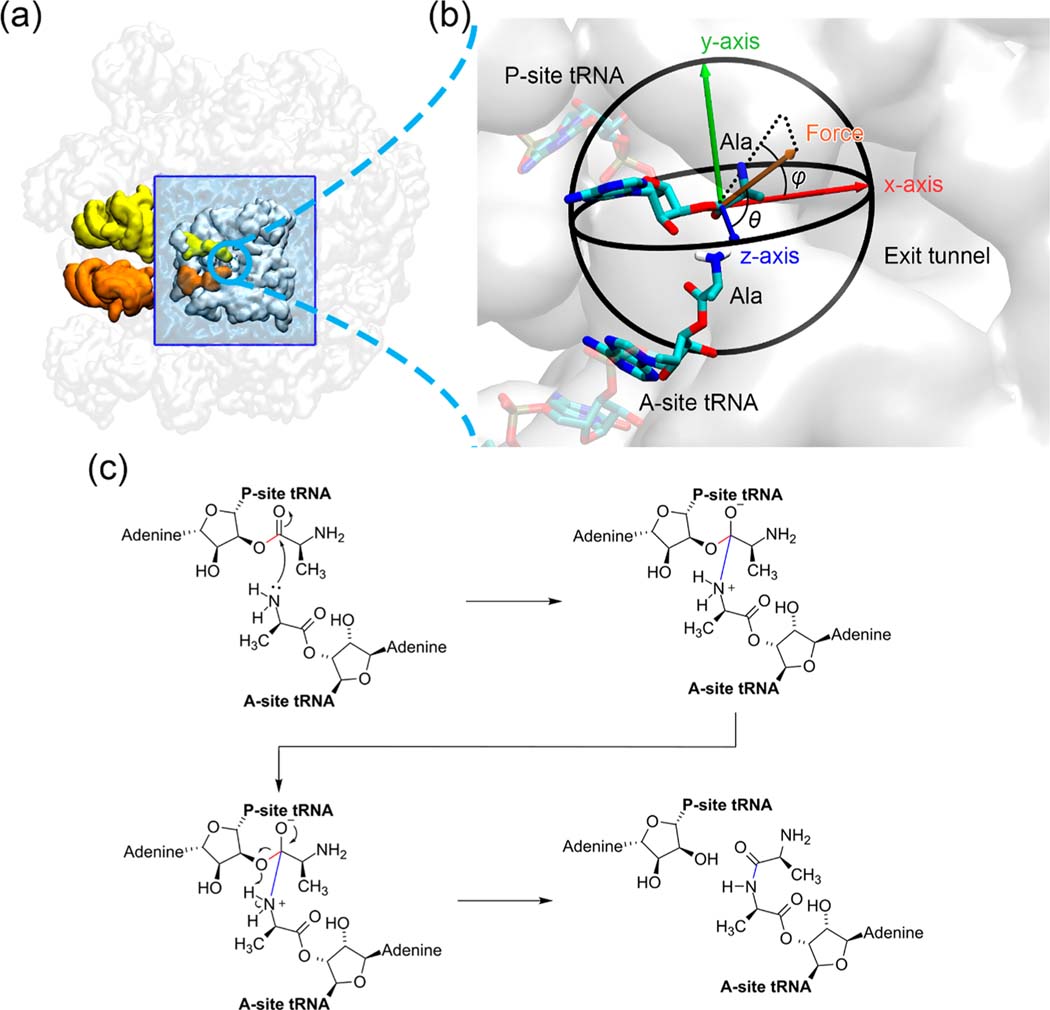
The high-resolution cryo-EM structure of the E. coli ribosome with PDB ID 5JTE¹⁵ was the starting point for modeling the ribosome. The P-site tRNA resolved in 5JTE is covalently bonded to a stalled nascent chain, while the A-site tRNA is bonded to a Lys residue. To model the Ala residues attached on the P- and A-site tRNAs, we only keep the C, Cα, N, O, and Cβ atoms of the last nascent chain residue on the P-site and the Lys residue on the A-site. The 50S ribosome structure, including the P- and A-site tRNAs and the attached amino acid residues, was trimmed to only include 6945 heavy atoms around the peptidyl transferase center (PTC, was centered around the A2602 nucleotide in the 23S rRNA; see Figure 1a). The trimming was made between residues so that all the residues in the truncated ribosome remain intact. The truncated ribosome was then solvated in a periodic TIP3P water box, whose boundary has the minimum distance of 10 Å away from the solute. The physiological salt concentration was additionally maintained by adding extra 2 Mg²⁺, 27 Na⁺, and 41 Cl⁻ ions (5 mM MgCl₂ and 100 mM NaCl, obtained from the previous study¹⁶) after the system was neutralized by 254 Na⁺ ions. The amino acid and nucleic acid residues were parametrized by using the Amber ff14SB force field¹⁷ and ff99OL3 force field,^18,19 respectively. The divalent metal ions and the monovalent ions were parametrized by using the dummy-atom model²⁰ and the Joung–Cheatham parameter set,²¹ respectively. The two Ala residues bonding on the P- and A-site tRNAs both have an unprotonated amino group (i.e., −NH₂ instead of −NH₃⁺).

Figure 1.

Simulation system of the peptidyl transfer reaction catalyzed by the E. coli ribosome. (a) Truncated 50S ribosome of the cryo-EM structure 5JTE from the Protein Data Bank. The entire 50S subunit is colored in transparent white. The truncated portion of the ribosome around the peptidyl transferase center (PTC) is shown in opaque white and embedded within a water box (blue). The A- and P-site tRNAs are shown in orange and yellow, respectively. (b) Spherical coordinate system of the pulling force applied on the carbonyl carbon atom of P-site Ala residue. It is a zoomed-in scene of the blue circled region in (a). The most probable structures of the Ala residues from molecular dynamics simulations in the reactant state are shown here, and the atoms treated quantum mechanically are represented as opaque sticks. (c) Reaction scheme of the peptidyl transfer reaction catalyzed by the ribosome and modeled in our QM/MM simulations. The breaking 3′ O–C bond in the P-site tRNA A76 nucleotide residue and the forming A- and P-site peptide bond, which are used to define the reaction coordinate, are highlighted in red and blue, respectively.

Preparing the System.

A series of MD simulations were performed to equilibrate the system density and ion distribution around the ribosome. This included an energy minimization phase with all ribosome atoms restrained except the two Ala residues: a 20 ps NVT heating phase that increases the temperature to 310 K, with all ribosome atoms restrained; an 11 ns NPT equilibration phase and a final energy minimization with all ribosome atoms restrained except the two Ala residues. We restrained all ribosome atoms during the NPT equilibration phase to keep the truncated ribosome identical with the cryo-EM structure. However, restraining such a large number of atoms in the NPT simulation resulted in an improper system density. To overcome this issue, we used the following strategy. During the equilibration phase, we first ran a 0.5 ns NPT simulation without any restraints to equilibrate the box size and the system density, then ran a 0.5 ns targeted MD simulation with an RMSD restraint toward the truncated ribosome structure that was obtained from the energy minimization to restore the ribosome to the original conformation (by decreasing the RMSD to zero), and finally ran a 10 ns NPT simulation with all ribosome atoms restrained by using a force constant 200 kcal/(mol Ų). The particle mesh Ewald (PME) method²² was used to calculate the long-range electrostatic interactions with a 10 Å cutoff. The NPT ensemble simulations were performed at 310 K temperature and 1 bar pressure via Langevin dynamics with a collision frequency of 1.0 ps⁻¹ and a coupling constant of 0.2 ps for both parameters. The SHAKE algorithm²³ was applied to the bonds involving hydrogen, allowing us to use a 2 fs integration time step. All the MD simulations were performed by Amber17.²⁴

Applying the Pulling Force on the P-Site Amino Acid Residue.

Using the equilibrated system, we applied an external pulling force in different directions on the P-site amino acid residue. In each case, a reference dummy atom, which has no electrostatic and van der Waals (vdW) interactions to any other atom in the system, was located 25 Å away from the carbonyl carbon atom (atom name is C) of the P-site Ala in a given direction. The force was applied via the following linear distance restraint between atom C and the dummy atom

$$U^{\text{ext }}(s)=F\left(s-s_0\right)$$ (1)

where F is the magnitude of the pulling force, which is 45 pN in our simulations; s is the distance between the reference dummy atom and the carbonyl carbon atom of the P-site Ala; and s₀ is the reference distance that was set as 1.5 Å. The position of the reference dummy atom was fixed during all the simulations.

Estimation of Peptidyl Transfer Reaction Transition State Barrier Using QM/MM Umbrella Sampling Simulations.

To estimate the activation free energy (ΔG^‡) for the peptidyl transfer reaction, QM/MM umbrella sampling simulations along the predefined reaction coordinate (RC) were performed on the equilibrated system, with different pulling forces applied. As shown in the reaction scheme (see Figure 1c), RCs were chosen as the difference of the breaking P-site 3′ O–C ester bond length (r_CO) at the P-site and the forming A- and P-site peptide bond length (r_CN), i.e., ξ = r_CO – r_CN. In total, 33 umbrella windows were chosen on the RC at −3.0, −2.8, −2.6, −2.4, −2.2, −2.0, −1.8, −1.6, −1.4, −1.2, −1.0, −0.8, −0.6, −0.4, −0.3, −0.2, −0.1, 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.2, 1.4, 1.6, 1.8, and 2.0 Å. Each umbrella window was run in the NPT ensemble at 310 K for 60 ps after a 1000-step energy minimization. The umbrella restraints were applied on the RCs with a force constant 250 kcal/(mol Ų). The QM region was chosen as the P- and A-site A76 (except the phosphate group) residues and the Ala residues. The QM region was simulated by using the third-order density functional tight binding (DFTB3) Hamiltonian²⁵ with 3ob-3–1 parameter set.^26–29 The MM region was simulated by using the same setup of the above classical preprocessing simulations. The QM/MM interface was built by inserting explicit link atoms (hydrogen atom). The interaction on the QM/MM interface was estimated by using the electrostatic embedding scheme. To enable the proton transfer, no SHAKE constraints were applied in the QM region. The MD integration time step was thus set as 1 fs. The potential of mean force (PMF) was unbiased and estimated by the WHAM equation³⁰ using the last 30 ps trajectories. ΔG^‡ was obtained as the difference between the maximum PMF value (transition state) and the minima before the maximum (reactant state). Note that in the umbrella sampling there are no actual transition state and reactant state structures simulated due to the discrete reaction coordinates used. All the transition state TS and reactant state R discussed in this paper refer to the average structures obtained from the umbrella windows closest to the corresponding states. The 95% confidence intervals (CIs) were estimated by using the Monte Carlo bootstrap error analysis³¹ with 100 trials. All the MD simulations were performed by Amber17.²⁴

Constructing the ΔΔG^‡ Surface by Using Linear Interpolation.

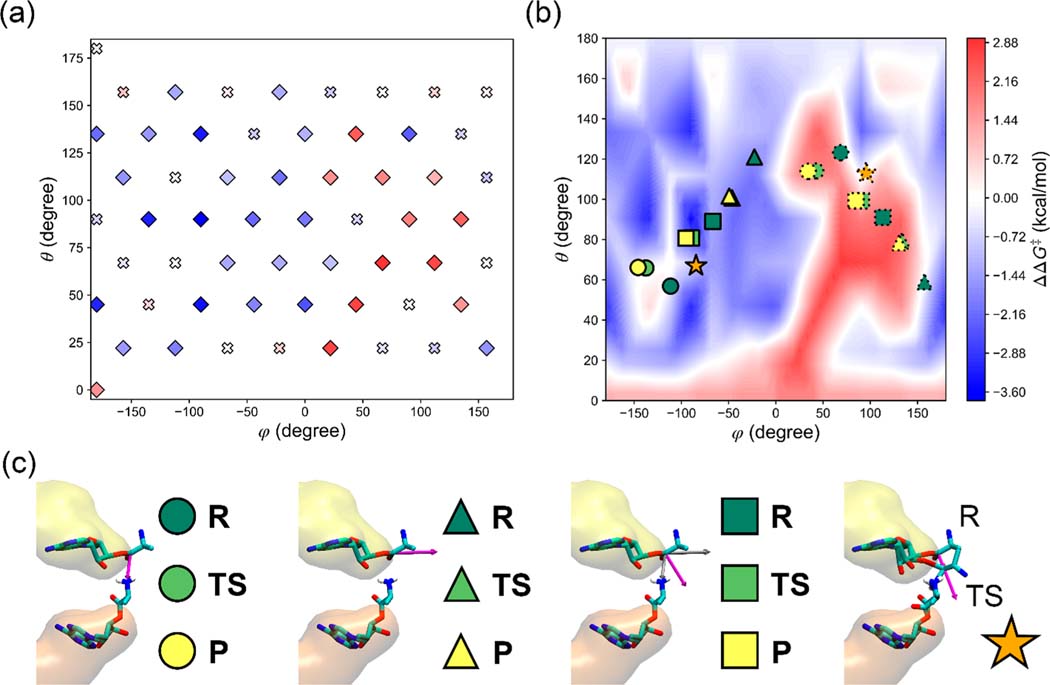
To systematically study the force-induced change of the activation free energy barrier height (ΔΔG^‡), we constructed the ΔΔG^‡ surface based on the QM/MM simulation data at a force magnitude of 45 pN. We converted the Cartesian coordinates of the force to a spherical coordinate system, where the force direction is denoted as (φ, θ), giving that φ is the azimuthal angle and θ is the polar angle (see Figure 1b). The activation free energy ΔG^‡ was estimated at each grid point on the (φ, θ) plane, where as shown in Figure 2a the grid points were chosen as the intersections of φ ∈ {−180°, −135°, −90°, −45°, 0°, 45°, 90°, 135°} and θ ∈ {45°, 90°, 135°}, the intersections of φ ∈ {−157.5°, −112.5°, −67.5°, −22.5°, 22.5°, 67.5°, 112.5°, 157.5°} and θ ∈ {22.5°, 67.5°, 112.5°, 157.5°}, and the two points at both poles (−180°, 0°) and (−180°, 180°). Thus, in total, we sampled 58 points on the (φ, θ) plane, and each point represents a different force direction. The activation free energy of the system without force applied ($\text{Δ}{G}_0^{{}^{‡}}$) was also estimated by using the same method. The force-induced change of the activation free energy barrier height was calculated as

$$\text{ΔΔ}{G}^{{}^{‡}}=\text{Δ}{G}^{{}^{‡}}-\text{Δ}{G}_0^{{}^{‡}}$$ (2)

Figure 2.

Change in the transition state barrier when 45 pN of force is applied as a function of (φ, θ)—the various directions of the applied force (Figure 1b). (a) ΔΔG^‡ (eq 2) values as a function of (φ, θ) at the discrete values used in the QM/MM simulations. Values that are not statistically different than zero are represented as crosses, while the others are represented as diamonds. All the points are colored according to the values based on the color bar in (b). (b) ΔΔG^‡ surface as a function of (φ, θ) by using a 2D linear interpolation between calculated points. The ΔΔG^‡ values are colored in a gradient from blue (a decrease in the energy barrier) to red (an increase in the energy barrier) with zero shown in white (no change in the energy barrier). Directions discussed in the main text are shown on the surface, where the force directions that are parallel and antiparallel with those directions are represented by the symbols outlined with solid and dotted lines, respectively. (c) An illustration of the relevant directions (magenta arrow) discussed in the main text. The A-site tRNA is on the bottom, while the P-site tRNA is on top. From left to right, the circles represent the direction (magenta) from the carbonyl C atom of the P-site Ala residue to the amino N atom of the A-site Ala residue. The triangles represent the direction (magenta) from the ribose 3′ O atom of the P-site tRNA A76 nucleotide residue to the carbonyl C atom of the P-site Ala residue. The squares represent the average direction (magenta) of the above two vectors (gray). The stars represent the direction (magenta) of the displacement of the carbonyl C atom of the P-site Ala residue from the reactant state R to the transition state TS. The reactant state (R), transition state (TS), and product state (P) are shown in dark green, light green, and yellow, respectively. Note that in most cases, when the force is applied parallel with these directions (symbols outlined by a solid line in Figure 2b), the energy barrier tends to decrease (i.e., they are found in blue regions), while antiparallel force directions (symbols outlined by dotted lines in Figure 2) tend to increase the energy barrier (they tend to be found in red regions).

The (φ, θ) plane is periodic due to the nature of angle; i.e., the ΔG^‡ values at any φ should be identical with the values at φ ± 2k × 180°, and the ΔG^‡ values at any θ should be identical with the values at ±θ ± 2k × 180°, where k is a natural number. To maintain this periodicity, we make four replicates of the ΔG^‡ samples on the positive and negative φ axis, respectively, and four replicates of the ΔG^‡ samples on the positive and negative θ axis, respectively (i.e., set k = 0, 1, 2, 3, 4), resulting in an extended area of φ ∈ [−9 × 180°, 9 × 180°) × θ ∈ [−9 × 180°, 9 × 180°]. At the poles, ΔG^‡ should be the same on the horizontal line of θ = ±k × 180°. We therefore insert grid points on those lines with an interval of 45° and with the ΔG^‡ value identical with that at (−180°, ±k × 180°). We then used the 2D linear interpolation to construct the ΔΔG^‡ surface on the extended area of the (φ, θ) plane and only present the surface on the central area φ ∈ [−180°, 180°) × θ ∈ [0, 180°]. The 95% CIs of ΔΔG^‡ were estimated by applying the uncertainty propagation rule to the 95% CIs of ΔG^‡ and $\text{Δ}{G}_0^{{}^{‡}}$, i.e., $\text{CI}\left(\text{ΔΔ}{G}^{{}^{‡}}\right)=\sqrt{\text{CI}{\left(\text{Δ}{G}^{{}^{‡}}\right)}^2+\text{CI}{\left(\text{Δ}{G}_0^{{}^{‡}}\right)}^2}$.

RESULTS

Change in Transition State Barrier ΔΔG^‡ as a Function of Force Direction.

To systematically study the force-induced changes in the activation free energy barrier height (ΔΔG^‡) to the peptidyl transfer reaction catalyzed by the ribosome, we calculated the ΔΔG^‡ in different force directions using QM/MM umbrella sampling simulations and then constructed the ΔΔG^‡ surface on the (φ, θ) plane in spherical coordinates (see the Methods section). In these simulations a force with a magnitude of 45 pN was used. This is on the order of magnitude of forces estimated to be generated by protein folding and electrostatic interactions between the nascent chain and ribosome exit tunnel wall. All of the simulations have converged, as indicated by the consistent PMFs computed from different blocks of time during the simulations (see Figure S1).

Plotting the interpolated surface of ΔΔG^‡ as a function of (φ, θ) (Figure 2b), we first analyzed whether any individual points were not significantly different than zero (Figure 2a). We did this by calculating the 95% confidence interval about ΔΔG^‡, and if the error bar overlapped with zero, then the p-value is not significant for a 0.05 threshold. We show these points in Figure 2a as crosses. For all other significant points we observe (Figure 2b) regions where certain force directions accelerate the reaction (i.e., decreased activation free energy, shown in blue), others decelerate the reaction (increased activation free energy, shown in red), and others cause no significant change in reaction speed (no change in the activation free energy, shown in white).

To make sense of these trends, we calculate time-averaged vectors that report on the progress of the peptidyl transfer reaction and plot their (φ, θ) values on the ΔΔG^‡ surface. Specifically, the vectors are along the peptide bond connecting the A- and P-site Ala residues that forms during the reaction (circles outlined by solid lines in Figure 2b,c), the P-site 3′ O–C ester bond connecting the tRNA and Ala residue that breaks during the reaction (triangles outlined by solid lines in Figure 2b and c), the average vector between these two (squares outlined by solid lines in Figure 2b,c), and finally the displacement vector of the carbonyl C atom of the P-site Ala residue from the reactant state R to the transition state TS (stars outlined by solid lines in Figure 2b,c).

With this information we observe that when the force is applied parallel to each of these directions the activation free energy is reduced, except for when force is along the peptide bond formation vector (φ ∈ [−150°, 110°] × θ ∈ [55°, 65°]). In this case, the applied force does not alter the barrier height. In contrast, when the force is applied antiparallel with these directions (i.e., in the opposite direction, marked as the symbols outlined by dotted lines in Figure 2b), the activation free energy increases in most of the cases, except for those along the opposite directions of the P-site 3′ O–C ester bond breaking at the reactant state (around the point at (155°, 55°)) and the displacement vector of the carbonyl C atom of the P-site Ala residue from the reactant state R to the transition state TS (around the point at (90°, 110°)) where no significant change is observed. This phenomenon is qualitatively consistent with the Bell model,^32,33 in which the influence of the force on the activation energy barrier is the negative of the work done by the force along the reaction coordinate.

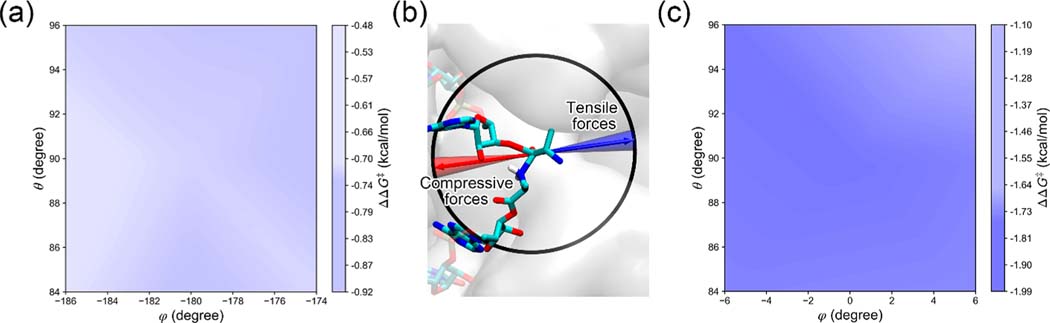
Tensile Forces along the Exit Tunnel Accelerate the Peptidyl Transfer Reaction.

We next focus on the influence of the pulling forces acting on the P-site carbonyl C atom and applied along the ribosome exit tunnel. This direction results in a tensile force as it extends the nascent chain and thereby induces tension. It has been computationally demonstrated that the tensile force generated by the unfolded nascent chains, which pulls the P-site residue along the long axis of the exit tunnel, could lower the activation energy barrier to the peptide bond formation.⁶ In this study, we not only focus on the exact direction that has been studied but also take into account fluctuations of the tensile force direction. Assuming the exit tunnel is a cylinder with a radius of 7.5 Å, a protein domain folds 80 Å from the P-site residue, resulting in a tensile force whose direction could diverge no greater than 6° (= arctan(7.5/80) ≈ 5.4°) from the long axis of the exit tunnel (see Figure 3b). The long axis of the exit tunnel coincides with the point (0°, 90°) on the (φ, θ) plane. We therefore focus on the influence of the force applied within the rectangular region φ ∈ [−6°, 6°] × θ ∈ [84°, 96°], as shown in Figure 3c. A 45 pN force applied within this region lowers the barrier height by 1–2 kcal/mol. This influence is statistically significant as illustrated at the grid point (0°, 90°) in Figure 2a. With such as change, we can estimate the change in reaction rate using Eyring’s equation:³⁴ $k/k_0={\text{e}}^{-\text{ΔΔ}{G}^{{}^{‡}}/k_{\text{B}}T}$, where k and k₀ are the reaction rates of the system in the presence and absence of the force, respectively, ΔΔG^‡ is the altered transition state barrier estimated by eq 2, k_B is the Boltzmann constant, and T is the temperature at 310 K. With this model the peptidyl transfer reaction would be accelerated by 5- to 25-fold.

Figure 3.

A subset of the ΔΔG^‡ surface when tensile and compressive forces are applied along the ribosome exit tunnel axis. (a) ΔΔG^‡ surface in the region φ ∈ [−186°, −174°] × θ ∈ [84°, 96°], representing the directions in which compressive forces are applied. (b) Directions of the tensile forces (blue arrow and cone) and compressive forces (red arrow and cone) applied respectively parallel and antiparallel along the exit tunnel axis. The PTC is represented in the same manner as in Figure 1b, except that the most probable transition state structure is shown. The cones represent 6° off axis from the arrows. (c) ΔΔG^‡ surface on the region φ ∈ [−6°, 6°] × θ ∈ [84°, 96°], representing the tensile forces applied along the exit tunnel. Panels a and c have the same colormap as used in Figure 2b but have a smaller range. Note that while the tensile force lowers the activation barrier by a statistically significant amount, the compressive force does not result in a statistically significant change in barrier height.

To examine the influence of compressive forces, i.e., those that push on the P-site, applied in the opposite direction of the exit tunnel axis, we focus on the rectangular region φ ∈ [−186°, −174°] × θ ∈ [84°, 96°] (see Figure 3a). A 45 pN force applied within this region lowers the barrier height by 0.5–0.9 kcal/mol. However, this effect is not statistically significant as illustrated at the grid point (−180°, 90°) of Figure 2a. According to the Bell model,^32,33 it is expected that increasing the magnitude of the compressive force will increase its effect on the barrier height, but whether it will accelerate or decelerate the peptidyl transfer reaction is unclear from these simulations.

Force Directions That Yield the Greatest Acceleration and Deceleration of the Peptidyl Transfer Reaction.

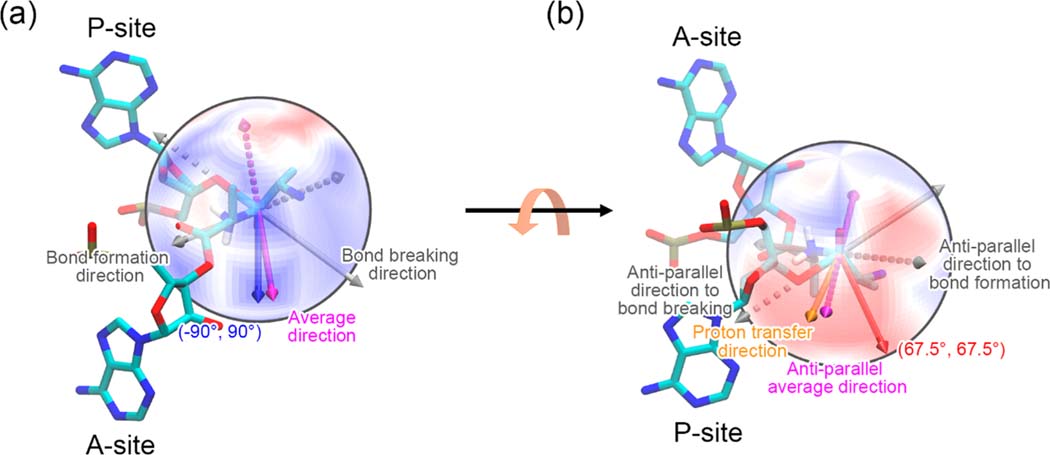
The applied force could both result in acceleration and deceleration for the peptidyl transfer reaction, as illustrated by the blue and red regions in Figure 2b, respectively. A maximum acceleration of 419 fold (estimated by the Eyring equation³⁴) is induced by the force applied in the direction of (−90°, 90°), where the activation free energy is reduced by 3.72 ± 0.90 kcal/mol. This direction nearly coincides with the average direction of the bonds that break and form during the reaction (denoted as squares outlined by solid lines in Figure 2b as well), as illustrated in Figure 4a. In this direction, the force performs the most work on the bonds that break and form, which pushes the reactants toward the transition state. The forces applied in nearby directions all have an effective force component in this direction and hence reduce the activation free energy. The maximum deceleration of 116-fold (estimated by the Eyring equation³⁴) is induced by the force applied in the direction of (67.5°, 67.5°), where the activation free energy is increased by 2.93 ± 1.00 kcal/mol. This direction is close to the opposite (antiparallel) average direction of those bonds that have broken and formed, as illustrated in Figure 4b. The force has a significant negative work acting on the bonds that break and form, which hinders the reactants from forming the transition state. The forces applied in the nearby directions all have an effective force component in this direction and hence increase the activation free energy.

Figure 4.

Illustration of the forces that cause the greatest acceleration (a) and deceleration (b) of the peptidyl transfer reaction. The ΔΔG^‡ surface is shown on a sphere instead of on the (φ, θ) plane. The color scheme is the same as in Figure 2b. Only the last nucleic acid residues of the A- and P-site tRNAs as well as the attached Ala residues are shown. The two Ala residues are shown in the transition state conformation. The bond breaking and formation directions are represented as gray arrows. The average of the above two directions is represented as a magenta arrow. The force directions that cause the greatest acceleration and deceleration are represented as a blue and a red arrow, respectively. The antiparallel directions that are opposite to the bond breaking/formation and the average directions are represented as dashed arrows with the same corresponding colors. The proton transfer direction is shown as an orange arrow in (b).

Generally, the force applied along the direction of the reaction, which we define as the average direction of bond formation and breaking, is expected to have the maximum influence on the activation free energy barrier and hence maximally alter the reaction rate.^32,33 This predicts a maximum barrier height change for a force applied in the direction of (−83.4°, 89.1°) (the magenta arrow in Figure 4a) based on the atomic coordinates in our transition state configuration. Consistent with this prediction, we observe in the simulations the greatest barrier decrease occurs at (−90°, 90°), which, due to our systematic sampling of (φ, θ) space, was the closest point we sampled to the expected value.

Conversely, the force applied opposite the direction of the reaction is expected to maximally increase the energy barrier, which would correspond to a force direction of (96.6°, 90.9°) (the dashed magenta arrow in Figure 4a). However, we observe that the force direction that actually increases the barrier the most is 37° from this, at (67.5°, 67.5°). We explain this observation by noting that there is a proton transfer step involved in the overall peptidyl transfer reaction, where the proton in the amino group of A-site Ala transfers to the 3′ O atom of the P-site tRNA A76 residue (Figure 1c) that is distinct from breaking of the P-site 3′ O–C ester bond and formation of the peptide bond. A force applied at (96.6°, 90.9°) coincides with the proton transfer direction, as illustrated in Figure 4b, indicating this force direction would enhance proton transfer by pushing the proton donor and acceptor closer. Thus, there are counterbalancing processes that cause the maximum increase in barrier height to be located at a different, nearby force direction.

Therefore, the asymmetric chemical environment of the ΔΔG^‡ surface shown in Figure 2b arises from the anisotropic environment at the catalytic core of the PTC.

Force-Induced Structural Changes in the Reactant State Ensemble.

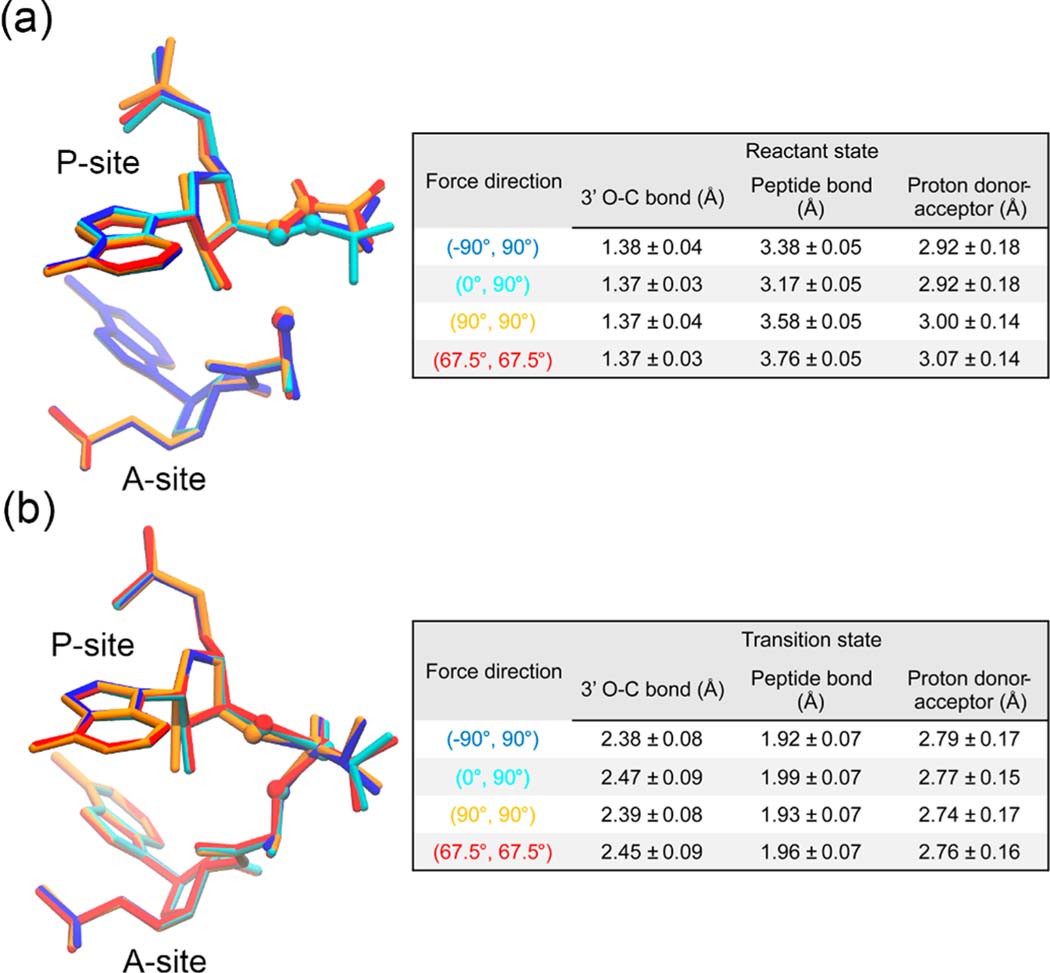
To examine how the pulling forces alter the activation free energy barrier at the molecular level, we checked the structural change of the reactant state and transition state, respectively. The structural change was characterized by the average lengths of the P-site 3′ O–C ester bond and the peptide bond as well as the distance between the proton acceptor (P-site tRNA A76 3′ O) and the proton donor (A-site amino N). As illustrated in Figure 5a, the reactant state structure of the P-site Ala residue was distorted by the pulling force. More specifically, both the force applied along (−90°, 90°), which at most accelerates the peptidyl transfer reaction, and the force applied along (0°, 90°), which is the tensile force along the exit tunnel, distort the structure of the P-site Ala residue and bring it closer to the A-site Ala residue. Both the force applied along (67.5°, 67.5°), which maximally decelerates the peptidyl transfer reaction, and the force applied along (90°, 90°), which almost coincides with the opposite direction of the reaction, distort the structure of the P-site Ala residue and shift it away from the A-site Ala residue. This is also confirmed by the bond lengths and distance shown in the right table in Figure 5a, where the peptide bond lengths have been changed by 0.2–0.6 Å. In contrast, the transition state structures do not have such a significant distortion, as shown in Figure 5b, where the geometries of the transition state are quite similar to each other with the bond lengths and distances changing less than 0.1 Å. This suggests that much of the alteration in the activation free energy barrier is caused by the distortion of the reactant state structures, which move closer to the transition state structure when the effective force component is parallel with the direction of the reaction.

Figure 5.

Force-induced structural changes. (a) The reactant state structures and (b) the transition state structures of the last nucleic acid residues of the A- and P-site tRNAs as well as the attached Ala residues are shown. The structures are obtained from the last 30 ps trajectories of the corresponding umbrella windows and are shown in blue, cyan, orange, and red for the systems with the pulling force applied along (−90°, 90°), (0°, 90°), (90°, 90°) and (67.5°, 67.5°), respectively. The P-site tRNA 3′ O atom, the P-site Ala carbonyl C atom, and the A-site Ala amino N atom are highlighted as spheres. In each panel, the average lengths (mean ± standard deviation) of the P-site 3′ O–C ester bond and the peptide bond and the distance between the proton acceptor (P-site tRNA A76 3′ O) and the proton donor (A-site amino N) for each system are reported in the table on the right.

DISCUSSION AND CONCLUSIONS

Most reports to date have focused on the effect of forces collinear with the long-axis of the exit tunnel in the direction toward the exit tunnel vestibule. These studies have found an acceleration of translation when such a force is applied. Here, we computationally examined the scenarios that can arise when forces acting in other directions influence the rate of peptide bond formation. Through this systematic study we observe three types of outcomes are possible. Depending on the applied direction the force acting on the P-site, the rate of peptide bond formation can accelerate, decelerate, or remain unaltered relative to the situation where no force is present. More specifically, we observe, consistent with previous results, that tensile forces applied along the exit tunnel tend to accelerate the reaction.⁶ But something new we find is that a compressive force, acting in the opposite direction, has no significant effect on the barrier height.

The most extreme acceleration of the reaction occurs when the force is applied along the direction of the reaction involving peptide bond formation between A- and P-site Ala residues and ester bond breaking between the P-site tRNA and Ala residue, as this force direction promotes bond breaking and formation of these bonds, while a force applied 37° away from the opposite direction results in the most deceleration. The reason the maximum deceleration does not occur in the exact opposite direction is because while peptide bond formation and/or ester bond breaking are inhibited, this direction of force brings the A-site amino group and the P-site tRNA A76 3′ O group closer together and thereby promotes proton transfer between them, which is an essential step in the reaction mechanism. One may ask why the maximum acceleration to peptide bond formation occurs in the exact direction of the reaction (and nearly opposite the direction of protons transfer) when proton transfer is an essential step. This can be explained by comparing the proton donor–acceptor distances presented in Figure 5. The proton donor–acceptor distances decreased from the reactant state to the transition state by 0.13, 0.15, 0.26, and 0.31 Å respectively for the forces along (−90°, 90°), (0°, 90°), (90°, 90°), and (67.5°, 67.5°). These distance changes have the same trend as the transition state barrier changes; that is, the system with a larger distance change is slower, as it is harder to overcome the larger distance (known as ground state stabilization). Although the change of the proton donor–acceptor distance in the system (90°, 90°) is smaller than that in the system (67.5°, 67.5°), it is still larger than the distances in other two accelerated systems. This indicates that when the force aligns with the direction of reaction, the distorted structures always promote proton transfer by bringing the proton donor and acceptor closer together, despite that the force may be applied opposite to the proton transfer direction.

These major directions we discussed have biological implications. In another computational study,³⁵ we examined the force generated by electrostatic interactions between the nascent chain and the exit tunnel. We observed various force directions as a consequence of these interactions. Negatively charged residues in the nascent chain could generate a force that moves the P-site residues toward the A-site, while positively charged residues could generate a force that moves the P-site residues away from the A-site. These force directions are, respectively, close to the direction (−83.4°, 89.1°) that maximally accelerates peptide bond formation and (67.5°, 67.5°) that maximally decelerates the reaction. Similarly, the steric interactions between the nascent chain and some certain peptidyl transfer inhibitors that bind in the exit tunnel would be expected to generate compressive forces due to the obstruction they create as the nascent chain passes through the exit tunnel.

We observe greater force-induced structural changes of the reactant structural ensemble compared to the transition state, which is reasonable as the transition state involves harder degrees of freedom than found in the reactant state. This suggests that the transition state location along an idealized reaction coordinate would not change much with force but the reactant location will. In some applied force directions the reacting molecules move closer together, while in others they move further apart, which anticorrelates with changes in barrier height.

These results are qualitatively consistent with the Bell model of force effects on transition state barrier heights, in which forces parallel or antiparallel with the reaction coordinate respectively decrease or increase the transition state barrier. That model is not quantitatively applicable for our system as the model assumes a 1-dimensional reaction coordinate, while the concerted bond breaking and formation between five different atoms does not permit description by a 1-dimensional reaction coordinate. We attempted using a higher-dimensional model but did not find a quantitative fit to our data.

More broadly, these results indicate that there is a richer set of scenarios of consequences for translation speed when force is applied that remain unexplored experimentally. Key to exploring these scenario’s experimentally is the creation of systems or experimental techniques that allow for the controlled creation of forces that act in directions other than the long axis of the ribosome exit tunnel. Systems could include the obstruction of the exit tunnel to generate compressive forces or functional groups incorporated into the nascent chain that could controllably interact with portions of the ribosome exit tunnel wall.