Abstract
Recent work has shown that convolutional neural networks (CNNs) trained on image recognition tasks can serve as valuable models for predicting neural responses in primate visual cortex. However, these models typically require biologically-infeasible levels of labeled training data, so this similarity must at least arise via different paths. In addition, most popular CNNs are solely feedforward, lacking a notion of time and recurrence, whereas neurons in visual cortex produce complex time-varying responses, even to static inputs. Towards addressing these inconsistencies with biology, here we study the emergent properties of a recurrent generative network that is trained to predict future video frames in a self-supervised manner. Remarkably, the resulting model is able to capture a wide variety of seemingly disparate phenomena observed in visual cortex, ranging from single-unit response dynamics to complex perceptual motion illusions, even when subjected to highly impoverished stimuli. These results suggest potentially deep connections between recurrent predictive neural network models and computations in the brain, providing new leads that can enrich both fields.
The fields of neuroscience and machine learning have long enjoyed productive dialogue, with neuroscience offering inspiration for how artificial systems can be constructed, and machine learning providing tools for modeling and understanding biological neural systems. Recently, as deep convolutional neural networks (CNNs) have emerged as leading systems for visual recognition tasks, they have also emerged—without any modification or tailoring to purpose—as leading models for explaining the population responses of neurons in primate visual cortex [1, 2, 3, 4]. These results suggest that the connections between artificial deep networks and brains may be more than skin deep.
However, while deep CNNs capture some important details of the responses of visual cortical neurons, they fail to explain other key properties of the brain. Notably, the level of strong supervision used to typically train CNNs is much greater than that available to our brain. To the extent that representations in the brain are similar to those in CNNs trained on, e.g., ImageNet [5], the brain must be arriving at these representations by different, largely unsupervised routes. Another key difference is that the majority of CNNs optimized for image recognition and subsequently used to predict neural responses are feedforward and thus fundamentally static, lacking recurrence and a notion of time (with notable recent exceptions [4, 6, 7]). Neuronal systems, in contrast, are highly dynamic, producing responses that vary dramatically in time, even in response to static inputs.
Here, inspired by past success in using “out-of-the-box” artificial deep neural networks as models of visual cortex, we explore whether modern predictive recurrent neural networks built for unsupervised learning can also explain critical properties of neuronal responses and perception. In particular, we consider a deep predictive coding network (“PredNet”; [8]), a network that learns to perform next-frame prediction in video sequences. The PredNet is motivated by the principle of predictive coding [9, 10, 11, 12]; the network continually generates predictions of future sensory data via a top-down path, and it sends prediction errors in its feedforward path. At its lowest layer, the network predicts the input pixels at the next time-step, and it has been shown to make successful predictions in real-world settings (e.g. car-mounted camera datasets [13]). The internal representations learned from video prediction also proved to be useful for subsequent decoding of underlying latent parameters of the video sequence, consistent with the suggestion of prediction as a useful loss function for unsupervised/“self”-supervised learning [14, 15, 16, 17, 18, 19, 20, 21, 22].
Self-supervised learning through video prediction has a rich history in machine learning literature and is a highly active area of current research [23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33]. Early implementations of spatiotemporal predictive learning include the work of Elman [20], Softky [14], and Hawkins [21]. Recent approaches have incorporated adversarial [23, 15, 16, 25] and variational [26, 24, 27] techniques, as well as novel recurrent units [34, 28]. With use cases including anomaly detection [35, 36] and robotic planning [37, 29], state-of-the-art models are capable of successful predictions in datasets ranging from action recognition [28, 24] to robotic arm movement [19, 31].
In the neuroscience community, predictive coding also has a rich history [38, 39, 40, 41, 42, 43, 44, 45, 46]. Rao and Ballard helped popularize the notion of predictive coding in neuroscience in 1999, proposing that spatial predictive coding could explain several extra-classical receptive field effects in primary visual cortex (V1), such as end-stopping [9]. Predictive coding has been proposed as an explanatory framework for phenomena in a variety of sensory systems [47, 48, 49]. The PredNet formulates temporal and spatial predictive coding principles in a deep learning framework to work on natural sequences, providing an opportunity to test a wide range of neuroscience phenomena using a single model.
Below, we show that despite being trained only to predict next frames in natural sequences, the PredNet captures a wide array of seemingly unrelated fundamental properties of neuronal responses and perception, even when probed with synthetic stimuli. We begin by demonstrating that the PredNet can mimic neuronal response properties at multiple levels of the visual hierarchy, including both spatial properties (end-stopping/length suppression) and temporal properties (on/off firing rate dynamics, temporal sequence learning effects). We then demonstrate that the PredNet can also capture aspects of perception, even under conditions where subjective interpretation is dissociated from visual input, such as the spatial completion in illusory contours and the dynamic illusion of the flash-lag effect.
RESULTS
The deep predictive coding network proposed in Lotter et al. (2017) [8] (“PredNet”) consists of repeated, stacked modules where each module generates a prediction of its own feedforward inputs, computes errors between these predictions and the observed inputs, and then forwards these error signals to subsequent layers (Figure 1, see also Methods). The residual errors from a given layer thus become the prediction targets for the layer above. The model consists of four components: targets to be predicted (Al), predictions (Âl), errors between predictions and targets (El), and a recurrent representation from which predictions are made (Rl). On an initial time step, the feedforward pass can be viewed as a standard CNN, consisting of alternating convolutional and pooling layers. Because of the pooling operation, the feedforward receptive field becomes twice as large at each successive layer. The pooling output of each layer is set as the prediction target for that layer, with the target at the lowest layer set to the actual input image itself, corresponding to the next frame in the input video sequence. Predictions are made in a top-down pass via convolutions over the representational units, which are first updated using the representational units from the layer above and errors from the previous time step as inputs. The error modules, El, are calculated as a simple difference between the targets (Al) and predictions (Âl), followed by splitting into positive and negative error populations. The network is trained to minimize the activations of the error units across the training set using (truncated) backpropagation through time, with the error units at each layer contributing to the total loss. Similar to the original work [8], the results presented here use a model trained for next-frame prediction on a car-mounted camera dataset (KITTI; [13]). Thus, the model is trained in a unsupervised or “self”-supervised manner which does not require any external labels or other forms of supervision. The model consists of four layers and, with 0-indexing used here, layer 1 would be analogous to primary visual cortex (V1).
Figure 1:
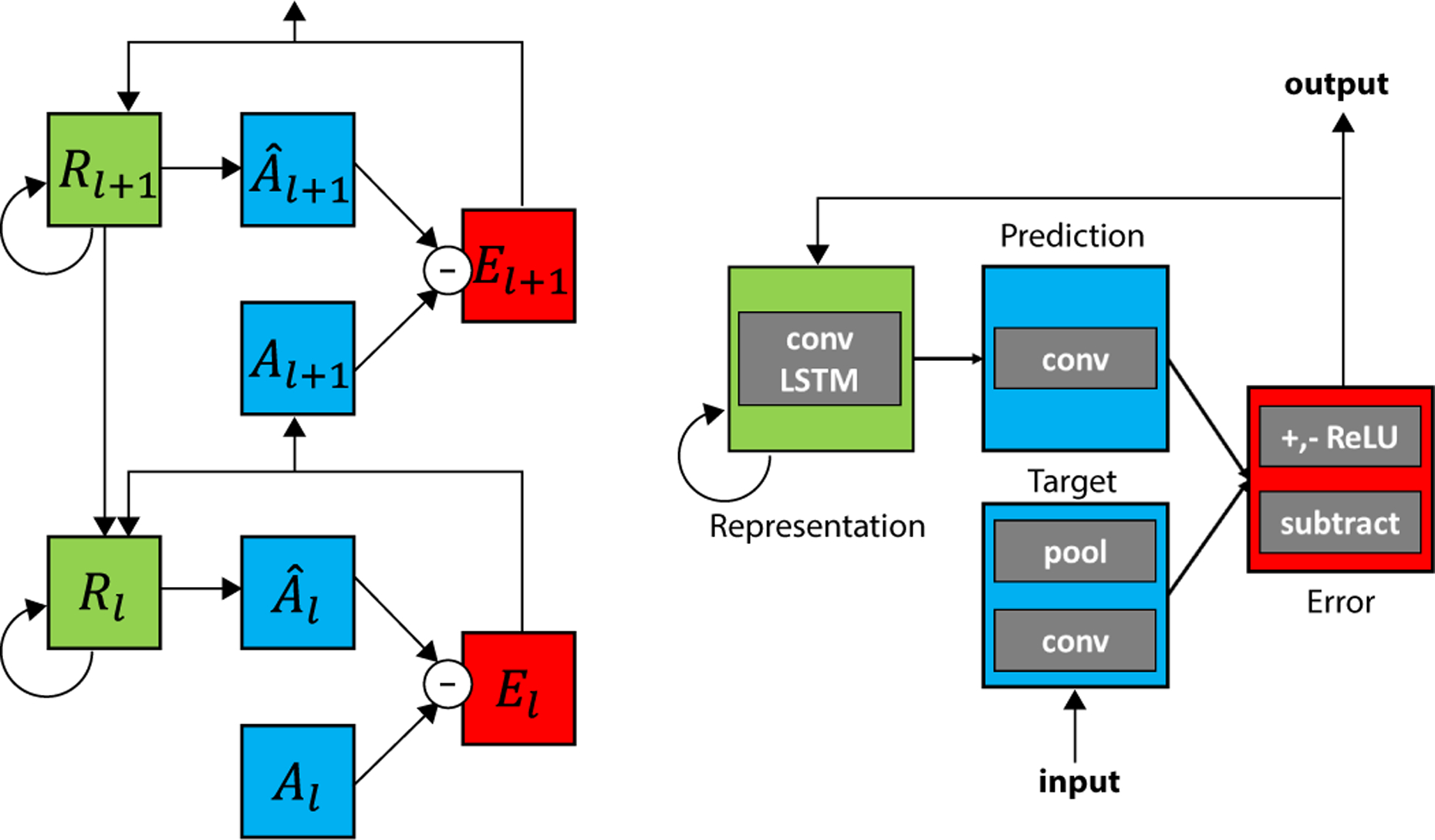
Deep Predictive Coding Networks (PredNets) [8]. Left: Each layer l consists of representation neurons (Rl), which output a layer-specific prediction at each time step (Âl), which is compared against a target (Al) to produce an error term (El), which is then propagated laterally and vertically in the network. Right: Module operations for case of video sequences. The target at the lowest layer of the network, A0, is set to the actual next image in the sequence. conv: convolution; conv LSTM: convolutional long short-term memory [50, 51]); pool: 2×2 max-pooling; ReLU: rectified linear unit activation.
PredNet can capture spatial and temporal single unit response properties
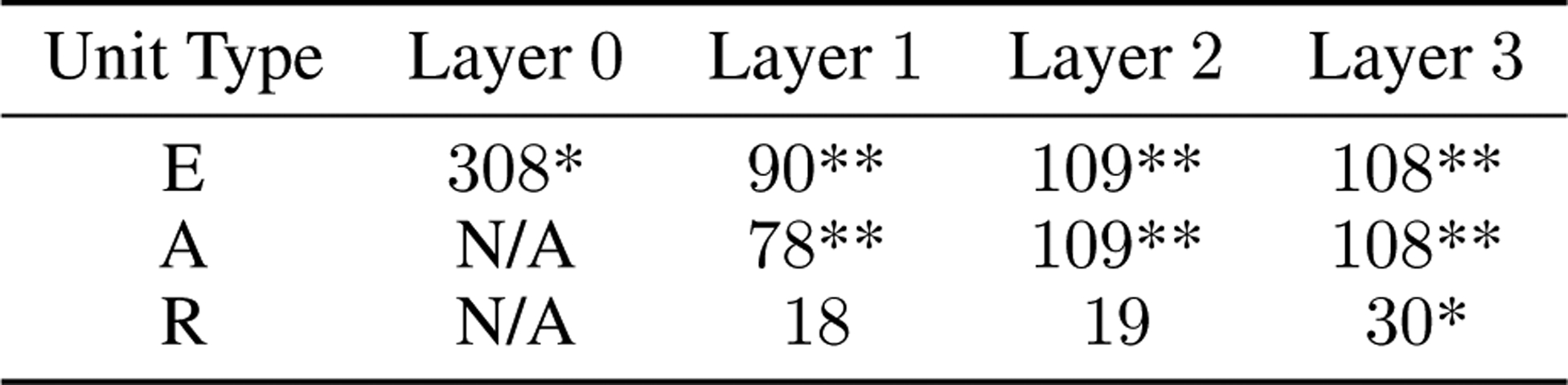
We begin by comparing the response properties of units in the PredNet to established single unit response properties of neurons in the primate visual system, which have been studied extensively using microelectrode recordings. We investigate both spatial and temporal properties, first illustrating that the spatiotemporally-trained PredNet can reproduce effects dependent on spatial statistics akin to the spatially-trained model of Rao and Ballard [9]. We then examine temporal aspects of responses in the network, demonstrating both short-term (“inference mode”) and long-term (“training mode”) properties that are consistent with biology. Throughout, we primarily compare responses in the PredNet’s error (“E”) units, the output units of each layer, to neuronal recordings in the superficial layers of cortex. In each comparison, we show that the PredNet qualitatively exhibits the effect and then provide a quantitative comparison to biology, primarily using the metrics defined in the original biological studies. For completeness, response properties of other units in the PredNet (e.g., the “R” units) are included in the Extended Data, and would likely map onto other parts of the cortical circuit (see Discussion).
End-stopping and length suppression.
One of the earliest non-linear effects discovered in recordings of visual cortex is the property of end-stopping [52]. End-stopping, or length suppression, is the phenomenon where a neuron tuned for a particular orientation becomes less responsive to a bar at this orientation, when the bar extends beyond its classical receptive field. The predictive coding explanation is that lines/edges tend to be continuous in nature, and thus the center of a long bar can be predicted from its flanks [9, 45]. A short, discontinuous bar, however, deviates from natural statistics, and responding neurons signal this deviation. One potential source for conveying the long range predictions in the case of an extended bar could be feedback from higher visual areas with larger receptive fields. This hypothesis was elegantly tested in Nassi et al. [53] using reversible inactivation of secondary visual cortex (V2), paired with V1 recordings in the macaque. As illustrated in the left side of Fig. 2, cryoloop cooling of V2 led to a significant reduction in length suppression, indicating that feedback from V2 to V1 is essential for the effect.
Figure 2:
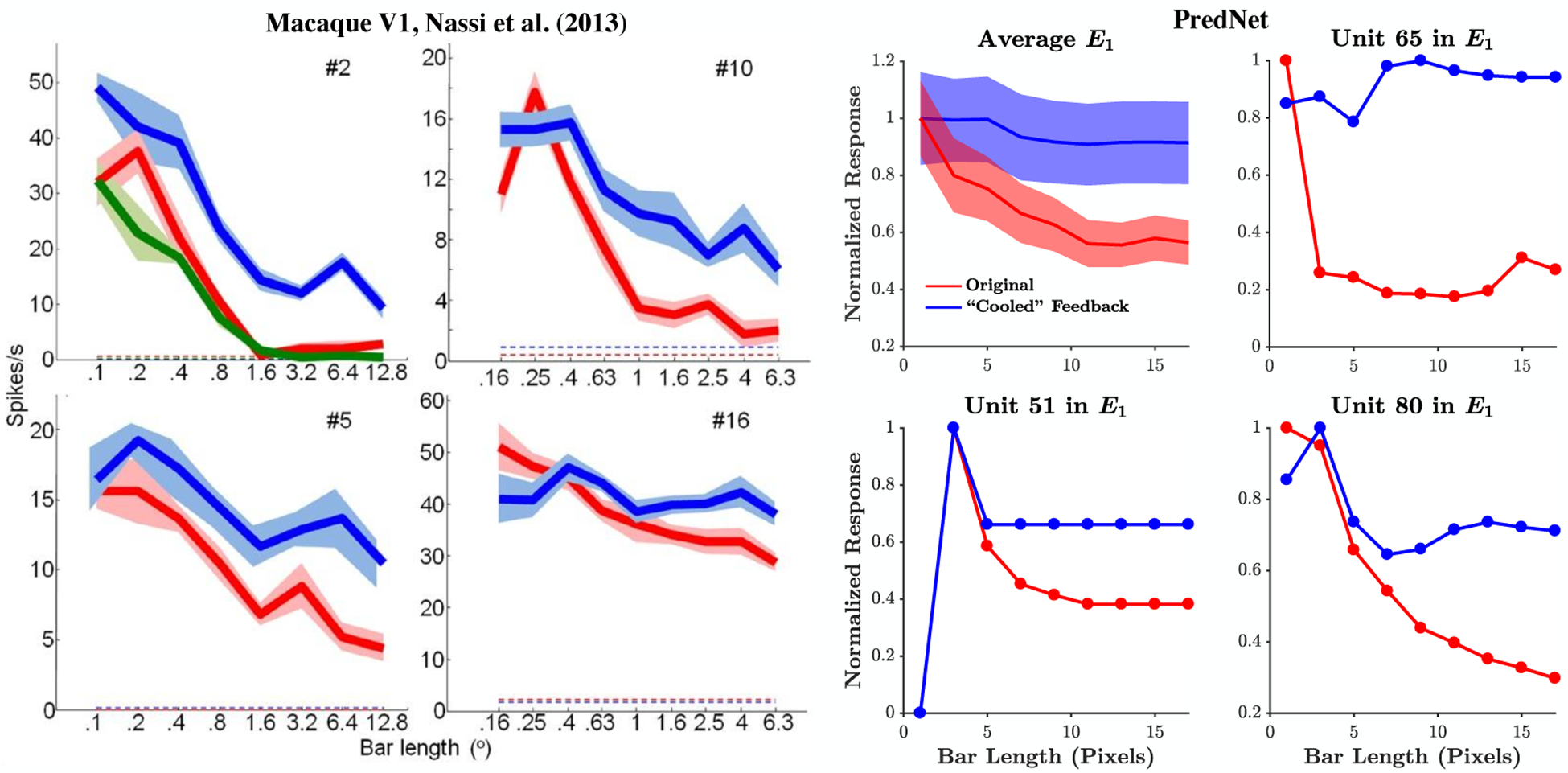
Length suppression. Left: Responses of example macaque V1 units to bars of different lengths before (red), during (blue), and after (green) inactivation of V2 via cryoloop cooling [reproduced from Nassi et al. [53]; dashed lines indicate spontaneous activity]. Right: PredNet after training on the KITTI car-mounted camera dataset [13] - Mean over E1 filter channels (± s.e.m.) and examples. Red: Original network. Blue: Feedback weights from R2 to R1 set to zero. We note that, in the PredNet, the “after” inactivation response (green trace in neural data) would be equivalent to the “before” inactivation response (blue). See Extended Data Fig. 1 for responses of A and R units.
The right side of Fig. 2 demonstrates that length suppression, and its mediation through top-down feedback, are also present in the PredNet. The upper left panel contains the mean normalized response for units in the E1 layer to bars of different lengths and the remaining panels contain exemplar units. The red curves correspond to the original network (trained on the KITTI dataset, [13]) and the blue curves correspond to zero-ing the feedback from R2 to R1. Quantifying percent length suppression (%LS) as , with r indicating the response, the mean decrease in %LS upon removing top-down signaling was 16 ± 7% (mean ± s.e.m.) for E1 units (p = 0.014, Wilcoxon signed rank test, one-sided, z = 2.2), which is similar to the 20% decrease observed in the V1 population upon cooling V2 by Nassi et al. [53].
On/off temporal dynamics.
Prediction in space and prediction in time are inextricably intertwined. A particular core temporal aspect of the visual cortical response that has a predictive quality is the on/off response trajectory to static stimuli. Figure 3a shows a typical response profile of a visual cortical neuron to a static input [54]. The neuron, recorded in the secondary visual cortex (V2) of a macaque monkey, produces a brief transient response to the onset of the visual stimulus, followed by near total suppression of that response. When the stimulus is removed, the neuron responds again with a transient burst of activity (known as an “off” response). The unpredictability of the stimulus and its precise onset correlate to the “on” response, which decays as the image remains fixed, consistent with the common, slow-moving or static nature of real-world objects. Finally, the sudden and unexpected disappearance of the object drives the “off” response. Fig. 3b shows the average response of PredNet E units in different layers over a set of 25 naturalistic objects appearing on a gray background. The on/off dynamics are apparent on the population average level, for all four layers of the network. One time step after image onset, the decay in average response ranges from 20% (E1) to 49% (E3). As a point of reference, macaque inferior temporal cortex (IT) data from Hung et al. [55] exhibits a 44% reduction in population response 100ms after post-onset peak of a static image on a gray background. This decay rate is thus of the same magnitude observed in the PredNet, given that one time step in the model is loosely analogous to 100ms, since the model was trained at a rate of 10 Hz. As the E units are the input drive to much of the rest of the network, it might be expected that the on/off dynamics are also present in the A and R layers, and indeed this is the case, as illustrated in Extended Data Figure 2.
Figure 3:
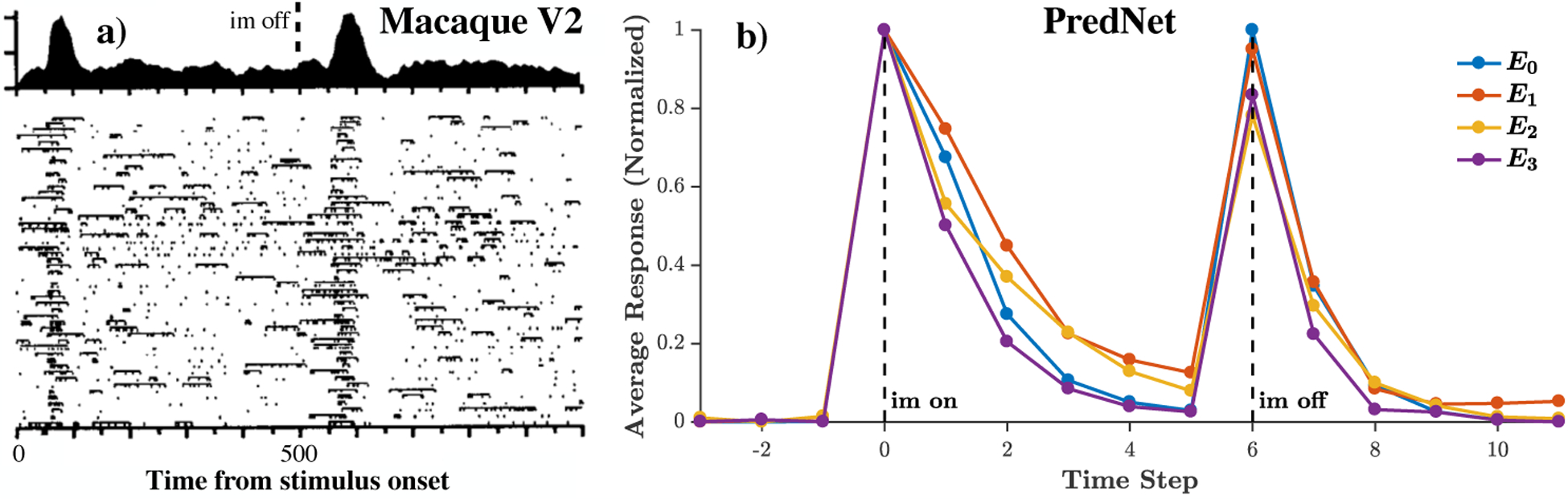
On/off temporal dynamics. Left: Exemplar macaque V2 neuron responding to a static image [adapted from Schmolesky et al. [54]]. Right: PredNet response to a set of naturalistic objects appearing on a gray background, after training on the KITTI car-mounted camera dataset [13]. Responses are grouped by layer for the E units, and averaged across all units (all receptive fields and filter channels) and all stimuli, per layer. The average response trace is then normalized to have a range from 0 to 1. The average response peaks upon image appearance and disappearance. Given the large number of units in each layer, the s.e.m is O(1%) of the mean. Responses of A and R units are contained in Extended Data Figure 2.
Sequence learning effects in visual cortex.
While the on/off dynamics of visual cortical responses may indeed reflect learned statistics of the natural world, there are perhaps even more striking examples of the sensitivity of neural responses to the long range temporal structure in the visual world. For instance, Meyer and Olson [56] demonstrated that neurons in IT could be strongly modulated by prior experience with sequences of presented images. After repeated presentations of arbitrary images with predictable transition statistics (e.g. “image B always follows image A”), neurons appeared to learn the sequence statistics, responding robustly only to sequence transitions that were unexpected. Fig. 4a shows the mean response of 81 IT neurons for predicted and unpredicted pairs. Fig. 4b demonstrates a similar effect in the PredNet after an analogous experiment. Initialized with the weights after training on the KITTI car-mounted camera dataset, the model was then trained on five image pairs for 800 repetitions, matching the number of trials in the Meyers & Olson experiment. The lower proportion of Fig. 4 contains an example sequence and the corresponding next-frame predictions before and after training on the image pairs. The model, prior to exposure to the images in this experiment (trained only on KITTI, [13]), settles into a noisy, copy-last-frame prediction mode. After exposure, the model is able to successfully make predictions for the expected image pair (row 2). Since the chosen image pair is unknown a priori, the initial prediction is the constant gray background when the first image appears. The model then rapidly copies this image for the ensuing three frames. Next, the model successfully predicts the transition to the second object (a stack of tomatoes in this case). In row 3, a sequence that differs from the training pair is presented. The model still makes the prediction of a transition to tomatoes, even though a chair is presented, but then copies the chair into subsequent predictions. Fig. 4b shows that the unexpected transitions result in a significantly larger average response in the final E layer of the network (E3; p = 0.002, paired t-test, one-sided, t(4) = 6.0). The PredNet E3 units and the IT neurons in Meyer and Olson [56] both, in fact, exhibit over a 2X increase in response to unpredicted vs. predicted stimuli (158% increase for IT, 108% increase for E3). In the PredNet, there is indeed a larger response to the unpredicted images in all layers and all unit types (E, A, R; Extended Data Figure 3).
Figure 4:
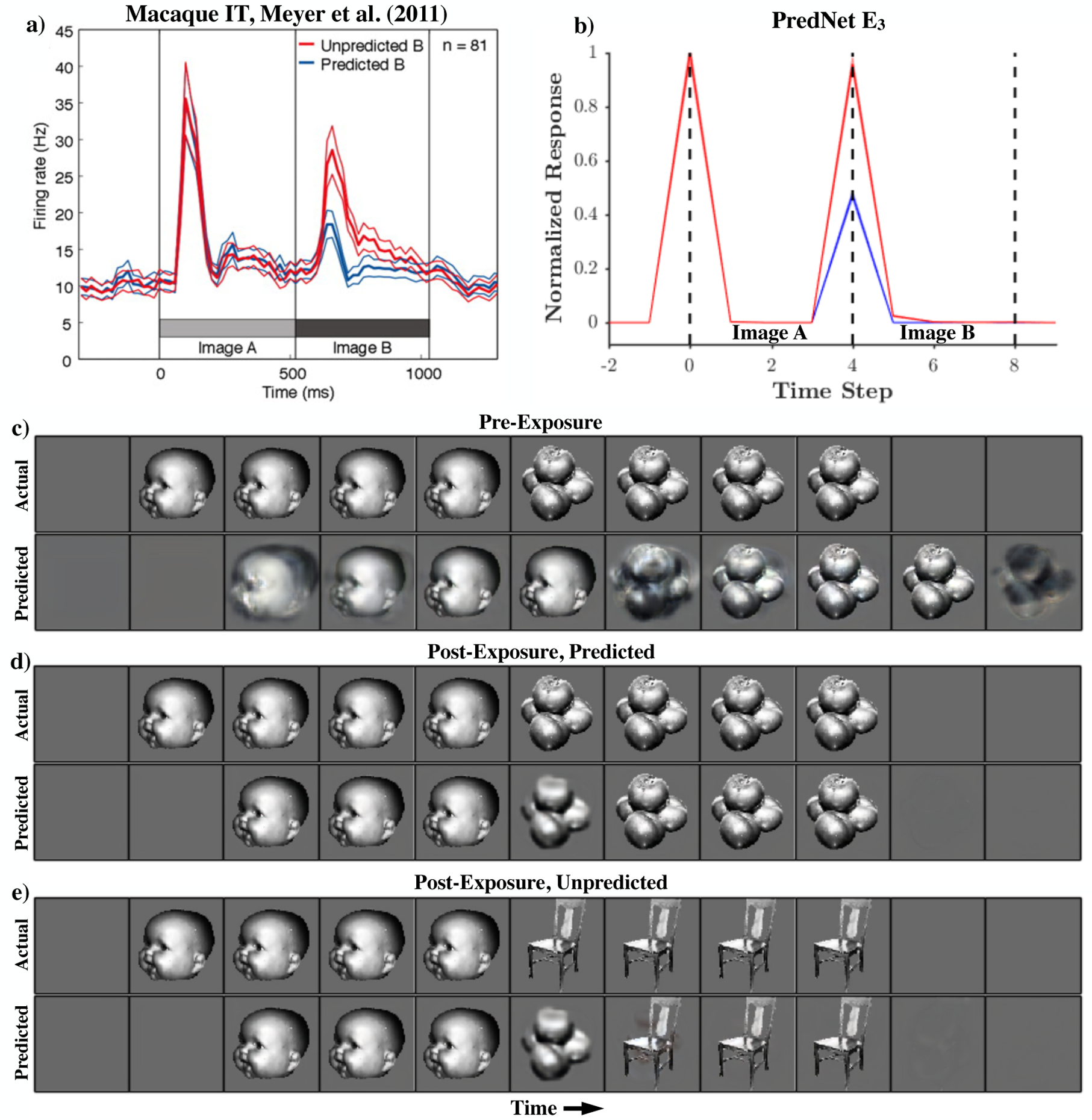
Image sequence learning effects. Top: Population responses to predicted vs. unpredicted image transitions. a) Mean of 81 neurons recorded in macaque IT [reproduced from Meyer and Olson [56]]. b) Mean (± s.e.m.) across all PredNet E3 units (all spatial receptive fields and filter channels). Bottom: Next-frame predictions by the PredNet. c) Predictions of a KITTI-trained PredNet model on an example sequence. d) PredNet predictions after repeated “training” on the sequence. e) PredNet predictions for an unpredicted image transition.
PredNet can capture spatial and temporal illusory aspects of visual perception
Visual illusions can provide powerful insight into the underpinnings of perception. Building upon the spatial and temporal single-unit response properties reproduced by the PredNet, we ask if the model can also capture complex aspects of visual perception when probed with spatial and temporal visual illusions. We examine the PredNet’s responses to illusory contours, a primarily spatially-predictive phenomenon, and the flash-lag illusion, which has aspects of both spatial and temporal prediction. We note also that the PredNet has recently been shown to predict the illusory motion perceived in the rotating snakes illusion [57]. In the following experiments, the network again has only been trained on the KITTI dataset and is evaluated in inference mode (i.e., there is no additional training for the specific stimuli used in this section).
Illusory contours.
Illusory contours, as in the Kanizsa figures [58], elicit perceptions of edges and shapes, despite the lack of enclosing lines. An example of such a figure is displayed at the bottom of Fig. 5. Importantly, the percept of the illusion is highly dependent on the spatial configuration of the components of the figure, as rotating these components lessens the effect (e.g., the “Rotated J” figure in the bottom of Fig. 5). Neural correlates of these illusions have been discovered in the responses of visual neurons. Lee and Nguyen [59] found that neurons in monkey V1 are responsive to illusory contours, albeit at a reduced response and increased latency compared to physical contours. Fig. 5a contains an example of such a neuron. The stimuli in the experiment consisted of sequences starting with an image of four circles, which then abruptly transitioned to one of numerous test images, including the illusion. Illustrated in Fig. 5b, the population average of 49 superficial V1 neurons responded more strongly to the illusion than similar, but non-illusory stimuli. This preference was also apparent in V2, with a response that was, interestingly, of a shorter latency compared to V1 (Fig. 5c).
Figure 5:
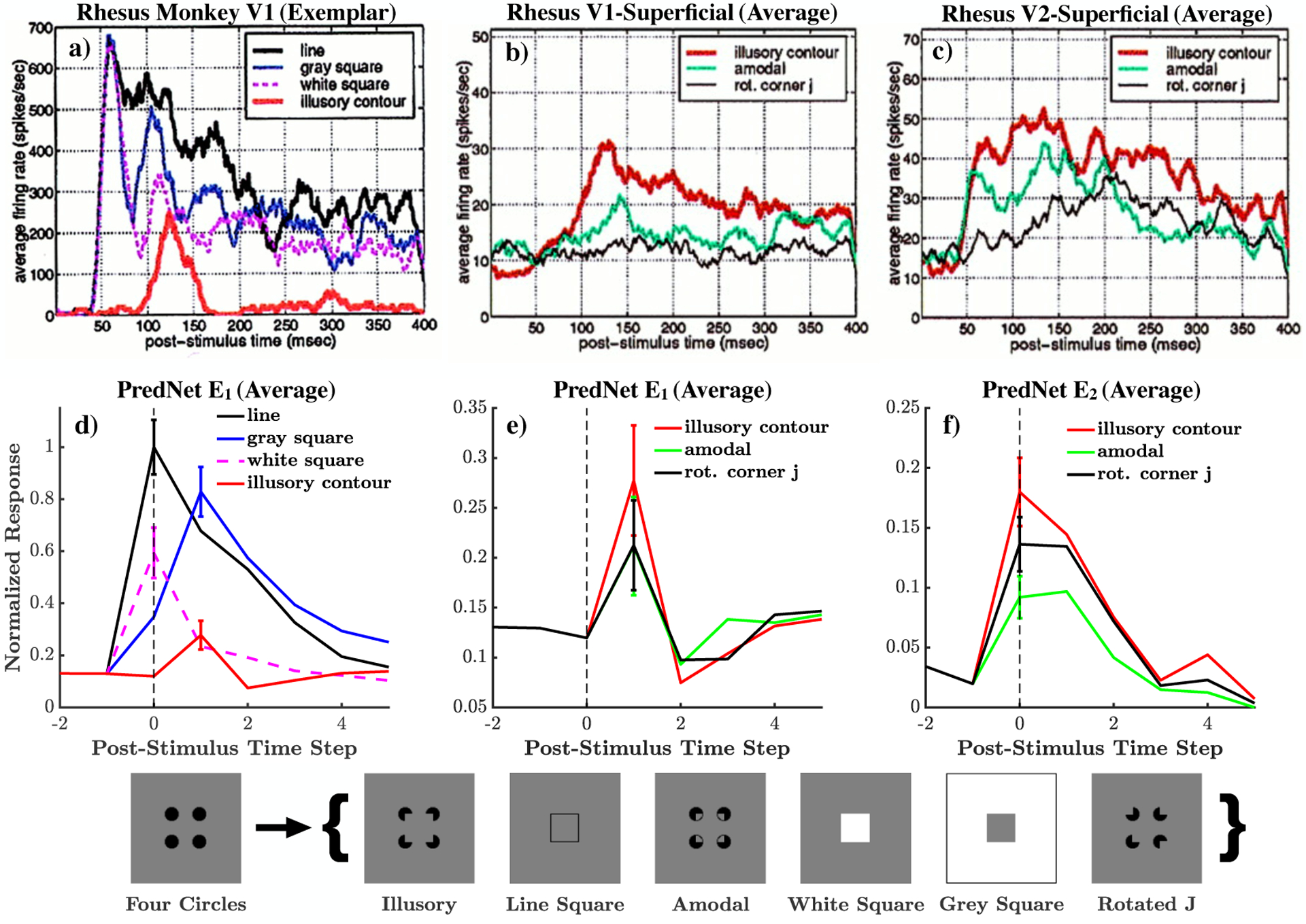
Illusory contours. Top: Data from electrophysiological recordings in the rhesus monkey [reproduced from Lee and Nguyen [59], Copyright (2001) National Academy of Sciences, U.S.A.]. Below: PredNet responses. a) An exemplar V1 neuron which exhibits a response to the illusory contour, at an increased latency compared to stimuli with true contours. b) V1 population average demonstrates a larger response to the illusory stimuli, compared to similar, control stimuli. c) V2 population average response is also larger for the illusory stimuli, and demonstrates an earlier latency than the V1 average. d) The PredNet E1 average activity also demonstrates a response to the illusory contour, at an increased onset latency compared to true contours. e) The E1 average response is moderately larger for the illusory contour than the control stimuli. f) The PredNet E2 response is also moderately larger for the illusory stimuli, with an earlier latency than E1. PredNet averages were computed across filter channels at the central receptive field. Error bars represent s.e.m. Bottom: Illustration of the stimuli and the presentation paradigm, using the nomenclature proposed by Lee and Nguyen [59]. For each trial in the monkey and PredNet experiments, the “four circles” stimuli is first presented, followed by one of the test stimuli (in brackets). See Extended Data Fig. 4 for the responses of the A and R units.
Fig. 5d–f demonstrate that the core effects discovered by Lee and Nguyen [59] are also largely present in the PredNet. In the population average of E1 units, there is indeed a response to the illusory contour, with an onset at an increased latency compared to the physical contours (Fig. 5d). Additionally, Fig. 5e illustrates that the average E1 response was moderately higher for the illusory contour than the response to the similar control images. This was also the case for E2 units, with a peak response one time step before E1 (Fig. 5f). Indeed, the size of the stimuli was chosen such that it was larger than the feedforward receptive field of the layer 1 neurons, but smaller than that of the layer 2 neurons (matching the protocol of [59]). Using metrics proposed by Lee and Nguyen [59] to quantify the preference of the illusion to the amodal and rotated images for each individual unit, we find that the average is positive (higher response to the illusion) for both comparisons and all tested layers in the PredNet (E1, E2, A1, A2, R1, R2), though not all statistically significant (see Extended Data Fig. 5).
The flash-lag effect.
Another illusion for which prediction has been proposed as having a role is the flash-lag effect. Fundamentally, the flash-lag effect describes illusions where an unpredictable or intermittent stimulus (e.g. a line or dot) is perceived as “lagging” behind the percept of a predictably moving stimulus nearby, even when the stimuli are, in fact, precisely aligned in space and time [60, 61, 62]. These illusions are sometimes interpreted as evidence that the brain is performing inference to predict the likely true current position of a stimulus, even in spite of substantial latency (up to hundreds of milliseconds) in the visual system [63, 64]. The version of the illusion tested here consists of an inner, continuously rotating bar and an outer bar that periodically flashes on. Fig. 6 contains example next-frame predictions by the PredNet on a sample sequence within the flash-lag stimulus. The model was again only trained on the KITTI car-mounted camera dataset, and then evaluated on the flash-lag stimulus in inference mode. The rotation speed of the inner bar in the clip was set to 6 degrees per time step. The first feature of note is that the PredNet is indeed able to make reasonable next-frame predictions for the inner rotating bar. If the model simply copied the last seen frame at every timestep instead of making an actual prediction, the angle between the inner rotating bar in the outputted “predicted” frame would be 6° behind the bar in the actual next frame. Instead, the inner bar in the PredNet predictions is on average only 1.4±1.2°(s.d.) behind the actual bar (see Methods for quantification of bar angle). As the model was trained on real-world videos, generalization to this impoverished stimulus is non-trivial. Second, the post-flash predictions made by the model tend to resemble the perceived illusion. In the PredNet next-frame predictions, the outer and inner bars are not co-linear, similar to the illusory percept (see additional post-flash predictions in Extended Data Fig. 6). As opposed to being aligned with a 0° difference in the actual image when the outer bar appears, the inner bar in the PredNet predictions lags the predicted outer bar by an average of 6.8±2.0°(s.d.). For rotation speeds up to and including 25 rotations per minute, we find that the average angular difference between the predicted bars in the PredNet aligns well with perceptual estimates (Extended Data Figure 8). Considering that the model was trained for next-frame prediction on a corpus of natural videos, this suggests that our percept matches the statistically predicted next frame (as estimated by the PredNet) more than the actual observed frame. These results thus support an empirical, natural statistics interpretation of the flash-lag illusion [65].
Figure 6:

The flash-lag effect. Top: A segment of the stimulus clip inputted to the PredNet. Bottom: PredNet predictions after training on the KITTI car-mounted camera dataset [13]. Each column represents the actual next frame in the sequence (above) and the outputted next frame prediction from the model (Â0; below). At the time step indicated as t0, the outer bar flashes on in the actual sequence and is co-linear with the inner bar. The PredNet’s post-flash prediction (corresponding to t+1) displays the two bars as not co-linear, similar to the perceptual illusion. Additional post-flash predictions are contained in Extended Data Fig. 6.
DISCUSSION
We have shown that a recurrent neural network trained to predict future video frames can explain a wide variety of seemingly unrelated phenomena observed in visual cortex and visual perception. These phenomena range from core properties of the responses of individual neurons, to complex visual illusions. Critically, while prior models have been previously used to explain subsets of the described phenomena, we illustrate that a single core PredNet model trained on natural videos can reproduce all the phenomena without being explicitly designed to do so (see Extended Data Figure 7). Our work adds to a growing body of literature showing that deep neural networks exclusively trained to perform relevant tasks can serve as surprisingly good models of biological neural networks, often even outperforming models exclusively designed to explain neuroscience phenomena.
A particular conceptual advantage of the PredNet training scheme, compared to typical supervised neural network training, is that it does not involve large amounts of supervision in the form of paired inputs and labels, which are neither required for biological learning nor are typically found in real life. Prediction is a learning signal is that comes for “free;” that is, it is a form of unsupervised or self-supervised learning. A prediction can be compared to the actual observed state of the world, and the errors in that prediction can drive learning directly. In addition, there is also intrinsic behavioral value in the ability to predict—both in time and in space. Temporal prediction enables more effective planning of actions and can also help mitigate lags found in the relatively slow processing pipeline of visual cortex, while spatial prediction, for instance, can help fill in information lost due to occlusion.
Analysis of model components in producing observed effects.
While the PredNet reproduces a diverse range of phenomena observed in the brain, we would not claim that the PredNet is a perfect or exact model of the brain, or that its precise architecture per se is required for the observed effects. Thus, it is useful to ask which features and components of the model are necessary to reproduce the biological phenomena described above. For instance, one key feature of the PredNet is recurrent connectivity, both within layers (intrinsic recurrent connections), and between layers (feedback connections). It is straightforward to see that some form of recurrence is required in order to observe temporal dynamics (such as “on” and “off” responses), since a strictly feedforward version of the PredNet would lack temporal dynamics altogether. Likewise, recurrent connections are essential for the PredNet to demonstrate phenomena such as length suppression and end-stopping in early layers. While it is possible that a strictly feedforward, nonlinear network could show end-stopping and surround suppression-like effects in higher layers, where receptive fields are large enough to include both the “center” and “surround,” such suppression is not possible in lower layers of the network without recurrence.
Related to recurrence, it is also clear that depth, with an associated increase in feedforward receptive field size over layers is necessary to produce the observed phenomena. For instance, the larger “classical” receptive field of the E2 layer vs. the E1 layer in the PredNet, combined with feedback, facilitates the effects observed in the illusory contour experiment, where both layers produce a response to the illusory figure, but the E2 response is earlier.
While recurrence, depth, and non-linearity can be seen to be essential from a “first principles” analysis of the PredNet, the necessity of other specific features of the PredNet is less obvious. One notable feature of the PredNet, motivated by predictive coding principles [9], is that it explicitly computes an error representation in a population of neurons, wherein predicted inputs are explicitly subtracted from actual inputs, and the activity of these “error” units is what is passed from layer to layer in a feedforward manner. One key feature that this kind of explicit representation and propagation of errors induces is a force that drives the activity of subpopulations of neurons towards zero. That is, with errors represented by the activity of explicit error-coding units, and a training objective based on reducing these errors, there is an explicit mechanism to encourage unit activity to go to zero. From a machine learning perspective, it is straightforward to design a version of the PredNet that is still trained to predict future inputs, but for which “errors” are not passed (Extended Data Fig. 9). Biologically, this could still correspond to a loss/errors being instantiated by neurons, but where these neurons do not serve as a core drive for activity in the rest of the network. Upon training a version of the PredNet with removal of the error passing in the network, we find that it generally less faithfully reproduces the neural phenomena presented here (Extended Data Fig. 10). For example, it might be expected that the decay in unit activity after an “on” response would be less dramatic in this control network than in the original PredNet and neural data, and indeed that is the case. Additionally, the control network actually exhibits enhanced length suppression upon the removal of top-down feedback and a decrease in response upon presentation of the illusory contours stimulus. However, some qualitative effects, such as a larger response to unexpected vs. expected stimuli in the sequence learning experiment are still present in this control network, suggesting that explicit error activity passing may or may not be essential to explain these phenomena. We note that as the explicit error passing in the PredNet seems to improve overall biological faithfulness here, it was also demonstrated to improve next-frame prediction performance in the original work [8]. Specifically, compared to a network with a similar architecture to the PredNet except for lacking layer-wise error computations, the PredNet performed better in next-frame prediction for both synthetic and natural stimuli. The biologically-inspired splitting of positive and negative errors at each layer was additionally illustrated to improve prediction performance.
Because the reduction of network activity induced by error propagation has some correlation with the observed effects in the PredNet, one might wonder whether other means of minimizing activity are sufficient to produce the effects, without necessarily requiring temporal prediction. For instance, sparse coding-style networks also tend to minimize overall activity, and sparse coding has been invoked as a possible explanation for phenomena such as end-stopping [66]. Sparse coding models are typically trained with a reconstruction loss, that is, a loss function based on representing the current stimulus, and critically, they impose an L1 penalty on activations. For static stimuli, it might be expected that reconstructive and predictive models will behave similarly. However, the predictive “what will appear next” nature of the sequence learning and flash-lag effect experiments described above lack an obvious explanation in the context of a purely static reconstructive loss. Nonetheless, it is certainly conceivable that various timeframes of sensory input estimation, from past to present (reconstruction) and future, are utilized as a learning signal and encoding strategy in the brain [67, 68].
Comparison of model components to biology.
Many of the core features of the PredNet architecture—recurrent connectivity, depth with increasing receptive field size, and activity minimization through explicit computation of errors— are central to reproducing the presented phenomena, but also correspond well with the known constraints of biological circuits. However, we note that the PredNet also contains elements that are not biologically plausible, or for which the mapping to biological implementation is not yet clear. Chief among these deviations from biology is the fact that the model uses scalar valued (“rate”) activations, rather than spiking, and that the model uses backpropagation for training. The extent to which these deviations matter is unclear. Some efforts have been made to show that rate-based models can be converted to spiking models [69], though there are numerous compelling computational proposals for ways that spike-based computation may be qualitatively different from rate-based computation [70, 71]. The backpropagation algorithm used to train the PredNet requires updating neuronal connections with non-local information, and thus, it is often cited as a key biologically-implausible element of artificial neural networks. However, recent work has suggested several avenues by which backpropagation-like computations might be implemented with biological neurons [72, 73].
To the extent that the PredNet might mimic the architecture of cortex, it is interesting to consider how the elements of the model might map onto the elements of real cortical microcircuits. Indeed, it has been suggested that there is a tight correspondence between the canonical microcircuit and the connectivity pattern implied by predictive coding [40]. The structure of a layer in the PredNet could also be seen as consistent with this mapping. In this view, the Al units in the PredNet would correspond to granular (L4) layer neurons in cortex, which largely serve as targets for feedforward inputs. The El units would correspond to superficial (L1/2/3) layers, which receive input from the Al/L4 neurons. The El (superficial) neurons then serve as outputs of the circuit, passing information to subsequent, higher areas. These neurons also output to deep (L5/6) layers within the same microcircuit, which would correspond to the Rl units in the PredNet. Finally, completing the circuit, the deep (Rl) units input onto the granular (Al/Âl) layer. Interestingly, we find that there is some variation in the response characteristics amongst the unit types in the PredNet; specifically, the average R response does not exhibit length suppression (Extended Data Fig. 1) and also shows a smaller “surprise” response compared to the A and E units (Extended Data Fig. 3). This raises an intriguing and testable question of whether such differences also exist between deep and superficial units in the brain. Lastly, we note that in the PredNet at least, it is partly notation whether it is said that the “activations” (Al) or the “errors” (El) are passed between layers, and the effects observed here in the E units are also present in the A units (Extended Data Figures 1, 2, 4, 3, 5). Overall, we do not intend to claim that there are precise classifications of “error” vs. “activation/feature” neurons per se, rather that both of these types of computation are important and could map to the canonical microcircuit, with potentially even individual neurons providing a combination of both computations.
Conclusion.
Neuroscience has been a longstanding inspiration for machine learning, where a core goal is to develop models with brain-like abilities. Conversely, developing computational models that reproduce and explain neural phenomena is a central aim in neuroscience. Here, we present an example of this cyclical dialogue, showing that a deep learning model inspired by theories of brain computation can reproduce a wide array of phenomena observed in visual cortex and visual perception. Importantly, the model was trained purely with a self-supervised, predictive loss. An especially salient motivation for pursuing such unsupervised/self-supervised methods is the ability of humans to excel in these regimes. Despite tremendous progress, AI systems today still lag well behind humans in critical properties including extrapolation across domains, few shot learning, and transfer learning. Thus, the ability of a self-supervised model to generalize from training on car-mounted camera videos to testing on impoverished, synthetic stimuli provides further inspiration for incorporating cognitive and neural constraints in designing AI models. In particular, that a simple objective-prediction-can produce such a wide variety of observed neural phenomena as demonstrated here underscores the idea that prediction may be a central organizing principle in the brain.
METHODS
PredNet background.
The original description of the PredNet can be found in Lotter et al. (2017) [8]. Briefly, the PredNet consists of a hierarchical stack of modules, where each module contains four different unit types: representational units (Rl) from which predictions are generated (Âl), targets to be predicted (Al), and error units (El); where l indicates the layer in the network. At each time step, the Rl units are first updated via a top-down pass, receiving input from both the error units at the same level (El) and the representational units from the layer above (Rl+1), which are first spatially upsampled (nearest-neighbor) to match the spatial size of layer l. The Rl units are implemented as convolutional long short-term memory (LSTM) units [50, 51]. After updating the Rl units, a bottom-up pass is made where first the predicted next frame is generated (Â0) via a convolution of the R0 units. The actual input frame, A0, is compared to Â0 via unit-wise subtraction, followed by the splitting into positive and negative error populations, forming E0. The splitting of the error populations is motivated by the existence of on-center/off-surround and off-center/on-surround neurons in the early visual system. E0 becomes the input into the next layer of the network, from which A1 is generated via a convolution over E0, followed by a 2×2 max-pooling operation. A prediction at this layer is generated via a convolution over R1, and then this process is repeated forward in the network until errors are calculated at each level. A summary of the computations performed by each unit is contained in equations Equations (1) to (4) below.
Given an input sequence of images, xt, the units at each layer l and time step t are updated according to:
| (1) |
| (2) |
| (3) |
| (4) |
The only modification to the original PredNet that we make here, for the sake of biological interpretability, is replacing the tanh output activation function for the LSTMs with a relu activation (relu(x) = max(x,0)), enforcing positive “firing rates”. On the KITTI dataset this leads to a marginally (8%) worse prediction mean-squared error (MSE) than the standard formulation, but it is still 2.6 times better than the MSE that would be obtained by simply copying the last frame seen (compared to 2.8 for tanh).
The loss function of the PredNet is implemented as the weighted sum of the error unit activations at each layer and time step. The model is thus “generative” in the sense that it generates predictions of future input data given previous input data, but not in the sense of an explicit probabilistic formulation, though future work could explore incorporating generative adversarial [74] or variational [75] components. We use the “Lall” version of the model here, placing a non-zero loss weight on each layer in the network. For model training, weights are updated via backpropagation [76] (through time) using the Adam optimizer [77]. The dataset used for training is the KITTI dataset [13], a collection of videos obtained from a car-mounted camera while driving in Germany. The same training and pre-processing procedures were used as in the original PredNet paper, including training using sequences of 10 frames, with each frame center-cropped and downsampled to 128×160 pixels. The number of filter channels (e.g. convolutional kernels) per layer for both the A and R modules are 3, 48, 96, and 198, from layers 0 to 3, respectively. Given a 128×160 image, this means that there are units in the A1 and R1 layers, for instance, given the 2×2 max-pooling between each layer. There are thus 122880 and 61440 units in the A2/R2 and A3/R3 layers, respectively. For each layer of the hierarchy, there are twice as many E units, given the splitting into positive and negative errors. Code for the PredNet, including training on the KITTI dataset, is contained at https://github.com/coxlab/prednet.
End-stopping and length suppression.
For each convolutional kernel in the PredNet, length suppression was evaluated at the central receptive field, with input images of size 128×128 pixels. We follow Nassi et al. [53] by first determining each unit’s preferred orientation, implemented by measuring responses to Gabor filters at different orientations. Filters with a wavelength and envelope standard deviation of 5 pixels were used and responses were summed over the presentation of 10 time steps, after the presentation of a gray background for 5 time steps. Given the preferred orientation for each unit, bars of width 1 pixel and varying length were presented at this orientation. For each bar, a gray background was again presented for 5 time steps and then the bar was presented for 10 time steps, with the total response quantified as the sum of the response over the 10 time steps. A population average over all units was quantified by following the procedure above and then normalizing each unit to have a maximum response of 1, followed by averaging. Removal of feedback was implemented by setting the connection weights from R2 to R1 to zero. Statistical analysis comparing the original network to the removal of feedback was performed using units that had a non-constant response in both conditions, which amounted to 28 out of 96 units in E1, 21 out of 48 units in A1, and 30 out of 48 units in R1 (see Extended Data Fig. 1 for A1 and R1 results).
On/off temporal dynamics.
The stimuli for the temporal dynamics experiment consisted of objects appearing on a gray background with images of size 128×128 pixels. A set of 25 objects were used, with examples displayed in Fig. 4. The input sequences consisted of a gray background for 7 time steps, followed by an object on the background for 6 time steps. For comparing response decay rates in the PredNet to the macaque IT data from Hung et al. [55], the population average of single unit activity in the IT data was used.
Sequence learning effects in visual cortex.
Stimuli for the sequence learning experiments in the PredNet consisted of 5 randomly chosen image pairs from a set of 25 images of objects appearing on a gray background of 128×128 pixels. Each image appeared in only one set of pairs. The training portion of the experiment (starting from the KITTI-trained weights) consisted of presenting each pair 800 times, matching the number of trials in the Meyer and Olson experiment [56]. Each trial consisted of a gray background for 4 time steps, followed by the first image for 4 time steps, then the second image for 4 time steps, and finally the gray background again for 4 time steps. For model updates, the Adam [77] optimizer was used with default parameters. For testing, unpredicted pairs were created by randomly permuting the second images across the pairs. The population response in Fig. 4 was quantified by averaging across all units and image pairs (5 predicted and unpredicted pairs), and normalizing this response to have a maximum of 1 across the duration of the trial. The difference between predicted and unpredicted responses was assessed at the peak of the response for the second image.
Illusory contours.
PredNet responses in the illusory contours experiment were evaluated using units at the central receptive field for each convolutional kernel, using input images of size 128×128 pixels. Similar to the neural experiments by Lee and Nguyen [59], the preferred orientation for each unit was first determined using a short bar stimulus, specifically a 1 pixel wide bar with a length of 8 pixels. Responses to the bar at different orientations were quantified as the sum of the response over a presentation of 10 time steps, after the presentation of a gray background for 5 time steps. Responses to the test stimuli were then evaluated when presenting at the optimal orientation for each unit, meaning that, for instance, one edge of the “line square” (see Fig. 5) was centered around the unit’s receptive field and oriented at the unit’s preferred orientation. The test sequences consisted of a gray background for 5 time steps, followed by the “four circles” image for 10 time steps, and finally one of the test images for 10 time steps. For the stimuli involving circles, the radius of the circles was set to 4 pixels with the distance between the centers of adjacent circles (or equivalently, the length of a side in the square stimuli) set to 16 pixels. These sizes were chosen because 4 pixels is twice the size of the feedforward receptive field in the E1 layer. The radius used in the Lee and Nguyen [59] experiments was also approximately twice as large as the mapped receptive fields in V1. In Fig. 5d–f, the population response was calculated as an average over the responses of individual units, where the response of each unit was first normalized by division of the unit’s max response over all stimuli. To be included in the population response as well as the statistical calculations of ICa and ICr (defined in main text), a unit had to have a non-zero response to the bar stimulus (at any orientation) and a non-zero response to at least one of the test sequences. The number of units meeting this criteria was 37 (out of 96) for E1, 32 (out of 192) for E2, 27 (out of 48) for A1, 32 (out of 96) for A2, 31 (out of 48) for R1, and 54 (out of 96) for R2 (see Extended Data Figures 4 and 5 for A and R results).
The flash-lag effect.
The flash-lag stimulus was created with a rotation speed of 6° per time step, with a flash every 6 time steps for 3 full rotations and an input size of 160×160 pixels. Angles of the bars in the predictions were quantified over the last two rotations to allow a “burn-in” period. The angles of the predicted bars were estimated by calculating the mean-squared error between the prediction and a probe bar generated at 0.1° increments and a range of centers, and taking the angle with the minimum mean-squared error.
Data Availability
The primary dataset used in this work is the KITTI Dataset [13], which can be obtained at: http://www.cvlibs.net/datasets/kitti/raw_data.php. All other data may be obtained via request to the authors.
Code Availability
Code for the PredNet model is made available at: https://github.com/coxlab/prednet. All other code may be obtained via request to the authors.
Extended Data
Extended Data Figure 1:
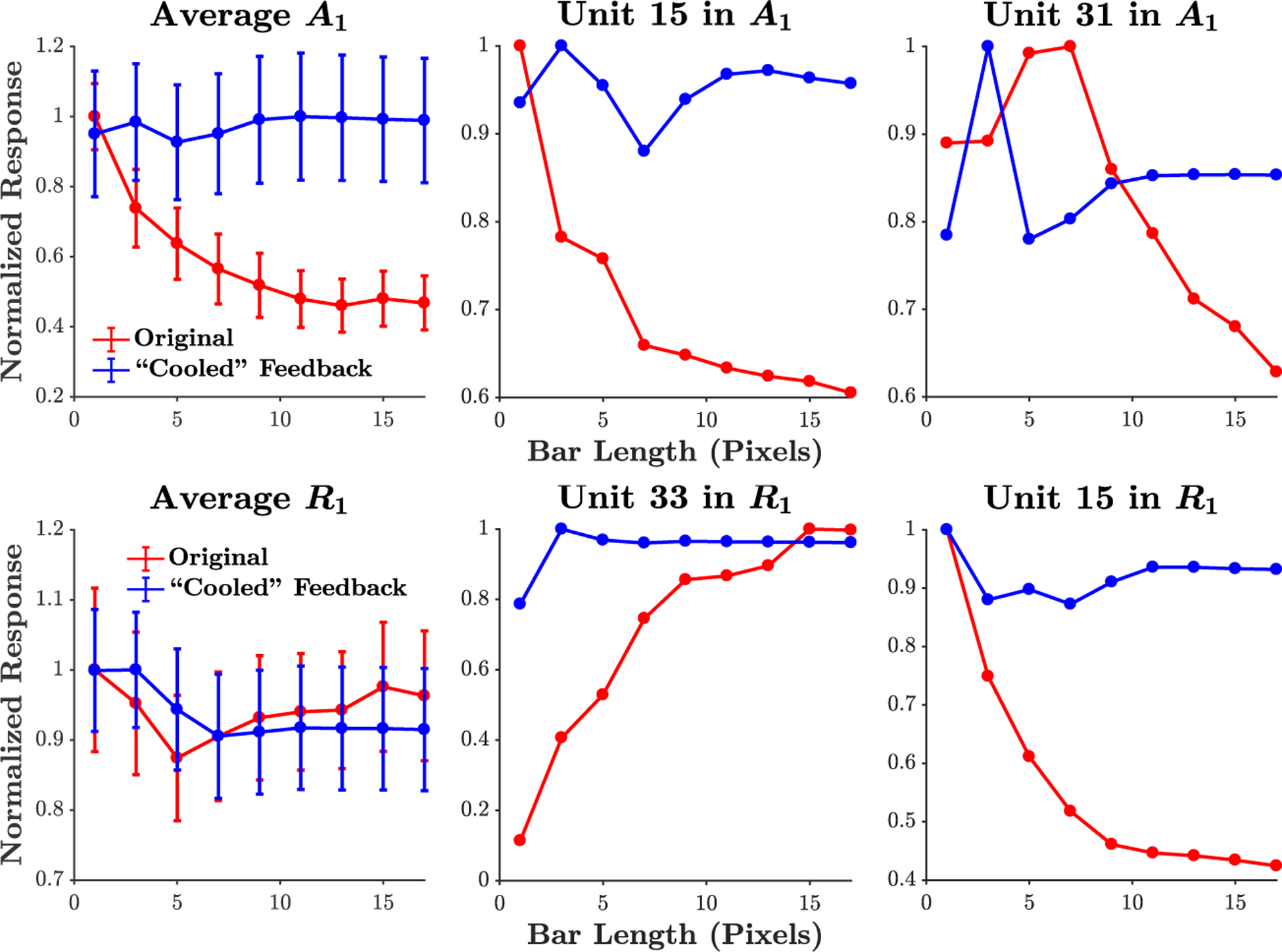
Length suppression analysis for A1 and R1 units. The average (± s.e.m) response of A1 and R1 units and exemplars are shown (expanding upon Fig. 2 in main text). Red: Original network. Blue: Feedback weights from R2 to R1 set to zero. The average A1 response demonstrates length suppression, whereas the average R1 response does not show a strong effect, with some units overall showing length suppression (e.g., unit 15 - bottom right panel) and other units showing an opposite effect (e.g., unit 33 - bottom middle panel). The removal of feedback led to a significant decrease in length suppression in A1, with a mean (± s.e.m) decrease in percent length suppression of 31 ± 7% (p = 0.0004, Wilcoxon signed rank test, one-sided, z = 3.3). The R1 units exhibited a mean %LS decrease of 5 ± 6% upon removal of feedback, which was not statistically significant (p = 0.18, z = 0.93).
Extended Data Figure 2:
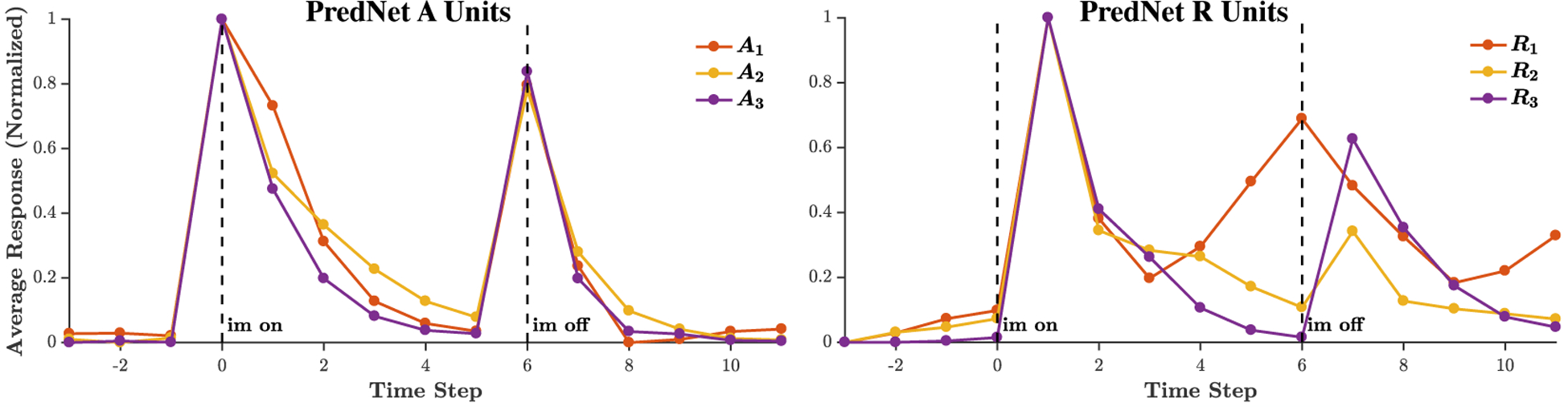
Temporal dynamics in the A and R units in the PredNet. The average response of A and R units to a set of naturalistic objects on a gray background, after training on the KITTI car-mounted camera dataset [13] is shown (expanding upon Fig. 3 in the main text). The A and R layers seem to generally exhibit on/off dynamics, similar to the E layers. R1 also seems to have another mode in its response, specifically a ramp up between time steps 3 and 5 post image onset. The responses are grouped per layer and consist of an average across all the units (all filters and spatial locations) in a layer. The mean responses were then normalized between 0 and 1. Given the large number of units in each layer, the s.e.m. is O(1%) of the mean. Responses for layer 0, the pixel layer, are omitted because of their heavy dependence on the input pixels for the A and R layers. Note that, by notation in the network’s update rules, the input image reaches the R layers at a time step after the E and A layers.
Extended Data Figure 3:
Response differential between predicted and unpredicted sequences in the sequence learning experiment. The percent increase of population peak response between predicted and unpredicted sequences is quantified for each PredNet layer. Positive values indicate a higher response for unpredicted sequences. *p < 0.05, **p < 0.005 (paired t-test, one-sided)
Extended Data Figure 4:
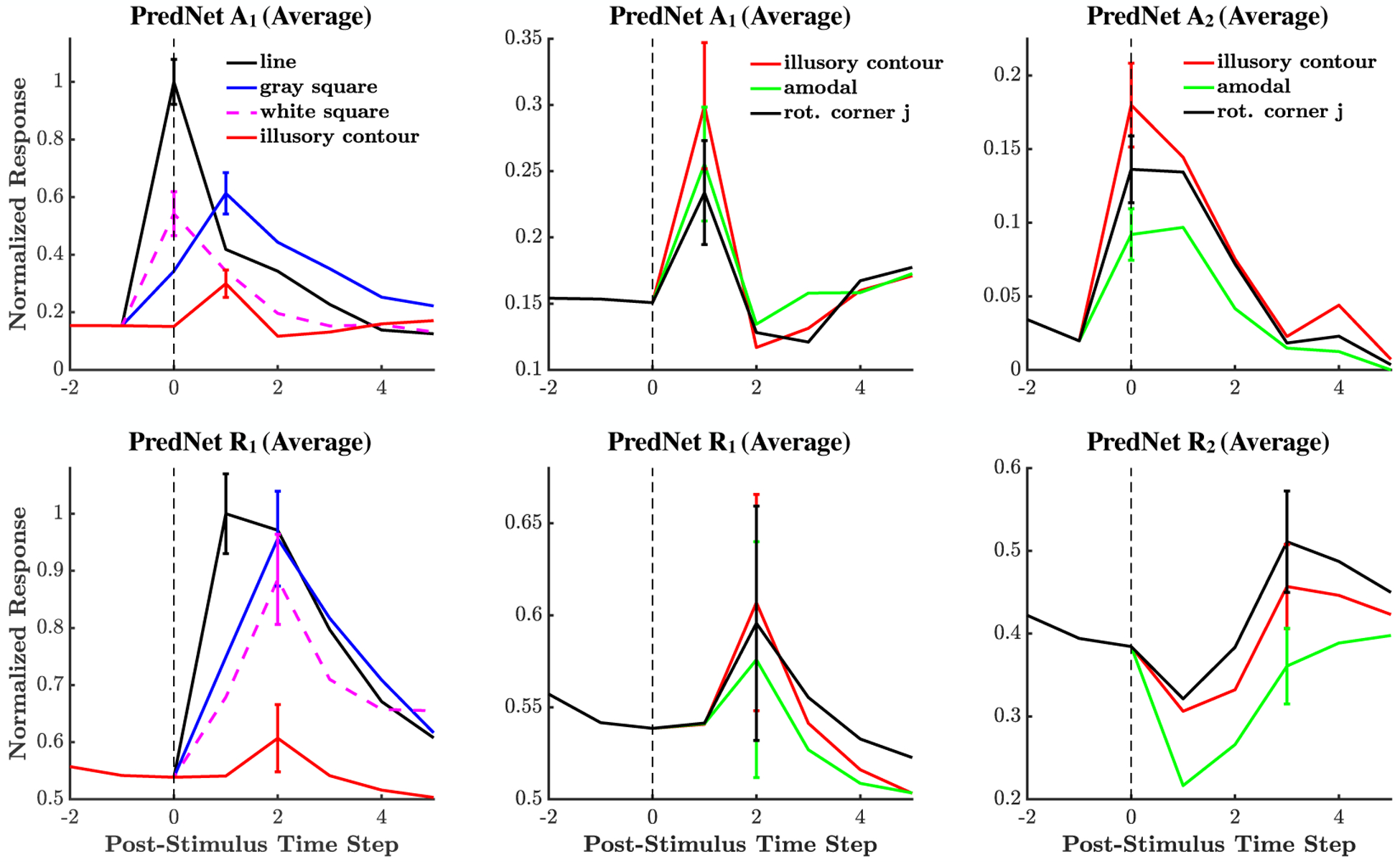
Illusory contours responses for A and R units in the PredNet. The mean ± s.e.m. is shown (expanding upon Fig. 5 in the main text). Averages are computed across filter channels at the central receptive field.
Extended Data Figure 5:
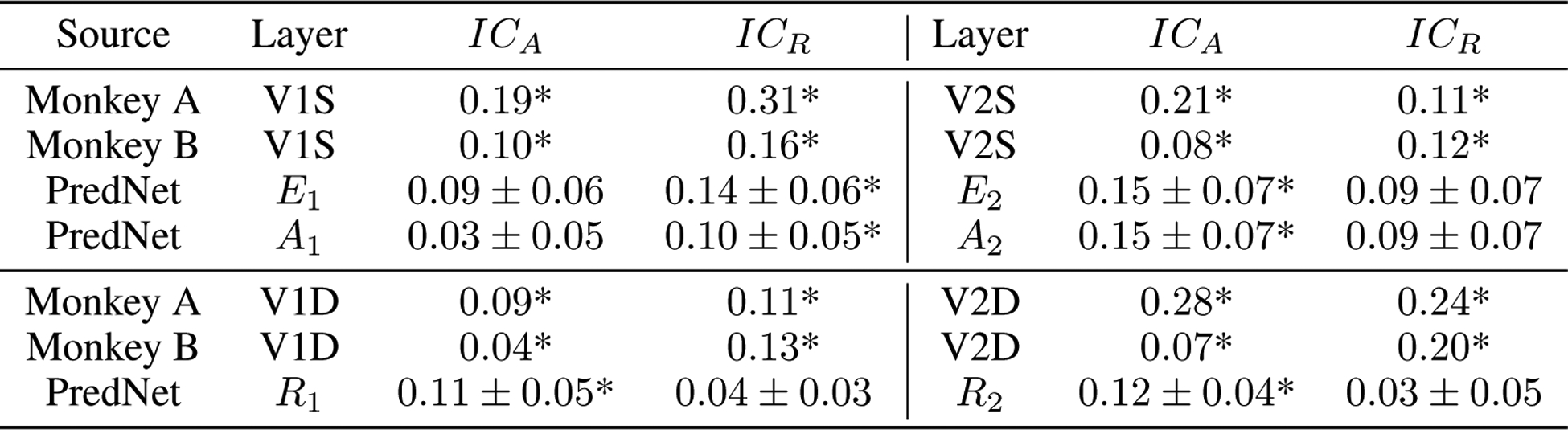
Quantification of illusory responsiveness in the illusory contours experiment. Units in the monkey recordings of Lee and Nguyen [59] are compared to units in the PredNet. We follow Lee and Nguyen [59] in calculating the following two measures for each unit: and , where Ri is the response to the illusory contour (sum over stimulus duration), Ra is the response to amodal stimuli, and Rr is the response to the rotated image. For the PredNet, these indices were calculated separately for each unit (at the central receptive field) with a non-uniform response. Positive values, indicating preferences to the illusion, were observed for all subgroups. Mean ± s.e.m.; *p < 0.05 (t-test, one-sided).
Extended Data Figure 6:

Additional predictions by the PredNet model in the flash lag experiment. The images shown consist of next-frame predictions by the PredNet model after four consecutive appearances of the outer bar. The model was trained on the KITTI car-mounted camera dataset [13].
Extended Data Figure 7:
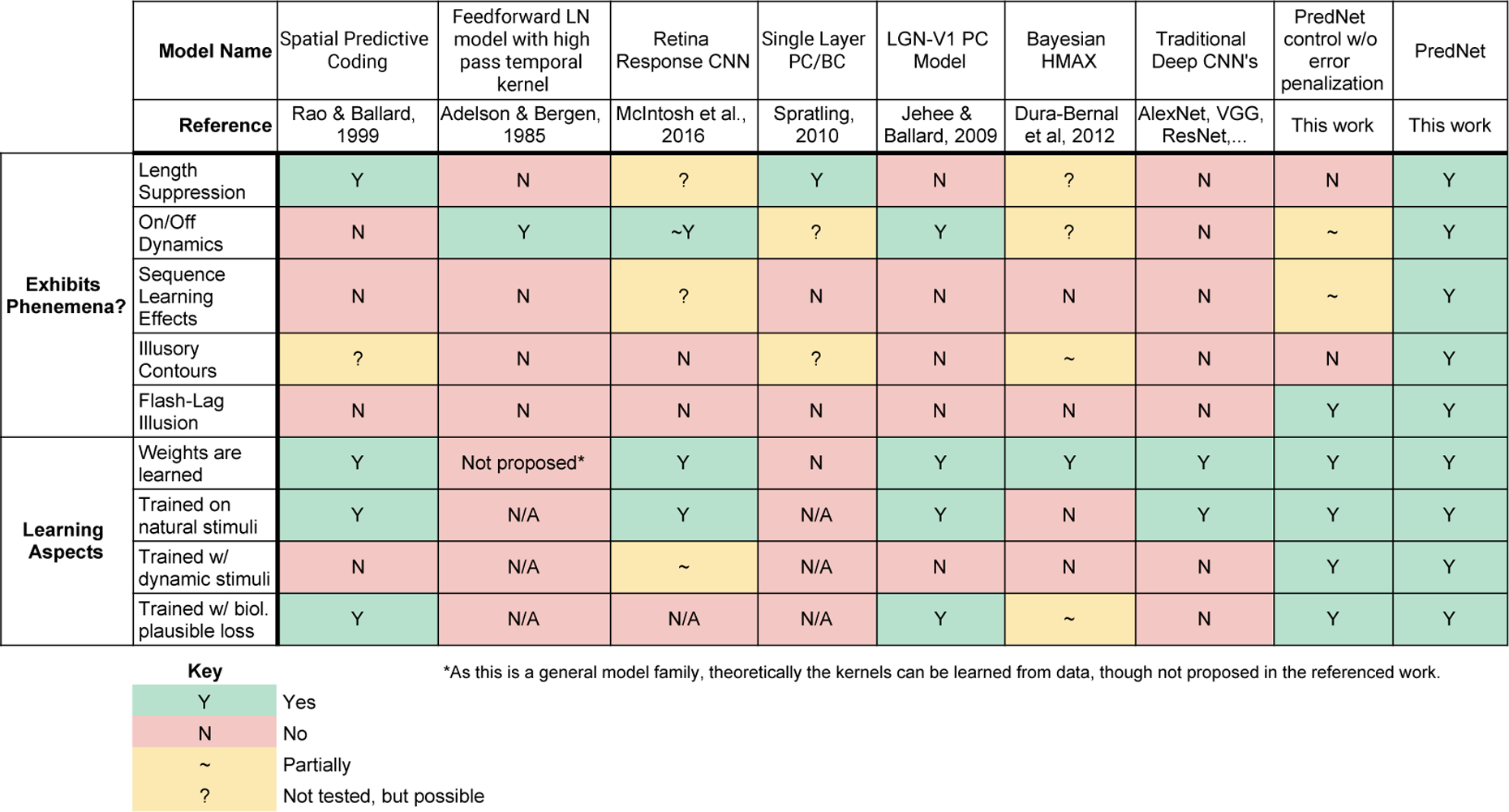
Comparison of the PredNet to prior models. The models under comparison are a (non-exhaustive) list of prior models that have been used to probe the phenomena explored here. The top section indicates if a given model (column) exhibits each phenomenon (row). The bottom section considers various learning aspects of the models. From left to right, the models considered correspond to the works of Rao and Ballard (1999) [9], Adelson and Bergen (1985) [78], McIntosh et al. (2016) [79], Spratling (2010) [45], Jehee and Ballard (2009) [46], and Dura-Bernal et al. (2012) [80]. Additionally, traditional deep CNNs are considered (e.g. AlexNet [81], VGGNet [82], ResNet [83]). The PredNet control (second column from right) refers to the model in Extended Data Figures 9 and 10.
Extended Data Figure 8:

Comparison of PredNet predictions in the flash-lag illusion experiment to psychophysical estimates. The psychophysical estimates come from Nijhawan, 1994 [60]. With the frame rate of 10 Hz used to train the PredNet as a reference, the average angular difference between the inner and outer bars in the PredNet predictions was quantified for various rotation speeds. The results are compared to the perceptual estimates obtained using two human subjects by Nijhawan [60]. Mean and standard deviation is shown. For rotation speeds up to and including 25 rotations per minute (RPM), the PredNet estimates align well with the psychophysical results. At 35 RPM, the PredNet predictions become noisy and inconsistent, as evidenced by the high standard deviation.
Extended Data Figure 9:
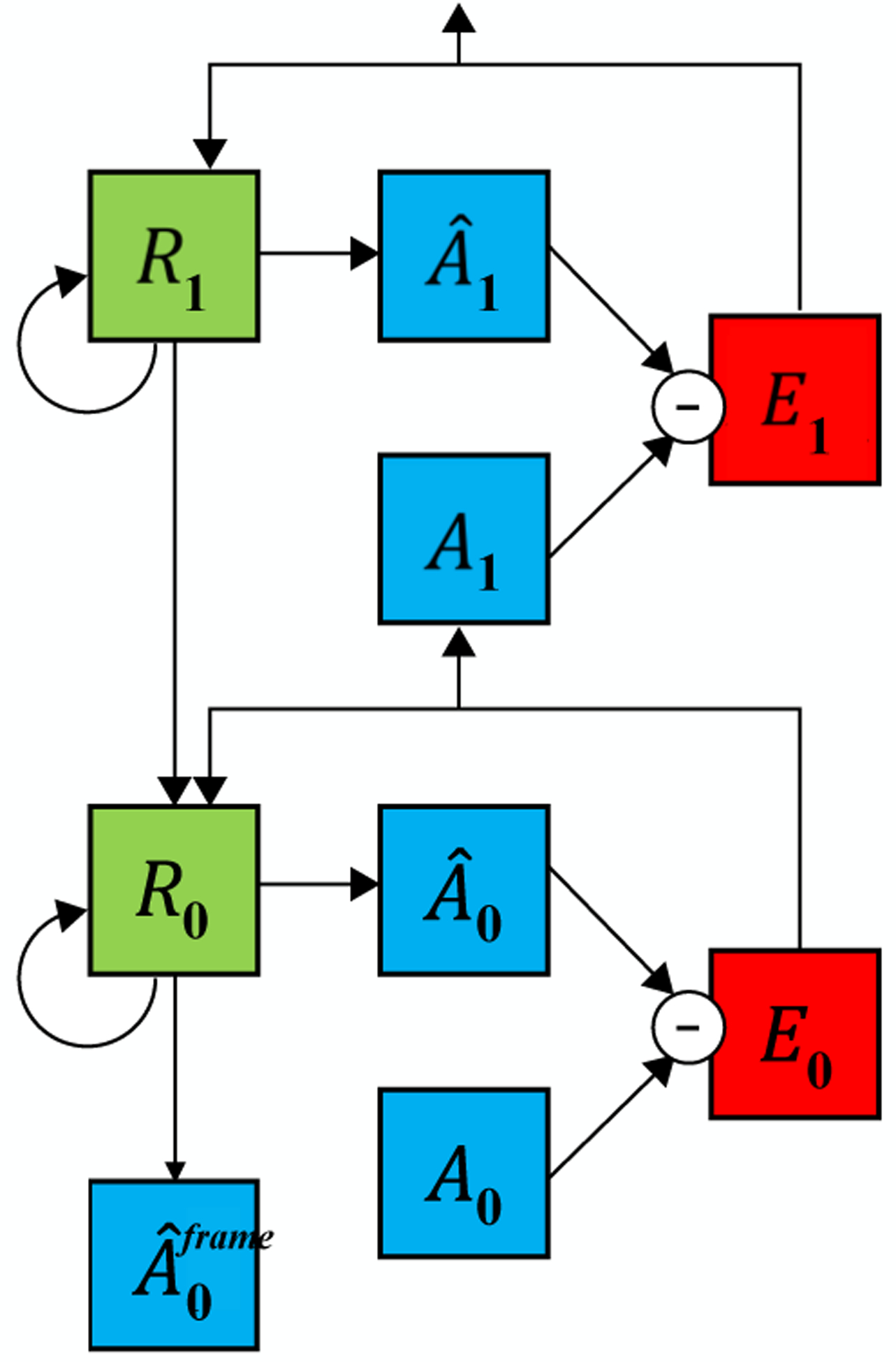
PredNet control model lacking explicit penalization of activity in “error units.” An additional convolutional block is added that generates the next-frame prediction given input from R0. The predicted frame is used in direct L1 loss, with the removal of the activity of the E units from the training loss altogether. Thus, in this control model, the E units are unconstrained and there is no explicit encouragement of activity minimization in the network.
Extended Data Figure 10:
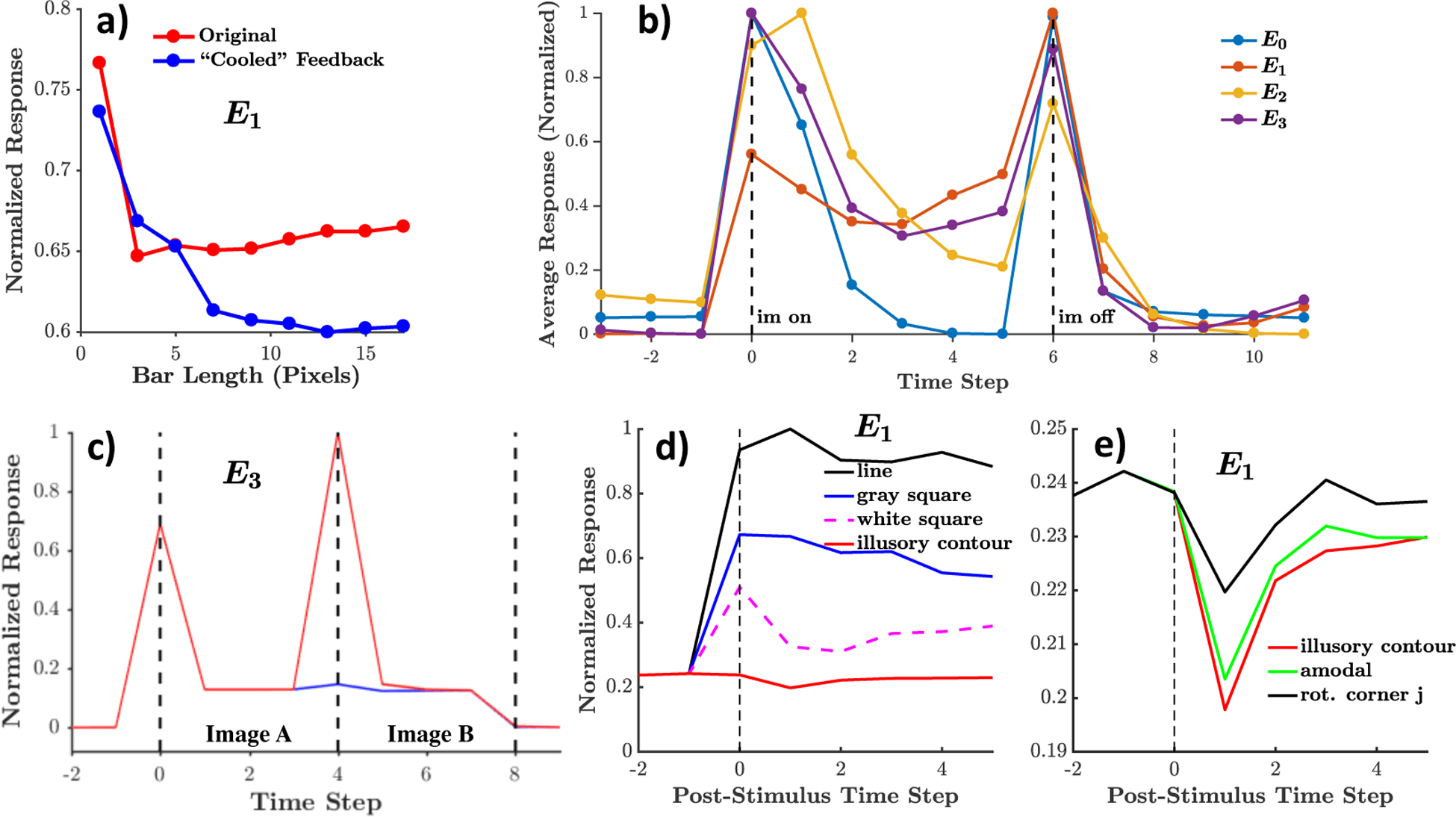
Results of control model with the removal of explicit minimization of “error” activity in the PredNet. Overall, the control model less faithfully reproduces the neural phenomena presented here. a) The control network E1 units exhibit enhanced length suppression when feedback is removed (opposite of the effect in biology and the original PredNet). b) The responses in the control network still peak upon image onset and offset, however the decay in activity after peak is non-monotonic in several layers and less dramatic overall than the results shown in Fig. 3. As opposed to the 20–49% decrease in response after image onset peak in the original PredNet and the 44% decrease in the Hung et al. [55] macaque IT data, the control network exhibited a 5% (E1) to 30% (E2) decrease. c) Response of the control network E3 layer in the sequence pairing experiment. The unpredicted images actually elicit a higher response than the first image in the sequence and the predicted images hardly elicit any response, both effects which are qualitatively different than the macaque IT data from Meyer and Olson [56] and the original PredNet. d,e) The average E1 response in the control network demonstrates a decrease in activity upon presentation of the illusory contour.
Acknowledgements
This work was supported by IARPA (contract D16PC00002), the National Science Foundation (NSF IIS 1409097), and the Center for Brains, Minds and Machines (CBMM, NSF STC award CCF-1231216).
Footnotes
Competing interests
The authors declare no competing interests.
References
- [1].Yamins DLK, Hong H, Cadieu CF, Solomon EA, Seibert D, and DiCarlo JJ Proceedings of the National Academy of Sciences 111(23), 8619–8624 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Yamins DLK and DiCarlo JJ Nature Neuroscience 19, 356–365 (2016). [DOI] [PubMed] [Google Scholar]
- [3].Khaligh-Razavi S-M and Kriegeskorte N PLOS Computational Biology 10, 1–29 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Nayebi A, Bear D, Kubilius J, Kar K, Ganguli S, Sussillo D, DiCarlo JJ, and Yamins DLK In Advances in Neural Information Processing Systems, 5290–5301. (2018). [Google Scholar]
- [5].Deng J, Dong W, Socher R, Li L-J, Li K, and Fei-Fei L In Computer Vision and Pattern Recognition, 248–255, (2009). [Google Scholar]
- [6].Tang H, Schrimpf M, Lotter W, Moerman C, Paredes A, Ortega Caro J, Hardesty W, Cox D, and Kreiman G Proceedings of the National Academy of Sciences 115(35), 8835–8840 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Kar K, Kubilius J, Schmidt K, Issa EB, and DiCarlo JJ Nature Neuroscience 22, 974–983 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Lotter W, Kreiman G, and Cox DD In International Conference on Learning Representations. (2017). [Google Scholar]
- [9].Rao RPN and Ballard DH Nature Neuroscience 2, 79–87 (1999). [DOI] [PubMed] [Google Scholar]
- [10].Friston K Philos Trans R Soc Lond B Biol Sci 360, 815–836 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Spratling MW Neural Computation 24, 60–103 (2012). [DOI] [PubMed] [Google Scholar]
- [12].Wen H, Han K, Shi J, Zhang Y, Culurciello E, and Liu Z In Proceedings of the 35th International Conference on Machine Learning, volume 80, 5266–5275, (2018). [Google Scholar]
- [13].Geiger A, Lenz P, Stiller C, and Urtasun R International Journal of Robotics Research 32, 1231–1237 (2013). [Google Scholar]
- [14].Softky WR In Advances in Neural Information Processing Systems, 809–815. (1996). [Google Scholar]
- [15].Lotter W, Kreiman G, and Cox D In International Conference on Learning Representations. (2016). [Google Scholar]
- [16].Mathieu M, Couprie C, and LeCun Y In International Conference on Learning Representations. (2016). [Google Scholar]
- [17].Srivastava N, Mansimov E, and Salakhutdinov R In Proceedings of the 32nd International Conference on Machine Learning, volume 37, 843–852. (2015). [Google Scholar]
- [18].Dosovitskiy A and Koltun V In International Conference on Learning Representations. (2017). [Google Scholar]
- [19].Finn C, Goodfellow IJ, and Levine S In Advances in Neural Information Processing Systems, 64–72. (2016). [Google Scholar]
- [20].Elman JL Cognitive Science 14, 179–211 (1990). [Google Scholar]
- [21].Hawkins J and Blakeslee S On Intelligence. (2004). [Google Scholar]
- [22].Luo Z, Peng B, Huang D-A, Alahi A, and Fei-Fei L In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 7101–7110, (2017). [Google Scholar]
- [23].Lee AX, Zhang R, Ebert F, Abbeel P, Finn C, and Levine S arXiv abs/1804.01523 (2018). [Google Scholar]
- [24].Villegas R, Pathak A, Kannan H, Erhan D, Le QV, and Lee H Advances in Neural Information Processing Systems, 81–91 (2019). [Google Scholar]
- [25].Villegas R, Yang J, Hong S, Lin X, and Lee H International Conference on Learning Representations (2017). [Google Scholar]
- [26].Denton E and Fergus R Proceedings of the 35th International Conference on Machine Learning, 1174–1183 (2018). [Google Scholar]
- [27].Babaeizadeh M, Finn C, Erhan D, Campbell RH, and Levine S International Conference on Learning Representations (2018). [Google Scholar]
- [28].Wang Y, Gao Z, Long M, Wang J, and Yu PS arXiv abs/1804.06300 (2018). [Google Scholar]
- [29].Finn C and Levine S In International Conference on Robotics and Automation, 2786–2793, (2017). [Google Scholar]
- [30].Hsieh J-T, Liu B, Huang D-A, Fei-Fei LF, and Niebles JC In Advances in Neural Information Processing Systems, 517–526. (2018). [Google Scholar]
- [31].Kalchbrenner N, van den Oord A, Simonyan K, Danihelka I, Vinyals O, Graves A, and Kavukcuoglu K In Proceedings of the 34th International Conference on Machine Learning, volume 70, 1771–1779, (2017). [Google Scholar]
- [32].Qiu J, Huang G, and Lee TS In Advances in Neural Information Processing Systems, 2662–2673. (2019). [Google Scholar]
- [33].Wang Y, Jiang L, Yang M-H, Li L-J, Long M, and Li F-F International Conference on Learning Representations (2019). [Google Scholar]
- [34].Wang Y, Long M, Wang J, Gao Z, and Yu PS In Advances in Neural Information Processing Systems, 879–888. (2017). [Google Scholar]
- [35].Liu W, Luo W, Lian D, and Gao S The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 6536–6545 (2018). [Google Scholar]
- [36].Tandiya N, Jauhar A, Marojevic V, and Reed JH In 2018 IEEE International Conference on Communications Workshops (ICC Workshops), (2018). [Google Scholar]
- [37].Ebert F, Finn C, Dasari S, Xie A, Lee AX, and Levine S arXiv abs/1812.00568 (2018). [Google Scholar]
- [38].Rao RPN and Sejnowski TJ In Advances in Neural Information Processing Systems, 164–170. (2000). [Google Scholar]
- [39].Summerfield C, Egner T, Greene M, Koechlin E, Mangels J, and Hirsch J Science 314, 1311–1314 (2006). [DOI] [PubMed] [Google Scholar]
- [40].Bastos AM, Usrey WM, Adams RA, Mangun GR, Fries P, and Friston KJ Neuron 76, 695–711 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Kanai R, Komura Y, Shipp S, and Friston K Philos Trans R Soc Lond B Biol Sci 370 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Srinivasan MV, Laughlin SB, and Dubs A Proceedings of the Royal Society of London B: Biological Sciences 216, 427–459 (1982). [DOI] [PubMed] [Google Scholar]
- [43].Atick JJ Network: Computation in neural systems 22, 4–44 (1992). [Google Scholar]
- [44].Murray SO, Kersten D, Olshausen BA, Schrater P, and Woods DL Proceedings of the National Academy of Sciences 99, 15164–15169 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Spratling MW Journal of Neuroscience 30, 3531–3543 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Jehee JFM and Ballard DH PLOS Computational Biology 5, 1–10 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Kumar S, Sedley W, Nourski KV, Kawasaki H, Oya H, Patterson RD III, M. A. H., Friston KJ, and Griffiths TD Journal of Cognitive Neuroscience 23, 3084–3094 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Zelano C, Mohanty A, and Gottfried JA Neuron 72, 178–187 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Mumford D Biological Cybernetics 66, 241–251 (1992). [DOI] [PubMed] [Google Scholar]
- [50].Hochreiter S and Schmidhuber J Neural Computation 9, 1735–1780 (1997). [DOI] [PubMed] [Google Scholar]
- [51].Shi X, Chen Z, Wang H, Yeung D, Wong W, and Woo W In Advances in Neural Information Processing Systems, 802–810. (2015). [Google Scholar]
- [52].Hubel DH and Wiesel TN The Journal of Physiology 195, 215–243 (1968). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Nassi JJ, Lomber SG, and Born RT Journal of Neuroscience 33, 8504–8517 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Schmolesky MT, Wang Y, Hanes DP, Thompson KG, Leutgeb S, Schall JD, and Leventhal AG Journal of Neurophysiology 79, 3272–3278 (1998). [DOI] [PubMed] [Google Scholar]
- [55].Hung CP, Kreiman G, Poggio T, and DiCarlo JJ Science 310, 863–866 (2005). [DOI] [PubMed] [Google Scholar]
- [56].Meyer T and Olson CR Proceedings of the National Academy of Sciences 108, 19401–19406 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Watanabe E, Kitaoka A, Sakamoto K, Yasugi M, and Tanaka K Frontiers in Psychology 9, 345 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Kaniza G Organization in Vision: Essays on Gestalt Perception. Praeger, (1979). [Google Scholar]
- [59].Lee TS and Nguyen M Proceedings of the National Academy of Sciences 98, 1907–1911 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Nijhawan R Nature 370, 256–257 (1994). [DOI] [PubMed] [Google Scholar]
- [61].Mackay DM Nature 181, 507–508 (1958). [DOI] [PubMed] [Google Scholar]
- [62].Eagleman DM and Sejnowski TJ Science 287, 2036–2038 (2000). [DOI] [PubMed] [Google Scholar]
- [63].Khoei MA, Masson GS, and Perrinet LU PLOS Computational Biology 13, 1–31 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Hogendoorn H and Burkitt AN eNeuro 6 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Wojtach WT, Sung K, Truong S, and Purves D Proceedings of the National Academy of Sciences 105, 16338–16343 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Zhu M and Rozell CJ PLOS Computational Biology 9, 1–15 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Chalk M, Marre O, and Tkačik G Proceedings of the National Academy of Sciences 115, 186–191 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Singer Y, Teramoto Y, Willmore BD, Schnupp JW, King AJ, and Harper NS eLife 7 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Hunsberger E and Eliasmith C arXiv abs/1611.05141 (2016). [Google Scholar]
- [70].Boerlin M, Machens CK, and Denève S PLOS Computational Biology 9, 1–16 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Maass W In Pulsed Neural Networks. (1999). [Google Scholar]
- [72].Nøkland A In Advances in Neural Information Processing Systems, 1037–1045. (2016). [Google Scholar]
- [73].Lillicrap TP, Cownden D, Tweed DB, and Akerman CJ Nature Communications 7, 13276 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, and Bengio Y In Advances in Neural Information Processing Systems, 2672–2680. (2014). [Google Scholar]
- [75].Kingma DP and Welling M In International Conference on Learning Representations. (2014). [Google Scholar]
- [76].Rumelhart DE, Hinton GE, and Williams RJ Nature 323, 533–536 (1986). [Google Scholar]
- [77].Kingma DP and Ba J In International Conference on Learning Representations. (2015). [Google Scholar]
- [78].Adelson EH and Bergen JR J. Opt. Soc. Am. A 2, 284–299 (1985). [DOI] [PubMed] [Google Scholar]
- [79].McIntosh L, Maheswaranathan N, Nayebi A, Ganguli S, and Baccus S In Advances in Neural Information Processing Systems, 1369–1377. (2016). [PMC free article] [PubMed] [Google Scholar]
- [80].Dura-Bernal S, Wennekers T, and Denham SL PLOS ONE 7, 1–25 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Krizhevsky A, Sutskever I, and Hinton GE In Advances in Neural Information Processing Systems 25, 1097–1105. (2012). [Google Scholar]
- [82].Simonyan K and Zisserman A International Conference on Learning Representations (2015). [Google Scholar]
- [83].He K, Zhang X, Ren S, and Sun J In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 770–778, (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The primary dataset used in this work is the KITTI Dataset [13], which can be obtained at: http://www.cvlibs.net/datasets/kitti/raw_data.php. All other data may be obtained via request to the authors.


