Dynamic Routing Capsule Networks for Mild Cognitive Impairment Diagnosis

Abstract

Alzheimer’s disease (AD) is a chronic neurodegenerative disease that could cause severe cognitive damage to the patients. Diagnosis of AD at its preclinical stage, i.e., mild cognitive impairment (MCI), could help to prevent or slow down AD progression. With machine learning, automatic MCI diagnosis could be achieved. Most of the previous studies mainly share a similar framework, i.e., building a classifier based on the features extracted from static or dynamic functional connectivity. Recently, inspired by the great successes achieved by deep learning in other areas of medical image analysis, researchers have introduced neural network models for MCI diagnosis. In this paper, we propose dynamic routing capsule networks for MCI diagnosis. Our proposed methods are based on a novel neural network fashion of capsule net. Two variants of capsule net are designed and discussed, which respectively uses the intra-ROIs and inter-ROIs dynamic routing to obtain functional representation. More importantly, we design a learnable dynamic functional connectivity metric in our inter-ROIs dynamic model, in which the functional connectivity is dynamically learned during network training. To the best of our knowledge, it’s the first time to propose dynamic routing capsule networks for MCI diagnosis. Compared with other machine learning methods and deep learning model, our method can achieve superior performance from various aspects of evaluations.

1. Introduction

As a chronic neurodegenerative disease, Alzheimer’s disease (AD) usually starts slowly and gradually worsens over time [1]. The preclinical stage of AD is mild cognitive impairment (MCI), and the early intervention in this stage is of great importance to slow the progression of AD and relieve the suffering of the patients. Resting-state functional MRI (RS-fMRI) is a non-invasive functional imaging method widely used in MCI studies. With the development of machine learning and computer-aided diagnosis (CAD) technology, some studies started focusing on designing CAD methods for distinguishing MCI patients from normal control (NC) subjects. Most of these methods share a two-step workflow: (1) extracting adequate feature representation from RS-fMRI; (2) designing a classifier or a series of boosted classifiers to categorize the obtained features into NC and MCI. In the first step, static functional connectivity (SFC) and dynamic functional connectivity (DFC) are calculated to construct brain networks the static and time-varying functional connectomics properties of the brain. For SFC, Pearson’s correlation coefficient (PCC) matrix of full-length BOLD signals is usually chosen as functional connectivity. When it comes to DFC, the functional connectivity features are obtained via high-order mining of SFCs with sliding windows at different time points of fMRI. Then, classifiers such as support vector machine (SVM) and Gaussian process regression (GPR) are applied to perform the classification of NC vs MCI [2, 3]. In recent years, deep learning methods have made breakthroughs in medical image analysis [4]. For the image-based AD diagnosis, deep neural network models [5, 6] are also reported to achieve competitive results. More recently, researchers propose a bidirectional long short-term memory (BiLSTM) model (a representative recurrent neural network (RNN) model) for MCI diagnosis [7]. Although the calculation of functional connectivity and classification are integrated into a network, the functional connectivity is not learnable during the training process.

Recently, a novel deep learning fashion named capsule network (CapsNet) was proposed [8]. Being different from existed neural networks, each node (capsule) within capsule layers contains a series of neurons. The activity of each capsule is represented by an activation vector (activation values of a series of neurons in it). The norm of this vector stands for the probability that an object exists in it. The key operation of CapsNet is called “dynamic routing by agreement”, which means capsules in lower-level layers predict the outcomes of that in higher-level layers, and the higher-level capsules get activated only if these predictions agree with each other. Some researchers have applied CapsNets to medical image analysis tasks to obtain competitive results [9–11]. Inspired by the dynamic routing strategy of CapsNet, we propose two dynamic routing CapsNet models for MCI diagnosis. To the best of our knowledge, it is the first time to introduce this novel deep learning model to fMRI-based MCI diagnosis. There are two variants of our CapsNet for MCI diagnosis: (1) Intra-ROIs dynamic CapsNet; (2) Inter-ROIs dynamic CapsNet. Compared with both traditional machine learning methods and the state-of-the-art deep learning model, the Intra-ROIs dynamic CapsNet obtains comparable diagnosis results while the Inter-ROIs dynamic CapsNet achieves superior performance. More importantly, our Inter-ROIs dynamic CapsNet provides a novel and learnable strategy to capture DFC during training of deep neural networks.

2. Method

The input to our CapsNet are timeseries of BOLD signal from the automated anatomical labeling (AAL) [12] template, which contains 116 brain ROIs. Since there are two variants of proposed CapsNet, which respectively mines intra-ROIs dynamic representation and inter-ROIs dynamic representation for MCI diagnosis, we detail network structures of them in the following subsections.

2.1. Intra-ROIs Dynamic CapsNet

Structures of our Intra-ROIs dynamic CapsNet are illustrated in Fig. 1. Before being fed into the Intra-ROIs dynamic CapsNet, the fMRI signals of different brain regions are computed from the AAL atlas template to obtain ROI-wise fMRI X = [x₁, …, x₂, …, x_N], N = 116 represents the number of ROIs. X is the input to Intra-ROIs dynamic representation layers which consist of two 1D convolution layers in the temporal dimension. F = [f₁, …, f_i, …, f_M] (M is the number of capsules in F) is the output of these layers. Then, F is fed into two capsule layers (High-order dynamic combination and Dynamic diagnosis in Fig. 1), successively obtaining high-order combination representation F_com = [f_1c, …, f_ic,…, f_Mc] and the diagnosis result F_d = [f_MCI,f_NC] (f_MCI and f_NC represent output of MCI capsule and NC capsule).

Fig. 1.

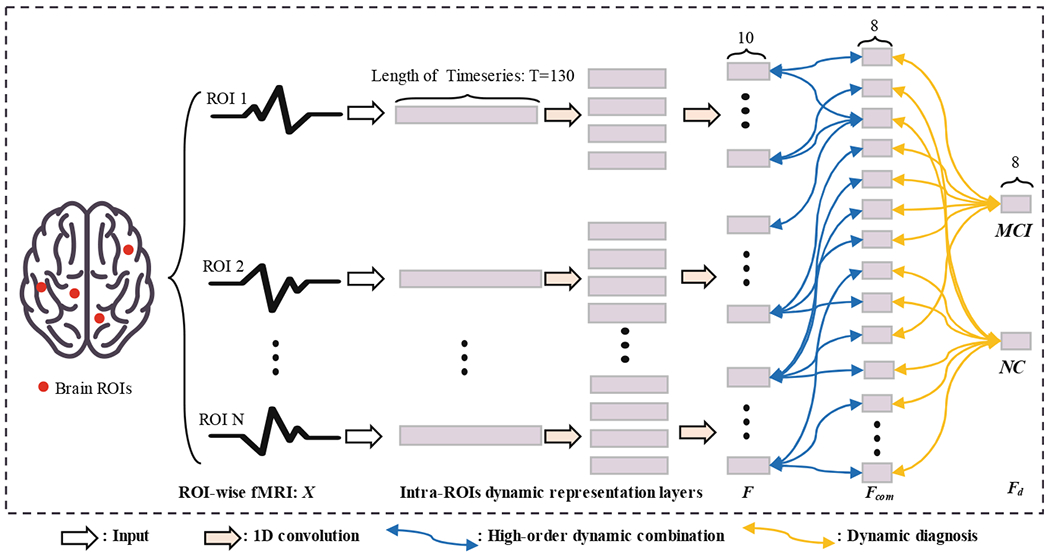
Illustration of our Intra-ROIs dynamic CapsNet. According to the AAL template, there are 116 ROIs in the preprocessed fMRI. The length of timeseries is 130. The ROI-wise input is successively propagated through Intra-ROIs dynamic representation layers and Dynamic diagnosis layer. Operations of these layers are listed in the bottom of this figure, and details of the network parameters are described in the Experiments and results section.

Capsules in these capsule layers (High-order dynamic combination and Dynamic diagnosis) are connected and optimized via “dynamic routing by agreement” algorithm [8]. Considering that μ_i is the output of capsule i in a capsule layer (For Intra-ROIs dynamic representation layers, μ_i is set as f_i. For High-order dynamic combination layers, μ_i is set as f_ic), the related prediction for its parent capsule j in next layer is:

$${\mu }_{j\mid i}={\mathit{W}}_{\mathit{ij}}{\mu }_i$$ (1)

where W_ij are learnable weights in the form of a matrix. The coupling c_ij between these two capsules is defined as Eq. 2:

$$c_{\mathit{ij}}=\frac{\mathit{exp}(b_{\mathit{ij}})}{{\sum }_k\mathit{exp}(b_{\mathit{ik}})}$$ (2)

where b_ij represents the probability that capsule i is coupled with capsule j, and it is initialized as 0 at the beginning of routing. So, s_j which stands for the input to capsule j can be computed as Eq. 3:

$${\mathit{s}}_j={\sum }_i{c}_{\mathit{ij}}{\mu }_{j\mid i}$$ (3)

Then, a squashing function is used to limit the norm of output value v_j from capsule j to [0, 1], which can make sure that the norm of this vector can act as a probability.

$${\mathit{v}}_j=\frac{{\Vert {\mathit{s}}_j\Vert }^2}{1+{\Vert {\mathit{s}}_j\Vert }^2}\frac{{\mathit{s}}_j}{\Vert {\mathit{s}}_j\Vert }$$ (4)

For the High-order dynamic combination layer, v_j is calculated as f_jc, and the norm of v_j represents the probability that a weighted combination of brain ROIs signals exist in capsule j; while for the Diagnosis capsule layer, v_j is calculated as f_MCI or f_NC, and the norm of v_j represents the probability that a scan belongs to MCI or NC.

The agreement a_ij between capsule i and its parent capsule j can be calculated in the form of inner product as Eq. 5:

$$a_{\mathit{ij}}={\mathit{v}}_j\cdot {\mu }_{j\mid i}$$ (5)

In the next iteration of dynamic routing, a_ij will be added to the b_ij to enhance the coupling between the capsule i and capsule j.

The dynamic routing strategy described above is performed in both the High-order dynamic combination and Dynamic diagnosis layers illustrated in Fig. 1. L_D is the loss function of the CapsNet, which is in the form of a margin loss as Eq. 6:

$$L_D=T_c\max {(0,m^{+}-\Vert {\mathit{v}}_c\Vert )}^2+\lambda (1-T_c)\max {(0,\Vert {\mathit{v}}_c\Vert -m^{-})}^2$$ (6)

T_c = 1 iff an instance from class c (MCI or NC) is present to the network, v_c is the output of the capsule which represent class c, and λ is a weight that is set as 0.5. m⁺ = 0.9 and m⁻ = 0.1 are the margins which are set as the recommended values in capsule net paper [8].

2.2. Inter-ROIs Dynamic CapsNet

Majority of traditional MCI diagnosis methods are based on the Inter-ROIs functional connectivity feature representation. Even though our Intra-ROIs dynamic CapsNet combines information from different ROIs in the High-order representation capsule layer, it cannot make full use of the rich information of inter-ROIs correlations. Thus, we further propose an inter-ROIs dynamic CapsNet which can capture the inter-ROIs dynamic representation for more superior diagnosis performance. Structures of Inter-ROIs CapsNet are illustrated in Fig. 2, which consist of Inter-ROIs dynamic representation layers and Dynamic diagnosis layer.

Fig. 2.

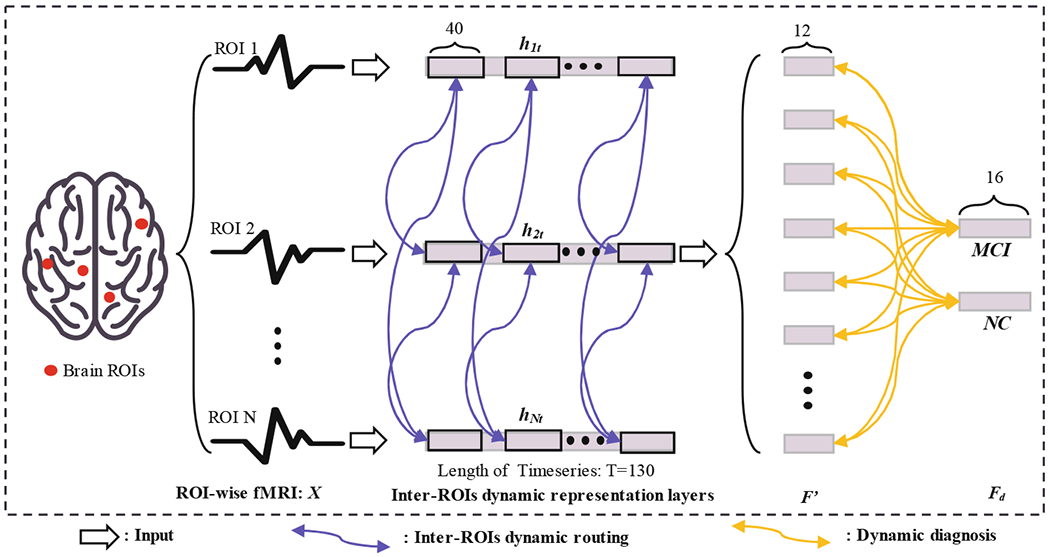
Illustration of our Inter-ROIs dynamic CapsNet. According to the AAL template, there are 116 ROIs in the preprocessed fMRI. The length of timeseries is 130. The ROI-wise input is successively propagated through Inter-ROIs dynamic representation layers and Dynamic diagnosis layer. Operations of these layers are listed in the bottom of this figure, and details of the network parameters are described in the Experiments and results section.

The Inter-ROIs dynamic representation layers can dynamically calculate correlations between ROIs. The dynamic correlation is defined as a weighted agreement f_ijt which is shown as Eq. 7. For each two brain ROIs, the agreement value of them at timepoint t is defined as a weighted inner product, h_it and h_jt are fMRI signal of i-th and j-th ROIs in temporal slide windows. Across the whole timeseries, there is an agreement vector f_ij = [f_ij1, f_ij2, …f_ijt, …f_ijNt], N_t is the total number of sliding windows, all agreement vectors form the input F′ to Dynamic diagnosis layers, F′ = [f₁₂,f₁₃, … f_ij, …f_N−1N].

$$f_{\mathit{ijt}}=w_{\mathit{ijt}}{\mathit{h}}_{\mathit{it}}\cdot {\mathit{h}}_{\mathit{jt}}$$ (7)

According to the number of ROIs N = 116, there are total N × (N − 1)/2 = 6670 nodes in F′ which stands for the output of these Inter-ROIs dynamic representation layers. Then, dynamic routings are performed between F′ and capsules in the diagnosis capsule layer. The dynamic routing strategy between these two layers is the same as that described in Sect. 2.1. Loss function of the Inter-ROIs dynamic CapsNet is also in the same form as Eq. 6.

3. Experiments and Results

In this section, we first describe the preprocessing of fMRI data, settings of experiments, and details of network structures. Then, we compare the proposed models with other diagnosis methods.

3.1. Data Preprocessing and Experiments

In this study, we use the ADNI dataset (http://adni.loni.usc.edu/) for training and testing the proposed methods. The RS-fMRI data are preprocessed by AFNI software package (1) According to a well-accepted pipeline, we performed first ten volumes removal, head motion correction, normalization, nuisance signals regression, detrend and bandpass filtering. (2) To minimize artifacts due to excessive motion, subjects with an average frame displacement greater than 0.5 mm were removed. Finally, RS-fMRI data were smoothed with 6 mm full width at half maximum Gaussian kernel.

Via the preprocess above, a dataset containing 395 scans of MCI patients and 485 scans of NC subjects is built. The number of scans for each subject varies from 1 to 8. The whole dataset is split to form the training set and testing set for 5 times. In each split, there are 25% of total scans (220 scans) in the testing set, while there are 75% of total scans (660 scans) in the training set. Since some subjects are scanned for more than once, scans of the same subject are split into either training set or test set to make the strict separation at the subject level. For training of our model, the optimizer is set as Adam, and the weights of network are initialized by Xavier. 20% instances in training set are used for validation to monitor the performance. Once the validation loss and validation error stop declining, the trained network parameters are applied to obtain diagnosis results on testing set. Our experiments are based on Pytorch [13].

3.2. Results and Analysis

We compare the proposed models with state-of-the-art traditional machine learning methods and deep learning model. The classification accuracy, sensitivity, specificity, and related standard deviations are listed in Table 1.

Table 1.

Diagnosis performance of comparison methods and ours.

Method	Accuracy(std)	Sensitivity(std)	Specificity(std)
Static SVM	0.630(0.021)	0.621(0.035)	0.636(0.029)
Dynamic SVM	0.651(0.030)	0.672(0.032)	0.639(0.033)
Static GPR	0.673(0.021)	0.570(0.044)	0.772(0.047)
Dynamic GPR	0.705(0.042)	0.641(0.038)	0.756(0.062)
Bi-LSTM	0.726(0.017)	0.725(0.039)	0.727(0.057)
Intra-ROIs CapsNet	0.729(0.023)	0.799(0.042)	0.673(0.065)
Inter-ROIs CapsNet	0.773(0.022)	0.771(0.027)	0.774(0.040)

In this table, Static SVM and Static GPR represent traditional methods based on SFC which is calculated by Pearson’s correlation between full-length BOLD signals. After building SFC matrix, the SVM or GPR are trained to classify the SFC matrix. Dynamic SVM and Dynamic GPR stand for dynamic connectivity methods in which dynamic representations are obtained from high-order analysis of functional connectivity at different slide windows [2, 3]. Construction of FC and selection of classifiers of these compared methods follow that in related studies. All these mentioned above are widely used and competitive traditional machine learning based MCI diagnosis methods.

In the other hand, Bi-LSTM is a recently proposed deep learning model for MCI diagnosis, which is in the form of bidirectional long short-term memory, and it has achieved competitive performance for diagnosing MCI. Besides, it is also based on dynamic functional connectivity. Intra-ROIs CapsNet and Inter-ROIs CapsNet stand for our CapsNet models. Network structures of Bi-LSTM follow the optimal ones which are chosen in the related MCI diagnosis study [7].

For Intra-ROIs CapsNet shown in Fig. 1, parameters of these two 1D convolution layers are set as (1) Conv1: kernel size = 1 × 20, number of kernels is 4, stride = 4; (2) Conv2: kernel size = 1 × 10, number of kernels is 4, stride = 2. Parameters of High-order representation capsule layer are set as: length of input = 10, length of output = 8; Parameters of diagnosis capsule layer are set as: length of input = 8, length of output = 16. For Inter-ROIs CapsNet shown in Fig. 2, parameters of inter-ROIs dynamic representation layer are set as width of slide window = 40, stride of slide window = 8; for the diagnosis capsule layer, length of input =12, length of output = 16. Parameters of the proposed models are selected according to both experiments and optimal values in capsule net paper [8].

As could be seen, according to the listed evaluations (Table 1), the inter-ROIs dynamic connectivity methods (Dynamic SVM, Dynamic GPR, BiLSTM, and Inter-ROIs CapsNet) can achieve superior performance than static ones and Inra-ROIs dynamic method (Static SVM, Dynamic GPR, Intra-ROIs CapsNet). The deep learning models (BiLSTM, Intra-ROIs CapsNet, and Inter-ROIs CapsNet) are more competitive than traditional machine learning based methods. The dynamic routing networks proposed in this paper outperformed both state-of-the-art traditional machine learning methods and deep learning model.

For further analysis, we also compare the receiver operating characteristic (ROC) curves and area under the curve (AUC) values of different methods in Fig. 3. Specifically, MCI is the positive class while NC is the negative class. As could be seen, our dynamic routing networks can achieve superior ROC performance and higher AUC values than other methods. Results in this figure can further demonstrate the efficiency of our CapsNets for MCI diagnosis.

Fig. 3.

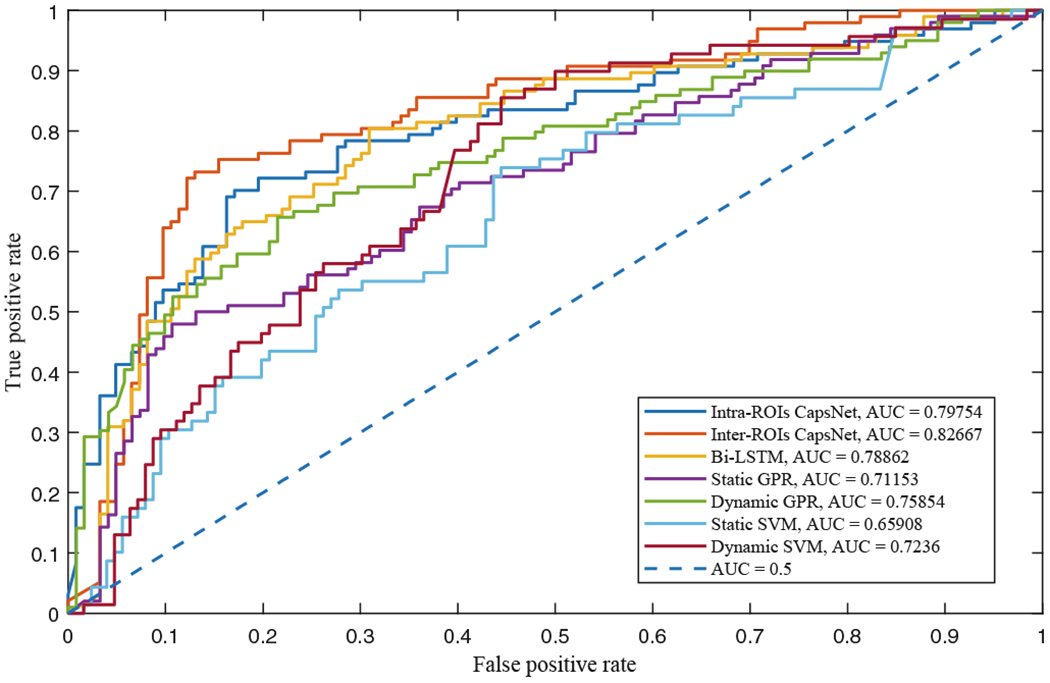
ROC curves and related AUC values of different diagnosis methods

4. Conclusions

In this study, we propose both two variants of CapsNet for MCI diagnosis. In the intra-ROIs model, temporal-dynamic representation of fMRI is first represented by ROI-wise convolutional networks. Then, high-order combinations of intra-ROIs representations are dynamically routed to obtain the diagnosis results. In the improved inter-ROIs dynamic variant, a novel weighted agreement metric is designed to capture the DFC across ROIs. With the help of our DFC metric, our Inter-ROIs dynamic CapsNet can achieve competitive diagnosis performance for MCI.