Compton PET: A Simulation Study for a PET Module with Novel Geometry and Machine Learning for Position Decoding

Abstract

This paper describes a simulation study of a positron emission tomography (PET) detector module that can reconstruct the kinematics of Compton scattering within the scintillator. We used a layer structure, with which we could recover the positions and energies for the multiple interactions of a gamma ray in the different layers. Using the Compton scattering formalism, the sequence of interactions can be estimated. The true first interaction position extracted in the Compton scattering will help minimize the degradation of the reconstructed image resolution caused by intercrystal scatter events. Because of the layer structure, this module also has readily available user-defined resolution for the depth of interaction. The semi-monolithic crystals enable high light collection efficiency and an energy resolution of ~10% has been achieved in the simulation. We used machine learning to decode the gamma ray interaction locations, achieving an average spatial resolution of 0.40 mm. Our proposed detector design provides a pathway to increase the sensitivity of a system without affecting other key performance features.

1. Introduction

High-resolution PET has attracted a lot of interest for its ability to conduct in vivo imaging of small animals and human brains [1]. However, the spatial resolution for most common high-resolution PET scanners is limited to around 1 to 2 mm [2] due to positron range, non-collinearity, the depth of interaction (DOI) effect, and Compton scatter inside the detector [3]. Thin detectors can be used to minimize the effect of depth of interaction and Compton scatter inside the detector, at the expense of reduced system sensitivity. The goal of this paper is to develop a design that allows DOI and Compton scatter information to be extracted without affecting system sensitivity.

Most current PET detector modules use pixelated crystal arrays with single-ended coupling to a photodetector. The position information comes from localizing individual crystals in the flood histogram, which provides only 2-dimensional position information. The missing DOI information leads to the parallax error, and degrades spatial resolution [4]. Several designs have been proposed to obtain DOI information [5]. With dual-ended readout detectors, DOI information has helped achieve 0.61 mm reconstructed spatial resolution [6], however, the additional photodetectors and very small-pitch crystal arrays in this design are very expensive. Moreover, the low cross-sectional area to height ratio significantly limited the amount of scintillation light that could be extracted from the crystals, which degrades the detector’s energy and timing resolution [7, 8].

For 511 keV gamma rays, there is a high probability of a Compton interaction between the gamma ray and the detector crystals, leading to inter-crystal scatter (ICS) events [9, 10]. If ICS happens, position decoding using the center of gravity method will provide incorrect gamma ray interaction positions, which affects both the spatial (transversal-axial direction) and DOI (radial direction) resolution. This blur in detector resolution causes degradation of the reconstructed image [11, 12]. Rejection of ICS events has been used to improve spatial resolution [13], however, this method also reduces system sensitivity. Several methods have been proposed to include the ICS events without deteriorating spatial resolution by identifying the earliest interaction using Compton kinematics [14–16]. However, the poor energy resolution for small-pitch pixelated arrays has limited the accuracy of this method. Detectors that utilize monolithic scintillators have better energy resolution, and have the ability to obtain 3-dimensional (3D) position information for a gamma ray interaction more accurately. However, monolithic scintillation detectors require dedicated calibration procedures [17–20] and Compton scattering inside the crystal results in a light distribution which is more complicated than the case with single photoelectric interactions, resulting in a more challenging task for position decoding [21].

To solve the two problems above, we propose to use a new PET module design, in which the scintillation crystal is divided into several layers along the radial direction with reflective films between layers. Each layer uses a continuous crystal, and the scintillation light is detected from the four sides of the crystals. Layered PET modules have been studied before, and this design can significantly increase the light collection efficiency, providing better energy resolution [22, 23]. However, the designs presented previously required more photodetectors than comparable designs with pixelated crystal arrays. In this paper, we propose a strategy which when scaled up, will use fewer or similar numbers of photodetectors compared to conventional pixelated array designs. In [24], the authors showed that, the side readout of monolithic crystals can achieve ~0.8 mm spatial resolution and 9.2% energy resolution when not including Compton scattering. In this paper, we include Compton scattering and employ machine learning for position decoding to improve spatial resolution [25, 26].

2. Materials and Methods

2.1. Detector

2.1.1. Module geometry

Figure 1 shows the schematics for three detector modules: two Compton PET modules of different sizes, and one traditional dual-ended readout module. The simulations in this paper used the detector module in Figure 1(a). It was composed of four layers of LYSO crystals, and the size of each crystal layer was 13.24×13.24×3.16 mm³. Both the top and bottom surfaces of each crystal were covered with enhanced specular reflective films (ESR). The scintillation light created in the crystal was collected by four SiPM arrays on the four sides of the crystals. There were 16 pixels (4 by 4) in each SiPM array, and the size of the array was 13.24×13.24 mm². The light collected in each pixel of the SiPMs was recorded individually, giving 64 signals in total. For each layer, the sum of the signals from all SiPM pixels on the sides provided the energy deposited in this layer, the pattern of how light was distributed in each SiPM was used to decode the position of the gamma ray interaction. The ultimate goal of this work is to build the detector shown in Figure 1(b), which is composed of six layers of LYSO crystals. Each crystal slab has a size of 50.40×50.40×3.16 mm³, and the isolation of light using ESR and the readout of light from four sides using SiPMs is the same as in Figure 1(a). For this geometry, the number of SiPMs required for readout is less than that required for dual-ended readout (Figure 1c). The module of Figure 1(a) is chosen for this study, to serve as a guide for first experimental work, which as a practical matter will utilize a smaller-scale prototype.

Figure 1.

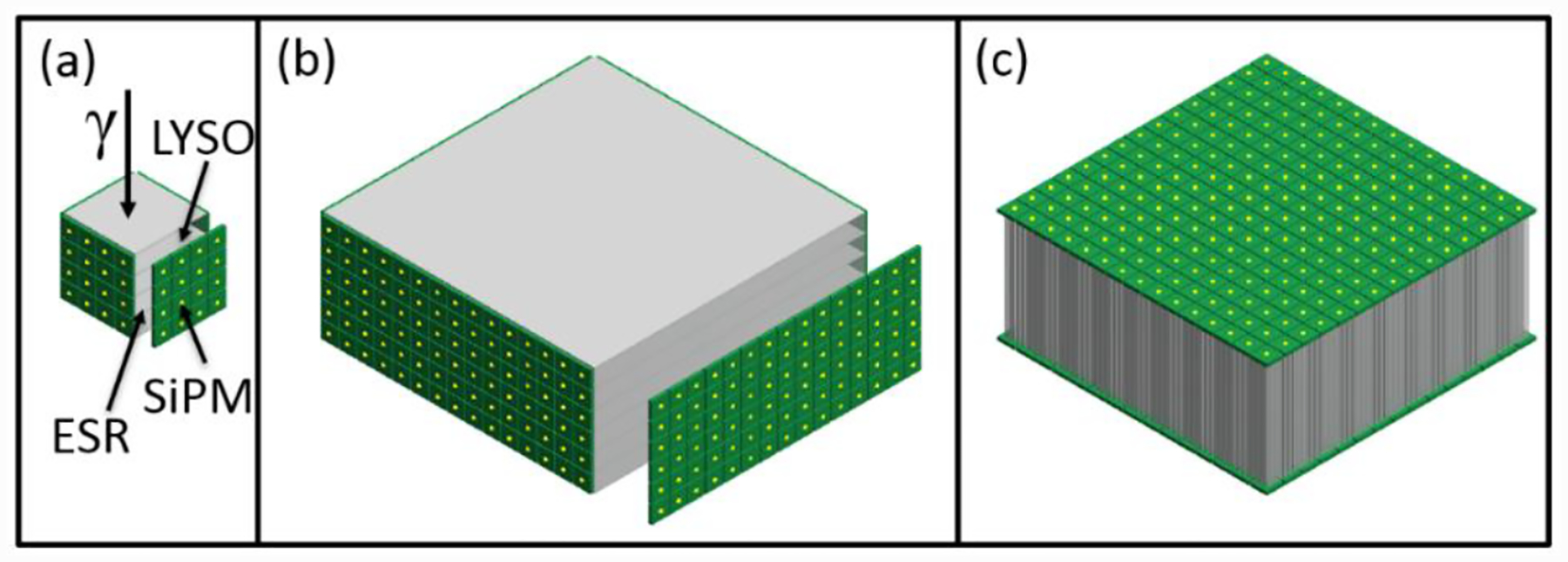
Detector module geometries. a) Geometry simulated in this work; b) Larger scale geometry for ultimate application. c) Dual-ended readout design with pixelated crystal array.

2.1.2. Features of the module

The proposed PET detector module has several features that offer the potential for superior performance, such as better DOI encoding, reconstruction of Compton kinematics, improved light collection, high gamma ray detection sensitivity, and efficient use of photodetectors. These features are described in more detail below.

The first feature of the module is that it has user-defined DOI resolution. Since each crystal layer is optically isolated from its neighbor crystals, the interaction depth can be determined by measuring the scintillation light generated in each layer. The DOI resolution is the layer thickness.

The second feature of the module is its ability to reconstruct the kinematics of Compton scattering inside the crystals. The position and energy of the recoil electrons in each layer can be determined within this module, from which the sequence of interaction can be estimated.

The third feature of this module is its high light collection efficiency. In traditional designs with single or dual-ended readout, some scintillation light is trapped inside the crystal due to total internal reflection. In this design, since the scintillation light is collected from four sides of the crystals, the light that is reflected on one side of the crystal due to total reflection will be able to be collected at its next incident position (Figure 2). For the interface between the LYSO crystal and optical grease, the critical angle for total reflection is: θ_c = 54° (assuming the index of refraction for LYSO and optical grease are 1.82 and 1.47, respectively). In Figure 2, if the first incident angle (θ₁) is larger than the critical angle, the second incident angle (θ₂) will be less than the critical angle, and the light has a high likelihood of passing through the interface at position B and being detected. The increased light collection will improve both energy resolution and timing resolution of the detector.

Figure 2.

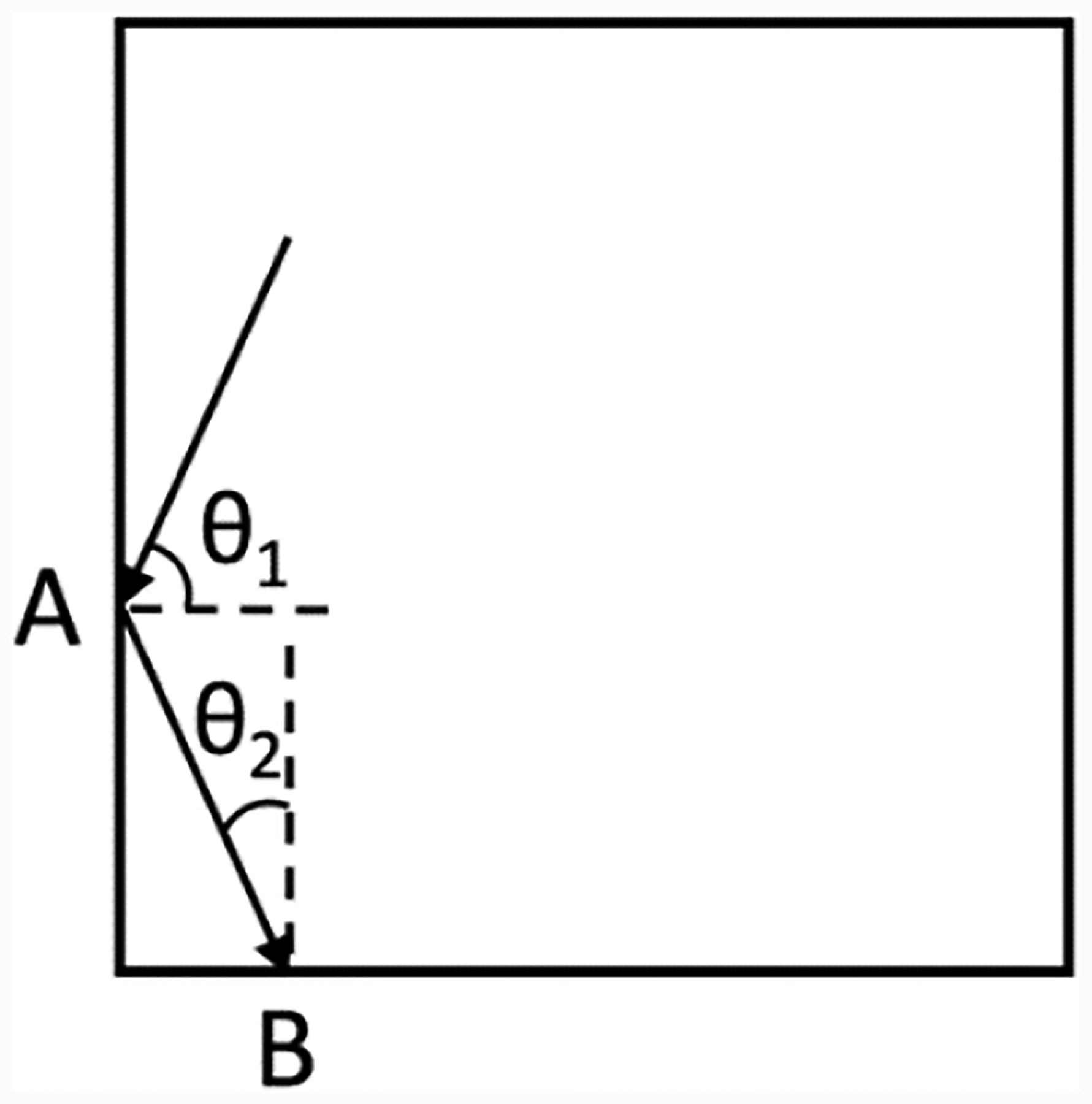
Schematic plot for scintillation light transportation inside the crystal. The light is reflected at position A due to total internal refection, but is transmitted to the photodetector at position B.

The fourth feature of this module is that it solves the trade-off between the system sensitivity and the spatial resolution. Since the spatial resolution is determined within each layer individually, increasing the number of layers will not affect the position decoding in each layer, and more layers will give higher sensitivity for gamma ray detection.

The fifth feature of this module is that it is possible to use fewer photodetectors than dual-ended detector modules. When the area of one side of the detector module is less than half of the area of the top of the module (see examples in Figure 1b and 1c), the number of photodetectors needed to cover the four sides is less than that needed to cover the top and bottom of the scintillator block.

2.2. Simulation setup

GATE v7.2 (Geant4 Application for Tomographic Emission) was used to simulate the performance of the Compton PET module [27]. The simulation consisted of three main parts: the radiation source, the scintillation crystals, and the photodetectors.

The following physics processes were included in the simulation: photoelectric interaction, Compton scattering, Rayleigh scattering, electron ionization, Bremsstrahlung, scintillation, optical scattering and absorption. For the scintillation process, we used the default parameters for LYSO crystals in GATE optical photon simulations which include 28 photons per keV for the scintillation yield, and 4.41 for the resolution scale [28]. The saturation effect for SiPMs [29] is not simulated in this study. Two kinds of optical boundaries were used to define the behavior of scintillating photons at the surface of the crystal. A dielectric-dielectric surface was used between the crystal and the ESR reflector (reflectivity: 0.95), and a dielectric-metal surface between the crystal and the photodetector (efficiency: 0.5, which accounts for the combination of optical transmission across the boundary and the photon detection efficiency of the SiPMs).

Two sets of simulations were conducted. In the first set, a point radiation source, which emits 511 keV gamma rays perpendicularly to the top surface of the crystal (Figure 3a), was used. To characterize the spatial resolution, a series of simulations with different source positions were conducted. Each simulation used a unique gamma ray incident position on the x-y surface of the module. In total, there were 625 incident positions (25×25 grid) with 0.5 mm pitch on the x-y (top) surface of the module, and ~4000 events were simulated for each incidence position. This set of simulated events was used for training the neutral network for position decoding using machine learning.

Figure 3.

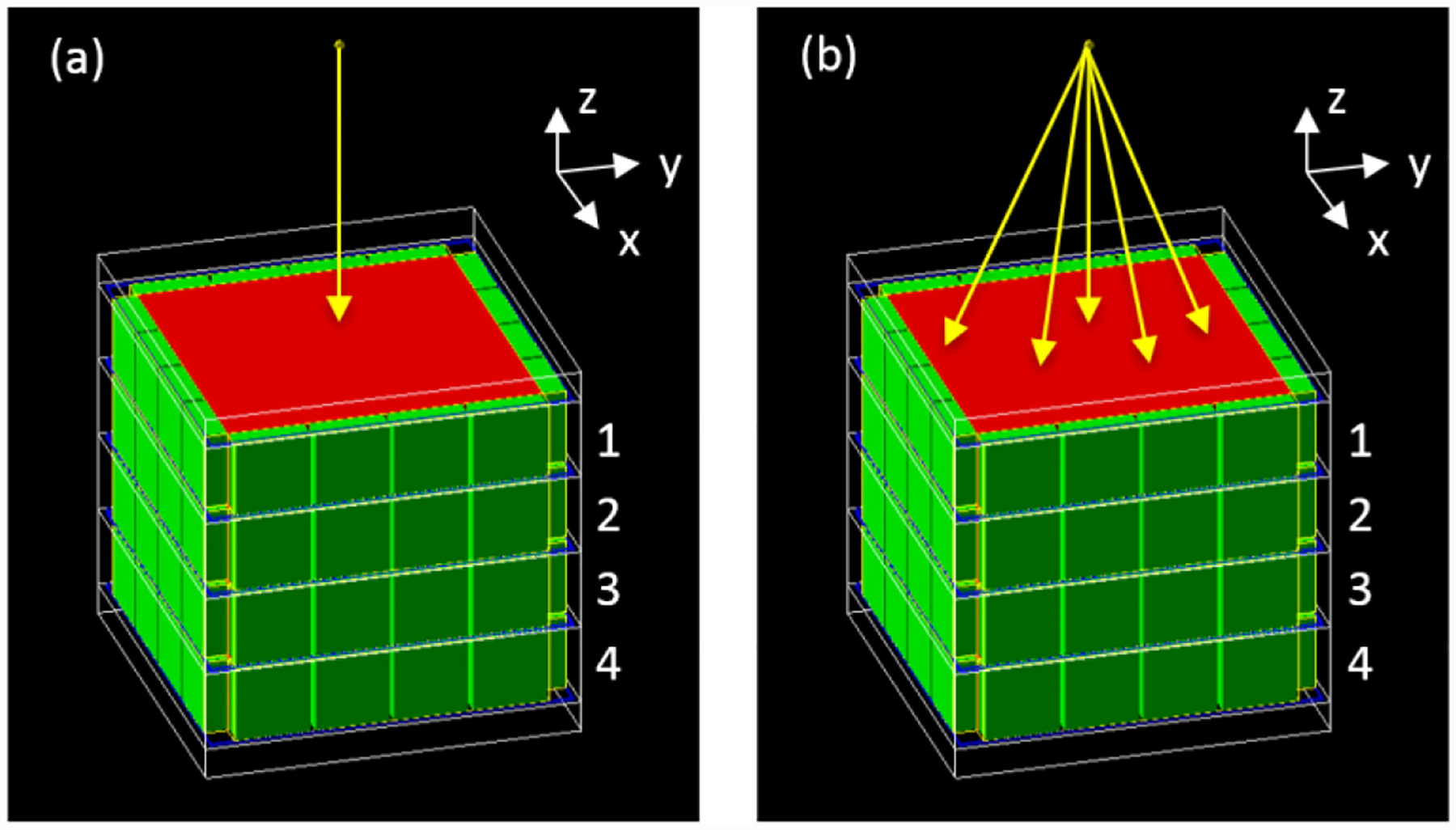
Schematic for simulating the Compton PET module in GATE. A point source emits 511 keV gamma rays perpendicularly (a) and isotropically (b) towards the front face of the 4-layer LYSO crystal module. The dimension of each crystal layer was 13.24×13.24×3.16 mm³, and the pitch along the DOI direction was 3.36 mm (ESR thickness was 0.2 mm). The layers are numbered 1 to 4 according to their distance from the radiation source. The scintillation light was collected by the 64 photodetectors on the four sides.

In the second set, the radiation source was changed to a point source which emits 511 keV gamma rays isotropically (Figure 3b), the point source was placed at the same 625 positions as in the first study. In this simulation, the gamma ray can enter the module with arbitrary positions and angles. This set of simulated events was used for testing the trained neural network from the first study.

2.3. Analysis methods

Two features were calculated from the simulated results: energy resolution and spatial resolution:

2.3.1. Energy resolution

The energy of the gamma ray detected by the module was assumed to be proportional to the total number of photons detected by the photodetectors. This assumption was verified using different gamma ray energies in the simulation. As shown in Figure 4, histograms of the total number of photons detected by the 64 photodetectors were plotted in (a), and a Gaussian fit was used to get the central values at the photopeaks for different gamma ray energies. Figure 4(b) shows the relationship between the number of photons corresponding to the photopeak and the gamma ray energy. The FWHM energy resolution for different photopeak energies is also plotted in Figure 4(b).

Figure 4.

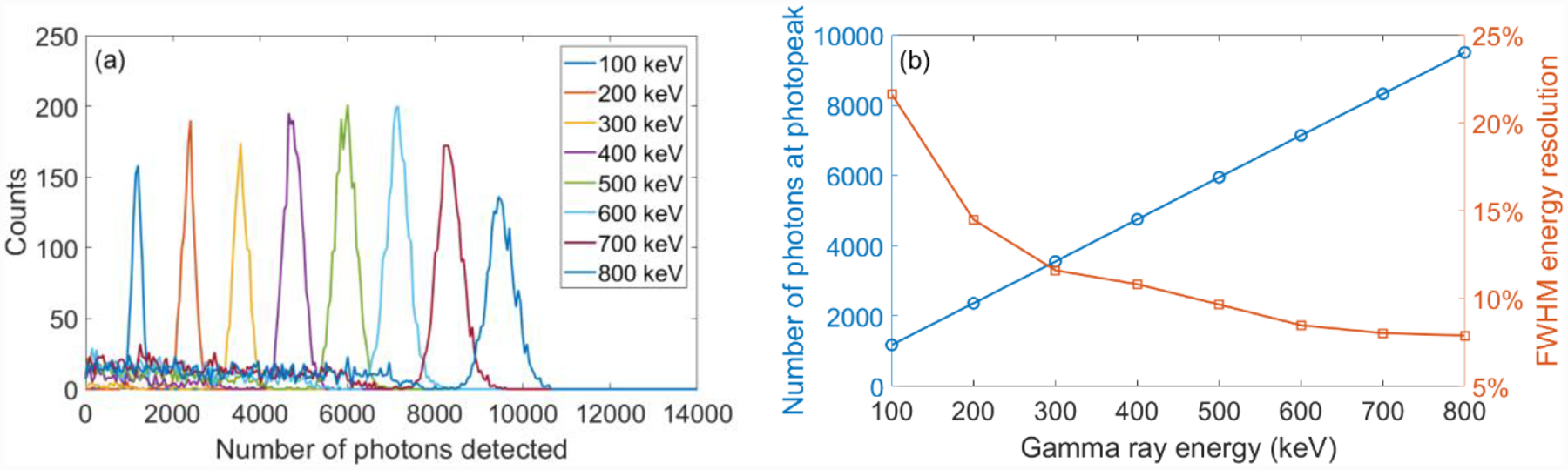
(a): histograms of the total number of photons detected by the 64 photodetectors for different gamma ray energies. (b): number of detected photons at the photopeak vs. gamma ray energy and photopeak FWHM energy resolution vs. gamma ray energy.

The total number of photons corresponding to the 511 keV photopeak changed for different gamma ray interaction locations, due to differing amounts of light absorption and different collection efficiencies. A calibration was performed to scale the energy histogram according to the known incident gamma ray position. After calibration, the FWHM of the 511 keV photopeak was calculated to be the energy resolution.

2.3.2. Spatial resolution

The Neural Network Toolbox in MATLAB R2017a was used to decode the first interaction position (FIP) between the incident gamma ray and the crystal. Supervised machine learning was used in this paper.

2.3.2.1. Ground truth determination for the FIP

For supervised machine learning, it is crucial to label the data with the correct ground truth value. In this application, the ground truth is the location of the first interaction position. The x and y coordinates of the FIP are known from the simulation, since the gamma rays hit the x-y plane of the detector perpendicularly (Figure 3a).

The z coordinate which gives information regarding the layer in which the FIP happened was obtained using two different methods in this study. In the first method, the z value was extracted from the GATE simulation, which gives the ground truth for first interaction layer (FIL). However, this method cannot be used in experiments where the depth is unknown.

In the second method, the FIL was derived from the Compton scattering kinematics. The energy and position for interactions in each layer are required to reconstruct the Compton scattering process according to Equation (1) [30].

$$\text{cos }\theta =1-\frac{E_1}{\gamma (E_0-E_1)},$$ (1)

where θ is the scattering angle of the gamma ray, E₀ is the gamma ray energy, E₁ is the energy of the recoil electron produced during Compton scatter, γ=E₀/m_ec², m_e is the mass of the electron and c is the speed of light. The energy information is readily available from measuring the light collected in each layer, the position information (for determining θ) would need an iterative process or a prior simulation study to be determined. However, there are cases where forward scatter and backward scatter give the same interaction positions and energies [31]. Moreover, the finite spatial and energy resolution, and possibility of multiple Compton scattering make it complicated to determine the interaction sequence unambiguously. In this paper, we only use the energy information to get the z value (FIL) [16, 31]. The following steps were used as the “FIL determination scheme”:

1. An energy window of 420–600 keV was applied around the 511 keV photopeak of the total absorbed energy in all layers. As shown in Figure 5(a), 66.7% of the total events have passed the energy window cut.

2. Events meeting the energy window selection were divided into four groups according to the number of the layers that the gamma ray interacted with. As shown in Figure 5(b), the percentage of events for each group were: 81.89% (one layer case), 17.13% (two layer case), 0.96% (three layer case), 0.02% (four layer case).

3. The FIL was determined for each group as follows:

   1. One layer case: In this case, the incident gamma ray deposits all its energy in one of the crystal layers, and the FIL can be determined unambiguously. However, this includes events that Compton scattering within that layer, and these events would degrade the spatial resolution in the x-y plane, but would not affect the prediction for the FIL.
   2. Two layer case: In this case, the FIL can either be the layer closer to the radiation source (forward scattering) or the layer further from the radiation source (backward scattering). According to the Klein-Nishina formula [32], the majority of the events are forward scattered events, thus for most of the events, we decided to use the interaction layer closest to the radiation source as the prediction for the FIL, namely the “closest layer scheme”. Figure 6(a) shows the histogram for the difference between the true FIL and the predicted FIL, in which the ground truth was from GATE simulation, and the prediction used the layer closest to the radiation source. The success rate for the “closest layer scheme” was 69.2% in Figure 6(a), which corresponds to the forward scattered events. The remaining 30.8% of the events were backward scattered events, which were wrongly predicted. To improve the success rate, we studied the energy histogram for the closest layer for the events with right and wrong predictions in Figure 6(b). We observed that in the energy window between 162 keV and 238 keV, 65% of the events were backward scattered events, and the “closest layer scheme” predicted events incorrectly. Since these events actually belong to the two layer case, we can swap the prediction for the FIL for events within this energy window, which will improve the success rate. Using this approach, the success rate for FIL prediction was improved from 69.2% to 81.3% as shown in Figure 7, where the “revised closest layer scheme” was used.
   3. Three layer case and four layer case: The events in these two cases only accounted for 0.98% of the total events (Figure 5b). The “closest layer scheme” was used to predict the FIL, with success rates of 93.4% and 96.8% respectively, as shown in Figure 8.

Figure 5.

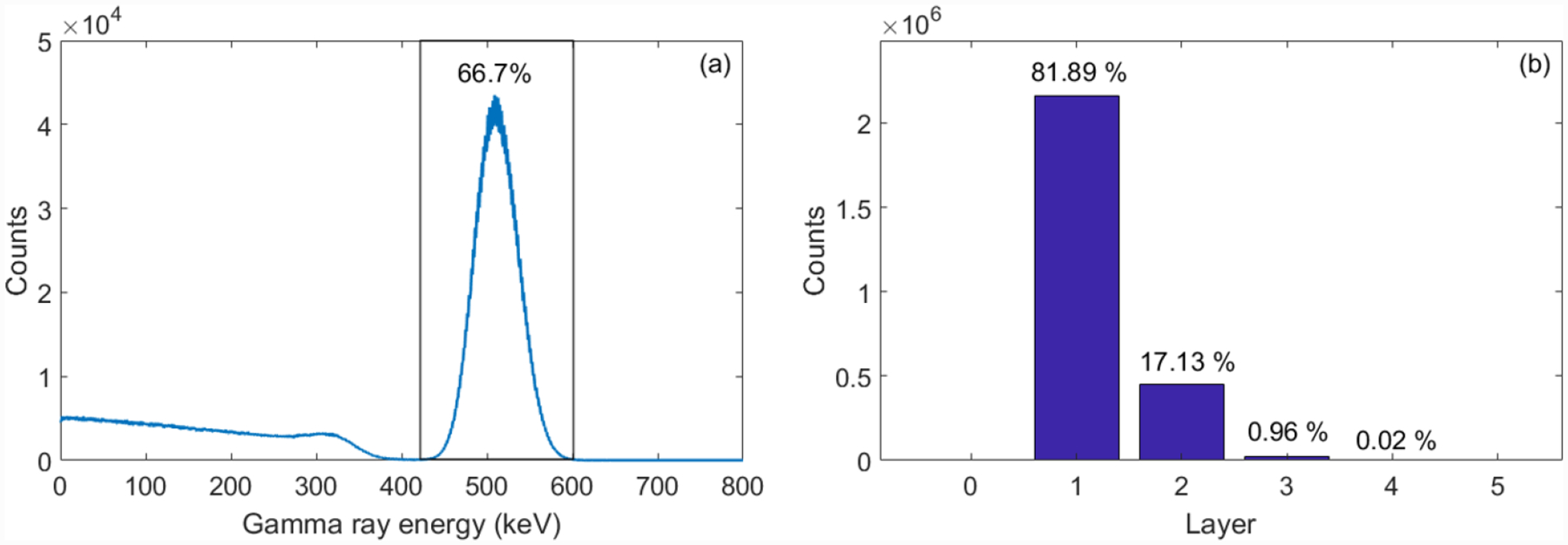
(a): Energy histogram for all the events, only the events within the energy window of 420–600 keV were used for FIL determination (b): Percentages for the number of layers the gamma ray interacted with (after the energy window cut).

Figure 6.

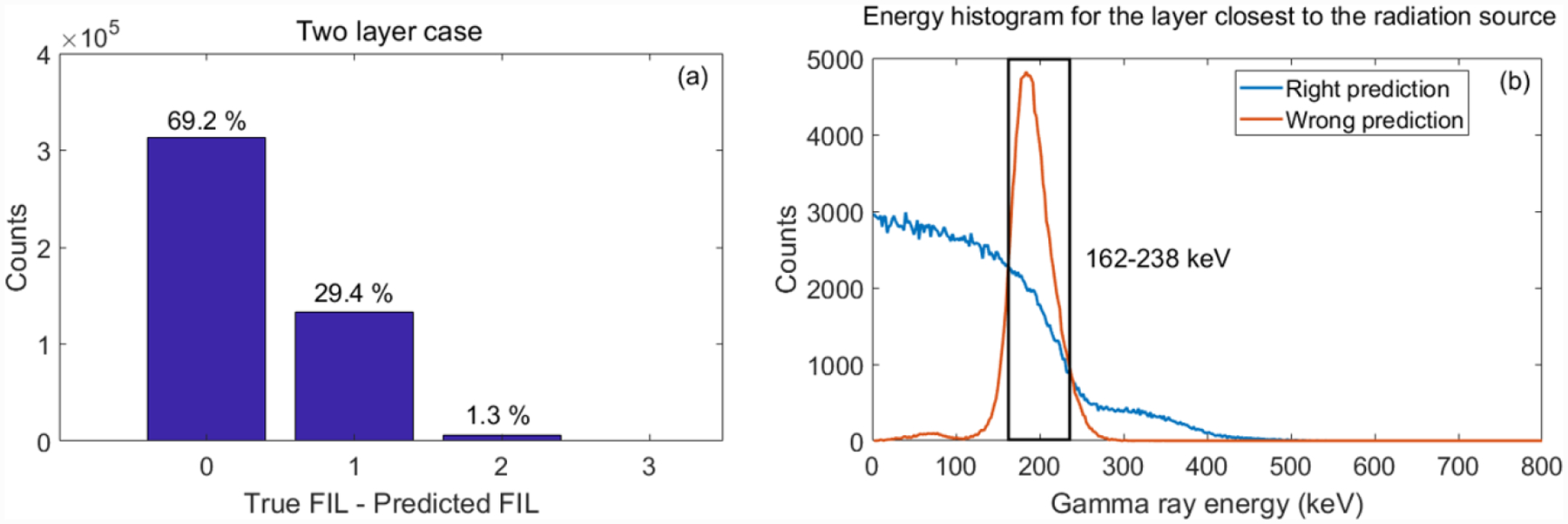
(a): Success rate of the “closest layer scheme” for predicting the FIL for the two-layer case. (b): Energy histograms for the layer closest to the radiation source with right and wrong prediction for the FIL using the “closest layer scheme”.

Figure 7.

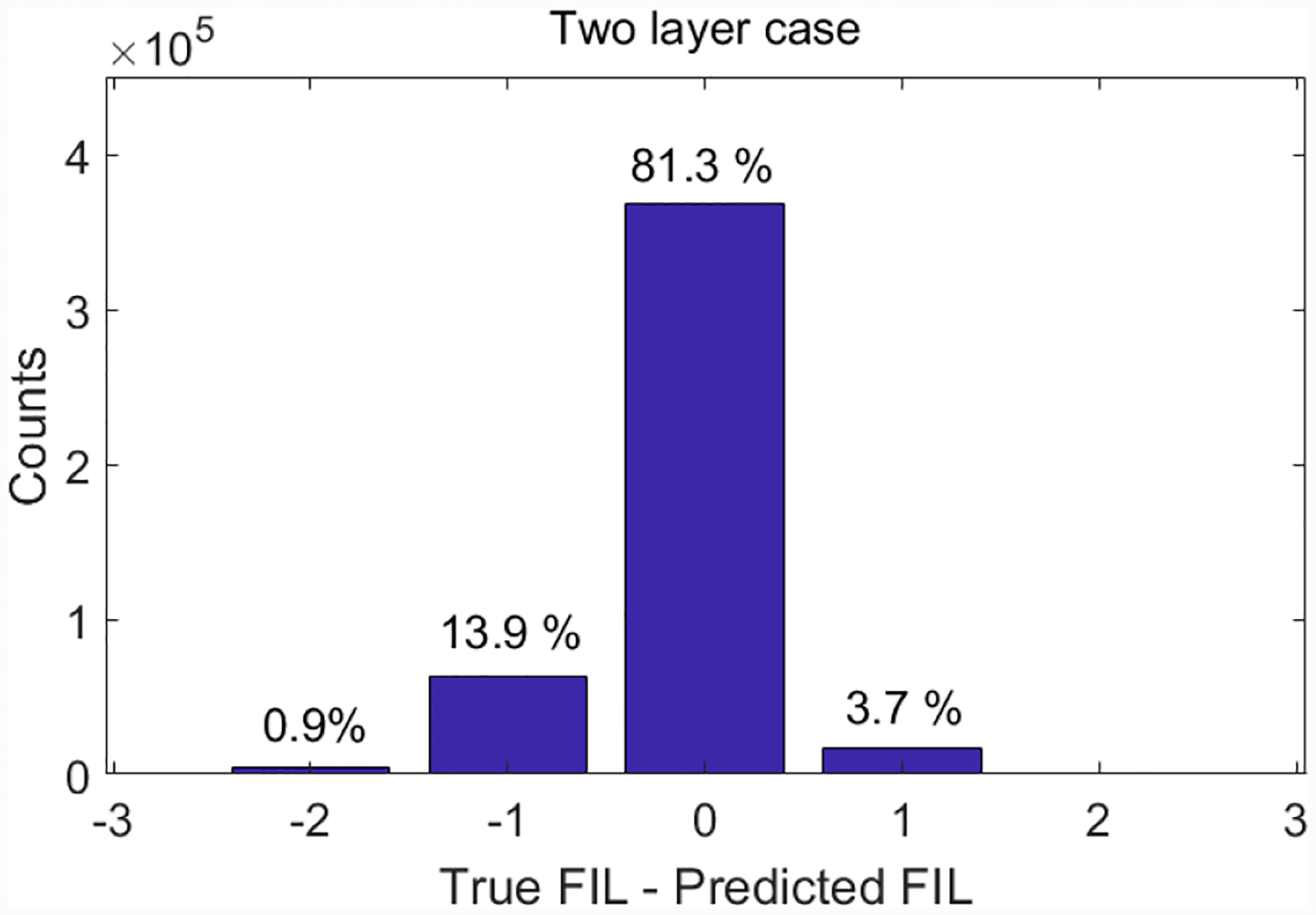
Success rate of the “revised closest layer scheme” for predicting the FIL for the two-layer case.

Figure 8.

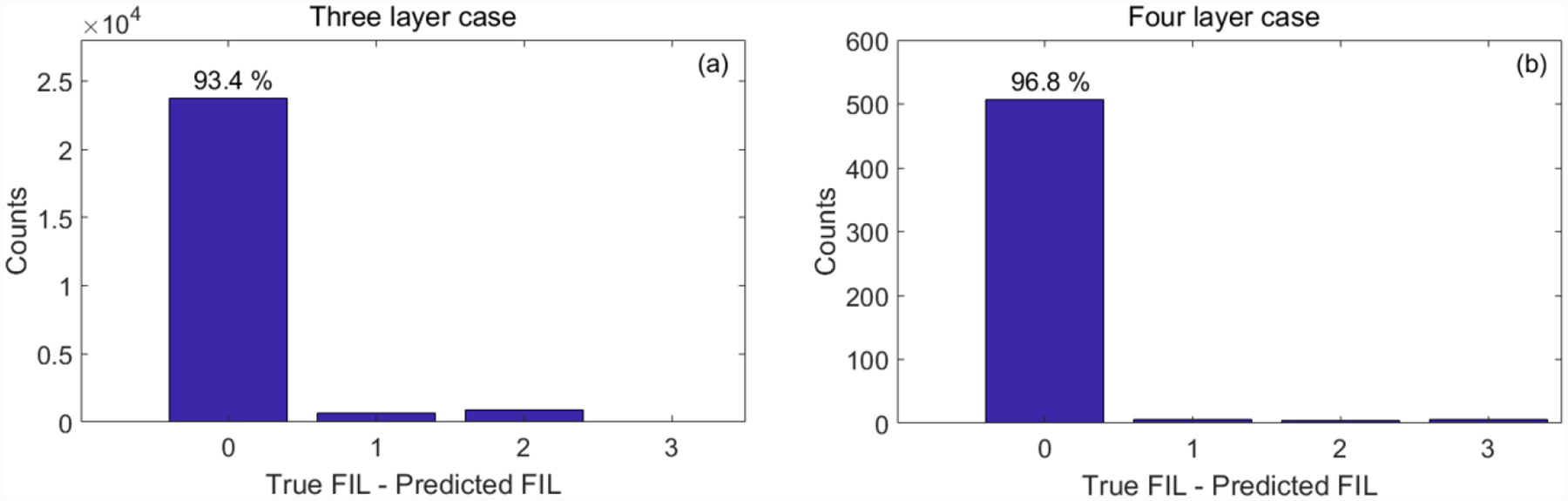
Success rate of the “closest layer scheme” for predicting the FIL for (a) the three-layer case and (b) the four-layer case.

2.3.2.2. Position decoding using machine learning

After the ground truth position for the FIP was determined, all the training events were divided into 625 groups corresponding to their known incidence position on the XY plane (Figure 3a). In each group, every event was represented by one 16×1 pixel image, which represents the light distribution detected by the photodetectors on the four sides of the FIL. Figure 9 shows how gamma rays interacting at different locations in the crystal layer produced different light distributions in the photodetectors. The task of the machine learning was to train a neural network to map the light distributions (16×1 pixel image) to gamma ray interaction positions.

Figure 9.

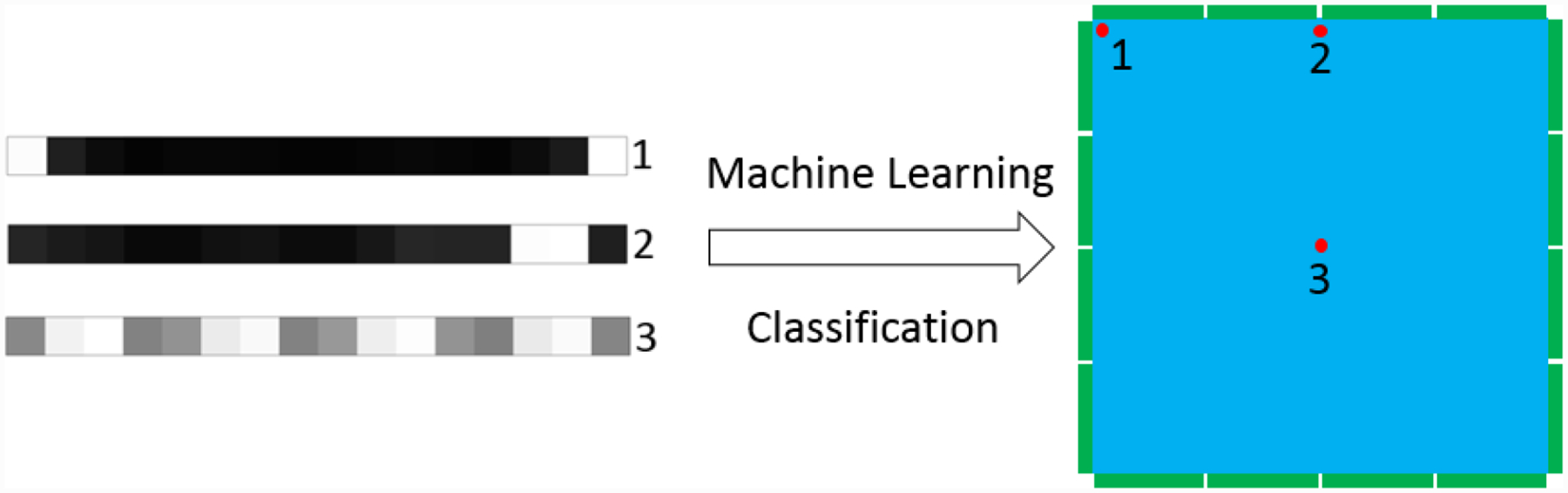
Schematic for the task of machine learning: mapping the 16×1 pixel image (light distribution on the 16 photodetectors) to gamma ray interaction position. Three examples are shown in the plots representing different interaction positions: corner (1), edge (2), center (3).

The structure of the network is shown in Figure 10: the input layer was a one dimensional 16 pixel image, only one convolution layer with 200 nodes was used, the rest of the layers were default layers used for classification problems. The neural network used a convolutional layer with 200 filters of size 1×1, the maximum number of epochs for training was 5, the loss function was the cross entropy loss, the initial learning rate is 0.0001, and the optimizer was the stochastic gradient descent with momentum.

Figure 10.

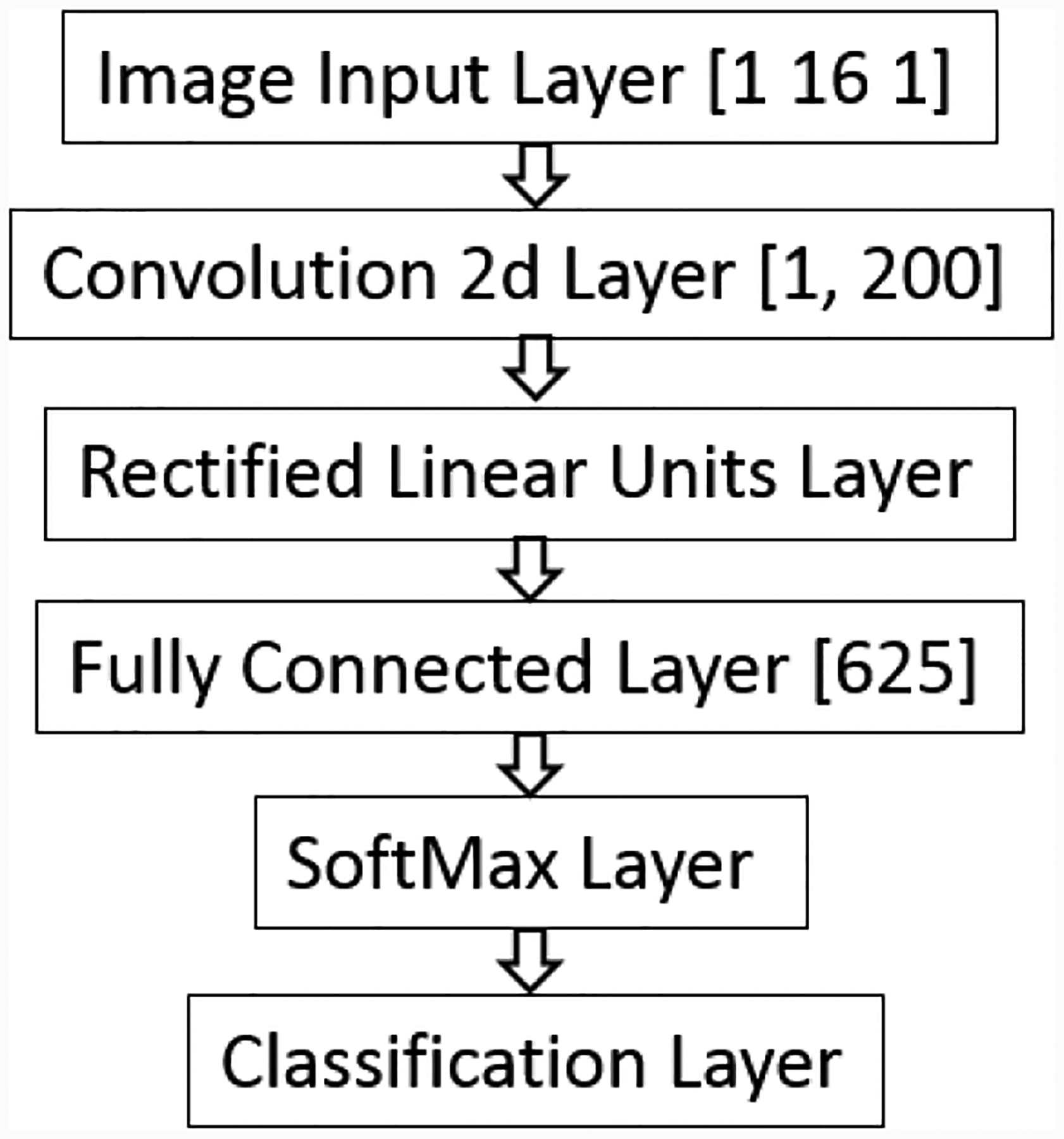
Structure of the neutral network.

The simulation study to quantify spatial resolution was designed such that it can be later replicated in experiments as well. The workflow for this process is shown in Figure 11. As described earlier, two simulation studies were conducted, one with a perpendicularly incident beam setup for training, the second with an isotropically emitting source producing obliquely incident photons. This second setup was designed to mimic the real-life situation and was used to test the trained neural network.

Figure 11.

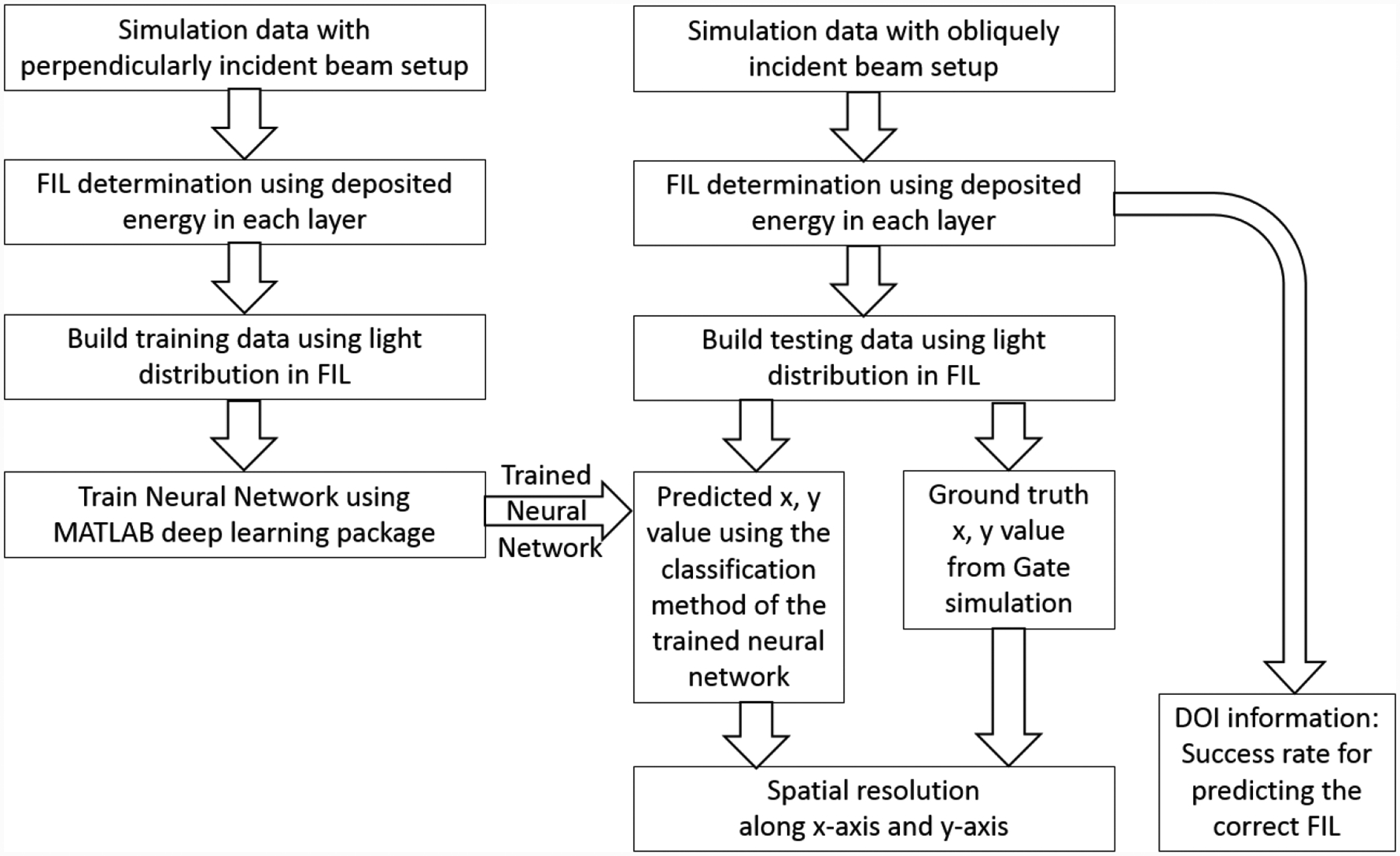
Workflow for quantifying the spatial resolution for the Compton PET module.

For each event in the second setup, two spatial locations were obtained: one was the ground truth value from GATE simulation, the other one was the predicted value using the output of the trained neutral network for x, y values and the “FIL determination scheme” for DOI (z value). Since a classification method was used, the output of the neural network for the testing data were the 625 discrete locations with different probabilities. An interpolation method was used for calculating the interaction location, in which the probabilities of a testing event being classified into each of the 625 positions were used as the weights in a center-of-mass calculation. A histogram was calculated for the difference between the ground truth and predicted interaction location. A Gaussian function was used to fit the histogram, and the FWHM of the fitted curve was reported as the spatial resolution for the x and y directions.

For the DOI information, the success rate of predicting the correct FIL was used as the figure-of-merit for DOI.

2.3.3. Electronic Noise

In order to study the effect of noise introduced by the photodetector and associated electronics, we added Gaussian noise to the number of photons detected by each SiPM. Gaussian noise with 5 different standard deviations were studied: 5, 10, 15, 20, 25 photons. The average number of photons detected by each SiPM was ~400. We defined the Gaussian noise percentage (Eq. 2) to indicate the amount of noise added. The effect of this noise on the energy and spatial resolution were studied.

$$\text{Gaussian noise percentage}=\frac{\text{standard devation of the Gaussian noise}}{\text{Average number photons detected}}$$ (2)

3. Results

3.1. Energy resolution

In section 2.3.1, it was shown that the number of photons detected by the photodetector was a good representation for the energy deposited by the gamma rays in the crystals. However, due to the loss of photons when scintillation light is travelling inside the crystal, the total number of detected photons varies by several percent for gamma ray interactions at different positions within the crystal. Figure 12 shows the 2D histogram of this variation. When the gamma ray interacts at the middle of the crystal, fewer photons were detected by the photosensors, due to longer average path the scintillation photons travelled before detection. A calibration according to the gamma ray incidence position was performed prior to calculating the energy resolution. After the calibration, the FWHM energy resolution improved from 11.7% to 9.3%.

Figure 12.

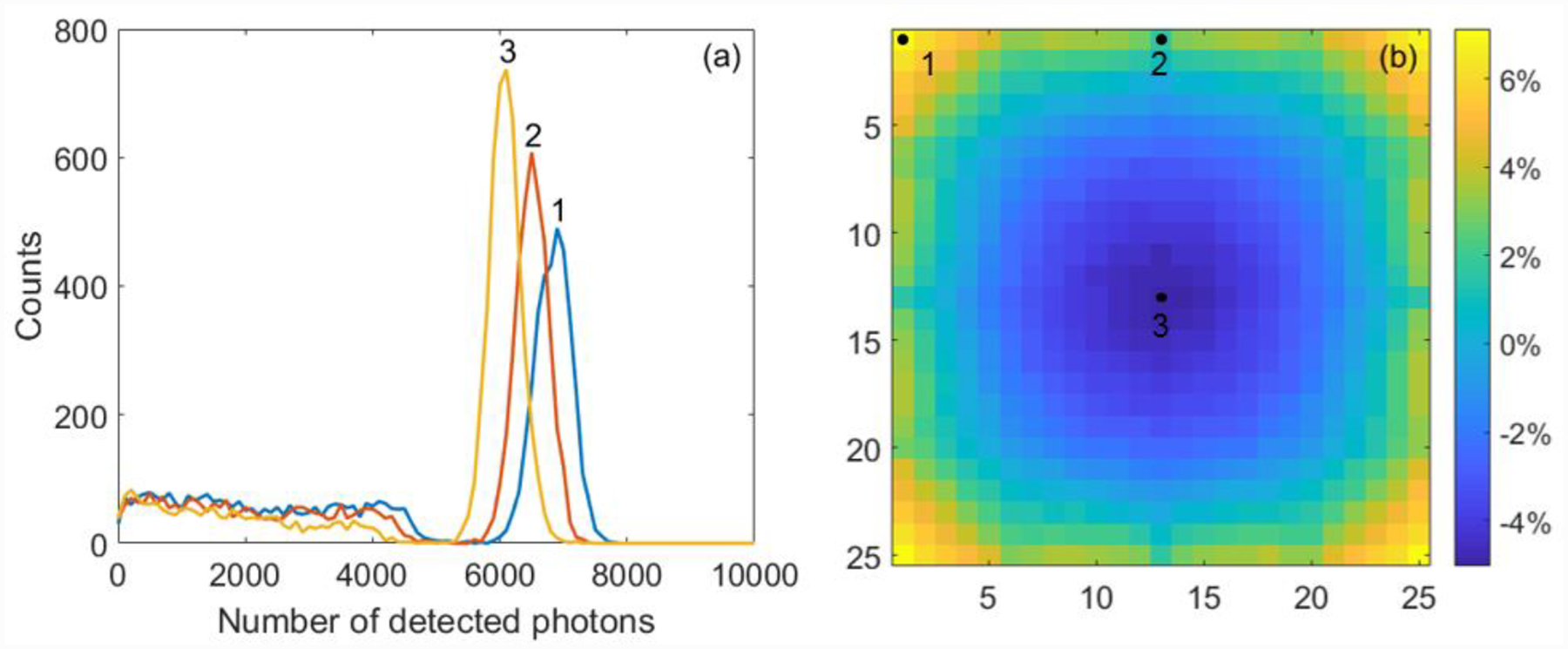
(a): Energy histograms for gamma rays interacting at different positions in the scintillation crystal: corner (1), edge (2), middle (3). (b): The 511 keV photopeak variation for different gamma ray incidence positions. The percentage is with respect to the average peak value (6270 detected photons).

3.2. Spatial resolution

Using the method described in section 2.3.2.2, the average FWHM spatial resolution (x direction, y direction) for the entire detector was (0.40 mm, 0.39 mm), as shown in Figure 13.

Figure 13.

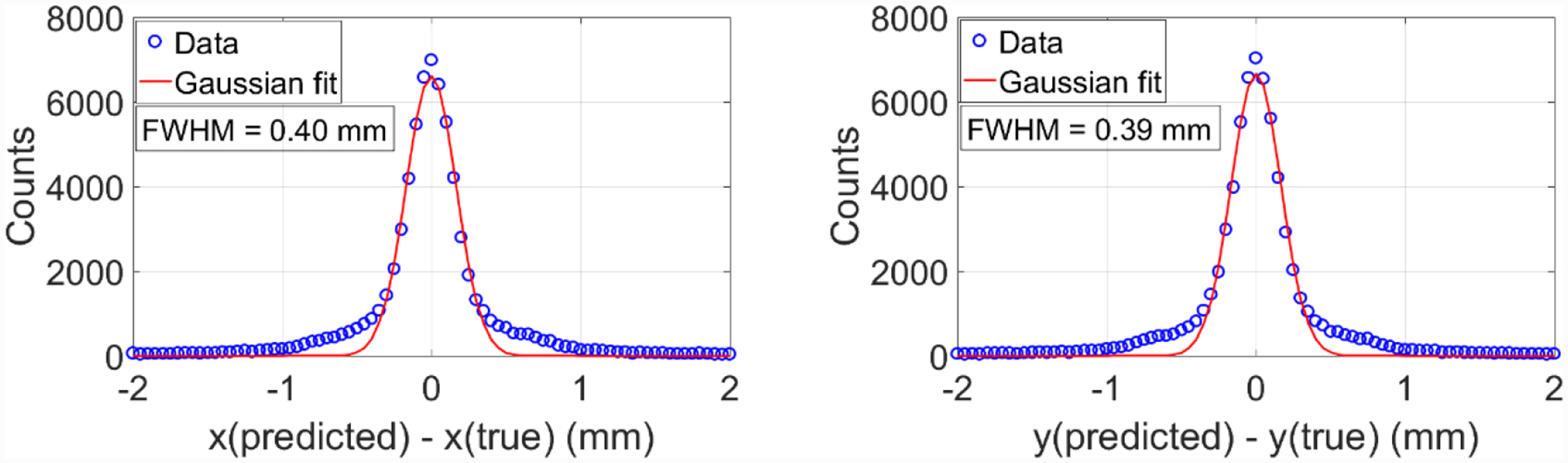
FWHM spatial resolutions along x and y directions.

In Figure 14, the FWHM spatial resolution (x direction, y direction) for different regions on the detector module were measured: center region (0.28mm, 0.27 mm), edge region (0.26 mm, 0.29 mm), and corner region (0.31 mm, 0.28 mm). The values for these local regions have better FWHM than the average across the entire detector, but the edge and corner regions show a position bias (Figure 14c and 14d). This bias is due to two reasons: first, the interpolation method can only give predicted values within the boundary formed by the outermost interpolation points, for interactions located outside the boundary, the prediction will be biased; second, compared to perpendicularly gamma rays used in collection training dataset, the testing dataset used obliquely incident gamma rays (Figure 3). Because the energy window applied around the 511 keV photopeak removes events in which scattered gamma rays escaping the crystal, but keeps events in which scattered gamma rays are reabsorbed by the crystal, this uneven action of the energy window will bias the position predictions for the testing dataset towards the center of the crystal. To study the bias of the predicted interaction locations, Figure 15 shows the dependence of the bias as two testing regions are moved along the x and y direction respectively. The maximum bias is 0.2 mm for the testing region at the edge of the crystal. Since all events with different incidence positions, and therefore different biases, were used to generate the histograms in Figure 13, the average FWHM spatial resolution for the entire detector is worse than that for the individual test regions in Figure 14.

Figure 14.

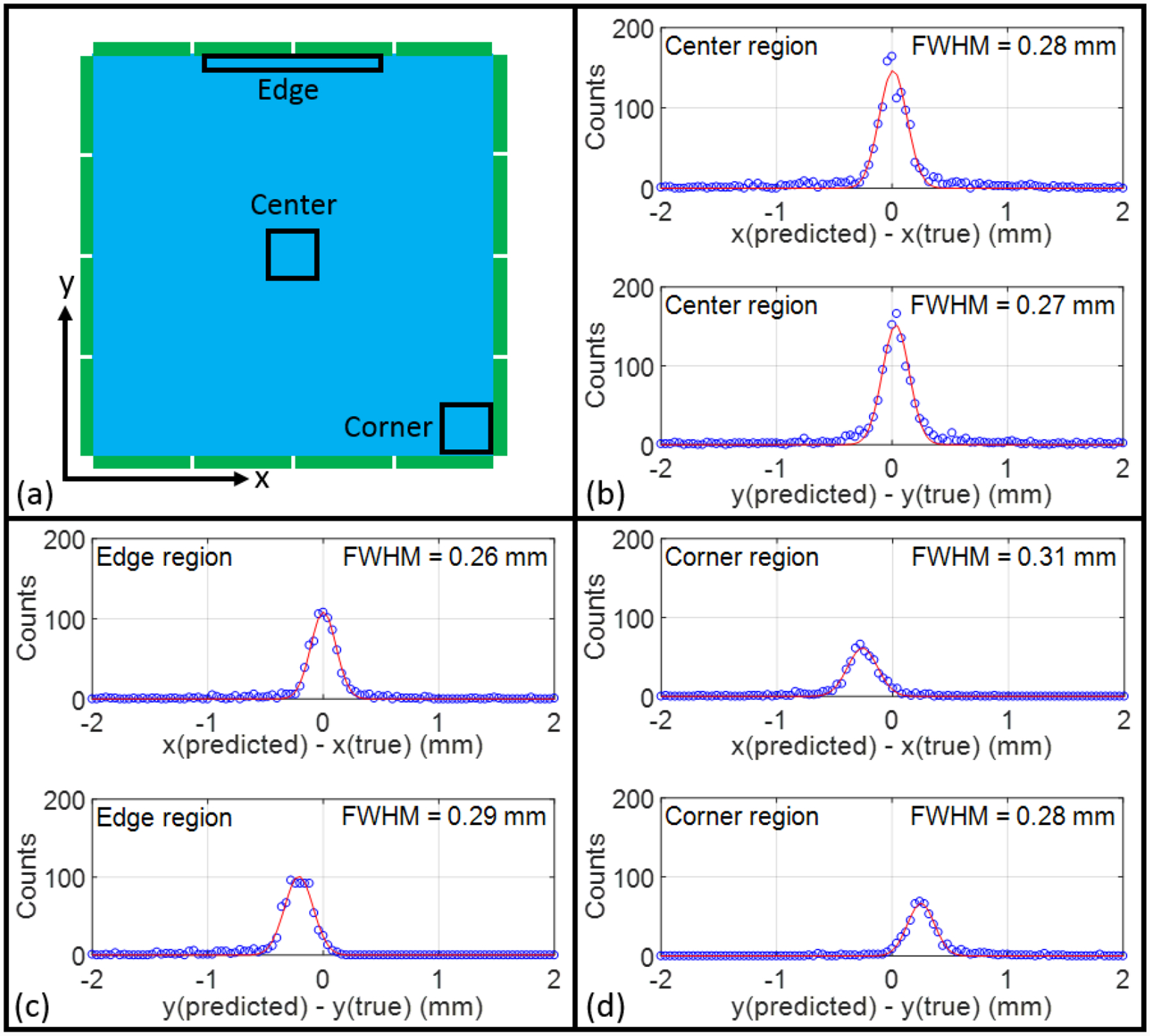
FWHM spatial resolutions along x and y directions for different regions.

Figure 15.

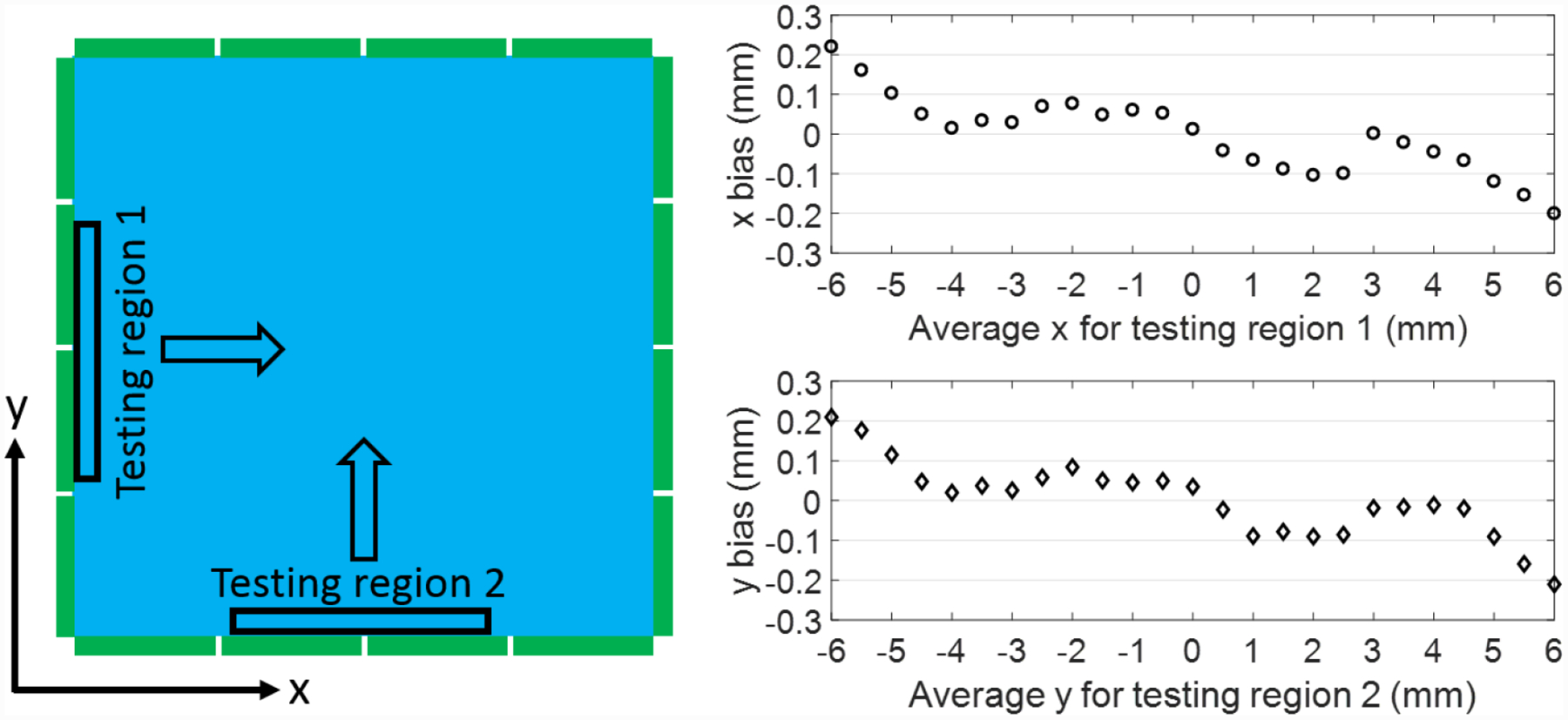
Study of the prediction bias (x bias, y bias) for testing region (1, 2) as the region scans along the (x, y) direction.

Figure 16 shows the histogram for the difference between the predicted z value and the true z value. The predicted z value was the z coordinate for the middle point of the predicted FIL, the true z value came from GATE simulation for the z coordinate of the first interaction point. For 96.6% of all the events, the difference was within ±1.68 mm, the thickness of one layer of the module (3.36 mm). Within the correctly predicted FIL, the events were not uniformly distributed, this was due to the fact that the predicted z value was for the middle point of the layer, but the probability of interaction between a gamma ray and the crystal follows an exponential curve with depth.

Figure 16.

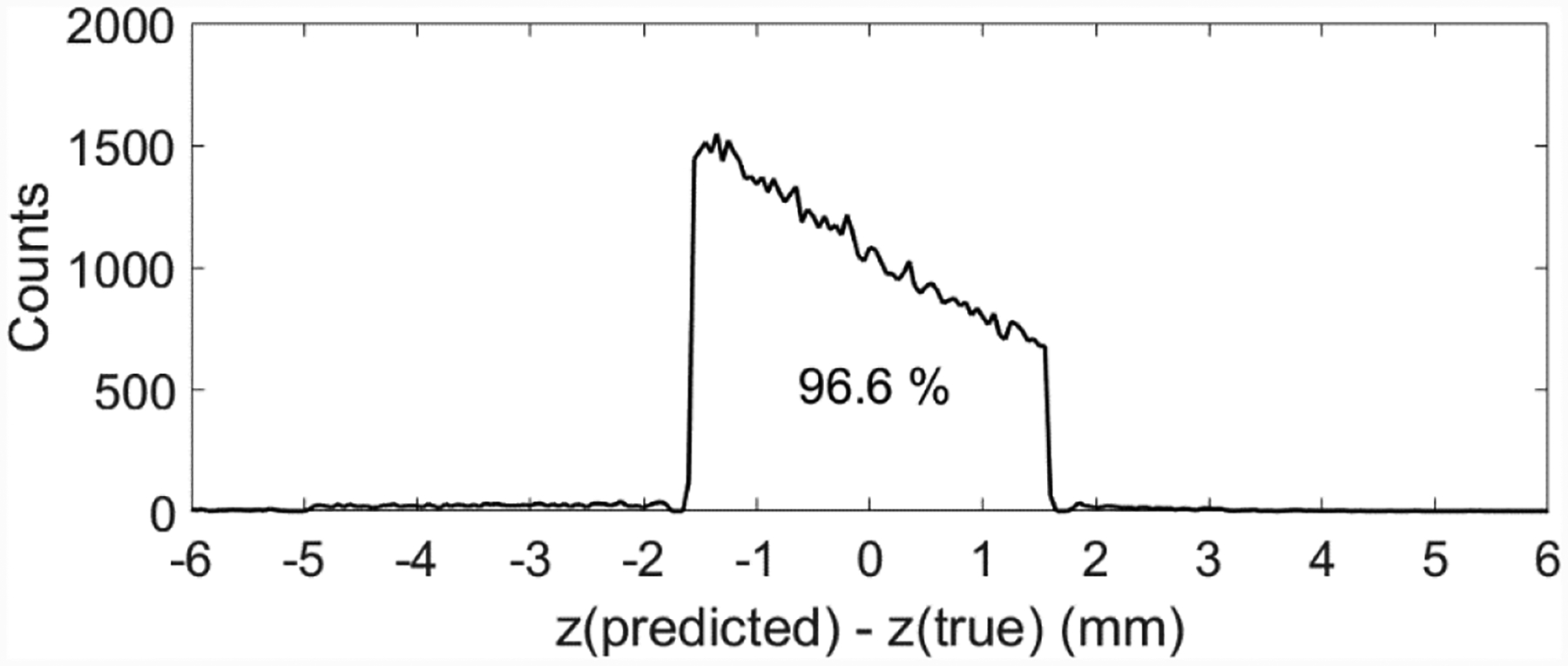
Histogram for the difference between the predicted and true interaction depth (z value).

3.3. Electronic Noise

Figure 17(a) shows that, as expected, the total number of photons at 511 keV is not affected by the added Gaussian noise, however, the FWHM energy resolution for the photopeak increases as more Gaussian noise is added. The spatial resolution also degrades with additional noise (Figure 17b). However, the effect on spatial resolution is small, and even at the highest noise level studied, the resolution did not degrade beyond 0.5 mm.

Figure 17.

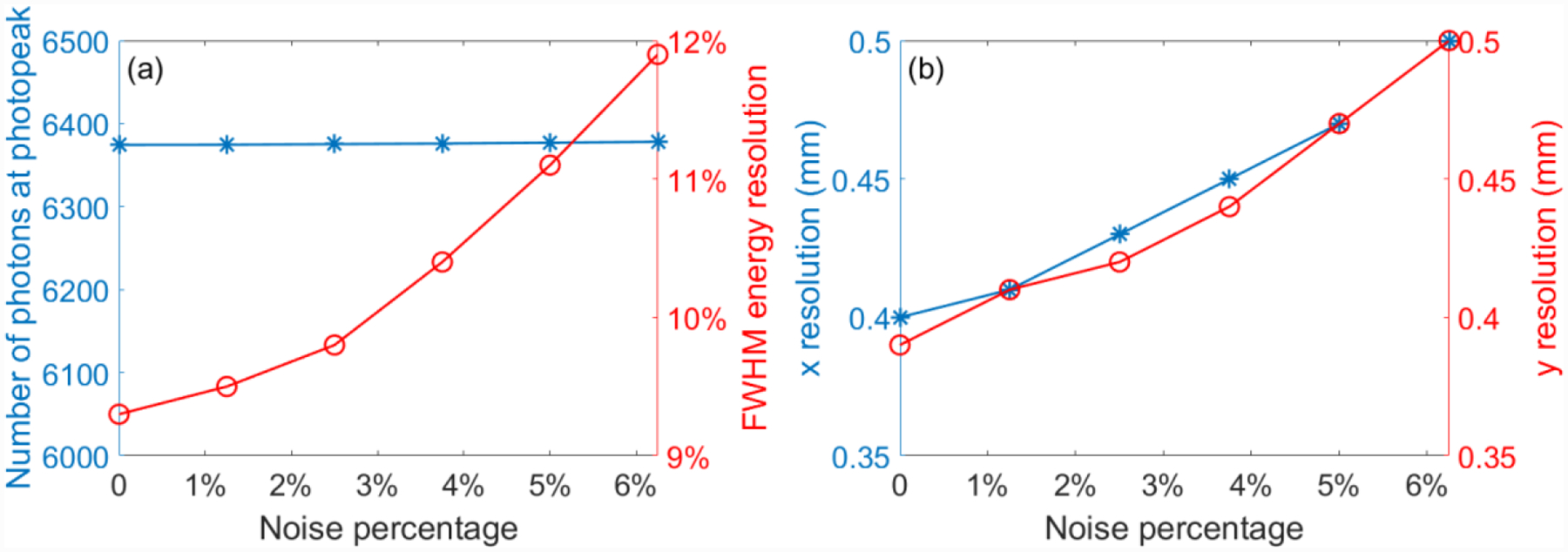
Effect of added electronic noise on (a) the position and FWHM energy resolution of the 511 keV photopeak, (b) spatial resolution along the x and y directions.

4. Discussion

In this paper, we proposed a PET detector module with a new geometry to extract more information regarding the first interaction point of a gamma ray and evaluated the performance using simulated data. The new detector module uses a layered structure with slabs of scintillation crystals stacked along the depth direction. The scintillation light was detected on the four sides of the module. Compared with conventional PET modules [6] with pixelated crystal arrays, more scintillation light can be collected in the new module, due to the decreased trapping of light caused by total internal reflection. The high light collection efficiency helped to improve the FWHM energy resolution to 9.3% in simulation. The semi-monolithic structure of the new module will be easier to manufacture, but poses a bigger challenge for position decoding. In this paper, we developed a position calibration procedure using machine learning. The advantage of machine learning is that the most time-consuming task was to train the neural network. Once the neural network has been trained, the position decoding is very fast using the classification method of the neural network.

In this work, we performed two sets of simulations with GATE. The first set of simulations used perpendicularly incident gamma rays for collecting data to train the neural network. This setup can be realized in experiments as well, in which the ground truth values for the first interaction position were readily available. In the second set of simulations, the gamma ray was allowed to hit the detector module at any position and at any angle. The trained neural network in the first study was used to decode the first interaction position for the second study. An average FWHM spatial resolution of 0.40 mm was achieved for both x and y directions. The addition of independent Gaussian noise of 5% to each detector element only degraded the overall positioning by 0.07 mm which shows the overall robustness of this approach. In the determination of DOI, Compton kinematics was used to find the first layer in which the gamma ray interacted. A figure-of-merit for DOI was defined using the success rate of predicting the correct FIL. In this study, 96.6% of the events were assigned to the correct FIL (3.36 mm thickness).

The next critical step to determine the usefulness of the new geometry is its scalability. Compared to the small module investigated here, we expect the performance of the large size module will be affected by the following issues. First, the dynamic range for the positioning bias (Figure 15) will become bigger, and the spatial resolution will become worse for the entire detector if the bias not corrected. But using a bias correction should minimize this effect. Second, for a large crystal slab, more SiPMs will be placed along the four sides of the crystal (Figure 1), and the average number of scintillation photons detected by each SiPM will be reduced. Assuming the same electronic noise, the effect of the noise on the performance of the module will be greater (section 3.3). This problem can be mitigated by decreasing the electronic noise of the system. Third, for the large size detector module, errors caused by non-uniformity within the crystal or among SiPMs will be more significant, requiring careful sourcing of components. Our plan for this project is next to demonstrate the performance of a small module experimentally, prior to scaling up simulation and experimental work.

The timing resolution is not studied in this paper. Compared to traditional detector designs, it is not clear if the average path length for the earliest arriving photons is longer or shorter in this detector design. In a traditional detector more events interact at the entrance face of the scintillator furthest from the photodetector, and photons often have to undergo multiple reflections before reaching the photodetector. It would be interesting to use Monte Carlo simulation to study the path lengths for the first arriving optical photons for the two different geometries, but that is beyond the scope of this work as the results are very geometry and surface-finish dependent.

One concern for using side readout is the effect of packing fraction on the system sensitivity. The SiPMs and the PCBs (print circuit boards) located along the four sides of the crystal slabs will introduce dead spaces between detector modules, thus decreasing the system sensitivity. The total thickness of the PCB (0.8 mm) and SiPMs (0.6 mm) is 1.4 mm, creating a minimum gap of 2.8 mm between modules in the new design. Comparing the packing fraction for the two designs shown in Figure 1b and 1c, the packing fraction for the Compton module with 50.40 × 50.40 mm² cross sectional area will be: (50.40/53.20)² = 89.8%. For a detector module with pixelated arrays (49 × 49 crystals with 1.09 mm pitch, thickness of reflective films between crystals of 0.07 mm), the packing fraction is: (50.04/53.4)² = 87.8%. The new design, therefore has slightly higher packing fraction than the traditional design using pixelated arrays.

5. Conclusion

In this paper, we studied a novel detector module for PET using GATE simulation. The x, y coordinates for the gamma ray interaction location were determined by decoding the scintillation light distribution on the four sides of the monolithic crystal slab using a trained neural network. The DOI of the gamma ray interaction was determined from the readily available layer structure. Since the x, y, and DOI (z) values indicate the first interaction location in this study, the effect of inter crystal scattering has been nearly eliminated. Since inter-crystal scattering has a stronger effect in high resolution PET detectors, the spatial resolution (0.40 mm) and DOI information that were achieved in this study make the new module a promising candidate for high-resolution PET scanners.