Abstract
During development, progenitor cells follow timetables for differentiation that span many cell generations. These developmental timetables are robustly encoded by the embryo, yet scalably adjustable by evolution, facilitating variation in organism size and form. Epigenetic switches, involving rate-limiting activation steps at regulatory gene loci, control gene activation timing in diverse contexts, and could profoundly impact the dynamics of gene regulatory networks controlling developmental lineage specification. Here, we develop a mathematical framework to model regulatory networks with genes controlled by epigenetic switches. Using this framework, we show that such epigenetic switching networks uphold developmental timetables that robustly span many cell generations, and enable the generation of differentiated cells in precisely defined numbers and fractions. Changes to epigenetic switching networks can readily alter the timing of developmental events within a timetable, or alter the overall speed at which timetables unfold, enabling scalable control over differentiated population sizes. With their robust, yet flexibly adjustable nature, epigenetic switching networks could represent central targets on which evolution acts to manufacture diversity in organism size and form.
Keywords: gene regulatory networks, cell differentiation, epigenetic switches, evolution, development, developmental timing
1. Introduction
How are the sizes and proportions of organs and body plans specified so precisely during multicellular development, yet so readily adjustable by evolution? For over a century, it has been recognized that the timetables of developmental events in the embryo are a central determinant of size and form [1–4]. Because progenitors grow and divide during development, the timing at which they specify different cell types will determine the final numbers and fractions of their differentiated progeny; consequently, changes in developmental timetables can engender variation in size or form. Changes to the timing of individual lineage specification events can give rise to innovations in shape or form [2,4,5], whereas changes to the speed at which developmental timetables unfold can generate proportionally scaled changes in organ and organism sizes [6,7].
As development is not coupled to an external clock, the timetables for developmental lineage specification must be encoded by the embryo itself [8,9]. In general, developmental timetables are the product of an interplay between cell-extrinsic factors, involving dynamic environmental signals, and cell-intrinsic factors, involving regulatory mechanisms inside the cell. Remarkably, in a range of contexts, there is evidence that these timetables are upheld primarily by cell-intrinsic timekeeping mechanisms that appear to operate autonomously after being triggered by external signals [10–15]. For example, during cerebral cortex development, progenitors generate different layers of cortical neurons in a defined order, giving rise to inner layer neurons before outer layer neurons. This same developmental timetable unfolds in vitro [16,17], even in the continual presence of strong inductive signals, suggesting it is largely set in a cell-autonomous manner. Furthermore, though progenitors from different species follow the same lineage specification schedule in vitro, they differ substantially in the speed at which they take to traverse this schedule, ranging from one week in mice to four months in humans [13,18–21]. These results show that timing mechanisms, operating autonomously in progenitor cells, can set defined timetables for developmental lineage specification, and that these timetables can be flexibly expanded or contracted across different species.
Gene regulatory networks control the dynamics of development, and ultimately dictate the timing with which cell lineage specification occurs in response to signals [22–25]. In order to account for the cell-autonomous timing mechanisms described above, these developmental gene networks need to be constructed such that their pace can be readily adjustable both in response to instructive signals or as a result of evolutionary changes. However, we currently lack a quantitative understanding of how these gene regulatory networks can set adjustable temporal schedules over developmental timescales spanning many days and cell generations. One major issue is that genes in regulatory networks are widely assumed to be regulated according to a quantitative framework derived largely from bacterial studies, whereby transcription factor levels determine rates of mRNA synthesis [22,26–28], as a result of their rapid DNA binding and polymerase recruitment. In this classical framework, genes respond to transcriptional inputs over timescales shorter than one cell cycle [29], because their dynamics are constrained by mRNA and protein stability and, by extension, cell cycle speed. Thus, gene regulatory networks regulated by transcription factor levels alone would be unable to set adjustable temporal schedules over developmental timescales spanning many days and cell generations.
In eukaryotes, the dynamics of gene transcription are determined not only by levels of transcription factors in the nucleus, but also by epigenetic mechanisms, involving heritable chromatin states which frequently switch in an all-or-none manner after long time delays spanning many cell generations [30]. In stem and progenitor cells, lineage-specifying genes are often held in a silent, compacted state facilitated by repressive histone modifications [31–33]. While transcription factors bind to these genes to remove repressive modifications at these gene loci, they often do so after many hours or even days [30,34], resulting in long time delays prior to gene activation and lineage specification. In our recent studies of the T cell lineage-specifying gene Bcl11b [35,36], we identified an epigenetic switching mechanism, where repressive chromatin modifications at individual gene loci finely tune the timing at which loci switch from a compacted silent state to an extended active state [37,38]. In contrast to mechanisms involving histone modifications alone [39,40], this methylation-compaction switching mechanism generates delays that are highly controllable at multiple levels of gene regulation—they can be tuned in an analogue manner by transcription factors, chromatin-modifying enzymes, as well as non-coding regulatory elements. With its modularity and ability to set long, tunable time delays, this timed epigenetic switch may constitute a building block for gene regulatory networks that set timetables during development, and implement temporal control functions that are harder to implement with classical networks alone. Indeed, models integrating epigenetic with classical transcriptional control, as investigated in the context of yeast phenotypic switching, plant adaptation and somatic cell reprogramming [41–44], also suggest that epigenetic switching mechanisms could explain some of the unique properties of network dynamics and cell decision making.
In this study, we investigate the temporal behaviours of gene regulatory networks composed of timed epigenetic switches. To do so, we first develop a mathematical framework for modelling such epigenetic switching networks. Using this framework, we then analyse a series of epigenetic switching networks of increasing complexity, starting from single timed epigenetic switches, to networks of two interacting epigenetic switches, to more elaborate networks based on different developmental systems. Through this work, we show that epigenetic switching networks can robustly maintain developmental timetables that span many cell generations and, in conjunction with an appropriate growth control strategy, generate precise numbers and proportions of differentiated cell types. We further show that these epigenetic switching networks can be tuned to alter both the timing of individual developmental events, as well as the speed at which entire timetables unfold, thus allowing for changes in organism size and form. Based on these findings, we propose that epigenetic switching networks underlie the ability of embryos to keep time during development, and are central targets on which evolution acts to facilitate variation in size and form.
2. Results
2.1. Modelling framework for epigenetic switching networks
We develop a quantitative framework for modelling gene regulatory networks composed of timed epigenetic switches. In this framework, we explicitly model the expression levels of network genes, as well as chromatin states at each of their loci. In accordance with our recent findings [37], we describe chromatin states at gene loci using a two-state model with heritable inactive and active states; however, we note that there could be additional hidden states that do not show observable differences in gene expression [30,45]. These epigenetic states are commonly thought to be stabilized by self-reinforcing histone modifications that create a positive feedback loop [39,40,46]; however, our recent study suggests that they may instead be stabilized by inter-nucleosomal interactions that result in the formation of a stable compacted chromatin structure [38]. Of note, this model can alone explain why histone modifications often correlate weakly with the gene activation state, and how rates of epigenetic switching can be tunably controlled by both transcription factors and chromatin regulators, in accordance with direct observations of stochastic epigenetic switching dynamics at the single-cell level [30,38]. Finally, we model growth and division of individual cells, together with its interplay with gene regulatory network activity.
Consider a network of N regulatory genes (figure 1a). Let Pi be the number of active loci of gene i in the cell (figure 1b). Let Xi be the copy number of its gene product. Let V(t) be the volume of the cell, such that xi = Xi/V is the concentration of protein i. The time evolution of these variables is given by the following rules:
| 2.1 |
| 2.2 |
| 2.3 |
| 2.4 |
Here, gene i switches from an inactive (active) to an active (inactive) epigenetic state with first-order kinetics, with a stochastic time constant of αi (βi). Consistent with work from our laboratory and others [30,38], both locus activation and silencing rates depend on x1 … xN, such that constants for epigenetic switching depend on regulatory input levels, which may either involve transcription factors or chromatin-modifying enzymes [38]. Once in an active state, gene i is synthesized with rate constant γi, and its encoded gene product Xi is then actively degraded with rate constant δi. PT is the total number of copies of each gene; in all simulations here, PT is taken to equal unity, under the assumption that copy number effects do not alter the emergent properties of the regulatory network considered here. Rates of promoter switching and protein degradation increase linearly with cell volume, reflecting an increase in molecular content with cell size; in accordance with previous observations [47], the rate of transcription also increases with cell volume, a mechanism that keeps steady-state protein concentration constant amid cell size variations. We note that, when the promoters of all genes are always in an active state, i.e. when Pi = 1, where i = 1 · · · N, this network reduces to one where individual genes are governed exclusively through classical gene regulation functions (figure 1c).
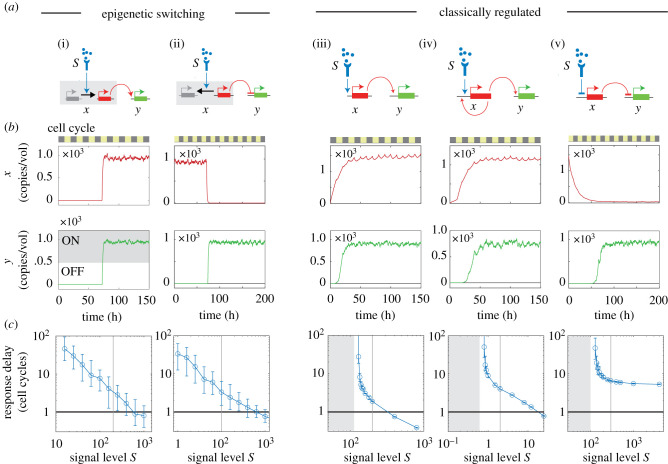
Figure 1.
Mathematical framework for modelling epigenetic switching networks. (a) Gene regulatory network, with single gene (i) highlighted. (b) Gene promoter undergoing epigenetic switching. (c) Classically regulated gene promoter. Xi gives the expression level of gene i; Pi gives the epigenetic state of gene promoter i. Also shown are rate constants for promoter activation αi, promoter silencing βi, protein synthesis γi and protein degradation δi. (d) Cell growth and division results in random partitioning of proteins, and inheritance of promoter states. (e) An epigenetic switch for gene X (left) is activated by an upstream signal S at t = 70 h. Plots show time evolution of copy number (X, top right) and concentration (x = X/V, bottom right), obtained using stochastic simulations. Zebra stripe indicates the timing of cell division events.
To model this gene regulatory network within cell lineages, we account for individual cells within lineage trees. Let M be the total number of cells in a given lineage, and let the mth cell in this lineage have promoter states and protein levels . Let this cell have volume Vm, birth time , and life time (figure 1d). Finally, let the cell cycle state of the cell be captured by a binary variable cm, that has a value of one when the cell is actively cycling, and zero when the cell has exited the cell cycle.
If cell m in the lineage is actively cycling cm = 1, its volume increases linearly during its lifetime to reflect cell growth (figure 1d):
| 2.5 |
where
| 2.6 |
At the end of its lifetime, cell m divides to generate two daughter cells, n and p. Its regulatory proteins partition randomly into the two daughters at the time of cell division, such that their numbers follow a binomial distribution:
| 2.7 |
On the other hand, gene promoters maintain their epigenetic states across cell division, such that
| 2.8 |
and
| 2.9 |
Cells that are not cycling (cm = 0) are taken to be irreversibly differentiated, and are not further analysed by modelling, though they are counted to obtain differentiated cell numbers. Following previous findings [48], the decision to exit the cell cycle is made at the cells’ birth, and will depend on both regulatory network state and cell division mechanism, as we discuss below.
To obtain regulatory network dynamics in a cell lineage, together with the structure of the lineage tree itself, we simulate the stochastic chemical reactions describing the network (equations (2.1)–(2.4)) in single cells using the Gillespie algorithm [49], while setting lifetimes, growth rates and initial conditions of simulated cells according to the rules above (equations (2.5)–(2.9)) (figure 1e). For each lineage, we begin by simulating a single progenitor cell. At the end of its lifetime, this cell divides; daughter cells inherit their mother’s regulatory network state (equations (2.8)–(2.9)), and also set their cycling states based of the states of their regulatory networks. Each daughter cell is then simulated, and this process continues iteratively until all cells withdraw from the cell cycle, or until a simulation time limit is reached. This algorithm generates a list of cells, a lineage tree showing the relationships between these cells, and Monte Carlo simulation results for each cell.
2.2. Epigenetic switches generate tunable timing delays
To understand the temporal properties of gene regulatory networks consisting of multiple interacting epigenetic switches, we first analyse networks consisting of single epigenetic switches. We compare these networks to those consisting of classically regulated genes, whose transcription factor levels alone determine transcription rates. For both types of gene networks, we measure the relationship between the magnitude of an input signal and the time delay to an output response, to determine the conditions under which they can robustly respond with delays that are tunably controlled by regulatory inputs.
Classically regulated genes typically respond to regulatory inputs within one cell generation, as their expression dynamics are shaped by the mRNA and protein half-life, which are in turn determined by cell cycle duration [22,29]. Epigenetic switching genes, on the other hand, could in principle respond and be controlled over a much wider range of timescales, as their switching dynamics are uncoupled from cell division and are instead determined by heritable chromatin conformation states at the gene locus. To test this idea, we analysed a series of simple gene regulatory networks, where a regulatory gene X receives an input from an upstream signal S and in turn activates a downstream response gene Y (figure 2a(i–v); electronic supplementary material, mathematical appendix, Part I). X is either regulated by a timed epigenetic switch, whose activation rate varies with input signal levels S (figure 2a(i,ii); see electronic supplementary material, table 1 for parameter values), or regulated classically, with transcription rates controlled by signal S (figure 2a(i,ii); see electronic supplementary material, table 1 for parameter values). For each network, we performed simulations to measure its response delay, defined as the time between signal onset and expression of the output gene above a threshold. We considered both signal-induced promoters, that promote response gene expression (figure 2a(i,iii,iv); see electronic supplementary material, tables 1 and 2 for parameter values); and signal-repressed promoters, that inhibit response gene expression (figure 2a(ii,v); see electronic supplementary material, tables 1 and 2 for parameter values). In all cases, we both performed stochastic simulations and calculated analytical expressions for response times (electronic supplementary material, mathematical appendix, Part II), to determine the generality of our findings.
Figure 2.
Epigenetic switches generate long, tunable delays in gene activation. Using stochastic simulations, we determined response times of different gene promoters (i–v), as indicated. Response times are defined as the delay between onset of an input signal S and activation of a response gene Y. For each promoter type, we show circuit diagrams (a), simulation time traces (b) and response delays, plotted against signal levels (c). Circles and error bars represent the median and inter-quartile range of the response time distribution, obtained over N = 100 simulations; the grey shaded area indicates the range of signals over which the circuit fails to respond.
From both simulations and analytical work, we find that epigenetic switches generated extended response delays that are tunable over a wide range of input signal levels. When exposed to strong signals, both signal-induced or signal-repressed promoters switched rapidly, resulting in rapid response gene induction; however, when signal levels decreased, gene switching rates decreased substantially, leading to longer delays spanning multiple cell generations in gene induction (figure 2b,c,(i,ii); see electronic supplementary material, table 1 for parameter values). Response delays were variable from cell-to-cell, reflecting the inherently probabilistic nature of switching. However, in both cases, response time distributions were well defined, with average values that could be controllably varied over a wide range of timescales by varying signal magnitude (electronic supplementary material, mathematical appendix, Part II).
Classically regulated genes, on the other hand, were more limited in their ability to generate long, tunable response delays. As these gene promoters express immediately upon signal exposure, the response delays they generate would depend on the time at which their expressed gene products reach a threshold for downstream gene induction. For signal-induced promoters, this threshold is either crossed within one cell generation, or, when signals are weak, not crossed at all (figure 2c(iii); see electronic supplementary material, table 2 for parameter values), resulting in a sharp divergence in response times below a certain threshold level of signal. This ‘now-or-never’ behaviour arises because signal strength S determines the final steady-state level of X, which may or may not exceed the response threshold. Furthermore, cell cycle duration imposes an upper limit on the half-life of the expressed protein, which determines its rise kinetics and the timing at which the response threshold is reached. Positive feedback on the gene prolonged response times, as previously observed (figure 2c(iv); see electronic supplementary material, table 2 for parameter values) [29]; however, delays exceeding one cell generation still occurred only over a narrow signal range, and there remained a large range of signals over which the system did not respond. To determine the generality of the result, we solved analytically for the system response times, both with and without positive feedback. In both cases, we found that defined response delays exceeding more than one cell generation could be upheld only over a very narrow range of system parameters; slight changes to the parameters resulted in either a failure to respond, or a substantial shortening of the response delay.
For a classical signal-repressed promoter, responses could be delayed over many cell generations, if the threshold level of X below which gene Y turns on is much lower than initial level of X (figure 2b(v); see electronic supplementary material, table 2 for parameter values). Furthermore, this response delay is much less variable from cell-to-cell when compared to those generated by epigenetically switching gene promoters (figure 2c(v)). However, simulations and analytical work revealed that this long response delay cannot be tuned by levels of S; it remains largely constant over a range of signals, and diverges below a critical threshold, resulting in a failure to respond (figure 2c(v)). Signal-dependent tuning of response delays could occur when signal levels were close to this critical threshold (electronic supplementary material, mathematical appendix, Part II); however, as with signal-induced genes, small changes in signal levels in this regime would lead to a failure to respond, or substantially shorten response delays. Taken together, these results indicate that classically regulated genes, in contrast to epigenetic switching genes, are fundamentally limited in their ability to generate tunable response delays that span multiple cell generations.
2.3. Networks of epigenetic switches uphold temporal schedules for gene expression
As networks with single epigenetic switches generate long, tunable delays in gene activation, networks with multiple interacting epigenetic switches could orchestrate more complex timetables for gene expression over long timescales. Here, we analyse the temporal properties of two epigenetic switching networks with different architectures that are frequently found in development contexts: negative feedback loops [50,51] and mutual inhibitory loops [22,52].
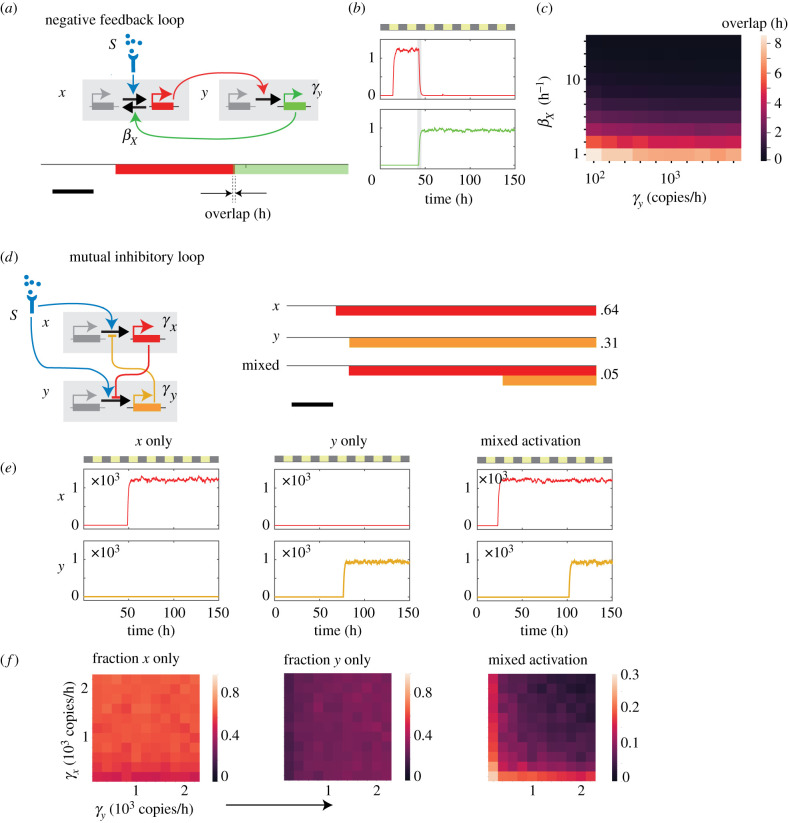
In the gene networks controlling nervous system development in flies and mammals [50,51,53], genes known as ‘temporal’ transcription factors form sequential negative feedback loops, where an upstream lineage-controlling transcription factor activates the expression of a downstream lineage-controlling transcription factor, which in turns inhibits expression of the preceding transcription factor. Such sequential negative feedback loops can restrict the expression of transcription factors to disjoint time windows. Using mathematical modelling, we ask whether negative feedback loops in regulatory networks of epigenetic switches can generate sequential temporal windows of regulatory gene expression. We consider a simple network, where a signal S activates the promoter of regulatory gene X (figure 3a, top left) (electronic supplementary material, mathematical appendix, Part II; see electronic supplementary material, table 3 for parameter values). X then activates the promoter of regulatory gene Y, which feeds back to inactivate the promoter of X. From Monte Carlo simulations, we found that this network generated sequential temporal windows for X and Y expression (figure 3a; bottom, right). These temporal windows each spanned multiple cell generations, and were largely mutually exclusive, though there were periods of temporal overlap in the expression of the two genes, whose durations depended on the rate of X promoter silencing by Y (figure 3c). These simulation results show that negative feedback between two epigenetic switches can generate sequential temporal windows of gene expression.
Figure 3.
Epigenetic switching networks uphold robust timetables for gene expression. (a–c) Negative feedback loops generate sequential time windows for expression. Shown are a network diagram (a, top), a timetable for gene expression (a, bottom) and a representative simulation trace (b), with temporal overlap in the expression of the two genes indicated in grey shading. Heatmap shows this temporal overlap plotted against the X promoter inactivation rate (βX) and the Y synthesis rate (γy). (d–f) Mutual inhibitory loops generate multiple concurrent timetables from the same starting cell population. Shown are a network diagram (d, left), timetables for cell expressing X, Y, or both genes in a mixed manner (d, right), and representative time traces for each of these populations (e). Heatmaps show the fractions of cells in each of these populations as a function of X synthesis rate γX, and Y synthesis rate γY.
Mutual inhibitory circuits, involving antagonistic interactions between two regulatory genes, can enable stabilization of multiple cell types during development [52,54,55]. When these interactions involve epigenetic switching genes, they may allow for stochastic establishment of mutually exclusive patterns of gene expression, and thus allow for multiple cell types to emerge in time from a common progenitor population [55]. To test this idea, we modelled a simple mutual inhibitory network consisting of two regulatory genes, X and Y, both of which are regulated by timed epigenetic switches. Both epigenetic switches activate in response to a common signal S, and both are inhibited in their activation by each other’s expression (figure 3d, left) (electronic supplementary material, mathematical appendix, Part III; see electronic supplementary material, table 3 for parameter values).
From simulations, we found that mutual inhibitory loops between epigenetic switches could generate multiple parallel temporal schedules for gene expression in response to same inducing signals. Two of these schedules involved the expression of either x or y alone, whereas the third schedule involved the concurrent expression of x and y in the same cell (figure 3d,e). When transcriptional rates of X or Y were decreased, the fraction of cells expressing either X or Y remained similar, indicating that the cell fractions are robust to changes in these parameters. However, the fraction of cells showing stable co-expression of the two regulatory genes increased, reflecting a weakened antagonism between these two genes (figure 3f). These results show that mutual inhibitory loops of epigenetic switches allow multiple timetables to unfold in parallel, and allow the fractions of these cells executing these different programmes to be tuned in a graded manner.
2.4. Networks of epigenetic switches generate multiple cell types in defined numbers
Developmental timetables set by epigenetic switching networks are variable from cell-to-cell due to the inherently stochastic nature of epigenetic switching (figure 2c(i,ii)); given this variability, it is unclear how these timetables could enable the generation of different cell populations with defined sizes.
Here, we analyse different coupling schemes by which gene regulatory networks control division and differentiation, to determine whether there are particular schemes that support robust population size control. We first considered a simple scheme, where gene activation directly induces differentiation (electronic supplementary material, mathematical appendix, Part IV). In this scheme, progenitors divide and self-renew until a signal S activates a gene Y that induces cell cycle exit and terminal differentiation (figure 4a(i,ii); see electronic supplementary material, table 4 for parameter values). Consistently, a number of regulatory genes can directly induce cell cycle exit and differentiation [56–58]. We then coupled this scheme to an epigenetic switching network, where activation of Y is controlled by an upstream epigenetic event on an upstream regulator X (figure 4a(ii)). For comparison, we also considered a classical regulatory gene network, where activation of Y occurs due to dilution of an upstream inhibitor X that is in turn repressed by signals (figure 4a(i)).
Figure 4.
Epigenetic switching networks enable the generation of multiple cell populations in defined sizes and fractions. Two cell division coupling schemes are considered: one where gene activation induces differentiation and cell cycle exit (a), and another where gene activation controls the duration of a competent state, where non-dividing progeny are generated by asymmetric division (b(i), c) or stochastic mechanisms (b(ii)). In the first scheme, gene activation is induced by repression of an upstream inhibitor (a(i)), or by epigenetic switching of an upstream activator (a(ii)). In the second scheme, epigenetic switching of an activator either induces a gene that promotes exit from a competent state (b), or promotes entry into second competent state (c). Each panel includes representative lineage trees superposed with coloured bars denoting when the gene is expressed, area plots showing averaged cell numbers over time, as well as additional plots as indicated. Vertical bars denote concentration ( (a(i)), (b(i)); red = (a(i,ii))), and horizontal scale bars denote time (10 h).
When gene activation was controlled through classical trans-mechanisms (figure 2(ii)), progenitors could expand to generate larger progeny numbers through multiple rounds of cell division (figure 4a(i)). However, when gene activation was controlled by epigenetic switching (figure 4a(ii)), progenitors were not able to generate fixed progeny numbers. When input signals were high (S > 4), gene activation and differentiation occurred quickly, within a single cell generation; in this regime, progenitors could give rise to defined progeny numbers, but only with a minimal degree of cell expansion. On the other hand, input signals decreased, gene activation timing became protracted over many cell generations; however, progenitor numbers increased in an unbounded manner, reflecting the inability of rare probabilistic events to curtail exponential growth.
In some developmental systems [50], regulatory genes may not directly induce differentiation, but instead control the entry or exit of progenitors from a competent state, where they can differentiate. Progenitors in this competent state differentiate by asymmetric cell division, where they give rise to a progenitor and a terminally differentiated cell. Such asymmetry could occur through uneven partitioning of fate determinants, as observed in a number of systems [59,60]. Alternatively, it could occur through a separate stochastic mechanism, where differentiated progeny are generated with a fixed probability during each cell division [61].
Here, we ask whether epigenetic switching networks, when coupled with a competent state control scheme, could generate defined numbers of differentiated cells (figure 4b). We first considered a simple network, where progenitors initially adopt a competent state, but eventually exit this state upon activation of a regulatory gene Y. Y is activated by X, whose promoter undergoes an epigenetic switching event controlled by signal S (figure 4a(ii)). We considered both differentiation strategies discussed above, where competent progenitors differentiate either by deterministic asymmetric cell division, or through stochastic mechanisms (figure 4b(i,ii); see electronic supplementary material, table 4 for parameter values).
From simulations, we found that coupling epigenetic switching to competent state exit allowed for generation of differentiated progeny from rare starting progenitors. For both asymmetric and stochastic strategies for differentiation control, individual starting progenitors gave rise to heterogeneous numbers of offspring, as expected; however, larger cohorts of starting progenitors showed precise final fold increases in cell number, by averaging across multiple cell lineages (figure 4b(i)). In this scheme, population sizes increased with decreasing signal strength, reflecting the lengthened period of time a progenitor cell spends in a competent state. For stochastic control strategies, defined output population sizes were maintained when differentiation probabilities were close to one half per cell generation (figure 4b(ii)). Notably, when competent state differentiation probabilities decreased beyond a threshold level, the number of output cells diverged in an unbounded manner (figure 4b(ii)), thus reflecting the importance for these probabilities to be specified within a narrow range. Such tight control of differentiation probabilities is important for adult stem cell homeostasis [61], and could also occur during embryonic development.
When developmental timetables set by epigenetic switching networks involve activation of multiple regulatory genes, they could give rise to multiple competent states that specify different cell types. Such a coupling may enable progenitors to not only control the numbers of different cell types, but also their relative proportions. To explore this idea, we analysed a simple epigenetic switching network that controls the switching of progenitors from one competent state to another. In this scheme, progenitors exist in a first competent state (figure 4c, blue), but enter a second competent state upon activation of Z by an upstream signal S (figure 4c, red). The expression of Z is controlled by an epigenetic switch, whose activation probability is tunably controlled by S. In both competent states, a second gene Y activated by an upstream regulator X works independently to drive cell cycle exit. The activation of X is controlled by an epigenetic switch on its locus. In both competent states, differentiated cells are generated through asymmetric cell division; however, similar conclusions are expected when differentiation from the competent state is controlled through stochastic mechanisms.
From simulations, we find that this epigenetic switching network, when used to control transitions between two competent states, generates two cell types with controllable numbers and proportions. As expected, progenitors switched from one competent state (blue) to the next (red), giving rise to the two progeny types in sequence (figure 4c). Increasing signal strength S, which accelerates switching to the second competent state, proportionally increased the numbers of the second cell type. Notably, changing signal levels S did not affect the total number of output cells, which would instead be modulated by the activation of gene Y and, consequently, by the activation timing of the epigenetic switch controlling the expression of X. Thus, regulatory inputs into epigenetic switching networks can be tuned to control the relative proportions of multiple cell types that emerge without altering their total numbers.
2.5. Flexible adjustment of developmental timetables during evolution
While developmental timetables are robustly defined in a developing embryo, they can vary widely across individuals and species, leading to variation in organ and organism sizes and proportions [5,9]. Below, by analysing mathematical models of epigenetic switching networks from different developmental systems, we show how evolutionary mutations can readily act on epigenetic switching networks to generate changes in organism size and form. In the first case, on body axis patterning by the Hox gene network, we show how non-coding mutations affecting epigenetic switching of individual genes can alter developmental events in timetables, and lead to shifts in cell type proportions. In the second case, on cerebral cortex development, we consider how changes to chromatin modifying enzymes can uniformly expand or contract developmental timetables, leading to scaled changes in total organism size.
2.6. Non-coding mutations affect developmental timing and cell type proportion
Patterning of the vertebrate body axis requires Hox genes, a family of transcription factors that form a regulatory network to specify segment identity. Hox genes follow a defined timetable for activation in the embryo, where those specifying the anterior turn on before those specifying the posterior (figure 5a; see electronic supplementary material, table 5 for parameter values) [9,62–65]. Changes in the relative timing of Hox gene activation, caused by mutations in non-coding regulatory sequences, can shift anterior/posterior proportions: targeted deletion of an enhancer for Hoxd11—a posterior-specifying Hox gene—delayed its activation, and shifted the sacrum towards the posterior [65]. Conversely, substitution of this enhancer for its more active fish counterpart accelerated gene activation, resulting in an anterior shift in sacrum positioning [66].
Figure 5.
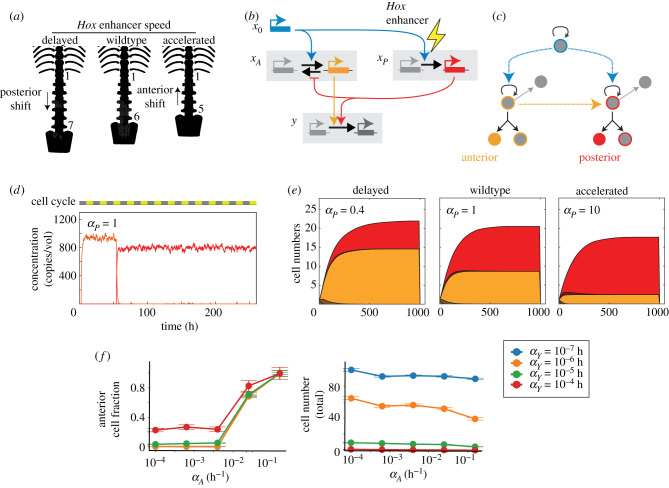
Non-coding mutations in epigenetic switching networks can alter developmental timing and cell type proportions. (a) Anterior–posterior positioning by Hox gene activation. (b) Minimal epigenetic switching Hox gene network, including an anterior Hox gene (xA), a posterior Hox gene (xP), an upstream regulator (x0) and a cell-cycle exit regulator (y). (c) Cell proliferation control scheme, showing anterior and posterior cells specified by these two regulators. (d) Representative time traces of anterior and posterior Hox gene levels (xA and xP) in simulated single progenitor lineages. (e) Area plots so averaged numbers of anterior- and posterior-specified cells over time, for three different relative rates of xP activation αP. (f ) Plots showing total cell number and fraction of anterior cells for different epigenetic activation rates of the anterior Hox gene, αA, and the cell-cycle exit regulator, αY. These two rates independently control the fraction of anterior cells (left) and the total number of cells (right), respectively.
This temporal progression of Hox gene activation may be regulated by timed, stochastic epigenetic switches. Hox gene activation requires active histone H3K27me3 removal controlled by PRC2 and demethylases [67,68], and also involves decompaction of individual gene loci [67,69]. Moreover, like Bcl11b, Hox genes show variable regulation not only between cells, but also between individual loci within individual cells [69,70], consistent with stochastic epigenetic control occurring at single loci. Based on these findings, we constructed a minimal model of a Hox gene epigenetic switching network, and asked whether non-coding mutations previously found to impact Hox gene expression [65,66] indeed alter gene activation timing and anterior/posterior proportions, as experimentally observed (figure 5b; see electronic supplementary material, table 5 for parameter values) [62,65] (electronic supplementary material, mathematical appendix, Part V). For simplicity, we aggregate anterior- and posterior-specifying Hox genes into two groups, xA and xP. Both anterior and posterior gene groups are activated by a common upstream input x0, whose function is to trigger an epigenetic switch leading to gene activation. Anterior (posterior) Hox genes have a faster (slower) time constant for activation, reflecting the order of activation encoded in the embryo. Once activated, posterior Hox genes silence anterior Hox gene expression, reflecting a phenomenon known as posterior dominance [63]. Gene silencing is taken to be fast, such that anterior and posterior Hox gene expression is mutually exclusive. When expressed, the anterior (posterior) Hox gene group cause progenitors to reside in a competent state, where they give rise to anterior (posterior) cell types. Here, we assume these progeny are generated through asymmetric cell division (figure 5c; see electronic supplementary material, table 5 for parameter values), as described (figure 4), though we expect similar conclusions when they are instead generated through stochastic mechanisms.
This minimal Hox gene epigenetic switching network recapitulated key features of anterior and posterior specification. As expected, Hox genes turned on in an ordered temporal sequence with the anterior Hox gene group turning on first, and with subsequent activation of the posterior Hox gene resulting in rapid anterior gene silencing (figure 5d). Gene activation led to concomitant generation of anterior and posterior cells, with both populations expanding to reach a defined final size. To model the effects of disrupting the Hoxd11 enhancer, we changed the activation rate constant for the posterior Hox gene group αP, either decreasing it to mimic deletion, or increasing it to mimic a more active variant. Consistent with experimental findings, lowering (raising) this rate constant diminished (enlarged) the posterior cell population relative to the anterior cell population, by shortening (lengthening) the time window over which this cell population was specified (figure 5e). Interestingly, total population sizes remained largely constant amid this change in posterior rate. Similarly, changing the epigenetic activation rates of the anterior Hox gene, αA, changed the fractions of anterior cells without changing population sizes, whereas changing activation rates of the cell cycle exit regulator, αY, altered the total population size while keeping population fractions constant. These results show how non-coding mutations affecting epigenetic switching rates in gene regulatory networks, by changing the timing of individual developmental events, can independently change cell population fractions and sizes.
2.7. Chromatin-modifying enzymes can scalably expand or contract developmental schedules
Evolutionary mutations lead not only to changes in the timing of events within developmental timetables, but also to differences in the speed at which these timetables unfold across different species [6,7], as is the case for cerebral cortex development and other developmental contexts [13,16–18,20] (figure 6a). Chromatin modifying enzymes, with their broad action and ability to modulate epigenetic switching at multiple gene loci, could globally alter the overall dynamics of epigenetic switching networks, and affect the speed at which temporal schedules set by these networks unfold. Consistently, disruption of chromatin modifying enzymes often results in changes to the speed of developmental transitions [38,71–73].
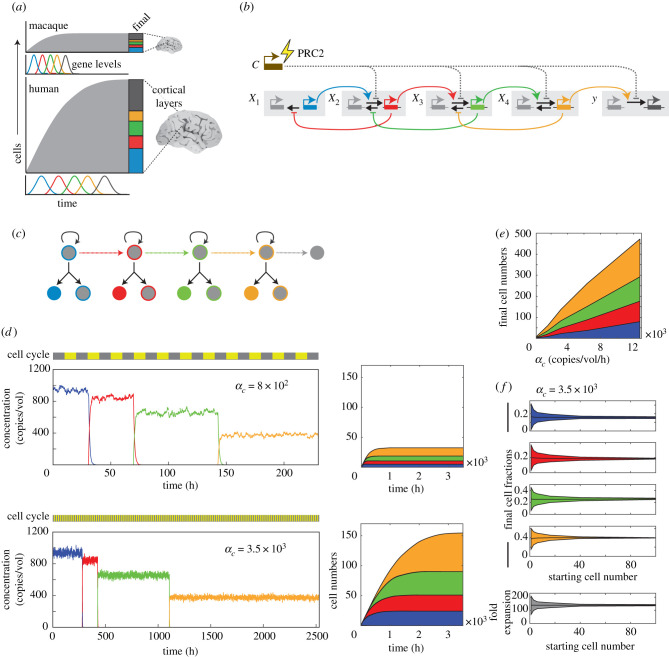
Figure 6.
Chromatin regulators can scalably expand or contract developmental timetables to modify total organ size. (a) Cerebral cortical layers in different species [13]. (b) Gene regulatory network controlling the specification of different cerebral cortical layers. (c) Asymmetric division scheme for neuronal differentiation, with cell states coloured according to expression of network regulators in (b). (d) Representative time traces (left) and averaged cell number area plots (right) for single lineage simulations, performed with higher (top) or lower (bottom) rates of chromatin regulator transcription αc. (e) Output numbers of different cortical layer neuron types as a function of αc. (f) Output fraction of neuron types (top), along with total fold expansion in cell number (bottom), plotted as a function of starting cell number. Line and shaded area represent mean and standard deviation. These results show that progenitors can generate multiple cortical layer neurons with precisely defined fractions, and that final cell numbers can be scalably adjusted by varying the chromatin regulator levels.
To test whether chromatin-modifying enzymes could act on epigenetic switching networks to control developmental speed, we developed a regulatory gene network model for cerebral cortex development. This network has a core architecture elucidated in work on Drosophila, but may also underlie neural development in vertebrates [50,53]. This architecture consists of a cascade of transcription factors that activate each other’s expression in succession (figure 6b; electronic supplementary material, mathematical appendix, Part VI; see electronic supplementary material, table 6 for parameter values). When activated, the regulators induce a competent state, where a distinct cortical neuron type is produced through asymmetric progenitor division, or, in the case of the last regulator in the sequence, induce cell cycle exit, as observed [50] (figure 6c; see electronic supplementary material, table 6 for parameter values). These regulators also repress their upstream activators in a negative feedback loop, to ensure their mutually exclusive expression (figure 6b). Finally, broadly acting chromatin regulators such as PRC2, which can act to control epigenetic switching rates [38], provide an additional input into all other regulatory genes in the sequence, working to dampen their rates of promoter activation.
From simulations, we found that regulatory genes in this cascade turned on in a defined temporal order, consistent with experimental findings. Activation of a gene led to rapid silencing of its preceding regulator, as expected (figure 6d, top), allowing these regulators to be expressed in sequential waves in single cell lineages. Activation times of regulators varied from cell to cell, leading to heterogeneity in the final numbers and fractions of different cortical layer types generated from a single progenitor (figure 6f). However, as starting progenitor numbers increased, variability in cell type fractions decreased, showing that timing control that is stochastic at the single cell level can lead to precise control of cell type proportions at the population level.
When chromatin regulator levels (αc) were increased, progenitors activated regulatory genes in the same order, but proceeded through this temporal schedule for activation at a slower speed (figure 6d, bottom). This scaled expansion of the timetable for cortical layer neuron specification, combined with an unchanged rate of cell division, led to larger final numbers of different cortical layer neuron types (figure 6d,e). Importantly, while total cell numbers increased, the proportions of neurons in different cortical layers remained the same. From an analytical solution of the system (electronic supplementary material, mathematical appendix, Part VI), we find that such scaled changes in timing and population sizes occur over a range of parameters, as long as the chromatin regulator similarly alters activation timing at all regulatory gene loci when perturbed. These results show that chromatin-modifying enzymes, acting on epigenetic switching networks, can scalably adjust the speed at which developmental schedules unfold and generate proportional changes in organ and organism sizes.
2.8. Independent growth and temporal control
Evolutionary changes in organ and organism sizes often arise not from changes to developmental timetables, but from changes in cell proliferation amid invariant developmental schedules. For example, while different dog breeds follow a similar embryonic timetable with a gestational period of two months [74,75], they have birth weights that can vary substantially between breeds, due to variants affecting rates of cell growth and proliferation such as the growth hormone/insulin-like growth factor (GH/IGF) pathway [76–78]. Mutations altering GH/IGF signalling activity change the overall rate of proliferation in the embryo without affecting the temporal schedules for organ formation, resulting in proportionately scaled body sizes at birth [76,79,80]. Similarly, decreasing c-Myc expression in mice reduces embryonic proliferation rates without affecting developmental schedules, resulting in neonates that retain their basic anatomical proportions but have fewer total cells [81,82].
As classical regulatory networks that generate long delays (figure 2(iii–v)) tend to rely on the cell cycle for setting response timescales, it is not clear how they can uphold constant developmental timetables amid changes in cell division rates. By contrast, timed epigenetic switches can work independently from cell division [38]; thus, epigenetic switching networks could potentially set developmental schedules invariant to cell proliferation changes (figure 7a). To examine this idea, we developed a toy regulatory network for body plan formation, and analysed this network to define the conditions under which epigenetic switching networks could generate invariant developmental schedules that allowed for tunable control of cell population sizes and fractions through control of cell division rate.
Figure 7.
Master growth regulators, acting on division-independent timetables set by epigenetic switching networks, can proportionally vary population sizes. (a) Perturbations to cell cycle speed regulators result in coordinated scaling of independently developing tissues. (b) Two gene regulatory networks for the two tissue types, each with an upstream regulator (XA, XB), a downstream regulator (YA, YB), and a cell cycle exit regulator (ZA, ZB). (c) Asymmetric division scheme for cell-type specification, with cell states coloured according to their corresponding regulators. (d) Representative time traces showing concentrations of regulatory genes, in single-cell lineages with slower (left) or faster (right) cell division rates. In both instances, we considered two parameter sets: one where YB is unstable (middle), and another where it is stable (bottom). (e,f) Averaged cell number plots (left) and final cell fractions (right), plotted as a function of cell cycle speed, obtained under regimes where YB is either unstable (e) or stable (f). These results show that changes in cell division rates can lead to proportional changes in cell population sizes, but only when regulators have short half-lives and, consequently, concentrations that do not vary with cell cycle speed.
To capture the autonomous development of multiple parts of a body plan, we incorporate into our model two epigenetic switching networks, each operating in parallel in different progenitor populations to generate a total of four differentiated cell populations (figure 7b,c) (electronic supplementary material, mathematical appendix, Part VII; see electronic supplementary material, table 6 for parameter values). While these progenitors develop independently from each other, they share a cell cycle control mechanism that can be adjusted by evolutionary mutations. These mutations could occur in the GH/IGF signalling pathway, as in the case for dogs, or in other cell division speed regulators, such as c-Myc or Akt/mTOR signalling [83,84]. We then simulate the time evolution of each regulatory network independently, to determine the effects of changing cell division rates on sizes and proportions of differentiated cell populations.
From stochastic simulations, we found that progenitors could maintain a constant developmental schedule over a range of cell cycle speeds (figure 7d, top and middle; figure 7e). When the speed of cell cycle progression increased, the population sizes of all differentiated cell types increased in a proportional manner, such that the fractions of different cell types remained largely constant.
Developmental schedules maintained constancy only when proteins encoded by regulatory network genes were all unstable, such that their half-lives were shorter than the cell cycle duration. When a regulatory protein in this network was set to be stable, such that its levels now varied with changing cell cycle length, there was a change in the activation timing of its target gene, which in turn led to disproportionate increase in the size of its corresponding cell population (figure 7d, bottom; figure 7f). These results indicate that rapid protein turnover in epigenetic switching networks, relative to cell division, is a requirement for maintaining developmental timetables that are independent of cell division speed.
3. Discussion
In this study, we sought to understand how progenitors can maintain autonomous timetables for cell lineage specification that robustly unfold over long developmental timescales, but are yet flexibly adjustable by evolution. We found that epigenetic switching networks, in contrast to classical networks governed by the bacterial quantitative paradigm, maintain robust timetables for gene activation and lineage specification. When used to control the transitions between different competent cell states for differentiation, epigenetic switching networks could generate multiple output cell types in defined numbers and proportions. Through analysing a series of case studies, we further show how evolution can act on epigenetic switching networks to alter developmental timetables and, consequently, organism size and proportion. Our results establish a quantitative paradigm for understanding how embryos can set and flexibly adjust developmental timetables for controlling organism size and proportions.
Epigenetic switching networks, in contrast to classical gene regulatory networks, can uniquely generate long response delays that are tunable by signalling inputs. While classical gene regulatory networks can also generate multi-generational response delays, these delays could only be tuned by signals over a narrow range. Furthermore, this tunable signal range was close to the lower signal threshold below which progenitors fail to respond, making them susceptible to stalling in a proliferative state. Thus, classically regulatory networks, while ideal for functional processes that require rapid responses, may be less suitable for developmental and physiological processes requiring protracted temporal control over many cell generations. Recent studies have found that species-specific differences in protein stability can also scalably affect developmental timetables [85,86]; however, as protein stability would perturb speed within timescales defined by cell division, additional mechanisms would have to account for larger, more protracted differences in developmental speed that span many cell generations, as is observed in cerebral cortex development and also in other developmental contexts [21].
Epigenetic switching networks can generate multiple cell types in defined sizes and proportions, provided that they control the transitions of progenitors between competent states that generate differentiated progeny through either asymmetric cell division—where fate determinants are unevenly partitioned during cell division—or through stochastic differentiation control (figure 4). In either case, cell populations grow linearly with time, allowing their sizes to be capped by stochastic timing delays that arise through epigenetic switching. There is evidence for both asymmetric and stochastic mechanisms in specific vertebrate developmental systems [59,61,87,88]; however, it will be useful to analyse developmental processes at the single lineage level in order to ascertain whether these competent states occur generally in the embryo. Emerging techniques for lineage reconstruction at the level of whole organisms may allow us to perform this analysis in a systematic manner [89].
Our studies in cerebral cortex development implicate epigenetic-modifying enzymes as master regulators of developmental speed (figure 6). Because of their broad sequence specificity, chromatin regulators likely bind and act on multiple genes within epigenetic switching networks [31,32]; consequently, changes in their levels or activity would alter network dynamics at a global level, and could potentially change the speed at which their temporal schedules unfold. Consistent with this idea, disruptions in polycomb complex activity accelerate differentiation across multiple cell lineages in different contexts [71,90–94]. Deletion of the PRC2 methyltransferase subunit, Ezh2, accelerates the temporal schedule for cerebral cortex development, leading to reduced cortical tissue size while preserving the temporal order of neuronal subtype differentiation [72]. Evolutionary changes in polycomb activity could stem from non-coding mutations affecting expression levels of polycomb components; however, because the PRC1 and PRC2 families have both undergone expansion during vertebrate evolution [95], it is also possible that such speed changes may also involve mutations that alter protein function. We point out that while H3K27me3 modifications modulate activation timing in our system, our modelling and experimental results indicate that they must collaborate with other chromatin modifications to set activation timing [38]. Thus, multiple chromatin systems may ultimately work together to dictate the pace of development. The repressive mark H3K9me3 also regulates lineage specification [33], and may coexist with H3K27me3 to establish repression at developmental genes [96,97]. Another intriguing chromatin regulator is HMGA2, a DNA-binding protein that controls body size and developmental timing in vertebrates [98,99]. HMGA proteins also have broad genome-specificity [100] and could operate on many loci simultaneously to control developmental speed.
Temporal control mechanisms, as implemented by epigenetic switching networks, must ultimately work together with spatial patterning mechanisms to ensure proper development. Spatial and temporal control mechanisms could work together through a range of possible strategies: for instance, temporal control mechanisms could set the size of domains on which spatial mechanisms act. For instance, some morphogen gradients can scale with the dimensions of a domain [101–103], though these gradients do not control the domain size itself [104,105]. Temporal mechanisms, with their ability to precisely specify output cell numbers, could work in conjunction with spatially scalable patterning mechanisms to ensure proportionality in both size and form. As another possibility, temporal control mechanisms could generate defined cell populations that then self organize in space. For example, during spinal cord development, an epigenetic switching network of mutually inhibitory genes is thought to drive motor neuron specification in the spinal motor column [55]. While these different motor neuron types are initially randomly distributed in space, they express unique cadherin combinations [106] that allow them to cluster together and generate defined structures. In general, future studies in developmental biology will benefit from closer consideration of how spatial and temporal control mechanisms work together to specify growth and form during multicellular development.
Acknowledgements
We thank members of the Kueh laboratory for discussions and feedback. We also thank James Briscoe for discussion and feedback on this study.
Data accessibility
The simulation code for the models in the paper is availability for download at https://github.com/KuehLabUW/Nguyen_and_Pease_et_al.2021.
Authors' contributions
P.N., N.A.P. and H.Y.K. designed the study and built the models. P.N. and H.Y.K. performed the simulations. P.N., N.A.P. and H.Y.K. wrote the manuscript.
Competing interests
We declare we have no competing interests.
Funding
This work was funded by an NIH Pathway to Independence Award 5R00HL119638 (to H.Y.K.), NIH/NHLBI R01HL146478 (to H.Y.K), and a Tietze Foundation Stem Cell Scientist Award (to H.Y.K.), University of Washington Institute for Stem Cell and Regenerative Medicine Scholarship (to N.A.P.) and an NIH F31 Fellowships F31HL151090 (to N.A.P.)
References
- 1.De Beer G. 1940. Embryos and ancestors. Oxford, UK: Clarendon Press. [Google Scholar]
- 2.Gould SJ. 1977. Ontogeny and phylogeny, reprint edn. Cambridge, MA: Harvard University Press. [Google Scholar]
- 3.Haeckel E. 1866. Generelle morphologie der organismen. Berlin, Germany: Georg Reimer. [Google Scholar]
- 4.Huxley JS, Pigliucci M, Müller GB. 1942. Evolution: the modern synthesis. London, UK: Allen and Unwin. [Google Scholar]
- 5.Alberch P, Gould SJ, Oster GF, Wake DB. 1979. Size and shape in ontogeny and phylogeny. Paleobiology 5, 296-317. ( 10.1017/S0094837300006588) [DOI] [Google Scholar]
- 6.Bonner JT. 1965. Size and cycle: an essay on the structure of biology. Princeton, NJ: Princeton University Press. [Google Scholar]
- 7.Calder WA. 1984. Size, function, and life history. North Chelmsford, MA: Courier Corporation. [Google Scholar]
- 8.Ebisuya M, Briscoe J. 2018. What does time mean in development? Development 145, dev164368. ( 10.1242/dev.164368) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Keyte AL, Smith KK. 2014. Heterochrony and developmental timing mechanisms: changing ontogenies in evolution. Seminars Cell Dev. Biol. 34, 99-107. ( 10.1016/j.semcdb.2014.06.015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Burton P, Raff M, Kerr P, Yacoub M, Barton P. 1999. An intrinsic timer that controls cell-cycle withdrawal in cultured cardiac myocytes. Dev. Biol. 216, 659-670. ( 10.1006/dbio.1999.9524) [DOI] [PubMed] [Google Scholar]
- 11.Gao FB, Durand B, Raff M. 1997. Oligodendrocyte precursor cells count time but not cell divisions before differentiation. Curr. Biol. 7, 152-155. ( 10.1016/S0960-9822(06)00060-1) [DOI] [PubMed] [Google Scholar]
- 12.Heinzel S, Binh Giang T, Kan A, Marchingo JM, Lye BK, Corcoran LM, Hodgkin PD. 2017. A Myc-dependent division timer complements a cell-death timer to regulate T cell and B cell responses. Nat. Immunol. 18, 96-103. ( 10.1038/ni.3598) [DOI] [PubMed] [Google Scholar]
- 13.Otani T, Marchetto MC, Gage FH, Simons BD, Livesey FJ. 2016. 2D and 3D stem cell models of primate cortical development identify species-specific differences in progenitor behavior contributing to brain size. Cell Stem Cell 18, 467-480. ( 10.1016/j.stem.2016.03.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rosello-Diez A, Arques CG, Delgado I, Giovinazzo G, Torres M. 2014. Diffusible signals and epigenetic timing cooperate in late proximo-distal limb patterning. Development 141, 1534-1543. ( 10.1242/dev.106831) [DOI] [PubMed] [Google Scholar]
- 15.Saiz-Lopez P, Chinnaiya K, Campa VM, Delgado I, Ros MA, Towers M. 2015. An intrinsic timer specifies distal structures of the vertebrate limb. Nat. Commun. 6, 8108. ( 10.1038/ncomms9108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Eiraku M. 2008. Self-organized formation of polarized cortical tissues from ESCs and its active manipulation by extrinsic signals. Cell Stem Cell 3, 519-532. ( 10.1016/j.stem.2008.09.002) [DOI] [PubMed] [Google Scholar]
- 17.Gaspard N et al. 2008. An intrinsic mechanism of corticogenesis from embryonic stem cells. Nature 455, 351-357. ( 10.1038/nature07287) [DOI] [PubMed] [Google Scholar]
- 18.van den Ameele J, Tiberi L, Vanderhaeghen P, Espuny-Camacho I. 2014. Thinking out of the dish: what to learn about cortical development using pluripotent stem cells. Trends Neurosci. 37, 334-342. ( 10.1016/j.tins.2014.03.005) [DOI] [PubMed] [Google Scholar]
- 19.Barry C et al. 2017. Species-specific developmental timing is maintained by pluripotent stem cells ex utero. Dev. Biol. 423, 101-110. ( 10.1016/j.ydbio.2017.02.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Espuny-Camacho I et al. 2013. Pyramidal neurons derived from human pluripotent stem cells integrate efficiently into mouse brain circuits in vivo. Neuron 77, 440-456. ( 10.1016/j.neuron.2012.12.011) [DOI] [PubMed] [Google Scholar]
- 21.Rayon T, Briscoe J. 2021. Cross-species comparisons and in vitro models to study tempo in development and homeostasis. Interface Focus 11, 20200069. ( 10.1098/rsfs.2020.0069) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Alon U. 2007. Network motifs: theory and experimental approaches. Nat. Rev. Genet. 8, 450-461. ( 10.1038/nrg2102) [DOI] [PubMed] [Google Scholar]
- 23.Briscoe J, Small S. 2015. Morphogen rules: design principles of gradient-mediated embryo patterning. Development 142, 3996-4009. ( 10.1242/dev.129452) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Davidson EH. 2010. Emerging properties of animal gene regulatory networks. Nature 468, 911-920. ( 10.1038/nature09645) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Georgescu C, Longabaugh WJR, Scripture-Adams DD, David-Fung ES, Yui MA, Zarnegar MA, Bolouri H, Rothenberg EV. 2008. A gene regulatory network armature for T lymphocyte specification. Proc. Natl Acad. Sci. USA 105, 20100-20105. ( 10.1073/pnas.0806501105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ackers GK, Johnson AD, Shea MA. 1982. Quantitative model for gene regulation by lambda phage repressor. Proc. Natl Acad. Sci. USA 79, 1129-1133. ( 10.1073/pnas.79.4.1129) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bintu L, Buchler NE, Garcia HG, Gerland U, Hwa T, Kondev J, Phillips R. 2005. Transcriptional regulation by the numbers: models. Curr. Opin. Genet. Dev. 15, 116-124. ( 10.1016/j.gde.2005.02.007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bolouri H, Davidson EH. 2002. Modeling transcriptional regulatory networks. BioEssays 24, 1118-1129. ( 10.1002/bies.10189) [DOI] [PubMed] [Google Scholar]
- 29.Levine JH, Elowitz MB. 2014. Polyphasic feedback enables tunable cellular timers. Curr. Biol. 24, R994-995. ( 10.1016/j.cub.2014.08.030) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bintu L, Yong J, Antebi YE, McCue K, Kazuki Y, Uno N, Oshimura M, Elowitz MB. 2016. Dynamics of epigenetic regulation at the single-cell level. Science 351, 720-724. ( 10.1126/science.aab2956) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Boyer LA et al. 2006. Polycomb complexes repress developmental regulators in murine embryonic stem cells. Nature 441, 349-353. ( 10.1038/nature04733) [DOI] [PubMed] [Google Scholar]
- 32.Lee TI et al. 2006. Control of developmental regulators by polycomb in human embryonic stem cells. Cell 125, 301-313. ( 10.1016/j.cell.2006.02.043) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nicetto D et al. 2019. H3K9me3-heterochromatin loss at protein-coding genes enables developmental lineage specification. Science 363, 294-297. ( 10.1126/science.aau0583) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mayran A, Khetchoumian K, Hariri F, Pastinen T, Gauthier Y, Balsalobre A, Drouin J. 2018. Pioneer factor Pax7 deploys a stable enhancer repertoire for specification of cell fate. Nat. Genet. 50, 259-269. ( 10.1038/s41588-017-0035-2) [DOI] [PubMed] [Google Scholar]
- 35.Kueh HY et al. 2016. Asynchronous combinatorial action of four regulatory factors activates Bcl11b for T cell commitment. Nat. Immunol. 17, 956-965. ( 10.1038/ni.3514) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rothenberg EV. 2019. Programming for T-lymphocyte fates: modularity and mechanisms. Genes Dev. 33, 1117-1135. ( 10.1101/gad.327163.119) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ng KK et al. 2018. A stochastic epigenetic switch controls the dynamics of T-cell lineage commitment. Elife 7, e37851. ( 10.7554/eLife.37851) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pease NA, Nguyen PHB, Woodworth MA, Ng KKH, Irwin B, Vaughan JC, Kueh HY. 2021. Tunable, division-independent control of gene activation timing by a polycomb switch. Cell Rep. 34, 108888. ( 10.1016/j.celrep.2021.108888) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dodd IB, Micheelsen MA, Sneppen K, Thon G. 2007. Theoretical analysis of epigenetic cell memory by nucleosome modification. Cell 129, 813-822. ( 10.1016/j.cell.2007.02.053) [DOI] [PubMed] [Google Scholar]
- 40.Zhang H, Tian XJ, Mukhopadhyay A, Kim K, Xing J. 2014. Statistical mechanics model for the dynamics of collective epigenetic histone modification. Phys. Rev. Lett. 112, 068101. ( 10.1103/PhysRevLett.112.068101) [DOI] [PubMed] [Google Scholar]
- 41.Artyomov MN, Meissner A, Chakraborty AK. 2010. A model for genetic and epigenetic regulatory networks identifies rare pathways for transcription factor induced pluripotency. PLoS Comput. Biol. 6, e1000785. ( 10.1371/journal.pcbi.1000785) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Berry S, Dean C, Howard M. 2017. Slow chromatin dynamics allow polycomb target genes to filter fluctuations in transcription factor activity. Cell Syst. 4, 445-457.e8. ( 10.1016/j.cels.2017.02.013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bhattacharyya B, Wang J, Sasai M. 2020. Stochastic epigenetic dynamics of gene switching. Phys. Rev. E 102, 042408. ( 10.1103/PhysRevE.102.042408) [DOI] [PubMed] [Google Scholar]
- 44.Gómez-Schiavon M, Buchler NE. 2019. Epigenetic switching as a strategy for quick adaptation while attenuating biochemical noise. PLoS Comput. Biol. 15, e1007364. ( 10.1371/journal.pcbi.1007364) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rodriguez J, Ren G, Day CR, Zhao K, Chow CC, Larson DR. 2019. Intrinsic dynamics of a human gene reveal the basis of expression heterogeneity. Cell 176, 213-226.e18. ( 10.1016/j.cell.2018.11.026) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Angel A, Song J, Dean C, Howard M. 2011. A Polycomb-based switch underlying quantitative epigenetic memory. Nature 476, 105-108. ( 10.1038/nature10241) [DOI] [PubMed] [Google Scholar]
- 47.Padovan-Merhar O et al. 2015. Single mammalian cells compensate for differences in cellular volume and DNA copy number through independent global transcriptional mechanisms. Mol. Cell 58, 339-352. ( 10.1016/j.molcel.2015.03.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Spencer SL, Cappell SD, Tsai FC, Overton KW, Wang CL, Meyer T. 2013. The proliferation-quiescence decision is controlled by a bifurcation in CDK2 activity at mitotic exit. Cell 155, 369-383. ( 10.1016/j.cell.2013.08.062) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gillespie DT. 1977. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340-2361. ( 10.1021/j100540a008) [DOI] [Google Scholar]
- 50.Kohwi M, Doe CQ. 2013. Temporal fate specification and neural progenitor competence during development. Nat. Rev. Neurosci. 14, 823-838. ( 10.1038/nrn3618) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Li X, Chen Z, Desplan C. 2013. Temporal patterning of neural progenitors in Drosophila. Curr. Top. Dev. Biol. 105, 69-96. ( 10.1016/B978-0-12-396968-2.00003-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Singh H, Khan AA, Dinner AR. 2014. Gene regulatory networks in the immune system. Trends Immunol. 35, 211-218. ( 10.1016/j.it.2014.03.006) [DOI] [PubMed] [Google Scholar]
- 53.Rossi AM, Fernandes VM, Desplan C. 2017. Timing temporal transitions during brain development. Curr. Opin. Neurobiol. 42, 84-92. ( 10.1016/j.conb.2016.11.010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Huang S, Guo YP, May G, Enver T. 2007. Bifurcation dynamics in lineage-commitment in bipotent progenitor cells. Dev. Biol. 305, 695-713. ( 10.1016/j.ydbio.2007.02.036) [DOI] [PubMed] [Google Scholar]
- 55.Johnston RJ, Desplan C. 2010. Stochastic mechanisms of cell fate specification that yield random or robust outcomes. Annu. Rev. Cell Dev. Biol. 26, 689-719. ( 10.1146/annurev-cellbio-100109-104113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Crescenzi M, Fleming TP, Lassar AB, Weintraub H, Aaronson SA. 1990. MyoD induces growth arrest independent of differentiation in normal and transformed cells. Proc. Natl Acad. Sci. USA 87, 8442-8446. ( 10.1073/pnas.87.21.8442) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kueh HY, Champhekar A, Champhekhar A, Nutt SL, Elowitz MB, Rothenberg EV. 2013. Positive feedback between PU.1 and the cell cycle controls myeloid differentiation. Science (New York, NY) 341, 670-673. ( 10.1126/science.1240831) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sorrentino V, Pepperkok R, Davis RL, Ansorge W, Philipson L. 1990. Cell proliferation inhibited by MyoD1 independently of myogenic differentiation. Nature 345, 813-815. ( 10.1038/345813a0) [DOI] [PubMed] [Google Scholar]
- 59.Knoblich JA. 2010. Asymmetric cell division: recent developments and their implications for tumour biology. Nat. Rev. Mol. Cell Biol. 11, 849-860. ( 10.1038/nrm3010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Venkei ZG, Yamashita YM. 2018. Emerging mechanisms of asymmetric stem cell division. J. Cell Biol. 217, 3785-3795. ( 10.1083/jcb.201807037) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Simons BD, Clevers H. 2011. Strategies for homeostatic stem cell self-renewal in adult tissues. Cell 145, 851-862. ( 10.1016/j.cell.2011.05.033) [DOI] [PubMed] [Google Scholar]
- 62.Juan AH, Ruddle FH. 2003. Enhancer timing of Hox gene expression: deletion of the endogenous Hoxc8 early enhancer. Development 130, 4823-4834. ( 10.1242/dev.00672) [DOI] [PubMed] [Google Scholar]
- 63.Mallo M, Alonso CR. 2013. The regulation of Hox gene expression during animal development. Development 140, 3951-3963. ( 10.1242/dev.068346) [DOI] [PubMed] [Google Scholar]
- 64.Wakamatsu Y, Suzuki K. 2019. Sequence alteration in the enhancer contributes to the heterochronic Sox9 expression in marsupial cranial neural crest. Dev. Biol. 456, 31-39. ( 10.1016/j.ydbio.2019.08.010) [DOI] [PubMed] [Google Scholar]
- 65.Zákány J, Gérard M, Favier B, Duboule D. 1997. Deletion of a HoxD enhancer induces transcriptional heterochrony leading to transposition of the sacrum. EMBO J. 16, 4393-4402. ( 10.1093/emboj/16.14.4393) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Gérard M, Zákány J, Duboule D. 1997. Interspecies exchange of a Hoxd enhancer in vivo induces premature transcription and anterior shift of the sacrum. Dev. Biol. 190, 32-40. ( 10.1006/dbio.1997.8679) [DOI] [PubMed] [Google Scholar]
- 67.Eskeland R et al. 2010. Ring1B compacts chromatin structure and represses gene expression independent of histone ubiquitination. Mol. Cell 38, 452-464. ( 10.1016/j.molcel.2010.02.032) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Soshnikova N, Duboule D. 2009. Epigenetic temporal control of mouse hox genes in vivo. Science 324, 1320-1323. ( 10.1126/science.1171468) [DOI] [PubMed] [Google Scholar]
- 69.Fabre PJ, Benke A, Manley S, Duboule D. 2015. Visualizing the HoxD gene cluster at the nanoscale level. Cold Spring Harb. Symp. Quant. Biol. 80, 9-16. ( 10.1101/sqb.2015.80.027177) [DOI] [PubMed] [Google Scholar]
- 70.Fabre PJ, Leleu M, Mascrez B, Lo Giudice Q, Cobb J, Duboule D. 2018. Heterogeneous combinatorial expression of Hoxd genes in single cells during limb development. BMC Biol. 16, 101. ( 10.1186/s12915-018-0570-z) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Ezhkova E, Pasolli HA, Parker JS, Stokes N, Su Ih, Hannon G, Tarakhovsky A, Fuchs E. 2009. Ezh2 orchestrates gene expression for the stepwise differentiation of tissue-specific stem cells. Cell 136, 1122-1135. ( 10.1016/j.cell.2008.12.043) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Pereira JD, Sansom SN, Smith J, Dobenecker MW, Tarakhovsky A, Livesey FJ. 2010. Ezh2, the histone methyltransferase of PRC2, regulates the balance between self-renewal and differentiation in the cerebral cortex. Proc. Natl Acad. Sci. USA 107, 15 957-15 962. ( 10.1073/pnas.1002530107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Vo LT et al. 2018. Regulation of embryonic haematopoietic multipotency by EZH1. Nature 553, 506-510. ( 10.1038/nature25435) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Mugnier A et al. 2019. Birth weight as a risk factor for neonatal mortality: breed-specific approach to identify at-risk puppies. Prev. Vet. Med. 171, 104746. ( 10.1016/j.prevetmed.2019.104746) [DOI] [PubMed] [Google Scholar]
- 75.Okkens A, Teunissen J, Van Osch W, Van Den Brom W, Dieleman S, Kooistra H. 2001. Influence of litter size and breed on the duration of gestation in dogs. J. Reproduction Fertility-Supplement 57, 193-197. [PubMed] [Google Scholar]
- 76.Baker J, Liu JP, Robertson EJ, Efstratiadis A. 1993. Role of insulin-like growth factors in embryonic and postnatal growth. Cell 75, 73-82. ( 10.1016/S0092-8674(05)80085-6) [DOI] [PubMed] [Google Scholar]
- 77.Rimbault M, Beale HC, Schoenebeck JJ, Hoopes BC, Allen JJ, Kilroy-Glynn P, Wayne RK, Sutter NB, Ostrander EA. 2013. Derived variants at six genes explain nearly half of size reduction in dog breeds. Genome Res. 23, 1985-1995. ( 10.1101/gr.157339.113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Verhaeghe J, Van Bree R, Van Herck E, Laureys J, Bouillon R, Van Assche FA. 1993. C-peptide, insulin-like growth factors I and II, and insulin-like growth factor binding protein-1 in umbilical cord serum: correlations with birth weight. Am. J. Obstet. Gynecol. 169, 89-97. ( 10.1016/0002-9378(93)90137-8) [DOI] [PubMed] [Google Scholar]
- 79.Gagliardi AD, Kuo EYW, Raulic S, Wagner GF, DiMattia GE. 2005. Human stanniocalcin-2 exhibits potent growth-suppressive properties in transgenic mice independently of growth hormone and IGFs. Am. J. Physiol.-Endocrinol. Metab. 288, E92-E105. ( 10.1152/ajpendo.00268.2004) [DOI] [PubMed] [Google Scholar]
- 80.Garfinkel BP, Arad S, Le PT, Bustin M, Rosen CJ, Gabet Y, Orly J. 2015. Proportionate dwarfism in mice lacking heterochromatin protein 1 binding protein 3 (HP1BP3) is associated with alterations in the endocrine IGF-1 pathway. Endocrinology 156, 4558-4570. ( 10.1210/en.2015-1668) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Hofmann J et al. 2015. Reduced expression of MYC increases longevity and enhances healthspan. Cell 160, 477-488. ( 10.1016/j.cell.2014.12.016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Trumpp A, Refaeli Y, Oskarsson T, Gasser S, Murphy M, Martin GR, Bishop JM. 2001. c-Myc regulates mammalian body size by controlling cell number but not cell size. Nature 414, 768-773. ( 10.1038/414768a) [DOI] [PubMed] [Google Scholar]
- 83.Chen WS et al. 2001. Growth retardation and increased apoptosis in mice with homozygous disruption of the akt1 gene. Genes Dev. 15, 2203-2208. ( 10.1101/gad.913901) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Peng XD et al. 2003. Dwarfism, impaired skin development, skeletal muscle atrophy, delayed bone development, and impeded adipogenesis in mice lacking Akt1 and Akt2. Genes Dev. 17, 1352-1365. ( 10.1101/gad.1089403) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Matsuda M et al. 2020. Species-specific segmentation clock periods are due to differential biochemical reaction speeds. Science 369, 1450-1455. ( 10.1126/science.aba7668) [DOI] [PubMed] [Google Scholar]
- 86.Rayon T et al. 2020. Species-specific pace of development is associated with differences in protein stability. Science 369, eaba7667. ( 10.1126/science.aba7667) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Fish JL, Dehay C, Kennedy H, Huttner WB. 2008. Making bigger brains—the evolution of neural-progenitor-cell division. J. Cell Sci. 121, 2783-2793. ( 10.1242/jcs.023465) [DOI] [PubMed] [Google Scholar]
- 88.Klein AM, Simons BD. 2011. Universal patterns of stem cell fate in cycling adult tissues. Development 138, 3103-3111. ( 10.1242/dev.060103) [DOI] [PubMed] [Google Scholar]
- 89.McKenna A, Findlay G, Gagnon J, Horwitz M, Schier A, Shendure J. 2016. Whole-organism lineage tracing by combinatorial and cumulative genome editing. Science 353, aaf7907. ( 10.1126/science.aaf7907) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Endoh M et al. 2017. PCGF6-PRC1 suppresses premature differentiation of mouse embryonic stem cells by regulating germ cell-related genes. eLife 6, e21064. ( 10.7554/eLife.21064) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Fujimura N, Kuzelova A, Ebert A, Strnad H, Lachova J, Machon O, Busslinger M, Kozmik Z. 2018. Polycomb repression complex 2 is required for the maintenance of retinal progenitor cells and balanced retinal differentiation. Dev. Biol. 433, 47-60. ( 10.1016/j.ydbio.2017.11.004) [DOI] [PubMed] [Google Scholar]
- 92.Mirzamohammadi F, Papaioannou G, Inloes JB, Rankin EB, Xie H, Schipani E, Orkin SH, Kobayashi T. 2016. Polycomb repressive complex 2 regulates skeletal growth by suppressing Wnt and TGF–signalling. Nat. Commun. 7, 12047. ( 10.1038/ncomms12047) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Xiao S, Zhang W, Manley NR. 2018. Thymic B cell development is controlled by the B potential of progenitors via both hematopoietic-intrinsic and thymic microenvironment-intrinsic regulatory mechanisms. PLoS ONE 13, e0193189. ( 10.1371/journal.pone.0193189) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Zhang J, Taylor RJ, La Torre A, Wilken MS, Cox KE, Reh TA, Vetter ML. 2015. Ezh2 maintains retinal progenitor proliferation, transcriptional integrity, and the timing of late differentiation. Dev. Biol. 403, 128-138. ( 10.1016/j.ydbio.2015.05.010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Sowpati DT, Ramamoorthy S, Mishra RK. 2015. Expansion of the polycomb system and evolution of complexity. Mech. Dev. 138, 97-112. ( 10.1016/j.mod.2015.07.013) [DOI] [PubMed] [Google Scholar]
- 96.Boros J, Arnoult N, Stroobant V, Collet J-F, Decottignies A. 2014. Polycomb repressive complex 2 and H3K27me3 cooperate with H3K9 methylation to maintain heterochromatin protein 1α at chromatin. Mol. Cell Biol. 34, 3662-3674. ( 10.1128/MCB.00205-14) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.de la Cruz CC, Kirmizis A, Simon MD, Isono K, Koseki H, Panning B. 2007. The polycomb group protein SUZ12 regulates histone H3 lysine 9 methylation and HP1 alpha distribution. Chromosome Res. 15, 299-314. ( 10.1007/s10577-007-1126-1) [DOI] [PubMed] [Google Scholar]
- 98.Chung J et al. 2018. High mobility group A2 (HMGA2) deficiency in pigs leads to dwarfism, abnormal fetal resource allocation, and cryptorchidism. Proc. Natl Acad. Sci. USA 115, 5420-5425. ( 10.1073/pnas.1721630115) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Lamichhaney S, Han F, Berglund J, Wang C, Almén MS, Webster MT, Grant BR, Grant PR, Andersson L. 2016. A beak size locus in Darwin's finches facilitated character displacement during a drought. Science 352, 470-474. ( 10.1126/science.aad8786) [DOI] [PubMed] [Google Scholar]
- 100.Ozturk N, Singh I, Mehta A, Braun T, Barreto G. 2014. HMGA proteins as modulators of chromatin structure during transcriptional activation. Front. Cell Dev. Biol. 2, 5. ( 10.3389/fcell.2014.00005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Ben-Zvi D, Shilo B-Z, Barkai N. 2011. Scaling of morphogen gradients. Curr. Opin. Genet. Dev. 21, 704-710. ( 10.1016/j.gde.2011.07.011) [DOI] [PubMed] [Google Scholar]
- 102.Inomata H. 2017. Scaling of pattern formations and morphogen gradients. Dev. Growth Differ. 59, 41-51. ( 10.1111/dgd.12337) [DOI] [PubMed] [Google Scholar]
- 103.Rogers KW, Schier AF. 2011. Morphogen gradients: from generation to interpretation. Annu. Rev. Cell Dev. Biol. 27, 377-407. ( 10.1146/annurev-cellbio-092910-154148) [DOI] [PubMed] [Google Scholar]
- 104.Averbukh I, Ben-Zvi D, Mishra S, Barkai N. 2014. Scaling morphogen gradients during tissue growth by a cell division rule. Development 141, 2150-2156. ( 10.1242/dev.107011) [DOI] [PubMed] [Google Scholar]
- 105.Fried P, Iber D. 2014. Dynamic scaling of morphogen gradients on growing domains. Nat. Commun. 5, 5077. ( 10.1038/ncomms6077) [DOI] [PubMed] [Google Scholar]
- 106.Price SR, Garcia NVDM, Ranscht B, Jessell TM. 2002. Regulation of motor neuron pool sorting by differential expression of type II cadherins. Cell 109, 205-216. ( 10.1016/S0092-8674(02)00695-5) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The simulation code for the models in the paper is availability for download at https://github.com/KuehLabUW/Nguyen_and_Pease_et_al.2021.