Linear parameter varying model of COVID-19 pandemic exploiting basis functions

Abstract

Current outbreaks of the COIVD-19 pandemic demonstrate a global threat. In this paper, a conceptual model is developed for the COVID-19 pandemic, in which the people in society are divided into Susceptible, Exposed, Minor infected (Those who need to be quarantined at home), Hospitalized (Those who are in need of hospitalization), Intensive infected (ventilator-in-need infected), Recovered and Deceased. In this paper, first, the model that is briefly called SEMHIRD for a sample country (Italy as an example) is considered. Then, exploiting the real data of the country, the parameters of the model are obtained by assuming some basis functions on the collected data and solving linear least square problems in each window of data to estimate the time-varying parameters of the model. Thus, the parameters are updated every few days, and the system behavior is modeled according to the changes in the parameters. Then, the Linear Parameter Varying (LPV) Model of COVID19 is derived, and its stability analysis is presented. In the end, the influence of different levels of social distancing and quarantine on the variation of severely infected and hospitalized people is studied.

1. Introduction

The World Health Organization (WHO) announced the outbreak of the COVID-19 pandemic, also known as the Coronavirus pandemic, on January 30th, 2020 [1]. This disease influences the respiratory system of patients [2]. COVID-19 strikes the immunity, and patients who are already dealing with another disease such as heart or lung disease are at higher risk. Therefore, more attention should be paid to these people [3].

Due to the rapid spread of the disease in the world, the prevention and control of Coronavirus as soon as possible are very important. Evidently, mathematical modeling of the pandemic disease can help in predicting and forecasting the spread pattern and helps in deciding about required governmental action against the virus.

In the literature, several models for the spread of the virus are presented [4], [5], [6], [7], [8], [9]. Inspiring the models previously developed for a similar pandemic (influenza) [10], various models for COVID-19 are proposed, which are all based on models developed through data analysis. In [1], a susceptible-exposed-infected-recovered (SEIR) model is developed that divides the people in society into four groups, excluding the passed away people. In [11], a more detailed model is proposed that considers the people in susceptible, infected, diagnosed, healed, ailing, recognized, threatened, and extinct based on being asymptomatic/symptomatic, detected/undetected, …

In [12], [13], [14], [15], [16] similar models are developed, and each study divides the people in society into various groups. However, all these papers provide models with constant variables, which is not able to fit the real data in the whole period of study.

In [17], the dynamics of the virus are modeled for the general population and regional hospital scale. In [18], for the pandemic model, an adaptive Bayesian inversion is proposed to obtain the uncertainty in the model parameters. In [19], a network model is presented, in which, connections between Chinese cities are considered. This model provides a spatial spread of the virus. While most papers develop a continuous model for COVID-19, in [20], [21], a discrete model is developed.

In [22], a deterministic model for the Coronavirus and the impact of the quarantine strategy on the model for Tunisia are described in two ways. In [11], [23], [24], fractional derivational order mathematical models are presented. In [25], a model with fractal-fractional is considered. In [26], a healthy, infected, and dead people (HID) model with one reversible reaction and a model by adding people with serious conditions to the HID model are proposed, and the impact of quarantine strategies in hospitals on the model are incorporated. A mathematical model for Nigeria is presented in [27]. A new epidemic model considering the impact of health care capacity has been developed in [28]. An epidemic model with a latency period is presented in [29]. In [30], artificial neural network approaches (autoregressive integrated moving average and nonlinear autoregressive artificial neural networks) have been used to model and forecast the prevalence of this epidemic in Egypt. Huang et al. [31] proposed a multi-input convolutional deep neural network model to predict the cumulative number of confirmed cases of COVID-19 in seven Chinese cities. In [32], a reinforcement learning-based agent was derived for tuning the model’s parameters of COVID-19 transmission dynamics. The authors took into account the healthcare system parameters, the pandemic’s characteristics, and the socio-economic aspects of the community.

Although several models for the COVID-19 pandemic are developed, still much effort is need to develop a model that can fit the real data in all pandemic waves, completely. On the other hand, most models cannot indicate whether the capacity of hospitals in full or, similarly, the capacity of ICU beds is completely occupied according to the model of disease.

In this paper, with generalizing the pandemic model based on the analysis of available data, infected people are classified according to the degree of their involvement in the disease, which considers their impacts on the usage of hospitals or ICU capacity. The reason for this model development is due to the shortage of hospital capacity or ventilators, which caused a panic in the peak of coronavirus disease in most countries.

The main usage of model development is to provide a detailed and accurate model which can fit the past and present data. Therefore, a time-varying model is developed in this paper to assure an appropriate model according to the historical data of a country. After being sure about the suitability of the model, it is used for developing an LPV model for the COVID-19 pandemic according to the time-varying parameters. Stability analysis of this model according to various social distancing levels can obviously be done by such an LPV model using LMI-based methods or the direct searching idea [33]. The LPV model is also appropriate for model-based stability analysis and controller design for the COVID19 pandemic, especially, the robust stability analysis and controller design approaches.

Unfortunately, many countries deal with a serious challenge of not being able to provide the required facilities for all patients. This inspired the significance of caring for this point in mathematical modeling. In this paper, the people in society are divided into SEMHIRD or Susceptible, Exposed, Minor infected (Those who need to be quarantined at home), Hospitalized (Those who are in need of hospitalization), Intensive infected (ventilator-in-need infected), Recovered and Deceased. Existing data provided by the Italian Health Organization are used in this study due to their completeness. The parameters of the proposed model are estimated via least-squares fitting. Then, according to a certain capacity in hospitals for people with severe care who need a ventilator to breathe and a certain capacity for hospitalization, the model is analyzed whether the present quarantine or social distancing rules are suitable for being continued in a country or a more sever strategy is required. Finally, the immaculate derived model is exploited in generating the COVID-19 LPV model.

The remainder of the paper is organized as follows. In Section 2, the suggested generalized mathematical model of pandemic Coronavirus is proposed. Section 3 presents the time-varying model identification strategy and the impact of various levels of quarantine. The COVID-19 LPV model is presented in Section 4. Numerical tests and comparisons between real and mathematical model behavior of coronavirus disease in a sample country are presented in Section 5. Also, this section includes the results of the LPV model analysis. Section 6 presents a discussion about the results and the state-of-the-art approaches. Finally, Section 7 concludes the paper.

2. Mathematical model of COVID-19

The purpose of this section is to provide an appropriate mathematical model for COVID-19 which can demonstrate the relation among different categories of people in society.

2.1. Conceptual model

In the proposed model, seven states are considered that represent different categories of people in the community who are associated with the disease. Susceptible people, S(t), exposed people, E(t), people with positive tests with mild symptoms of the disease as minor infected people, $M\left(t\right)$, hospitalized with symptoms people, $H\left(t\right)$, people in intensive infected, $I\left(t\right)$, recovered people, $R\left(t\right)$, and deceased people, $D\left(t\right)$. The state $I\left(t\right)$ shows the people who need a ventilator for breathing.

The flow diagram of the proposed model is shown in Fig. 1 .

Fig. 1.

Flow diagram of SEMHIRD mathematical model of COVID-19.

In this diagram, ${\alpha }_E$, ${\alpha }_M$ and ${\alpha }_H$ show the contact factors of exposed, minor infected, and hospitalized people with susceptible people, which can lead to their transition to exposed people. Also, $k_1$, $k_2$, ${\delta }_1$, ${\delta }_2$,${\theta }_1$ and ${\theta }_2$ coefficients demonstrate the transfer from exposed to minor infected, from exposed to hospitalized, from minor infected to hospitalized, hospitalized to minor infected, from hospitalized to intensive infected and from intensive infected to hospitalized, respectively.

According to the proposed model, recovered people have come from the exposed, minor infected, hospitalized and critical people with transfer coefficient $\rho$, $\beta$, $\eta ,$ and $\phi$, respectively.

Deceased people are from critical people with transfer coefficient $\mu$. Similarly, the rest of the parameters indicate the transfer coefficient of each group to another group. The compartmental representation of Fig. 1 is equivalent to the following set of differential equations:

$$\frac{\mathit{dS}\left(t\right)}{\mathit{dt}}=-{\alpha }_{E}S\left(t\right)E\left(t\right)-{\alpha }_{M}S\left(t\right)M\left(t\right)-{\alpha }_{H}S\left(t\right)H\left(t\right)$$ (1)

$$\frac{\mathit{dE}\left(t\right)}{\mathit{dt}}={\alpha }_{E}S\left(t\right)E\left(t\right)+{\alpha }_{M}S\left(t\right)M\left(t\right)+{\alpha }_{H}S\left(t\right)H\left(t\right)-\left(k_1+k_2\right)E\left(t\right)-\rho E\left(t\right)$$ (2)

$$\frac{\mathit{dM}\left(t\right)}{\mathit{dt}}=k_{1}E\left(t\right)-\beta M\left(t\right)-\delta M\left(t\right)$$ (3)

$$\frac{\mathit{dH}\left(t\right)}{\mathit{dt}}=k_{2}E\left(t\right)+\delta M\left(t\right)-\theta H\left(t\right)-\eta H\left(t\right)-\zeta H\left(t\right)$$ (4)

$$\frac{\mathit{dI}\left(t\right)}{\mathit{dt}}=\theta H\left(t\right)-\phi I\left(t\right)-\mu I\left(t\right)$$ (5)

$$\frac{\mathit{dR}\left(t\right)}{\mathit{dt}}=\rho E\left(t\right)+\beta M\left(t\right)+\eta H\left(t\right)+\phi I\left(t\right)$$ (6)

$$\frac{\mathit{dD}\left(t\right)}{\mathit{dt}}=\mu I\left(t\right)+\zeta H\left(t\right)$$ (7)

$$N\left(t\right)=S\left(t\right)+E\left(t\right)+M\left(t\right)+H\left(t\right)+I\left(t\right)+R\left(t\right)+D\left(t\right)$$ (8)

where $N\left(t\right)$ is the total population of the considered country. Dividing equation (8) by $N\left(t\right)$, the number of people in each group will be proportional to the total population. With considering the relative population for each group, the following equation is obtained:

$$S\left(t\right)+E\left(t\right)+M\left(t\right)+H\left(t\right)+I\left(t\right)+R\left(t\right)+D\left(t\right)=1$$ (9)

The algebraic relationship (9) helps to make the model simpler by reducing one state. $S\left(t\right)$ can be removed from state equations. Table 1 indicates the parameter information in the simulation.

Table 1.

Parameter Information.

Parameter	Description
${\alpha }_E$	Contact factor of exposed to susceptible
${\alpha }_M$	Contact factor of minor infected to susceptible
${\alpha }_H$	Contact factor of hospitalized to susceptible
$k_1$	Transition rate of exposed to minor infected
$k_2$	Transition rate of exposed to hospitalized
$\rho$	Transition rate of exposed to recovered
$\beta$	Transition rate of minor infected to recovered
$\eta$	Transition rate of hospitalized to recovered
$\delta$	Transition rate of minor infected to hospitalized
$\phi$	Transition rate of intensive infected to recovered
$\theta$	Transition rate of hospitalized to intensive infected
$\mu$	Transition rate of intensive infected to deceased
$\zeta$	Transition rate of hospitalized to deceased

In the sequel, some explanatory notes about the conceptual model (1–8) are given to understand its concepts and aspects, completely.

First, it must be emphasized that the mentioned groups have their own dynamics, properties, and influences on the virus transmission dynamics. For instance, the minor and major infected people have different dynamics and have cross-influences on the other groups. Indeed, the proposed categorization is adopted from the nature of the virus spread.

Second, the proposed model (1–8) can be rewritten as given below:

$$\left[\begin{array}{c}\dot{E}\\ \dot{M}\\ \dot{H}\\ \dot{I}\\ \dot{R}\\ \dot{D}\end{array}\right]=\left[\begin{array}{cccccc}-k_1-k_2-\rho +{\alpha }_{E}S& {\alpha }_{M}S& {\alpha }_{H}S& 0& 0& 0\\ k_1& -\beta -\delta & 0& 0& 0& 0\\ k_2& \delta & -\theta -\eta -\zeta & 0& 0& 0\\ 0& 0& \theta & -\phi -\mu & 0& 0\\ \rho & \beta & \eta & \phi & 0& 0\\ 0& 0& \zeta & \mu & 0& 0\end{array}\right]\left[\begin{array}{c}E\\ M\\ H\\ I\\ R\\ D\end{array}\right]$$ (10)

The non-zero entries of the system’s matrix in (10) indicate the conceptual connections between the mentioned groups. The connections are consistent with the real transmission dynamics of the virus, in both definition and causality aspects. For example, the deceased people cannot influence the other groups, while the exposed or infected ones can significantly impact the other groups.

In (10), the off-diagonal entries of the system’s matrix are non-negative, which means the matrix is Metzler and the proposed model is positive [34]. Hence, the states will remain non-negative in the simulation times whenever initial conditions are non-negative. This fact mathematically describes the sign of off-diagonal entries that are obviously consistent with the positive nature of the real model. The diagonal entries of the system’s matrix in (10) are supposed to be non-positive to satisfy the wave shape of the model’s states. Thus, the states should individually have a damping mechanism to suppress their values independent of the values of the other groups. It is apparent that this property can be held by restricting the diagonal entries to be non-positive. Consequently, the proposed model satisfies necessary conditions adopting from the definitions and causality conditions of the real virus spread model. It means the structure of the model must be considered as (1–8) based on the existed restrictions and conceptual definitions of the model’s states.

2.2. Parameter concepts and formulations

In this model, birth is not considered, and death is only considered for this disease. The reason is the negligible number of death and birth in a short period of study. It is assumed that recovered people are immune to the disease, and only people in need of intensive care may die. With considering the susceptible people in the community who get the disease if they are exposed to it, the spread of the virus is through the communication of susceptible people with exposed people at the risk of the disease who are asymptomatic, people who have few symptoms of the disease, and people admitted to the hospital. Also, it is assumed that intensive infected are completely isolated from the outside environment. These communications are shown by ${\alpha }_{E}S\left(t\right)E\left(t\right)$, ${\alpha }_{M}S\left(t\right)M\left(t\right)$ and ${\alpha }_{H}S\left(t\right)H\left(t\right)$ terms. It seems that ${\alpha }_E$ is greater than ${\alpha }_M$ because people are more likely to avoid the people with symptoms of the disease, but ${\alpha }_E$ is reduced strongly by implementing social distancing. ${\alpha }_H$ may be greater than ${\alpha }_E$ and ${\alpha }_M$ because of the severity of the disease.

Exposed people do not have the symptoms of the disease, and the disease can be transmitted to others. People who have been recovered may also transmit the disease for a period of time. Therefore, in this paper, these people are also considered those who can spread the disease to exposed people. Parameter $\rho$ indicates the rate of recovery of these people. It is difficult to measure the number of people in this category due to the lack of symptoms and their avoidance of visiting medical centers. However, these people may have symptoms after a period of time. People with low symptoms and high symptoms may transfer to the minor infected people group and hospitalized people group with rates $k_1$ and $k_2$, respectively.

Minor infected people may get worse over time and be hospitalized, and this conversion rate is shown by $\delta$. Hospitalized people may recover, be transferred to the part of intensive infected or die with rates $\eta$, $\theta$ and $\zeta$, respectively. Intensive infected people may recover or die with rates $\phi$ and $\mu$, respectively.

The vector of all parameters is denoted by $\theta \left(t\right)={[{\alpha }_E,{\alpha }_M,{\alpha }_H,k_1,k_2,\rho ,\beta ,\eta ,\delta ,\phi ,\theta ,\mu ,\zeta ]}^T$ for the convenience of the notations. Obviously, these parameters surely have time-varying nature because the amounts of their related contact factors or transition rates (based on Table 1) are continuously changed over time. Furthermore, the consideration of time-varying parameters increases the number of free variables in the least square problem that intuitively improves its results which is described later in this paper. To represent this time-varying nature, each parameter such as ${\alpha }_E\left(t\right)$ is considered as an extension of $n$ basis functions:

$${\alpha }_E\approx \sum _{i=1}^n{\omega }_{{\alpha }_{E_i}}{b}_i\left(t\right)$$ (11)

where notations ${\left\{{\omega }_{{\alpha }_{E_i}}\right\}}_{i=1}^n$ and ${\left\{b_i\left(t\right)\right\}}_{i=1}^n$ are two sets of real coefficients and radial basis functions with the following definition:

$$b_i=\frac{\mathrm{e}\mathrm{x}\mathrm{p}(-{\sigma |t-c_i|}^2)}{\sqrt{\frac{\sigma }{\pi }}}$$ (12)

In fact, $b_i$ is the $i$ ^th basis function which is a Gaussian basis function in which $c_i$ is the center of each basis function and $\sigma$ is its variance. All parameters can similarly be formulated as (11) that implies the structure of a network of $n$ radial basis functions as follows:

$$\theta \left(t\right)=\sum _{i=1}^n{\omega }_i{b}_i\left(t\right)$$ (13)

where;

$${\omega }_i={\left[{\omega }_{{\alpha }_{E_i}},{\omega }_{{\alpha }_{M_i}},{\omega }_{{\alpha }_{H_i}},{\omega }_{k_{1_i}},{\omega }_{k_{2_i}},{\omega }_{{\rho }_i},{\omega }_{{\beta }_i},{\omega }_{{\eta }_i},{\omega }_{{\delta }_i},{\omega }_{{\phi }_i},{\omega }_{{\theta }_i},{\omega }_{{\mu }_i},{\omega }_{{\zeta }_i}\right]}^T$$ (14)

The time-varying nature of the parameters is represented by (13) that is a combination of some radial basis functions given in (12). This particular time-varying structure is considered according to the universal approximation theorem that states there exist coefficients ${\left\{{\omega }_i\right\}}_{i=1}^{n\left(\epsilon \right)}$ for each threshold error value $\epsilon >0$ that satisfy condition (15) (Please, note that the number of the basis functions $n\left(\epsilon \right)$ depends on the threshold error value $\epsilon$):

$$\forall t:\left|\theta \left(t\right)-\sum _{i=1}^{n\left(\epsilon \right)}{\omega }_i{b}_i\left(t\right)\right|\le \epsilon$$ (15)

Regarding the universal approximation theorem, the time-dependent parameters $\theta \left(t\right)$ can be approximately considered as given in (13). The theorem provides a mathematical reason for the time-varying representation (13).

3. Modeling strategy

The linear parameters of the proposed model can be obtained from system identification. Endeavor to fit a constant-variable model to real database of a country demonstrates that the behavior of coronavirus spread is so complex that it cannot be modeled only by constant variables. Therefore, the attempt is made to fit the model by time-varying parameters. To ensure accurate and appropriate model of the Coronavirus transmission dynamics, all the parameters in (1)- (8) are considered as a function of basis functions, and the parameters of the basis functions are determined, assuring least square errors.

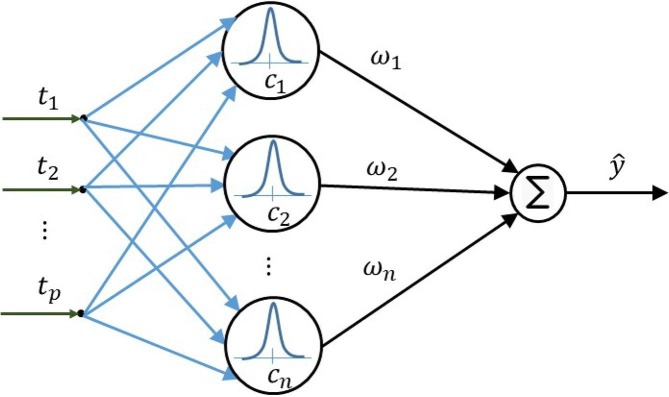
A sample basis function network is shown in Fig. 2 [35].

Fig. 2.

A sample basis function network.

In Fig. 2, $t_i$ is the time which is considered from $t_1$ to $t_p$ corresponding to the length of data, ${\omega }_i$ is a coefficient vector and the output $\widehat{y}$ is the estimation of the parameters in equations (1)-(8).

The proposed model (1)-(8) contains a set of unknown variables which are the weights of the radial basis functions in equation (13). The variables are estimated through the least square method, which is presented in the following. For this purpose, the following matrices should be firstly defined:

$$x={\left[EMHIRD\right]}^T$$ (16)

$$A\left(S,\theta \right)=\left[\begin{array}{cccccc}-k_1-k_2-\rho +{\alpha }_{E}S& {\alpha }_{M}S& {\alpha }_{H}S& 0& 0& 0\\ k_1& -\beta -\delta & 0& 0& 0& 0\\ k_2& \delta & -\theta -\eta -\zeta & 0& 0& 0\\ 0& 0& \theta & -\phi -\mu & 0& 0\\ \rho & \beta & \eta & \phi & 0& 0\\ 0& 0& \zeta & \mu & 0& 0\end{array}\right]$$ (17)

$$S\left(t\right)=1-x_1\left(t\right)-\cdots -x_6\left(t\right)$$ (18)

Using (16), (17), the dynamics of the model can be rewritten as follows:

$$\dot{x}\left(t\right)=A\left(S\left(t\right),\theta \left(t\right)\right)x\left(t\right)$$ (19)

The above model is a nonlinear time-varying model, even though it seems to be a linear model. This paper presents this nonlinear time-varying model by a Linear Parameter Varying (LPV) model since its parameters are time-varying according to (13).

To implement the least square method, the above model is firstly discretized as given below, in which notations $T$ and $k$ stand for the step time and time index, respectively:

$$x\left(\left(k+1\right)T\right)=A\left(S\left(kT\right),\theta \left(kT\right)\right)x\left(kT\right)$$ (20)

On the other hand, (13) leads to the following result:

$$\theta \left(kT\right)=\sum _{i=1}^n{\omega }_i{b}_i\left(kT\right)$$ (21)

Upon substituting (21) in (20), one can find the following equation:

$$x\left(\left(k+1\right)T\right)=\sum _{i=1}^{n}A\left(S\left(kT\right),b_i\left(kT\right){\omega }_i\right)x\left(kT\right)$$ (22)

For the convenience of the notations, $x\left(\left(k+1\right)T\right)$ and $x\left(kT\right)$ are replaced by $x_{k+1}$ and $x_k$ in the above equation, as follows:

$$x_{k+1}=\sum _{i=1}^{n}A\left(S\left(kT\right),b_i\left(kT\right){\omega }_i\right)x_k$$ (23)

Please note that, vector $x_k$ is adopted from the recorded data which is the $k^{\mathit{th}}$ record. Using this fact, the following equation can be found from (23):

$$\begin{array}{c}\forall j=1,\cdots ,6:\hfill \\ e_j^T{x}_{k+1}=\sum _{i=1}^n\sum _{l=1}^{13}\left(e_j^{T}A\left(S\left(kT\right),{\stackrel{\_}{e}}_l{b}_i\left(kT\right)\right)x_k\right){\omega }_{i,l}\hfill \end{array}$$ (24)

where $e_j$ and ${\stackrel{\_}{e}}_l$ are the $j^{\mathit{th}}$ and $l^{\mathit{th}}$ columns of the identity matrices of $I_6$ and $I_{13}$ (Please, note that, there are 13 parameters in the model). Let $N$ be the number of the recorded data that means there exists ${\left\{x_k\right\}}_{k=0}^N$ records. Using this assumption, the identification problem will briefly be obtained as follows:

$$G\omega =g$$ (25)

with the following matrix definitions and considering $S_k=S\left(kT\right)$ and $b_{i,k}=b_i\left(kT\right)$:

$$G=\left[\begin{array}{ccccc}{e}_1^{T}A\left(S_0,{\stackrel{\_}{e}}_1{b}_{1,0}\right)x_0& \cdots & e_1^{T}A\left(S_0,{\stackrel{\_}{e}}_{13}{b}_{1,0}\right)x_0& \cdots & e_1^{T}A\left(S_0,{\stackrel{\_}{e}}_{13}{b}_{n,0}\right)x_0\\ e_2^{T}A\left(S_0,{\stackrel{\_}{e}}_1{b}_{1,0}\right)x_0& \cdots & e_2^{T}A\left(S_0,{\stackrel{\_}{e}}_{13}{b}_{1,0}\right)x_0& \cdots & e_2^{T}A\left(S_0,{\stackrel{\_}{e}}_{13}{b}_{n,0}\right)x_0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ e_6^{T}A\left(S_0,{\stackrel{\_}{e}}_1{b}_{1,0}\right)x_0& \cdots & e_6^{T}A\left(S_0,{\stackrel{\_}{e}}_{13}{b}_{1,0}\right)x_0& \cdots & e_6^{T}A\left(S_0,{\stackrel{\_}{e}}_{13}{b}_{n,0}\right)x_0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ e_1^{T}A\left(S_k,{\stackrel{\_}{e}}_1{b}_{1,k}\right)x_k& \cdots & e_1^{T}A\left(S_k,{\stackrel{\_}{e}}_{13}{b}_{1,k}\right)x_k& \cdots & e_1^{T}A\left(S_k,{\stackrel{\_}{e}}_{13}{b}_{n,k}\right)x_k\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ e_6^{T}A\left(S_k,{\stackrel{\_}{e}}_1{b}_{1,k}\right)x_k& \cdots & e_6^{T}A\left(S_k,{\stackrel{\_}{e}}_{13}{b}_{1,k}\right)x_k& \cdots & e_6^{T}A\left(S_k,{\stackrel{\_}{e}}_{13}{b}_{n,k}\right)x_k\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ e_1^{T}A\left(S_N,{\stackrel{\_}{e}}_1{b}_{1,N}\right)x_N& \cdots & e_1^{T}A\left(S_N,{\stackrel{\_}{e}}_{13}{b}_{1,N}\right)x_N& \cdots & e_1^{T}A\left(S_N,{\stackrel{\_}{e}}_{13}{b}_{n,N}\right)x_N\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ e_6^{T}A\left(S_N,{\stackrel{\_}{e}}_1{b}_{1,N}\right)x_N& \cdots & e_6^{T}A\left(S_N,{\stackrel{\_}{e}}_{13}{b}_{1,N}\right)x_N& \cdots & e_6^{T}A\left(S_N,{\stackrel{\_}{e}}_{13}{b}_{n,N}\right)x_N\end{array}\right]$$ (26)

$$g={\left[e_1^T{x}_1\cdots e_6^T{x}_1\cdots e_1^T{x}_{N+1}\cdots e_6^T{x}_{N+1}\right]}^T$$ (27)

$$\omega ={\left[{\omega }_{1,1}\cdots {\omega }_{1,13}\cdots {\omega }_{n,1}\cdots {\omega }_{n,13}\right]}^T$$ (28)

The least square method is used to solve the algebraic equations (25)-(28). To evaluate the cross validation, the algebraic equation is decomposed such as $G_{\mathit{train}}$ and $G_{\mathit{test}}$ and the test dataset are randomly selected from the rows of matrix $G$. Similarly, vectors $g_{\mathit{train}}$ and $g_{\mathit{test}}$ are correspondingly selected from the rows of the main vector $g$. Using these decompositions, the algebraic equation (25) is equivalently converted to the following equations:

$$G_{\mathit{train}}\omega =g_{\mathit{train}}$$ (29)

$$G_{\mathit{test}}\omega =g_{\mathit{test}}$$ (30)

The algebraic equation (29) is solved via the least square method as the train equation. Then, the results are cross validated by the test equation (30) to check their accuracy.

4. LPV modeling of SEMHIRD and its stability assessment

Consider the system (10). It can be seen that in this system the parameters

$$\left\{p_i\right\}=\left\{{\alpha }_E,{\alpha }_M,{\alpha }_H,k_1,k_2,\rho ,\beta ,\eta ,\phi ,\delta ,\theta ,\mu ,\zeta \right\}$$ (31)

belong to a predefined interval $\left[0\stackrel{\_}{p_i}\right]$. Also, each state variable of the system (10) belongs to the set $\left[01\right]$.

The LPV model of system (10) can be written as [36]:

$$\dot{x}=A\left(p\right)x$$ (32)

where $p$ represents the interval change of parameters $\left\{p_i\right\}$, and matrix $A$ is

$$A=\underset{\_}{A}\odot \left(1-C\right)+\overline{A}\odot C$$ (33)

And

$$\underset{\_}{A}=\left[\begin{array}{cccccc}-\stackrel{\_}{k_1}-\stackrel{\_}{k_2}-\stackrel{\_}{\rho }& 0& 0& 0& 0& 0\\ 0& -\stackrel{\_}{\beta }-\stackrel{\_}{\delta }& 0& 0& 0& 0\\ 0& 0& -\stackrel{\_}{\theta }-\stackrel{\_}{\eta }-\stackrel{\_}{\zeta }& 0& 0& 0\\ 0& 0& \theta & -\phi -\mu & 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$$

$$\stackrel{\_}{A}=\left[\begin{array}{cccccc}\stackrel{\_}{{\alpha }_E}& \stackrel{\_}{{\alpha }_M}& \stackrel{\_}{{\alpha }_H}& 0& 0& 0\\ \stackrel{\_}{k_1}& 0& 0& 0& 0& 0\\ \stackrel{\_}{k_2}& \stackrel{\_}{\delta }& 0& 0& 0& 0\\ 0& 0& \stackrel{\_}{\theta }& 0& 0& 0\\ \stackrel{\_}{\rho }& \stackrel{\_}{\beta }& \stackrel{\_}{\eta }& \stackrel{\_}{\phi }& 0& 0\\ 0& 0& \stackrel{\_}{\zeta }& \stackrel{\_}{\mu }& 0& 0\end{array}\right]$$

$$C=\left[\begin{array}{cccccc}{\mathrm{c}}_1& {\mathrm{c}}_2& {\mathrm{c}}_3& 0& 0& 0\\ {\mathrm{c}}_4& 0& 0& 0& 0& 0\\ {\mathrm{c}}_5& c_6& 0& 0& 0& 0\\ 0& 0& c_7& 0& 0& 0\\ c_8& c_9& c_{10}& c_{11}& 0& 0\\ 0& 0& c_{12}& c_{13}& 0& 0\end{array}\right]$$ (34)

The corner points of matrix $A$ can be found by setting each varying parameter ${c_i\}}_{i=1}^{13}$ a value of one or zero. Therefore, there are $2^{13}$ corner points in the COVID-19 LPV model. In the above model, the varying parameters $c_i$ can change freely in the interval $\left[01\right]$.

Lemma 1.

The system (10) is stable if there exists a positive definite symmetric matrix $P$ such that:

$$A_i^{T}P+P{A}_i<0,forallcornerpoints{A}_i.$$ (35)

Proof.

The system (10) can be rewritten as:

$$\dot{x}=\sum _{i=1}^{2^{13}}{a}_i{A}_{i}x,$$ (36)

where $a_i$ represents the coordinates of matrix $A$ in the convex space formed by the corner points $A_i$. Now, consider the Lyapunov function $V=x^{T}Px$. Its derivative can be found as:

$$\dot{V}=\sum _{i=1}^{2^{13}}{a}_i{x}^T{A}_i^{T}Px+a_{i}P{A}_{i}x=a_i{x}^T\left(\sum _{i=1}^{2^{13}}{A}_i^{T}P+P{A}_i\right)x$$ (37)

If all the elements in the parentheses are negative definite, it can be concluded that $\dot{V}$ is negative definite.

To check the COVID-19 LPV system stability, we use both the LMIs in (37) and the concept of direct search approach [37]. Evidently, we have an uncertain system that includes many time varying parameters that should be assessed whether it is stable. Due to the large uncertain space of parameters, the LMIs in (37) may become infeasible. To be sure that we can find the system stability status exactly, we exploit the direct search approach. The methodology is to consider the whole uncertain space and then divide it into small simplexes. Then, check whether the simplices in the uncertain space assure stability of the model or not. The stability assessment is based on the exposed edges lemma. In each simplex, if the corner points are stable and the convex combination of the corner points does not entail any critical points, then the whole simplex is stable. The detailed proofs of the method are given in [37].

In the direct search approach, the goal is to check the system stability by searching the solution space of the parameters.

At first, we check if the COVID-19 model is inherently stable, and we may encounter a non-satisfying answer that it is not stable. Then, we can apply some control measures such as increasing social distancing level and repeat the test. This method can lead to a useful conclusion for controlling the COVID-19 spread.

5. Simulation results

To show the appropriateness of the proposed approach in modeling the Coronavirus transmission dynamics and assessing its stability, the sample data of a country is exploited. According to the completeness of data in [38], the real data of Italy is considered. Then, the model is developed based on the basis function model, and the behavior of the model in the past and present is evaluated. After being sure about the time-varying model parameters, the effects of social distancing and quarantine levels on the severity of the Coronavirus infections and death are investigated.

The proposed model can be used for different countries, however, in this article, the data of Italy is used due to its completeness.

5.1. Model study

In this section, the data provided by the Italian Ministry of Health, [38], are used to determine the parameters of the proposed model of COVID-19. The total population of the mentioned groups for Italy is considered 60,381,361 people [39].

At first, the model without using basis functions is considered and by using constant parameters, the model is simulated. Fig. 3 shows the results of the model with constant parameters and a comparison of the states model with real data for 454 days. As shown in Fig. 3, the model is not fitted on the real data.

Fig. 3.

Variation of number of states of the model with constant parameters which shows inappropriate modeling result: ${\alpha }_E=0.342$, ${\alpha }_M=0686$, ${\alpha }_H=0.2955$, $k_1=0.0123$, $k_2=0.0021$, $\rho =7.8126e^{-4}$, $\beta =0.0153$, $\eta =0.1180$, $\delta =0.0055$, $\phi =0.0750$, $\theta =0.0123$, $\mu =0.0152$ , $\zeta =0.0016$.

In the following, the basis functions model mentioned in section 3 is implemented to simulate the model. In this simulation, for some different $c_i$, the Gaussian functions are chosen as basis functions. The number of basis functions is $n=$130.$\sigma$ = 0.15 and $N$ is the population of Italy. Fig. 4 shows the considered basis functions in this simulation (for better display, it is only shown for 150 days).

Fig. 4.

Basis functions.

According to the obtained data, the least square approach is exploited to determine the model parameters.

The variation of quantities in the mathematical model for the Italy database for 454 days is shown in Fig. 5 . The maximum error in the fitting of the model to the real data is 0.0115. The results of Mean Squared Error (MSE), Sum Squared Error (SSE), and Root Mean Squared Error (RMSE) are given in Table 2 . As shown in Fig. 5, the number of minor infected people, hospitalized people, and intensive infected increased in the early days, and these populations experience a peak, and after that, with the regulations related to this disease, given by WHO, the trend is decreasing. Again, after some time, the pandemic experiences its second wave.

Fig. 5.

Variation of number of people in different categories in the proposed model a) Exposed people b) Minor infected people, c) Hospitalized people, d) Intensive infected people, e) Recovered people, and f) Deceased people.

Table 2.

Error in Statistical Tests.

State	MSE	SSE	RMSE
$E$	1.7134$\times {10}^{-4}$	0.0778	0.0353
$M$	9.3893$\times {10}^{-6}$	0.0043	0.0083
$H$	2.5102$\times {10}^{-8}$	1.1396$\times {10}^{-5}$	4.2733$\times {10}^{-4}$
$I$	2.7961$\times {10}^{-9}$	1.2694$\times {10}^{-6}$	1.4262$\times {10}^{-4}$
$R$	5.7608$\times {10}^{-4}$	0.2615	0.0647
$D$	2.0986$\times {10}^{-6}$	9.5275$\times {10}^{-4}$	0.0039

Fig. 6 to Fig. 10 show the results of parameter estimation using real data from Italy. The parameters are time-varying, and every 3.5 days change.

Fig. 7.

Variation of parameters that express the transfer rates of exposed people to the minor infected and hospitalized people.

Fig. 8.

Variation of parameters that express the transfer rates to the recovered people.

Fig. 9.

Variation of parameters that state the transmission rates of different degrees of disease to each other.

Fig. 6.

Variation of parameters that affect the spread of the virus.

Fig. 10.

Variation of parameters that state the transmission rates to deceased people.

5.2. Discussion about shortage in hospital capacity and ventilator capacity

The hospital capacity of Italy is 3.18 beds per 1000 people and the ventilator capacity for Italy is 5,324 [40], and the need for these devices has to be at most equal to the number of available devices. This number is about 8.9 per 100,000 people. Since some people are already hospitalized in the country according to a disease other than Coronavirus, it is assumed that the 30% of hospital capacity and 80% of ventilator capacity can be devoted to this disease, approximately. The capacities are shown by a red line in Fig. 11 and Fig. 12 .

Fig. 11.

Hospitalized people compared to hospital capacity.

Fig. 12.

Intensive infected people compared to ventilator capacity.

To analyze the model for the future, we can consider the above model and assume that the level of quarantine is changed. In model (1)-(2), the social distancing and the quarantine levels can affect the parameter ${\alpha }_E$, and ${\alpha }_H$, respectively. At the same time, the social distancing and quarantine strategies may change, which can influence the curve variations in the future.

It is assumed that the social distancing is divided into 5 categories: 100%, 75%, 50%, 25%, and 0%, according to the level of social distancing imposed by the government. Obviously, 100% means complete lockdown, and 0% means no social distancing is applied. In other categories, different levels of social distancing are considered. For instance, we can assume 75% social distancing means all people stay at home and only the shops are open provided that they keep on the sever regulations of WHO (covering most parts of their shop with glass or plastics to avoid direct contact with the customers). The 50% social distancing level can be assumed as the case that added to the shops, subways, MTR and transportation facilities, work, and finally, 25% social distancing refers to the case that except conferences, university and school classes that are held electronically, all other activities in the city are followed, regularly. Obviously, these numbers are not estimated exactly and they are just mentioned to give a sense of different social distancing levels.

Added to the different social distancing levels, different cases of quarantine in hospitals are assumed. In these cases, people (doctors, nurses, and those who are supposed to work at hospitals) who visit the patients may or may not wear special clothes, and the patients may or may not be kept in isolated rooms. The more the contaminated person is kept isolated, the more severe quarantine level is considered.

5.2.1. Effects of quarantine strategy on hospitalized and Intensive-infected people

The effect of decreasing quarantine strategy with increasing ${\alpha }_H$ on the population of hospitalized people and intensive infected people are shown in Fig. 13 . Similarly, Fig. 13 reveals that to avoid a shortage of ICU beds, it is necessary to quarantine the hospitalized people. This indicates the isolation of COVID-19 patients to protect doctors, nurses, and those who are supposed to work at hospitals. It is concluded that the isolation should be kept at the highest level to assure enough ICU capacity for intensive infected people.

Fig. 13.

Effect of decreasing quarantine of hospitalized people with increasing ${\alpha }_H$. a) The effect of different levels of quarantine on the hospitalized people. b) The effect of different levels of quarantine on the intensive infected people.

5.2.2. Effects of social distancing on hospitalized and Intensive-infected people

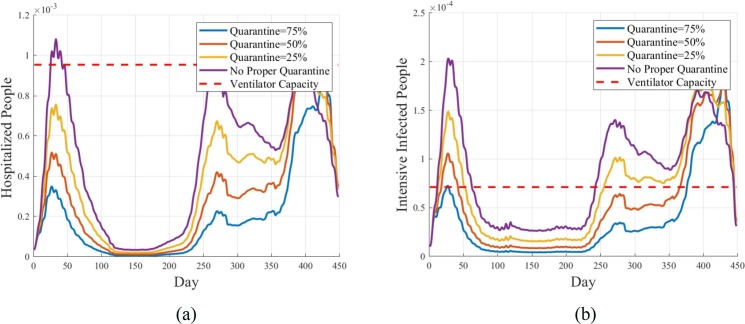
The effect of decreasing social distancing with increasing ${\alpha }_E$ on the population of hospitalized people and intensive infected people are shown in Fig. 14 .

Fig. 14.

Effect of decreasing social distancing with increasing ${\alpha }_e$. a) The effect of different levels of social distancing on the hospitalized people. b) The effect of different levels of social distancing on the intensive infected people.

Fig. 14a indicates that if no social distancing is applied, the capacity of hospitals is not enough for patients. However, Fig. 14b determines the essential social distancing level of at least 75% to assure that ICU beds are enough for Coronavirus patients who are in need of a ventilator.

5.3. LPV model stability analysis

According to the results given in Fig. 6- Fig. 10, the variation of the parameters in the LPV model of COVID-19 in (10) is derived as follows:

$$\begin{array}{c}{\alpha }_E∊\left[0,3.45\right],{\alpha }_M∊\left[0,2.92\right],{\alpha }_H∊\left[0.07,3.41\right],\hfill \\ k_1∊\left[0,1.38\right],k_2∊\left[0,1.36\right],\rho ∊\left[0,0.15\right],\beta ∊\left[0,0.46\right],\hfill \end{array}$$

$$\begin{array}{c}\eta ∊\left[0.02,2.55\right],\phi ∊\left[0.23,2.59\right],\delta ∊\left[0,2.66\right],\hfill \\ \theta ∊\left[0.17,1.32\right],\mu ∊\left[0,0.06\right],\zeta ∊\left[0,0.07\right]\hfill \end{array}$$ (38)

At first, the stability is assessed by solving the set of LMIs in (35) using the YALMIP toolbox [41]. The result shows no feasible solution. To be sure that whether the problem is unstable per se or it can be stable, the direct searching approach is exploited.

The approach shows total infeasible solution space, which means intensive care and quarantine strategies are needed to stabilize the model. Since the direct search approach is non-conservative, this means that the LPV model is unstable. For further study, the quarantine and social distancing levels are increased, which is equal to decreasing the values of ${\alpha }_E,{\alpha }_M,{\alpha }_H$. Setting these levels to 75% shows a stable model that guarantees the states' convergence to constant values.

6. Discussion

The data of COVID-19 in case study Italy for 454 days from March 2nd, 2020 to May 29th, 2021 are collected and a model for the spread of Coronavirus is suggested. It is shown that without using basis functions and by using constant parameters, the model is not fitted on the collected data. Then, according to section 3, some basis functions are used, and the parameters are estimated dynamically. As is given in section 4, the results show the capability of the proposed model to follow the real data. There are some papers that work on COVID-19 modeling, but they didn’t compare modeling results with real data [4], [11]. In some other works, only in the early days of the outbreak, the model has been tested to fit the data [22], [27], [29], and in some others, the model has not fitted appropriately for all days [13], [42]. However, in this paper, the comparison of data and the proposed model is given and the accuracy of fitting the proposed model to the data is 99.33% in the total data.

In sections 5.2.1 and 5.2.2, it is shown that without applying appropriate quarantine and social distancing, the required number of hospital beds and ventilators exceeds the available capacities. The results show the need for social distancing and quarantine rules.

It is essential to mention that the social distancing level depends on the physical distance of the people. Therefore, it is not essential for the model whether lockdown policy is imposed or the people themselves obey WHO's suggestions. In some countries, the government imposed severe regulations, while in some other countries, governments just suggest people follow WHO regulations. For the proposed model of this paper, both of these strategies are the same. The result is important: the people should not come closer to others (whether by force or by their own decision).

In the last part of the paper, the modeling results are used to derive the LPV model of COVID-19 disease. Fortunately, the methodology is successful in presenting an approach for COVID-19 LPV model derivation. Then, the stability tools can be used to assess the model stability.

7. Conclusion

In this paper, a mathematical model for the spread of COVID-19 is proposed. In this model, the people involved with the disease are divided into seven groups, including susceptible people, exposed people, minor infected, home isolation people, hospitalized people, intensive care people, intensive infected, recovered people, and deceased. After estimating the time-varying parameters in the model, the effects of social distancing and quarantine are studied on the model. It is concluded that the model is suitable for fitting the past and present curves and can be used for determining the level of quarantine and social distancing in a city. In addition, the time-varying parameters of the model are used in deriving the COVID-19 LPV model. The model can be used for robust stability assessment or controller design (vaccine injection rate) approaches, exploiting the theory of LPV systems.

CRediT authorship contribution statement

Roozbeh Abolpour: Conceptualization, Methodology, Software, Validation. Sara Siamak: Software, Resources, Data curation, Writing – original draft. Mohsen Mohammadi: Data curation, Methodology, Writing - review & editing. Parisa Moradi: Formal analysis, Writing – original draft. Maryam Dehghani: Conceptualization, Supervision, Project administration, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.