An on-board surgical tracking and video augmentation system for C-arm image guidance

Abstract

Purpose

Conventional tracker configurations for surgical navigation carry a variety of limitations, including limited geometric accuracy, line-of-sight obstruction, and mismatch of the view angle with the surgeon’s-eye view. This paper presents the development and characterization of a novel tracker configuration (referred to as “Tracker-on-C”) intended to address such limitations by incorporating the tracker directly on the gantry of a mobile C-arm for fluoroscopy and cone-beam CT (CBCT).

Methods

A video-based tracker (MicronTracker, Claron Technology Inc., Toronto, ON, Canada) was mounted on the gantry of a prototype mobile isocentric C-arm next to the flat-panel detector. To maintain registration within a dynamically moving reference frame (due to rotation of the C-arm), a reference marker consisting of 6 faces (referred to as a “hex-face marker”) was developed to give visibility across the full range of C-arm rotation. Three primary functionalities were investigated: surgical tracking, generation of digitally reconstructed radiographs (DRRs) from the perspective of a tracked tool or the current C-arm angle, and augmentation of the tracker video scene with image, DRR, and planning data. Target registration error (TRE) was measured in comparison with the same tracker implemented in a conventional in-room configuration. Graphics processing unit (GPU)-accelerated DRRs were generated in real time as an assistant to C-arm positioning (i.e., positioning the C-arm such that target anatomy is in the field-of-view (FOV)), radiographic search (i.e., a virtual X-ray projection preview of target anatomy without X-ray exposure), and localization (i.e., visualizing the location of the surgical target or planning data). Video augmentation included superimposing tracker data, the X-ray FOV, DRRs, planning data, preoperative images, and/or intraoperative CBCT onto the video scene. Geometric accuracy was quantitatively evaluated in each case, and qualitative assessment of clinical feasibility was analyzed by an experienced and fellowship-trained orthopedic spine surgeon within a clinically realistic surgical setup of the Tracker-on-C.

Results

The Tracker-on-C configuration demonstrated improved TRE (0.87 ± 0.25)mm in comparison with a con ventional in-room tracker setup (1.92 ± 0.71)mm (p < 0.0001) attributed primarily to improved depth resolution of the stereoscopic camera placed closer to the surgical field. The hex-face reference marker maintained registration across the 180° C-arm orbit (TRE = 0.70 ± 0.32 mm). DRRs generated from the perspective of the C-arm X-ray detector demonstrated sub-mm accuracy (0.37 ± 0.20 mm) in correspondence with the real X-ray image. Planning data and DRRs overlaid on the video scene exhibited accuracy of (0.59 ± 0.38) pixels and (0.66 ± 0.36) pixels, respectively. Preclinical assessment suggested potential utility of the Tracker-on-C in a spectrum of interventions, including improved line of sight, an assistant to C-arm positioning, and faster target localization, while reducing X-ray exposure time.

Conclusions

The proposed tracker configuration demonstrated sub-mm TRE from the dynamic reference frame of a rotational C-arm through the use of the multi-face reference marker. Real-time DRRs and video augmentation from a natural perspective over the operating table assisted C-arm setup, simplified radiographic search and localization, and reduced fluoroscopy time. Incorporation of the proposed tracker configuration with C-arm CBCT guidance has the potential to simplify intraoperative registration, improve geometric accuracy, enhance visualization, and reduce radiation exposure.

Introduction

Fluoroscopy and/or surgical navigation are widely used to localize anatomy with respect to surgical instruments and guide the accurate placement of spinal instrumentation while avoiding injury to neurovascular structures. Fluoroscopy provides real-time radiographic views of the surgical field but lacks depth information and imparts radiation dose to the surgeon and patient. On the other hand, surgical navigation enables visualization of tracked surgical tools relative to the anatomy as registered to 3D preoperative images, potentially reducing the reliance on fluoroscopy and improving 3D visualization. Integration of tracking systems and intraoperative fluoroscopy/cone-beam computed tomography (CBCT) imaging is a prevalent trend, allowing navigation and visualization using up-to-date 3D images that properly reflect deformation and/or tissue excision during the intervention. Various studies have proposed navigation incorporating a tracking system and mobile C-arm capable of CBCT reconstruction [1–5]. The tracker in such systems is conventionally positioned in the operating room at a typical distance of 100–300 cm from the surgical field (Fig. 1) and can be susceptible to line-of-sight occlusion.

Fig. 1.

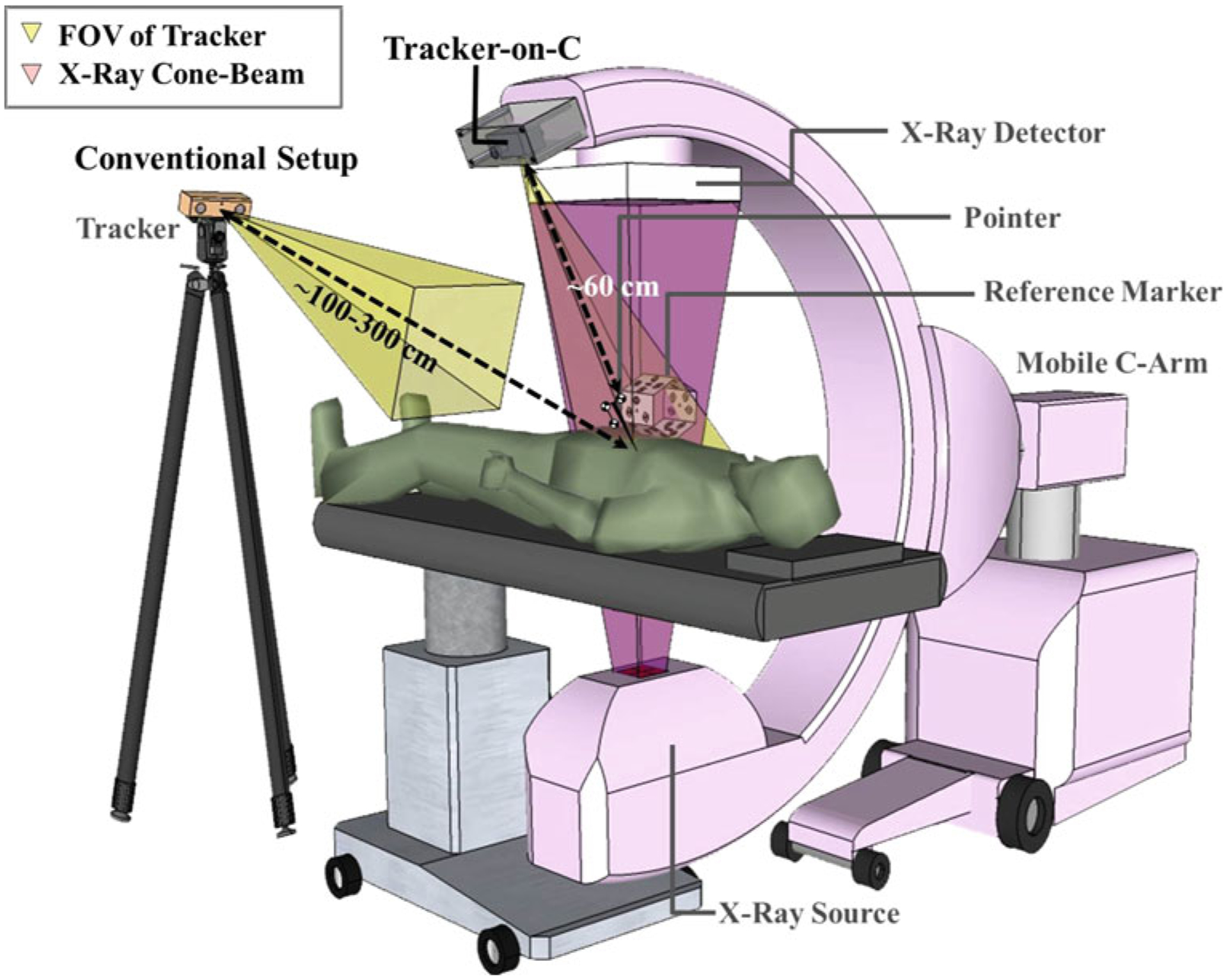
Illustration of the Tracker-on-C configuration. The system employs a tracker mounted on the C-arm and reference marker visible from all rotation angles to provide real-time tracking, DRR capabilities, and video augmentation. Also, shown is a conventional configuration in which the tracker is placed in the room (typically at ~100–300 cm distance from the surgical field)

Meanwhile, positioning the C-arm accurately with respect to the surgical target for 2D/3D imaging can be a time-consuming task and can involve multiple fluoroscopic acquisitions to position the C-arm at the region of interest [6,7]. To reduce fluoroscopy time in C-arm setup and target localization, digitally reconstructed radiographs (DRRs) generated from 3D volumetric data (e.g., intraoperative or preoperative computed tomography (CT)) and the known perspective of the C-arm (e.g., as measured by the tracking system) may be helpful. Dressel [8] proposed an intraoperative C-arm positioning system using a camera-augmented mobile C-arm (CAMC) [9] in which a video camera was incorporated on the C-arm (adjacent to the X-ray tube placed over the table) as a tracking and localization system. The system demonstrated excellent utility in a variety of orthopedic surgery applications.

Similarly, video augmentation can be used to better visualize the spatial relationship between surgical tools and anatomy. Fluoroscopy-based navigation systems can visualize the trajectory of a surgical tool on X-ray projections [10–12]. Surgical tools can also be visualized with respect to tomographic slices (axial, sagittal, and coronal) and surface models generated from 3D images (e.g., CT, MR, and CBCT) [13–15]. Other systems have integrated a video camera within the surgical guidance system to enable video augmentation. For example, Hayashibe et al. [16] developed a system overlaying volume-rendered images generated from intraoperative CT on the video scene captured by a video camera attached to the back of a ceiling-mounted monitor. Navab et al. [9] developed an image overlay system in which 3D planning data or simulated X-ray images were overlaid on real-time video images captured from the perspective of the C-arm-mounted video camera in CAMC. Fusion of video images and real X-ray projections has also been shown using a double mirror construction that aligns the principle axis of the video camera and X-ray imaging system (i.e., direct optical matching to X-ray field) [17]. In addition, a video-based tracker employed in conventional navigation systems allows video augmentation from the perspective of the tracker; however, in the conventional, room-based setup, such a perspective is mismatched to the surgeon’s viewpoint, and an additional video camera was required to capture the operating field.

This paper describes a novel tracker configuration for a 3D mobile C-arm guidance system, referred to as Tracker-on-C. In the proposed configuration (illustrated in Fig. 1), the tracker is mounted on the C-arm gantry next to the flat-panel detector (FPD) over the table at a distance of approximately 60 cm from the C-arm isocenter. The position of the tracker on the gantry was hypothesized to improve geometric accuracy and reduce line-of-sight obstruction. The proposed configuration also facilitated DRR generation from the perspectives defined by a tracked tool or the C-arm itself. For the specific case in which a video-based tracker is used (e.g., a stereoscopic video camera system such as the MicronTracker, Claron Inc., Toronto, ON, Canada), the Tracker-on-C configuration allows video augmentation from a perspective similar to the surgeon’s-eye view over the table. Segmented anatomical structures, planning data, DRRs, and the X-ray field-of-view (FOV) can be superimposed onto the video scene to assist localization of target anatomy and positioning the C-arm at tableside such that target anatomy is in the FOV. The proposed Tracker-on-C system is distinct from systems mentioned above in a variety of respects: (1) the tracking system may employ video-based, optical/infrared, or electromagnetic trackers (although only the first was investigated below); (2) for cases in which the system uses a tracker employing a video camera (e.g., a video-based tracker like the one described below or some optical/infrared trackers), it provides the capability for video augmentation; (3) the capabilities of the proposed system are based on 3D/3D registration (not, for example, direct optical matching to the X-ray field [17]); (4) the proposed system uses the geometric calibration of the C-arm and does not require hardware modification of the C-arm (aside from the mounting of the tracker); and (5) the proposed system allows C-arm operation in the usual (detector-over-table) configuration. Typical workflow associated with the Tracker-on-C system could include off-line calibration and quality assurance (e.g., camera distortion calibration and C-arm geometric calibration), preoperative imaging (e.g., acquisition of CT (or MR) images and definition of planning data therein), preoperative setup (registration of the tracker, patient, and image data), and intraoperative use (e.g., C-arm positioning assistant, surgical navigation, and use of virtual fluoroscopy to reduce X-ray exposure time). A recent study specifically examined conventional workflow for C-arm setup (a potential bottleneck in CBCT guidance) in comparison with the setup assisted by Tracker-on-C, suggesting a significant benefit to workflow associated with the video augmentation capabilities of the proposed system [18]. The proposed system was evaluated quantitatively in terms of geometric accuracy and qualitatively by an expert spine surgeon within a realistic preclinical (cadaver) setup of the Tracker-on-C to assess the feasibility and potential utility in the early stages of system development.

Materials

Tracker-on-C configuration

A schematic of the proposed tracker configuration is illustrated in Fig. 1. We employed the implementation on a prototype mobile C-arm for intraoperative CBCT reported by Reaungamornrat et al. [19], and we provide a brief summary here. The tracker was mounted on the C-arm next to the detector at a distance of ~60 cm from isocenter. The registration between the tracker and the patient is maintained at any C-arm angulation by the use of a “hex-face” reference marker visible from any angle. While the proposed Tracker-on-C configuration is compatible with various tracking modalities (e.g., infrared, video, and electromagnetic), a video-based tracker (MicronTracker Sx60, Claron Technology Inc., Toronto, ON, Canada) as shown in Fig. 2a was used in the current work.

Fig. 2.

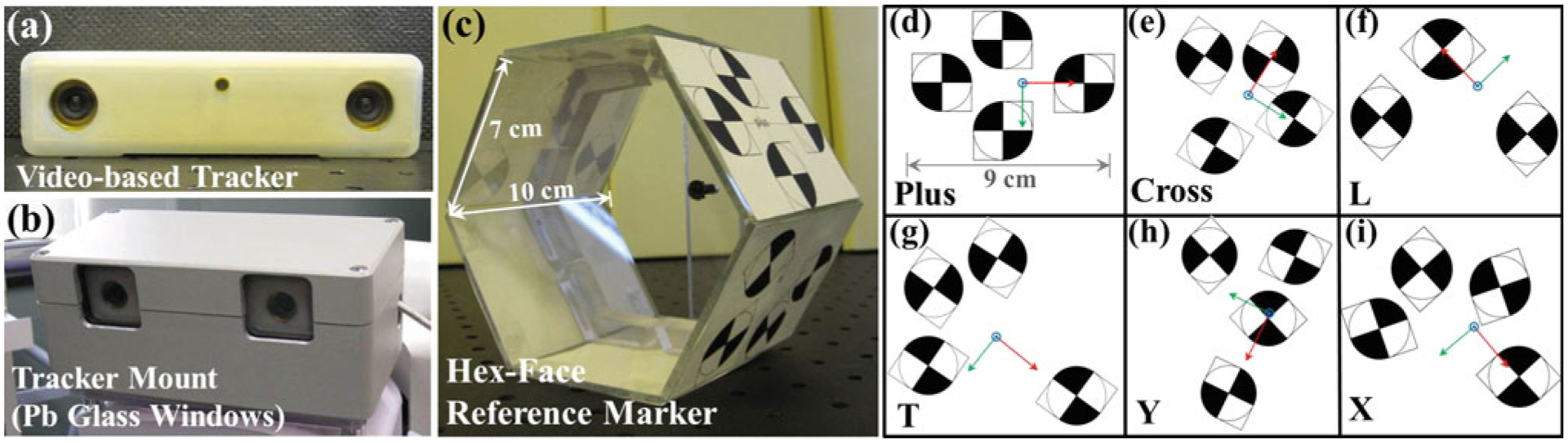
a Video-based tracker. b Tracker mount incorporating a metallic enclosure and Pb glass window. c Hex-face reference marker with six planar faces. d–i Xpoint configuration, name (lower left), and coordinate system associated with each face (x-axis in red, y-axis in green, and z-axis in blue)

Mobile isocentric C-arm

A prototype mobile C-arm developed in academic–industry collaboration (Siemens Healthcare, Erlangen, Germany) for intraoperative CBCT was used [20]. The isocentric C-arm incorporated a FPD, motorized rotation, geometric calibration, and software for 3D reconstruction. The FPD (PaxScan 3030 CB, Varian Imaging Products, Palo Alto, CA, USA) provided real-time, distortionless readout (30 × 30 cm², 768 × 768 pixel format, 0.388 mm pixel size) for high-quality CBCT. The tracker mount—installed next to the FPD—incorporated a steel enclosure and a Pb glass window to shield the tracker from radiation (Fig. 2b). The Tracker-on-C configuration allows tracking of the object from various C-arm angulations while permitting normal use and configuration of the C-arm (detector-over-table).

Tracking system

The video-based tracker (MicronTracker, Claron Inc., Toronto, ON, Canada) employed in the current work is illustrated in Fig. 2a. The tracker uses visible light to observe markers constructed from black-and-white checkerboard patterns called Xpoints (Fig. 2d–i). Unique geometric configurations of Xpoints allow marker recognition and pose measurement. The tracker provides a field-of-measurement (FOM) of ~30–160 cm distance from the tracker at a rate of 48Hz, and a video stream of 640 × 480 pixels. It interfaces with a PC workstation via a standard IEEE-1394a (Firewire) with a data transfer rate of 400 Mbps. The tracker was integrated with the TREK surgical navigation system previously described for CBCT-guided interventions [21,22], using two main open-source libraries: computer-integrated surgical systems and technology (CISST) (Johns Hopkins University, Baltimore MD, USA) [23–25] and 3D Slicer (Brigham and Women’s Hospital, Boston, MA, USA) [26,27]. Visualization and image analysis were implemented in 3D Slicer, while numerical computation, multi-threading, hardware interfaces, and control/image capture of the video-based tracker were handled by CISST. A complete description of the TREK architecture binding of CISST and 3D Slicer libraries can be found in the literature [22].

Reference marker

A reference marker was used to establish a coordinate system associated with the patient, so that intraoperative tracking can be accomplished relative to the patient coordinate system rather than the tracker coordinate system, thereby eliminating measurement errors due to the movement of the tracker. Similar to other optical trackers, the video-based tracker requires unobstructed line of sight to tracked markers. The line-of-sight requirement and size of the tool impose challenges in the design of a marker visible across 180°–360° (i.e., across all C-arm rotation angles). A reference marker visible from 360° was designed to define the world reference frame and maintain registration at any C-arm angulation. The work below involved (detector-over-table) C-arm rotation of ~180°, so only the top three faces were typically used. Referred to as a “hex-face” reference marker, it comprised six faces attached to six acrylic planar surfaces aligned in a hexahedral shape (Fig. 2c). The initial prototype reference marker was fairly large (~1.4 cm diameter of an Xpoint), and a smaller version (~0.7 cm diameter of an Xpoint) is under development. Each face contained a unique geometry of Xpoints defining the coordinate system associated with each face as illustrated in Fig. 2d–i. The size and configuration of these marker arrangements were found through repeat experimentation to be a suitable starting point for testing and early application to the Tracker-on-C system.

Methods: Tracker-on-C registration and functionality

Clinical workflow for the Tracker-on-C system, as illustrated in Fig. 3, could include, for example: (1) acquisition of preoperative CT images, (2) preoperative surgical planning (definition of target structures and tool trajectories), (3) preoperative off-line calibration (e.g., camera calibration and C-arm geometric calibration), (4) attachment of the reference marker to the patient (intraoperative, immediately before procedure), (5) paired-point registration (intraoperative, immediately before procedure), and (6) intraoperative imaging and guidance based on 2D (fluoroscopy), 3D (CT and/or cone-beam CT).

Fig. 3.

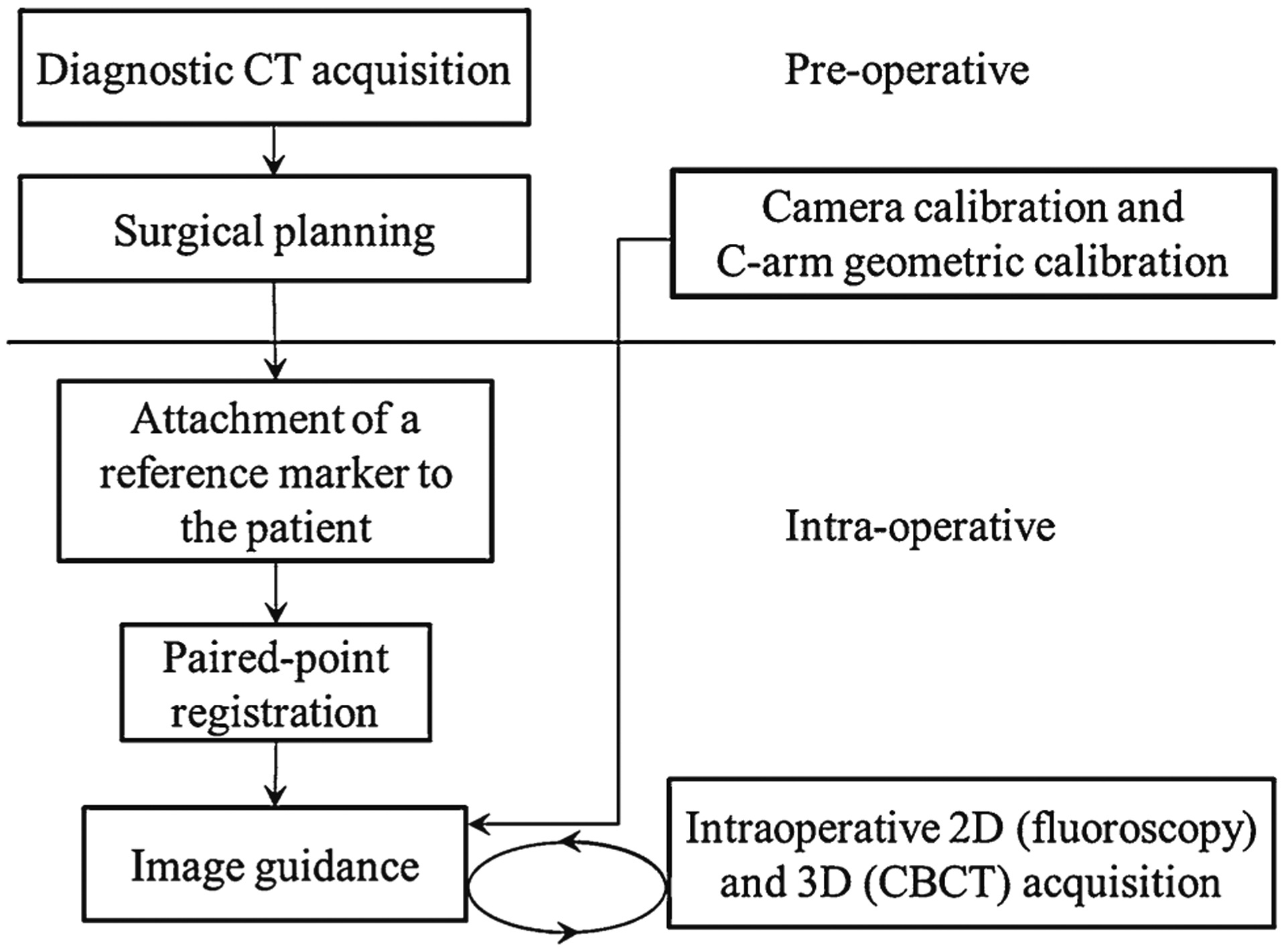
Clinical workflow of the Tracker-on-C system

The section below describes the registration methods and three main functionalities of the Tracker-on-C system, including surgical tracking, generation of DRRs, and video augmentation. Experimental measurement of the geometric accuracy of each functionality is detailed in “Methods: Experimentation and assessment.” Terms and notation for the system geometry and geometric relationships between coordinate systems are summarized in Table 1.

Table 1.

Nomenclature for coordinate systems and transforms

ATB	Transformation from coordinate system B to A
${}^A{\overrightarrow{P}}_B$ or (ApB,x, ApB,y, ApB,z)	Position of point B (x, y, and z location) in coordinate system A
$A_{\overrightarrow{x}}$, $A_{\overrightarrow{y}}$, $A_{\overrightarrow{z}}$	Axes (x, y, and z) of coordinate system A
T	Coordinate system of the tracker
R	Coordinate system of the reference marker
F	Coordinate system of the reference marker Face
M	Coordinate system of the marker (tool)
VC	Coordinate system of the video camera
S	Coordinate system of the x-ray source
FPD	Coordinate system of the flat-panel detector
CT	Coordinate system of the CT image
CBCT	Coordinate system of the CBCT image
CP	Coordinate system of the calibration phantom

Tool calibration

Tool tracking is a process by which the position and orientation of the patient and a surgical tool are first determined in the world coordinate system (i.e., the coordinate system of a reference marker or a tracker). Then, a registration process allows transformation of positions from the world coordinate system to that of a 3D medical image (and vice versa). In this work, the paired-point registration method proposed by Arun et al. [28] was used to estimate the translation vector and rotation matrix that produced a least-squares fit of the point sets (fiducials) in the world and image coordinate systems. Paired-point registration is a common and well-accepted method yielding equivalent geometric accuracy to the combination of paired-point matching and surface matching while requiring less registration time [29]. The matched points (fiducials) in the world reference frame and in the medical image coordinate system were identified manually. This section describes the tool calibration performed to allow pose measurements of a tool tip and the hex-face reference marker. In “Methods: Experimentation and assessment,” geometric accuracy of these registrations was evaluated in terms of the target registration error (TRE) as the distance between anatomical target points in the coordinate systems of the world and medical images after registration [30].

Real-time pose measurement of the tip of rigid surgical tools (e.g., pointers, suction, drills, and endoscopes) is one key feature of surgical navigation. A pivot calibration provides a least-square solution of the transformation from the coordinate system attached to the tool handle to the coordinate system at the tip position [31,32]. For calibration of the hex-face reference marker, a custom calibration procedure was developed to determine the relative transformation between the coordinate systems associated with each face. The rigid tool construction assured the relative transformation to be constant. The relative transformation between face i and i + 1 was computed using Eq. (1),

$${}^i{T}_{i+1}={\left({}^T{T}_i\right)}^{-1}{}^T{T}_{i+1}$$ (1)

where the transformations from face i(^T T_i) and i + 1 (^T T_i + 1) to the tracker coordinate system were measured directly by the tracker. The “zeroth” face (i.e., that to which other faces were registered) was selected as the one at the center of the C-arm rotational arc to minimize error and simplify pose measurement.

For pose measurements in which more than one face is visible to the tracker, the face presenting the least obliqueness was used for registration in order to reduce fiducial localization errors. The obliqueness was determined as:

$$\theta ={\text{cos}}^{-1}\left(\frac{{}^T\overrightarrow{z}{}^F\overrightarrow{z}}{|{}^T\overrightarrow{z}||{}^F\overrightarrow{z}|}\right)$$ (2)

where θ is the obliqueness, ${}^T\overrightarrow{z}$ is the z-axis of the tracker, and ${}^F\overrightarrow{z}$ is the normal vector of the face.

Tracker-on-C for guidance with digitally reconstructed radiographs (DRRs)

DRRs are simulated projection images computed from the 3D data set of either CT or CBCT using specified virtual camera perspectives. The Tracker-on-C facilitates two DRR functionalities, including DRRs from the perspective of a tracked tool (X-ray Flashlight) and from the C-arm itself (Virtual Fluoroscopy). These functionalities and calibration procedures for the two virtual camera perspectives are described below. In “Methods: Experimentation and assessment,” geometric accuracy of DRRs from the perspective of the C-arm was measured as the projection error (the distance between corresponding projected points in real and virtual fluoroscopic images).

Geometric calibration

Geometric calibration of the Tracker-on-C system was performed to enable the generation of DRRs from the pose of the C-arm. The geometric calibration computed the homogeneous transformation between the coordinate systems of the tracker and the FPD (^FPDT_T), as shown in Fig. 4a. The calibration phantom consisted of two sets of steel ball bearings (BBs): a set of 16 BBs located in two circular patterns embedded in an acrylic cylinder [33] (referred to as “Cylinder BBs”) and a set of 4 BBs placed at the centers of Xpoints in a rigidly affixed reference marker (referred to as “Xpoint BBs”). Figure 4b shows a zoomed-in photograph of the phantom overlaid with red circles and green squares around the Cylinder BBs and the Xpoint BBs, respectively, and Fig. 4c shows a corresponding projection image. The cylindrical phantom and associated C-arm geometric calibration were adapted from Cho et al. [33]. A CBCT reconstruction of the phantom was acquired at a voxel size of 0.3×0.3×0.3 mm³ to define the locations of the BBs in the CBCT coordinate system.

Fig. 4.

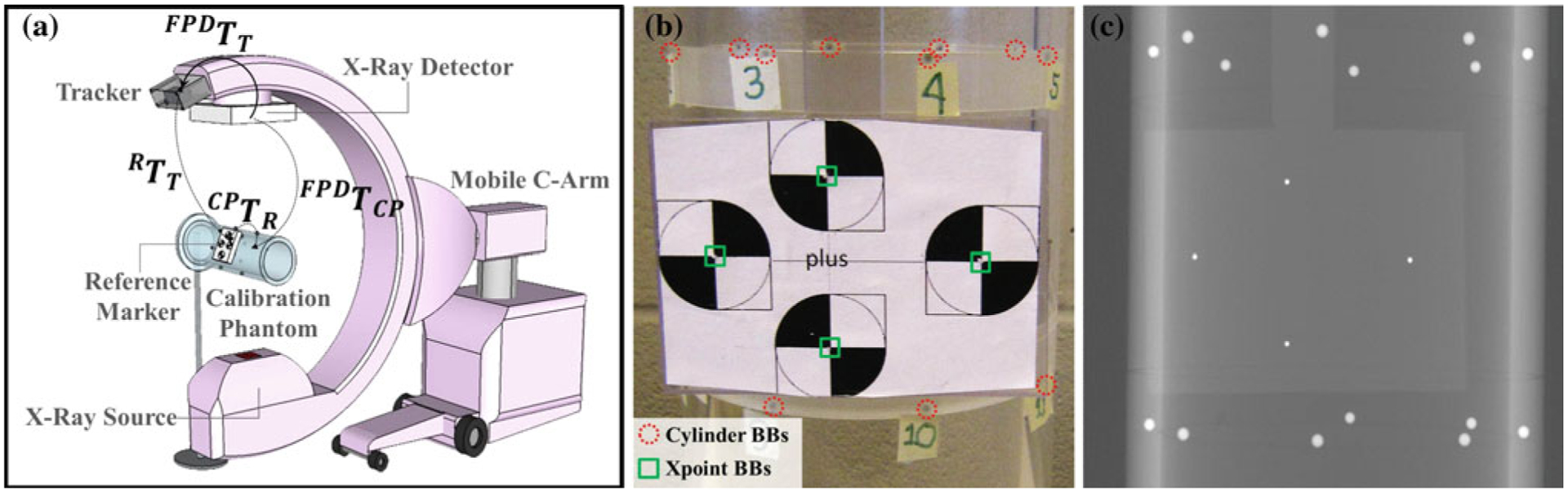
a System geometry for the tracker-to-detector calibration. b Zoomed-in view of the calibration phantom with red circles around BBs used for C-arm calibration (16 “Cylinder BBs”) [33] and green squares around BBs placed at the center of Xpoints (4 “Xpoint BBs”). c Zoomed-in view of a radiograph of the calibration phantom

The location of the Cylinder BBs was obtained from the CAD model of the phantom. The Xpoint BBs and the CBCT images of the phantom were used to compute the transformation between the coordinate systems of the phantom and the reference marker (^CPT_R):

$${}^{\text{CP}}{T}_R{=}^{\text{CP}}{T}_{\text{CBCT}}{}^{\text{CBCT}}{T}_R$$ (3)

where the transformation between the reference marker and the CBCT coordinate system (^CBCTT_R) was computed by paired-point registration of the 4 Xpoint BB locations in the reference marker coordinates and in the CBCT images. Likewise, the transformation between the CBCT coordinate system and the phantom (^CPT_CBCT) was computed using the 16 Cylinder BBs. The transformation ^CPT_R was constant since the Xpoint reference marker was rigidly fixed to the cylindrical calibration phantom.

The transformation between the coordinate systems of the tracker and the detector (^FPDT_T) was computed as:

$${}^{\text{FPD}}{T}_T{=}^{\text{FPD}}{T}_{\text{CP}}{}^{\text{CP}}{T}_R{}^R{T}_T$$ (4)

where the transformation ^R T_T was obtained directly by tracker measurements, and the transformation between the coordinate systems of the calibration phantom and the detector (^FPDT_CP) was computed as in Cho et al. [33] and Daly et al. [34] in which each projection of the cylindrical phantom provides a complete pose determination of the C-arm at that angulation. The transformation ^FPDT_CP was dependent on C-arm angulation due to mechanical flex of the gantry, so projection errors of DRRs generated from the pose of the C-arm were examined in which the full (angle-dependent) calibration was employed in comparison with that using a single nominal angle (suffering error due to gantry flex).

Functionalities using DRR

The Tracker-on-C system integrated a GPU-based projector library for DRR computation that speeds the computationally expensive process of DRR generation through parallelization and higher computational performance on multiple GPUs (NVIDIA GeForce/Quadro, NVIDIA Corporation, Santa Clara, CA, USA). Two projection algorithms were implemented: (1) a simple grid interpolation algorithm using texture memory on the GPU; and (2) Siddon’s radiological path computation [35] which provides a more accurate line integral with the disadvantage of increased computation time. The geometry of the C-arm imaging system, including the extrinsic and intrinsic parameters required to project 3D data to 2D images, was specified via a 3 × 4 projection matrix [36,37]. The library was designed as a cross-platform, compiler-independent, shared library implemented using CUDA 4.0 and C++ and allowing scripting via other programming languages (e.g., MATLAB and Python). The following two functions for specifying the DRR perspective were implemented.

1. Tool-Driven DRR (“X-ray Flashlight”) DRRs generated from the perspective of a tracked tool (e.g., a handheld pointer) use the extrinsic parameters (^M T_CT) specifying the transformation between the volume image (e.g., CT or CBCT) and the tracked tool coordinate system, computed as:

   $${}^M{T}_{\text{CT}}{=}^M{T}_R{}^R{T}_{\text{CT}}$$ (5)

   where the transformation between the volume image and reference marker coordinate system (^RT_CT) was computed from paired-point registration. The transformation from the reference marker to the tracked tool coordinate system (^M T_R) was measured by the tracker. The implementation allowed free adjustment (in software) of the virtual source position of the X-ray flashlight along the tool trajectory to achieve desired image magnification.
2. C-Arm-driven DRR (“Virtual Fluoroscopy”) DRRs generated from the pose of the C-arm provide a virtual fluoroscopic view based on the extrinsic parameters (^ST_CT) describing the transformation between the volume image (CT or CBCT) and the X-ray source coordinate systems, computed as:

   $${}^S{T}_{\text{CT}}{=}^S{T}_{\text{FPD}}{}^{\text{FPD}}{T}_T{}^T{T}_R{}^R{T}_{\text{CT}}$$ (6)

   where the transformation from the tracker to the detector coordinate system (^FPDT_T) was computed using Eq. (4), and the transformation between the source and the detector coordinate system (^ST_FPD) was computed from C-arm geometry calibration. The intrinsic parameters of the C-arm, including the focal length and image center, change during rotation due to mechanical flex of the arm [34], so they were estimated at each angulation. The focal length was computed from the known pixelsize of the C-arm and the position of the detector in the z-axis of the source coordinate system, and the image center was computed from the pixel size, image size, and the position of the detector in x and y-axes of the source coordinate system.

Tracker-on-C for video augmentation

The video-based tracker employed in the Tracker-on-C configuration enabled video augmentation from the perspective of the tracker above the OR table. This section describes the camera calibration and distortion correction for this specific video camera and the three video augmentation functionalities supported by the Tracker-on-C system, including planning data overlay, virtual filed light overlay, and DRR overlay. The geometric accuracy of video augmentation was examined in “Methods: Experimentation and assessment.”

Camera calibration and distortion correction

Camera calibration is the process of determining the location, orientation, and intrinsic parameters of the camera required for rendering 3D models or images over the video scene [38–40]. The extrinsic parameters describe the pose of the video camera with respect to the world reference frame (i.e., the tracker coordinate system), and the intrinsic parameters represent the projection geometry of the camera. In this work, we used the intrinsic calibration parameters provided by the manufacturer through the built-in application programming interface (API). These calibration parameters—internally used for triangulation in the tracking of Xpoints—provide the direction that each pixel element faces, which we approximate to a simple pinhole model for overlay of 3D objects using a standard pinhole-based rendering technique. These parameters represent the projection ray from the ith CCD element to the center of the video camera containing that CCD element as:

$${\overrightarrow{r}}_i={\overrightarrow{t}}_i+d_i{\overrightarrow{l}}_{i(i=1,2,\dots ,N)(N:\text{ number of rays })}$$ (7)

where ${\overrightarrow{r}}_i$ denotes a projection ray in the tracker coordinate system, d_i denotes the scale factor, ${\overrightarrow{t}}_i$ denotes the origin of the ray on the ith pixel of the CCD, and ${\overrightarrow{l}}_i$ denotes a unit vector along the ray direction. Note there are projection rays from the CCD elements in each camera to the center of that camera (i.e., left and right cameras).

The camera center in the tracker coordinate system, the image center, and the pixel size were fitted to the parameters provided by the manufacturer in a least-square sense as follows. The camera center in the tracker coordinate system (${}^T{\overrightarrow{P}}_{\text{VC}}$; 3 × 1 vector) was computed as the point that minimized the sum of distances from all rays (Eq. 8), interpreted intuitively as the most probable intersection of those rays:

$${}^T{\overrightarrow{P}}_{\text{VC}}=\widehat{\overrightarrow{P}}=\underset{\overrightarrow{P}}{\text{arg min}}\sum _{i=1}^N\Vert \overrightarrow{P}-\left({\overrightarrow{t}}_i+d_i{\overrightarrow{l}}_i\right)\Vert$$ (8)

We defined the orientation of the camera coordinate system to be parallel to the tracker coordinate system. The extrinsic parameters were therefore given by:

$${}^T{T}_{\text{VC}}=\left[\begin{array}{cc}I& {}^T{\overrightarrow{P}}_{\text{VC}}\\ 000& 1\end{array}\right]$$ (9)

where ^T T_VC denotes the transformation from the camera to the tracker coordinate system and I denotes a 3 × 3 identity matrix. The intrinsic parameters, including the image center and the pixel size, were estimated from the relationship between the projection rays and the 2D pixel locations on the image plane. The tracker coordinates of the ith pixel $\left({}^T{\overrightarrow{P}}_i\right)$ on the image plane were computed from the projection ray (r_i in Fig. 5) and from the image coordinates of the ith pixel:

$${}^T{\overrightarrow{P}}_i=\left[\begin{array}{c}{}^{T}p{}_{i,x}\\ {}^{T}p{}_{i,y}\\ {}^{T}p{}_{i,z}\end{array}\right]=\left[\begin{array}{c}{u}_i\cdot s_x+o_x\\ v_i\cdot s_y+o_y\\ T_{p_{i,z}}\end{array}\right]$$ (10)

where (^T p_i,x, ^T p_i,y, ^T p_i,z) denotes the position of the ith pixel in x, y, and z axes of the tracker coordinate system computed from the projection ray, (s_x, s_y) denotes the pixel size, (u_i, v_i) denotes the image coordinates of the ith pixel, and (o_x, o_y) denotes the image center in tracker coordinates.

Fig. 5.

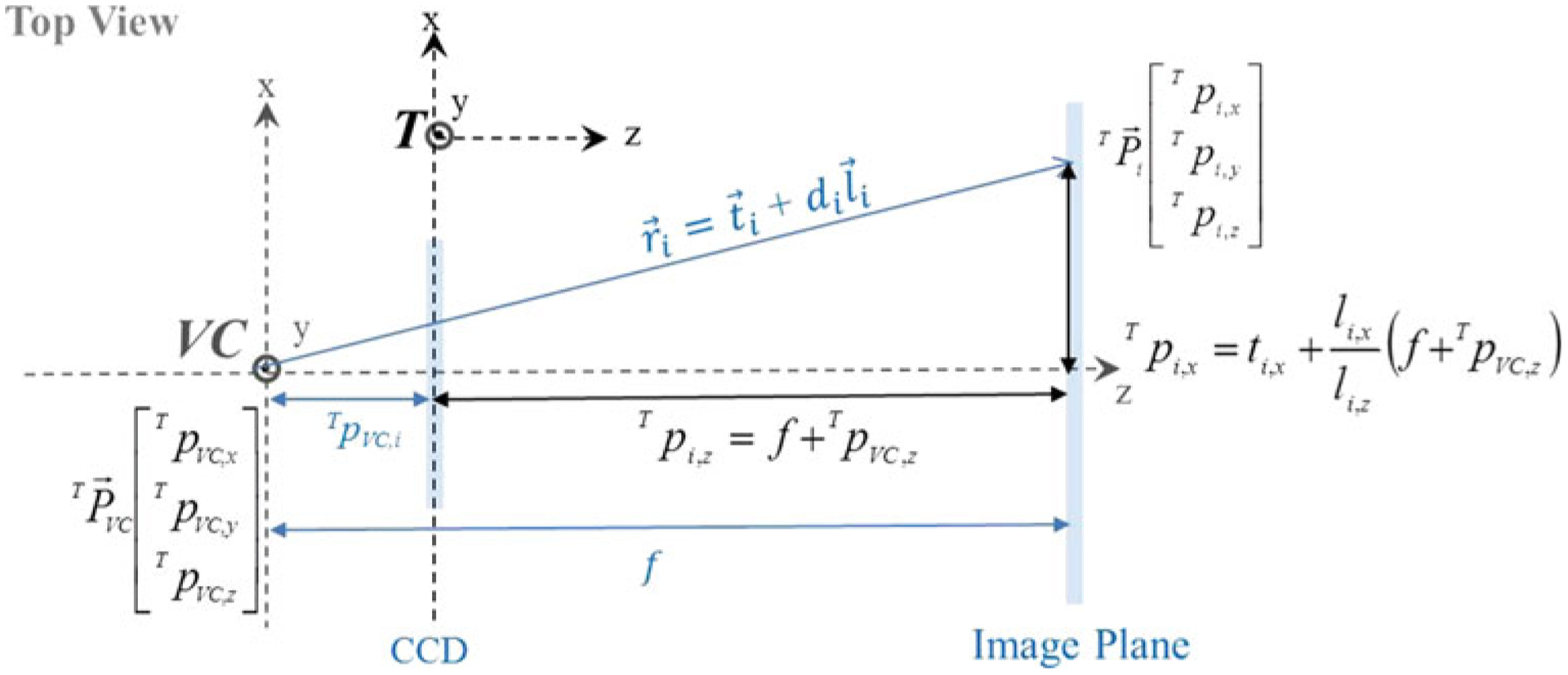
Video camera geometry for the calculation of the tracker coordinate of the ith pixel $\left({}^T{\overrightarrow{P}}_i\right)$ on the image plane from the projection ray in 3D, where (^T p_i,x, ^T p_i,y, ^T p_i,z) denotes the position of the ith pixel, (^T p_VC,x, ^T p_VC,y, ^T p_VC,z) denotes the camera center, (t_i,x, t_i,y, t_i,y) denotes the position of the origin of the ray on the ith pixel, and (l_i,x, l_i,y, l_i,y) denotes a unit vector along the ray direction in x, y, and z axes of the tracker coordinate system, supposing a focal length (f) as the distance between the image plane and the camera center

A least-squares solution of Eq. (11) minimizes the distance between ${}^T{\overrightarrow{P}}_i$ computed from the projection ray in 3D and the image coordinate in 2D, and solves for the image center and the pixel size:

$$\left({\widehat{s}}_x,{\widehat{s}}_y,{\widehat{o}}_x,{\widehat{o}}_y\right)=\underset{s_x,s_y,o_x,o_y}{\text{arg min}}\sum _{i=1}^N\Vert \left[\begin{array}{c}{}^T{p}_{i,x}\\ {}^T{p}_{{}_{i,y}}\end{array}\right]-\left[\begin{array}{c}{u}_i\cdot s_x+o_x\\ v_i\cdot s_y+o_y\end{array}\right]\Vert$$ (11)

Since there exists a discrepancy between the camera model provided by the manufacturer and the simple pinhole model, described above, a distortion correction was required to achieve a correct overlay of the rendered image. A built-in API function that provides the calibrated image coordinates for a given set of 3D tracker coordinates was used. A lookup table was created to store the mapping between locations of distorted and corrected pixel locations, which significantly reduced computation time and allowed real-time distortion correction. The intensity value of the calibrated pixel was computed from the four neighbors of the distorted pixel using bilinear interpolation.

Video augmentation functionalities

The following functions for video augmentation were implemented:

1. Planning data overlay 3D planning data include volumetric segmentations, desired tool trajectories, etc. described in the context of preoperative images. Superimposing such models onto the video scene used the geometric relationship between the coordinate systems of the preoperative images and the video camera:

   $${}^{\text{VC}}{T}_{\text{CT}}{=}^{\text{VC}}{T}_T{}^T{T}_R{}^R{T}_{\text{CT}}$$ (12)

   where the transformation between the coordinate systems of the preoperative CT images and the reference marker (^RT_CT) was computed from paired-point registration between fiducials in the coordinate systems of the CT and the reference marker, the transformation between the coordinate systems of the reference marker and the tracker (^T T_R) was measured by the tracker, and the transformation ^VCT_T was computed using Eq. (9). Any Xpoint reference marker can be used—e.g., the hex-face reference marker used for TRE measurements, the triple-face BB embedded marker used for DRR measurements, and/or a single-face reference marker. In the work described herein, hex-face or triple-face markers were used to maintain visibility of the reference marker from the tracker perspective on the C-arm. The intrinsic parameters computed from Eq. (11) were used to project the data onto the video image plane.
2. Virtual field light overlay Superimposing the X-ray FOV onto the video scene was implemented to assist C-arm positioning, conveying both a projection “field light” as well as the (~ 15 × 15 × 15 cm³) cylindrical FOV of the CBCT reconstruction volume. Overlaying the FOV on the video scene used the geometric relationship between the FOV and the video camera (^VCT_CBCT), computed as:

   $${}^{\text{VC}}{T}_{\text{CBCT}}{=}^{\text{VC}}{T}_T{}^T{T}_{\text{FPD}}{}^{\text{FPD}}{T}_{\text{CBCT}}$$ (13)

   where the transformation between the coordinate systems of the tracker and the FPD (^T T_FPD) and the transformation ^VCT_T were described in Eqs. (4) and (9), respectively.

3. DRR overlay DRRs generated from the perspective of the tracker video and superimposed on the video scene show virtual radiographic renderings of anatomical structures projected from either preoperative CT or intraoperative CBCT. The transformation between the coordinate systems of the volume image (CT or CBCT) and the video camera (^VCT_CT) computed using Eq. (12) was given by the extrinsic parameters used to generate DRRs, and the intrinsic parameters were those of the projection geometry of the tracker video, computed using Eq. (11).

Methods: Experimentation and assessment

Geometric accuracy of the Tracker-on-C functionalities including surgical tracking, virtual fluoroscopy, and video augmentation was evaluated in this section.

Target registration error measurement (tool tracking)

The Tracker-on-C configuration was first evaluated in terms of the TRE measured as the distance between target points measured by the tracking system and the “true” target locations defined in a previously acquired diagnostic CT image following transformation by the estimated registration. The experiments used a rigid plastic skull phantom containing 12 built-in surface divots, shown in Fig. 6a. The phantom was scanned on a diagnostic CT scanner (Somatom Definition Flash, Siemens Healthcare, Forcheim, Germany) and reconstructed at a voxel size of 0.4 × 0.4 × 0.2 mm³. Six divots in the plastic skull (labeled 2, 4, 6, 8, 10, and 12 in Fig. 6a) were defined as target points, and the other 6 divots (labeled 1, 3, 5, 7, 9, and 11) were used as fiducial points for paired-point registration [28] of the tracker and CT image coordinate systems. The 6 registration fiducials were selected in a manner generally consistent with the “rules” of good fiducial configuration (i.e., non-colinear, non-coplanar, and broadly distributed with center of mass near the target [41,42]) and consistent with the number of fiducials typically selected in other research and in clinical practice [43–46]. There was no attempt to “optimize” the fiducial number or arrangement, which were instead held fixed for each experiment below to examine the effect of TRE on the tracker setup (not the fiducial arrangement). Each divot was localized manually 20 times in the CT image using 3D Slicer to define the “true” locations in the CT coordinate system [43,47–49]. For TRE measurement, a tracked pointer tool was used to localize the divots in the tracker coordinate system, also 20 times for each divot. The mean of the 20 samples was used as the fiducial or target location in the coordinate systems of both the CT and the tracker. The experiments were performed in the laboratory setup on the experimental tabletop (Fig. 6b) and the actual C-arm. The following measurements of TRE were obtained to quantify the geometric accuracy of the proposed configuration (i.e., MicronTracker in a Pb glass enclosure in a moving reference frame at a tracker-to-target distance, d_target, of ~60 cm) in comparison with a more conventional setup (i.e., the same tracker placed stationary in the OR at d_target ~ 100–200 cm). The experiments employed a setup giving fairly good registration accuracy (i.e., a rigid phantom, a workbench, and an arrangement of registration fiducials scattered about the target points) in order to elucidate effects and trends in TRE that would be difficult to assess by numerical simulation alone—for example, whether or not the TRE changes in the presence of the Pb glass and whether or not TRE was maintained in a rotating coordinate system. The resulting TRE is typically low and consistent with other laboratory measurements [43,50,51], but the experiments certainly do not guarantee that this level of registration accuracy will be achieved in a real clinical scenario in which the arrangement of registration fiducials is different, the target undergoes deformations, etc.

Fig. 6.

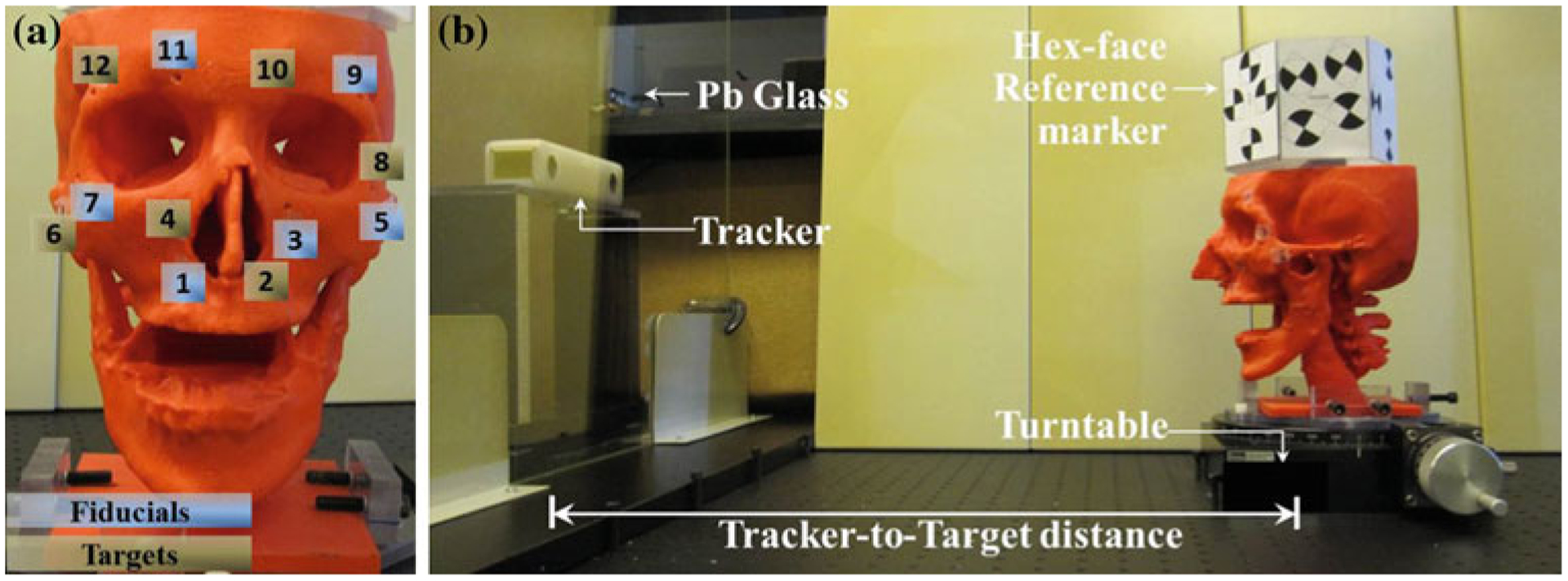
a A plastic skull phantom with 12 built-in surface divots: six registration fiducial divots (1, 3, 5, 7, 9, 11) and six target divots (2, 4, 6, 8, 10, 12). b Experimental tabletop setup showing a tracker-to-target distance of ~60 cm for the Tracker-on-C configuration

TRE with and without Pb glass

TRE was measured with and without Pb glass to evaluate the feasibility of tracking from within the X-ray-shielded enclosure. The pointer tool and the hex-face reference marker were calibrated with and without Pb glass. The pivot calibrations with and without glass achieved residual error of 0.43 and 0.41 mm, respectively, which suggests successful calibration for either setup. Tool calibration with glass was used in the Tracker-on-C setup, whereas tool calibration without glass was used in the conventional setup. Paired-point registration [28] was applied to the fiducials in the coordinate systems of the tracker and the CT image to compute the transformation between the two coordinate systems (^T T_CT). The transformation ^T T_CT was computed under 2 different setups: (i) with Pb glass (8 mm thick Pb-impregnated window glass equivalent to >2 mm Pb) and (ii) without Pb glass. For each setup, the target points in the CT coordinate system were transformed using the transformation ^T T_CT, and TRE was computed as the distance between the targets and the transformed targets in the tracker coordinate system.

TRE at variable tracker-to-target distance

It is generally well known that the geometric accuracy (specifically, fiducial localization error, FLE) of a tracking system depends on the tracker-to-target distance and improves near the “sweet spot” of the FOV, which for a stereoscopic camera system like the MicronTracker is likely to be at a shorter tracker-to-target distance giving improved triangulation of marker locations. It was therefore hypothesized that the proposed configuration (d_target ~ 60 cm) would exhibit improved TRE in comparison with a more conventional (in-room) configuration (d_target > 100 cm). To quantify the improvement, the TRE was measured for the proposed and conventional tracker setup with the tracker positioned at ~60 cm (with Pb glass) and ~110 cm (without Pb glass), respectively. In addition, the TRE was measured as a function of tracker-to-target distance over the range 50–170 cm at 10 cm steps (with Pb glass). TRE computation was the same as in experiment (1).

TRE in a rotating frame of reference (hex-face marker)

To test the feasibility and geometric accuracy of tracking in the proposed configuration in which the tracker is in a moving reference frame (specifically, mounted to a rotating C-arm), the TRE was measured with the hex-face reference marker across a rotation of 180° at 30° steps on the benchtop and the actual C-arm. In the experimental tabletop setup, the skull phantom attached with the hex-face reference marker was mounted on a turntable to simulate rotation of the C-arm (Fig. 5b). In the actual C-arm setup, the phantom was placed on a carbon-fiber operating room (OR) table near C-arm isocenter. At each rotation angle, the position of each divot in the reference marker coordinate system was computed using the relationship:

$${}^R{\overrightarrow{P}}_i{=}^R{T}_T{}^T{\overrightarrow{P}}_{i(i=1,2,\dots ,12)}$$ (14)

where divot i in the tracker coordinate system $\left({}^T{\overrightarrow{P}}_i\right)$ was transformed to reference marker coordinates $\left({}^R{\overrightarrow{P}}_i\right)$ using the transformation between the coordinate systems of the tracker and the reference marker (^RT_T) measured by the tracker. Paired-point registration was applied to the fiducials in the coordinate systems of the reference marker and the CT to compute the transformation between the two coordinate systems (^RT_CT). The target points in the CT coordinate system were transformed to the reference marker coordinates, and the TRE was measured as the distance between the target locations and the transformed target locations in the reference marker coordinate system.

Geometric accuracy of DRRs

Virtual fluoroscopy was evaluated by measuring the projection errors of BB locations in virtual fluoroscopy for all C-arm angulations at 10° increments using the aforementioned cylindrical geometric calibration phantom. A “triple-face BB-embedded” reference marker (comprising the top 3 faces of the hex-face marker described above) was used in which BBs were placed at the center of Xpoints. The triple-face reference marker was visible over a 180° arc. A CBCT image of the reference marker was used to compute the transformation ^CBCTT_R. The triple-face BB-embedded reference marker and ^CBCTT_R were also used in the evaluation of video augmentation (“Geometric accuracy of video augmentation”).

A CBCT image of the cylindrical phantom with the reference marker and an additional 5 BBs (for projection error measurement) was acquired with voxel size of 0.3 × 0.3 × 0.3 mm³. At each C-arm angle, a real fluoroscopic image of the phantom and the transformation ^T T_R were collected, and the C-arm geometric calibration was computed. Equation (6) was used to generate two sets of DRRs using the C-arm geometric calibration: (1) for each angle, referred to as “full-calibration” and (2) for one particular angle (~60° in this work), referred to as “single-pose calibration.” The BBs in the virtual and the real fluoroscopic images were identified using a Hough transform applied to each image, and the projection error between the true and virtual BB locations was computed. These experiments provided quantitative assessment of geometric accuracy for “Virtual Fluoroscopy,” but a similar assessment was not performed for “X-ray Flashlight” for the lack of ground truth (i.e., how to obtain a real X-ray projection at the exact pose as the handheld tool); however, since the two functionalities involve similar registration and DRR calculation methods, we anticipate a similar level of geometric accuracy.

Geometric accuracy of video augmentation

The following functionalities for video augmentation were evaluated:

Accuracy of planning data overlay

The accuracy of overlay of the planning data was evaluated by measuring projection errors across 180° rotations of the C-arm at 30° step angles using a skull phantom with divots on the skin surface. The triple-face BB-embedded reference marker was used to define the world coordinate system and computes the transformation between the CBCT and the reference marker coordinate systems. Each divot on the skull phantom was localized manually 10 times in CBCT images of the phantom (0.3 × 0.3 × 0.3 mm³voxels). At each C-arm angulation, the projection error between the divot positions in the video image and the virtually projected image was computed. The divot positions in the video image were localized by applying a Hough transform to the video image of the skull phantom. The divot positions in the virtually projected image were computed by projecting those divots in the CBCT coordinate system onto the video image coordinate system.

Accuracy of DRR overlay

The geometric accuracy of DRR overlay was evaluated by computing projection errors across 180° angulations of the C-arm in 30° steps using a phantom incorporating 13 BBs in a rectangular acrylic prism (referred to as the “BB phantom”). CBCT reconstructions (0.3 × 0.3 × 0.3 mm³voxels) of the phantom attached with the triple-face BB-embedded reference marker were acquired to identify the relative transformation between the phantom and the reference marker coordinate systems. A video image was captured, and the DRR was generated at each angle. The 2D positions of four BBs in the DRR and video image were identified manually once. The projection errors were computed as the difference in positions of BBs in the DRR and the video image.

Preclinical assessment

Preclinical evaluation by an expert spine surgeon involved phantom and cadaver studies as illustrated in Fig. 7. Each of the Tracker-on-C functionalities described above was qualitatively assessed in a series of mock trials examining: (1) real-time tracking (e.g., potential advantages in line of sight and implications for modified marker designs), (2) virtual fluoroscopy (including both the “X-ray flashlight” and “virtual fluoro” modes), and (3) video augmentation (including overlay of planning data, X-ray FOV, and DRRs on the video scene). The purpose of the qualitative study was to ascertain potential clinical applications at an early stage of system development for which these capabilities might be of greatest utility. A quantitative evaluation of the effects on workflow in comparison with conventional surgical navigation systems was beyond the scope of these initial studies, which was limited to qualitative expert feedback as a guide to system development and future clinical performance studies.

Fig. 7.

Preclinical assessment of the Tracker-on-C in cadaver and phantom studies

Results

Target registration error

The geometric accuracy in tool tracking with the Tracker-on-C configuration is summarized in Figs. 8, 9, and Table 2. The “box and whisker” plots in Figs. 8, 9 show the TRE median (red horizontal line), first and third quartiles (rectangular box), and total range (dashed vertical lines with end-caps). The TRE measured with and without Pb glass is shown in the box plots of Fig. 8a. There was no statistically significant difference in TRE (p = 0.5) with and without Pb glass: (0.87 ± 0.25)mm versus (0.83 ± 0.25)mm, respectively. Note that in the case of tracking with Pb glass, the tracked tool and hex-face reference marker were calibrated with the Pb glass in place. An (inadvisable) alternative scenario was also investigated in which calibration performed without the Pb glass was used for tracking in the presence of Pb glass, and an increase in TRE was observed: (1.33 ± 0.56) mm. This supports the feasibility of tracking from within the X-ray-shielded enclosure of Fig. 2, provided that calibration is also performed with the tracker inside the enclosure.

Fig. 8.

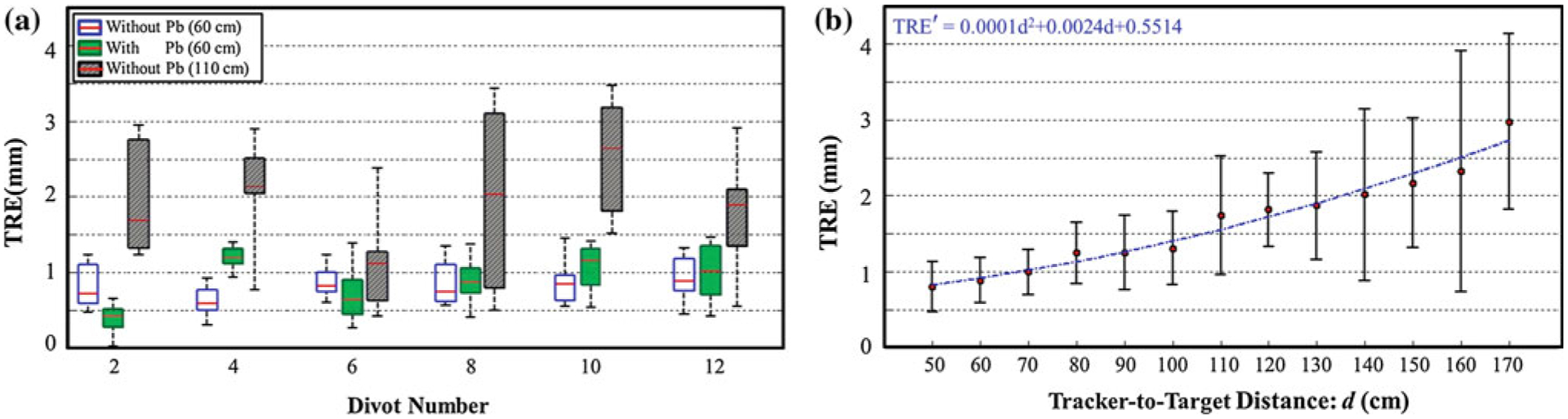
Accuracy of surgical tracking. a TRE measured without and with Pb glass at a tracker-to-target distance of ~60 cm demonstrated by the blue and green box plots, respectively. The TRE without Pb glass at tracker-to-target distance of ~110 cm (conventional setup) is shown by the gray box plot. b TRE measured as a function of tracker-to-target distance. A quadratic fit to the measurements is overlaid

Fig. 9.

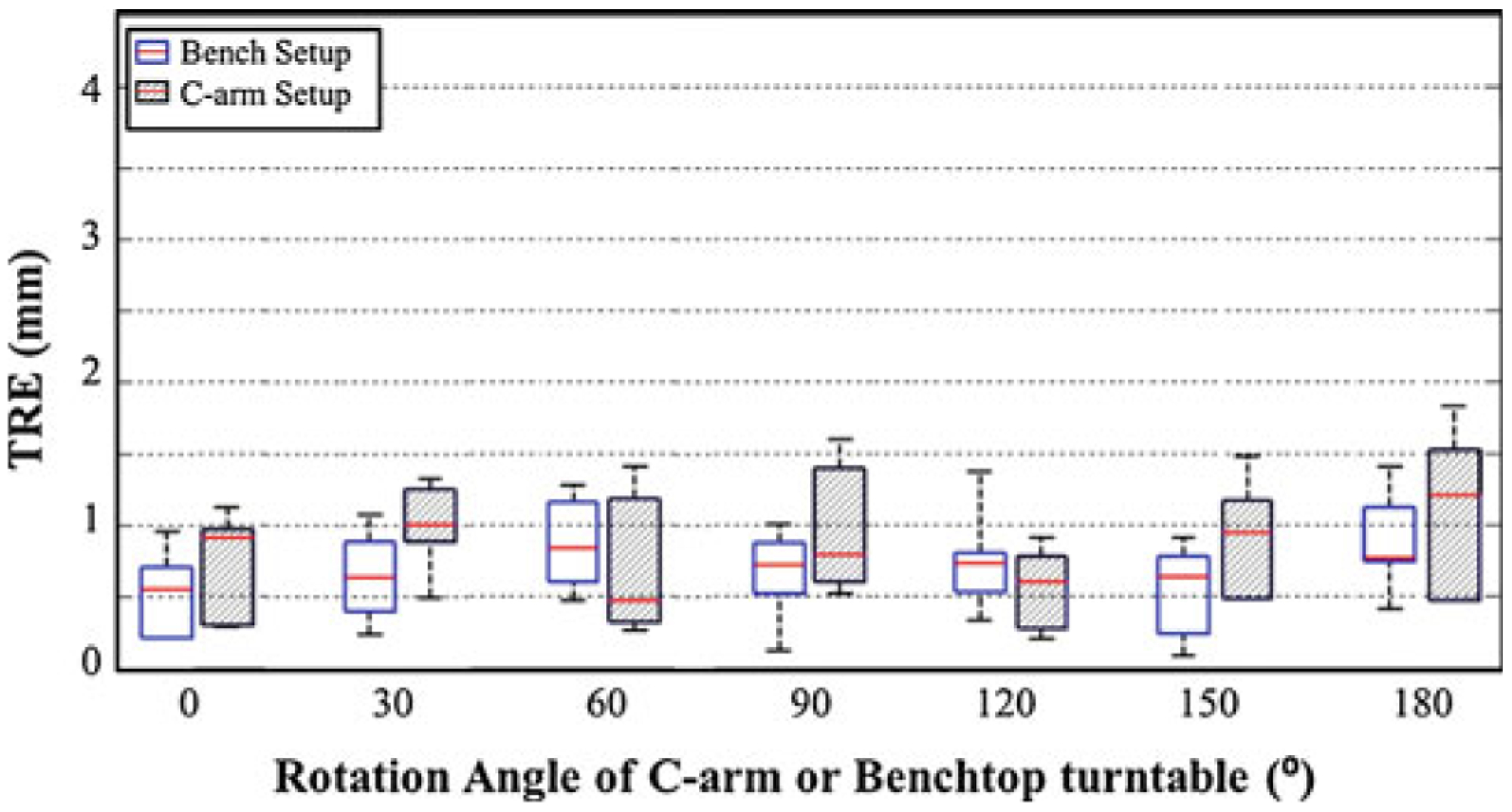
TRE for the bench and C-arm setup demonstrated by the blue and gray box plots, respectively

Table 2.

Summary of TRE measurements

	Experiment	Description	TRE (mm)	p value
1	Pb glass	Without Pb glass	0.83 ± 0.25	0.5
		With Pb glass	0.87 ± 0.25
2	Tracker-to-target distance	Tracker-on-C setup	0.87 ± 0.25	<0.0001
		Conventional setup	1.92 ± 0.71
3	Rotating frame of reference	Bench setup	0.70 ± 0.32	0.11
		C-arm setup	0.86 ± 0.43

The TRE measured at various tracker-to-target distances is shown in Fig. 8. Figure 8a shows the TRE for the conventional tracker configuration (~110 cm tracker-to-target distance) in comparison with TRE for the proposed tracker configuration (~60 cm tracker-to-target distance). The same video-based tracker was used in both configurations, and both cases are within the manufacturer-specified (~30–160 cm) FOM. The proposed configuration yielded an improvement in TRE from (1.92 ± 0.71) mm to (0.87 ± 0.25) mm which was statistically significant (p < 0.0001) and was attributed to the expected improvement in depth resolution (stereoscopic triangulation) at shorter tracker-to-target distance. Figure 8b shows that TRE increases as a smooth function of tracker-to-target distance, increasing from (0.80 ± 0.33)mm at 50 cm to (2.98 ± 1.16) mm at 170 cm. These results agree with the analysis in the literature, which suggests that depth measurement errors are quadratically related to target distance [52–54], and a quadratic fit is shown for comparison. The TRE at target distance less than 50 cm could not be measured in the current setup because the marker tool was out of the FOM frustum of the tracker.

The TRE measured from a rotating frame of reference (using the hex-face reference marker) is shown in Fig. 9, including measurements on the benchtop (blue) and the C-arm (gray). The consistency in TRE for both cases across 180° rotation demonstrates the feasibility and stability of the hex-face reference marker to maintain registration. There was no statistically significant difference in TRE measured between the benchtop and the C-arm setups (p = 0.11), and there was no statistically significant difference between the results of Fig. 9 (rotating coordinate system) and Fig. 8 (fixed coordinate system) (p = 0.88).

Tracker-on-C for DRR

DRR capabilities enabled by the Tracker-on-C included the “X-ray flashlight” and “virtual fluoroscopy” functionality described above. The GPU-accelerated projection libraries provided real-time DRR generation in each of these functionalities—for example, initial implementation giving 58.6 fps virtual fluoroscopy (768×768, 0.388 mm² pixels) generated from a (512 × 512 × 512, 0.3 × 0.3 × 0.3 mm³) voxel volume image on GeForce GTX470 (NVIDIA, Santa Clara, CA, USA). The potential clinical utility is discussed in “Discussion and conclusions,” and the geometric accuracy of DRRs (viz., virtual fluoroscopy) is detailed in Fig. 10.

Fig. 10.

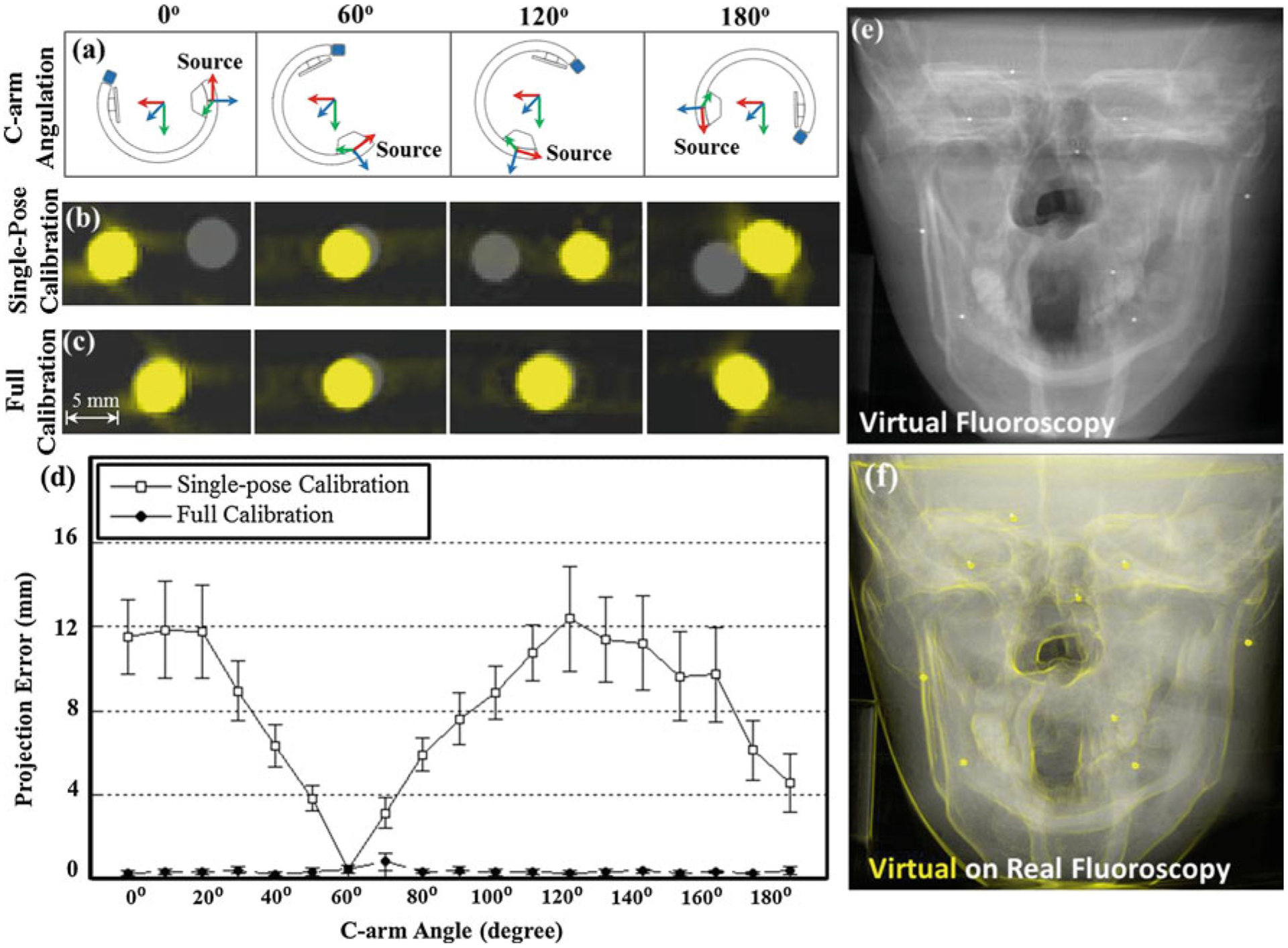
Tracker-on-C for virtual fluoroscopy. a Illustration of C-arm pose at 0°, 60°, 120°, and 180° angulations. b, c Zoomed-in view of DRRs (yellow) overlaid on real fluoroscopic images (gray) for (b) single-pose calibration and (c) full calibration. d Projection error of virtual fluoroscopy measured as a function of C-arm angle. Note the sub-mm projection error achieved with full, angle-dependent calibration. e Virtual fluoroscopy (DRR) of the skull phantom. f Gradient of the virtual fluoroscopy images overlaid in yellow over a real fluoroscopy image

The C-arm pose at approximately 0°, 60°, 120°, and 180° angulation is illustrated in Fig. 10a. Figure 10b and c show zoomed-in views of the DRR (yellow) overlaid on real fluoroscopic images (gray) in the region of a single BB for single-pose calibration and full calibration, respectively. Each image corresponds to the respective C-arm angulation shown in Fig. 10a. Single-pose calibration (Fig. 10b) is seen to fail at angles departing from that at which the system was calibrated (e.g., 60°), whereas full calibration provides good spatial correspondence between the DRR and real fluoroscopy. Figure 10d further quantifies the geometric accuracy of virtual fluoroscopy, for which single-pose calibration is seen to result in projection error that depends strongly on C-arm angle (mean error of (8.21 ± 3.47) mm, square symbols), compared to full angle-dependent calibration, which gives stable, sub-mm projection error for all angulations (mean error (0.37 ± 0.20) mm, circular symbols). The degradation in accuracy for the single-pose calibration is attributed to mechanical flex of the C-arm. Virtual fluoroscopy of the skull phantom generated from a PA view (90° angulation) is shown in Fig. 10e, and its gradient is superimposed in yellow on the corresponding real fluoroscopy image in Fig. 10f for visual comparison. The image provides qualitative evaluation of projection accuracy and suggests excellent correspondence between the virtual and real projection. The projection error measured in the 9 BBs on the skull phantom was (1.48 ± 0.27) mm.

Tracker-on-C for video augmentation

Applications and geometric accuracy of the Tracker-on-C system for video augmentation are illustrated in Fig. 11. As shown in these examples, the Tracker-on-C configuration provided visualization of planning data, device trajectories, the X-ray FOV, and underlying anatomy accurately superimposed on real-time video images from a natural perspective of the surgical field at any C-arm angulation over the operating table. The overlay of planning data on the video image of a thorax phantom (Fig. 11b) shows segmented vertebrae, registration fiducials, and target trajectories of T5 and T7 pedicle screws. The virtual field light overlay (Fig. 11c) displays the CBCT FOV as a purple cylinder superimposed on the video image. DRR overlay (Fig. 11d) shows the underlying anatomical structures of the thorax phantom. The overlay of planning data achieved a projection error of (0.59 ± 0.38) pixels depicted by the blue plot in Fig. 11a, and the DRR overlay achieved projection error of (0.66 ± 0.36) pixels as illustrated by the gray plot in Fig. 11a. Each box and whisker plot comprises 4 projection errors (i.e., the projection error evaluated in 4 target points). The data at 180° were excluded from the plot, since it comprises only 2 projection errors (since only 2 target points were visible in the video images at that angle).

Fig. 11.

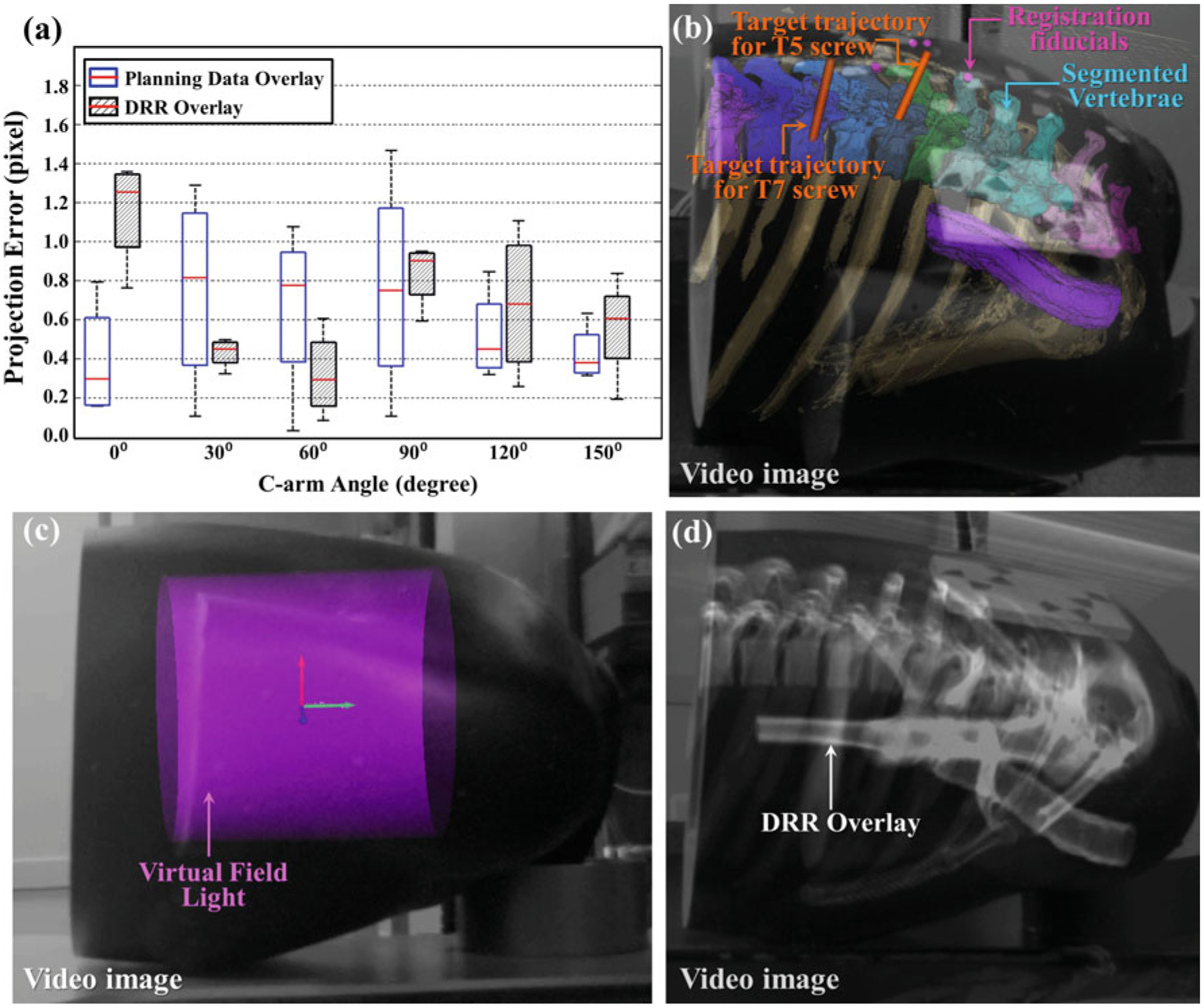
Tracker-on-C for video overlay. a Summary of projection errors for planning data and DRR overlay. b Overlay of segmented vertebrae, registration fiducials, and planned trajectories for T5 and T7 pedicle screws on the video image of a thorax phantom. (The software implementation allowed free adjustment of alpha blending values such that 3D models could be overlaid on the video images with variable opacity—from fully opaque to transparent.) c Virtual field light overlay on the video image of the thorax phantom. d DRR overlay on the video image of the thorax phantom. Any or all of these three video overlay functionalities can be combined within an augmented scene derived from the tracker video stream

Discussion and conclusions

The direct mounting of a surgical tracker on a rotational C-arm (Tracker-on-C) offers potential performance and functional advantages in comparison with a conventional in-room tracker configuration. Key functionality implemented on the current prototype system includes tracking, virtual fluoroscopy, and video augmentation. As detailed above, the configuration demonstrated improved TRE compared to the same tracker in a conventional in-room configuration, and there was no degradation due to mounting the tracker within an X-ray shielded enclosure (behind Pb glass) to protect CCD elements from radiation damage, provided the tool and reference marker calibration was performed in the presence of the Pb glass. The increase in TRE is attributed to refraction in the Pb glass that had not been accounted in the calibration without Pb glass. The discrepancy is resolved if the tool is calibrated and the tracker is registered with the Pb glass in place (and not moved).The hex-face reference marker demonstrated capability to maintain registration in a dynamic reference frame across the full C-arm range of rotation and, by virtue of its perspective over the operating table, could reduce line-of-sight obstruction commonly attributed to the occlusion of the tracker view by personnel about tableside. While the current system used a hex-face marker in which (during C-arm rotation) the face presenting the least obliqueness to the tracker was used for registration, alternative methods such as using as many faces as visible for any pose measurement are also under development. Tracker-on-C capabilities using DRRs (e.g., the “X-ray flashlight” tool and virtual fluoroscopy generated from any C-arm angulation) demonstrated sub-mm accuracy, and video augmentation (e.g., overlay of preoperative planning data and DRRs on the tracker video stream) demonstrated sub-pixel accuracy.

The reference marker thereby maintains tracking capability (as well as virtual fluoroscopy and video augmentation) as the C-arm rotates about the table for fluoroscopy or CBCT—as long as the reference marker is within its FOV. This implies, of course, that the Tracker-on-C system is only functional when the C-arm remains at tableside (as common in fluoroscopically guided procedures) with the reference marker in the FOV. This may be perfectly consistent with workflow and logistics of many minimally invasive procedures that utilize fluoroscopy throughout the operation (e.g., minimally invasive spine surgery), but for procedures in which the C-arm is used only intermittently and then pushed aside (e.g., skull base surgery), Tracker-on-C capabilities would only be available when the C-arm is at tableside. A combined tracker arrangement immediately comes to mind—for example, a conventional tracker configuration in the OR to allow surgical navigation throughout the procedure, augmented by the Tracker-on-C when the C-arm is at tableside, giving added capability for tracking (at higher geometric accuracy by virtue of two trackers), virtual fluoroscopy, and video augmentation. Initial assessment of clinical utility and workflow was limited to qualitative expert feedback in the context of spine surgery. Recent work expanded on such evaluation to include quantitative analysis of workflow—for example, the virtual field light utility offering nearly a factor of 2 improvement in the time required to position the C-arm accurately at tableside (with the target in the FOV and without collision of the C-arm and table/patient) [18]. The same studies indicated a reduction in X-ray exposure from ~2–7 radiographs acquired for C-arm positioning in the conventional (un-assisted) approach, compared to 0–2 for the Tracker-on-C approach. The overall preclinical assessment by an expert spine surgeon suggested potential benefit of the Tracker-on-C configuration in procedures that commonly rely on fluoroscopy, including spine surgeries such as percutaneous screw placement, other minimally invasive spine procedures (lateral access and transforaminal fusions), vertebral augmentation procedures (vertebroplasty and kyphoplasty), and interventional pain procedures (epidural injections, nerve root block, and facet injections). In such procedures, up-to-date fluoroscopic visualization is essential, so the C-arm is positioned at tableside in a manner consistent with the proposed Tracker-on-C arrangement. Although the configuration demonstrated reduced line-of-sight obstruction, it introduced implications for modified marker designs to allow tool tracking from any C-arm angle.

The real-time DRR capabilities assisted the surgeon in C-arm setup and radiographic search/localization of target anatomy without X-ray exposure. Such functionality could reduce fluoroscopy time expended in tasks such as vertebral level counting/localization, selection of specific PA/LAT/oblique views, and aligning the C-arm at tableside. With the increasing concern regarding radiation exposure to physicians, such technology presents a welcome addition to methods for improving OR safety. The virtual flashlight was useful in assisting anatomical localization and level counting, whereas virtual fluoroscopy assisted positioning the C-arm to achieve a desired X-ray perspective prior to radiation exposure. Virtual fluoroscopy was helpful in precisely aligning the C-arm to acquire the desired perspectives of “true” AP (where the spinous process appears in the middle of the pedicles), the “true” lateral (showing a clean edge on upper and lower endplates and a single pedicle), and the tear-down view in pelvic injury. Virtual fluoroscopy could therefore provide speed and reduce radiation exposure in “hunting” for complex oblique views of specific anatomical features, such as the “bullseye” view for transpedicle needle insertion and localization of the tip of the humerus as an entry point for humeral nail insertion. Since virtual fluoroscopy can be computed from either preoperative CT or intraoperative CBCT (typically the former), it can be used even in complex patient setups that challenge or prohibit 180° rotation of the C-arm for CBCT acquisition—for example, the lithotomy position in prostate brachytherapy and the “beach-chair” position in shoulder surgery. In fact, the Tracker-on-C could be implemented on C-arms not allowing intraoperative CBCT (i.e., conventional fluoroscopic C-arms) and would still provide tracking, virtual fluoroscopy, and video augmentation in the context of preoperative images.

The video-based tracker used in the current work allowed video augmentation from a natural perspective (surgeon’s eye view) over the operating table. Overlay of the virtual field light assisted in positioning the C-arm to align the CBCT FOV to the target region without X-ray exposure. Overlay of DRRs and preoperative planning and/or image data onto the video stream provided intuitive visual localization of surgical tools with respect to images and/or planning structures. Rigid fixation of the tracker with respect to the X-ray detector facilitated quick, accurate intraoperative registration using the tracker-to-detector transformation and geometric calibration of the C-arm. The proposed configuration presented streamlined integration of C-arm CBCT with real-time tracking and demonstrated potential utility in a spectrum of image-guided interventions (e.g., spine surgery) that could benefit from improved accuracy, enhanced visualization, and reduced radiation exposure. Video augmentation showed potential value in minimally invasive spine surgery by allowing the surgeon to localize target anatomy relative to the patient’s skin surface. Planning data overlay facilitated quick localization of target tissues and margins. DRR overlay on real-time video was found to assist vertebral level counting and localization by showing anatomical structures with respect to the skin surface of the patient.

Overall workflow steps for the Tracker-on-C system include, for example: (1) off-line calibration, registration, and distortion correction of the tracker, C-arm, and tracked instruments; (2) acquiring preoperative images (CT); (3) planning the procedure (e.g., planning target screw trajectories and segmenting target tissues); (4) exporting 3D models of the planning data; (5) attaching the reference marker to the patient; (6) registering the patient to the preoperative images (and associated planning data); (7) acquiring intraoperative 3D images; and (8) tracking and updating the display (e.g., DRR and video augmentation). Step 1 is an off-line procedure likely performed by a technologist in the process or regular quality assurance. Steps 2–4 are preoperative items performed before the procedure on a patient-specific basis. Steps 5–6 are performed in the operating room, likely with the patient under anesthesia but before the operation has begun. Steps 7–8 are performed at any time during the procedure on command from the operating surgeon. Step 6 could be repeated (e.g., registering instead to the most up-to-date intraoperative CBCT image) if the registration to preoperative images becomes invalid (e.g., anatomical deformation). The robustness of this transformation could be evaluated, for example by measuring the pose of the detector with respect to the tracker coordinate system and computed the difference in the pose periodically. A thorough evaluation of such workflow items is beyond the scope of this paper and is being addressed in ongoing work—for example, assessment of workflow in C-arm setup assisted by the virtual field light [18]. Use of the system in a realistic surgical context would require the hex-face reference marker to be minimized and positioned in a manner that does not interfere with the surgical field but provides line of sight to the tracker from any rotation angle over the table. Such considerations will be evaluated in a future development phase and will certainly depend on the surgical application—for example, cranial surgery versus spine surgery. The system employs pair-point registration to match the tracking data to equivalent areas on the medical images, typically requiring ~5–20min on average [45,55,56] for setup and registration. Visualization of the video augmentation could be improved by optimizing the blending factor (e.g., alpha value) and blending technique specific to a given surgeon’s visual preference. The time required for calibration and registration of the Tracker-on-C system is comparable to other image-guided surgical navigation systems—for example, image-to-world registration as in [45,55,56]. Future work includes more streamlined implementation in the TREK [22] guidance system and assessment of accuracy, radiation exposure, procedure time, and workflow in specific surgical scenarios.