Wearable sensors enable personalized predictions of clinical laboratory measurements

Abstract

Vital signs, including heart rate and body temperature, are useful in detecting or monitoring medical conditions, but are typically measured in the clinic and require follow-up laboratory testing for more definitive diagnoses. Here we examined whether vital signs as measured by consumer wearable devices (that is, continuously monitored heart rate, body temperature, electrodermal activity and movement) can predict clinical laboratory test results using machine learning models, including random forest and Lasso models. Our results demonstrate that vital sign data collected from wearables give a more consistent and precise depiction of resting heart rate than do measurements taken in the clinic. Vital sign data collected from wearables can also predict several clinical laboratory measurements with lower prediction error than predictions made using clinically obtained vital sign measurements. The length of time over which vital signs are monitored and the proximity of the monitoring period to the date of prediction play a critical role in the performance of the machine learning models. These results demonstrate the value of commercial wearable devices for continuous and longitudinal assessment of physiological measurements that today can be measured only with clinical laboratory tests.

A routine clinic visit consists of a physical examination with vital sign measurements and blood and urine tests to examine overall health and detect abnormalities due to illnesses such as infection or chronic disease^1,2. Although vital signs like heart rate, body temperature, blood pressure, respiration rate, height and weight do not generally enable a specific diagnosis, they are useful for assessing overall health and triaging patients rapidly in both routine and emergency settings. Laboratory evaluation of blood and urine, referred to as ‘clinical labs’, is a less rapid and often more specific method to quantitatively assess health³. Traditional clinical examinations have drawbacks that include requirements for in-person visits, potentially invasive tests, infrequent sampling, a highly controlled setting, a lack of tools to systematically incorporate past visit information, and challenges with interpreting clinical measurements at the boundaries of normal values. Studies that examine the relationship between vital signs and clinical labs have been limited.

Over the past several years, interest in assessing consumer wearables (wearables) for healthcare and longitudinal monitoring has increased^4–6. Several groups have demonstrated that it is possible to extract accurate information from wearables in both a clinical and ‘real-world’ environment^7–9. Wearables can capture vital signs continuously and longitudinally during daily life, but the utility of this continuous information remains in question. Recent studies applied machine learning to wearables data to predict cardiovascular^10–13 (for example, the presence of arrhythmias like atrial fibrillation), diabetic¹⁴ and infection statuses¹⁵ using electrocardiogram (ECG) or photoplethysmogram (PPG) signals from wearables. Moreover, individual baselines can be established and deviations assessed as possible signs of acute and chronic disease rather than relying on population-based norms⁸. This prior work suggests that wearables may have clinical utility, particularly when incorporated into personalized, predictive models. However, the ability of vital signs, and particularly those measured by wearables, to predict clinical labs has not been evaluated.

In this study, we explored parameters that would hasten the adoption of wearables into healthcare. We first examined whether vital signs measured continuously and remotely by wearables (wVS) can accurately represent vital signs measured in the clinic (cVS). We further explored whether vital signs can be used as a non-invasive proxy measurement of clinical labs by developing models of the relationship between wVS and clinical labs. Finally, we investigated whether increasing model and feature complexity, increasing the amount of time monitored, or personalizing models would improve their prediction accuracy (Fig. 1a).

Fig. 1 |. Overview of the iPOP wearables study.

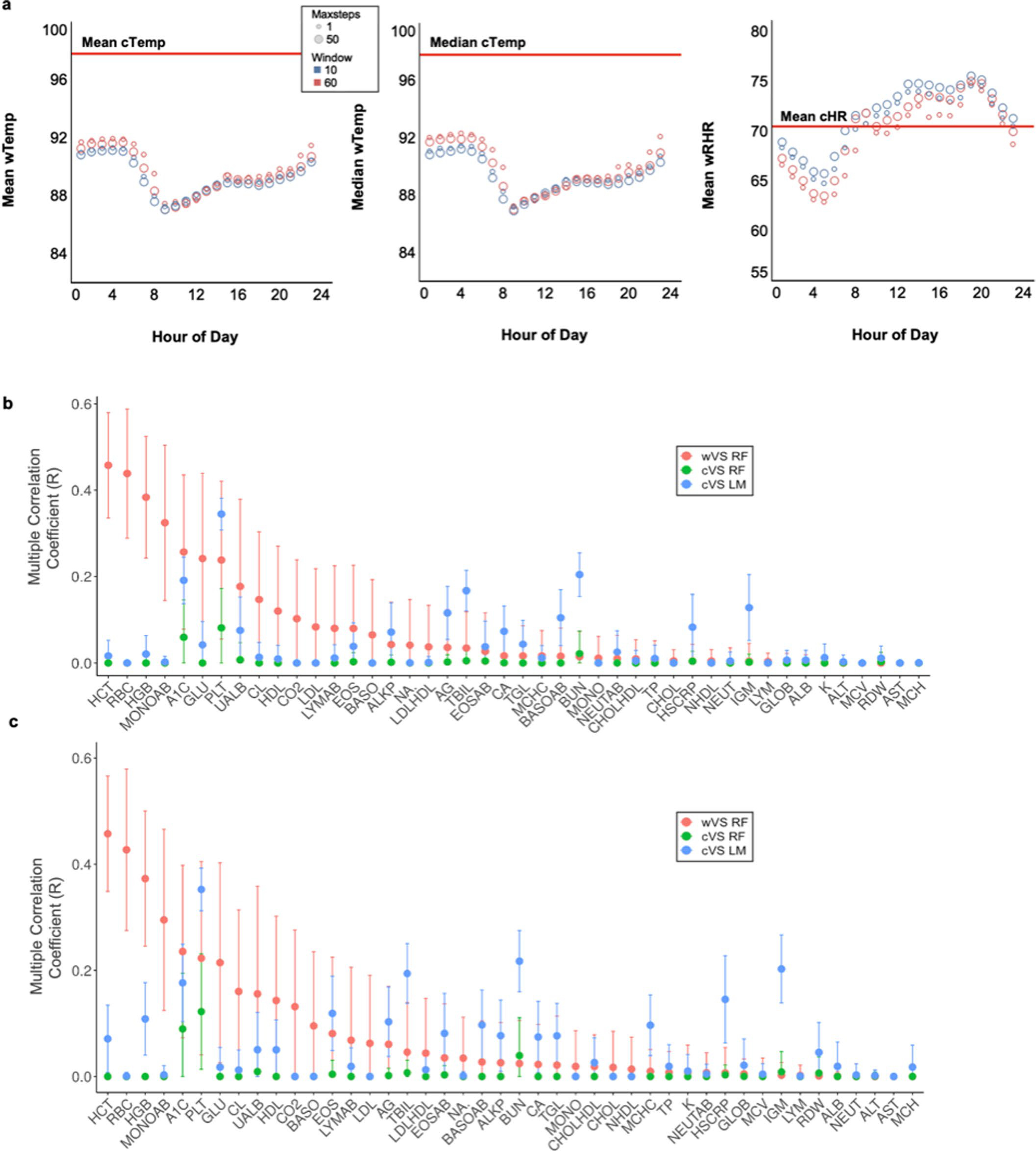
a, Study design. b, Timespan of clinical monitoring per participant in the iPOP wearables cohort (left), and the total number of clinic visits per person (right). Each clinic visit included clinical lab tests. n = 54 study participants in each plot. c, Distribution of vital signs measured in the clinic and by the watch in the iPOP wearables cohort (n = 226 measurements). The values of wRHR and wRTemp were computed by averaging the wHR and wTemp during periods in which no steps were taken, including all such periods that occurred 2 weeks before clinic visits during the same time period as the clinic visits (7:00 to 9:00). Median values are indicated by dark blue vertical lines. d, Daily variation in median wRHR using multiple resting definitions (no steps or steps < 50 for a duration of 10 or 60 min) (n = 54 participants with at least one cHR and cTemp measurement (2,145 observations in total) during wearables monitoring). e, Variance of wRHR using multiple resting definitions (no steps for a duration of 60, 10 or 5 consecutive min). Measurements of wRHR are taken from hours of the day corresponding to typical clinic visit times for a duration of either 1 week, 2 weeks or 1 month before the clinic visit. The average variance of wRHR across the nine different resting definitions is 53.2 and the variance of cHR is shown as a horizontal line at 93.2 bpm. n = 54 participants.

Results

Vital signs collected by wearables versus in the clinic

We first explored how well wearables capture baseline physiology by comparing routine vital sign measurements from a smart watch with vital signs measured in the clinic using our integrative personal omics profiling (iPOP) cohort^8,16–19. Fifty-four iPOP participants wore an Intel Basis smart watch measuring heart rate, skin temperature, accelerometry and electrodermal activity (EDA). The diverse cohort (Supplementary Table 1d) comprising 30 females (aged 40 to 70 years; mean 56 years) and 24 males (aged 35 to 76 years; mean 58 years) was clinically monitored for an average of 3.3 years with an average of 42 clinic visits per individual during the clinical monitoring period (Fig. 1b)^8,16,17. Participants wore the smart watch for 343 days on average (s.d. 241 days); an average of 313 days overlapped the clinical monitoring period. In the clinic we measured six vital signs (cVS), including heart rate and oral temperature (Supplementary Table 1a and Fig. 1c).

We first compared watch-based measurements of resting heart rate (wRHR; Fig. 1c) with clinic-based measurements of heart rate (cHR) by aggregating watch measurements from the same time as the clinic visits (7:00 to 9:00) for 1 week, 2 weeks or 1 month before the date of the clinic visit. We explored multiple definitions of rest by varying the time windows for capturing inactivity (5-, 10- and 60-min intervals with no steps) and found that shorter windows were associated with higher wRHR (Fig. 1d), as expected for residual effects of activity on heart rate. Intermediate resting periods with no steps for 10 consecutive minutes during the 2 weeks before the clinic visit was chosen for all subsequent analyses. For wRHR, the median was 71 (s.d. 6.7) beats per minute (bpm) and for cHR, the median was 71 (s.d. 9.4) bpm (n = 226). For all resting definitions tested, our estimates had negligible bias and the variance in wRHR was significantly lower than that in cHR (Fig. 1c,e and associated source data), indicating that wRHR are more consistent in measuring the typical resting heart rate than the intermittent cHR, presumably because many observations of resting heart rate measured longitudinally capture more consistent heart rate values than a single measurement in the clinic. Longer wRHR monitoring periods prior to the clinic visit resulted in lower variance of wRHR, as expected, and increased similarity between wRHR and cHR values (Fig. 1e and associated source data).

Watch-based measurements of resting skin temperature (wRTemp) at the wrist were lower than oral temperatures measured in the clinic (cTemp): cTemp = 97.9 ± 0.4 °F; wRTemp = 89.2 ± 2.2 °F (Fig. 1c and Supplementary Table 1a,c). In contrast to heart rate, clinically measured oral temperature was a more consistent and stable physiological temperature metric than wearable-measured skin temperature, which, even at rest and with correction for ambient temperature, is much more variable. We conjecture that differences between cTemp and wRTemp reflect differences due to the measurement location at the wrist as well as a variety of environmental and physiological factors.

wRHR and wRTemp exhibited daily circadian patterns (Fig. 1d and Extended Data Fig. 1a); this variation was consistent across resting definitions, indicating that time of day is a key factor that affects the variance of day-to-day clinic measurements within an individual, consistent with other studies²⁰. Overall, our results indicate that wRHR provide more consistent heart rate measurements than do cHR, whereas cTemp are more consistent than wRTemp.

Predicting clinical laboratory measurements from wearables.

As our findings indicated that heart rate, skin temperature and physical activity were associated with infection and insulin sensitivity⁸; we explored the concept that clinical labs could be modeled using vital signs from wearables or clinic visits. Given that PPG detects differences in subcutaneous blood volume, wearable PPG is potentially capable of measuring hemoglobin and glycated hemoglobin (HbA1c) levels^21,22. Furthermore, EDA measures the electrical properties of the skin, which change with epidermal hydration status²³. Therefore, we examined to what extent wVS can be used to predict specific clinical labs (Fig. 1a) using the iPOP cohort. The wVS included heart rate, skin temperature, EDA and physical activity (Supplementary Table 1c). The 44 clinical laboratory panels included those with diagnostic utility in a primary care setting, such as the complete blood count with differential, comprehensive metabolic panel, and cholesterol panel (Fig. 3a and Supplementary Table 1b).

Fig. 3 |. Predicting clinical laboratory measurements from vital signs collected using wearables.

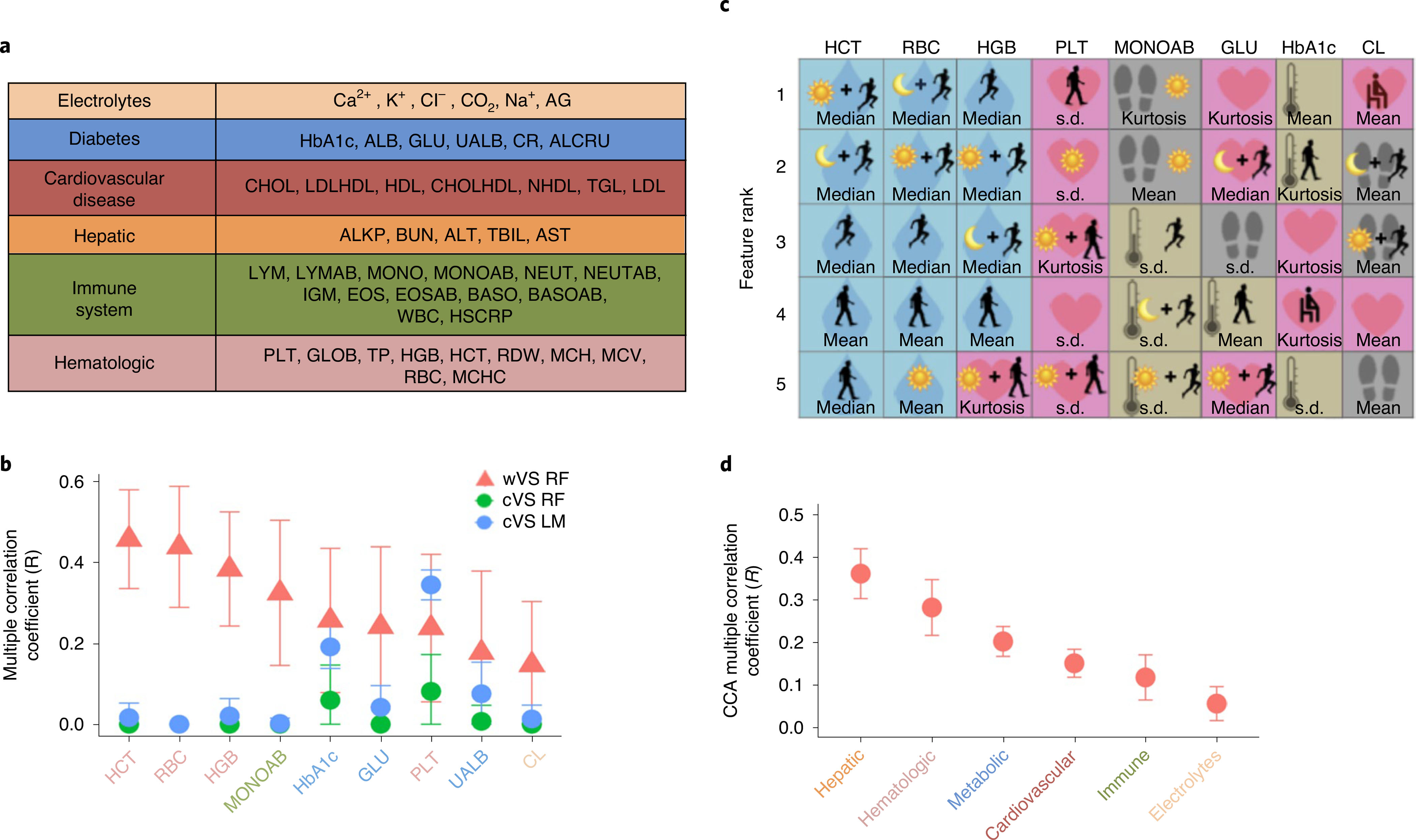
a, Physiological categories of clinical laboratory tests performed at clinic visits. ALB, albumin; ALKP, alkaline phosphatase; ALRCU, aluminum/creatinine ratio; ALT, alanine aminotransferase; AST, aminotransferase; BASO, relative basophil count; BASOAB, absolute basophil count; BUN, blood urea nitrogen; CHOL, total cholesterol; CHOLHDL, high-density lipoprotein/total cholesterol ratio; CR, creatinine; EOS, relative eosinophil count; EOSAB, absolute eosinophil count; GLOB, globulin; HbA1c, glycated hemoglobin; HDL, high-density lipoprotein; HSCRP, high-sensitivity C-reactive protein; IGM, immunoglobulin M; LDL, low-density lipoprotein; LDLHDL, LDL/HDL ratio; LYM, relative lymphocyte count; LYMAB, absolute lymphocyte count; NEUT, relative neutrophil count; NEUTAB, absolute neutrophil count; MCH, mean corpuscular hemoglobin; MCHC, mean corpuscular hemoglobin concentration; MCV, mean corpuscular volume; NHDL, non-HDL cholesterol; RDW, red-cell distribution width; TBIL, total bilirubin; TGL, triglycerides; TP, total protein; UALB, urine albumin; WBC, white-blood-cell count. b, The models that most accurately predict clinical laboratory tests using vital signs measured by the watch (wVS, red triangles) compared to the clinic (cVS, blue and green circles) (P < 0.05 for all except serum chloride (CL); correlation between observed and predicted values with Bonferroni correction). Points correspond to the mean R statistic derived by leave-one-person-out cross validation for n = 54 study participants, and error bars represent the 95% confidence intervals derived by bootstrap with the procedure repeated 1,000 times. The wVS are random forest models using the 153 digital biomarkers from part c calculated on watch data from the day before the clinic visit. The cVS models are bivariate linear (blue) or random forest (green) models with cHR and cTemp as model features. All of the models are cross validated using leave-one-person-out cross validation and confidence intervals are established using bootstrapping (P < 0.05). Clinical laboratory test colors correspond to physiology subsets from part a. c, The most accurate digital biomarkers selected out of the 153 features in the wVS models in part b. The colors and large icon in the background of the squares correspond to the different wVS in the left side of Fig. 2a (pink heart, heart rate; blue droplet, EDA; tan thermometer, skin temperature; gray footprints, steps), and the foreground icons correspond to the thresholding criteria on the right side of Fig. 2a. Interpretations of colors and symbols are provided in part a. d, CCA using physiology categories from part a as outcome variables and the 153 digital biomarkers from Fig. 2a as model features (P < 0.05 for all CCA models). Points correspond to the mean correlation derived by leave-one-person-out cross validation for n = 54 study participants, and error bars represent 95% confidence intervals derived by bootstrap with the procedure repeated 1,000 times.

We developed a feature engineering pipeline (Fig. 2a) that converted the longitudinal wVS measurements into 153 features (for example, mean heart rate during high intensity activity, overnight variability in skin temperature; see Methods and Supplementary Table 2a) and used statistical learning models (that is, random forest, Lasso and canonical correlation analysis (CCA)) to combine these features and predict clinical labs (Fig. 2b). Of the 44 clinical labs, we found the highest correlation between the observed and predicted values for four hematologic tests (Extended Data Fig. 1b,c). Specifically, the wVS random forest models explained 6–21% of the variation in hematocrit (HCT), red blood cell count (RBC), hemoglobin (HGB) and platelet count (PLT) values (P < 0.05 with Bonferroni correction; Fig. 3b, red triangles). As the random forest models significantly outperformed the Lasso (two-sided Wilcoxon signed rank test, P < 1 × 10⁻⁵), we chose the random forest models for subsequent analysis due to their robustness and performance.

Fig. 2 |. Methodology for predicting clinical laboratory measurements from vital signs collected using wearables.

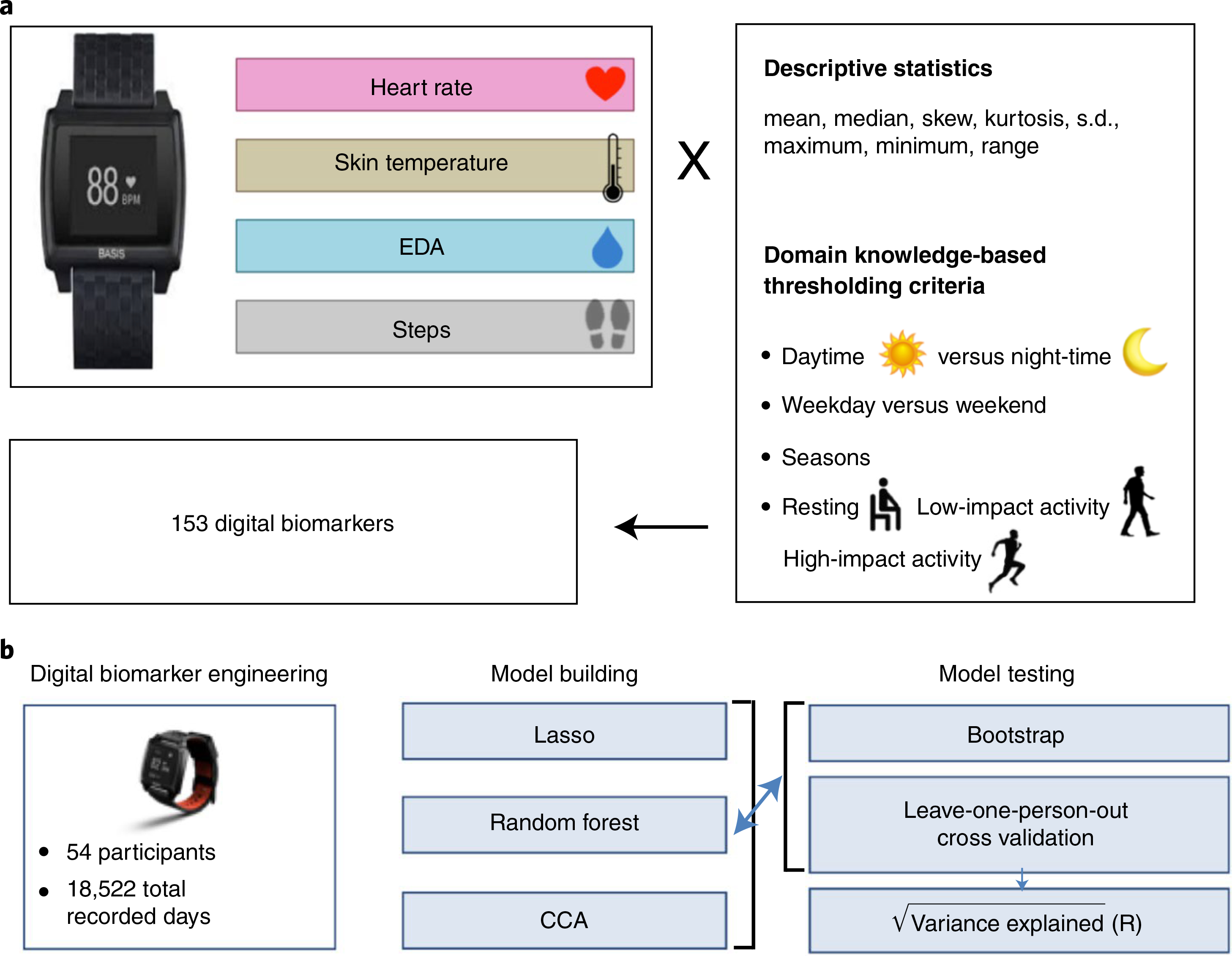
a, Feature engineering pipeline to calculate potential digital biomarkers from continuous, longitudinal smart watch data. Statistical moments of the wVS, including heart rate, skin temperature, EDA and step counts, were subjected to thresholding based on the time of day, impact level of physical activity, and domain knowledge to reduce the size of the feature set. b, Overview of the modeling and analysis approach for this study, including the input data (left), statistical learning methods employed (middle) and model evaluation methodology (right).

The best predictive features in the wVS models are depicted in Fig. 3c (see also Supplementary Table 2b). Surprisingly, the five most important features for predicting HCT, HGB and RBC were all, except for one, permutations of EDA. EDA is a wVS that currently does not have a corollary clinical vital sign and is measured clinically only in highly specialized settings. The non-EDA feature, kurtosis of heart rate during daytime low intensity activity, had relatively high importance for predicting HGB. Kurtosis is a measure of how many outliers are in the distribution and how extreme these are. The five features that best predicted PLT were all based on heart rate, that best predicted absolute monocyte counts (MONOAB) were based on steps and skin temperature, and that best predicted HbA1c, fasting plasma glucose, and serum chloride were a combination of skin temperature, steps and heart rate, indicating that diverse features from physiological signals are predictive of different clinical measures, and that prediction performance is improved by integrating the diverse features into a single model.

As individual clinical labs are often correlated, particularly those with related physiological processes, we generated summary scores for each of these physiological processes by projecting related labs onto a single index. We assigned labs to physiological groups (electrolytes, metabolic, cardiovascular, hepatic, immune, hematologic; Fig. 3a) used as the outcomes in regularized CCA using the 153 wVS features as predictors (Fig. 3d, Supplementary Table 2a and source data for Fig. 3d). The hepatic and hematologic CCA models performed best, with wVS explaining 12% and 7% of the variance, respectively (P < 0.05) (Fig. 3d). Interestingly, the wVS random forest models performed better for the four individual hematologic tests compared to the overall hematologic physiology group, indicating that there are nonlinear relationships between wVS and HCT, RBC, HGB and PLT that are captured by the random forest models but not by CCA. Taken together, these results demonstrate that the complex physiological features and indices that we developed can reduce a large number of variables to summarize the categorical health²⁴.

Predicting clinical laboratory measurements from wVS and cVS.

The previous analysis revealed a correlation between physiological wearables measurements and clinical biochemical and cellular measurements. To determine whether these relationships also exist between clinically measured vital signs and clinical labs, and how they compare to the wVS and clinical labs associations, we next built models to predict clinical labs using cVS measurements (cHR and cTemp) as predictors instead of wVS measurements. The number of cVS variables (2) was dramatically lower than the number of wVS variables (153) due to the intermittent cVS sampling, compared to the longitudinal and continuous wVS sampling and the additional watch sensors (accelerometry and EDA). We therefore developed bivariate linear regression and random forest models using the iPOP cVS data (Fig. 3b). We found that wVS random forest models significantly outperformed cVS random forest and linear models for the vast majority (37) of the 44 clinical labs (two-sided Wilcoxon rank sum test, P < 1 × 10⁻⁵) (Extended Data Fig. 1b,c and source data for Fig. 3a), presumably because wearables capture variation in vital signs for an extended period before the laboratory test, whereas clinical vital signs provide only a single moment snapshot. Different time windows for computing wVS features yield substantially different model performance (Fig. 4a). Moreover, features such as standard deviation or kurtosis are highly predictive in several of the wVS models (Supplementary Table 3b), and these metrics do not exist in cVS models.

Fig. 4 |. Relationship between duration and proximity of monitoring and model accuracy.

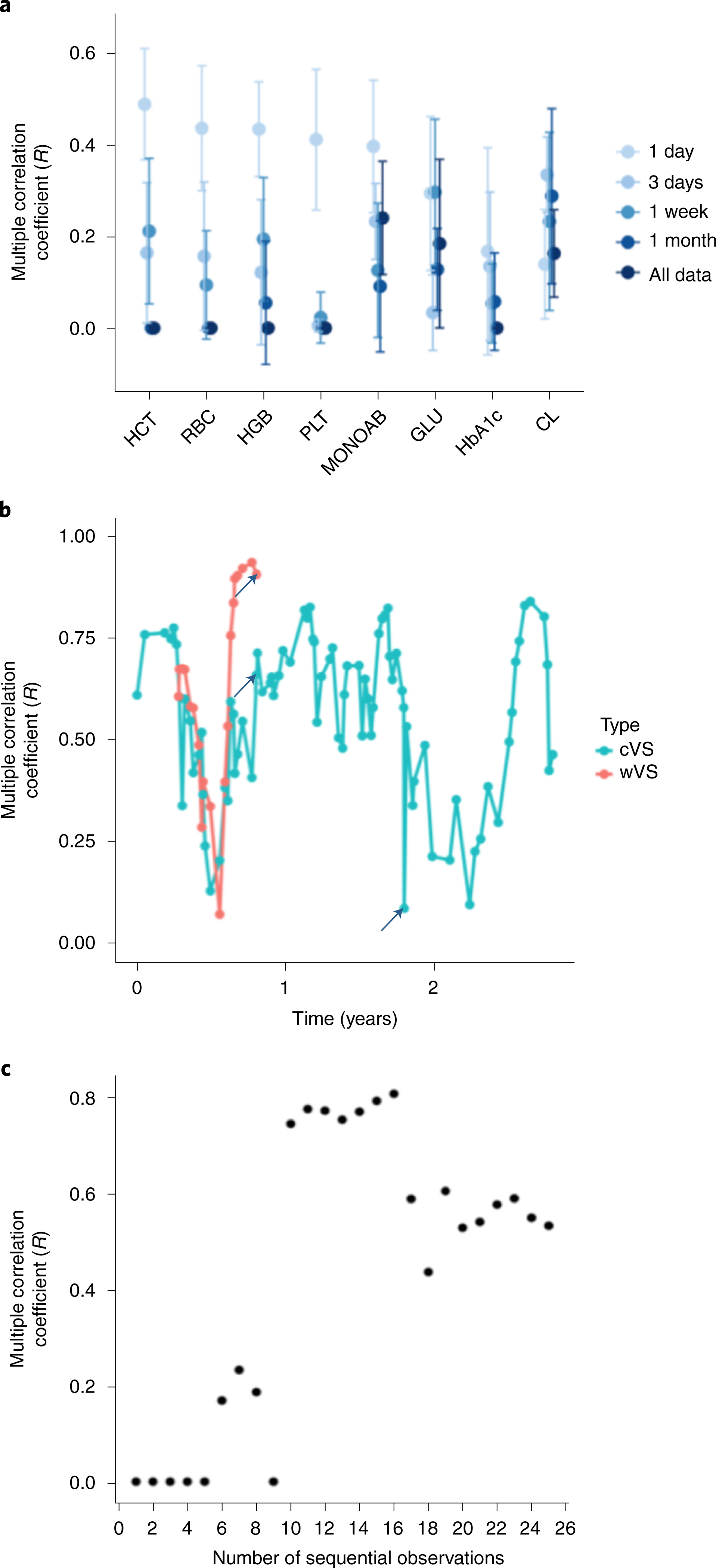
a, The eight most accurate random forest models using varying time windows of wVS monitoring before the clinic test for calculating features as in Fig. 2a, and using leave-one-person-out cross validation for n = 54 study participants. Points correspond to the mean R statistic and error bars represent 95% confidence intervals derived by bootstrap with the procedure repeated 1,000 times. b, Multiple correlation coefficient (R) of the predicted versus observed values in the personal HCT cVS mixed effects model and wVS personal random forest model over time for the most frequently sampled iPOP study participant (a mainly healthy individual), with simultaneous smart watch monitoring and frequent clinic sampling over a 2.5-year period. The clinic visits demarcated with arrows correspond to a viral infection (left and middle arrows) and a traumatic biking accident resulting in an ED visit (right arrow). c, Accuracy (R) of the HCT ~ All Vitals model in the iPOP participant from part a versus the number of clinic visits that were used to develop the model.

Timing and personalization improve accuracy of models.

We reasoned that temporal change in physiology was a likely contributor to unexplained variance in our models. Hence, we explored whether varying the duration or proximity of monitoring improved the prediction of clinical labs from wVS. Relevant time scales for monitoring clinical laboratory biomarkers vary by physiological processes. For example, blood glucose responds to dietary stimulus within minutes, whereas HbA1c reflects overall blood glucose over several months. Therefore, to find the optimal duration of monitoring by wearables, we analyzed clinical laboratory models using wVS collected at set time windows proximal to the clinical laboratory test date (Fig. 4a). We found that most of the top models perform best with features calculated from shorter time periods before the laboratory test date (for example, HCT, RBC, HGB and MONOAB random forests), and for some laboratory tests the time window has only a minor impact on model accuracy (for example, HGB Lasso model) (Fig. 4a and Extended Data Fig. 2a). The Lasso model performed slightly better with longer timescales than the random forest model (Fig. 4a and Extended Data Fig. 2a). Of the physiological categories (Fig. 3a), the hematologic category performed best using a shorter monitoring period, with R values of 0, 0.093, 0.130 and 0.411 with wVS from 1 month, 1 week, 3 days and 1 day before the clinic visit, respectively.

Another likely source of unexplained variance in the clinical laboratory models is inter-subject variability (Extended Data Fig. 3a). To address the potential reduction in performance caused by inter-subject variability, we developed personalized models to account for differing individual baselines (Figs. 4 and 5a). As more historical data (simultaneous clinical labs and vital signs) were required to build personalized models than were available in the iPOP cohort, we used the Stanford EHR (SEHR) dataset (28,694 individuals, 38,058 observations) to build models that used longitudinal data for an individual (213 patients with ≥50 observations). We developed cVS personalized models (multivariate linear and random forest) that used a patient’s personal mean of the clinical labs as a baseline prediction for that patient, and calculated patient-specific parameters to model individual variability around that personal baseline (Fig. 5a,b). Personalized models explained, on average, 43% more variance than population-level models (two-sided Wilcoxon signed rank test, P < 1 × 10⁻⁵).

Fig. 5 |. Personalized models improve predictions of clinical laboratory tests from vital sign measurements.

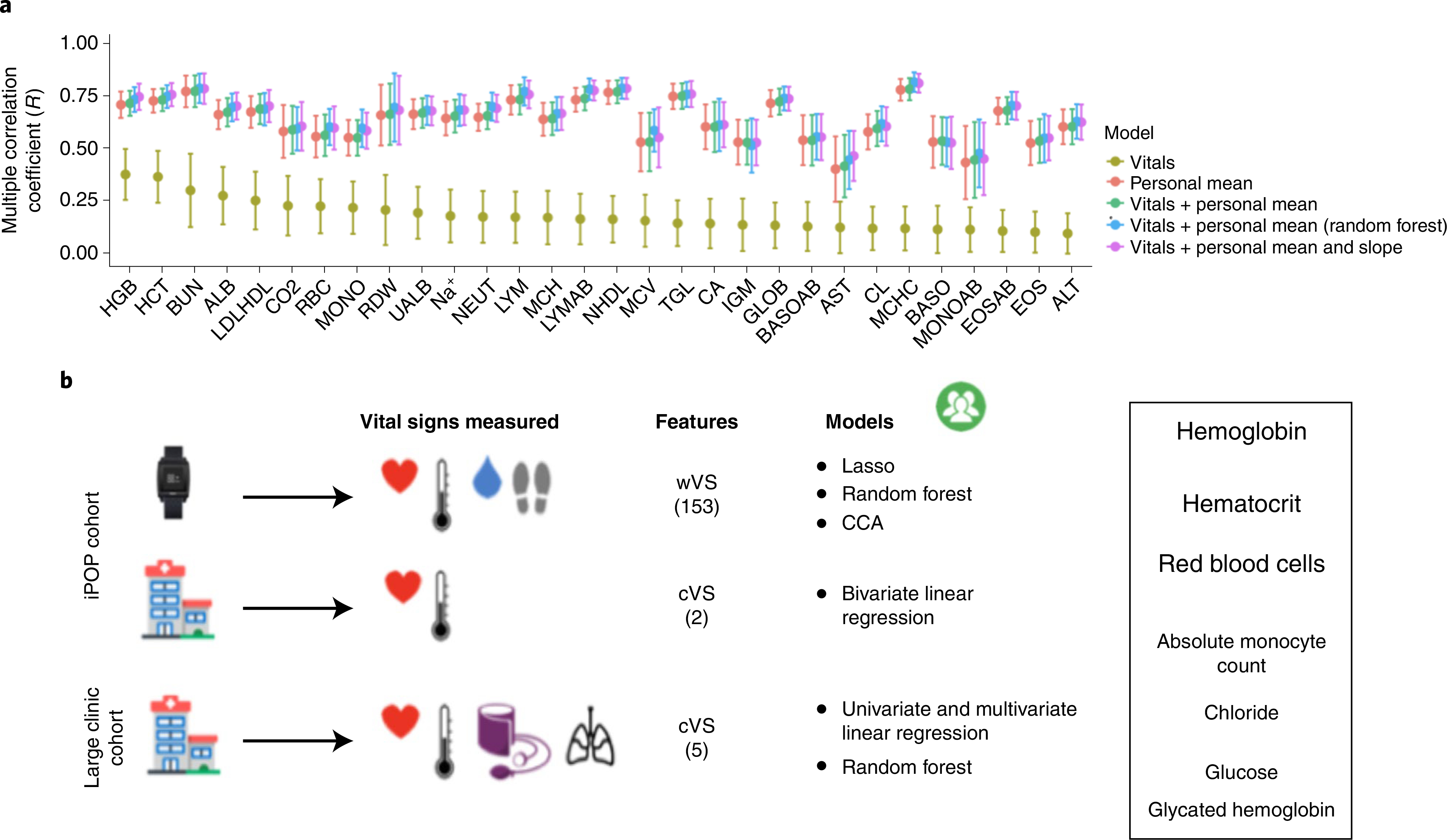
a, Comparison of five models predicting clinical laboratory test values in the SEHR dataset for patients with more than 50 observations for each clinical laboratory test (average n = 117 patients per test; the number of patients varies for each test). The models include the personal mean of the test for a patient (red), the linear clinic vitals (cVS) model (~All Vitals) (olive green), the personal mean + linear cVS model (green), the personal cVS random forest model (blue), and the linear mixed effects models using the personal mean and slope + cVS (purple). Points correspond to the mean R statistic derived by cross validation and error bars represent 95% confidence intervals derived by bootstrap, repeating the procedure 1,000 times. b, Study summary and results. Font sizes of clinical labs correspond to the overall predictive ability of the models developed in this study.

As a proof of principle for building personalized health models, we conducted a case study with a relatively healthy and frequently sampled iPOP participant who had sufficient wearables and clinical vital sign measurements to potentially establish accurate personalized cVS and wVS models of HCT (Fig. 4b). We explored how the number of observations and the duration of monitoring affect the variance explained by a personalized model, how personalized model accuracy changes over time, and how the change in accuracy is related to the dynamically changing health of an individual.

As expected, the performance of the personalized models for the case study varied over time, and health events caused shifts that required updated clinical information to re-establish high performance (Fig. 4b). The individual’s personalized HCT wVS model outperformed the personalized cVS model 84% of the time (Fig. 4b). We found that personalized models built using more observations or from a dense monitoring period had increased accuracy if the monitoring period was of appropriate length. For the HCT cVS model, 10 sequential clinic visits were needed to observe an R improvement from near zero to 0.74 (Fig. 4c). We also found that the personalized models often performed comparably to the population-level models if the prior observations were not in close proximity to the test that we aimed to predict (Fig. 4c). Thus, in contrast to our initial hypothesis, more visits did not always equate to more accurate models because the timespan of observations was often longer and therefore included observations that were more distanced in time from the clinic visit with the relevant laboratory test. A more complex modeling scheme is required to effectively incorporate all available data; for example, by down-weighting observations that are distant from the clinical visit.

Another key finding was that the ability to build an accurate model for an individual varied based on their health fluctuations. In the SEHR dataset, individuals with the most clinic visits are also those that are the most sick, and the dynamic nature of their personalized model performance may reflect their dynamic health status (Extended Data Fig. 2b)²⁵. Interestingly, dramatic decreases in personalized model accuracy coincided with major health events (for example, myocardial infarction, emergency department visit or viral illness), suggesting that major shifts in physiology can influence the quality of the model (Fig. 4b and Extended Data Fig. 2b), and in turn that changes in model performance can signal major health events. So far, such large-scale analysis of variability in health has been possible only in sick populations, because data on healthy individuals are usually sparse. With wearables, we can also analyze health variations in healthy populations.

Discussion

Here we demonstrate that (1) heart rate vital signs collected from wearables provide a more consistent depiction of resting heart rate than measurements taken in the clinic; (2) wVS are associated with several clinical labs, with hematologic clinical laboratory tests most consistently predictable using wVS models; (3) specific physiological features are associated with clinical features (for example, EDA and HCT) providing insights into links between clinical biochemical tests and physiology; (4) in the majority of cases, wVS models outperform cVS models; (5) the amount of time monitored, the proximity of the monitoring period to the date of prediction, and health events play a critical role in the accuracy of the models; and that (6) personalized models perform significantly better than population-level models. These findings build upon our previous study in which we found that it is possible to determine personal vital sign baselines and detect illness from wearables⁸, and hence are a starting point for improved diagnostics using wearables.

cHR are used to monitor acute and chronic health status, including infection, anemia, hypoxia and cardiovascular disease risk²⁶. Previous studies demonstrated that single clinic visits do not sufficiently capture average heart rate among patients with cardiovascular disease and hypertension^20,27. We demonstrate that circadian heart rate variations cannot be captured through intermittent clinic visits, and therefore cHR taken at different times of day are of limited utility for tracking health over time. Heart rate variations throughout the course of the day are an important consideration given that most clinic visits do not occur at the same time of day, complicating the interpretation of cHR²⁰.

Calculating wRHR over varying time and activity thresholds revealed that wRHR decrease with longer durations of inactivity. Current cHR guidelines only require 5 min of rest and do not account for physical activity or stress levels immediately prior to the clinic visit. We also found that wRHR are more representative of typical resting heart rate than intermittent cHR, and that longer monitoring periods for capturing wRHR decreased variance. This underscores the importance of time window selection for individual ‘baselining’. This window will vary for different types of physiological measurements depending on how much variability is expected, how variation occurs over time, and how measurements covary with other factors (for example seasonality). This information can be collected and factored into wearables measurements in the future.

Although in the past clinical labs were routinely collected at annual visits, there has been a shift from routine collection due to lack of evidence of benefit²⁸. Using prediction models to pre-screen for risk of abnormal labs may enable providers to better identify those who might benefit from laboratory testing, avoiding the cost and effort of performing routine clinical laboratory testing on all patients. Presently, we do not anticipate diagnostic use of the current models; however, they can be used to suggest further clinical testing. These models could also be extremely useful in an emergency room setting, as information about the risk for abnormal clinical labs could be available the moment that the patient arrives.

We found that the majority of wVS models outperform cVS models, presumably because wVS provide more measurements throughout the duration of monitoring and the ability to engineer more complex model features (Extended Data Fig. 3b). The finding that the variance of wRHR is lower than that of cHR, combined with our previous validation studies that compared wRHR with simultaneous clinical gold standard measurements^5,8, demonstrates that many longitudinal observations of resting heart rate enable us to capture more consistent HR values than could be captured in a clinic.

Among the 44 laboratory tests, there are a few groups of tests that are strongly correlated, and several models were found to predict the correlated tests. However, no laboratory tests are redundant, and even strongly correlated laboratory tests have distinct clinical applications. For example, although there is great heterogeneity among our predictive models of clinical labs, we consistently found that two components of the complete blood count clinical lab panel—HCT and HGB—were best predicted from vital signs alone. These two tests are strongly correlated, but they are derived differently and contain complementary information. HGB is a direct measurement of hemoglobin, whereas HCT is calculated from RBC count and mean corpuscular volume. Wearable-measured EDA was a strong predictor of HCT, HGB and RBC, consistent with existing literature on sympathetic activation and hemoconcentration²⁹. In the outpatient setting these models may help to identify individuals who would benefit from screening for anemia as well as those suffering from dehydration. The potential to detect dehydration using wearables may be particularly useful in older adults who are at heightened risk of dehydration due to age-related physiological changes, including decreased thirst³⁰. Hospitalizations for dehydration are extremely costly and are considered by US Medicare to be preventable³¹. The potential of wearables to establish a reliable baseline and detect changes from the baseline may be a valuable tool to address this problem and other emerging uses in older people (for example, fall detection). Given that one in five people in the United States regularly wears a smartwatch, and their use is increasing, there will often be sufficient data for practical implementation of these methods by physicians.

PPG uses light absorption by hemoglobin to calculate heart rate, and therefore we expected that HGB would be the most likely test to be predictable by PPG-based heart rate measurements. Indeed, we found that the wVS heart rate features comprised 20–40% of the most-predictive features in our best HGB model, whereas cVS, which does not use PPG, could only explain 2–7% of the variance in HGB measurements.

Daytime and night-time high intensity activity were strong predictors of fasting plasma glucose, as were wRHR and wRTemp. This is consistent with our previous work showing that the difference between daytime and night-time wRHR and daily steps are associated with insulin resistance⁸. Although the random forest method does not illustrate direction of prediction and only ranks the feature importance, we infer that high daytime activity may be associated with better fitness, an important factor in glucose control. On the other hand, high night-time activity may be disruptive of circadian rhythms, which is also important to blood glucose control. Daytime physical activity and skin temperature changes during physical activity were predictive of MONOAB, as might be expected given that these become disrupted during infection. Additional research will help to uncover the underlying biological mechanisms of the relationship between biomolecular measurements and physiological signals.

Although we were able to build useful models of clinical chemistry from wearables data in our relatively small iPOP cohort, the cohort size was limited. Therefore the models that we developed here, although predictive, are less generalizable to the overall population. To obtain similar results in another specified group of patients, models should be trained on data from those cohorts in which the model is intended to be applied. In the future, larger datasets like the Health eHeart Study³² and the All of Us Research Initiative that capture both clinical information and simultaneous wearables information will dramatically improve the field of digital biomarker development and training of models on specific populations. Such datasets may also support the development of more accurate, but also more complex and potentially less interpretable deep learning models. Here, we aimed to develop accurate yet interpretable models because understanding the logic underlying a model’s output is critical in the clinical setting.

As technology advances, present-day clinical labs may be frequently measured outside of the clinic^33,34. There have been several successful examples of continuous monitoring of clinical labs via wearable biosensors; for example, continuous blood glucose^35,36, cortisol³⁷, and sweat analyte³⁸ monitors. These sensors are not without challenges as they require access to bodily fluids, often through invasive methods, and usually require frequent recalibration. We anticipate that in the future, using new wearables that measure additional parameters such as systolic and diastolic blood pressure and respiration rate will further improve the wVS personalized models. Moreover, a combination of clinical and wearable metrics may provide a more holistic picture of the patient, with intermittent but precise measurements in the clinic and noisier but continuous monitoring using wearables, complementing clinical practice.

Overall, our findings suggest that wearables enable continuous health monitoring, health monitoring outside of the clinic, and detection of deviations from personal healthy baselines that can be used to identify the need for more formal clinical laboratory evaluation. The personalized monitoring and modeling framework presented here can be readily generalized to other types of data and clinical measurements, enabling broad implementation of personalized health monitoring through wearables.

Methods

Wearables cohort.

Participants were enrolled in the iPOP study under institutional review board (IRB)-approved protocols (IRB-23602 and IRB-34907 at Stanford University) with written consent. All clinical measurements were covered by IRB-23602, the enrollment criterion of which is a minimum age of 18 years. All wearable measurements were covered by IRB-34907, the enrollment criterion of which is a minimum age of 13 years. Cohort demographics are reported in Supplementary Table 1d. Participants were recruited with efforts to enroll those at risk for type 2 diabetes (SSPG ≥150 mg dl⁻¹, fasting plasma glucose ≥ 100 mg dl⁻¹, oral glucose tolerance test ≥ 140 mg dl⁻¹, HbA1c > 5.6%) and healthy controls. We simultaneously collected wearables data from a subset of our cohort consisting of 54 individuals. Clinical laboratory tests were performed at every clinic visit, which occurred roughly four times per year for ‘healthy visits’ (regular check-ins with no specific reason for the visit; e.g., no reported illness, stressful event, travel, etc.). Clinic visits were performed in the mornings between 7:00 and 9:00, and resting heart rate was measured after 5 min of sitting, according to American College of Cardiology (ACC) and American Heart Association (AHA) guidelines^20,39. The data collected included 44,402 clinical laboratory test results and 3,987 vital sign measurements (2,391 cHR and 1,596 cTemp) using the gold standard Welch Allyn 6000 series instrument, which is routinely used at the clinical laboratory services at Stanford University (average values and number of observations for each test are given in Supplementary Table 1a,b). Participants wore a smart watch for an average of 343 days. Average values for the smart watch are reported in Supplementary Table 1c. For each individual, the number of days monitored by the clinic and by the wearable were calculated by the time between the date of the first and the final clinic visit, and the total amount of time that the watch was worn, respectively.

Retrospective clinical record cohort.

Overall, we analyzed clinical records from 28,694 patients at Stanford Hospital (IRB-37859). The records contained 31,543,209 laboratory test results (87,972 from our 44 clinical labs of interest that have corresponding vital signs measurements) and 885,966 vital signs measurements (552,145 cHR and 333,821 cTemp, 86,515 and 75,187 of which, respectively, have corresponding clinical laboratory tests from our 44 tests of interest) (average values and numbers of observations for each test are given in Supplementary Table 3a,b, and cohort demographics are given in Supplementary Table 3c)³. These records were from 10,000 individuals with prediabetes, 8,694 with type II diabetes, and 10,000 individuals who were normoglycemic based on fasting plasma glucose. We used clinical vital signs that occurred on the same date as our clinical laboratory tests of interest, using only observations between 20–230 bpm (heart rate), 90–115°F (oral temperature), 70–220 mmHg (systolic blood pressure), 35–130 mmHg (diastolic blood pressure) and 2–130 breaths per min (respiration rate). The average cHR was 77.51 (s.d. 14.12) (n = 86,515 cHR observations) and the average cTemp was 97.96 (s.d. 0.50) (n = 75,187 cTemp observations) (Supplementary Table 3a). These numbers are similar to the clinical measures from the iPOP wearables cohort (mean cHR = 71, cTemp = 97.9) although the cHR in the large cohort is elevated.

Clinical record data cleaning.

To address possible data entry errors, for each of the clinical laboratory tests we removed outliers (values greater than three standard deviations from the mean for that laboratory). We compiled a list of 44 clinical laboratory tests based on their ubiquity in standard clinical practice, their frequency in our clinical records, and their relevance to physiology (Supplementary Tables 1b and 3b). The number of days monitored by the clinic was calculated by the time between the date of the first and the final visit.

wVS data pre-processing steps.

We collected a total of 157,068,268 wearables measurements using four sensors (heart rate photoplethysmography, skin temperature thermopile, EDA and accelerometer at a rate of 1 measurement per sensor per min) from 54 individuals over a total of 18,522 days of recording using the Intel Basis smart watch. We removed outliers using the same method as above.

Evaluating the relationship between cVS and wVS.

Previous research shows that the Intel Basis watch accurately measures heart rate in the resting range^7,8,40. To explore the correspondence between clinically measured vital signs and vital signs measured using the wearable (cVS and wVS, respectively), we calculated the resting values of heart rate and skin temperature measured from the smart watch (wRHR and wRTemp, respectively) during 5-, 10-, and 60-min rolling windows during the 24 hours prior to the clinic visit, for which there were no steps taken or the number of steps was less than 50. We averaged the wRHR during each hour of the day to explore the circadian variation in wRHR and to compare wRHR at each hour of the day to the average of the single clinic cHR. To compare the variation in wRHR with the variation cHR, we used the watch measurements during 1 week, 2 weeks and 1 month prior to the date of the clinic visit during the same time as the clinic visits (7:00 to 9:00). In the clinic, participants are required to rest by sitting upright for 5 min before the cHR measurement according to ACC and AHA guidelines³⁹. We had n = 54 participants with cHR and cRTemp taken during smart watch wear (that is, with simultaneous clinical and wearables measurements). We compared the mean and variance of wRHR and wRTemp to cHR and cTemp and calculated the correlation coefficient between wRHR and cHR, and wRTemp and cTemp.

Wearable data feature engineering.

Our wVS feature engineering pipeline used a systematic, unbiased approach for subsetting and calculating standard descriptive statistics (eight statistical moments) on the continuous wearables data. From this pipeline we compiled a list of 5,736 possible features in our model. Based on discussion with five clinicians, we selected 153 features out of the 5,736 that were most likely to be directly altered in a physiological state change that could be detected by the 44 clinical laboratory tests (Supplementary Table 2a). The digital biomarkers generated using the schema in Fig. 2a were used as inputs into the model development pipeline (Fig. 2b). The time window of wVS measurements used in the feature calculations can vary. We first chose the 24-h period immediately preceding the clinic visit where the clinical laboratory test was done. Below, we demonstrate how the choice of time window affects the model accuracy.

Evaluating the relationship between wVS and clinical laboratory tests.

We built and tested models of varying complexity to predict clinical laboratory test values from wVS. We evaluate model performance as a function of the observed and predicted values of the dependent variable using the multiple correlation coefficient R corrected for leave-one-person-out cross validation.^41,42 More specifically, we calculate the square root of the per cent variance explained by the model using the formula:

$$R=\sqrt{1-\frac{{\text{RSS}}_{\text{m}}}{{\text{RSS}}_0}}$$ (1)

where RSS_m is the residual sum of squares of the trained model on the test data and RSS₀ is the equivalent for the null model. We define RSS as:

$$RSS={\sum _i\left(o_i-p_i\right)}^2$$ (2)

where o_i are observed values and equation (1) is equivalent to the classical coefficient of determination, R². For nonlinear models this value can be similarly interpreted as the proportion of variance of the dependent variable that is explained by the model. Moreover, the quantity RSS_m/n, where n is the number of observations, is equivalent to the mean squared error.

We chose to report the R² statistic rather than absolute errors in order to make all models presented in the study compatible, regardless of the machine learning methods used and the clinical labs being predicted. Algebraic transformations enable conversion from R² to units of the laboratory test by computing

$$\text{RMSE}=\sigma \sqrt{\left(1-R^2\right)}$$ (3)

where RMSE is the root mean squared error and σ is the standard deviation of the laboratory test. We provide standard deviations of all laboratory tests in Supplementary Table 1b. Models were initially generated using only wVS, excluding demographic covariation, because we were interested in understanding how much of the variation in clinical laboratory tests could be explained directly by vital signs when no additional information is available (Fig. 3b). We also later tested the same models including demographic covariation. Testing models with and without demographic covariation is important for determining the robustness of the models and whether they can use sensor data alone to generate insights. Models that operate well with fewer inputs are more useful in low resource settings or in high privacy environments where gathering additional information about a patient can be difficult. To test and compare the wVS models, we built univariate and multivariate linear regression, least absolute shrinkage and selection operator (Lasso) regularized regression, random forest, and canonical correlation models using the stats, glmnet, randomForest and PMA packages, respectively (R version 3.3.3). The univariate used only mean wRHR or mean wRTemp to predict each clinical laboratory test. The bivariate model included both wRHR and wRTemp, and the multivariate model included both the mean and standard deviation of these values. The 153 wVS engineered features were used in the Lasso and random forest models (Supplementary Table 3a). We used leave-one-person-out cross validation (LOPOCV) and the R reporting statistic to assess the accuracy of the models. In LOPOCV, for each subject in the dataset we train a model using a dataset without that subject and then we test model performance on that subject. Next, we average the errors across all subjects to obtain an estimate of the error outside of the training set.

Lasso.

To develop a regression model that can take advantage of the higher feature complexity made possible by using wVS as opposed to cVS, we used Lasso^43,44 with the 153 wVS features as predictors and each of the 44 clinical laboratory tests as outcomes (Supplementary Table 3a)⁴⁴. We used the glmnet package (R version 3.3.3) to build each Lasso model LOPOCV loop to develop the overall model and an internal n-fold cross-validation loop in which the model training data set from the outer loop is decomposed into a subsequent training or validation set to tune the lambda shrinkage parameter over 100 possible values for lambda (nlambda = 100). We explored lambdas that minimize the cross-validated error (lambda.min) or that minimize the cross-validated error plus one standard deviation (lambda.1se), which generally results in a more robust and parsimonious model. We determined the best fit Lasso models for each of the 44 clinical laboratory tests and explored the features that appeared the most frequently among the 44 Lasso models as well as features with the highest coefficients overall and in particular models. We also explored how varying the timespan used to calculate the model features affected the overall accuracy of the Lasso models (Extended Data Fig. 2a).

Random forest.

Given our finding that the slopes of the relationships between cVS and clinical labs often vary oppositely, we decided to use random forest nonlinear models⁴⁵. We used the randomForest package in R to build separate models for each test. We evaluated the model following the same LOPOCV method and R reporting statistic. We used the default package parameters of 500 trees and 51 variables randomly chosen at each split (the number of features divided by 3).

Canonical correlation analysis.

An extension of linear models in the context of high-dimensional data is to predict a weighted sum of tests rather than individual tests. Conceptually, this is motivated by the fact that variability in individual clinical laboratory tests from a certain group (for example, metabolic tests) can be correlated and therefore we may want to project them onto a single index to summarize this variability. To accomplish this, we searched to maximize the correlation between a linear combination of a subset of clinical laboratory tests and a linear combination of predictors. We grouped the clinical laboratory tests by physiological groups (Fig. 3a), which we use as the outcomes in the regularized CCA models, where the wVS features are the same as were used in the random forest and lasso models⁴⁶. We used internal cross-validation over combinations c₁, c₂ ∈ (0.1, 0.5, 0.7) corresponding to aggressive, medium and conservative penalties, respectively, to choose the optimal parameters for each groups of tests⁴⁶. We used LOPOCV and the R reporting statistic to assess the canonical correlation. CCA is a useful tool for finding relations between sets of variables, however it can handle only linear relations and, while we attempted to use a regularized version of CCA, there is no gold standard technique for solving the problem of sparse CCA. In light of recent developments in this area of high-dimensional statistics we may expect further improvements in the robustness of these tools^46,47.

Evaluating relationship between cVS and clinical laboratory tests.

We also built and tested models of varying complexity to predict clinical laboratory test values from cVS. For direct comparability with the wVS models built for the iPOP cohort, we built random forest and bivariate linear cVS models in the iPOP cohort using LOPOCV, using only individuals with ten or more observations of that clinical lab test. These cVS models used cHR and cTemp as variables, which are the two vital signs that were measurable both in the clinic and by the watch. We ran 1,000 bootstrapping trials to establish confidence bounds of the reporting statistic R. In each bootstrapping trial i we sampled observations with replacement, ran the training procedure, and recorded the R_i statistic on the test set. We report the mean of R_i as our R statistic and use the standard deviation of R to establish confidence bounds and P values. We defined the most accurate cVS models as those with P < 0.05 for correlation between observed and predicted values using Bonferroni correction for multiple hypothesis testing. For the Bonferroni correction we multiply the P values of models of all clinical tests by 44 (the number of models).

Exploring the importance of duration and proximity of monitoring.

We sought to discover whether there is an optimal number of observations, length of monitoring period, and proximity of monitoring to the date of the test being predicted to achieve the most accurate possible predictions. To explore how time affects the accuracy of the model predictions, we analyzed how the cVS mixed effects model accuracy changes with respect to the number of observations used to generate the model and the proximity of those observations to the date of the test being predicted. We used a relatively healthy iPOP participant with more than 60 clinic visits to test this concept. For the personal cVS model, we divided the number of visits in half and on each half we built models to predict the last three observations (test set). We trained the model using the last K observations prior to the observation that we want to predict. We varied K between 1 and 25 to find the number of observations optimal for predictions. We computed R from all six test values (three from each half). We used this approach to evaluate the models predicting HCT from cVS for this subject.

For the individual with the largest number of observations in both datasets we analyzed temporal variability of accuracy of cVS and iPOP models. Beginning from the tenth visit, we built a linear model to predict HCT for each subsequent visit using the last 10 visits. Given a small number of observations we aimed at building parsimonious models. For the cVS model we use pulse, temp, systolic and diastolic blood pressure, and respiration. For the iPOP model we use mean heart rate, skin temperature, galvanic skin response, step count and resting heart rate. We predicted values of HCT using that model for the current and subsequent time points, and we computed the R statistic.

To explore the importance of the overall amount of wearables data from each individual used to develop the wVS model features, and the timespan of monitoring relative to the date of the clinical test, we developed retrospectively expanding windows of time from the date of the clinical laboratory test (1 day, 3 days, 1 week and 1 month before the date of the clinical laboratory test) where the data collected in that time window was used to calculate the wVS features. We also created a time window containing all wVS data collected before the clinical laboratory test. For each prediction, we tested five sets of wVS features, one per timespan, to regenerate the lasso and random forest models including demographics, and compared the accuracy of the models.

Personalized models.

To explore the capabilities of cVS models at the population level, we developed univariate and multivariate linear models and random forest models using the large population-level clinical dataset (n = 28,694 patients at Stanford Hospital). The most complex cVS multivariate linear model included all vital signs measured in the clinic (cHR, cTemp, systolic and diastolic blood pressure, and respiration rate), and we tested this model with and without demographic covariation. We also performed random forests using the same features from the complex multivariate model (see Methods, section on wVS model building). As the number of features in the cVS models was significantly lower than in the wVS models (5 cVS features versus 153 wVS features), we did not perform the Lasso regression on the cVS models because it was not necessary to perform feature selection. We estimated the R reporting statistic used through cross-validation, dividing data into 50 equal partitions at the patient level, where each laboratory test in each partition was separated into 60% training data and 40% test data. To derive confidence bounds we repeated the procedure 1,000 times, sampling data with replacement.

We enhanced the most accurate wVS and cVS models that we developed previously, through design of personalized models that use the historical data from an individual as an additional input into the model. For the wVS and cVS random forest models, we included the personal identifier as a categorical feature. For the cVS linear regression models, we explored three methods of personalizing the models. First, we explored the personal mean; a simple intercept-only model using the personal mean (for example the mean of all previous results for the clinical laboratory test for that individual). Second, we examined cVS + personal mean; a model combining the personal mean and the multivariate cVS model. Last, we examined cVS + personal mean + personal slope; a mixed effects model allowing for variability of slope coefficients for each individual to account for random effects. To ensure a sufficient amount of historical data per individual in the cVS models, we chose only individuals with more than 50 clinic visits (213 people, mean of 111 and median of 117 patients per test). The second and the last of these models were generated using the loess function from the stats package in R for local polynomial regression and personal slopes in the mixed effects models were generated using the lmer function from the lme4 package in R. To test the accuracy of the personal cVS linear models, we performed leave-one-test-result-out cross validation, holding out the last observation for each patient to be predicted using the model trained on all patients (including the one from which the observation was held out). We used bootstrapping to calculate the confidence bounds of R, the multiple correlation coefficient between the observed and predicted values.

Reporting Summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Data availability

Intel Basis watch data are available on the Stanford iPOP site (http://ipop-data.stanford.edu/wearable_data/Stanford_Wearables_data.tar) and in the Digital Health Data Repository⁴⁸ (https://github.com/DigitalBiomarkerDiscoveryPipeline/Digital_Health_Data_Repository/tree/main/Dataset_StanfordWearables). Data that are unique to this study are included as source data and in the supplementary tables. Source data are provided with this paper.

code availability

R version 3.3.3 was used with the base packages and the following additional CRAN packages: stats, glmnet, lme4, randomForest and PMA. Custom scripts were used for data analysis and are open source via github.com/jessilyn/wearables_vitalsigns (https://doi.org/10.5281/zenodo.4661493), and wearables data pre-processing scripts are available on the Digital Biomarker Discovery Pipeline (https://DBDP.org)⁴⁸.

Extended Data

Extended Data Fig. 1 |. Wearables temperature variations and extended modeling results.

a, Variations in wRTemp over course of the day. b, R statistics based on LOOCV for all tests from Fig. 3b. c, R statistics based on K-fold CV for all tests from Fig. 3b.

Extended Data Fig. 2 |. Model accuracy changes over time based on window of historical data from an individual.

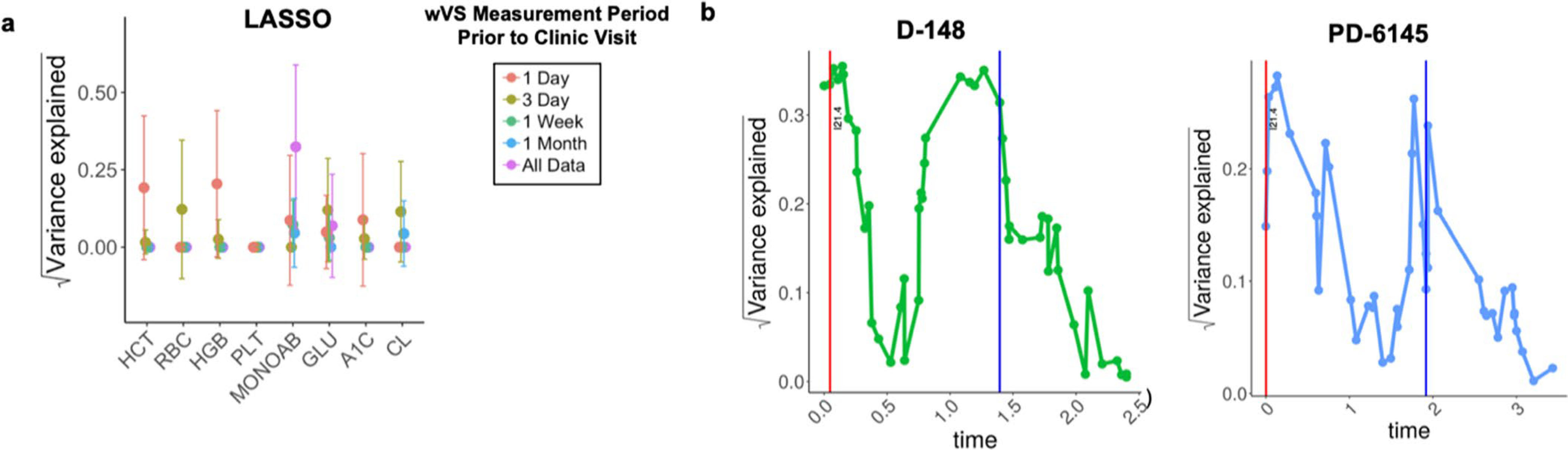
a, Lasso regularized regression using features calculated using different windows of wearable device monitoring. b, Accuracy of the HCT cVS mixed effects models over time for two example patients that were monitored between 2.5–5 years at Stanford hospital with >50 HCT observations at separate clinic visits. The HCT cVS mixed effects models demonstrate that the model accuracy changes over time, and particularly with a dramatic health event like a myocardial infarction (ICD code I21.4) (red vertical line) or a life-threatening ED visit (blue vertical line; CPT code 99285).

Extended Data Fig. 3 |. Increasing amounts of personalized data open up new study and model possibilities.

a, Summary of different biomedical data collection modalities and the typical amount of data they result in. b, Demonstration of how the amount and modality of data collection (longitudinal continuous vs. discrete measurements) constrain the type and complexity of models that can be built from the data.