Abstract
The prevalence of dropout events is a serious problem for single-cell Hi-C (scHiC) data due to insufficient sequencing depth and data coverage, which brings difficulties in downstream studies such as clustering and structural analysis. Complicating things further is the fact that dropouts are confounded with structural zeros due to underlying properties, leading to observed zeros being a mixture of both types of events. Although a great deal of progress has been made in imputing dropout events for single cell RNA-sequencing (RNA-seq) data, little has been done in identifying structural zeros and imputing dropouts for scHiC data. In this paper, we adapted several methods from the single-cell RNA-seq literature for inference on observed zeros in scHiC data and evaluated their effectiveness. Through an extensive simulation study and real data analysis, we have shown that a couple of the adapted single-cell RNA-seq algorithms can be powerful for correctly identifying structural zeros and accurately imputing dropout values. Downstream analysis using the imputed values showed considerable improvement for clustering cells of the same types together over clustering results before imputation.
Keywords: single cell Hi-C, single cell RNA-seq, imputation, dropout, structural zero
Introduction
Thanks to the rapid development of high-throughput sequencing technologies, single-cell assays, including RNA sequencing (RNA-seq) [1] and Hi-C [2], now allow us to study cellular genomic features and dynamic functions at the single-cell resolution. However, single-cell assays usually suffer from high dropout rates due to insufficient sequencing depth, i.e. smaller than needed read counts. The prevalence of dropout events may bring bias and/or computational complexities to downstream analyses, including single cell clustering [3] (RNA-Seq or Hi-C data), and structural studies such as A/B compartments [4], topologically associating domain (TAD) [5] and 3D chromatin structure models (Hi-C data) [6]. To complicate things further, the excess of zeros typically seen in high-throughput data also includes a large proportion that are due to inherent biological properties rather than insufficient sequencing depth: the so-called structural zeros [7].
Although numerous methods have been proposed for identifying structural zeros and imputing the underlying values of dropouts for single-cell RNA-Seq (scRNA) data, methodologies for single-cell Hi-C (scHiC) data for the same purposes are lacking behind, potentially due to greater data complexity of scHiC, as discussed in this section. Nevertheless, the importance of scHiC data quality for downstream analyses is widely discussed, including several methods that introduce an intermediate step for improving data quality before clustering or 3D structure recapitulation. In particular, HiCRep [8] is developed to calculate the reproductivity of Hi-C data, and it takes a 2D mean filter approach to replace each contact with the average count of its neighbors. GenomeDISCO [9] is a concordance measure, which smooths a Hi-C matrix by random walks on the contact map graph. HiCPlus [10] is a supervised learning technique that infers a high-resolution Hi-C matrix from a low-resolution Hi-C matrix based on deep convolution neural network, with the assumption that a Hi-C matrix is composed of repeating local patterns that are spatially correlated in a neighborhood. scHiCluster [5] first performs a convolution-based step and then a random walk step, taking information from both the linear genome and experimentally measured interactions of neighbors. Although these methods may be adapted for scHiC imputation of observed zeros, none of them utilizes information from similar single cells. Furthermore, these methods are not designed to separate structural zeros from dropouts.
The landscape for identification of structural zeros and imputation of dropouts is much different for scRNA. Single-cell RNA-seq data are usually organized as a scRNA matrix of gene expression levels, with rows representing genes and columns representing cells. Numerous methods have been developed to address the challenge of imputing dropout events; an incomplete list of existing methods is provided in Table 1. For example, scImpute [11] proposes a two-step approach that estimates dropout probabilities and imputes the expression levels for those with high probabilities. Markov Affinity-based Graph Imputation of Cells (MAGIC) [12], on the other hand, is a data diffusion approach that shares information among similar cells through local neighbors. Another method, scRMD [13], applies a robust matrix decomposition algorithm [14] to estimate the mean expression level of a gene from the same cluster of cells and make imputation at the determined dropout positions. McImpute [15] and SCRABBLE [16] are based on a low-rank matrix completion algorithm, which is mathematically akin to the Netflix movie recommendations problem [17]. In particular, McImpute uses the nuclear norm minimization algorithm to recover the low-rank scRNA matrix. On the other hand, although SCRABBLE [16] is also under the low-rank matrix completion framework, it goes one step further by taking bulk RNA-seq data as a constraint for the imputation. Note that neither MAGIC nor SCRABBLE separates observed zeros into structural zeros or dropouts. Comprehensive evaluations and comparisons of eight imputation methods, including ScImpute and MAGIC, were carried out in a recent publication [3].
Table 1.
Summary of several single cell RNA-seq imputation methods/packages
| Package | Method | Using information of similar single cells | Using information of bulk data | Using information from neighborhood | Criterion for inferring structural zeroes |
|---|---|---|---|---|---|
| MAGIC | Graph imputation | Y | N | N | N |
| McImpute | Low-rank matrix completion | Y | N | Y | Y |
| scImpute | Two-component mixture model | Y | N | N | Y |
| SCRABBLE | Matrix regularization | Y | Y | Y | N |
| scRMD | Robust matrix decomposition | Y | N | Y | Y |
In high-throughput genomic analysis, it is not uncommon that methods devised for one platform are used for analyzing data from another platform. In particular, methods for analyzing microarray gene expression data have been routinely used for analyzing RNA-seq data. It is also seen that methods developed for RNA-seq data, such as limma or DESeq2, have been used to analyze DNA methylation data [18]. In the spirit of such prior work, in this paper, we study whether imputation methods for scRNA as listed in Table 1 can be adapted effectively for use in scHiC data. One particularly attractive feature of the methods curated in Table 1 is that all of them make use of information of similar single cells, which effectively increases the information for imputation. As described earlier, such a feature is missing in current scHiC analysis methods for data quality improvement. Another desirable feature for some of the methods is that structural zeros are also inferred in addition to imputing for dropouts, which is another deficiency in current scHiC methods.
Despite these potential benefits, one difficulty in adapting scRNA methods for scHiC data lies in the differences in these two types of data. As already mentioned, scRNA data are typically organized as a scRNA matrix of gene expression levels, with rows representing genes and columns representing cells. On the other hand, scHiC data characterizes pairwise interactions using a 2D contact matrix, with complicated spatial correlation structures, especially among neighboring positions. Another difficulty, due to the increase in data dimension, is data coverage. For single-cell technologies, coverage is typically low; coverage for RNA-seq is typically 5–10% [5]. For single-cell interaction data such as scHiC, the coverage is one degree of magnitude lower, with coverage typically in the range of 0.25–1% [5]. Therefore, in this paper, we will focus especially on addressing the dependency structure in scHiC data and excess of zeros. We evaluate and compare the methods described in Table 1 using both simulated and real data.
Methods and their adaptations for scHiC data
We have selected several methods to use in study whether imputation methods for scRNA can be adapted effectively for use in scHiC data for both inferences about structural zeros and imputations for dropouts. We included McImpute, scImpute, MAGIC and SCRMD as part of our comparison methods since they have been shown to be superior for scRNA imputation in prior studies [3, 13], in addition to other desirable features described earlier. We also included SCRABBLE, which appears to be the only imputation method for scRNA that can take bulk RNA-Seq information into consideration.
Since scHiC chromatin interaction data are represented as a 2D contact matrix, whereas scRNA data are a vector of gene expression levels for each single cell, we first vectorized the scHiC matrix for each single cell by concatenating the columns, but only using the lower triangular values from the scHiC matrix. Then we combined vectors from multiple single cells into a new scHiC data matrix with rows representing locations (pairs of interacting loci in the genome) and columns representing cells. In this way, all imputation methods for single cell RNA-seq can be directly applied to scHiC data. We briefly describe each of the comparison methods and their adaptation for scHiC in the following.
MAGIC
MAGIC [12] takes an approach involving four steps: (a) preprocessing the data (scHiC matrix with rows denoting contact counts and columns denoting cells) with library size normalization (dividing by the library size in each cell—column sum—and then multiplying by the median of column sums), denoted by D, and applying Principal Components Analysis (PCA) to the original matrix (before normalization), keeping only the leading PCs that collectively account for at least 70% of the variability; (b) calculating a cell–cell Euclidian distance matrix (Dist) using the leading PCs in (1) and converting Dist to the affinity matrix (A) by an adaptive Gaussian kernel: 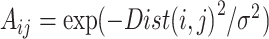 ; (c) symmetrizing
; (c) symmetrizing 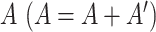 and normalizing it by row sum to get a Markov transition matrix
and normalizing it by row sum to get a Markov transition matrix  ; (d) making the imputation using
; (d) making the imputation using 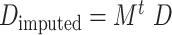 , where t is the diffusion time that is selected to remove noise without over-smoothing (default value is 3 or it may be automatically determined by the algorithm). Those with imputed values less than 0.5 are treated as structural zeros to be consistent with the other procedures, although we note that MAGIC itself does not provide a default threshold value.
, where t is the diffusion time that is selected to remove noise without over-smoothing (default value is 3 or it may be automatically determined by the algorithm). Those with imputed values less than 0.5 are treated as structural zeros to be consistent with the other procedures, although we note that MAGIC itself does not provide a default threshold value.
McImpute
McImpute [15] uses nuclear norm minimization algorithm to recover the low rank matrix. The observed data matrix (with rows denoting contact counts and columns denoting cells in scHiC data) is normalized in the following manner: dividing by the library size in each cell (column sum) and then multiplying by the median of column sums. Further, a  -transformation is applied to each pseudo-count (adding 1 to the count). McImpute solves the matrix completion problem to obtain the predicted matrix by minimizing an objective function, which involves two terms. The first term is the sum of the squared differences between the pseudo-count matrix and the predicted matrix only for the observed non-zero positions. The second term represents a penalty on the rank of the predicted matrix, which includes not only the predicted for observed non-zeros but also values for the zero positions. All the imputed values smaller than 0.5 are replaced with a 0, effectively declaring them to be structural zeros. One advantage of McImpute is that it does not make any assumption on the data distribution, and values in the entire matrix are taken into consideration for imputation.
-transformation is applied to each pseudo-count (adding 1 to the count). McImpute solves the matrix completion problem to obtain the predicted matrix by minimizing an objective function, which involves two terms. The first term is the sum of the squared differences between the pseudo-count matrix and the predicted matrix only for the observed non-zero positions. The second term represents a penalty on the rank of the predicted matrix, which includes not only the predicted for observed non-zeros but also values for the zero positions. All the imputed values smaller than 0.5 are replaced with a 0, effectively declaring them to be structural zeros. One advantage of McImpute is that it does not make any assumption on the data distribution, and values in the entire matrix are taken into consideration for imputation.
scImpute
scImpute [11] applies a similar normalization procedure as McImpute: it normalizes the raw scRNA matrix by library size and then takes a 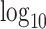 -transformation on the pseudo count (count +1.01). scImpute then clusters cells into subpopulations by PCA transformation and spectral clustering. For each contact count within a subpopulation, the intensity level is assumed to follow a mixture distribution of Gamma and Normal, with the proportion of Gamma as the dropout rate parameter. All parameters are estimated by the Expectation-Maximization (EM) algorithm. A dropout probability is defined to be the ratio of density between Gamma component and the overall mixture distribution. For the set of the data with dropout probabilities smaller than a threshold (default value is 0.5), no imputation is carried out as such data are treated as structural zeros. For the complementary set of data (i.e., those with probabilities greater than the threshold), non-negative least squares regression is applied to impute expression data by borrowing information from cells in the same subpopulation.
-transformation on the pseudo count (count +1.01). scImpute then clusters cells into subpopulations by PCA transformation and spectral clustering. For each contact count within a subpopulation, the intensity level is assumed to follow a mixture distribution of Gamma and Normal, with the proportion of Gamma as the dropout rate parameter. All parameters are estimated by the Expectation-Maximization (EM) algorithm. A dropout probability is defined to be the ratio of density between Gamma component and the overall mixture distribution. For the set of the data with dropout probabilities smaller than a threshold (default value is 0.5), no imputation is carried out as such data are treated as structural zeros. For the complementary set of data (i.e., those with probabilities greater than the threshold), non-negative least squares regression is applied to impute expression data by borrowing information from cells in the same subpopulation.
SCRABBLE
SCRABBLE [16] imputes dropout events by minimizing an objective function of three terms. The first two terms compose the objective function of McImpute, except the first term of SCRABBLE is divided by 2. The third term is the sum of squared differences between the bulk data (if such are available) and the aggregated single cell data, which is the unique characteristic of SCRABBLE—it is the only algorithm among the ones adapted that can utilize information from bulk data. The final output matrix is the predicted matrix that minimizes the objective function.
scRMD
scRMD [13] preprocesses data in the same way as scImpute: normalizing the matrix by the library size and transforming the pseudo-counts. An important assumption of scRMD is that dropout events may happen only on a candidate set  where observed values are lower than a threshold, with the default being the 0.05 quantile of nonzero values. scRMD then decomposes the normalized matrix (Y) into (L-S) via a robust matrix decomposition algorithm, where L represents mean expected counts and S indicates whether a dropout happens: if a dropout happens, the corresponding value in S is greater than 0. Otherwise, the value is 0. scRMD only replaces the candidate positions (set
where observed values are lower than a threshold, with the default being the 0.05 quantile of nonzero values. scRMD then decomposes the normalized matrix (Y) into (L-S) via a robust matrix decomposition algorithm, where L represents mean expected counts and S indicates whether a dropout happens: if a dropout happens, the corresponding value in S is greater than 0. Otherwise, the value is 0. scRMD only replaces the candidate positions (set 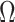 ) in Y with the corresponding values in
) in Y with the corresponding values in 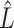 for those positions that have positive values in
for those positions that have positive values in 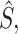 where
where 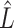 and
and 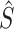 are the estimates at the conclusion of the matrix decomposition algorithm.
are the estimates at the conclusion of the matrix decomposition algorithm.
McImpute-block
As described above, to make it possible to apply methods designed for analyzing scRNA data to scHiC, we vectorized the scHiC matrix. However, doing so results in the loss of the most important feature of a contact matrix, which is the spatial correlation within neighborhood regions inherent in such data [19]. To alleviate this problem, we further consider a CUT step in conjunction with a scRNA imputation method (using McImpute as a template in our naming convention), which effectively takes contacts in neighboring positions into consideration in a more precise way to enrich information and reduce noise. This step essentially entails a partition of the whole scHiC matrix into blocks so that imputations can be carried out for each block separately. A schematic diagram depicting how to partition the 2D contact matrix into blocks is shown in Figure 1, in which we focus on the lower triangular part of the matrix below the red squares. The partition of blocks allows McImpute and other scRNA imputation methods to take advantage of information contained in neighboring positions of a 2D matrix. Specifically, suppose the dimension of an scHiC matrix is N by N with a block size of M. Then, the number of blocks for each row (and column) is the ceiling of P=N/M. Shown in Figure 1 is an example with N = 14 and M = 5. A couple technical issues are further explained. First, the diagonal blocks (P1, P3 and P6 in Figure 1) are of different sizes compared to the complete blocks (P2, P4 and P5 in Figure 1). Second, if P is not an integer, then the last block (before ‘padding’) would have a smaller block size than the rest. One way to solve this problem is to enforce the block size of the last block to still be M by overlapping the last block with the one prior to it (as shown in Figure 1). Each block is then analyzed one at a time using McImpute as before by vectorizing data contained in the block and combining across multiple cells into an scRNA-like matrix. Since some positions in the original 2D matrix may be overlapped as described in the CUT step, the imputed value for an overlapped position is taken to be the average from all involved blocks.
Figure 1 .

Schematic diagram of the result of a CUT Step. There are three diagonal blocks and three non-diagonal blocks. To make each block have the same numbers of rows and columns, overlapping may be necessary, as indicated in the plot.
Simulation study
To evaluate the performance of the methods describe above, we simulated 2D contact matrices using two types of underlying 3D structures: structures estimated from three K562 cells [20] and a helix model that has been used in the literature for evaluating methods for 3D structure recapitulation [21]. Several criteria are used to assess the performance of the methods. In the following, we will first provide details on the two kinds of 3D structures. Then we will describe the simulation procedure for producing the scHiC contact matrices. Finally, we will discuss the criteria devised for evaluating the results.
Two kinds of underlying 3D structures
K562 model
The first kind of underlying 3D structure we used for our simulation study was recapitulated based on three single cells (GSM2109974, GSM2109985 and GSM2109993) from a K562 scHiC dataset [20] (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE80006). We constructed the structure using SIMBA3D [21]; for each of them, we used a substructure with 61 consecutive loci on chromosome 1 (i.e., 61 consecutive segments of the same length as a underlying 3D K562 model for the first simulation study. Therefore, for each 3D structure, we have the 3D coordinates for all the loci: 
Helix model
The second kind of 3D structures we considered was from a helical model, which has been used to model chromatin structure in previous studies [21]. In this study, a 3D helix structure with 61 loci is determined by two parameters  and L at each locus
and L at each locus 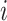 in the genome:
in the genome:
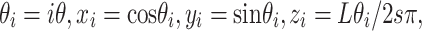 |
where  is the 3D coordinate for locus
is the 3D coordinate for locus 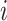 ,
, 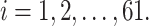
Simulation procedure
We used the following simulation procedure to generate a 2D contact matrix for each single cell based on a given underlying 3D structure (either from the K562 model or the helix model):
Step 1. Generate distance matrix d = (
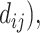 where
where 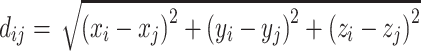 , and
, and  and
and 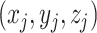 are the 3D coordinates of loci
are the 3D coordinates of loci 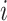 and
and 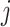 .
.- Step 2. Use the following relation to generate the
 matrix,
matrix,
where
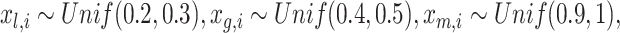 and they may be thought of as covariates and act as normalizing factors [22]. We restrict
and they may be thought of as covariates and act as normalizing factors [22]. We restrict 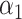 to be negative so that contact frequency and 3D distance follows an inverse relationship [4]. Further,
to be negative so that contact frequency and 3D distance follows an inverse relationship [4]. Further,  are set to control the sequencing depth. For each of three 3D K562 structures, their parameter values are as displayed in Table 2(A), representing three underlying ‘cell types.’ For the helix structure, we considered three sets of parameter values displayed in Table 2(B), which are also taken to represent three underlying ‘cell types.’
are set to control the sequencing depth. For each of three 3D K562 structures, their parameter values are as displayed in Table 2(A), representing three underlying ‘cell types.’ For the helix structure, we considered three sets of parameter values displayed in Table 2(B), which are also taken to represent three underlying ‘cell types.’
Table 2.
Parameter settings for simulation
| (A) For structures inferred from three K562 single cells | ||||||||||
| Type | GSM # |

|
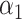
|
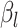
|
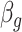
|

|
Sequencing depth | # True 0 positions | Range of 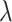 values values |
|
| K562 T1 | 2109974 | 5.6 | −1 | 0.9 | 0.9 | 0.9 | 6800 | 91 | 0.90–16.07 | |
| K562 T2 | 2109985 | 6.3 | −1 | 0.9 | 0.9 | 0.9 | 12,000 | 91 | 0.89–34.41 | |
| K562 T3 | 2109993 | 6.7 | −1 | 0.9 | 0.9 | 0.9 | 13,410 | 91 | 0.87–50.31 | |
| (B) For a structure generated from the helix model | ||||||||||
| Type |

|
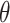
|

|
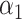
|
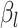
|
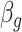
|
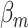
|
Sequencing depth | # true 0 positions | Range of 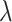 values values |
| Helix T1 | 0.04 |
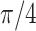
|
1.0 | −1 | 0.1 | 0.1 | 0.1 | 6637 | 91 | 0.83–44.84 |
| Helix T2 | 0.04 |

|
1.1 | −1 | 0.1 | 0.1 | 0.1 | 6702 | 91 | 0.91–49.80 |
| Helix T3 | 0.04 |
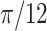
|
1.2 | −1 | 0.1 | 0.1 | 0.1 | 6437 | 91 | 1.02–53.96 |
Step 3. Denote the lower
 quantile of
quantile of 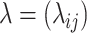 as
as  . For those
. For those 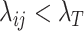 , randomly select (1-r)/2 of them and set their
, randomly select (1-r)/2 of them and set their  values to be exactly 0; these are the structural zero positions shared across all single cells. For each of the remaining r/2 positions, they may be set as a structural zero with 50% chance for each single cell; therefore, whether each of these positions represents a structural zero position or not varies from cell to cell. The resulting matrix after setting the structural zero positions for a single cell is denoted as
values to be exactly 0; these are the structural zero positions shared across all single cells. For each of the remaining r/2 positions, they may be set as a structural zero with 50% chance for each single cell; therefore, whether each of these positions represents a structural zero position or not varies from cell to cell. The resulting matrix after setting the structural zero positions for a single cell is denoted as  . For our simulation, we set r = 0.2, leading to the number of true zero positions and the range of
. For our simulation, we set r = 0.2, leading to the number of true zero positions and the range of 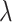 values as indicated in Table 2.
values as indicated in Table 2.Step 4. Use the underlying matrix
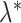 to generate a 2D contact matrix for each single cell treating each
to generate a 2D contact matrix for each single cell treating each 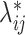 as the Poisson intensity parameter if
as the Poisson intensity parameter if 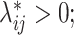 otherwise, the contact count is set to be zero.
otherwise, the contact count is set to be zero.
Based on the simulation procedure and each 3D structure and cell type, we first generated single cell contact matrices for three sample sizes: n = 10, 50, and 100 single cells. This led to the average sequencing depths (over the 100 single cells) as shown in Table 2. As can be seen there, type I of the K562 structure (K562 T1, based on single cell GSM2109974) and the three cell types of the helix structure all have sequencing depths of around 7000; hence, they are referred to as the ‘7K’ data. For cell types II and III of the K562 model (K562 T2 and K562 T3), we randomly subsampled the 2D matrix to arrive at an ‘7K’ sequencing depth for comparison purpose. Two other data resolutions were also created similarly for all cell types and structures, leading to data with ‘4K’ and ‘2K’ sequencing depths.
Since SCRABBLE can incorporate bulk data into its analysis, we also generated such information. An additional 220 single cells of each K562 cell type were simulated and combined to form a bulk dataset with sequencing depth of approximately 7 million. Similarly, an additional 350 single cells for each of the three helix cell types were simulated, leading to a (combined) bulk dataset of also about 7 million in sequencing depth. Note that we created the two bulk data sets with a mixture of cells and cell types to evaluate whether the utilization of such data for making inference about the observed zeros would lead to better separating of structural zeros from sampling zeros as well as imputation accuracy.
Whole genome settings
Taking computational constraints into consideration (since some algorithms such as scImpute and MAGIC are extremely computationally intensive for large scHiC datasets based on our experience – more details are provided in results), we have opted to carry out our main comprehensive simulation study under 54 settings for 3D substructures each with only 61 loci. More specifically, each of the five algorithms are studied for all 54 settings; this requires considerable computational time, especially given our desire to gauge computational feasibility on a single computer (rather than the use of a cluster) with reasonably good computational power. Nevertheless, we do recognize the importance of studying whole genome capability of the algorithms; therefore, we also carry out a smaller-scale study examining only the three K562 3D structures, each with 10 single cells but considering the whole genome.
Evaluation criteria
We considered four main criteria to evaluate the performance of the imputation methods. In addition, we also looked into the accuracy of clustering single cells before and after imputation as an additional criterion for comparison with a scHiC method. Among the four main criteria, the first one is true positive (TP) rate, which is defined as the ratio of the number of correctly identified structure zeroes to the number of underlying structural zeroes. For MAGIC and SCRABBLE, since default values for declaring structural zeros were not provided, we labelled those with imputed count less than 0.5 as structural zeros. For the other methods, we used their default criteria in the corresponding packages for structural zeros inference. The second is true negative (TN) rate, which is the ratio of the number of correctly identified sampling zeroes (dropouts) to the number of true dropouts. To measure imputation accuracy, we computed the Spearman correlation (COR)—our third criterion—between the imputed value and the corresponding underlying true mean value for those that are observed zeros. We further used the mean absolute error (MAE), our fourth main criteria, to measure imputation accuracy, which is the absolute difference between the predicted value and the corresponding underlying true mean value, again for those that are observed zeros. Note that for those classified as structural zeros, their corresponding predicted values are 0; whereas for those classified as dropouts, their predicted values are the imputed ones from the respective methods.
Results
K562 3D structures
The results for applying the methods listed in Table 1 to the simulated data from the underlying K562 3D structures are presented in Figure 2. In terms of correct identification of structural zeros, all methods performed well for all cell types across all sequencing depths and sample sizes (Figure 2A). Nevertheless, even though all methods have detection rate of above 85%, there are obvious separation among the methods in some settings. MAGIC and scRMD performed the best across the board, and especially with larger sample sizes and higher sequencing depth. In terms of correct identification of dropouts, the performance is a much greater mix (Figure 2B). McImpute and scImpute performed the best for all three cell types and across all sequencing depths and sample sizes. Although MAGIC performed as well in a couple of the settings, its performance dropped quite a bit in other settings, especially at sequencing depth 2K with a small sample size of 10 single cells. On the other hand, SCRABBLE had the worst performance, with correct identification rate falling down to zero in most settings (due to their low imputed values). The correlation between the imputed values and the true underlying mean values of the observed zeros are all above 0.75 for McImpute and scImpute, the best performers among the methods across all settings, with MAGIC and scRMD following not too far behind. However, the performance of SCRABBLE continued to be the worst overall, in fact with negative correlations in most of the settings (Figure 2C). Finally, evaluating imputation accuracy in terms of absolute difference between the imputed and expected, McImpute performed better (for the 4K and 2K scenarios) or at least as well (cell types 2 and 3) as the other methods across all settings except for cell type I with the 7k sequencing depth, in which it is clearly outperformed by MAGIC (Figure 2D). In addition to the means provided in Figure 2, we provide the corresponding standard deviations in Supplementary Table S1 to give further details.
Figure 2 .

Performance comparisons among several packages for the K562 structures. The comparisons are done for a combination of 27 settings, with factors including cell type (K562 T1, K562 T2 and K562 T3), sample size (10, 50 and 100 single cells) and sequencing depth (7K, 4K and 2K). (A) Proportion of true positives (TP; rate for identifying true structural zeros: larger value indicating better performance); (B) proportion of TNs (rate for identifying true dropouts: larger value indicating better performance); (C) Spearman correlation between predicted values and the underlying expected values (larger correlation indicating better performance); (D) mean absolute error (smaller value indicating better performance).
Helix 3D structure
The results for carrying out the same analyses as for the K562 structures are summarized in Supplementary Figure S1. The results are similar, by and large, to those from the K562 structures in terms of the relative performances of the different methods, but some minor discrepancies also exist. All methods performed well for structural zeros inference. Nevertheless, although all the other methods achieved a TP rate of close to 90% or above, the TP rate for SCRABBLE fell below 80% for several of the settings, especially for cell type 3. For correct identification of dropouts, scImpute and McImpute were the best performers. On the other hand, scRMD joined SCRABLE as having the worse performance, with close to 0 or practically zero TN rate for most settings. Reasonably high correlations are observed for McImpute and scImpute (between 0.5 and 0.75), but SCRABBLE produced mostly negative correlations between the imputed values and the true underlying mean values. For imputation accuracy, McImpute was the undisputed winners considering all settings, with MAGIC performing similarly well except for the low sample size (n = 10) scenarios. Numerical values of the means and corresponding standard deviations are provided in Supplementary Table S2.
Overall, considering the results from both kinds of 3D structures and taking all four main evaluation criteria into consideration, McImpute had the most stable performance across all simulation settings, including the 3D structures, cell types, sequencing depths and sample sizes. scImpute had a stable performance comparable with McImpute in terms of structural zeros and dropout identifications, but lagged behind McImpute for imputation accuracy. Nevertheless, given its consistent performance in all the considered 3D structures and simulation models, which are different from the scImpute analysis model, it appears that scImpute, the only model-based method among those investigated here, is insensitive to model misspecification, at least for those considered here. On the other hand, MAGIC performed reasonably well, especially for identifying structural zeros, but its performance was more sensitive to sequencing depth and sample size. The performance of scRMD was similar to MAGIC, but more stable. Finally, SCRABBLE had the worst performance among all the packages evaluated for their effectiveness of analyzing scHiC data.
McImpute versus McImpute-Block
Considering all 54 simulation settings, McImpute is seen as the top performer or near the top for all evaluation criteria; therefore, we were interested in further investigating whether the addition of the CUT step, which carves out more highly spatially correlated blocks for separate analysis, would further improve its performance. To better evaluate block choices, we chose a larger segment (250 loci) of the three K562 structures to simulate scHiC data, following the same parameter settings in Table 2A. The results based on the same four evaluation criteria are presented in Figure 3. As can be seen from Figure 3A and B, McImpute-Block has much greater ability for correct identification of dropout events compared to McImpute regardless of the block sizes; however, McImpute-Block has a bit lower rate of detecting the underlying structural zeros, especially for those with smaller block sizes, for all three types of single cells. These results are not surprising, as correct identifications of structural zeros and dropouts are usually negatively correlated. In particular, with the addition of the CUT step, we allowed each block matrix to have its own latent factors, which decreased the sparsity of the predicted overall matrix, leading to a lower TP and a higher TN. The Spearman correlations between the predicted and the true underlying expected values for both McImpute and McImpute-Block are similar, although the latter is a little bit better for K562 T1 and T3 (Figure 3C). The estimation accuracy, on the other hand, is much improved with McImpute-Block, especially for small to moderate block sizes (Figure 3D)—again, not surprising given the spatial correlation of neighboring counts within each block when the CUT step is activated. The corresponding standard deviations, in addition to the means shown in Figure 3, are provided in Supplementary Table S3. In summary, for this simulation, we observed that the addition of the CUT step for a wide range of block sizes (especially for blocks with moderate sizes, say 50–100) can lead to a significant reduction in correct identification of dropouts and estimation accuracy, due to the utilization of correlated information while cutting down the noise of uncorrelated ones outside of the block.
Figure 3 .

Performance comparison between McImpute and McImpute-Block for the three K562 structures. (A) TP; (B) NP; (C) Spearman Correlation (Jitter plot to avoid overlaps) and (D) mean absolute errors, all as described in the legend of Figure 2. The three cell types, K562 T1, K562 T2 and K562 T3, are as described in Table 2A. The sample size is 10 single cells of each type.
Clustering
Although we have considered several criteria for evaluating the effectiveness of using scRNA packages for imputing scHiC data, the question of whether downstream analysis is improved with imputed data for scHiC analyses remained unanswered. To address this, we considered clustering results before and after imputation, as the importance and accuracy of clustering is an issue often considered in scRNA analysis [11,15] and tackled by a number of scHiC methodologies, including HiCRep [8]. We applied the K-means clustering algorithm with Euclidean distance to the data before imputation, after imputation with scImpute and with McImpute (two of the best performers evaluated), and after data quality improvement (smoothing step) using HiCRep. Ten cells from each of the three types of single cells of sub-K562 3D structures with 15 loci and around 75% observed zeros were generated following the same settings of 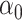 ,
, 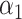 ,
, 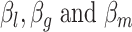 in Table 2A. We chose the sub-K562 structures at this level of zeros so that the k-means clustering algorithm would have trouble correctly separating the three cell types (see Supplementary Figure S2 as an example). Our results of misclassification rate and the adjusted rand index (ARI, a number between 0 and 1 measuring clustering consistency with the known grouping, with 1 being in complete agreement [18]), presented in Figure 4, are based on 100 replications. Several observations are apparent from the results. First, the median misclassification rate is among the highest, and the ARI for measuring agreement is among the lowest, before imputation. Second, the two imputation methods investigated in this paper, scImpute and McImpute, greatly improve the quality of clustering, evidenced by the smaller misclassification rate and larger ARI’s: over 75% of the replicates have zero misclassification rates and over 50% have an ARI of 1. On the other hand, data after HiCRep imputation did not lead to obvious improvements for the scenario considered, although extreme outliers were avoided after imputation.
in Table 2A. We chose the sub-K562 structures at this level of zeros so that the k-means clustering algorithm would have trouble correctly separating the three cell types (see Supplementary Figure S2 as an example). Our results of misclassification rate and the adjusted rand index (ARI, a number between 0 and 1 measuring clustering consistency with the known grouping, with 1 being in complete agreement [18]), presented in Figure 4, are based on 100 replications. Several observations are apparent from the results. First, the median misclassification rate is among the highest, and the ARI for measuring agreement is among the lowest, before imputation. Second, the two imputation methods investigated in this paper, scImpute and McImpute, greatly improve the quality of clustering, evidenced by the smaller misclassification rate and larger ARI’s: over 75% of the replicates have zero misclassification rates and over 50% have an ARI of 1. On the other hand, data after HiCRep imputation did not lead to obvious improvements for the scenario considered, although extreme outliers were avoided after imputation.
Figure 4 .

Clustering results before imputation and after imputation with three methods for data generated from the three K562 structures. Shown are results based on 10 singles cells from each of the three cell types. (A) Boxplots of misclassification rate of the three underlying cell types using the K-means algorithm. The dots (100 total) representing the individual misclassification rates for the 100 replicates are superimposed on the boxplot. (B) Boxplots of ARI (the larger the value the better performance) for measuring correct clustering of the three underlying cell types using the K-means algorithm. The dots (100 total) representing the individual ARI for the 100 replicates are superimposed on the boxplot.
Whole genome study
We applied each of the four algorithms—MAGIC, McImpute, scImpute and scRMD—to each of the whole genome datasets generated from the three K562 3D structures. We did not consider SCRABBLE in this analysis because it was shown not to be competitive in the above investigations. First, we explored the possibility of analyzing the entire genome. We were able to run McImpute and scRMD on the entire dataset for each K562 structure; the input matrix was of approximate dimensions 3,650,000 X 10, where the 10 columns represent the 10 single cells of a K562 structure, and the number of rows corresponds to the number of pairs of approximately 2700 loci in the genome. However, we were not successful in running MAGIC nor scImpute on a Linux machine with the following specifications: Intel(R) Xeon(R) CPU E5–2690 v3 @ 2.60GHz; RAM:128 GB. Next, we considered our Algorithm-Block methods, where Algorithm can be any of the four methods named above, and the block size was set to be 100 for all analyses. This time, all methods were able to run successfully, with their performance evaluated by the same four criteria used above (results are presented in Supplementary Figure S4). Comparing among the Algorithm-Block methods, one can see that the results are qualitatively the same as those from the 61-loci study. First, all methods achieved very high TP: over 99% of structural zeros were correctly identified by all methods. In terms of correct identifications of dropouts (TN) and correlation (COR) between expected and imputed for sampling zeros, scImpute and McImpute are superior to MAGIC and scRMD, the same as what we observed for the 61-loci results. Finally, McImpute outperformed the other methods in terms of accuracy (MAE) in estimating the interaction counts for the sampling zeros, which again is consistent with the 61-loci results. For McImpute and scRMD, since results are available for the whole genome analysis without the need to cut the 2D contact matrix into blocks, we also plotted the results on the same figure (Supplementary Figure S4) for comparison. For McImpute, results from the whole genome analysis were inferior to those from McImpute-Block. In particular, none of the dropouts were correctly identified, leading to a TN of 0 and the unavailability of COR (thus, COR was unavailable in Supplementary Figure S4). For scRMD, the difference between whole and block are not that drastic, but overall, scRMD-Block slightly outperformed the other. These results are consistent with our motivation for designing the additional CUT step in conjunction with the scRNA-seq imputation algorithm for analyzing scHiC data, as spatial correlations in the 2D contact matrix are much better utilized. The numerical values on the means and the corresponding standard deviations are provided in Supplementary Table S4.
As described in the earlier investigation on the block size, we shew that McImpute-Block generally improves the performance of dropout identification and estimation accuracy. Although the improvement on dropout identification appears to be irrespective of block size, improvement on estimation accuracy decreases as block size increases, although there are still appreciable gains in estimation accuracy even with moderate (but on the larger end) block sizes (e.g. block size = 100) compared to results without the CUT step. This latter observation is important, as there is a trade-off between block size and computational efficiency. For McImpute and scRMD, analyzing the entire genome without cutting is in fact more efficient (Table 3) than with the corresponding Algorithm-Block methods with a block size of 100. With an even smaller block size of say 50, then the computational time will further increase because there are now more blocks (about quadruple the number of blocks) to analyze separately. On balance, we recommend using a moderate block size (50–100) for whole genome analysis, keeping it on the lower end if computational power permits. As a comparison, Table 3 also presents the computational times for MAGIC-Block and scImpute-Block, which are an order of magnitude higher (in the thousands of seconds compared to the hundreds). Note that for these two methods, the computational time is prohibitively large without the CUT step. In summary, it is seen that matrix decomposition/completion methods (McImpute and scRMD) are much faster and can handle high-dimensional data. In contrast, modeling-based approach such as scImpute or methods requiring traditional manipulations with the entire matrix (e.g. MAGIC) may not be amenable for large dimensional matrices, but their Block version is a way of providing a feasible solution for whole genome analysis.
Table 3.
Time and memory requirementa for analyzing whole genome scHiC data
| Methodb | Time | Memory |
|---|---|---|
| MAGIC-Block | 2704 s | <4Gb |
| McImpute-Block | 331 s | <4Gb |
| scImpute-Block | 2343 s | <4Gb |
| scRMD-Block | 156 s | <4Gb |
| McImpute | 170 s | 8.7Gb |
| scRMD | 132 s | 8.2Gb |
aThe computational time (in seconds) and memory are based on a Linux machine with the following specifications: Intel(R) Xeon(R) CPU E5-2690 v3 @ 2.60GHz; RAM:128 GB.
bBlock size of 100 was used for all Algorithm-Block methods. Further, for McImpute and scRMD, computational time was also provided for whole genome analysis without the CUT step.
Analyses of two scHi-C datasets
We illustrate the use of scRNA-seq imputation methods for scHiC inference with two publicly available datasets. In both applications, we demonstrated the improvement on clustering of single cells after inferring structural zeros and imputing dropouts. In the first application, we only chose a segment on chromosome 1 in our analysis since this limited information led to a substantial misclassification rate and an opportunity to demonstrate improvement after imputation. In the second application, we used the entire genome for our analysis. A number of single cells were misclassified in this dataset before imputation to improve data quality, even with information from the entire genome, thus also providing us an opportunity to illustrate the utility of the methods investigated in this paper.
Clustering of GM and PBMC single cells
We considered a single cell Hi-C dataset (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE117876) composed of two cell lines: lymphoblastoid (GM) and peripheral blood mononuclear cell (PBMC); we downloaded the data processed by hickit. Although 17 GM cells and 18 PBMC cells were listed in the database, only data for 14 of the 17 GM cells were downloadable, resulting in a total of 32 single cell datasets available for our analysis. Since cells of the same type are believed to be more similar, we were interested in understanding whether imputation improves the accuracy of grouping these 32 cells according to their cell types. To perform this assessment, we first selected 30 consecutive loci on chromosome 1 (summary statistics of their sequencing depths and percentage of observed zeros are given in Supplementary Table S4); the use of which led to a substantial misclassification rate (25%) and a poor ARI index (0.23) (Figure 5) before imputation. Specifically, one GM cell was classified with the PBMC cluster, while seven PBMC cells were classified with the GM cluster. From the figure, it can be seen that HiCRep does not improve the misclassification rate nor the ARI agreement index—with two misclassified GM and six misclassified PBMC cells. On the other hand, clustering using the data imputed by scImpute reduces the misclassification rates to 20% and improves the ARI to 0.371—with three GM cells classified with the PBMC cluster and three PBMC cells classified with the GM cluster. Finally, the clustering results from the data imputed with McImpute achieves the best result, with a misclassification rate of 6.25% (2 misclassifications), and an ARI of 0.758. The results show that scImpute and McImpute have significantly improved the clustering quality, whereas the results after HiCRep imputation remain the same, consistent with the results presented in the simulation study.
Figure 5 .

Clustering results (misclassification rate and Adjusted Rand Index) before imputation and after imputation with three methods for 32 scHiC datasets composed of two types of cell: lymphoblastoid (GM) and PBMC.
Clustering of brain prefrontal cortex cells
In our second application, we considered the scHiC data produced by a recent single-nucleus methyl-3C sequencing technique that simultaneously captures both DNA methylation and 3C data [23]. Single cell Hi-C data are available for over 4000 single human brain prefrontal cortex cells (https://github.com/dixonlab/scm3C-seq) [23]. In total, 14 cortical cell subtypes were identified from the DNA methylation data by first identifying non-neuronal cells with CG methylation and then further subclustering neuronal cells with non-CG methylation. We considered two analyses with the data.
In the first analysis, we focused on two subtypes: L6 (an excitatory neuron subtype, 86 single cells) and NN1 (non-neuronal cell type 1, 100 single cells) to illustrate the utility of the scRNA-seq imputation methods using whole genome data. Among the 186 single cells considered, we were able to identify 2158 common loci at the 1 MB resolution (we removed all loci that did not interact at all with any other loci in the genome. Before imputation, one L6 cell and one NN1 cell were misclassified out of the total of 186 cells using K-means. Given that McImpute is able to handle genome-wide data without difficulty and appears to perform better, or at least as well as other methods consistently, we only applied McImpute to make inference about structural zeros and impute the dropouts. With the improved data, K-means was able to find two clusters, with all 86 L6 cells in one cluster and all 100 NN1 cells in another cluster, resulting in no misclassification, an improvement over results before applying McImpute.
In the second analysis, we considered a much harder problem. In the original analysis of the data [23], eight neuronal subtypes were all clustered together based on scHi-C data without imputation. In particular, L4 and L5 are two excitatory neuronal subtypes among the eight, but they are located in different cortical layers. Our analysis before imputation showed that 58 (44%) of the L4 cells and 88 (49%) of the L5 cells were misclassified, representing an overall misclassification rate of 0.469. After imputation using McImpute, the number of misclassified cells reduce to 48 for L4 and 69 for L5, resulting in a misclassification rate of 0.376, a 20% reduction.
Discussions
In this paper, we adapted and evaluated several single cell RNA-seq imputation methods—McImpute, scImpute, MAGIC, scRMD and SCRABBLE—for their effectiveness in imputing dropouts and identifying structural zeros for single cell Hi-C contact matrices. Due to the spatially correlated nature of Hi-C contact matrices, we also evaluated McImpute-Block, a modification of the McImpute algorithm by applying an extra CUT step to divide a contact matrix into spatially (more homogeneously) correlated blocks before applying McImpute to each block (i.e. the submatrices). An extensive simulation study was performed varying a number of factors, leading to a total of 54 settings. Among the various factors considered was the underlying 3D structure, for which we considered two diverse settings: a set of three structures recapitulated based on three K562 single cells using a recent single cell 3D reconstruction method, and a helix model utilized in previous studies in the literature. It was observed that the adapted McImpute algorithm was effective in structural zeros inference and in imputation accuracy for dropout events. scImpute also performed well in most of the simulation settings, but was not as consistent as McImpute and tended to be less accurate in the imputed values. MAGIC and scRMD also performed well in some of the evaluation criteria. On the other hand, SCRABBLE underperformed in all aspects compared to the other methods adapted and investigated. We further carried out another study to investigate the practical utility of the adapted methods for analyzing whole genome scHiC data. Our results show conclusively that the CUT step is recommendable for whole genome analysis, either for computational efficiency (for scImpute and MAGIC) or for improved performance (McImpute) by taking spatial correlation in neighboring contact counts into consideration. As long as the block size is moderate (50–100 for whole genome analysis), the results are robust, non-sensitive and computationally efficient. Although there may be potential boundary effects (i.e. those on the boundary of a block would benefit less from spatial correlations with their neighbors), we did not see substantial problems in our study. One way to lessen the potential boundary effect is to use a sliding-window approach, but this would lead to a substantial increase in the number of blocks and thus greater computational demand.
It is surprising to see that the only method that can utilize bulk data, SCRABBLE, did not perform as well as one would expect based on scRNA studies. One possible reason might be that its default parameter settings that are suitable for scRNA imputation may not be appropriate for scHiC imputation. Therefore, the fact that the utilization of additional bulk data did not help improves the performance of a method does not necessarily imply that bulk data are not useful. Further studies are needed to fully understand the operational characteristics of SCRABBLE for making inferences on scHiC observed zeros.
Although the ability to separate structural zeros from sampling zeros (dropouts) are extremely important for downstream analysis, among the methods adapted for scHiC data, MAGIC and SCRABBLE do not explicitly provide a criterion for making such an inference. To adapt them for scHiC data, we considered a natural threshold of 0.5, which is also used by some other methods (McImpute and scRMD): imputed values less than 0.5 were treated as structural zeros whereas those greater than 0.5 were treated as the imputed dropout values. This threshold is ‘natural’ because interaction counts on a 2D matrix are whole numbers; therefore, a number less than 0.5 would be rounded to 0 whereas a number greater than that would be rounded to a positive integer. However, other threshold values may be considered, as setting this threshold is really an act of compromise between the correct identification of structural zeros and dropouts: a larger threshold generally leads to a higher proportion of correct identification of structural zeros at the expense of correctly identifying dropouts, and vice versa, as we illustrated in Supplementary Figure S3. Nevertheless, since the threshold of 0.5 appears to be a good compromise for most of the variety of settings in our simulation study, we would suggest using such a value in data applications, as we have done in our real data analysis.
The effectiveness of the McImpute method for statistical inference on the observed zeros in scHiC data is also seen through two real data analyses to separate cell types, GM and PBMC in one study and L6 and NN1, L4 and L5, in another study. Processing data with the adapted McImpute algorithm clearly improved the correct clustering of the single cells in both studies. In the first application, although scImpute was also seen to lead to improved separation of GM and PBMC cells compared to the results before imputation, the improvement was not as great as that of McImpute. Interestingly, for HiCRep, a method proposed specifically for improving HiC data quality, its performance on clustering was not as good as the two adapted methods proposed for scRNA data. Nevertheless, demonstrating the effectiveness of some of the adapted scRNA imputation methods for scHiC data is not, in anyway, a substitute for the need to develop methodologies tailored for scHiC data, as appropriate utilization of the unique features of scHiC data, as demonstrated in McImpute-Block, can lead to improvement in imputation accuracy. Finally, although we focus on single cell clustering as a downstream analysis to demonstrate improved performance after imputation, there are other aspects of HiC research that can be used to evaluate improved performance, including calling of topologically associated domains and loop identification, but these are not within the scope of the current paper.
Key Points
Observed zeros happen in large proportions in single cell Hi-C data; however, how to deal with such data is a difficult problem that has not received adequate attention in the literature.
The problem of large proportions of observed zeros also happens in single cell RNA-seq data, but unlike in the single cell Hi-C situation, plenty of methods have been proposed in the literature to sort observed zeros into structural zeros and dropouts, with efficient algorithms for imputing the values for the latter.
We adapted and evaluated several methods from the single cell RNA-seq literature for their effectiveness in making inferences for observed zeros in single cell Hi-C data.
For a large number of simulation scenarios and real data, a couple of the adapted single cell RNA-seq algorithms show consistent and effective performance for correctly identifying structural zeros and accurately imputing dropout values.
Downstream analysis using the imputed values from the adapted methods has demonstrated considerable improvement for clustering cells of the same types together over clustering results before imputation.
Supplementary Material
Acknowledgements
The authors would like to thank two anonymous reviewers for their constructive comments and suggestions.
Chenggong Han and Qing Xie are both graduate students in the Interdisciplinary PhD Program in Biostatistics at the Ohio State University.
Shili Lin is a Professor in the Department of Statistics and the Interdisciplinary PhD Program in Biostatistics, and an affiliated member in the Translational Data Analytics Institute at the Ohio State University.
Contributor Information
Chenggong Han, Ohio State University.
Qing Xie, Ohio State University.
Shili Lin, Translational Data Analytics Institute at the Ohio State University.
Funding
The National Institutes of Health (grant 1R01GM114142-01).
References
- 1. Wu AR, Neff NF, Kalisky T, et al. Quantitative assessment of single-cell RNA-sequencing methods. Nat Methods 2014;11:41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Wang S, Su J-H, Beliveau BJ, et al. Spatial organization of chromatin domains and compartments in single chromosomes. Science (80-) 2016;353:598–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Zhang L, Zhang S. Comparison of computational methods for imputing single-cell RNA-sequencing data. IEEE/ACM Trans Comput Biol Bioinforma 2020;17:376–89. [DOI] [PubMed] [Google Scholar]
- 4. Lieberman-Aiden E, Van Berkum NL, Williams L, et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science (80-) 2009;326:289–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Zhou J, Ma J, Chen Y, et al. Robust single-cell hi-C clustering by convolution- and random-walk–based imputation. Proc Natl Acad Sci U S A 2019;116:14011–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Carstens S, Nilges M, Habeck M. Inferential structure determination of chromosomes from single-cell hi-C data. PLoS Comput Biol 2016;12:e1005292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Kaul A, Davidov O, Peddada SD. Structural zeros in high-dimensional data with applications to microbiome studies. Biostatistics 2017;18:422–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Yang T, Zhang F, Yardımci GG, et al. HiCRep: assessing the reproducibility of hi-C data using a stratum-adjusted correlation coefficient. Genome Res 2017;27:1939–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Ursu O, Boley N, Taranova M, et al. GenomeDISCO: a concordance score for chromosome conformation capture experiments using random walks on contact map graphs. Bioinformatics 2018;34:2701–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Zhang Y, An L, Xu J, et al. Enhancing hi-C data resolution with deep convolutional neural network HiCPlus. Nat Commun 2018;9:750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Li WV, Li JJ. An accurate and robust imputation method scImpute for single-cell RNA-seq data. Nat Commun 2018;9:997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Dijk D, Sharma R, Nainys J, et al. Recovering gene interactions from single-cell data using data diffusion. Cell 2018;174:716–729.e27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Chen C, Wu C, Wu L, et al. scRMD: imputation for single cell RNA-seq data via robust matrix decomposition. Bioinformatics 2020;36:3156–61. [DOI] [PubMed] [Google Scholar]
- 14. Hsu D, Kakade SM, Zhang T. Robust matrix decomposition with sparse corruptions. IEEE Trans Inf Theory 2011;57:7221–34. [Google Scholar]
- 15. Mongia A, Sengupta D, Mcimpute MA. Matrix completion based imputation for single cell RNA-seq data. Front Genet 2019;10:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Peng T, Zhu Q, Yin P, et al. SCRABBLE: single-cell RNA-seq imputation constrained by bulk RNA-seq data. Genome Biol 2019;20:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems. Computer (Long Beach Calif) 2009;42:30–7. [Google Scholar]
- 18. Urdinguio RG, Torró MI, Bayón GF, et al. Longitudinal study of DNA methylation during the first 5 years of life. J Transl Med 2016;14:160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Eckhardt F, Lewin J, Cortese R, et al. DNA methylation profiling of human chromosomes 6, 20 and 22. Nat Genet 2006;38:1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Flyamer IM, Gassler J, Imakaev M, et al. Single-nucleus hi-C reveals unique chromatin reorganization at oocyte-to-zygote transition. Nature 2017;544:110–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Xiao G, Wang X, Khodursky AB. Modeling three-dimensional chromosome structures using gene expression data. J Am Stat Assoc 2011;106:61–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Hu M, Deng K, Qin Z, et al. Bayesian inference of spatial organizations of chromosomes. PLoS Comput Biol 2013;9:e1002893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Lee D-S, Luo C, Zhou J, et al. Simultaneous profiling of 3D genome structure and DNA methylation in single human cells. Nat Methods 2019;16:999–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


