Deep-joint-learning analysis model of single cell transcriptome and open chromatin accessibility data

Abstract

Simultaneous profiling transcriptomic and chromatin accessibility information in the same individual cells offers an unprecedented resolution to understand cell states. However, computationally effective methods for the integration of these inherent sparse and heterogeneous data are lacking. Here, we present a single-cell multimodal variational autoencoder model, which combines three types of joint-learning strategies with a probabilistic Gaussian Mixture Model to learn the joint latent features that accurately represent these multilayer profiles. Studies on both simulated datasets and real datasets demonstrate that it has more preferable capability (i) dissecting cellular heterogeneity in the joint-learning space, (ii) denoising and imputing data and (iii) constructing the association between multilayer omics data, which can be used for understanding transcriptional regulatory mechanisms.

Introduction

The rapid development of single-cell sequencing offers an unprecedented resolution to study complex biological systems or processes, including cancer, immune system and cellular differentiation [1–3]. With the advancement of the scalable methods for single-cell RNA sequencing (scRNA-seq), such as 10X Chromium, and Smart-seq2 [4], technologies for measuring other molecular types, i.e. single-cell chromatin accessibility sequencing (scATAC-seq) [5], DNA methylation [6], proteomics [7] and metabolomics [8] have been developed. More recently, technological innovations allow for measuring multiple types of molecules in the same individual cell, such as sci-CAR-seq [9], scCAT-seq [10] and SNARE-seq [11]. The resulting single-cell multiomics data potentially provide richer information associated with cell states beyond the transcriptome [12]. That is to say that multiomics data can capture complementary but converging information about a cell.

Gene expression is regulated through a set of transcription factors (TFs) binding to its cis-regulatory genomic regions. scRNA-seq characterize the gene expression level of a cell, and epigenomic changes such as scATAC-seq reflect the openness of cis-regulation elements in the nearby genes. The integration of such two-omics data can provide new insights regarding the regulatory layers associated with cellular heterogeneity [13]. Many integration tools have been designed for bulk data [14]. For example, MOFA, a generalization of principal component analysis (PCA), was proposed to process bulk data, and also can be applied to single-cell datasets [15]. IntNMF, an extension of non-negative matrix factorization (NMF), was developed to integrate multiomics data for disease subtype classification, and was evaluated to handle single-cell datasets [16, 17]. However, recent research has found that single-cell data has its unique characteristics, different from bulk data, and thus novel methods are required to be developed [18].

Integration of single-cell multiomics data is still a great challenge due to the inherent highly sparse, great heterogeneity because of assaying noise, the great dimensional difference between scATAC-seq and scRNA-seq data, about 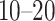times [19], and increasingly large-scale datasets [20]. A large number of methods have been developed for scRNA-seq data integration, however, only a few methods were proposed for integrating single-cell multiomics data, and these methods were developed for the omics data collected from different cells but drawn from the same cell population [21–24]. For example, Coupled MMF was proposed to perform clustering of scRNA-seq and scATAC-seq data through constructing a coupled non-negative matrix for the gene and cis-regulatory elements [23]. MATCHER was proposed to predict correlation between scRNA-seq and scATAC-seq by using Gaussian process latent variable models to infer pseudotime for each cell [24]. Recently, Seurat (version 3) [25] and LIGER [22] were developed for integrating scRNA-seq and scATAC-seq data. Both of these methods firstly transform the scATAC-seq data into gene activity data like gene expression data and then identify anchors between the scRNA-seq data and gene activity data through aligning each other in the low-dimensional space. However, the alignment efficiency between two-omics/two-layer-omics data often requires similar clustering performance from both measurements. It is hard to define cell clusters through scATAC-seq data due to its extremely sparsity property (i.e. over 99% zeros in sci-CAR-seq). Hence, this improper alignment for these two methods likely affects the downstream analysis.

Deep generative models have emerged as a powerful framework to model the high-dimensional data [26, 27]. Particularly, VAE, which learns low-dimensional features from the input data by an encoder, and recovers the input data by a decoder, this can be done by maximizing the likelihood between recovered data and input data, and minimizing the Kullback–Leibler (KL) divergence between learned latent features and true posteriors. Recently, single-cell variational inference (scVI) adapting a standard VAE was proposed to analyze scRNA-seq data [26]. However, a standard VAE uses a single isotropic multivariable Gaussian distribution over the latent variables and often underfits the sparsity data [28]. SCALE adapting a VAE that uses Gaussian Mixture Model (GMM) as the prior over the latent variables was proposed to analyze scATAC-seq data, the analysis results indicate that the framework integrating VAE and GMM can be used to process highly sparsity data and learn a more disentangled and interpretable latent features [27]. Recent rapid development of deep-learning multimodal technologies [29, 30] and successful application in integrating multiview biological data [31], demonstrate their great potential to solve the difficulty of the current analysis on single-cell multiomics data.

Here, we proposed single-cell multimodal variational autoencoder (scMVAE) for the integrative analysis of scRNA-seq and scATAC-seq data that are measured from the same single-cell by using three types of joint-learning strategies. scMVAE model uses stochastic optimization and multimodal encoder, firstly to aggregate the two-omics data across similar cells and features to approximate the joint latent features to where GMM is prior, and then to reconstruct the observed expression values by a decoder per omics data while accounting for the normalization of each type of data, which can be trained for very large datasets. In particular, through joint-learning of two-omics data in an unsupervised manner, scMVAE model (i) yields biologically meaningful low-dimensional features that simultaneously represent both these multilayer profiles, allowing cell visualization and clustering; (ii) denoises and imputes two-omics data; and (iii) constructs the association between two-layer data, which can be used to infer the new regulatory relations. To demonstrate its efficiency, we applied scMVAE model and other integration methods to both simulated and real datasets, which demonstrated that scMVAE model performs more favorably than current state-of-the-art methods.

Methods

scMVAE probabilistic model

scMVAE models the distribution of scRNA-seq and scATAC-seq from the same cell through three joint-learning strategies: PoE inference network (detailed in Material S1), neural network, and direct concatenation of features of two-omics data (Figure 1A–C). To balance the large dimensional difference between scRNA-seq and scATAC-seq data, we converted the peak level count matrix of scATAC-seq data to the gene activity data like gene expression values of the scRNA-seq data, and modeled each omics data drawn from one zero-inflated negative binomial (ZINB) distribution. Specifically, given the 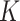clusters, the joint-learning features 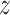could be obtained through the multiomics encoder network via the reparameterization, and 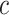is a categorical variable whose probability is discrete. 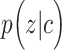is a mixture of Gaussians distribution parameterized by mean value vector 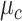and covariance matrix 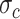conditioned on 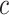. 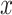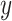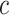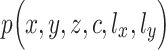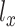Considering that , and are independently conditioned on z, then the multimodal joint learning distribution where and 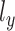are one-dimensional Gaussian variables that serve as the library size factors of scRNA-seq and scATAC-seq data, respectively, can be factorized as:

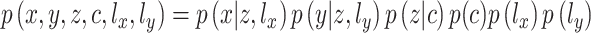Figure 1 .

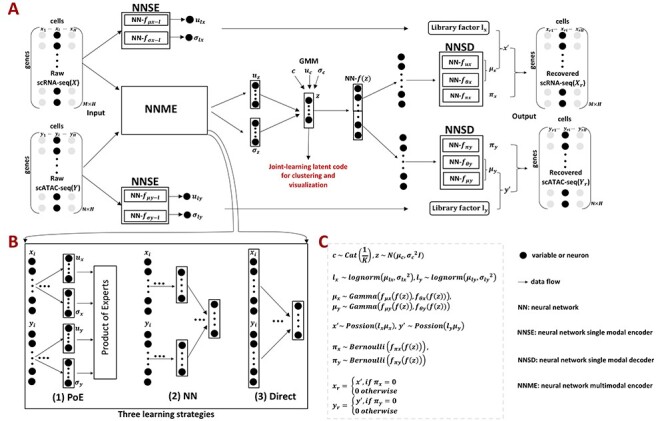
Overview of scMVAE model with three joint-learning strategies. (A) Overall framework of the scMVAE model. Given the scRNA-seq data (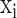 with 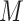variables) and scATAC-seq data ( 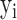with 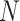variables) of the same cell 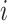as input, the scMVAE model learned a nonlinear joint embedding (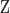) of the cells that can be used for multiple analysis tasks (i.e. cell clustering and visualization) through a multimodal encoder with three learning strategies described as (B), and then reconstructed back to the original dimension as output through a decoder for each omics data. Note: the same cell orders for both omics data ensure that one cell corresponds to a point in the low-dimensional space. (B) Illustration model of three learning strategies: (i) ‘PoE’ framework was used to estimate the joint posterior by a product of posterior of each omics data (detailed in Material S1), (ii) ‘NN’ was used to learn the joint-learning space by using a neural network to combine the features extracted by a sub encoder network for each layer data and (iii) ‘Direct’ strategy was used to learn together by directly using the concatenation of the original features of two-layer data as input. Here, the neural networks: 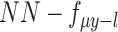, , 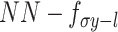, , 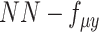, 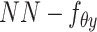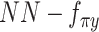were removed from the total network under this learning condition. (C) The distribution to where each variable of scMVAE model belongs. Each omics data were modeled as one ZINB distribution. The detailed description for each variable is given in datasets and preprocessing.

Each factorized variable defined as follows:

, .

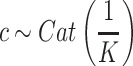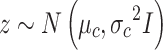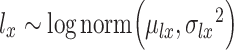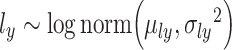Besides, each gene expression level f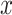or or 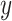was independently from the following generation process:

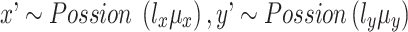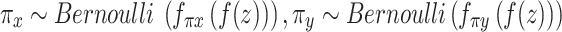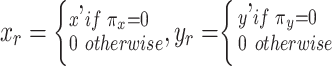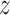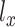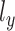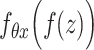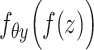GMM prior to is used in MVAE to generate highly realistic samples by learning more disentangled and interpretable latent representations, which has been applied to the scRNA-seq and scATAC-seq in the previous work separately [27, 32]. and are regarded as the log-normal distribution that is expected to be strongly correlated with the empirical log-library size. and indicate the feature-specific inverse desperations that are estimated by the variational Bayesian inference. Neural network 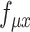and 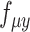are constrained during the inference to encoder the mean proportional genes expressed across all genes in one cell by the use of the ‘softmax’ activation function at the last layer, for the scRNA-seq and scATAC-seq data, respectively. Neural network 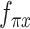and 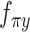encoder whether each gene has been dropped out because of the capturing efficiency and sequencing depth, by using the ‘sigmoid’ function at the last layer, for each of two-omics data.

The training of scMVAE model is to maximize the log-likelihood of the observed scRNA-seq and scATAC-seq data, however, since this is intractable, the evidence lower bound (ELBO) is instead optimized:

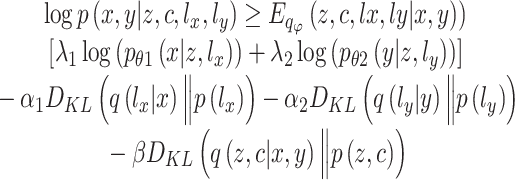Two reconstruction terms and regularization terms of KL divergence associated with library size factor 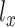and 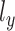were encouraged to do the data normalization, denoising and imputing. The KL divergence for the latent variable 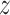was used to regulate it to be a GMM manifold, to enhance the association with multiomics data. The parameters 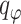, 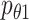and 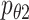are the multimodal encoders, a decoder for scRNA-seq, and scATAC-seq data, respectively.

All neural networks use dropout regularization and batch normalization. Each neural network has one or two fully connected layers, with 128 or 256 nodes per layer. The activation functions between two hidden layers are ‘relu’ function. The Adam optimizer with a 1e⁻⁶ weight decay is used to maximize the ELBO. The scMVAE model is implemented with the pytorch package, among them, GMM is constructed with the Python scikit-learn package. Source code is available at the GitHub repository: https://github.com/cmzuo11/scMVAE.

Datasets and preprocessing

Real data

Two datasets including paired profiles used in our study were generated by the SNARE-seq technology [11]. Specifically, (i) the cell line mixture dataset consisting of 1047 cells is derived from mixtures of cultured human BJ, H1, K562 and GM cells; to check if our model is robust with the sparsity data, we randomly dropout out nonzero values of two-omics data to zero value, with the proportion ranges from 0.1 to 0.3, thus generating nine datasets; (ii) the AdBrainCortex dataset including 10 309 cells is derived from the adult mouse cerebral cortex. Besides, 549 cells derived from the human HCT116, HeLa-S3, K562, PDX1 and PDX2 cell lines generated by scCAT-seq technology [10] were used to validate our method.

Simulated data: three simulated dataset with paired profiles generated by the following strategy: (i) a scRNA-seq data with two clusters of cells was simulated by Splatter [33], with the following parameters: batchCells = 3000, nGenes = 200, dropout.type = experiment, dropout.mid = 5, dropout.shape = −1, de.prob = 0.3; and a scATAC-seq data consisting of 3000 cells and 500 peaks (nPeaks = 500) were generated by the following pipeline: the peaks formed two clusters, with each cluster consisting of 250 specific peaks; and these specific peaks had a value of 1 or 2 (ratio 1:4) in the cells of the corresponding clusters, and 0 in other cells. The noised data were further generated from real data by randomly dropping out nonzero values by 0.75, and followed by setting the zero values to 1 or 2 (ratio 1:4) by 0.2; (ii) a scRNA-seq data with three clusters was simulated by the same parameters as (i) but with nGenes = 500, the dropout ratio for nonzero values of scATAC-seq data is 0.7, and the noise ratio for zero values is 0.25; and (iii) a scRNA-seq data with four clusters was simulated by the same parameters as (i) but with nGenes = 600, and the dropout ratio for nonzero values of scATAC-seq data is 0.5 and noise ratio for zero values is 0.4, as well as nPeaks = 600 with each cluster containing 300 specific peaks.

Preprocessing: the features of scRNA-seq and scATAC-seq data of the cell line mixture datasets expressed in at least 1% of cells were firstly kept; the peak level count matrix data were collapsed into ‘gene activity matrix’ by the simplifying assumption that a gene’s activity can be quantified by summing all counts within the gene body 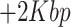upstream, by the ‘CreateGeneActivityMatrix’ function in the Seurat; and then Laplace score method [34] was used to order features for each omics data based on its power on preserving data local structure, evaluated by Pearson correlation between cells, respectively. For the efficiency of the scMVAE and other compared methods, the top 500 features per omics data were selected for the input of the method. For the AdBrainCortex dataset, same processing strategy was used to deal with two-omics data, but the top 3000 features per data were selected for the method comparison. Besides, the same processing method was used to handle two-omics data of scCAT-seq technology, and the top 500 features per data were selected for the input of the compared methods.

Visualization and clustering

The uniform manifold approximation and projection (UMAP) algorithm from uwot R package was applied to map the raw data and extracted latent features to two-dimension, and then the ‘Dimplot’ and ‘FeaturePlot’ functions from the Seurat were used to visualize the cell embedding and gene expression level between different cell population. Additionally, ‘K-means’ from the Python package ‘scikit-learn’ was used to cluster the cells based on the extracted low-dimensional features. The random seed 200 was set to repeat the result.

Evaluation of clustering results

The Rand Index (RI) quantifies the clustering similarity between two classifications by considering matched and unmatched assignment pairs independent of the number of clusters. The Adjusted RI (ARI) score is calculated by considering grouping by chance with RI by

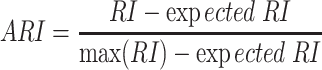The ARI score ranges from 0 to 1, with 0 indicating random labeling and 1 indicating completely matching.

Normalized mutual information (NMI)

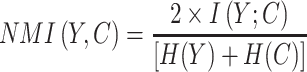Where 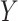and 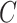are categorical distribution for the real class and predicted cluster labels, 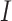is the mutual entropy function and H is the Shannon entropy function.

Evaluation of clustering results for the real datasets

We defined the clustering score to evaluate if the predicted cell clustering dissects the real cellular heterogeneity. Specifically, we created the contingency table based on two clustering methods: classification of each cell based on whether its expression level of 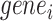(i.e. known marker gene for one cluster) is larger than 0 or not; and classification of each cell predicted by each computational method. Fisher exact test was used to test if these cells expressing 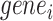were significantly enriched in cluster_m. The cluster_m is considered as cell population expressing gene_j if the corresponding P-value < 0.05. Here, the formula 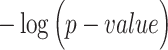is regarded as the clustering score.

Besides, we applied the Gini-index (GI) [35] based measure to quantify a cluster-specific score by considering the association between marker gene and cell clustering. Specifically, the average of each marker and housekeeping gene were calculated for each cluster; the GI for each gene including marker gene and housekeeping gene was calculated by the ‘gini’ function from reldist [36]; and then the fold-change between GI per each marker and the average of that of all housekeeping genes as the AGI to evaluate the specific level of each marker gene for a cluster cluster_m. The higher AGI score, the better the cell clustering.

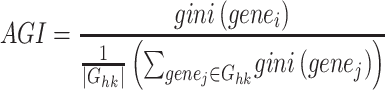where G_hk indicates the gene set of the housekeeping genes that are downloaded from the previous study [37], and 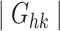is the number of housekeeping genes. Also, we applied this metric to evaluate the quality of denoised scRNA-seq data, by considering the information of marker genes, housekeeping genes and cell clustering predicted by the latent features that are extracted from the compared computational methods.

Evaluation of consistency between two-omics data

Kappa coefficient, a statistical measure to test the reliability of interrater, is used to assess the consistency between cell clusters predicted by each omics data [38]. Specifically, we applied the Seurat to assign cell cluster for each recovered omics data, and then used ‘Kappa.test’ function from fmsb [39] to calculate the kappa coefficient between two cell assignments. Calculation of Cohen’s kappa can be performed as follows:

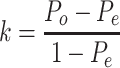Where 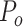indicates the actually observed consistency between two raters, and P_e indicates the hypothetical probability of chance consistency.

Pearson and Spearman correlation methods were used to assess the similarity level of the same gene from each denoised omics data. Besides, the known transcriptional regulations between TFs and target genes (TGs) of human and mouse were downloaded from the TRRUST v2 database [40] to biologically interpret the similarity of two denoised data by assessing how much these denoised data can recover these known relations between TFs (indicated by scRNA-seq) and TGs (indicated by scATAC-seq). Here, the correlation of each regulation larger than 0.3 is regarded as it is recovered.

Prediction and validation of transcriptional regulatory relationships

We adopt the following steps to predict the relations between TF and TG. (i) We identify TF motifs enrichment in each locus based on the raw scATAC-seq data by chromVAR [41], with the default parameters. Note that we focused on the 70 689 loci covered by 3000 genes on AdBrainCortex dataset. (ii) We infer a possible TF–TG pair if a TF can bind to at least one loci of a TG. (iii) We calculate the Pearson correlation between each TF (indicated by scRNA-seq) and TG pair (indicated by scATAC-seq), and determine if each pair significantly happens based on the empirical test: a 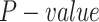of the correlation of each TF–TG pair can be estimated by comparing it with the correlation of randomly selected gene pairs, 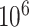times, and the 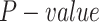of each pair less than 0.05 is regarded as it is a final prediction of the regulations.

We validate the predicted TF–TG pairs with RegNetwork database [42], a comprehensive set of experimentally observed and predicted transcriptional regulatory relationships, in the following way. Specifically, regarding 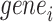among all 128 TFs collected in the chromVAR, 98 TFs are founded in RegNetwork, 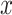of which regulate 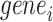among our identified 12 TFs using chromVAR, and 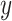of which regulate 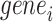. The fold-change enrichment 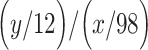for 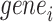larger than 1 is regarded as our predicted TF–TG pairs, which are over-represented in the RegNetwork database.

Prediction of cluster numbers K

For each omics data, we followed SC3 [43] method to determine the suitable cluster number 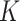, by the following steps: (i) calculating the eigenvalues of 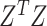, where 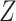is the z-score matrix of the raw count matrix; (ii) determining 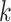based on the number of eigenvalues that are significantly different from the Tracy-Widom distribution with mean and s.d. [44]. The minimum value of 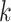for multiomics data is regarded as the final predicted cluster number.

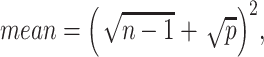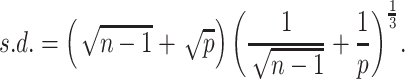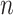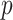Where and indicate the number of genes and cells, respectively.

Results

scMVAE model for joint-learning single-cell multiomics data

scMVAE model combines the MVAE and the GMM to model the joint-learning distribution of two-omics data from the same individual cells, by using three learning strategies (Figure 1A–C). To balance the large dimensional difference between two-omics data, we converted scATAC-seq data to the gene activity data, and modeled each of these two datasets drawn from a ZINB distribution, as used in the previous study [45]. Specifically, we modeled the observed gene expression data 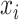(from scRNA-seq data 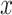) and gene activity data 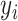(from scATAC-seq data y) in the same cell i drawn from a generative model of the form 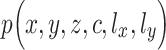, where 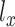and 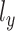are different one-dimensional Gaussian variables that serve as the cell-specific normalized factors of scRNA-seq and scATAC-seq data, respectively; the joint-learning features 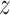is a low-dimensional latent vector representing remaining variation of these multilayer profiles, which is used to represent each cell as a point in the low-dimensional space, to do the visualization and clustering; and 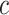is one specific clustering pattern of cells with 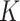clusters, or one of the components of GMM over 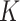clusters. Since z is conditioned on c, and x and y are independently conditioned on z or f(z), 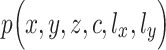can be written as 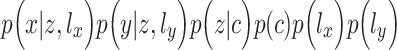, where 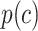is a discrete distribution of 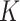clusters, 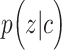follows a mixture of Gaussian distribution with a mean vector 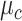and a covariance matrix 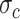for each clustering pattern c. In our work, we used three types of strategies to transform two-layer omics data (x_i,y_i) of each cell 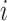to the d-dimensional vector of latent features z_i on the manifold learned by a multimodal encoder network, to construct the complex association between two-layer data, and then mapped the latent features through two decoder networks back to the original dimensionality to represent both omics data of each cell, respectively (Figure 1A–C).

Model evaluation and comparison on the simulated multiomics datasets

We compared the scMVAE model with several benchmark methods for visualization and clustering using three simulated two-omics datasets, which was generated by Splatter and an in-house program, respectively. Available cell labels as the ground truth were used to evaluate the clustering result. Specifically, we simulated three datasets of 3000 cells containing two, three and four cell types, with different sparsity and separation for scRNA-seq data and scATAC-seq data, respectively (Figure 2A, Figure S1A). By default, scMVAE and scVI extract 10 features from the input data. We also applied the MOFA to reduce the input data to the 10 features, but only one feature was retained after running the software. We then visualized these features extracted by these tools with the top two factors: principal components (PCs) or UMAPs, as well as raw data as a comparison. Besides, Seurat was used to process each omics data as follows: extracting top 10 PCs, and then reducing these PCs to two-dimensions for visualization. Since IntNMF needs the predefined cell cluster number, we preset it to two, three and four, respectively. In summary, each cell type was assigned almost by different feature embeddings from scMVAE, compared to MOFA, IntNMF and all other single-omics methods, especially for the complex scenarios, which indicates that the nonlinear joint-learning of multiomics data from the same cell can capture more useful feature representation than that from linear joint-learning PCA or NMF, and single-omics method; MOFA and IntNMF perform better than single-omics methods in the simple scenario, but reversely on the complex dataset, which indicates that the linear joint-learning method cannot efficiently detangle the complex relationship between two-omics data; and the embeddings inferred by the PoE and NN strategy were almost different from one cell type to another, compared to those by the shallow direct concatenation, particularly in the complex conditions (Figure 2A).

Figure 2 .

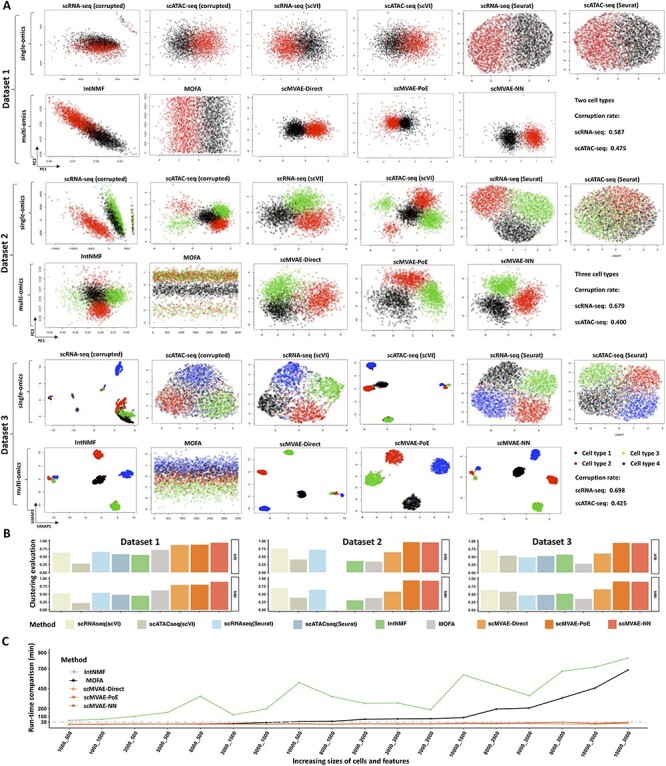
Visualization, clustering and run-time comparison on the simulated datasets. (A) Dot plot of the top two factors (PCs for Dataset1 and 2; UMAPs for Dataset 3) extracted from each of corrupted omics data of three simulated datasets, and latent features extracted by single-omics methods: scVI and Seurat for each omics data (upper layer for each dataset), and joint-learning latent features extracted by IntNMF, MOFA and scMVAE model, respectively (lower layer for each dataset). Cells are colored by their true cell types. For each dataset, the final subplot indicates its corruption rate of each omics data. (B) Clustering accuracy was evaluated by ARI and NMI between true cell label and predicted cell cluster by single-omics methods: scVI and Seurat; and multiomics methods: IntNMF, MOFA and scMVAE model, respectively, for each of three simulated datasets. (C) Run-time comparison for fitting four models on the 18 simulated datasets which were generated by randomly selected different sizes of cells and features from AdBrainCortex datasets with 3000 features per omics data. Algorithms were tested on a machine with one 40-core Intel(R) Xeon(R) Gold 5115 CPU addressing with 132GB RAM, and two NVIDIA TITAN V GPU addressing 24GB.

We then applied K-means clustering on the latent features extracted by above computational methods, and assessed their clustering accuracy based on the ARI and NMI by comparing predicted cell clusters with the ground truth. Note: the default method in Seurat was used to predict cell clusters for each omics data. The results show: scMVAE performs better than MOFA, IntNMF and all single-omics methods, except that scMVAE-Direct performs worse in the complex scenarios; MOFA performs better than IntNMF and all single-omics methods, but worse than those in the complex conditions (Figure 2B). Additionally, these original count data for each technology were used to validate the recovery accuracy. We calculated the correlation of recovered data and original data by spearman correlation for each method (Figure S1B), which shows that scMVAE performs best.

To assess the scalability of training, we randomly subsampled 18 datasets with different sizes of cells and genes from AdBrainCortex dataset of about 10 000 mouse brain cells [11]. To facilitate the comparison with state-of-the-art algorithms for modeling of the single-cell multiomics data, we limited the maximum number of variables for each omics data to the 3000 variables selected by Laplace score. We found that all methods were able to process those big data, but scMVAE performs faster compared to MOFA and IntNMF (Figure 2C), thanks to its reliance on a fixed number of cells at each iteration of iterative stochastic optimization. It is emphasized that scMVAE can get the optimal solution converged at most 30 min across all simulated datasets, but MOFA and IntNMF both reach 700 min, increasing with the size of cell or feature.

scMVAE captures cellular heterogeneity in the joint-learning latent space

We next evaluated the extent to which the latent features inferred by scMVAE characterize biological variability between cells. By default, scMVAE model extracts four-dimensional features from the original cell line mixture datasets with paired profiles. For comparison, we also applied single-omics methods: PCA and scVI to separately map the scRNA-seq and scATAC-seq data to four dimensions, and two-omics methods: CCA, IntNMF and MOFA to simultaneously map two-omics data to four dimensions, and then visualized these four-dimensional features as well as raw data with UMAP. In summary, the feature embeddings extracted by multiomics methods except IntNMF were better separated between cell types than those by single-omics methods, scMVAE and MOFA perform better than CCA; and the features extracted from scRNA-seq by any single-omics method perform better than those from scATAC-seq data, which indicates that scRNA-seq data have richer information about cell state compared to scATAC-seq data (Figure 3A and B).

Figure 3 .

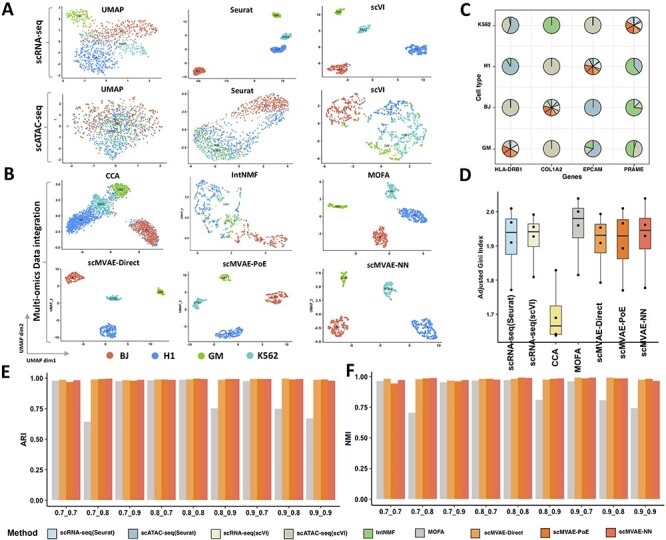
Feature embedding and clustering comparison on the original cell line mixture datasets. (A) UMAP visualization of the raw data and features separately extracted from scRNA-seq (upper layer) and scATAC-seq (lower layer), by Seurat and scVI, respectively. (B) UMAP visualization of the extracted features from the multiomics method: CCA, IntNMF, MOFA and scMVAE model. (C) Clustering accuracy was evaluated by clustering score between cell cluster predicted by nine computational methods (i.e. Seurat, scVI (scRNA-seq), IntNMF, MOFA, CCA, scVI (scATAC-seq) and scMVAE model) and cell assignments based on whether each cell expresses one marker gene. Each subpie plot shows the clustering score of nine methods for each cluster, and ideally, it is distributed on the diagonal. X and Y axis indicate marker genes and cell clusters, respectively. (D) Clustering accuracy was evaluated by AGI score based on the clustering assignment predicted by computational methods (i.e. Seurat, scVI, MOFA and scMVAE model) and the expression level of marker gene and housekeeping genes. Note: the higher the score, the better the clustering performance. (E) Clustering accuracy was assessed by ARI to compare different methods under the nine datasets with different sparsity levels of scRNA-seq and scATAC-seq data. (F) Clustering accuracy was assessed by NMI to compare different methods under the nine datasets with different sparsity levels of scRNA-seq and scATAC-seq data.

We then applied the K-means clustering on the low-dimensional features extracted by scMVAE model and assessed the clustering performance by comparing the results with the single-omics method: scVI and Seurat for each omics data, separately, and two-omics method: MOFA, IntNMF and CCA. Due to the lack of the ground truth for the real data, we evaluated clustering accuracy by clustering score and AGI. The results show that the multiomics methods (except IntNMF) perform better than single-omics methods, and the CCA method has poor performance when integrating two-omics data simultaneously (Figure 3C and D). Besides, 1004 cells of the cell line mixture datasets (96%) have the same cell type annotation based on the prediction of MOFA and scMVAE, and are kept for further comparison.

Finally, by generating nine datasets, the nonzero values of two-omics data of 1004 cells randomly dropped out to zero with ranging from 10% to 30% were used to test whether scMVAE is robust with the sparsity data. For comparison, we used the same deep-learning structure of our scMVAE model to process these nine datasets. ARI and NMI were applied to compare the clustering accuracy between scMVAE and MOFA. We found that scMVAE has a stable and higher clustering accuracy than MOFA under various combinations of scRNA-seq and scATAC-seq sparsity data (Figure 3E and F).

Besides, we noted that scMVAE and MOFA accurately capture the cellular variability of multiomics data generated from scCAT-seq technology, but IntNMF cannot (Figure S2A); and the clustering accuracy based on ARI and NMI of scMVAE and MOFA is significantly higher than that of IntNMF (Figure S2B), which indicates that there are some specific properties of single-cell that bulk multiomics methods cannot capture efficiently.

Additionally, motivated by the recent study [46], we benchmarked the influence of the ZINB and NB distribution on two cell line mixture datasets from two technologies (Figure S2A and B, Figure S3A–C), found that the clustering accuracy difference between ZINB and NB distribution is generally small (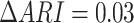, 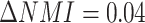for scCAT-seq data, 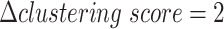for SNARE-seq data), and scMVAE model with ZINB distribution performs slightly better than NB distribution on SNARE-seq, but slightly worse than scCAT-seq data. Hence, we implemented both distributions in our code to improve its adaptability. We also observed that ZINB or NB distribution with GMM prior performs slightly better than Gaussian prior on the cell clustering (Figure S2A and B, Figure S3A–C).

We further investigate if our clustering estimated method can find suitable clusters on the real datasets (Methods). The results show that the estimated clusters are close to that of the references, clustering results are similar to the reference sets, feature embeddings are not influenced by the cluster numbers, and cell clustering and feature embeddings of scMVAE model with ZINB or NB distribution, GMM and Gaussian priors are not influenced by the cluster number (Figure S4A–C and S5A–C).

scMVAE model significantly enhances the consistency between two-omics data on the denoised datasets compared to original noisy datasets

An important feature for scMVAE is the ability to enhance the consistency between two-omics data which usually have very low correlation due to inherent highly sparse, great heterogeneity resulting from assaying noise. This estimation of scMVAE could be used to denoise each data and enhance the consistency between two-omics data by using the joint learning of two-omics data. We compared the consistency of cell clustering between two-omics data of cell line mixture datasets of SNARE-seq denoised by scMVAE model, CCA, MOFA and each scVI model for each omics data, as well as the raw data. All these denoised data come from the same model as used in scMVAE captures cellular heterogeneity in the joint-learning latent space. The similarity of cell clustering is assessed by Kappa coefficients. Generally, the interrater reliability between two denoised omics data learned by deep-learning models is higher than other methods; scMVAE is better than scVI model that processes each omics data separately, which indicates that deep-joint-learning models can construct the association between different modalities data; and the Kappa coefficients of MOFA was the same with raw data, which indicates that MOFA is unable to denoise or improve the raw multiomics data in this case (Figure 4A, Figure S6).

Figure 4 .

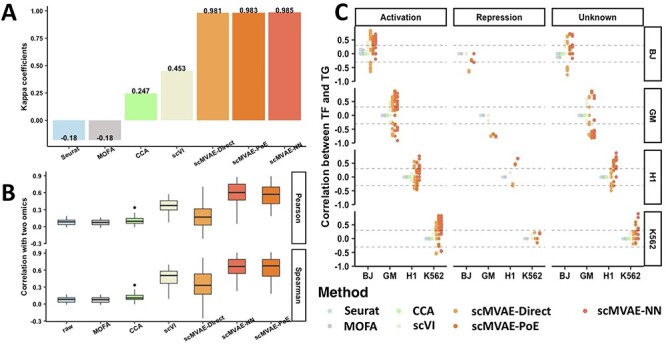
Consistency of clustering and features between two-omics data on the denoised cell line mixture datasets by scMVAE. (A) The consistency was evaluated by the Kappa coefficient between the clustering assignment of two-omics data denoised by MOFA, CCA, scVI and scMVAE model, as well as raw data. (B) Features similarity was assessed by Pearson and Spearman correlation between two-omics data denoised by MOFA, CCA, scVI and scMVAE, as well as raw data. (C) Pearson correlation between known TF–TG pairs of two-omics data denoised by MOFA, CCA, scVI and scMVAE model, as well as raw data.

Next, we applied the correlation methods including Pearson and Spearman to evaluate the similarity of the expression level of the same genes of two denoised omics data. In summary, the correlation between two denoised data learned by deep-learning models is significantly higher than that by other models; and among them, the correlation of scMVAE model with scMVAE-NN and scMVAE-PoE strategies are significantly higher than scMVAE-Direct, which is consistent with the previous study that this shallow model scMVAE-Direct with the concatenation of the original features of two-layer data as input is hard to construct the associations between different modalities [47]; and the correlation of CCA is higher than MOFA; and the correlation of MOFA model is the same with raw data (Figure 4B), which is consistent with the conclusion about cell clustering as Figure 4A.

Besides, we check whether two denoised omics data learned by scMVAE model can reflect real transcriptional regulations. Specifically, we calculated the Pearson correlation between a TF quantified by scRNA-seq data and a TG quantified by scATAC-seq data within each cell cluster. The results show that scMVAE model with two strategies: scMVAE-NN and scMVAE-PoE can identify 100% of known TF–TG pairs [40]; scMVAE-Direct and scVI can identify 87% and 53% of total known pairs; but the correlations by CCA and MOFA are almost as the same as raw data, which indicates that scMVAE can construct the associations between the modalities by the way of joint-learning (Figure 4C).

Finally, we tested whether scMVAE model is robust to improve the consistency between the modalities under the sparsity data, which is evaluated based on the same dropout out datasets as used in Figure 3E and F. After processing each data by MOFA and scMVAE model, we compared the similarity of cell clustering and expression level between these methods. The results show that scMVAE model has a more stable and higher consistency than MOFA between two denoised omics data under nine combinations of scRNA-seq and scATAC-seq data (Figure S7).

Similarly, scMVAE can improve the consistency of two-omics data of scCAT-seq technology (Figure S2C). Besides, we noted that the consistency differences between ZINB and NB distribution (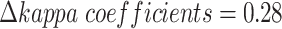 for SNARE-seq, 0.005 for scCAT-seq), and between GMM and Gaussian prior ( 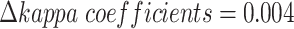for SNARE-seq, 0.05 for scCAT-seq) are generally small (Figure S2C, and S3D), and the differences of feature similarity of two-omics data denoised by scMVAE model with ZINB or NB distribution, GMM and Gaussian priors are generally small (Figure S2D and S3E). Additionally, the consistency between two denoised data is not influenced by the estimated cluster number 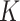(Figure S4D and S5D).

scMVAE model is scalable to the large-scale real dataset

We further examined AdBrainCortex dataset of 10 309 cells with two-omics data to investigate whether scMVAE model works for large datasets [11]. The study inferred nine main cell types with 22 finer subtypes by using the graphic clustering on the scRNA-seq data. By default, scMVAE model extracts 22 features from the input data. For comparison, we applied single-omics methods: PCA and scVI to separately map each omics data to 22 dimensions, and two-omics methods: CCA, IntNMF and MOFA to simultaneously map two-omics data to 22 dimensions, and then used the UMAP to reduce these 22-dimensional features as well as raw data to two-dimensional features for visualization. To facilitate the comparison with the clusters defined by the previous study, we used the same clustering method with the study to define cell clusters for each scRNA-seq data denoised by the scVI, MOFA, and scMVAE model, as well as raw data. Due to the lack of the real cell type from the literature as a benchmark, we did the same clustering assessment as the cell line mixture dataset. Overall, most of the major reference clusters have a corresponding one identified by the scMVAE model, nevertheless, some small and highly similar subtypes defined by the previous study are combined into one group. That is because we adopt a novel strategy to select high-information features for further analysis, and six markers (Pvalb, Vip, Pdgfra, Rgs5, Vtn, Kdr) corresponding to five subtypes defined by this study were removed out due to their expression proportion among all cells less than 1% (ranging from 0.19% to 0.64%).

In summary: (i) the feature embeddings extracted by scMVAE and MOFA models were better separated between different cell clusters, compared with other methods (Figure 5A), but of which scMVAE was better than MOFA, which indicates that joint latent features extracted by our nonlinear scMVAE model cover more information than those by the generalized linear MOFA model; (ii) the clustering score between scVI for scRNA-seq and scMVAE model for multilayer data is more similar than other methods, but the feature embeddings extracted by scMVAE model are better separated than scVI (Figure 5A and B), which indicates that the joint-learning scMVAE model accurately captures two-layer information; (iii) the IntNMF model works worst in integrating two-layer data (Figure 5A); (iv) the clustering score between scMVAE (with GMM prior) with ZINB and NB distribution is basically same, but the feature embeddings of ZINB distribution are better than that of NB distribution (Figure S8A–C); (v) the clustering score of scMVAE (with either ZINB or NB distribution) with GMM is higher than that with Gaussian prior, also the feature embeddings of GMM prior are better than that of Gaussian prior, which indicates that the GMM prior constraints on the latent code can help scMVAE to learn more disentangled and interpretable latent representations on the complex dataset (Figure S8A–C); and (vi) scMVAE-PoE model seems to perform better than scMVAE-NN, and scMVAE-NN performs better than scMVAE-Direct, either GMM or Gaussian prior, ZINB or NB distribution (Figure S8A–C).

Figure 5 .

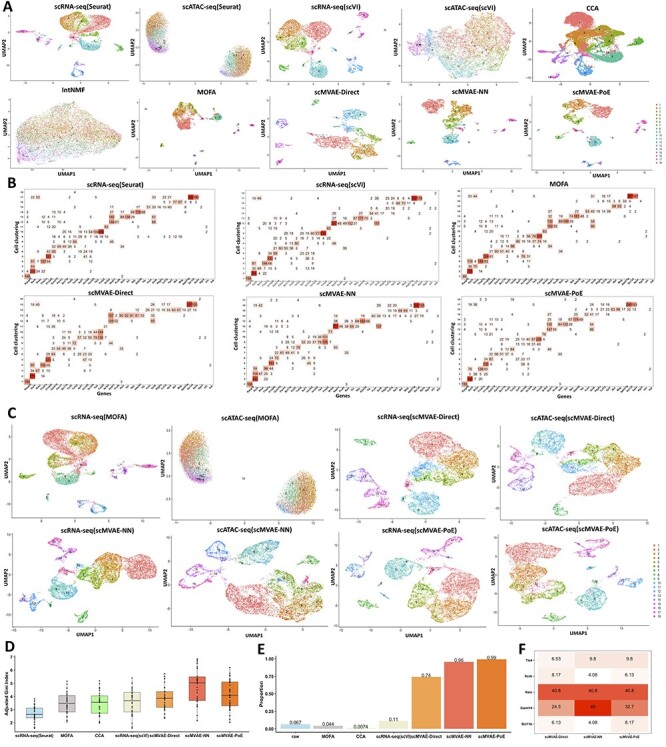
scMVAE model works well on AdBrainCortex (a large dataset). (A) UMAP visualization of the latent features extracted by one-omics methods (i.e. Seurat and scVI) for scRNA-seq and scATAC-seq data, separately; and by two-omics methods (i.e. CCA, IntNMF, MOFA and scMVAE model) for multilayer data. (B) Clustering accuracy was evaluated by clustering score between cluster assignments predicted by computational methods and cell assignment based on whether each cell expresses a marker gene. (C) UMAP visualization of the denoised data from MOFA and scMVAE model. (D) Clustering and denoised quality were assessed by AGI score based on the cell clustering predicted by computational methods (i.e. Seurat, scVI, MOFA and scMVAE model) and gene expression level of marker gene and housekeeping genes denoised by these methods. (E) The proportion of 135 TF–TG pairs inferred by two-omics data denoised from scVI, MOFA and scMVAE, as well as raw data, by Pearson coefficients larger than 0.3 within at least one cell cluster. (F) Fold-change enrichment of the predicted regulations of known five marker genes, which are validated by the RegNetwork database.

Not surprisingly, feature embeddings of scATAC-seq data extracted by Seurat cannot clearly separate cell types annotated from scRNA-seq data by Seurat. However, the feature embeddings extracted by scMVAE are better separated between different cell clusters than other methods, which indicates that the scMVAE model can improve the quality of scRNA-seq and scATAC-seq data simultaneously. Additionally, the denoised data from MOFA have the same information as raw data in terms of clustering, which is consistent with the conclusion that MOFA is unable to denoise the data for clustering (Figure 5C).

Next, we evaluated the quality of two denoised data as follows: (i) the AGI score that was calculated by both clustering and denoised markers (also housekeeping genes) was used to evaluate the denoised quality (Figure 5D). The AGI score of scMVAE model is significantly higher than other methods including scVI for scRNA-seq, which indicates that scMVAE model can simultaneously improve the cell clustering and two-omics data denoising; (ii) the correlation of the same gene from two-omics data denoised by scMVAE model is significantly higher than other methods (Figure S9A); and (iii) scMAVE-NN and scMVAE-PoE model can recover more than 95% of the known transcriptional regulations between two denoised omics data whereas other methods only recover about 5% of relationships (Figure 5E, Figure S9B). These comparison results demonstrate that scMVAE model can be trained for large-scale datasets, with higher quality.

Finally, we further investigate the quality of the predictions of TF–TG pairs based on the denoised data by scMVAE (Methods). Totally, we inferred 8840 interactions between 12 TFs and 2440 TGs, 8422 interactions between 12 TFs and 2427 TGs, and 8429 interactions between 12 TFs and 2426 TGs from the data denoised by scMVAE-Direct, scMVAE-NN and scMVAE-PoE, respectively, and among them, regulations of 1626 (66.6%), 1607 (66.2%), and 1618 (66.7%) TGs are validated by RegNetwork database, respectively (Figures S10 and S11). For example, we observed that the regulations of five known marker genes: Rorb, Galnt14, Bcl11b, Tle4 and Reln, are over-represented in the RegNetwork database (Figure 5F).

Discussion

scMVAE model was proposed to analyze scRNA-seq and scATAC-seq measured from the same individual cells in a biological meaning manner, to account for its inherent highly sparse, great heterogeneity, by combining MVAE and GMM model, which can be scalable to large datasets. To our best knowledge, this is the first deep-joint-learning model for processing single-cell multiomics data.

By comparing the scMVAE with scVI that processes each omics data separately, we found that scMVAE model has a better performance in terms of denoising, imputation and the association between two-layer data, which is attributed to the subsequent mutual learning designed by our model after bottom layer of the scMVAE. Besides, the feature embeddings extracted by scMVAE model are better separated than scVI model for each omics data, which indicates that the joint-learning representation of multiomics data can yield a deeper and more useful representation.

Overall, we noted that scMVAE-NN and scMVAE-PoE strategies perform better than scMVAE-Direct, especially for the association between two-omics data. This is consistent with the conclusion from the previous study [47]. scMVAE-PoE and scMVAE-NN strategies have comparable performances on these analysis tasks, but the total network parameters of scMVAE-PoE are less than scMVAE-NN. With the rapid accumulation of large-scale single-cell multiomics data [48], scMVAE model can be easily adjusted to adapt it by adding the corresponding network for each omics data. Recently, many methods have been proposed to consider the specific properties for each data while integrating data from multiple sources [22]. Luckily, our scMVAE-PoE strategy is scalable and can disentangle omics-specific and modality-invariant factors for two-omics data [49].

Key Points

• A single-cell multimodal variational autoencoder (scMVAE) model was proposed to learn the joint latent features that accurately represent transcriptomic and chromatin accessibility profiles that are both measured in the same cell, to account for their inherent sparse and heterogeneous property;

• Studies on both simulated datasets and real datasets demonstrate that scMVAE has more preferable capability (i) dissecting cellular heterogeneity in the joint-learning space, (ii) denoising and imputing data and (iii) constructing the association between multilayer omics data, which can be used for understanding transcriptional regulatory mechanisms;

• With the rapid accumulation of large-scale single-cell multiomics data, scMVAE is scalable to easily process large and multilayer data.

Chunman Zuo is a post-doctor in the Key Laboratory of Systems Biology, Shanghai Institute of Biochemistry and Cell Biology, Center for Excellence in Molecular Cell Science, Chinese Academy of Sciences, Shanghai 200031, China. Her research includes computational biology, bioinformatics and machine learning.

Luonan Chen is a professor and executive director in the Key Laboratory of Systems Biology, Shanghai Institute of Biochemistry and Cell Biology, Center for Excellence in Molecular Cell Science, Chinese Academy of Sciences, Shanghai 200031, China; Hangzhou Institute for Advanced Study, University of Chinese Academy of Sciences, Chinese Academy of Sciences, Hangzhou 310024, China; and Center for Excellence in Animal Evolution and Genetics, Chinese Academy of Sciences, Kunming 650223 China. His interests include systems biology, computational biology, bioinformatics and applied mathematics.

Data availability

The datasets used in the study are available from the Gene Expression Omnibus (GEO) repository under the accession number: GSE126074 [11], and supplementary data of previous study [10].

Funding

This work was supported by National Key R&D Program of China (No. 2017YFA0505500), Priority Research Program of the Chinese Academy of Sciences (No. XDB38040400), the National Natural Science Foundation of China (Nos. 31930022 and 31771476), Shanghai Municipal Science and Technology Major Project (No. 2017SHZDZX01), and Shanghai Super Postdoctoral Fellow Program.

Conflict of interest: The authors declare that no conflict of interest exists.