Abstract
Due to the high cost of flow and mass cytometry, there has been a recent surge in the development of computational methods for estimating the relative distributions of cell types from the gene expression profile of a bulk of cells. Here, we review the five common ‘digital cytometry’ methods: deconvolution of RNA-Seq, cell-type identification by estimating relative subsets of RNA transcripts (CIBERSORT), CIBERSORTx, single sample gene set enrichment analysis and single-sample scoring of molecular phenotypes deconvolution method. The results show that CIBERSORTx B-mode, which uses batch correction to adjust the gene expression profile of the bulk of cells (‘mixture data’) to eliminate possible cross-platform variations between the mixture data and the gene expression data of single cells (‘signature matrix’), outperforms other methods, especially when signature matrix and mixture data come from different platforms. However, in our tests, CIBERSORTx S-mode, which uses batch correction for adjusting the signature matrix instead of mixture data, did not perform better than the original CIBERSORT method, which does not use any batch correction method. This result suggests the need for further investigations into how to utilize batch correction in deconvolution methods.
Keywords: deconvolution methods, digital cytometry, DeconRNASeq, CIBERSORT, ssGSEA, SingScore
Introduction
There are many players involved in the tumorigenesis and inflammatory processes triggered by cancer treatments, including necrotic cells, wild-type and mutant epithelial cells and immune cells such as dendritic cells (DCs), macrophages and T cells. It has been shown that prognosis is strongly correlated with the quality of immune reactions in tumors regardless of the stage of the cancer [1]. For instance, a high expression of Th17 markers is linked to poor prognosis in patients with colorectal cancer, whereas patients with high expression of the Th1 markers have improved survival [2].
In many cancers, including colon cancer, microbial antigens trigger and maintain an inflammatory response. For example, in some colon cancers, DCs are maturated by falsely recognizing commensals as pathogens. Mature or activated DCs promote differentiation of naive T cells into effector T cells and natural killer T cells [3]. Activated effector T cells stimulate macrophages by releasing pro-inflammatory cytokines, and activated pro-inflammatory macrophages produce IL-6, IL-12 and TNF-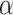
[4, 5], which promote the release of IL-6 by CD4
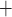T cells [6, 7]. The release of IL-6 by macrophages and CD4
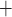T cells enhances tumor cells’ growth in colon cancer [8–10]. As a result, mutant and wild-type epithelial cells receiving proliferation signals compete to divide and take over the available empty spaces generated by treatments. The rate of occurrences of each of these reactions depends on the number of each cell type in the tumor. For this reason, the outcome of cancer treatments depend on the number and interaction networks of each cell type.
Many experimental approaches such as single-cell analysis tools (including immunohistochemistry, flow cytometry and mass cytometry) have been utilized to document tumor immune infiltrates. However, these methods are expensive and time-consuming [11] because they require laboratories, professionals and equipment. Obtaining the gene expression levels of a bulk of cells has become easier and cheaper thanks to new advances in high-throughput RNA-sequencing tools [12]. Therefore, several deconvolution methods (DMs) have been developed in recent years to estimate the relative abundance of each cell type in a bulk of cells, such as tumors, from their gene expression profiles. This process of digitally estimating the distribution of cell types from bulk gene expression data has also been referred to as digital cytometry [13].
In 2009, Abbas et al. [14] proposed estimating the percentage of cell types from microarray data with a linear model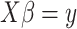 
. In this simple model, the vector 
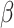is the percentage of each cell type in the mixture data 
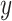and 
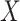is a signature matrix, in which each column is a reference expression vector of a cell type and the rows are genes. To get more robust results, in 2015, Newman et al. [15] used the machine learning technique of support vector regression (SVR) to estimate the vector 
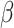. Additionally, score-based models that use the single-sample gene set enrichment analysis (ssGSEA) [16] and single-sample gene set scoring (SingScore) [17] methods have been developed. These methods use reference sets of genes that are upregulated and downregulated in each cell type, in place of a signature matrix, and use a rank-based metric to evaluate the relative enrichment of a gene set within mixture data. More recently, in 2019, Newman et al. [13] developed CIBERSORTx by extending their original CIBERSORT method with a batch correction step to eliminate the effect of cross-platform variations in data sets. Here, we provide a review of these five digital cytometry methods that have been used for tumor deconvolution.
Methods
There are two main categories of digital cytometry methods: linear models and rank-based models. Here, we review three common linear models—Deconvolution of RNA-Seq (DeconRNASeq) [18], CIBERSORT [15] and CIBERSORTx [13]—and two rank-based models [19], ssGSEA DM [16] and Single-sample Scoring of molecular phenotypes Deconvolution Method (SingScore) DM [17].
Linear models
Deconvolution of RNA-Seq
DeconRNASeq [18] treats the deconvolution task as a linear regression model with constraints on the model coefficients. This method assumes that the total expression level of a gene in a sample is the sum of all the expression levels of the given gene in all cells in the sample.
DeconRNASeq takes as input the gene expression profile of a sample tissue, called mixture data, and a ‘signature matrix’ where each column is a ‘typical’ gene expression of a cell type. The method outputs the fractions of each cell type included in the signature matrix for the given sample. The general formula for this model is given as
 |
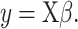(1) |
Here, 
denotes the observed gene expression level vector of a sample (mixture data), 
denotes the signature matrix where each column is the gene expression level of a specific cell type and 
is the vector of estimated proportions of cell types.
DeconRNASeq finds the estimated proportions of cell types (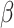
) by minimizing the following objective function:
 |
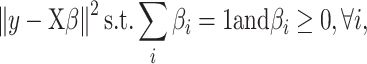(2) |
where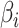 
is the estimated proportion of cell 
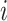in the sample. By minimizing this objective function, the linear regression model finds the coefficients that result in the smallest sum of squared difference between the observed and the predicted expression levels in the sample. The constraints are designed to make sure that the cell proportions are positive and add up to 
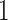. The optimization procedure is done using quadratic programming [20–22].
Cell-type Identification By Estimating Relative Subsets Of RNA Transcripts (CIBERSORT)
Like DeconRNASeq, CIBERSORT [15] assumes that the total expression level of a gene in a sample is the sum of expression levels of that gene in all the cells in that sample. CIBERSORT utilizes a machine learning technique called Support Vector Regression (SVR) for estimating cell proportions. Unlike linear regression, which tries to find the linear function that minimizes the sum of squared error, SVR tolerates a margin of error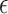 
and only tries to minimize the sum of absolute error of data points that lie outside this margin of error. In particular, CIBERSORT uses the 
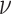-SVR algorithm for this task. The general formula for CIBERSORT is the same as DeconRNASeq (Equation (1)). Similar to DeconRNASeq, CIBERSORT takes mixture data and a signature matrix as input and returns the model coefficient 
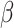as estimated fractions of each cell type in the sample. The only difference between these two methods is their optimization procedure; CIBERSORT finds 
by minimizing the following objective function:
 |
(3) |
s.t. 
and 
and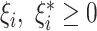 
. Here, 
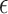is the margin of error and 
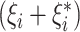is the absolute error of data points that lie outside the margin of error 
. 
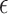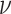is a model hyperparameter that gives an upper bound on the fraction of training error and a lower bound on the fraction of support vectors. Thus, the value of 
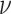is between 0 and 1.
Since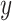 
is a linear combination of 
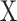(Equation (1)), CIBERSORT uses a linear kernel in 
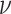-SVR. Unlike DeconRNASeq, CIBERSORT does not put any constraints on the model coefficient 
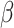during optimization, and there is no guarantee that elements of 
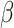will be nonnegative and add up to 1. Thus, after the optimization process, CIBERSORT sets any negative coefficients to 0 and then normalizes the coefficients such that they sum to 1.
CIBERSORTx method
Since the gene expression data sets can be collected through completely different experimental settings with the use of different experimentation plans, platforms and methodologies, there are undesired batch effects in the gene expression values. These technical variations can in some cases be as large as the biological variations between different cell types [23]. It has been shown that the ComBat algorithm [24] can effectively remove these unwanted variations from bulk RNA-Seq data [23]. Newman et al. [13] introduced CIBERSORTx, which extends CIBERSORT by adding batch correction using ComBat to address the possible cross-platform variations in gene expression data sets. CIBERSORTx introduces two strategies for batch correction: B-mode and S-mode.
CIBERSORTx B-mode. As in CIBERSORT, mixture datum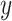 
is modeled as a linear combination of signature matrix 
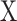and cell fractions 
.
 |
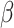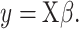The algorithm of CIBERSORTx B-mode is as follows:
Use CIBERSORT to obtain estimated fractions
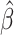from mixture data 
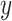and signature matrix 
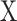.Create estimated mixture data
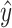, where 
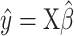.Use ComBat [24] to eliminate the cross-platform variation between
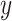and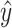 
, producing adjusted mixture data 
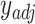.Use CIBERSORT to estimate final cell fractions
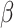from 
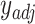and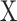 
.
CIBERSORTx S-mode. When the technical variation between signature matrix and mixture data is more severe, Newman et al. [13] recommend to use S-mode, which adjusts the signature matrix instead of mixture data. As input, S-mode requires the mixture data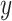 
and the set of single-cell reference profiles 
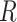from which the signature matrix 
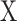was derived. 
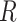consists of single-cell transcriptomes from different cell types, typically multiple transcriptomes per cell type. The gene expression profile of each cell type in 
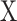is constructed by aggregating the corresponding single-cell transcriptomes in 
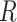. CIBERSORTx S-mode estimates cell fractions in the following way:
(1) Let
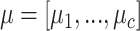be the fractions of each cell type from 
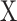in 
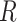and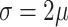 
.(2) Generate artificial cell fractions
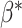by drawing from normal distribution 
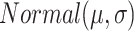.(3) Set negative values of
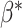to 0 and normalize 
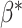so its components sum to 1.(4) Sample single-cell transcriptomes from
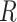according to 
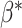and add them together to create artificial mixture data 
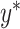.(5) Use ComBat [24] to eliminate the cross-platform variation between
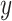and 
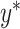, producing adjusted mixture data 
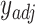and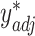 
.(6) Use nonnegative least squares to find
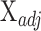that minimizes 
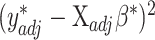such that 
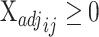for all 
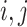.(7) Use CIBERSORT to estimate final cell fractions
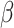from original 
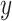and 
.
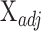Rank-based models
Single sample Gene Set Enrichment Analysis Deconvolution Method (ssGSEA DM)
All above-mentioned linear models rely on a signature matrix to deconvolve a bulk of cells using its gene expression profile. However, obtaining an accurate signature matrix is very challenging in practice because factors such as variations in experimental settings and laboratory measurements can bias the signature matrix [25]. Fortunately, the most highly expressed genes for any given cell type are usually consistent across different laboratories and conditions. The DM based on single sample gene set enrichment analysis (ssGSEA) only uses these highly expressed genes of each cell type, here called cell signatures or upregulated gene sets, instead of a signature matrix.
The ssGSEA method [25], which is a modification of gene set enrichment analysis (GSEA) [26], was developed in order to get an enrichment score for a single sample instead of two groups of samples. Here, we call the method developed by Senbabaoglu et al. [16], which utilizes the ssGSEA score specifically for the digital cytometry task, ssGSEA DM. This method takes mixture data and sets of highly expressed genes for each cell type as input and returns the enrichment score for each cell type. The algorithm of ssGSEA DM is as follows:
Order mixture data by absolute expression from highest to lowest.
Replace gene expression values in mixture data by their ranks.
- For each gene
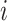, in the ordered rank data from step 2, compute the following: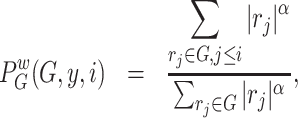 
(4)
where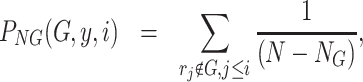
(5) 
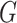is the given cell signature, containing 
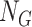upregulated genes, 
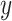is the mixture data, containing 
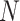genes, 
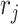is the rank of a gene 
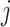, and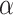 
is a parameter in 
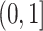. - The enrichment score for the sample
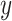and cell signature 
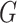is given by: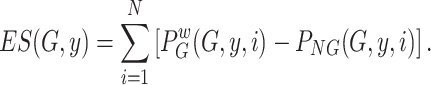 
(6)
The enrichment score of the cell signature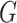 
tells us the relative fraction of the cell type with cell signature 
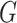. For example, assume T cells and B cells respectively have the cell signatures 
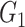and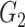 
. If the enrichment score of the cell signature 
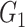is higher than the enrichment score of the cell signature 
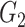, we conclude that the number of T cells is higher than the number of B cells in the mixture data.
SingScore DM
SingScore [17] stands for single-sample scoring of molecular phenotypes. Similar to ssGSEA DM, SingScore DM uses enriched gene sets instead of a signature matrix for performing digital cytometry. While ssGSEA DM only uses a set of upregulated genes for each cell type, SingScore DM has the option to use both upregulated and downregulated gene sets for each cell type. Thus, SingScore DM takes as input a set of upregulated genes and an optional set of downregulated genes for each cell type along with the mixture data and outputs a score for each cell type. The algorithm of SingScore DM is as follows:
Order mixture data by gene expression levels from highest to lowest.
Use the top half of genes in the sample as the up-set and the bottom half as the down-set. An important remark is that these up-set and down-set genes of the sample are different from the upregulated and downregulated gene sets of each cell type.
Rank these genes in ascending order for up-set and descending order for down-set.
- For a given cell type and its upregulated gene set
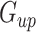and downregulated gene set 
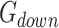, calculate the following:
where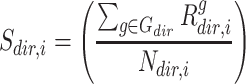
(7) 
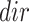is the gene set direction (up-/down-regulated), 
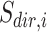is the score for sample 
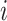against the directed gene set, 
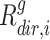is the rank of gene 
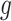in the directed set from the sample (up-set or down-set), 
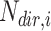is the number of genes in 
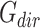that are observed within the mixture data. - Calculate the normalized score:
where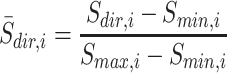
(8) 
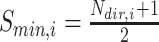and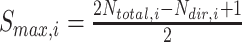 
- Calculate output score for sample i:
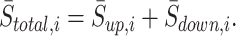
(9)
Similar to ssGSEA DM, the output scores of SingScore DM algorithm are the relative levels of each cell type in the sample, rather than the actual fractions.
Approach
To compare the performance of the above-mentioned methods on the deconvolution task, we generate simulation data with known mixing fractions and signal-to-noise ratio (SNR) ranging from 100:5 to 100:50 (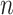
= 100 samples for each SNR). We use two different signature matrices: LM22 [15] and LM6 [27] for DeconRNASeq, CIBERSORT and CIBERSORTx. LM22 is derived from microarray data and consists of 547 gene expressions for 22 leukocytes, while LM6 is derived from RNA-Seq data and has 684 gene expressions for 6 leukocytes. These signature matrices are also used to derive the upregulated gene sets used for ssGSEA DM and SingScore DM. We note that the single-cell reference profiles needed to run CIBERSORTx S-mode are not available for the LM6 signature matrix; hence, this method is excluded from the LM6 results.
We construct the simulation data in the following manner: first, ‘known’ mixing fractions for a sample are obtained by drawing random numbers from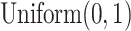 
and then normalized so that the fractions in a sample sum to 1. Mixture data are then formed by a linear combination of the LM22 source gene expression profile and the known mixing fractions, where LM22 source gene expression profile is the gene expression profile used to create LM22, before the gene selection step. Noise is induced to the simulation data by adding values drawn from 
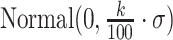, where 
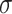is the global standard deviation of the original simulation data without noise and 
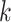is an integer. This results in an SNR ratio of 
:
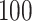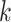for a given value of 
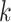. We create 10 sets of simulated data with 
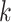chosen from 
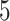to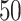 
, in steady increments of 
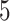, resulting in SNR ratios ranging from 
:
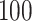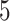to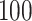 
:
.
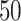It is conceivable to encounter mixture data that consist of more cell types than those available in the signature matrix. To test for each method’s robustness to this phenomenon, we delete a few cell types in the signature matrix LM22 and run all five methods using the simulated mixture data with two signature matrices: reduced LM22 and the original LM6.
We also apply these methods on two experimental data sets: whole blood RNA-Seq data with ground truth cell fractions estimated by flow cytometry (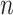
= 12) (available on Gene Expression Omnibus under the accession number GSE127813 [13]) and PBMC microarray data with ground truth fractions estimated by flow cytometry (
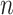= 20) (available on Gene Expression Omnibus under the accession number GSE65133 [15]). Although these data sets come from different platforms, we cannot make any conclusive statements that these methods perform better on RNA-Seq than on microarray data due to the limited availability of data sets with ground truth fractions. For each experimental data set, we run all five methods with the original LM22 and the original LM6.
To facilitate a fair comparison of the performance of the five DMs, we want the signature matrix used in linear methods to come from the same database as the gene sets used in rank-based methods. Thus, we use the data sources of LM22 to create upregulated gene sets for ssGSEA DM and SingScore DM by applying a method similar to [28]. First, we separate the samples in the single-cell reference profiles of LM22 into groups according to their cell type. For each gene, we calculate the difference between the minimum expression in the group of interest and the highest mean expression of all other groups. If this difference is greater than a threshold, we select this gene as an upregulated gene for the cell type of the analyzed group. We do this for every group to select the highly expressed genes in each cell type-specific group. We apply the same technique to derive upregulated gene sets from LM6. However, since we do not have access to the reference profiles of LM6, we apply this technique on LM6 itself. These gene sets derived from LM22 and LM6 are available for download on our GitHub page (see Data Availability section).
We ran the above digital cytometry methods using the following software:
DeconRNASeq package in R for DeconRNASeq,
CIBERSORT’s R source code for CIBERSORT,
CIBERSORTx’s website application for CIBERSORTx,
gsva package in R for ssGSEA DM,
SingScore package in R for SingScore.
Each of these methods has its own form of normalization in its algorithm. In ssGSEA DM and SingScore DM, the normalization is not applied on the input mixture data, and since input gene sets are only lists of gene names, no normalization can be applied here either. The only normalization in rank-based methods is applied on output scores at the end of the algorithm, thus making output scores nicer for visualization without changing the correlation of the predicted values with the ground truth fractions. On the other hand, CIBERSORT and CIBERSORTx use z-score normalization on their inputs (the signature matrix and mixture data) as a mandatory initial step in their software, and DeconRNASeq software provides an option to first standardize the input mixture data. The results of these linear models with normalization will differ from those without. CIBERSORT and CIBERSORTx also have optional quantile normalization on the input mixture data. This quantile normalization is recommended for microarray data but not for RNA-Seq data. Since the PBMC microarray data set has been previously normalized with the limma package in R, using ‘normexp’ background correction with negative controls [15], and the whole blood data set is RNA-Seq data, we use CIBERSORT and CIBERSORTx without quantile normalization in this study. For DeconRNASeq, ssGSEA DM and SingScore DM, we use normalization (which is the default setting for these methods).
We note that since rank-based methods output relative scores as opposed to frequencies, we cannot use traditional metrics such as mean square error to compare the performance of each method to the original data. Thus, we instead consider four different measures of correlation: Pearson correlation per sample, Pearson correlation per cell, Spearman correlation per sample and Spearman correlation per cell. Correlation per sample between estimated and true fractions tells us how well a method estimates the relative frequency of all cell types in a given sample, while correlation per cell tells us how well a method estimates the relative frequency of a given cell type between all samples.
Results
Analysis of simulation data
We create simulation data as described in the Approach section and apply each of the above-mentioned methods with both the reduced LM22 and the original LM6 signature matrices (or corresponding derived gene sets for rank-based methods). For all methods and signature matrices, the Pearson and Spearman correlation results are consistent with one another. With reduced LM22, the more noise is added to the data set, the lower the correlations observed between the ground truth fractions and the methods’ predictions, with the following exceptions: the sample-level correlation of DeconRNASeq, ssGSEA DM and SingScore DM does not vary much when the signal to noise changes (Figure 1A and B). For LM22, CIBERSORT and CIBERSORTx B-mode perform best on data with high signal to noise. The batch correction in CIBERSORTx does not appear to improve the method for this simulated data; however, we note that the simulated data and signature matrix are both derived from LM22, and therefore, there should not be any cross-platform variation to eliminate. Interestingly, DeconRNASeq with reduced LM22 performs just as well as CIBERSORT and CIBERSORTx when the noise level is high.
Figure 1 .
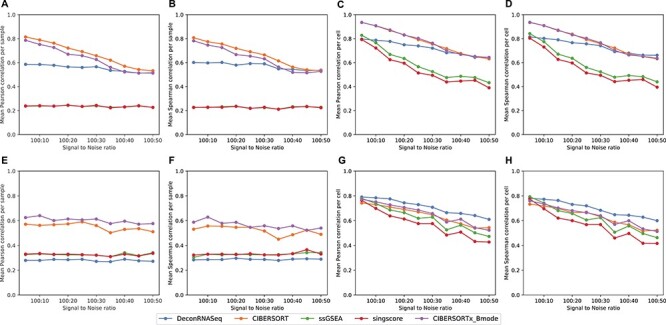
Results on simulation data with different SNR from 100:5 to 100:50. Note in A and B, the ssGSEA results align with SingScore. A–D: mean correlation between flow cytometry cell fractions and predicted cell fractions obtained from running methods with reduced LM22, across different noise levels. A: sample-level Pearson correlation, B: sample-level Spearman correlation, C: cell-level Pearson correlation, D: cell-level Spearman correlation. F–I: mean correlation between flow cytometry cell fractions and predicted cell fractions obtained from running methods with LM6, across different noise levels. F: sample-level Pearson correlation, G: sample-level Spearman correlation, H: cell-level Pearson correlation, I: cell-level Spearman correlation.
For all methods with LM6, cell-level correlations with true fractions again decrease as noise increases, but sample-level correlations stay roughly the same across all noise levels (Figure 1E–H). The insensitivity to the noise levels of sample-level results with LM6 could be due to the fact that simulation data were created using LM22 source gene expression profile instead of LM6. When LM6 is used, CIBERSORT and CIBERSORTx B-mode again perform best per sample, although correlations are lower than with reduced LM22. Figure 1E and F shows that CIBERSORTx B-mode outperforms CIBERSORT with LM6, suggesting that CIBERSORTx B-mode is better than CIBERSORT when the signature matrix and mixture data are from different platforms. Interestingly, DeconRNASeq with LM6 performs worst per sample (Figure 1E and F) but best per cell (Figure 1G and H). The poor performance per sample of DeconRNASeq with LM6, but strong performance with LM22, may indicate DeconRNASeq’s lack of robustness when signature matrix comes from a different platform than mixture data. It is worth noting that the rank-based methods perform poorly across all noise levels with both signature matrices. In particular, rank-based methods produce very low sample-level correlations with ground truth fractions (Figure 1A, B, E and F).
In addition to examining the mean correlations, we created box plots of the 100 different sample-level correlations and the 16 (LM22) or 6 (LM6) different cell-level correlations, using the simulation data generated with SNR 100:10 (Figure 2). We observe in Figure 2A, B, E and F that the variances in sample-level correlations, particularly with LM6, are quite large for all methods. The cell-level correlation plots (Figure 2C and D) show that while CIBERSORT and CIBERSORTx with LM22 produce results that are highly correlated (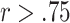
) with the ground truth for all individual cell types besides CD4 memory resting T cells, the other methods show a larger variation in performance among the different cell types. In particular, we note that DeconRNASeq does a poor job predicting the number of resting NK cells, bringing down the method’s mean correlation per cell with LM22. However, this observation does not hold when LM6 is used. This may help explain the discrepancy in DeconRNASeq’s performance in mean cell-level correlation with LM22 and LM6. With LM6, all methods besides DeconRNASeq do a poor job predicting the relative number of CD4 T Cells but do a great job predicting the relative level of neutrophils.
Figure 2 .
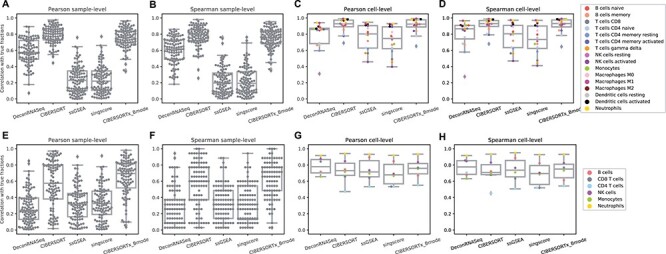
Results on simulation data with SNR 100:10. A–D: box plots of correlations between ground truth cell fractions and predicted cell fractions obtained from running methods with LM22. A: sample-level Pearson correlation, B: sample-level Spearman correlation, C: cell-level Pearson correlation, D: cell-level Spearman correlation. F–I: box plots of correlations between ground truth cell fractions and predicted cell fractions obtained from running methods with LM6. F: sample-level Pearson correlation, G: sample-level Spearman correlation, H: cell-level Pearson correlation, I: cell-level Spearman correlation.
Analysis of whole blood data
We obtain the ground truth fractions of neutrophils, lymphocytes, monocytes, T cells, CD8+ T cells, CD4+ T cells, B cells and NK cells for whole blood data (GSE127813) from CIBERSORTx [13] and compare them with the corresponding estimated fractions obtained using the above-mentioned methods. Since LM22 has 22 leukocytes, we sum the estimated fractions of certain cell sub-types to match them with the ground truth cell types. For example, we sum the estimated fractions of CD4+ naive T cells, CD4+ memory resting T cells and CD4+ memory-activated T cells to compare it with the ground truth fraction of CD4+ T cells. However, there are still eight leukocytes that do not have a similar match to the categories of the ground truth cells, and so we exclude them from our analysis. These cell types are macrophages (M0, M1, M2), DCs (resting, activated), mast cells (resting, activated) and eosinophils. Hence, we do not expect estimated percentages to sum precisely to 1. A similar procedure is applied to the results obtained with LM6, and we end up comparing estimated fractions and ground truth fractions in neutrophils, monocytes, T cells, CD8+ T cells, CD4+ T cells, B cells and NK cells.
In agreement with the simulation data results, the linear methods perform better in overall than the rank-based methods in terms of correlation per sample (Figure 3A, B, F and G). Of all the methods, CIBERSORT and CIBERSORTx B-mode again perform best per sample, both with LM22 and LM6, while CIBERSORTx S-mode performs worse than these two. DeconRNASeq performs much better in terms of Pearson correlation (and slightly better in terms of Spearman correlation) with the use of LM22 than with LM6. On the other hand, ssGSEA DM and SingScore DM perform very poorly with gene sets from LM22 (Figure 3A and B) but do a better job with gene sets from LM6 (Figure 3F and G). We should note that sample-level Pearson correlations of ssGSEA DM and SingScore DM are low for both gene sets, but since Pearson correlation is not a good measure for rank-based results, we should focus on Spearman correlation when analyzing the performance of these two methods.
Figure 3 .
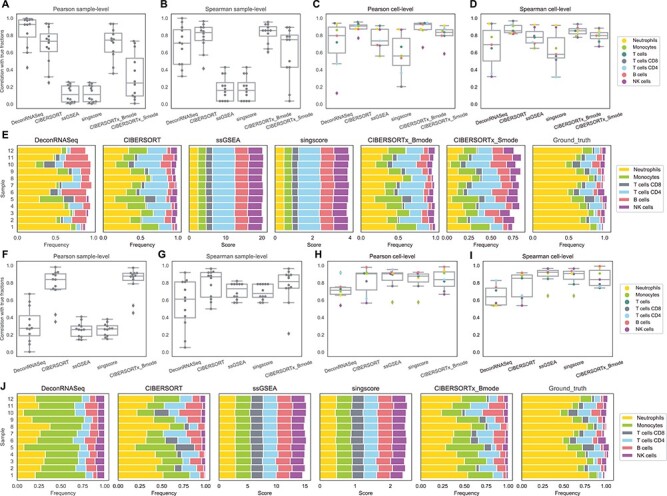
Results on whole blood data. A–D: box plots of correlations between flow cytometry cell fractions and predicted cell fractions obtained from running methods with LM22. A: sample-level Pearson correlation, B: sample-level Spearman correlation, C: cell-level Pearson correlation, D: cell-level Spearman correlation. E: stacked bar charts of predicted cell fractions by each method with LM22 and ground truth flow cytometry cell fractions. F–I: box plots of correlations between flow cytometry cell fractions and predicted cell fractions obtained from running methods with LM6. F: sample-level Pearson correlation, G: sample-level Spearman correlation, H: cell-level Pearson correlation, I: cell-level Spearman correlation. J: stacked bar charts of predicted cell fractions by each method with LM6 and ground truth flow cytometry cell fractions.
With regard to correlation per cell, CIBERSORT and CIBERSORTx B-mode perform best with LM22 (Figure 3C and D). In contrast to the simulation data results, rank-based methods perform best with LM6 (Figure 3H and I), though CIBERSORT and CIBERSORTx B-mode are not far behind. DeconRNASeq performs the worst out of all methods with LM6 but still achieves cell-level Pearson and Spearman correlations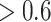 
. CIBERSORTx S-mode performs very well but still worse than original CIBERSORT and CIBERSORTx B-mode. In particular, all linear methods do a somewhat poor job predicting NK cells, compared with other cell types and rank-based methods do a poor job at predicting monocytes.
Overall, CIBERSORT and CIBERSORTx give the best results for the whole blood data set (Figure 3). Among CIBERSORT models, CIBERSORTx S-mode performs poorly but still gives relatively good results in terms of Spearman correlation with ground truth fractions (Figure 3 B and D). The comparison between Figure 3A and F shows that DeconRNASeq results are very different between LM22 and LM6, suggesting that DeconRNASeq is very sensitive to the signature matrix. In combination with the analysis of DeconRNASeq in simulation data, this result indicates that DeconRNASeq’s performance is highly dependent on the compatibility between signature matrix and mixture data.
Lastly, we compare the cellular profiles generated by each method to the ground truth fractions in Figure 3E and J. Since ssGSEA DM and SingScore DM return enrichment scores instead of estimated fractions, the total sum of the output scores for each sample does not need to be less than or equal to 1. As mentioned earlier, since they are rank-based, we should not expect them to produce scores close to ground truth fractions, but rather hope to see their output scores consistent with the ranks of true fractions (i.e. if neutrophils have the highest number in the ground truth data, we would expect these methods to give neutrophils the highest score among all cell types). However, ssGSEA DM and SingScore DM estimate similar scores of cell types for different samples, even though ground truth fractions differ across samples (Figure 3E and J). Linear methods, on the other hand, are able to capture the difference in distribution of fractions across samples. Although fractions estimated by CIBERSORT and CIBERSORTx do not completely match the ground truth fractions, these methods do succeed in capturing important patterns such as the relative levels of neutrophils, T cells, B cells and NK cells in samples. All methods overestimate the fraction of B cells, and all but DeconRNASeq with LM22 drastically underestimate the fraction of neutrophils (Figure 3E). The two rank-based methods, ssGSEA DM and SingScore DM, produce similar output scores to each other. CIBERSORT and CIBERSORTx are expected to give similar estimated fractions since they both use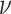 
-SVR and the only difference is that CIBERSORTx uses batch correction before applying 
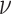-SVR. We observe a slight improvement in performance with CIBERSORTx compared with CIBERSORT for this data set.
Analysis of PBMC data
PBMC data, (GSE65133) [15], includes flow cytometry fractions for naive B cells, memory B cells, CD8+ T cells, CD4+ naive T cells, CD4+ memory resting T cells, CD4+ memory-activated T cells,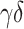 
T cells, NK cells and monocytes. Following the same procedure as mentioned before, we compare the estimated fractions to flow cytometry fractions of naive B cells, memory B cells, CD8+ T cells, CD4+ naive T cells, CD4+ memory resting T cells, CD4+ memory-activated T cells, 
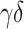T cells, NK cells and monocytes for LM22 and B cells, CD8+ T cells, CD4+ T cells, NK cells and monocytes for LM6.
We repeat the correlation analysis with the PBMC data set, and the sample-level results are somewhat different from our findings from the whole blood data set. In general, the rank-based methods perform much better in terms of correlation per sample on the PBMC data than on the other two data sets, while DeconRNASeq performs considerably worse. With LM6, sample-level Spearman correlations show high variance across samples for all methods (Figure 4F and G). This implies that all methods have an inconsistent behavior, i.e. for some samples they perform better than other samples. However, it is worth noting that there are only five cell types overlapping between LM6 cell types and ground truth cell types. The sample-level correlation across only five cell types is susceptible to being low when only one or two cell types are poorly predicted, and as seen in Figure 4H and I, these methods do a poor job estimating the relative frequency of B cells with LM6. In fact, we also observe high variance in LM6 sample-level results on the simulation data (Figure 2G), where the number of cell types (six) is small as well and the poor estimation of CD4 T cells likely contributes to some samples having low correlation with true fractions with all methods. Overall, CIBERSORT, CIBERSORTx B-mode, ssGSEA DM and SingScore DM perform better per sample than DeconRNASeq and CIBERSORTx S-mode with LM22 (Figure 4A and B), and Figure 4F and G indicates no significant differences in performance between linear models and rank-based methods with LM6.
Figure 4 .
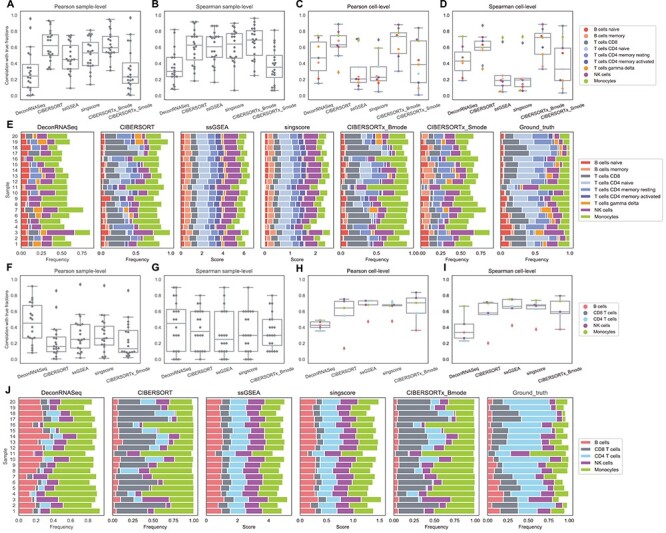
Results on PBMC data. A–D: box plots of correlations between flow cytometry cell fractions and predicted cell fractions obtained from running methods with LM22. A: sample-level Pearson correlation, B: sample-level Spearman correlation, C: cell-level Pearson correlation, D: cell-level Spearman correlation. E: stacked bar charts of predicted cell fractions by each method with LM22 and ground truth flow cytometry cell fractions. F–I: box plots of correlations between flow cytometry cell fractions and predicted cell fractions obtained from running methods with LM6. F: sample-level Pearson correlation, G: sample-level Spearman correlation, H: cell-level Pearson correlation, I: cell-level Spearman correlation. J: stacked bar charts of predicted cell fractions by each method with LM6 and ground truth flow cytometry cell fractions.
With regard to cell-level correlation, CIBERSORT and CIBERSORTx B-mode again perform best with the LM22 signature matrix, while the rank-based methods perform considerably worse compared with the whole blood and simulation data (Figure 4C, D, H and I). However, when LM6 is used, the rank-based methods outperform the linear models (Figure 4H and I). All methods except DeconRNASeq with LM22 signature matrix do well on predicting the number of CD8+ T cells and monocytes. Additionally, all methods but DeconRNASeq with LM6, ssGSEA DM and SingScore DM with LM22 show high correlations with the ground truth for NK cells. CIBERSORT and CIBERSORTx B-mode with LM22 signature matrix are the only methods for which the majority of cell types have correlation coefficients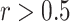 
. However, even these methods struggle to accurately predict the number of CD4+ memory resting T cells and 
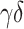T-cells with LM22 (Figure 4C and D), as well as the number of B cells when using LM6 (Figure 4H and I).
Similar to the whole blood data set, we also plot the predicted cellular profiles estimated by the methods in a stacked bar chart, along with the ground truth fractions (Figure 4E and J). We again note that we have omitted cell types that were present in the signature matrix but not in the PBMC data. Hence, we do not expect the frequencies to necessarily sum to 1. The rank-based methods do a slightly better job at capturing variations among samples in this data set as compared with the whole blood data. However, the CIBERSORT methods, particularly CIBERSORTx B-mode, again exhibit the best overall performance.
Discussion
As mentioned in the Approach section, the normalization in linear methods can affect their performance on the deconvolution of bulk gene expression data. Unlike CIBERSORT and CIBERSORTx, DeconRNASeq does not have clear guidance on whether to use its normalization and when to use it. We tried DeconRNASeq both with and without normalization on our data sets. DeconRNASeq with normalization gives overall better results in the whole blood and PBMC data sets and gives similar results to without normalization in simulation data. However, we would like to note that just because DeconRNASeq with normalization works better on these specific data sets does not mean it would work better on other data sets as well. One positive aspect of the linear methods’ normalization is that it helps these algorithms converge faster and easier, which reduces the run time significantly.
We provide a comparison of each of these methods’ run time per sample in Table 1. The run time for each of the three data sets was calculated as the average of 20 runs, using a 2.5 GHz Intel Core i7 CPU with 16 GB of RAM, and then normalized by the number of samples in the data set. All methods besides CIBERSORTx were run in R. We note that the CIBERSORTx team provides a web portal to run their software, removing any dependencies on hardware or software. Therefore, it would not be a fair comparison to include this method in Table 1. While the original CIBERSORT also has a web portal to run the method, we used the CIBERSORT R source code to record time to compute while making sure that the results from the R code are identical to those from the web portal. We note that CIBERSORTx takes longer than CIBERSORT, since the method runs batch correction before applying CIBERSORT. SingScore is the fastest of the five methods, followed by DeconRNASeq, while ssGSEA and CIBERSORT are significantly slower. Unsurprisingly, all methods run faster with the smaller LM6 signature matrix than with LM22. In general, the run time per sample also decreases for data sets with a smaller number of genes per sample.
Table 1.
Method run times per sample (mean +/- standard deviation, in milliseconds)
| Whole blood | PBMC | Simulation | ||||
|---|---|---|---|---|---|---|
| (58 581 genes/sample) | (34 694 genes/sample) | (11 845 genes/sample) | ||||
| LM22 | LM6 | LM22 | LM6 | LM22 | LM6 | |
| DeconRNASeq |
|
|
|
|
|
|
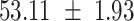
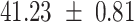
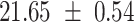
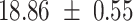
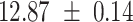
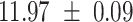
| CIBERSORT |
|
|
|
|
|
|
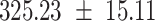
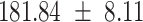
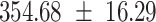
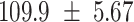
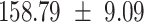
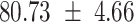
| ssGSEA |
|
|
|
|
|
|
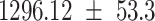
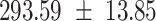
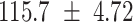
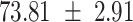
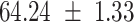
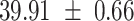
| SingScore |
|
|
|
|
|
|
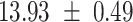
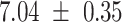
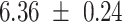
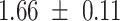
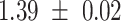
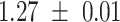
As discussed in the Results section, rank-based methods tend to estimate very similar scores across samples, while linear models are able to capture some variations in fractions among samples (Figure 3E and J and Figure 4E and J). Since rank-based methods use the rank of the genes instead of the actual expression value in the calculation of output score, as long as the genes have the same ranks across samples, ssGSEA DM and SingScore DM will output the same scores across samples (even when these genes have very different expression values across samples). Thus, rank-based methods can still successfully estimate the ranks of frequencies between cell types but might fail to estimate the relative frequencies of a given cell type in samples. This is, in fact, the main disadvantage of rank-based methods, as mentioned in Table 2 where we discuss the advantages and disadvantages of each digital cytometry method. There has been a novel attempt, introduced by Aran et al. [29], to transform enrichment scores to make them more comparable with cell fractions. These transformed enrichment scores are intended to be more on the same range with cell fractions but are not designed to be used in place of cell fractions. Converting enrichment scores to cell fractions is generally a hard problem, since enrichment scores are derived using only ranks of the genes instead of gene expression values themselves.
Table 2.
Advantages and disadvantages of methods
| Methods | Advantages | Disadvantages |
|---|---|---|
| DeconRNASeq | ∙ Outputs are cell fractions ∙ Open-source implementations available in Python and R ∙ Quick run time | ∙ Requires a signature matrix as an input ∙ Performance is highly dependent on the compatibility between signature matrix and mixture data |
| CIBERSORT | ∙ Outputs are cell fractions ∙ Open-source implementations available in Python and R ∙ Web portal available for running method ∙ Good performance on digital cytometry task | ∙ Requires a signature matrix as an input ∙ Slow run time |
| CIBERSORTx B-mode | ∙ Outputs are cell fractions ∙ Web portal available for running method ∙ Good performance on digital cytometry task ∙ Eliminates the batch effect between signature matrix and mixture data by adjusting mixture data | ∙ Requires a signature matrix as an input |
| CIBERSORTx S-mode | ∙ Outputs are cell fractions ∙ Web portal available for running method ∙ Eliminates the batch effect between signature matrix and mixture data by adjusting signature matrix | ∙ Requires a signature matrix as an input ∙ Does not perform as well as CIBERSORTx B-mode |
| ssGSEA DM | ∙ Does not require a signature matrix; it only uses the upregulated gene sets of each cell type ∙ Open-source implementations available in Python and R | ∙ Outputs are scores for each cell type rather than cell fractions ∙ Produces similar scores for samples with varying distributions of cell types ∙ Slow run time |
| SingScore DM | ∙ Does not require a signature matrix; it can use both upregulated and downregulated gene sets of each cell type ∙ Open-source implementations available in Python and R ∙ Quick run time | ∙ Outputs are scores for each cell type rather than cell fractions ∙ Produces similar scores for samples with varying distributions of cell types |
The rank-based methods generally perform better in terms of all four correlation metrics when the upregulated gene sets came from the same platform as the mixture data. In particular, for the microarray PBMC and simulation data, ssGSEA DM and SingScore DM results have higher correlations with the ground truth when using LM22 (derived from microarray data) compared with LM6 (derived from RNA-Seq data). Similarly, for the RNASeq whole blood data, ssGSEA DM and SingScore DM results are more correlated with ground truth fractions when using LM6 compared with LM22.
We further note that the rank-based methods analyzed in this study were originally introduced for the task of analyzing the enrichment of a gene set in a single sample and have recently been adopted for the digital cytometry task. Enrichment analysis refers to a group of methods for determining a set of enriched genes either in a sample or between two groups of samples. There are three generations of enrichment analysis methods: overrepresentation analysis, functional class sorting techniques and pathway topology-based techniques [19]. Both ssGSEA and SingScore belong to the second-generation, functional class sorting techniques. To the best of our knowledge, among all enrichment analysis methods, only these two single-sample enrichment methods have been used for digital cytometry. It would be worth exploring whether adopting other single-sample enrichment methods for digital cytometry would lead to better results.
In terms of linear methods, throughout this study, we have seen good performance from both CIBERSORT and CIBERSORTx B-mode. Since CIBERSORTx uses batch correction to account for cross-platform variation between the signature matrix and mixture data, we should expect CIBERSORTx to perform at least as well as CIBERSORT when signature matrix and mixture data come from different platforms. Indeed, we see marginal improvements of CIBERSORTx B-mode over CIBERSORT in both PBMC and simulation data with LM6 (Figures 1E–H and 4F—I) where mixture data come from microarray data and signature matrix comes from RNA-Seq data, and qualitatively similar performance between CIBERSORTx B-mode and CIBERSORT in whole blood data with LM22 (Figure 3A–D) where mixture data comes from RNA-Seq data and signature matrix comes from microarray data. In fact, CIBERSORTx B-mode slightly outperforms CIBERSORT in both PBMC and whole blood experimental data sets regardless of signature matrix used. However, CIBERSORTx B-mode underperforms CIBERSORT by a small margin in the simulation data with LM22, raising the possibility that batch correction may negatively affect the performance of CIBERSORT if signature matrix and mixture data come from the exact same platform.
Newman et al. [13] mention that CIBERSORTx B-mode should be used when signature matrix is derived from bulk sorted reference profile or when the technical variation between signature matrix and mixture data is moderate, while CIBERSORTx S-mode should be used when this variation is high. Figures 3A–D and 4A–D show that CIBERSORTx S-mode performs worse than both original CIBERSORT and CIBERSORTx B-mode in both experimental data sets, suggesting that the technical variation between LM22 and these data sets is not high. These results also suggest that it is better to use CIBERSORTx B-mode than CIBERSORTx S-mode when the technical variation between signature matrix and mixture data is low. We would like to mention that many studies on tumor micro-environment have recently utilized digital cytometry methods, most commonly CIBERSORT/x [30–35] and ssGSEA [36–40], and two separate studies on blood leukocyte and tumor infiltrating leukocytes enumeration indicate that iSort, a transcriptome DM based on CIBERSORTx, achieves highly accurate and robust results for both blood and tumor samples [41, 42].
Conclusion
We compare five common digital cytometry methods, including three linear models and two rank-based methods, on simulation data, whole blood RNA-Seq data and PBMC microarray data. Rank-based methods ssGSEA DM and SingScore DM give conflicting results between sample-level and cell-level correlation with ground truth fractions and overall perform worse than linear methods. DeconRNASeq’s performance depends heavily on how comparable the signature matrix and mixture data are. CIBERSORT and CIBERSORTx B-mode perform the best among all mentioned methods based on sample-level and cell-level Pearson and Spearman correlation with ground truth cell fractions for all three data sets, regardless of the signature matrix used. CIBERSORTx B-mode tends to slightly outperform CIBERSORT, especially when signature matrix and mixture data come from different platforms. CIBERSORTx S-mode, however, does not perform as well. This suggests further investigation into the way batch correction is used for adjusting the signature matrix in order to eliminate the technical variations between signature matrix and mixture data.
Key Points
Linear digital cytometry methods perform better than ranked-based methods.
The rank-based ssGSEA and SingScore DMs estimate similar scores for cell types across different samples, even though ground truth fractions differ across samples.
CIBERSORTx B-mode outperforms DeconRNASeq, CIBERSORT, CIBERSORTx S-mode, ssGSEA and SingScore DMs.
Although the batch correction method introduced in CIBERSORTx B-mode to adjust the mixture data improves the performance of the model, the batch correction method used in CIBERSORTx S-mode, to adjust the signature matrix rather than the mixture samples, does not improve performance for the tests performed.
Data Availability
The PBMC data set and its flow cytometry fractions are available on the CIBERSORT website at https://cibersort.stanford.edu under the name ‘Fig 3a PBMCs Gene Expression’ and ‘Fig 3a PBMCs Flow Cytometry’, respectively. The whole blood data set is available on Gene Expression Omnibus with identifier GSE 127813, and its flow cytometry fractions are available on the CIBERSORTx website at https://cibersortx.stanford.edu under the name ‘Ground truth whole blood (txt)’. The simulation data created for this study, as well as the upregulated gene sets we derived from LM22 and LM6, can be found on our github page. The data portion of our github repository is located at https://github.com/ShahriyariLab/Tumor Decon/tree/master/TumorDecon/data. The simulation data and gene sets can be found under the names ‘Simulation_data’, ‘LM22_up_genes.csv’ and ‘LM6_up_genes.csv’, respectively.
Acknowledgments
We are grateful to G. Bindea for sharing their method of selecting highly expressed genes in immune cell types from single-cell gene expression profiles.
Funding
This work was supported by the National Cancer Institute of the National Institutes of Health [R21CA242933 to L.S.].
Trang Le is a PhD student in statistics program at the University of Massachusetts Amherst. Her current research focuses on improving tumor deconvolution methods.
Rachel Aronow is a software engineer in the Department of Mathematics and Statistics at the University of Massachusetts Amherst.
Arkadz Kirshtein is a postdoctoral research associate in the Department of Mathematics and Statistics at the University of Massachusetts Amherst. His current research focuses on modeling cell interaction networks in colon cancer.
Leili Shahriyari is an assistant professor at the University of Massachusetts Amherst. Her current research focuses on the development of frameworks to combine machine learning, statistical and mathematical models to arrive at personalized cancer treatments.
Contributor Information
Trang Le, University of Massachusetts Amherst.
Rachel A Aronow, Department of Mathematics and Statistics at the University of Massachusetts Amherst.
Arkadz Kirshtein, Department of Mathematics and Statistics at the University of Massachusetts Amherst.
Leili Shahriyari, University of Massachusetts Amherst.
References
- 1. Galon J, Costes A, Sanchez-Cabo F, et al. Type, density, and location of immune cells within human colorectal tumors predict clinical outcome. Science 2006; 313(5795):1960–4. [DOI] [PubMed] [Google Scholar]
- 2. Tosolini M, Kirilovsky A, Mlecnik B, et al. Clinical impact of different classes of infiltrating T cytotoxic and helper cells (Th1, th2, treg, th17) in patients with colorectal cancer. Cancer Res 2011; 71(4):1263–71. [DOI] [PubMed] [Google Scholar]
- 3. Baumgart DC, Carding SR. Inflammatory bowel disease: cause and immunobiology. Lancet 2007; 369:1627–40. [DOI] [PubMed] [Google Scholar]
- 4. Beutler B, Greenwald D, Hulmes JD, et al. Identity of tumour necrosis factor and the macrophage-secreted factor cachectin. Nature 1985;316(6028):552–4. [DOI] [PubMed] [Google Scholar]
- 5. Grivennikov SI, Greten FR, Karin M. Immunity, inflammation, and cancer. Cell 2010;140 (6):883–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Popivanova BK, Kitamura K, Wu Y, et al. Blocking TNF-alpha in mice reduces colorectal carcinogenesis associated with chronic colitis. J Clin Invest 2008;118(2):560–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Waldner MJ, Neurath MF. Colitis-associated cancer: the role of T cells in tumor development. Semin Immunopathol 2009; 31(2):249–56. [DOI] [PubMed] [Google Scholar]
- 8. Mudter J, Neurath MF. IL-6 signaling in inflammatory bowel disease: pathophysiological role and clinical relevance. Inflamm Bowel Dis 2007; 13(8):1016–23. [DOI] [PubMed] [Google Scholar]
- 9. West NR, McCuaig S, Franchini F, et al. Emerging cytokine networks in colorectal cancer. Nat Rev Immunol 2015;15(10):615–29. [DOI] [PubMed] [Google Scholar]
- 10. Ca H, Sa J. IL-6 as a keystone cytokine in health and disease. Nat Immunol 2015;16(5):448–57. [DOI] [PubMed] [Google Scholar]
- 11. Heath JR, Ribas A, Mischel PS. Single-cell analysis tools for drug discovery and development. Nat Rev Drug Discov 2016; 15(3):204–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Kukurba KR, Montgomery SB. RNA sequencing and analysis. Cold Spring Harb Protoc 2015; 2015(11):951-69. pdb-top084970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Newman AM, Steen CB, Liu CL, et al. Determining cell type abundance and expression from bulk tissues with digital cytometry. Nat Biotechnol 2019;37(7):773–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Abbas AR, Wolslegel K, Seshasayee D, et al. Deconvolution of blood microarray data identifies cellular activation patterns in systemic lupus erythematosus. PLoS One 2009; 4(7):e6098–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Newman AM, Liu CL, Green MR, et al. Robust enumeration of cell subsets from tissue expression profiles. Nat Methods 2015;12(5):453–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Şenbabaoğlu Y, Gejman RS, Winer AG, et al. Tumor immune microenvironment characterization in clear cell renal cell carcinoma identifies prognostic and immunotherapeutically relevant messenger RNA signatures. Genome Biol 2016;17 (1): 231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Foroutan M, Bhuva DD, Lyu R, et al. Single sample scoring of molecular phenotypes. BMC Bioinformatics 2018;19(1): 404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Gong T, Hartmann N, Kohane IS, et al. Optimal deconvolution of transcriptional profiling data using quadratic programming with application to complex clinical blood samples. PLoS One 2011; 6(11): 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Zyla J, Marczyk M, Domaszewska T, et al. Gene set enrichment for reproducible science: comparison of CERNO and eight other algorithms. Bioinformatics 2019; 35(24):5146–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Lawson CL, Hanson RJ. Solving Least Squares Problems. Philadelphia, PA: Society for Industrial and Applied Mathematics, 1995. [Google Scholar]
- 21. Bertsekas DP. Nonlinear Programming. Belmont, MA: Athena Scientific, 1999. [Google Scholar]
- 22. Mackey MD, Mackey DJ, Higgins HW, et al. CHEMTAX—a program for estimating class abundances from chemical markers: application to HPLC measurements of phytoplankton. Mar Ecol Prog Ser 1996; 144(1–3):265–83. [Google Scholar]
- 23. Gustafsson J, Held F, Robinson J, et al. Sources of variation in cell-type RNA-seq profiles. 2020. [DOI] [PMC free article] [PubMed]
- 24. Johnson WE, Li C, Rabinovic A. Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics 2007; 8(1):118–27. [DOI] [PubMed] [Google Scholar]
- 25. Barbie DA, Tamayo P, Boehm JS, et al. Systematic RNA interference reveals that oncogenic KRAS-driven cancers require TBK1. Nature 2009;462(7269):108–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Subramanian A, Tamayo P, Mootha VK, et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci U S A 2005;102(43):15545–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Chen B, Khodadoust MS, Liu CL, et al. Profiling tumor infiltrating immune cells with CIBERSORT. Meth Mol Biol 2018; 1711:243–59. Clifton, NJ. [DOI] [PMC free article] [PubMed]
- 28. Bindea G, Mlecnik B, Tosolini M, et al. Spatiotemporal dynamics of intratumoral immune cells reveal the immune landscape in human cancer. Immunity 2013;39(4):782–95. [DOI] [PubMed] [Google Scholar]
- 29. Aran D, Hu Z, Butte AJ. xCell: digitally portraying the tissue cellular heterogeneity landscape. Genome Biol 2017; 18(1):1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Ali HR, Chlon L, Pharoah PD, et al. Patterns of immune infiltration in breast cancer and their clinical implications: a gene-expression-based retrospective study. PLoS Med 2016; 13(12): e1002194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Zeng D, Li M, Zhou R, et al. Tumor microenvironment characterization in gastric cancer identifies prognostic and immunotherapeutically relevant gene signatures. Cancer Immunol Res 2019; 7(5):737–50. [DOI] [PubMed] [Google Scholar]
- 32. Gentles AJ, Newman AM, Liu CL, et al. The prognostic landscape of genes and infiltrating immune cells across human cancers. Nat Med 2015; 21(8):938–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Zhou R, Zhang J, Zeng D, et al. Immune cell infiltration as a biomarker for the diagnosis and prognosis of stage I–III colon cancer. Cancer Immunol Immunother 2019; 68(3):433–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Zeng D, Zhou R, Yu Y, et al. Gene expression profiles for a prognostic immunoscore in gastric cancer. Br J Surg 2018; 105(10): 1338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Su S, Akbarinejad S, Shahriyari L. Immune classification of clear cell renal cell carcinoma. bioRxiv 2020;1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Jia Q, Wu W, Wang Y, et al. Local mutational diversity drives intratumoral immune heterogeneity in non-small cell lung cancer. Nat Commun 2018; 9(1):1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Wang S, Zhang Q, Yu C, et al. Immune cell infiltration-based signature for prognosis and immunogenomic analysis in breast cancer. Brief Bioinform 2020. [DOI] [PubMed] [Google Scholar]
- 38. Yoshihara K, Shahmoradgoli M, Martínez E, et al. Inferring tumour purity and stromal and immune cell admixture from expression data. Nat Commun 2013; 4(1): 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Tian X, Zhu X, Yan T, et al. Differentially expressed lncRNAs in gastric cancer patients: a potential biomarker for gastric cancer prognosis. J Cancer 2017; 8(13): 2575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Şenbabaoğlu Y, Gejman RS, Winer AG, et al. Tumor immune microenvironment characterization in clear cell renal cell carcinoma identifies prognostic and immunotherapeutically relevant messenger RNA signatures. Genome Biol 2016; 17(1):1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Newman AM, Nakao A, Li K, et al. Analytical validation of digital cytometry (iSort) for leukocyte enumeration using stored blood. 2020. American Society of Clinical Oncology.
- 42. Newman AM, Nakao A, Li K, et al. Analytical validation of iSort digital cytometry for leukocyte enumeration in clinical tumor specimens. 2020. American Society of Clinical Oncology.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The PBMC data set and its flow cytometry fractions are available on the CIBERSORT website at https://cibersort.stanford.edu under the name ‘Fig 3a PBMCs Gene Expression’ and ‘Fig 3a PBMCs Flow Cytometry’, respectively. The whole blood data set is available on Gene Expression Omnibus with identifier GSE 127813, and its flow cytometry fractions are available on the CIBERSORTx website at https://cibersortx.stanford.edu under the name ‘Ground truth whole blood (txt)’. The simulation data created for this study, as well as the upregulated gene sets we derived from LM22 and LM6, can be found on our github page. The data portion of our github repository is located at https://github.com/ShahriyariLab/Tumor Decon/tree/master/TumorDecon/data. The simulation data and gene sets can be found under the names ‘Simulation_data’, ‘LM22_up_genes.csv’ and ‘LM6_up_genes.csv’, respectively.