Abstract
This paper applies image processing metrics to tracking of perturbations in mechanical phase delay in a multi-axis microelectromechanical system (MEMS) scanner. The compact mirror is designed to scan a laser beam in a Lissajous pattern during the collection of endoscopic confocal fluorescence images, but environmental perturbations to the mirror dynamics can lead to image registration errors and blurry images. A binarized, threshold-based blur metric and variance-based sharpness metric are introduced for detecting scanner phase delay. Accuracy of local optima of the metric for identification of phase delay is examined, and relative advantages for processing accuracy and computational complexity are assessed. Image reconstruction is demonstrated using both generic images and sample tissue images, with significant improvement in image quality for tissue imaging. Implications of non-ideal Lissajous scan effects on phase detection and image reconstruction are discussed.
Index Terms—: Image Processing, Phase correction, Endoscopes, Microelectromechanical Systems, Lissajous scanning, Microscopy, Dynamics
I. Introduction
Imaging by scanning a laser beam has many applications in biomedical imaging [1], scanning probe microscopy [2], 3D printing [3], single pixel cameras [4], scanning electron microscopy (SEM), laser scanning based projectors [5], and LiDAR (light detection and ranging). Various beam steering patterns, such as raster, spiral, and Lissajous, can be chosen depending on the application and scanning actuator capabilities. For instance, Lissajous scanning is obtained when both axes of motion are operated with constant sinusoidal inputs of differing frequency and phase [6]. The scan pattern has a direct effect on image resolution, field-of-view (FOV), and frame rate (FR). Lissajous scanning is a popular choice in imaging applications as it can be easily implemented using galvo mirrors or, especially, miniaturized MEMS (microelectromechanical system)-based scanners. For many scanning actuators, a large FOV can be achieved by operating the scanner near resonant frequencies. Unlike raster scanning, Lissajous does not require the two operating frequencies to be widely separated, simplifying the MEMS design.
However, the effectiveness of a Lissajous scan and accuracy of image reconstruction is very sensitive to the phase of the axes. In miniaturized devices, such as MEMS mirrors, the resonant frequency of a scanner (i.e. resonant micro-mirror) can drift by several degrees of phase angle due to environmental perturbations. This drift, in turn, produces a change in phase delay between mirror motion and the periodic input driving signal. There has been limited analysis of phase compensation as a mechanical phenomena in Lissajous scanning, as distinct from other phase information that may be compensated during imaging, such as focal depth or wavefront geometry. Previous methods for compensating for mechanical phase shift in resonant devices include temperature-based calibration [7], on-chip capacitive sensing [8], and design to limit temperature sensitivity, but these suffer from poor repeatability, poor signal-to-noise ratios, and material limitations when using small MEMS devices in severely space-constrained applications such as endoscopy. Various feedback controllers have also been proposed [9]–[11], but these are also susceptible to sensing limitations in small, in vivo instruments and they increase system complexity. Most recently, information from the spatial Fourier transform of image information was proposed for MEMS mirror phase identification, but this requires substantial computation and tracked only small perturbations in phase [12].
This paper proposes methods for high-accuracy mechanical phase detection using (i) an image sharpness-based variance metric, (ii) an image blur-based threshold metric; the latter metric relies on binary pixel counting from thresholded intensity data during Lissajous scanning. Sharpness-based metrics comparable to (i) are often used in other autofocus applications [13]. Blur-based algorithms similar to (ii) were first proposed as criteria during development of early autofocus techniques for microscopy [14]. However, we demonstrate the first application (to the best of the authors’ knowledge) of these classes of criteria to the problem of mechanical phase tracking encountered by multi-axis MEMS scanners. Moreover, while the approach of thresholded pixel counting as in the blur metric has not been widely adopted as an autofocus criteria because the value for an optimal focusing parameter (i.e. focal depth) can vary with threshold level [15], we will show that it is much less sensitive to this limitation under the conditions of Lissajous scanning, with accompanying advantages for computation time.
In this work, we thus demonstrate that variance and thresholded pixel count metrics are well-suited to the compensation of unknown phase perturbations in Lissajous scanning with MEMS mirrors, with some trade-offs between them for robustness of parameter selection versus computational efficiency. In addition, we will discuss how these phase detection algorithms interact with other potential limitations of Lissajous scan design, such as fill factor (FF) versus frame rate and non-uniform scan density, and will suggest practical approaches for managing these trade-offs for the MEMS scanner. Sample images from a fluorescent confocal endomicroscope using a 2-axis parametrically-resonant micro-mirror are presented.
II. Scanner model and phase drift
To begin, we examine the interaction of MEMS mirror dynamic perturbations with Lissajous-scan image reconstruction. The model for scanner dynamics in each axis of a two-axis parametrically-resonant MEMS scanner, such as shown in fig. 1(a), are described following [16] by
where subscript k denotes parameters for a respective axis (x or y), J is rotational inertia, c is a damping constant, K is a torsional spring stiffness, V is input voltage, and d and b are parameters approximating roll-off of capacitance between electrostatic comb fingers that actuator mirror motion as an exponential decay. Let the scanner be driven into motion about an axis with a driving voltage given by
| (1) |
where Ak is input amplitude, fk is the driving frequency close to resonance of the x or y axis, and ψk is the phase of the driving voltage applied to the electrodes of different axis. The angular motion of scanner along the respective axis, and the laser position (x, y) on the object plane can be closely approximated as
| (2) |
| (3) |
Fig. 1.
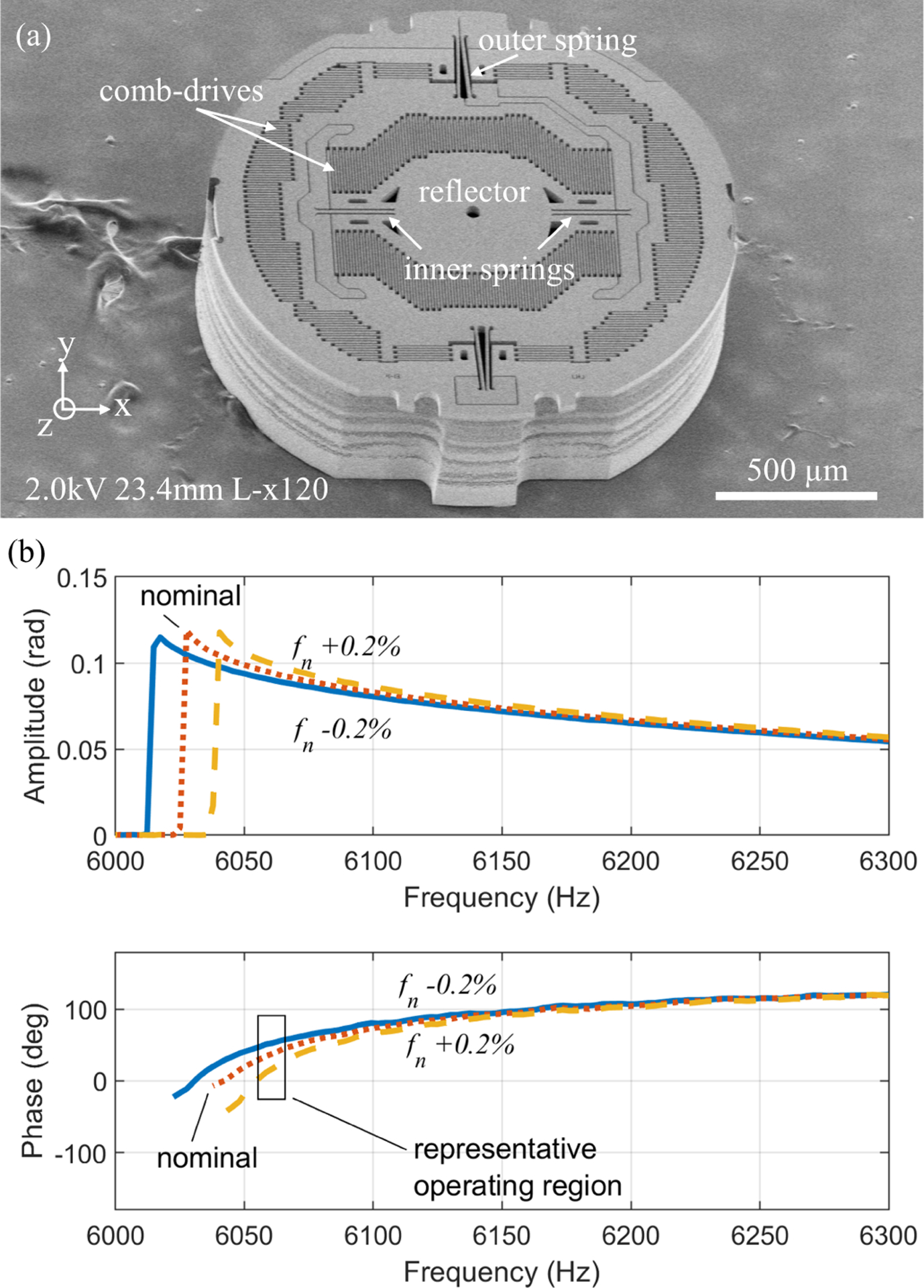
(a) A 2-axis electrostatic actuated parametrically-resonant MEMS scanner, (b, c) Phase delay variation near maximum amplitude scanning is substantial with small perturbations of natural frequency. Sample frequency response generated by methods from [16], [17], with nominal Jx =0.013 mg mm2, cx =0.003 μN-mm-s/rad, Kx =4860 μN-mm/rad, bx =0.0006 rad2, dx =0.003 μN-mm-rad, and corresponding linear natural frequency, fn, of 6405 Hz perturbed by adjusting Kx.
Here, Dk is the peak amplitude of the mirror motion, ϕk(t) is the phase difference between scanner motion and input voltage at the current driving frequency, and L is the distance from the mirror to the focal point of the laser being scanned. Note that the scanner oscillates at half the frequency of the input voltage due to parametric resonance as described in [16].
In fluorescence endomicroscopy, the distance of an instrument from a tissue sample is not precisely controlled, and thus the exact FOV of the image, (±LDx, ±LDy) is neither expected to be exactly known, nor critical to producing a clear image, so long as the tissue surface is within the working distance of the instrument. Thus, perturbations to mirror dynamics affecting motion amplitude are of limited importance. However, perturbations to the mechanical phase difference between scanner input and motion output will rapidly degrade image quality if changes in delay cannot be identified.
To elaborate, an image can be reconstructed if one knows the trajectory of the laser beam on the object plane as a function of time. As described by eqs. (2) and (3), the beam motion depends on parameters fk, ψk, ϕk(t), and . In practice, fk, and ψk are known, and as noted above has comparatively modest impact on image quality. Phase information ϕk, however, can be a major contributor to image misregistration. Mechanical phase drifts in one or both axes can be attributed to numerous factors such as variation in environmental conditions including temperature, changes in material property over time, etc, with sample behavior shown in fig. 1(b, c). This makes the phase ϕk(t) a slow function of time and creates difficulty in image reconstruction. There is also the possibility of dynamic coupling of axes, but this can be mitigated in parametrically-resonant scanners by ensuring that the natural frequencies of the two axes are sufficiently far from an integer multiple of one another, as by design procedures discussed in [4]. The phase ϕk(t) can be experimentally determined in a controlled lab environment to reconstruct the image. However, in practical application, the phase determined in the lab will not remain constant indefinitely. It is sometimes possible to adjust the phase manually to compensate the drift for sparse images. However, this requires substantial user experience and it becomes almost impossible to adjust the phase for images of structures that are new to the user. Thus, there is a need to determine the correct phase at a regular interval of time with minimal disruption to the endoscopy procedure.
III. Lissajous scan image reconstruction
To generate a grey scale imaging via single point scanning, points (x(t), y(t)) on an object H are sequentially sampled at constant sampling frequency (T is sampling time). The intensity of light, H (x(pT), y(pT)), from pth point is stored as data sample R(p). By this process, the 2D image of an object H(x, y) is translated into 1D time series data R, referred to as raw data henceforth. The sequence of sampled points (x, y) on the object plane H is determined by the Lissajous scanning pattern given by eqs. (2) and (3), Where t = pT, and p ∈ N. Image reconstruction becomes an inverse problem where one must map intensity values R(p) to a 2D image space (discrete) I(i, j), where I is a grey image (M × N matrix) of an object H. Thus, it is essential to know each ordered pair (i, j) as a function of p.
The mapping of R to I is many-to-one because of non-uniform scan density (the number of data points sampled per unit area) over the FOV and rounding of the location of sample instance to the nearest pixel location. One way to get a unique intensity value at a pixel (i, j) is to average all such values of R(p)’s that are mapped to that pixel. The schematic for the process of object scanning and image reconstruction is shown in fig. 2 and summarized by the calculations:
| (4) |
| (5) |
Where ⌈ ⌉ denotes a greatest integer function (ceiling), and and are the normalized co-ordinates given by
| (6) |
| (7) |
A key characteristic of the impact of drift on image reconstruction is duplicative appearance of features along each axis when pixels are misregistered due to erroneous phase used for reconstruction. As illustration, consider that a given from eqs. (6) and (7) is also satisfied by
| (8) |
| (9) |
Under conditions of phase uncertainty, the phase ϕk(t) can be written as
| (10) |
where is a constant and Δϕk(t) is phase drift. When Δϕx = Δϕy = 0, all intensities assigned to a pixel (i, j) are obtained from the same, correctly-registered, point in the FOV. However, non-zero phase drift assigns intensity measurements to either side of the nominal pixel location.
Fig. 2.
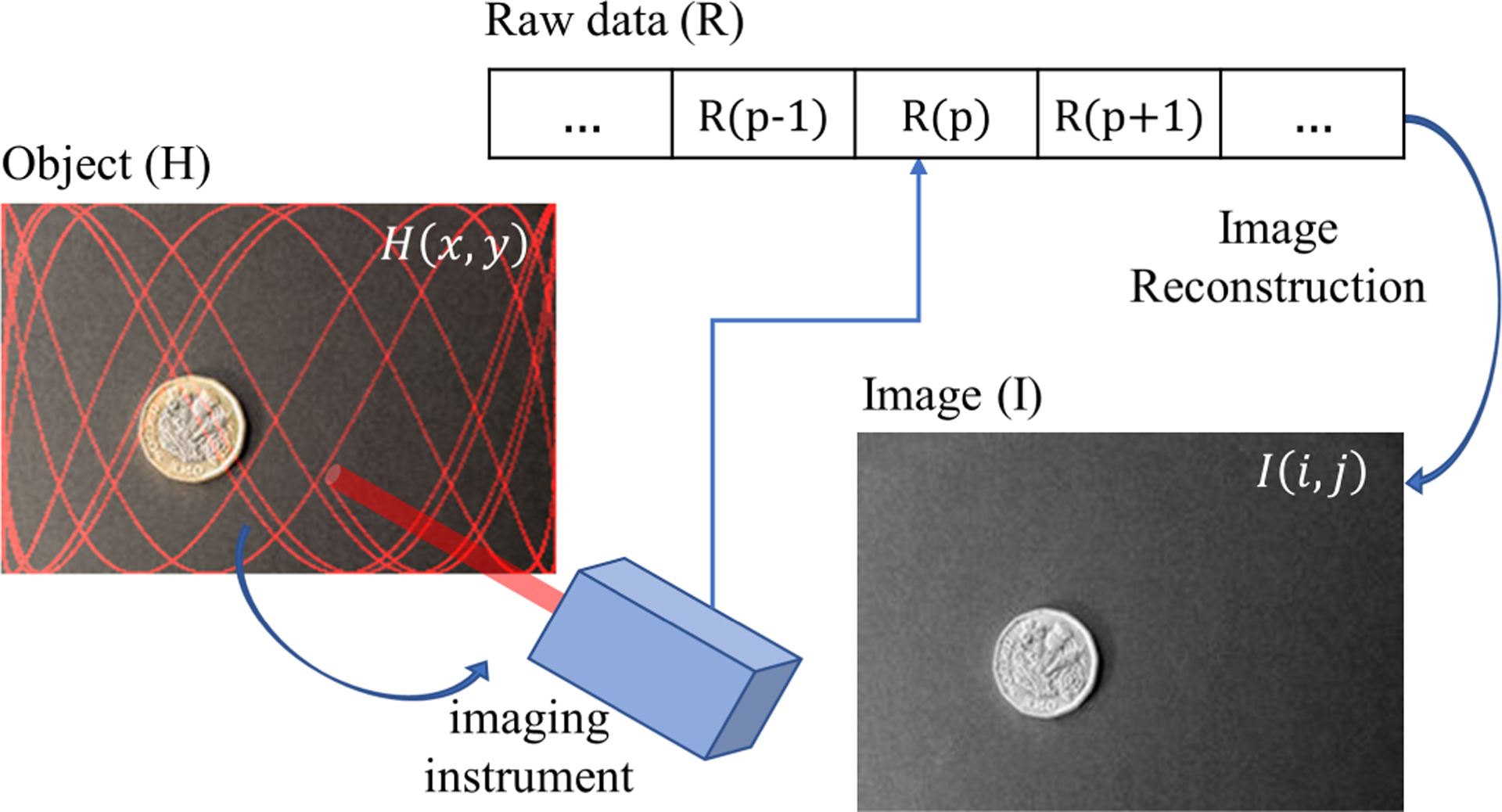
Schematic for image reconstruction in a single pixel scanning camera (Image credits: ID 90250929 ©Jevanto | Dreamstime.com).
To demonstrate the resulting effect, we generate a set of raw data by sampling the demonstration image, shown in fig. 3(a), in Lissajous style. Arbitrary scanning frequencies and phases of fx = 19251 Hz, fy = 3315 Hz, and ϕx = 2.8456 rad, ϕy = 0.3989 rad were chosen to simulate the laser scan pattern. A total of 106 samples were recorded assuming a sampling rate of 107 samples/sec. The location of the simulated laser point at any sampling instance was rounded to the nearest pixel location.
Fig. 3.

(a) original image, (b) image reconstructed with phase error ϕx = ϕy = π/8 rad.
If we introduce an exaggerated error or drift of rad for phases in both axes (Δϕx and Δϕy), the reconstructed image will have four overlapping images as shown in fig. 3(b). As a consequence of eqs. (6) to (9), we can say the output image is an overlap of four original images offset by corresponding phase of Δϕx and Δϕy in each axis. Moreover, the offset between right and left scan images is not a linear function of Δϕ as it is mapped via the sinusoidal functions above. This demonstration gives an exaggerated view of a problem, but even a small error in phase leads to a blurry image, significantly affecting image resolution. This puts a stringent requirement on the accuracy with which the phases should be predicted or detected.
IV. Phase estimation using image-based metrics
Autofocusing techniques regularly rely on metrics drawn from image properties to perform an optimization on an autofocus parameter. A common example is metrics for sharpness, frequently defined based on pixel variance within an image [18]. Estimation of the phase delay (ϕ*) under a metric is an optimization problem where the estimated value is the argument of a minimization or maximization problem, i.e.
| (11) |
where, the objective function g(ϕx, ϕy) can be any combination of metrics expected to improve the image quality upon optimization. As established in section III, the phase error in each axis independently produces the effect of overlapping images. Thus, optimizing the objective function g(ϕx, ϕy) with respect to two variables ϕx and ϕy simultaneously can be an overkill and computationally expensive. We simplify eq. (11) with the independent assumption and rewrite as
| (12) |
and perform a sequential optimization starting arbitrarily with either ϕx or ϕy.
Conceptually a variety of autofocus-type algorithms could be applied to this problem, with most such algorithms depending on metrics such as intensity variance or properties of spatial Fourier transform. However, these are comparatively computationally expensive and can be implemented only after fully reconstructing the image for each candidate phase angle. Motivated by this characteristic impact of phase drift on Lissajous image reconstruction, we instead first describe our method for rapidly assessing image blur when using a MEMS micro-scanner. We will then introduce a variance-based approach in section IV–B for comparison, which is more similar to widely-used autofocus metrics from other applications, though implemented in MEMS scanner phase tracking for the first time.
A. Threshold-based blur metric
We propose a threshold-based blur metric that functions as a “shorthand” method to signify the amount of repetition in the image with low computational complexity. In this method, a threshold (σ, constant for a given phase detection step) is used to convert the time series raw data R to a binary vector, Rσ = {0, 1}. Then, all pixels within the image are assigned a binary value, IB(i, j), with value equal to one if entry in Rσ assigned to a pixel (i, j) under a candidate phase estimate is a one. This can also be written
| (13) |
In other words, if at any instance during reconstruction a pixel is assigned an intensity greater than the threshold, it takes on a value of 1. The final normalized threshold metric, B, is then defined as the total number of white pixels in the B/W image, (i.e. sum of all ones) divided by the total number of pixels
| (14) |
Conceptually, the rationale behind eq. (14) is that when an inaccurate phase is used to generate the image, the information is spread across the image, and ones (or bright pixels) will be spread across the image and increase the value of B. An exaggerated phase error example is demonstrated in fig. 4. For B to serve as an indicator of phase, we desire B to be a minimum when Δϕx = Δϕy = 0. To do this, we assume that
- σ is selected according to
(15) there exist non-empty sets of pixels with R(p) < σ, and that are oversampled during the Lissajous scan period of interest.
Fig. 4.

Demonstration of intuition behind threshold metric, the value of the threshold metric B (number of bright pixels) increases from 0.0434 to 0.1640 with increase in phase error from 0 to 0.075π for (a) and (b) respectively.
Under these assumptions, if the image is correctly registered (i.e. Δϕx = Δϕy = 0), there will be finite numbers of both one and zero entries in IB, and associated boundaries between “black” and “white” regions in the binarized image. As phase error increases, the number of white pixels increases due to pixels in the black regions drawing samples from the white regions due to eqs. (6) to (9) and the asymmetric thresholding conditions of eq. (13). Critically, due to eqs. (6) to (9) and assumption (ii), the number of white pixels must increase for perturbations of Δϕx and Δϕy in either direction, and Δϕx = Δϕy = 0 will be at least a local minimum.
The critical result for this method is that the combination of, oversampling and locally-symmetric misregistration characteristic of Lissajous scanning prevents the minimum value of B from being dependent on threshold value, so long as assumption (i) is satisfied. Thus, this approach is highly-suitable for phase correction in Lissajous scanning despite application to other autofocus scenarios being less effective. Furthermore, the approach requires less computational effort than more conventional autofocus techniques. While binarized pixels do need to be assigned to locations in image space based on candidate phase delays, minimal additional computation is required to calculate B, as opposed to full computation of reconstructed image properties by metrics such variance or spatial frequency calculations.
A limitation of the metric in eq. (14) is that a global search is not proven to be robust and not guaranteed to provide the correct optimum value for all possible selections of the threshold. However, as will be examined in the following section, we have observed to date that the threshold metric is always at least locally minimized at , regardless of the choice of the threshold value.
B. Variance-based sharpness metric
In this method, a variance-based sharpness metric is used to predict the phase. This metric is inspired by other autofocus applications and adapted to MEMS scanner phase tracking as a comparison for the more specialized approach above. In a sharp image, the pixel intensity values are well separated and thereby increase the variance of pixel intensities. Thus, the variance of pixel intensities can be a sharpness metric, S, in this case using pixel intensity of an image reconstructed from a test phase delay,
| (16) |
| (17) |
Such that optimal phase is selected based on eq. (12) with g = −S.
V. Results
In this section, we examine the results of the proposed phase detection algorithm through application to a set of test images and images acquired from in vivo endomicroscopy. We will compare effectiveness of both metrics proposed in section IV in estimating the phase. The effect of phase error on the image quality can be assessed by using a target error previously established [19]. Let the maximum uncertainty in intensity location that produces acceptable image quality be δr. Then, in an image size of M × N, the error in estimation of a phase along respective axes is upper bounded by,
| (18) |
Where the uncertainty in intensity location δr2 = δx2 + δy2.
A. Phase correction implementation using global and local search
The simulated raw data described in section III is first used as a demonstration of the proposed blur versus sharpness-based phase prediction methods. A global search was made independently along x and y axes by evaluating either metrics at each candidate phase between [0, π] incremented in step of 0.02 rad. To mitigate the missing pixels during the algorithm implementation, the image was constructed at 9/16 of the size of original image (3/4 along each axis). In fig. 5(a)–(b) the global minimum can be seen at the true phase values. The results were fine-tuned by a local search where phase was incremented in steps of 1 mrad in the vicinity of the minimizer obtained from the global search. The results can be seen in fig. 5(c)–(d). The comparison of the predicted phase by both methods with the true phase is given in table I.
Fig. 5.
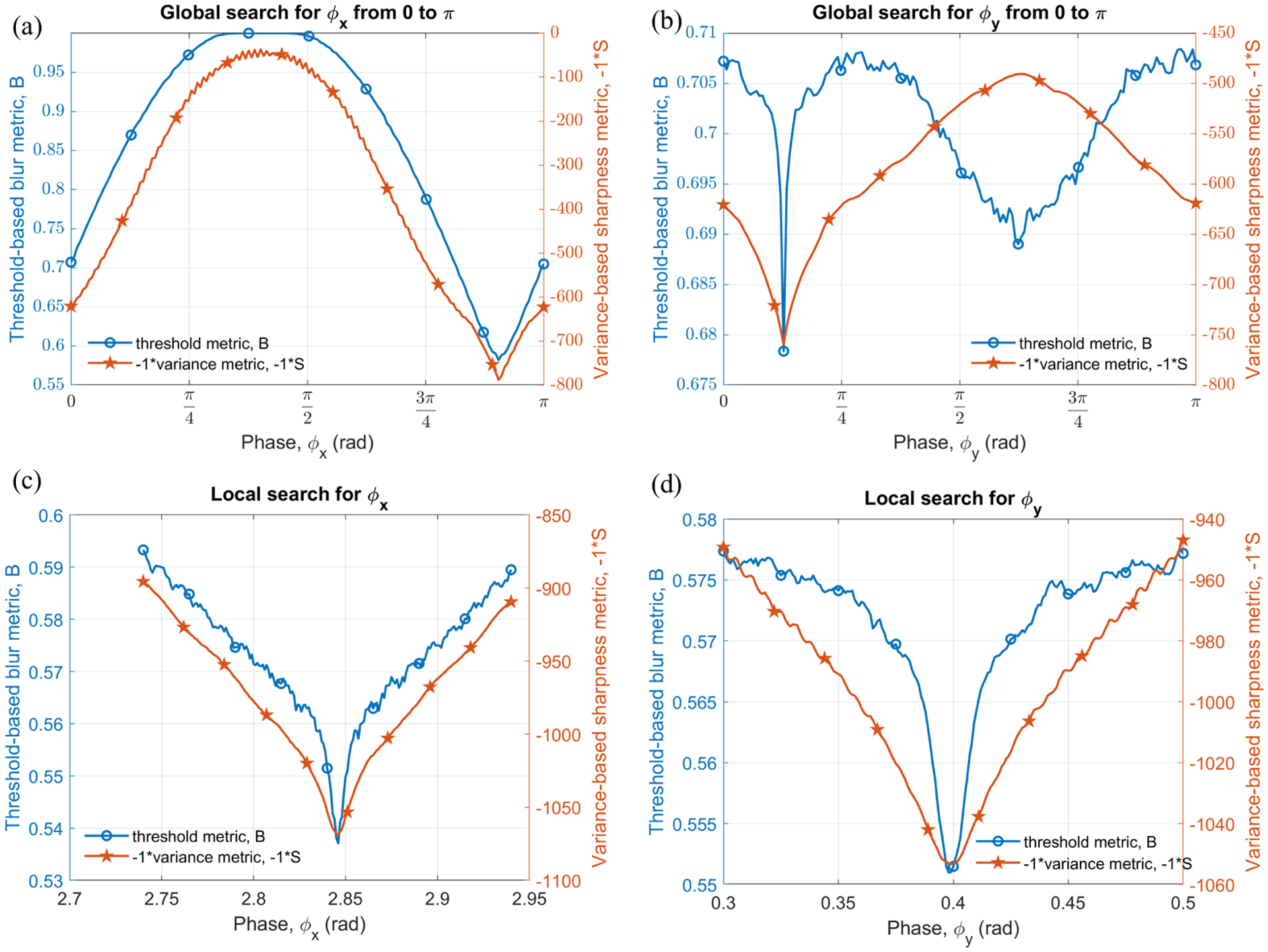
Plots of threshold and negative variance metric vs phase x and y; (a) and (b) global search from 0 to π, (c) and (d) local search around initial approximation given by global search.
TABLE I.
Sample image result comparison
|
ϕx (rad) |
δϕx (mrad) |
ϕy (rad) |
δϕy (mrad) |
|
|---|---|---|---|---|
| True phase | 2.8456 | 0 | 0.3989 | 0 |
| Estimated phase | ||||
| • threshold metric | 2.8460 | 0.4 | 0.3980 | −0.9 |
| • variance metric | 2.8460 | 0.4 | 0.3980 | −0.9 |
B. Algorithm testing on simulated data using generic images
The effectiveness and versatility of the phase detection algorithm and proposed metrics is next evaluated by testing it on several images. For demonstration purpose, results for both biological images such as a widefield endoscopic image of human colon, confocal microscopic image of sessile serrated (SS) adenoma tissue and normal tissue from human colon, and couple of images commonly used in the image processing community like ‘chemical plant’, and ‘lake’, are shown in fig. 6. These images were first converted to grayscale and resize to 256×256 pixels. Raw data for each image was generated by simulating Lissajous scanning as described in section III. For comparison, we used the same arbitrary scanning frequencies and phases of fx = 19251 Hz, fy = 3315 Hz, and ϕx = 2.8456 rad, ϕy = 0.3989 rad to simulate the laser scan pattern for each image. Global and local search, as mentioned in section V–A, were performed using Matlab to predict the phase value and results are shown in fig. 6 and summarized in table II. As evident from the results, the algorithms successfully predict the phase value with maximum absolute error of 0.6 mrad. The accuracy could be further improved by reducing the step size of 1 mrad used during the local search. To put this error in a perspective, in view of eq. (18), for M = N = 256 pixels, |δϕ| = 0.6 mrad, the maximum possible pixel shift is δr ≈ ±0.1086 pixel. In other words, the maximum error in the inferred location of an intensity value is less than 10.86% of a pixel dimension.
Fig. 6.
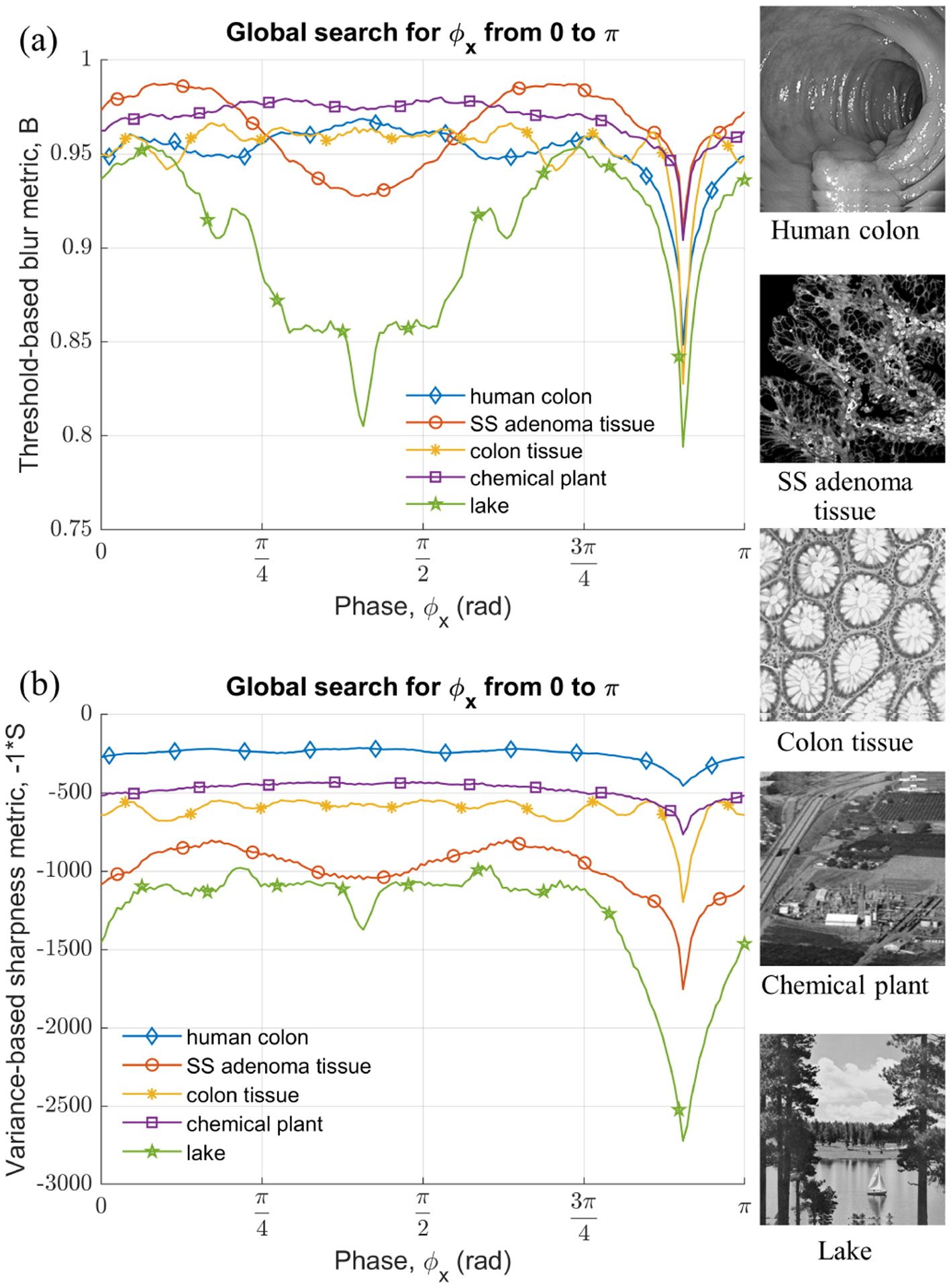
Plots of global search sweep along x axis from 0 to π for generic test images; (a) threshold-based blur metric, (b) variance-based sharpness metric (negative).
TABLE II.
Phase and error estimation in test images
| Threshold metric | Variance metric | |||
|---|---|---|---|---|
|
δϕx (mrad) |
δϕy (mrad) |
δϕx (mrad) |
δϕy (mrad) |
|
| Human colon | 0.4 | 0.1 | 0.4 | 0.1 |
| SS adenoma tissue | 0.4 | 0.1 | 0.4 | 0.1 |
| Colon tissue | 0.4 | 0.1 | 0.4 | 0.1 |
| Chemical plant | 0.4 | 0.1 | 0.4 | 0.1 |
| Lake | −0.6 | 0.1 | 0.4 | 0.1 |
C. In-vivo tissue imaging demonstration
The effectiveness of the algorithm was applied to a two-axis MEMS scanner installed in a front-view single-axis confocal endomicroscope during in-vivo imaging [20]. The animal study was approved by the University Committee on the Use and Care of Animals (UCUCA) at the University of Michigan. During imaging, the mouse was anesthetized with inhaled isoflurane. Fluorescein sodium at a concentration of 5%, 200 μL was administered intravenously into the tail vein of a nude mouse to generate contrast. Fluorescence images were collected at 10 and 25 fps from the mucosal surface of the colon and the hind limb, respectively (fig. 7). The probe was placed in contact with the tissue surface and was moved manually across the area of interest.
Fig. 7.
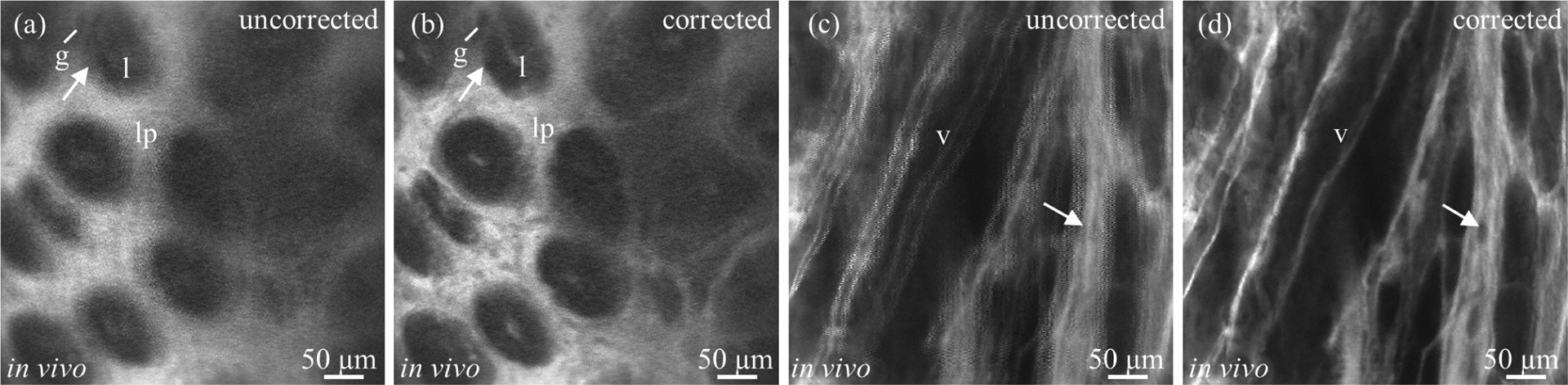
(a, b) Comparison of in vivo fluorescence images before and after phase correction. A normal colonic mucosa from a mouse was imaged. Individual crypts (arrow), including glands (g), lumen (l), and lamina propria (lp), could be identified in the corrected image. (c,d) A saphenous vein from the hind limb of a mouse was imaged. Individual vessels (v) and blood cells (arrow) could be identified in the corrected image. Contrast was provided by intravenous injection of fluorescein.
The scanner in the probe used for mouse colon imaging had parametric resonance at fx= 27680 Hz, fy= 6540 Hz. The phase of ϕx = 17.143 deg, ϕy = 11.543 deg were identified by using a generic fluorescence target before the in-vivo experiment. LabVIEW was used for real-time in-vivo imaging, and it is hypothesized that the MEMS scanner experienced phase shift due to environmental variation, producing blurred images shown in fig. 7(a). Environmental factors, such as temperature variations and mechanical stress were most likely to be the cause of phase perturbations. Phase correction was performed offline using LabVIEW and the estimated phase values are tabulated in table III. The estimates by both the metrics agree with each other. During the implementation of algorithm the problem of missing pixels, as discussed in section VI–A, was tackled by reconstructing the image at reduced size during global search, however, for the local search full size image was used. Remaining missing pixels were filled using moving median with window size of 5 pixels.
TABLE III.
Phase and error estimation for in-vivo images
| Mouse colon fx = 27680 Hz, fy = 6540 Hz |
Mouse hind limb thigh fx = 24200 Hz, fy = 5650 Hz |
||||||
|---|---|---|---|---|---|---|---|
| Lab-setting | Threshold | Variance | Lab-setting | Threshold | Variance | ||
| Estimated phase along x-axis | 17.143 | 19.710 | 19.824 | 9 | 11.516 | 11.459 | |
| Estimated phase change | - | 2.567 | 2.681 | - | 2.516 | 2.459 | |
| Estimated phase along y-axis | 11.543 | 12.834 | 12.949 | 1.8 | 1.375 | 1.490 | |
| Estimated phase change | - | 1.291 | 1.406 | - | −0.425 | −0.310 | |
Representative improvements in image quality after phase correction using threshold metric can be seen in fig. 7(b). The image produced using variance metric has no appreciable difference compared to fig. 7(b), and is not shown here in view of limited space. The fluorescence image of mouse hind limb thigh was taken at 25 fps using another probe with scanning parameters as mentioned in the table III. The image (fig. 7(d)) after phase correction shows significant improvement in the image quality, for instance, blood cells (arrow) could be clearly identified. It can be concluded that the phase along the fast axis drifted by almost 2.5 deg for both the experiments, while the average phase drift along the slow axis is 1.345 deg and −0.367 deg in mouse colon and thigh imaging respectively. It should be noted that only these drifts in phase should correspond directly to changes in the underlying dynamics, while the absolute measures of phase may include additional delays due to data acquisition and pre-processing, unknown but considered fixed for a given hardware configuration.
VI. Discussion
A. Effect of missing pixels
We note that the Lissajous scan trajectory depends on driving frequencies and the relative phase difference between them. A repeating or non-repeating pattern is obtained depending on whether the ratio of driving frequencies, , is a rational or irrational number, respectively. A non-repeating curve is often desired as different pixels are scanned in each cycle (i.e. one cycle of the lower frequency), thereby covering more area on the object plane and improving the fill factor (FF). FF can be defined as a ratio of the number of pixels scanned at least once to the total possible number of pixels in the image. In a high definition (HD) image, FF can be made sufficiently high by scanning for a long time, which results in lower frame rate. This leads to a trade-off between FR and FF; it is difficult to maximize both for an HD image. In a high FR application using Lissajous scan, it is inevitable to have some missing pixels in the reconstructed image. As a mitigating factor, various algorithms can be used to fill these missing pixels in a post-processing step after initial image reconstruction, or an image with reduced size can be reconstructed. However, it is difficult to eliminate these missing pixels during the phase prediction as this step precedes all others.
As mentioned earlier a total of 106 samples were taken to simulate the raw data from the image in fig. 3(a), which is 26 times the total number of pixels in the image. These many samples were enough to reconstruct the image such that there are no missing pixels. However, to study the effect of missing pixels on blur and sharpness metric, we tested phase tracking using only quarter of total samples in the raw data i.e. the first 0.25 × 106 samples. The missing pixels are flagged by a separate color in the image reconstructed with true phase information as shown in fig. 8(a). The plot of the threshold metric vs phase is shown in fig. 8(b) with a solid line. As compared to the fig. 5(b) this time the threshold metric has more high frequency variation with respect to ϕy. The percentage of missing pixels in an image as a function of ϕy is plotted on the right y-axis of the plot given in fig. 8(b). As evident from the plot, the high frequency noise peaks in the threshold metric match with the missing pixels. The sharpness-based phase prediction method will also suffer if the image has missing pixels as shown in fig. 8(c). In the extreme case, the phase prediction method may fail if the contribution of missing pixels to the variance metric exceeds the depth of the global minimum at the true phase.
Fig. 8.
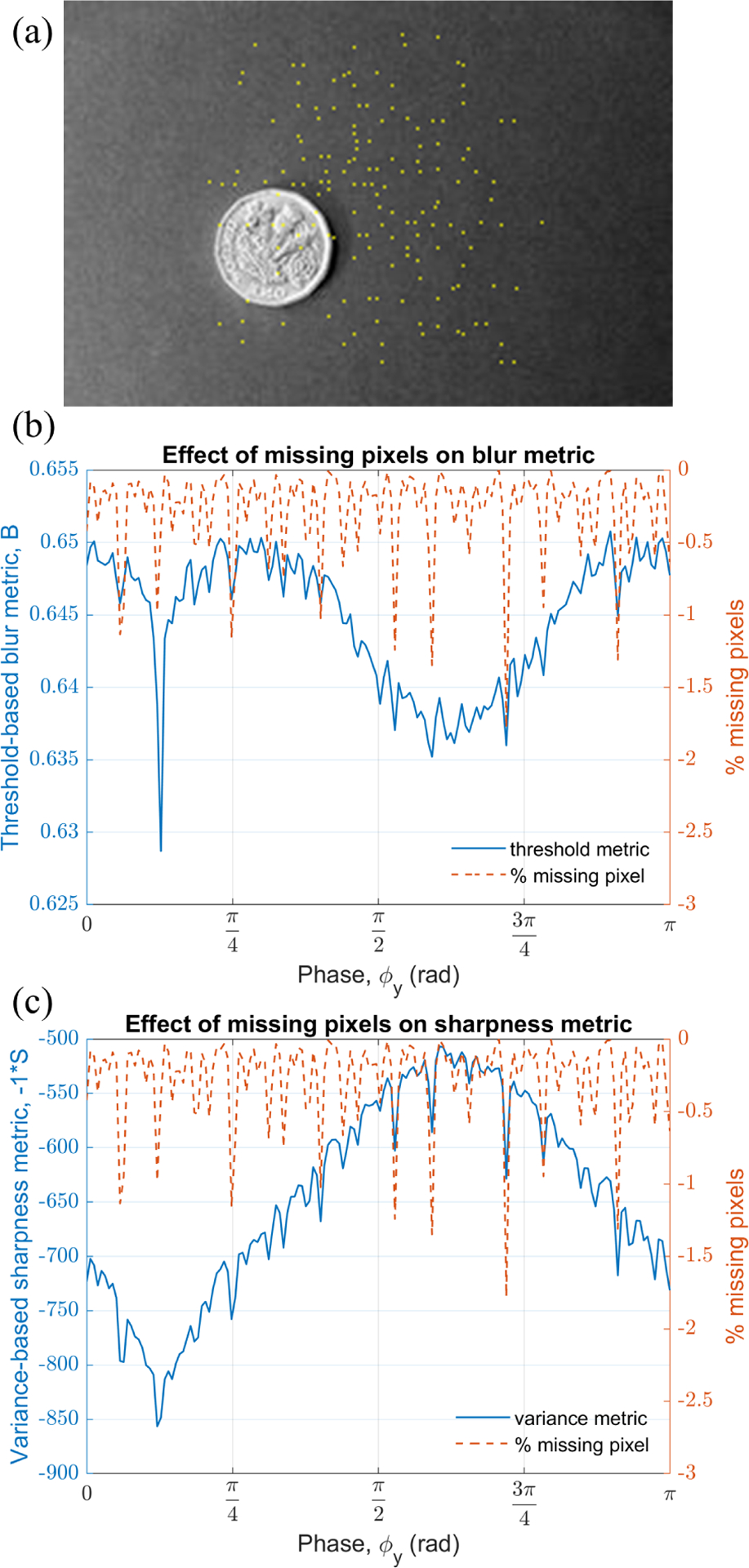
(a) High FR image with missing pixels, (b) and (c) plot of threshold and variance metric, respectively, with respect to phase y demonstrating the effect of missing pixels.
B. Practical choice of threshold used for binarizing
As a practical matter, the algorithm works most effectively when the threshold (σ) is selected close to the mean of the raw data, i.e. when because this approximately balances the count of zeroes and ones in binarized data. Selecting a smaller value for the threshold increases the count of ones, and in the reconstructed image there will be some overlap of ones at all candidate phase. Thus, the sensitivity of the threshold metric to the change in candidate phase is reduced. If ones are too sparse, i.e., the threshold metric is almost constant with respect to phase and has a very steep slope near the true phase value. As a result, true phase may be missed by discrete steps taken while sweeping candidate phase values.
C. Effect of binarizing before or after image reconstruction
In a threshold-based blur metric, there are two potential ways to binarize the data. First, the raw data R itself can be binarized to construct the B/W image using eq. (13) directly. Second, a grey image I can be made from raw data and later binarized to a B/W image. In this section, we study the effect of binarizing the raw data R vs a grey image I. fig. 9(a) represents the first case where raw data R is binarized using threshold values and fig. 9(b) shows a grey image I binarized using threshold values. As seen from the fig. 9(a) all the pseudo images of the coin are preserved and remain evident on choosing an appropriate threshold value. While in case (b), some of the pseudo images of the coin are lost. Thus, it is important to binarize the raw data before the image is formed for better detection of phase with increased sensitivity.
Fig. 9.

(a) A binary filter applied to raw data to obtain B/W image directly, (b) A binary filter applied to grey image constructed from raw data.
D. Computation time comparison
In Lissajous scanning, to mitigate the missing pixels one need to oversample the object by an order of magnitude more compared to total number of pixels in the targeted image, as discussed in section VI–A. This poses a big challenge for phase prediction in real time imaging. The computation time to predict phase error using either sharpness or blur metric is dominated by the step in which enormous samples in a raw data R are mapped to respective pixel location for each test phase. As the memory location is not accessed sequentially due to Lissajous scanning, this becomes the bottleneck in speeding up the algorithm. However, most operations in evaluating the threshold metric are binary, because of eq. (13), making it faster compared to the variance metric in predicting the phase errors. We compared the time taken by both the methods in estimating the phase by performing a global search (158 test phases) on standard images with parameters same as described in sections V–A and V–B. Matlab was used to run 12 iterations of the global search on a machine having 8GB RAM, Intel(R) Core(TM) i7-7700HQ CPU, 2.80GHz, on a single processor, and the average time taken for evaluating metrics per test phase is reported in table IV. The threshold metric took on an average 17.49 ms compared to 19.45 ms by the variance metric. On an average, the estimated computation time breakdown for threshold and variance metric algorithm, respectively, is as follows: the image reconstruction steps took 17.42 ms and 19.34 ms, while evaluation of metrics itself just took 0.02 ms and 0.04 ms, and rest of the time was spent on other computations. It should be noted that all these figures represent qualitative performance of the metrics. The overheads due to time profiling may affect the relative proportion of actual time spent on each line of code. The total computation time may significantly differ on optimizing the code, implementing the code in different coding language, and/or machine.
TABLE IV.
Qualitative comparison of average computation time taken to evaluate a metric per test phase
| Threshold metric time (ms) | Variance metric time (ms) | |
|---|---|---|
| Human colon | 17.96 | 19.79 |
| SS adenoma tissue | 17.84 | 19.69 |
| Colon tissue | 17.29 | 19.21 |
| Chemical plant | 17.23 | 19.29 |
| Lake | 17.14 | 19.26 |
| Mean | 17.49 | 19.45 |
E. Comparison between threshold and variance metrics
We have discussed particular cases of sharpness and blur metric application, i.e., variance and threshold-based metrics, respectively, that can determine the phase value for high quality image reconstruction of a Lissajous-scanned image. A summary of the strengths and weaknesses of the two methods are as follows: In the threshold-based blur metric the global phase search results may be sensitive to the value of threshold parameter σ. The optimum value of σ may be different for different images which make the implementation of threshold-based method less robust. The variance metric is threshold-free, making it very robust in predicting the phase. However, the computation time for the threshold metric is 10% less than the variance metric as the former involves working with binary variables. The faster method can be desirable in some real-time imaging applications such as endomicroscopy, especially if computational resources are limited. In addition, the threshold-based metric is also observed to provide a more prominent local minimum than the variance-based sharpness metric in all sample images.
VII. Conclusion
In this paper, sharpness-based image processing metrics to correct for phase delay in a Lissajous-style MEMS scanner are introduced. A novel threshold-based blur metric is developed which binarizes the raw data to predict the phase error in the reconstructed image in a computationally efficient form. A variance-based sharpness metric is also implemented to able to successfully determine the true phase value. In high FR imaging application, missing pixels being inevitable adversely affects both the metrics and may lead to error in results. It is observed that threshold metric is less robust compared to the variance metric in global search, however, the threshold metric is faster as it involves calculation with binary variables and is better suited to real-time phase correction. Both of these metrics have been experimentally demonstrated to be effective in compensating for phase error in practical implementation with a MEMS-based endomicroscope. Similar algorithms could be extended to other potential applications involving single pixel imaging or projection.
As future work, a variety of other image-based metrics inspired by autofocus and related algorithms could conceptually be adapted for use in MEMS scanner phase tracking. The proposed blur and sharpness metrics were selected based on potential for leveraging specific Lissajous properties versus correspondence to high-popularity approaches in other applications, respectively, but we acknowledge that this is not an exhaustive exploration of candidate criteria. Other potential improvements include dynamic thresholding of binary data and/or further analysis to reduce computation time, in order to further facilitate high-speed, real-time endoscopic imaging.
Acknowledgment
The authors thank Jing Chen, and Sangeeta Jaiswal for helping in taking the in-vivo and ex-vivo tissue images. The authors thank the National Institutes of Health, award R01-EB-020644, for support of this work. The authors thank staff and members of the Lurie Nanofabrication Facility at the University of Michigan for providing support during the fabrication of devices.
This work was supported in part by the National Institutes of Health (Grant R01-EB-020644).
Biographies

Mayur Birla received the B.Tech. degree in mechanical engineering from Visvesvaraya National Institute of Technology, Nagpur, India in 2011 and the M.E. mechanical engineering from Indian Institute of Science (IISc), Bangalore, India in 2015. He is currently pursuing the M.S. in electrical engineering and the Ph.D. in mechanical engineering at University of Michigan, Ann Arbor, USA.
From 2011 to 2013, he was a Systems Engineering at BrahMos aerospace private limited, India. His research interest includes development of two photon endomicroscopy system compatible with commercially used endoscopes. He is recipient of ‘Best student’ in mechanical engineering at IISc, Bangalore and member of honor societies Tau Beta Pi, and Phi Kappa Phi.

Xiyu Duan received the B.S degree in electrical engineering from Hong Kong University of Science and Technology, Hong Kong, China, in 2010, and the Ph.D. degree in biomedical engineering from the University of Michigan, Ann Arbor, MI, USA, in 2016.
His research focued on MEMS based fiber endomicroscopes to for real time optical biopsy. He is currently an hardware engineer at Apple Inc.

Haijun Li received the Ph.D. degree in microelectronics and solid-state electronics from Jilin University, Changchun, China, in 2007. He held a post-doctoral position at Nanyang Technology University, Singapore, from 2008 to 2011. He was a Senior Engineer at the Hebei Semiconductor Research Institute, Shijiazhuang, China, from 1997 to 2008.
He is currently a Research Investigator with the University of Michigan, Ann Arbor, MI, USA, where he is involved in the development of MEMS-based endomicroscope. His research interests include MEMS, uncooled infrared detectors, epi-MEMS technology, and wafer level packaging technologies.

Miki Lee received the B.S.E. degree in aerospace engineering from the University of Michigan, Ann Arbor, USA, in 2015, and the M.E. degree in space engineering from the University of Michigan, Ann Arbor, USA, in 2016.
She is currently a Research Lab Specialist Inter. with the Department of Internal Medicine, University of Michigan. Her research focuses on the development of MEMS-based endomicroscopy imaging systems.

Gaoming Li received the Ph.D. degree in Optics from Xiamen University, Xiamen, Fujian, China, and post-doctoral training at the Nanyang Technological University, Singapore and the University of Michigan, Ann Arbor, MI, USA. He is currently a research investigator with the University of Michigan. His research interests include optical endomicroscopy, photoacoustic, optical design and speckle.

Thomas D Wang received the B.S. degree in mathematics and physics from Harvey Mudd College, Claremont, CA, USA, in 1985, and the Ph.D. degree in medical engineering and medical physics from the Massachusetts Institute of Technology, Cambridge, MA, USA, in 1996.
He is currently a Professor of Medicine, Biomedical Engineering, and Mechanical Engineering at the University of Michigan and the H. Marvin Pollard Collegiate Professor of Endoscopy Research. He has developed a number of microsystems-based technologies to perform scanning and actuation for high speed imaging with large working distance in endomicroscopy. His research interests are in the field of biomedical optics, multiplexed detection, and molecular imaging.

Kenn R Oldham received the B.S. degree in mechanical engineering from Carnegie Mellon University, Pittsburgh, PA, USA, in 2000, and the Ph.D. degree in mechanical engineering from the University of California at Berkeley, Berkeley, CA, USA, in 2006.
He is currently an Associate Professor of Mechanical Engineering at the University of Michigan. His research focuses on the intersection of control systems and micro-scale sensing and actuation, with interests in design for controllability, optimal and robust control, microsystem estimation and identification, and novel sensor and actuator design. Applications include terrestrial micro-robotics, endoscopic microscopy, and inertial and physiological sensing.
Contributor Information
Mayur Birla, Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI, 48109 USA.
Xiyu Duan, University of Michigan, Ann Arbor, MI 48109, USA; Apple Inc., Cupertino, CA 95014, USA.
Kenn Oldham, Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI, 48109 USA.
References
- [1].Duan X, Li H, Wang F, Li X, Oldham KR, and Wang TD, “Three-dimensional side-view endomicroscope for tracking individual cells in vivo,” Biomedical optics express, vol. 8, no. 12, pp. 5533–5545, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Salapaka SM and Salapaka MV, “Scanning probe microscopy,” IEEE Control Systems Magazine, vol. 28, no. 2, pp. 65–83, 2008. [Google Scholar]
- [3].Lee S-H, Moon JJ, and West JL, “Three-dimensional micropatterning of bioactive hydrogels via two-photon laser scanning photolithography for guided 3d cell migration,” Biomaterials, vol. 29, no. 20, pp. 2962–2968, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Li H, Duan X, Qiu Z, Zhou Q, Kurabayashi K, Oldham KR, and Wang TD, “Integrated monolithic 3d mems scanner for switchable real time vertical/horizontal cross-sectional imaging,” Optics express, vol. 24, no. 3, pp. 2145–2155, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Holmström ST, Baran U, and Urey H, “Mems laser scanners: A review,” Journal of Microelectromechanical Systems, vol. 23, no. 2, pp. 259–275, 2014. [Google Scholar]
- [6].Hwang K, Seo Y-H, Ahn J, Kim P, and Jeong K-H, “Frequency selection rule for high definition and high frame rate lissajous scanning,” Scientific reports, vol. 7, no. 1, pp. 1–8, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Ishikawa N, Ikeda K, and Sawada R, “Temperature dependence of the scanning performance of an electrostatic microscanner,” Journal of Micromechanics and Microengineering, vol. 26, no. 3, p. 035002, 2016. [Google Scholar]
- [8].Csencsics E and Schitter G, “Design of a phaselocked-loop-based control scheme for lissajous-trajectory scanning of fast steering mirrors,” in 2017 American Control Conference (ACC), IEEE, 2017, pp. 1568–1573. [Google Scholar]
- [9].Pannu S, Chang C, Muller R, and Pisano A, “Closed-loop feedback-control system for improved tracking in magnetically actuated micromirrors,” in 2000 IEEE/LEOS International Conference on Optical MEMS (Cat. No. 00EX399), IEEE, 2000, pp. 107–108. [Google Scholar]
- [10].Csencsics E and Schitter G, “System design and control of a resonant fast steering mirror for lissajous-based scanning,” IEEE/ASME Transactions on Mechatronics, vol. 22, no. 5, pp. 1963–1972, 2017. [Google Scholar]
- [11].Morrison J, Imboden M, and Bishop DJ, “Tuning the resonance frequencies and mode shapes in a large range multi-degree of freedom micromirror,” Optics express, vol. 25, no. 7, pp. 7895–7906, 2017. [DOI] [PubMed] [Google Scholar]
- [12].Loewke NO, Qiu Z, Mandella MJ, Ertsey R, Loewke A, Gunaydin LA, Rosenthal EL, Contag CH, and Solgaard O, “Software-based phase control, video-rate imaging, and real-time mosaicing with a lissajous-scanned confocal microscope,” IEEE Transactions on Medical Imaging, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Santos A, Ortiz de Solórzano C, Vaquero JJ, Pena JM, Malpica N, and del Pozo F, “Evaluation of autofocus functions in molecular cytogenetic analysis,” Journal of microscopy, vol. 188, no. 3, pp. 264–272, 1997. [DOI] [PubMed] [Google Scholar]
- [14].Groen FC, Young IT, and Ligthart G, “A comparison of different focus functions for use in autofocus algorithms,” Cytometry: The Journal of the International Society for Analytical Cytology, vol. 6, no. 2, pp. 81–91, 1985. [DOI] [PubMed] [Google Scholar]
- [15].Mendelsohn ML and Mayall BH, “Computer-oriented analysis of human chromosomes—iii. focus,” Computers in biology and medicine, vol. 2, no. 2, pp. 137–150, 1972. [DOI] [PubMed] [Google Scholar]
- [16].Shahid W, Qiu Z, Duan X, Li H, Wang TD, and Oldham KR, “Modeling and simulation of a parametrically resonant micromirror with duty-cycled excitation,” Journal of Microelectromechanical Systems, vol. 23, no. 6, pp. 1440–1453, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Li H, Barnes P, Harding E, Duan X, Wang TD, and Oldham KR, “Large-displacement vertical electrostatic microactuator dynamics using duty-cycled softening/stiffening parametric resonance,” Journal of Microelectromechanical Systems, vol. 28, no. 3, pp. 351–361, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Yao Y, Abidi B, Doggaz N, and Abidi M, “Evaluation of sharpness measures and search algorithms for the auto-focusing of high-magnification images,” in Visual Information Processing XV, International Society for Optics and Photonics, vol. 6246, 2006, 62460G. [Google Scholar]
- [19].Chen Y, Lee M, Birla MB, Li H, Li G, Duan X, Wang TD, and Oldham KR, “Motion estimation for a compact electrostatic microscanner via shared driving and sensing electrodes in endomicroscopy,” IEEE/ASME Transactions on Mechatronics, vol. 25, no. 2, pp. 661–672, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Li G, Duan X, Lee M, Birla M, Chen J, Oldham KR, Wang TD, and Li H, “Ultra-compact microsystems-based confocal endomicroscope,” IEEE Transactions on Medical Imaging, vol. 39, no. 7, pp. 2406–2414, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]


