DIFFEOMORPHIC REGISTRATION FOR RETINOTOPIC MAPPING VIA QUASICONFORMAL MAPPING

Abstract

Human visual cortex is organized into several functional regions/areas. Identifying these visual areas of the human brain (i.e., V1, V2, V4, etc) is an important topic in neurophysiology and vision science. Retinotopic mapping via functional magnetic resonance imaging (fMRI) provides a non-invasive way of defining the boundaries of the visual areas. It is well known from neurophysiology studies that retinotopic mapping is diffeomorphic within each local area (i.e. locally smooth, differentiable, and invertible). However, due to the low signal-noise ratio of fMRI, the retinotopic maps from fMRI are often not diffeomorphic, making it difficult to delineate the boundaries of visual areas. The purpose of this work is to generate diffeomorphic retinotopic maps and improve the accuracy of the retinotopic atlas from fMRI measurements through the development of a specifically designed registration procedure. Although there are sophisticated existing cortical surface registration methods, most of them cannot fully utilize the features of retinotopic mapping. By considering unique retinotopic mapping features, we form a quasiconformal geometry-based registration model and solve it with efficient numerical methods. We compare our registration with several popular methods on synthetic data. The results demonstrate that the proposed registration is superior to conventional methods for the registration of retinotopic maps. The application of our method to a real retinotopic mapping dataset also results in much smaller registration errors.

1. INTRODUCTION

It is an important topic in vision science and neurobiology to identify and analyze visual areas of the human brain (i.e. the visual atlas) [1, 2]. Retinotopic mapping with functional magnetic resonance imaging (fMRI), provides a non-invasive way to delineate the boundaries of the visual areas [3, 4]. It is well known in neurophysiology that retinotopic mapping is locally diffeomorphic (i.e. smooth, differentiable, and invertible) within each local area [5, 4]. However, the decoded visual coordinates from fMRI retinotopic mapping studies are not guaranteed to be diffeomorphic because of the low signal-noise ratio of fMRI. The non-diffeomorphic problem is more severe near the most important fovea region because the size of the neuronal receptive field is much smaller and the retinotopic organization is more complicated [2]. As a result, it is difficult and unreliable to directly delineate the visual atlas from a single subject’s retinotopy.

To get a better visual atlas, especially for the fovea, it is preferable to use more subjects and take advantage of the group average. However, individuals’ visual regions are different in size, shape and even location [6]. Directly averaging several individuals’ retinotopic maps cannot improve the result. Indeed, there are lots of methods and packages to register cortical surfaces, e.g. FreeSurfer [6], FSL [7], and BrainSuite [8]. Although very advanced, most of the methods are designed for diffeomorphic cortical wrapping using anatomical scalar information (e.g. curvature, thickness) only.

There is an opportunity to use retinotopic maps to improve registration of cortical areas. First, unlike image registration where only scalar features are available, retinotopic mapping associates an estimated visual coordinate (although noisy) to each location of the visual cortex. Second, the quality of the estimated visual coordinates can be assessed with performance metrics, which can help us emphasize high-quality locations and under-weight poor-quality locations [3]. Benson and colleagues[9] have taken advantage of these features to register retinotopic measurements to a template. Their algorithm morphs the subject’s surface to fit template data and introduces several penalties to avoid overstretching. However, these penalties severely compromise registration accuracy.

Can we model retinotopic registration, especially the diffeomorphic constraint? It is easy to quantify visual coordinate differences after registration, e.g., with Euclidean distance. The question is how to define and quantify diffeomorphism. Fortunately, diffeomorphism has been long discussed in geometry. We use the Beltrami coefficient [10], an important concept in quasiconformal geometry, to quantify the diffeomorphic condition and model the registration as a function optimization problem with constraints. Our method eliminates redundant registration limitations and ensures diffeomorphic result. Then we apply the linear Beltrami solver [11] to solve the registration model. Our model may also adopt human-based landmarks as a rough/precise guideline to help registration. The proposed method improves the accuracy and robustness of retinotopic map registration.

2. PROBLEM RESTATEMENT

2.1. Retinotopic Mapping

We briefly introduce the idea of retinotopic mapping via fMRI. Assume a unit illumination light spot is on point $v=\left(v^{(1)},v^{(2)}\right)\in {ℝ}^2$ in the visual field, as shown in Fig. 1. After the visual system’s processing, the light spot will eventually activate a population of neurons. The main purpose of retinotopic mapping is to find, the center v and the extent $\sigma \in {ℝ}^{+}$ of its receptive field on the retina, for each point $P=(X,Y,Z)\in {ℝ}^3$ on visual cortex.

Fig. 1.

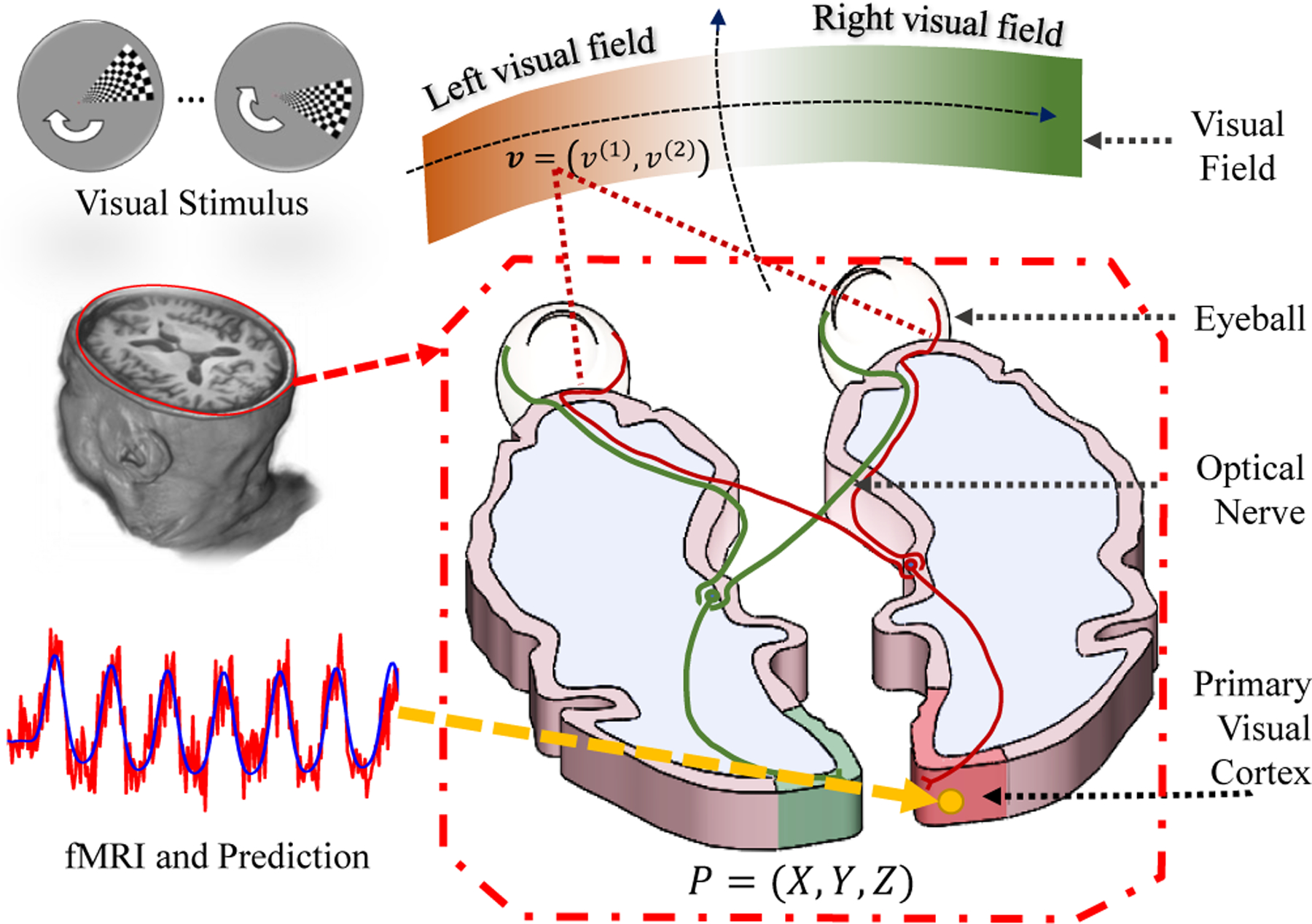
Illustration of the visual system.

fMRI provides a noninvasive way to determine v and σ for P, based on the following procedure. (1) Design a stimulus time sequence s (t; v), such that the stimulus sequence is unique for every visual coordinate, i.e., s (t; v₁) ≠ s (t; v₂), ∀ v₁ ≠ v₂; (2) Present the stimulus sequence to an individual and record the fMRI signals from the visual cortex; (3) For each fMRI time sequence on a cortical location, y (t; P), determine the corresponding receptive field, including its central location v and its size σ on the retina, that most-likely generated the fMRI signals. Specifically, given the neurons’ spatial response r (v′; v, σ) (a predefined model depicts of neural response around v) and the hemodynamic response function h (t) (a model of the time course of neural activation to a stimulus), the predicted fMRI signal can be written as:

$$\widehat{y}(v,\sigma )=\beta \left(\int r\left(v\prime ;v,\sigma \right)s\left(t;v_x,v_y\right)dv\prime \right)*h(t)$$ (1)

where, β is a coefficient that converts the units of response to the unit of fMRI activation, and * is the convolution operator. Then the perceptive center v and perceptive field size σ are estimated by minimizing the difference between predicted signal and measurement,

$$(v,\sigma )=\text{arg}\underset{(v,\sigma )}{\text{min}}\int |\widehat{y}(v,\sigma )-y(t;P){|}^{2}dt,$$ (2)

The retinotopic mapping of the entire visual cortex is obtained when (v,σ) is solved for every point on the cortical surface. The goodness of the estimation for each location is inferred by the variance explained, $R^2=\int |\widehat{y}-\overline{y}{|}^{2}dt/\int |y-\overline{y}{|}^{2}dt$.

2.2. Mathematical Model

In practice, cortical surface S is usually represented by a set of vertices P_S = {P₁, P₂, …, P_n} = {P_i} and triangular faces F_S = {F_i}, denoted by S_S = (F_S,P_S). The fMRI signal is decoded for each location on cortical surface P_i ∈ P_S according to Eq. (2). The decoding process generates a raw visual coordinate v_i, perception size σ_i and variance explained $R_i^2$ for each vertex P_i. We use $S=\left(F_S,P_S,v_s,{\sigma }_s,R_s^2\right)$ to denote the bundle data of cortical surface as well as the raw retinotopic measurements. Here we use capitalized subscript to denote all data of a subject, e.g. P_S means all the point collection of the subject, and lowercase subscript to denote data of a point, e.g. P_i is for i–th point of the subject. If the visual coordinate v_S is accurate, then the visual atlas is of high quality. However, v_S is greatly influenced by the fMRI signal-noise ratio, head movement, subject’s behavior and so on [12].

How can we assign a new visual coordinate $\widehat{v}$, such that it is most likely inferred by the measurements from all the subjects’ data? One promising approach is registering each subject to a presumed template or mathematical model [9, 13] and then assigning the registered template value to the subject. In this work, we wish to find a registration method and a presumed template $T=\left(F_T,P_T,v_T,{\sigma }_T,R_T^2\right)$, such that the overall registration cost from all subjects’ data to the template is minimal, i.e., T = arg min_T ∑_J R(T, S_J), where R is the registration cost between the template T and J-th subject’s data S_J.

The remaining problem is to define the diffeomorphic registration function and its cost. Obviously, it is easier to discuss the problems on 2D instead of the original 3D cortical surface. If we can find a diffeomorphic function from the cortical surface to a parametric domain, then the 3D registration can be simplified as a 2D problem, because the composite of two diffeomorphic functions is still diffeomorphic. Fortunately, a discrete conformal (angle preserving) mapping of the occipital region is handy [14]. Specifically, as shown in Fig. 2, we first define a feature point that corresponds to the fovea as the center point. We then calculate the geodesic distances from all vertices to the center point [15]. We only consider the portion of cortical surface whose geodesic distance to the center point is within a certain value, and map this patch to a unit disk, $c:P\mapsto u,u=\left(u^{(1)},u^{(2)}\right)\in {ℝ}^2$. Similarly, we obtain a similar portion of cortical surface and map it to a parametric space, $c\prime :P\prime \mapsto u\prime ,u\prime =\left(u{\prime }^{(1)},u{\prime }^{(2)}\right)\in {ℝ}^2$ for template cortical surface (Fig. 2(c) gray color region). If we find a registration function f : u ↦ u′ in the parametric space, we can get the registration for the two cortical mesh as P′ = c⁻¹ ○ f ○ c (P). Ideally, f tries to: (1) minimize the retinotopic visual coordinate differences between the subject and the template, i.e. ∫ w |v_s (f) − v_T |² du (w is proportional to the variance R²); (2) ensure diffeomorphism; (3) introduces some smoothness. In geometry, diffeomorphism can be quantified by Jacobian, Beltrami coefficient, and etc.

Fig. 2.

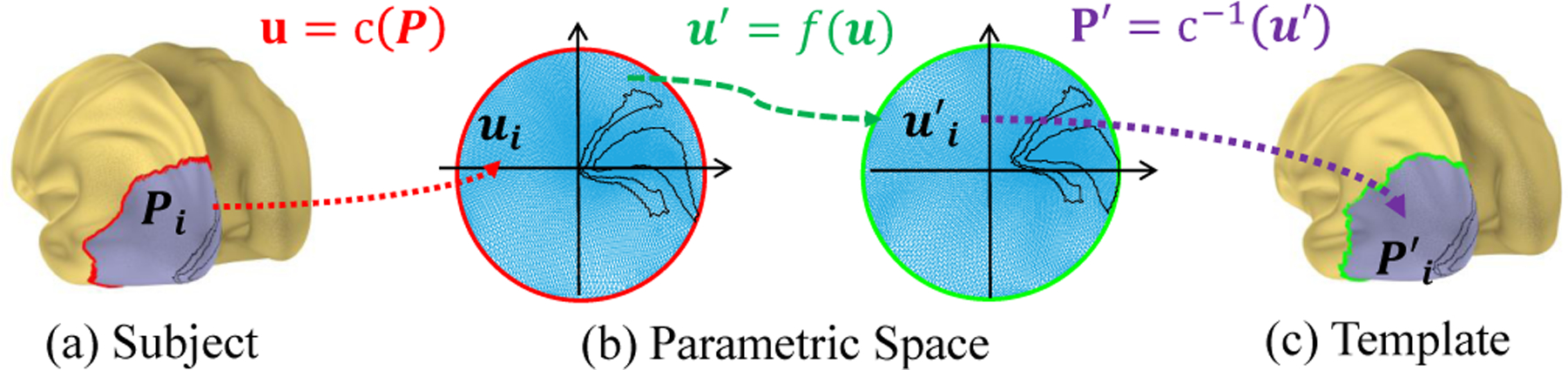
Illustration of several spaces and registration.

We adopt Beltrami coefficient to quantify the diffeomorphism, considering that Beltrami coefficient also quantifies angle deviation. The reason we care about angle deviation is that previous work shows retinotopic mapping preserve angle to a considerable extent [16]. Since cortical surface is conformal to visual space to some extent and we map cortical surface to the parametric space by conformal mapping, the registration f should also preserve the angle to some extent. The Beltrami coefficient, associated with f is defined as,

$${\mu }_f=\left(\frac{\partial f}{\partial u^{(1)}}+i\frac{\partial f}{\partial u^{(2)}}\right)/\left(\frac{\partial f}{\partial u^{(1)}}-i\frac{\partial f}{\partial u^{(2)}}\right).$$ (3)

If |μ_f|1 < 1 then f is diffeomorphic. Considering the diffeomorphic condition, angle minimization, and smoothness requirements, we seek f minimizing the energy in Eq. (5),

$$E=\int w{|v_S(f)-v_T|}^2+{\lambda }_1{|{\mu }_f|}^2+{\lambda }_2|\nabla f{|}^{2}du.$$ (4)

2.3. Numerical Method

It is extremely costly to minimize energy in Eq. (4) directly as it mixes Beltrami coefficient μ_f and mapping function f. The solution is to alternatively solve with respect to the mapping function and Beltrami coefficient in separate steps. Unavoidably, we need tools to convert the mapping function and Beltrami coefficient back and forth.

2.3.1. Beltrami Coefficient

Given the explicit form of function f, we can compute the Beltrami coefficient μ_f according to (Eq. 3). In the discrete case, f is interpreted linearly on each triangle. As shown in Fig. 3(a), for u within the triangle, f (u) = α_iv_i + a_jv_j + α_kv_k, where v_i = f_c (u_i) , v_j = f_c (u_j), and v_k = f_c (u_k). The coefficients α_i,α_j,α_k are called the barycentric coefficients. Specifically, α_i (similarly for α_j and α_k) is the area portion of triangle Δuu_ju_k relative to Δu_iu_ju_k, i.e. α_i = Area (Δuu_ju_k) / Area (Δu_iu_ju_k). Now we can compute the Beltrami coefficient ${\mu }_{f_c}$ according to (Eq. 3).

Fig. 3.

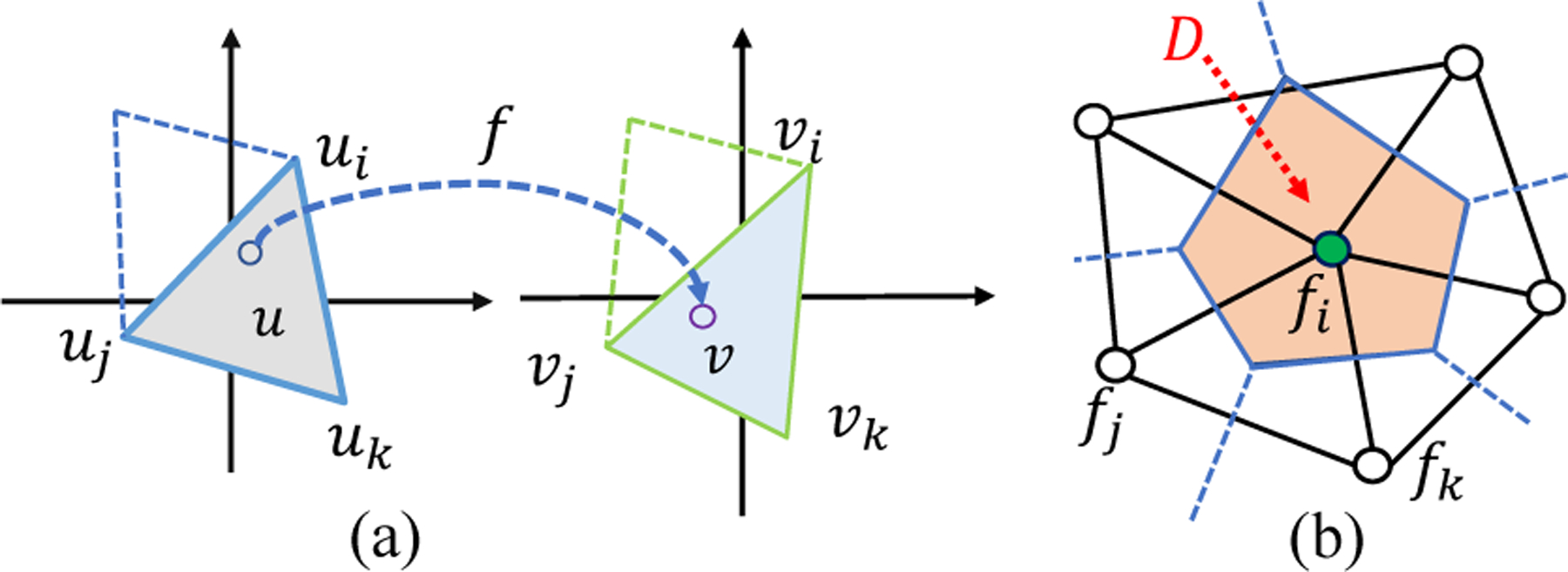
(a) Illustration of approximate the mapping in discrete; (b) The divergence approximation on the vertex ring.

2.3.2. Linear Beltrami Solver (LBS)

We briefly introduce the LBS to recovery function f = (f⁽¹⁾, f⁽²⁾) for the given Beltrami coefficient μ = ρ + iτ. It is first introduced in [17, 11]. According to the definition, i.e. Eq. (4), we have,

$$\left(\frac{\partial f}{\partial u^{(1)}}+i\frac{\partial f}{\partial u^{(2)}}\right)/\left(\frac{\partial f}{\partial u^{(1)}}-i\frac{\partial f}{\partial u^{(2)}}\right)=\rho +i\tau .$$ (5)

After re-organizing Eq. (5) and eliminating f⁽²⁾, we derive,

$$\nabla \cdot A\nabla f^{(1)}=0,$$ (6)

where $A=\left(\begin{array}{ll}{\alpha }_1\hfill & {\alpha }_2\hfill \\ {\alpha }_2\hfill & {\alpha }_3\hfill \end{array}\right)$, ${\alpha }_1=\frac{{(\rho -1)}^2+{\tau }^2}{1-{\rho }^2-{\tau }^2}$, ${\alpha }_2=\frac{-2\tau }{1-{\rho }^2-{\tau }^2}$ and ${\alpha }_3=\frac{1+2\rho +{\rho }^2+{\tau }^2}{1-{\rho }^2-{\tau }^2}$, ∇f⁽¹⁾ = (∂f⁽¹⁾/∂u⁽¹⁾ + ∂f⁽¹⁾/∂u⁽²⁾), and the divergence ∇ on vector G = A∇f⁽¹⁾ = (G⁽¹⁾, G⁽²⁾) is defined as ∇·G = ∂G⁽¹⁾/∂u⁽¹⁾+∂G⁽²⁾/∂u⁽²⁾. By solving the partial equation Eq. (6) with certain boundary conditions, we can solve f⁽¹⁾. Similarly, f⁽²⁾ can be solved.

In the discrete case, gradient operator ∇f⁽¹⁾ (u) can be written out with the linear interpretation. For discrete divergence ∇ · G operator, it is approximated on each vertex of its dual-cell (a cell consisted of neighboring triangles’ circum-centers). In specific, as shown in Fig. 3(b), consider the center vertex with its neighbors N(u_i), we approximate ∇ · G (u_i) as the average of divergence on D, which is written as,

$$\nabla \cdot G=\frac{1}{\left|D\right|}{\int }_{\partial D}Gds=\frac{1}{|D|}\sum _{T_j\in N\left(z_i\right)}{G}_{T_j}\cdot \left(u_k-u_j\right).$$ (7)

According to these approximations, we have a set of linear equations for f_i and its neighbors. Finally, we can write Eq. (6) in a matrix form and solve f efficiently.

2.3.3. Laplacian Smoothing and Chopping

Now we can convert between the mapping function and Beltrami coefficient back and forth. During the registration, we apply the smooth operation to the function f to make the registration smooth, namely the Laplacian smoothing. In specific, for a scalar function g, we get a smooth version of g′ by solving the following equation,

$$g\prime =\text{arg}\underset{g}{\text{min}}\int |\nabla g{|}^2+\lambda \int {\left|g-g\prime \right|}^2,$$ (8)

where λ is a constant. Eq. (8) can be efficiently solved by its Euler-Lagrange equation, i.e. (−∇ · ∇ + 2λI) ν = 2λμ. We apply the smooth process to f⁽¹⁾ and f⁽²⁾, separately.

As we discussed, for diffeomorphic mapping, the Beltrami coefficient |μ| < 1. Equivalently, if there is a point whose |μ| > 1, the mapping is non-diffeomorphic. To pursue a diffeomorphic mapping, we will shrink the magnitude of |mu| and keep the argument arg μ (notice μ is a complex function), i.e. ν′ = ν/ |ν|, if |ν| > 1. This is called Chop.

2.3.4. Simple Registration Regardless Diffeomorphism

To take advantages of the features from retinotopic mapping, instead of updating the registration function using scalar features, we search (by brute-force) retinotopic visual coordinates within the nearby cortical surface region $\left|f_i^{\prime }-f_i\right|<r_0$, and update the registration by,

$$f_i^{\prime }=\text{arg}\underset{f_i^{\prime }}{\text{min}}{\left(v_{\text{S}}\left(f_i^{\prime }\right)-v_T\right)}^2,\left|f_i^{\prime }-f_i\right|<r_0$$ (9)

2.3.5. Algorithm

The overall registration process is summarized in Alg. 1.

3. RESULTS

3.1. Performance on Synthetic Data

We generate synthetic subject and template data in the scenario of retinotopic mapping according to the double-sech model, proposed by Schira et al. [13]. The subject and template data are generated by two different sets of parameters. The subject data is added with a small and big amount of uniform noise, respectively. We calculate the ground truth registration displacement from the subject to the template. Then we use several methods to register the noisy subject data to the predefined template and get registration displacement. Eventually, we report the registration error (difference between method’s registration displacement and ground truth displacement) in Tab. 1. We found (1) the proposed algorithm achieves the smallest registration error and ensures diffeomorphism (2) LDDMM and QCHR can also achieve almost diffeomorphic result, however, our method is more precise; (3) TPS is fast, but the method’s accuracy is bad; (4) LDDMM, D-Demos, and QCHR ensure diffeomorphism for image registration, however, they cannot guarantee overall diffeomorphism when we consider the visual coordinates as intensity of image; (5) Because of an alternative scheme in our method, it usually takes approximately 100 to 150 seconds to register.

Table 1.

Compare registration performance relative to the ground truth. Results for small noise and big noise cases are reported respectively (Running time is reported in average). Landmarks/anchors are given for methods with “*” a symbol.

Method	Registration Error		# Overlap Triangles	Time/(s)
	Mean	Max
TPS* [18]	0.75/4.47	1.87/14.43	2/18	0.36
Bayesian* [9]	3.89/3.98	6.59/9.45	2079/2469	110
D-Demos [19]	1.12/1.20	2.34/2.59	2377/2473	1.6
LDDMM [20]	0.59/0.64	1.27/1.49	1/1	86
QCHR* [11]	0.06/0.10	0.62/0.47	1/0	173
Proposed*	0.04/0.08	0.12/0.19	0/0	123

3.2. HCP Data

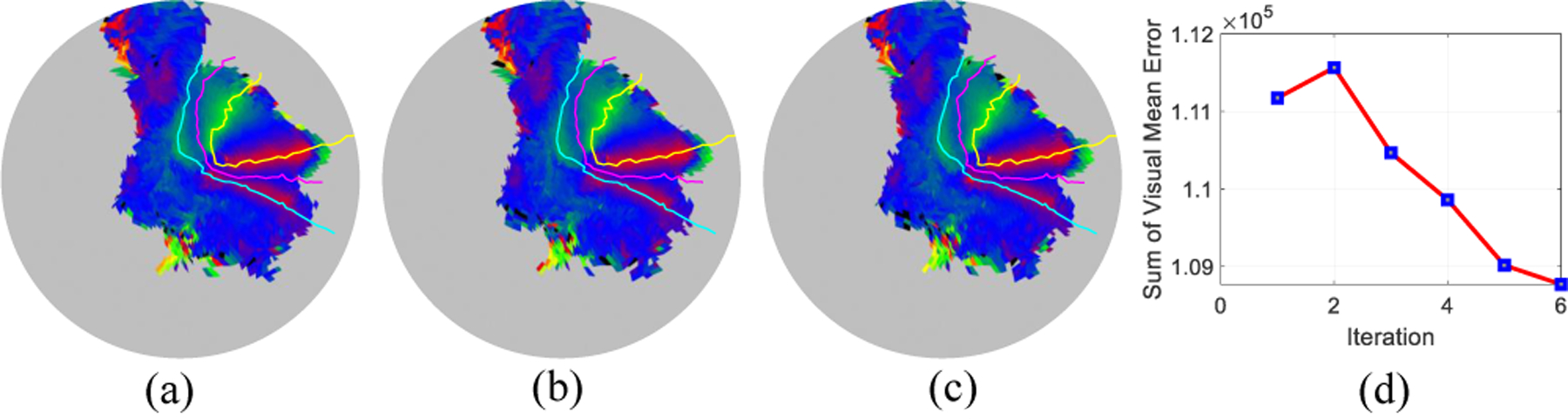
We apply our registration to the first twenty subjects of the Human Connectome Project (HCP) retinotopic dataset [21]. The original retinotopic result is available at [22]. We initialize a template by averaging the subjects’ data. Then we register all subjects’ data to the initial template. Fig. 5 shows one subject’s registration process. The curves are the boundaries of V1/V2/V3 inferred from the template. We see the before our registration (Fig. 5(a)), the boundary is not perfectly aligned especially in the fovea region. We shall mention the readers that, Fig. 5(a) result is indeed from a registration result which used both the structural as well as some fMRI feature [12]. This means our alignment can further improve the result by incorporation more retinotopic information. Besides the subject registration, We further define the overall registration cost as the sum of visual coordinate error across subjects in the dataset. After registering all subjects’ data, we take the average of the subjects and use the same method to register the template to the average data. This process is repeated until we are satisfied. Fig. 6(a)–(c) shows the first, second, and last iteration of the template, respectively. Fig. 6(d) shows the registration cost, overall visual error, is decreased during the process. The decreased overall visual error means we slightly improved the template for human retinotopic maps.

Fig. 5.

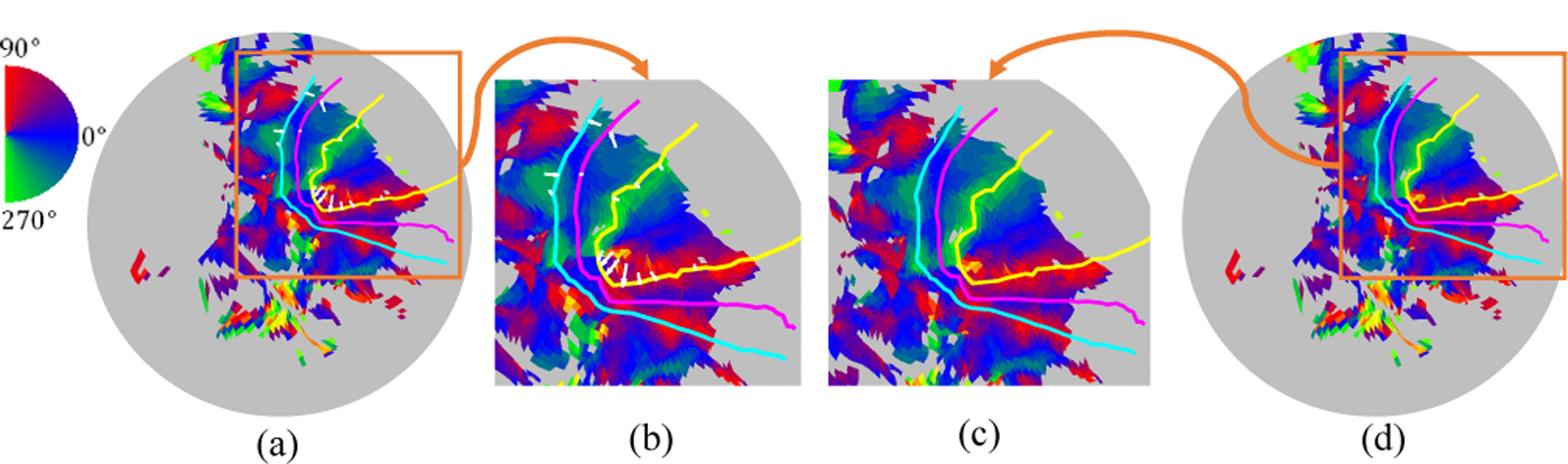
Before (left two figures) and after registration (right two figures) of the left hemisphere of the subject ‘102816’.

Fig. 6.

The template morphing process.

4. CONCLUSION AND FUTURE WORK

We proposed a model for the retinotopic registration. We plan to use this framework for higher visual regions.

Fig. 4.

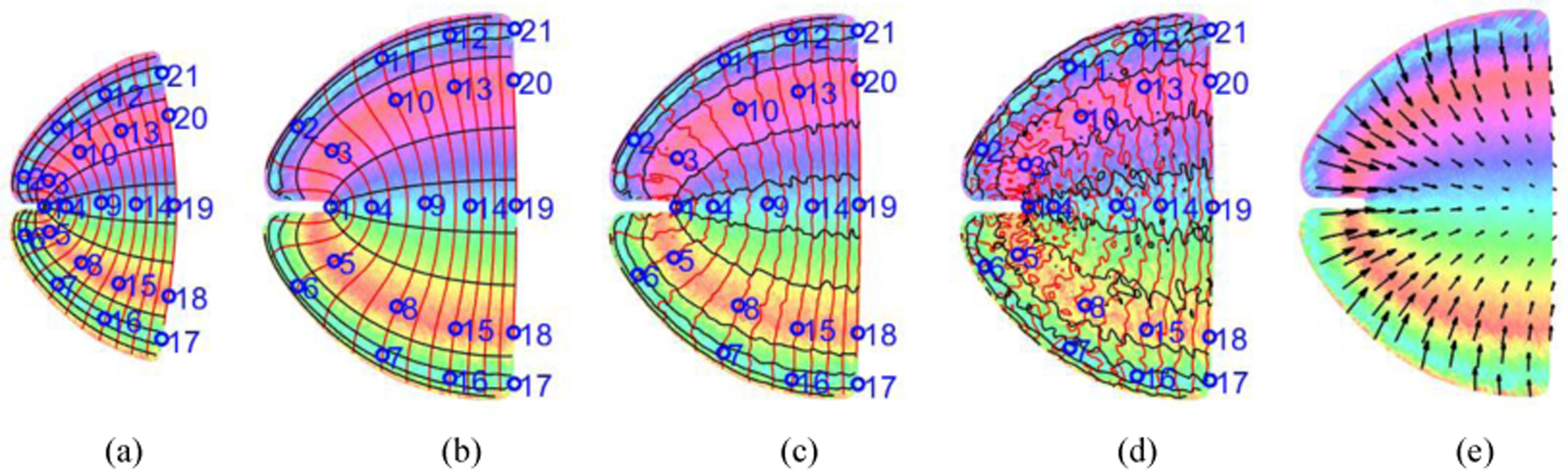
Template and subject: (a) Template; (b) Perfect subject; (c) Subject data with a small added noise (Peak Signal-Noise Ratio is 20 dB); (d) Subject data with a big added noise (Peak Signal-Noise Ratio is 10 dB); (e) Ground truth displacement. Red/black curves are for eccentricity/angle contour. Landmarks are marked for (a)-(d).