Network sampling coverage III: Imputation of missing network data under different network and missing data conditions

Abstract

Missing data is a common, difficult problem for network studies. Unfortunately, there are few clear guidelines about what a researcher should do when faced with incomplete information. We take up this problem in the third paper of a three-paper series on missing network data. Here, we compare the performance of different imputation methods across a wide range of circumstances characterized in terms of measures, networks and missing data types. We consider a number of imputation methods, going from simple imputation to more complex model- based approaches. Overall, we find that listwise deletion is almost always the worst option, while choosing the best strategy can be difficult, as it depends on the type of missing data, the type of network and the measure of interest. We end the paper by offering a set of practical outputs that researchers can use to identify the best imputation choice for their particular research setting.

Introduction

Network data are often incomplete, with nodes and edges missing from the network of interest. Missing data can create problems when analyzing network data because network measures are often defined with respect to a fully observed graph (Borgatti et al., 2006; Smith and Moody, 2013). For example, measures that depend on the paths between all actors (e.g., closeness centrality and betweenness centrality) tend to be particularly sensitive to missing data (Kossinets, 2006; Smith et al., 2017; Rosenblatt et al., 2020). A researcher faced with incomplete network data must decide what, if any, imputation should be employed to limit the biasing effect of missing data (Huisman, 2009; Žnidaršič et al., 2018). Unfortunately, there are few clear guidelines for making imputation decisions. Recent work has shown that imputation can reduce the bias resulting from missing data, but we are only beginning to understand the returns to imputation (e.g., Koskinen et al., 2010; Gile and Handock, 2017; de le Haye et al., 2017; Krause et al., 2018a,b, 2020). For instance, is it always best to impute network data, or can we sometimes get away with doing nothing? And more pressing, how should a researcher choose which imputation method is optimal? Does one approach offer a universally robust option, or does it depend on the circumstances of the study?

This paper is part of a three-paper series on missing network data, with the overall goal of offering practical advice and tools for network researchers faced with missing data (Smith and Moody, 2013; Smith et al., 2017). We focus on a common situation: where the network data is incomplete because a subset of actors has provided no information about their network ties (e.g., Galaskiewicz, 1991; Costenbader and Valente, 2003; Silk et al., 2018). For example, a network study of high school students may miss students because they were absent the day of the survey, or simply because they refused to participate in the study. Even automated data (e.g., based on Bluetooth proximity) may suffer from missing data problems (Wang et al., 2012).

Paper 1 and paper 2 of this series explored the effect of missing data on network measures across a wide range of networks and missing data scenarios. We find that bias can vary dramatically across settings, where the level of bias depends crucially on the measure of interest, the network being analyzed and the type of missing data (see also Frantz et al., 2009; Huisman, 2009; Martin and Niemeyer, 2019). For example, the same measure (e.g., Bonacich centrality) calculated on the same network can yield very different levels of bias, depending on if the missing nodes are central or peripheral actors (Smith et al., 2017).

In this paper, we focus on the question of imputation: how do different imputation methods fare under different research settings—in terms of measures, network features and missing data types.¹ In this way, we combine the literature on missing data effects (where is missing data most problematic?) with the literature on imputation (what kinds of strategies can we use to impute network data?). We consider a range of imputation methods, from simple imputation to more complex model- based approaches (Žnidaršič et al., 2017; Krause et al., 2018a,b, 2020). Simple imputation approaches attempt to ‘rebuild’ the network as best as possible from the information found in the data itself (i.e., if i nominates j and j is missing we might impute a tie from j to i) (Huisman, 2009). Model-based approaches use sophisticated statistical models to probabilistically fill in the missing data (Koskinen et al., 2010; Wang et al., 2016). From the perspective of a researcher, it is crucial to know which approaches will work for their particular setting. An approach that is effective for one measure and/or network type may be ineffective for another. The effectiveness of the approach may even depend on the type of missing data.

Our ultimate goal is to offer a set of practical outputs for researchers trying to decide what imputation approach to implement. A researcher will be able to identify the case closest to their own (in terms of measures, missing data type, and network features) and then use our results to look up the optimal imputation choice. A researcher would, of course, have to balance the performance of the imputation method (in terms of lowering bias) with the difficulty of implementing it. Our results will make it easier for a researcher to perform such cost-benefit analyses, given the features of their research setting.

We begin the paper with a short background section on missing network data and imputation. We then describe the imputation methods of interest, as well as the networks, measures and sampling setup that will form the basis of the analysis. Our analysis follows past work in the literature. We begin by taking a complete network and simulating different missing data scenarios. We then impute the missing data (on the now incomplete network), recalculate the measures of interest, and compare the resulting value to the true value. We present results for three types of network measures: centrality, centralization and topology.

Theory

Our paper contributes to a growing literature on non-response treatments to missing network data (Wang et al., 2016; Žnidaršič et al., 2017; Krause et al., 2018a,b). We focus on a key form of missing data, actor non-response. We define a non-respondent as an actor that fails to offer any nomination information (i.e., no information on out-going ties). We assume that non-respondents are not completely missing, however, and can still be nominated by other actors.² This is a common form of missing data, particularly in well-defined, bounded settings. For example, in a school, a student may be out sick the day of the survey but still be on the roster, so that other students could nominate them. In this way, we have observations of a non-respondent’s in-coming ties but not of their out-going ties.

The two most common approaches for inferring missing ties are simple imputation and model-based imputation. We discuss each in turn.

Simple imputation leverages information about the incoming ties to non-respondents to help reconstruct the network (Stork and Richards, 1992; Huisman, 2009). If node k is a non-respondent and is nominated by i and j (who are not missing), we begin by including the ties from i→k and j→k. Additional heuristics can then be applied to help fill in the network. For example, a researcher may assume reciprocal ties going out from the non-respondents to those who nominated them, imputing k→i and k→j. Assuming reciprocity, however, runs the risk of adding ties that do not really exist, while doing no further imputation may fail to add ties that do exist. Much of the methodological work on simple imputation has asked how well such methods work in practice. For example, Huisman (2009) compared an imputation strategy based on the observed network’s density to a preferential attachment strategy and a unit imputation strategy. He found that simple imputation generated stable estimates of reciprocity, mean degree, and inverse geodesic distance for undirected networks with a 40 % non-response rate or less, but preformed less well for directed networks.

Recent work has considered more complicated (non-model based) imputation methods; where the rules for adding ties are dependent on other properties of the graph, like the reciprocity rate or the indegree of a node’s nearest neighbors (Žnidaršič et al., 2017). For example, Žnidaršič et al. (2017) explored a range of actor non-response treatments, finding that imputing ties based on the incoming ties of ego’s k-nearest neighbors significantly reduces non-response bias in valued networks, but that the macro-structure of the network (e.g., core periphery networks, networks with cohesive subgroups, and hierarchical networks) significantly influences the effectiveness of such strategies (see also Žnidaršič et al., 2018).

Model-based imputation methods are an alternative approach for inferring missing data (Robins et al., 2004; Kolaczyk and Csárdi 2014´ ). As with simple imputation, model-based methods begin by leveraging the information provided by the incoming ties to non-respondents. Model-based approaches, however, go further by proposing a parametric model that derives the likelihood of the observed data as a marginalization of the complete-data likelihood over the possible states of the missing variable (in our case a given adjacency matrix) (Gile and Handcock, 2017). The advantage of this approach is that it allows the researcher to incorporate more information about the network’s nodes, dyads, and local structure when estimating the likelihood of a given tie, as well as information about the survey instrument such as number of alters each respondent could nominate (Wang et al., 2016). Similarly, a model-based approach makes it possible to impute ties between non-respondents, which is difficult with simple imputation approaches. Model-based imputation also has the advantage of considering multiple plausible states of the network to generate a summary measure that accounts for the increased variability of parameter estimates due to imputation (Huisman and Krause, 2017). In this way, a researcher is better able to take into account the uncertainties in the imputation process, consistent with best practices from the literature on multiple imputation (Allison, 2002).

For example, Wang et al., 2016 used an imputation method based on exponential random graph models (ERGM); they found, on average that, 73 % of the missing ties could be effectively imputed, although smaller, sparser networks were harder to fit. Krause et al., 2018a,b expanded on this approach by employing a Bayesian ERGM (see also Koskinen et al., 2013) to impute missing ties, finding that Bayesian models are particularly useful when the percentage of missing data approaches 50 % and the measure in question is sensitive to misspecification (such as with transitivity). The main disadvantage of model-based imputation is that it can be difficult to implement (given the need to specify and estimate a model). Model-based imputation may also introduce bias by over generalizing tendencies observed in information rich parts of the network to the entire network. Nevertheless, these methods are often warranted, particularly in longitudinal network analysis where missing data is likely due to the repeated nature of the sampling, and where biases present in the initial network will affect the estimates of all subsequent networks (Hipp et al., 2015; Krause et al., 2018a,b).

Imputation strategies thus have great potential to limit bias due to missing data. Nevertheless, the practical problem remains of how to choose an imputation approach in a given research setting, especially as an imputation method that works well in one setting may not work well in another (Hipp et al., 2015). Different factors such as the network type, the kind of missing data, and the measure of interest are likely to influence the performance of different imputation methods, as different conditions magnify (or hide) the relative weaknesses of each approach. For example, we might expect that estimates of transitivity for a directed core-periphery network are particularly vulnerable to approaches that add reciprocated ties, as this runs the risk of inflating the estimated number of closed triads. In this case, the researcher should avoid reciprocated imputation; but what imputation strategy should be used, and are there other cases where reciprocated imputation works well?

In short, different approaches are likely to work better/worse in different settings, and it is crucial for a researcher to understand the consequences of different imputation choices. With this is mind, our analysis will extend past work by considering different imputation options across a much wider range of network types, measures and missing data features than is typically considered. It is only by considering such a complex set of conditions that we can begin to offer practical advice to researchers, as we can say under what conditions a given imputation approach is most appropriate.

Data

We examine the efficacy of different imputation methods across twelve empirical networks, seven directed networks and five undirected networks. These networks vary widely in terms of network features and substantive contexts, although all networks are limited to under 1000 nodes. Medium to small networks are sensitive to missing data and are conducive to additional data collection efforts, making them particularly appropriate for the study of missing data and imputation methods (Gile and Handcock, 2017). All networks are binary. Binary network data are still commonly used, and it is important to understand how missing network information affects this baseline case. The networks are the same as in papers I and II of this study.³ They include: “data on elites (corporate interlocks: “Mizruchi Interlock” and “River City Elite”), young youth networks (“Gest 6^th graders”, “Prosper s220”)⁴, adolescent and young adult networks (“Sorority Friendship”, “High School (p13 & p24)”, the Gagnon prison network (MacRae, 1960), science networks (the sociological abstracts collaboration graph, the Social Networks article co-citation graph, and the biotechnology exchange network) and epidemiological networks (Colorado Springs HIV risk network - Morris and Rothenberg, 2011)⁵ _“ (quoted from Smith and Moody, 2013). See Fig. 1 for plots and summary statistics (Table 1).

Fig. 1.

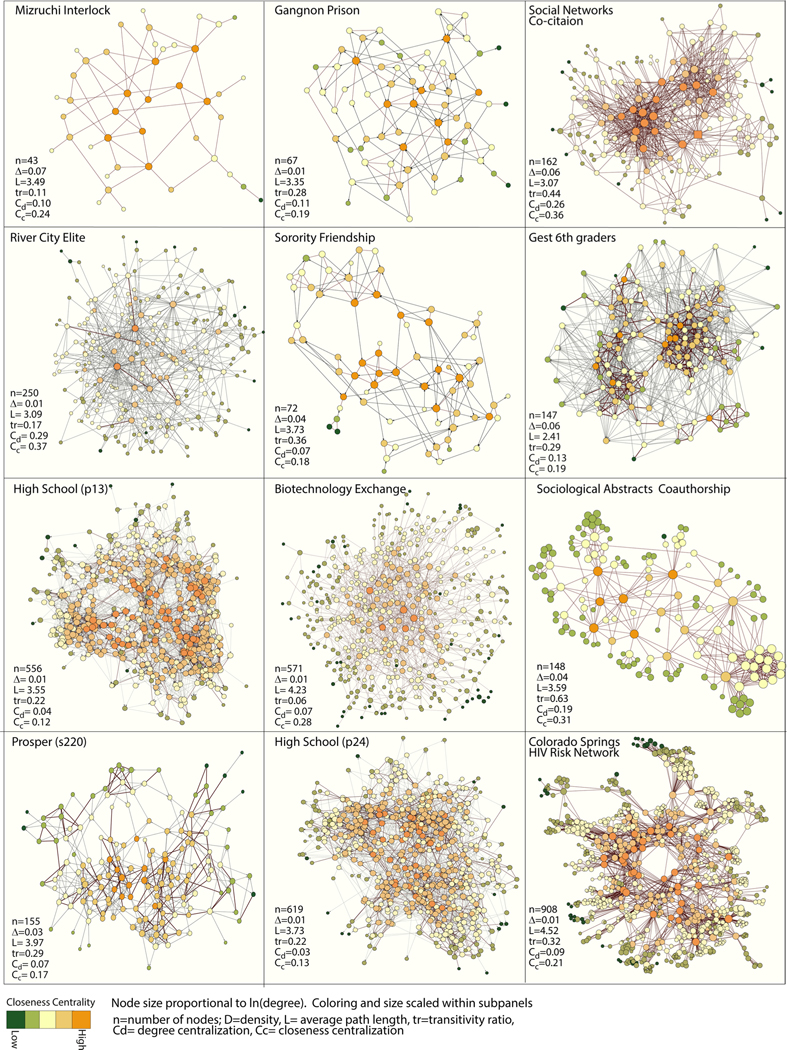
Networks Used for Sampling Simulations.

Table 1.

Sample network descriptive statistics.

	Inter-lock	Prison	Sorority	6th Grade	Co-author	Prosper	Co-citation	Elite	HS 13	Bio-tech	HS24	HIV Risk
Directed?	No	Yes	Yes	Yes	No	Yes	No	Yes	Yes	No	Yes	No
Centrality
In – Degree	3.02	2.72	2.89	8.86	6.16	3.83	9.32	2.39	6.06	3.85	5.71	6.05
	(1.93)	(2.02)	(1.75)	(5.26)	(5.98)	(2.69)	(10.62)	(7.59)	(4.42)	(4.99)	(3.96)	(8.12)
Out – Degree	3.02	2.72	2.89	8.86	6.16	3.83	9.32	2.39	6.06	3.85	5.71	6.05
	(1.93)	(1.48)	(1.85)	(4.67)	(5.98)	(2.36)	(10.62)	(1.63)	(2.90)	(4.99)	(2.99)	(8.12)
Symmetric Degree	3.02	5.43	5.78	17.7	6.16	7.65	9.32	4.78	12.1	3.85	11.43	6.05
	(1.93)	(2.73)	(2.88)	(7.73)	(5.98)	(3.85)	(10.62)	(7.83)	(6.04)	(4.99)	(5.84)	(8.12)
Closeness	0.36	0.18	0.15	0.35	0.32	0.18	0.38	0.03	0.22	0.26	0.2	0.25
	(0.08)	(0.08)	(0.09)	(0.12)	(0.06)	(0.09)	(0.09)	(0.02)	(0.05)	(0.04)	(0.06)	(0.04)
Betweenness	0.06	0.03	0.04	0.01	0.02	0.02	0.01	0	0.01	0.01	0.01	0
	(0.07)	(0.05)	(0.05)	(0.02)	(0.06)	(0.03)	(0.02)	(0)	(0.01)	(0.02)	(0.01)	(0.02)
Bonacich Power	0.82	0.86	0.86	0.9	0.58	0.82	0.63	0.64	0.83	0.6	0.83	0.57
	(0.58)	(0.52)	(0.51)	(0.43)	(0.82)	(0.57)	(0.78)	(0.77)	(0.55)	(0.8)	(0.56)	(0.82)
Centralization
In – Degree	0.10	0.08	0.06	0.14	0.19	0.08	0.26	0.29	0.04	0.07	0.03	0.09
Out – Degree	0.10	0.08	0.06	0.15	0.19	0.02	0.26	0.03	0.01	0.07	0.01	0.09
Symmetric Degree	0.10	0.06	0.05	0.08	0.19	0.05	0.26	0.15	0.03	0.07	0.02	0.09
Closeness	0.27	0.12	0.17	0.16	0.35	0.11	0.48	0.06	0.08	0.36	0.08	0.28
Betweenness	0.20	0.17	0.16	0.06	0.37	0.16	0.12	0.01	0.05	0.24	0.03	0.17
Bonacich Power	0.20	0.18	0.14	0.13	0.26	0.16	0.22	0.41	0.13	0.29	0.12	0.23
Topology
Component Size	43	67	72	147	148	155	162	250	556	571	619	908
Bicomponent Size	27	62	59	145	75	147	118	195	545	336	605	517
Distance	0.36	0.18	0.15	0.35	0.32	0.18	0.38	0.03	0.22	0.26	0.2	0.25
Transitivity	0.11	0.28	0.36	0.29	0.63	0.29	0.44	0.17	0.22	0.02	0.22	0.32
TauRC	−0.91	2.35	4.65	17.75	17.65	7.22	−27.36	163.6	23.66	−91.61	22.91	−104.22

Standard deviations are in parentheses.

Measures

Our analysis includes 16 different measures which we broadly divide into three classes: centrality, centralization and topology. By looking at a wide range of measures, we can better describe the conditions under which different imputation approaches offer the best choice.

Centrality

Our centrality measures include in-degree, total degree, Bonacich power centrality, closeness and betweenness. For the undirected networks, we only include a measure of degree (as total degree, out-degree, and in-degree are the same). Note that Bonacich power centrality is calculated on a symmetrized version of the network (for the directed networks). We calculate closeness centrality based on the inverse distance matrix, so that disconnected nodes have a value of 0 and directly connected nodes have a value of 1. We use the inverse distance matrix so that the summation does not include undefined values, a problem when pairs of people in the network cannot reach one another.

Centralization

Centralization measures the variation in the distribution of the given centrality measure, and is a graph-level statistic (whereas centrality captures an individual-level characteristic). We include centralization scores for each of our centrality measures. Our measure of centralization is a simple standard deviation of the individual centrality scores.

Topology

We include six topological measures. We include two global measures of connectivity, component size and bicomponent size. We measure component size as the proportion in the largest component. We first calculate the number of actors in the largest component, defined as the largest set of actors connected by at least one path. We then divide by the size of the network, defined as the number of nodes in the network being analyzed (i.e., the observed network after any nodes have been removed as part of the missing data treatment). A bicomponent is defined as a set of actors connected by at least two independent paths (Moody and White, 2003). As with component size, we divide the size of the largest bicomponent by the size of the network being analyzed, yielding the proportion in the largest bicomponent. Our third measure is distance, measured as the mean inverse distance between pairs of nodes (meaning that higher values actually indicate lower distances). We scale the value by the log of network size.⁶ Our fourth measure is transitivity, measured as the relative number of two-step paths that also have a direct path; more substantively, transitivity captures the tendency for a “friend of a friend to be a friend”. Our fifth measure is the tau statistic, a weighted summary statistic based on the triad distribution (Wasserman and Faust, 1994). The tau statistic captures the local processes that govern tie formation (like clustering and hierarchy). The tau statistic is a summation over the specified triads, conditioned on the dyad distribution in the network. Here, we use the ranked-cluster (RC) weighting scheme.⁷ Our last topological measure is based on blockmodeling the network (White et al., 1976). We begin by partitioning the full network into a set of equivalence blocks, where nodes with similar pattern of ties are placed together.⁸ We use the Rand statistic (Rand, 1971) to compare the partitioning found in the incomplete data to the partitioning observed in the full, true network. The unadjusted Rand statistic shows the proportion of pairs in one partition (the true partitioning) that are placed together in a second partition (the partitioning under missing data).

Missing data

Our study is focused on the efficacy of different imputation methods under different conditions of missing data. In order to explore different level of missing data), we identify a portion of the nodes as non-imputation approaches, it is first necessary to generate missing data respondents, individuals for whom we have no information on out- from the observed data in a controlled, systematic way. We follow a going edges. We construct the observed (incomplete) network by standard protocol when inducing missing data: for each network (and removing the out-going edges from the non-respondents. Once the appropriate edges are removed, we apply different imputation methods to the same network, with the same missing data. We repeat this process 1000 times for each level of missing data: 1 %, 2 %, 5 %, 10 %, 15 %, 20 %, 25 %, 30 %, 40 %, 50 %, 60 %, 70 %.⁹

We also consider different types of missing data, defined by which nodes are most likely to be non-respondents: central nodes, peripheral nodes, or nodes selected at random. Past work has shown that missing more central nodes generally yields larger bias (at least when the researcher takes no action to impute the missing cases) (Smith et al., 2017). Research contexts vary with respect to who is most likely to be a non-respondent. For example, central actors are less likely to provide nomination data when studying organizations (e.g., public officials in an elite network), where central actors are more likely to have scheduling conflicts and may be less willing to cooperate. Peripheral actors are more likely to be non-respondents in settings like schools, where actors who are not socially embedded in the network are more likely to be disengaged and thus less likely to take the survey. Network measures are typically robust to missing peripheral members of the network, but imputation procedures may struggle in such cases. We have very little information about nodes on the periphery (as few people nominate them), making it harder to impute where ties should be added for those actors. It is unclear how different imputation procedures will fare when periphery nodes are non-respondents (compared to more central nodes).

Formally, our missing data conditions are set based on the correlation between centrality and the probability of being a non-respondent. We have five correlation values: strong negative correlation (−.75), weak negative correlation (−.25), missing at random (0), weak positive correlation (.25) and strong positive correlation (.75). Cases with a negative correlation between centrality and missingness correspond to situations where those on the periphery are more likely to be non- respondents. A zero correlation corresponds to random selection of non-respondents, while a positive correlation means that more central actors are more likely to be non-respondents. We consider two definitions of central actors, one based on closeness and one based on in- degree. There are thus 9 different missing data types (−.75 closeness, −.75 in-degree, −.25 closeness, −.25 in-degree, 0, .25 closeness, .25 in- degree, 75 closeness, and .75 in-degree). We will not distinguish between the closeness and in-degree results here as they offer very similar findings, so we simply aggregate them in the final figures and tables.

Imputation methods

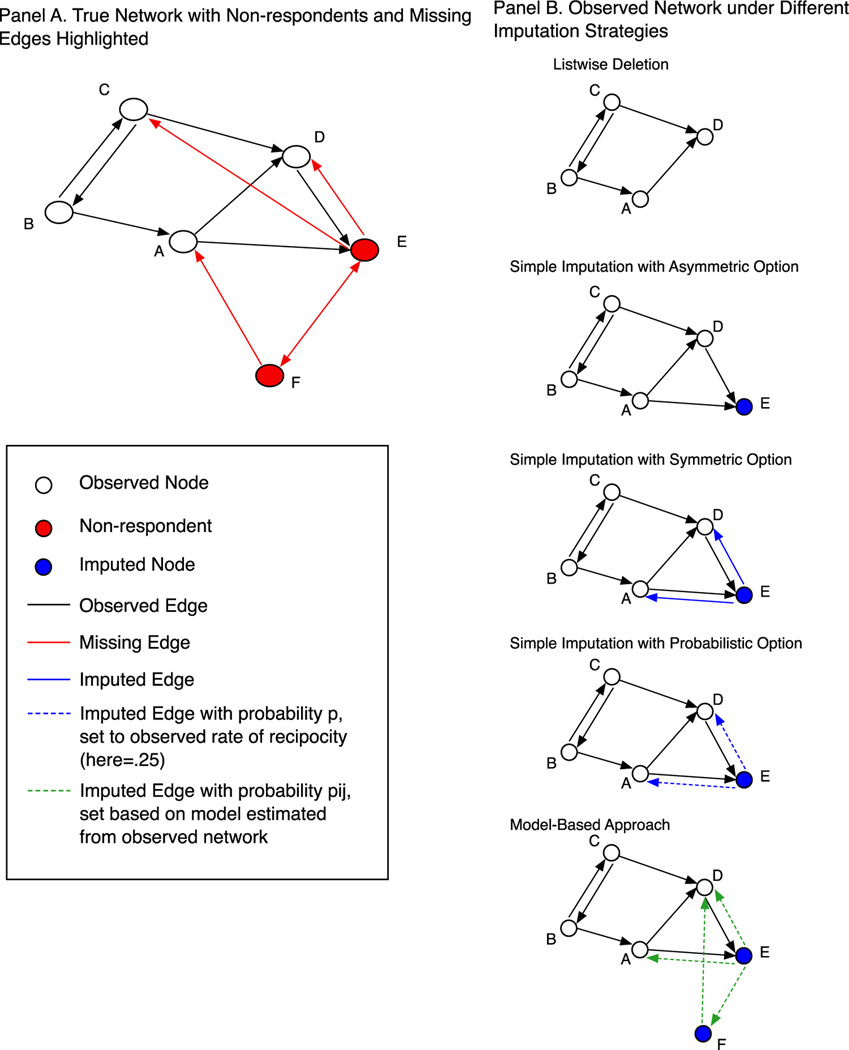
We consider the effectiveness of six different approaches for dealing with missing data. In each case, we first construct a network with missing data, where a subset of nodes is treated as non-respondents, with no out-going edge information. We then take the incomplete network and impute the missing edges using different imputation approaches. Fig. 2 presents the different imputation options in a simple network with 5 nodes. On the left-hand panel, we have the complete network with non-respondents and edges highlighted in red. Here, we see that nodes E and F are missing. All edges going from E or F to other actors (like E→D) will not be observed, including any edges between the non-respondents (see Handcock and Gile, 2010). A researcher will, however, typically have information on edges going to non-respondents (for example D→E), and we assume that this is the case for our analysis.

Fig. 2.

Demonstrating Imputation Strategies on Toy Network.

Given these conditions, we break out the imputation methods into three large classes: listwise deletion, simple imputation and model-based. The simple imputation methods include asymmetric, symmetric and probabilistic treatments; the model-based methods include simple and complex exponential random graph models. Thus, we consider six approaches: listwise deletion, asymmetric, symmetric, probabilistic, model-based simple and model-based complex.

Listwise deletion

The simplest option is to remove all nodes with incomplete information from the network. This is pictured in the top right-hand plot in Fig. 2. Here, non-respondents are not present in the network, while all incoming ties to non-respondents are not considered. This amounts to listwise deletion, where only those cases with full information, or those present at the time of data collection, are included in the network used for analysis. In this case, E and F and all ties going to and from E and F are missing. Note that this is the typical strategy for most network studies (Smith et al., 2017; Silk et al., 2015). Also, note that listwise deletion will yield a network that is smaller than the true network.

Simple imputation

The second class of imputation methods that we consider is simple imputation. Here, the researcher uses the tie information from the observed nodes to the non-respondents to help ‘fill in’, or reconstruct, the network (Huisman, 2009). The basic idea is that when an actor who is present in the survey nominates someone who is absent; that this is useful information that should not be thrown away, as is done in listwise deletion. For example, in Fig. 2, nodes A and D nominate E, who has missing data on all out-going ties. A simple imputation approach would begin by putting E back into the network with edges from A→E and D→E. This is demonstrated in the simple imputation plots in Panel B. Note that node F, who is also a non-respondent, is not put back into the network as none of the observed nodes nominated them. Once the missing nodes are put back, the researcher must decide on how to impute the missing edges from the non-respondents to the nodes who nominated them. No other ties are imputed. This means that all potential ties between non-respondents who were put back into the network are assumed not to exist, taking a value of 0 in the matrix.¹⁰ In our little example, we need to impute whether E sends ties back to A and D. Note that for undirected networks this choice is simple as all ties are reciprocated. The directed case is more difficult and we consider three different options.

Asymmetric imputation

First, a researcher could employ an asymmetric approach, where no ties from non-respondents are added to the nodes who nominated them (past work has also labeled this null tie imputation; Žnidaršič et al., 2017). In the second plot in Panel B, we see that there are ties from D to E and A to E but no ties from E, the non-respondent, back to D or A. This strategy privileges the observed data by removing from consideration ties from the non-respondents to the respondents who nominated them. The downside of this approach is that it assumes that an asymmetry exists between all non-respondents and respondents, an assumption that is unlikely to be true in many cases. It could, however, be useful for certain measures, especially those where adding an incorrect tie badly biases the results (like transitivity).

Symmetric imputation

The second option is symmetric imputation (also referred to as reconstruction in past work: Huisman, 2009; Žnidaršič et al., 2017). Here, a researcher always assumes that an edge from a non-respondent to a respondent is reciprocated. In our example, the edges from A and D to E (non-respondent) is returned, so we impute edges E→A and E→D. In this case, a researcher would get the E→D edge correct but would incorrectly add the E→A edge. A symmetric option is likely to work well when the reciprocity rate is high. It is also likely to work well in cases where the measure of interest does not rely heavily on the direction of the ties or in cases where missing edges are more consequential than adding incorrect edges.

Probabilistic imputation

The last simple imputation option is probabilistic imputation. Here, edges from non-respondents to the respondents who nominated them are imputed probabilistically, based on the rate of reciprocity in the observed network. A researcher first calculates the reciprocity rate as the proportion of ties that exist such that if i nominates j then j also nominates i. For this initial calculation, we only include dyads where both i and j are observed nodes (i.e., both respondents). For our example network in Fig. 2, the reciprocity rate in the observed, incomplete network is .25. A researcher would then take this rate and use it to impute the ties from non-respondents to respondents. Here, our researcher would basically flip a weighted coin, adding an edge with the probability set to .25. This would be done, in this case, for E→A and E→D. This process can itself be repeated a number of times (as there will be stochastic variation). Each iteration will yield a slightly different network, which can then be used in subsequent analysis. One could then summarize the results over the imputed networks. In our analysis, we repeat the imputation process over 100 networks, using the mean value (for the statistic of interest) over the 100 networks as the summary measure of interest. A probabilistic option falls somewhere between the asymmetric and symmetric options, in terms of adding or not adding edges. The probabilistic option is likely to be a fairly safe choice, although it may not always be the best option in every setting.

Overall, the simple imputation methods have the advantage of being very easy to implement while taking advantage of data from the survey itself. The disadvantage is that these methods miss any edge from non- respondents to other non-respondents (such as E↔F). It also systematically misses any asymmetric edge from a non-respondent to an observed node (such as E→C). Couple these built-in biases with the possibility of adding edges that are not really there, and it is unclear how far we can push simple imputation options, particularly given difficult combinations of measures and missing data types.

Model-based

The third class of imputation methods is model-based approaches. Here, a researcher takes the observed network, and estimates a statistical network model predicting the presence/absence of a tie between all ij pairs. The researcher then takes the underlying model and uses the model to predict, probabilistically, the ties that exist for nodes that are missing. For example, we know that networks tend to be homophilous (i. e., two actors who are similar are more likely to form a tie). A researcher can estimate the strength of this tendency (e.g., in terms of race or gender) and then use that information to help predict if a missing edge exists. We assume that the researcher has basic information on all actors, even the missing cases. Thus, an actor may have missing network data but basic demographic (or other) information about them may still be available. This may be acquired through administrative records, third hand reports or even from the ‘missing’ respondent, as they may begin the survey but not finish it.

A model-based imputation approach is depicted at the bottom of Panel B in Fig. 2. We assume that a researcher employing a model-based approach will begin by first performing a simple asymmetric imputation of the data. For example, in Fig. 2, Actor E is put back into the network and edges from A→E and D→E are added. The researcher will then take the remaining non-respondents, those who received no nominations from the observed nodes and put them back into the network. In our example actor F would be added to the network. The next step is to estimate a model predicting an edge between actors, only including the observed edges in the model.

We use exponential random graph models (ERGM) to impute the missing data. There are a number of possible options, but ERGM is a commonly used model and is quite flexible, making it an ideal choice. ERGMs are statistical models used to test hypotheses about network structure and formation (Hunter et al., 2008; Wasserman and Pattison, 1996). Formally, we define a network, Y_ij, over the set of nodes N, where Y is equal to 1 if a tie exists and 0 otherwise. Define y as the observed network. Y is then a random graph on N, where each possible tie, ij, is a random variable. ERGMs estimate the Pr(Y=y), where the “independent variables” are counts of local structural features in the network (Goodreau et al., 2009; Robins et al., 2007), such as number of ties and homophily. The model can be written as:

$$P(Y=y)=\frac{exp\left({\theta }^{T}g(y)\right)}{\kappa (\theta )}$$ (1)

where g(_y) is a vector of network statistics, θ is vector of parameters, and κ_(θ) is a normalizing constant.

In this case, the model is estimated based on the incomplete network, where edges from non-respondents to other nodes are unobserved. Note that all missing edges are treated as NAs when estimating the model (i.e., missing instead of 0 s), and are thus not included in the estimation of the coefficients. The estimated coefficients may be biased, depending on the terms included and the type of missing data. It is, nonetheless, our best guess (given the data at hand) at what the underlying local tendencies are for the network. We can then take that estimated model and predict the missing edges. This amounts to simulating networks from the underlying model. Note that this includes missing edges from non-respondents to respondents (E→A) as well as edges between non-respondents (E and F). All observed edges (including edges from respondents to non-respondents) are held fixed and not allowed to vary as different networks are generated from the estimated model. In Fig. 2, we have plotted an example simulated network, with the missing edges colored green. This represents one possible imputation, or draw form the underlying model; another generated network would look slightly different (with different ‘green’ edges added to the network). A researcher could repeat this process a number of times, calculating the statistics of interest for each simulated network (with observed edges held fixed), summarizing over all of the calculated values.

The main benefit of a model-based approach is that we are able to recover nodes that are non-respondents and received no nominations from respondents (actor F in Fig. 2). We are also able to apply a better model to recover the edges between respondents and non-respondents (i.e., going beyond just reciprocity). Model-based approaches are thus likely to fare well when looking at measures that capture structural features at an aggregate level, like component size. The main drawback to a model- based approach is that the imputed network will deviate further from the raw data than with any of the simple imputation approaches. Measures that are sensitive to getting the specific edges correct, such as centrality measures, may be more difficult for a model-based approach.

We consider two versions of model-based imputation. One we denote as ‘simple’ and the other we denote as ‘complex’. Each has the same basic form but the simple model includes fewer terms, and is thus easier to estimate.

Simple model-based

The simple model-based approach includes three basic terms. First, we include a term for the base rate of tie formation in the network (edges). Second, we include terms for homophily on two attributes.¹¹ We assume these attributes are known for both non-respondents and respondents. Third, for directed networks, we include a term capturing reciprocity, the count of the number of dyads where ij exists and ji exists. We then take the estimated model¹², based on number of edges, reciprocity, homophily and simulate a set of networks from the underlying model. Only the missing edges are allowed to vary run to run, as the observed edges are held fixed.¹³

Within these simulations, we put constraints on the outdegree of each node, constraining the simulations so that each node has the same out- degree as the observed values (these values are imputed for the non-respondents).¹⁴ In this way, we ensure that out-degree in the simulated networks is consistent with the observed data, matching the respondents and matching our best guess for non-respondents. In the end, we calculate the statistics of interest for each generated network (we generate 100 networks each time)¹⁵ and take the mean over all networks as the measure of interest. All models are estimated in R using the ergm package (Handcock et al., 2019).

Complex model-based

The complex model-based approach is exactly the same as the simple approach expect that it includes a term to capture triadic processes. The simple model only includes terms at the node or dyadic level. For the complex model, we take the same model and add a GWESP (geometrically weighted edgewise shared partner) term to the model. GWESP is a weighted summation of the counts of how many shared partners each ij pair have (restricted to cases where i and j have a tie), capturing the tendency for groups (or local clusters) to emerge in the network. Adding GWESP allows us to capture tendencies towards transitivity and higher order closure. It also makes the model harder (and longer) to estimate.

In short, the model-based approach is more complicated than with simple imputation approaches. A researcher must make a number of difficult modeling choices (terms, constraints, etc.), and must then actually estimate and simulate from the specified model. Thus, one of the main questions of this study is about the relative payoffs and tradeoffs between simple imputation and model-based approaches. Simple imputation approaches are much easier to implement. But will they yield valid results? And if the model-based approach yields better estimates, is the improvement worth the added effort that a model-based approach requires? Thus, we want to identify the conditions (measure of interest, type of missing data, etc.) where one can ‘get away with’ the simpler network options, compared to the conditions where a more complicated model-based approach is necessary.

It is worth noting that our model-based imputation approaches employ particular forms, with particular terms and constraints included. It is possible that alternative specifications (i.e., using a Bayesian approach) would offer better results than that presented here (Krause et al., 2018a,b). Our results are, however, still instructive, as they represent the kinds of tradeoffs and models that a researcher in the field is likely to consider.

Presentation of results

Our results offer a presentation challenge. We have 12 networks, 5 missing data types, 12 missing data levels, 16 measures, and 6 imputation approaches. For each of these combinations, there are 1000 iterations (with different actors treated as non-respondents each time). The combinatorics make it difficult to present the results in a raw form. Our strategy is to calculate summary statistics across these iterations and then to use different plots and regression models as a means of summarizing the results.

For each scenario (network, measure, and missing data type), we begin by comparing the true values to that observed in the networks with missing data—where a subset of nodes are treated as non- respondents and different imputation strategies are used to deal with the missing data. We first calculate a bias score, capturing how far the observed value is from the true value. The observed value is the measure calculated on the imputed networks (i.e., the network we observe the imputation is performed). For the centrality scores, we calculate the centrality of the nodes in the complete network (no missing data), calculate it again using the networks with imputed data, and correlate these two vectors. The higher the correlation, the greater is the effectiveness of that imputation method for that missing data scenario. To make this a bias score, we calculate 1 minus the correlation between the true and observed centrality scores.

$$bias{}_{centrality}=1-cor\text{(}True\text{,}Observed\text{)}$$ (2)

When we correlate the two vectors, we only include respondents, thus excluding non-respondents that we have brought back into the network through the imputation process. This makes the calculations consistent across different imputation strategies. It is also the likely choice that researchers would make in their own analysis (as the bias will be much higher for non-respondents). We have also performed an analysis where we keep all actors in the calculation (respondents and non-respondents). The imputation strategies fare much worse in this case, suggesting some of the costs of including the missing cases. The results for this additional analysis are presented in Table A13 in the Appendix.¹⁶

We use a standardized bias score for our graph level measures of centralization and topology. We define bias as:

$$bias{}_{centralization;topology}=\left|\frac{True-Observed}{True}\right|$$ (3)

A bias score captures how much the observed score (in the imputed networks) differs from the true value. The bias scores are relative to the size of the true value, making it easier to compare across networks and statistics. The bias scores can be negative (over-estimates) or positive (under-estimates). For simplicity, we take the absolute value of the bias scores, making them comparable in all analyses.

We begin each set of results with a bias ratio table. The bias ratio tables show the total improvement in the measure for each imputation type relative to listwise deletion. We first calculate the total bias that results from doing listwise deletion. We calculate the bias score (for the given measure) under listwise deletion, summing up the bias at each level of missing data to arrive at a total bias score. We then repeat this process for the same network and missing data, but now we assume that the data are imputed under different approaches. We take the total bias under each imputation approach and divide that by the total bias under listwise deletion, multiplying it by a 100 to arrive at a percent decrease in bias (or improvement in fit). Larger values are better, with negative values suggesting that the imputation method actually performed worse than listwise deletion.

For our second set of analyses, we take the bias scores and regress them on the level of missing data. We thus predict bias for each scenario as a function of percent missing nodes: $bias={\beta }_0+{\beta }_1\left(\frac{\%missing}{10}\right)$. The estimated slope coefficient, β₁, captures the expected increase in bias for a 10 % increase in number of non-respondents. The slope coefficients (β 1) are used as a summary measure, showing how quickly bias increases as the level of missing data goes up.

We then use a series of regression models to summarize the results, providing an overall picture of bias across all networks, measures, missing data types and imputation approaches. We run separate Hierarchical Linear Models (HLM) for each measure, using the bias slopes (β₁) as the dependent variable (bias slopes are nested within networks). Larger coefficients mean that bias is predicted to be higher, as bias increases at a faster rate as missing data increases. Our main independent variable is the type of imputation, represented by a set of dummy variables: Asymmetric, Probabilistic, Symmetric, Model-based simple and Model-based complex. Listwise deletion serves as the reference category. We also include a variable for missing data type, ranging from −.75 (low degree nodes are more likely to be non-respondents) through .75 (high degree nodes are more likely to be non-respondents). The remaining variables capture network properties that may be correlated with higher levels of bias. We include predictors for network size (logged) and concentration (measured as the standard deviation of in- degree). We run separate models for the directed and undirected networks. We also include interactions between imputation type and the missing data type, as well as interactions between imputation type and network features. In this way, we can see the relative effectiveness of different imputation strategies under a variety of conditions. See Tables A2, A4, A6, A8, A10, and A12 in the Appendix.

We use the estimated regression models to produce a series of summary plots. We present two basic figures for each measure type (centrality, centralization, topology). The first figure focuses on the effectiveness of different imputation approaches across different measures and types of missing data. For each subplot, the x-axis is the level of missing data and the y-axis is the expected bias, under the scenario of interest. The results are based on a network with moderate features, one that is medium sized and moderately/weakly centralized. We have results for each measure and three different types of missing data (missing low centrality nodes, random missing data and missing high centrality nodes). Within each subplot there are 6 lines, one for each of the imputation approaches. The lines represent the predicted bias based on the regression model, using the regression coefficients for that model and setting the network features to the scenario of interest. Higher values in the plot indicate more bias and thus worse performing imputations. The second set of figures focuses on the effectiveness of imputation approaches across networks with different features. Here, we systemically vary the size and centralization of the networks, but hold the type of missing data fixed (only looking at random missing data). We include 4 combinations of size and centralization: large centralized, small centralized, large decentralized, small decentralized. The key question is how well different imputation methods fare for different measures under different conditions.

Results

Centrality

We begin our discussion of centrality by examining the undirected networks as they represent the simpler case. Table 2 captures a qualitative summary of the ‘best’ imputation approach under different conditions, while the main numerical results are presented in Fig. 3 and Tables A1 and A2. Table A1 is our bias ratio table, where each value in the table reports the decrease in total bias (over all levels of missing data and all runs) for that imputation approach compared to listwise deletion. Fig. 3 presents example predicted bias plots for one network for 3 different missing data types. The results are based on the HLM results presented in Table A2, predicting bias as a function of the missing data type and network characteristics.

Table 2.

Summary of Best Imputation Options for Centrality Measures.

Measure	Directed or Undirected	Non-response Type	Size and Centralization	Best Imputation Option
Degree	Undirected	Any	Any	Any strategy except Listwise Deletion
Bon Power	Undirected	Central Nodes	Any	Model-Baseda
Betweenness
Closeness
Bon Power	Undirected	Less Central Nodes	Any	Any strategy except Listwise Deletion
Betweenness
Closeness
Indegree	Directed	Central Nodes	Any	Probabilistic
Indegree	Directed	Less Central Nodes	Any	Probabilistic, Listwise Deletion or Asymmetric
Total Degree	Directed	Any	Any	Asymmetric or Probabilistic
Bon Power	Directed	Any	Any	Probabilistic, Symmetric or Asymmetric
Closeness	Directed	Any	Any	Model-Based
Betweenness	Directed	Any	Any	Probabilistic

Notes.

^a:The model-based approach is assumed to correspond to complex or simple unless explicitly noted.

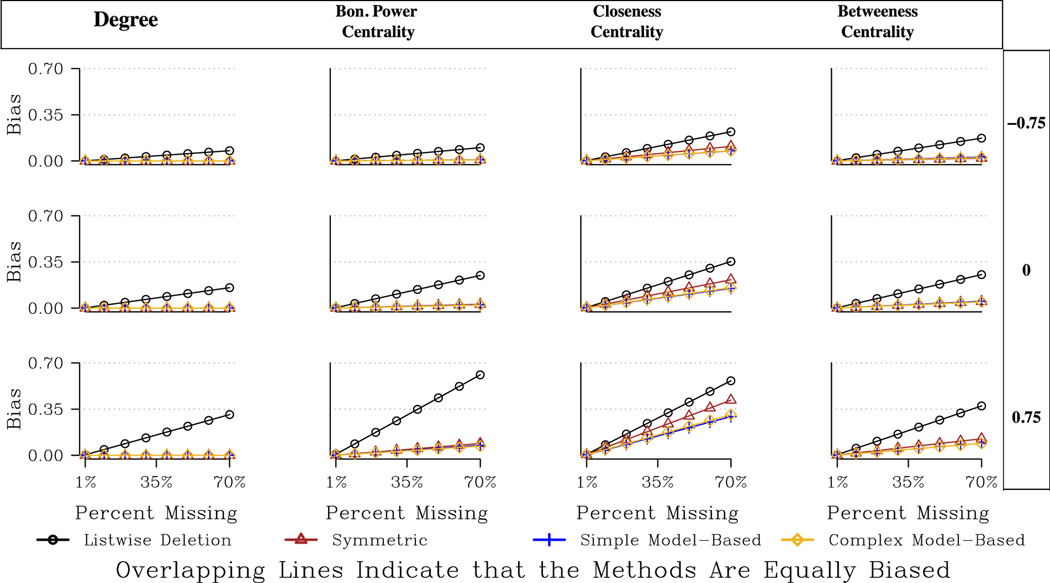
Fig. 3.

Predicted Bias for Centrality Measures for a Large, Undirected, Moderately Centralized Network.

The results for degree are very straightforward. We see that all imputation methods lower the bias to 0, or perfectly impute the missing data. The imputation methods add ties between i and j in cases where i nominates j and j is a non-respondent. There is no error possible here as the return tie (j to i) is assumed to be reciprocated, as the network is undirected. Note that this perfect correlation only holds if we restrict our attention to the degree of the respondents in the network (as there could be still unobserved edges between the missing cases that leads to bias).¹⁷

Bonacich, closeness and betweenness centrality offer a slightly more complicated story. In general, we find that the model-based imputation methods offer the best option, although the differences between the model-based and symmetric approaches are relatively small, especially for Bonacich centrality. For example, looking at closeness for the Biotech network, total bias decreases by 83 % using the model-based approaches and 78 % using the symmetric option, assuming we are missing high centrality nodes. The differences are even smaller when missing low centrality nodes, where the symmetric option is even sometimes preferred. More generally, we see that imputing (using any option) drastically reduces the bias compared with listwise deletion. Looking at betweenness with 40 % of the network missing and missing high degree nodes (assuming the network is medium-sized and decentralized), we would expect a bias of .21 under listwise deletion, .07 under the symmetric approach, and .052 under the simple and complex model-based approaches. The symmetric approach is particularly attractive here because it is so simple to implement, but still yields results that are close to the more onerous model-based approaches. See Fig. 3 for the full results.

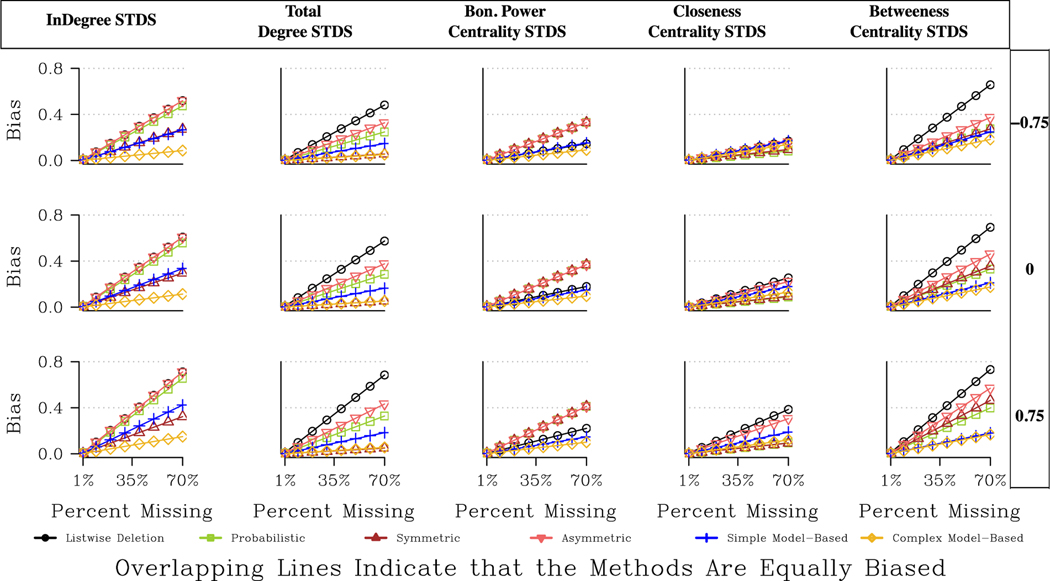
We now turn to the directed networks, where the results are more variable across measures and networks. The main results are presented in Tables A3 and A4 and Fig. 4. We will also refer to Table 2, capturing the best option for each scenario (in terms of measure, missing data type, etc.). Looking at indegree, we see that the probabilistic imputation method fares the best, although the real story is how badly imputation methods perform in general. The probabilistic approach is only marginally better than listwise deletion, while the symmetric and model-based approaches are actually worse than listwise deletion.

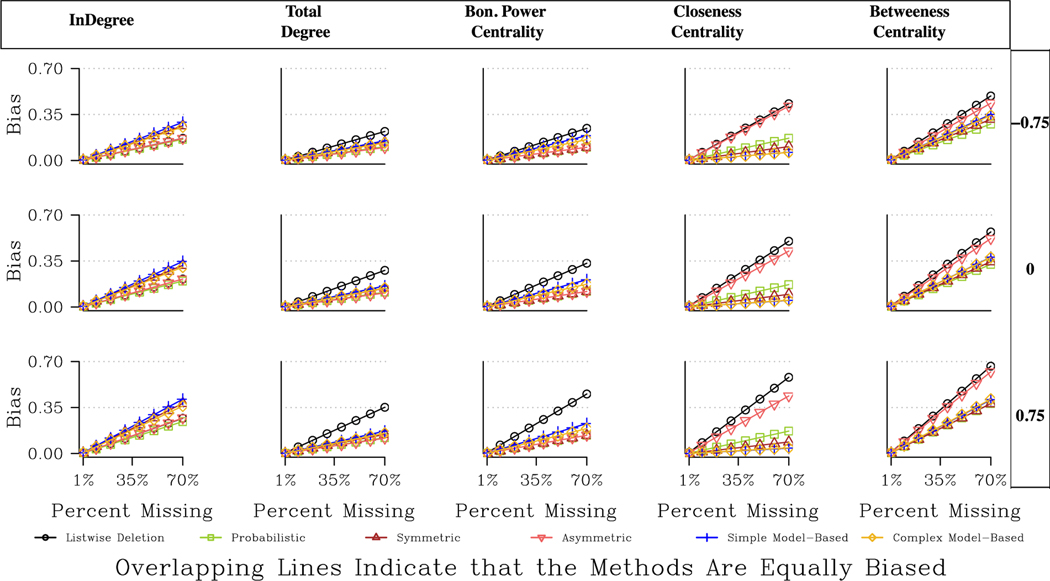
Fig. 4.

Predicted Bias for Centrality Measures for a Large, Directed, Moderately Centralized Network.

Looking at Table A3, the bias ratio table, we see negative numbers for the symmetric and model-based approaches, suggesting higher bias than listwise deletion. Indegree is difficult to impute because it is based on the specific number of nominations sent to each actor. An imputation method will add ties that are generally consistent with the existing data, but this does not mean that it will add the specific ties sent to a specific actor.

The imputation methods are more effective for total degree and Bonacich power centrality. With total degree, for example, the probabilistic and asymmetric approaches are almost always better than listwise deletion, and typically outperform the model-based and symmetric approaches. For example, in our large, moderately centralized network, the expected bias under 30 % missing data (with high degree nodes) is .049, .052, .062, .073, and .15 for the asymmetric, probabilistic, symmetric, model-based (simple) and listwise deletion approaches respectively. Fig. 4 also makes clear that the differences between listwise deletion and the imputation methods are highest when central nodes are more likely to be non-respondents. The returns to imputation are larger when central nodes are non-respondents because the bias under listwise deletion can be quite high (see Smith et al., 2017), while the imputation methods see only a slight increase in bias when missing central actors. The imputation methods tend to fare well when central nodes are non-respondents because there is so much information about central nodes (i.e. many people nominate them), making it easier to impute ties for those actors.

The exceptional case, as it often is, is the RC elite network, where imputation using the model-based or symmetric approaches are worse than listwise deletion, especially when missing less central nodes (the probabilistic and asymmetric approaches are similar to listwise deletion). The RC elite network is highly centralized, meaning if low centrality nodes are non-respondents, and we add reciprocated ties from the highly centralized node back to the peripheral nodes, and they do not exist, then we may greatly deviate from the true centralities in the network. There is, in that sense, the danger of over fitting/imputing what is essentially a hub and spoke structure.

Closeness offers a different story than the degree-based measures. All imputation methods are still better than listwise deletion, but here the model-based approaches fare considerably better. The model-based approaches are generally the best option, except for a few cases in the smaller networks (most noticeably the Sorority network where the probabilistic approach is best). For example, in the Proper network, the improvement using the model-based approach (simple or complex) is around 79 % compared to 61 % with probabilistic imputation or 67 % with symmetric imputation (missing high degree nodes).

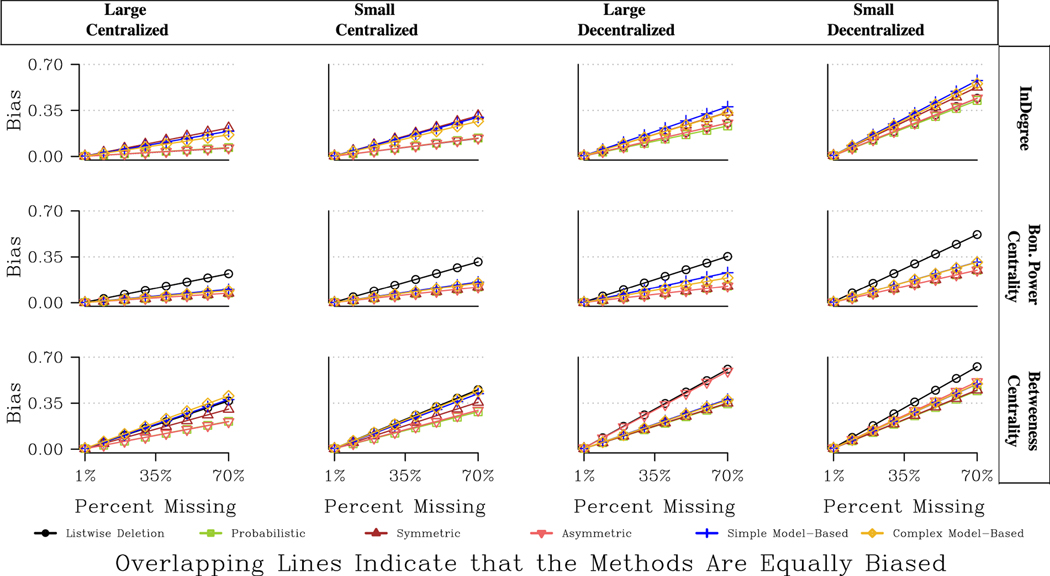
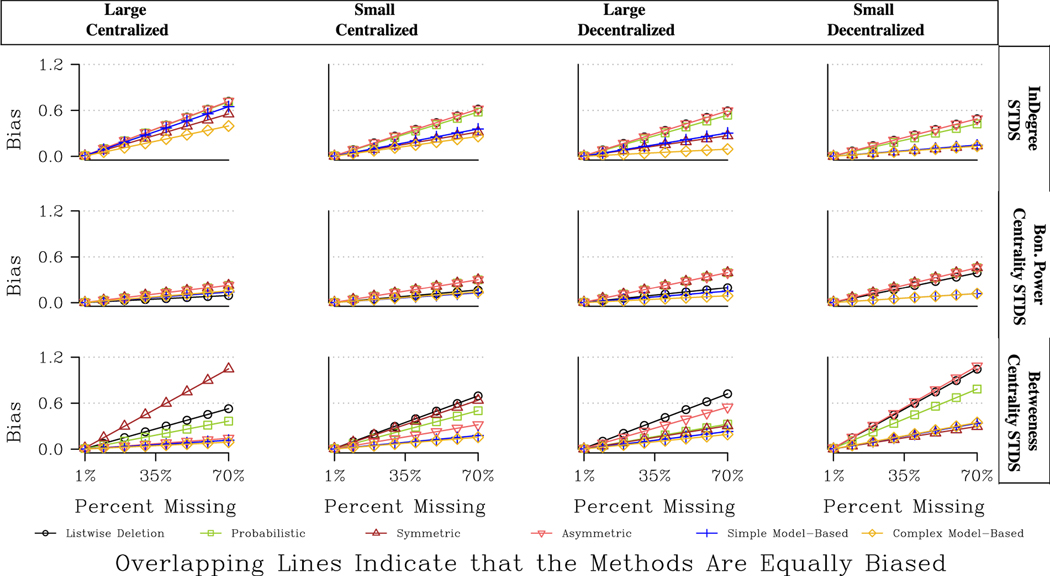
Fig. 5 offers a final set of comparisons, focusing on the performance of different imputation approaches in networks with different features. The figure presents the predicted bias for four different example networks, with varying combinations of size and centralization. The results are presented for directed networks with random non-response (also the case for Figs. 8 and 11) We focus on the results for betweenness centrality as the effect of centralization is so stark here. Overall, the probabilistic approach is consistently the best for betweenness, but otherwise the results are quite contingent. When the network is decentralized, the model-based and symmetric approaches perform adequately, offering better results than listwise deletion (although not as good as the probabilistic option). When the network is centralized, however, the model-based approach is the worst option, often little better than listwise deletion. We get similar results for closeness, where the model-based approaches are particularly preferred in large, decentralized networks (although the differences are less extreme). The symmetric and model- based approaches fare less well in centralized networks because both approaches tend to add more ties to the reconstructed network, potentially underestimating the centrality of the key actors while overestimating the centrality of the peripheral actors.

Fig. 5.

Predicted Bias for Centrality Measures for Four Network Types.

Fig. 8.

Predicted Bias for Centralization Measures for Four Network Types.

Fig. 11.

Predicted Bias for Topology Measures for Four Network Types.

Overall, for the directed networks, simple imputation strategies are preferred when estimating degree-based centrality measures, with probabilistic, asymmetric or sometimes even listwise deletion faring quite well. These imputation methods are less biased when estimating degree-based measures because they stick close to the actual data, and thus are better at recovering the specific number of alters. In contrast, with the path-based measures (particularly closeness), more complicated model-based approaches perform well, along with the probabilistic approach. For these path-based measures, the advantage of recovering more of the paths tends to outweigh the risk of (potentially) inflating the degree of any one node, as the model-based approaches are able to recover the pattern of ties. The probabilistic approach is unique in that it performs well in almost every case, a robust option when measuring centrality scores on directed networks.

Centralization

The centralization results are presented in Figs. 6 and 7, as well as Tables A5–A8. Table 3 offers a broad qualitative summary of the findings. We again start with a brief discussion of the undirected networks. Looking at degree centralization, all methods fare equally well in reducing bias and all outperform listwise deletion by a considerable margin (although some bias remains even after imputation). The returns to imputation are especially large when central nodes are more likely to be missing. For example, for an undirected, large, moderately centralized network with 40 % missing data, the predicted bias is .48 under listwise deletion and .13 after applying any of the imputation methods (assuming central nodes are more likely to be missing).

Fig. 6.

Predicted Bias for Centralization Measures for a Large, Undirected, Moderately Centralized Network.

Fig. 7.

Predicted Bias for Centralization Measures for a Large, Directed, Moderately Centralized Network.

Table 3.

Summary of Best Imputation Options for Centralization Measures.

Measure	Directed or Undirected	Non-response Type	Size and Centralization	Best Imputation Option
Degree Std	Undirected	Any	Any	Any strategy except Listwise Deletion
Bon Power Std	Undirected	Any	Small	Model-Baseda
Bon Power Std	Undirected	Any	Medium/Large	Listwise Deletion
Closeness Std	Undirected	Any	Any	Model-Based
Betweenness Std	Undirected	Any	Any	Any strategy except Listwise Deletion
Indegree Std	Directed	Any	Any	Model-Based (complex)
Total Degree Std	Directed	Any	Any	Model-Based (complex) or Symmetric
Bon Power Std	Directed	Any	Any	Model-Based
Closeness Std	Directed	Central Nodes	Decentralized	Model-Based (complex) or Symmetric
Closeness Std	Directed	Less Central Nodes	Decentralized	Symmetric or Probabilistic
Closeness Std	Directed	Any	Centralized	Probabilistic or Listwise Deletion
Betweenness Std	Directed	Any	Decentralized	Model-Based or Symmetric
Betweenness Std	Directed	Any	Centralized	Model-Based or Probabilistic

Notes.

^a:The model-based approach is assumed to correspond to complex or simple unless explicitly noted.

The results are quite different for Bonacich Power centralization, as listwise deletion is actually a better option than any of the imputation methods for every network but the small Interlock network (see Table A5 and Fig. 6). In general, the bias for Bonacich Power centralization is quite low, even when high degree nodes are non-respondents and we use listwise deletion. Thus, any imputation method that adjusts the centrality of the respondents (while excluding the missing cases from the calculation) runs the risk of adding bias where little was present to begin with.

The closeness results show the clearest differentiation between imputation options, with the model-based approaches (simple or complex) being preferred over listwise deletion and the symmetric approach. This holds across all missing data types and networks. For example, for the Co-authorship network, the total decrease in bias is 85 % for the complex model (compared to listwise deletion) and 73 % under the symmetric option. The median bias for the Co-authorship network with 30 % missing data is less than .05 with the model-based approach (under random missing nodes); compare this to .88 bias under listwise deletion.

Overall, the undirected networks for the centralization measures yield a straightforward story. In every case besides Bonacich Power, it is better to impute than listwise deletion, and in most cases any of the imputation approaches will work, making simple imputation particularly attractive. Note that the returns to imputation are typically larger when more central nodes are non-respondents, as imputation tends to weaken the deleterious effects of missing central actors.

We now turn to the directed networks, presented in Fig. 7 and Table A7 (the bias ratio table). We start with indegree centralization. The results clearly point to the complex model-based approach offering the greatest reduction in bias, followed by the symmetric approach and the simple model-based approach. The asymmetric and probabilistic methods do not offer much (or any) improvement over listwise deletion. For example, looking at Fig. 7, the expected bias for a large, moderately centralized network (under random missing nodes) with 30 % missing data is about .05 for the complex-model imputation, .127 for symmetric imputation, and .26 for listwise deletion and asymmetric imputation. The results are similar for total degree centralization, although here the asymmetric and probabilistic approaches are somewhat better than listwise deletion. Additionally, the symmetric approach offers no worse estimates than the model-based approach, and is often the best option. For example, the decrease in total bias for the HS 24 network (missing low degree nodes) is 87 % for both the symmetric and the complex model-based approach. The decrease is 31 % for the asymmetric option and 48 % for the probabilistic option.

The Bonacich centralization results mirror the undirected results in many ways, with most imputation methods offering worse estimates than listwise deletion under conditions of missing data (note that the symmetric, asymmetric and probabilistic are all equivalent in this case). The exceptions are the model-based approaches, which consistently outperform listwise deletion for all directed networks, save for the RC elite network (where listwise deletion is preferred). Thus, while a symmetric imputation would be a good option for indegree or total degree centralization, this does not extend to the case of Bonacich power. Boncacich centrality depends on the degree of one’s neighbors, while the symmetric approach only imputes the degree of the missing nodes in a limited way, compared to the model-based approach. Symmetric imputation, thus, tends to overestimate the level of centralization in the network for Bonacich centrality (as the method potentially underestimates the degree of one’s neighbors).

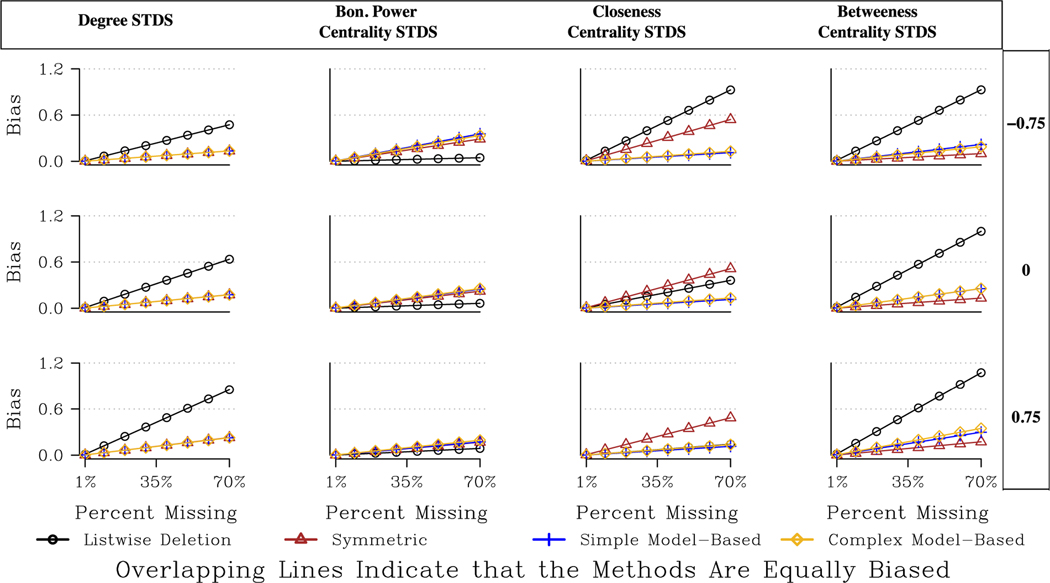
Closeness and betweenness centralization offer more contingent, complicated stories. The best imputation approach for closeness centralization depends heavily on the features of the network and the kinds of nodes that are missing. When the network exhibits low to moderate centralization and central nodes are more likely to be non-respondents (bottom row in Fig. 7), the best option is either the model- based or the symmetric approach. On the other hand, when low centrality nodes are more likely to be non-respondents, the best options are the probabilistic or symmetric approaches. For example, consider the Prison network, which has low centralization. When low degree nodes are non-respondents, the median bias is .11, .12 and .15 under the probabilistic, symmetric and model-based approaches, assuming 40 % missing data. When high degree nodes are non-respondents, the analogous values are: .20 (probabilistic), .15 (symmetric), and .10 (model- based). In this case, the symmetric approach would be a robust choice, although not necessarily the best one in terms of lowering bias. Simple imputation works less well for the more centralized networks. Listwise deletion is often just as good (or even better) as the imputation methods, especially when the network is very centralized (such as the RC elite network) or the non-respondents are less central. See Table A7 for the full results.

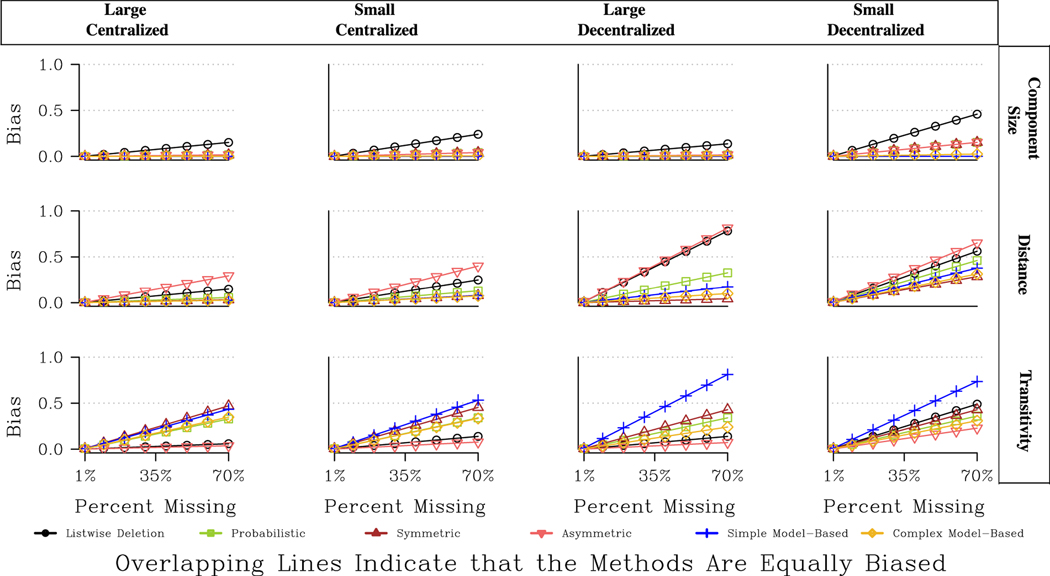
For betweenness, the results also depend heavily on the features of the network, and we can see this most clearly in Fig. 8. Fig. 8 presents the expected bias (based on the regression results presented in Table A8) for four different kinds of networks: large centralized, small centralized, large decentralized and small decentralized. The bottom row shows the results for betweenness. For the decentralized networks, the model- based and symmetric approaches are clearly preferred. For moderately centralized networks, the model-based approaches remain a good option. The model-based approaches fare quite poorly, however, for the RC elite network, the most centralized network. Here taking a model-based approach yields worse bias than listwise deletion, making the probabilistic and asymmetric approaches more appropriate. More striking, perhaps, is the poor performance of the symmetric option. In centralized networks, measures of betweenness centralization are sensitive to any imputation that changes the paths from the most central actors; thus, strategies that tend to add more ties (and thus paths between actors), like symmetric imputation, perform worse when the network is very centralized. Thus, the best option for decentralized networks is not an ideal choice for centralized ones.

In sum, the story is simple with undirected networks. All imputation methods are better than listwise deletion, with simple imputation methods being particularly attractive due to their ease of use. The case of directed networks is harder, as the ideal choice depends on the measure, the type of missing data and the type of network. In general, when there are contingent choices, the model-based approach performs comparatively well when the network is decentralized and/or the non-respondents have high degree.

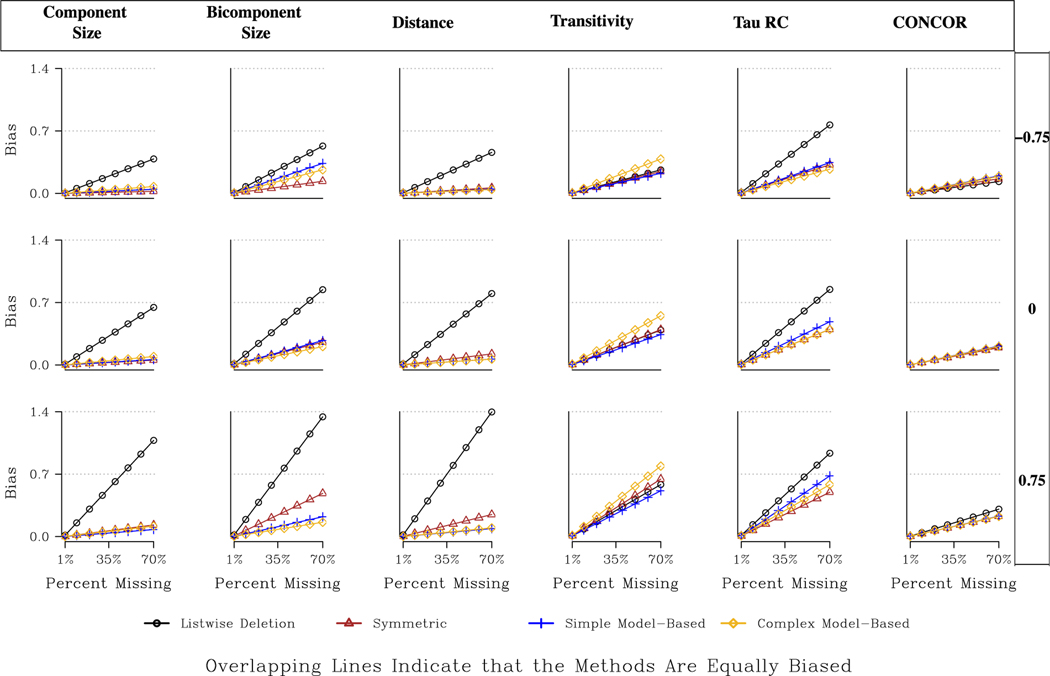
Topology

We end the results section with a discussion of the topology measures, again starting with the undirected networks. The results are presented in Fig. 9 and Table A9. See Table 4 for an overall picture of the best imputation methods. Looking at Fig. 9, we can see that all imputation methods fare better than listwise deletion for component size, bicomponent size and distance, and that there are large returns to imputation. We also see that the ideal choice of imputation method depends on the type of missing data. When high centrality nodes are more likely to be non-respondents, the best choice is the model-based approach (simple or complex). For example, the expected bias for bicomponent size when the network is large, moderately centralized, and missing 30 % of the data (in Fig. 9) is .57 when listwise deletion is applied, .20 for the symmetric strategy, and .07 for the complex model- based strategy. The analogous values when low centrality nodes are non-respondents are: .23 (listwise deletion), .06 (symmetric), and .11 (model-based) suggesting that the symmetric approach is actually favored when missing less central nodes, although the model-based approach remains a good option.

Fig. 9.

Predicted Bias for Topology Measures for a Large, Undirected, Moderately Centralized Network.

Table 4.

Summary of Best Imputation Options for Topology Measures.

Measure	Directed or Undirected	Non-response Type	Size and Centralization	Best Imputation Option
Component	Undirected	Central Nodes	Any	Model-baseda
Bicomponent
Distance
Component	Undirected	Less Central	Any	Symmetric
Bicomponent
Distance	Undirected	Less Central	Any	Any strategy except Listwise Deletion
Transitivity	Undirected	Any	Decentralized	Model-based (simple)
Transitivity	Undirected	Any	Centralized	Listwise Deletion
Tau	Undirected	Any	Any	Model-based
CONCOR	Undirected	Central Nodes	Any	Any strategy except Listwise Deletion
CONCOR	Undirected	Less Central	Any	Symmetric
Component	Directed	Any	Any	Model-based
Bicomponent
Distance	Directed	Central Nodes	Any	Model-based or Symmetric
Distance	Directed	Less Central	Any	Probabilistic or Symmetric
Transitivity	Directed	Any	Any	Asymmetric or Listwise Deletion
Tau	Directed	Any	Any	Probabilistic
CONCOR	Directed	Any	Any	Any strategy, including Listwise Deletion

Notes.

^a:The model-based approach is assumed to correspond to complex or simple unless explicitly noted.

The transitivity results show a different kind of pattern, where the best choice depends on the network being analyzed. When the network is decentralized, the simple model-based approach is the best option, followed by symmetric imputation (in most cases).¹⁸ The results are very different for the centralized networks, however. Here, all of the imputation methods perform poorly and listwise deletion is the most viable option. For example, looking at Table A9, we see negative values for the bias reduction in the HIV network and the Co-citation network (two highly centralized networks), meaning the imputation methods perform worse than listwise deletion. The imputation methods perform poorly in the centralized networks because transitivity tends to be unevenly distributed across the network (i.e., we may have lower levels with the most centralized actors), making imputation difficult for methods that do explicitly account for such variation.

Finally, looking at the CONCOR results, we see that the bias is quite low overall and the returns to imputation are small. For example, for the Co-authorship network, the median bias at 50 % missing is only .25 for listwise deletion and .20 for any of the imputation methods.

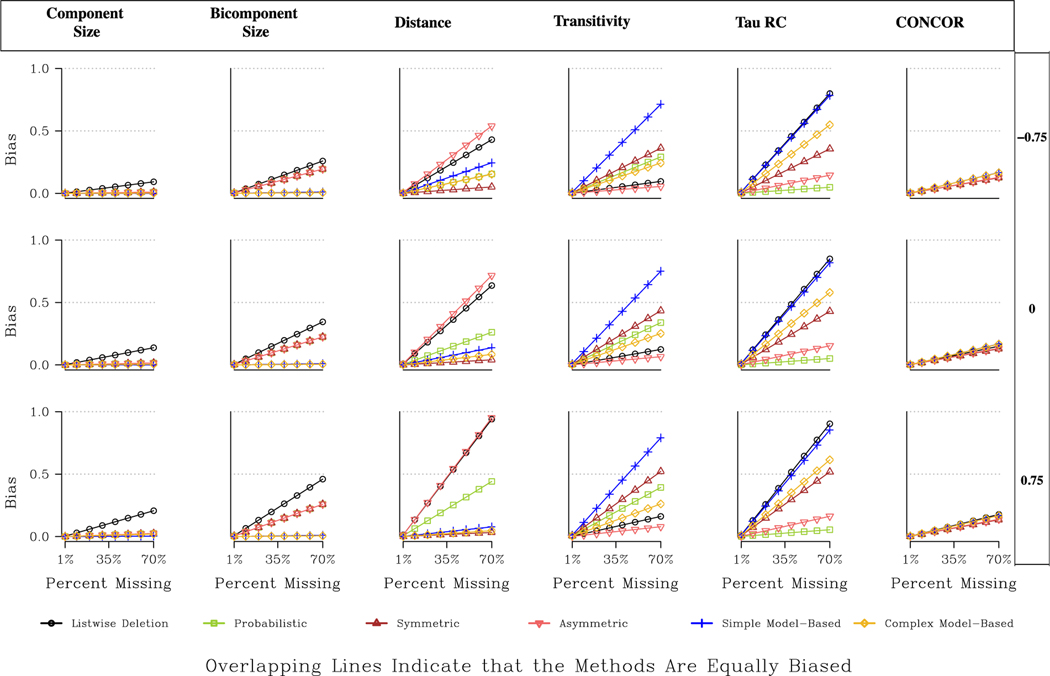
The results for the directed networks are presented in Fig. 10 and Table A11. Component and bicomponent size are similar to what we saw in the undirected case, but here the model-based approaches (simple or complex) are more uniformly the best option, followed by the simple imputation approaches.¹⁹ For example, for bicomponent size, the drop in total bias (compared with listwise deletion) under the model-based approach is 95 % for the Prosper network under random missing data; compare this to only 39 % using simple imputation. Or, looking at Fig. 10, the expected bias is almost 0 under the model-based approaches, outperforming the simpler options in all cases (but especially so when high degree nodes are more likely to be non-respondents).

Fig. 10.

Predicted Bias for Topology Measures for a Large, Directed, Moderately Centralized Network.

The distance results are much more sensitive to the type of missing data. For example, for the Prosper network under missing high degree nodes, the decrease in total bias is 81 % for the model-based approach, 73 % for the symmetric approach and 33 % for the probabilistic approach.²⁰ When low centrality nodes are non-respondents, the model- based approach actually yields 7 % more bias than listwise deletion while the symmetric approach has a slight improvement over listwise deletion, with a 15 % decrease in total bias. The probabilistic approach offers the best option in this case, with a decrease of 35 %. The symmetric and probabilistic strategies are both relatively information light methods (assuming either full reciprocation or reciprocation based on the observed reciprocity rate), and thus tend to perform comparatively better when there is little information about the non-respondents, as is true when trying to impute ties for peripheral nodes. Note that the asymmetric option performs quite poorly in these cases, offering worse or similar estimates as listwise deletion.

The transitivity results are straightforward in the directed case. The only consistently viable option that performs better than listwise deletion is the asymmetric imputation approach. Thus, the worse option for distance is the best option for transitivity. For example, looking at Fig. 10, the expected bias for our directed, moderately centralized network is .03 under the asymmetric approach, .053 under listwise deletion, .11 under the model-based approach, .145 under the probabilistic approach, and .18 under the symmetric approach (assuming 30 % missing random data). These results indicate that imputation that attempts to go beyond the raw data alters the underlying transitivity estimate in a way that is worse than listwise deletion, which has low bias in itself. See Fig. 10 and Table A11 for tau statistic and CONCOR results.

Fig. 11 offers a different kind of comparison, presenting the predicted bias for four example networks with different combinations of size and centralization. The figure is limited to three measures, component size, distance and transitivity. Overall, looking at Fig. 11, the best imputation method does not strongly depend on the features of the network. The best choice for large decentralized networks tends to be the best choice for small centralized networks (making the choice easier from the point of view of the researcher). There are, however, differential returns to different methods, depending on the features of the network and the measure of interest. For example, for distance, the returns to symmetric imputation (in terms of how much is gained relative to listwise deletion) is highest in decentralized networks—especially large decentralized networks where the bias is high if listwise deletion is applied. For transitivity, we see that the asymmetric approach is consistently the best, but that the model-based and probabilistic approaches fare relatively better in the decentralized networks.

Overall, the topology results suggest that the best imputation choice depends on the type of missing data, the type of network and the measure of interest. For example, we see measures that capture large structural features, like component size or distance, are best imputed based on the model-based or symmetric options. Other measures that are more local, like transitivity, are harder to impute and often listwise deletion is the best option. The type of missing data also matters greatly here, as the model-based approaches tend to perform better when more central nodes are missing, with this being true in both the directed and undirected cases.

Conclusion

Missing data is a difficult problem faced by network researchers. Traditional measures assume a full census of a bounded population (Laumann et al., 1983; Wasserman and Faust, 1994). In practice, a full census is often difficult to come by, as nodes and/or edges may be missing, offering an incomplete picture of the full network structure. It is thus important to understand how much bias results from missing data and how successful different imputation methods are under different conditions. This can be difficult to gauge, however, as there are few general, practical guidelines on how to address missing network data. This paper takes up this problem directly, showing how different imputation methods fare across a range of circumstances, including different networks, missing data types and measures of interest. We also consider a number of different imputation methods, ranging from simple network imputation to more complicated model-based approaches. The hope is that our results will make it easier for a researcher to choose an imputation method, given the particular features of their study.

Overall, we find that doing listwise deletion is almost always the worst option. Which imputation method performs best, however, is quite contingent, depending on the type of missing data, the type of network and the measure of interest. In this way, it is an easy choice to impute, but a harder choice to decide which method to employ. For example, for degree-based measures of centrality (on directed networks), we see that very simple approaches, including the asymmetric option, fare well. On the other hand, path-based measures (like closeness and betweenness) tend to require more complicated options, either probabilistic imputation or a model-based approach. In a similar way, we find that model-based approaches are particularly effective for structural measures, like bicomponent size or distance, but fare less well when estimating more local measures, like transitivity. The results also suggest that the type of network and missing data affect the performance of the imputation methods (Žnidaršič et al., 2018; Krause et al., 2020). For example, the model-based approaches are comparatively more effective when the network is decentralized and non-respondents have high degree.

How to choose an imputation strategy

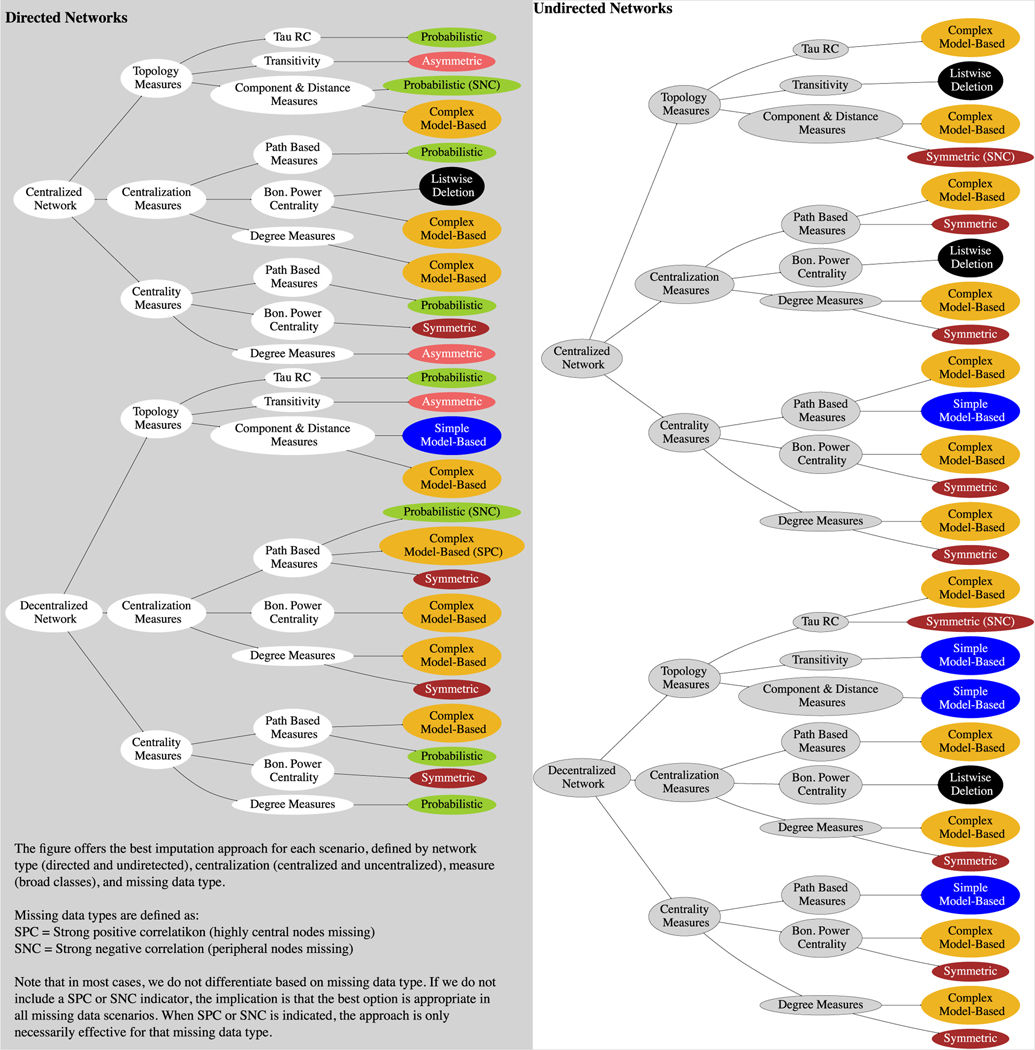
In short, different imputation methods are appropriate in different research settings, depending on the particular combination of missing data type, network and measure. Thus, a researcher must navigate a set of complex dependencies when making imputation decisions, especially since the size and type of network (e.g., large bipartite graphs) can make model-based imputation approaches intractable. To make this task easier, we have summarized our results in a simplified format in Fig. 12.

Fig. 12.

Summary Figure of Best Imputation Approach by Network Type, Measure, and Missing Data Condition.

The goal of Fig. 12 is to provide a user-friendly guide to imputation decisions. The figure is organized around a number of key factors, such as network type (directed/undirected; centralized/decentralized) and measure of interest.²¹ The figure is presented as a kind of branching structure, or decision tree, with the final branch showing the optimal choice of imputation method, given the features along the path. In selecting the optimal imputation strategy, we have tried to balance the best performing method with the difficulty of implementation. A researcher would simply follow the relevant path for their research setting and choose the best imputation method (noting that other imputation strategies may also offer reasonable results). For example, a researcher with a directed, decentralized network measuring betweenness or closeness centralization would do well using a symmetric imputation approach. The same researcher with a centralized network would do better using a probabilistic option. Such contingent decisions are hard to make without a guide, showing the clear utility of Fig. 12, as well as the more detailed summary tables presented earlier in the text.

It is important to note that Fig. 12 focuses on the optimal imputation method, but there are other factors that should be considered when making an imputation choice. First, a researcher must balance the performance of a method with the difficulty of implementing it. For example, a model-based approach can be difficult and expensive (time- wise) to implement. A researcher must already have a working knowledge of statistical network models, decide on the specific model to estimate, estimate the model, and so on. This is quite burdensome compared to the simple imputation options, which in many cases offer similar results. Thus, it is conceivable that a researcher would opt for simple imputation even when the model-based approach offers strictly lower bias. Of course, even with simple imputation options, a researcher must do a considerable amount of careful consideration, picking the right option for their particular scenario. In a similar way, a researcher may opt for a ‘safe’ choice that performs well across many settings, even if it is not necessarily the best (predicted) option in their particular case. Our results suggest that the probabilistic approach to network imputation is robust to different measures and networks, making it a good option overall. Finally, we note that a model-based approach may fare better under different specifications (e.g., Bayesian), as a better-specified model (i.e., one that captures the true tie formation processes) will offer improved estimates.

Limitations and considerations

Our analysis rests on a number of assumptions that must be considered when interpreting the results. For example, we assumed that the non-respondents are identifiable, so that respondents could still nominate them. This implicitly assumes a well-bounded, clearly defined population. Such conditions will not hold in all research settings, however, with important implications for the viability of different imputation strategies. Most clearly, the simple imputation approaches cannot be applied when missing nodes are unable to be identified (as there is no information to reconstruct the network). Model-based approaches could, in theory, still be used, as long as the size of the population was known, but their effectiveness will likely be reduced. There is no edge information on the missing nodes, making it difficult to predict how the missing nodes fit into the larger network. Listwise deletion could, of course, still be applied without complication.

Our analysis also assumes that the observed network is recorded without error. This assumption is unlikely to strictly hold in practice. Actors may forget to nominate people they should have (Brewer, 2000; Bell et al., 2007), while potentially nominating those they should not; for example, nominating an aspirational friend who is, in fact, not actually a friend (Almaatouq et al., 2016). Finally, there could be conflicting reports about the nature of the relationship (An and Schramski, 2015). Any measurement error in the observed data will end up being factored into the imputation process, and thus may lead to somewhat poorer results than reported in our own analysis. This may be particularly deleterious to the simple imputation approaches. If a researcher imputes a tie from j→i because i nominates j, then it is problematic if i→j does not really exist and is simply measurement error; as one imputes based on a false premise. Model-based approaches may fare better, as the model imputes probabilistically, based on general tendencies observed throughout the whole network, thus minimizing the effect of particular mistakes in the data.²² Ultimately, these are open questions deserving of more concerted work in the future.

Final thoughts

This set of papers began with a simple goal — to describe the consequences of missing data for typically used network measures (Smith and Moody, 2013). Overall, we have shown that the effect of missing data is highly contingent, depending on the circumstances of the study, as well as the actions of the researcher. Here, we emphasize the role of the researcher in reducing bias. Our results suggest that a researcher choosing an effective imputation method for their setting can greatly reduce the bias due to missing data, even in cases with difficult conditions (i.e., non-respondents tend to be central to the network). A study with over 50 % non-respondents can, potentially, still yield valid estimates. In the end, the hope is that our results can be used as a practical guide for researchers choosing an imputation strategy, and, more generally, dealing with the difficult problem of missing network data.

Appendix A

Table A1.

Percent Decrease in Total Bias under Different Imputation Strategies: Centrality Measures for Undirected Networks.

Measure	Imputation	Interlock			Coauthor			Co-citation			Biotech			HIV
		Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality
		−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75
Degree	Symmetric	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100
	Model-based Simple	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100
	Model-based Complex	100	100	100	100	100	100	100	100	100	100	100	100	100	100	100
Bon Power	Symmetric	96	93	91	96	95	89	95	94	93	95	92	92	90	88	86
	Model-based Simple	95	95	94	98	97	91	97	96	96	96	93	93	91	90	89
	Model-based Complex	93	94	94	98	96	91	98	97	97	96	94	93	93	92	92
Closeness	Symmetric	91	85	80	89	82	75	92	90	86	85	83	78	88	86	82
	Model-based Simple	93	91	87	90	86	80	94	94	92	91	89	84	91	90	85
	Model-based Complex	93	91	86	91	85	77	93	93	91	90	88	83	91	89	84
Betweenness	Symmetric	86	79	67	86	78	56	83	74	49	90	88	79	87	82	62
	Model-based Simple	87	86	77	74	81	68	79	74	60	88	88	84	65	75	70
	Model-based Complex	86	84	76	83	82	64	78	73	62	88	88	81	79	82	73

Table A2.

Centrality Bias Slope Regressions: Undirected Networks.

Variables	Model 1 Degree	Model 2 Bon. Power	Model 3 Closeness	Model 4 Betweeness
Intercept	−1.925***	−2.572	−2.834**	−1.802
	(0.46)	(1.7)	(0.94)	(1.33)
Correlation with Centrality	0.92***	1.199***	0.626***	0.517***
	(0.15)	(0.11)	(0.05)	(0.07)
In-degree Std. Dev.	−0.166***	−0.174	−0.075	−0.041
	(0.03)	(0.13)	(0.07)	(0.1)
Log of Size	−0.166	0.016	0.035	−0.206
	(0.09)	(0.35)	(0.19)	(0.27)
Symmetric Imputation	−40.255***	−3.407**	−2.313**	−0.397
	(0.6)	(1.06)	(0.89)	(0.63)
Simple Model-Based Imputation	−39.492***	−3.772***	−2.771*	−1.214
	(1.22)	(1.1)	(1.21)	(0.87)
Complex Model-Based Imputation	−39.492***	−3.31**	−2.712*	−0.703
	(1.59)	(1.09)	(1.1)	(0.58)
Correlation with Centrality* Symmetric Imputation	−0.871***	0.292	0.261***	0.68***
	(0.21)	(0.16)	(0.08)	(0.1)
Correlation with Centrality* Simple Model-Based Imputation	−0.718***	0.225	0.267***	0.234*
	(0.21)	(0.16)	(0.08)	(0.1)
Correlation with Centrality* Complex Model-Based Imputation	−0.718***	0.232	0.291***	0.34***
	(0.21)	(0.16)	(0.08)	(0.1)
In-degree Std. Dev.* Symmetric Imputation	0.146**	−0.03	−0.064	0.085
	(0.04)	(0.08)	(0.07)	(0.05)
In-degree Std. Dev.* Simple Model-Based Imputation	0.198*	−0.071	−0.054	0.116
	(0.09)	(0.08)	(0.09)	(0.07)
In-degree Std. Dev.* Complex Model-Based Imputation	0.198	−0.111	−0.045	0.113*
	(0.12)	(0.08)	(0.08)	(0.04)
Log of Size* Symmetric Imputation	0.211	0.224	0.337	−0.257*
	(0.12)	(0.22)	(0.18)	(0.13)
Log of Size *Simple Model-Based Imputation	0.029	0.294	0.345	−0.15
	(0.25)	(0.23)	(0.25)	(0.18)
Log of Size* Complex Model-Based Imputation	0.029	0.241	0.333	−0.242*
	(0.33)	(0.22)	(0.23)	(0.12)
N	180	180	180	180
Networks	5	5	5	5

Note: The regression uses the betas slopes from each line as the dependent variable. The betas represent the expected drop in correlation (between the empirical and the observed) for a 10 % increase in the amount of missing data. Larger numbers mean larger bias with more missing data. The correlation with centrality takes four values: − .75, − .25, .25, and .75.

Table A3.

Percent Decrease in Total Bias under Different Imputation Strategies: Centrality Measures for Directed Networks.

Measure	Imputation	Prison			Sorority			6th Grade			Prosper			RC Elite			HS 13			HS 24
		Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality
		−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75
Indegree	Probabilistic	4	5	6	6	14	20	−6	−2	2	2	3	3	−1	−1	−1	6	7	9	10	12	15
	Symmetric	−31	−25	−27	−24	−7	5	−103	−92	−71	−54	−51	−50	−226	−238	−277	−42	−41	−41	−29	−25	−21
	Asymmetric	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Model-based Simple	−52	−44	−42	−44	−29	−15	−68	−59	−46	−78	−63	−52	−218	−254	−262	−71	−64	−57	−59	−51	−40
	Model-based Complex	−43	−37	−34	−35	−20	−9	−63	−52	−37	−65	−51	−41	−168	−190	−210	−50	−44	−34	−42	−33	−22
Total Degree	Probabilistic	60	63	68	69	74	77	52	55	61	61	63	67	0	6	47	57	60	67	63	66	71
	Symmetric	51	56	63	64	71	76	34	40	52	49	53	60	−120	−108	−15	44	48	57	53	58	66
	Asymmetric	60	62	67	67	71	74	57	58	63	62	63	67	1	7	48	59	62	67	64	66	71
	Model-based Simple	40	47	53	52	60	67	39	43	51	37	43	51	−79	−79	−10	35	41	50	43	48	57
	Model-based Complex	43	48	55	55	62	68	43	47	55	41	47	55	−45	−44	7	42	47	57	48	53	62
Bon Power	Probabilistic	55	57	62	56	60	64	57	58	60	57	57	61	66	73	87	63	66	73	64	67	70
	Symmetric	55	57	62	56	60	64	57	58	60	57	57	61	66	73	87	63	66	73	64	67	70
	Asymmetric	55	57	62	56	60	64	57	58	60	57	57	61	66	73	87	63	66	73	64	67	70
	Model-based Simple	40	49	57	38	48	57	42	49	57	29	37	49	53	60	80	31	41	53	37	45	56
	Model-based Complex	39	49	57	36	47	56	47	53	61	32	40	52	57	63	80	43	51	63	44	52	62
Closeness	Probabilistic	49	56	62	55	59	64	79	84	88	51	56	61	48	49	51	62	66	70	67	72	75
	Symmetric	36	51	62	42	48	54	83	90	93	58	64	67	−77	−58	−46	78	83	86	78	83	87
	Asymmetric	33	39	46	40	47	54	32	32	34	21	28	35	49	49	53	8	9	12	7	9	13
	Model-based Simple	49	65	73	33	52	61	87	94	95	66	76	80	0	15	18	79	85	88	84	89	91
	Model-based Complex	49	63	71	37	52	59	88	94	96	67	76	79	10	24	23	81	86	89	85	89	91
Betweenness	Probabilistic	30	32	32	22	21	22	29	35	34	28	29	28	23	21	13	37	37	34	46	46	45
	Symmetric	3	13	20	4	4	6	−18	−3	4	1	14	16	−151	−136	−95	10	12	11	25	28	29
	Asymmetric	24	24	24	13	13	13	19	15	13	11	10	10	51	46	38	9	8	7	10	9	8
	Model-based Simple	−22	−3	9	−8	−2	3	−4	6	8	−10	6	11	−145	−144	−110	−6	0	1	10	15	19
	Model-based Complex	−15	1	11	−1	4	6	7	16	15	−1	12	14	−120	−109	−80	7	12	12	19	23	27

Table A4.

Centrality Bias Slope Regressions: Directed Networks.

Variables	Model 1 Indegree	Model 2 Total Degree	Model 3 Bon. Power	Model 4 Closeness	Model 5 Betweeness
Intercept	−2.598***	−2.476***	−2.198***	−2.973*	−2.652***
	(0.7)	(0.6)	(0.23)	(1.37)	(0.19)
Correlation with Centrality	0.309***	0.31***	0.411***	0.197***	0.202***
	(0.04)	(0.03)	(0.03)	(0.05)	(0.02)
In-degree Std. Dev.	−0.356***	−0.273***	−0.138***	−0.058	−0.114***
	(0.06)	(0.06)	(0.02)	(0.13)	(0.02)
Log of Size	0.107	0.073	−0.037	0.094	0.103**
	(0.15)	(0.13)	(0.05)	(0.29)	(0.04)
Asymmetric Imputation	0.019	−0.845	−0.286	−2.184***	−0.822
	(0.2)	(0.57)	(0.35)	(0.57)	(0.44)
Simple Model-Based Imputation	0.448	−0.506	−0.868*	0.723	0.466
	(0.57)	(0.92)	(0.44)	(1.97)	(0.42)
Complex Model-Based Imputation	0.544	−0.483	−0.491	0.938	0.556
	(0.5)	(0.81)	(0.34)	(2.15)	(0.45)
Probabilistic Imputation	0.145	−0.915	−0.286	−0.909	0.046
	(0.24)	(0.51)	(0.34)	(2.26)	(0.35)
Symmetric Imputation	0.544	−0.811	−0.286	0.358	0.262
	(0.42)	(0.97)	(0.32)	(1.5)	(0.32)
Correlation with Centrality* Asymmetric Imputation	0.01	−0.196***	−0.193***	−0.158*	0.035
	(0.06)	(0.04)	(0.04)	(0.07)	(0.03)
Correlation with Centrality* Simple Model-Based Imputation	−0.075	−0.224***	−0.286***	−0.475***	−0.098**
	(0.06)	(0.04)	(0.04)	(0.07)	(0.03)
Correlation with Centrality* Complex Model-Based Imputation	−0.077	−0.215***	−0.292***	−0.431***	−0.077*
	(0.06)	(0.04)	(0.04)	(0.07)	(0.03)
Correlation with Centrality* Probabilistic Imputation	−0.033	−0.219***	−0.193***	−0.192**	0.009
	(0.06)	(0.04)	(0.04)	(0.07)	(0.03)
Correlation with Centrality* Symmetric Imputation	−0.064	−0.284***	−0.193***	−0.32***	−0.074*
	(0.06)	(0.04)	(0.04)	(0.07)	(0.03)
In-degree Std. Dev.* Asymmetric Imputation	0.003	0.207***	−0.046	−0.055	−0.102*
	(0.02)	(0.05)	(0.03)	(0.05)	(0.04)
In-degree Std. Dev.*Simple Model-Based Imputation	0.168**	0.229**	−0.069	0.108	0.088*
	(0.05)	(0.09)	(0.04)	(0.18)	(0.04)
In-degree Std. Dev.*Complex Model-Based Imputation	0.154***	0.205**	−0.064*	0.109	0.105*
	(0.05)	(0.07)	(0.03)	(0.2)	(0.04)
In-degree Std. Dev.* Probabilistic Imputation	0.029	0.21***	−0.046	−0.041	−0.017
	(0.02)	(0.05)	(0.03)	(0.21)	(0.03)
In-degree Std. Dev.* Symmetric Imputation	0.218***	0.318***	−0.046	0.059	0.059*
	(0.04)	(0.09)	(0.03)	(0.14)	(0.03)
Log of Size* Asymmetric Imputation	−0.005	−0.163	−0.087	0.358**	0.187*
	(0.04)	(0.12)	(0.08)	(0.12)	(0.09)
Log of Size *Simple Model-Based Imputation	−0.111	−0.169	0.111	−0.553	−0.2*
	(0.12)	(0.2)	(0.09)	(0.42)	(0.09)
Log of Size* Complex Model-Based Imputation	−0.138	−0.171	0.019	−0.584	−0.227*
	(0.11)	(0.17)	(0.07)	(0.46)	(0.1)
Log of Size * Probabilistic Imputation	−0.055	−0.145	−0.087	0.002	−0.085
	(0.05)	(0.11)	(0.07)	(0.48)	(0.07)
Log of Size* Symmetric Imputation	−0.175	−0.201	−0.087	−0.359	−0.163*
	(0.09)	(0.21)	(0.07)	(0.32)	(0.07)
N	378	378	378	378	378
Networks	7	7	7	7	7

Note: The regression uses the betas slopes from each line as the dependent variable. The betas represent the expected drop in correlation (between the empirical and the observed) for a 10 % increase in the amount of missing data. Larger numbers mean larger bias with more missing data. The correlation with centrality takes four values: −.75, −.25, .25, and .75.

Table A5.

Percent Decrease in Total Bias under Different Imputation Strategies: Centralization Measures for Undirected Networks.

Measure	Imputation	Interlock			Coauthor			Cocitation			Biotech			HIV
		−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75
Degree	Symmetric	64	76	64	62	83	67	52	84	64	54	79	56	58	85	62
	Model-based Simple	63	76	64	63	83	68	52	84	64	54	79	55	58	84	62
	Model-based Complex	63	76	64	63	83	68	52	84	64	54	79	55	58	84	62
Bon Power	Symmetric	−9	15	43	−313	−251	−89	−374	−583	−158	−588	−249	−82	−815	−411	−130
	Model-based Simple	28	54	63	−229	−107	−61	−391	−492	−70	−701	−300	−95	−922	−509	−176
	Model-based Complex	25	54	61	−175	−76	−131	−308	−226	−100	−689	−292	−134	−855	−413	−127
Closeness	Symmetric	78	66	61	82	73	65	79	80	77	80	77	76	86	83	84
	Model-based Simple	86	82	77	89	86	78	87	87	78	93	93	91	96	95	91
	Model-based Complex	85	81	77	90	85	76	88	88	78	93	93	90	95	94	92
Betweenness	Symmetric	81	74	62	80	83	76	76	64	44	78	78	67	83	89	86
	Model-based Simple	78	79	76	69	58	50	88	85	77	66	72	69	88	81	69
	Model-based Complex	77	78	75	79	66	54	87	78	66	67	73	67	90	83	68

Table A6.

Centralization Bias Slope Regressions: Undirected Networks.

Variables	Model 1 Degree	Model 2 Bon. Power	Model 3 Closeness	Model 4 Betweeness
Intercept	−2.723***	−2.284	−2.387	−1.912***
	(0.35)	(1.35)	(1.22)	(0.21)
Correlation with Centrality	0.39**	0.423***	−1.254***	0.097
	(0.13)	(0.1)	(0.06)	(0.07)
In-degree Std. Dev.	0.016	−0.147	0.042	−0.011
	(0.03)	(0.1)	(0.09)	(0.02)
Log of Size	0.038	−0.265	−0.123	0.003
	(0.07)	(0.27)	(0.25)	(0.04)
Symmetric Imputation	−1.378*	−0.881	−0.749	0.107
	(0.61)	(1.37)	(0.99)	(0.82)
Simple Model-Based Imputation	−1.324*	−3.054**	0.096	−0.942
	(0.65)	(0.94)	(1.43)	(1.46)
Complex Model-Based Imputation	−1.324	−3.16**	−0.211	−0.878
	(1.1)	(1.02)	(1.63)	(1.09)
Correlation with Centrality* Symmetric Imputation	−0.036	−0.784***	1.18***	0.271**
	(0.18)	(0.15)	(0.09)	(0.1)
Correlation with Centrality* Simple Model-Based Imputation	−0.044	−0.909***	1.265***	0.111
	(0.18)	(0.15)	(0.09)	(0.1)
Correlation with Centrality* Complex Model-Based Imputation	−0.044	−0.788***	1.291***	0.311**
	(0.18)	(0.15)	(0.09)	(0.1)
In-degree Std. Dev.* Symmetric Imputation	−0.01	0.184	−0.132	0.098
	(0.05)	(0.1)	(0.07)	(0.06)
In-degree Std. Dev.* Simple Model-Based Imputation	−0.011	0.178*	−0.05	−0.081
	(0.05)	(0.07)	(0.11)	(0.11)
In-degree Std. Dev.* Complex Model-Based Imputation	−0.011	0.099	−0.063	−0.025
	(0.08)	(0.08)	(0.12)	(0.08)
Log of Size* Symmetric Imputation	0.022	0.189	0.277	−0.413*
	(0.13)	(0.28)	(0.2)	(0.17)
Log of Size *Simple Model-Based Imputation	0.014	0.555**	−0.158	−0.003
	(0.13)	(0.19)	(0.29)	(0.3)
Log of Size* Complex Model-Based Imputation	0.014	0.638**	−0.075	−0.056
	(0.22)	(0.21)	(0.33)	(0.22)
N	180	180	180	180
Networks	5	5	5	5

Note: The regression uses the beta slopes from each line as the dependent variable. The direction of the bias is ignored when calculating the regressions. The betas represent the expected increase in bias for a 10 % increase in the amount of missing data. Larger numbers mean larger bias with more missing data. The correlation with centrality takes four values: −.75, −.25, .25, and .75.

Table A7.

Percent Decrease in Total Bias under Different Imputation Strategies: Centralization Measures for Directed Networks.

Measure	Imputation	Prison			Sorority			6th Grade			Prosper			RC Elite			HS 13			HS 24
		Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality
		−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75
Indegree	Probabilistic	4	5	5	14	15	16	7	7	8	6	6	5	0	0	0	6	6	7	9	10	10
	Symmetric	43	44	44	58	66	70	49	50	55	51	50	51	6	6	8	36	40	44	46	51	54
	Asymmetric	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	Model-based Simple	54	50	45	54	60	60	42	37	32	55	50	44	6	4	6	36	35	33	43	42	39
	Model-based Complex	56	62	58	36	62	68	77	70	61	66	73	65	27	20	17	72	67	60	79	74	66
Total Degree	Probabilistic	43	42	39	60	66	67	60	61	63	58	59	57	7	7	8	39	43	46	48	52	54
	Symmetric	52	66	72	40	58	66	78	79	80	70	77	81	20	19	22	76	82	87	87	92	93
	Asymmetric	25	25	23	38	42	42	43	45	48	38	40	40	7	6	8	26	30	33	31	35	37
	Model-based Simple	57	64	61	56	69	76	72	72	72	76	79	77	13	10	13	57	60	61	66	69	70
	Model-based Complex	45	61	67	33	61	71	80	82	82	62	76	82	33	26	23	83	83	80	87	89	85
Bon Power	Probabilistic	1	10	19	−13	−7	1	−86	−79	−62	−58	−43	−25	−213	−192	−203	−74	−69	−55	−82	−82	−63
	Symmetric	1	10	19	−13	−7	1	−86	−79	−62	−58	−43	−25	−213	−192	−203	−74	−69	−55	−82	−82	−63
	Asymmetric	1	10	19	−13	−7	1	−86	−79	−62	−58	−43	−25	−213	−192	−203	−74	−69	−55	−82	−82	−63
	Model-based Simple	47	58	58	53	66	67	25	40	44	26	33	32	−361	−200	−186	21	28	10	16	10	−4
	Model-based Complex	46	57	59	56	64	66	40	56	52	35	46	39	−391	−227	−233	45	51	30	46	46	25
Closeness	Probabilistic	7	23	28	24	33	36	−18	20	25	19	45	43	−106	−48	34	−4	53	57	−8	59	71
	Symmetric	−14	14	37	26	47	56	−12	19	−18	34	68	72	−1824	−2102	−1381	−19	12	−3	5	48	35
	Asymmetric	−3	−8	−4	−13	−5	1	−12	−3	15	−11	2	6	−80	−26	44	3	3	5	5	15	17
	Model-based Simple	−27	25	46	9	36	50	−10	7	−47	4	50	54	−566	−540	−317	−32	−7	−26	−9	11	−4
	Model-based Complex	−33	28	52	23	53	63	−12	16	−25	15	70	75	−264	−223	−127	−36	35	17	−9	52	33
Betweenness	Probabilistic	46	40	36	48	42	39	35	30	25	62	56	50	35	30	27	65	58	51	50	36	25
	Symmetric	72	72	68	71	69	64	7	−2	−16	67	64	62	−771	−675	−556	43	33	19	45	30	14
	Asymmetric	15	11	8	10	7	5	58	44	25	26	16	11	24	19	16	35	12	−20	40	7	−33
	Model-based Simple	67	67	67	58	61	62	0	−3	−2	25	34	38	−1231	−1073	−886	9	12	11	−22	−25	−21
	Model-based Complex	69	68	66	63	65	63	34	32	27	42	50	53	−939	−724	−526	42	43	39	21	18	19

Table A8.

Centralization Bias Slope Regressions: Directed Networks.

Variables	Model 1 Indegree	Model 2 Total Degree	Model 3 Bon. Power	Model 4 Closeness	Model 5 Betweeness
Intercept	−2.877***	−3.012***	−2.12***	−3.022***	−1.443
	(0.15)	(0.14)	(0.62)	(0.9)	(0.79)
Correlation with Centrality	0.21***	0.234***	0.28***	0.556***	0.072
	(0.03)	(0.04)	(0.05)	(0.1)	(0.04)
In-degree Std. Dev.	0.06***	0.074***	−0.228***	−0.278	−0.103
	(0.01)	(0.01)	(0.06)	(0.15)	(0.13)
Log of Size	0.027	0.029	−0.085	0.148	−0.066
	(0.03)	(0.03)	(0.13)	(0.22)	(0.19)
Asymmetric Imputation	0	−0.611	−0.658*	0.751	−0.02
	(0.15)	(0.47)	(0.29)	(0.69)	(0.24)
Simple Model-Based Imputation	−1.808***	−1.489	−2.423**	−0.973	−1.321
	(0.42)	(0.92)	(0.82)	(0.81)	(1.2)
Complex Model-Based Imputation	0.346	1.953	−1.173	−0.567	−0.969
	(1.16)	(1.03)	(1.1)	(0.97)	(1.06)
Probabilistic Imputation	−0.176	−1.426	−0.658	1.792*	0.844
	(0.28)	(0.82)	(0.42)	(0.91)	(0.79)
Symmetric Imputation	−1.773	2.302*	−0.658	0.209	−1.055
	(1.03)	(1.03)	(0.74)	(1.39)	(1.1)
Correlation with Centrality* Asymmetric Imputation	0	−0.048	−0.133	−0.13	0.21***
	(0.04)	(0.06)	(0.07)	(0.14)	(0.05)
Correlation with Centrality* Simple Model-Based Imputation	0.101*	−0.085	−0.302***	−0.487***	−0.283***
	(0.04)	(0.06)	(0.07)	(0.14)	(0.05)
Correlation with Centrality* Complex Model-Based Imputation	0.159***	−0.19***	−0.219**	−0.659***	−0.134*
	(0.04)	(0.06)	(0.07)	(0.14)	(0.05)
Correlation with Centrality* Probabilistic Imputation	0.005	−0.047	−0.133	−0.46**	0.177**
	(0.04)	(0.06)	(0.07)	(0.14)	(0.05)
Correlation with Centrality* Symmetric Imputation	−0.094*	−0.319***	−0.133	−0.572***	0.28***
	(0.04)	(0.06)	(0.07)	(0.14)	(0.05)
In-degree Std. Dev.* Asymmetric Imputation	0	0.054	0.094***	−0.008	−0.257***
	(0.01)	(0.04)	(0.03)	(0.11)	(0.04)
In-degree Std. Dev.*Simple Model-Based Imputation	0.173***	0.223**	0.231**	0.32*	−0.083
	(0.04)	(0.09)	(0.08)	(0.13)	(0.2)
In-degree Std. Dev.*Complex Model-Based Imputation	0.223*	0.249**	0.32**	0.388*	−0.116
	(0.11)	(0.1)	(0.1)	(0.16)	(0.17)
In-degree Std. Dev.* Probabilistic Imputation	0.024	0.129	0.094*	0.135	0.046
	(0.03)	(0.08)	(0.04)	(0.15)	(0.13)
In-degree Std. Dev.*Symmetric Imputation	0.159	0.308**	0.094	0.384	0.376*
	(0.1)	(0.1)	(0.07)	(0.23)	(0.18)
Log of Size* Asymmetric Imputation	0	−0.008	0.153*	−0.135	0.119*
	(0.03)	(0.1)	(0.06)	(0.17)	(0.06)
Log of Size *Simple Model-Based Imputation	0.07	−0.119	0.193	−0.126	0.079
	(0.09)	(0.2)	(0.18)	(0.19)	(0.29)
Log of Size* Complex Model-Based Imputation	−0.477	−0.86***	−0.137	−0.288	0.016
	(0.25)	(0.22)	(0.23)	(0.23)	(0.25)
Log of Size * Probabilistic Imputation	−0.002	0.025	0.153	−0.546*	−0.283
	(0.06)	(0.17)	(0.09)	(0.22)	(0.19)
Log of Size*Symmetric Imputation	0.055	−0.958***	0.153	−0.459	−0.202
	(0.22)	(0.22)	(0.16)	(0.34)	(0.27)
N	378	378	378	324	324
Networks	7	7	7	7	7

Note: The regression uses the betas slopes from each line as the dependent variable. The betas represent the expected drop in correlation (between the empirical and the observed) for a 10 % increase in the amount of missing data. Larger numbers mean larger bias with more missing data. The correlation with centrality takes four values: −.75, −.25, .25, and .75.

Table A9.

Percent Decrease in Total Bias under Different Imputation Strategies: Topology Measures for Undirected Networks.

Measure	Imputation	Interlock			Co-author			Co-citation			Biotech			HIV
		−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75
Component	Symmetric	89	86	74	95	92	83	94	94	93	94	94	91	96	96	96
	Model-based Simple	81	89	86	95	96	96	86	92	97	85	88	91	91	93	94
	Model-based Complex	79	88	85	86	90	91	75	87	93	84	87	90	82	87	90
Bicomponent	Symmetric	68	67	55	81	82	73	76	85	82	77	79	77	87	89	85
	Model-based Simple	41	79	80	−100	−1	42	−28	49	83	63	80	92	17	50	74
	Model-based Complex	44	80	79	−22	38	66	16	62	89	68	83	93	45	68	85
Distance	Symmetric	30	72	59	70	83	68	14	81	68	92	90	78	89	91	81
	Model-based Simple	38	80	70	67	92	88	18	84	76	93	93	84	83	97	91
	Model-based Complex	39	80	70	72	91	85	19	84	77	93	93	85	87	97	90
Transitivity	Symmetric	75	70	72	−8	−31	−51	30	−101	−58	74	47	33	−140	−92	−45
	Model-based Simple	76	79	82	−42	−56	−64	5	−123	−55	79	61	48	−217	−159	−97
	Model-based Complex	39	50	67	22	3	−7	35	−52	−2	45	31	4	−112	−69	−27
Tau	Symmetric	39	53	20	−27	−16	−12	57	49	63	86	68	46	72	82	64
	Model-based Simple	40	42	28	13	7	−3	79	72	74	71	60	48	88	82	66
	Model-based Complex	13	16	13	47	28	12	75	53	61	72	61	50	89	85	70
CONCOR	Symmetric	44	42	46	50	49	52	54	42	38	39	36	40	47	43	44
	Model-based Simple	21	30	42	22	31	44	38	30	33	30	31	38	37	37	41
	Model-based Complex	21	29	42	36	41	51	39	32	37	29	31	37	44	43	46

Table A10.

Topology Bias Slope Regressions: Undirected Networks.

Variables	Model 1 Component Size	Model 2 Bicomponent Size	Model 3 Distance	Model 4 Transitivity	Model 5 Tau RC	Model 6 CONCOR
Intercept	−2.752***	−2.78***	−3.262***	−0.538	−1.648	−3.82***
	(0.44)	(0.45)	(0.42)	(1.68)	(0.84)	(0.24)
Correlation with Centrality	0.685***	0.619***	0.742***	0.53***	0.132	0.56***
	(0.07)	(0.06)	(0.13)	(0.05)	(0.08)	(0.02)
In-degree Std. Dev.	−0.061	−0.08*	−0.086**	−0.236	−0.005	−0.034
	(0.03)	(0.03)	(0.03)	(0.13)	(0.06)	(0.02)
Log of Size	0.106	0.168	0.24**	−0.184	−0.07	0.07
	(0.09)	(0.09)	(0.08)	(0.34)	(0.17)	(0.05)
Symmetric Imputation	−0.326	0.125	1.064*	−2.167	2.207*	−0.272
	(0.46)	(0.26)	(0.52)	(1.75)	(1.1)	(0.36)
Simple Model-Based Imputation	−1.659	−0.327	0.914	−2.951	1.553	−0.128
	(1.26)	(1.67)	(0.67)	(2.08)	(1.11)	(0.31)
Complex Model-Based Imputation	−1.605***	−0.077	1.052	−1.784	2.683	−0.145
	(0.42)	(1.53)	(1.15)	(1.53)	(1.38)	(0.24)
Correlation with Centrality* Symmetric Imputation	0.481***	0.231**	0.179	0.117	0.161	−0.341***
	(0.1)	(0.09)	(0.18)	(0.08)	(0.12)	(0.03)
Correlation with Centrality* Simple Model-Based Imputation	−0.326**	−0.896***	−0.332	0.02	0.322**	−0.458***
	(0.1)	(0.09)	(0.18)	(0.08)	(0.12)	(0.03)
Correlation with Centrality* Complex Model-Based Imputation	−0.404***	−0.951***	−0.2	−0.051	0.378**	−0.446***
	(0.1)	(0.09)	(0.18)	(0.08)	(0.12)	(0.03)
In-degree Std. Dev.* Symmetric Imputation	−0.078*	−0.096***	0.045	0.227	−0.001	0.02
	(0.03)	(0.02)	(0.04)	(0.13)	(0.08)	(0.03)
In-degree Std. Dev.* Simple Model-Based Imputation	−0.078	0.085	0.067	0.308*	−0.126	0.021
	(0.09)	(0.13)	(0.05)	(0.16)	(0.08)	(0.02)
In-degree Std. Dev.* Complex Model-Based Imputation	−0.026	0.07	0.062	0.1	−0.066	0.018
	(0.03)	(0.12)	(0.09)	(0.11)	(0.1)	(0.02)
Log of Size* Symmetric Imputation	−0.277**	−0.132*	−0.497***	0.164	−0.465*	0.021
	(0.09)	(0.05)	(0.11)	(0.36)	(0.22)	(0.07)
Log of Size *Simple Model-Based Imputation	−0.051	−0.193	−0.59***	0.2	−0.233	0.012
	(0.26)	(0.34)	(0.14)	(0.42)	(0.23)	(0.06)
Log of Size* Complex Model-Based Imputation	−0.03	−0.265	−0.61**	0.257	−0.49	0.013
	(0.09)	(0.31)	(0.23)	(0.31)	(0.28)	(0.05)
N	180	180	180	180	180	180
Networks	5	5	5	5	5	5

Note: The regression uses the beta slopes from each line as the dependent variable. The direction of the bias is ignored when calculating the regressions. The betas represent the expected increase in bias for a 10 % increase in the amount of missing data. Larger numbers mean larger bias with more missing data. The correlation with centrality takes four values: -.75, -.25, .25, and .75.

Table A11.

Percent Decrease in Total Bias under Different Imputation Strategies: Topology Measures for Directed Networks.

Measure	Imputation	Prison			Sorority			6th Grade			Prosper			RC Elite			HS 13			HS 24
		Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality			Correlation with Centrality
		−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75	−.75	0	.75
Component	Probabilistic	69	69	68	61	62	59	77	76	77	73	76	76	85	86	91	82	82	86	80	81	84
	Symmetric	69	69	68	61	62	59	77	76	77	73	76	76	85	86	91	82	82	86	80	81	84
	Asymmetric	69	69	68	61	62	59	77	76	77	73	76	76	85	86	91	82	82	86	80	81	84
	Model-based Simple	83	89	93	89	92	91	97	98	98	85	91	93	84	87	92	94	95	97	90	92	94
	Model-based Complex	79	86	91	84	88	87	90	89	92	81	88	91	78	81	89	86	88	92	85	88	91
Bicomponent	Probabilistic	30	36	39	30	33	33	−101	−36	19	30	39	43	74	73	79	−10	11	38	−1	20	43
	Symmetric	30	36	39	30	33	33	−101	−36	19	30	39	43	74	73	79	−10	11	38	−1	20	43
	Asymmetric	30	36	39	30	33	33	−101	−36	19	30	39	43	74	73	79	−10	11	38	−1	20	43
	Model-based Simple	86	88	89	74	84	87	47	69	84	93	95	95	66	77	84	85	90	94	90	94	96
	Model-based Complex	83	86	87	80	87	87	59	78	89	92	93	93	81	88	91	92	95	96	93	96	96
Distance	Probabilistic	36	33	27	24	38	33	27	40	36	35	38	33	8	16	19	64	57	52	68	59	51
	Symmetric	−19	49	63	−35	41	51	−47	47	73	15	74	73	−2616	−2138	−1463	55	75	82	59	81	85
	Asymmetric	−22	−13	−8	−26	−15	−9	−42	−83	−40	−22	−11	−7	−3	−6	−3	−23	−16	−10	−23	−14	−9
	Model-based Simple	−35	46	71	−127	2	46	−54	42	78	−40	47	72	−1075	−662	−392	32	58	76	22	56	76
	Model-based Complex	−10	59	74	−74	32	59	−27	59	76	−7	67	81	−663	−353	−202	60	80	93	50	78	92
Transitivity	Probabilistic	16	35	45	12	4	8	−131	−135	−121	−53	−26	−8	48	51	64	−109	−141	−107	−94	−135	−101
	Symmetric	8	26	34	4	−2	0	−196	−207	−197	−85	−68	−52	−222	−195	−82	−162	−204	−162	−125	−171	−134
	Asymmetric	34	41	45	45	50	53	35	35	39	29	40	44	53	55	71	41	42	47	40	40	44
	Model-based Simple	−82	−48	−20	−142	−112	−74	−379	−365	−301	−282	−235	−171	−190	−147	−46	−538	−583	−396	−490	−534	−355
	Model-based Complex	8	31	41	16	24	32	−154	−149	−115	−49	−22	5	6	25	54	−128	−130	−55	−85	−79	−17
Tau	Probabilistic	36	36	36	32	31	28	62	65	67	68	71	71	0	6	21	89	89	87	89	88	85
	Symmetric	−132	−69	−15	21	24	20	−4	3	6	−27	3	19	−16	−23	−36	6	18	32	9	22	31
	Asymmetric	11	15	22	−7	6	12	43	45	45	55	65	70	1	7	22	78	80	81	76	79	80
	Model-based Simple	15	20	24	8	10	6	−16	−15	−12	0	7	10	−19	−11	6	−10	−5	4	−15	−8	−3
	Model-based Complex	22	27	37	42	42	38	12	14	16	35	39	40	−1	6	23	22	26	32	14	20	25
CONCOR	Probabilistic	6	12	19	12	17	21	9	8	7	21	23	29	11	20	39	17	20	25	21	23	26
	Reciprocated	7	12	19	10	16	21	8	7	6	22	24	29	4	14	32	17	20	25	22	24	27
	Directed	5	11	18	13	17	21	6	5	4	20	22	28	11	20	39	17	20	25	21	23	26
	Model-based Simple	−13	−3	8	−9	2	11	−7	−6	−3	−4	2	11	−15	−3	21	−5	−1	6	3	7	14
	Model-based Complex	−10	0	11	−4	6	15	−7	−4	−2	−2	4	14	−14	−3	22	0	4	11	7	10	17

Table A12.

Topology Bias Slope Regressions: Directed Networks.

Variables	Model 1 Component Size	Model 2 Bicomponent Size	Model 3 Distance	Model 4 Transitivity	Model 5 Tau RC	Model 6 CONCOR
Intercept	−0.553	−0.979	−4.062***	−0.957*	−2.251***	−3.754***
	(3.77)	(1.45)	(0.37)	(0.46)	(0.11)	(0.41)
Correlation with Centrality	0.537	0.383***	0.521***	0.348***	0.081**	0.224***
	(0.66)	(0.04)	(0.07)	(0.03)	(0.03)	(0.01)
In-degree Std. Dev.	−0.089	−0.084	−0.333***	−0.303***	0.014	0.045
	(0.35)	(0.13)	(0.06)	(0.08)	(0.01)	(0.04)
Log of Size	−0.471	−0.262	0.496***	−0.274*	0.013	−0.046
	(0.81)	(0.31)	(0.09)	(0.11)	(0.02)	(0.09)
Asymmetric Imputation	0.696	−0.141	0.71*	−0.84**	1.884	−0.117
	(7.31)	(0.97)	(0.35)	(0.26)	(1.37)	(0.33)
Simple Model-Based Imputation	−14.491	−0.026	1.411*	−1.834***	−0.588	−0.392***
	(41.66)	(1.17)	(0.68)	(0.39)	(0.62)	(0.11)
Complex Model-Based Imputation	−3.342	1.705***	2.204**	−1.509**	−0.981*	−0.506***
	(7.28)	(0.44)	(0.69)	(0.48)	(0.49)	(0.14)
Probabilistic Imputation	0.696	−0.141	0.925	−1.934***	4.558***	−0.212
	(4.26)	(1.01)	(0.72)	(0.48)	(1.1)	(0.3)
Symmetric Imputation	0.696	−0.141	4.024***	−1.784***	−0.78	−0.262
	(6.8)	(0.98)	(0.59)	(0.49)	(1.15)	(0.31)
Correlation with Centrality* Asymmetric Imputation	0.056	−0.194**	−0.142	−0.112*	−0.007	−0.172***
	(0.93)	(0.06)	(0.11)	(0.05)	(0.04)	(0.02)
Correlation with Centrality* Simple Model-Based Imputation	2.348*	−0.443***	−1.288***	−0.28***	−0.024	−0.209***
	(0.93)	(0.06)	(0.11)	(0.05)	(0.04)	(0.02)
Correlation with Centrality* Complex Model-Based Imputation	1.109	−0.346***	−1.31***	−0.301***	−0.005	−0.211***
	(0.93)	(0.06)	(0.11)	(0.05)	(0.04)	(0.02)
Correlation with Centrality* Probabilistic Imputation	0.056	−0.194**	0.176	−0.149**	−0.005	−0.169***
	(0.93)	(0.06)	(0.11)	(0.05)	(0.04)	(0.02)
Correlation with Centrality* Symmetric Imputation	0.056	−0.194**	−0.82***	−0.106*	0.168***	−0.176***
	(0.93)	(0.06)	(0.11)	(0.05)	(0.04)	(0.02)
In-degree Std. Dev.* Asymmetric Imputation	−0.107	−0.119	0.131*	0.05	0.346**	−0.018
	(0.68)	(0.09)	(0.06)	(0.04)	(0.13)	(0.03)
In-degree Std. Dev.*Simple Model-Based Imputation	−2.292	0.319**	−0.145	0.175**	0.053	−0.016
	(3.86)	(0.11)	(0.11)	(0.06)	(0.06)	(0.01)
In-degree Std. Dev.*Complex Model-Based Imputation	−0.261	0.236***	−0.056	0.361***	0.117*	−0.002
	(0.67)	(0.04)	(0.11)	(0.08)	(0.05)	(0.01)
In-degree Std. Dev.* Probabilistic Imputation	−0.107	−0.119	−0.083	0.29***	0.423***	−0.019
	(0.39)	(0.09)	(0.12)	(0.08)	(0.1)	(0.03)
In-degree Std. Dev.* Symmetric Imputation	−0.107	−0.119	0.098	0.323***	0.218*	−0.009
	(0.63)	(0.09)	(0.1)	(0.08)	(0.11)	(0.03)
Log of Size* Asymmetric Imputation	−0.377	0.038	−0.185*	−0.002	−0.811**	0.013
	(1.56)	(0.21)	(0.09)	(0.06)	(0.29)	(0.07)
Log of Size *Simple Model-Based Imputation	2.96	−0.774**	−0.364*	0.452***	0.05	0.091***
	(8.9)	(0.25)	(0.16)	(0.09)	(0.13)	(0.02)
Log of Size* Complex Model-Based Imputation	0.209	−1.084***	−0.629***	0.098	0.013	0.098***
	(1.56)	(0.09)	(0.17)	(0.12)	(0.1)	(0.03)
Log of Size * Probabilistic Imputation	−0.377	0.038	−0.229	0.262*	−1.461***	0.028
	(0.91)	(0.21)	(0.17)	(0.11)	(0.23)	(0.06)
Log of Size* Symmetric Imputation	−0.377	0.038	−1.14***	0.254*	−0.137	0.024
	(1.45)	(0.21)	(0.14)	(0.12)	(0.25)	(0.07)
N	378	378	324	324	378	378
Networks	7	7	7	7	7	7

Note: The regression uses the betas slopes from each line as the dependent variable. The betas represent the expected drop in correlation (between the empirical and the observed) for a 10 % increase in the amount of missing data. Larger numbers mean larger bias with more missing data. The correlation with centrality takes four values: − .75, − .25, .25, and .75.

Table A13.

Maximum percent missing to retain target correlation of .9 with true score.

Network	Imputation Type	In-Degree		Out-Degree		Total Degree		Bonacich Power		Closeness		Betweenness
		Non-respondents in Correlation		Non-respondents in Correlation		Non-respondents in Correlation		Non-respondents in Correlation		Non-respondents in Correlation		Non-respondents in Correlation
		No	Yes	No	Yes	No	Yes	No	Yes	No	Yes	No	Yes
Undirected Networksa	Listwise Deletion	55.8	NAb	55.8	NA	55.8	NA	47.6	NA	5	NA	30.2	NA
	Symmetric	70c	46.8	70	46.8	70	46.8	70	52.6	56.8	39.2	65.6	44.8
	Model-Based Simple	70	56.4	70	56.4	70	56.4	70	58.2	64.8	28.8	69.4	45.2
	Model-Based Complex	70	58.4	70	58.4	70	58.4	70	59.4	64.4	24.4	67.8	48.2
Directed Networksa	Listwise Deletion	39	NA	25.6	NA	33.7	NA	26.3	NA	21.6	NA	15.4	NA
	Probabilistic	40.9	39	70	9.6	58.6	24.4	51.1	23.9	42.3	9	20.4	11.1
	Symmetric	30.9	30.6	70	12.4	50.1	29.1	51.1	23.9	43.3	12.3	9.7	5.4
	Asymmetric	39	38.4	70	6.7	59.4	20.7	51.1	23.9	26.3	3.9	19.3	7.7
	Model-Based Simple	27.7	28.4	70	13.3	45.7	25.3	42	24	49.9	11.4	9.1	4.7
	Model-Based Complex	30	31.3	70	12.6	48.7	27.3	44	24.9	50.4	10.7	11.4	6.9

The maximum percent missing was calculated based on a quadratic fit to the data.

^aValues represent the means (for the maximum percent missing to retain target correlation) taken over all directed or undirected networks.

^bListwise deletion has no value for the case of non-respondents being kept in the correlation calculation.

^cCases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means.