Classification of SARS-CoV-2 and non-SARS-CoV-2 using machine learning algorithms

Abstract

Due to the continued evolution of the SARS-CoV-2 pandemic, researchers worldwide are working to mitigate, suppress its spread, and better understand it by deploying digital signal processing (DSP) and machine learning approaches. This study presents an alignment-free approach to classify the SARS-CoV-2 using complementary DNA, which is DNA synthesized from the single-stranded RNA virus. Herein, a total of 1582 samples, with different lengths of genome sequences from different regions, were collected from various data sources and divided into a SARS-CoV-2 and a non-SARS-CoV-2 group. We extracted eight biomarkers based on three-base periodicity, using DSP techniques, and ranked those based on a filter-based feature selection. The ranked biomarkers were fed into k-nearest neighbor, support vector machines, decision trees, and random forest classifiers for the classification of SARS-CoV-2 from other coronaviruses. The training dataset was used to test the performance of the classifiers based on accuracy and F-measure via 10-fold cross-validation. Kappa-scores were estimated to check the influence of unbalanced data. Further, 10 × 10 cross-validation paired t-test was utilized to test the best model with unseen data. Random forest was elected as the best model, differentiating the SARS-CoV-2 coronavirus from other coronaviruses and a control a group with an accuracy of 97.4 %, sensitivity of 96.2 %, and specificity of 98.2 %, when tested with unseen samples. Moreover, the proposed algorithm was computationally efficient, taking only 0.31 s to compute the genome biomarkers, outperforming previous studies.

Graphical abstract

1. Background

Coronavirus is an RNA virus comprising of single-stranded positive-sense RNA, of approximately 32 kb in length [1,2]. Coronavirus is part of the Coronaviridae family, which consists of alpha, beta, delta, and gamma coronaviruses [3]. As the name signifies, the spherical external protein exhibits a characteristic crown shape when it is under an electron microscope [4]. A wide range of mammalian hosts, including humans, can be infected by it. Infected human hosts display asymptomatic to severe symptoms in their genitalia, digestive, respiratory, enteric nervous, cardiovascular, and endocrine systems [3]. Humans are known to be infected by six coronaviruses. Of these, OC43, NL63, 229E, and HKU1 usually produce mild cold-like symptoms, whereas, in 2003, the Severe Acute Respiratory Syndrome-Coronavirus (SARS-CoV), and in 2012, the Middle East Respiratory Syndrome-Coronavirus (MERS-CoV), caused severe respiratory illnesses [5].

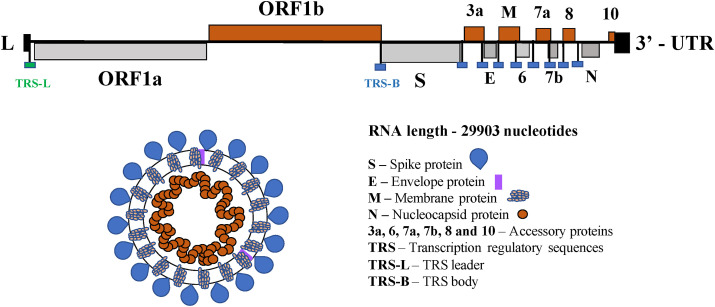
SARS-CoV-2/COVID19 was originated from a local market in Wuhan, China in late 2019 [6]. From there, it has extensively spread worldwide, with infections and deaths of 186.06 and 4.02 million, respectively (July 8, 2021 [7]). Fig. 1 depicts the full-length genomic RNA of the highly pathogenic human coronaviruses that cause SARS-CoV-2. It comprises 29,903 nucleotides, which functions as an mRNA, where the open reading frames ORF1a, and ORF1b are translated into proteins. In addition, nine major sub-genomic RNAs are produced, see Fig. 1, which are translated into accessories proteins of SARS-CoV-2.

Fig. 1.

SARS-CoV-2 genome organization [1] and ordering/location of the various encoded proteins.

Symptoms of COVID19 identified to date include fever, cough, myalgia, headache, shortness of breath, chills, sore throat, runny nose, chest pain, rash, nausea, vomiting, diarrhea, and fatigue. Since many of the symptoms resemble those of the common cold and influenza, an accurate molecular result is critical for a final diagnosis. The real-time polymerase chain reaction is a well-known molecular method [8] but has suffered from a high false-negative rate and (30–50 %) detection rate [6,9]. Due to the variation of viral RNA sequences within virial species (see Fig. 1), and the viral load in various anatomic sites [10]. In addition, COVID19 assays can result in low sensitivity if not aligned properly with the virus template, as the virus is strongly related to other coronavirus species. Moreover, SARS-CoV-2 may present with other lung infections that makes it even more challenging to identify [11].

Thus, researchers worldwide applied various digital signal processing (DSP) methods such as discrete Fourier transform (DFT) [12], digital filter [13], time-domain periodogram (TDP) [14], modified average magnitude difference function (AMDF) [15], singular value decomposition (SVD) [16] and modified SVD [17], which include forward-backward filtering to detect three-base periodicity (or period-3 property) for the prediction of exon locations in the DNA sequence [12]. These methods could be potentially useful in suppressing the SARS-CoV-2 spread by discrimination other coronaviruses.

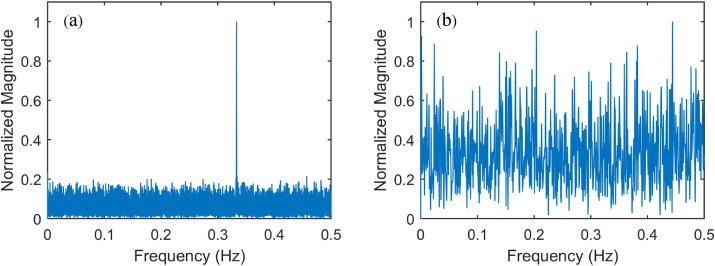
Three-base periodicity is an intrinsic property of protein-coding regions (known as exons) of DNA [12], It can be used to distinguish protein-coding sequences from non-coding sequences (known as introns) that do not show the same periodicity. Fig. 2 shows that the Fourier spectrum of DNA sequences (SARS-CoV-2 isolate Wuhan-Hu-1) exhibit a strong spectral component at frequency 1/3 Hz (Fig. 2a) compared with a control sample (Fig. 2b).

Fig. 2.

Normalized Fourier spectrum analysis (a) of SARS-CoV-2, and (b) a control sample.

Numerous studies report the distinction of the virus using various classification approaches such as support vector machine (SVM) [18], decision trees (DT) [19], Gaussian radial basis function neural network [20], random forest (RF) [21], gapped Markov Chain with SVM [22], k-nearest neighbor (k-NN) [23], and convolutional neural network [24]. Besides, k-mers (oligomers of length k) based SVM, ML-DSP, and MLDSP have been utilized effectively in virology, including HIV-1 genomes, influenza, dengue and COVID19 classification [[25], [26], [27]]. However, k-mers do not work well with short length sequences, and the use of higher k-mer, exponentially increases the number of features, which poses a significant computational challenge. Further, there can be less tolerance when proteins contain errors or mutations as k-mers must be contiguous. Lopez-Rincon et al. [28] proposed a deep learning approach for the classification of SARS-CoV-2, with specificity 99.39 % and sensitivity 100 %. However, disadvantages of all deep learning methods are the lack of interpretability and being computation expensive and prone to overfitting.

We employed the electron-ion interaction potential (EIIP) [20] scheme for the numerical representation of complementary (cDNA), as a simple way of enumerating the four different cDNA bases, hereafter referred as DNA, three-base periodicity property to extract the genome biomarkers, and ML models to classify SARS-CoV-2. This work illustrates how DSP, biomarker selection, and ML give a computationally rapid alignment-free classification of novel coronavirus. Herein, the converted DNA sequence into genomic signal was used for the computation of the magnitude spectrum and its average by applying DFT, in addition to the peak-to-average ratio of the magnitude spectrum as biomarkers.

Further, AMDF, SVD, and TDP were utilized as biomarkers with zero-phase filtering, in contrast to traditional filters [[13], [14], [15], [16]] and without filtering. Filter-based Pearson correlation coefficient (PCC) via ANOVA tests, and correlation-based feature section (CFS) were employed to identify the most significant biomarkers for the classification of SARS-CoV-2. Filter techniques can easily scale to large datasets, are computationally simple, fast, and independent from the classifier. Following this, the ranked biomarkers were fed into the k-NN, DT, RF, and SVM classifiers. The proposed method is efficient, computationally inexpensive, and able to correctly distinguish the SARS-CoV-2 from non-SARS-CoV-2, which includes the rest of coronavirus and a control group without a priori biological knowledge.

2. Methodology

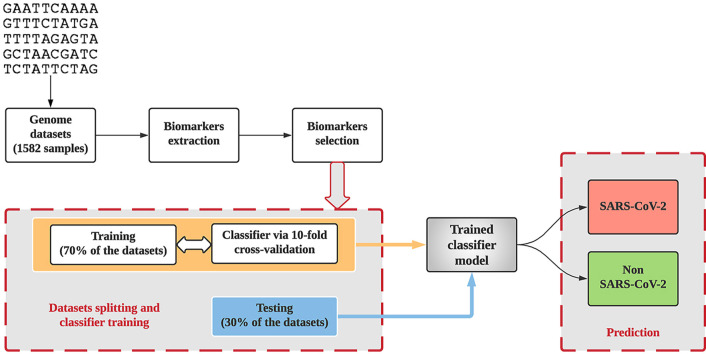
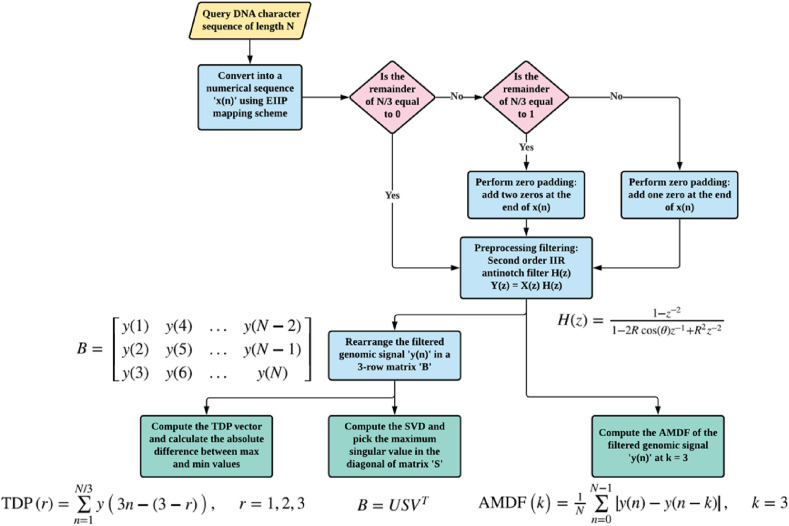
The proposed method for the distinction of SAR-CoV-2 comprises five steps: (1) Data collection: a total of 1582 samples, including 615 SARS-CoV-2 and 967 non-SARS-CoV-2 samples, (2) Conversion of the DNA “characters” into numeric values for rapid and more efficient processing, (3) Three-base periodicity property detection for the extraction of genome biomarkers using DSP, (4) Biomarkers selection, and (5) ML implementation. Eight biomarkers were derived using the three-base periodicity property and selected based on PCC [29], and CFS [30], as some of the biomarkers may contain irrelevant and/or redundant information that may reduce the performance of the classifier if not removed [21]. The selected biomarkers were fed into the classifiers.

2.1. Database sources

COVID19 Wuhan-Hu-1 whole reference genome of 29903bps was downloaded from the National Center for Biotechnology Information (NCBI), along with the genome sequences in the FASTA format with the queries: SARS-CoV-2, Sequence Data (Nucleotides), Select Records (download all records), and FASTA definition line (use default) from the NCBI (https://www.ncbi.nlm.nih.gov/labs/virus) and Global Initiative on Sharing All Influenza Database (GISAID, https://www.gisaid.org/) [27]. COVID19 data comprises the complete genome, the complete coding sequence (CDS), and partial CDS, which length varies from 64 to 29945bps. Besides, other human, mammals, and birds’ coronaviruses [31], were incorporated into the non-SARS-CoV-2 group to assess the robustness and effectiveness of the proposed algorithms. We also downloaded a control sample from the Epitranscriptomics and RNA Dynamics Lab (Novoa Lab) and the Bioinformatics Core Facility (BioCore) at the Center for Genome Regulation [32]. Table 1 depicts information on coronavirus species, sample size, and designated label for both SARS-CoV-2 and non-SARS-CoV-2 groups. The description of DNA numerical mapping is presented in Supplementary. Methodology for the extraction of genome biomarkers using the three-base periodicity property is elucidated in the following sections.

Table 1.

Lists the name of the coronavirus species, number of samples, and designated labels.

Coronavirus species	Number of samples	Label
SARS-CoV-2	615	1
Control sample	27	0
Anatid alphaherpesvirus 1	13	0
HCoV-OC4	170	0
Bos Taurus Polyomavirus	4	0
Chiropteran bocaparvovirus 1	2	0
Galliform aveparvovirus 1	4	0
Human coronavirus 229E	60	0
Human coronavirus HKU1	39	0
Human Coronavirus NL63	66	0
MERS-CoV	520	0
SARS-CoV	7	0
PREDICT_CoV-35 [31]	4	0
PREDICT_CoV-47 [31]	2	0
PREDICT_CoV-82 [31]	3	0
PREDICT_CoV-92 [31]	36	0
PREDICT_CoV-93 [31]	3	0
PREDICT_CoV-96 [31]	5	0
bat-SL-CoVZC45	1	0
bat-SL-CoVZXC21	1	0

2.2. Genome biomarkers extraction using the three-base periodicity property

Herein, a robust DSP algorithm is developed to investigate the strength of the three-base periodicity to extract the significant genome. We selected eight biomarkers using various DSP-based methods, namely average magnitude spectrum, peak-to-average ratio of the magnitude spectrum, SVD, SVD with filtering, AMDF, AMDF with filtering, TDP, and TDP with filtering. DSP techniques are implemented in MATLAB (R2015a) on an Intel® Core™ i7, 2.5 GHz with 16 GB RAM.

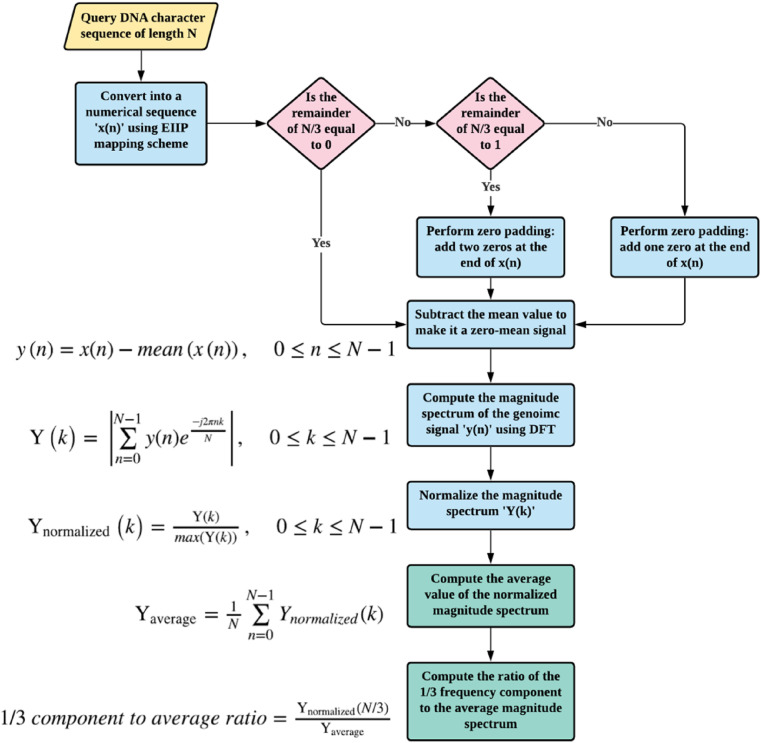
2.2.1. Three-base periodicity detection using discrete fourier transform

Fig. 3 exhibits the procedure for the computation of three-base periodicity detection using discrete Fourier transform. Herein, frequency-domain representation (spectrum) refers to breaking down a signal into its constituent sinusoids. That is, the spectrum of a signal is a representation of its frequency content [33]. Considering a zero-mean genomic signal ‘y(n)’, of length ‘N’, as in Eqs. (1) and (2).

$$y\left(n\right)=x\left(n\right)-{\mu }_{x}0\le n\le N-1$$ (1)

where μ _x is the mean of the signal ‘x(n)’, calculated as follows,

$${\mu }_x=\frac{1}{N}\sum _{n=0}^{N-1}x\left(n\right)$$ (2)

Fig. 3.

Flowchart of the DFT-based features.

The purpose of subtracting the mean is to suppress the zero-frequency component [34], since direct current component is not significant in the context of detecting the three-base periodicity. The magnitude spectrum of ‘y(n)’ is computed using the DFT as depicted in Eq. (3) – (5).

$$Y\left(k\right)=\left|\sum _{n=0}^{N-1}y\left(n\right)e^{\raisebox{1ex}{$-j2\pi nk$}\!\left/ \!\raisebox{-1ex}{$N$}\right.}\right|0\le k\le N-1$$ (3)

where ‘k’ is the frequency ‘f’ and the sampling frequency ‘f _s’ of the signal.

$$k=\frac{Nf}{f_s}$$ (4)

When dealing with DNA sequences, the value ‘f _s’ uses one sample per second [35] and thereby,

$$f=\frac{k}{N}$$ (5)

The magnitude spectrum is, then, normalized as follows in Eq. (6).

$$Y_{normalized}\left(k\right)=\frac{Y\left(k\right)}{\max \left[Y\left(k\right)\right]}0\le k\le N-1$$ (6)

This normalization examines the strength of the 1/3 frequency component relative to the whole magnitude spectrum. Thus, the average of the normalized magnitude spectrum is estimated using Eq. (7):

$$Y_{average}=\frac{1}{N}\sum _{n=0}^{N-1}{Y}_{normalized}\left(k\right)$$ (7)

Subsequently, the magnitude of the 1/3 spectral component (f = 1/3 Hz) is calculated by setting ‘k’ to N/3 as performed in Ref. [35]. Then, computing the ratio between the magnitude of this 1/3 spectral component and its average is performed using Eq. (8):

$$Y_{1/3-to-average}=\frac{Y_{normalized}(N/3)}{Y_{average}}$$ (8)

This feature is expected to be relatively higher if the DNA is a protein-coding sequence (e.g. viral genome), as the nucleotides exhibit three-base periodicity.

2.2.2. Enhanced approach for three-base periodicity detection using filtering

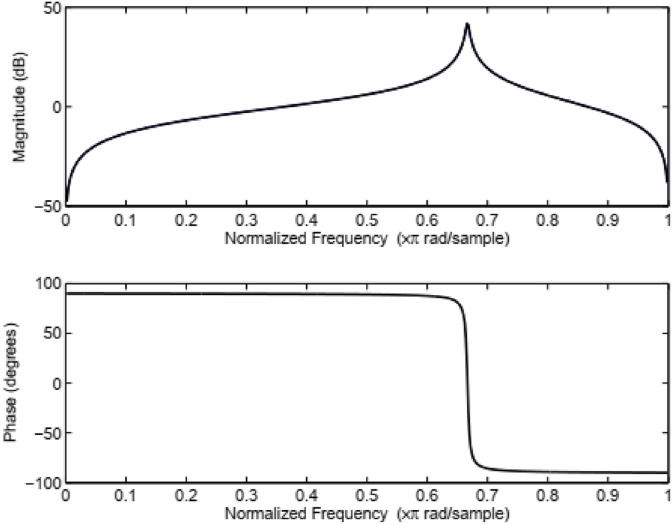
Fig. 4 illustrates the steps to estimate the AMDF, SVD, and TDP. Herein, the genomic signal x(n) is filtered to emphases the three-base periodicity and point out the protein-coding region in the DNA sequence employing conventional filtering methods [12,33], see Fig. 5 . However, we employed zero-phase filtering, instead of traditional filtering, to overcome the non-linear phase distortion. In addition, we investigated the impact of AMDF, SVD, and TDP approaches without filtering, which may enhance the computational efficiency of the proposed algorithms. See the supplementary material for the illustration of anti-notch filter and the mathematical description of AMDF, SVD, and TDP.

Fig. 4.

Flowchart of the AMDF, SVD and TDP-based features.

Fig. 5.

Magnitude and phase responses of the IIR anti-notch filter.

3. Biomarker selection

Our main aim is to employ the minimum number of best biomarkers to maximize the performance of each classifier for the problem in consideration. Herein, filter-based biomarker selection is employed, instead of wrapper approaches since they compute the relevance of biomarkers by their correlation with the dependent class. On the other hand, wrapper techniques measure the effectiveness of a subset of biomarkers by training a classifier via cross-validation (CV) [36], limiting the use of more than one classifier at a time. Moreover, filter-based techniques reduce the risk of overfitting, the computation cost, and the selection is independent of any classifier [37,38]. Herein, two filter techniques were deployed: PCC and CFS [39]. The explanations about the PCC and CFS are included in the Supplementary. Further, the probability density functions (PDFs) are computed using the kernel density estimation method for the best biomarker to provide a qualitative assessment between the SARS-CoV-2 and non-SARS-CoV-2 groups [40].

4. Machine learning classifiers

Herein, k-NN, DT, RF, and SVM were used for the classification of SARS-CoV-2 and non-SARS-CoV-2. ML techniques have proven to be powerful tools for addressing such tasks [[25], [26], [27], [28]]. ML refers to a series of algorithms driving their functionality learning from unlabeled or labeled data, rather than using predefined sets of functions and rules [41]. This property is ideal to predict histopathological characteristics, clinical outcomes, molecular biomarkers, or treatment responses [41]. To augment generalizability, and limit overfitting, ML includes training, validation, and external testing in separate datasets [41]. CV uses the training and validation datasets to fit the classifier, evaluate its performance, and optimize its hyper parameters [41] based on arbitrary sub-separation and iterative cycles of training and validation [42]. The testing dataset is kept completely independent from development and is utilized to assess the final model and verify its performance and generalizability. Short descriptions about k-NN, DT, RF, and SVM are included in the following paragraphs.

k-NN has widely been used due to its simple implementation and high efficiency [26]. It is a very versatile algorithm since it can be applied to classification, regression, and missing value imputation problems. The key idea of the standard k-NN is to search for all the K nearest neighbors for a given test sample. The two main elements that affect its performance is the selection of a proper K value and selecting the best distance function for identifying the K classes.

DT is one of the most well-known machine learning methods for data classification. It is a tree-based technique in which the model is represented as a set of nodes and hierarchical connections that represents relationships. The connections form a path that starts from a root node, and it is described by a sequence where data is recursively separated until reaching a Boolean outcome in a leaf node. DTs are considered a powerful method in terms of accuracy, simple analysis, predictive power, and fast convergence [27].

RF [25] is based on the idea that aggregating multiple decision trees cause a decrease of variance in the outcome compared to a single model. RF has received significant attention, and several benchmarking studies demonstrated that currently, this method is one of the most robust and flexible machine learning techniques in solving both classification and regression problems.

SVM [27,38] a supervised learning technique for classification and regression, based on the structural risk minimization principle and statistical learning theory. SVM maps the original observations into a higher-dimensional space to find an optimum separating hyperplane. This factor makes the algorithm particularly powerful over other traditional machine learning approaches.

In this study, the total number of samples (1582 samples) was divided into two sets via resampling. The first set consists of 70 % (1107 samples) from both classes SARS-CoV-2 (424 samples) and non-SARS-CoV-2 (683 samples), which were used to train the model via ten-fold CV. The second set contained 30 % (475 samples) from both classes SARS-CoV-2 (189 samples) and non-SARS-CoV-2 (286 samples) and was used as a testing dataset with the trained model. The classifiers were validated via ten-fold CV, and the best model was selected based on the F-measure [43], which balances the recall and precision of the model. In addition, the efficacy of the model was evaluated on the accuracy matrix via the corrected 10 × 10 fold CV paired t-test [44]. This method compares the means of two groups of compatible data, determining which one is lower or whether they are equivalent, prior to apply the test dataset in the trained model. Moreover, Kappa-score was utilized to verify the influence of imbalance data between the two classes as one class (non-SARS-CoV-2) comprises 61.15 % compared with the SARS-CoV-2 class 38.85 %.

In this study, the DT, and RF are deployed with default parameters, while k-NN uses K = 3, and SVM uses radial basis function (RBF) kernel that was implemented by the C++ LIBSVM library [45]. The hyper parameters of RBF (penalty constant, C, kernel width, γ) were optimized by a grid-search to achieve the maximum result. All four ML experiments provided in this study were conducted using WEKA [44].

The performance of the trained model on the testing dataset was evaluated using confusion matrices (refer Supplementary) in terms of sensitivity, specificity, and accuracy [46]. Herein, sensitivity assesses if the SARS-CoV-2 data is correctly recognized by the classifier, whereas specificity reveals how well the non-SARS-CoV-2 data was identified. The accuracy assesses the total amount of samples that were well classified.

5. Results

We employed a DSP-ML-based algorithm for the classification of SARS-CoV-2 and non-SARS-CoV-2. A total of eight biomarkers were extracted based on the three-base periodicity property. Supplement Figure 1 provides the results of three-base periodicity property using DFT in terms of frequency and magnitude spectrum for one sample of each class, that shows the variation in magnitude spectrum to the corresponding frequency at 1/3 Hz. The algorithms source code is in Supplementary. Supplementary Table 1 lists the investigated genome biomarkers with the respective sequence length statistics, mean, and standard deviation (SD) for SARS-CoV-2 and non-SARS-CoV-2. The deviation of each biomarker from their mean is very low (Supplementary Table 1), which shows the consistency of the proposed biomarkers and provide kind of surety that these biomarkers will perform similarly even with a greater number of samples. Table 2 depicts the result of the genome biomarkers selection. The biomarker (GB5) had an “r” value of 0.32, followed by GB3, GB2, GB1, and GB4 with “r” values 0.18, 0.12, 0.13, 0.12, respectively, which illustrates the weak positive correlation compared with the rest of biomarkers, which had no relation (r < 0.1). Further, ANOVA test was performed, confirming that GB1 to GB5 are significantly better (p < 0.0001) than GB6, GB7, and GB8, which is consistent with the F-value listed in Table 3 . Hence, we used for the classification a set of five biomarkers, removing those biomarkers, with no relation (r < 0.1). CFS method utilized the subsets of biomarkers that are highly linked with the class, while having low intercorrelation. Table 2 shows that biomarkers GB4 and GB5 possess higher discrimination capabilities with a merit of 0.67. Thus, both were used as input biomarker vectors. Besides, PDF of GB5 and scatter plot of GB4 and GB5 for 100 samples from both classes are presented in Supplementary Figs. 2 and 3.

Table 2.

Genome biomarkers correlation values.

Genome Biomarkers	Genome biomarker index	Pearson ‘r’ cross-correlation coefficient (Correlation ranking filter)		Correlation Based Feature Selection
		‘r’ value	Ranked biomarkers based on ‘r’ value
Average magnitude	GB1	0.13	GB5	GB4
Peak-to-average ratio	GB2	0.14	GB3	GB5
SVD	GB3	0.18	GB2
SVD with filtering	GB4	0.12	GB1
AMDF	GB5	0.32	GB4
AMDF with filtering	GB6	0.08
TDP	GB7	0.08
TDP with filtering	GB8	0.09

SVD-singular value decomposition, SVD with filtering – SVD with anti-notch IIR filtering, AMDF-average magnitude difference function, AMDF with filtering-average magnitude difference function with anti-notch IIR filtering, TDP- time-domain periodogram, TDP with filtering-time-domain periodogram with anti-notch IIR filtering, GB1-genome biomarkers and 1 represents the index number.

Table 3.

ANOVA analysis for proposed features.

Parameters	GB1	GB2	GB3	GB4	GB5	GB6	GB7	GB8
F-value	26.20	33.06	55.34	25.02	182.81	11.78	12.23	13.16
p-value	<0.0001	<0.0001	<0.0001	<0.0001	<0.0001	0.001	0.000	0.000

Herein, the SVM-RBF classifier was optimized via Grid search and evaluated using ten-fold CV on the training dataset. The performance of the classifier was assessed based on the accuracy. Table 4 shows, for CFS and correlation, the values of the optimized parameters-penalty constant (C) and width (γ), were 100, 0.001 and 1000, 0.001. Further, the optimized parameters and same training dataset were used for comparison with other classifiers, while assessing the performance of the SVM.

Table 4.

Classification of SARS-CoV-2 and non-SARS-CoV-2 via ten-fold CV on the training data.

Classifiers	Genome biomarkers selection methods	Accuracy (%) (mean ± SD)	F-measure (mean ± SD)	Kappa-score (mean ± SD)	Model built time (second)
k-NN	CFS	96.47 ± 0.89	0.96 ± 0.01	0.92 ± 0.02	0.002
	Correlation	97.56 ± 1.35	0.97 ± 0.02	0.95 ± 0.03	0.01
SVM-RBF	CFS (C-100, gamma-0.001)	97.29 ± 1.96	0.96 ± 0.03	0.94 ± 0.04	0.2
	Correlation (C-1000, gamma-0.001)	97.73 ± 1.43	0.96 ± 0.02	0.96 ± 0.03	0.29
DT	CFS	96.47 ± 1.74	0.95 ± 0.02	0.93 ± 0.04	0.14
	Correlation	97.46 ± 1.41	0.96 ± 0.02	0.94 ± 0.03	0.04
RF	CFS	97.92 ± 1.66	0.97 ± 0.02	0.96 ± 0.03	0.22
	Correlation	98.78 ± 1.09	0.98 ± 0.02	0.98 ± 0.02	0.27

k-NN – k-nearest neighbors; SVM-RBF: Support vector machine-radial basis function; DT-Decision tree; RF-Random forest, CFS-correlation-based feature selection, Correlation-Pearson correlation coefficient.

Table 4 presents the results of the classifiers via ten-fold CV in terms of the mean and SD, which utilized the CFS and correlation-based ranked biomarkers. The latter performed better than CFS, achieving slightly higher accuracy. The RF shows slightly greater F-measure (mean, 98 % and SD, 2 %) compared with other classifiers. This means that RF will possibly sustain acceptable precision and recall. In addition, Kappa-scores (>0.9) elucidates that the employed classifiers can well balance the disproportionate amount of data of both groups. However, the F-measure of SVM-RBF, DT, and RF stands close to the k-NN, see Table 4. Hence, prior to apply the model on unseen data, a corrected 10 × 10 fold CV paired t-test was performed to assess the model performance based on accuracy.

Table 5 depicts the results of the corrected 10 × 10 fold CV paired t-test. It can be seen that the RF holds victory (v), whereas k-NN, DT and RF neither contains asterisk (*) nor ‘v’, which shows that they could be statistically significant but unable to conclude via t-test. Therefore, RF was selected and deployed for further testing on the unseen data.

Table 5.

Paired t-test analysis for model selection via 10 × 10 fold CV.

Test	Model evaluation parameters	k-NN	SVM-RBF	DT	RF
Paired t-test analysis	Accuracy	97.37	97.80	97.83	98.98 v

(v//*) reflects as follows: v-victory, * - poorly statistically significant, blank – unable to say.

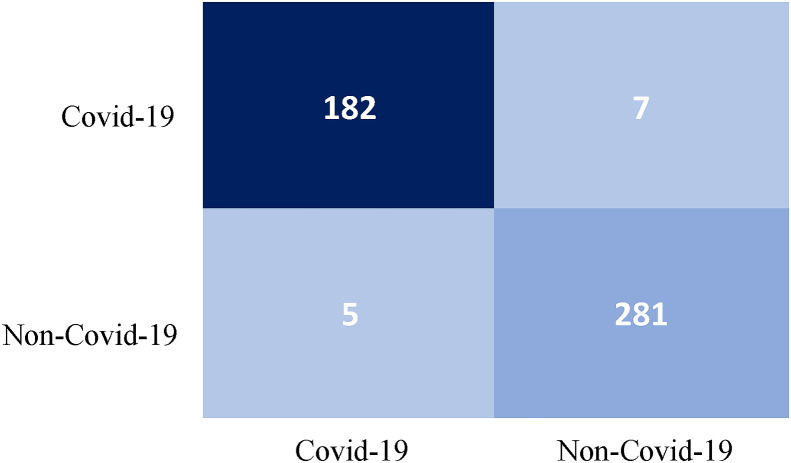
The selected RF model was trained and deployed for testing using the 30 % unseen samples. Table 6 illustrates that the elected model can correctly classify the SARS-CoV-2 (sensitivity, 96.29 %) and non-SARS-CoV-2 (specificity, 98.25 %) with accuracy of 97.47 %. Fig. 6 illustrates a confusion matrix for the classification results of RF on unseen dataset. Besides, the total execution time (biomarkers extraction and RF model build time) is approximate 0.31 s, that tells the proposed algorithm is computationally inexpensive and efficient to be implemented in a real-time scenario.

Table 6.

Classification results using RF on unseen testing dataset.

	Sensitivity (%)	Specificity (%)	Accuracy (%)
RF	96.29	98.25	97.47

SARS-CoV-2 – severe acute respiratory syndrome coronavirus 2; non-SARS-CoV-2-non severe acute respiratory syndrome coronavirus 2; RF- Random forest.

Fig. 6.

Confusion matrix for the classification results of random forest on unseen dataset.

6. Discussion

Based on the history of SARS-CoV-2, previous studies suggest an origin from bats earlier to zoonotic transmission [47]. So far, the early SARS-CoV-2 virus genomes, which are sequenced and uploaded are more than 99 % similar, advocating these viruses result from a recent cross-species event [48]. These earlier examinations are based on alignment-based techniques to recognize relationships between the SARS-CoV-2 and other coronaviruses with amino acid sequence and nucleotide resemblances. When examining the reserve replicase domains of ORF1ab for coronavirus species categorization, almost 94 % of amino acid residues were similar to SARS-CoV, reaching 70 %, on the whole genome resemblance, which confirms that the SARS-CoV-2 virus was genetically distinct [49]. Within the RNA-dependent RNA polymerase (RdRp) zone, it was discovered that the bat coronavirus, RaTG13, formed via a different lineage from other bat SARS-similar coronaviruses [48], was the nearest relation to the SARS-CoV-2. A group of researchers found that two bat SARS-similar coronaviruses, bat-SL-CoVZXC21 and bat-SL-CoVZC45, were also very similar to SARS-CoV-2 [47]. Yet, whether the SARS-CoV-2 virus started from a recombination event is still unknown [48].

We included distinct types of SARS-CoV-2 data including complete genome, partial genome, partial and complete CDS, from different regions such as RdRP, 3″-to-5″ exonuclease, non-structural protein 3. The length of data, that varies from 64bps to 29945bps compared with 2000-50000bps from earlier studies [27,28], were included in this study, which shows the robustness of the proposed approach. Further, we proposed a new biomarker based on the three-base periodicity property for the prediction of SARS-CoV-2 virus.

In this work, eight biomarkers, GB1-GB8, were extracted based on the three-base periodicity properties, by applying various DSP techniques. Descriptive statistical analysis was performed to know the distribution of data, that helps to detect typos and outliers and allows us to identify associations among biomarkers. It can be seen (Supplementary Table 1) that there were minor deviations in the biomarker from their mean value, which were found to be distinct for both the SARS-CoV-2 and non-SARS-CoV-2 groups. Thus, the biomarker selection methods, PCC and CFS were deployed to enhance the efficiency of ML (Table 2). It can be observed that the results achieved by GB5 (AMDF) possess higher discrimination abilities for the classification with 32 % of correlation coefficient. The outcome agrees with an earlier study [50], wherein a correlation coefficient r ≥ 0.3 is suggested to be significant for medical diagnosis. Therefore, even the sequences collected from distinct zones with varied compositions can be simply compared quantitatively by employing the propose biomarker (AMDF), with uniformly meaningful results as when comparing SARS-CoV-2 sequences. Further, ANOVA test was applied to the biomarkers. Correlation coefficients <0.3, and p-values <0.05 were assumed statistically significant [51] and were included as the most significant biomarkers. Table 3 shows that GB1 to GB8 had p-values <0.05. However, GB1 to GB6 reported lower p-values compared with GB7 and GB8. Hence, GB1-GB6 were taken as features for the classification. On the other hand, CFS based method revealed GB4 and GB5 as the most notable biomarkers compared with other biomarkers (Table 3). The three-base periodicity DSP approach is simple and effective, which took an average 0.4 μseconds/nucleotide compared with k-mers, suggested in Ref. [27]. Further, the selected biomarkers from both methods were fed into the classifiers and assessed based on their accuracy.

Table 4 illustrates that PCC and CFS were comparable as biomarker selection techniques. However, PCC outperformed CFS as the accuracy was comparatively higher for all the classifiers. Further, Kappa test was performed to confirm the influence of the imbalanced data between the different groups. It is shown (Table 4) that all the classifiers achieved > 0.9 Kappa-score, which means that the results were not affected. Thereafter, the F-measure shows values closed to each other. Hence, 10-times 10-fold CV paired t-test was performed using the accuracy to identify the best model to test afterwards on unseen samples. It can be observed from Table 5 that the accuracy and F-measure achieved by k-NN, SVM-RBF, DT, and RF exhibited very close scores. However, paired t-test revealed that RF had the best replicability. Therefore, RF was chosen to be tested with the unseen data, achieving 96.29 % sensitivity, 98.25 % specificity with an accuracy of 97.47 % (Table 7 ), which are very near to the findings of the previous employed algorithms. Besides, it can be seen that the studies on SARS-CoV-2 based on k-mers and deep neural network (DNN) conducted by Randhawa et al. [27] and Lopez-Rincon et al. [28] achieved 100 % and 98.73 % accuracy, respectively which seems to be slightly higher than the proposed approach, but the computation time of our work is comparatively lower. However, some concern arises from these studies as Randhawa et al. performed the training on the data without reporting any hyperparameter values for the classifiers, which restricts the reproducibility of their experiments. Also, they used a small number of samples from the SARS-CoV-2 group and did not perform any overfitting countermeasures. The study revealed 100 % accuracies for their six classifiers over three different tests. This may be due to overfitting, which means that the finding may not be generalize over unseen data. On the other hand, Lopez-Rincon et al., used a significant imbalanced dataset, where SARS-CoV-2 represents only the 11.93 % of samples. Additionally, they utilized DNN, which requires a huge amount of data, is computationally extremely expensive, and features are unknown. Further, proposed approaches can only distinguish SARS-CoV-2 from other coronaviruses without including the control group. Hence, these works are not capable of knowing whether someone is infected with these types of virus or not. In contrast, the proposed DSP-ML based approach depicts comparatively acceptable classification results for the discrimination of SARS-CoV-2 and non-SARS-CoV-2, by employing newly proposed biomarkers, which only required genome sequence as input. DSP-ML is an alignment-free approach, ultrafast as it can be seen by the time-performance of ML via 10-fold CV for training datasets presented in Table 7.

Table 7.

SARS-CoV-2 classification using DSP-ML and DNN-based approach.

Algorithm	Method	Sensitivity (%)	Specificity (%)	Accuracy (%)	Computation time (sec)
Proposed algorithm	Three-base periodicity, ML	96.29	98.25	97.47	0.31
Randhawa's et al. algorithm	k-mers, ML	–	–	100	2.14
Lopez-Rincon's et at. algorithm	DNN	–	100	98.73	–

DSP-ML took only 0.31 s to compute the genome biomarkers (including conversion of DNA sequences into numeric form, estimating the magnitude spectrum, average magnitude, peak-to-average ratio using DFT, SVD, SVD with filtering, AMDF, AMDF with filtering, TDP, TDP with filtering based on the characteristics of three-base periodicity property and classification of SARS-CoV-2 and non-SARS-CoV-2 groups. The robust validation approach is fast and can cope with low length of DNA sequences. Hence, it can be deployed in more efficient ways for the prediction SARS-CoV-2 condition by using raw cDNA sequences as input. However, the study is restricted by the limited number of samples and will be required further investigation with larger data to confirm the efficacy of the proposed approach. The genome sequence data consists of partial CDS that has short length of sequence, which may perhaps enhance and/or degrade the results. The conventional mapping scheme could be replaced with the Pseudo-EIIP DNA symbolic-to-numeric mapping scheme, which may possibly reduce the computational overhead. We also use the raw data without any pre-processing. That may possibly influence the outcomes.

7. Conclusion

This study explores the significance of three-base periodicity for the prediction of SARS-CoV-2 virus. We derived eight biomarkers based on the three-base periodicity properties, using DSP techniques, and ranked those based on a filter-based biomarker selection method, which reduces the computation time and enhances the efficiency of the classifiers. The ranked biomarkers were fed to distinct classifiers for the prediction of SARS-CoV-2 coronavirus from other coronaviruses and a control group via 10-fold CV. In addition, a 10 × 10 CV paired t-test was performed to select the best model to test with the unseen data. The combination of ranked biomarkers (GB1 to GB5), and best supervised model (RF), is capable of differentiating the SARS-CoV-2 coronavirus with an accuracy of 97.47 % and computation time of 0.31 s, which outperforms previous studies. Our work includes various types SARS-CoV-2 data like complete genome, partial genome, partial and complete CDS, from the different regions that varies in length from 64bps to 29945bps, which shows the robustness and effectiveness of proposed approach and also ensures that our results are not affected by the imbalance dataset. Further, we plan to convert the proposed procedure into a computer-aided system that will allow the timely and efficiently differentiation of SARS-CoV-2 viruses from other viruses as early screening of novel viral outbreaks, which can lead to avoid the community transmission and decrease the mortality rate. Additionally, we plan to test the feasibility of proposed features for the classifications of different mutant of SARS-CoV-2 by deploying a multi-class classifier.

Declaration of competing interest

The authors declare no competing interests.

Appendix A. Supplementary data

The following is the Supplementary data to this article: