Abstract
Alcohol intoxication is well known to impair a number of cognitive abilities required for sound decision making. We tested whether an intoxicating dose of alcohol altered whether individuals satisfied a basic property of rational decision making, transitivity of preference. Our study was within-subjects in design and our analysis teased apart stable, yet error-prone, preferences from variable, error-free preferences. We find that alcohol intoxication does not appear to play a major role in determining whether subjects violate transitivity. For a minority of individuals, we find that alcohol intoxication does impact how they select among and/or perceive lotteries with similar attribute values. This, in turn, can cause them to alter various aspects of their preference structure.
Keywords: Alcohol, Decision Making, Transitivity, Lexicographic Semiorders
Introduction
Transitivity of preference is often considered a basic requirement for sound decision making. It is an intuitive and plausible condition requiring only that, for any three choice alternatives, a, b, and c, a decision maker who prefers a over b, and b over c, must also prefer a over c. For example, a decision maker with transitive preferences who prefers an apple over a banana, and a banana over a carrot, must also prefer the apple over the carrot. A decision maker who violates transitivity can be taken advantage of via the classic “money pump” technique (Anand, 1993) in which he is repeatedly traded a good or service, at a cost, only to be sold back an inferior one, leaving the person financially worse off than where he started.
Transitivity of preference is also a fundamental assumption in any theory of rational choice that is based on utility maximization, such as Expected Utility Theory (Von Neumann & Morgenstern, 1947) and Cumulative Prospect Theory (Tversky & Kahneman, 1992). This assumption has been subjected to intense empirical scrutiny over the years, with the majority of research in psychology and economics concluding that most individuals do demonstrate transitive preferences (Birnbaum & Gutierrez, 2007; Birnbaum & LaCroix, 2008; Birnbaum & Schmidt, 2008; Cavagnaro & Davis-Stober, 2014; Regenwetter & Davis-Stober, 2012; Regenwetter, Dana, & Davis-Stober, 2011; Myung, Karabatsos, & Iverson, 2005; Karabatsos, 2006; Mellers & Biagini, 1994). While the vast majority of these experiments were carried out under ideal laboratory conditions, research on transitivity has found it to be robust to several environmental manipulations, such as reducing the time available to make a decision (Cavagnaro & Davis-Stober, 2014) and how choice alternative information is displayed (Davis-Stober, Brown, & Cavagnaro, 2015). Dai (2017a) recently reported strong support for transitive preferences in an inter-temporal choice task.
Manipulating aspects of the choice task or the choice environment, such as a time pressure manipulation, only places indirect cognitive constraints on the decision maker. In contrast, real-world applications of decision making often involve the direct reduction of the decision maker’s cognitive capacity. For example, a sleep-deprived parent may have to decide whether a child’s cough is serious enough to warrant a trip to the hospital. An intoxicated individual may have to decide whether to drive home or call a ride service after a night of carousing. Circumstances such as these pose an interesting and untested question – do underlying properties of a person’s decision making process change under direct reduction of cognitive capacity?
In this paper, we investigate whether transitivity of preference is robust to direct reduction of the decision maker’s cognitive capacity via acute alcohol intoxication. Acute alcohol intoxication forms an ideal paradigm for evaluating basic properties of rationality, such as transitivity of preferences. Alcohol intoxication is well known to impair a range of cognitive abilities required for sound decision making (McCarthy et al., 2012); including attentional capacity (Mocaiber et al., 2011; Steele & Josephs, 1990), memory retrieval (Kirchner & Sayette, 2003; Sayette, 1993), and inhibitory control (Marczinski et al., 2005; Noël et al., 2010). Thus, our analysis of transitivity under alcohol intoxication speaks to the robustness of this basic property of rational decision making at the individual level, and to the external validity of choice theories that require transitivity more generally. Should transitivity of preferences be satisfied even under the intoxication condition, this would provide strong support for transitivity as an invariant property of decision making.
As an alternative to the theory that preferences are strictly transitive, we consider the possibility that they are instead formed through a lexicographic heuristic. In a lexicographic heuristic, the decision maker searches sequentially through the attributes of the choice alternatives until an attribute is found that discriminates between the alternatives. The alternative with the superior attribute is then selected. For properly chosen stimuli, a decision maker using this type of strategy would systematically violate transitivity (Fishburn, 1991; Tversky, 1969).
Researchers have argued that lexicographic heuristics require less cognitive effort to apply compared to rational (i.e., transitive) approaches involving utility maximization (Brandstätter, Gigerenzer, & Hertwig, 2006; Gigerenzer, Todd, & the ABC Research Group, 1999; Rieskamp & Hoffrage, 2008), as less information is needed to arrive at a decision. This raises the question of whether individuals with otherwise transitive preferences could be induced to violate the transitivity axiom and/or utilize a lexicographic heuristic under direct cognitive impairment, such as acute alcohol intoxication. The answer to this question also has important implications for how such individuals evaluate risky trade-offs. A decision maker who utilizes an intransitive choice strategy, such as a lexicographic heuristic, could evaluate choice options without incorporating all relevant information. For example, such a decision maker may not consider the probability of causing a serious accident when deciding whether or not to drive home, basing his decision instead on the hassle of retrieving his car the next morning (McCarthy, Pederson, Thompsen, & Leuty, 2006).
In our analysis, we test transitivity by casting it as a formal mathematical model, which can then be directly compared against competing models that are not necessarily transitive, such as the lexicographic heuristic. Following Cavagnaro and Davis-Stober (2014), Dai (2017a), and Regenwetter et al. (2017), we employ Bayesian model selection methodology. This approach allows competing theories to be tested against each other, rather than against chance, and has been supported as a favorable alternative to null hypothesis significance testing (Marewski & Olsson, 2009; Rouder, Speckman, Sun, Morey, & Iverson, 2009). Moreover, it avoids many of the logical and statistical pitfalls (e.g., simply counting violations) that have plagued previous assessments of transitivity (Regenwetter, Dana, & Davis-Stober, 2011).
Furthermore, in a comment on Dai (2017a), Scholten (2017) argued that a lack of transitivity violations does not necessarily constitute evidence against attribute-wise theories, see also Dai (2017b) for his reply. In our analysis, we directly compare general models of transitivity to a lexicographic competitor theory that allows, but does not require, intransitive preference. In this way, we avoid the problem of indirectly inferring rejection of a particular class of theories through supportive evidence for another.
Our formalizations of these preference structures also account for different types of choice variability. When presented with the same choice multiple times, decision makers are often not consistent in their responses. A considerable amount of research has been directed towards understanding and modeling such choice variability (see, e.g., Ballinger & Wilcox, 1997; Busemeyer, Weg, Barkan, Li, & Ma, 2000; Haruvy, Stahl, & Wilson, 2001; Hey, 2001; Hey & Orme, 1994). The major models of choice variability include single strategy “error” models (Birnbaum & Bahra, 2012; Bröder, 2010; Glöckner, 2009; Harless & Camerer, 1994) as well as multi-strategy “mixture” models (Carbone & Hey, 2000; Davis-Stober & Brown, 2011; Loomes & Sugden, 1995). In error models, preferences are fixed but responses are variable; in mixture models, preferences are allowed to be variable, i.e., decision makers are allowed to utilize multiple decision strategies over the course of the choice task. As argued by Hey (2005), which model of choice variability is used to analyze data matters a great deal and not all decision makers exhibit the same type of choice variability. To this end, we dissociate structural properties of preference (transitivity, lexicographic semiorders) from the nature of individual choice variability by considering transitive and lexicographic semiorder models under both error and mixture specifications.
To our knowledge, only one prior study has investigated the effect of direct impairment of cognitive capacity via alcohol intoxication on fundamental properties of decision making. Burghart, Glimcher, and Lazzaro (2013) conducted a field study of bar patrons, where participants completed a choice task designed to evaluate the Generalized Axiom of Revealed Preferences (GARP). GARP is a basic econometric property that is both necessary and sufficient for preferences to be described by utility maximization. Burghart et al. found that participants’ obtained breath alcohol concentration (BrAC) was unrelated to whether or not participants satisfied GARP. Our study builds upon Burghart et al. in two important ways. First, while GARP is related to transitive preference, our models of transitivity provide tests for alternative models of utility, including random utility and weak utility models (see Davis-Stober et al., 2017, for a recent discussion). Second, Burghart et al.’s field study was observational in nature and could only uncover correlational information regarding GARP and BrAC. In contrast, our study was a within-subjects laboratory experiment, evaluating whether participants satisfy transitivity in both sober and intoxicated states.
Methods
Participants
Participants were recruited from the University of Missouri and surrounding community via posted advertisements and electronic newsletters. Prospective subjects completed a phone interview to assess recent drinking behavior and were excluded if they were currently seeking substance abuse treatment or attempting to restrict current drinking behavior. Additionally, subjects were excluded if they reported a condition that would be exacerbated by consuming alcohol, were currently pregnant or nursing, or reported any history of psychiatric illness. The sample (N=36) was primarily Caucasian (94.9%) and was 22.32 years old on average (SD=1.87). A majority (79.4%) of subjects reported drinking once to twice a week, consuming 4.24 drinks per occasion (SD=2.32).
Measures
Demographic information.
A self-report questionnaire was used to collect demographic information, including age, gender, race, and education.
Breath Alcohol Concentration (BrAC)
Intoximeters’ Alco-Sensor FST (Alco-Sensor FST, Intoximeters Inc) was used to assess BrAC.
Decision Making Task.
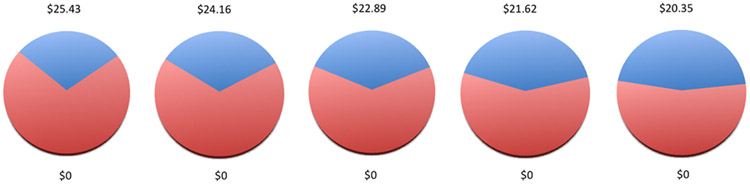
Our experiment followed a very similar design to that of the classic Tversky (1969) study on intransitive preference. Participants were repeatedly presented pairs of binary gambles on a computer screen and asked to select the gamble they preferred via a keyboard press. Our experiment deviates from that of Tversky in that participants were allowed to indicate indifference between the presented gambles. This design follows that of Regenwetter and Davis-Stober (2012), and has been shown to permit more general and more powerful tests of preference structures. In our experiment, there were five distinct binary gambles in the stimulus set (Figure 1), thus a total of 10 possible gamble pairs. Our gamble stimuli were designed to induce intransitive choices arising from a lexicographic semiorder (Tversky, 1969).
Figure 1.
The five binary gambles used in our experiment. The shaded proportion of the circle corresponds to the probability of winning the dollar amount displayed above the circle and the unshaded region corresponds to the probability of winning nothing. The expected values for the five gambles, reading left to-right, are equal to: $7.42, $8.05, $8.58, $9.01, and $9.33.
Procedure
Data for the current study were collected as part of a larger alcohol administration study (Morris et al, 2014). Target sample size for this experiment was 30, but 6 additional participants were enrolled prior to stopping due to scheduling and logistical issues – no data relevant to this project were examined prior to study completion. The experiment consisted of two sessions for each participant, an alcohol session and a comparison no-beverage/sober session, in counterbalanced order. Participants were paid $12 an hour for participation in this study. This payment was based solely on time and was not conditional on task performance. Prior to each session, participants were required to abstain from alcohol and other substances for 24 hours. A breath test was used to confirm sobriety. Female participants completed a urine pregnancy test - no participants were excluded as a result of a positive test.
For each session, all pairwise comparisons of the gambles in Figure 1 were randomly presented to each participant a total of 5 times each, totaling 50 trials in each session, counterbalancing whether a gamble showed up on the left- or right-hand side of the screen. The number of trials per session was determined via simulations and provided sufficient posterior evidence regarding the Bayesian order-constrained methodology (Klugkist & Hoijtink, 2007) we applied.
During the intoxicated session, subjects ingested a dose of alcohol consisting of one part 100 proof vodka (50% alcohol by volume) and four parts non-caffeinated tonic. The beverage was calculated by participant body mass and used a .75 g/kg dose for men and .65 g/kg for women, resulting in an approximate peak BrAC of .075-.08%. The total beverage was subsequently divided into three drinks of equal volume and administered in three five-minute intervals. After consumption, participants were allotted a 15 minute absorption period. The decision making task was administered 60 minutes post beverage consumption at approximately peak BrAC (mean BrAC before task = .079%, mean BrAC after task =.078%). There was no significant effect of gender on BrAC both before and after the decision making task, t(32)= −.426, p>.05, and t(32)=−.848, p>.05, respectively.
The no-beverage/sober session was nearly identical to the alcohol session. It differed in that it commenced at an earlier time (eleven in the morning versus one in the afternoon) and subjects completed a brief questionnaire packet prior to the task blocks. Task blocks were initiated at 15 minute intervals post-survey, and the decision making task was administered 60 minutes after the completion of the survey.
Models
We construct both mixture and error specifications of both transitive and (potentially intransitive) lexicographic semiorder models of choice. We describe each in turn.
As a transitive model of choice with a mixture specification of choice variability, we consider the Weak Order Mixture Model (WOMM) of Regenwetter and Davis-Stober (2012). Under the WOMM, an individual is allowed to have dynamically changing preferences over time with the restriction that all choices made by the individual are consistent with weakly ordered, transitive preferences. The WOMM places no restrictions on when, or how, or even if, an individual dynamically changes her preferences. This model is a generalization of the mixture model of transitive preferences of Regenwetter, Dana, and Davis-Stober (2011), previously used in recent tests of the transitivity axiom (Cavagnaro & Davis-Stober, 2014; Dai, 2017a). Despite its apparent generality, the proportion of choice probabilities (for our five choice alternative experiment), out of all possible, that conform to WOMM is equal to .00045. This value was obtained by Monte Carlo simulation methods as reported in Regenwetter and Davis-Stober (2012).
As a transitive model of choice with an error specification of choice variability, we consider a Weak Order Error Model (WOEM). Applying the QTest framework developed by Regenwetter et al. (2014), we define WOEM as all possible weak orders under a modal choice specification with .5 maximum response error – see Regenwetter et al. (2014) for details. Under WOEM, an individual has a single preference state that is weakly ordered and is allowed to generate choices such that the maximum error must not exceed .5. The WOEM can be considered a generalization of weak stochastic transitivity (Davidson & Marschak, 1959) to two-alternative, non-forced choice; i.e., WOEM restricted to linear orders (as opposed to weak orders) results in weak stochastic transitivity.
An alternative to the theory that preferences are transitive is that they conform to a lexicographic semiorder structure, defined as an ordered collection of semiorders. The core idea of a semiorder is that “small” differences in attribute values are ignored by the decision maker (Luce, 1956). For example, if a decision maker was deciding between two automobiles, and their prices differed by only a dollar, then this person would likely not use price when making her choice, i.e., a dollar would be below her price “threshold.” A decision maker chooses according to a lexicographic semiorder if, when comparing any two choice alternatives, attribute values are compared sequentially until a set of attribute values are reached upon which the choice alternatives differ by a sufficient margin. At that point, the process stops and the alternative that is superior based on that attribute is preferred. For properly chosen stimuli, such as ours, a decision maker using this type of strategy would systematically violate transitivity (Fishburn, 1991; Tversky, 1969). Throughout, our models are based on simple lexicographic semiorders as defined in Davis-Stober (2010; 2012). A simple lexicographic semiorder is a lexicographic semiorder restricted to choice alternatives with two attributes, where the two attributes “trade-off” with one another, i.e., as one attribute becomes more favorable the other becomes less so. Our choice stimuli satisfy these properties.
As a lexicographic semiorder model of choice under a mixture specification of choice variability, we consider the Lexicographic Semiorder Mixture Model (LSMM) of Davis-Stober (2012). Similar to the WOMM, the LSMM allows an individual to have dynamically changing preferences over time with the restriction that all choices made by the individual are consistent with preferences that satisfy a lexicographic semiorder structure. The LSMM places no restrictions on an individual’s permissible preferences other than that he must make choices consistent with a lexicographic semiorder structure at all sampled time points (Davis-Stober, 2012). For the binary gamble stimuli we use in our experiment, there are two possible orders in which the attribute values could be considered: a decision maker could consider payoff values before considering the probability of winning or vice versa. Thus, we consider two such mixture models: LSMM1 will be the model defined by considering probability of winning first and LSMM2 will be the model defined by considering payoff values first (Davis-Stober, 2012)1. Both LSMM1 and LSMM2 are extremely parsimonious. The proportion of choice probabilities (for our five choice alternative experiment), out of all possible, that conform to LSMM1 is equal to .0000013. The value for LSMM2 is identical. This value was obtained by Monte Carlo simulation methods. The LSMMs are two orders of magnitude more parsimonious than the WOMM.
As a lexicographic semiorder model of choice under an error specification of choice variability, we consider the Lexicographic Semiorder Error Model (LSEM). Following the QTest framework in Regenwetter et al. (2014), we consider all simple lexicographic semiorders with a modal choice specification with .5 maximum response error. As above, we consider two LSEMs; LSEM1, which corresponds to a modal choice specification over all simple lexicographic semiorders such that probability of winning is considered first, and LSEM2, which corresponds to a modal choice specification over all simple lexicographic semiorders such that payoff values are considered first. Said simply, the LSEMs capture the choice behavior of individuals who choose, with error, according to a single lexicographic semiorder preference. To remove overlap with the WOEM specification, we removed the 81 preference states (for each LSEM model) that are also consistent with weak orders, leaving 513 lexicographic semiorder preference states that are not also weak orders.
In our analysis, we compare all six of the above models against an “unconstrained” model that places no restrictions on preferences. If our analysis favors the unconstrained model over all six substantive models, we would conclude that transitivity is violated for that participant and that their choices are not well-explained by a lexicographic semiorder structure.
Results
For each session, we calculated the proportion of times that each individual chose a particular gamble over another for all paired comparisons. Our statistical approach follows that of Davis-Stober et al. (2015) and Cavagnaro and Davis-Stober (2014). We assessed the degree to which each of the seven models accounted for these data using the order-constrained Bayes factor methodology of Klugkist and Hoijtink (2007). A Bayes factor provides a method of model comparison that properly accounts for model complexity and goodness of fit (Kass & Raftery, 1995) and can be interpreted as a statement about posterior odds. For example, if we compare WOMM to the unconstrained model and obtain a Bayes factor of 10, then we would conclude that WOMM is 10 times more likely to have generated the data for that subject than the unconstrained model. Following the standard Jeffreys' (1961) interpretation scale, a Bayes factor of 1-3 is weak evidence for the model, values between 3 and 10 are strong evidence, and a Bayes factor greater than 100 is decisive evidence. We classified subjects’ behavior according to the model with the highest Bayes factor, with the requirement that the highest Bayes factor (versus the unconstrained model) must be greater than or equal to 3.
Provided in the online supplement is a table that presents Bayes factors for all 36 participants in both sober and intoxicated conditions. Table 1 provides a summary of the marginal classifications for the sober and intoxicated conditions. The distribution of model classifications was roughly equal across the two conditions, suggesting that alcohol intoxication did not have an effect on model classification rates. Ignoring model of choice variability, participants were classified according to transitive models roughly as often as lexicographic semiorder models. The WOEM had the largest number of classifications, followed by LSMM1. Next, we turn to questions concerning individual-level classification stability.
Table 1:
Number of data sets (out of 72 total data sets, 36 participants times two conditions) for which each model provided the highest Bayes factor among substantive models and achieved a Bayes factor of at least 3.15 against the unconstrained model. Classification rates according to the more stringent criterion of achieving a Bayes factor of at least 3.15 against both the unconstrained model and the second-best substantive model are in parentheses.
| Model | Sober | Intox. | Overall |
|---|---|---|---|
| WOMM | 2(0) | 5(3) | 7(3) |
| LSMM1 | 9(4) | 8(5) | 17(9) |
| LSMM2 | 1(0) | 1(1) | 2(1) |
| WOEM | 14(9) | 14(11) | 28(20) |
| LSEM1 | 3(1) | 2(1) | 5(2) |
| LSEM2 | 5(5) | 4(3) | 9(8) |
| Total | 34(19) | 34(24) | 68(43) |
Only 3 subjects’ data (out of 36) failed to be classified according to one of the six substantive models for both conditions. Among the remaining 33 subjects, two-thirds remained stable with respect to whether their best fitting model was transitive or a lexicographic semiorder across conditions, ignoring the model of choice variability. More than half of the subjects who were stable (12) were classified according to a transitive model, and the rest (10) were classified according to a lexicographic semiorder model. Of the 11 subjects who changed in their classification across conditions, 4 subjects switched from a transitive model (sober condition) to a lexicographic semiorder model (intoxicated condition), and 7 switched from a lexicographic semiorder model (sober condition) to a transitive model (intoxicated condition).
Our analysis also allows us to investigate the stability of choice variability models (i.e., error models vs. mixture models). The results show that 19 out of 33 subjects were stable within either an error or mixture specification across conditions, ignoring whether the model was transitive or lexicographic semiorder. Among those who changed across conditions according to their best-performing model of choice variability, 8 subjects switched from error specification (sober) to mixture specification (intoxicated), and 6 switched from mixture (sober) to error (intoxicated)2.
It is worth noting that among the subjects who switched from an error model (sober) to a mixture model (intoxicated), none of them switched from a lexicographic semiorder model (sober) to a transitive model (intoxicated). All subjects who switched from a mixture model (sober) to an error model (intoxicated), on the other hand, were either stable in their transitive/lexicographic semiorder classification or switched from a lexicographic semiorder model (sober) to a transitive model (intoxicated). Given the small sample size of the current study, it is hard to say that such interaction effects can be generalized to other samples, but it suggests the possibility that alcohol effects have an underlying pattern.
We carried out a series of post-hoc analyses to better understand the impact of alcohol intoxication on participants’ choices. Across all participants, and all choice pairs, the indifference response was selected at a higher rate in the intoxicated condition (15.3% of responses) than in the sober condition (10.9% of responses). This difference is significant at the .05 alpha level for a Wilcoxon signed rank test, p = .0058. Further, there was greater total variability in choice responses for the intoxicated condition than the sober condition, but this difference was not significant at the .05 alpha level for a Wilcoxon signed rank test3 The greater use of the indifference response under the intoxicated condition manifested in an interesting way. Among all 6 participants who switched in their classification from any substantive model sober to an LSMM model intoxicated, there was a marked increase in the rate of using the indifference response for adjacent gambles. Adjacent gambles are defined as gamble pairs in which the attribute values differ by only one level, i.e., in Figure 1, if we label the five binary gambles (left-to-right) as: a,b,c,d,e; the adjacent gamble pairs are: (a,b), (b,c), (c,d), and (d,e). For these 6 participants, the average proportions of indifference responses for the four adjacent gamble pairs are nearly twice as large as in the sober condition:
Indifference of (a,b) .83 (intoxicated) 95% CI (.73, .99); .20 (sober) 95% CI (0, .44)
Indifference for (b,c) .57 (intoxicated) 95% CI (.37, .78); .13 (sober) 95% CI (0, .34)
Indifference for (c,d) .60 (intoxicated) 95% CI (.43, .83); .17 (sober) 95% CI (0, .40)
Indifference for (d,e) .43 (intoxicated) 95% CI (.23, .67); .10 (sober) 95% CI (0,.34).
The above differences between intoxicated and sober conditions are significant at the .05 alpha level for choice pairs (a,b), (b,c), and (c,d). We carried out confidence interval estimation using the methodology of Glaz and Sison (1999) and applied a Bonferroni correction for multiple tests. Average indifference rates for non-adjacent gambles were roughly similar across the two conditions for these 6 participants.
We also examined data from other participants who changed in their model classification in the intoxicated condition. For individuals who switched from any model classification sober to the WOMM intoxicated there is an indication of “probability splitting” for adjacent gamble pairs, where an individual exhibited a strong preference for one gamble (within an adjacent pair) sober only to prefer both gambles equally often intoxicated. Participant 3 exhibits this behavior by selecting gamble b over a (also c over b) 100% of the time sober, but then selecting b over a (also b over c) only 40% of the time intoxicated. Again, this suggests a similar effect with regard to adjacent gambles as individuals who switched classification to LSMM while intoxicated. We stress, however, that the sample size for these participants are too small to carry out a statistical test and that this interpretation should only be considered for designing future studies.
Discussion
Our results suggest three major takeaways. First, alcohol intoxication does not appear to play a major role in whether subjects violated the transitive models. Second, 2/3 of the classified participants were invariant in whether they were classified according to a transitive or a lexicographic semiorder model across both conditions. Taken together, these two points suggest that preference structure (either transitive or lexicographic) is a robust property of decision making for many participants. Third, a majority of the classified participants were invariant in their model of choice variability across both conditions – suggesting that this too may be a stable property of choice for many individuals. Our results are consistent with the Burghart et al. (2013) study, which found that GARP violations were unrelated to BrAC level. Overall, participants were classified according to transitive models in roughly equal number as lexicographic semiorder models.
It is worth discussing that 1/3 of our participants switched with regard to transitive/lexicographic semiorder classification across conditions, although not in a simple, directional fashion, contrary to our hypothesis. This rate is larger than has been observed in previous studies manipulating time pressure (Cavagnaro & Davis-Stober, 2014) and stimulus display (Davis-Stober et al., 2015). This final point suggests that alcohol’s effect on preference structure is not a simple, directional effect toward heuristic decision making and warrants future investigation. Our post-hoc analysis revealed that many of these participants were more likely to indicate indifference between adjacent gambles under alcohol intoxication, suggesting alcohol’s influence in how they perceive and/or evaluate gambles with similar attribute values.
The fact that many individuals continued to satisfy transitivity when intoxicated does not indicate that these preferences would necessarily result in rational or optimal choices. An extensive literature indicates that alcohol intoxication increases the likelihood of “poor” behavioral decisions (e.g., aggressive behavior, driving while impaired; Giancola, 2004; McCarthy et al. 2012). Our results are not inconsistent with this literature, but suggest that intoxication increases risk for such behaviors by other means, without altering the underlying structure of the decision making process. Rather than alter how individuals combine and evaluate choice information when making a decision, intoxication may instead influence what choice information goes into the decision making strategy. Changing which attributes and/or alternatives are considered when making a decision is consistent with alcohol’s deleterious effect on attention (Mocaiber et al., 2011) and with the alcohol myopia (attention allocation) model (Steele & Josephs, 1990), which posits that alcohol intoxication narrows attentional capacity to the most salient aspects of stimuli. Future studies could examine multi-dimensional choice sets, which would allow for isolating the effects of alcohol on the allocation of attention and the use of decision strategy. An additional direction for future research is to examine decision making strategies for externally relevant choices often associated with alcohol-related negative consequences (e.g., sexual behavior, aggression, driving while intoxicated).
Our results suggest that, while other aspects of the decision making process could change as a function of direct cognitive impairment, whether an individual uses a transitive or lexicographic semiorder decision strategy appears to be a relatively stable property of decision making. This work parallels recent empirical findings in the decision making literature (Cavagnaro & Davis-Stober, 2014; Davis-Stober et al. 2015). Taken together, these results suggest that preference structure is a more ‘automatic’ cognitive process (Glöckner & Betsch, 2008; Glöckner & Herbold, 2011) as opposed to a ‘deliberate’ process (Brandstätter, 2011).
One limitation of our study is the small sample size for testing the role of individual differences. To be clear, given the design and methodological approach, we did not lack power for the main findings. All six of the substantive models we considered are extraordinarily parsimonious in that only a small fraction of possible observable data conform to either model, and our calculated Bayes factors reflected decisive evidence for model classification. We also note that 36 subjects is, to date, one of the largest samples for an experimental test of transitivity that follows a within-subject design (see Cavagnaro & Davis-Stober, 2014, for a review). An important direction for future research is to examine individuals who do switch in their transitive/lexicographic semiorder classification when intoxicated. Are some individuals particularly sensitive to disruptions of preference structure under alcohol intoxication? If so, future studies can explore whether such sensitivity is associated with engagement in alcohol-related problem behaviors or with risk factors for alcohol problems, e.g., response to alcohol (King, deWit, McNamara, & Cao, 2011) and impulsivity (Sher & Trull, 1994).
Supplementary Material
Acknowledgments
Funding for this work was provided by National Institute on Alcohol Abuse and Alcoholism Grant R01 AA 019546 to Denis M. McCarthy and Grant K25AA024182 to Clintin P. Davis-Stober.
Footnotes
All choice data and code are available for download at: https://figshare.com/articles/AlcPaperMaterials_zip/4650274
One could also consider a mixture model in which a decision maker varied in the order that they considered the two attributes, i.e., a mixture model over all preferences satisfying LSMM1 and LSMM2. We leave this for future work. Care would have to be taken in specifying such a model because as the number of attributes increases such a model could accommodate many (possibly all) binary preferences.
We tested whether BrAC or subjective intoxication (assessed both before and after task completion) differed for those who switched between the intoxicated and sober session, compared to those who did not switch. We examined this separately for individuals who switched between a transitive model and a lexicographic semiorder (n = 11) vs. those who did not (n = 22), and for those who switched from an error to a mixture model (n = 14) vs. those who did not (n = 19). There were no significant differences as a function of switching for either index of impairment at the .05 Type I error level.
We measured total variability in choice responses by estimating the variance for the multinomial random variable corresponding to each choice pair and then summing these values across all participants and choice pairs; estimated total variances for the intoxicated and sober conditions were 398 and 378 respectively, p>.05.
Contributor Information
Clintin P. Davis-Stober, University of Missouri
Denis M. McCarthy, University of Missouri
Daniel R. Cavagnaro, California State University, Fullerton
Mason Price, University of Missouri.
Nicholas Brown, University of Missouri.
Sanghyuk Park, University of Missouri.
References
- Alco-Sensor FST [Apparatus]. St Louis, MO: Intoximeters Inc. 2010. [Google Scholar]
- Anand P (1993). The philosophy of intransitive preference. The Economic Journal,337–346. [Google Scholar]
- Ballinger TP, & Wilcox NT (1997). Decisions, error and heterogeneity. The Economic Journal, 107, 1090–1105. [Google Scholar]
- Birnbaum MH, & Bahra JP (2012). Testing transitivity of preferences using linked designs. Judgment and Decision Making, 7, 524–567. [Google Scholar]
- Birnbaum MH, & Gutierrez RJ (2007). Testing for intransitivity of preferences predicted by a lexicographic semiorder. Organizational Behavior and Human Decision Processes, 104, 96–112. [Google Scholar]
- Birnbaum MH, & LaCroix AR (2008). Dimension integration: Testing models without trade-offs. Organizational Behavior and Human Decision Processes, 105, 122–133. [Google Scholar]
- Birnbaum MH, & Schmidt U (2008). An experimental investigation of violations of transitivity in choice under uncertainty. Journal of Risk and Uncertainty, 37, 77–91. [Google Scholar]
- Brandstätter E (2011). On the stability of choice processes. Frontiers in Psychology, 2, dii: 10.3389/fpsyg.2011.00295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandstätter E, Gigerenzer G, & Hertwig R (2006). The priority heuristic: Making choices without trade-offs. Psychological Review, 113, 409–432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bröder A (2010). Outcome-based strategy classification. In Glöckner A & Witteman C (Eds.), Foundations for tracing intuition: Challenges and methods (pp. 61–82). New York: Psychology Press. [Google Scholar]
- Burghart DR, Glimcher PW, & Lazzaro SC (2013). An expected utility maximizer walks into a bar…. Journal of Risk and Uncertainty, 46, 215–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busemeyer JR, Weg E, Barkan R, Li X, & Ma Z (2000). Dynamic and consequential consistency of choices between paths of decision trees. Journal of Experimental Psychology: General, 129, 530–545. [DOI] [PubMed] [Google Scholar]
- Carbone E, & Hey JD (2000). Which error story is best? Journal of Risk and Uncertainty, 20, 161–176. [Google Scholar]
- Cavagnaro DR, & Davis-Stober CP (2014). Transitive in our preferences but transitive in different ways: An analysis of choice variability. Decision, 1, 102–122. [Google Scholar]
- Dai J (2017a). Are intertemporal preferences transitive? A Bayesian analysis of repeated individual intertemporal choices. Decision, 4, 1–24. [Google Scholar]
- Dai J (2017b). Using test of transitivity to evaluate psychological models of intertemporal choice for individuals: Reply to Schloten (in press). In press at Decision. [Google Scholar]
- Davidson D, & Marschak J (1959). Experimental tests of a stochastic decision theory. In Churchman CW & Ratoosh P (Eds.), Measurements: Definitions and theories (pp.233–269). New York, NY: Wiley. [Google Scholar]
- Davis-Stober CP (2010). A bijection between a set of lexicographic semiorders and pairs of non-crossing Dyck paths. Journal of Mathematical Psychology, 54, 471–474. [Google Scholar]
- Davis-Stober CP (2012). A lexicographic semiorder polytope and probabilistic representations of choice. Journal of Mathematical Psychology, 56, 86–94. [Google Scholar]
- Davis-Stober CP, & Brown N (2011). A shift in strategy or “error”? Strategy classification over multiple stochastic specifications. Judgment and Decision Making, 6(8), 800–813. [Google Scholar]
- Davis-Stober CP, Brown N, & Cavagnaro DR (2015). Individual differences in the algebraic structure of preferences. Journal of Mathematical Psychology, 66, 70–82. [Google Scholar]
- Davis-Stober CP, Brown N, Park S, & Regenwetter M (2017). Recasting a biologically motivated computational model within a Fechnerian and random utility framework. Journal of Mathematical Psychology, 77, 156–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishburn PC (1991). Nontransitive preferences in decision theory. Journal of Risk and Uncertainty, 4, 113–134. [Google Scholar]
- Giancola P (2004). Executive functioning and alcohol-related aggression. Journal of Abnormal Psychology, 113, 541–555. [DOI] [PubMed] [Google Scholar]
- Gigerenzer G, Todd PM, & the ABC Research Group. (1999). Simple heuristics that make us smart. Oxford University Press. [Google Scholar]
- Glaz J, & Sison CP (1999). Simultaneous confidence intervals for multinomial proportions. Journal of Statistical Planning and Inference, 82, 251–262. [Google Scholar]
- Glöckner A (2009). Investigating intuitive and deliberate processes statistically: The multiple-measure maximum likelihood strategy classification method. Judgment and Decision Making, 4, 186–199. [Google Scholar]
- Glöckner A, & Betsch T (2008). Multiple-reason decision making based on automatic processing. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34,1055–1075. [DOI] [PubMed] [Google Scholar]
- Glöckner A, & Herbold AK (2011). An eye-tracking study on information processing in risky decisions: Evidence for compensatory strategies based on automatic processes. Journal of Behavioral Decision Making, 24, 71–98. [Google Scholar]
- Harless DW, & Camerer CF (1994). The predictive utility of generalized expected utility theories. Econometrica, 62, 1251–1289. [Google Scholar]
- Haruvy E, Stahl DO, & Wilson P (2001). Modeling and testing for heterogeneity in observed strategic behavior. Review of Economics and Statistics, 83,146–157. [Google Scholar]
- Hey JD (2001). Does repetition improve consistency? Experimental Economics, 4, 5–54. [Google Scholar]
- Hey JD (2005). Why we should not be silent about noise. Experimental Economics, 8, 325–345. [Google Scholar]
- Hey JD,& Orme C (1994). Investigating generalizations of expected utility theory using experimental data. Econometrica, 62, 1267–1326. [Google Scholar]
- Jeffreys H (1961). Theory of Probability. Oxford University Press. [Google Scholar]
- Karabatsos G (2006). Bayesian nonparametric model selection and model testing. Journal of Mathematical Psychology, 50, 123–148. [Google Scholar]
- Kass RE, & Raftery AE (1995). Bayes factors. Journal of the American Statistical Association, 90, 773–795. [Google Scholar]
- King AC, de Wit H, McNamara PJ, & Cao D (2011). Rewarding, stimulant, and sedative alcohol responses and relationship to future binge drinking. Archives of General Psychiatry, 68, 389–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirchner TR, & Sayette MA (2003). Effects of alcohol on controlled and automatic memory processes. Experimental and Clinical Psychopharmacology, 11, 167–175. [DOI] [PubMed] [Google Scholar]
- Klugkist I, & Hoijtink H (2007). The Bayes factor for inequality and about equality constrained models. Computational Statistics and Data Analysis, 51, 6367–6379. [Google Scholar]
- Loomes G, & Snugden R (1995). Incorporating a stochastic element into decision theories. European Economic Review, 39, 641–648. [Google Scholar]
- Luce RD (1956). Semiorders and a theory of utility discrimination. Econometrica, 24, 178–191. [Google Scholar]
- Marczinski CA, Abroms BD, Selst MV, & Fillmore MT (2005). Alcohol-induced impairment of behavioral control: Differential effects on engaging vs. disengaging responses. Psychopharmacology, 182, 452–459. [DOI] [PubMed] [Google Scholar]
- Marewski JN, & Olsson H (2009). Beyond the null ritual: Formal modeling of psychological processes. Zeitschrift für Psychologie / Journal of Psychology, 217, 49–60. [Google Scholar]
- McCarthy DM, Pedersen SL, Thompsen DM & Leuty ME (2006). Development of a measure of drinking and driving expectancies for youth. Psychological Assessment, 18,155–164. [DOI] [PubMed] [Google Scholar]
- McCarthy DM, Niculete ME, Treloar HR, Morris DH, & Bartholow BD (2012). Acute alcohol effects on impulsivity: associations with drinking and driving behavior. Addiction, 107, 2109–2114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mellers BA, Biagini K (1994). Similarity and choice. Psychological Review, 101, 505–518. [Google Scholar]
- Mocaiber I, David IA, de Oliveria L, Pereira MG, Volchan E, Figueria I, Vila J, & Machado-Pinheiro W (2011). Alcohol, emotion and attention: Revisiting the alcohol myopia theory. Psicologia: Reflexão e Critica, 24, 403–410. [Google Scholar]
- Morris DH, Treloar HR, Niculete ME, & McCarthy DM (2014). Perceived danger while intoxicated uniquely contributes to driving after drinking. Alcoholism: Clinical and Experimental Research, 38, 521–528. doi: 10.1111/acer.12252 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myung JI, Karabatsos G, Iverson GJ (2005). A bayesian approach to testing decision making axioms. Journal of Mathematical Psychology, 49, 205–225. [Google Scholar]
- Noël X, Bechara A, Brevers D, Verbanck P, & Campanella S (2010). Alcoholism and the loss of willpower: A neurocognitive perspective. Journal of Psychophysiology, 24, 240–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regenwetter M, Cavagnaro DR, Popova A, Guo Y, Zwilling C, Lim SH, & Stevens JR (2017). Heterogeneity and Parsimony in Intertemporal Choice. In press at Decision. [Google Scholar]
- Regenwetter M, Davis-Stober CP, Lim SH, Guo Y, Popova A, Zwilling C, Cha Y-S, & Messner W (2014). QTest: Quantitative testing of theories of binary choice. Decision, 1, 2–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regenwetter M, & Davis-Stober CP (2012). Choice variability versus structural inconsistency of preferences. Psychological Review, 119, 408–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regenwetter M, Dana J, & Davis-Stober CP (2011). Transitivity of preference. Psychological Review, 118, 42–56. [DOI] [PubMed] [Google Scholar]
- Rieskamp J, & Hoffrage U (2008). Inferences under time pressure: How opportunity costs affect strategy selection. Acta Psychologica, 127, 258–276. [DOI] [PubMed] [Google Scholar]
- Rouder JN, Speckman PL, Sun D, Morey RD, & Iverson G (2009). Bayesian t-tests for accepting and rejecting the null hypothesis. Psychonomic Bulletin & Review, 16, 225–237. [DOI] [PubMed] [Google Scholar]
- Sayette MA (1993). An appraisal-disruption model of alcohol's effects on stress responses in social drinkers. Psychological Bulletin, 114, 459–476. [DOI] [PubMed] [Google Scholar]
- Scholten M (2017). Thoughts on analyses of intransitive intertemporal preference. In press at Decision. [Google Scholar]
- Sher KJ, & Trull TJ (1994). Personality and disinhibitory psychopathology: Alcoholism and antisocial personality disorder. Journal of Abnormal Psychology1, 103, 92–102. [DOI] [PubMed] [Google Scholar]
- Steele CM, & Josephs RA (1990). Alcohol myopia: Its prized and dangerous effects. American Psychologist, 45, 921–933. [DOI] [PubMed] [Google Scholar]
- Tversky A (1969). Intransitivity of preferences. Psychological Review, 76, 31–48. [Google Scholar]
- Tversky A, & Kahneman D (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297–323. [Google Scholar]
- von Neumann J, & Morgenstern O (1947). The theory of games and economic behavior. Princeton University Press. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.