Penalized Geodesic Tractography for Mitigating Gyral Bias

Abstract

In this paper, we introduce a penalized geodesic tractography (PGT) algorithm for mitigating gyral bias in cortical tractography, which is essential for improving cortical connectomics. Unlike deterministic and probabilistic tractography algorithms that perform one-way tracking, PGT solves a global optimization problem in estimating the pathways connecting multiple regions, instead of local step-by-step orientation tracing. PGT is unconfounded by local false-positive or false-negative fiber orientations and ensures that fiber streamlines that are intended to connect two regions do not terminate prematurely. We show that PGT reduces gyral bias by allowing streamlines to make sharper turns into the cortical gyral matter and results in a significantly more uniform spatial distribution of cortical connections.

1. Introduction

Diffusion magnetic resonance imaging (DMRI) [1] allows brain white matter pathways to be reconstructed in-vivo and non-invasively by tracing local fiber orientations, which capture the diffusion patterns of water molecules. In connectomic studies that investigate cortico-cortical connectivity [2,3], fiber tracking often needs to be performed across gray-white matter boundaries in gyral blades of complex cortical convolutions. This process can be challenging due to factors such as partial volume effects and gyral bias [1].

A vast majority of tractography algorithms begin tracking from a seed point and propagate a streamline until some termination criterion is met [4,5]. This is a one-way tracking (OWT) process and can cause unsatisfactory outcome in noisy conditions due to error accumulation, often resulting in prematurely terminated tracts that fall short of reaching the cortex. OWT methods are also susceptible to gyral bias with streamlines preferentially terminating at gyral crowns rather sulcal banks or fundi. The bias can be observed for a wide range of tractography algorithms (deterministic and probabilistic), diffusion models, diffusion weightings, and even for gradient directions with very high angular resolution [6].

In this work, we introduce a novel algorithm, called penalized geodesic tractography (PGT), for determining the shortest streamlines that connect different brain regions. We show that PGT overcomes the gyral bias problem, giving a significantly more uniform spatial distribution pattern of cortical connections. PGT determines the shortest paths connecting the regions via backtracking of the distance maps computed by solving the eikonal equation on a Finsler manifold with an anisotropic metric induced by the fiber orientation distribution function (FODF). Unlike existing methods that solve for shortest paths based on local costs [7–10], PGT determines a globally minimal path by minimizing a cost function that penalizes both tract curvature and length using a penalized manifold metric. This avoids the error stemming from the step-by-step tracing of the distance map and provides a global solution of the shortest path. Using in-vivo data, we demonstrate that PGT overcomes gyral bias and results in an improved coverage of the cortex.

2. Methods

2.1. Geodesic Tractography

The aim of geodesic tractography is to determine the shortest paths (i.e., geodesics) connecting a seed region and a target region based on an orientation field. The shortest paths can be determined using a distance map in relation to the seed region. The distance map is calculated by solving an eikonal equation, which is a partial differential equation (PDE) that describes the time of arrival at each point in space as a function of the local speed based on the orientation field.

In this work, the local speed is determined based on the FODF. This is reflected by the Finsler metric $\mathcal{F}$ [11], which defines at each point $x\in {ℝ}^3$ a positive norm ${\mathcal{F}}_x(u_x)\equiv \mathcal{F}(x,u_x)>0$ whenever orientation $u_x\in {\mathbb{S}}^2$ is nonzero. The Finsler metric is more flexible than the Riemannian metric and naturally provides the geometric generalization suitable for analysis of more complex fiber configurations, such as crossings [11]. Given a Lipschitz regular path $\gamma (t)\in {ℝ}^3$ with boundary conditions $\gamma (0)=x_0$ and $\gamma (T)=x_T$, the length of the path ℓ(γ) can be measured as

$$\ell (\gamma )={\int }_0^T\mathcal{F}(\gamma (t),\dot{\gamma }(t))dt,$$ (1)

with the convention $\dot{\gamma }(t)≔\frac{d}{dt}\gamma (t)$. Let U(x) be the distance function starting from an arbitrary seed point $x_0\in {ℝ}^3$. U(x_T) is then the minimal value of (1) for a geodesic connecting x₀ and x_T. The distance function satisfies the eikonal equation

$$\nabla U^T{\mathcal{F}}^{-1}\nabla U=1\mathrm{s.t.}U(x_0)=0$$ (2)

where ∇U is the spatial gradient of U. Solving for U via (2) can be done effectively using the fast marching algorithm. The shortest path from x₀ to x_T can be determined by solving an ordinary differential equation (ODE):

$$\dot{\gamma }\propto {\mathcal{F}}^{-1}\nabla U.$$ (3)

Note that for implementation, the paths are lifted into the configuration space ${ℝ}^3\times {\mathbb{S}}^2$ of positions and orientations [12].

2.2. Penalized Finsler Metric

To ensure a well-behaving distance map that is continuous and smooth, we employ a penalized Finsler metric in the position-orientation space [10,12]:

$${\mathcal{F}}_{(x,u_x)}^2(\dot{x},{\dot{u}}_x)≔c{(x,u_x)}^2({\langle u_x,\dot{x}\rangle }_{+}^2+{\epsilon }^{-2}{\langle u_x,\dot{x}\rangle }_{-}^2+{\epsilon }^{-2}{\Vert u_x\times \dot{x}\Vert }^2+{\zeta }^2{\Vert {\dot{u}}_x\Vert }^2),$$ (4)

where $(x,u_x)\in {ℝ}^3\times {\mathbb{S}}^2$ is a position in the configuration space and $(\dot{x},{\dot{u}}_x)$ is a tangent vector at this position. Note that $\langle u_x,{\dot{u}}_x\rangle =0$ by construction since $u_x\in {\mathbb{S}}^2$. The parameter $\zeta >0$ balances the cost of motion in the position and angular spaces, in other words, the amount of curvature penalization. The term ${\epsilon }^{-2}{\Vert u_x\times \dot{x}\Vert }^2$ penalizes any position motion that is not colinear with the current orientation u, and forbids such motion in the limit as ε → 0. The negative part of their scalar product $\langle u_x,\dot{x}\rangle$ is penalized to forbid reverse motion. We define the local cost function at each position (x, u_x) based on the FODF field $\mathcal{V}$ as

$$c(x,u_x)={\left\{1+\delta \left|\frac{{\mathcal{V}}_{+}(x,u_x)}{{\Vert {\mathcal{V}}_{+}\Vert }_{\infty }}\right|\right\}}^{-1},$$ (5)

where δ > 0, ‖⋅‖_∞ the supremum norm and ${\mathcal{V}}_{+}(x,u_x)=\max \{0,\mathcal{V}(x,u_x)\}.$ Based on the penalized Finsler metric, the distance map U can be computed by solving the eikonal Eq. (2) using Hamilton fast marching with adaptive stencils [13].

2.3. Tractography with Optimized Shortest Path

Given the distance map U, PGT determines a shortest path connecting a seed position to a region of interest (ROI) with curvature penalization. We define the curvature-penalized cost of a path γ(t) as

$$\psi (\gamma )={\int }_0^T\mathcal{F}(\gamma (t),\dot{\gamma }(t))\mathcal{C}(\Vert \ddot{\gamma }(t)\Vert )dt,$$ (6)

where $\mathcal{C}(\Vert \ddot{\gamma }(t)\Vert )=\sqrt{1+{(\zeta \Vert \ddot{\gamma }(t)\Vert )}^2}$ is the Reeds-Shepp cost with a typical radius of curvature ζ [12]. Given the seeds $x_0\in {ℝ}^3$, target region $x_T\in {ℝ}^3$, and tangents $u_{x_0},u_{x_T}\in {\mathbb{S}}^2,$ PGT aims to find the path $\gamma :[0,T]\to \mathcal{W}\subset {ℝ}^3\times {\mathbb{S}}^2$ obeying the boundary conditions and globally minimizing the cost ψ(γ) by solving

$$\underset{\gamma }{\min }\psi (\gamma )\mathrm{s.t.}\{\begin{array}{c}\hfill \gamma :[0,T]\to \mathcal{W},\forall t,\Vert \dot{\gamma }(t)\Vert =1,\hfill \\ \hfill \gamma (0)=x_0,\gamma (T)=x_T,\dot{\gamma }(0)=u_{x_0},\dot{\gamma }(T)=u_{x_T}.\hfill \end{array}$$ (7)

The shortest path can be determined (7) with the following equations:

$$\dot{\gamma }(t)=L(t-1){\mathcal{F}}_{\gamma (t)}^{-1}dU(\gamma (t))\text{with}\{\begin{array}{c}\hfill {\dot{u}}_x(t)=L(t-1)c{(\gamma (t))}^{-1}{\nabla }_{{\mathbb{S}}^2}U(\gamma (t))\hfill \\ \hfill \dot{x}(t)=L(t-1)c{(\gamma (t))}^{-1}{D}_{u_x(t)}{\nabla }_{{ℝ}^3}U(\gamma (t))\hfill \\ \hfill \gamma (0)=x_0,\gamma (T)=x_T\hfill \\ \hfill \dot{\gamma }(0)=u_{x_0},\dot{\gamma }(T)=u_{x_T}\hfill \end{array}$$ (8)

where L(t) is the length of the path at t, D_ux is the 3 × 3 symmetric positive definite matrix with eigenvalue 1 in the direction u_x, and eigenvalue ε² in the orthogonal directions. That is, D_ux ≔ u_x ⊗ u_x + ε²(3I − u_x ⊗ u_x) [10]. Solving for the optimal path can be done effectively using the forward Euler integration of the partial differential equations in (8).

2.4. Datasets and Processing

A DMRI dataset (Subject ID: 105923) from the Human Connectome Project (HCP) [14] was used to validate our method. The dataset has an isotropic spatial resolution of 1.25 mm, with three b-values (b = 1000, 2000, 3000 s/mm²), a total of 270 gradient directions (90 per shell), and 18 non-diffusion-weighted images. Cortical and sub-cortical parcellation was performed on the T1-weighted image using FreeSurfer. The cortical GM map generated by FSL using the T1-weighted MR image was used to define tractography seed voxels. The FODFs were estimated using multi-tissue spherical deconvolution (MTSD) [15]. We employed the WM FODFs to compute the local costs in (5). Qualitative and quantitative comparisons were performed with respect to three algorithms in MRtrix3 [16], i.e., iFOD1 [16], iFOD2 [17], and a SD-based deterministic (DET) [16], with default parameters. 50 million streamlines were generated with each of the three methods. For PGT, 3 seed points were randomly selected for each GM voxel.

3. Results

Table 1 shows the quantitative results for iFOD1, iFOD2, DET, and PGT. Here, a streamline is said to be valid when its endpoint is within a radius of 2 mm from a cortical GM voxel. PGT yields significantly more streamlines that reach the cortical regions with a much smaller rate of prematurely terminated streamlines.

Table 1.

Fiber statistics for the various tractography approaches.

	Subcortical-cortical			Whole brain
	Initial	Valid	%	Initial	Valid	%
DET	1M	703709	70.37%	50M	36772925	73.55%
iFOD1	1M	718306	71.83%	50M	41630557	83.26%
iFOD2	1M	676357	67.64%	50M	38935000	77.87%
PGT	953956	936923	98.21%	42335648	41624624	98.32%

To evaluate the uniformity of the spatial distribution of the streamline endpoints at the cortex, we computed the standard deviations of the fiber densities (count per volume) across voxels in different cortical regions. The results in Fig. 1 indicate that PGT yields much lower standard deviations than other methods. The same analysis was performed with only the valid streamlines. The results, shown in Fig. 2, indicate that the density variability increases significantly at both gyral and sulcal for DET, iFOD1, and iFOD2.

Fig. 1.

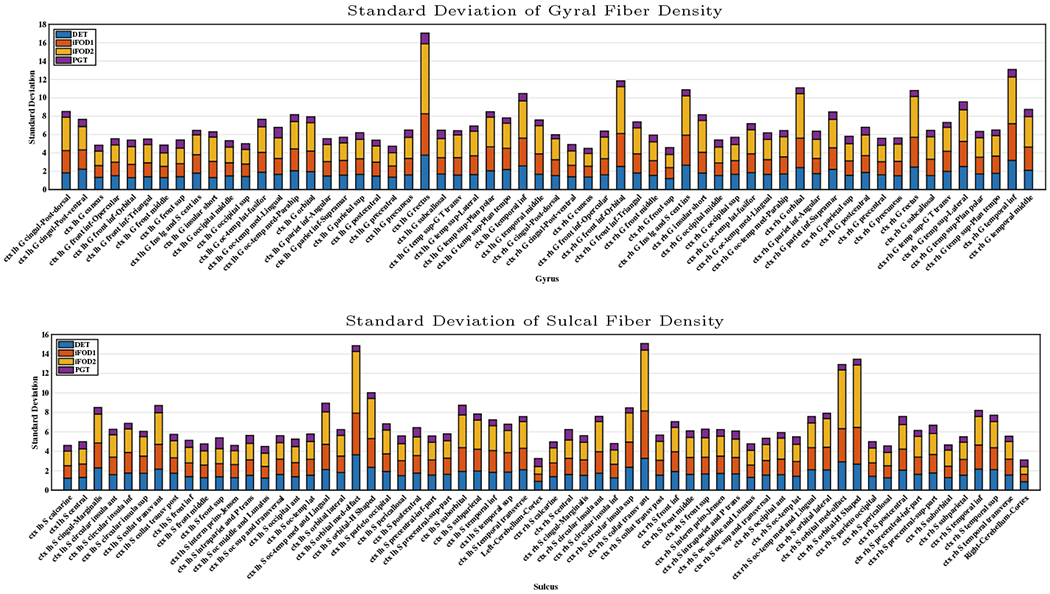
Standard deviations of fiber densities at WM-GM boundaries at gyri and sulci.

Fig. 2.

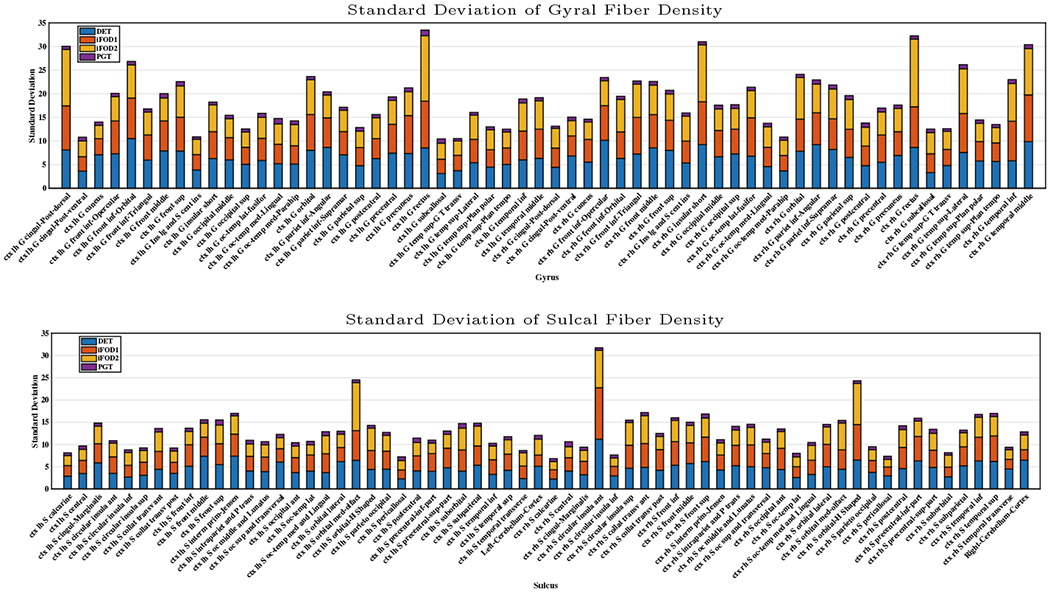
Standard deviations of fiber densities of valid streamlines at WM-GM boundaries at gyri and sulci.

Figure 3 shows a mapping of the endpoints of the streamlines onto the cortical surface, which confirms that PGT gives a fuller coverage of the cortex. Other methods are generally biased towards the gyral crowns.

Fig. 3.

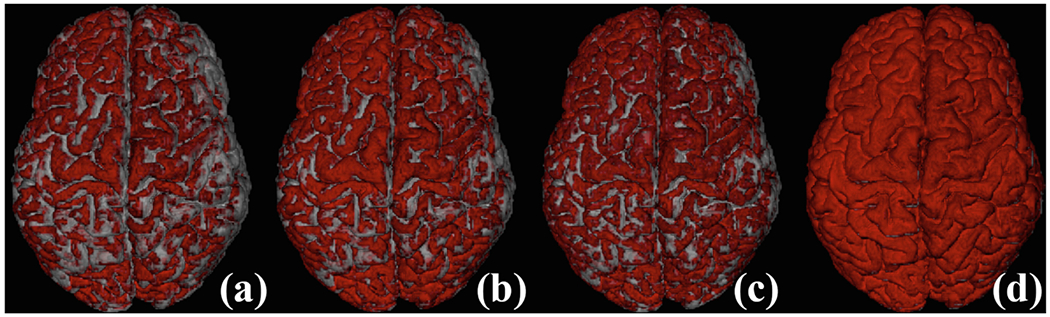
Coverage of streamline endpoints at WM-GM interface: (a) DET; (b) iFOD1; (c) iFOD2; (d) PGT.

We extracted the corticospinal tract (CST) using the white matter query language (WMQL) [18], which is based on FreeSurfer cortical parcellations. In WMQL, the CST streamlines are defined as those connecting the postcentral and precentral gyri and the brain stem. The results, shown in Fig. 4, indicate that PGT yields fiber streamlines that fully cover both postcentral and precentral gyri (orange arrows). PGT also reduces false-positive streamlines (white arrows).

Fig. 4.

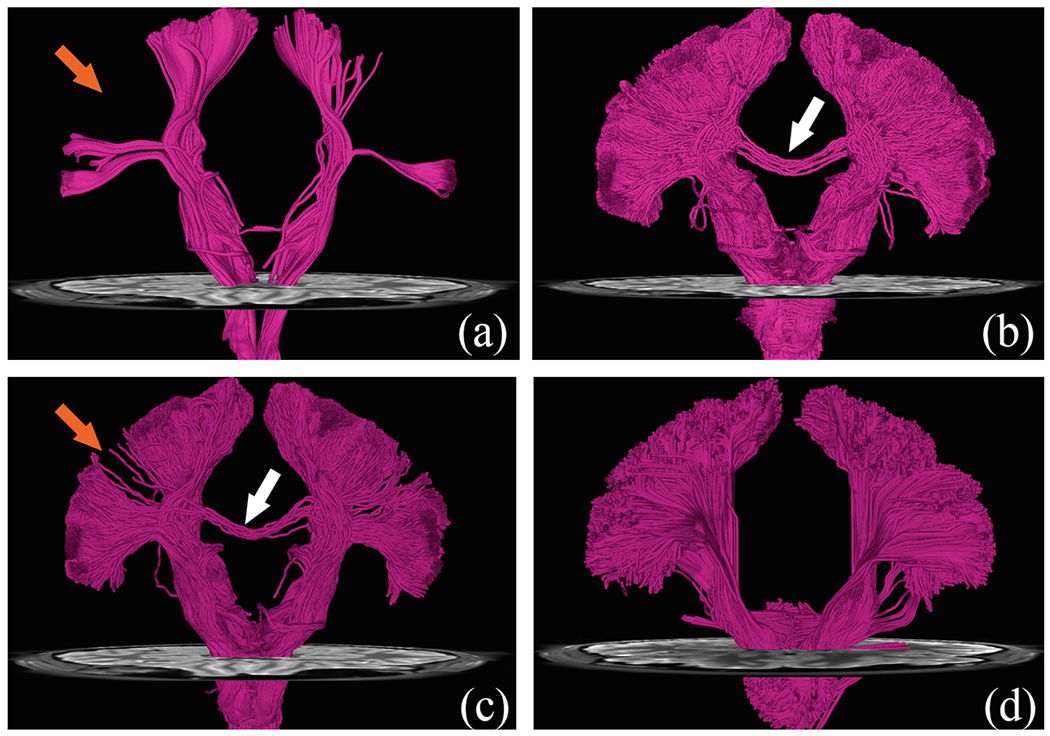
Cortiospinal Tract (CST): (a) DET; (b) iFOD1; (c) iFOD2; (d) PGT.

4. Conclusion

We have presented penalized geodesic tractography (PGT) for cortical tractography and have demonstrated that PGT can be used to overcome gyral bias. Our method extends the fast marching method by employing a penalized manifold metric that balances the costs in positions and orientations. We have shown with HCP data that PGT improves tract coverage of the cortex and results in a spatially uniform tract density distribution.