Global waves synchronize the brain’s functional systems with fluctuating arousal

Traveling waves spatiotemporally organize brain-wide activity in synchrony with ongoing arousal fluctuations.

Abstract

We propose and empirically support a parsimonious account of intrinsic, brain-wide spatiotemporal organization arising from traveling waves linked to arousal. We hypothesize that these waves are the predominant physiological process reflected in spontaneous functional magnetic resonance imaging (fMRI) signal fluctuations. The correlation structure (“functional connectivity”) of these fluctuations recapitulates the large-scale functional organization of the brain. However, a unifying physiological account of this structure has so far been lacking. Here, using fMRI in humans, we show that ongoing arousal fluctuations are associated with global waves of activity that slowly propagate in parallel throughout the neocortex, thalamus, striatum, and cerebellum. We show that these waves can parsimoniously account for many features of spontaneous fMRI signal fluctuations, including topographically organized functional connectivity. Last, we demonstrate similar, cortex-wide propagation of neural activity measured with electrocorticography in macaques. These findings suggest that traveling waves spatiotemporally pattern brain-wide excitability in relation to arousal.

INTRODUCTION

Organisms continuously regulate multiple physiologic variables. This regulation is supported by autonomic arousal fluctuations that coordinate body-wide physiology in relation to anticipated behavioral demands, e.g., cycling between “fight-or-flight” versus “rest-and-digest” modes (1). Accumulating evidence indicates that global brain function is also temporally structured in relation to these arousal fluctuations (2). Thus, in awake rodents, fluctuations in physiological (e.g., pupil size) and behavioral (e.g., locomotor activity) variables over tens of seconds are correlated with changes in global brain state, indexed by neural oscillations, incidence of sharp-wave ripples, or the extracellular environment (2–4). Recently, massively parallel neural recordings have demonstrated that these ongoing arousal fluctuations account for a substantial fraction of variability in single-unit firing rates throughout the brain (5, 6). These findings appeal to a broader literature implicating an endogenous, infra-slow (<~0.1 Hz) neuromodulatory process that temporally organizes brain-wide function in relation to arousal (7, 8).

A separate line of investigation has described the spatial organization of brain function. Thus, mammalian brains have been characterized in terms of multiple anatomically segregated functional systems [e.g., somatomotor, visual, and higher-order cognitive systems (9)]. These functional-anatomic systems are arranged along a continuous axis extending from unimodal (e.g., somatomotor and visual) to transmodal (higher-order) systems (10, 11). At the broadest scale, this axis separates the brain into two complementary “macro” systems: an “extrinsic” system that is more directly linked to the immediate sensory environment and an “intrinsic” system whose activity preferentially relates to changing higher-level, internal context (12, 13). It is unclear how this spatial organization relates to the infra-slow arousal regulation of brain-wide function.

Notably, the current understanding of spatially segregated function has been informed by spontaneous infra-slow fluctuations of the blood oxygen level–dependent (BOLD) functional magnetic resonance imaging (fMRI) signal (14, 15). These fluctuations are correlated within brain regions to an extent that reflects their functional relatedness [functional connectivity (FC)]. Thus, BOLD FC is widely used to hierarchically partition the brain into functional modules (“networks”) at multiple granularities [e.g., 2, 7, and 17 FC networks (16, 17)]. Apart from functional mapping, substantial evidence indicates that spontaneous BOLD signal fluctuations exhibit globally organized structure [e.g., (11, 18, 19)] and dynamics [e.g., (20–24)], with a multitude of behavioral and electrophysiological correlates [e.g., (25–27)]. However, to date, this expansive literature lacks a unifying physiological and phenomenological theoretical framework.

We propose that available behavioral, electrophysiological, and neuroimaging evidence is consistent with a model in which coordinated cortical and subcortical traveling waves spatiotemporally pattern brain-wide excitability in relation to infra-slow arousal fluctuations. This parsimonious account is motivated by mounting evidence of an endogenous physiological process underlying infra-slow fluctuations in electrophysiology and in the BOLD signal (28–30). Accordingly, this model constitutes a generative account of the canonical spatiotemporal features of spontaneous BOLD signal fluctuations, including the global organization of FC.

Four major predictions follow from this traveling wave model. First, BOLD signal fluctuations throughout the brain should be coherent with arousal fluctuations. Second, regional phase shifts of the BOLD signal, relative to physiological indices of arousal, should be organized according to FC network identity. Third, these phase shifts should systematically vary along the principal, unimodal-transmodal axis of FC (11). Fourth, similarly organized traveling waves should also be apparent in electrophysiological recordings. We provide novel support for each of these predictions, presenting converging evidence across multiple human fMRI datasets, multiple indices of arousal, and hemisphere-wide electrocorticography (ECoG) in macaque monkeys. We characterize several additional features of these waves that, together, offer a parsimonious account for many spatiotemporal features of spontaneous BOLD signal fluctuations, including large-scale FC structure. In sum, our results suggest that infra-slow arousal waves are a physiologically integrative process supporting an intrinsic spatiotemporal organization of brain-wide excitability.

Theory

Figure 1 illustrates our proposed framework, which casts infra-slow arousal fluctuations as a [quasiperiodic (31)] spatiotemporal cycle that endogenously regulates brain-wide physiology (Fig. 1A). Global brain states and behavior vary according to the phase of ongoing arousal fluctuations (2). Likewise, we hypothesize that different phases within a canonical arousal cycle are associated with different topographies of enhanced excitability. These different topographies should be organized according to the major functional systems of the brain (Fig. 1A), which systematically vary along the unimodal-transmodal axis in their relation to the immediate sensory environment (11). Accordingly, the proposed spatiotemporal process comprises large-scale, topographically organized patterns of excitability (involving coordinated metabolic and electrophysiological changes) that evolve over tens of seconds in parallel with arousal. We propose that this topographically organized modulation is the predominant physiological process that is reflected in spontaneous, spatially patterned fluctuations in the BOLD signal. For this reason, the proposed spatiotemporal arousal process, described below, also amounts to a generative mechanism underlying BOLD FC.

Fig. 1. Infra-slow arousal fluctuations as a global, spatiotemporal process.

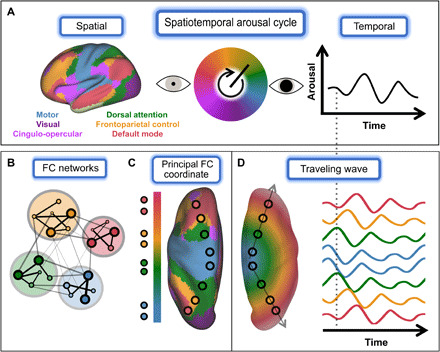
(A) We propose that infra-slow arousal fluctuations can be understood as a spatiotemporal cycle, within which different temporal phases correspond to different spatial patterns of enhanced excitability. These spatial patterns correspond to the major functional systems of the brain [left; (16)], such that activity within each system fluctuates over tens of seconds in accordance with arousal (right). (B to D) The proposed mechanism linking FC networks to global arousal fluctuations. (B) FC networks are often defined using tools from graph theory (15), where “edges” are defined by the strength of zero-lag correlation (FC) between the spontaneous BOLD fluctuations observed in any two regions. Brain regions (here, small circles) are assigned to modules (large circles) such that connections are stronger within rather than between modules. Module assignments [e.g., those shown in (A)] do not preserve global (i.e., intermodule) relationships. (C) Without enforcing modularity, FC is seen to evolve along a principal, cortex-wide “coordinate”; this principal FC coordinate corresponds to the unimodal-transmodal axis of brain functional organization (11). Canonical FC networks occupy characteristic positions along this continuous axis, as apparent from the dorsal view shown here. Notably, process does not enter to this picture of FC. (D) This continuous, gradient-like organization of FC can be parsimoniously explained by traveling waves. A global wave would introduce propagation delays that gradually increase with distance from the wave source. Thus, activity would be in-phase (i.e., strongly correlated at zero lag) between regions that are approximately equidistant from the source [compare with (C)]. The vertical dashed line highlights various in-phase and out-of-phase relationships between brain regions. Last, if this wave process is linked to arousal fluctuations, then different sets of regions (i.e., networks) will be preferentially active at different phases of arousal [(A), above].

An immediate question follows from our assertion that spontaneous BOLD signal fluctuations reflect, to a large extent, a global arousal process. Namely, how can a global process account for the classical picture of segregated FC networks? We hypothesize that this global arousal process is instantiated by topographically organized traveling waves. Traveling waves are a ubiquitous source of spatiotemporal organization in nature (32, 33). Figure 1 (B to D) illustrates how global wave propagation can account for spatially organized FC structure.

Figure 1B takes, as a starting point, the familiar representation of FC as discrete networks. FC networks are defined as sets of regions that share temporally coincident BOLD signal fluctuations, assessed by the strength of zero-lag correlation (i.e., FC) (15). Discrete networks are often obtained by first representing all pairwise FC relationships as a graph, with nodes corresponding to brain regions and edges corresponding to time-averaged correlations (15). This graph representation can then be subjected to clustering or community detection algorithms that assign brain regions to one of several modules (“FC networks”), such that edges are stronger within rather than between modules (Fig. 1B).

These modular descriptions of FC have proven useful for mapping large-scale functional systems [e.g., see canonical FC networks shown in Fig. 1 (A and B) (16)]. However, emphasis on identifying discrete FC networks obscures the global and spatially embedded nature of FC organization. Thus, canonical networks exhibit organized FC and anatomical positions in relation to one another (Fig. 1C) (11, 18). These aspects of FC are well captured by analyses that do not enforce modular descriptions (e.g., manifold learning). These analyses have described a principal, unimodal-to-transmodal axis of global FC organization [e.g., (11, 19, 34)] (Fig. 1C). From this perspective, canonical FC networks are understood as sets of regions that occupy characteristic positions along cortex-wide spatial gradients. Thus, the “principal functional gradient” [i.e., the first coordinate of a low-dimensional embedding of FC structure (11, 35)] maps gradual variation in FC to gradual changes over anatomical space. A dynamical process underlying this correspondence has not been proposed.

We suggest that this global, gradient-like picture of FC can be parsimoniously explained by traveling waves that propagate along the unimodal-transmodal axis (Fig. 1D). In this simple model, the FC between two regions (i.e., the degree to which their fluctuations are temporally coincident) will vary inversely with difference in propagation delay (arrival time) of the global wave at these regions. In turn, the difference in propagation delay between any two regions will reflect the difference in anatomical position of these two regions in relation to the wave source (22). Accordingly, wave propagation along the unimodal-transmodal axis (Fig. 1C) would instantiate a topographic spatial gradient of time delays [phase shifts (36)] (Fig. 1D) and, consequently, a spatial gradient in FC structure. Last, in this model, global waves are linked to neuromodulators that underlie arousal fluctuations (37). Consequently, global waves would temporally segregate functional systems within a canonical arousal cycle (effectively, propagation along the unimodal-transmodal axis spatiotemporally instantiates the canonical arousal cycle). In this way, a global, spatiotemporal process can parsimoniously link the spatial patterns described by FC and global arousal fluctuations.

The proposed model serves as a guiding framework for the novel results presented in the remainder of this paper. These results include empirical support for the following core predictions of the model: (i) BOLD signal fluctuations are globally coherent with arousal, (ii) phase shifts of the BOLD signal relative to arousal are network-dependent in cortical and subcortical structures, (iii) these phase shifts are ordered along unimodal-transmodal gradients, and (iv) these phase relations also manifest in electrophysiology. We describe additional properties of arousal waves that highlight their explanatory potential as a parsimonious, theoretically grounded, mechanistic account of many previously described features of resting-state fMRI time series. We anticipate that future studies will more systematically examine various properties of these waves and their relation to an expansive resting-state fMRI literature.

RESULTS

BOLD fluctuations exhibit brain-wide coherence with arousal

Our model predicts that spontaneous BOLD signal fluctuations should be coherent with physiological indices of arousal throughout the brain. This hypothesis concerns spontaneous BOLD fluctuations in general; it is not a hypothesis concerning specific brain regions that we believe to regulate arousal. We examined coherence between BOLD signals and autonomic activity in a large dataset comprising simultaneously collected resting-state fMRI and physiological data [the Human Connectome Project (HCP) (38)]. First, we examined BOLD signal fluctuations averaged within canonical large-scale networks (Fig. 2A). Consistent with our predictions, spectral analysis revealed strong, broadband coherence of BOLD signal fluctuations with infra-slow fluctuations in respiratory volume [respiratory variation (RV)] present across cortical networks (Fig. 2B). Notably, RV coherence exhibited a broad peak centered on ~0.025 Hz, consistent with prior reports of a biphasic cross-correlation between arousal measures and spontaneous BOLD signal fluctuations [e.g., (39)]. This coherence peak at 0.025 Hz was not observed in relation to the global BOLD signal (fig. S1), implying that it is specific to the relation between BOLD signals and arousal [and is not a consequence of inability to resolve very-low-frequency peaks in BOLD fMRI runs of finite duration (15 min)]. Thus, the low-frequency coherence peak is consistent with an intrinsically rhythmic, autonomic-related infra-slow process (7, 8, 40, 41).

Fig. 2. Global and topographically organized coherence with fluctuating arousal.

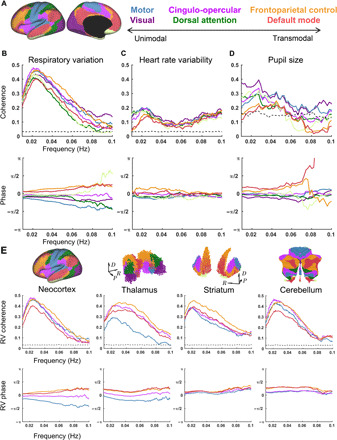
(A) Functional organization of brain structures as previously estimated from FC (seven-network parcellation) (16). (B) Group-average coherence magnitude (top) and phase (bottom) of cortical network–averaged signals in relation to RV. RV was computed as the temporal SD of respiratory belt data over 6-s sliding windows. Cross-spectra were averaged across a large sample (N = 190 individuals). The displayed phase spectra are shifted to remove a constant (frequency independent) ~−7-s lag (BOLD preceding RV). Note substantial phase shifts over a broad frequency range. (C) Same as in (B), but for heart rate variability (HRV), measured as the (inverse) mean beat-to-beat interval derived from pulse oximetry within 6-s sliding windows. Data obtained from the same N = 190 individual sample as in (A). Note that weaker HRV coherence is likely related to technical factors (see Materials and Methods); BOLD:HRV coherence is similar in magnitude to RV:HRV coherence (fig. S1E). (D) Same as in (B) but for pupil size. Data were acquired in an independent sample (N = 20) (42). (E) Same as in (B) but for four major networks in the neocortex, thalamus, striatum, and cerebellum. FC network parcellations obtained from prior studies (16, 98–100). Black dashed lines in coherence plots indicate 99th percentile of the null distribution computed from 500 random shuffles. Direction labels indicate dorsal (D), posterior (P), and anatomical rightward (R). Three-dimensional (3D) maps of subcortical structures were generated from MNI152 voxel coordinates. A flatmap representation is shown for the cerebellum [following (34)].

Next, we examined the phase of coherence across networks. Inspection of RV phase spectra confirmed a topographic organization of coherence phase: Throughout the canonical infra-slow frequency range (0.01 to 0.1 Hz), functional networks maintained substantial phase shifts relative to one another in their relation to RV. Notably, this result indicates that phase relations among networks, rather than time delays, are preserved across infra-slow frequencies (note S1). Network phase shifts generally progressed from unimodal cortex [“motor” (includes primary somatomotor, somatosensory, and auditory cortices (16)) and “visual” networks] to transmodal (e.g., “frontoparietal control” and “default mode” networks). Similar patterns were observed in relation to two other measures of autonomic activity: heart rate variability (HRV) (Fig. 2C) and, in an independent dataset (42), pupil size (Fig. 2D) (37). Thus, the temporal structure of spontaneous BOLD fluctuations appears to reflect an association with general physiological arousal.

Last, we asked whether phase relationships with arousal measures are similarly mirrored in subcortical structures. Of the physiological measures, cortical coherence was strongest with RV; accordingly, subsequent analyses focused on this measure. We found that the thalamus, striatum, and cerebellum each exhibit strong coherence with RV (Fig. 2E). Phase spectra in these structures also indicated appreciable phase shifts over a broad frequency range that topographically parallel neocortex. Thus, BOLD time series are globally coherent with fluctuating arousal but phase-shifted in a consistent order according to network identity.

Global waves recapitulate FC structure

We next sought to test our hypothesis that BOLD signal phase shifts, relative to arousal, are spatially organized as traveling waves. To investigate this possibility, we obtained regional phase shifts of BOLD fluctuations relative to RV using Hilbert transform analysis within the frequency range of strongest coherence (0.01 < f < 0.05 Hz) (Fig. 3A). This procedure allows us to infer traveling waves from time-averaged phase relationships in spontaneous activity, relative to RV, rather than from the delay times of evoked responses. The RV phase map revealed parallel, coordinated unimodal-to-transmodal waves within the cerebral cortex, thalamus, striatum, and cerebellum (Fig. 3B).

Fig. 3. Arousal-related global waves closely relate to large-scale FC structure.

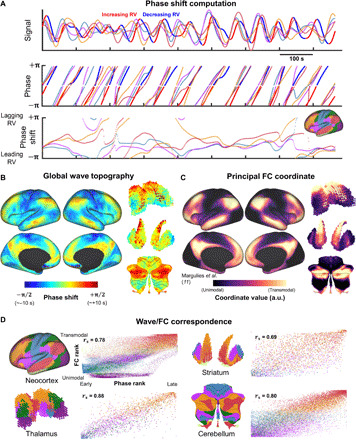
(A) Phase shift analysis for a representative time epoch from a single individual. Top: RV (color-coded red and blue according to phase) and multiple network-averaged BOLD time series (color-coded by networks shown in Fig. 2A) after filtering between 0.01 and 0.05 Hz. Middle: These time series were Hilbert transformed to extract instantaneous phase values. The RV minus BOLD phase differences (modulo 2π) are shown in the bottom part of (A). Bottom: Time series of instantaneous phase shifts of network-averaged signals relative to RV. (B) Time- (and individual-) averaged maps of instantaneous phase shifts relative to RV (zero-centered). The equivalence between a phase shift of π/2 and a time delay of ~10 s reflects that this analysis was conducted on narrowband signals centered at ~0.025 Hz. (C) Principal neocortical, cortico-striatal, cortico-thalamic, and cortico-cerebellar FC diffusion coordinates (35) (principal functional gradients). Principal coordinate in cerebral cortex was obtained from (11). Coordinates in the thalamus, striatum, and cerebellum were computed de novo (see the “Diffusion maps” section in Materials and Methods). The unimodal-transmodal gradient is reflected in the gradual increase in coordinate values progressing from primary sensorimotor regions (black) to higher-order association regions (yellow). a.u., arbitrary units. (D) Correspondence between maps shown in (B) and (C). Voxels sorted by FC coordinate rank (vertically) and phase rank (horizontally) and color-coded according to FC network identity. Color codes are shown in Fig. 2A. r_s denotes the Spearman’s rank correlation coefficient.

The phase shifts shown in Fig. 3B indicate propagation delays on the order of several seconds (see Fig. 3B caption). These long delays are consistent with our model in which slowly propagating waves can account for features of BOLD FC measured at zero lag. More specifically, we hypothesized that propagating waves can account for the gradient-like structure of FC (Fig. 1C). Accordingly, we assessed the spatial correspondence between the RV phase map (Fig. 3B) and the principal FC coordinate described by Margulies et al. (11) (Fig. 3C).

We confirmed that cortical RV phase map is strongly correlated with the principal FC coordinate in the neocortex (spatial Spearman’s rho = 0.78) (Fig. 3D). Our model further predicts topographically consistent wave propagation in the thalamus, striatum, and cerebellum. To investigate this possibility, we computed the principal FC coordinate within the thalamus, striatum, and cerebellum based on their FC with the neocortex. Principal FC coordinates were obtained via diffusion map embedding (35), as in (11) (see the “Diffusion maps” section in Materials and Methods). In each structure, we found strong spatial correlation between the principal FC coordinate and the RV phase map (Fig. 3C) [Spearman’s rho = 0.88, 0.69, and 0.80 in the thalamus, striatum, and cerebellum, respectively; P < 0.01 in each structure following correction (see Materials and Methods)].

Brain-wide propagation dynamics

The preceding results suggest that global arousal waves can account for the principal organizational feature of FC; namely, the unimodal-transmodal axis of FC organization (11). However, traditionally, FC structure has been understood in terms of discrete, hierarchically nested networks with (proportionately) sharp boundaries (16, 43). Thus, FC most strongly distinguishes between two major, distributed functional brain systems (12, 17): an extrinsic system comprising sensorimotor and “task-positive” (44) regions and an intrinsic system comprising the default mode network (“task-negative”) and frontoparietal regions that preferentially respond to changing task conditions (45). How might global waves account for this feature?

To answer this question, we sought to visualize wave propagation across a canonical arousal cycle. Thus, rather than obtaining an average RV phase value for each voxel (as in Fig. 3B), we computed an average spatial map of the BOLD signal at each RV phase (discretized into 40 phase bins). The resulting sequence of maps describes the evolution of voxelwise BOLD signals in relation to RV phase. These maps reveal a succession of spatially distributed motifs resembling canonical FC networks (Fig. 4, A and B, and movie S1). As suggested by voxelwise maps of average phase (Fig. 3B), FC network motifs are embedded in waves that propagate from somatomotor and higher-order visual cortices (note S2) toward transmodal, association cortex. In parallel, unimodal → transmodal propagation occurs within the thalamus, striatum, and cerebellum. In line with previous observations, global waves begin with suppression of activity in the midline thalamus arousal center (46, 47). Hippocampal and brainstem activity similarly exhibit organized activity patterns that are time-locked to these waves (fig. S3 and movie S2).

Fig. 4. Visualizing propagation dynamics.

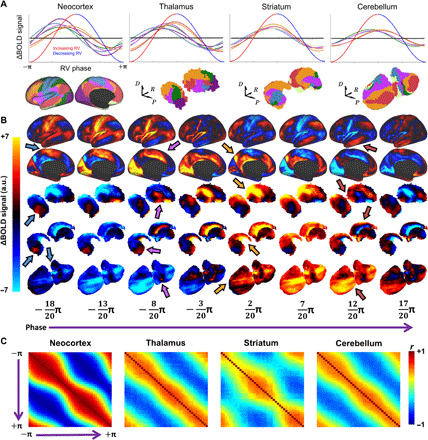
(A) Mean FC network BOLD signals averaged (across time and individuals) within each of 40 equally spaced RV phase bins and subsequently plotted as a canonical RV cycle (see Fig. 3A). Black lines at the center of each plot indicate 99th percentile values from null distribution (500 random shuffles of physiological and BOLD time series across individuals). Color-coded network topographies are shown below. Increasing and decreasing RV broadly correspond to sympathetic and parasympathetic activity, respectively (although note that interpretation of BOLD versus RV timing may not be straightforward). (B) Group-averaged BOLD signal maps shown for 8 (of 40) evenly spaced phase bins across the canonical RV cycle. This illustrates the temporal evolution (“animation”) of the BOLD signal topography over a canonical arousal cycle. Each column displays the average BOLD signal topography at a particular arousal phase. To enhance spatial specificity (for visualization only), the global mean time course across all phase bins was subtracted from the time course at each voxel. Thus, for a given phase, (B) illustrates how each voxel differs from the brain-wide mean BOLD value at that phase. Color-coded arrows highlight canonical FC network topographies (motor, cingulo-opercular, frontoparietal control, and default mode) appearing simultaneously across the cerebral cortex, thalamus, striatum, and cerebellum. (C) Frame-by-frame spatial correlation matrices computed from (B). Each element in these matrices represents the spatial correlation of BOLD maps at two different phase bins. Thus, these matrices represent spatial correlations between temporal units (in contrast to conventional FC matrices, which represent temporal correlations between spatial units). Matrices indicate relatively smooth progression (i.e., strong correlations surrounding diagonals) between anticorrelated topographies (blue off-diagonal regions). However, the narrowing of the diagonal near the middle of this matrix (where phase = ~0), particularly in the neocortex, indicates that most time is spent with one of the two anticorrelated topographies. Positive correlation in corners reflects intrinsic periodicity (20) [data in (C) were unfiltered beyond a gentle 0.0005-Hz temporal high-pass filter (97)].

Figure 4C illustrates propagation between the abovementioned intrinsic and extrinsic brain systems. This propagation between complementary topographies occurs in both cortical and subcortical structures, with an intrinsic periodicity of ~40 s (20). Notably, the BOLD signal topography changes relatively rapidly during the transition between the extrinsic and intrinsic systems (Fig. 4C and movie S2). This observation is consistent with prior accounts of the extrinsic and intrinsic systems as two temporal “metastates” (20, 23), such that activity gradually increases in one state before rapidly switching to the other (42).

Transitions between the extrinsic and intrinsic topographies appear to involve multiple coordinated, rotating waves within cortex and subcortex (Fig. 4B and movies S1 and S2), which are less apparent from the RV phase map shown in Fig. 3B. We characterized these complex propagation features in two ways. First, we applied optical flow analysis to the cortical dynamics shown in Fig. 4B (i.e., the canonical RV cycle) (Horn-Schunck algorithm; see Materials and Methods). The resulting flow fields revealed vortex- or spiral-like propagation in several locations (Fig. 5A). For example, on the lateral surface, propagation from motor cortex broadly follows a clockwise trajectory—sequentially passing through insula, inferior frontal regions, and dorsolateral prefrontal cortex—before propagating back toward motor cortex (Fig. 5A). Thus, a transmodal → unimodal propagation pattern completes the spatiotemporal cycle.

Fig. 5. Wave decomposition.

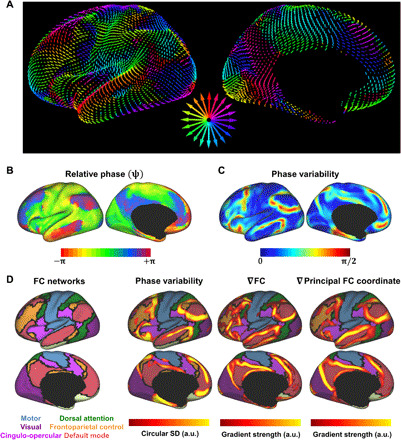
(A) Flow fields computed from (Fig. 4B) using optical flow analysis (see Materials and Methods). Arrow magnitude and orientation indicate the local velocity and direction of propagation within 3D Euclidean space. To facilitate visualization, arrows are color-coded according to direction within the 2D plane of the page based on color wheel at center. See also movies S1 and S2. (B) Phase mapping of movie shown in Fig. 4B. ψ illustrates the rotating nature of the propagation dynamics (effectively, curl of the vector field; divergence shown in fig. S6). Phase maps were referenced to a common region; hence, exact phase value in this map is arbitrary. Note pinwheel-like structures where many phases come together in close proximity (e.g., anterior insula, premotor cortex, and angular gyrus). (C) Local phase variability of the map shown in (B). Phase variability is computed as the (circular) SD (standard deviation) of phase values within a 10-mm radius of each vertex. (D) Regions with high phase variability (C) overlap regions where FC exhibits abrupt changes, particularly at the boundary dividing the extrinsic and intrinsic systems. From left to right: Canonical FC networks (16); thresholded version of map shown in (C); spatial gradient of the FC similarity matrix (43); and spatial gradient of the principal FC diffusion coordinate (shown in Fig. 3C) (11). ∇ is the differential operator indicating gradient computation.

To further characterize rotation, we represented the “movie” in Fig. 4B as a new phase function, ψ(r,t), where r indexes voxels and t indexes time points (i.e., RV phase bins). ψ, defined via Hilbert transform (see Materials and Methods), represents each frame of the RV movie as a spatial map of instantaneous phase shifts (48). After referencing each frame of ψ to a common region (the visual network), the (circular) mean of ψ across movie frames (Fig. 5B) captures the dynamics of brain regions in relation to one another (thus, “relative phase”) within a canonical RV cycle, rather than peak times in relation to RV. Figure 5B reveals, embedded within the globally coherent wave process, many sharp phase boundaries. Notably, these include several apparent phase singularities [i.e., centers of pinwheel-like structures, at which all phases come arbitrarily close together (32)], e.g., in the anterior insula, premotor cortex, and angular gyrus [effectively, Fig. 5B represents the curl of the flow field (48); divergence of the flow field identifies sources in several nearby, attention-related regions (fig. S6)].

If phase within this global wave cycle determines FC structure (as in the proposed framework), phase should be most variable at locations where FC is also most variable. By computing local variability of ψ (i.e., circular SD within a 10-mm radius; see Materials and Methods), greatest phase variability is observed at the boundary separating the extrinsic and intrinsic systems (Fig. 5B). Thus, similar to FC, phase within the global wave cycle is most variable at the boundaries circumscribing the default mode (red) and frontoparietal control (yellow) FC networks (Fig. 5D). The principal FC coordinate also changes abruptly at these boundary regions (Fig. 5D) (11). Accordingly, the globally coherent wave process, as well as the unimodal-transmodal coordinate of FC, preserves the sharp distinction between the extrinsic and intrinsic systems.

Global waves in macaque ECoG

The preceding analyses link topographically organized BOLD signal fluctuations to global arousal fluctuations indexed by RV, HRV, and pupil size. Similar results are also obtained in relation to spontaneous head movements, which are intimately linked to arousal (see Supplementary Text and fig. S5). The interpretation of BOLD signal fluctuations linked to these indices is a matter of ongoing debate [e.g., (39, 49–51); see Discussion]. However, our model posits that propagating BOLD signal fluctuations observed with fMRI are physiologically coupled to electrophysiological waves reflecting neuronal activity. Accordingly, the question now emerges as to whether the results obtained on the basis of BOLD fMRI signals can also be demonstrated with infra-slow electrophysiology.

The power envelope of broadband “gamma” (40 to 100 Hz) local field potentials is a reliable correlate of the BOLD signal [e.g., (52, 53)]. Gamma band-limited power (BLP) exhibits spontaneous, infra-slow fluctuations that are closely coupled to infra-slow electrical potentials (<0.1 Hz) (which are not typically recorded in conventional electrophysiology) (28). These power fluctuations mirror the long-distance coordination characteristic of BOLD FC [e.g., (54) and references therein]. Thus, our model predicts that the FC topographies of gamma BLP are embedded within globally propagating arousal waves.

A series of studies in macaque monkeys have defined an electrophysiological index of arousal transitions, involving cortex-wide fluctuations in gamma BLP recorded with ECoG (55). These gamma BLP fluctuations occur as part of a stereotypical temporal sequence of changes to >1-Hz cortical spectral content, termed sequential spectral transitions (SSTs) and are closely linked to global fluctuations observed with fMRI [reviewed in (56)]. Together, SSTs emerge as a likely electrophysiological correlate of infra-slow arousal waves. Accordingly, although SSTs are currently understood to be globally synchronous events, we hypothesized that the gamma component of SSTs should manifest as a traveling wave.

Testing this hypothesis requires large-scale electrophysiological recordings of sufficient spatial resolution and coverage. Accordingly, we examined spontaneous cortical activity measured from hemisphere-wide ECoG arrays in two highly sampled macaques (57). We identified SST events using previously described criteria (55). Averaging over SST events (N = 1145 events total; monkey 1, N = 656; monkey 2, N = 489), we found that fluctuations in gamma BLP propagate as traveling waves across macaque neocortex (Fig. 6, A to C). Propagation dynamics strongly resembled results obtained by analysis of human fMRI data, specifically, propagation from sensorimotor regions to distributed association regions in frontal, parietal, and temporal cortices (Fig. 6D and movies S3 and S4).

Fig. 6. Electrophysiological arousal transients propagate as global waves across macaque neocortex.

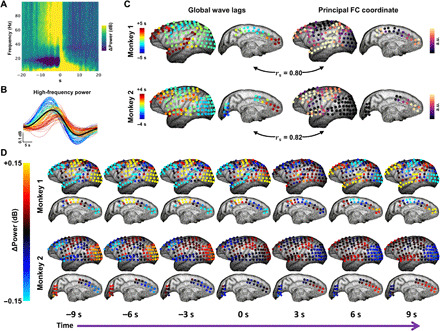
(A) Spectrogram depicting a sequential spectral transition (SST) event (55) averaged over hemisphere-wide electrodes (128) in two macaque monkeys across several awake recording sessions (N = 1145 events in total). SSTs comprise a stereotypical sequence of changes in power within multiple frequency bands. (B) The high-frequency portion of the mean SST spectrogram (gamma; 40 to 100 Hz), plotted as a separate time series for each electrode in one monkey. Time series (color-coded by mean latency) reveal a range of time delays. (C) Left: Lag maps of global high-frequency power during SST events, derived from cross-correlation, follow gradients that indicating large-scale traveling waves. In each monkey, this propagation delay map strongly correlates with the principal functional gradient obtained from diffusion embedding of the FC matrix computed across all electrodes (similar to Fig. 3C). r_s denotes the Spearman’s rank correlation coefficient. (D) Spatiotemporal evolution of high-frequency power during SST events in two monkeys. Global mean time course subtracted from (D) for visualization only (as in Fig. 4B). As in human fMRI, activity propagates over several seconds from sensorimotor regions to association areas in frontal, parietal, and temporal cortices. See also movies S3 and S4.

Similar to fMRI results in humans, we examined the correspondence of propagation patterns to the principal diffusion coordinate of the FC matrix in each monkey. We found that principal FC coordinates obtained from gamma BLP (Fig. 6C) varied from unimodal to transmodal cortex. Thus, the principal FC coordinate obtained with macaque electrophysiology was homologous to the principal, fMRI-derived functional gradient in humans (Fig. 3C) and corresponded well with previous descriptions of structural and FC gradients across macaque neocortex (11, 58). As in the human fMRI data, we observed strong correlation between propagation delays and functional gradients in both monkeys (Fig. 6C). These results demonstrate an electrophysiological basis for slowly propagating waves that spatiotemporally pattern high-frequency neuronal dynamics in relation to arousal.

DISCUSSION

Here, we have proposed an intrinsic, infra-slow physiological process that spatiotemporally patterns brain-wide excitability in relation to arousal. We have empirically confirmed the central prediction of this model: topographically organized traveling waves that slowly propagate in cortical and subcortical structures in synchrony with arousal fluctuations. We suggest that these waves are the predominant, intrinsic physiological process reflected in spontaneous BOLD signal fluctuations. Accordingly, infra-slow arousal waves constitute a generative mechanism of FC and spatiotemporal structure as assessed with resting-state fMRI.

A key feature of these waves is that they link together, within a unifying physiological framework, many previously described features of resting-state fMRI time series. Thus, arousal waves relate to and may provide a parsimonious account of large-scale FC structure (11, 17), anticorrelated systems (12, 17, 44), quasiperiodic patterns (20, 59), and BOLD temporal sequences described at multiple time scales (21, 23, 36), SSTs (55, 56), “transition zones” in the neocortex (discussed below) (60, 61), as well as the BOLD correlates of head motion: global and temporally extended signal changes and distance-dependent FC changes (49). To be clear, many of these features reflect properties of large-scale functional anatomy (e.g., functional systems, structural connectivity, and spatial embedding). Waves offer a mechanistic account of how this functional anatomy manifests in BOLD spatiotemporal structure (e.g., zero-lag FC). [Note that FC is sometimes assessed via coherence (i.e., not necessarily zero lag), particularly in electrophysiology [e.g., (62)]. The present paper uses “FC” interchangeably with “zero-lag correlation,” which is the primary measure of interest in resting-state fMRI research (15)].

Phase singularities may link together several additional themes in the literature. Singularities lie at the boundary of the extrinsic and intrinsic systems [a similar observation was recently described in mouse cortex (63)]. Regions proximal to this boundary have been implicated in diverse contexts relating to integration [e.g., (61, 64); see (65) for further discussion and results in individuals]. Attention and salience-related regions (66, 67) may drive rotation about these singularities (fig. S6): Recent studies indicate that the structural connectome intrinsically biases propagation to occur along the unimodal-transmodal axis (68), whereas attention-related regions are well positioned to flexibly reroute propagation along this axis (69). These regions may have the ability to interrupt (effectively, phase reset) an ongoing infra-slow arousal cycle (31, 70). Notably, this potential for phase resetting suggests one way in which global waves may substantially contribute to observed task-evoked brain responses (71).

Regardless of their functional interpretation, phase singularities provide a parsimonious account for multiple FC-related observations. Thus, if FC network assignments are determined by phase shifts in relation to global waves, then the phase singularities of these waves, where all phases converge, should correspond to regions where many networks appear to converge. Relatedly, regions lacking a well-defined phase shift should also lack a reliable FC network affiliation, even in individuals. These interpretations appear consistent with published results (12, 17, 61, 72) [for results in individuals, see (65) and figures S10 to S11 in (73)]. Last, because regions of poorly defined phase lie at the junction between two anticorrelated systems, interindividual variability in the precise location of these points [likely determined by gyral patterns (32, 74)] is expected to yield highly variable FC patterns across individuals. Consistent with this prediction, interindividual variability in FC is maximal at the boundary between the extrinsic and intrinsic systems (75, 76). This adds nuance to the notion that phylogenetically recent transmodal regions exhibit greatest interindividual FC variability (77). Notably, boundary regions also hold greatest explanatory value in studies relating interindividual variability in FC to interindividual variability in behavioral measures (77) or task-evoked BOLD responses (60).

The second-order statistics of BOLD signal fluctuations (e.g., correlation structure and spectral content) index arousal on a time scale of minutes (referred to here as “vigilance,” to avoid confusion) (78). These slower changes are consistent with increasing magnitude of spontaneous waves during lower vigilance states. Thus, reduced vigilance is marked by increased BOLD signal amplitude and FC within sensorimotor cortex (consistent with dispersive propagation beginning in these locations), increased “global signal” amplitude, and decreasing anticorrelations between the default mode network and attention systems [reviewed previously in (56, 78, 79)]. These slower fluctuations in vigilance have emerged as an important explanatory factor for time-varying FC, as well as its behavioral and electrophysiological correlates (56). We suggest that these results are consistent with relative suppression of spontaneous waves during higher-vigilance states, recapitulating the widely observed negative relationship between spontaneous and task-evoked brain activity [e.g., (80, 81)]. Nonetheless, we expect that the persistence of these waves during task states is likely to account for a substantial fraction of variability observed in task-evoked brain responses and behavioral performance (2, 28, 82).

The full explanatory potential of this framework, as well as the extent to which additional intrinsic physiological processes need to be invoked, remains to be determined. The present study focuses on a dominant global wave pattern and its association with arousal. Resting-state BOLD signal fluctuations also include contributions from other wave patterns with state-dependent probability (30, 83), and other mechanisms may contribute to more fine-scale FC structure (84). These mechanisms include experimentally unconstrained evoked activity (i.e., not an intrinsic physiological process). Nonetheless, we note that the spatiotemporal dependencies inherent to traveling waves pose a widely recognized challenge to spatiotemporal decomposition. Conventional decomposition techniques, which typically assume spatial and/or temporal independence, can be expected to assign different features of these waves to statistically (but not phenomenologically) independent components, thereby inflating the estimated dimensionality (and, correspondingly, underestimating the amount of variance attributable to the propagating wave) (85, 86).

Implications for BOLD imaging

The BOLD signal reports local changes in blood oxygenation. These changes are tightly linked to millisecond-scale neuronal activity through a complex neurovascular cascade. However, many biochemical agents (e.g., blood gases) can influence cerebral hemodynamics outside this classical cascade. As these factors all are regulated to some extent by autonomic activity, the BOLD correlates of autonomic fluctuations are generally regarded as nuisance variables, particularly in the context of functional brain mapping. In contrast, our proposed framework follows from accumulating, multimodal evidence demonstrating that systemic physiological processes are fundamentally linked to infra-slow neural activity (6, 8, 87). This evidence has emerged against a backdrop of empirical and theoretical support for the centrality of autonomic processes to global brain function [e.g., (88) and references therein; see (89) for historical overview of arousal, behavior, and the brain]. These results warrant a more nuanced view of physiological variables in fMRI.

The coordination of neural, metabolic, and systemic physiology underlies the success of BOLD-based imaging in the study of human brain function. It is unsurprising, then, that infra-slow neurophysiology is intimately related to each of these factors. The relevant biology is wide-ranging and likely includes many metabolic and nonneuronal process that slowly modulate neuronal excitability [see (8, 28) and references therein]. Although reference limits preclude proper treatment of this literature, we note likely essential roles for redox metabolism (90, 91), ion fluxes (3, 92), and glial physiology [including upstream of the neurovascular cascade (4, 93)]. These interrelated factors are each influenced by neuromodulators that track behavioral state over infra-slow time scales (4, 37, 94). More generally, our work builds upon substantial evidence implicating infra-slow oscillations in the autonomic-related coupling of brain and body [reviewed in (87, 95)].

This extent of integrative physiology raises practical and, more importantly, theoretical challenges for distinguishing “neuronal” versus “nonneuronal” sources of BOLD signal fluctuations. Global waves are inherently associated with physiological variables and head movements, yet are likely to significantly contribute to the spatiotemporal features of interest in BOLD time series, and are apparent from electrophysiology (Fig. 6). Further, the broad distribution and frequency invariance of regional phase shifts (Fig. 2) imply that removal of widely shared variance (e.g., with global signal regression), although useful for enhancing spatial specificity (96), alters rather than eliminates the manifestation of global waves in BOLD time series. The available evidence supports this interpretation (22, 51, 59). Our results pose a challenge to the commonly held view that BOLD associations with physiological variables, even if related to neuronal activity, are purely a “nuisance” in investigations not explicitly concerned with fluctuating arousal. The possibility should be considered that autonomic activity is fundamental to spontaneous infra-slow brain activity.

MATERIALS AND METHODS

A more comprehensive version of this section is provided in the Supplementary Materials.

Datasets

Dataset 1: HCP (fMRI and physiology)

Simultaneously collected resting-state fMRI and physiological data were analyzed from a previously described subset of 190 individuals (51) from the WU-Minn HCP 1200 Subject Release. Details regarding the HCP dataset are published elsewhere (97). Two 15-min, eyes-open resting-state fMRI sessions (multiband factor = 8, repetition time (TR) = 0.72 s; 2.0-mm isotropic voxels, one left-to-right and one right-to-left phase-encoding direction) were obtained at each of two experimental sessions, for a total of four runs per individual. Physiological data were collected at 400 Hz via a bellow placed around the chest (respiration) and a pulse oximeter placed on the fingertip (pulse). We analyzed all runs from the 190 individuals that included full duration BOLD and physiological time series (22 of 760 possible scans were omitted from RV analyses; 31 were omitted from HRV analyses).

Dataset 2: Weizmann Institute dataset (fMRI and pupil size)

Simultaneously collected resting-state fMRI and eye-tracking data were acquired from 22 individuals as part of the main (i.e., “rest fixation”) experiment described in (42). Briefly, each individual provided one 8-min, eyes-open resting-state scan (TR = 2.0 s, 3.0 mm by 3.0 mm by 4.0 mm voxels). Pupil diameter was acquired at 500 Hz using an MR-compatible infrared EyeLink 100 (SR Research, Osgoode, ON, Canada) eye tracker. Two individuals were excluded based on excessive movement or eye-tracking artifacts (42), leaving 20 individuals for analysis in the present work.

Dataset 3: Genomics Superstruct Project (fMRI)

We additionally analyzed resting-state fMRI data from 1139 individuals of the Harvard-MGH (Massachusetts General Hospital) Brain Genomics Superstruct Project (GSP). Details regarding the GSP dataset are published elsewhere (16). Two 6-min fMRI runs (TR = 3.0 s, 3.0-mm isotropic voxels) were acquired per individual included in the present analyses.

Dataset 4: Neurotycho (ECoG)

Resting-state electrophysiological data were obtained from a publicly available database (neurotycho.org) (57). We used ECoG data from two macaque monkeys each chronically implanted with a subdural, 128-channel electrode array spanning the cerebral cortex of the left hemisphere. Details of this dataset are published elsewhere (55, 57). As previous studies find that arousal shifts most closely associated with the fMRI global signal are most prominent in the eyes-closed state (55), we analyzed data obtained during the awake, eyes-closed resting state. A total of eight sessions were used for monkey 1 (“Chibi”) and nine sessions for monkey 2 (“George”), each lasting 10 to 20 min.

Data processing and analysis

Physiological data preprocessing

RV and HRV were computed as previously (51). Thus, temporal SD of the respiratory trace and mean beat-to-beat interval was computed within 6-s sliding windows centered on each TR (i.e., every 0.72 s). Beat-to-beat interval was estimated using the built-in findpeaks MATLAB function. Pupil size estimates were obtained from the EyeLink system and preprocessed as previously (42).

fMRI preprocessing

See Supplementary Methods for a detailed description of fMRI preprocessing. All fMRI data were analyzed in CIFTI format, which represents cortical voxels as vertices on a surface mesh while retaining volumetric time series from the subcortex and cerebellum. We used the standard HCP “grayordinate” parcellation, comprising 59,000 cortical vertices and 66,000 subcortical/cerebellar gray matter voxels (38).

Network parcellations

Neocortical, thalamic, striatal, and cerebellar network parcellations, defined on the basis of zero-lag FC, were obtained from previously published works (16, 98–100).

Coherence analysis

Cross-spectral analysis of BOLD and physiological data was performed using multitaper spectral estimates (see Supplementary Methods). Time series were averaged within networks and complex-valued cross-power spectral density (CPSD; P_xy) was computed at the individual level and subsequently averaged across individuals. Magnitude and phase of coherence were derived from the group-averaged PSD and CPSD estimates. A null distribution of coherence estimates was obtained by shuffling physiological time series across individuals and recomputing the group-averaged CPSD. This procedure was repeated 500 times.

All group-level phase spectra contained a group delay term of ~7 s corresponding to the temporal lag of the physiological time series relative to BOLD fluctuations. To emphasize between-network phase shifts, this delay was removed from network phase spectra by subtracting out the group-level global signal phase spectrum (relative to the relevant physiological term).

Phase maps

To generate phase maps shown in Fig. 3, physiological and BOLD time series were filtered between 0.01 and 0.05 using a fourth-order zero-phase Butterworth filter. Instantaneous phase was computed via Hilbert transform. Mean phase shifts were computed for each voxel as the circular mean of instantaneous phase shifts (relative to the physiological time series) across all time points and individuals. Thus,

$${\text{PLV}}_n=\frac{1}{T}\mid {\displaystyle \sum _{t=1}^T}\text{exp}(i({\mathrm{\theta }}_{\text{RV},t}-{\mathrm{\theta }}_{n,t}))\mid$$

where θ_{RV, t} and θ_{n, t} are the instantaneous phases, at time t, of RV and the BOLD signal at a given voxel n. PLV is the complex phase-locking value, which is subsequently averaged across individuals. Figure 3B displays the angle of the group-average PLV; magnitude of the group-average PLV is shown in fig. S2.

Phase-locked dynamics

Movies of a canonical arousal cycle (Fig. 4) were obtained by averaging BOLD signals within 40 phase bins spanning the interval (−π, π] based on the instaneous phase of the filtered RV time series [similar to (37)]. For results shown in Fig. 4 (A and B), BOLD data were additionally filtered between 0.01 and 0.05 Hz, and the resulting 40-frame movie was smoothed using a sliding-window average of three phase bins in either direction. Last, subcortical and cerebellar voxels were smoothed with a 4-mm Gaussian kernel (following the above steps). These maneuvers did not materially change the results; propagation dynamics without denoising, temporal filtering, or averaging across phase bins are shown in fig. S4. Propagation displays (both image frames and videos) are shown following subtraction of the global mean time course from the final, group-level result, to aid visualization of spatial specificity.

Optical flow estimation and wave decomposition

Vector flow fields (Fig. 5A) were constructed via optical flow analysis. Optical flow was estimated from the spatial and temporal derivatives of the RV movie shown in Fig. 4B (movies S1 and S2) using the Horn-Schunck algorithm (see Supplementary Methods). Here, flow fields are used primarily as a visualization technique, with fig. S6 (divergence) being the only analysis performed directly on the flow field.

The rotational component of propagation was obtained by defining a new phase function ψ(r, t) via Hilbert transform of the RV cycle shown in Fig. 4B (movies S1 and S2), where r indexes cortical vertex and t indexes movie frame. (Note that this procedure does not make use of the flow field computed above.) To summarize as a single map, the phase topography at each time point of ψ was referenced to a common region (the visual network) and subsequently averaged across the 40 frames. The resulting map, ψ_avg, is shown in Fig. 5B. See Supplementary Methods for further details of analyses presented in Fig. 5 and fig. S6.

ECoG processing and analysis

Two channels from monkey 2 (George) were excluded [as previously (55)] based on anomalous spectral content. Notch filtering at 50 Hz and harmonics was used to remove line noise. SST events were identified on the basis of a low-frequency synchronization index following an identical procedure as in (55). Thus, spectrograms were generated for each channel, yielding time series of 1- to 100-Hz power in 1-Hz frequency bins (see Supplementary Methods). BLP was computed for each channel by averaging the mean-subtracted spectrograms across frequencies within a given frequency band. A low-frequency spatial synchronization index was defined as the fraction of channels at each time point (every 0.2 s) whose delta (1 to 4 Hz) BLP exceeded +1 SD. SSTs were defined as the 40-s period surrounding time points at which the low-frequency synchronization index surpassed a threshold of 0.4 (i.e., 40% of channels showing increased delta power). Threshold crossings occurring within 3 s of a preceding crossing were excluded. In total, 1145 SST events were identified across sessions (monkey 1, N = 656; monkey 2, N = 489). SSTs were averaged within and across sessions to yield an average SST spectrogram for each channel in each monkey.

Broadband gamma (40 to 100 Hz) BLP was similarly averaged across all SST instances to yield dynamics shown in Fig. 6D. Gamma BLP waveforms at each channel were cross-correlated with the mean waveform averaged across channels (analogous to global signal; fig. S1) to yield a time delay for each channel (Fig. 6C). A global mean SST spectrogram (Fig. 6A) was obtained by averaging SST spectrograms across channels and monkeys.

Diffusion maps

We obtained principal FC coordinates via diffusion map embedding (35), as in (11). A detailed description of this procedure is provided in Supplementary Methods. Briefly, a low-dimensional embedding of the original data points (here the FC “seed map” of each voxel/electrode) is obtained by constructing a random walk on the graph representation of the data, in which edges are given by some a priori definition of pairwise similarity. The eigenvectors of a transition probability matrix based on this graph can be understood as coordinates of the data (diffusion coordinates).

The principal FC diffusion coordinate (first nonconstant eigenvector) for the neocortex, previously derived by diffusion map embedding of fMRI FC, was obtained from publicly available results from Margulies et al. (11). Similarly, we used diffusion maps to obtain a principal coordinate for cortico-striatal, cortico-thalamic, and cortico-cerebellar FC, using the publicly available HCP S1200 Subject Release group-average FC matrix (available from https://db.humanconnectome.org). Furthermore, a principal FC coordinate was defined for each macaque monkey using FC matrices constructed from broadband gamma power. See Supplementary Methods for further details.

Statistical analyses

All spatial correlations were computed as Spearman’s rho values. Statistical significance of spatial correlation values was evaluated in all cases by comparison against a null distribution obtained from maps with similar spatial autocorrelation. We assessed spatial correspondence by comparison with a null distribution (500 random shuffles) obtained via Moran spectral randomization (see Supplementary Methods).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/30/eabf2709/DC1

View/request a protocol for this paper from Bio-protocol.