Multi-objective optimization challenges in perioperative anesthesia: a review

Abstract

Physicians use perioperative decision-support tools to mitigate risks and maximize benefits to achieve the most successful outcome for patients. Contemporary risk-assessment practices augment surgeon’s judgement and experience with decision-support algorithms driven by big data and machine learning. These algorithms accurately assess risk for a wide range of postoperative complications by parsing large datasets and performing complex calculations that would be cumbersome for busy clinicians. Even with these advancements, large gaps in perioperative risk assessment remain; decision-support algorithms often cannot account for risk-reduction therapies applied during a patient’s perioperative course, and do not quantify tradeoffs between competing goals of care (e.g., balancing postoperative pain control with the risk of respiratory depression or balancing intraoperative volume resuscitation with risk for complications from pulmonary edema). Multi-objective optimization solutions have been applied to similar problems successfully, but have not yet been applied to perioperative decision-support. Given the large volume of data available via electronic medical records, including intraoperative data, it is now feasible to successfully apply multi-objective optimization in perioperative care. Clinical application of multi-objective optimization would require semiautomated pipelines for analytics and reporting model outputs and a careful development and validation process. Under these circumstances, multi-objective optimization has the potential to support personalized, patient-centered, shared decision-making with precision and balance.

Article summary:

Risk calculators and decision-support tools estimate the probability of individual or composite outcomes, yet approaches and techniques in multi-objective optimization are unknown to most clinicians. Here we describe the potential for multi-objective optimization methods to quantify tradeoffs among competing outcomes in perioperative medicine.

Single objectives versus reality

Historically, assessing the risks of undergoing surgery relied solely on surgeon experience and intuition. Preoperative risk assessments have evolved into an evidence-based practice using objective clinical data and validated risk-assessment tools. Risk-scoring systems such as the American College of Surgeons National Surgical Quality Improvement Program Risk Calculator, the Surgical Risk Preoperative Assessment System, MySurgeryRisk, Predictive OpTimal Trees in Emergency Surgery Risk Calculator, and others aim to provide patients and clinicians with estimates of risk for postoperative complications.^1–4 These calculators leverage large volumes of data, regression modeling, and machine-learning techniques to accurately predict postoperative complications. These predictions can inform shared decision-making processes involving patients, their caregivers, and clinicians.

One major weakness of most existing surgical risk calculators is that they fail to incorporate a dynamic mathematical adjustment for change in the probability of outcomes or complications that is expected to occur when various treatments are applied. Instead, the calculators estimate static risk for individual complications or composite outcomes. Risk estimates for composite outcomes better represent aggregate risk for a larger, more comprehensive set of complications, but they often group rare events with common events and group severe complications with minor complications; the resulting predictions lack granularity and interpretability.⁵ Even when risk estimates are accurate, granular, and interpretable, they often do not identify the specific clinical decisions that are the primary drivers of clinical outcomes, much less suggest an optimal management strategy to optimize outcomes.

Perioperative decision-support tools predicated on numerical rating scales present numerous challenges. The definition of pain as a fifth vital sign by the American Pain Society and subsequent emphasis by the Joint Commission led to an implicit administrative goal to minimize patient-reported pain.⁶ This single-objective optimization is easily accomplished by administering high-dose fentanyl in the postanesthesia care unit, although this may not lead to improvement in overall patient outcome. Thoughtful clinicians also seek to avoid respiratory depression, nausea, emesis, pruritus, constipation, opioid dependence, and adverse opioid-related events.^7–11 These other important outcomes may be monitored, reported, and valued separately, inappropriately, or not at all, leading to a treatment approach that fails to achieve the ultimate goal of restoring function (e.g., breathing, return of bowel function, and ambulation). In a sentinel investigation by Vila et al.,¹² an opioid-based quality improvement program was associated with a 6% improvement in patient satisfaction with pain management and a 223% increase in postoperative safety events, demonstrating the potential consequences of single-objective optimization.

Principles of multi-objective optimization

Many real-life decision-making situations involve multiple goals. For example, a stock broker designing a portfolio seeks a high return on investment and low risk, a mechanical engineer building an engine seeks high horsepower and low fuel consumption, and an anesthesiologist caring for a patient in the postoperative period seeks low pain severity and early return to function. The common thread across these decision problems is conflict between the goals cited. Financial portfolios that have high returns tend to be risky, powerful cars use more gasoline, and high-dose opioids can impair postoperative function. In addition, these problems typically have a set of good solutions rather than a single best solution. Often, to improve one goal, the decision-maker must sacrifice another goal. Only two conflicting goals are considered in these examples; tradeoffs can incorporate many goals or objectives.

It is possible to form complex decision-making scenarios as mathematical optimization problems with multiple objectives. These formulations are called multi-objective optimization problems. A decision (or a solution) is represented by assigning values to variables, for example the amount of intravenous fluid administered during surgery. Let x_i represent the i^th decision variable and x = (x₁,…,x_n) the collection of decision variables. An objective, in this context, is a function that maps decisions to a goal. Let f_j(x) represent the j^th goal as a function of a decision. Formally, the associated optimization problem is stated as

$$\underset{x\in X}{\min }{f}_1\left(x\right),\dots ,f_m\left(x\right)$$

where x is a decision contained within X, which represents the decision space, or the set of all feasible decisions. This example arbitrarily minimizes the objectives; it is possible to minimize some objectives while maximizing others. The set of all possible outcomes that can result from all possible decisions is called the objective space. The goal is to find a solution that optimizes all functions.

Consider the portfolio optimization problem described by Harry Markowitz, in which one is interested in creating a portfolio of stocks with high expected return and low risk. Assume that an investor wants to invest a total of $1, distributed among 3 available stocks. Her decision space, X, is represented by the amount she invests in each stock. A solution, x, might look like, x=(0,0.25,0.75), representing no investment in stock 1, 25 cents in stock 2, and 75 cents in stock 3. Expected portfolio return is a weighted sum of each stock’s expected return, which can be written as f1(x)=x1μ1+x2μ2+x3μ3, where μi is the expected return of stock i. Similarly, objective 2, portfolio-wide risk, can be written as f2(x)=x12σ12+x22σ22+x32σ32, where σi2 is the variance of stock i’s return (for simplicity, we assume that stock returns are independent of one another). The associated optimization problem is maxf1(x),minf2(x),subject tox1+x2+x3=1,x1,x2,x3≥0.

The solution to this problem is a set of points known as the efficient frontier. The solutions in the frontier are called efficient solutions. One solution is said to dominate another solution if it is strictly better in 1 objective and not worse in others. The efficient frontier is composed of solutions that are not dominated by any other solution. Figure 1 represents a sampling of portfolios in the objective space (i.e., risk versus return). The solution corresponding to point A is nondominated because there is no portfolio that has lower risk than A. Portfolio A dominates B because it has both higher returns and lower risk, but A does not dominate C. C is dominated by D. This example depicts multiobjective optimization problems as having sets of solutions rather than a single solution. Given this set of solutions, if there are additional preferences not previously included in the model criteria, then such preferences may help decision-makers choose among available solutions for a given multiobjective optimization problem.¹³

Fig. 1.

Risk vs. return profiles of stock portfolios.

Multi-objective optimization in clinical practice

Multi-objective optimization challenges abound in surgery and perioperative medicine. Perhaps one of the simplest rubrics is in postoperative pain management, which has the goals of minimizing pain while minimizing opioids and maximizing indicators of surgical recovery, such as breathing, return of bowel function, and ambulation. Tradeoffs among these goals are illustrated in Figure 2.

Fig. 2.

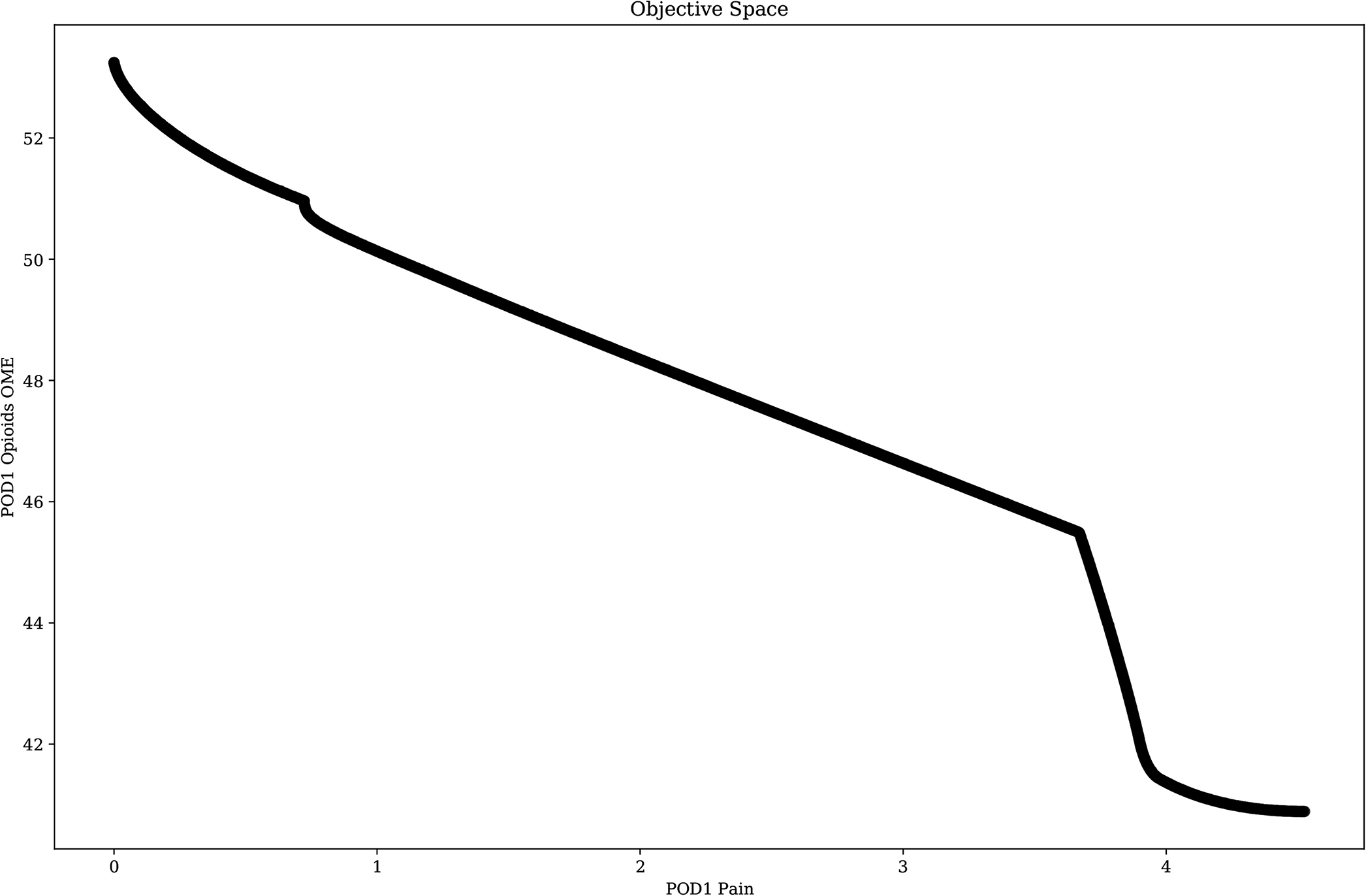
Postoperative day one (POD1) mean pain intensity vs. oral morphine milligram equivalents.

Decisions on perioperative fluid management, vasopressor and inotropic support, ventilation management, antibiotic selection, and blood glucose management typify those hourly decisions, which may impart multiple and imbalanced consequences.^13–20 Notably, while decision heuristics commonly aim to restore “normal” parameters, many patients suffer comorbid factors that may transiently or permanently challenge this underlying strategy.²¹ From a broader perspective, decisions on the timing of surgery are common in older adults with hip fractures, with data supporting early repair as well as correcting reversible clinical abnormalities, which may conflict with early repair.^22–24 Perioperative neurocognitive disorders (e.g., delirium and postoperative cognitive change), which are the most common postoperative complications in older adults, may be exacerbated by pain intensity and opioids, suggesting further opportunities for optimization across competing endpoints.^25–31

Prior limited experience for clinical multi-objective optimization

The authors are unaware of any published applications of multi-objective optimization in perioperative decision-making. However, similar concepts have been applied in performing partial hepatectomy for multifocal hepatocellular carcinoma. Liver surgeons seek to maximize complete resection or destruction of the target lesions and the size and function of the liver remnant. Multi-objective optimization has been formally deployed in exploring the distribution of Level 1, 2, and 3 trauma centers in Colorado, minimizing total system access time and the number of casualties who could not reach the desired level of care.³² Similar work has been performed regarding the Scottish trauma system.³³ Multi-objective optimization has been used in surgical device design and development for cochlear implants, coronary stents, and numerous orthopedic implants.^34–36 Generally, these designs attempt to minimize the risk of insertion and device-specific complications while maximizing device longevity and functionality. Multi-objective optimization has also been applied to simulated radiation therapy for brain lesions, seeking to maximize normal neuroanatomy around the lesion while delivering a theoretically sufficient dose of radiation to destroy the lesion.³⁷ Similar methods have been applied to electrostimulation for acetabular bone reformation.³⁸ This work focused on arranging electrodes to achieve a homogenous field distribution and optimal simulation interval, objectives that occasionally conflict.

Challenges and future directions in clinical implementation of multi-objective optimization

The increasing availability of large volumes of data from electronic health records offers opportunities to apply advanced data science techniques to frame clinical challenges as multi-objective optimization problems that balance tradeoffs among competing goals. Conceptually, this approach seems preferable to traditional decision-support tools that estimate probabilities for individual outcomes in isolation or estimate probabilities for composite outcomes that lack granularity and interpretability. However, evidence supporting the clinical efficacy of multi-objective optimization is lacking. Future investigations should seek retrospective validation followed by prospective clinical application with comparison to standard decision-making and traditional decision-support tools. This would require semiautomated pipelines for analytics and reporting model outputs. If successful, multi-objective optimization has the potential to support personalized, patient-centered, shared decision-making with precision and balance.

Highlights.

Topic:

Multi-objective optimization in perioperative decision-making

Purpose:

Describe a framework for achieving balance among several competing goals of care

State-of-the-Art:

Multi-objective optimization can quantify tradeoffs among several outcomes of interest, offering advantages over traditional, single-objective optimization

Knowledge Gaps:

The feasibility and efficacy of multi-objective optimization in augmenting surgical decision-making have not been reported

Technology Gaps:

Clinical application of multi-objective optimization would require semiautomated pipelines for analytics and reporting model outputs

Future Directions:

Retrospective development and validation of multi-objective optimization decision-support tools, followed by clinical application in a prospective, observational setting