Computational analysis of the binding mode of 8-oxo-guanine to formamidopyrimidine-DNA glycosylase

Abstract

8-oxo-guanine (8OG) is the most prevalent form of oxidative DNA damage. In bacteria, 8OG is excised by formamidopyrimidine glycosylase (Fpg) as the initial step in base excision repair. To efficiently excise this lesion, Fpg must discriminate between 8OG and an excess of guanine in duplex DNA. In this study, we explore the structural basis underlying this high degree of selectivity. Two structures have been reported in which Fpg is bound to DNA, differing with respect to the position of the lesion in the active site, one structure showing 8OG bound in the syn conformation, the other in anti. Remarkably, the results of our all-atom simulations are consistent with both structures. The syn conformation observed in the crystallographic structure of Fpg obtained from B. stearothermophilus is stabilized through interaction with E77, a non-conserved residue. Replacement of E77 by Ser, creating the Fpg sequence found in E. coli and other bacteria, results in preferred binding of 8OG in the anti conformation. Our calculations provide novel insights into the roles of active site residues in binding and recognition of 8OG by Fpg.

DNA is a major target of oxidative damage which, in turn, has been linked to human diseases associated with aging, including cancer (1, 2). 8-oxoguanine (8OG) (3) is one of the most common forms of oxidative DNA damage(4); failure to repair this lesion prior to DNA replication leads to G:C to A:T transversion mutations in bacterial and mammalian cells(5).

In E. coli, Fpg (MutM), MutY and MutT work in concert to counter the potentially deleterious effects of 8OG (6, 7). Fpg is an 8-oxoguanine-DNA glycosylase/AP lyase which excises 8OG from oxidatively damaged DNA. This multi-step process is initiated by nucleophilic attack on C1′ by the N-terminal proline of Fpg, forming a Schiff base intermediate. Proton abstraction leads to β- elimination of the 3′ phosphate, followed by hydrolysis of the Schiff base and δ-elimination, generating a single base gap (8, 9).

In the present context, damage recognition refers to the process by which a specific lesion, 8OG, is selected for excision by Fpg in a vast sea of unmodified DNA. The problem may be considered in two parts; how the enzyme “finds” the lesion embedded in DNA and how the modified base, once encountered, is accommodated as a Michaelis complex in the enzyme’s active site. The current model for damage recognition involves a) non-specific binding to duplex DNA b) scanning the groove(s) by facilitated diffusion c) damage recognition mediated by hydrogen bonds or thermodynamic instability d) formation of a transient enzyme-DNA complex e) eversion of damaged nucleotide from helix and f) binding in the active site pocket (10).

While the catalytic mechanism by which 8OG is excised from DNA has been extensively investigated by structural methods(11–17), little is known regarding the mechanism by which Fpg recognizes its cognate lesion and whether discrimination between the oxidized base and guanine occurs during one or several stages of binding. 8OG differs from guanine at the N7 and O8 positions in that N7 is protonated and the C8 hydrogen is replaced by oxygen (Figure 1). It seems likely that that these structural differences account, at least in part, for the ability of Fpg to recognize and bind 8OG in its active site.

Figure 1.

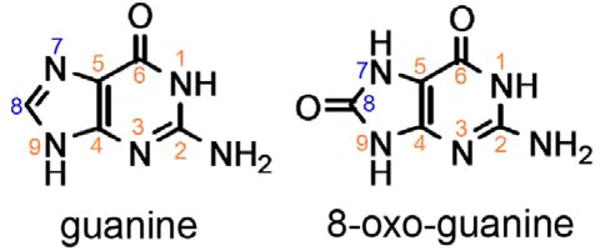
Structures of guanine and 8-oxoguanine.

The initial challenge in determining structural requirements for binding specificity through X-ray crystallographic analysis was presented by the difficulty in trapping the Fpg-DNA complex before base excision occurs. Two approaches have been used to circumvent this problem. Gilboa et al. used sodium borohydride to trap the Schiff base intermediate by forming a covalently- bound intermediate (15). The resulting crystal structure of the E. coli Fpg-DNA complex lacked the damaged base; moreover, the βFα10 loop (residues 217–224) does not appear in the resulting electron density map. Thus, direct evidence for substrate recognition was lacking.

More recently, Fromme and Verdine reported the crystal structure of the Fpg-DNA complex containing the damaged base (14) (Figure 2). In this case, Bacillus stearothermophilus (B. st.) Fpg was used for the study with its catalytic activity eliminated by use of an E2Q mutant (18). This approach generated a structure with 8OG bound to Fpg in the syn conformation, in which a single hydrogen bond between the lesion N7 and Ser219’s backbone carbonyl oxygen is formed. The mutation involves replacement of an ionizable (Glu) side chain with a neutral residue (Gln) that was observed to directly interact with the lesion, thus the details of the resulting structure could differ from those of the active, wild type enzyme.

Figure 2.

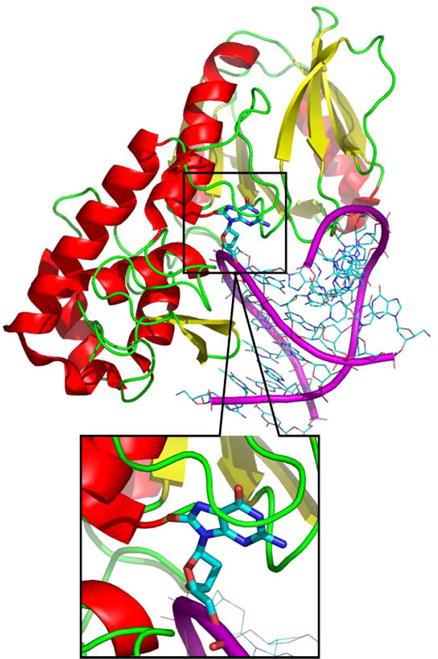
Structure of B. st. Fpg bound to 8OG DNA (pdb code: 1R2Y). Atomic detail is shown for the DNA duplex and the protein is represented with a cartoon diagram.

Simulation studies (19, 20) have been conducted in which the missing base in the structure reported by Gilboa et al was modeled into the crystallographic structure(15). Based on their data, the authors proposed a different binding mode for 8OG than that deduced for the E2Q mutant by Fromme and Verdine. These simulations suggested that the 8OG binds to Fpg in the anti conformation, making hydrogen bonding contacts to both N7 and O8 of 8OG. In contrast, the crystal structure from Fromme and Verdine show the damaged base to be in the syn conformation, with only N7 involved in hydrogen bonding with Fpg(14).

Unlike its human analog, hOGG, Fpg displays no significant π-π interactions with 8OG, resulting in a more spacious binding pocket. Thus, one possible explanation for the apparently contradictory results is that 8OG may bind to Fpg either in anti or in syn, although this does not fully explain the divergent observations. We previously used a computational approach to study the preference for anti and syn 8OG conformations in a variety of sequence contexts in duplex DNA(21). In the present study, we employ all-atom molecular dynamics simulations and free energy calculations to gain insight into the interactions involved in the complex between 8OG and wild type Fpg. We address two specific questions: what is the preferred conformation of 8OG in the Fpg active site, and what are the interactions between 8OG and Fpg that provide for lesion recognition or a secondary discrimination against guanine prior to base excision? We make the remarkable observation that our simulations are consistent with both models of the Fpg-8OG complex. Additional calculations provide insight into the role of specific Fpg residues in the binding of DNA containing 8OG.

MATERIALS AND METHODS

System preparation

All initial structures were built using the Leap module of Amber (version 8) (22), based on the crystal structure of the B. st. Fpg/DNA complex with 8OG in the syn conformation (1R2Y.pdb)(14). The sequence of the DNA duplex was d[GTAGACCTGGAC]·[GTCCAG*GTCTAC] (where G* is 8OG). All water molecules in the crystal structure were retained. The anti conformation was built by rotating the glycosidic angle of 8OG using the molecular modeling software MOIL-VIEW(23). Protein mutants were generated by manual editing of the pdb file, with the new side chain built using Leap. These structures were minimized for 100 cycles of steepest descent and then solvated in truncated octahedron boxes with a minimum 6 Å buffer between the box edge and the nearest protein atom. The TIP3P model(24) was used to explicitly represent water molecules. Following previous studies(19, 20), the N-terminal proline was modeled as neutral to mimic the stage directly before the reaction. The parameters for neutral N-terminal proline were obtained from Perlow-Poehnelt et al. (20). Force field parameters for 8OG were obtained from Miller et al.(25). Zinc was modeled using the Stote non-bonded model (q = +2e-, σ = 1.7 Å, ε = 0.67 kcal/mol)(26). The remaining protein and nucleic acid parameters employed Amber ff99 (27, 28), with modified protein backbone parameters to reduce the alpha-helical bias of those force fields(29). Previous calculations showed a large pKa shift for glutamate in the active site of T4 Endonuclease V (30). However, Fromme and Verdine suggested(14) that Glu2 is unlikely to be protonated since it is at the N-terminus of an α-helix; it has been shown that acidic residues in this position tend to have low pKa values (31). In this study we calculated the pKa value of Glu2’s using two approaches, Jensen’s empirical method(32) and Onufriev’s H++ method(33); these methods resulted in Glu2 pKa values of 5.69 and 6.78, respectively. To mimic the crystallization pH (7.5)(14) we therefore simulated Glu2 in its deprotonated state unless specified otherwise. We also repeated selected simulations and umbrella sampling calculations using protonated Glu2 to examine the sensitivity of the results to the ionization state.

Molecular Dynamics simulations

All molecular dynamics simulations were carried out with the SANDER module in Amber. Solvated systems were minimized and equilibrated in three steps: (i) 50 ps MD simulation (22) with protein and DNA atoms constrained and movement allowed only for water; (ii) five 1000-step cycles of minimization, in which the positional restraints on the protein and DNA were gradually decreased; (iii) Four cycles of 5000 steps MD simulation with decreasing restraints on protein and DNA. A final 5000 steps of MD were performed without restraints. The resulting structures were used in the production runs.

SHAKE(34) was used to constrain bonds involving hydrogen atoms. The non-bonded cutoff was 8 Å. The particle mesh Ewald method(35, 36) was used to calculate long-range electrostatics. Constant pressure (1 atm) and temperature (300 K) were maintained by the weak coupling algorithm (37).

Structural analysis

The root mean square deviation (RMSD) of three regions of the complex were calculated separately: (i) protein, which is calculated using the Cα atom of all protein residues; (ii) DNA, which includes the backbone heavy atoms of only the 8OG:C and flanking base pairs; (iii) loop, which includes the Cα atom of residues in the base binding loop (222 – 231), with the RMSD calculated for this region after best-fit of the coordinates of the entire protein. The glycosidic angle of 8OG is defined using atoms O4′ –C1′ –N9–C4. The RMSD and glycosidic angle calculations, along with distance calculations, were carried out using the ptraj module.

Umbrella sampling and potential of mean force calculations

Umbrella sampling (38–41) was used to calculate the potential of mean force (PMF) as a function of 8OG glycosidic angle in the binding site. 36 starting structures were generated using MOIL-VIEW(23) by rotating 8OG glycosidic angle in 10° increments from 10° to 360°. These initial structures were energy minimized and one independent 200ps simulation (i.e. one umbrella sampling window) was performed for each structure. The glycosidic angle was restrained to the initial value using a harmonic restraint with a force constant of 50 kcal mol-1radian-2. Residues farther than 10 Å from 8OG were restrained using positional restraints (force constant 2 kcal mol-1 Å-2). The other parameters of these simulations were the same as the standard MD simulations. The resulting PMF was obtained by WHAM analysis(39–41) of the data using a program provided by Alan Grossfield (freely available at dasher.wustl.edu/alan).

MM-GBSA

The MM-PBSA method has become widely used for calculation of free energies of binding(42). The MM-GBSA variant, in which the GB solvation model is used, was shown to successfully reproduce relative affinities and selectivities for a range of matrix metalloprotease inhibitors(43). In this study, we treated the protein+DNA(without 8OG) as the “receptor” and the 8OG nucleotide as the “ligand”. The relative binding energy of 8OG in anti or syn conformations represents the contribution of protein-8OG interactions to the relative stability of these two binding modes. The absolute binding free energy is calculated by the equation 1:

$$\begin{array}{l}\mathrm{\Delta }{G}_{\mathit{binding}}=G_{\mathit{COMP}}-G_{\mathit{receptor}}-G_{\mathit{ligand}}\\ G_x=E_{\mathit{VDW}}+E_{\mathit{EEL}}+G_{\mathit{pol}}+G_{\mathit{non-pol}}\end{array}$$

Equation 1. The equations for calculating MM-GBSA binding free energy.

The van der Waals energy (EVDW) and intramolecular electrostatic energy (EEEL) were calculated using SANDER(22, 44). The polar part of solvation free energy (Gpol) was calculated using the GB-OBC solvent model (44, 45). The nonpolar solvation free energy (Gnon-pol) was calculated by using the solvent accessible surface area (SASA) and a surface tension of 5 cal mol-1Å-2 (46). Energy calculations for the isolated ligand (8OG) and receptor (Fpg) used coordinates sets obtained from the trajectory of the complex.

The images in this article were made using VMD(47) and pymol(48).

Results and Discussion

Effect of the E2Q mutation

In the crystal structure of B. st. E2Q-inactivated Fpg with DNA, the damaged base binds to the active site in the syn conformation(14) and the βFα10 binding loop is ordered. However, due to the proximity of the Glu2 side chain to the 8OG base (~3 Å), the electrostatic effects arising from the E2Q mutation may be significant. Perlow-Poehnelt et al. suggested this mutation as one possible reason for the difference in 8OG conformation in the E2Q B. st. crystal structure and the E. coli computational model(20). We used two sets of simulations to test this possibility and also to investigate the general influence of the mutation on the structure of the complex. One simulation used the same E2Q mutant B. st. Fpg-DNA complex that was studied crystallographically and the other employed wild type B. st. Fpg in the complex. Three independent 2ns simulations were used for each sequence to evaluate precision.

Stability of the wt and E2Q systems

To analyze the stability of the structures under the simulation conditions, the RMSDs of protein Cα atoms, lesion site residues (8OG:C and flanking base pairs) and the βFα10 loop were computed for each of the six independent simulations. The flexibility of the βFα10 loop was proposed to play an important role in the recognition and excision of the damaged base(12–16, 19, 20, 49). Both systems are quite stable in all six 2ns simulations. For the DNA lesion site, the RMSD plateau values are 0.5-1.0 Å with either protein sequence, while the RMSDs of the entire protein and the βFα10 loop region are both slightly larger at ~1.0 Å (Figure S1). The loop shows greater fluctuations about this average than the protein or DNA. We thus conclude that the simulations provide stable dynamics and that the mutation does not have any dramatic effect on the overall structure and stability of the complex.

Influence of the E2Q mutation on the active site geometry

Detailed analysis of the trajectories brought to light several small but interesting differences in the behavior of the two sequences. In the crystal structure of E2Q Fpg, a hydrogen bond forms between the Nε of Gln2 and O8 of 8OG. This interaction is reproduced in the E2Q simulations (shown in Figure 3), with an average distance between these atoms of 3.04 Å (Figure S2), in excellent agreement with the value of 3.08 Å observed in the crystal structure(14). However, this hydrogen bond cannot form in the wild type sequence since the amide nitrogen is not present. In particular, unfavorable electrostatic interactions are present in the wild type between the Glu2 carboxylate and O8 of 8OG, resulting in a shift of the protein strand containing Glu2 away from 8OG in the wt simulations (Figure 3).

Figure 3.

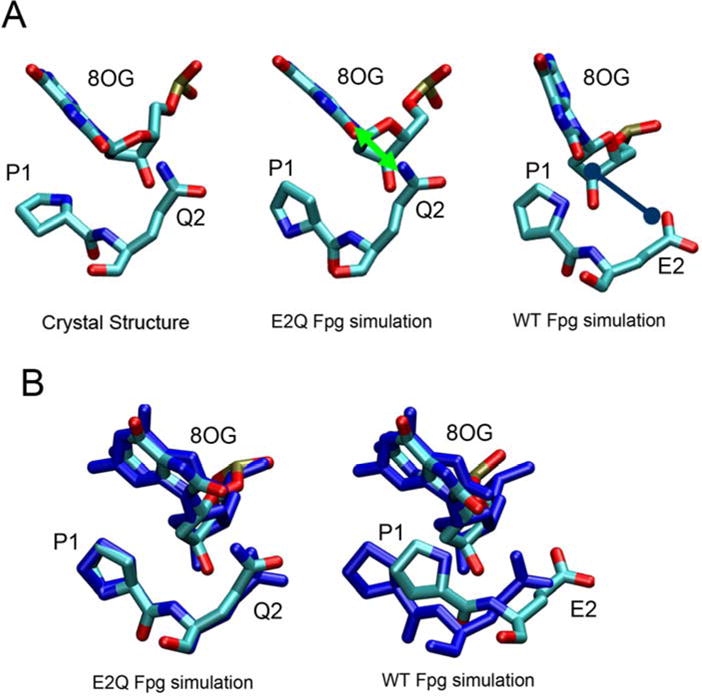
Comparison of conformation of the region containing 8OG, Pro1 and Gln2 (Glu2 in wt) between the crystal structure, the E2Q Fpg simulation and the wild type Fpg simulation. The favorable interaction between Q2 and the O8 of 8OG is indicated by a green line and the unfavorable interaction between WT E2 and the O8 of 8OG is indicated with a blue line. Panel B shows the region after best-fit of 8OG, in which the crystal structure is shown in dark blue simulation structures are colored by atom. The E2Q simulations reproduce the E2Q crystal structure, but a shift in P1/E2 relative to 8OG is apparent in the wild type simulation.

This difference between the E2Q mutant and wt Fpg causes two obvious effects. First, due to repulsion between 8OG and Glu2, the purine ring rotates slightly, increasing the distance between O8 and the Glu2 carboxylate. The glycosidic angle of 8OG in E2Q simulations is 108 ± 21° (uncertainty denotes the standard deviation), similar to 101° in the crystal structure(14) suggesting that the simulation is reasonable. In the wild type simulations, however, this angle is significantly different at 57° ± 14°.

The second effect observed is that the average distance between N of Pro1 and C1′ of 8OG is shorter in the wild type than in the E2Q mutant. In the proposed mechanism of 8OG excision, C1′ of 8OG undergoes nucleophilic attack by the N of Pro1 (9, 50). In simulations of wild type Fpg, the average distance is ~4.2 Å. The E2Q mutant samples two minima at 4.5 Å and 5.8 Å, with a preference for the longer distance resulting in an average of ~5.3 Å (Figure S1). In the crystal structure, this value is 3.4 Å, much shorter than we observe in the simulation of the same sequence. This apparent inconsistency arises from ~180º rotation of the Pro1 ring in the simulation such that the nitrogen moves farther from 8OG. Interestingly, the rotated ring from the E2Q Fpg simulation still overlaps well with the crystal structure (but with exchange of the positions of N and C) and thus the structure would be expected to remain in good agreement with the electron density (Figure 3B). Therefore, the different orientation of the Pro1 ring in our E2Q Fpg simulation and x-ray structure could result from the difficulty of distinguishing between carbon and nitrogen from the electron densities.

Thus, while the control simulations of the E2Q mutant reproduced the crystallographic data with high accuracy, analogous simulations on the wild type sequence resulted in a slight rearrangement of the residues in contact with the lesion. These include loss of a hydrogen bond present with Glu2 and shift of Glu2 away from 8OG, resulting in shortening of the average distance between the Pro1 nucleophile and the 8OG sugar ring. These observations are consistent with the proposed catalytic mechanism.

Previous calculations have suggested that the pKa of glutamate in the active site of T4 Endonuclease V can be shifted to a higher value (30). However, Fromme and Verdine have suggested that Glu2 in Fpg is unlikely to be protonated at neutral pH(14), due to the observation that glutamates at N-termini of α-helices (such as Glu2 in Fpg) are less likely to be protonated (31). We calculated the pKa value for Glu2 and obtained values of 5.7 and 6.8 depending on the method used for the calculation (see Methods). Since this value is reasonably close to neutral pH, we repeated the simulation using Glu2 with a protonated side chain carboxyl group. The resulting structure was similar to that observed in both the E2Q x-ray structure and the E2Q mutant simulation (Figure S1), with a hydrogen bond between O8 of 8OG and Glu2 acidic hydrogen analogous to the hydrogen bond observed between O8 of 8OG and Nε2 of Gln2 in the E2Q mutant. Due to the uncertainty of the ionization state of Glu2 and lack of experimental structure data for the wild type sequence with 8OG bound in the active site, we conclude that it is not possible from these simulations to determine which of these active site hydrogen bonding patterns is adopted under physiological conditions.

Structural and energetic analysis of the anti and syn 8OG binding modes

The glycosidic angle of 8OG in the simulations described above was observed to depend somewhat on the sequence; the glycosidic angle changed from high syn (108°) in the E2Q mutant simulation (101° in the x-ray crystal structure) to syn (57°) in the wild type sequence. However, a full transition to anti was not observed in any of the six simulations. Two scenarios could account for this observation; either the syn 8OG conformation is thermodynamically favored, or 8OG also can bind in an anti conformation, but the energy barrier between these two conformations is sufficiently large that transitions occur more slowly than the nanosecond time scale of our simulations. Thus we cannot infer from solely this data whether the 8OG’s conformation is more favorable in syn or anti.

To directly compare the stability of the alternate binding modes in the wild type sequence, we constructed a complex containing 8OG in the anti conformation by rotation of the glycosidic angle. Simulations of the wild type sequence, for both syn and anti conformations, utilized two independent methods, umbrella sampling and MM-GBSA, to estimate the relative free energy of these binding modes. These methods differ significantly in their approach and thus provide a measure of the reliability of the conclusions. In addition, umbrella sampling has the advantage of being able to estimate the barrier for rotation about the 8OG glycosidic bond in the complex, while MM-GBSA can readily provide estimates for the contribution of different interactions to the relative free energies of the two conformations. Thus the methods are independent but highly complementary. We first examine the relative stability of the conformations (since the anti form has not been observed crystallographically) and then examine the relative free energies.

Stability of the anti 8OG and syn 8OG binding modes

Simulations were performed for 7 ns for each of the two systems (anti and syn for wt Fpg). As shown in Figure 4, all four conformations are stable during the fully unrestrained simulations, with plateau RMSD values of ~1Å for the proteins and DNA fragments. The RMSDs of the loop region (residues 222-231) fluctuate between 1 and 2 Å, with greater flexibility apparent in the anti 8OG systems.

Figure 4.

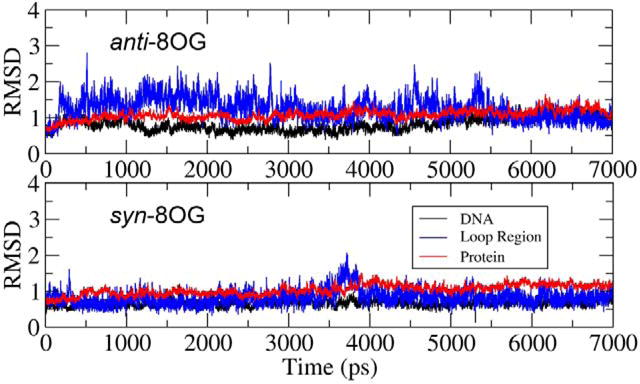
RMSD values for the protein, DNA and binding loop during simulations of the WT Fpg/DNA complex with anti (upper) and syn (lower) conformations for 8OG.

Specific interactions between 8OG and Fpg in the two binding modes

Figure 5 shows the anti and syn binding modes of 8OG in the final structures from the simulations. Comparison of the structures reveals surprising similarity in the hydrogen bonding patterns of the two binding modes. Both conformations of 8OG fit in the binding pocket without significantly changing the conformation of the βFα10 loop. In the syn conformation (Figure 5a), 8OG forms four hydrogen bonds to Fpg: between 8OG N1 and T223 Oγ, between 8OG N7 and the backbone O in S219, between 8OG N2 and E77 Oε and a network of hydrogen bonds between 8OG N6 and the N atoms of residues 221 to 224.

Figure 5.

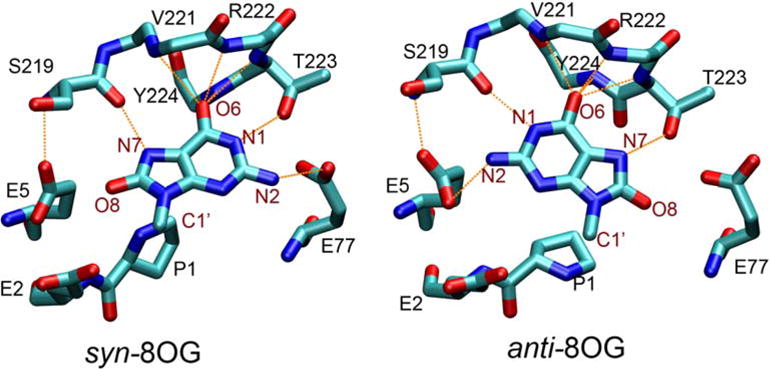
8OG and surrounding residues in the Fpg-DNA complex with (a, left) syn 8OG as observed in the crystal structure and (b, right) anti 8OG built by rotation around the glycosidic bond of 8OG. Protein residues are labeled in black, and atoms of 8OG are labeled in maroon. Hydrogen bonds are indicated by orange dashed lines. Only the base group of 8OG is shown (the remaining atoms linked to C1′ are not shown).

In the anti conformation (Figure 5b), because of the rotation of the base about the glycosidic bond, N1 and N7 swap their respective partners, with N7 now forming a hydrogen bond with T223’s Oγ and N1 hydrogen bonding to the O of S219. N2 acts as hydrogen bond donor to a different Glu residue, E5. N6 maintains its hydrogen bonds with the four residues 221 to 224.

To examine the stability of these interactions during our simulations, we used histogram analysis to compute the distributions of the distances corresponding to these contacts. The results, shown in Figure 6, confirm that these hydrogen bond interactions are stable throughout the simulations. In both conformations, 8OG O6 forms a hydrogen bond network with the N atoms of V221, R222, T223 and Y224. For simplicity, the average distance between O6 and these four N atoms is denoted “VRTY”. The distributions of the average distances between O6 and the four “VRTY” residues are similar in the two binding modes.

Figure 6.

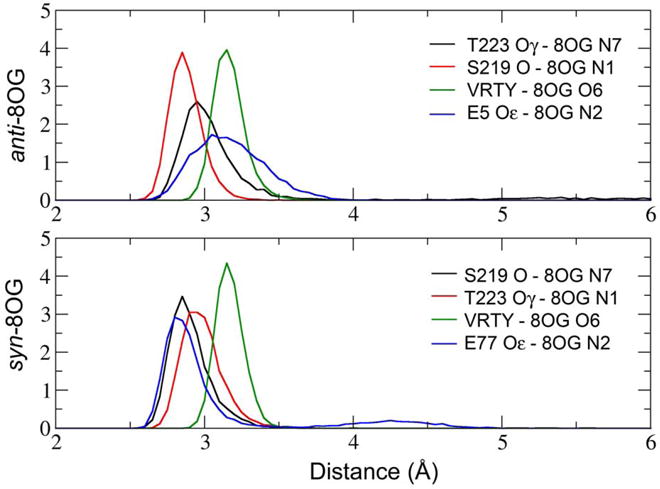
Histograms of distances corresponding to hydrogen bonds between Fpg and 8OG. “VRTY” represents the average distance between 8OG O6 and the backbone N atoms in residues 221 through 224.

Figure 6 also shows that the distribution of the distance between S219 and N7 in syn 8OG is similar to that for S219 and N1 in the anti 8OG binding mode. This also is the case for the distances involving T223, reflecting the exchange of these hydrogen bonds resulting from rotation about the glycosidic bond (Figure 5). 8OG N2 forms a slightly shorter hydrogen bond with E77 in syn 8OG than it does with E5 in anti 8OG. The longer hydrogen bond distance for 8OG-E5 may arise from the interaction of E5 with S219 in addition to 8OG, while E77 does not form hydrogen bonds with residues other than 8OG and therefore has more freedom to optimize its interaction with 8OG.

8OG differs from guanine in hydrogen bonding ability by having an acceptor O8 and conversion of N7 from acceptor to donor. Specific interactions with either group could be employed by Fpg as a final step in allowing the enzyme to discriminate between 8OG and deoxyguanine. In the crystal structure reported by Fromme and Verdine, 8OG N7 in the syn conformation forms a specific hydrogen bonding interaction with S219 (14). In contrast, previous simulations of E. coli Fpg (19, 20) suggested that the O8 of anti 8OG interacts with K217 (R222 in B. st. Fpg).

Interestingly, the binding pocket in our simulations appears not only able to accommodate both anti and syn 8OG, but a similar set of specific hydrogen bonds are formed in each. Both conformations have hydrogen bonds that could be used to differentiate 8OG from guanine. In our simulations, the hydrogen bond interaction formed to N7 of syn 8OG involves S219, consistent with the crystal structure reported by Fromme and Verdine(14). In the anti conformation, T223 is the key residue in recognizing the oxidized base, and not R222. Experimental data indicates that 8OG binding affinity is reduced approximately fourfold in the K217T E. coli Fpg mutant (19). We calculated the distance between R222 and O8 during the simulations, and found no significant interaction. However, since R222 is next to T223, mutation of the basic residue in this position may affect the conformation of T223 and thus the binding affinity of 8OG.

We also examined the effect of the anti vs. syn change on the distance between P1 nitrogen and the C1′ of 8OG. As described above, P1 N acts as a nucleophile attacking C1′ of the 8OG in the initial step of the glycosylase reaction (9, 50). The distance between these two atoms is significantly different in the two binding modes. In syn 8OG, this distance is 4.2 ± 0.3 Å. In anti 8OG, this distance is 3.5 ± 0.3 Å. The shorter distance in anti 8OG could suggest that this conformation may be more reactive; however other factors are likely to be involved.

Does Fpg preferentially bind syn or anti 8OG, and what is the role of sequence conservation?

The MD simulations described above demonstrate that 8OG can adopt both anti or syn conformations in the active site. However, no transitions between these two conformations are observed in these simulations. Similarly, Perlow-Poehnelt et al. reported no anti/syn transitions in their simulations of E. coli Fpg (20). Therefore, we cannot directly obtain the relative stabilities of these conformations by comparing their populations. Instead, we used two other approaches, umbrella sampling and MM-GBSA, to calculate the relative stability of each of these conformations in the Fpg binding site.

We also used these MD simulations to investigate the role of the E77 side chain in 8OG binding. Figure 5 demonstrates that E5 and E77 appear to have opposite effects for syn and anti 8OG conformations. E77 stabilizes syn 8OG by forming a hydrogen bond with 8OG N2. On the other side of the binding pocket, the E5 side chain has Coulombic repulsion with 8OG O8. In anti 8OG, these roles are reversed; E5 forms a hydrogen bond with 8OG N2, and the side chain carbonyl of E77 repels 8OG O8.

Importantly, E5 is strictly conserved while E77 is not. In 85 sequences of Fpg found in the Swiss-Prot database, 48 have serine at the position corresponding to E77, 11 have threonine, and 26 have glutamate. This residue is serine in E. coli Fpg. Due to the direct interaction of E77 with 8OG and its different role with anti and syn 8OG conformations, sequence changes at this position could significantly affect the binding mode. To investigate this possibility, two additional systems were prepared for the E77S Fpg mutant with syn and anti 8OG.

Using the umbrella sampling procedure described in Methods, the potential of mean force for rotation of the 8OG glycosidic bond in the Fpg binding pocket was calculated for each of the two sequences (wt and E77S). The results are shown in Figure 7, and detailed values including statistical uncertainties are provided in Table S1. There are two obvious energy minima in the free energy profiles for both systems. One, located at about 55°, represents the syn conformation of 8OG. The other, at about −67°, corresponds to a high anti 8OG.

Figure 7.

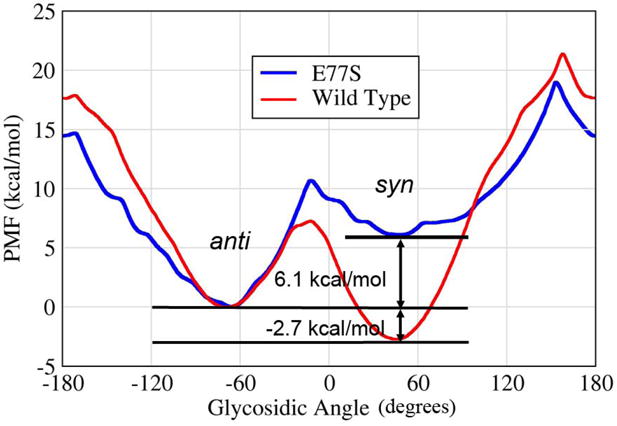
The potential of mean force (free energy profile) for rotation around the 8OG glycosidic bond in the Fpg binding pocket. Data is shown for the B. st. wild type (red curve) and the E77S mutant (blue). To aid the comparison, the free energy of the anti minimum was assigned a value of zero for both data sets.

Although the two energy minima have the same location in wild type and E77S Fpg, the relative free energy of these two minima is highly sensitive to the effect of this mutation. This is consistent with the interactions shown in Figure 5, in which E77 makes favorable hydrogen bonding interactions with syn 8OG but shows unfavorable Coulombic repulsion with anti 8OG. With E77, syn 8OG is 2.7 kcal/mol more stable than anti 8OG, consistent with observation of the syn conformation in the crystal structure of this sequence. In the E77S mutation, however, anti 8OG becomes 6.1 kcal/mol more stable than syn. Thus the E77S mutation has an important impact on the relative stability of the two binding modes.

As described above, the ionization state of Glu2 affected the local conformations of the active site. Therefore, we investigated whether the Glu2 protonation would affect the free energy profile for rotation of 8OG by repeating the umbrella sampling calculation with protonated Glu2 in wild type sequence and compared with the profile obtained with deprotonated Glu2. We observe that the ionization state of Glu2 has little effect on the relative free energies of anti and syn or on the height of the transition state connecting these minima (at glycosidic angles near zero) (Figure S4). Larger differences are observed near the highest energy barrier (~150) where the statistical uncertainties in the data are large (Table S1).

To further confirm these data from umbrella sampling calculations, MM-GBSA was also used to calculate the relative free energies of anti and syn binding by Fpg using deprotonated Glu2. The advantage of MM-GBSA is that it is possible to obtain approximate contributions to the total free energy from various types of interactions, including van der Waals, electrostatics, and solvation free energy. Results of this analysis are provided in Table 1.

Table 1.

The relative anti and syn 8OG binding free energies (kcal/mol), calculated by MM-GBSA, in both B. st. wild type Fpg and the E77S mutant. Positive values indicate that the anti conformation is higher in free energy and therefore less favorable. Total free energies are provided as well as individual components of the free energy. Data are discussed in the text. (VDW: van der Waals, EEL: electrostatic, POL: electrostatic component of solvation free energy, SASA: nonpolar solvation energy using the solvent accessible surface area).

	Wild Type	E77S
ΔΔE(VDW)	2.2±0.1	2.0±0.1
ΔΔE(EEL)	0.4±0.8	−11.5±0.5
ΔΔG(POL)	1.1±0.1	1.0±0.5
ΔΔG(SASA)	−0.1±0.0	0.1±0.0
ΔΔG(total)	3.7±0.6	−8.3±0.1

The results of the MM-GBSA calculations are in good agreement with those obtained by umbrella sampling. For the wild type B. st. Fpg, syn 8OG is 3.7 kcal/mol more stable than anti 8OG (2.7 kcal/mol from umbrella sampling). For the E77S mutant, anti 8OG is 8.3 kcal/mol more stable than syn (6.1 kcal/mol from the umbrella sampling calculations).

In addition to providing additional support to the umbrella sampling results, MM-GBSA also supplies estimates of the contribution from each energy term. In wild type B. st. Fpg, the total anti/syn energy difference arises mainly from van der Waals interaction (2.2 out 3.7 kcal/mol). The solvation free energy also favors syn 8OG by ~ 1 kcal/mol. The electrostatic energy does not favor either, which is reasonable since there are the number of hydrogen bonds in each conformation are the same(Figures 5 and 6).

The MM-GBSA energy decomposition for the E77S mutant is also shown in Table 1. The differences from van der Waals, solvation and solvent accessible area between the two binding modes are roughly the same as were observed with E77. However, the electrostatic energy difference has changed dramatically, with the anti conformation stabilized by electrostatic interactions, ~ 11 kcal/mol more than syn. This result is consistent with the discussion above concerning changes in the role of E77 between anti and syn. The electrostatic energy in E77S favors anti 8OG so strongly that it becomes the preferred conformation, despite slightly less favorable van der Waals and solvation free energy.

Summary and Conclusions

X-ray crystallography continues to be the main source of information for understanding mechanisms of DNA damage recognition at the molecular level. The need for high quality, diffracting crystals and the requirement of catalytically inactive damaged DNA-protein complexes are frequently addressed by the introduction of single amino acid mutations or, even, by the deletion of a short protein segment. The perturbations that such changes may cause to the structure of the complex can be very difficult to evaluate. In contrast, computational methods are ideally suited to evaluate these putative mutation-derived perturbations by comparing the structures of complexes with the mutated and wild type proteins.

We have focused on the role of the Fpg inactivating E2Q mutation on the specific interactions involved in binding and, perhaps excision of 8OG. Simulations of a complex between the E2Q mutant and DNA provided results consistent with the crystal structure of the same sequence. Simulations of the complex with wild type E2 sequence produced very similar results, with small changes arising from loss of the group on Q2 that hydrogen bonds to 8OG in both the E2Q crystal structure and simulations. The glycosidic angle of 8OG changed from 108° (E2Q) to 57° (wt) and the N-terminal proline moved closer to 8OG, reducing the distance between the P1 nitrogen and the 8OG C1′. In both wild type and E2Q, the syn conformation of 8OG and the other key interactions between 8OG and Fpg were maintained as seen in the crystal structure.

We built a model of the wt B. st. Fpg-DNA duplex containing anti 8OG by using the crystal structure of the complex with syn 8OG and rotating the 8OG glycosidic bond. Subsequent unrestrained molecular dynamics simulations resulted in the interesting observation that the binding site (including the βFα10 loop) can readily accommodate both anti and syn 8OG without significantly changing its conformation. Additionally, hydrogen bonds seen in the crystal structure and simulations of the syn 8OG complex were replaced by a nearly equivalent set for anti 8OG. Free energy calculations showed that syn 8OG is 2.7 kcal/mol more stable in this binding site than anti 8OG.

As suggested by early studies(30), the pKa value of Glu2 can have a large shift towards protonated state. Therefore, we also simulated the complex with protonated Glu2. The results indicate that the details of the hydrogen bonding between 8OG and Glu2 depend on the ionization state, however, its effect on the relative free energies of 8OG’s two binding modes is not significant (Figure S4).

Previous studies also suggested that 8OG could possibly be accommodated by Fpg in either the anti or syn conformation but that anti is favored(19, 20), based on simulation of anti and syn 8OG that were modeled into the E. coli Fpg crystal structure with a homology-modeled substrate binding loop. In those simulations, the anti conformation was shown to make stable contacts that were consistent with existing mutation data, while the syn conformation did not. The authors suggested that the E2Q mutation used for crystallization was one possible reason for the disagreement between their results and the crystal structure. In the present study, we find that the syn 8OG conformation that is preferred with wt B. st. Fpg arises from favorable interaction with the non-conserved E77 side chain, which also destabilizes the anti conformation. This position in E. coli Fpg and many other Fpg sequences is occupied by serine, which has a shorter, neutral side chain. We hypothesized that the residue at this position could alter the preferred conformation of bound 8OG, and tested this postulate through free energy calculations using the B. st. E77S mutant. These revealed that anti 8OG is indeed more stable than syn when E77 is replaced by serine.

While our simulations resolved an apparent discrepancy between two proposed models of binding of 8OG by Fpg, the simulations do not reveal any evolutionary advantage for using different binding conformations by E. coli and the thermophilic B. st. Moreover, the effect that the syn or anti 8OG binding site conformation, including hydrogen bonds specific to 8OG, has on the mechanism of lesion extrusion and/or damage recognition remains to be established. Future computations will address these points. It is interesting to note, however, that our simulations demonstrated that the anti/syn conformational change that makes a large difference in the properties of duplex DNA appears to make relatively little difference in the ability of Fpg to specifically bind the lesion.

Supplementary Material

Figure S1: Comparison of conformation of the region containing 8OG, Pro1 and Gln2 (Glu2 in wt) between the crystal structure wild type Fpg simulation. In this simulation the Glu2 was modeled in its protonated state. The crystal structure is shown in dark blue, and the simulation structure is colored by atom.

Figure S2: The RMSDs of the E2Q mutant and wild type systems. In protein the results are calculated by the Cα atom of all residues in protein. The results for DNA are calculated based on the backbone heavy atoms of 8OG:C base pair and its upstream and downstream base pairs. Loop inclu7des the Cα atom of residues in the base binding loop (222 – 231), with fitting the reference structure using the coordinates of whole protein.

Figure S3: Distance analysis for the six independent simulations. Panel A shows the results from E2Q Fpg simulations, in which two distances are shown: the distance between N of catalytic residue Pro1 and C1′ of 8OG (labeled as P1 to C1′), and the distance between Nε of Q2 and O8 of 8OG (labeled as Q2 to O8). Panel B shows the results from wild type Fpg simulations. The first distance is the one between Pro1’s N and 8OG’s C1′ (labeled as P1 to C1′), and the distance between Oε of E2 and O8 of 8OG (labeled as E2 to O8).

Figure S4: The potential of mean force (free energy profile) for rotation around the 8OG glycosidic bond in the Fpg binding pocket. Data is shown for the B. st. wild type with Glu2 deprotonated (red curve) and with Glu2 protonated (blue). To aid the comparison, the free energy of the anti minimum was assigned a value of zero for both data sets.

Table S1. Output from WHAM analysis on WT-Glu2 umbrella sampling. The first column is the coordinate of the free energy profile (8OG’s glycosidic angle). The second column is the free energy value. The third column is the statistical free energy uncertainty.

Abbreviations

Fpg

formamidopyrimidine-DNA glycosylase from Escherichia coli

8OG

8-oxo-7,8-dihydroguanine

E. coli

Escherichia coli

B. st

Bacillus stearothermophilus

MM-GBSA

molecular mechanics-generalized Born-surface area method

PMF

potential of mean force

WHAM

weighted histogram analysis method