Abstract

d9-Butanol or 1-butan-d9-ol (D9B) is often used as an OH radical tracer in atmospheric chemistry studies to determine OH exposure, a useful universal metric that describes the extent of OH radical oxidation chemistry. Despite its frequent application, there is only one study that reports the rate coefficient of D9B with OH radicals, k1(295 K), which limits its usefulness as an OH tracer for studying processes at temperatures lower or higher than room temperature. In this study, two complementary experimental techniques were used to measure the rate coefficient of D9B with OH radicals, k1(T), at temperatures between 240 and 750 K and at pressures within 2–760 Torr. A thermally regulated atmospheric simulation chamber was used to determine k1(T) in the temperature range of 263–353 K and at atmospheric pressure using the relative rate method. A low-pressure (2–10 Torr) discharge flow tube reactor coupled with a mass spectrometer was used to measure k1(T) at temperatures within 240–750 K, using both the absolute and relative rate methods. The agreement between the two experimental aproaches followed in this study was very good, within 6%, in the overlapping temperature range, and k1(295 ± 3 K) was 3.42 ± 0.26 × 10–12 cm3 molecule–1 s–1, where the quoted error is the overall uncertainty of the measurements. The temperature dependence of the rate coefficient is well described by the modified Arrhenius expression, k1 = (1.57 ± 0.88) × 10–14 × (T/293)4.60±0.4 × exp(1606 ± 164/T) cm3 molecule–1 s–1 in the range of 240–750 K, where the quoted error represents the 2σ standard deviation of the fit. The results of the current study enable an accurate estimation of OH exposure in atmospheric simulation experiments and expand the applicability of D9B as an OH radical tracer at temperatures other than room temperature.
1. Introduction
Atmospheric simulation chambers have been used for decades to study the physicochemical processes that occur in our atmosphere such as the oxidation mechanism and products of volatile organic compounds (VOCs), secondary organic aerosol formation, and photochemical aging.1,2 Many research groups have developed a variety of atmospheric simulation chambers that range from the traditional indoor and outdoor Teflon chambers to the more recent temperature-regulated simulation chambers and oxidation flow reactors that can simulate multi-day atmospheric oxidation. These chambers are often highly equipped with state-of-the-art instrumentation to follow stable gaseous and particulate species and in several cases for direct or indirect detection of radical species.1−3
OH radicals are the main driver of daytime VOC oxidation in the atmosphere,4 and therefore, OH-initiated VOC oxidation is frequently studied in simulation chambers. In the past few years, the OH exposure (measured as the time-integrated OH concentration) is reported in chamber studies to provide a useful universal metric for atmospheric modeling studies that simulate the various physicochemical processes. While direct detection of OH radicals in atmospheric simulation chambers is feasible via laser-induced fluorescence or chemical ionization mass spectrometric detection,5−7 indirect methods of OH radical detection are often preferred due to the ease of use and low cost of this approach.8−10 For instance, indirect measurement of OH concentration is performed by following the decay of a tracer compound, due to its reaction with OH, using available detection techniques such as gas chromatography or proton-transfer reaction mass spectrometry (PTR-MS). Recently, Barmet et al. reported the use of n-butanol-d9, CD3(CD2)3OH (referred to as D9B hereinafter), as a useful tracer to measure OH exposure or OH “clock” in atmospheric simulation chamber experiments.9 Barmet et al. showed that D9B is detected by PTR-MS, a commonly used technique in chamber experiments, at a mass peak (m/z 66) that is expected to be free of interferences even under complex conditions where multiple VOC species and degradation products are present. Since D9B reacts predominantly with OH radicals and can be unambiguously detected even with quadrupole PTR-MS (unit mass resolution), other research groups have applied this useful technique to measure OH exposure in a variety of simulation chamber studies.
The use of D9B as a tracer for OH exposure measurements requires the accurate knowledge of its reaction rate coefficient with OH in a wide temperature range to provide extended applicability in simulation chambers. As part of the Barmet et al. study, the room temperature rate coefficient, k1(295 K), for the reaction of OH with D9B was measured to be (3.40 ± 0.88) × 10–12 cm3 molecule–1 s–1.9
| 1 |
Barmet et al. used the well-established relative rate technique where the loss of D9B due to reaction with OH radicals was measured relative to that of a reference compound, in this case 2-butanone. The authors discuss the complications related to the OH rate coefficient measurement in their study, such as potential loss of the reference compound, other than OH reaction, and report an uncertainty of ∼26%.
Despite the uncertainties mentioned, D9B has been widely applied as a tracer of OH radicals in smog chamber experiments for almost a decade.8−36 Nevertheless, the errors associated with the rate coefficient determination of the OH tracer could propagate high uncertainties (≥26%) to the concentration of OH radicals during the chamber experiments and thus potentially lead to poor interpretation of the experimental observations. Besides, to the best of our knowledge, the rate coefficient of the tracer has been determined solely at 295 K, and thus, it limits the application of the method proposed by Barmet et al. to room temperature studies. However, in several cases, the simulation and understanding of the physicochemical processes occurring in the atmosphere require studies at lower or higher temperatures than 295 K.37−42 In addition, the possible application of the OH clock method in other domains (e.g., combustion, catalysis, etc.) where higher temperatures are required should not be excluded.
The objective of the current study was twofold—on one hand, to conduct kinetic experiments and determine accurately the rate coefficient of D9B with OH radicals (reaction 1) at room temperature and, on the other hand, to measure the rate coefficient of the title reaction as a function of temperature and to extend the applications of the method proposed by Barmet et al. In particular, the title reaction was studied in a wide temperature range, 240–750 K, and at pressures within 2–760 Torr, using two different experimental approaches, that is, a temperature-regulated atmospheric simulation chamber at atmospheric pressure and a temperature-regulated low-pressure flow tube reactor. The two approaches followed here allow us to systematically explore the reaction under a wide range of conditions and to measure the OH rate coefficient, k1(T), at high accuracy using both absolute and relative rate methods. The results of this study are compared with those of the only available literature study of Barmet et al. at 295 K.
2. Experimental Section
The OH reaction rate coefficient, k1, was measured at atmospheric pressure and at temperatures between 263 and 353 K deploying the THALAMOS (Thermally regulated Atmospheric simulation chamber) facility and applying the well-established relative rate method. At pressures between 2 and 10 Torr and at temperatures between 240 and 750 K, a discharge flow tube reactor coupled with a modulated molecular beam mass spectrometer was used to determine the rate coefficient of the title reaction employing both absolute and relative rate methods. The two complimentary techniques used in this study have been discussed in detail before, and only the details related to this work are given below.
2.1. THALAMOS Simulation Chamber
THALAMOS is an indoor atmospheric simulation chamber where temperature-dependent studies of homogeneous or heterogeneous processes are carried out (Figure 1).43,44 THALAMOS consists of a 0.6 m3 Teflon chamber placed inside a climatic box (Vötsch industrietechnik VT-4100, effective volume of 1.2 m3) to control the temperature between 231 and 453 K. Several fans are used inside the climatic box and inside the Teflon chamber to ensure fast temperature equilibration of the air surrounding the walls of the Teflon chamber and the homogeneous mixing of reagents inside the Teflon chamber, respectively. The temperature, pressure, and relative humidity (RH) inside the chamber are continuously monitored and recorded with appropriately calibrated probes.
Figure 1.
General description of the THALAMOS facility. The wide vertical arrows indicate the cleaning process of the THALAMOS chamber, that is, the continuous flashing and pumping of the chamber. During a typical experiment, the Teflon pump is recirculating the gas mixture between the chamber and the SIFT-MS instrument (dash arrows).
Generated dry air (RH < 5%) was used as bath gas for the majority of the experiments, while a few measurements were carried out under 50% RH. D9B, H2O2, and reference compounds were injected in their liquid form via a septum inlet and introduced into the chamber using a stream of dry air. To facilitate the evaporation of compounds, the inlet line was temperature-controlled using a heating tape at 323 K. Gas mixture homogenization inside THALAMOS, at 293 K, is achieved within ∼1 min, but it is also dependent on compound volatility and THALAMOS temperature.
In order to induce photo-oxidation reactions, the climatic box is equipped with a light irradiation system capable of hosting 20 lamps, (i) 10 UV-A lamps (Philips PL-L 24W/10/4P) with a maximum at λmax = 365 nm and (ii) 10 mercury lamps (OSRAM HNS-L 24W 2G11) emitting in the UV-C region, λmax at 254 nm. In the current study, UV-C lamps were used to photolyze H2O2 and produce OH radicals via the reaction
| 2 |
A Restek Sulfinert-treated stainless-steel tube was used to sample the reaction mixture off the chamber. Selected ion flow tube mass spectrometry (SIFT-MS) was deployed for the real-time monitoring of reactants. The standard sampling flow of the instrument is 25 mL min–1. A recirculating Teflon diaphragm pump, 4 L min–1, is used to create a closed loop between the chamber and the SIFT-MS instrument to ensure the fast response of the mass spectrometer to the modifications in the gas mixture occurring in the chamber.
The SIFT-MS (Voice 200 ultra) is a mass spectrometer based on the chemical ionization of the analytes. Further information about the operation principles of SIFT-MS technology can be found elsewhere, and only a brief description will be given herein.45,46 A microwave discharge is used for the simultaneous generation of three precursor ions, H3O+, NO+, and O2+, which are sequentially selected using a first quadrupole mass filter. Then, the precursor ions are injected inside a low-pressure flow tube reactor (pressure in the range of 500–900 mTorr) using nitrogen (N2), as carrier gas. At the same time, the sample is injected at the upstream end of the reactor. The precursor ions react with the analytes along the flow tube to produce new characteristic ionized molecules.45,46 Finally, the gas flow passes through a skimmer, located at the downstream end of the flow tube reactor, and is injected in a high-vacuum chamber for mass analysis and ion counting using a second quadrupole mass spectrometer. The mass spectrometric ion peaks selected to monitor the concentration profiles of reference and target molecules used in the current study are listed in Table 1.
Table 1. Mass Spectral Ion Intensities Selected to Monitor the Concentration Profiles of the Compounds Used in the Kinetic Study.
| SIFT-MS (atmospheric pressure study) | |||
|---|---|---|---|
| compounds | product ions | m/z | precursor ions |
| d9-butanol (C4D9OH) | C4D9+ | 66 | H3O+ |
| [C4D9OH]H+ | 84 | ||
| [C4D9OH]H3O+ | 102 | ||
| [C4D8OH]+ | 81 | NO+ | |
| [C4D8OH+]H2O | 99 | ||
| C3D6O+ | 64 | O2+ | |
| toluene (C7H8) | [C7H8]H+ | 93 | H3O+ |
| C7H8+ | 92 | NO+ | |
| C7H8+ | 92 | O2+ | |
| propanol (C3H7OH) | C3H7+ | 43 | H3O+ |
| C3H7O+ | 59 | NO+ | |
| 1-butanol (C4H9OH) | C4H9+ | 57 | H3O+ |
| C4H9O+ | 73 | NO+ | |
| C4H8+ | 56 | O2+ | |
| ethanol (C2H5OH) | [C2H6O]H+ | 47 | H3O+ |
| C2H5O+ | 45 | NO+ | |
| C2H5O+ | 45 | O2+ | |
| Modulated QMS (Low-Pressure Study) | |||
| nitrogen oxide (NO) | [NO]+ | 30 | |
| nitrogen dioxide (NO2) | [NO2]+ | 46 | |
| molecular bromine (Br2) | [Br2]+ | 160 | |
| atomic bromine (Br•) | [Br]+ | 80 | |
| hypobromous acid (BrOH) | [BrOH]+ | 96/98 | |
| molecular fluorine (F2) | [F2]+ | 38 | |
| atomic fluorine (F•) | [F]+ | 19 | |
| d9-butanol (C4D9OH) | [C4D9OH]+ | 83 | |
| [C3D6O]+ | 64 | ||
2.1.1. Mass Spectrometric Pattern of D9B with SIFT-MS
The mass spectrometric pattern of D9B has been recorded under dry conditions (RH < 5%) after injection and well mixing of 1.2 × 1014 molecule cm–3 in the Teflon chamber. The time and mass resolution of the instrument were set to 1 s and 1 amu, respectively. Figure 2 displays the recorded mass spectra and the major fragments/mass spectrometric peaks identified for each of the three precursor ions of SIFT-MS. Concerning the H3O+ ion, the most intense peak noticed was the one with m/z 66 that corresponds to the [C4D9]+ fragment.9 In addition, the protonated parent peak with m/z 84 ([C4D9OH]H+) was also observed along with another mass peak with m/z 102 that corresponds to [C4D9OH]H3O+. Interestingly, the ratio of mass peaks 66/102 was decreased when RH in the chamber was increased to 50%. Apparently, the increase in RH in the sampling flow results in an increase in water absolute concentration in the flow tube of the SIFT-MS instrument, enhancing the formation of the first hydronium water cluster (m/z = 37) and thus the reaction probability for the formation of the [C4D9OH]H3O+ cation. Using NO+ as a precursor ion, two major peaks were noticed with m/z ratios of 81 and 99 that correspond to [C4D8OH]+ and [C4D8O]H3O+, respectively. Regarding O2+, the major peak observed was at 64 amu corresponding to the [C4D8]+ cation. Several other fragments with lower relative abundances were noticed and attributed as displayed in Figure 2.
Figure 2.
Mass spectrum of D9B recorded with SIFT-MS recorded after introduction of 1.2 × 1014 molecule cm–3 in the chamber under dry conditions and 293 K. Mass scan resolution of the SIFT-MS instrument was set to 1.
To monitor the concentration profiles of D9B in the kinetic experiments (see Table 1), four selection criteria were applied based on the (i) stability of the mass peaks in the absence of reaction after injecting a known amount of D9B in the chamber, (ii) stability of the mass peaks after introducing in the chamber a known quantity of H2O2/H2O solution (OH radical precursor) in the absence of reaction, (iii) absence of contribution to the peaks of D9B after injection of the reference compound(s) in the chamber, and (iv) absence of contribution to the peaks of D9B after the OH-initiated oxidation of reference compounds. Consequently, under dry conditions where the majority of the experiments were carried out, the mass peaks with an m/z of 66, 99, and 64 arising from H3O+, NO+, and O2+, respectively, were used to monitor D9B.
2.1.2. Relative Rate Coefficient Determination
The rate coefficient k1 of OH radical reaction with D9B was investigated under atmospheric pressure in the temperature range of 263–353 K applying the relative rate method (RR). In the RR methodology, the temporal loss of D9B is measured relative to that of a reference compound (REF) provided that the observed changes are solely in the gas phase due to their reaction with the oxidant of interest, that is, the OH radicals
| 1 |
| 3 |
In all measurements presented herein, the dark and photolytic loss of D9B and reference compounds was negligible as verified by initial testing before each rate coefficient determination experiment.
The RR method has been widely used in the literature,47,48 and the relative rate coefficient is derived by the expression49
where [D9B]0, [REF]0, [D9B]t, and [REF]t are the initial concentrations of d9-butanol and those of the reference at reaction time t = 0 and at discrete times, t, after reaction mixture irradiation, respectively, and k1 and kREF are the corresponding second-order rate coefficients. A relative rate plot, ln[D9B]0/[D9B]t versus ln[REF]0/[REF]t, should be linear, with a slope equal to rate coefficient ratio, k1/kREF, and a zero intercept. Therefore, the rate coefficient for the reaction of interest can be determined from the relative rate data fitting relative to the known rate coefficient of the reference reaction, kref.49 Toluene, propanol, 1-butanol, and ethanol were used as reference compounds. The corresponding rate coefficient values of the reference molecules with OH radicals were obtained by the temperature-dependent expressions recommended by the IUPAC panel: k(toluene+OH) = 1.8 × 10–12 exp(340/T) cm3 molecule–1 s–1 recommended over 210–350 K, k(propanol+OH) = 4.6 × 10–12 exp(70/T) cm3 molecule–1 s–1 recommended over 260–380 K,47k(1-butanol+OH) = 5.3 × 10–12 exp(140/T) cm3 molecule–1 s–1 recommended over 260–380 K,47 and k(ethanol+OH) = 6.7 × 10–18T2 exp(511/T) cm3 molecule–1 s–1, recommended over 216–599 K.47
2.2. Low-Pressure Discharge Flow Tube Reactor
Absolute and relative kinetic measurements were conducted at a total pressure of 2.0–8.4 Torr (He bath gas) using a conventional fast-flow reactor combined with a molecular beam-sampling electron-impact ionization mass spectrometer.50−52 Depending on the temperature range, two different flow reactors were used. The low-temperature reactor (Figure S1), used at T = 240–335 K, consisted of a Pyrex tube (45 cm length and 2.4 cm i.d.) surrounded by a jacket through which thermostated ethanol was circulated. To reduce the heterogeneous loss of OH radicals, the inner surface of the reactor and of the movable injector of the OH radicals was coated with halocarbon wax. For higher temperatures (T = 310–750 K), a reactor consisting of a Quartz tube (45 cm length and 2.5 cm i.d.) with an electrical heater and water-cooled attachments was used (Figure S2).52
Hydroxyl radicals were produced in the movable injector through a rapid reaction of H atoms with excess NO2, hydrogen atoms being generated by dissociation of H2, diluted in He, in a microwave discharge (Figure S1)
| 4 |
with a rate coefficient k4 = (1.47 ± 0.26) × 10–10 cm3 molecule–1 s–1 recommended over 195–2000 K.53
OH radicals were monitored at m/z 96 and 98, (HOBr+), after being scavenged with excess Br2 ([Br2] = (3–5) × 1013 molecule cm–3), added in the end of the reactor, 5 cm upstream of the sampling cone, as shown in Figure S1
| 5 |
with a rate coefficient k5 = 2.16 × 10–11 exp(207/T) cm3 molecule–1 s–1 recommended over 220–950 K.50
This reaction was also used for the determination of the absolute concentrations of OH radicals through their chemical conversion to HOBr in excess of Br2, [OH] = [HOBr] = Δ[Br2], that is, concentration of OH (HOBr) was determined from the consumed fraction of [Br2]. The detailed discussion on the possible influence of secondary chemistry on this method of OH detection and determination of the absolute concentrations of the radicals is presented in previous publications.54,55
The D9B was delivered to the reactor by flowing the bath gas (He) over liquid D9B and was detected by MS at its parent and fragment peaks at m/z = 83 and m/z = 64, respectively (Table 1). The absolute calibration of the mass spectrometer for D9B was realized under experimental conditions of kinetic measurements (pressure, temperature, and total flow of bath gas) through injection of known amounts (generally, 0.6 μL) of D9B into a helium flow in the reactor and recording its mass peak at m/z = 64, which was by a factor of 100 more intensive than the parent one. The integrated area of the mass spectrometric signal, corresponding to the known total number of D9B molecules injected into the reactor, allowed the determination of the calibration factor. Another method employed for the absolute calibration of D9B was to link its concentration to that of Br2. It consisted in titration of the same concentration of F atoms, generated after dissociation of F2 in a microwave discharge, with excess Br2 ([F]0 = Δ[Br2]) and D9B ([F]0 = Δ[D9B]). This procedure allowed the absolute calibration of D9B signals using that of Br2. The absolute concentrations of D9B determined with two employed methods were consistent within 10%. Absolute concentrations of stable species (NO2 and Br2) were calculated from their flow rates obtained from the measurements of the pressure drop of their manometrically prepared mixtures in He stored in calibrated volume flasks.
2.2.1. Absolute Rate Coefficient Determination
The absolute measurements
of k1 were
carried out at a total pressure of 2.0–2.2 Torr (He bath gas)
under pseudo-first-order conditions, monitoring kinetics of OH consumption,
[OH]0 = 2–3 × 1011 molecule cm–3, in an excess of D9B. Under such conditions, 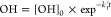 , with the pseudo-first-order rate constant k1′ = k1[D9B] + kw, where kw represents the heterogeneous
loss of OH radicals. All the pseudo-first-order rate constants, k1, were corrected for axial and radial diffusion of OH radicals,56 with the diffusion coefficient of OH in He calculated
as D0 = 660 × (T/298)1.85 Torr cm–2 s–1.57 The corrections were typically <8%,
being somewhat higher in a few kinetic runs (up to 14%).
, with the pseudo-first-order rate constant k1′ = k1[D9B] + kw, where kw represents the heterogeneous
loss of OH radicals. All the pseudo-first-order rate constants, k1, were corrected for axial and radial diffusion of OH radicals,56 with the diffusion coefficient of OH in He calculated
as D0 = 660 × (T/298)1.85 Torr cm–2 s–1.57 The corrections were typically <8%,
being somewhat higher in a few kinetic runs (up to 14%).
2.2.2. Relative Rate Coefficient Determination
Relative rate measurements were conducted using the reaction of OH with Br2 as a reference
| 1 |
| 5 |
The experiments were carried out at total pressures in the reactor in the range of 2.0–8.4 Torr and consisted in a fast consumption of OH in reaction with a mixture of Br2 and D9B and the measurements of HOBr yield as a function of the [D9B]/[Br2] ratio.
The fraction of the initial concentration of OH radicals, [OH]0, transformed to HOBr in reaction 5, is
After rearrangement of this expression, one has
At a constant concentration of Br2, the second term of the last equation is constant, and k1/k5 can be determined as a slope of the linear dependence of (([OH]0/[HOBr])–1) on the [D9B]/[Br2] ratio.
2.3. Materials
The purities of the gases/liquids used in the current study were as follows: He (>99.9995%, Alphagaz), passed through a liquid nitrogen trap; H2 (>99.998%, Alphagaz); Br2 (>99.99%, Aldrich); and NO2 (>99%, Alphagaz) and D9B (isotopic purity 98%, Aldrich), toluene (≥99.5% Aldrich), ethanol (≥99.5%, Aldrich), propanol (≥99.5%, Aldrich), 1-butanol (≥99.5%, Aldrich), and H2O2 (30% in water). Zero air was produced using an oil-free air compressor and then was driven through a zero air generator (Claind AZ-2020) operated at 673 K to catalytically convert the organics present in the air flow to CO2. The RH in the gas flow at room temperature, 293 K, was below 5%
2.4. Error Analysis
In this section, we discuss possible uncertainties in the determination of the rate coefficient values. Considering the different experimental systems deployed and rate coefficient methods applied, the uncertainties are discussed separately. Deploying the THALAMOS chamber and the relative rate ratios, the linear fitting of experimental results (see also Figure 3) provides the 2σ standard deviation of the measurement, which was always better than 3% (see also Table 2). Considering that a combination of several mass peaks of D9B and the reference compound was used, the values of each k1ion/kREF measurement were averaged, and the 2σ standard error of the mean is given as an estimated uncertainty (see also Table 2). To estimate the accuracy of each measurement, we add in quadrature the 2σ standard error of the average value, other systematic uncertainties, such as temperature readings (estimated to be always below 1%), and the error in the rate coefficient of the reference compound (10% for toluene and propanol, 15% for butanol, and 6% for ethanol). The final value of k1 at each temperature is derived after performing a weighted average of individual measurements. The weighted average takes into account the accuracy of each measurement. The overall uncertainty denoted for k1 values measured with the THALAMOS chamber (see also Figure 6) corresponds to the 2σ standard error of the mean value, reflecting the total uncertainty of the measurements.
Figure 3.

Example of relative rate plots for the reaction of D9B with OH radicals obtained at 293 K and atmospheric pressure using the reference compounds labeled on the graph. For the relative rate data displayed, the H3O+ precursor ion of the SIFT-MS instrument was selected to monitor in real time the concentrations of D9B and the reference. The lines are linear least-squares fits of the experimental data.
Table 2. Summary of the Experimental Conditions and Rate Coefficients Obtained in This Work for the Gas-Phase Reaction of d9-Butanol with OH Radicals.
| reference: toluene. k(toluene+OH) = 1.8 × 10–12 exp(340/T) cm3 molecule–1 s–1, IUPAC recommended over 210–350 K | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T (K) | [D9B]0a | [toluene]0a | [H2O2]0a |
|
|
|
kD9B/ktoluene all ionsc | k1 (10–12)c cm3 molecule–1 s–1 | |||
| 263 | 2.95 | 2.46 | 95.9 | 0.69 ± 0.01 | 0.69 ± 0.01 | 0.64 ± 0.01 | 0.67 ± 0.03 | 4.39 ± 0.13 | |||
| 273 | 2.95 | 2.71 | 68.9 | 0.67 ± 0.01 | 0.62 ± 0.01 | 0.63 ± 0.01 | 0.64 ± 0.03 | 4.00 ± 0.12 | |||
| 293 | 5.41 | 4.67 | 54.1 | 0.65 ± 0.01 | 0.62 ± 0.01 | 0.57 ± 0.01 | 0.61 ± 0.04 | 3.50 ± 0.14 | |||
| 293 | 6.15 | 4.67 | 54.1 | 0.64 ± 0.01 | 0.62 ± 0.01 | 0.57 ± 0.01 | 0.61 ± 0.04 | ||||
| 313 | 5.66 | 4.92 | 56.6 | 0.69 ± 0.01 | 0.62 ± 0.01 | 0.56 ± 0.01 | 0.62 ± 0.06 | 3.30 ± 0.20 | |||
| 333 | 5.90 | 5.41 | 61.5 | 0.75 ± 0.01 | 0.64 ± 0.01 | 0.68 ± 0.01 | 0.69 ± 0.06 | 3.45 ± 0.21 | |||
| 353 | 3.94 | 3.44 | 88.6 | 0.94 ± 0.01 | 0.89 ± 0.01 | 0.76 ± 0.01 | 0.86 ± 0.10 | 4.06 ± 0.36 | |||
| reference: propanol. k(propanol+OH) = 4.6 × 10–12 exp(70/T) cm3 molecule–1 s–1, IUPAC recommended over260–380 K | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T (K) | [D9B]0a | [Propanol]0a | [H2O2]0a |
|
|
|
kD9B/kpropanol all ionsc | k1 (10–12)c cm3 molecule–1 s–1 | |||
| 263 | 4.67 | 5.90 | 192 | 0.79 ± 0.01 | 0.74 ± 0.01 | Not usedd | 0.76 ± 0.01 | 4.58 ± 0.29 | |||
| 263 | 2.95 | 3.44 | 477 | 0.79 ± 0.01 | 0.79 ± 0.01 | 0.79 ± 0.01 | 4.73 ± 0.05 | ||||
| 273 | 4.92 | 6.15 | 98.4 | 0.68 ± 0.01 | 0.66 ± 0.01 | 0.67 ± 0.01 | 3.95 ± 0.06 | ||||
| 293 | 5.41 | 6.64 | 106 | 0.60 ± 0.01 | 0.55 ± 0.01 | 0.58 ± 0.04 | 3.36 ± 0.23 | ||||
| 313 | 5.66 | 7.13 | 113 | 0.60 ± 0.01 | 0.55 ± 0.01 | 0.58 ± 0.04 | 3.30 ± 0.23 | ||||
| 333 | 5.90 | 7.38 | 120 | 0.62 ± 0.01 | 0.58 ± 0.01 | 0.60 ± 0.03 | 3.40 ± 0.17 | ||||
| 353 | 6.40 | 7.87 | 128 | 0.66 ± 0.01 | 0.61 ± 0.01 | 0.64 ± 0.04 | 3.60 ± 0.22 | ||||
| reference: 1-butanol. k(1-butanol+OH) = 5.3 × 10–12 exp(140/T) cm3 molecule–1 s–1, IUPAC recommended over 260–380 K | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T (K) | [D9B]0a | [1-butanol]0a | [H2O2]0a |
|
|
|
kD9/kbutanolall ionsc | k1 (10–12)c cm3 molecule–1 s–1 | |||
| 263 | 4.67 | 4.92 | 479.7 | 0.51 ± 0.01 | 0.50 ± 0.01 | 0.52 ± 0.01 | 0.51 ± 0.01 | 4.60 ± 0.18 | |||
| 263 | 1.97 | 1.97 | 479.7 | 0.46 ± 0.01 | 0.48 ± 0.01 | 0.47 ± 0.01 | 0.47 ± 0.01 | 4.24 ± 0.08 | |||
| 273 | 4.92 | 4.92 | 496.9 | 0.39 ± 0.01 | 0.38 ± 0.01 | 0.40 ± 0.01 | 0.39 ± 0.01 | 3.45 ± 0.10 | |||
| 293 | 5.41 | 5.41 | 216.5 | 0.37 ± 0.01 | 0.34 ± 0.01 | 0.35 ± 0.01 | 0.35 ± 0.02 | 2.98 ± 0.23 | |||
| 333 | 5.90 | 6.15 | 120.5 | 0.40 ± 0.01 | 0.39 ± 0.01 | 0.38 ± 0.01 | 0.39 ± 0.01 | 3.15 ± 0.17 | |||
| 353 | 6.40 | 6.40 | 127.9 | 0.45 ± 0.01 | 0.44 ± 0.01 | 0.41 ± 0.01 | 0.43 ± 0.02 | 3.39 ± 0.22 | |||
| reference: ethanol. k(ethanol+OH) = 6.7 × 10–18 T2 exp(511/T) cm3 molecule–1 s–1, IUPAC recommended over 216–599 K | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||||||||
| T (K) | [D9B]0a | [ethanol]0a | [H2O2]0a | 102/47 | 81/47 | 66/47 | 99/45 | 81/45 | 64/45 | kD9/kethanol all ionse | k1 (10–12)e cm3 molecule–1 s–1 | |||
| 293f | 5.29 | 8.46 | 54.1 | 1.10 ± 0.01 | 1.07 ± 0.01 | 1.13 ± 0.02 | 1.00 ± 0.01 | 0.92 ± 0.01 | 0.95 ± 0.01 | 1.04 ± 0.10 | 3.43 ± 0.33 | |||
| 293f | 5.29 | 8.46 | 103 | 1.00 ± 0.01 | 1.00 ± 0.01 | 1.10 ± 0.02 | 1.00 ± 0.01 | 1.08 ± 0.01 | 0.99 ± 0.01 | 1.06 ± 0.10 | 3.49 ± 0.33 | |||
| 293f | 5.29 | 8.46 | 54 | 1.03 ± 0.01 | 0.97 ± 0.01 | 0.96 ± 0.01 | 1.13 ± 0.01 | 1.03 ± 0.01 | 1.06 ± 0.01 | 1.03 ± 0.06 | 3.39 ± 0.20 | |||
| 313f | 5.66 | 9.05 | 113 | 1.08 ± 0.01 | 1.02 ± 0.01 | 1.10 ± 0.01 | 1.00 ± 0.01 | 0.96 ± 0.01 | 1.00 ± 0.01 | 1.03 ± 0.07 | 3.46 ± 0.24 | |||
| 333f | 5.66 | 9.05 | 221 | 1.19 ± 0.01 | 1.16 ± 0.01 | 1.10 ± 0.01 | 1.07 ± 0.01 | 1.02 ± 0.01 | 1.06 ± 0.01 | 1.10 ± 0.06 | 3.79 ± 0.21 | |||
Units of 1013 molecule cm–3.
The errors represent the 2σ fit precision (standard deviation).
The quoted uncertainty is the 2σ standard error of the mean values.
Ion relative ratios not used due to mass peak contribution.
The mean values of the relative ratios for each precursor ion were averaged. The quoted uncertainty is the 2σ standard error of the mean values.
Experiment carried out at 50% RH.
Figure 6.
Summary of the kinetic measurements performed with the two complementary experimental setups. Regarding chamber experiments, the relative rate kinetic data (filled squares) were calculated for a weighted average (i.e., average that takes into account the accuracy of each measurement). The error bars correspond to the total estimated uncertainties. For kinetic data at low pressure of this work (empty squares for relative rate measurement and open circles for absolute measurements), the error bars correspond to the total estimated uncertainties. The literature value of Barmet et al.9 is also displayed (triangle). The dash line is the fitting of experimental results with a modified Arrhenius expression. The solid line is the temperature dependence of the rate coefficient of 1-butanol with OH radicals using the temperature expression proposed in the work of McGillen et al.65
The accuracy in the absolute rate coefficient measurements of k1 is estimated to be around 11% by adding in quadrature the statistical error (i.e., 2σ standard deviation, which was always better than 4%), the absolute concentration of D9B (∼10%), flows (3%), pressure (2%), and temperature (1%). For the high-temperature absolute measurements (above 595 K), a conservative uncertainty of 20% was also included (in quadrature) due to OH regeneration (see Section 3.2.1), and the total uncertainty was increased to 23%. The total error (accuracy) of the measurements deploying the relative rate method in the low-pressure flow tube was estimated to be ca. 20% by adding in quadrature the precision of the measurements (2σ standard deviation, ∼8%) and errors in D9B (10%) and Br2 (5%) concentration and that of the reference compound (Br2, 15%).
Finally, the estimated total uncertainty of the room temperature value was derived after a weighted average of the individual kinetic measurements carried out under atmospheric and low pressures. The error quoted to the mean value is the 2σ standard error, indicating the total uncertainty of the measurement.
3. Results
3.1. Atmospheric Pressure Kinetic Measurements inside the THALAMOS Simulation Chamber
Table 2 summarizes the conditions under which experiments
were carried out, the relative rate ratios, and the obtained rate
coefficients measured at each temperature. The initial concentrations
of D9B and reference compounds were between 1.97 and 9.05 × 1013 molecule cm–3, while those of H2O2 ranged between 54 and 497 × 1013 molecule
cm–3. Besides the kinetic runs carried out using
propanol as a reference, with the three precursor ions H3O+, NO+, and O2+, the
characteristic mass intensities of each compound (see also Table 1) were used to determine
the relative rate ratios for each pair of precursor ions, that is, 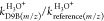 ,
, 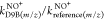 , and
, and  , respectively. The final relative rate
ratio reported represents the average value of the ions’ precursor
ratios, and the corresponding uncertainty is the 2σ standard
error of the mean. Typical relative rate plots with the four reference
compounds at 293 K using H3O+ as a precursor
ion are given in Figure 3. As displayed in Table 2, the variation in experimental conditions,
such as the concentrations of D9B and the reference molecules, the
OH radical precursor, the RH, and so forth, resulted in similar rate
coefficient values (within experimental uncertainties) at a given
temperature. Furthermore, the rate coefficients determined with the
four reference compounds are in excellent agreement between each other.
, respectively. The final relative rate
ratio reported represents the average value of the ions’ precursor
ratios, and the corresponding uncertainty is the 2σ standard
error of the mean. Typical relative rate plots with the four reference
compounds at 293 K using H3O+ as a precursor
ion are given in Figure 3. As displayed in Table 2, the variation in experimental conditions,
such as the concentrations of D9B and the reference molecules, the
OH radical precursor, the RH, and so forth, resulted in similar rate
coefficient values (within experimental uncertainties) at a given
temperature. Furthermore, the rate coefficients determined with the
four reference compounds are in excellent agreement between each other.
In the range of 263–353 K where chamber experiments were performed, no significant variation in the rate coefficient was noticed (see also Figure 6). Nevertheless, moving away from room temperature to both hot and cold temperature extremes, the rate coefficient was slightly increased. To further evaluate the temperature dependence of the title reaction, kinetic measurements were carried out with the low-pressure discharge flow tube reactor where a significant broad temperature range was achieved.
3.2. Low-Pressure Kinetic Measurements inside the Discharge Flow Tube Reactor
3.2.1. Absolute Measurements of k1
The absolute rate coefficient measurements were carried out in the temperature range of 298–750 K. The concentration of OH radicals used in the kinetic runs was in the order of 2–3 × 1011 molecule cm–3 and Br2 0.13–11.2 × 1013 molecule cm–3. Results are summarized in Table 3. Figure S3 displays examples of the exponential decays of OH radicals in the presence of different concentrations of D9B in the reactor. Typical second-order plots are displayed in Figure 4. It is worth mentioning that the intercepts in the examples shown in Figure 4, kw, are in the range 30–40 s–1, which is somewhat higher than the values measured in the absence of D9B in the reactor, kw = 10–20 s–1. This indicates the contamination of the surface of the reactor by D9B and/or the products of reaction (1). The effect was more pronounced at lower temperatures in both uncoated quartz (at T ≤ 500 K) and halocarbon wax-coated (at T < 298 K) reactors. The rate of OH radical consumption rapidly increased upon addition of even very low concentrations of D9B. As one can see in Figure S4, the intercept of the linear fit to the experimental data observed at T = 500 K (≈90 s–1) is much higher than the value of kw (≈20 s–1) measured in the absence of D9B in the reactor. In all cases, the reaction rate constant was determined from the slope of the linear fit to the experimental data observed in the presence of D9B in the reactor (straight lines in Figures 4 and S4), that is, under the assumption that heterogeneous contribution to the loss of OH radicals is independent of D9B concentration in the gas phase and considering that the intercept is significantly lower than the measured maximum values of k1′. However, due to this effect, the lowest temperature of the absolute kinetic measurements was limited to 425 and 298 K in the quartz and halocarbon wax-coated reactors, respectively.
Table 3. Summary of the Absolute Measurements of k1a.
| T (K) | number of kinetic runs | [D9B] (1013molecule cm–3) | k1 (10–12) cm3 molecule–1 s–1 |
|---|---|---|---|
| 298b | 9 | 0.80–10.1 | 3.60 ± 0.41 |
| 335b | 11 | 0.55–9.68 | 3.40 ± 0.39 |
| 425c | 9 | 0.49–8.78 | 4.11 ± 0.47 |
| 500c | 9 | 0.13–11.1 | 4.70 ± 0.54 |
| 595c | 8 | 0.67–11.2 | 5.79 ± 1.32d |
| 670c | 11 | 0.14–5.14 | 8.12 ± 1.85d |
| 750c | 7 | 0.32–4.36 | 9.80 ± 2.23d |
The total pressure in the reactor was 2 Torr, with the linear flow velocity in the reactor between 1980 and 2100 cm s–1 and OH radical concentrations in the range of (2–3) × 1011 molecule cm–3. The combined uncertainty on k1 was estimated to be about 11% by adding in quadrature the statistical error (≤4%) and that on the measurements of the absolute concentration of D9B (∼10%), flows (3%), pressure (2%), and temperature (1%).
Halocarbon wax-coated reactor.
Uncoated quartz reactor.
The error includes the systematic uncertainty and 20% conservative error to include OH regeneration of high-temperature studies.
Figure 4.
Pseudo-first-order rate constant (k1′) as a function of the concentration of D9B at T = 298 K (open symbols) and 750 K (filled symbols). Error bars represent estimated uncertainties (≤5%) on the determination of k1.
The highest temperature of the study (T = 750 K) was limited by a chain reaction in the zone of OH conversion to HOBr at high temperatures
| 1 |
| 5 |
| 6 |
| 7 |
| 8 |
where R1 and R2 are the radicals formed upon abstraction of a D atom from D9Br by OH and Br. Although this side chemistry (operative at high temperatures only) has a negligible impact on the concentrations of D9B (due to the low initial concentrations of OH radicals), it led to the formation of the species contributing to m/z = 96/98 (most likely, the fragment of CD3Br), that is, to the mass peaks where OH radicals were detected (as HOBr).
Another point, which should be discussed, is the potential regeneration of OH at high temperatures—in particular, the D or H atom abstraction pathways by hydroxyl radicals at all four sites of D9B (α-CD3CD2CD2C•DOH, β-CD3CD2C•DCD2OH, γ-CD3C•DCD2CD2OH, δ-C•D2CD2CD2CD2OH, and O radical-CD3CD2CD2CD2O•). Anticipating a similar reaction mechanism with 1-butanol, these abstraction pathways are temperature-dependent, and thus, they contribute differently to the overall rate coefficient.58 In all cases, the corresponding radicals formed can isomerize or decompose (forming different products), a temperature- and pressure-dependent process.58−60 The decomposition of the β-radical can result in 1-d8-butene (or 1-butene in the case of 1-butanol) formation and OH radical regeneration58,59,61
| 9 |
According to the theoretical work of Zhang et al.,60 the unimolecular decomposition rate of the β-radical is important at high temperatures (e.g., below 50 s–1 at 500 K, 1000 s–1 at 600 K, and ∼1 × 104 at 750 K at 1 Torr total pressure) and can bias high-temperature kinetic measurements. Overall, the majority of literature data report an OH regeneration of around 20% in the case of 1 butanol reaction with OH radicals. Considering a comparable site-specific reactivity distribution with 1 butanol and similar temperature and pressure dependence of the β-radical, we anticipate that the OH regeneration can bias the absolute kinetic measurements carried out at temperatures above ca. 550 K. In particular, the absolute kinetic measurements were carried out always in excess of NO2 and NO in our reactor (ca. 5 × 1013 molecule cm3 for both species), and in their presence, the β-radicals formed (but not limited to) can be scavenged. Based on the studies of Rissanen et al.62,63 who studied the reactivity of C2 carbon-centered free hydroxyalkyl radicals as a function of temperature, the corresponding rate coefficients of the hydroxyalkyl radicals with NO2 and NO at 550 K are expected to be 2 × 10–11 and 7 × 10–12 cm3 molecule–1 s–1, respectively. Considering similar rate coefficients for the hydroxybutyl radicals, the first-order rate constant of radical scavenging is around 1000 s–1 and thus around 10 times higher than that of the decomposition of β-radicals that leads to OH regeneration.60 At 600 K, the total rate coefficient of scavenging is comparable with that of β-radical decomposition. To account for the effect of OH regeneration, besides the estimated systematic uncertainties, we have included an extra 20% error in our high-temperature measurements (>595 K). In conclusion, the absolute kinetic measurements at 595 K and above should be considered as the overall rate coefficient of the process.61
3.2.2. Relative Rate Measurements of k1
Besides absolute rate coefficient measurements, the relative rate method described in Section 2.2.2 was applied to determine the rate coefficient of k1 in the range of 240–540 K. In these experiments, HOBr was monitored in both the D9B-free system, corresponding to [OH]0, and the Br2 and D9B-containing system, corresponding to the fraction of [OH]0 reacted with Br2. Reaction time was 0.02–0.04 s, [OH]0 = (2–5) × 1011 molecule cm–3, and the concentrations of D9B and Br2 were 0.24–27.2 × 1013 and 0.71–1.38 × 1013 molecule cm–3 respectively. In Table 4, all the experimental conditions and the k1 values measured with the relative rate method are summarized. Typical examples of the experimental data are shown in Figures 5 and S5. The values of kw calculated from the y-intercepts in Figure 5 are around 40 s–1 at T = 540 and 460 K and nearly 110 s–1 at T = 275 K. As expected, kw derived from the data observed at lower temperatures (Figure S5) is significantly higher (around 200 s–1). The low-pressure kinetic measurements obtained with the relative rate and absolute rate approaches were in excellent agreement with each other.
Table 4. Summary of the Relative Measurements of k1 with the Reaction OH + Br2 as a Referencea.
| T (K) | number of kinetic runs | [D9B]b | [Br2]b | k1/k3 | k1 (10–12) cm3 molecule–1 s–1 |
|---|---|---|---|---|---|
| 240c | 8 | 0.58–23.9 | 1.28 | 0.107 | 5.48 ± 1.10 |
| 245c | 8 | 1.08–27.2 | 1.22 | 0.095 | 4.79 ± 0.96 |
| 252c | 8 | 0.71–17.4 | 1.06 | 0.106 | 4.91 ± 0.98 |
| 260c | 8 | 0.82–17.4 | 1.32 | 0.091 | 4.36 ± 0.87 |
| 268d | 7 | 1.46–15.3 | 1.23 | 0.091 | 4.26 ± 0.85 |
| 275d | 8 | 1.13–16.4 | 1.38 | 0.078 | 3.59 ± 0.72 |
| 283d | 8 | 0.64–23.6 | 0.95 | 0.078 | 3.52 ± 0.70 |
| 310d | 12 | 0.72–13.3 | 0.71 | 0.087 | 3.66 ± 0.73 |
| 320c | 9 | 0.41–17.4 | 1.01 | 0.083 | 3.41 ± 0.68 |
| 360d | 6 | 0.30–11.9 | 1.17 | 0.096 | 3.69 ± 0.74 |
| 405e | 9 | 0.55–8.39 | 0.85 | 0.106 | 3.80 ± 0.76 |
| 460e | 10 | 0.24–9.83 | 1.20 | 0.127 | 4.30 ± 0.86 |
| 540e | 9 | 0.35–7.05 | 0.88 | 0.162 | 5.15 ± 1.03 |
The quoted overall uncertainty is 20% and includes the precision of the measurements (∼8%) and errors in D9B (10%) and Br2 (5%) concentration and that of the reference compound (Br2, 15%).
Units of 1013 molecule cm–3.
Halocarbon wax-coated reactor, P = (8.2–8.4) Torr.
Halocarbon wax-coated reactor, P = 2.15 Torr.
Uncoated quartz reactor, P = (2.0–2.2) Torr.
Figure 5.
Yield of HOBr from OH radical titration with Br2 + D9B mixtures at 275 K (filled squares), 460 K (open circles), and 540 K (filled circles). Partially shown error bars represent typical uncertainties of the measurements (≤10%). For clarity, the data for T = 275 are Y-shifted by −0.17.
4. Discussion
Figure 6 summarizes the rate coefficients measured with the two complementary techniques. Concerning the chamber experiments, in Figure 6 are presented the average values of the rate coefficients determined with the different references at each temperature. The error bars correspond to the 2σ standard error of the mean values derived from the weighted fitting of all individual measurements (see also the Error Analysis section) and reflect the overall uncertainty of the measurements. In the temperature range where kinetic data can be compared, there is an excellent agreement between the rate coefficients measured with the two setups despite the significant differences in the experimental conditions used, that is, pressure–no pressure dependence of the rate coefficient is noticed, methods applied, OH radical generation, detection of compounds, and so on. The cross-validation of the kinetic measurements confirms that the rate coefficients reported in this study are not affected by any systematic uncertainties related to experimental conditions.
To obtain the room temperature (295 ± 3 K) rate coefficient of D9B with OH radicals, an error-weighted average of the individual kinetic measurements carried out under atmospheric and low pressures was performed. k1 at 295 ± 3 K was found to be k1 = (3.42 ± 0.26) × 10–12 cm3 molecule–1 s–1, where the estimated uncertainty corresponds to the 2σ standard error of the mean value and includes the overall uncertainty of the measurements (see the Error Analysis section). k1 measured in the current study is in excellent agreement with the only literature measurement of Barmet et al.,9k1 = (3.40 ± 0.88) × 10–12 cm3 molecule–1 s–1. However, the uncertainty between the two measurements is significantly different, with our measurement being highly precise (uncertainty of ca. 8%) compared with the literature value, where the estimated uncertainty was ca. 26%.9 Based on the IUPAC-recommended rate coefficient value, for the reaction of OH radicals with 1-butanol at 298 K, k(1-butanol) = 8.5 × 10–12 cm3 molecule–1 s–1,47 the observed kinetic isotope effect is ca 2.5, which is consistent with that previously observed for the case of ethanol.64
Figure 6 includes the data measured in this study that describe the temperature dependence of k1. The kinetic data at all temperatures are well represented by the modified Arrhenius expression
While the rate coefficient values measured within 300–400 K shows very small dependence on temperature, increased values were noticednear the temperature extremes. This observed temperature dependence indicates a complex reaction mechanism that includes direct H atom elimination at high temperatures and/or the formation of pre-reactive complexes at low temperatures. In particular, it is well established in the literature that OH radicals form pre-reactive complexes with oxygenated species and with n-butanol.58 At low temperatures, the pre-reactive complex is thermally stabilized, increasing its lifetime, that is, the complex has sufficient time to distribute the excess of energy, and thus, the probability of the reaction leading to products is enhanced, increasing the overall rate coefficient. At elevated temperatures, the contribution of the pre-reactive complex formation is diminished, and the overall rate coefficient is defined by the direct H atom abstraction mechanism (similar to alkanes + OH reactions). Furthermore, the temperature dependence of k1 is consistent with that previously observed for the case of 1-butanol.65 However, at higher temperatures, the apparent kinetic isotope effect seems to decrease, indicating differences in the reaction rate temperature dependence for one or more of the available reactivity sites (α, β, γ, and δ positions) between D9B and 1-butanol. While further exploration on the site-specific reactivity and its temperature dependence is required to better understand the observed kinetic behavior, it was beyond the scope of this study.
5. Conclusions
In the framework of the current study, the rate coefficient of D9B with OH radicals has been measured in a wide temperature range, applying both absolute and relative rate methods under atmospheric and low pressures. Under atmospheric pressure, the room temperature rate coefficient was determined to be (3.42 ± 0.26) × 10–12 cm3 molecule–1 s–1 with an accuracy of 8%. This value is significantly more precise than the existing value in the literature (uncertainty of 26%), and thus, it allows a more accurate determination of OH radicals when D9B is used as a tracer in chamber experiments. Low-pressure and atmospheric pressure kinetic data are in excellent agreement in the overlapping range applied. Combining all kinetic measurements, the temperature dependence of the reaction has been determined. To conclude, the kinetic data of the current study can be used for a more accurate determination of OH radicals in chamber experiments (commonly performed under atmospheric temperature conditions, i.e., <320 K) or in possible future applications at combustion temperatures.
Acknowledgments
This work is part of the CaPPA project funded by the ANR through the PIA under contract ANR-11-LABX-0005-01, the “Hauts-de-France” Regional Council, and the European Regional Development Fund (ERDF).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c01942.
Low-pressure flow tube reactors, examples of temporal profiles of OH radicals for absolute measurements, plot of the pseudo-first-order rate constant k1′ at 500 K, and relative rate data where the yield of HOBr from OH radical titration with Br2 + D9B mixtures at different temperatures is plotted (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Barnes I.; Rudzinski K. J.. Environmental Simulation Chambers: Application to Atmospheric Chemical Processes; Springer: Dordrecht, Netherlands, 2004; Vol. 1. [Google Scholar]
- Eurochamp . Eurochamp > Eurochamp 2020, 2020; Vol. 2020.
- Yuan B.; Koss A. R.; Warneke C.; Coggon M.; Sekimoto K.; de Gouw J. A. Proton-Transfer-Reaction Mass Spectrometry: Applications in Atmospheric Sciences. Chem. Rev. 2017, 117, 13187–13229. 10.1021/acs.chemrev.7b00325. [DOI] [PubMed] [Google Scholar]
- Heard D. E.; Pilling M. J. Measurement of OH and HO2 in the Troposphere. Chem. Rev. 2003, 103, 5163–5198. 10.1021/cr020522s. [DOI] [PubMed] [Google Scholar]
- Fuchs H.; Dorn H.-P.; Bachner M.; Bohn B.; Brauers T.; Gomm S.; Hofzumahaus A.; Holland F.; Nehr S.; Rohrer F.; et al. Comparison of OH Concentration Measurements by DOAS and LIF during SAPHIR Chamber Experiments at High OH Reactivity and low NO Concentration. Atmos. Meas. Tech. 2012, 5, 1611–1626. 10.5194/amt-5-1611-2012. [DOI] [Google Scholar]
- Flores J. M.; Zhao D. F.; Segev L.; Schlag P.; Kiendler-Scharr A.; Fuchs H.; Watne Å. K.; Bluvshtein N.; Mentel T. F.; Hallquist M.; et al. Evolution of the Complex Refractive Index in the UV Spectral Region in Ageing Secondary Organic Aerosol. Atmos. Chem. Phys. 2014, 14, 5793–5806. 10.5194/acp-14-5793-2014. [DOI] [Google Scholar]
- Fuchs H.; Albrecht S.; Acir I. H.; Bohn B.; Breitenlechner M.; Dorn H.-P.; Gkatzelis G. I.; Hofzumahaus A.; Holland F.; Kaminski M.; et al. Investigation of the Oxidation of Methyl vinyl ketone (MVK) by OH Radicals in the Atmospheric Simulation Chamber SAPHIR. Atmos. Chem. Phys. 2018, 18, 8001–8016. 10.5194/acp-18-8001-2018. [DOI] [Google Scholar]
- Tritscher T.; Dommen J.; DeCarlo P. F.; Gysel M.; Barmet P. B.; Praplan A. P.; Weingartner E.; Prévôt A. S. H.; Riipinen I.; Donahue N. M.; et al. Volatility and Hygroscopicity of Aging Secondary Organic Aerosol in a Smog Chamber. Atmos. Chem. Phys. 2011, 11, 11477–11496. 10.5194/acp-11-11477-2011. [DOI] [Google Scholar]
- Barmet P.; Dommen J.; DeCarlo P. F.; Tritscher T.; Praplan A. P.; Platt S. M.; Prévôt A. S. H.; Donahue N. M.; Baltensperger U. OH clock Determination by Proton Transfer Reaction Mass Spectrometry at an Environmental Chamber. Atmos. Meas. Tech. 2012, 5, 647–656. 10.5194/amt-5-647-2012. [DOI] [Google Scholar]
- Platt S. M.; El Haddad I.; Zardini A. A.; Clairotte M.; Astorga C.; Wolf R.; Slowik J. G.; Temime-Roussel B.; Marchand N.; Ježek I.; et al. Secondary Organic Aerosol Formation from Gasoline Vehicle Emissions in a new Mobile Environmental Reaction Chamber. Atmos. Chem. Phys. 2013, 13, 9141–9158. 10.5194/acp-13-9141-2013. [DOI] [Google Scholar]
- Bruns E. A.; El Haddad I.; Slowik J. G.; Kilic D.; Klein F.; Baltensperger U.; Prévôt A. S. H. Identification of significant precursor gases of secondary organic aerosols from residential wood combustion. Sci. Rep. 2016, 6, 27881. 10.1038/srep27881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Platt S. M.; Haddad I. E.; Pieber S. M.; Huang R.-J.; Zardini A. A.; Clairotte M.; Suarez-Bertoa R.; Barmet P.; Pfaffenberger L.; Wolf R.; et al. Two-stroke scooters are a dominant source of air pollution in many cities. Nat. Commun. 2014, 5, 3749. 10.1038/ncomms4749. [DOI] [PubMed] [Google Scholar]
- Henry K. M.; Donahue N. M. Photochemical Aging of α-Pinene Secondary Organic Aerosol: Effects of OH Radical Sources and Photolysis. J. Phys. Chem. A 2012, 116, 5932–5940. 10.1021/jp210288s. [DOI] [PubMed] [Google Scholar]
- Bruns E. A.; El Haddad I.; Keller A.; Klein F.; Kumar N. K.; Pieber S. M.; Corbin J. C.; Slowik J. G.; Brune W. H.; Baltensperger U.; et al. Inter-comparison of laboratory smog chamber and flow reactor systems on organic aerosol yield and composition. Atmos. Meas. Tech. 2015, 8, 2315–2332. 10.5194/amt-8-2315-2015. [DOI] [Google Scholar]
- Bruns E. A.; Krapf M.; Orasche J.; Huang Y.; Zimmermann R.; Drinovec L.; Močnik G.; El-Haddad I.; Slowik J. G.; Dommen J.; et al. Characterization of primary and secondary wood combustion products generated under different burner loads. Atmos. Chem. Phys. 2015, 15, 2825–2841. 10.5194/acp-15-2825-2015. [DOI] [Google Scholar]
- Stirnweis L.; Marcolli C.; Dommen J.; Barmet P.; Frege C.; Platt S. M.; Bruns E. A.; Krapf M.; Slowik J. G.; Wolf R.; et al. Assessing the influence of NOx concentrations and relative humidity on secondary organic aerosol yields from α-pinene photo-oxidation through smog chamber experiments and modelling calculations. Atmos. Chem. Phys. 2017, 17, 5035–5061. 10.5194/acp-17-5035-2017. [DOI] [Google Scholar]
- Molteni U.; Bianchi F.; Klein F.; El Haddad I.; Frege C.; Rossi M. J.; Dommen J.; Baltensperger U. Formation of highly oxygenated organic molecules from aromatic compounds. Atmos. Chem. Phys. 2018, 18, 1909–1921. 10.5194/acp-18-1909-2018. [DOI] [Google Scholar]
- Pfaffenberger L.; Barmet P.; Slowik J. G.; Praplan A. P.; Dommen J.; Prévôt A. S. H.; Baltensperger U. The link between organic aerosol mass loading and degree of oxygenation: an α-pinene photooxidation study. Atmos. Chem. Phys. 2013, 13, 6493–6506. 10.5194/acp-13-6493-2013. [DOI] [Google Scholar]
- Tiitta P.; Leskinen A.; Hao L.; Yli-Pirilä P.; Kortelainen M.; Grigonyte J.; Tissari J.; Lamberg H.; Hartikainen A.; Kuuspalo K.; et al. Transformation of logwood combustion emissions in a smog chamber: formation of secondary organic aerosol and changes in the primary organic aerosol upon daytime and nighttime aging. Atmos. Chem. Phys. 2016, 16, 13251–13269. 10.5194/acp-16-13251-2016. [DOI] [Google Scholar]
- Bruns E. A.; Slowik J. G.; El Haddad I.; Kilic D.; Klein F.; Dommen J.; Temime-Roussel B.; Marchand N.; Baltensperger U.; Prévôt A. S. H. Characterization of gas-phase organics using proton transfer reaction time-of-flight mass spectrometry: fresh and aged residential wood combustion emissions. Atmos. Chem. Phys. 2017, 17, 705–720. 10.5194/acp-17-705-2017. [DOI] [Google Scholar]
- Bertrand A.; Stefenelli G.; Jen C. N.; Pieber S. M.; Bruns E. A.; Ni H.; Temime-Roussel B.; Slowik J. G.; Goldstein A. H.; El Haddad I.; et al. Evolution of the chemical fingerprint of biomass burning organic aerosol during aging. Atmos. Chem. Phys. 2018, 18, 7607–7624. 10.5194/acp-18-7607-2018. [DOI] [Google Scholar]
- Suarez-Bertoa R.; Zardini A. A.; Platt S. M.; Hellebust S.; Pieber S. M.; El Haddad I.; Temime-Roussel B.; Baltensperger U.; Marchand N.; Prévôt A. S. H.; et al. Primary emissions and secondary organic aerosol formation from the exhaust of a flex-fuel (ethanol) vehicle. Atmos. Environ. 2015, 117, 200–211. 10.1016/j.atmosenv.2015.07.006. [DOI] [Google Scholar]
- Hunter J. F.; Carrasquillo A. J.; Daumit K. E.; Kroll J. H. Secondary Organic Aerosol Formation from Acyclic, Monocyclic, and Polycyclic Alkanes. Environ. Sci. Technol. 2014, 48, 10227–10234. 10.1021/es502674s. [DOI] [PubMed] [Google Scholar]
- Gkatzelis G. I.; Papanastasiou D. K.; Florou K.; Kaltsonoudis C.; Louvaris E.; Pandis S. N. Measurement of nonvolatile particle number size distribution. Atmos. Meas. Tech. 2016, 9, 103–114. 10.5194/amt-9-103-2016. [DOI] [Google Scholar]
- Zhou J.; Zotter P.; Bruns E. A.; Stefenelli G.; Bhattu D.; Brown S.; Bertrand A.; Marchand N.; Lamkaddam H.; Slowik J. G.; et al. Particle-bound reactive oxygen species (PB-ROS) emissions and formation pathways in residential wood smoke under different combustion and aging conditions. Atmos. Chem. Phys. 2018, 18, 6985–7000. 10.5194/acp-18-6985-2018. [DOI] [Google Scholar]
- Bertrand A.; Stefenelli G.; Pieber S. M.; Bruns E. A.; Temime-Roussel B.; Slowik J. G.; Wortham H.; Prévôt A. S. H.; El Haddad I.; Marchand N. Influence of the vapor wall loss on the degradation rate constants in chamber experiments of levoglucosan and other biomass burning markers. Atmos. Chem. Phys. 2018, 18, 10915–10930. 10.5194/acp-18-10915-2018. [DOI] [Google Scholar]
- Kaltsonoudis C.; Jorga S. D.; Louvaris E.; Florou K.; Pandis S. N. A portable dual-smog-chamber system for atmospheric aerosol field studies. Atmos. Meas. Tech. 2019, 12, 2733–2743. 10.5194/amt-12-2733-2019. [DOI] [Google Scholar]
- Kilic D.; El Haddad I.; Brem B. T.; Bruns E.; Bozetti C.; Corbin J.; Durdina L.; Huang R. J.; Jiang J.; Klein F.; et al. Identification of secondary aerosol precursors emitted by an aircraft turbofan. Atmos. Chem. Phys. Discuss 2018, 18, 7379–7391. 10.5194/acp-18-7379-2018. [DOI] [Google Scholar]
- Zhou J.; Elser M.; Huang R.-J.; Krapf M.; Fröhlich R.; Bhattu D.; Stefenelli G.; Zotter P.; Bruns E. A.; Pieber S. M.; et al. Predominance of secondary organic aerosol to particle-bound reactive oxygen species activity in fine ambient aerosol. Atmos. Chem. Phys. 2019, 19, 14703–14720. 10.5194/acp-19-14703-2019. [DOI] [Google Scholar]
- Stefenelli G.; Jiang J.; Bertrand A.; Bruns E. A.; Pieber S. M.; Baltensperger U.; Marchand N.; Aksoyoglu S.; Prévôt A. S. H.; Slowik J. G.; et al. Secondary organic aerosol formation from smoldering and flaming combustion of biomass: a box model parametrization based on volatility basis set. Atmos. Chem. Phys. 2019, 19, 11461–11484. 10.5194/acp-19-11461-2019. [DOI] [Google Scholar]
- Alroe J.; Cravigan L. T.; Mallet M. D.; Ristovski Z. D.; Miljevic B.; Osuagwu C. G.; Johnson G. R. Determining the link between hygroscopicity and composition for semi-volatile aerosol species. Atmos. Meas. Tech. 2018, 11, 4361–4372. 10.5194/amt-11-4361-2018. [DOI] [Google Scholar]
- Jorga S. D.; Kaltsonoudis C.; Liangou A.; Pandis S. N. Measurement of Formation Rates of Secondary Aerosol in the Ambient Urban Atmosphere Using a Dual Smog Chamber System. Environ. Sci. Technol. 2020, 54, 1336–1343. 10.1021/acs.est.9b03479. [DOI] [PubMed] [Google Scholar]
- Faiola C. L.; Pullinen I.; Buchholz A.; Khalaj F.; Ylisirniö A.; Kari E.; Miettinen P.; Holopainen J. K.; Kivimäenpää M.; Schobesberger S.; et al. Secondary Organic Aerosol Formation from Healthy and Aphid-Stressed Scots Pine Emissions. ACS Earth Space Chem. 2019, 3, 1756–1772. 10.1021/acsearthspacechem.9b00118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein F.; Baltensperger U.; Prévôt A. S. H.; El Haddad I. Quantification of the impact of cooking processes on indoor concentrations of volatile organic species and primary and secondary organic aerosols. Indoor Air 2019, 29, 926–942. 10.1111/ina.12597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang N.; Kostenidou E.; Donahue N. M.; Pandis S. N. Multi-generation chemical aging of α-pinene ozonolysis products by reactions with OH. Atmos. Chem. Phys. 2018, 18, 3589–3601. 10.5194/acp-18-3589-2018. [DOI] [Google Scholar]
- Kostenidou E.; Karnezi E.; Kolodziejczyk A.; Szmigielski R.; Pandis S. N. Physical and Chemical Properties of 3-Methyl-1,2,3-butanetricarboxylic Acid (MBTCA) Aerosol. Environ. Sci. Technol. 2018, 52, 1150–1155. 10.1021/acs.est.7b04348. [DOI] [PubMed] [Google Scholar]
- Kristensen K.; Jensen L. N.; Glasius M.; Bilde M. The effect of sub-zero temperature on the formation and composition of secondary organic aerosol from ozonolysis of alpha-pinene. Environ. Sci.: Processes Impacts 2017, 19, 1220–1234. 10.1039/c7em00231a. [DOI] [PubMed] [Google Scholar]
- Knopf D. A.; Alpert P. A.; Wang B. The Role of Organic Aerosol in Atmospheric Ice Nucleation: A Review. ACS Earth Space Chem. 2018, 2, 168–202. 10.1021/acsearthspacechem.7b00120. [DOI] [Google Scholar]
- Quéléver L. L. J.; Kristensen K.; Normann Jensen L.; Rosati B.; Teiwes R.; Daellenbach K. R.; Peräkylä O.; Roldin P.; Bossi R.; Pedersen H. B.; et al. Effect of temperature on the formation of highly oxygenated organic molecules (HOMs) from alpha-pinene ozonolysis. Atmos. Chem. Phys. 2019, 19, 7609–7625. 10.5194/acp-19-7609-2019. [DOI] [Google Scholar]
- Li Z.; Tikkanen O.-P.; Buchholz A.; Hao L.; Kari E.; Yli-Juuti T.; Virtanen A. Effect of Decreased Temperature on the Evaporation of α-Pinene Secondary Organic Aerosol Particles. ACS Earth Space Chem. 2019, 3, 2775–2785. 10.1021/acsearthspacechem.9b00240. [DOI] [Google Scholar]
- Coates J.; Mar K. A.; Ojha N.; Butler T. M. The influence of temperature on ozone production under varying NOx conditions – a modelling study. Atmos. Chem. Phys. 2016, 16, 11601–11615. 10.5194/acp-16-11601-2016. [DOI] [Google Scholar]
- Mu Q.; Shiraiwa M.; Octaviani M.; Ma N.; Ding A.; Su H.; Lammel G.; Pöschl U.; Cheng Y. Temperature effect on phase state and reactivity controls atmospheric multiphase chemistry and transport of PAHs. Sci. Adv. 2018, 4, eaap7314 10.1126/sciadv.aap7314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osseiran N.; Romanias M. N.; Gaudion V.; Angelaki M. E.; Papadimitriou V. C.; Tomas A.; Coddeville P.; Thevenet F. Development and Validation of a Thermally Regulated Atmospheric Simulation Chamber (THALAMOS): A Versatile Tool to Simulate Atmospheric Processes. J. Environ. Sci. 2020, 95, 141–154. 10.1016/j.jes.2020.03.036. [DOI] [PubMed] [Google Scholar]
- Grira A.; Amarandei C.; Romanias M. N.; El Dib G.; Canosa A.; Arsene C.; Bejan I. G.; Olariu R. I.; Coddeville P.; Tomas A. Kinetic Measurements of Cl Atom Reactions with C5–C8 Unsaturated Alcohols. Atmosphere 2020, 11, 256. 10.3390/atmos11030256. [DOI] [Google Scholar]
- Spanel P.; Smith D. Advances in On-line Absolute Trace Gas Analysis by SIFT-MS. Curr. Anal. Chem. 2013, 9, 525. 10.2174/15734110113099990017. [DOI] [Google Scholar]
- Smith D.; Španěl P. Selected Ion Flow Tube Mass Spectrometry (SIFT-MS) for On-Line Trace Gas Analysis. Mass Spectrom. Rev. 2005, 24, 661–700. 10.1002/mas.20033. [DOI] [PubMed] [Google Scholar]
- Atkinson R.; Baulch D. L.; Cox R. A.; Crowley J. N.; Hampson R. F.; Hynes R. G.; Jenkin M. E.; Rossi M. J.; Troe J. Evaluated Kinetic and Photochemical Data for Atmospheric Chemistry: Volume II - Gas Phase Reactions of Organic Species. Atmos. Chem. Phys. 2006, 6, 3625–4055. 10.5194/acp-6-3625-2006. [DOI] [Google Scholar]
- Burkholder J. B.; Sander S. P.; Abbatt J.; Barker J. R.; Huie R. E.; Kolb C. E.; Kurylo M. J.; Orkin V. L.; Wilmouth D. M.; Wine P. H.. Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 18; JPL Publication 15-10; Pasadena, 2015. [Google Scholar]
- King M.The Relative-Rate Technique for Determining Rate Constants. ECG Environmental Briefs, 2016, ECGEB No 13.
- Bedjanian Y. Temperature-Dependent Rate Constant for the Reaction of Hydroxyl Radical with 3-Hydroxy-3-methyl-2-butanone. J. Phys. Chem. A 2019, 123, 10446–10453. 10.1021/acs.jpca.9b08714. [DOI] [PubMed] [Google Scholar]
- Bedjanian Y.; Morin J.; Romanias M. N. Reactions of OH Radicals with 2-methyl-1-butyl, neopentyl and 1-hexyl nitrates. Structure-Activity Relationship for Gas-Phase Reactions of OH with Alkyl nitrates: An Update. Atmos. Environ. 2018, 180, 167–172. 10.1016/j.atmosenv.2018.03.002. [DOI] [Google Scholar]
- Morin J.; Romanias M. N.; Bedjanian Y. Experimental Study of the Reactions of OH Radicals with Propane, n-Pentane, and n-Heptane over a Wide Temperature Range. Int. J. Chem. Kinet. 2015, 47, 629–637. 10.1002/kin.20936. [DOI] [Google Scholar]
- Su M.-C.; Kumaran S. S.; Lim K. P.; Michael J. V.; Wagner A. F.; Harding L. B.; Fang D.-C. Rate Constants, 1100 ≤ T ≤ 2000 K, for H + NO2 → OH + NO Using Two Shock Tube Techniques: Comparison of Theory to Experiment†. J. Phys. Chem. A 2002, 106, 8261–8270. 10.1021/jp0141023. [DOI] [Google Scholar]
- Bedjanian Y.; Le Bras G.; Poulet G. Kinetic Study of the Reactions of Br2 With OH And OD. Int. J. Chem. Kinet. 1999, 31, 698–704. . [DOI] [Google Scholar]
- Bedjanian Y.; Le Bras G.; Poulet G. Kinetic Study of OH + OH And OD + OD Reactions. J. Phys. Chem. A 1999, 103, 7017–7025. 10.1021/jp991146r. [DOI] [Google Scholar]
- Kaufman F. Kinetics of Elementary Radical Reactions in the Gas Phase. J. Phys. Chem. 1984, 88, 4909–4917. 10.1021/j150665a024. [DOI] [Google Scholar]
- Ivanov A. V.; Trakhtenberg S.; Bertram A. K.; Gershenzon Y. M.; Molina M. J. OH, HO2, and Ozone Gaseous Diffusion Coefficients. J. Phys. Chem. A 2007, 111, 1632–1637. 10.1021/jp066558w. [DOI] [PubMed] [Google Scholar]
- McGillen M. R.; Baasandorj M.; Burkholder J. B. Gas-Phase Rate Coefficients for the OH + n-, i-, s-, and t-Butanol Reactions Measured Between 220 and 380 K: Non-Arrhenius Behavior and Site-Specific Reactivity. J. Phys. Chem. A 2013, 117, 4636–4656. 10.1021/jp402702u. [DOI] [PubMed] [Google Scholar]
- Seal P.; Oyedepo G.; Truhlar D. G. Kinetics of the Hydrogen Atom Abstraction Reactions from 1-Butanol by Hydroxyl Radical: Theory Matches Experiment and More. J. Phys. Chem. A 2013, 117, 275–282. 10.1021/jp310910f. [DOI] [PubMed] [Google Scholar]
- Zhang P.; Klippenstein S. J.; Law C. K. Ab Initio Kinetics for the Decomposition of Hydroxybutyl and Butoxy Radicals of n-Butanol. J. Phys. Chem. A 2013, 117, 1890–1906. 10.1021/jp400155z. [DOI] [PubMed] [Google Scholar]
- Sime S. L.; Blitz M. A.; Seakins P. W. Rate coefficients for the reactions of OH with butanols from 298 K to temperatures relevant for low-temperature combustion. Int. J. Chem. Kinet. 2020, 52, 1046–1059. 10.1002/kin.21422. [DOI] [Google Scholar]
- Rissanen M. P.; Arppe S. L.; Timonen R. S. Kinetics of Several Oxygenated Carbon-Centered Free Radical Reactions with NO2. J. Phys. Chem. A 2013, 117, 3902–3908. 10.1021/jp401999e. [DOI] [PubMed] [Google Scholar]
- Rissanen M. P.; Ihlenborg M.; Pekkanen T. T.; Timonen R. S. Kinetics of Several Oxygen-Containing Carbon-Centered Free Radical Reactions with Nitric Oxide. J. Phys. Chem. A 2015, 119, 7734–7741. 10.1021/acs.jpca.5b01027. [DOI] [PubMed] [Google Scholar]
- Carr S. A.; Blitz M. A.; Seakins P. W. Site-Specific Rate Coefficients for Reaction of OH with Ethanol from 298 to 900 K. J. Phys. Chem. A 2011, 115, 3335–3345. 10.1021/jp200186t. [DOI] [PubMed] [Google Scholar]
- McGillen M. R.; Carter W. P. L.; Mellouki A.; Orlando J. J.; Picquet-Varrault B.; Wallington T. J. Database for the Kinetics of the Gas-Phase Atmospheric Reactions of Organic Compounds. Earth Syst. Sci. Data Discuss. 2020, 12, 1203. 10.5194/essd-12-1203-2020. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.







