Abstract
In project management, agility concept has emerged for overcoming the limitations of traditional methodologies that are sequential and linear. An agile project contains planned processes as well as iterations. In global competitive areas, achieving agility in outsourcing processes enables the companies to cope with changes and dynamic issues. This paper introduces an integrated cognitive map-based intuitionistic fuzzy multiple criteria decision aid to rank agile outsourcing provider alternatives and then determine the best performing one. Intuitionistic fuzzy sets are employed for dealing with uncertain and vague data along with the loss of information that may be occurred in numerical operations with fuzzy numbers. Intuitionistic fuzzy cognitive map tool is used to weight the evaluation criteria that are interrelated with each other with causal links. The most appropriate agile outsourcing provider alternative is identified via intuitionistic fuzzy complex proportional assessment technique, which aims to obtain a solution relative to the ideal solution. In order to demonstrate the robustness of the proposed intuitionistic fuzzy decision aid, a case study is conducted in Turkish white goods industry. As a comparative study, a scenario analysis is provided to understand the impacts of COVID-19 pandemic on agile provider evaluation/selection decision. According to the results obtained from the scenario analysis, it is worth noting that home office procedures are appropriate for maintaining agility in outsourcing processes of project management.
Keywords: Intuitionistic fuzzy sets, Intuitionistic fuzzy cognitive map, Intuitionistic fuzzy complex proportional assessment, Agile provider selection, Project management, COVID-19 pandemic
Introduction
Agile project management concept is introduced in 2001 to handle ineffectiveness in defining the requirements of the customers, managing the changes of the project needs, and saving cost. It has been emerged from unpredictable characteristics of customer needs, developing technology, and unstability of business problems (Lei et al. 2017). Agile concept was required in project management in order to eliminate the shortcomings of Waterfall project management methodology, which is linear and sequential. In an agile project, processes are planned and then managed in iterative manner. The representatives of stakeholders of the project criticize and review each iteration of the agile project. The outcomes achieved from an iteration lead to construct the following project stage (Totten 2017).
In increasing competition of the markets, agility concept has become more and more crucial in managerial issues. Accordingly, agility in outsourcing processes has emerged in order to deal with changes and dynamic environment (Liu et al. 2008). Outsourcing provides disintegration of the jobs by collaborating with a provider in lieu of insourcing an activity (Tsai et al. 2010). In the recent past, outsourcing is a component of strategic management as well as a part of operations management, although it was firstly employed in the early 1990s in information technologies (IT) to achieve cost savings and technical efficiency (Tjader et al. 2014). For the employer, the selection of the outsourcer has a major impact on the cost and quality of the project. Selecting the wrong provider may lead to delayed completion and increased costs (Chen et al. 2021a).
The objective of this paper is to develop an integrated intuitionistic fuzzy decision framework that identifies the most suitable agile provider alternative. The presence of uncertain, vague, and hesitative data led to utilize intuitionistic fuzzy numbers in order to express interrelationships among the evaluation criteria and the ratings of the alternatives with regard to the criteria. Intuitionistic fuzzy cognitive map (IFCM) technique is employed to handle cause-and-effect relationships among the criteria. Selection procedure is completed using intuitionistic fuzzy complex proportional assessment (IFCOPRAS) methodology that obtains a solution relative to the ideal solution. To illustrate the proposed integrated decision framework, a case study is conducted in a white goods manufacturer that aims to determine the most appropriate agile outsourcing provider for an IT-oriented project. In order to understand whether COVID-19 pandemic causes to a change in rank-order of the alternatives or not, a scenario analysis is provided and then a comparative analysis is demonstrated.
The contributions of the proposed method to the literature can be listed as follows. First, the proposed method allows to utilize intuitionistic fuzzy numbers to express the experts’ opinions. Uncertain and vague data can be easily handled by fuzzy decision analyses representing the data by linguistic terms. However, fuzzy decision making approaches cannot incorporate hesitative data or lack of information of the decision-makers. For that purpose, intuitionistic fuzzy decision aid framework is proposed in order to be able to cope with hesitation in data. Second, IFCM methodology allows to transform the cause-and-effect relationships among the criteria into the intuitionistic fuzzy numbers by considering hesitation. Third, the presented intuitionistic decision framework obtains the best performing alternative using IFCOPRAS methodology that finds a solution relative to the ideal solution. Fourth, this is the paper that combines IFCM and IFCOPRAS throughout the literature. Fifth, there is not another work that ranks agile provider alternatives in white goods sector. Sixth, a scenario-based comparative analysis is provided in order to understand the impacts of COVID-19 pandemic on agile provider evaluation/selection decision framework.
The remaining parts of the paper are organized as follows. Section 2 explains a detailed literature review on outsourcing provider evaluation/selection problem. Section 3 outlines materials and methods along with the proposed decision aid. Conducted case study is given in the subsequent section. Section 5 gives an evaluation of COVID-19 effect by providing a scenario analysis. Managerial implications and discussion are delineated in Sect. 6. Concluding remarks as well as future research directions are provided in the last section.
Literature review
In the recent past, researchers have contributed to the “provider evaluation/selection” literature by proposing various approaches. In this section, providing a deep literature survey related to this field and demonstrating the gap in the literature are aimed. For that reason, the online databases namely “Science Direct”, “Taylor & Francis”, “Springer”, and “Emerald” were examined, and the research papers that were published from 2006 to 2020 and related to “provider evaluation/selection” problem are observed. “Provider evaluation”, “provider selection” and “decision” are utilized as keywords while searching the related papers in the literature. In order to give a detailed and apparent structure while surveying the literature, categorization of the reviewed papers is provided. According to the methods applied in the reviewed works, two main categories named as “decision-making-based approaches” and “optimization-based approaches” are created.
In total, 63 research papers are reviewed, 73% of them utilized decision making based approaches, whereas 27% of them employed optimization-based techniques for solving provider evaluation/selection problem. 45% of the reviewed papers that used decision making based approaches were published in the past 5 years, 55% of them were published earlier. Besides, 35% of the reviewed papers that used optimization-based approaches were published in the past 5 years, and 65% of them were published earlier. 51% of the reviewed papers that utilized decision-making-based approaches introduced individual decision making methodology, and 49% of them presented integrated decision aid methods. On the other hand, 41% of the reviewed papers that employed optimization-based approaches introduced individual decision framework and 59% of them presented integrated decision support.
First, the studies that introduce decision-making-based approaches for provider selection problem are reviewed, and table format is given in Table 1. Bottani et al. (2006) ranked third-party logistics (3PL) provider alternatives and selected the most suitable one using fuzzy technique for order preference by similarity to ideal solution (TOPSIS) method. Likewise, Jharkharia et al. (2007) identified the best performing 3PL provider alternative by employing analytic network process (ANP) methodology. Wang et al. (2007) combined analytic hierarchy process (AHP) and preference ranking organization method for enrichment evaluations (PROMETHEE) II techniques for selecting the most suitable information systems project provider incorporating both quantitative and qualitative data into the decision framework.
Table 1.
Reviewed papers that propose decision making-based approaches for outsourcing provider selection problem
| Author(s) | Year | AHP | ANP | TOPSIS | PROMETHEE | VIKOR | DEMATEL | QFD | ELECTRE | Delphi |
|---|---|---|---|---|---|---|---|---|---|---|
| Bottani et al | 2006 | x | ||||||||
| Jharkharia et al | 2007 | x | ||||||||
| Wang et al | 2007 | x | x | |||||||
| Efendigil et al | 2008 | x | ||||||||
| Hsu and Hsu | 2008 | x | x | |||||||
| Büyüközkan et al | 2009 | |||||||||
| Chen et al | 2009 | x | ||||||||
| Kahraman et al | 2009 | x | ||||||||
| Chen et al | 2010 | x | x | |||||||
| Cheng et al | 2010 | x | ||||||||
| Lin et al | 2010 | x | ||||||||
| Tjader et al | 2010 | x | ||||||||
| Kahraman et al | 2010 | x | ||||||||
| Liou et al | 2010 | x | x | x | ||||||
| Chen et al | 2011 | x | ||||||||
| Kumar et al | 2011 | x | ||||||||
| Cao et al | 2012 | x | ||||||||
| Erkayman et al | 2012 | x | x | |||||||
| Ho et al | 2012 | x | x | |||||||
| Kaya | 2012 | x | ||||||||
| Low et al | 2012 | x | x | |||||||
| Govindan et al | 2013 | x | x | |||||||
| Hsu and James | 2013 | x | x | |||||||
| Hsu et al | 2013 | x | x | |||||||
| Uygun et al | 2014 | x | x | |||||||
| Alkhatib et al | 2015 | x | x | x | ||||||
| Faisal and Raza | 2016 | |||||||||
| Govindan et al | 2016 | x | ||||||||
| Lin | 2016 | x | ||||||||
| Sen et al | 2017 | x | ||||||||
| Shahrasbi et al | 2017 | x | x | x | ||||||
| Büyüközkan et al | 2017 | x | x | |||||||
| Ecer | 2018 | x | ||||||||
| Ji et al | 2018 | x | ||||||||
| Sremac et al | 2018 | |||||||||
| Singh et al | 2018 | x | x | |||||||
| Li et al | 2018 | x | ||||||||
| Chen | 2018 | x | x | |||||||
| Percin | 2019 | x | x | |||||||
| Govindan et al | 2019 | x | ||||||||
| Ljubojevic et al | 2019 | x | ||||||||
| Zarbakhshnia et al | 2020 | x | ||||||||
| Rani et al | 2020 | |||||||||
| Liu et al | 2020 | x | ||||||||
| Gireesha et al | 2020 | |||||||||
| Mishra et al | 2020 | x |
| Author(s) | Year | EDAS | ANN | Entropy | Choquet integral | Grey relation analysis | MABAC | SWARA | WASPAS | AD | BWM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bottani et al | 2006 | ||||||||||
| Jharkharia et al | 2007 | ||||||||||
| Wang et al | 2007 | ||||||||||
| Efendigil et al | 2008 | x | |||||||||
| Hsu and Hsu | 2008 | x | |||||||||
| Büyüközkan et al | 2009 | x | |||||||||
| Chen et al | 2009 | ||||||||||
| Kahraman et al | 2009 | ||||||||||
| Chen et al | 2010 | ||||||||||
| Cheng et al | 2010 | ||||||||||
| Lin et al | 2010 | ||||||||||
| Tjader et al | 2010 | ||||||||||
| Kahraman et al | 2010 | ||||||||||
| Liou et al | 2010 | ||||||||||
| Chen et al | 2011 | ||||||||||
| Kumar et al | 2011 | ||||||||||
| Cao et al | 2012 | x | |||||||||
| Erkayman et al | 2012 | ||||||||||
| Ho et al | 2012 | ||||||||||
| Kaya | 2012 | ||||||||||
| Low et al | 2012 | ||||||||||
| Govindan et al | 2013 | ||||||||||
| Hsu and James | 2013 | ||||||||||
| Hsu et al | 2013 | x | |||||||||
| Uygun et al | 2014 | ||||||||||
| Alkhatib et al | 2015 | ||||||||||
| Faisal and Raza | 2016 | x | |||||||||
| Govindan et al | 2016 | ||||||||||
| Lin | 2016 | ||||||||||
| Sen et al | 2017 | ||||||||||
| Shahrasbi et al | 2017 | ||||||||||
| Büyüközkan et al | 2017 | ||||||||||
| Ecer | 2018 | x | |||||||||
| Ji et al | 2018 | x | |||||||||
| Sremac et al | 2018 | x | x | ||||||||
| Singh et al | 2018 | ||||||||||
| Li et al | 2018 | ||||||||||
| Chen | 2018 | ||||||||||
| Percin | 2019 | x | x | ||||||||
| Govindan et al | 2019 | ||||||||||
| Ljubojevic et al | 2019 | ||||||||||
| Zarbakhshnia et al | 2020 | ||||||||||
| Rani et al | 2020 | x | |||||||||
| Liu et al | 2020 | x | x | ||||||||
| Gireesha et al | 2020 | x | |||||||||
| Mishra et al | 2020 |
Efendigil et al. (2008) aimed to solve the most appropriate third-party reverse logistics (3PRL) provider alternative by combining fuzzy AHP and artificial neural network (ANN). Hsu and Hsu (2008) evaluated information systems provider selection criteria using Delphi method, calculated criteria weights by Entropy technique, and identified the best alternative employing TOPSIS methodology. Büyüközkan et al. (2009) proposed a 2-additive choquet integral method to fourth party logistics service provider selection problem by conducting a case study in a logistics firm that performs in Turkey. Chen et al. (2009) introduced an efficient delivery approach and evaluated possible providers employing fuzzy viekriterijumsko kompromisno rangiranje (VIKOR) method for an IT outsourcing project. Likewise, Kahraman et al. (2009) identified the best performing IT service provider for a furniture company located in Konya, Turkey, by utilizing fuzzy TOPSIS methodology. Chen et al. (2010) integrated fuzzy AHP and fuzzy TOPSIS methods for selecting the most appropriate outsourcing manufacturing partner in pharmaceutical research and development. Cheng et al. (2010) employed ANP to rank 3PRL providers for high-technology manufacturing firms by conducting a case study in electronics sector in Taiwan. In a similar way, Lin et al. (2010) used ANP to propose a hybrid multi-criteria decision making (MCDM) approach to deal with complicated manufacturing outsourcing provider evaluation and selection by providing an application for a semiconductor company in Taiwan. Likewise, Tjader et al. (2010) made use of ANP method to decide the best off-shore policy between client and vendor by using decision-makers, influence groups and stakeholder’s perspective for roughly 50 factors.
Kahraman et al. (2010) determined the most appropriate enterprise resource planning (ERP) project outsourcing provider alternative by employing fuzzy AHP technique. Liou et al. (2010) integrated DEMATEL, ANP, and VIKOR methods to evaluate the criteria of outsourcing providers and ranking the priorities of the alternatives in airline industry. Chen et al. (2011) employed fuzzy PROMETHEE for evaluating the service providers in order to provide a guideline to managers for being able to manage outsourcing decisions efficiently. Kumar et al. (2012) weighted the criteria of 3PL provider selection problem through consistent fuzzy preference relation and ranked the alternatives with VIKOR method. Cao et al. (2012) utilized Dodgson function to identify potential providers, ANP to weight selection criteria, and grey relation analysis to rank the providers alternatives in finance sector. Erkayman et al. (2012) combined fuzzy AHP and fuzzy TOPSIS methods for ranking 3PL service providers. Likewise, Ho et al. (2012) solved 3PL provider selection problem by integrating quality function deployment (QFD) and fuzzy AHP. Kaya (2012) assessed and selected the most appropriate waste electrical and electronic equipment (WEEE) outsourcing firm in Turkey using fuzzy AHP. Low et al. (2012) evaluated the criteria of cloud-based hospital information technologies service provider by combining fuzzy Delphi method and fuzzy AHP. Govindan et al. (2013) ranked the priorities of 3PRL provider selection criteria with AHP and evaluated the alternatives with ANP methodology by conducting an illustrative case study in an automobile company. Hsu and James (2013) identified the most suitable provider in airline industry by integrating the decision making trial and evaluation laboratory (DEMATEL) and ANP. Similarly, Hsu et al. (2013) determined the most suitable provider in airline industry combining DEMATEL, ANP, and grey relation methods. Uygun et al. (2015) combined DEMATEL and fuzzy ANP methods for provider evaluation in telecommunication sector.
In the last 5 years, Alkhatib et al. (2015) proposed 3PL provider selection framework in which fuzzy DEMATEL is used to weight evaluation criteria, fuzzy TOPSIS is employed to rank the alternatives, and fuzzy VIKOR is utilized to test stability of the ranking results. Faisal and Raza (2016) constructed a grey theory-based decision framework for IT outsourcing provider selection for academic institutions. Govindan et al. (2016) revealed the interrelationships among 3PL provider selection criteria and then proposed a selection framework using grey DEMATEL in automotive industry. Lin (2016) applied fuzzy AHP technique for service provider selection in Taiwanese tourism industry. Sen et al. (2017) solved 3PL provider selection problem using grey-TOPSIS methodology. Shahrasbi et al. (2017) ranked the alternatives of security service providers using group decision making and applied fuzzy TOPSIS, fuzzy VIKOR, and fuzzy elimination et choix traduisant la realité (ELECTRE) methods by making use of Hamming, Chebyshev, Euclidean, and Manhattan distances. In order to obtain a single final rank-order, they employed an aggregation technique. Büyüközkan et al. (2017) combined intuitionistic fuzzy DEMATEL and intuitionistic fuzzy ANP methodologies for evaluating customer relationship management partners.
More recently, Ecer (2018) integrated fuzzy AHP and evaluation-based on distance from average solution (EDAS) for 3PL provider selection in marble industry. Ji et al. (2018) combined multi-attribute border approximation area comparison (MABAC) and ELECTRE methods for outsourcing provider selection in the presence of neutrosophic fuzzy numbers. Sremac et al. (2018) utilized rough stepwise weight assessment ratio analysis (SWARA) and rough weighted aggregated sum product assessment (WASPAS) methods by integrating rough Dombi aggregation operator into the 3PL provider evaluation framework. Likewise, Singh et al. (2018) developed fuzzy AHP and fuzzy TOPSIS combined approach for 3PL provider selection for a cold supply chain in food industry. Li et al. (2018) solved 3PRL provider selection using cumulative prospect theory and then provided a comparative analysis employing fuzzy TOPSIS technique for an electronics company. Chen (2018) solved sustainable supplier selection problem by employing QFD and TOPSIS methods in the hesitative environment.
Recently, Percin (2019) identified the best performing outsourcing provider in chemical industry combining fuzzy SWARA and fuzzy axiomatic design (AD) methodologies and then provided a sensitivity analysis in order to compare the results with those of other decision making techniques namely fuzzy TOPSIS and fuzzy VIKOR. Govindan et al. (2019a, b) proposed ELECTRE-based stochastic multi-criteria acceptability analysis for 3PRL provider selection for an Indian manufacturer. Ljubojevic et al. (2019) proposed two-stage decision framework for outsourcing provider selection in transportation sector. The hybrid two-stage method combines DEMATEL with a novel outranking methodology. In a similar manner, Zarbakhshnia et al. (2020) identified the best 3PRL provider that performs for car parts production company by integrating fuzzy AHP and grey multi-objective optimization by ratio analysis. Rani et al. (2020) evaluated mobile telephone service providers incorporating intuitionistic fuzzy sets into grey relation analysis. Likewise, Mishra et al. (2020) proposed intuitionistic fuzzy ELECTRE technique for ranking and selecting mobile phone service providers. Liu et al. (2020) introduced best worst method (BWM) and Entropy integrated TOPSIS methodology for blockchain service provider selection problem in hesitative environment. Gireesha et al. (2020) developed an improved interval-valued intuitionistic fuzzy sets (IIVIFS) based WASPAS technique for cloud outsourcing provider selection. Chen et al. (2021b) employed hesitant fuzzy linguistic term set into a MCDM methodology for 3PRL provider selection problem. Moreover, they compared the ranking results of the proposed approach with different MCDM techniques, namely TOPSIS, VIKOR, COPRAS, and MULTIMOORA.
Throughout the literature, few researchers have focused on optimization-based decision support for outsourcing provider evaluation and selection framework, the tableau format of the review is given in Table 2. Araz et al. (2007) assessed the providers for a textile company and selected the most appropriate vendor by integrating PROMETHEE and fuzzy goal programming (GP) approaches. Cao et al. (2007) optimize provider selection framework by proposing two-stage combinatorial optimization model. Isiklar et al. (2007) developed fuzzy compromise programming (CP) model for 3PL provider selection for a big holding company located in Turkey. Wu and Chien (2008) constructed a decision framework to evaluate outsourcing providers and to solve order allocation problem by proposing a mixed integer linear programming (MILP) model. Wong (2012) proposed a fuzzy ANP integrated preemptive fuzzy integer GP to 3PL provider selection. Likewise, Azadi et al. (2011) ranked the efficiency of 3PRL providers by developing chance-constrained data envelopment analysis (DEA) based model. Liou et al. (2011) developed DEMATEL and ANP integrated fuzzy preference programming model to service provider selection for airline industry in Taiwan. Ukor et al. (2012) combined integer programming (IP) model, tree-search heuristic, and genetic algorithm for provider selection problem. Gonzalez-Gomez et al. (2013) compared water services outsourcing companies’ (public, private, public–private) efficiency using 80 water plants data performing in Southern Spain. For that reason, they developed a DEA model.
Table 2.
Reviewed papers that propose optimization-based approaches for outsourcing provider selection problem
| Author(s) | Year | GP | CP | IP | MILP | NLMIP | Combinatorial Optimization |
DEA | Fuzzy programming | Heuristics |
|---|---|---|---|---|---|---|---|---|---|---|
| Araz et al | 2007 | x | ||||||||
| Cao et al | 2007 | x | ||||||||
| Isiklar et al | 2007 | x | ||||||||
| Wu and Chien | 2008 | x | ||||||||
| Wong | 2010 | x | ||||||||
| Azadi et al | 2011 | x | ||||||||
| Liou et al | 2011 | x | ||||||||
| Ukor et al | 2011 | x | x | |||||||
| Gonzalez-Gomez et al | 2013 | x | ||||||||
| Percin and Min | 2013 | x | ||||||||
| Li et al | 2014 | x | ||||||||
| Wan et al | 2015 | x | ||||||||
| Tavana et al | 2016 | x | ||||||||
| Hu and Yu | 2016 | x | ||||||||
| Govindan et al | 2019 | x | ||||||||
| Lai et al | 2020 | x | ||||||||
| Wang et al | 2020 | x |
| Author(s) | Year | Genetic algorithm | Fuzzy regression | AHP | ANP | Fuzzy ANP |
DEMATEL | PROMETHEE | TOPSIS | QFD |
|---|---|---|---|---|---|---|---|---|---|---|
| Araz et al | 2007 | x | ||||||||
| Cao et al | 2007 | |||||||||
| Isiklar et al | 2007 | |||||||||
| Wu and Chien | 2008 | |||||||||
| Wong | 2010 | x | ||||||||
| Azadi et al | 2011 | |||||||||
| Liou et al | 2011 | x | x | |||||||
| Ukor et al | 2011 | x | ||||||||
| Gonzalez-Gomez et al | 2013 | |||||||||
| Percin and Min | 2013 | x | x | |||||||
| Li et al | 2014 | |||||||||
| Wan et al | 2015 | x | ||||||||
| Tavana et al | 2016 | x | ||||||||
| Hu and Yu | 2016 | x | ||||||||
| Govindan et al | 2019 | x | ||||||||
| Lai et al | 2020 | |||||||||
| Wang et al | 2020 | x |
Percin and Min (2013) proposed QFD-integrated fuzzy linear regression and zero–one goal programming models to 3PL provider selection problem. Likewise, Li et al. (2014) developed a fuzzy linear programming model for IT outsourcing provider selection. Wan et al. (2015) introduced a TOPSIS-integrated intuitionistic fuzzy linear programming model for outsourcing provider evaluation. Tavana et al. (2016) ranked the best 3PRL provider alternatives by incorporating strengths, weaknesses, opportunities, and threats (SWOT) analysis into the intuitionistic fuzzy AHP methodology employing an extension of intuitionistic fuzzy preference programming model. The proposed model is illustrated via a case study that is conducted in a pipe joint manufacturer. Hu and Yu (2016) proposed AHP integrated goal programming model for solving contract provider selection problem. Govindan et al. (2019a, b) proposed a goal programming model-based integrated fuzzy decision aid for evaluating 3PRL providers in Indian electronics industry. They combined fuzzy AHP and fuzzy TOPSIS methodologies, and considered environmental, economic, and social indicators for selecting the best performing alternative. Lately, Lai et al. (2020) proposed a compromise programming model that obtains the best performing cloud outsourcing service provider alternative. Wang et al. (2020) introduced a nonlinear mixed integer multi-objective programming model for 3PL provider selection and order allocation decision problems and then made use of genetic algorithm to convert multi-objective programming model into a single-objective model.
Although researchers have focused on outsourcing provider selection problem by proposing several decision making approaches throughout the literature, there is no work that considers cause-and-effect relationships among evaluation criteria by taking into account vagueness, uncertainty, and hesitation in interrelations. Moreover, IFCOPRAS method, which determines a solution relative to the ideal solution, has not been employed before for the selection process of the related problem. This paper aims to fill these gaps in the provider selection literature.
Materials and methods
In this section, materials and methods that are utilized in this paper are explained. Intuitionistic fuzzy sets are used for handling uncertain and vague data along with the loss of information that may be occurred in numerical operations with fuzzy numbers. Intuitionistic fuzzy cognitive map technique is employed to weight the evaluation criteria that are interrelated with each other with causal links. The most appropriate agile outsourcing provider alternative is identified via intuitionistic fuzzy complex proportional assessment technique, which aims to obtain a solution relative to the ideal solution.
Intuitionistic fuzzy sets
Fuzzy set theory was initially presented by Zadeh (1965) to cope with the decision problems that contain uncertain and vague data. Fuzzy set theory has been applied in various research studies that provide applications in different sectors. It assumes that the membership degree of an element is a single value that is between zero and one. However, the non-membership degree of an element may not always be equal to one minus the membership degree due to the hesitation degree (Otay et al. 2017). For that reason, Atanassov (1986) proposed intuitionistic fuzzy sets (IFS), which become the extension of fuzzy sets. IFS take into account the degree of hesitation that is computed as one minus the sum of membership and non-membership degrees. On the other hand, apart from IFS, throughout the literature, there are several different approaches that cope with uncertainty and vagueness with the loss of information in numerical operations named as pythagorean fuzzy sets (Yang et al. 2018), q-rung orthopair fuzzy sets (Yang et al. 2021), and proportional hesitant fuzzy linguistic term sets (Chen et al. 2016).
The basic notions and some operations of IFS are given as.
Definition 1
(Kahraman et al. 2017). Let be a given set. An IFS in E is an object Y described in
| 1 |
where and satisfy the condition for every Hesitancy is equal to one minus the sum of membership and non-membership degrees as
| 2 |
Definition 2
(De et al. 2000). Let Y and Z be two IFSs in the set E. Namely, and
The operations of summation and multiplication between and are defined as
| 3 |
| 4 |
Definition 3
(De et al. 2000). For any positive integer number k, is defined as
| 5 |
where and .
Definition 4
(Xu 2007). Let , be an intuitionistic fuzzy number. The score of is defined as follows:
| 6 |
where .
Definition 5 (
Xu et al. 2015). Let , be an intuitionistic fuzzy number. The normalized score of is defined as
| 7 |
where .
Intuitionistic fuzzy cognitive maps
Axelrod (1976) initially proposed cognitive maps (CM) as a modelling tool in political and social sciences. Directed edges and causal links have been the main elements of CMs, which may be employed as a modelling tool in various departments of the companies namely forecasting, planning, research & development.
Binary relations called as “increase” and “decrease” are used in CMs. Moreover, experts are forced to utilize crisp numbers while creating conventional CM. This situation may lead insufficient information, like different data from different experts or different data from the same expert on different days (Dursun et al. 2020). For that reason, fuzzy cognitive map (FCM) technique is developed in order to express causal links rather than numerical terms (Ross 2010). FCM combines fuzzy logic and neural networks, and enables to include fuzzy numbers or linguistic variables to determine the power of causal relations among the concepts/factors (Kosko 1986).
is the set of concepts/factors, edges show how much factors Ci cause factor Cj. The weight of each factor is computed, taking into account the effect of the other factors on the evaluated factor, by running the iterative formulation of FCM until the system will be stable as
| 8 |
where is the value of concept Ci at pth iteration, is the weight of the connection from Cj to Ci, and f is a threshold function, which is sigmoid function in this paper (Goker and Dursun 2019).
In the recent past, intuitionistic extensions of FCM are developed in order to handle the hesitation, and thus, IFSs are incorporated into the cognitive map framework (Goker et al. 2020). IFCM make use of intuitionistic fuzzy numbers for determining the power of causal links in a cognitive map (Dogu and Albayrak, 2018). The application steps of IFCM are listed as
Step 1 Define evaluation criteria and power of causalities among them by reaching consensus between decision-makers.
Step 2 Determine intuitionistic fuzzy scale and convert the causalities among the factors into the intuitionistic fuzzy numbers according to this scale.
Step 3 Identify membership, non-membership, and hesitation values.
Step 4 Construct the weight matrix.
- Step 5 Start the following iterative formulation and run it until the system will be stabilized (Dursun and Gumus 2020).
where and represent the weight matrices that refer to membership values and hesitation values of causalities, respectively.9
Intuitionistic fuzzy complex proportional assessment methodology
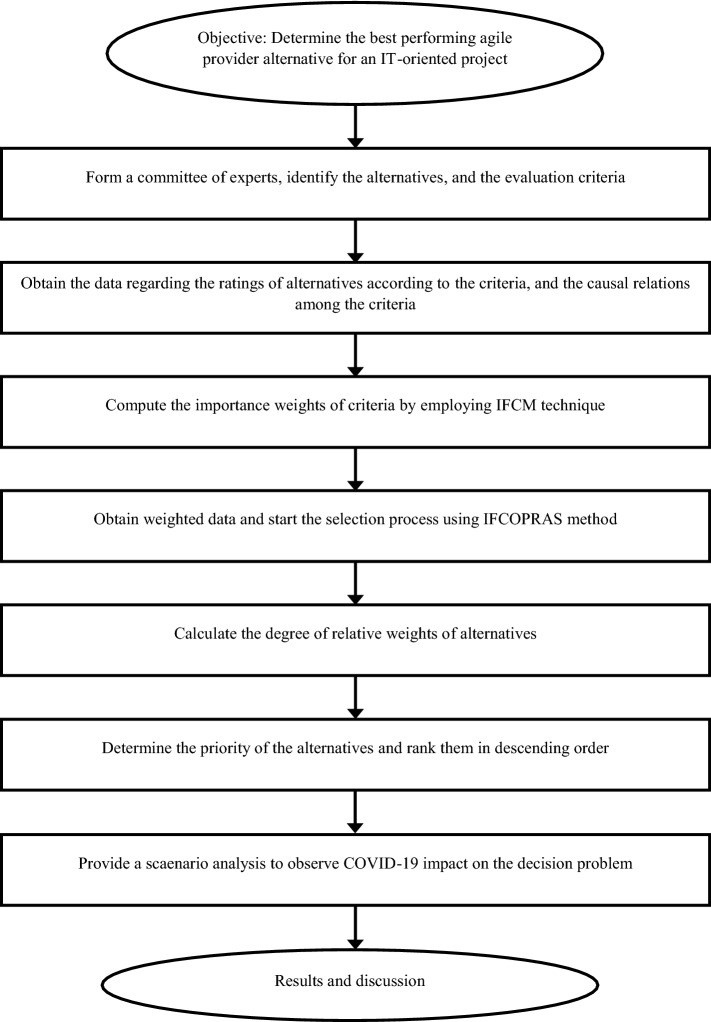
Decision problems in business life often require numerous criteria, which are conflicted and related to each other. Besides, crisp numbers may not always be available while collecting the data. In such circumstances, fuzzy set theory is suitable to cope with vagueness and imprecision in data. On the other hand, fuzzy set theory fails to handle the evaluation of membership and non-membership because of the lack of information, and thus hesitancy occurs. IFS theory is proposed to deal with hesitation in decision processes. In this paper, an integrated intuitionistic fuzzy decision aid framework is introduced. Weighting process is completed via IFCM tool, whereas IFCOPRAS method is employed for selection procedure. The complex proportional assessment (COPRAS) technique, which was initially presented by Zavadskas and Kaklauskas (1996), is an MCDM method that determines a solution relative to the ideal solution. The stepwise illustration of the developed framework, which is represented in Fig. 1, is as
Fig. 1.
The stepwise illustration of the developed framework
Step 1 Form a committee of experts, identify the alternatives (Ar = 1,2,…,m), and the evaluation criteria Ci (i = 1,2,…,n).
Step 2 Obtain the data regarding the ratings of alternatives according to the criteria, and the causal relations among the criteria.
Step 3 Compute the importance weights of criteria by following the steps of IFCM mentioned in Sect. 3.2.
- Step 4 Normalize the importance weights employing Eq. (10)
where represent the normalized weight of criterion i.10 - Step 5 Start the selection process using IFCOPRAS method. Obtain weighted data using Eq. (11)
where represents the rating of the rth alternative regarding ith criterion and is the weight of the ith criterion, and11 -
Step 6 Sum the cost and benefit criteria values.
Let be a set of cost criteria, i.e. the minimum values refer to superior option. Calculate values for each alternative employing Eq. (12).12 - Step 7 Let be a set of benefit criteria, i.e. the maximum values represent superior choice. Calculate values for each alternative employing Eq. (13).
13 - Step 9 Determine the priority of the alternatives () using Eq. (15) and rank the alternatives in descending order.
15
Case study
Agility concept becomes more and more important in white goods sector in the recent past in order to manage the projects in a more efficient manner and survive in competitive environment. Agile project management is a crucial managerial process that should be managed properly. Agile provider selection is a decision problem that contains numerous conflicting criteria and imprecision in data. For that reason, it may be solved by proposing MCDM procedure that can be employed when data are imprecise. The objective of this paper is to propose an integrated intuitionistic fuzzy decision aid to identify the most appropriate agile project provider. The application of the developed decision aid is illustrated by conducting a case study in Turkish white goods industry. The case firm has five potential providers and wants to identify the most appropriate alternative for an IT-oriented project that is supposed to be managed with agile project management methodology, and thus, a decision framework that determines the most suitable agile provider alternative is required.
Initially, agile provider selection criteria, which are listed in Table 3, are determined by conducting literature review along with collecting decision-makers’ opinions from project management department of the case firm. The first three criteria are denoted as cost criteria while the other are benefit criteria.
Table 3.
Agile provider selection criteria
| Label | Criterion | Definition |
|---|---|---|
| C1 | Cost | Refers to the cost paid to the provider |
| C2 | Complexity perception | Refers to how project provider team perceives the complexity of the project |
| C3 | Lead time | Refers to the time when the provider submits the outsourced project to the client |
| C4 | Customer participation | Refers to the participation of the client into the outsourcing process |
| C5 | Communication | Refers to the communication among project team members |
| C6 | Ability to react to change | Refers to the ability of project team for reacting in changes |
| C7 | Self-organization | Refers to the self-organizing ability of project team members |
| C8 | Operational efficiency | Refers to the operational efficiency of the provider while performing outsourced project processes |
| C9 | Responsiveness | Refers to the frequency of feedbacks of the outsourcing provider when the client requests something which is related to the corresponding outsourced process |
| C10 | Productivity | Refers to the productivity as well as the overall performance of the project team |
| C11 | Innovative skills | Refers to the innovative capabilities of the provider in order to keep up with changing and improving technology, and increasing innovation demands of the market in various business processes |
| C12 | IT capability | Refers to the innovative capabilities of the service provider in order to keep up with changing and improving technology, and increasing innovation demands of the market in various business processes |
| C13 | Reliability | Refers to the reliability of the provider for keeping the private and confidential information of the client firm |
A committee of three decision-makers, i.e. two project management managers and an agile management specialist who have all been working for more than three years in case firm, conducted the evaluation. A questionnaire, which contains the evaluation of outsourcing providers with respect to criteria as well as interrelationships among criteria, is prepared. The decision-makers expressed their opinions by reaching a consensus, and they utilized the linguistic scale given in Table 4.
Table 4.
Linguistic scale
| Linguistic variables | IFS |
|---|---|
| Very High (VH) | < 0.95, 0.05 > |
| High (H) | < 0.70, 0.25 > |
| Medium (M) | < 0.50, 0.40 > |
| Low (L) | < 0.25, 0.70 > |
| Very Low (VL) | < 0.05, 0.95 > |
First, the decision-makers identified whether there is a causal link between pair of evaluation factors, or not. Second, they determined the power of relationship according to the linguistic scale mentioned in Table 4. Linguistic data for interrelationships among criteria are given in Table 5.
Table 5.
Linguistic data for interrelationships among criteria
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | – | – | – | – | – | – | – | – | – | – | – | L | L |
| C2 | – | – | H | L | – | H | – | VL | VL | L | – | – | – |
| C3 | – | – | – | – | – | – | – | – | – | – | – | – | – |
| C4 | – | – | M | – | – | VH | – | – | VH | – | – | – | – |
| C5 | – | – | H | – | – | L | – | L | – | M | VL | – | – |
| C6 | – | – | M | – | – | – | – | H | VH | – | – | – | M |
| C7 | – | – | M | – | – | M | – | – | M | VL | – | – | – |
| C8 | – | – | H | – | – | – | – | – | – | – | – | – | – |
| C9 | – | – | – | H | – | H | – | – | – | – | – | – | H |
| C10 | – | – | – | – | – | – | – | – | – | – | – | – | – |
| C11 | – | – | – | – | – | – | – | – | – | – | – | – | – |
| C12 | – | – | VL | – | – | VL | – | L | – | – | VL | – | – |
| C13 | – | – | – | – | – | – | – | – | – | – | – | – | – |
Linguistic data collecting from the decision-makers are converted into intuitionistic fuzzy numbers associated with intuitionistic fuzzy scale, and power of relationship matrix is determined as follows (Table 6).
Table 6.
Power of relationship matrix
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | – | – | – | – | – | – | – | – | – | – | – | < 0.25,0.70 > | < 0.25,0.70 > |
| C2 | – | – | < 0.70,0.25 > | < 0.25,0.70 > | – | < 0.70,0.25 > | – | < 0.05,0.95 > | < 0.05,0.95 > | < 0.25,0.70 > | – | – | – |
| C3 | – | – | – | – | – | – | – | – | – | – | – | – | – |
| C4 | – | – | < 0.50,0.40 > | – | – | < 0.95,0.05 > | – | – | < 0.95,0.05 > | – | – | – | – |
| C5 | – | – | < 0.70,0.25 > | – | – | < 0.25,0.70 > | – | < 0.25,0.70 > | – | < 0.50,0.40 > | < 0.05,0.95 > | – | – |
| C6 | – | – | < 0.50,0.40 > | – | – | – | – | < 0.70,0.25 > | < 0.95,0.05 > | – | – | – | < 0.50,0.40 > |
| C7 | – | – | < 0.50,0.40 > | – | – | < 0.50,0.40 > | – | – | < 0.50,0.40 > | < 0.05,0.95 > | – | – | – |
| C8 | – | – | < 0.70,0.25 > | – | – | – | – | – | – | – | – | – | – |
| C9 | – | – | – | < 0.70,0.25 > | – | < 0.70,0.25 > | – | – | – | – | – | – | < 0.70,0.25 > |
| C10 | – | – | – | – | – | – | – | – | – | – | – | – | – |
| C11 | – | – | – | – | – | – | – | – | – | – | – | – | – |
| C12 | – | – | < 0.05,0.95 > | – | – | < 0.05,0.95 > | – | < 0.25,0.70 > | – | – | < 0.05,0.95 > | – | – |
| C13 | – | – | – | – | – | – | – | – | – | – | – | – | – |
To apply IFCM method, Eq. (9) is activated with an initial vector . Equation (9) is run until the value of the updated vector will no longer change, in other words, until the system will be stable. Sigmoid function is employed as a threshold function of Eq. (9) since it is suitable function restricting the values of in the interval of [0, 1] (Goker and Dursun 2019). FCMapper software is used for computational operations of IFCM. The weights of the criteria are provided in Table 7.
Table 7.
Weights of the criteria
| Label | Weight |
|---|---|
| C1 | 0.6590 |
| C2 | 0.6590 |
| C3 | 0.9676 |
| C4 | 0.8290 |
| C5 | 0.6590 |
| C6 | 0.9618 |
| C7 | 0.6590 |
| C8 | 0.8566 |
| C9 | 0.9502 |
| C10 | 0.7679 |
| C11 | 0.6784 |
| C12 | 0.7046 |
| C13 | 0.8863 |
The evaluations of the providers regarding the data collected from the decision-makers are identified as in Table 8. Criteria weights are normalized using Eq. (10), and then evaluation data are weighted using Eq. (11).
Table 8.
Evaluations of the providers
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | H | VH | H | M | VH | VL | M | VH | L | H | L | VL | H |
| A2 | H | H | M | M | M | VH | M | H | M | H | L | H | VL |
| A3 | M | H | H | VH | VL | M | VH | H | L | M | M | H | M |
| A4 | VH | M | H | L | M | L | M | H | VL | M | H | VH | H |
| A5 | L | VH | VH | L | M | L | L | M | VH | M | M | H | M |
In this step, selection process starts, and IFCOPRAS steps are followed. The sum of cost and benefit criteria values are calculated by employing Eqs. (11) and (12). Degree of relative weights as well as the priorities of the alternatives are computed using Eqs. (13) and (14), and the alternatives are ranked in descending order according to their priorities. Overall computational outcomes of IFCOPRAS methodology are given in Table 9.
Table 9.
Overall computational outcomes
| Rank | |||||||
|---|---|---|---|---|---|---|---|
| A1 | < 0.3189,0.6616 > | 0.2413 | < 0.5474,0.4208 > | 0.5633 | 0.6991 | 0.8107 | 3 |
| A2 | < 0.1979,0.7672 > | 0.1535 | < 0.5455,0.4057 > | 0.5698 | 0.7834 | 0.9084 | 2 |
| A3 | < 0.2101,0.7564 > | 0.1263 | < 0.5819,0.3761 > | 0.6029 | 0.8623 | 1 | 1 |
| A4 | < 0.2962,0.6819 > | 0.2169 | < 0.4970,0.4548 > | 0.5210 | 0.6721 | 0.7794 | 5 |
| A5 | < 0.3901,0.6072 > | 0.1923 | < 0.4985,0.4479 > | 0.5253 | 0.6958 | 0.8068 | 4 |
The proposed integrated intuitionistic fuzzy decision aid is applicable when the data are uncertain, vague, and hesitative. The developed approach leads to employ intuitionistic fuzzy numbers in order to express interrelationships among the evaluation criteria and the ratings of the alternatives with regard to the criteria. IFCM tool is utilized to cope with cause-and-effect relationships among the criteria. Besides, selection process is completed using IFCOPRAS method that obtains a solution relative to the ideal solution. The proposed framework aims to solve the decision problems that consist of multiple and conflicting criteria with interrelationships among them.
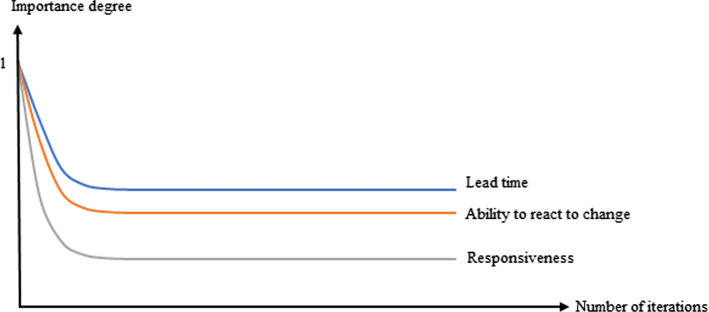
The application of these two techniques, in other words, combination of them provide solving decision problems in a cost-effective manner due to computational efficiency. The expert knowledge-based system enables the decision-makers to reach a consensus to express their opinions; hence, an expert-friendly and easily applicable mathematical decision framework is constructed. IFCM technique provides obtaining the importance degrees of evaluation criteria in hesitative environment. The iterative formulation of IFCM is run until the system reaches stability; in other words, the weights of the factors will no longer change. The stabilization of each criterion is obtained after different number of iterations, approximately 20 iterations are required for all the factor weights remain same, and this process takes just few seconds. As an example, a graph, which gives the change of the importance degrees of the three most effective factors on agile provider selection process named as “lead time”, “ability to react to change”, and “responsiveness” according to the number of iterations, is provided in Fig. 2.
Fig. 2.
Variation of the importance degrees of the three most effective factors
Evaluation of COVID-19 effect with scenario analysis
In order to observe the impacts of pandemic on the presented decision problem in this study, second reviewing process with the experts is completed. A scenario analysis is provided to understand the effects of COVID-19 on agile provider selection, in other words, whether the ranking of providers varies or not when considering the impacts of pandemic on criteria weights. At the initial step of the analysis, the decision-makers are supposed to determine whether there is any change on importance degrees of evaluation criteria in post-pandemic period when home office become widely used procedure by the organizations. Second, they told us remote working decreases directly the importance weights of four criteria, namely customer participation, communication, responsiveness, and productivity. Thus, they reached a consensus and equalled the weights of these four factors to 0.15, 0.10, 0.15, and 0.20, respectively. Subjective opinions of the experts are made use in assigning weights for the scenario analysis.
Using the updated weights, IFCM process is run again, scenario analysis is provided via FCMapper software, and the final weights for criteria are recomputed as in Table 10. Afterwards, IFCOPRAS method is them employed for agile provider selection problem utilizing recalculated weights of criteria.
Table 10.
Weights of the criteria obtained via scenario analysis
| Label | No change | Weight obtained via scenario analysis |
|---|---|---|
| C1 | 0.6590 | 0.6590 |
| C2 | 0.6590 | 0.6590 |
| C3 | 0.9676 | 0.9354 |
| C4 | 0.8290 | 0.15 |
| C5 | 0.6590 | 0.1 |
| C6 | 0.9618 | 0.8643 |
| C7 | 0.6590 | 0.6590 |
| C8 | 0.8566 | 0.83 |
| C9 | 0.9502 | 0.15 |
| C10 | 0.7679 | 0.2 |
| C11 | 0.6784 | 0.6705 |
| C12 | 0.7046 | 0.7046 |
| C13 | 0.8863 | 0.8040 |
The results of the COVID-19 analysis are given in Table 11. The decrease in the importance weights of 4 criteria caused to some differences in the results. After applying scenario analysis, the weight differences between “no change” and “weight obtained via scenario analysis” can be observed. According to the results, the importance level of lead time decreases after COVID-19 pandemic period. That situation is caused by home office processes, and thus the tolerances for determining the delivering time of a project increase. Besides, the effect of the ability to react to change on the agile provider selection problem is decreased due to increasing volatility in every project management process in pandemic period. Moreover, the importance of operational efficiency decreases since efficient operation processes are still provided in home office. In addition, the importance level of reliability decreases because it becomes harder to reach to agile providers in COVID-19 pandemic period, and hence the outsourcers may accept to work with the outsourcing firms that are not the most reliable ones.
Table 11.
Overall computational outcomes after scenario analysis
| Rank | |||||||
|---|---|---|---|---|---|---|---|
| A1 | < 0.4097,0.5675 > | 0.3181 | < 0.4830,0.4884 > | 0.4972 | 0.6807 | 0.7345 | 4 |
| A2 | < 0.2611,0.6953 > | 0.2063 | < 0.5344,0.4294 > | 0.5525 | 0.8354 | 0.9014 | 2 |
| A3 | < 0.2751,0.6832 > | 0.1707 | < 0.5609,0.3910 > | 0.5849 | 0.9267 | 1 | 1 |
| A4 | < 0.3822,0.5918 > | 0.2876 | < 0.5471,0.4117 > | 0.5676 | 0.7705 | 0.8314 | 3 |
| A5 | < 0.4895,0.5074 > | 0.2562 | < 0.3845,0.5505 > | 0.4170 | 0.6447 | 0.6956 | 5 |
After the scenario analysis, the first two providers remain same; however, third, fourth, and fifth provider vary. Hence, remote working does not lead to significant changes since the clients will select only the best performing provider, which remains same after COVID-19 analysis. Thus, agile provider selection decision in white goods sector is not affected by home office procedure that is applied due to the pandemic. As s strategic management component, remote working may remain for maintaining agility in outsourcing processes.
Managerial implications and discussion
In global markets, organizations must follow changes and handle competition while managing their operations. Companies that take into account responsiveness, cost, flexibility, and quality as performance measures may achieve competitive advantages. In some circumstances, these measures are optimized by disintegrating organizational concepts to focus on the core competencies, and thus outsourcing processes become more and more crucial. Being a managerial term, outsourcing, refers to disintegrating firms’ activities to third-party service providers in lieu of hiring new personnel for carrying a job. Outsourcing, which is one of the strategic management components, influences the entire performance of value chain. It also provides cost saving and flexibility. Moreover, the clients can easily focus on their core competencies via outsourcing the peripheral activities to the providers.
Firms can make use of outsourcing when they need to manage the functions more efficiently. Thus, the efficient usage of the sources positively influences the profitability of firms. Alternatively, outsourcing the material-focused activities to an external provider is an essential application, which provides the transformation of fixed assets to current assets. Therefore, the current ratio and cash ratios, and then the flexibility will be improved. Transferring or utilizing the information of the service provider firms brings fast growth rate. The firms have know-how skills; however, they can fail to possess technical capabilities for generating and then maintaining the process. Hence, they outsource technical processes to an expert for surviving in competitive markets.
In this study, outsourcing processes in project management are taken into consideration. In competitive environments, firms need to adapt different strategies to the managerial components in order to survive in the market. A successful project should have such a management methodology that can keep up with dynamic environment and cope with uncertainty and unpredictability when changes occur. In the recent past, “agility” has emerged and then become widely utilized concept in project management. Agile project management refers to an iterative approach for delivering a project in its whole life cycle, which contains incremental steps. Software development projects are widely conducted via iterative approaches in order to move faster and improve adaptability skills since these iterations provide correcting mistakes throughout the path rather than following one linear path. The main objective of agile approach is to provide benefits in entire process rather than only at the end. Moreover, agile approach supports the concepts of flexibility, collaboration, and empowerment.
An agile project should consist of quickness, flexibility, and responsiveness characteristics. In order to achieve agility in project management process, collaborating with agile providers is necessary. Hence, agile provider evaluation and selection framework, which contains conflicting criteria, is in the position of managerial MCDM problem. To determine the most appropriate agile provider alternative, evaluation factors related to agility are required to be included into the decision analysis.
The objective of this paper is to identify the most suitable agile provider alternative for an IT-oriented project of a firm that performs in Turkish white goods industry. 13 evaluation criteria, which are interrelated with causal links, are determined by conducting a literature survey as well as reviewing with decision-makers from the case firm. These cause-and-effect relationships are coped with cognitive mapping, uncertain, vague, and hesitative data are to be handled with IFCM technique that results in weighting evaluation criteria. In order to identify the best performing agile provider alternative, IFCOPRAS method, which is dealt with uncertainty and hesitation in data, is employed.
The IFCM technique enables the researchers to provide several scenario analyses on the related decision problem for understanding the effects of a change on the importance level of specific factor(s). Accordingly, the results of the new analysis can be obtained in a practical way rather than resolving the whole problem. The scenario analyses are very useful in dynamic decision systems. In this paper, a scenario analysis is employed to evaluate COVID-19 effect on agile provider selection problem; however, it can be enhanced by applying different scenario analyses considering the conditions of the environment. Hence, one shall also note that the scenario analysis can be performed in various case studies.
The contributions of the introduced decision making procedure to the literature can be summarized as follows.
The proposed method allows to utilize intuitionistic fuzzy numbers to express the experts’ opinions, and thus it copes with hesitation in data.
IFCM methodology enables to convert the causal links among the criteria into the numerical terms by taking into account hesitation.
The developed intuitionistic decision aid yields the most suitable alternative using IFCOPRAS method that finds a solution relative to the ideal solution.
This is the first work that combines IFCM and IFCOPRAS throughout the literature.
There is not another study that aims to rank agile provider alternatives in white goods sector.
A scenario-based comparative analysis is provided in order to understand the impacts of COVID-19 pandemic on agile provider evaluation/selection decision framework.
As a managerial implication, the obtained results are shared with the case company, and thus the proposed framework has become a guideline for the firm that can be utilized for provider evaluation and selection problem in agile environment. Upon the request of the project managers of the case company, scenario analysis, which aims to observe the effects of COVID-19 pandemic on the related decision problem, is provided, and thus the results obtained from the scenario analysis are also shared with the firm. The feedbacks are collected from the company, and the choice of the best performing agile provider alternative is observed. The firm has decided to collaborate with the most suitable provider as identified in the proposed decision framework.
Concluding remarks
In this work, an integrated cognitive mapping-based intuitionistic fuzzy MCDM procedure that determines the best performing agile provider is introduced. Uncertainty and vagueness in data are handled by employing IFSs, which deal with the loss of information that may be occurred in numerical operations with fuzzy numbers. The evaluation criteria are weighted using IFCM tool that takes into account the causal links among the factors. The selection process is conducted employing IFCOPRAS method that finds a solution relative to the ideal solution, and thus the most appropriate agile provider is identified. A case study, which is conducted in Turkish white goods sector, is provided in order to demonstrate the robustness of the proposed decision methodology.
The limitations of the proposed decision aid and the future research directions can be summarized as follows. First, in this paper, the experts express their opinions using linguistic variables and reaching consensus in the presence of hesitative data. In this situation, the decision-makers may be influenced by each other and change their own opinions. Thus, the data and thus the outcomes obtained from the proposed methodology may be affected by the consensus. In order to eliminate that risk, a group decision making procedure, in which the experts do not hear the others’ opinions, can be a topic of the future research related to this field. Second, IFCM process starts with the initial vector , which is widely used initial vector throughout the literature (Goker et al. 2020). However, an additional technique, which starts the algorithm by obtaining the initial values assigned to each factor, may be proposed. Hence, more sensitive results of the importance degrees of the concepts can be achieved in that manner. This additional technique will probably be developed in the future research. Third, a scenario analysis is restricted to provide to understand the effects of COVID-19 on agile provider selection in this paper. Unfortunately, COVID-19 pandemic has not finished yet, and continues to affect all the managerial and decision processes of the organizations. In this study, the effect of COVID-19 pandemic on agility concept is investigated and observed in the selection procedure, but in the future, researchers may be focused on the other components of strategic management that are influenced by the pandemic. Such studies will be decision support for the managers who are supposed to take crucial managerial decisions during this difficult period for the entire world. Finally, group decision making problems in various sectors apart from white goods industry that need to consider hesitation in data will be a probable topic of future research.
Acknowledgements
This study was supported by Galatasaray University Research Fund.
Declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Alkhatib SF, Darlington R, Yang Z, Nguyen T. A novel technique for evaluating and selecting logistics service providers based on the logistics resource view. Expert Syst Appl. 2015;42(20):6976–6989. [Google Scholar]
- Araz C, Ozfirat PM, Ozkarahan I. An integrated multicriteria decision-making methodology for outsourcing management. Comput Oper Res. 2007;34(12):3738–3756. [Google Scholar]
- Atanassov K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986;20:87–96. [Google Scholar]
- Axelrod R. Structure of decision. Princeton, New York: Princeton University Press; 1976. [Google Scholar]
- Azadi M, Saen RF. A new chance-constrained data envelopment analysis for selecting third-party reverse logistics providers in the existence of dual-role factors. Expert Syst Appl. 2011;38(10):12231–12236. [Google Scholar]
- Bottani E, Rizzi A. A fuzzy TOPSIS methodology to support outsourcing of logistics services. Supply Chain Manag Int J. 2006;11(4):294–308. [Google Scholar]
- Buyukozkan G, Feyzioglu O, Ersoy MS. Evaluation of 4PL operating models: a decision making approach based on 2-additive Choquet integral. Int J Prod Econ. 2009;121(1):112–120. [Google Scholar]
- Büyükozkan G, Güleryüz S, Karpak B. A new combined IF-DEMATEL and IF-ANP approach for CRM partner evaluation. Int J Prod Econ. 2017;191:194–206. [Google Scholar]
- Cao Q, Qiong W. Optimizing vendor selection in a two-stage outsourcing process. Comput Oper Res. 2007;34(12):3757–3768. [Google Scholar]
- Cao J, Cao G, Wang W. A hybrid model using analytic network process and gray relational analysis for bank's IT outsourcing vendor selection. Kybernetes. 2012;41(7–8):994–1013. [Google Scholar]
- Chen LH, Hung CC. An integrated fuzzy approach for the selection of outsourcing manufacturing partners in pharmaceutical R & D. Int J Prod Res. 2010;48(24):7483–7506. [Google Scholar]
- Chen LY, Wang TC. Optimizing partners' choice in IS/IT outsourcing projects: the strategic decision of fuzzy VIKOR. Int J Prod Econ. 2009;120(1):233–242. [Google Scholar]
- Chen YH, Wang TC, Wu CY. Strategic decisions using the fuzzy PROMETHEE for IS outsourcing. Expert Syst Appl. 2011;38(10):13216–13222. [Google Scholar]
- Chen ZS, Chin KS, Li YL, Yang Y. Proportional hesitant fuzzy linguistic term set for multiple criteria group decision making. Inf Sci. 2016;357:61–87. [Google Scholar]
- Chen ZS, Zhang X, Govindan K, Wang XJ, Chin KS. Third-party reverse logistics provider selection: a computational semantic analysis-based multi-perspective multi-attribute decision-making approach. Expert Syst Appl. 2021;166:114051. [Google Scholar]
- Chen ZS, Zhang X, Rodriguez RM, Pedrycz W, Martinez L. Expertise-based bid evaluation for construction-contractor selection with generalized comparative linguistic ELECTRE III. Autom Constr. 2021;125:103578. [Google Scholar]
- Chen ZS (2018) Sustainable supplier selection using two-phase QFD and TOPSIS within PD-HFLTS context. In: World Scientific Proceeding Series on Computer Engineering and Information Science. Data Science and Knowledge Engineering for Sensing Decision Support, 1168–1175
- Cheng YH, Lee F. Outsourcing reverse logistics of high-tech manufacturing firms by using a systematic decision-making approach: TFT-LCD sector in Taiwan. Ind Mark Manag. 2010;39(7):1111–1119. [Google Scholar]
- De SK, Biswas R, Roy AR. Some operations on intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000;114:477–484. [Google Scholar]
- Dogu E, Albayrak YE. Criteria evaluation for pricing decisions in strategic marketing management using an intuitionistic cognitive map approach. Soft Comput. 2018;22:4989–5005. [Google Scholar]
- Dursun M, Gumus G. Intuitionistic fuzzy cognitive map approach for the evaluation of supply chain configuration criteria. Math Methods Appl Sci. 2020;43(13):7788–7801. [Google Scholar]
- Dursun M, Goker N, Mutlu H. A cognitive map integrated intuitionistic fuzzy decision-making procedure for provider selection in project management. J Intell Fuzzy Syst. 2020;39(5):6645–6655. [Google Scholar]
- Ecer F. Third-party logistics (3PLs) provider selection via fuzzy AHP and EDAS integrated model. Technol Econ Dev Econ. 2018;24(2):615–634. [Google Scholar]
- Efendigil T, Onut S, Kongar E. A holistic approach for selecting a third-party reverse logistics provider in the presence of vagueness. Comput Ind Eng. 2008;54(2):269–287. [Google Scholar]
- Erkayman B, Gundogar E, Yilmaz A (2012) An integrated fuzzy approach for strategic alliance partner selection in third-party logistics. Sci World J 1:1–6 [DOI] [PMC free article] [PubMed]
- Faisal MN, Raza SA. IT outsourcing intent in academic institutions in GCC countries an empirical investigation and multi-criteria decision model for vendor selection. J Enterp Inf Manag. 2016;29(3):432–453. [Google Scholar]
- Gireesha O, Somu N, Krithivasan K, Sriram VSS. IIVIFS-WASPAS: an integrated multi-criteria decision-making perspective for cloud service provider selection. Future Gener Comput Syst Int J Sci. 2020;103:91–110. [Google Scholar]
- Goker N, Dursun M. A fuzzy scenario-based approach to analyzing neuromarketing technology evaluation factors. Soft Comput. 2019;23:12295–12304. [Google Scholar]
- Goker N, Dursun M, Cedolin M. A novel IFCM integrated distance based hierarchical intuitionistic decision making procedure for agile supplier selection. J Intell Fuzzy Syst. 2020;38:653–662. [Google Scholar]
- Gonzalez-Gomez F, Garcia-Rubio MA, Alcala-Olid F, Ortega-Diaz M. Outsourcing and efficiency in the management of rural water services. Water Resour Manag. 2013;27(3):731–747. [Google Scholar]
- Govindan K, Sarkis J, Murugesan P. An analytic network process-based multicriteria decision making model for a reverse supply chain. Int J Adv Manuf Technol. 2013;68(1–4):863–880. [Google Scholar]
- Govindan K, Khodaverdi R, Vafadarnikjoo A. A grey DEMATEL approach to develop third-party logistics provider selection criteria. Ind Manag Data Syst. 2016;116(4):690–722. [Google Scholar]
- Govindan K, Agarwal V, Darbari JD, Jha PC. An integrated decision making model for the selection of sustainable forward and reverse logistic providers. Ann Oper Res. 2019;273:607–650. [Google Scholar]
- Govindan K, Kadzinski M, Ehling R, Miebs G. Selection of a sustainable third-party reverse logistics provider based on the robustness analysis of an outranking graph kernel conducted with ELECTRE I and SMAA. Omega. 2019;85:1–15. [Google Scholar]
- Ho W, He T, Lee CKM, Emrouznejad A. Strategic logistics outsourcing: an integrated QFD and fuzzy AHP approach. Expert Syst Appl. 2012;39(12):10841–10850. [Google Scholar]
- Hsu PF, Hsu MG. Optimizing the information outsourcing practices of primary care medical organizations using entropy and TOPSIS. Qual Quant. 2008;42(2):181–201. [Google Scholar]
- Hsu CC, James JH. An outsourcing provider decision model for the airline industry. J Air Transp Manag. 2013;28:40–46. [Google Scholar]
- Hsu CC, James JH, Chuang YC. Integrating DANP and modified grey relation theory for the selection of an outsourcing provider. Expert Syst Appl. 2013;40(6):2297–2304. [Google Scholar]
- Hu KJ, Yu VF. An integrated approach for the electronic contract manufacturer selection problem. Omega Int J Manag Sci. 2016;62:65–81. [Google Scholar]
- Isiklar G, Alptekin E, Buyukozkan G. Application of a hybrid intelligent decision support model in logistics outsourcing. Comput Oper Res. 2007;34(12):3701–3714. [Google Scholar]
- Jharkharia S, Shankar R. Selection of logistics service provider: an analytic network process (ANP) approach. Omega Int J Manag Sci. 2007;35(3):274–289. [Google Scholar]
- Ji P, Zhang H, Wang J. Selecting an outsourcing provider based on the combined MABAC–ELECTRE method using single-valued neutrosophic linguistic sets. Comput Ind Eng. 2018;120:429–441. [Google Scholar]
- Kahraman C, Engin O, Kabak O, Kaya I. Information systems outsourcing decisions using a group decision-making approach. Eng Appl Artif Intell. 2009;22(6):832–841. [Google Scholar]
- Kahraman C, Beskese A, Kaya I. Selection among ERP outsourcing alternatives using a fuzzy multi-criteria decision making methodology. Int J Prod Res. 2010;48(2):547–566. [Google Scholar]
- Kahraman C, Parchami A, Onar SC, Oztaysi B. Process capability analysis using intuitionistic fuzzy sets. J Intell Fuzzy Syst. 2017;32:1659–1671. [Google Scholar]
- Kaya I. Evaluation of outsourcing alternatives under fuzzy environment for waste management. Resour Conserv Recycl. 2012;60:107–118. [Google Scholar]
- Kosko B. Fuzzy cognitive maps. Int J Man Mach Stud. 1986;24:65–75. [Google Scholar]
- Kumar R, Harwinder S, Dureja JS. An approach to analyze logistic outsourcing problem in medium-scale organization by CFPR and VIKOR. J Manuf Technol Manag. 2012;23(7):885–898. [Google Scholar]
- Kumari R, Mishra AR. Multi-criteria COPRAS method based on parametric measures for intuitionistic fuzzy Sets: application of green supplier selection. Iran J Sci Technol Trans Electr Eng. 2020;44:1645–1662. [Google Scholar]
- Lai H, Liao HC, Wen Z, Zavadskas EK, Al-Barakati A. An improved CoCoSo method with a maximum variance optimization model for cloud service provider selection. Inz Ekon Eng Econ. 2020;31(4):411–424. [Google Scholar]
- Lei H, Ganjeizadeh F, Jayachandran PK, Ozcan P. A statistical analysis of the effects of Scrum and Kanban on software development projects. Robot Comput Integr Manuf. 2017;43:59–67. [Google Scholar]
- Li DF, Wan SP. Fuzzy heterogeneous multi attribute decision making method for outsourcing provider selection. Expert Syst Appl. 2014;41(6):3047–3059. [Google Scholar]
- Li YL, Ying CS, Chin KS, Yang HT, Xu J. Third-party reverse logistics provider selection approach based on hybrid-information MCDM and cumulative prospect theory. J Clean Prod. 2018;195:573–584. [Google Scholar]
- Lin SW. The critical success factors for a travel application service provider evaluation and selection by travel intermediaries. Tour Manag. 2016;56:126–141. [Google Scholar]
- Lin YT, Lin CL, Yu HC, Tzeng GH. A novel hybrid MCDM approach for outsourcing vendor selection: a case study for a semiconductor company in Taiwan. Expert Syst Appl. 2010;37(7):4796–4804. [Google Scholar]
- Liou JJH, Chuang YT. Developing a hybrid multi-criteria model for selection of outsourcing providers. Expert Syst Appl. 2010;37(5):3755–3761. [Google Scholar]
- Liou JJH, Wang HS, Hsu CC, Yin SL. A hybrid model for selection of an outsourcing provider. Appl Math Program. 2011;35(10):5121–5133. [Google Scholar]
- Liu LB, Berger P, Zeng A, Gerstenfeld A. Applying the analytic hierarchy process to outsourcing location decision. Supply Chain Manag Int J. 2008;13(6):435–449. [Google Scholar]
- Liu S, Hu YN, Zhang X, Li YF, Liu L. Blockchain service provider selection based on an integrated BWM-Entropy-TOPSIS method under an intuitionistic fuzzy environment. IEEE Access. 2020;8:104148. [Google Scholar]
- Ljubojevic S, Pamucar D, Jovanovic D, Vesovic V. Outsourcing transport service: a fuzzy multi-criteria methodology for provider selection based on comparison of the real and ideal parameters of providers. Oper Res Int J. 2019;19:399–433. [Google Scholar]
- Low C, Chen YH. Criteria for the evaluation of a cloud-based hospital information system outsourcing provider. J Med Sys. 2012;36(6):3543–3553. doi: 10.1007/s10916-012-9829-z. [DOI] [PubMed] [Google Scholar]
- Mishra AR, Singh RK, Motwani D. Intuitionistic fuzzy divergence measure-based ELECTRE method for performance of cellular mobile telephone service providers. Neural Comput Appl. 2020;32(8):3901–3921. [Google Scholar]
- Otay I, Oztaysi B, Onar SC, Kahraman C. Multi-expert performance evaluation of healthcare institutions using an integrated intuitionistic fuzzy AHP&DEA methodology. Knowl Based Syst. 2017;133:90–106. [Google Scholar]
- Percin S. An integrated fuzzy SWARA and fuzzy AD approach for outsourcing provider selection. J Manuf Technol Manag. 2019;30(2):531–552. [Google Scholar]
- Percin S, Min H. A hybrid quality function deployment and fuzzy decision-making methodology for the optimal selection of third-party logistics service providers. Int J Logist Res Appl. 2013;16(5):380–397. [Google Scholar]
- Rani P, Mishra AR, Ansari MD, Ali J. Assessment of performance of telecom service providers using intuitionistic fuzzy grey relational analysis framework (IF-GRA) Soft Comput. 2020 doi: 10.1007/s00500-020-05269-w. [DOI] [Google Scholar]
- Ross TJ. Fuzzy logic with engineering applications. 3. Hoboken: Wiley; 2010. [Google Scholar]
- Sen DK, Datta S, Mahapatra SS. Decision support framework for selection of 3PL service providers: dominance-based approach in combination with grey set theory. Int J Inf Technol Decis Mak. 2017;16(1):25–57. [Google Scholar]
- Shahrasbi A, Shamizanjani M, Alavidoost MH, Akhgar B. An aggregated fuzzy model for the selection of a managed security service provider. Int J Inf Technol Decis Mak. 2017;16:1–60. [Google Scholar]
- Singh R, Gunasekaran A, Kumar P. Third party logistics (3PL) selection for cold chain management: a fuzzy AHP and fuzzy TOPSIS approach. Ann Oper Res. 2018;267:531–553. [Google Scholar]
- Sremac S, Stevic Z, Pamucar D, Arsic M, Matic B. Evaluation of a third-party logistics (3PL) provider using a rough SWARA-WASPAS model based on a new rough Dombi aggregator. Symmetry. 2018;10:1–25. [Google Scholar]
- Tavana M, Zareinejad M, Di Caprio D, Kaviani MA. An integrated intuitionistic fuzzy AHP and SWOT method for outsourcing reverse logistics. Appl Soft Comput. 2016;40:544–557. [Google Scholar]
- Tjader YC, Shang JS, Vargas LG. Offshore outsourcing decision making: a policy-maker's perspective. Eur J Oper Res. 2010;207(1):434–444. [Google Scholar]
- Tjader Y, May JH, Shang J, Vargas LG, Gao N. Firm-level outsourcing decision making: a balanced scorecard-based analytic network process model. Int J Prod Econ. 2014;147:614–623. [Google Scholar]
- Totten J (2017) Critical success factors for agile project management in non-software related product development teams. Ph.D. thesis, Western Michigan University
- Tsai WH, Leu JD, Liu JY, Lin SJ, Shaw MJ. A MCDM approach for sourcing strategy mix decision in IT projects. Expert Syst Appl. 2010;37:3870–3886. [Google Scholar]
- Ukor R, Carpenter A. Service selection and horizontal multi-sourcing in process-oriented capability outsourcing. J Softw Evol Process. 2012;24(3):259–283. [Google Scholar]
- Uygun O, Kacamak H, Kahraman UA. An integrated DEMATEL and Fuzzy ANP techniques for evaluation and selection of outsourcing provider for a telecommunication company. Comput Ind Eng. 2015;86:137–146. [Google Scholar]
- Wan SP, Wang FL, Lin LL, Dong JY. An intuitionistic fuzzy linear programming method for logistics outsourcing provider selection. Knowl Based Syst. 2015;82:80–94. [Google Scholar]
- Wang JJ, Yang DL. Using a hybrid multi-criteria decision aid method for information systems outsourcing. Comput Oper Res. 2007;34(12):3691–3700. [Google Scholar]
- Wang GX, Hu XJ, Li XZ, Zhang Y, Feng S, Yang AF. Multiobjective decisions for provider selection and order allocation considering the position of the CODP in a logistics service supply chain. Comput Ind Eng. 2020;140:106216. [Google Scholar]
- Wong JT. DSS for 3PL provider selection in global supply chain: combining the multi-objective optimization model with experts' opinions. J Intell Manuf. 2012;23(3):599–614. [Google Scholar]
- Wu JZ, Chien CF. Modeling strategic semiconductor assembly outsourcing decisions based on empirical settings. Or Spectrum. 2008;30(3):401–430. [Google Scholar]
- Xu ZS. Intuitionistic fuzzy aggregation operators. IEEE Trans Fuzzy Syst. 2007;15(6):1179–1187. [Google Scholar]
- Xu GL, Wan SP, Xie XL (2015) A selection method based on MAGDM with interval-valued intuitionistic fuzzy sets. Math Prob Eng 1:1–13
- Yang Y, Chen ZS, Chen YH, Chin KS. Interval-valued pythagorean fuzzy frank power aggregation operators based on an isomorphic frank dual triple. Int J Comput Intell Syst. 2018;11(1):1091–1110. [Google Scholar]
- Yang Y, Chen ZS, Rodriguez RM, Pedrycz W, Chin KS. Novel fusion strategies for continuous interval-valued q-rung orthopair fuzzy information: a case study in quality assessment of Smart Watch appearance design. Int J Mach Learn Cybern. 2021 doi: 10.1007/s13042-020-01269-2. [DOI] [Google Scholar]
- Zadeh LA. Fuzzy sets. Inf Control. 1965;8:338–353. [Google Scholar]
- Zarbakhshnia N, Wu Y, Govindan K, Soleimani H. A novel hybrid multiple attribute decision-making approach for outsourcing sustainable reverse logistics. J Clean Prod. 2020;242:118–461. [Google Scholar]
- Zavadskas EK, Kaklauskas A (1996) Determination of an efficient contractor by using the new method of multicriteria assessment, in Langford, D. A., Retik, A. (Eds.), International Symposium for “The Organisation and Management of Construction”. Shaping Theory and Practice. Vol. 2: Managing the Construction Project and Managing Risk. CIB W 65; London, Weinheim, New York, Tokyo, Melbourne, Madras. London: E and FN SPON, 94–104.