Sensorimotor strategies and neuronal representations for shape discrimination

Abstract

Humans and other animals can identify objects by active touch, requiring the coordination of exploratory motion and tactile sensation. Both the motor strategies and neural representations employed could depend on the subject’s goals. We developed a shape discrimination task that challenged head-fixed mice to discriminate concave from convex shapes. Behavioral decoding revealed that mice did this by comparing contacts across whiskers. In contrast, a separate group of mice performing a shape detection task simply summed up contacts over whiskers. We recorded populations of neurons in the barrel cortex, which processes whisker input, and found that individual neurons across the cortical layers encoded touch, whisker motion, and task-related signals. Sensory representations were task-specific: during shape discrimination but not detection, neurons responded most to behaviorally relevant whiskers, overriding somatotopy. Thus, sensory cortex employs task-specific representations compatible with behaviorally relevant computations.

eTOC Blurb

Mice use their whiskers to identify objects, akin to human fingertips. Rodgers et al. show that mice discriminate shapes by comparing the number of contacts across whiskers. In a surprising violation of cortical topography, neurons in barrel cortex (which processes whisker input) dramatically reconfigured their tuning to support this computation.

Introduction

In active sensation, animals choose how to move their sensory organs to most effectively gather information about the world (Gibson, 1962; Yang et al., 2016b). A key challenge in neuroscience is to understand the strategies animals use to explore the world and how they interpret the resulting sensory input.

We investigated this problem in the mouse whisker system. Freely moving rodents actively move their whiskers to identify objects and obstacles (Brecht et al., 1997; Grant et al., 2018; Hutson and Masterton, 1986; Lyon et al., 2012; Stüttgen and Schwarz, 2018; Voigts et al., 2015) but the sensorimotor strategies and neuronal mechanisms that enable whisker-based object recognition are not well understood. In freely moving animals, it is difficult to track the whiskers (Petersen et al., 2020; Voigts et al., 2008) and to ensure that whiskers alone are used, instead of vision, olfaction, or touch with skin (Mehta et al., 2007). Head fixation enables better whisker tracking and stimulus control, but most tasks for head-fixed mice focus on spatially simple features, like the location or orientation of a pole, or the texture of sandpaper (Chen et al., 2013; Kim et al., 2020; O’Connor et al., 2010a). Indeed, the head-fixed mouse is often trimmed to a single whisker, though a few studies have considered multi-whisker behaviors (Brown et al., 2021; Celikel and Sakmann, 2007; Knutsen et al., 2006; Pluta et al., 2017).

We asked how mice discriminate concave from convex objects. Curvature is one of the fundamental components of form, and discriminating curvature requires integrating information over space (Connor et al., 2007; Lederman and Klatzky, 1987). Shape discrimination has never been studied with precise whisker tracking (although cf. Anjum et al., 2006; Brecht et al., 1997; Diamond et al., 2008; Harvey et al., 2001; Polley et al., 2005). Curved stimuli have been used in visual and somatosensory experiments in primates, but were typically presented passively (Nandy et al., 2013; Yau et al., 2009), whereas active sensation is critical for shape discrimination in humans and other species (Chapman and Ageranioti-Bélanger, 1991; von der Emde, 2010; Klatzky and Lederman, 2011).

We set out to understand the sensorimotor strategies and neuronal representations of two tasks: shape discrimination and shape detection. Behavioral decoding revealed that shape discrimination mice compared contacts across whiskers whereas shape detection mice summed up contacts across whiskers. Populations of individual neurons in barrel cortex encoded the mouse’s choice in addition to other sensory, motor, and task variables. Most importantly, neural representations were task-specific, overriding even basic cortical topography. Our behavioral decoding approach revealed why these task-specific representations were useful in object recognition.

Results

The shape discrimination and detection tasks

We developed a shape discrimination task in which head-fixed mice licked left for concave and right for convex shapes to obtain water rewards (Supplemental Video 1). On each trial, a linear actuator moved a curved shape (either convex or concave) into range of the whiskers on the right side of the face, stopping at one of three different positions (termed close, medium, or far; Fig 1A,B). At all positions, mice had to actively move their whiskers to contact the shape. The use of different positions ensured that mice did not simply memorize the location of a single point on the object. Mice could generalize to flatter shapes that were more difficult to discriminate (Supplemental Fig 1A). Trimming off all the whiskers caused performance to fall to chance, demonstrating that mice could not use non-whisker cues to choose correctly (Supplemental Fig 1B). Lesioning the contralateral barrel cortex, which processes whisker input, substantially and significantly degraded the performance of untrimmed mice for multiple days (Fig 1C–D). Thus, mice relied on whiskers and on barrel cortex to discriminate shape.

Figure 1. The shape discrimination and shape detection tasks.

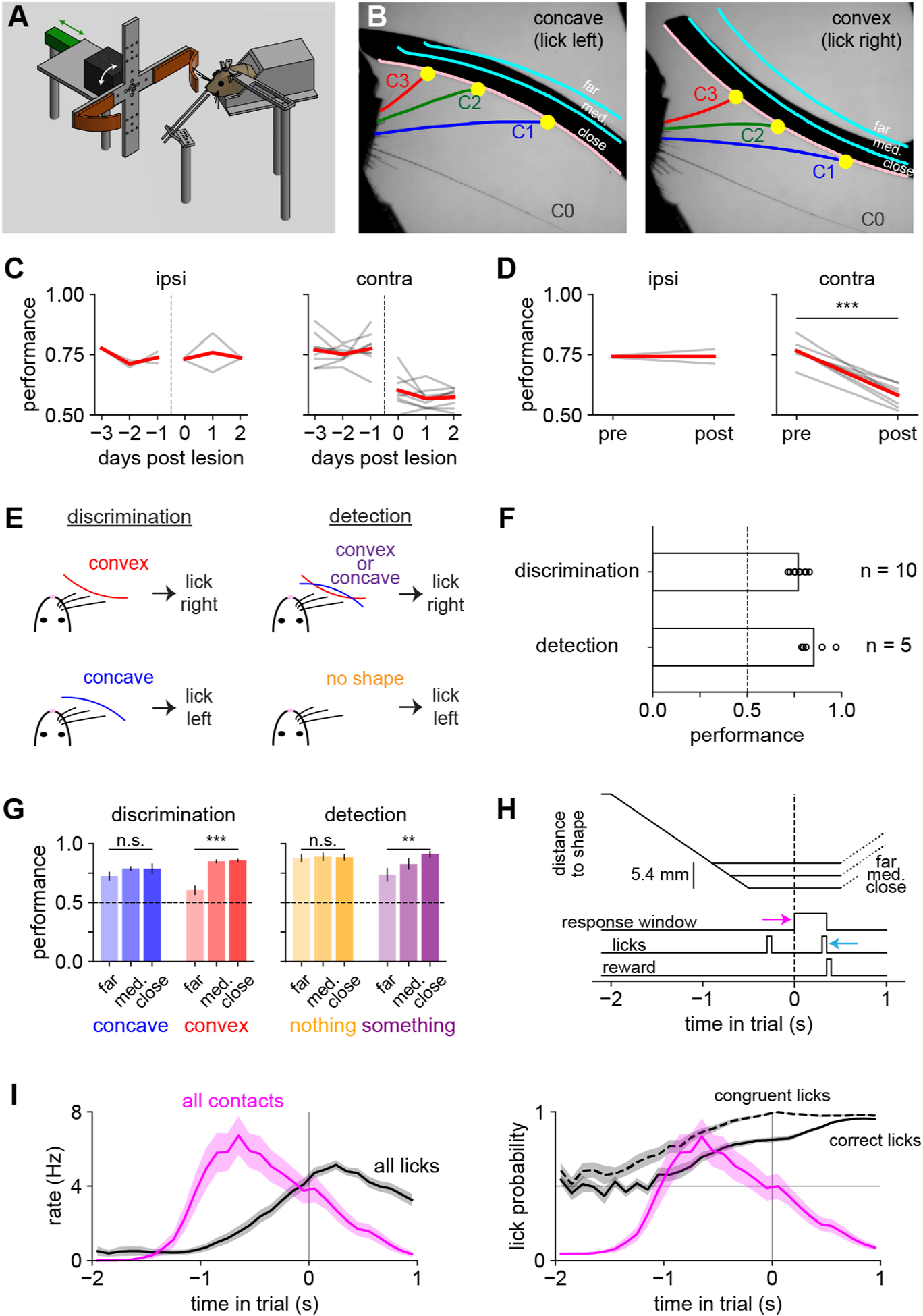
A) Diagram of the behavioral apparatus. A motor (black) rotated a shape (orange) into position, and a linear actuator (green) moved it toward the whiskers.

B) Example high-speed video frames. Shapes were presented at one of three different positions (pink and cyan lines labeled close, medium, and far).

C) Lesioning right barrel cortex (ipsilateral to shapes) had no effect on shape discrimination (left; n = 2 mice) whereas contralateral lesions impaired performance, with no sign of recovery over three days (right; n = 8 mice).

D) Same as panel (C), averaging over three days. Paired t-test.

E) Task rules.

F) Mouse performance (fraction of correct trials) on both tasks exceeded chance (dashed line).

G) Mouse performance by task, stimulus, and position. On the “nothing” condition, the actuator moves to the correct position, but no shape is present. One-way repeated-measures ANOVA.

H) Trial timeline. Pink arrow: opening of response window. Cyan arrow: choice lick.

I) Left: total lick rate regardless of lick direction (black) and total contact rate (pink) on the same timescale as panel H, pooled across tasks. Right: probability that licks were correct (solid) or congruent (dashed; i.e., in the same direction as the eventual choice lick).

Error bars: SEM over mice.

Throughout the manuscript: * p < 0.05; ** p < 0.01; *** p < 0.001.

To assess which features of the behavioral and neural responses were specific to the task, we trained a separate group of mice on shape detection (Fig 1E). These mice learned to lick right for either shape and to lick left on trials when the actuator presented an empty position with no shape. The trial timing and shapes were identical in both tasks, which differed only in the rule governing which direction the mice should lick to receive reward.

Both groups of mice learned to perform well above chance (Fig 1F; n = 5 detection and 10 discrimination mice). Detection mice more accurately reported the presence of a shape when it was closer (Fig 1G). Discrimination mice identified concave shapes equally well at all locations, but were more likely to identify convex shapes correctly when closer. Thus, shape discrimination relied on “detecting convexity”, an observation we return to below.

Precise video tracking of multiple whiskers

To permit unambiguous identification of each whisker in videography, we gradually trimmed off whiskers until only the middle row of whiskers remained. Mice were initially impaired by each trim but could recover with training (Supplemental Fig 1C), suggesting that they initially used many rows but could learn to rely on just one. Within the spared middle row, C1 is the caudal-most and longest whisker, and C3 is the rostral-most and shortest whisker still capable of reaching the shapes. The straddler whisker (β or γ, denoted “C0”) rarely made contact and was therefore excluded from analysis.

To reveal how mice identified the shapes, we acquired video of their whiskers at 200 frames per second. This large dataset—15 mice, 88.9 hours, 115 sessions, 18,514 trials, 63,979,800 frames—necessitated high-throughput automated tracking. To do this, we used the human-curated output of a previous-generation whisker tracking algorithm (Clack et al., 2012) to bootstrap the training of a deep convolutional neural network (Insafutdinov et al., 2016; Mathis et al., 2018; Pishchulin et al., 2015). This method precisely tracked the full extent of the whiskers (accuracy >99.7%; Supplemental Fig 2A–D) even as they moved rapidly, became obscured, or contacted the shape.

The timing of sensory evidence and behavioral reports

We used the timing of the contacts and licks within each trial to understand when the mice made their decisions (Fig 1H). Each trial began with the linear actuator moving the shape into the mouse’s whisker field, and the “response window” always opened 2.0 seconds after the trial began. The direction of the first lick in the response window (the “choice lick”) determined whether the trial was correct or incorrect. The opening of the response window (defined as t = 0 throughout our analyses) was not explicitly cued. The shape reached its final position in the interval −0.8 < t < −0.4, depending on whether it was a close, medium, or far trial.

Mice could move their whiskers, contact the shape, and lick at any time during the trial, although “early licks” (i.e., t < 0) had no effect on the outcome. We defined “correct early licks” as those in the direction that would be rewarded, and “congruent early licks” as those in the same direction as the choice lick (Fig 1I). Early in the trial (−2.0 < t < −1.5), mice made few or no contacts, and accordingly their rate of correct licking was near the chance level of 0.5. As the mice made the bulk of their contacts (−1.5 < t < 0), the rate of correct and congruent licks steadily increased. After the choice lick on error trials, the mice could infer their error from the absence of reward and often switched their lick direction, even though this had no effect on the outcome. The rate of contacts peaked before the rate of licking did, indicating that contacts were not an incidental effect of licking: mice first collected evidence and then registered their decision.

Contact count, but not whisking or contact force, differs between discrimination and detection

Trained mice whisked in stereotyped patterns that could differ widely across individuals (Fig 2A). We decomposed whisker motion into individual cycles (Fig 2B, n = 882,893 whisks from 15 mice, excluding intertrial intervals). Mice made contacts near the peak of the whisk cycle (Fig 2C), synchronously across whiskers (Fig 2D; cf. Sachdev et al., 2001). During both tasks, performance increased with the number of contacts made on each trial (Fig 2E).

Figure 2. Mice briefly tapped the shapes with multiple whiskers.

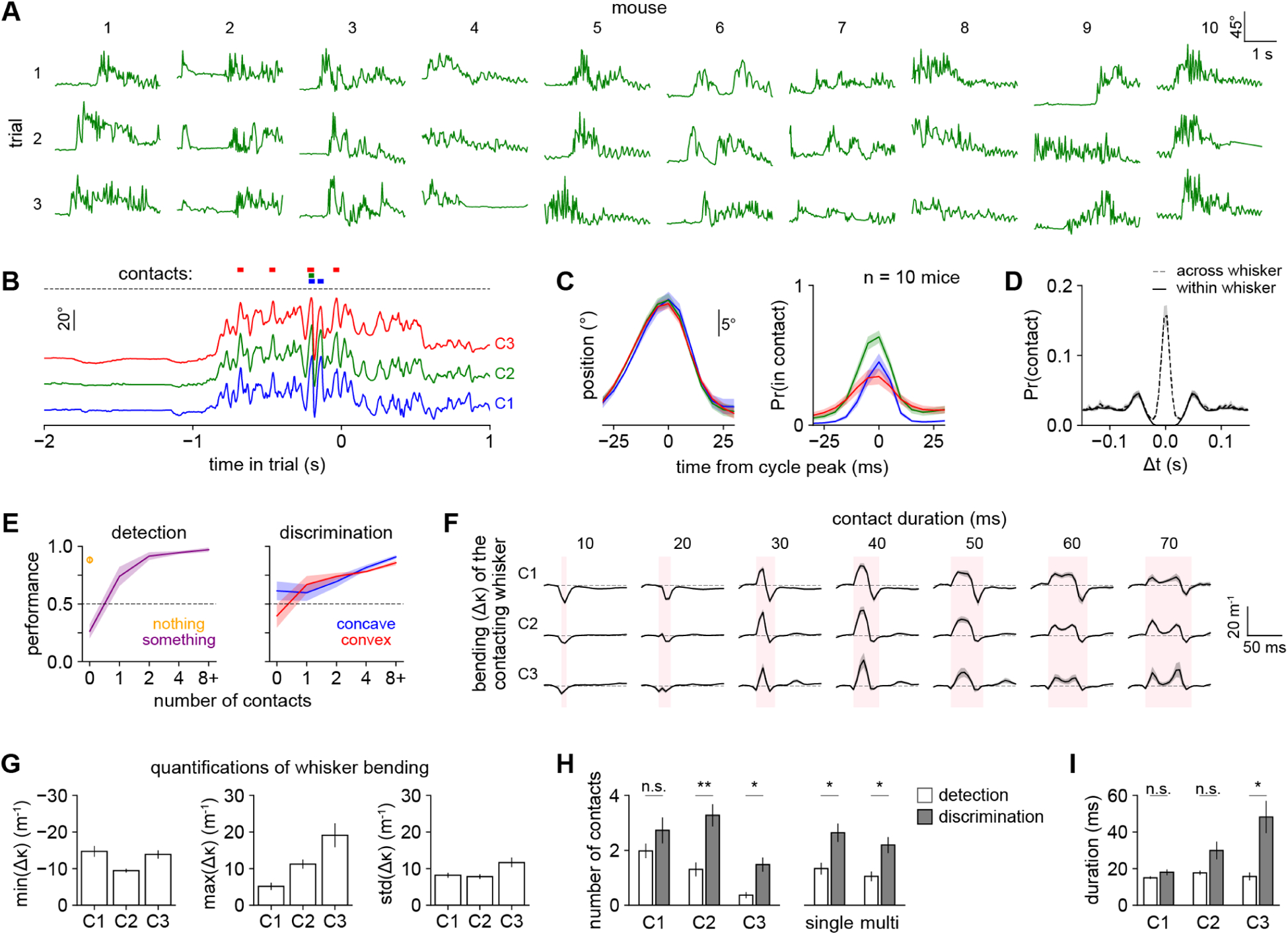
A) Angular position of the C2 whisker on three representative correct trials from each of ten mice.

B) Angular position of C1, C2, and C3 over a single trial using timescale in Fig 1H. Colored bars: whisker contacts.

C) Left: mean angle of each whisker aligned to the C2 whisk cycle peak. Right: probability that each whisker was in contact, aligned to the same time axis as on left. For both, n = 94,999 whisk cycles during which ≥1 whisker made contact.

D) Autocorrelation of contact times within each whisker (solid) and cross-correlation of contact times across pairs of adjacent whiskers (dashed).

E) Performance versus the number of contacts in the detection (left) or discrimination (right) task. Orange circle: trials during detection when no shape is present. We excluded mice from any bin in which they had <10 trials.

F) Mean whisker bending (Δκ) over time during each contact aligned to its onset and relative to the pre-contact baseline (dashed line), plotted separately for each whisker (row) and contact duration (column). Pink shaded area: duration of contact. Not all mice made contacts of all possible durations; data points with <10 contacts per mouse were excluded.

G) Whisker bending quantified as the minimum, maximum, and standard deviation of Δκ over the duration of each contact.

H) Compared to detection mice, discrimination mice made significantly more contacts with C2 and C3 (left) and significantly more contacts with a single whisker and with multiple whiskers (right). Unpaired t-test.

I) Mean duration of contacts. C3 contacts are significantly longer during discrimination. Unpaired t-test.

Error bars: SEM over mice.

All panels include 10 discrimination mice. E, H, and I also include 5 detection mice.

Surprisingly, the statistics of whisker motion and contact kinematics were similar in both shape discrimination and detection (Supplemental Fig 2E–F), and in both cases differed strikingly from previously published tasks. For instance, we exclusively observed tip contact, whereas mice localizing poles make contact with the whisker shaft (Hires et al., 2013, cf. a similar observation in rats discriminating texture in Carvell and Simons, 1990). We never observed animals dragging their whiskers across the objects’ surfaces, as they do with textured stimuli (Carvell and Simons, 1990; Jadhav et al., 2009; Ritt et al., 2008). In both shape detection and discrimination, contacts were brief (median 15 ms, IQR 10–25 ms, n = 167,217; Supplemental Fig 2G). Whisker bending, a commonly used proxy for contact force (Birdwell et al., 2007; but see also Quist et al., 2014; Yang and Hartmann, 2016), was dynamic (Fig 2F): a whisker could bend slightly while pushing into a shape and then bend in the other direction while detaching. Occasionally we observed double pumps, a signature of active exploration (Wallach et al., 2020). The contact forces we observed were much smaller than in many studies: the typical maximum bend (Δκ) was 5.1 +/− 1.0 m⁻¹ for C1, 11.2 +/− 1.2 m⁻¹ for C2, and 19.1 +/− 3.3 m⁻¹ for C3 (mean +/− SEM over mice; Fig 2G; Supplemental Fig 2F), much less bent than the 50–150 m⁻¹ typical of pole localization (Hires et al., 2015; Hong et al., 2018; Huber et al., 2012). The sensorimotor strategy we observe here is similar to the “minimal impingement” mode used by freely moving rodents (Grant et al., 2009; Mitchinson et al., 2007).

Though the whisking and contact kinematics were in large part similar between shape discrimination and detection, two specific differences suggested task-specific processing. Compared with the detection group, mice performing shape discrimination made more single- and multi-whisker contacts, and they made significantly more contacts with C2 and C3, though not with C1 (Fig 2H). They also made much longer duration contacts with the C3 whisker than the shape detection group did (Fig 2I). In sum, these analyses suggested that mice rely more on contact number than on contact force to discriminate shape.

Behavioral decoding reveals sensorimotor strategies

To pinpoint the strategies mice used to perform these tasks, we developed an analysis termed behavioral decoding that identifies the sensorimotor events driving behavioral choice (Fig 3A). In this approach, we first quantified a large suite of sensorimotor features from the video (e.g., contact location, cross-whisker contact timing) as well as task-related variables (choice and reward history). All 31 features are listed in Supplemental Table 1.

Figure 3. Behavioral decoding reveals sensorimotor strategies.

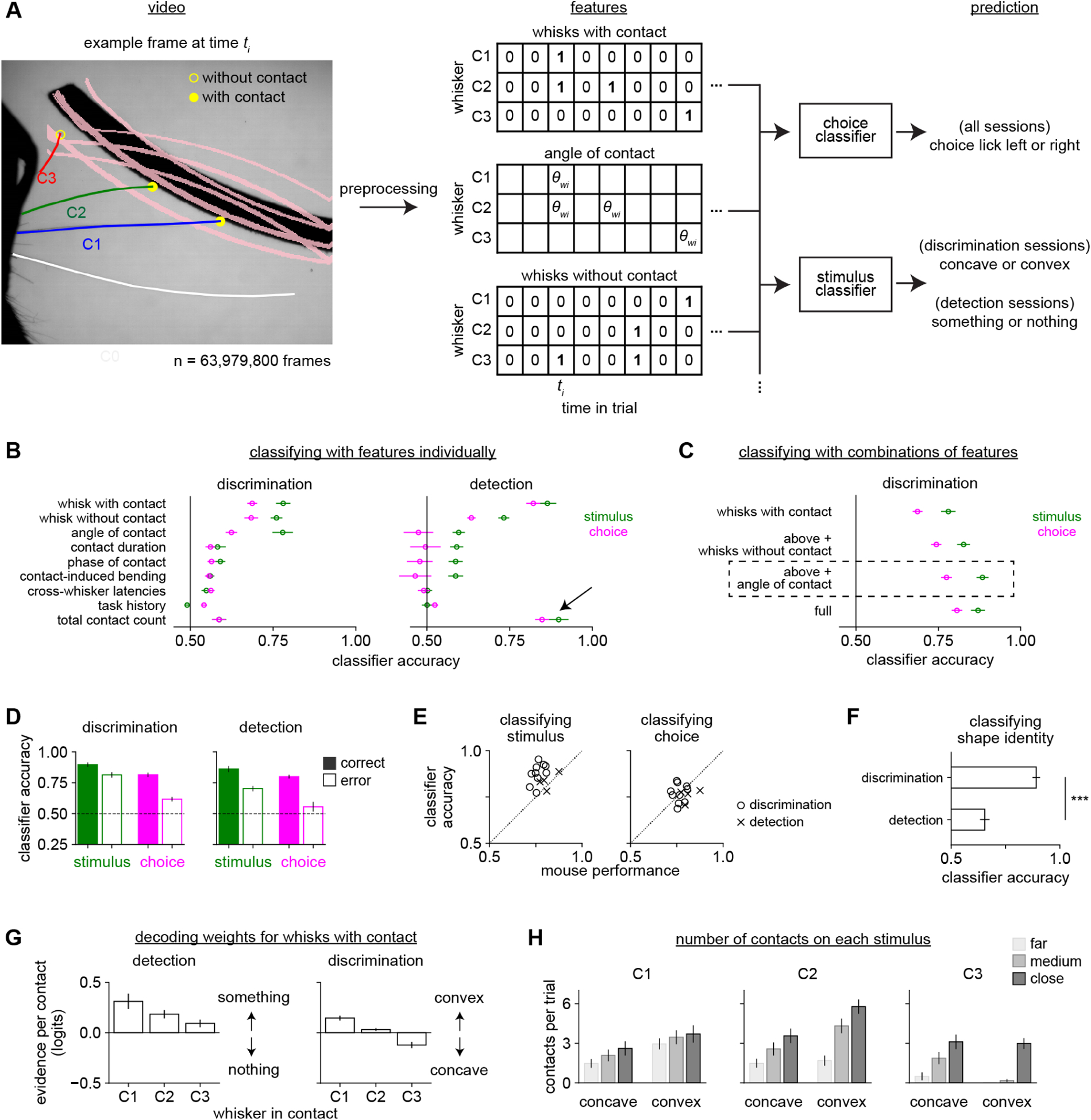
A) Behavioral decoding. We used 31 contact, whisking, and task-related features (Supplemental Table 1) to predict the stimulus or choice. Left: Example frame showing the peak of a sampling whisk. C1-C3 protracted enough to reach the shapes at some positions (pink lines); C1 and C2 were scored as “with contact” and C3 as “without contact”. Middle: Example features, each an array over whisker (rows) and 250 ms time bins (columns). Example frame in third column. Sampling whisks were binarized as “with contact” or “without contact”. Continuous variables like “angle of contact” were defined only during contact and were otherwise null. Right: Logistic regression classifiers predicted stimulus or choice.

B) Accuracy of behavioral decoders trained on a single feature to identify stimulus (green) or choice (pink). During shape detection (right), the total number of contacts (black arrow) was the most informative feature, but was much less useful during discrimination.

C) Features were combined in a stepwise fashion to create a simple model that captured behavior. Shown is the accuracy of decoders trained on 1) whisks with contact only, 2) also including whisks without contact, 3) also including angle of contact, 4) including all features in the entire dataset. The third model (dashed box, “optimized behavioral decoder”) performs as well as the full model while using far fewer features.

D) The optimized behavioral decoder predicts stimulus and choice well during both shape discrimination and detection, though less accurately when the mouse made an error (open bars).

E) Accuracy of the decoder at identifying stimulus and choice versus the performance of each mouse.

F) The decoder more accurately predicted shape identity for mice performing shape discrimination than detection. Unpaired t-test.

G) The weights assigned by the decoder to the “whisks with contact” feature, separately plotted by which whisker made contact. Weights were relatively consistent over the trial time course (data not shown) and are averaged over time here for clarity. They are expressed as the change in log-odds (logits) per additional contact.

H) The mean number of contacts per trial for each whisker during shape discrimination, separately by shape identity and position (cf. Fig 1B). Although each whisker may contact one shape more frequently, no whisker touches a single shape exclusively.

Error bars: SEM over mice. n = 10 shape discrimination mice and 4 shape detection mice. Behavioral decoding requires error trials and one detection mouse made too few errors to be included.

We distinguished between “sampling whisks” (those on which mice protracted far enough to reach the closest possible position of either shape) and “non-sampling whisks” (all other whisks). Because non-sampling whisks could not have touched any shape on any trial, they could not be informative, and were discarded from analysis. The remaining sampling whisks were divided into “whisks with contact” (those that contacted the shape) and “whisks without contact” (those that did not; Fig 3A). We used two-dimensional arrays over whisker and time to represent “whisks with contact”, “whisks without contact”, and continuous values like “angle of contact”.

Next, we trained linear classifiers using logistic regression to predict either the stimulus identity (concave vs convex for discrimination; something vs nothing for detection) or the mouse’s choice (lick left or lick right) on each trial using all of these features. Predicting the stimulus indicated which features carried information about shape whereas predicting choice indicated which features might have influenced the mouse’s decision (Nogueira et al., 2017). However, stimulus and choice are correlated; indeed, they are perfectly correlated on correct trials. To address this, we weighted error trials in inverse proportion to their abundance, such that correct and incorrect trials were balanced (i.e., equally weighted in aggregate). This notably improved our ability to predict the mouse’s errors (Supplemental Fig 3A). Numerical simulations validated the accuracy and statistical efficiency of this method in comparison with other techniques (Supplemental Fig 3B,C).

Contact count is the most informative feature about stimulus and choice

To identify the most important features, we compared the accuracy of separate decoders trained on every individual feature during shape discrimination (Fig 3B, left). The most informative feature for decoding both stimulus and choice was “whisks with contact”—which whiskers made contact. The next most informative feature was “whisks without contact”—which whiskers were protracted enough to rule out the presence of some shapes. The “angle of contact” feature was also useful for predicting the stimulus, likely due to the geometrical information it contains, but less useful for predicting choice, suggesting that mice did not exploit that information despite its utility. The remaining 28 analyzed features were relatively uninformative about choice (Supplemental Fig 3D), including mechanical/kinematic variables like speed or contact-induced whisker bending, contact timing across whiskers or within the trial or whisk cycle, and task variables like choice history.

We tested our hypothesis that mice used different information for discrimination and detection by comparing the usefulness of each feature across tasks. During shape detection, the total contact count summed over whiskers explained stimulus and choice better than any other variable (Fig 3B, right). Total contact count was far less informative during discrimination. This reflects the fundamental difference between these tasks: detection required the mouse only to know that contacts occurred whereas discrimination required additional information—most critically, the identities of the contacting whiskers.

A combination of a few features suffices to explain behavior

Having assessed the relative importance of each feature, we asked whether the most important features contained redundant information or could be combined to improve decoding. We gradually added features in decreasing order of usefulness until the model’s performance plateaued (Fig 3C). The model improved after including whisks with contact, whisks without contact, and contact angle, and these three features together performed as well as the full model with all 31 measured features. Therefore we used the reduced 3-feature model (the “optimized behavioral decoder”; dashed box, Fig 3C) for all further analyses. Dropping individual features or whiskers from the optimized behavioral decoder impaired its performance, confirming their individual importance (Supplemental Fig 3E–F).

The optimized behavioral decoder accurately predicted either stimulus or choice on both correct and error trials during both detection (Fig 3D; stimulus: 83.5 ± 2.2%; choice: 75.9 ± 1.8%; mean ± SEM) and discrimination (stimulus: 87.7 ± 1.8%; choice: 76.9 ± 1.6%). It outperformed the mice on shape discrimination (Fig 3E), indicating that the mice did not optimally use this sensory information. In sum, this decoder constitutes a model of behavior capable of either identifying the stimulus or predicting the mouse’s choice, even on error trials. To achieve this, the model primarily required binary information about which whiskers made contact, rather than the fine temporal dynamics of those contacts.

This decoder’s ability to identify shapes could have been a trivial consequence of mice whisking onto distinct objects or an important reflection of the behavioral goals of the mice. To test this, we compared the optimized behavioral decoder’s ability to classify shape identity in mice performing shape discrimination versus mice performing shape detection. Although the same shapes were used in both tasks and the same features were quantified in all cases, the decoder was substantially better able to classify shape identity in mice performing shape discrimination than detection (Fig 3F). Thus, more information about shape identity is collected by mice actively attempting to discriminate those shapes.

Mice compare the prevalence of contacts across whiskers to discriminate shape

We next used the weights of the optimized behavioral decoder to reveal the strategy used for each task. Whether predicting stimulus (Fig 3G) or choice (Supplemental Fig 3G), this decoder assigned strikingly different weights to contacts made by each whisker. For shape detection, all weights were positive, meaning contact by any whisker signaled the presence of an object (Fig 3G, left). In sharp contrast, weights of different whiskers had opposite signs during shape discrimination (Fig 3G, right): each C1 contact indicated a greater likelihood of convex whereas each C3 contact indicated a greater likelihood of concave. These results were not affected by early licking or trial balancing (Supplemental Fig 3H,I).

Thus, mice compare the prevalence of contacts across whiskers to discriminate an object’s curvature whereas they sum up contacts across whiskers to detect an object. Critically, this is not because any given whisker can only reach one of the shapes—all whiskers can touch both shapes (Fig 3H). Instead, the whisking strategy employed for discrimination biases contact prevalence across whiskers. To visualize this process of spatial sampling, we registered all of our whisker video into a common reference frame (Fig 4A). The C1 whisker sampled the region in which contacts indicated convexity and absence of contacts indicated concavity, and the reverse was true for C3 (Fig 4B,C). The location that mice chose to sample even in the absence of contacts was also informative about their upcoming choice (Supplemental Fig 4; Dominiak et al., 2019).

Figure 4. Mice compare information across whiskers to discriminate shape.

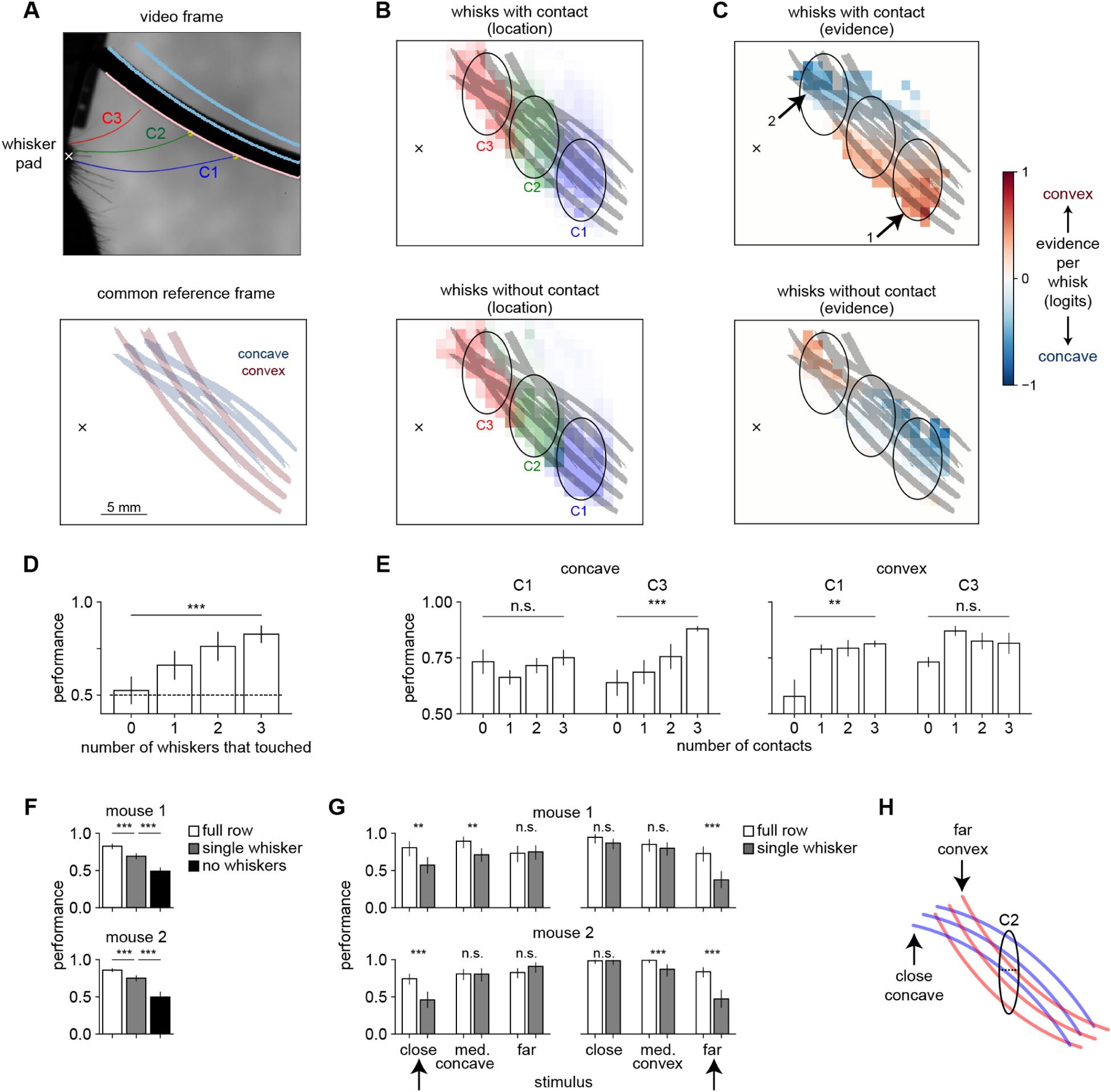
A) Videos for all sessions were registered into a common reference frame defined by the shape positions. Top: example frame. Bottom: location of the concave (blue) and convex (red) shapes in the common reference frame. Whisker pad marked with an X.

B) Location of the peak of each whisk with contact (top) or without contact (bottom) in the common reference frame. Each whisker samples distinct regions of shape space (ovals).

C) Same data from panel B, now colored by the evidence each whisk contains about shape, using the decoder weights. Top: C1 mainly contacts convex shapes (arrow 1) whereas C3 mainly contacts concave shapes (arrow 2). Bottom: On whisks without contact, the mapping between whisker and shape identity is reversed.

D) Performance on shape discrimination increases with the number of whiskers making contact (p < 0.001). One-way ANOVA. In panels D and E, error bars show SEM over mice.

E) Performance on concave shapes increases with C3 contacts (left, p < 0.001) and on convex shapes with C1 contacts (right, p < 0.01). One-way ANOVA.

F) After trimming to a single whisker (C2), performance on shape discrimination is significantly lower but still above chance (p < 0.001, Fisher’s exact test). For individual mouse data in panels F and G, error bars show 95% Clopper-Pearson confidence intervals.

G) Trimming to a single whisker impairs performance on specific combinations of shape and position (marked with black arrows). Thus, mice can discriminate shape with a single whisker, but not in a position-invariant way.

H) With a single C2 whisker, mice can only sample the area indicated by the black oval, where close contacts indicate convex and far contacts concave. This strategy will fail on the closest concave and furthest convex shapes, as shown in panel G.

We confirmed these results with other analyses that did not rely on behavioral decoding. Mouse performance on shape discrimination significantly increased with the number of whiskers making contact (Fig 4D), indicating that they benefited from combining information across whiskers. Mice better identified convex shapes when they made C1 contacts, and concave shapes when they made C3 contacts (Fig 4E). When trimmed to a single whisker, mice were still able to discriminate shape above chance, but they showed a specific pattern of errors indicating that this ability was no longer invariant to stimulus position (Fig 4F–H). Similarly, although humans discriminate shapes better when they scan with multiple fingers, they can still perform above chance when forced to use an inferior strategy relying on a single finger (Davidson, 1972).

In summary, behavioral decoding produced a computational model of the distinct sensorimotor strategies that mice adopted in two different tasks. Mice summed up contacts across whiskers to detect shapes whereas they compared contacts across whiskers to discriminate shape identity. Behavioral decoding could be used to dissect other large behavioral tracking datasets to reveal the strategies used in other tasks and by other model organisms.

Barrel cortex neurons encode movement, contacts, and choice

We next asked how neural activity in barrel cortex mediated these strategies by recording populations of individual neurons across the cortical layers using an extracellular electrode array (Fig 5A–D; Supplemental Video 2). We recorded 675 neurons from 7 shape discrimination mice and 301 neurons from 4 shape detection mice. Putative inhibitory interneurons were identified from their narrow waveform width (Fig 5B). Neurons responded to individual contact events but not licks (Fig 5E; Supplemental Fig 5A).

Figure 5. Whisker motion and contacts drive barrel cortex neurons.

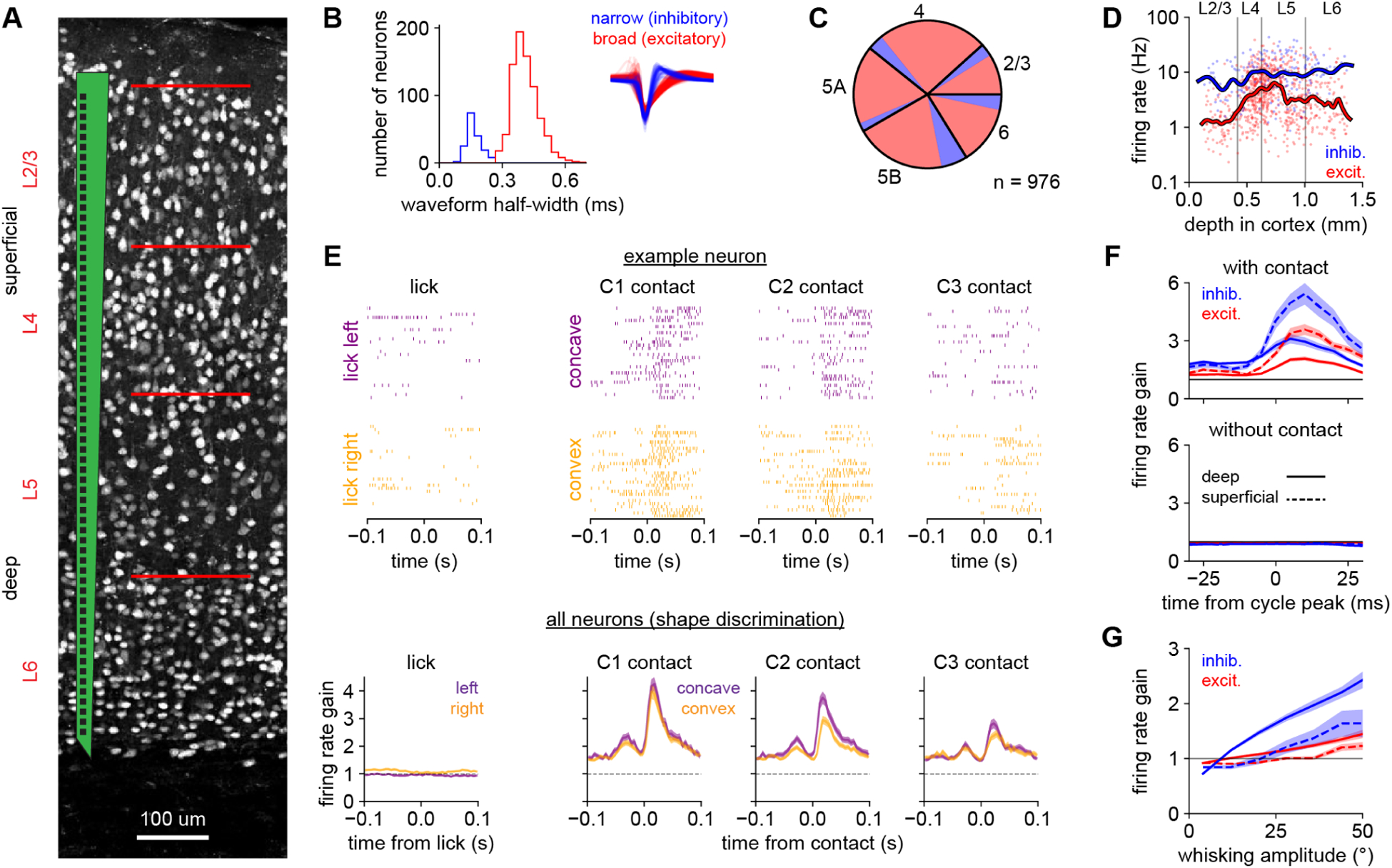
A) Schematic of the multi-electrode recording array overlaid on image of NeuN-labeled neurons spanning all cortical layers.

B) The bimodal distribution of extracellular waveform half-widths (the time between peak negativity and return to baseline) permits classification into narrow-spiking (putative inhibitory; blue) and broad-spiking (putative excitatory; red) cell types. Inset: normalized average waveforms from individual neurons.

C) Relative fraction of excitatory (red) and inhibitory (blue) neurons recorded in each layer.

D) Firing rates of individual neurons (meaned over the entire session) versus their depth in cortex. Inhibitory and deep-layer neurons typically exhibit higher firing rates. Lines: smoothed with a Gaussian kernel.

E) Top: Spike rasters from an example L2/3 inhibitory neuron in the C3 cortical column aligned to licks or to contacts of individual whiskers. Bottom: Responses to those events averaged over all neurons recorded during shape discrimination. To compare across neurons with different baseline firing rates, we defined the firing rate gain as the evoked response divided by each neuron’s mean firing rate over the session, so that 1.0 indicates no evoked response.

F) Firing rate gain of each cell type locked to the whisk cycle (cf. Fig 2C). Absolute firing rates in Supplemental Fig 5B.

G) Firing rate gain of each cell type on individual whisk cycles versus the amplitude of that whisk cycle, excluding cycles with contact. Deep inhibitory neurons (solid blue line) are modulated most strongly.

In panels B–D, F, and G n = 976 neurons from both tasks, pooled because the results were similar. In panel E, n = 675 neurons recorded during shape discrimination only. Error bars: SEM over neurons.

Because the whisk cycle correlates contacts across whiskers and over time (Fig 2C,D), we analyzed responses on individual whisk cycles. Neurons exhibited rapid transient responses to whisks with contact but not to whisks without contact (Fig 5F, Supplemental Fig 5B). Contact responses were stronger in the superficial layers and in inhibitory neurons, likely reflecting greater thalamocortical input to this cell type (Bruno and Simons, 2002; Cruikshank et al., 2007). Firing rate tracked the amplitude of each individual whisk, especially in deep inhibitory neurons (Fig 5G). Thus, neurons encoded whisking amplitude in a graded fashion, while also responding phasically to individual contacts.

Beyond encoding these rapid sensorimotor variables, some neurons encoded the mouse’s choice through slower changes in firing rate over the trial (example: Fig 6A). We quantified this effect by decoding stimulus and choice from the neural population, again using trial balancing (Fig 6B, left and middle). We also asked whether this information was local (i.e., contained in individual whisk cycles; Isett et al., 2018) or continuous (integrated over the trial). We removed local information about contacts by setting the spike count to zero on “sampling whisks” (those large enough to reach the shapes at their closest position). This largely abolished the encoding of stimulus but not choice (Fig 6B, right), demonstrating that barrel cortex transiently carries stimulus information during sampling whisks but encodes choice more persistently. Choice encoding was not explained by early licking (Supplemental Fig 6). In sum, on fine timescales barrel cortex neurons respond to whisker movement and contacts (but not licks), and on longer timescales they encode cognitive variables like choice.

Figure 6. Barrel cortex persistently encodes choice.

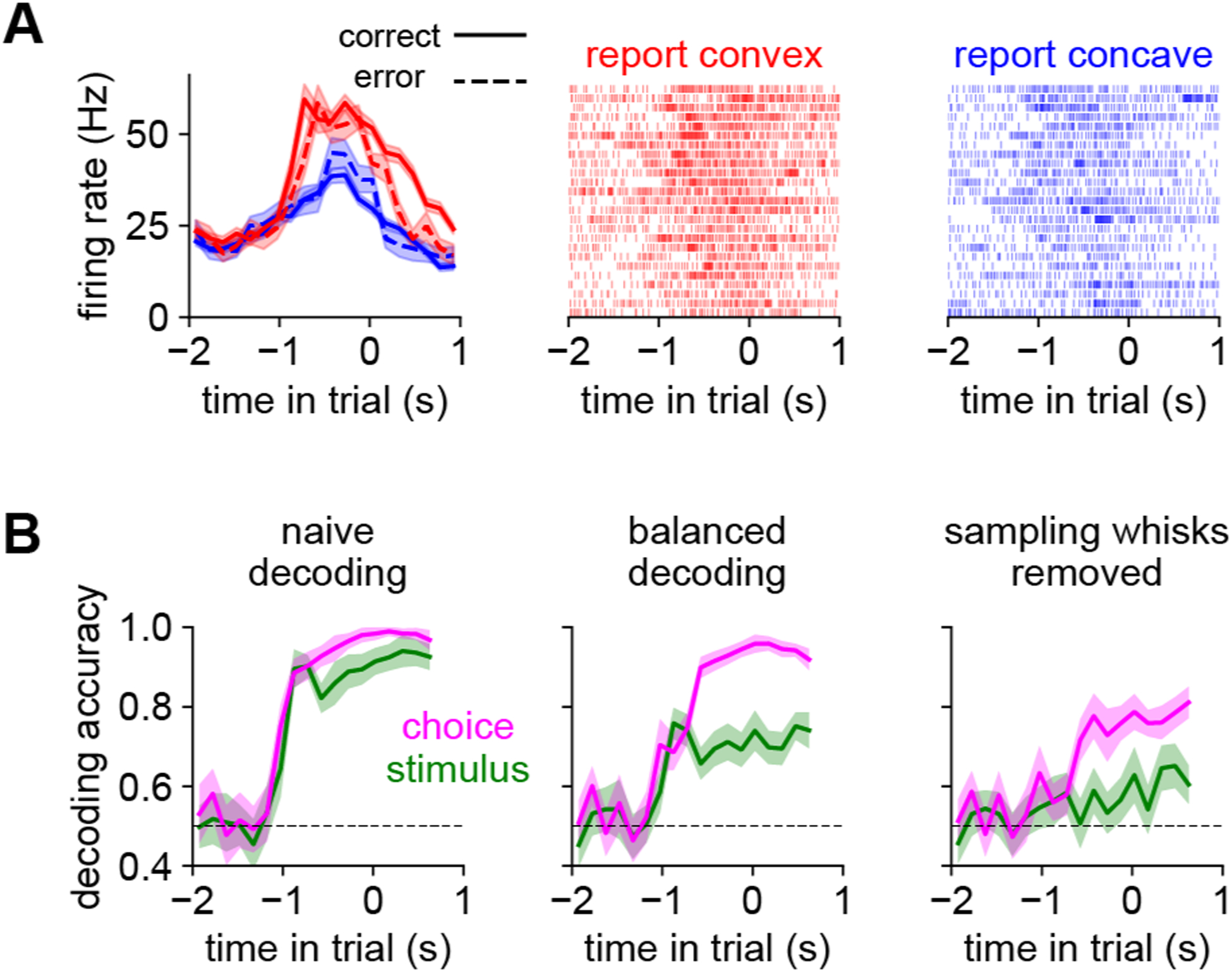
A) An example L5 excitatory neuron that encodes choice. Left panel: mean spike rate over trials for convex (red) or concave (blue) choices, separately by correct (solid) and incorrect (dashed). Right two panels: example spike rasters from randomly chosen trials. This neuron’s firing rate is elevated for convex choices, regardless of the identity of the shape. Error bars: SEM over trials.

B) Stimulus (green) or choice (pink) can be decoded from a pseudopopulation (n = 450 neurons) aggregated across shape discrimination sessions (timescale as in Fig 1H). Left: With a naive (unbalanced) approach, stimulus or choice can be decoded with similar accuracy. Middle: Equally balancing correct and incorrect trials decouples stimulus and choice. Right: Removing spike counts from all sampling whisks (i.e., whisks sufficiently large to reach the shapes) largely abolishes stimulus information while preserving choice information. Dashed line: chance. Error bars: 95% bootstrapped confidence intervals.

Distributed coding of sensorimotor variables

We next used regression to assess how neurons encoded whisker motion, contacts, and task-related features like choice. Because these features are correlated with each other, determining their relative importance is analytically challenging. We assessed the contribution of all features together using multivariate regression (a generalized linear model, or GLM; Fig 7A, Supplemental Fig 7A), similar to receptive field mapping by reverse correlation with natural stimuli (Park et al., 2014; Sharpee, 2013). Rather than binning the spikes into arbitrary time bins or averaging over trials, we sought to make predictions on individual whisk cycles. Our observation that the whisk cycle packetized contacts (Fig 2C) and spikes (Fig 5F) supported this level of granularity.

Figure 7. Distributed coding in barrel cortex.

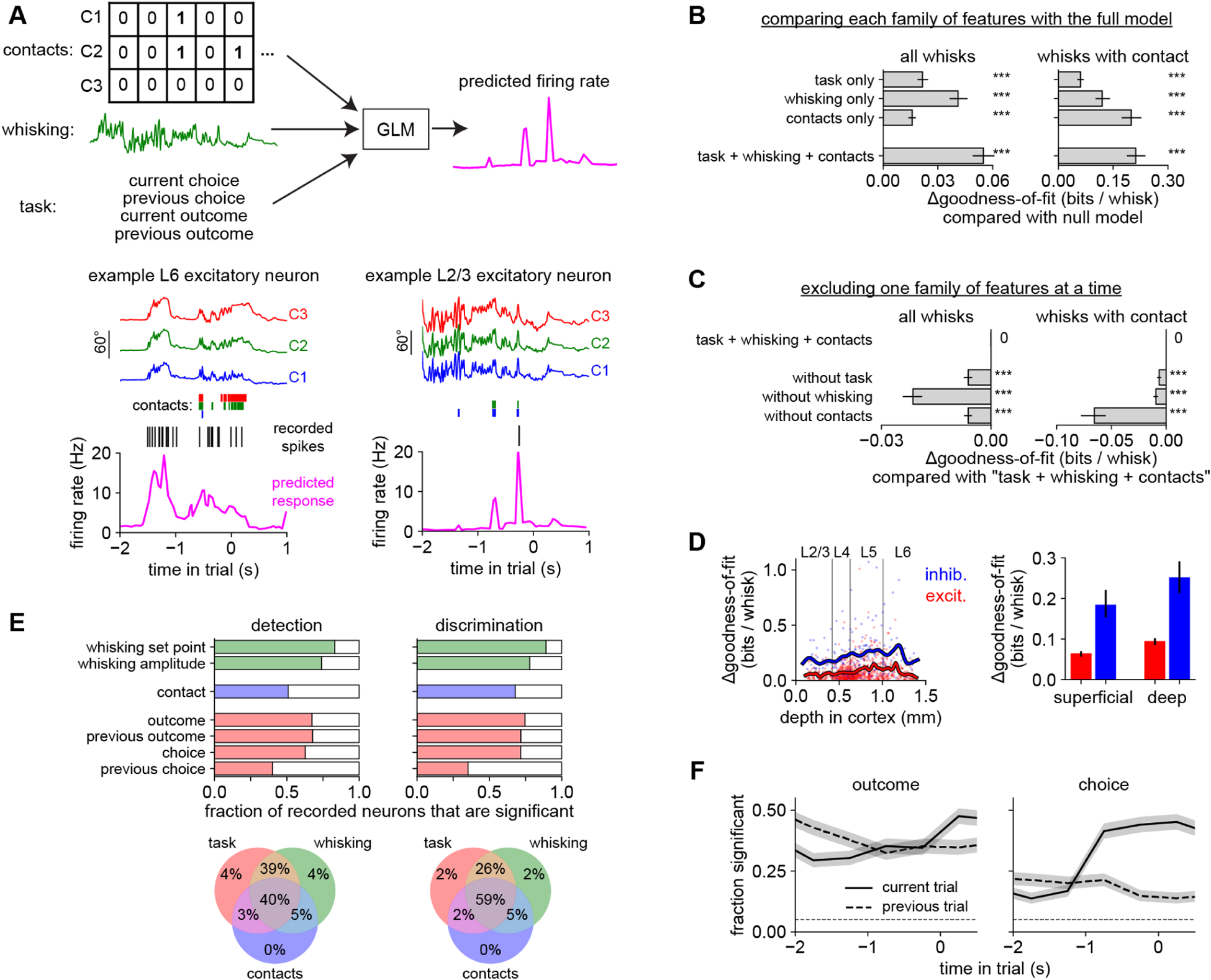
A) A GLM used features about contacts (whisker identity), whisking (amplitude and set point), and task (choice and reward history) to predict neural responses on individual whisk cycles. Bottom left: Predicted firing rate (pink) for an example neuron (black raster: recorded spikes) given the position of each whisker (colored traces) and contacts (colored bars). This L6 neuron mainly responded to whisking, regardless of contacts. Bottom right: This L2/3 neuron mainly responded to contacts regardless of whisking. Models were always evaluated on held-out trials.

B) The goodness-of-fit (ability to predict neural responses) of the GLM using features from the task, whisking, or contact families. Each feature family significantly improves the log-likelihood over a null model that used only information about baseline firing rate (p < 0.001, Wilcoxon test). The full model (“task + whisking + contacts”) outperforms any individual feature family. Similar results are obtained when testing on the entire dataset (left) or only on whisks with contact (right).

C) The effect on goodness-of-fit of leaving out one family at a time from the full “task + whisking + contacts” model.

D) Goodness-of-fit versus cortical depth (left) and grouped by cell type (right) in the “task + whisking + contacts” model.

E) Top: Proportion of neurons that significantly (p < 0.05, permutation test) encoded each variable during each task. Bottom: Venn diagram showing percentage of neurons significantly encoding features from task (red), whisking (green), and contact (blue) families during each task. <1% of neurons did not significantly encode any of the features.

F) Proportion of neurons significantly modulated by the outcome or choice of the previous (dashed) or current (solid) trial. Timescale as in Fig 1H.

n = 301 neurons during shape detection and 675 neurons during shape discrimination, pooled in panels B–D and F because the results were similar. Error bars: 95% confidence intervals, obtained by bootstrapping (B–D) or Clopper-Pearson binomial (F).

To quantify the importance of each feature for predicting neural responses, we fit different GLMs on individual families of features—contact (“whisks with contact” as above), whisking (amplitude and set point), and task-related (choice and outcome of the current and previous trial)—and compared their goodness-of-fit on held-out data. Each family alone had explanatory power, and a combined “task + whisking + contacts” model surpassed any individual family (Fig 7B, Supplemental Fig 7B). Dropping any family decreased the goodness-of-fit, indicating that each contained unique information (Fig 7C). Goodness-of-fit varied widely across the population but was generally higher in inhibitory and deep-layer neurons (Fig 7D, Supplemental Fig 7C).

In both tasks, we found that >99% of neurons were significantly modulated by at least one of the variables we measured (task, whisking or contacts; Fig 7E). A plurality of neurons were significantly modulated by all three variables. Thus, across these behaviors, individual neurons in barrel cortex are typically tuned for a combination of sensorimotor and task-related features and only rarely for a single feature (Rigotti et al., 2013).

Finally, we asked how neurons encoded task-related variables over the course of the trial. Early in the trial, neurons encoded the previous outcome whereas later in the trial they encoded the choice on that trial (Fig 7F). This is related to our observation that choice could be decoded from neural activity (Fig 6B), but that analysis did not distinguish between coding of choice per se versus coding of sensorimotor signals that might correlate with choice. The GLM analysis disentangles these variables and demonstrates that, in addition to coding for sensorimotor variables, barrel cortex neurons also persistently encode choice and outcome.

Cell type-specific encoding of movement and contact

The tuning of individual neurons varied with cell type (excitatory or inhibitory) and laminar location (superficial or deep). The most prominent effect was that whisking strongly drove deep-layer inhibitory neurons (Fig 8A–C). Indeed, almost all (94 / 107 = 87.9%) inhibitory neurons in the deep layers were significantly excited by whisking (mean increase in firing rate: 23.9% per 10° of whisking amplitude). Excitatory neurons and superficial inhibitory neurons also encoded whisking, but were as likely to be suppressed as excited.

Figure 8. Task-specific contact responses are formatted for shape discrimination.

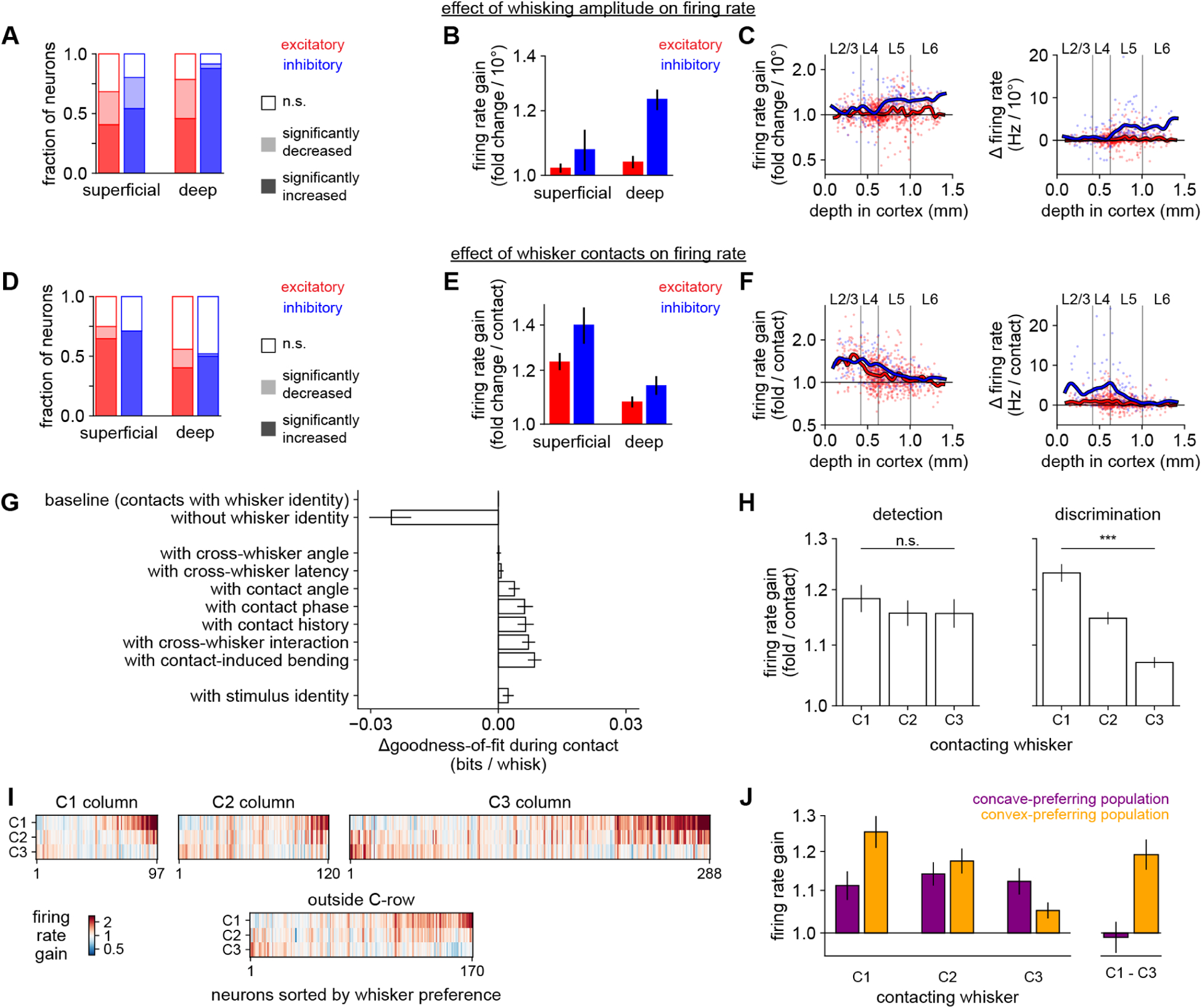
A) Proportion of neurons of each cell type whose activity is significantly (p < 0.05, permutation test) increased, decreased, or unmodulated by whisking amplitude. In panels A–C, n = 301 neurons during shape detection and n = 675 neurons during shape discrimination, pooled because the results were similar.

B) Firing rate gain per each additional 10 degrees of whisking amplitude, grouped by cell type.

C) Data in (B) for individual neurons versus cortical depth. Lines: smoothed with a Gaussian kernel.

D–F)Like panels (A–C), but for whisker contacts (averaged across C1, C2, and C3 whiskers). In (D–H), n = 235 neurons during shape detection and n = 675 neurons during shape discrimination. We excluded neurons for which too few whisker contacts occurred to estimate a response.

G) Goodness-of-fit of models incorporating contact-related features, compared to the “task + whisking + contacts” model (top row, “baseline”). Removing whisker identity (second row) markedly decreases the quality of the fit. Adding contact-related parameters only slightly improves fit, even when including stimulus identity (bottom row).

H) Response to contacts made by each whisker. Left: During shape detection, the population responds nearly equally to each whisker (p > 0.05; one-way ANOVA). Right: During shape discrimination, the population strongly prefers C1 contacts (p < 0.001).

I) Contact response of each individual neuron during shape discrimination (n = 675), split by location within barrel cortex. Neurons preferring C1 contacts (upper right corner of each heatmap) are more common in each location.

J) Similar to the right panel of H, but separately for neurons that preferred convex (n = 110; orange) or concave choices (n = 76; purple), as assessed by the decoder analysis in Fig 6B. Neurons that prefer convex choices respond more strongly to C1 contacts than to C3 contacts (p < 0.001; t-test), similar to the weights used by the optimized behavioral decoder to identify convex shapes in the right panel of Fig 3G.

Logarithmic y-axis in B–C, E–F, H, and J. Error bars: 95% bootstrapped confidence intervals in B, E, and G; SEM over neurons in H and J.

In contrast, whisker contacts on the shapes more strongly modulated superficial cells, including both L2/3 and L4, than those in deep layers (Fig 8D–F). Suppression by contact was less frequent than excitation in all cell types. Thus, movement and contact have their greatest impact on the deeper and superficial layers, respectively.

Contact responses are dominated by whisker identity, not finer sensorimotor parameters

We next asked which features of these contacts drove neurons. Barrel cortex is arranged topographically with neurons in each cortical column typically responding to the corresponding whisker (somatotopy). However, barrel cortex neurons are also tuned for multiple whiskers, contact force, cross-whisker timing, and global coherence, among other features (Brumberg et al., 1996; Drew and Feldman, 2007; Ego-Stengel et al., 2005), though this is less well understood in the behaving animal.

To assess the importance of each contact-related feature in our dataset, we compared the goodness-of-fit of GLMs that had access to each. Whisker identity (which whisker made contact) was the most critical element determining neural firing (Fig 8G, Supplemental Fig 8A). The exact kinematics of contacts were less important.

We considered the possibility that some alternative kinematic feature that was not measured (e.g., due to limitations in frame rate) might be driving neural activity. We therefore fit a model that also included the identity of the shape (concave or convex) on which each contact was made. If any unmeasured kinematic feature drove neural activity differently depending on the stimulus, this feature should capture some variability. However, it only slightly improved the model (Fig 8G, bottom bar). This rules out, at least in a GLM framework, a latent variable that differentiates the stimuli and strongly drives neural activity. Thus, contact responses in barrel cortex are mainly driven by the identity of the contacting whisker, which alone almost fully accounts for the neural encoding of shape.

Task-specific representation of contacts

Because the behavioral meaning of contacts made by each whisker differed between detection and discrimination (Fig 3–4), we asked whether neural tuning was also task-specific using the weights that the GLM assigned to each whisker (Supplemental Fig 8B,C). In shape detection mice, the population of recorded neurons as a whole responded nearly equally to contacts made by C1, C2, and C3 (Fig 8H, left). Individual neurons could prefer any of the three whiskers, and in keeping with the somatotopy of barrel cortex, superficial neurons tended to prefer the whisker corresponding to their cortical column (Supplemental Fig 8D).

In marked contrast, we observed a widespread and powerful bias in shape discrimination mice: at the population level, neurons responded much more strongly to C1 contacts than to contacts by C2 or C3 (Fig 8H, right). Neurons preferring C1 were more prevalent in all cell types and in all recording locations, including the C2 and C3 cortical columns (Supplemental Fig 8E,F; individual neurons in Fig 8I). This task-specific tuning could not be explained by the shape stimuli, our analyses, or the whisker trimming procedures because all of these were the same for both tasks. Contact force could not explain this effect (Supplemental Fig 8G). Thus, whisker tuning was task-specific and overrode somatotopy.

Whisker-specific tuning explains the population choice signal

The task-specific neural tuning we observed corresponds to the different weights assigned to each whisker by the behavioral decoders (compare Fig 3G, right and Fig 8H, right), suggesting that neurons might be tuned to C1 in order to promote convex choices. This mirrors our behavioral observation (Fig 1G) that mice seemed to rely on a “convexity detection” strategy. In theory, the population could instead have been tuned to C3 in order to promote concave choices, but we did not observe this.

We asked whether neurons’ coding of choice could be explained by their whisker tuning. Specifically, we assessed the tuning of two subpopulations of neurons preferring either concave or convex choices (i.e., those assigned positive or negative weights by the neural decoder in Fig 6B). Indeed, the convex-preferring subpopulation strongly preferred C1 contacts (Fig 8J, orange bars).

In summary, our neural encoder model (Fig 7–8) explains how the neural decoder (Fig 6) was able to predict stimulus and choice: neurons were tuned for sensory input that the mouse had learned to associate with convex shapes. These representations were task-specific (Fig 8H) and could not be explained solely by simple geometrical aspects of the stimuli or whiskers. Indeed, the representations matched weights used by the behavioral decoders to identify shapes. Our results link the tuning of individual neurons for fine-scale sensorimotor events to the more global and persistent representations of shape and choice. This bridging of local features to global identity is the essential computation of shape recognition.

Discussion

In this study, we developed a novel head-fixed shape discrimination behavioral paradigm. Mice accomplished this task by comparing contacts made across whiskers. Barrel cortex neurons exhibited distributed coding of sensory, motor, and task-related signals. Deep inhibitory neurons robustly encoded motion signals, and all populations of neurons coded for contacts with a bias toward the whisker (C1) that preferentially contacted convex shapes. In shape detection mice, we observed similar coding of exploratory motion signals and of choice and outcome-related signals, but not the whisker-specific bias in contact responses. Thus, neural tuning for motion and choice is shared across tasks, whereas tuning for contacts is task-specific.

Behavioral decoding reveals sensorimotor strategies

Understanding neural computations begins with defining the subject’s strategy (Krakauer et al., 2017; Marr and Poggio, 1976). Our approach was to measure as many sensorimotor parameters as was feasible and then to use behavioral decoding to predict the stimulus and choice from these data. This allowed us to identify informative variables and understand the corresponding task-specific neural responses. Our approach could readily be extended to other tasks, modalities, and model organisms.

Some variables, such as contact count, were important for both stimulus and choice. Others, such as contact angle, were more important for predicting stimulus than choice, suggesting that mice did not (or could not) effectively exploit it. This effect is likely due to the incomplete information mice have about the instantaneous location of the whisker tips (Fee et al., 1997; Hill et al., 2011; Moore et al., 2015; Severson et al., 2019).

In most tasks, stimulus and choice are correlated, especially when the subject’s accuracy is high. We disentangled stimulus and choice through trial balancing—overweighting incorrect trials so that in aggregate they are weighted the same as correct trials. Other approaches include separately fitting correct and incorrect trials, comparing stimulus prediction with choice, and so on (Campagner et al., 2019; Isett et al., 2018; Waiblinger et al., 2018; Zuo and Diamond, 2019). A benefit of trial balancing is that it jointly optimizes over correct and incorrect trials.

Mice compare the number of contacts across whiskers to discriminate shape

Shape discrimination fundamentally differs from pole localization and texture discrimination because it explicitly requires integration over different regions of space. Thus, comparing input across whiskers was a reasonable strategy for mice to pursue. Although rodents can perform other tasks better with multiple whiskers (Carvell and Simons, 1995; Celikel and Sakmann, 2007; Knutsen et al., 2006; O’Connor et al., 2010a), those cases likely reflect statistical pooling of similar information from multiple sensors, as in our shape detection control task (Krupa et al., 2001). Our results go beyond statistical pooling. We are unaware of any published examples of mice assigning opposite behavioral meaning to input from different nearby whiskers. This strategy mirrors the way primates compare across fingers when grasping objects (Davidson, 1972; Thakur et al., 2008).

For shape discrimination, the identity of the contacting whiskers was the most important feature determining both behavioral choice and neural responses. Cross-whisker contact timing has been hypothesized to be an important parameter for shape discrimination (Benison et al., 2006; cf. primate fingertips in Johansson and Flanagan, 2009) but was uninformative in our task. This may be because whisker flexibility during movement adds too much variability to this parameter. It had also been proposed that the pattern of forces over the whiskers as they “grasp” an object could be informative about shape (Bush et al., 2016; Hobbs et al., 2016a), but we observed little contribution of whisker bending. In sum, whisker identity during contact was the critical parameter for shape discrimination (Hobbs et al., 2016b).

Adaptive motor exploration strategies simplify the sensory readout

Reflecting this difference in strategy, mice interacted with shapes in a fundamentally different way than in many other tasks. In our task, mice lightly tapped the stimuli with the tips of multiple whiskers simultaneously. This “minimal impingement” approach (Mitchinson et al., 2007) is likely the natural mode of the whisker system (Grant et al., 2009; Ritt et al., 2008). Multiple light touches could also engage adaptation circuits within the somatosensory pathway, enhancing their ability to perform fine discrimination (Wang et al., 2010). In contrast, mice locate and detect poles by contacting them with high enough force to cause substantial whisker bending (Hong et al., 2018; Pammer et al., 2013). This likely drives a strong neural response, an adaptive strategy for detection (Campagner et al., 2016; O’Connor et al., 2010b; Ranganathan et al., 2018) though perhaps more useful for nearby poles than for surfaces.

A common thread running through the literature of whisking behavior is that animals learn a motor exploration strategy optimized for the task at hand: targeting whisking to a narrow region of space to locate objects (Cheung et al., 2019; O’Connor et al., 2010a), rubbing whiskers along surfaces to generate the high-acceleration events that correlate with texture (Isett et al., 2018; Jadhav et al., 2009; Schwarz, 2016), or targeting contacts to specific whiskers in the present work. Thus, animals pursue a motor strategy that simplifies the sensory readout, e.g. to a threshold on spike count (O’Connor et al., 2013). Performance is consequently limited by errors in motor targeting rather than in sensation (Cheung et al., 2019).

Similarly, humans learn adaptive motor strategies for directing gaze and grasp (Gamzu and Ahissar, 2001; Yang et al., 2016a). The challenge of these tasks may lie in learning a skilled action that enhances active perception rather than in drawing fine category boundaries through sensory representations as in classical perceptual learning. Behavior may thus be considered a motor-sensory-motor sequence combining purposive exploration and sensory processing to guide further actions (Ahissar and Assa, 2016).

Distributed coding of sensorimotor signals in barrel cortex

In natural behavior, active sensing is the norm: animals explore by moving their heads, eyes, and ears and by sniffing, chewing, or grasping objects. Motion signals should perhaps be expected in sensory areas because they provide context for interpreting sensory input. In the barrel cortex, recent studies have variously found that neurons respond to whisking onset (Muñoz et al., 2017; Yu et al., 2016), that whisking phase modulates contact responses (Curtis and Kleinfeld, 2009; Hires et al., 2015), or that whisking simply has mixed effects on neuronal firing (Ayaz et al., 2019; O’Connor et al., 2010b; Peron et al., 2015). Technical limitations of whisker tracking perhaps explain these disparate results (Krupa et al., 2004).

We measured all of these variables with high-speed video and considered them together using multivariate regression. This approach was critical to understanding the structure of neural responses, because it allowed us to compare the relative importance of each sensorimotor variable even when they were correlated with each other. We have recently observed that barrel cortex encodes nonlinear combinations of motion and contact signals, even though such combinations are not necessary for this task (Nogueira et al., 2021).

Motion encoding was widespread but had a strong cell type-specific bias: inhibitory neurons in the deep layers were robustly and consistently excited by whisking, consistent with previous reports (Muñoz et al., 2017; Yu et al., 2019). These inhibitory neurons receive direct input from primary motor cortex (Kinnischtzke et al., 2014) and can potently suppress the entire cortical column (Bortone et al., 2014; Frandolig et al., 2019). Inhibitory coding of motion could allow the brain to predict and account for the sensory consequences of movement (Yu et al., 2016) as in the auditory cortex (Schneider et al., 2018).

The superficial and deep layers of cortex can encode sensory stimuli independently (Constantinople and Bruno, 2013), but they can also strongly interact (Pluta et al., 2019). We observed stronger touch responses in the superficial layers and stronger whisking responses in the deep layers, potentially useful for simulating the effects of motor exploration (Brecht, 2017). More generally, whisker motion signals may be analogous to the preparatory saccade signals identified in visual cortex. Like whisking, saccades are motor actions directed toward collecting information, and the cortex predicts the resulting change in sensory input (Steinmetz and Moore, 2010).

It is an open question why sensory cortex is required for some perceptual tasks and not others. We recently found that barrel cortex was dispensable for detecting textured surfaces but essential for discriminating them (Park et al., 2020). Here, we also find barrel cortex to be essential for discriminating shape. Barrel cortex may thus be generally necessary for discriminating objects, but dispensable for detecting them.

Motor strategies and neural representations are adapted to the task

At first glance, the whisker system may appear to be a labeled-line system due to its somatotopic organization in the brainstem, thalamus, and cortex. Indeed, neurons in thalamorecipient layer 4 typically respond best to stimulation of an anatomically corresponding whisker. However, outside of L4 the preference for any particular whisker is much weaker (Brecht et al., 2003; Clancy et al., 2015; Jacob et al., 2008; De Kock et al., 2007; Peron et al., 2015; Pluta et al., 2017; Ramirez et al., 2014), and attending to whisker input actually decreases somatotopy (Wang et al., 2019).

Rather than maintaining a labeled-line code, the barrel cortex may encode multi-whisker sequences, a map of scanned space, or entire tactile scenes (Bale and Maravall, 2018; Estebanez et al., 2018; Laboy-Juárez et al., 2019; Pluta et al., 2017; Vilarchao et al., 2018). Similarly, auditory cortex is now thought to encode high-level sound features rather than strict tonotopy (Bandyopadhyay et al., 2010; Carcea et al., 2017; Rothschild et al., 2010). Ethologically, integrating information across sensors would seem more useful than maintaining in higher-level areas a strict segregation based on peripheral organization.

We suggest that sensory cortex learns to accentuate the sensory features that are most relevant for the animal’s goals (Ramalingam et al., 2013). An important question for future work will be whether these task-specific representations arise from local plasticity induced by training or from long-range inputs signaling the context of the task (Rodgers and DeWeese, 2014). In future work we plan to investigate the timescale over which these representations emerge (Driscoll et al., 2017).

Neurons in visual cortex and auditory cortex can increase their responses to, or slightly shift their tuning toward, rewarded stimuli (David et al., 2012; Fritz et al., 2003; Khan et al., 2018; Poort et al., 2015). Our results are fundamentally different. First, no whisker was “rewarded” or “punished” in our task, and indeed all whiskers could touch both objects. Second, the neurons did not subtly shift their tuning, but rather changed the whisker they most responded to, akin to a V1 receptive field center moving to a new retinal location. Indeed, the magnitude of the effect we observe is more similar to the massive reconfiguration that is driven by extreme manipulations such as stitching an eye shut or removing a finger (Horton and Hocking, 1997; Merzenich et al., 1984) but in our case arises solely through behavioral training.

Our work provides a new conceptual way to think about task-specific neural representations. We decompose the response to the shape into the responses to the individual sensorimotor events that indicate curvature. It was not a priori obvious that any particular whisker would be associated with either shape, and so our approach was to first identify the behavioral meaning of each whisker’s contacts, which then explained the corresponding neural response. A similar retuning could give rise to the enhanced responses to rewarded stimuli observed in other tasks.

Although the details of these effects are specific to this task and stimulus geometry, we suggest that analogous computations in other brain areas and species could also implement object recognition by comparing input across different sensors in the context of exploratory motion. Recent results have demonstrated an unexpectedly widespread coding of motion across the brain (Musall et al., 2019; Stringer et al., 2019; reviewed in Parker et al., 2020). These motion signals could be critical for interpreting sensory input in the context of behavioral state. The common structure of cortex across regions of disparate functionality (Douglas and Martin, 2004) may be a signature of this common computational goal.

STAR Methods

Resource Availability

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Randy M. Bruno (randybruno@columbia.edu).

Materials Availability

This study did not generate any unique reagents.

Data and Code Availability

The datasets and code generated during this study are available at https://github.com/cxrodgers/Rodgers2021 and https://dx.doi.org/10.5281/zenodo.4743837 (Rodgers, 2021).

Experimental Model and Subject Details

We report data here from 26 adult mice (14 females and 12 males) of the C57BL6/J strain bred in the Columbia University animal facilities. The mice were used for the following experiments.

• 10 mice (“shape discrimination group”; 6 females and 4 males) were used for shape discrimination experiments throughout the manuscript.

• 5 mice (“shape detection group”; 4 females and 1 male) were used for shape detection experiments throughout the manuscript.

• 8 mice (“lesion group”; 3 females and 5 males) were used for the lesion experiments in Fig 1C–D.

• 1 female (from a different anatomical study) was used for the image in Fig 5A.

• 1 male was used only for the single-whisker trim experiments (Fig 4F–G). 1 other male from the “shape discrimination group” was also used for those experiments.

• 1 male was used only for the discrimination with flatter shapes (Supplemental Fig 1A). 1 male and 2 females from the “shape discrimination group” were also used for those experiments.

Mice in our colony are continuously backcrossed to C57BL/6J wild-type mice from Jackson Laboratories. Some mice expressed Cre, CreER, Halorhodopsin, Channelrhodopsin2, and/or EGFP for ongoing and unpublished studies. Some received tamoxifen, but this was done well before any behavioral training or surgical manipulations. Mice received no probes, substances, viruses, or any other surgical interventions relating to optogenetics or other genetic manipulations. We noted no difference in the results regardless of the genes expressed and therefore pooled the data here.

Mice were group-housed (unless they did not tolerate this) and lived in a pathogen-free barrier facility. All experiments were conducted under the supervision and approval of the Columbia University Institutional Animal Care and Use Committee.

Method Details

Surgeries

Mice were implanted with a custom-designed stainless steel headplate (manufactured by Wilke Enginuity) between postnatal day 90 and 180. They received carprofen and buprenorphine and were anesthetized with isoflurane throughout the stereotaxic procedure. Using aseptic technique, we removed the scalp and fascia covering the dorsal surface of the skull. We then positioned the headplate over the skull and affixed it with Metabond (Parkell).

After behavioral training (see below), some mice underwent another procedure to permit electrophysiological recording. First, we used a dental drill to thin the cement and skull over barrel cortex, rendering it optically transparent, and coated it with cyanoacrylate glue (Vetbond). We used intrinsic optical signal imaging (described below) to locate the cortical columns of the barrel field corresponding to the whiskers on the face. We then used a scalpel (Fine Science) to cut a small craniotomy directly over the columns of interest. Between recording sessions, the craniotomy was sealed with silicone gel (Dow DOWSIL 3–4680, Ellsworth Adhesives) and/or silicone sealant (Kwik-Cast, World Precision Instruments).

Some mice (n = 8) were lesioned to test the necessity of barrel cortex in this task (Fig 1C–D). After these mice completed behavioral training, we used intrinsic signal optical imaging to localize barrel cortex in the left and/or right hemispheres. Using aseptic technique, we cut a craniotomy over barrel cortex on one side and aspirated all layers of cortex with a sterile blunt-tipped needle connected to a vacuum line. These lesions had a diameter of 2–3 mm and were centered on the C2 column. Of these eight mice, six were lesioned on the left side (contralateral to the stimulus), and two were lesioned on the right side (ipsilateral to the stimulus). The two mice lesioned on the ipsilateral side were tested for any impairment, then lesioned again on the contralateral side, and then tested again. Because the contralateral lesions produced similar results regardless of whether the ipsilateral side had already been lesioned, the results for all contralateral lesions are pooled. Some of these mice were performing simpler versions of the shape discrimination task (e.g., before trimming to one row, or only for a subset of the possible shape positions).

Intrinsic signal optical imaging

Individual barrel-related cortical columns were located with intrinsic imaging. While the mice were anesthetized with isoflurane, individual whiskers were deflected one at a time by a piezoelectric stimulator (8 pulses in the rostral direction at 5 Hz, with ~30 s between trains). We used custom software written in LabView (National Instruments) to acquire images of the cortical surface through the transparent thinned skull under a red light source with a Rolera CCD camera (QImaging). Videos were averaged over 20–60 trains of pulses. We repeated this procedure for the C1, C2, and C3 whiskers to locate the region of maximal initial reflectance change corresponding to each.

Behavioral apparatus

The behavioral apparatus was contained within a black box (Foremost) with a light-blocking door. It was built with posts (Thorlabs) and custom-designed laser-cut plastic pieces on an aluminum bread board (Edmund Optics, Thorlabs, or Newport). A stepper motor (Pololu 1204) rotated a custom-designed curved shape 3D-printed with ABS plastic (Shapeways) into position, and a linear actuator (Actuonix L12-30-50-6-R) moved it within reach of the mouse’s whiskers. Rewards (~5 μL of water, chosen based on the mouse’s weight and how many trials it typically completed) were delivered by opening a solenoid valve (The Lee Co. LFAA1209512H) that allowed water to flow to the mouse from a reservoir to a thin stainless steel tube (McMaster).

An Arduino Uno, in communication with a desktop computer over a USB cable, controlled the motors. It also monitored licking by sampling beam breaks of the mouse’s tongue through infrared proximity detectors (QRD1114, Sparkfun) or capacitive touch sensors (MPR121, Sparkfun) in front of and slightly to the left or right of the mouse’s mouth, inspired by a published two-choice design (Guo et al., 2014). Between trials only, the Arduino activated a white “house light” (LE LED; Amazon B00YMNS4YA) that prevented mice from fully dark-adapting, preventing the use of visual cues. A computer fan (Cooler Master; Amazon B005C31GIA) continuously blew air slowly over the shape such that the mouse’s nose was upwind from the shape, preventing the use of olfactory cues. We never observed mice exploiting auditory or vibrational cues from the motors and thus no masking noises were necessary.

At a fine timescale the trial structure was controlled by the Arduino using a custom-written sketch. At the level of individual trials, the desktop PC chose the stimulus and correct response and logged all events read from the Arduino to disk using custom Python code. The training parameters for each mouse were stored in a custom-written django database and updated manually or semi-manually by the experimenters depending on each mouse’s progress.

Two-alternative task design

In this two-alternative design, the mouse can lick left, lick right, or do nothing. If 45 seconds elapsed without any lick, the trial was marked as “spoiled” and discarded from analysis. Such trials typically only occurred at the end of the session when the mouse was satiated. Thus, all included trials are either correct (licked the correct direction) or incorrect (licked the incorrect direction). There is no equivalent to the “false positive” or “miss” outcome of go/nogo tasks.

On some trials the mouse made no contacts. We included these trials in all analyses. On the detection task, the mouse could not possibly make any contacts on the “stimulus-absent” trial type, and it would not have made sense to exclude those trials. For parity, we included these trials in our analysis of the discrimination task. Choices on these trials were scored exactly the same—correct or incorrect—as on trials with contact.

Behavioral training

Throughout, the mice were denied access to water in the home cage and learned to receive their water during behavioral training. We closely monitored their water intake, weight, and general health to ensure they did not become dehydrated. Ad libitum water was provided if necessary to ensure health.

Each mouse in our study learned either shape detection or shape discrimination throughout its training, rather than progressing from one task to the other. Neither task was used as an initial shaping stage for the other. The number of training sessions did not significantly differ between the two tasks: detection animals received 94.8 sessions on average (individual mice: 89, 93, 147, 121, 24) and discrimination animals received 118.0 sessions on average (individual mice: 107, 118, 93, 120, 157, 133, 106, 110).

Mice were trained to perform either the shape discrimination or detection tasks using a process of gradual behavioral shaping described below.

1. “Lick training.” Mice initially learned to lick to receive water. They were advanced through each step of this stage only once they learned to receive sufficient daily water from the apparatus. First, they were placed in the apparatus without head-fixing and allowed to drink freely from the water pipes, which rewarded every lick. Next, we head-fixed the mice directly in front of a single lick pipe and rewarded every lick. Finally, mice were presented with two lick pipes (left and right) and learned to lick alternately from each of them, first in blocks of ten licks and gradually decreasing to a single lick on each side. This stage required 12.5 sessions on average.

2. “Forced alternation”. We introduced the complete trial structure for the first time, presenting shapes and rewarding the mouse only for correct responses and punishing it with a timeout for incorrect responses. During this stage the shape on each trial was not random; instead, mice were repeatedly presented with the same shape trial after trial until it gave the correct response. After a correct response, the other stimulus was presented. Thus, mice could perform at 100% by alternating responses from trial to trial. The timeout was initially 2 s and then increased to 5 s and finally 9 s as the mice became accustomed to it. This stage required 11.3 sessions on average.

3. “Stimulus randomization with bias correction”. During this stage, stimulus identity was randomized on each trial and only presented at the closest position. Each session began with 45 trials of “forced alternation” to ensure that mice were able to lick both directions. After that, trials were generally random. The software continuously monitored their performance for biases; when a strong bias was detected, it stopped presenting trials randomly and began presenting trials designed to counteract the bias. For instance, if mice responded on the left ≥20% more than on the right, the software would deliver only right trials. Alternatively, if the mice showed a significant perseverative bias (ANOVA “choice ~ stimulus + side + previous_choice”, p < 0.05 on previous_choice), the software would deliver “forced alternation” trials. Critically, we only ever analyzed truly random trials from the session. Non-random trials were used only for behavioral shaping and were discarded from behavioral and neural analyses.

4. “Range of positions”. We now presented shapes at the first 2 positions (close and medium) and then all 3 positions (close, medium, and far). Position was randomized across trials. The same automatic training and bias-prevention procedures as before were used.

5. “Flatter shapes”. Some mice were now presented with flatter shapes as well as the shapes of the original curvature. Other mice skipped this stage and were never presented with flatter shapes.

6. “Whisker trimming”. We gradually trimmed whiskers off the right side of the face: first we trimmed the A and E rows, then the B row, then the D row. After any trimming, we allowed mice to recover to high performance before trimming additional rows. We retrimmed previously trimmed whiskers as necessary to ensure they could not reach the shapes. Stages 3–6 required a total of 109.1 sessions on average.

Sometimes it was necessary to return mice to an earlier stage of training temporarily to facilitate learning (e.g., reducing the number of positions at which the shapes were presented or returning to “forced alternation” trials only). Mice that successfully progressed through all stages of the training procedure—those who could identify both shapes at all three positions with only the C-row of whiskers—were deemed fully trained. We only took high-speed video or neural recordings from fully trained mice.

Videography

For videography and electrophysiology, we moved the behavioral setup to a different light-blocking box mounted on a vibration-isolating air table (TMC). We took video of fully trained mice using a high-speed camera (Photonfocus DR1-D1312IE-100-G2-8) with a 0.15 ms exposure time to prevent motion blur. We used a lens with a 25 mm focal length (Fujinon HF25HA-1B) to prevent “fisheye” distortion. An aperture (F-stop) of approximately 6.0 optimized depth of field.

We designed and built a custom infrared backlight with a 7×8 grid of high-power surface-mount infrared (850 nm) LEDs (Digikey VSMY2853G) soldered to a custom-designed PCB (manufactured by OSH Park) that allocated power to each LED through current-limiting resistors. Diffusion paper mounted above the LEDs homogenized the light. The backlight was placed below the mouse and pointed toward the camera so that the whiskers would show up as high-contrast black on a white background. The Arduino pulsed this backlight off for 100 ms at the beginning of each trial, allowing us to synchronize the behavioral and video data. We used Matlab’s Image Acquisition Toolbox to store the video data to an SSD.

Electrophysiology

To record neural activity, we head-fixed the mouse in the behavioral arena as usual and removed the temporary sealant over the craniotomy. We lowered an electrode array (Cambridge Neurotech H3) using a motorized micromanipulator (Scientifica PatchStar), noting its depth at initial contact and at final position. We used an OpenEphys acquisition system (Siegle et al., 2017) with two digital headstages (Intan C3314) to record 64 channels of neural data at 30 kHz at the widest possible bandwidth (1 Hz to 7.5 kHz). The backlight sync pulse was acquired with an analog input to synchronize the neural, behavioral, and video data.

We used KiloSort (Pachitariu et al., 2016) to detect spikes and to assign them to putative single units. Single units had to pass both subjective and objective quality checks. First, we used Phy (Rossant et al., 2016) to manually inspect every unit, merging units that appeared to be from the same origin based on their amplitude over time and their auto- and cross-correlations. Units that did not show a refractory period (i.e. a complete or partial dip in the auto-correlation within 3 ms) were deemed multi-unit and discarded. Second, single units had to pass all of the following objective criteria: ≤5% of the inter-spike intervals less than 3 ms; ≤1.5% change per minute in spike amplitude; ≤20% of the recording at <5% of the mean firing rate; ≤15% of the spike amplitude distribution below the detection threshold; ≤3% of the spike amplitudes below 10 μV; ≤5% of the spikes overlapping with common-mode artefacts.

We identified inhibitory neurons from their waveform half-width, i.e. the time between maximum negativity and return to baseline on the channel where this waveform had highest power. Neurons with a half-width below 0.3 ms were deemed narrow-spiking and putatively inhibitory. We measured the laminar location of each neuron (using the boundaries in Hooks et al., 2011) based on the manipulator depth and the channel on which the waveform had greatest RMS power. Neurons in L1 or the cortical subplate were discarded from this analysis because they were difficult to sort and showed variable properties across mice.

Histological reconstruction

We used a camera mounted on a surgical microscope to take a picture of the area around barrel cortex on every session from the time of intrinsic signal imaging to the end of the experiment. We aligned all of these images with each other using the TrakEM2 plugin (Cardona et al., 2012) in Fiji using surface vasculature. These images, referenced to individual barrel column locations determined by intrinsic signal imaging, were used to guide the placement of the craniotomy and the electrode. We also photographed and aligned images of the location of the implanted electrode array each day.

On the last day, we inserted a glass pipette coated with DiI (Sigma-Aldrich 468495) into the barrel field twice to leave two landmarks, one anterior and one posterior, which were also photographed and aligned. At the conclusion of the experiment, we deeply anesthetized the mice with pentobarbital, transcardially perfused them with 4% paraformaldehyde, and removed the brain for histological processing.

The left hemisphere was sectioned tangentially to the barrel field using a Vibratome or freezing microtome to cut 50 or 100 μm sections. We stained for barrels with fluorescently conjugated streptavidin and imaged the sections on an epifluorescent microscope to reveal the location of the barrels and the DiI landmarks. In this way we confirmed the exact location of each recording site with respect to both the anatomical and functional barrel map.

Quantification and statistical analysis

Statistics

Throughout this manuscript, “*” indicates p < 0.05; “**” indicates p < 0.01; “***” indicates p < 0.001; and “n.s.” indicates “not significant”.

To non-parametrically estimate the width of certain non-normal distributions, we used “bootstrapped confidence intervals”. This means resampling the data with replacement 1000 times, taking the average of each resampled dataset, and then taking the interval that spans the central 95% of this distribution of averages across resampled datasets.

Whisker video analysis

We used a lightly modified fork of the ‘pose-tensorflow’ package (Insafutdinov et al., 2016; Pishchulin et al., 2015) to train and use a deep convolutional neural network to identify and track whiskers in the video. This network is based on Resnet (He et al., 2015) and is the same “feature detector” network incorporated into the first version of DeepLabCut (Mathis et al., 2018). We generated an initial training set using the software ‘whisk’ (Clack et al., 2012) to track individual whiskers and custom semi-automated code to classify them.

Eight equally spaced points along each tracked whisker were provided as the “joints” for the neural network to identify. We iteratively improved the neural network by evaluating it on new frames, choosing difficult frames from the result, semi-automatically improving the labels, swapping in the results from ‘whisk’ as necessary, and then using this new training set to train a new version of the network. This procedure is described in greater detail in the following section. Whiskers of below-threshold confidence or below-threshold smoothness at any joint were discarded. We optimized these thresholds with a cross-validated grid search.

Sessions with inaccurate labeling were discarded: we required that every whisker be labeled in ≥95% of the frames, that ≤2% of the contact events contained even a single frame with a missing label, and that the arcs traced out over the entire session by the whisker contained no discontinuities or jumps suggestive of tracking errors. In the remaining well-traced sessions we interpolated whiskers over any missing frames.

We identified the shape stimulus in each frame by thresholding and segmenting the frame and selecting the segment of the appropriate size and location. We identified contacts on the shape based on proximity (≤10 pixels Cartesian distance) between the tip of each whisker and the edge of the shape.

To estimate each whisker’s bending moment, we first fit a spline through its 8 identified joints and used the “measure” function of ‘whisk’ to estimate curvature (κ). κ is the spatial rate of change of direction of the whisker at each point along its length, i.e. the reciprocal of the radius of curvature at that point, and is measured in units of m⁻¹. ‘whisk’ averages κ over the entire length of the traced whisker and we followed this convention. For comparison with other studies, we note that 1 m⁻¹ is equal to 0.001 mm⁻¹ due to this reciprocal. κ = 0 for a straight line. In our study, κ > 0 for a whisker pushing into a shape and κ < 0 for the reverse curvature, typically encountered while detaching from the shape.

To register all videos within a common reference frame for visualization (Fig 4A–C), we extracted the location of the shape edge at each location (close, medium, or far). Because we knew the exact distance between edges in reality, we used the vector between adjacent locations in the image to measure the angle and scale for that particular video. After compensating for this angle and scale, we used the peak in the 2D cross-correlation to find the offset that best aligned the videos with each other.

Quantification of whisker tracking accuracy

The simplest metric of tracking accuracy is the mean distance between the true label and the predicted label, which is 2.8 pixels in our case. However, this is not a particularly informative metric, because the scientific utility of such an algorithm is limited by the prevalence of rare but large errors (e.g., misclassifying C1 as C2) which are too rare to affect such a metric. Indeed, there are multiple additional kinds of errors to consider, such as false negatives and false positives, each of which has varying severity depending on the analysis.

Moreover, performance on the average frame is not particularly important, because in the majority of frames in the dataset the whiskers are at rest or near rest, and in these frames tracking is easy. Mice make contact with the shapes in diverse ways, and although this constitutes a tiny minority of the frames in the dataset, these are precisely the frames where accurate tracking is most difficult and most important. Finally, before accurate training is available, such frames with whisker contacts cannot be a priori identified for use in a training set or quantifying accuracy. Thus, for all these reasons, quantifying the accuracy of tracking algorithms in general remains challenging.

We began by defining four disjoint types of whisker tracking errors, all defined with respect to a training set curated by a human (C.R.).

• “poorly traced”: The extent of the whisker is not traced correctly. For example, the tip is missing, or the trace “jumps” from one whisker to another. This was defined by calculating the Cartesian distance between ground truth and reported location of each joint in the whisker, and identifying whiskers where this distance was greater than 20 pixels for the tip or for the mean over all joints.

• “incorrectly classified”: The wrong label is assigned. For example, whisker C2 is correctly traced, but is labeled as C1. If the whisker is both poorly traced and incorrectly classified, it is labeled as incorrectly classified.

• “false positive”: A non-whisker object is reported as a whisker, or the same whisker object is labeled as two different whiskers.

• “false negative”: The whisker is present in the frame, but is not labeled. This is possible because our algorithm applies a confidence and smoothness threshold to the output of the neural network, and outputs that do not pass these thresholds are simply dropped.

We used an iterative procedure to train our algorithm, which was critical to its success.

1. First, we chose n = 7433 frames randomly from all sessions for which we had video, applied a previous generation whisker tracking algorithm (whiski), and manually labeled the identity of each whisker after verifying that it was correctly traced. This is “curated dataset 1”, representative of typical frames in the video.

2. We trained a neural network on that dataset, and used it to label all the frames in all the videos.

3. Of all these frames, we chose the frames on which the network was most likely to have made mistakes. We did this in several parallel ways: identifying frames where the reported confidence values were intermediate (i.e., unsure of presence or absence of the whisker), where the whiskers were near the extreme ends of their typical ranges, where any whisker was missing, and when any whisker was missing during a contact event. These are “challenge frames”, because they were chosen for their difficulty.

4. We manually evaluated and corrected every challenge frame, using the previous generation whisker tracking algorithm as a backup method when necessary.

5. We repeated steps 2–4 four times, to generate curated datasets 2–5.

Each type of error is nearly zero (<0.2%) on dataset 1, which is the only dataset representative of typical frames (Supplemental Fig 2D). The most common type of error is the false negative, because we used a relatively strict confidence threshold. However, false negatives are also the least problematic, because we interpolated missing whiskers over frames. Error rates increase with each subsequent set of challenge frames, because as the algorithm improves, the frames on which it still makes errors become more and more difficult.

Decomposition of individual whisks

We defined the whisker’s angle as the Cartesian angle between base and tip. We decomposed the whisking signal into individual whisk cycles using the Hill transform (Hill et al., 2011). Briefly, we bandpassed the data from 8 to 50 Hz and applied the Hilbert transform to extract phase. Peaks and troughs were defined as frames where the phase crossed zero or π. We defined set point as the angle of each whisker at the trough of each whisk cycle, and amplitude as the angular difference between peak and trough on each cycle for the C2 whisker. The whisking amplitude was very consistent across whiskers, so we used the amplitude of the C2 whisker only. In contrast the relative set point of each whisker could vary, so we used the set point of each as regressors in the neural GLM analysis. To smooth these amplitude and set point parameters, we applied a triangular window that weighted one cycle before and after half as much as the current cycle.

To identify sampling whisks (those large enough to reach the shapes if they had been at their closest position), we aligned the frames to the response window and found the convex hull of the edges of the shape (i.e., the boundary of closest points to the whisker pad) versus time from the response window. A “whisk without contact” was one on which the whiskers crossed this boundary. This could happen if, for instance, the C3 whisker investigated the space where the medial portion of the closest concave shape would be, but actually a convex shape was present or a concave shape at a further position (example: Fig 3A). A “whisk with contact” is any whisk on which contact was made. Sampling whisks are defined as either “whisks with contact” or “whisks without contact”. All other whisks (non-sampling whisks) are those which did not cross the convex hull described above and did not make contact with the shapes. Not all trials contained contacts, but the vast majority of trials included at least one sampling whisk.

Lick rates (Fig 1I)

We recorded the times of all licks, even those before the response window that had no effect on the trial outcome. In rare cases our detector recorded a single lick as many licks (the “switch bouncing” effect) and so for analysis we binned licks in 100 ms bins and discarded any surplus licks above one per bin.

To plot the rate of correct or concordant licks, we calculated the rate of licking on each side on every trial and defined each lick as “correct/incorrect” depending on whether it matched the correct side, and as “concordant/discordant” depending on whether it matched the direction of the choice lick (i.e., the first lick in the response window, which determined trial outcome). We then meaned the lick rates for each trial type (correct, incorrect, concordant, discordant) within each mouse. Finally we divided the rate of correct licks by the rate of all licks, and the rate of concordant licks by the rate of all licks, to generate the results plotted in Fig 1I.

Behavioral decoding analysis (Figure 3)

We first selected only trials in which the mouse responded within the first 0.5 s of the response window in order to ensure that behavior was roughly aligned across trials. This procedure excluded only a small fraction of trials. In some sessions we used optogenetic stimulation for separate studies; any trial with optogenetic stimulation was discarded from all analysis in this manuscript. In some sessions we also presented flatter shapes (performance data: Supplemental Fig 1A) but for behavioral decoding and all neural analyses we discarded any trials with the flatter shapes.

We then extracted all whisking and contact data from each trial from −2.0 to +0.5 s of the opening of the response window and obliviated (set to zero or the mean value) all data after the time of the choice lick to ensure that only pre-choice activity was included in the analysis. Each feature was measured on every individual whisk (e.g., presence of contact, cross-whisker latency within that contact, interaction terms for multiple-whisker contact; complete list in Supplemental Table 1). We then aggregated each feature within 250 ms bins locked to the response window opening, so that trials with different numbers of whisks could be directly compared. Most features were aggregated by meaning within the bin, but count-related features (like contact count) were aggregated by summing within the bin.

Finally we concatenated some task-related features like previous choice and previous outcome that did not depend on the whisk cycle. Even if the previous trial was itself excluded (for instance, due to optogenetic stimulation), the “previous outcome” and “previous choice” variables were still taken from that excluded trial.

If a feature was not defined for a time bin (for instance, cross-whisker contact timing and contact-induced bending have no meaning if no contacts occurred), it was left as null (NaN). Because these parameters were only measured during contacts, they implicitly contained information that a contact had occurred. Specifically, they were null at all times other than during contact. During feature standardization (described below), we ensured that these features could have no effect on the coefficients or goodness-of-fit when they were null. The net result of this procedure is that these features could only be informative conditioned on the presence of a contact. This permits their interpretation as modulating the information gleaned by the mouse about each contact, above and beyond the mere presence of a contact per se.

The result of this feature selection process was 725 scalar features per trial, some of which (e.g., contact count) depended on time bin and some of which (e.g., previous choice) did not. For each session, we standardized all features by scaling them to zero mean and unit standard deviation. At this point we imputed null (NaN) features with zero, so that they could not affect the coefficients obtained. We used the same procedures to fit individual features (Fig 3B) or combinations of features (Fig 3C).

We also asked whether the three features (whisks with contact, whisks without contact, and angle of contact) in the optimized behavioral decoder (Fig 3C; dashed box) contained unique information or were potentially redundant with one another. To do this, we dropped one feature at a time, refit the decoder, and assessed the decrease in its accuracy on predicting stimulus or choice (Supplemental Fig 3E,F). That decrease is taken as that feature’s “unique contribution” to the decoder’s accuracy (Musall et al., 2019).

Choice decoders were trained to predict which way the mouse would lick (left or right). For shape discrimination sessions, stimulus decoders were trained to predict the shape identity (concave vs convex). For shape detection sessions, stimulus decoders were trained to predict the presence of a shape (concave or convex, vs nothing). The only exception to this is in Fig 3F, in which the decoder was trained to predict shape identity (concave vs convex) regardless of the task.

Cross-validation scheme

Each session was fit separately—classifiers were never fit on one session and then applied to another session, even from the same mouse. We grouped the trials into 4 separate “strata”, with one stratum for each combination of choice and stimulus (concave/convex for discrimination; something/nothing for detection). We split the data into 7 “folds” for cross-validation, equally sampling trials from each stratum. Each trial was in the “testing” set for one fold, the “tuning” set for one fold, and the “training” set for five folds. For each fold, we fit a logistic regression model (‘sklearn.linear_model.LogisticRegression’) on the training set over a range of different regularization parameters, always using L2 regularization. We then evaluated the model on the held-out tuning set and chose the regularization that optimized classifier accuracy over all sessions. Finally we evaluated the model with the chosen regularization on the doubly held-out testing set and took that score as the model’s overall accuracy.

To analyze the weights of the classifier for the session as a whole, we averaged the weights across folds. To analyze the prediction on an individual trial, we used the classifier for which that trial was in the testing (doubly held-out) set. Because each trial was in the testing set in exactly one fold, there was only one unique prediction per trial.

The need to disentangle stimulus and choice

As a thought experiment, imagine a neuron that purely encodes the stimulus and is completely unaffected by choice, similar to what we might expect in the sensory periphery. For instance, this neuron could respond with 1 spike to concave shapes (stimulus A) and 0 spikes to convex shapes (stimulus B).

If a mouse is performing 75% correct, the results might look like this:

• stimulus: {A, A, A, A, B, B, B, B}

• choice: {A, A, A, B, B, B, B, A}

• neuron: {1, 1, 1, 1, 0, 0, 0, 0}

By design, we know that this noiseless neuron is completely driven by stimulus and not at all by choice. Indeed, the variables “stimulus” and “spikes” are perfectly correlated. However, the variables “choice” and “spikes” are also correlated: they are matched on 6 of 8 trials (the correct trials). The naive approach of correlating the neural response with choice would report a spurious choice encoding, but this is in fact due to stimulus encoding coupled with a preponderance of correct trials (schematized in Supplemental Fig 3B).

The most straightforward way to deal with this is by trial dropping—including correct and incorrect trials in equal proportion. For instance, for each stimulus we could include 1 correct trial (out of 3 total) and 1 error trial (out of 1 total). The data would then look like this:

• stimulus: {A, A, B, B}

• choice: {A, B, B, A}

• neuron: {1, 1, 0, 0}

After this procedure, “stimulus” and “neuron” are still perfectly correlated, but “choice” and “neuron” are perfectly uncorrelated (2 matches out of 4 trials). Thus, this procedure indeed reveals the true relationship in the data. However, it is woefully underpowered, because it requires discarding a large proportion of the data—in this case, half the dataset was dropped. This lack of power becomes more acute as the mouse’s performance increases and the error trials become rarer.

The procedure that we developed for this paper—trial balancing—achieves the same result as trial dropping but without the loss of statistical power. In this example, instead of keeping 1/3 of the correct trials, we would include all of the correct trials but weight them 1/3 as much as the each error trial. We implemented this using the ‘sample_weight’ argument in sklearn.linear_model.LogisticRegression. In calculating the cost function to optimize, the decoder weights the cost of each datapoint in accordance with its sample weight. The overall result is that correct and incorrect trials of each stimulus are all equally weighted in aggregate, thus disentangling stimulus and choice.

Validation of trial balancing

We validated that trial balancing accurately and efficiently disentangles stimulus and choice using a simulation in which we know the ground truth that the method should discover. We present this in the context of behavioral decoding (inferring stimulus or choice from sensorimotor features) but the mathematical argument is identical for the case of neural decoding (inferring stimulus or choice from neural responses).

To assess this, we generated simulated data for a hypothetical sensorimotor feature (e.g., contact angle) that is purely driven by the stimulus identity and has no causal relationship with the mouse’s choice (Supplemental Fig 3B). This hypothetical feature is positive for stimulus B (blue) and negative for stimulus A (red), regardless of choice (solid vs dashed lines). A well-calibrated decoder algorithm should reveal the presence of stimulus evidence in this data while rejecting the presence of choice evidence. The naive decoder would draw a vertical line at zero, which clearly discriminates the two stimuli (red and blue). Critically, this same naive decoder would also discriminate choice A on the left (solid) and choice B on the right (dashed). Essentially, this error occurs because stimulus and choice are correlated with one another. The decoder would thus report spurious choice evidence in these data, which we know from construction is not true.

We argue that trial balancing and trial dropping can be used to prevent this false conclusion. The simulation bears this out. All three decoders (naive, trial-balanced as in the manuscript, and trial-dropping) correctly infer that this feature has evidence about stimulus (Supplemental Fig 3C; left three bars). However, the naive decoder incorrectly infers that this feature has evidence about choice, whereas both trial balancing and trial dropping give the correct result of no evidence in this case (Supplemental Fig 3C, right three bars). In practice, we prefer trial balancing over trial dropping, because in real data the number of errors on a given stimulus can be small, resulting in an unacceptably small trial count. Trial balancing allows us to use all of the data while still successfully disentangling stimulus and choice and inferring evidence correctly.

Finally, we compared the results obtained with trial balancing to those obtained from trial dropping, now using the actual data collected from the mice instead of simulated data. As with trial balancing, we divided the trials into four groups: correct and incorrect trials on each stimulus. However, instead of weighting each trial in inverse proportion to its prevalence (“trial balancing”), we now perform “trial dropping” by identifying the size of the smallest of the four groups (N), and selecting N random trials from each of the four groups.

The results with both methods are qualitatively similar (Supplemental Fig 3I). However, because trial dropping discards most of the data, it is less statistically powerful than trial balancing is. Thus, the weights obtained are much smaller, because the cross-validation procedure adopts a stronger regularization to account for the higher noise level. Because of this higher noise, decoders using trial dropping were also less accurate. Thus, the trial balancing procedure we describe here yields similar results as trial dropping, but with greater statistical power.

Aggregation

To aggregate results across mice (e.g., Fig 3D,F) we averaged the accuracy of the classifier across sessions within each mouse first. The sample size for error bars and statistical tests was then equal to the number of mice.

To plot the weights of the classifier in Fig 3H, we first averaged the weights over time for simplicity. Because the coefficients plotted in Fig 3H are related to contact counts, we multiplied the coefficients by the standard deviation of the corresponding column in the feature matrix before standardization. This effectively reverses the standardization, and puts the coefficient in more-interpretable “per contact” units rather than “per standard deviation of contact count” units. This was for visualization only and did not affect the results.

To plot the evidence in Fig 4C, we applied the weights of the decoder to each individual whisk cycle and meaned this evidence over all whisks with a peak within that spatial bin. For visualization in this panel, we used a model that incorporated the peak angle of whisks without contact.

Neural decoding analysis (Fig 6B)

To decode stimulus and choice from neural activity, we used a resampling/bootstrapping approach to combine neural data across sessions and mice. First the trials were split into five equally sized “folds”, one of which was the “test fold” and the rest “train folds”. No tuning set was necessary because we fixed the regularization at 1.0 in this analysis. For each shape (concave or convex), we randomly chose a single trial with that shape from the test fold in each session. We concatenated all of the neural data from those trials into a “pseudopopulation” as if all the neurons had been recorded simultaneously. We then repeated this process 30 times to construct 30 pseudotrials of the test fold. Then, we repeated the process for the train folds, to generate 120 pseudotrials of the train folds. By construction, the same trial could never be included in both the test and train folds.

The classifier was trained on the train fold and evaluated on the test fold. Because correlations can have a strong impact on the amount of information encoded by a neuronal population (Nogueira et al., 2020), we maintained the correlation structure between simultaneously recorded neurons. Specifically, for each pseudotrial we sampled the same trial from each simultaneously recorded neuron. The entire process was repeated 100 times to generate the confidence intervals displayed in the plot, which we obtained by fitting a normal distribution to the accuracy over repeats.

We call the procedure above the “naive” approach because it does not balance hits and errors; hence, it confounds stimulus and choice. This naive approach is used in the left panel of Fig 6B. We also used a “balanced” approach to disentangle stimulus and choice in the middle and right panels of Fig 6B. Specifically, we first divided all the trials into 4 strata (concave hit, concave error, convex hit, convex error) instead of the 2 strata (concave or convex) used in the naive approach. We then repeated the same resampling approach to draw pseudotrials from each of the 4 strata. This ensures equal weighting of correct and incorrect trials; hence, it is balanced. We used disjoint train and test folds just as in the naive approach.

In all cases, to train the classifier we first standardized the firing rate of each neuron in the pseudopopulation to zero mean and unit variance. We provided these normalized firing rates to a classifier (‘sklearn.linear_model.LogisticRegression’) and trained it to predict either the stimulus or choice on each trial. We trained separate classifiers on every time bin in the training fold. We used the classifiers to predict stimulus or choice on each trial in the held-out test fold.

For both naive and balanced classifiers, we repeated the entire procedure five times, such that each trial was included in the test fold exactly once (and in the training fold the other four times). We averaged the classifier’s accuracy over each of the four held-out test sets (never including the training set) and reported this as the classifier’s overall cross-validated accuracy in Fig 6B.

For the right panel of Fig 6B, we zeroed out the spikes on all “sampling whisks” (defined above in the videographic methods). We also zeroed out spikes on the cycle preceding and the two cycles following each sampling whisk to ensure complete removal of whisk-locked stimulus information. This procedure removed phasic contact-evoked or whisk-evoked stimulus responses, but spared long-timescale persistent representations.

We asked whether early licks could affect the results of behavioral decoding or neural decoding. To address this, we excluded all trials in which the mouse made even a single lick in the interval −2 < t < −1. (As always, we use the timeline schematized in Fig 1H, with t = 0 representing the opening of the response window.) We chose this period of time because it precedes the bulk of the whisker contacts, and so licks during this time must be unrelated to the animal’s sampling strategy. This analysis resulted in essentially identical results for behavioral decoding (Supplemental Fig 3H) and for neural decoding (Supplemental Fig 6), indicating that our evaluation of the sampling strategy and neural decoding is not affected by impulsive licks.

Neural encoding analysis (Fig 7, 8)

For this analysis, we began with the same features (contact count, etc.) from the behavioral analysis. Rather than aggregate within arbitrary time bins, we used the feature measurements on individual whisk cycles. We added some additional features that could affect neural firing: the amplitude (peak-to-trough angle) of each whisk and the set point (start angle) of each individual whisker at the beginning of each whisk.

We also added some additional trial-related features: current choice, previous choice, current outcome (rewarded or not), and previous outcome. Because the effect of these features could vary over the course of the trial, we used separate temporal indicator variables (Park et al., 2014). Specifically, we divided all whisks into 500 ms bins with respect to the response window opening. If the current choice was “left”, we marked the temporal indicator variable corresponding to left choices within that whisk’s bin as 1, and left all other variables as zero. We repeated this for each task variable.

Finally, we added two “nuisance features” for firing rate drift and cycle duration. For firing rate drift, we divided each session into 10 blocks and assessed the mean firing rate of each neuron within that block. We provided the logarithm of this value as a feature to the GLM. The timescale of each block was far too long (~several minutes) to contain any information about individual whisks, but it captured the baseline firing rate of the neuron, as well as any long-timescale variations, for example due to satiety. The second nuisance feature was the logarithm of the duration of each individual whisk cycle. This is because a whisk cycle that is twice as long should be expected to emit twice as many spikes, all else equal. The use of a logarithm in both cases accounts for the exponential link function in the GLM. Both of these nuisance features are highly predictive of neural firing by design and were important for fitting the data but were not analyzed further for scientific conclusions.

We fit the data using a GLM for Poisson data like spike counts (i.e., with an exponential link function) using the ‘pyglmnet’ module (Jas et al., 2020). We used 5-fold cross-validation, ensuring that each trial was in the test set exactly once and evaluating the GLM on these held-out test sets only. We always used L2 regularization but we varied the strength of this regularization. We typically used the regularization value that optimized the model fit for that neuron, but when comparing coefficients across neurons (e.g., Fig 8) the same value of regularization was used for all neurons to ensure coefficients were on the same scale.

In order to obtain the null distributions of each coefficient and thereby significance, we also trained 40 additional GLMs for each neuron using permuted features. Specifically we permuted the rows but not the columns of the feature matrix, which maintains the correlation structure of the features but randomizes the mapping to neural responses. Each row of data contains any necessary history terms, and the rows are always kept together. For instance, one column corresponds to the current whisk amplitude, and another column to the previous whisk amplitude. No matter how the rows are arranged in the design matrix, they retain the same current and previous cycle information. Thus, our current approach always preserves whisk-to-whisk information in the features, regardless of whether they are aligned with the neural responses (the real fit) or randomly permuted with respect to the neural responses (the null distribution).

The distribution of each coefficient over permutations had a near-zero mean but a non-zero standard deviation. To assess significance of individual coefficients (e.g. Fig 7E–F) we divided the actual coefficient by the standard deviation of the coefficients obtained on the permutations to obtain the z-score of the coefficient. We then converted this into a two-tailed p-value by integrating the standard normal beyond this z-score. We validated that this approach controlled the false positive rate at α = 0.05 by including a spurious regressor that was drawn from a random distribution and ensuring that the random regressor was found significant no more than 5% of the time (indeed, that the resulting p-value distribution was uniform; data not shown).

To assess goodness-of-fit of any GLM, we took the log-likelihood of the data under the best fit and compared it to the log-likelihood of the data under a null model. The null model had access only to the “nuisance features” described above: baseline firing rate and whisk cycle duration. We subtracted the log-likelihood of the null from the log-likelihood of the fit model, and divided by the total number of whisks in that session in order to permit comparison across datasets of different duration. We used a logarithm of base 2 to permit presentation in “bits”. This is not an estimate of the information contained by the neural spike train, but rather an estimate of the change in the KL-divergence between [the true (unknown) distribution of the data and the distribution predicted by the model under consideration] versus [the same quantity, but replacing the model under consideration with the null model].

We also present the same data quantified as the pseudo R² in Supplemental Figures 7 and 8, using the function ‘pyglmnet.metrics.pseudo_R2’. This quantity is defined as (LLM – L0) / (LS – L0), where LLM is the log-likelihood for the fit model, L0 the null model that always predicts the mean firing rate, and LS the saturated model which predicts the data exactly. The saturated model is not actually achievable by any real fitting procedure, but provides an upper bound on performance for all possible models.

Direct comparison of task-specific neural responses while controlling for contact force

To determine whether the change in whisker-specific tuning that we observed during shape discrimination could be explained by the intensity of the contacts, we directly compared neural responses to contacts made by each whisker while controlling for contact force (Supplemental Fig 8G). We observed that the neural response increases with contact force in both tasks and on all whiskers. In mice performing the detection task, the relationship is quite similar regardless of which whisker makes contact. In mice performing the discrimination task, the response to C1 is much larger than the response to C3, even as we now control for identical contact forces. Similar results were obtained for other kinematic parameters (data not shown). This analysis, which does not use a GLM, directly validates the original GLM-based conclusions: C1 contacts induce a larger neural response than C3 contacts in mice performing discrimination, but not in mice performing detection, even after controlling for contact force.

Analysis software

We used the Python packages ipython (Perez and Granger, 2007), pandas (McKinney, 2010), numpy (Van Der Walt et al., 2011), scipy (Virtanen et al., 2020), scikit-learn (Pedregosa et al., 2011), scikit-image (Van Der Walt et al., 2014), statsmodels (Seabold et al., 2010), pyglmnet (Jas et al., 2020), and matplotlib (Hunter, 2007) to investigate, analyze, and present the data.

Supplementary Material

2

Supplemental Video 1, related to Figure 1.

Whisker tracking during shape discrimination

This video demonstrates some example trials of the shape discrimination behavior. A single frame is shown here for illustration. The whisker tracking is overlaid (C0, blue; C1, green; C2, red; C3, cyan; circles indicate individually tracked “joints”). Yellow circles appear when any tip contacts the edge of the shape (pink line). Four example correct trials (two concave and two convex) are included. The playback speed is 0.15x real-time.

3

Supplemental Video 2, related to Figure 5.

Synchronized whisker tracking and neural responses during shape discrimination

This video demonstrates simultaneously recorded neural activity and behavior. A single frame is shown here for illustration. The left half of the frame shows the behavior, as in Supplemental Video 1 (excluding the tracked joints for clarity). The right half of the frame shows the neural spiking, synchronized with the behavior. Individual neurons (red: excitatory; blue: inhibitory) are plotted as separate rows. Neurons are sorted from superficial (top) to deep (bottom). The small text labels next to each row indicate the unit number and, in parentheses, the depth in microns from the cortical surface. An audio track plays the spikes from single example neurons, as annotated throughout the video. As in Supplemental Video 1, the playback speed is 0.15x real-time.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Anti-NeuN Antibody (rabbit)	Sigma-Aldrich	Cat# ABN78
Chemicals, peptides, and recombinant proteins
DiI (1,1’-Dioctadecyl-3,3,3’,3’-tetramethylindocarbocyanine perchlorate)	Sigma-Aldrich	CAS# 41085-99-8
Streptavidin, Alexa 647 conjugate	ThermoFisher	Cat# S21374
Deposited data
Raw and analyzed data	This paper	https://dx.doi.org/10.5281/zenodo.4743837
Experimental models: Organisms/strains
Mouse, C57BL/6J, bred at Columbia University from Jackson lines	The Jackson Laboratory	Stock# 000664
Software and algorithms
ImageJ	Schneider et al., 2012	https://imagej.nih.gov/ij/
ImageJ plugin: TrakEM2	Cardona et al., 2012	https://imagej.net/TrakEM2
Matlab	MathWorks	https://www.mathworks.com/products/matlab.html
Matlab toolbox: Image Acquisition Toolbox	MathWorks	https://www.mathworks.com/products/image-acquisition.html
Python	https://www.python.org/	https://www.python.org/
Python package: ipython	Perez and Granger, 2007	http://ipython.org/
Python package: pandas	McKinney, 2010	https://pandas.pydata.org/
Python package: numpy	Van Der Walt et al., 2011	https://numpy.org/
Python package: scipy	Virtanen et al., 2020	https://www.scipy.org/
Python package: scikit-learn	Pedregosa et al., 2011	https://scikit-learn.org
Python package: scikit-image	Van Der Walt et al., 2014	https://scikit-image.org/
Python package: statsmodels	Seabold et al., 2010	https://www.statsmodels.org
Python package: pyglmnet	Jas et al., 2020	https://github.com/glm-tools/pyglmnet
Python package: matplotlib	Hunter, 2007	https://matplotlib.org/
Python package: pose-tensorflow (forked)	Insafutdinov et al., 2016	https://github.com/cxrodgers/PoseTF

Highlights.

• Head-fixed mice learned to discriminate or detect shapes with their whiskers

• Mice compared the number of contacts across whiskers to discriminate shape

• Individual barrel cortex neurons encoded motion, touch, and task-related signals

• Task-specific neural representations were aligned with behavioral requirements