Polygenic risk modeling with latent trait-related genetic components

Abstract

Polygenic risk models have led to significant advances in understanding complex diseases and their clinical presentation. While polygenic risk scores (PRS) can effectively predict outcomes, they do not generally account for disease subtypes or pathways which underlie within-trait diversity. Here, we introduce a latent factor model of genetic risk based on components from Decomposition of Genetic Associations (DeGAs), which we call the DeGAs polygenic risk score (dPRS). We compute DeGAs using genetic associations for 977 traits and find that dPRS performs comparably to standard PRS while offering greater interpretability. We show how to decompose an individual’s genetic risk for a trait across DeGAs components, with examples for body mass index (BMI) and myocardial infarction (heart attack) in 337,151 white British individuals in the UK Biobank, with replication in a further set of 25,486 non-British white individuals. We find that BMI polygenic risk factorizes into components related to fat-free mass, fat mass, and overall health indicators like physical activity. Most individuals with high dPRS for BMI have strong contributions from both a fat-mass component and a fat-free mass component, whereas a few “outlier” individuals have strong contributions from only one of the two components. Overall, our method enables fine-scale interpretation of the drivers of genetic risk for complex traits.

Introduction

Heritable common diseases like diabetes and heart disease are leading causes of death and financial burden in the developed world [1]. Polygenic risk scores (PRS), which sum effects from many risk loci for a trait, have been used to identify individuals at high risk for conditions like cancer, diabetes, heart disease, and obesity [2–5]. Although many versions of PRS can be used to estimate risk [6–8], previous work suggests that a “palette” model which decomposes genetic risk into pathways could better describe complex disease [9]. Such a model would center common components of disease over outlier events or black-box genetic effects.

Meanwhile, recent methodological advances have allowed researchers to further interrogate the molecular and clinical underpinnings of common diseases. Of note are methods to partition trait heritability across biological pathways and cell types [10], and to leverage genetic associations from multiple traits to identify and validate disease subtypes [11]. In particular, these techniques have offered key insights into the cellular mechanisms and shared etiology of metabolic diseases (e.g., diabetes and coronary heart disease) [10–13]—traits for which variability in clinical presentation has been a long-standing challenge [9, 14]. Thus far, however, PRS have not explicitly considered this within-trait diversity, even as the best-performing scores have added sophisticated models of linkage disequilibrium [15–17].

Here, we present a polygenic model based on latent trait-related genetic components identified using Decomposition of Genetic Associations (DeGAs) [18]. Where standard PRS for a trait models genetic risk as a sum of effects from genetic variants, the DeGAs polygenic risk score (dPRS) models risk as a sum of contributions from DeGAs components [18]. Each DeGAs component consists of a set of variants which affect a subset of the traits (Fig. 1). The component’s genetic loading is a component PRS (cPRS) that approximates risk for a weighted combination of relevant traits. Instantiated cPRS values for an individual are then used to create a profile that describes their disease risk and informs subtyping for each trait.

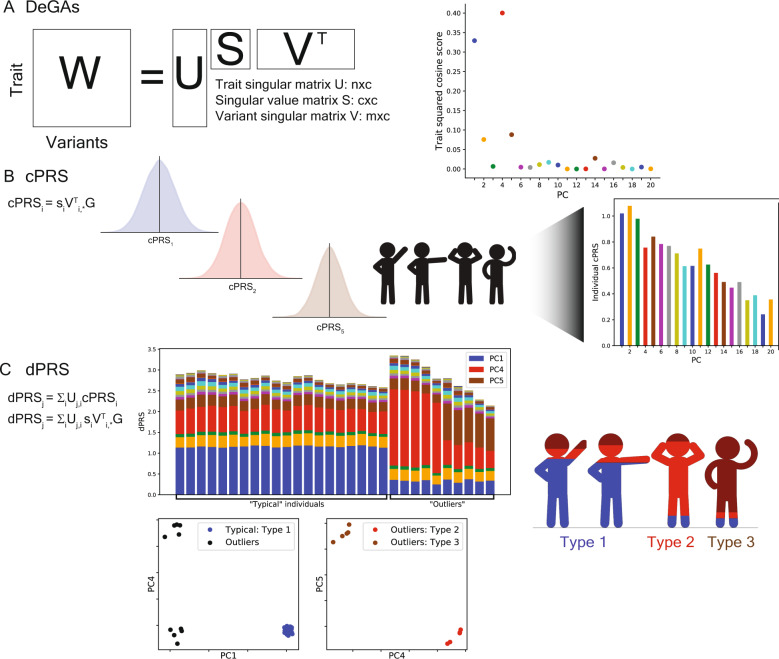
Fig. 1. Study overview.

A Matrix Decomposition of Genetic Associations (DeGAs) is performed by taking the truncated singular value decomposition (TSVD) of a matrix W (n × m) containing summary statistics from GWAS of n = 977 traits over m = 469,341 variants from the UK Biobank. The squared columns of the resulting singular matrices U (n × c) and V (m × c) measure the importance of traits (variants) to each component; the rows map traits (variants) back to components. The squared cosine score (a unit-normalized row of US) for some hypothetical trait indicates high contribution from PC1, PC4, and PC5. B Component polygenic risk scores (cPRS) for the ith component are defined as S_IV^T_I, *G (ith singular value in S and ith row in VT), for an individual with genotypes G. C DeGAs polygenic risk scores (dPRS) for trait j are recovered by taking a weighted sum of cPRS_I, with weights from U (j, ith entry). We also compute DeGAs risk profiles for each individual (see “Methods”), which measure the relative contribution of each component to genetic risk. We “paint” the dPRS high-risk individuals with these profiles and label them “typical” or “outliers” based on similarity to the mean risk profile (driven by PC1, in blue). Outliers are clustered on their profiles to find additional genetic subtypes: this identifies “Type 2” and “Type 3,” with risk driven by PC4 (red) and PC5 (tan). Clusters visually separate each subtype along relevant cPRS (below). Image credit: VectorStock.com/1143365 (color figure online).

As proof of concept, we compute DeGAs using summary statistics generated from genome-wide associations between 977 traits and 469,341 independent common variants in a subset of unrelated white British individuals (n = 236,005) in the UK Biobank [19] (see “Methods”). We then develop a series of dPRS models and evaluate their performance in additional independent samples of unrelated white British individuals (n = 33,716 validation set; n = 67,430 test set), and in UK Biobank non-British whites (n = 25,486 extra test set). Here, we highlight results for body mass index (BMI/obesity) and myocardial infarction (MI/heart attack), motivated by their high prevalence among older individuals in this cohort [20].

Material and methods

Study population

The UK Biobank is a large longitudinal cohort study consisting of 502,560 individuals aged 37–73 at recruitment during 2006–2010 [19]. The data acquisition and study development protocols are online (http://www.ukbiobank.ac.uk/wp-content/uploads/2011/11/UK-Biobank-Protocol.pdf). In short, participants visited a nearby center for an in-person baseline assessment where various anthropometric data, blood samples, and survey responses were collected. Additional data were linked from registries and collected during follow-up visits.

We used a subsample consisting of 337,151 unrelated individuals of white British ancestry for genetic analysis. We split this cohort at random into three groups: a 70% training population (n = 236,005), a 10% validation population (n = 33,716), and a 20% test population (n = 67,430). We used the training population to conduct genome-wide association studies for DeGAs and the validation population to evaluate dPRS model performance for various DeGAs hyperparameters. We report final associations and performance measures from the test population. An additional cohort of unrelated non-British White individuals (n = 25,486, with self-reported white but not British ancestry) was used as an extra test population. The “white British” and “non-British white” populations were defined using genotype PCs from UK Biobank’s PCA calculation and self-reported ancestry (UK Biobank Field 21000) [19, 21], with additional sample quality control and population groupings as previously described [18, 19].

Genome-wide association studies in the UK Biobank

PLINK v2.00a [22] (April 2, 2019) was used for genome-wide associations of 805,426 directly genotyped variants, 362 human leukocyte antigen (HLA) allelotypes, and 1815 non-rare (AF > 0.01%) copy number variants [23] (CNV) in the UKB training population. We used the --glm Firth-fallback option to apply an additive-effect model across all sites. Quantitative trait values were rank normalized using the --pheno-quantile-normalize flag. The following covariates were used: age, sex, the first four genetic principal components, and, for variants present on both of the UK Biobank’s genotyping arrays, the array which was used to genotype each sample.

Genotyped sites and samples have been subject to rigorous quality control by the UK Biobank [19]. Prior to use in downstream methods, we performed additional variant quality control on array-genotyped variants, including more stringent filters on missingness (>1%), gross departures (p < 10⁻⁷) from Hardy–Weinberg equilibrium, and other indicators of unreliable genotyping [24]. As with previous versions of DeGAs, we further filtered variants by minor allele frequency (MAF > 0.01%), array-specific missingness (<5%), and LD independence [18]. The LD independent set was computed with “--indep-pairwise 50 5 0.5” in PLINK v1.90b4.4 (May 21, 2017). MAF and LD filters were applied within and across each array-genotyped group. This process resulted in a set of 469,341 variants (467,427 genotyped variants, 118 HLA allelotypes, and 1796 CNVs) for our analysis.

Binary disease outcomes were defined from UK Biobank resources using a previously described method which combines self-reported questionnaire data and diagnostic codes from hospital inpatient data [24]. Additional traits like biomarkers, environmental variables, and self-reported questionnaire data like health outcomes and lifestyle measures were collected from fields curated by the UK Biobank and processed using previously described methods [24, 25]. In all, we collected 977 traits with at least 1000 observations (quantitative traits) or cases (binary traits). These comprise most common traits in the Global Biobank Engine [26], excluding imaging features and traits which were subject to manual curation. A full list of traits and their Global Biobank Engine IDs is in Data S1. Summary statistics from all GWAS described here are publicly available on the Global Biobank Engine (Web Resources).

Risk modeling using Decomposition of Genetic Associations (DeGAs)

Given GWAS summary statistics, we computed DeGAs as previously described [18]. First, a sparse matrix of genetic associations W (n × m) was populated with effect size estimates (or z-statistics) between the n = 977 traits and m = 469,341 independent common variants (see GWAS “Methods” section). Only variants with at least two associations were used (p < 10⁻⁶; Fig. S1 has additional cutoffs). After filtration, rows of W were standardized to zero mean and unit variance, to give traits equal relative weight.

Next, we performed a truncated singular value decomposition (TSVD) on W using the TruncatedSVD function in the scikit-learn python module [27, 28] to identify the top c = 500 trait-related genetic components. TSVD outputs three matrices whose product approximates W: a trait singular matrix U (n × c), a variant singular matrix V (m × c), and a diagonal matrix S (c × c) of singular values s_i (Fig. 1A). W is approximated by U, S, and V as below:

$$W={\mathrm{USV}}^T$$

The matrices U, S, and V are then used to compute cPRS. The cPRS for the ith DeGAs component can be written as follows:

$${\mathrm{cPRS}}_i=S_{i,*}{V}^{T}G$$

for an individual with genotypes G (m × 1) over the variants used in DeGAs. Here, S_i,* is the ith row of S. With cPRS, we define the dPRS for the jth trait:

$${\mathrm{dPRS}}_j=\sum _i{U}_{j,i}{\mathrm{cPRS}}_i$$

where U_j,i is the (j,i)'th entry of U. In terms of the matrices U, S, and V, this can be rewritten as follows:

$${\mathrm{dPRS}}_j=U_{j,*}S{V}^{T}G$$

For interpretability, the population distribution of dPRS for each trait j is scaled to zero mean and unit variance, independently of the distributions of dPRS for other traits.

We further relate individuals to traits via components using a measure we call the DeGAs risk profile (dRP). An individual’s DeGAs risk profile for a phenotype j is a vector over the c DeGAs components, where the value for the ith component is proportional to:

$${\mathrm{dRP}}_{j,i}~\max \left(0,{\mathrm{dPRS}}_j\times {\mathrm{cPRS}}_i\right)$$

with a denominator introduced for normalization so that these values sum to one. Note we only consider component scores, which have the same sign as the overall risk score when estimating their contribution to an individual’s genetic risk, hence the max operator. The DeGAs risk profile is therefore a normalized measure which, for high-risk individuals with positive dPRS, is the fraction of risk owing to driving components. Analogously, for low-risk individuals with negative dPRS, it measures the contribution from protective components.

Computing polygenic risk scores

As a baseline model for dPRS, we computed single-trait PRS with a pruning and thresholding approach using the same summary statistics which were input to DeGAs. As DeGAs requires variants filtered on LD independence and for p < p* based on a critical value p* (see above), we used only the variants present in the DeGAs input matrix W in each PRS. Specifically, PRS weights for trait j were taken from the jth row of W. The PRS was then computed with PLINK v1.90b4.4 (May 21, 2017) using the --score flag, with the “sum,” “center,” and “double-dosage” modifiers. These correspond to the assumptions that variants make additive contributions across sites; that the mean distribution of risk is zero; and that alleles have additive effects. These are the same assumptions used in our GWAS.

In a similar fashion, polygenic scores (cPRS) for all DeGAs components were computed with PLINK2 v2.00a2 (April 2, 2019) using the --score flag, with “center” and “cols = scoresums” modifiers. These modifiers correspond to the same assumptions as in the PRS: that genetic effects are additive across sites (this is the default genotype model for --score); that each component is zero centered; and that alleles make additive contributions. We then computed dPRS and DeGAs risk profiles for each trait using the formulas above.

In some analysis, PRS and dPRS were further adjusted by age, sex, and four genetic principal components from UK Biobank’s PCA calculation. Covariate adjustment was performed by fitting a multiple regression model with dPRS (or PRS) and covariates in the validation population (Supplementary Methods). We also fit a covariate-only model using the same procedure (without either polygenic score) and used its performance as baseline for the joint models (Fig. 2).

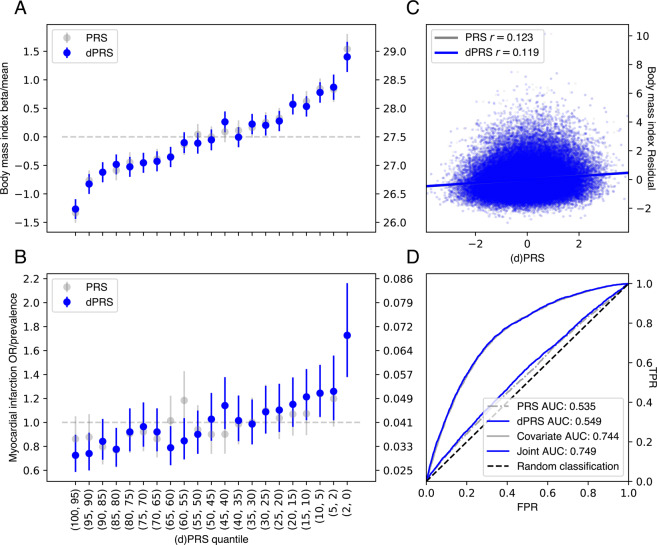
Fig. 2. Performance of dPRS.

A, B Effect of increased risk (dPRS or PRS) on BMI and MI. Beta/OR (left axis) were estimated by comparing the quantile of interest (x-axis) with a middle quantile (40–60%), adjusted for these covariates: age, sex, 4 PCs (see “Methods”). Trait mean or prevalence (right axis) was computed within each quantile; error bars denote the 95% confidence interval of each estimate. C Correlation between dPRS or PRS and covariate-adjusted BMI. D Receiver operating curves with area under curve (AUC) values for MI using dPRS, PRS, covariates, and a joint model with covariates and dPRS. Models with covariates were fit in the validation set; all evaluation was in the test set (see “Methods”).

Classifying genetic risk profiles from DeGAs components

In order to assess whether our method could identify subtypes of genetic risk, we analyzed the DeGAs risk profiles of high-risk individuals whose dPRS is driven by an “atypical” combination of DeGAs components. We used the Mahalanobis distance (D_M) to identify outlier individuals whose z-scored distance from the mean DeGAs risk profile exceeded 1:

$$D_M=\sqrt{\left(x-\mu \right)S^{-1}{\left(x-\mu \right)}^T}$$

where x is the DeGAs risk profile; μ is the mean profile; and S is the identity matrix. Traditionally, S is taken to be the covariance matrix for each of the features across all x. However, for this measure, we treat each component as having equal variance. This results in the above formula reducing to the Euclidean distance between a profile x and the mean profile μ, which can be used to identify “atypical” individuals rather than statistical outliers.

We then intersected this set of outlier individuals with the top 5% of dPRS to create the “high-risk outlier” group. Here, we define the mean risk profile for a trait as the component-wise mean across all individuals’ DeGAs risk profiles in a high-risk set (top 5% of dPRS). To identify subtypes among high-risk outliers, we performed a k-means clustering of their DeGAs risk profiles using the KMeans function from the python scikit-learn module [28]. The number of clusters k was determined by optimizing a statistic over putative values of k ranging from 1 to 20. Specifically, we used the gap-star statistic in the python “gap-statistic” module [29, 30] as the statistic for selecting a value k. We then evaluated which components drove risk in each cluster by computing a mean risk profile for the group (defined as above), which was then renormalized to one for visualization.

Results

Genome-wide associations between 977 traits and 469,341 independent HLA allelotypes, CNVs [23], and array-genotyped variants were computed in a training set of 236,005 unrelated white British individuals from the UK Biobank study [19] (see “Methods”). We applied DeGAs [18] to scaled beta- or z-statistics from these GWAS with varying p value thresholds for input (Fig. 1A). We then defined PRS for each DeGAs component (cPRS; Fig. 1B) and used them to build the dPRS (Fig. 1C). The model with optimal out-of-sample prediction (Fig. S1) corresponded to DeGAs on beta values with significant (p < 10⁻⁶) associations.

To validate this model, we estimated disease prevalence (or, for BMI, mean BMI) at several quantiles of risk in a held-out test set of white British individuals in the UK Biobank (n = 67,430). For all example traits, we observed increasing severity (quantitative) or prevalence (binary) at increasing quantiles of dPRS (Fig. 2A, B) adjusted for age, sex, and the first four genotype principal components from UK Biobank’s PCA calculation [19]. This trend was most pronounced at the highest risk quantile (2%) for each trait. At this stratum, we observed 1.40 kg/m [2] higher BMI (95% CI: 1.14–1.67) and 1.73-fold increased odds of MI (95% CI: 1.38–2.16), over the population average in the test set (total n = 67,235 individuals for BMI; 2812 MI cases).

Furthermore, we found dPRS to be comparable to prune- and threshold-based PRS using the same input data (Fig. S2). Although there was some discrepancy between the individuals considered high risk by each model (Fig. S4 and Table S2), we observe similar effects at the extreme tail of PRS as with dPRS. The top 2% of PRS for each trait had 1.54 kg/m² higher BMI (95% CI: 1.28–1.81) and 1.72-fold increased odds of MI (95% CI: 1.38–2.16) (Fig. 2A, B) using the same covariate adjustment as dPRS. Population-wide predictive measures were also similar, with BMI residual r = 0.21 and PRS AUC (not adjusted for covariates) 0.54 for MI (Fig. 2C, D). We also note similar performance for BMI dPRS predicting obesity (defined as BMI > 30; Fig. S6), with OR = 1.7 at the 2% tail and AUC = 0.56. On balance, despite the reduced rank of the DeGAs risk models—the input matrix W is reduced from ~1000 traits to a 500-dimensional representation—we achieve performance equivalent to traditional PRS for these example traits and observe a similar trend for the other traits (Fig. S2 and Data S1).

However, we note that dPRS and PRS add little population-wide predictive value over factors such as age, sex, and demographic effects that are captured by genomic PCs (Fig. 2C, D). At the population level, we found r = 0.12 between covariate-adjusted dPRS and residualized BMI, and the area under the receiver operating curve (AUC) was 0.55 for MI dPRS and 0.56 for obesity (using BMI dPRS) without covariate adjustment. Adjusting for covariates, the marginal increase in AUC is modest: only 0.005 for MI.

Characterizing DeGAs components

We describe the latent structure identified through DeGAs by annotating each component with its contributing traits and variants, aggregated by gene. The relative importance of traits to components is measured using the trait contribution score [18], which corresponds to a squared column of the trait singular matrix U. The relative importance of components to each trait is measured using the trait squared cosine score [18], which is a normalized squared row of US. The contribution and squared cosine scores are defined analogously for variants and genes using the variant singular matrix V. For each example trait, we highlight five components of interest (ranked by the trait squared cosine score) and describe them by their respective trait contribution scores (Fig. 3) and gene contribution scores. The trait and gene contribution scores for all components can be found in Data S2 and S3, respectively.

Fig. 3. Top 5 DeGAs components for each example trait.

Top 5 DeGAs components for BMI (left) and MI (right), ordered from top to bottom, as ranked by their respective trait squared cosine scores. Each component is labeled with its top 10 traits, as determined by the trait contribution score (squared column of U), and with its relative importance (squared cosine score). Traits are displayed for a component if their contribution score for the component exceeds 0.02.

BMI is a polygenic trait with associated genetic variation relevant to adipogenesis, insulin secretion, energy metabolism, and synaptic function [18, 31]. Here, the DeGAs trait squared cosine score (Fig. 3) indicates strong contribution from components related to body size and fat-free mass (PC1; 23.6%), fat mass (PC2; 35.9%), as well as risk factors for obesity like body size at age 10 and trunk fat percentage (PC363; 4,5%). Components related to exercise (PC206; 2.4%) and diabetes (PC6; 1.7%) also contribute.

Genetic variation proximal to STC2 and MC4R contribute strongly to both PC1 and PC2 (Data S3). STC2 is a stanniocalcin-related protein most highly expressed in cardiomyocytes and skeletal muscle. It has previously been associated with lean mass traits in humans [32, 33] and has been shown to restrict postnatal growth in mouse [34]. MC4R is a melanocortin receptor in the G-protein coupled receptor family. It is primarily expressed in the brain, is known to play a role in energy homeostasis and somatic growth [35, 36], and has been associated with fat-mass and obesity-related traits in humans [37]. Both components also have contribution from variation proximal to FTO and DLEU1, both of which associate with traits affecting body size in adults [38, 39]. FTO is an alpha-ketoglutarate-dependent dioxygenase whose causal role in BMI has been questioned [40]; DLEU1 is a tumor-suppressing lncRNA named for its frequent deletion in patients with chronic lymphocytic leukemia [41]. These components reflect the roles of adipogenesis and growth regulation pathways in high BMI.

MI is a polygenic outcome with well-established risk factors attributable to common and rare genetic variation [5], age, sex, and lifestyle attributes like diet and smoking. DeGAs components important to this trait are related to measures of lung function, as well as usage of medications for an array of conditions which are comorbid with MI (Fig. 3). These medications include aspirin, ibuprofen, and cholesterol-lowering medications (e.g., statins), which are represented across PC12 (22.9%; also includes reticulocyte measurements), PC32 (10.4%; also includes hearing problems and angina), and PC30 (6.4%; also includes headaches). A component related to blood pressure medications also contributes (PC16; 5.8%). Another relevant component (PC11; 13.4%) has contribution from measures of lung function like forced expiratory volume in 1 s (FEV1), forced vital capacity (FVC), and the ratio of the two (FEV FVC ratio).

Two of these components, PC11 and PC12, have contribution from variation proximal to the lipoprotein gene LPA, at the 9p21.3 susceptibility locus (CDKN2B), and in the brain-expressed solute carrier SLC22A3 [42] (Data S3). Variation in these three genes also contributes to PC32, as does variation proximal to the transcription factor STAT6 (which has been associated with adult-onset asthma and inflammatory response to mosquito bites) [43, 44]. PC30 also has contribution from STAT6, as well as the phosphatase and actin regulator PHACTR1, which has been identified in prior coronary artery disease GWAS [45]. These components reflect the diversity of conditions and risk factors which are comorbid with MI.

Painting DeGAs risk profiles

To further characterize the genetic architecture of these traits, we “painted” the genetic risk profiles of each high-risk individual (top 5% of dPRS). For this, we decomposed each individual’s dPRS across DeGAs components into a vector we call the DeGAs risk profile (see “Methods”). The DeGAs risk profile is an individual-level measure over the (in this case) c = 500 DeGAs components and is normalized such that the entries in the vector sum to one. For individuals with above average risk (dPRS > 0), it describes the contributions from components, which contribute positively to risk; for individuals with below average risk (dPRS < 0), it describes the contributions from components which have protective effects. As an individual rather than population-level measure, the DeGAs risk profile can be used to further examine the underlying genetic diversity among high-risk individuals (Fig. 4A, B) in a way which complements the trait and gene squared scores from DeGAs.

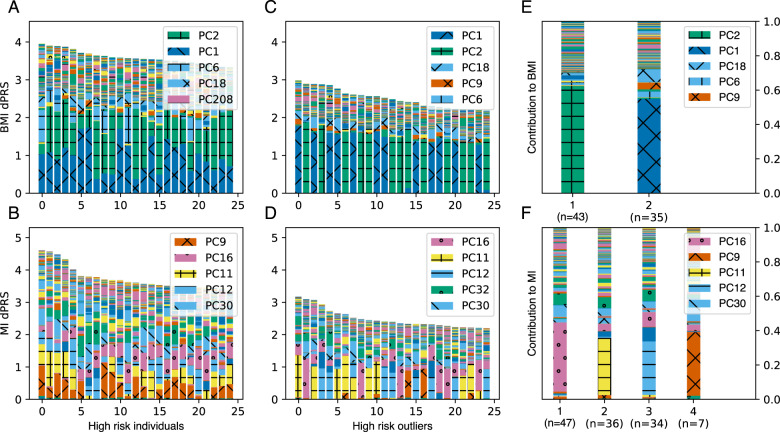
Fig. 4. Painting components of genetic risk.

A, B Component-painted risk for the 25 individuals or C, D 25 outliers with highest dPRS for each trait in the test set. Each bar represents one individual; the height of the bar is the covariate-adjusted dPRS, and the colored components of the plot are the individual’s DeGAs risk profile, scaled to fit bar height. Colors for the five most represented components in each box are shown in its legend in rank order. E, F Mean DeGAs risk profiles from k-means clustering of high-risk outlier risk profiles, annotated with cluster size (n). Phenotype groups for selected components in this figure include: PC1 (fat-free mass); PC2 (fat mass); PC9 (leukocytes and viral antigens); PC11 (lung function); PC12 (aspirin and cholesterol medication); PC16 (blood pressure medication); PC32 (hearing, ibuprofen, and cholesterol medication) (color figure online).

We therefore investigated the diversity of components which drive risk among high-risk individuals, using their DeGAs risk profiles. We used the Mahalanobis criterion (see “Methods”) to find individuals in the test population whose risk profiles significantly differed from average. We then found high-risk individuals (top 5% of dPRS) among these outliers (z-scored Mahalanobis distance > 2) to identify a group of “high-risk outliers”. For these individuals (Fig. 4C, D), genetic risk is often driven by the same components as for other high-risk individuals (Fig. 4A, B), but the degree to which certain components contribute can differ. For example, while the trait squared cosine score for MI identifies PC11 and PC12 (lung function and cholesterol medications) as the top components (Fig. 3), the DeGAs risk profile suggests PC9 (immune function) can drive genetic risk for some individuals with high MI dPRS (Fig. 4B). This suggests that the DeGAs risk profile can identify individuals with high genetic risk whose pathology may differ from “typical”.

To better describe genetic diversity among outlying individuals, we attempted to identify genetic subtypes of each example trait in the high-risk outlier population. We performed a k-means clustering of this group using DeGAs risk profiles as the input; k was chosen by optimizing the gap-star statistic across an array of potential values (see “Methods”). We described each cluster using its mean risk profile (Fig. 4A, B) and noticed that cluster membership divides individuals based on cPRS for relevant components (Fig. 4C, D).

For BMI, we identify two risk clusters (Fig. 4E): one driven by the fat-mass component (PC2; 59.0%, n = 43) and the other by the fat-free mass component (PC1; 70.4%, n = 35). Some outlying individuals at risk for high BMI have genetic contribution from the near exclusively fat-related component (PC2), hence their deviation from “typical”. However, other individuals are outlying due to contribution from the lean mass component (PC1). Genetic risk from this cluster comes mainly from variant loadings related to fat-free mass-related traits like whole-body water and fat-free mass. That this cluster is distinct from other outliers at risk for high BMI implies relevant differences between individuals, which may suggest alternative preventative and therapeutic approaches across groups.

We also find five clusters of risk for MI, four of which are driven primarily by components which were identified as important via the phenotype cosine score (Fig. 3). These were PC11 (lung function; 34.8%; n = 47), PC12 (high cholesterol; 32.9%; n = 33), PC16 (blood pressure; 40.2%; n = 31), and PC32 (hearing and cholesterol; 27.0%; n = 6), all of which have additional contribution from medications commonly used for conditions comorbid with MI (Fig. 4F). The fifth cluster is driven primarily by PC9 (37.0%; n = 7), which has high phenotype contribution from leukocyte measures, vitamin B9, and an array of viral antigens. Its genetic contribution is primarily from variants proximal to the HLA genes, and other genes in 6p21.3 like the butyrophilin-like protein BTNL2 and the testis sperm-binding protein TSBP1. Though these clusters could offer therapeutic insights for MI, the components are less clear to interpret than those underlying risk for BMI.

Discussion

In this study, we introduce a new technique to model polygenic traits using components of genetic associations. We build an example model using data from unrelated white British individuals in the UK Biobank and show that our method adds an interpretable dimension to traditional polygenic risk models by expressing disease, lifestyle, and biomarker-level elements in trait-related genetic components. Predicting genetic risk with these components led us to infer disease pathology beyond variant-trait associations without loss of predictive power from reducing model rank (Fig. S2).

For two phenotypes of interest (BMI and MI), we showed that the DeGAs risk profile offers meaningful insight into the genetic drivers of trait risk for an individual. We then used this measure to identify clusters of high-risk individuals who share similar genetic risk profiles for each of the traits. We find, as in previous work [18], that genetic risk for BMI can be decomposed into fat-mass and fat-free mass-related components. We also show that while many individuals have risk for BMI driven by a combination of the two components, there exist “outlier” individuals who have strong contributions from only one of them. Our results further indicate that this diversity of contributory genetic risk is not limited to BMI and MI (Supplementary Results; Fig. S3). However, extracting biological insights for other traits will likely require deeper phenotyping, or other rich resources like single cell data.

We further demonstrated the generalizability of dPRS by assessing its performance in independent test sets of white British and non-British white individuals (Fig. S5; all traits in Data S1) from the UK Biobank. Among non-British whites, the top 2% of dPRS carries OR = 1.9 for MI (Fig. S5), compared to 1.7 in the test set individuals (Fig. 2). Likewise, the top 2% of dPRS risk has 1.63 kg/m² higher BMI in non-British whites compared to 1.40 kg/m² in the test set. Though dPRS performance is similar in these groups for these traits, concerns about the generalizability of traditional clump-and-threshold PRS across groups also apply to dPRS. This may be compounded by our choice to LD-prune variants prior to analysis with DeGAs instead of using clumping or fine-mapping. One benefit of our approach is that it is agnostic to fine-scale patterns of association within LD blocks, which avoids the problem of having distinct (but highly correlated) causal variants across traits within a locus. However, pruning may leave dPRS more vulnerable to overfitting patterns of LD in the GWAS population compared to approaches which use fine mapped variants. This may be worth revisiting in future work, especially as DeGAs is agnostic to choices in input summary statistics. Here, we use GWAS effect sizes and z-statistics—however, coefficients from linear mixed models (e.g., BOLT-LMM [46]), regularized regression (e.g., bigsnpr [47], BASIL [8]), or polygenic risk models which explicitly consider LD (e.g., PRScs [16], LDPred [7]) may also be used, and would likely improve the predictive performance of dPRS.

We also note that our analysis of subtypes may not be robust to different choices of input traits or study population. Taking MI as an example, our study finds four clusters of outliers (Fig. 4F), two of which seem to measure clinical biomarkers by proxy—namely, cholesterol and blood pressure medications. However, residual confounding and reverse causation (among other sources of bias) are always worth considering when using data from observational studies such as UK Biobank [20]. We therefore advise careful deliberation when selecting analysis traits for DeGAs, and when interpreting trait risk associated with DeGAs components. Although our trait selection in this work was deliberately broad, so as to highlight the wide scope of application areas for our method, we were sure to exclude traits that may have noisy or confounded associations: specifically, rare conditions (n < 1000 in the UK Biobank) or traits that correlate with social measures like socioeconomic status.

In future work, more careful phenotype curation could result in insights beyond those we describe here. Several trait groupings may be of interest for follow-up, particularly diseases with known biomarkers (e.g., blood lipids, pulmonary anthropometry, and cardiovascular disease). Trait groups need not be clinically established risk factors to be informative—in particular, biological pathways and networks [48] or genetic correlation estimates [49] may provide sufficient prior evidence of shared biology to produce meaningful findings with DeGAs. We encourage replication efforts, and to facilitate further study we have made all DeGAs risk models from this work available on the Global Biobank Engine [18] (Web resources).

Looking forward, we anticipate many potential applications of component-aware polygenic risk models like dPRS. Since DeGAs requires only summary-level data, it is possible to build a component model of genetic risk without the need to rerun genome-wide association tests. It is also possible to build dPRS on GWAS from one cohort (even several) and use it to assess genetic risk and identify trait subtypes in another. Such analyses will help elucidate the diversity of polygenic risk for complex traits across individuals and populations.

Web resources

Supplementary data, including weights for the final DeGAs model, are available on the Global Biobank Engine [28]: https://biobankengine.stanford.edu/downloads.

Author contributions

MAR conceived and designed the study. MA and MAR carried out statistical and computational analyses. MA, YT, GRV, and MAR carried out quality control of the data. RT and TH aided in statistical design and conception. We thank Johanne Justesen, Michael Wainberg, and members of the Rivas Lab for comments on the paper. The paper was written by MA and MAR and revised by all the co-authors. All co-authors have approved of the final version of the paper.

Compliance with ethical standards

Conflict of interest

Some of the material in this work has been filed as a patent under Nonprovisional Application S19-332 (S31-06348).

Supplementary information

The online version contains supplementary material available at 10.1038/s41431-021-00813-0.