Blood Flow Velocimetry in a Microchannel During Coagulation Using Particle Image Velocimetry and Wavelet-Based Optical Flow Velocimetry

Abstract

This article describes novel measurements of the velocity of whole blood flow in a microchannel during coagulation. The blood is imaged volumetrically using a simple optical setup involving a white light source and a microscope camera. The images are processed using particle image velocimetry (PIV) and wavelet-based optical flow velocimetry (wOFV), both of which use images of individual blood cells as flow tracers. Measurements of several clinically relevant parameters such as the clotting time, decay rate, and blockage ratio are computed. The high-resolution wOFV results yield highly detailed information regarding thrombus formation and corresponding flow evolution that is the first of its kind.

Introduction

Hemostasis is a complex and multifaceted process, regulated by a series of orchestrated biochemical reactions to maintain normal blood flow through the vascular system while reacting to any vascular injuries by initiating the blood coagulation process [1]. The biology of blood coagulation is extremely complex and involves the interplay between many proteins and cellular structures, such as clotting factors [2], platelets [3], and red blood cells [4]. The coagulation cascade can be triggered by either the intrinsic pathway (contact activation) [5] or extrinsic pathway (tissue factor activation) [6], both resulting in the formation of a thrombus due to fibrin polymerization. An imbalance in this tightly regulated system can lead to either excessive bleeding or abnormal thrombus formation, which can lead to lethal consequences if not treated [7].

The dynamics of blood flow play a critical role in spatial and temporal propagation of thrombi [8,9]. The local shear stress may initially increase in response to a small thrombus and significantly reduce in the event of a microvascular stenosis with a large drop in pressure [10]. Low shear stress has been shown to induce platelet adhesion and thrombin generation downstream, which contributes to continuing growth of the thrombus [11,12]. Furthermore, alteration of blood flow causes endothelial cells to possess a prothrombotic phenotype in the vicinity of the thrombus [13,14]. Transportation of hemostatic proteins and cellular components is also crucial for the process of thrombus formation and largely impacted by the local flow conditions [10]. Therefore, monitoring of temporal changes in blood flow relative to thrombus formation during a clotting process will provide unique insights in the context of hemostasis.

Microfluidic devices offer the ability to monitor clotting dynamics of whole blood under a precisely controlled flow environment while implementing surface characterization and blood perfusion chemistry to mimic intravascular conditions [7,15–17]. Microfluidic systems typically require small blood samples (submilliliter) and allow the study of multicellular interactions and their effect on thrombus formation at a single cell level. Functionalization of microchannel surfaces with the appropriate biological substrate, such as collagen [18], tissue factor [19], thrombin [20], or fibrinogen [21], is also key to understanding the molecular mechanisms of thrombus formation and propagation. Moreover, these microfluidic devices can be designed to provide multiple shear stress regions or a gradient of shear stress within the same platform to mimic low venous and high arterial shear conditions, which may have unique implications in the kinetics of thrombus growth [22–24]. Microfluidic assessment of thrombus formation and spatiotemporal evolution is usually carried out via monitoring of brightfield or fluorescent images of cellular components (e.g., platelets and white blood cells) or performing endpoint measurements (e.g., electrical impedance, clot mechanics, and quartz crystal microbalance) [25–27]. Microfluidic approaches to characterize altered blood flow and its evolution during thrombus growth are lacking mainly due to the difficulties associated with experimental flow measurement techniques. Conventional particle image velocimetry (PIV) [28] cannot be performed because the thickness of the laser sheet used to illuminate particles which track the flow is large compared to the length scales of the microfluidic devices. One solution is to use a confocal micro-PIV (μ PIV) system [29]; however, these systems are very complex and rather expensive, and the resulting velocity measurements have poor in-plane spatial resolution compared to relevant length scales during coagulation.

In this study, we utilize a microfluidic platform integrated with both PIV and wavelet-based optical flow velocimetry (wOFV) processing to monitor changes in whole blood rheology as well as spatiotemporal variations in local blood velocity, respectively, during coagulation. The flow is imaged using volumetric illumination with a simple experimental setup. The images are path-integrated through the height of the microchannel, so velocimetry yields the average velocity over that height. The flow and coagulation dynamics are primarily two-dimensional, however, so the path integration does not present significant practical limitations. Moreover, microscopic images of the flow field allow thrombus growth to be quantified over time, in relation to the local and average flow velocities. These parameters are expected to demonstrate a unique behavior from a clinical perspective, in which people with clotting disorders may present abnormal thrombus growth rate and associated blood flow dynamics, which will be a function of total pressure drop and the shape of thrombus [30–32]. The microfluidic approach described here may also be utilized to evaluate the effect of emerging therapeutic approaches on clotting dynamics and thrombus formation. It should be noted that this work is only relevant for capillary flows, as arterial or venous thrombosis requires somewhat larger blood vessels and hence higher Reynolds numbers than those realized here.

Particle image velocimetry is a mature experimental technique that is widely employed in fluid mechanics across a wide range of flow regimes [33]. The details of PIV processing are outside the scope of this work, but they are given in many articles in the literature as well as several reference texts such as the one by Adrian and Westerweel [34]. Fundamentally, PIV is based on the cross-correlation of image subregions, or inter-rogation spots, each of which contains groups of small particles which follow the flow. The particles are illuminated, typically by a laser, and appear as bright spots in an otherwise dark background in images. The displacement of the tracer images between successive frames is interpreted as velocity given the known interframe time. While PIV processing has many strengths, including robustness to noise and its ability to evaluate large interframe displacements, it is not well suited to so-called natural images, i.e., those which contain continuously variable textures or other features instead of discrete, isolated bright points [28]. Optical flow velocimetry (OFV) is a recently developed methodology that, along with other advantages compared to conventional PIV, performs very well using natural images as inputs, in part because the optical flow methods from which OFV is derived were originally developed in the computer vision community to process natural images [35].

Experimental Setup

The whole blood sample for this work was drawn into a 3.2% sodium citrate containing vacutainer from a single healthy donor under an Institutional review board-approved protocol at University Hospitals Cleveland Medical Center. The blood sample was stored at 4${}^{°}$ C upon collection and was processed within 24 h. The microfluidic channels were fabricated as previously described in Refs. [36–40]. Briefly, a double-sided adhesive and a polymethyl methacrylate top cover were laser micromachined and then assembled with a standard microscope glass slide. The microchannel dimensions defined by the double-sided adhesive are $4\times 25\times 0.05$ mm (width × length × height). The assembled microchannels were washed with phosphate-buffered saline (PBS, 1X) and absolute ethanol (100%), which was followed by tubing assembly. To induce blood coagulation, a CaCl₂ stock solution was prepared by dissolving calcium chloride dehydrate in PBS at a concentration of 600 mM. Prior to the experiment, the whole blood sample was recalcified with the stock solution to obtain a final concentration of 100 mM CaCl₂. Although a CaCl₂ concentration of 100 mM is relatively high compared to the physiological range, calcium concentration does not significantly change coagulation time after a certain level as we have shown in our previous work [26]. We decided to use a high level of calcium concentration to ensure proper coagulation of Na-citrate containing blood sample for this proof-of-concept study. The control experiment was performed by mixing the whole blood sample with PBS. Thereafter, the mixed blood sample was immediately injected into the microfluidic channel at a constant inlet pressure of 20 mBar by means of a Flow-EZ pressure control unit (Fluigent Inc., North Chelmsford, MA), as shown in Fig. 1. The constant supply pressure implies that the flow rate is reduced as the blood coagulates [41]. The maximum initial shear rate was approximately 10 s^–1, and the shear rate reduced to zero as the flow slowed and eventually stopped due to microchannel blockage as coagulation occurred. The microfluidic channel was placed on an inverted microscope (Olympus IX83), and a video was recorded simultaneously under 4X magnification using a high-resolution camera (EXi Blue EXI-BLU-R-F-M-14-C) at 10 frames per second as soon as the flow was started. The field of view was centered on the microfluidic channel, and one pixel in the images corresponds to 1.58 μm.

Fig. 1.

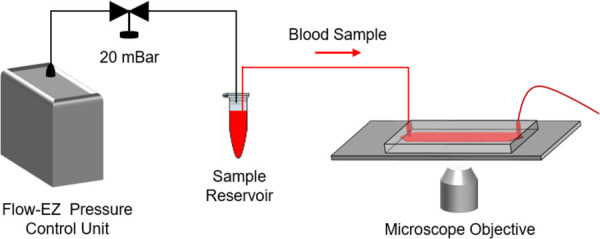
Schematic view of the experimental setup. A pressure control unit was utilized to inject the blood sample into the microfluidic channel at a constant pressure of 20 mBar. The microfluidic channel was placed on an inverted microscope, and the blood flow was recorded under 4X magnification using a high-resolution microscope camera.

Wavelet-Based Optical Flow Velocimetry

Wavelet-based optical flow velocimetry is a novel technique for determining fluid velocity in image sequences first devised by Wu et al. [42]. Further developments were made by various other researchers in recent years [43–46]. The basis for the wOFV algorithm used in this work is presented by Schmidt and Sutton [47], and the reader is referred there for more details. A brief summary of the wOFV methodology is given here.Wavelet-based optical flow velocimetry belongs to the larger class of optical flow velocimetry (OFV) methods. The objective of OFV is to determine a velocity field from a pair of images containing some flow tracer. Like nearly every OFV approach, wOFV assumes the conservation of image intensity $I(\underset{¯}{x},t)$ in an image sequence, i.e., I is only changed via advection by a velocity field $\underset{¯}{v}(\underset{¯}{x},t)$. The change in I thus takes the form of an advection equation, commonly encountered in fluid mechanics

$$\frac{\partial I\left(\underset{¯}{x},t\right)}{\partial t}+\underset{¯}{v}\left(\underset{¯}{x},t\right)·\underset{¯}{\nabla }I\left(\underset{¯}{x},t\right)=0$$ (1)

The unknown velocity field $\underset{¯}{v}$ is usually determined by integrating Eq. (1) in time over an interval $\Delta t=t_1-t_0$ and performing an inverse Taylor expansion in space. This yields the displaced frame difference equation

$$I_0(\underset{¯}{x})-I_1(\underset{¯}{x}+\underset{¯}{v}(\underset{¯}{x})\Delta t)=0$$ (2)

$\underset{¯}{v}$ is found from Eq. (2) by solving a minimization problem of the form

$$\widehat{\underset{¯}{v}}=\underset{\underset{¯}{v}}{\text{argmin}}\hspace{0.17em}\hspace{0.17em}{J}_D(I_0,I_1,\underset{¯}{v})+\lambda J_R(\underset{¯}{v})$$ (3)

The two terms in Eq. (3) are the data term, J_D, and the regularization term, J_R, which are balanced by a scalar parameter λ that is determined semi-empirically. J_D is a penalty function formed from the displaced frame difference Eq. (2), and J_R enforces smoothness on the velocity field. Schmidt and Sutton [47] use the div-curl operator of Corpetti et al. [48] for J_R, which is well suited for high Reynolds number turbulent flows. The microscale flow in this study, however, has a very small Reynolds number ($\text{Re}\ll 1$), so it is well within the regime of laminar flow. Therefore, J_R in this work is based on the Laplace operator

$$J_R={\int }_{\Omega }|\left|{\underset{¯}{\nabla }}^2\underset{¯}{v}(\underset{¯}{x})\right|{|}^2\mathrm{d}\underset{¯}{x}$$ (4)

where Ω is the image domain. In this form, J_R penalizes the magnitude of the vector Laplacian of the velocity field via quadratic penalization. Laplacian filtering and smoothing is ubiquitous in image processing and is ideal for naturally smooth fields, such as laminar fluid flows [49].Wavelet-based optical flow velocimetry differs from classical OFV methods in that it does not perform the minimization in Eq. (3) over the velocity field $\underset{¯}{v}$ in the spatial domain, but rather in the wavelet domain by operating on the wavelet transform of $\underset{¯}{v}$

$$\underset{¯}{\psi }=\Psi (\underset{¯}{v})$$ (5)

The minimization is performed sequentially from coarse scales in the wavelet domain to finer ones as described in Ref. [47], building in a natural multiresolution analysis [50]. Additionally, regularization is performed in the wavelet domain by performing differentiation on the wavelet bases, eliminating the need for complex finite difference schemes to handle the challenging Euler–Lagrange equations resulting from Eq. (4). The estimated velocity field has one velocity vector at each pixel in the original images, and therefore wOFV can produce velocity fields with orders of magnitude higher spatial resolution compared to PIV, which produces one vector per interrogation spot.

Results and Discussion

As stated previously, two sets of images from different experiments are considered in this study. For both cases, the entire image sequence is first processed using a state of the art commercial PIV code (TSI Inc. Insight 4G) to determine the bulk properties of the blood flow and observe averaged trends over time. wOFV is then applied to later images in the 100 mM CaCl₂ case to demonstrate a detailed analysis of the coagulation dynamics.

An example blood flow image for the 100 mM CaCl₂ case after spontaneous clots have formed through the microchannel is shown in Fig. 2. The flow is from left to right. The images are preprocessed prior to performing velocimetry with three preprocessing steps: first, mean filtering with a 3 × 3-pixel kernel, followed by intensity normalization and finally edge-aware local Laplacian filtering [49] to enhance contrast. The mean filtering reduces imaging noise while the other two processes improve motion estimation from the images. Individual red blood cells (erythrocytes) appear as small dots in the image, creating a speckle-like pattern. The erythrocytes are used by both PIV and wOFV as flow tracers to estimate velocity.

Fig. 2.

Example blood flow images from the 100 mM CaCl₂ case at $t=230-380$ s at intervals of 50 s, showing the development of coagulation. Flow is from left to right. The flow has coagulated in the dark regions of the bottom three images. The images have been preprocessed using the steps described in the text. The horizontal line in the lower left of the image at t = 330 s indicates the scale (1 mm).

Particle Image Velocimetry Analysis

Particle image velocimetry analysis was performed for both cases using Insight 4 G. The algorithm used multiple passes with grid deformation, starting with 128-high × 192-wide pixel interrogation spots and moving to a final spot size of 32 × 64 pixels. The initial and final interrogation spots are overlapped by 50% in both directions, so the spacing between PIV vectors is 25.28 and 50.56 μm in the spanwise and streamwise directions, respectively. Figure 3 shows the horizontal component of velocity averaged over the image domain for both cases as a function of time. The difference in mean velocity at t = 0 s between the cases is due primarily to the CaCl₂ content in the 100 mM CaCl₂ case, which lowers its viscosity, increasing the velocity for the same driving pressure. Note that while the bulk velocity for the control case is relatively constant over the entire 400-second image sequence, indicating minimal activation of the coagulation cascade, the 100 mM CaCl₂ case shows a dramatic drop in velocity around t = 220 s corresponding to the formation of large thrombi made up of heterotypic cellular aggregates that are visible under the microscope (Fig. 2). We postulate that this large drop in mean blood flow velocity is indicative of clotting time, during which the resistance inside the microchannel significantly increases because of thrombus formation, thereby slowing down the flow. Some noise is apparent in both time traces, but it is likely random and can be smoothed out to determine global trends such as the velocity decay rate, which could be calculated between t = 220 s and when the average velocity becomes relatively constant again, around t = 300 s. The increased noise in the control case beginning around t = 270 s is likely due to the presence of small thrombi in the image domain which cause errors in the PIV processing. This will be investigated in future studies.

Fig. 3.

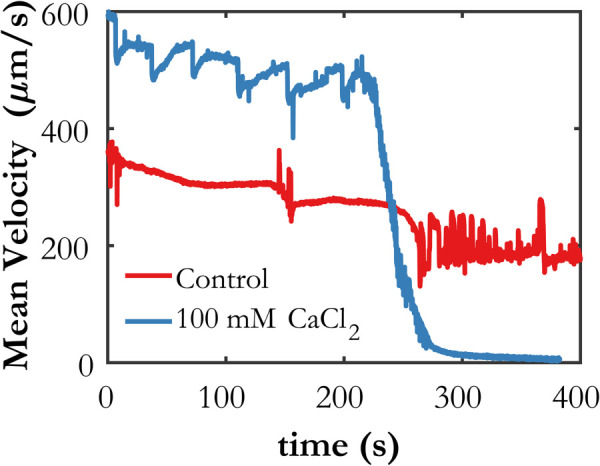
Mean horizontal velocity for each case determined by PIV. The clotting time is observed to be 220 s.

An important factor for the accuracy of both PIV and wOFV is the displacement of the flow tracers between consecutive frames, or the interframe displacement. The accepted rule of thumb for PIV processing is that the maximum interframe displacement should be less than one quarter of the size of the largest interrogation spot [28]. For wOFV, peak accuracy for particle images occurs for displacements of less than about five pixels [46]. The factor between interframe displacement and velocity in μm/s is 15.8, i.e., a displacement of one pixel corresponds to a velocity of 15.8 μm/s. Referencing Fig. 3, the interframe displacement prior to coagulation in the 100 mM CaCl₂ case is 30–35 pixels, which is suitable for PIV processing and the selected interrogation spot size according to the aforementioned rule of thumb. It is much too large for wOFV processing, however, and wOFV does not become accurate until the maximum velocity at a given time drops below 80 μm/s. The average velocity meets this threshold at about t = 260 s, but the maximum velocity in the image domain at a given time instance does not drop below 80 μm/s until much later, around 320 s.

Wavelet-Based Optical Flow Velocimetry Analysis

Wavelet-based optical flow velocimetry was applied to images from the 100 mM CaCl₂ case toward the end of the sequence when coagulation has reduced the flow velocity, from t = 280 s to t = 380 s. The optimal value of the regularization parameter in Eq. (3) was determined to be $\lambda ={10}^{-1.8}$. Two important features of the flow under consideration in this study in the context of wOFV are that (1) the flow is incompressible, and (2) the flow is entirely two-dimensional. As a result, the accuracy of wOFV can be enhanced substantially by projecting the estimated velocity field to divergence free space via a Helmholtz decomposition. This can be done because not only is the true flow divergence-free (because it is incompressible), but there is no apparent divergence in the images due to out-of-plane velocity [51]. Increasing the accuracy of OFV methods by employing a Helmholtz decomposition is used extensively when assessing their accuracy with synthetic data from incompressible, two-dimensional flows [52–54]. Furthermore, incompressibility and two-dimensionality can be exploited to a greater degree in wOFV methods in particular, where the velocity can be restricted to divergence-free space during computation by using divergence-free wavelet bases [45]. This is not implemented in this study and is left for future work, but the estimated flow is projected to divergence-free space after computation via Helmholtz decomposition here.

The results in this section are not meant to serve as a detailed analysis of blood coagulation in general or even in this specific case with CaCl₂ addition. Rather, they are intended to give a flavor of the kind of information that can be extracted from blood flow images using wOFV, and indicate the types of analyses that could be performed in future work to foster new insights regarding blood flow and coagulation dynamics. Figure 4 shows an example instantaneous snapshot of the magnitude of the velocity field at t = 330 s for PIV and wOFV. One can immediately see the dramatic increase in the amount of detail afforded by wOFV due to its much finer spatial resolution. The vector spacing for wOFV is the same as the pixel spacing, or 1.58 μm. The thrombi grow during the coagulation process, so the length scales in the problem evolve, shrinking in time. From the data shown in Fig. 4, at t = 330 s, the length scales of the thrombi appear to be of the order of tens to hundreds of microns. Additionally, it is apparent from manual inspection of the image pair for the velocity field in Fig. 4 that PIV is underestimating the displacements, while wOFV is capturing them accurately. This is likely due both to wOFV being better suited to natural images than PIV, and because of the sharp spatial velocity gradients on the border of the flow channels that have formed around the thrombi.

Fig. 4.

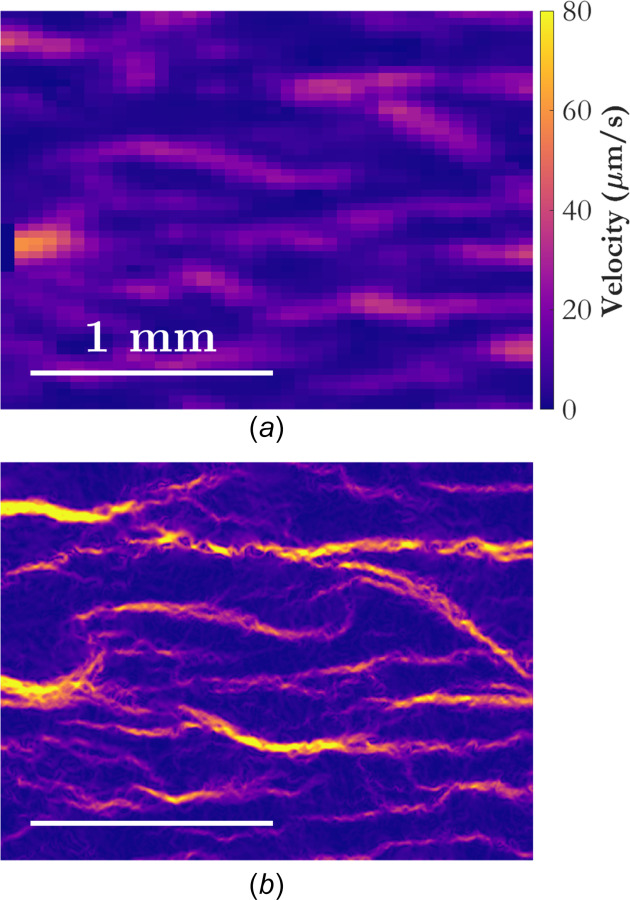
Instantaneous snapshots of the velocity field at t = 330 s for (a) PIV and (b) wOFV. The velocity field is colored according to velocity magnitude, and the spatial scale is shown in the lower left of each subfigure.

As a first step in further analysis of the wOFV results, velocity vectors are superimposed on the velocity field in Fig. 5(a). The vectors complement the velocity magnitude data by giving an indication of flow direction. Alternative flow markers, which are even more informative, are the streamlines shown in Fig. 5(b). Streamlines are curves that are everywhere tangent to the local flow velocity. They are calculated by seeding the velocity field at starting locations along the left and right borders of the domain, and then marching parametrically from those locations in space according to the velocity field. Streamlines from starting locations seeded at the right edge of the domain are computed by marching backward, i.e., using $-\underset{¯}{v}$ instead of $\underset{¯}{v}$. A total of 520 equally spaced starting locations are seeded on each side of the domain, for a total number of 1040 potential streamlines. The high spatial resolution afforded by wOFV allows the streamlines to be computed accurately from the velocity field at each instant in time. Not all starting locations will yield a streamline which traverses the domain, however, and only streamlines, which do so are shown in Fig. 5(b). Other streamlines, which are the ones seeded into locations where there are no flow channels, i.e., inside of thrombi, do not propagate from their initial locations because the local flow velocity is zero.

Fig. 5.

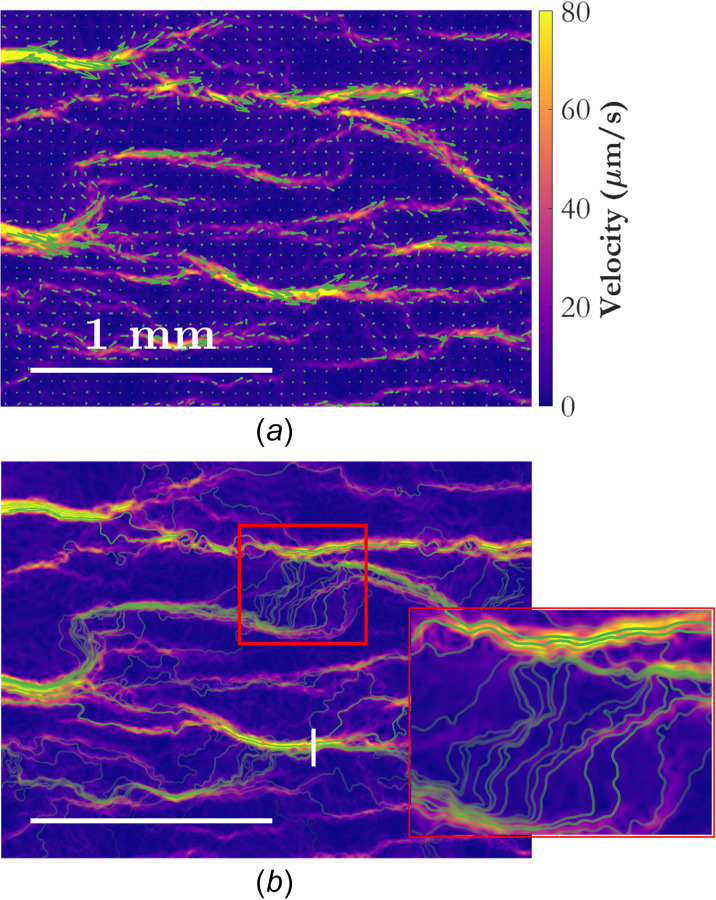
Instantaneous snapshots of the velocity field at t = 330 s for wOFV showing (a) velocity vectors and (b) streamlines, each shown in green. The velocity field is colored according to velocity magnitude. Velocity vectors are subsampled by a factor of 30 in both dimensions and scaled by a factor of 20 to aid in visualization. The transparency for each streamline is set according to the mean residence time along that streamline, with more transparency indicating a longer residence time (lower average velocity). The vertical white line in (b) is referenced in Fig. 7. The horizontal white lines indicate the spatial scale. A zoomed-in image of the region marked by a red rectangle in (b) shows the streamlines in finer detail.

The transparency of the streamlines in Fig. 5 represents the residence time of a fluid element (or a single erythrocyte) along that streamline, normalized by the length of the streamline. Figure 6 shows a histogram, normalized as a probability density function, of normalized residence times for the streamlines in Fig. 5(b). The streamlines with a shorter normalized residence time correspond to higher average velocity along a flow path, indicating a higher flow rate of erythrocytes. It is possible that the residence time of a streamline may have some use in predicting which channels are more likely to close due to coagulation.

Fig. 6.

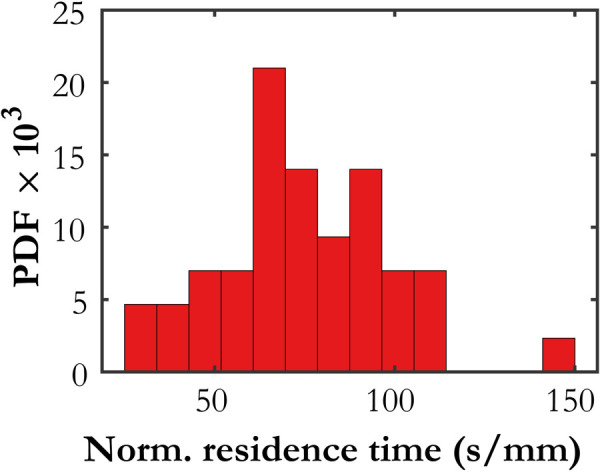
Histogram of normalized residence times for the streamlines shown in Fig. 5(b)

A more rigorous analysis of this type would use pathlines instead of streamlines, because pathlines explicitly follow Lagrangian fluid elements instead of being tangent to the local velocity. For steady flows, pathlines and streamlines coincide. The flow in this study is steady enough over the timescale of a fluid element traversing the image domain in one of the faster-moving channels that those streamlines and pathlines would be very similar, but Fig. 6 indicates that the median time for a fluid element to traverse the 2.2 mm-long domain is of the order of 150–200 s, so some features of the flow field certainly change over that time interval. Pathlines are more difficult to compute than streamlines, however, because they require good temporal resolution of the evolving velocity field [55], which is why they are not computed here. Nonetheless, the investigation of local flow properties along pathlines would likely be a worthwhile avenue to pursue in future studies with more highly resolved data.

Further quantitative information can be extracted from the temporal evolution of the velocity field and streamlines. Figure 7(a) shows a quantity designated as the blockage ratio as a function of time. In this work, the blockage ratio is defined as the number of streamlines that traverse a significant portion of the domain divided by the total number of seeded streamline starting locations. For instance, at t = 320 s, the blockage ratio is about 0.5, indicating that 50% of the starting locations along the left and right edges of the velocity field yield a valid streamline; that is, one that traverses the domain. The blockage ratio defined this way is expected to closely approximate the fraction of the cross-sectional area of the channel that remains open to blood flow.

Fig. 7.

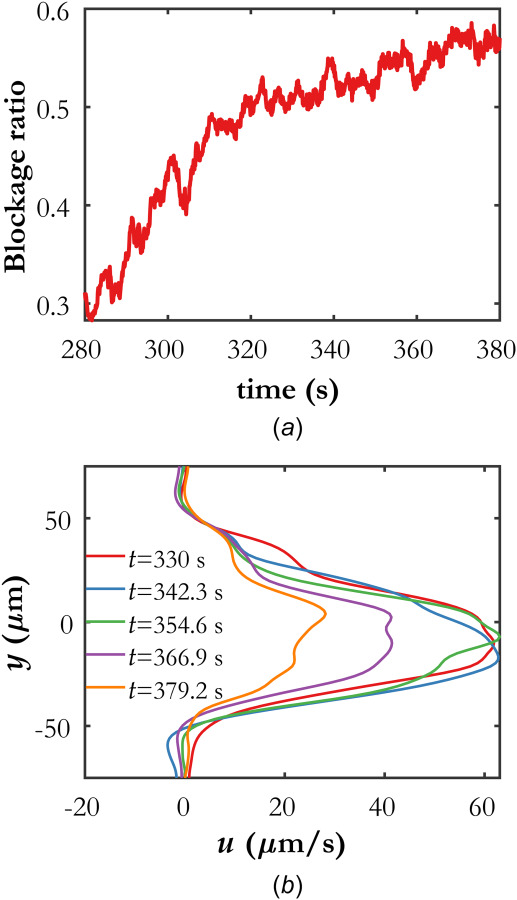
(a) Temporal evolution of the computed blockage ratio, quantified by the number of streamlines that traverse a majority of the domain to the total number of seeded streamline starting locations. (b) Temporal evolution of the horizontal component of velocity along the flow channel marked with a vertical white line in Fig. 5(b). The origin on the y-axis is arbitrary.

Figure 7(b) shows the evolution of profiles of the horizontal component of velocity, sampled along the vertical white line in Fig. 5(b). Each profile is averaged over 5 consecutive temporal snapshots, or 0.5 s, to reduce noise. The reduction in velocity in the flow channel as a function of time can be clearly observed, beginning between t = 354 s and t = 366 s. Using data from wOFV processing, future studies can analyze the velocity profile evolution in isolated flow channels to investigate coagulation dynamics.

Finally, Fig. 8 gives a global view of the temporal evolution of the velocity field. Not only can the connections between primary flow channels be observed at a single instant, but one can track how a given channel changes in time. These changes might include shape, width, velocity, or its relationship with other flow passages. The entire sequence of velocity fields can readily be converted into a movie, which can be played simultaneously with a movie of the recorded images. The videos can be studied to identify regions of interest for further analysis.

Fig. 8.

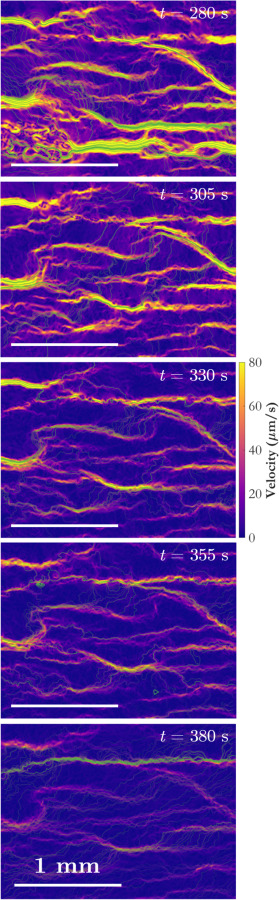
Evolution of the velocity field determined using wOFV as a function of time. Coloration indicates velocity magnitude, and the streamlines are colored according to mean residence time. Horizontal white lines indicate the spatial scale.

As an example, a particular feature of interest in Fig. 8 is the long, wide channel of high-velocity flow toward the bottom center of the frame at t = 280 s (top image). It appears to conduct a significant amount of flow, and the erythrocytes are fast-moving, so intuitively one might not expect coagulation to occur in that location. Yet, by t = 305 s, the flow in that region has significantly diminished and by t = 330 s the channel has almost completely disappeared, indicating thrombus formation. The reason for this can be observed in the top two frames in Fig. 8. The large channel occupies about two thirds of the width of the frame on the right-hand side, but the velocity field at t = 280 s reveals that it is fed by a complex network of a large number of small, low-velocity channels on the left-hand side of the domain. This network experienced coagulation shortly after t = 280 s, and as that region begins to clot, the flow feeding the large channel is choked off. The velocity in the large channel decreases rapidly as the channel is deprived of its supply, allowing a thrombus to form. Observations from Fig. 8 indicate that the rapid increase in blockage ratio observed in Fig. 7(a) between t = 280 s and t = 320 s is primarily due to the obstruction of this particular large channel.

Conclusions

Particle image velocimetry and wOFV have been applied for the first time to a series of microscopic images of whole blood flow in a microchannel during coagulation. Each method offers its own set of strengths, depending on the details of the experiment and the desired data to be acquired. PIV is well suited to compute average velocity over the entire image domain, particularly when the interframe displacements are larger than five pixels, but it fails to accurately capture fine flow features as the blood begins to coagulate. wOFV, on the other hand, offers orders of magnitude higher spatial resolution and is well-suited to determining velocity from natural images, such as the erythrocytes in whole blood. This enables much more detailed investigations of the flow field evolution during coagulation, potentially offering new insights into coagulation dynamics in future work.

The most significant limitation of wOFV processing in this application is its accuracy for flows with large interframe displacements. This facet prevents wOFV from being applied at the onset of coagulation in this study, where the displacements are much greater than the limiting value of five pixels. The issue of interframe displacement can be resolved by reducing the flow velocity in the experiment, but this is not always practical as higher velocities may be of interest. Alternatively, the magnification can be decreased such that the apparent motion in the image domain covers fewer pixels, but this must be balanced against the size of the erythrocytes and the width of the flow channels that form around thrombi during coagulation. The ideal solution for reducing the interframe displacement is to decrease the interframe time, either by using a higher speed camera than the one in this study or by using a setup with multiple cameras and staggered image acquisition (see, e.g., Biswas and Qiao [56]). The demonstration of the benefits of wOFV processing and the new analyses it enables motivate future investigations of whole blood flow dynamics where the issue of interframe displacement is addressed from the onset.

The microfluidic platform integrated with PIV and wOFV described in this work holds great promise for potential future applications from a clinical perspective. For example, assessment of clotting time and decay rate for a clinically diverse patient population can enable monitoring of disease status and the impact of therapeutical interventions on variations in these parameters. More importantly, functionalization of microchannel surface via relevant biological substrates (e.g., heparin, thrombin, Factor XII, etc.) may alter fluid dynamics and thrombus formation in a patient-specific fashion and warrants further research. Further, the efficacy of emerging therapies against thrombus-targeting fibrinolysis can be quantitatively evaluated under physiologically relevant shear conditions using this approach.

Funding Data

• National Science Foundation CAREER (Award No. 1552782; Funder ID: 10.13039/100000001).

• National Heart, Lung, and Blood Institute (NHLBI) (Grant No. R01HL133574; Funder ID; 10.13039/100000050).

Nomenclature

I =

image intensity

J_D =

data term

J_R =

regularization term

PIV =

particle image velocimetry

Re =

Reynolds number

t =

time (s)

$\underset{¯}{v}$ =

velocity (μm/s)

wOFV =

wavelet-based optical flow velocimetry

$\underset{¯}{x}$ =

spatial coordinate (μm)

$\Psi$ =

wavelet transform operator

$\underset{¯}{\psi }$ =

wavelet transform of the velocity field

Ω =

image domain