Plasticity and Enzymatic Degradation Coupled With Volumetric Growth in Pulmonary Hypertension Progression

Abstract

Pulmonary hypertension (PH) is one of the least understood and highly elusive cardiovascular conditions associated with elevated pulmonary arterial pressure. Although the disease mechanisms are not completely understood, evidence has accumulated from human and animal studies that irreversible processes of pulmonary arterial wall damage, compensated by stress-mediated growth, play critical roles in eliciting the mechanisms of disease progression. The aim of this study is to develop a thermodynamic modeling structure of the pulmonary artery to consider coupled plastic-degradation-growth irreversible processes to investigate the mechanical roles of the dissipative phenomena in the disease progression. The proposed model performs a model parameter study of plastic deformation and degradation processes coupled with dissipative growth subjected to elevated pulmonary arterial pressure and computationally generates in silico simulations of PH progression using the clinical features of PH, found in human morphological and mechanical data. The results show that considering plastic deformation can provide a much better fitting of the ex vivo inflation tests than a widely used pure hyperelastic model in higher pressure conditions. In addition, the parameter sensitivity study illustrates that arterial damage and growth cause the increased stiffness, and the full simulation (combining elastic-plastic-degradation-growth models) reveals a key postpathological recovery process of compensating vessel damage by vascular adaptation by reducing the rate of vessel dilation and mediating vascular wall stress. Finally, the simulation results of luminal enlargement, arterial thickening, and arterial stiffness for an anisotropic growth are found to be close to the values from the literature.

1 Introduction

Pulmonary hypertension (PH), which is associated with elevated pulmonary arterial pressure, is a complex cardiovascular disease characterized by progressive vascular remodeling [1]. Unlike in systemic hypertension for which patients have had effective pharmacological management for decades, PH prognosis remains poor with 15% mortality within 1 year even with current access to modern clinical managements [2]. PH's pathological features are smooth muscle hypertrophy, endothelial dysfunction, fragmented elastin, and deposition of collagen [3]. There have been accumulating evidences from human and animal studies that irreversible processes of pulmonary arterial wall damage, compensated by stress-mediated growth, play critical roles in eliciting the mechanisms of disease progression.

In studies on PH pathophysiology, increased activity of elastolytic enzymes has been suggested to play an important role in understanding the disease progression [3,4]. Particularly, via disturbed balances of matrix metalloproteinases (MMPs), MMP-2, MMP-7, and MMP-9, and tissue inhibition of MMPs (TIMPs), the elastolytic activities/inhibitions contribute to the processes of vascular damage (e.g., fragmentation of the internal elastic lamina) and remodeling for the establishment of PH [5]. Tan et al. [6] suggested that a high pulsatility of the pulse pressure/flow was correlated to inflammatory cellular signaling, followed by pulmonary arterial stiffening. Interestingly, animal models of PH have shown that treatment with an elastase inhibitor, which halts the process of wall damage, showed significant declines in pulmonary artery pressure and reductions in medial hypertrophy [7,8].

On the other hand, adventitial layers of the arterial wall mainly consist of collagen fibers, shown by the crystal structure of triple-helical collagen-related peptides. Damage to load bearing collagen is suggested to be responsible for the pathological conditions through mechanisms such as stress-softening or material yielding to the process [9–12]. A biomaterial study also found that intermolecular hydrogen bonds play a key role in determining the resistance against slip via a mechanism of load transmission inside collagen fibrils and fibers [13]. in vitro tests with pulmonary arteries revealed that collagen fibers carry most of the load at high pressure, while the elastic layer bears only the load in the low blood pressure range [14]. Wang et al. [15] further illustrated plastic yielding of the porcine pulmonary artery that was induced by over-pressurization in an ex vivo inflation test, at which a narrow range of blood pressure (50–60 mmHg) was consistently observed for permanent damage.

While those dissipative processes (elastin degradation and collagen damage) would be indispensable for modeling the disease progression, collagen accumulation in PH should be another key contributor to proximal pulmonary artery stiffening [16]. The injury-sensing tissue, in response to the increased vascular stress and arterial damage, activates a multitude of biological processes of arterial growth and remodeling in PH [17]. In the course of the disease progression, the mean pulmonary arterial pressure (mPAH) is generally elevated, and the pulse pressure is linearly increased [18], whereby these changes, with other pathological conditions, may induce potential damage to the arterial wall followed by a compensatory mechanism of collagen accumulation.

The current understanding of PH, however, has largely been obtained through animal models. Those animal models are not able to fully reproduce the pathology of human PH [19], and therefore, computational modeling can help provide physical insights on dissipative and growth processes during PH disease progression. In particular, continuum models have brought significant contributions to understanding the mechanisms of inelastic material behavior and biological tissue remodeling. Typical inelastic models have long been used with the standard formulation, which separates the total deformation gradient multiplicatively into elastic and inelastic parts [20]. Based on this theory, volumetric growth models have been developed for two decades by replacing the plastic deformation gradient with a growth deformation gradient for biological tissues [21–23]. In the cardiovascular system, various growth models have been implemented in studying vascular diseases [24–26] and cardiac diseases [27,28]. Most of the reported models have focused on the hyperelastic and volumetric growth, but plastic deformation with enzymatic degradation in the disease has been rarely studied.

The aim of this study is ultimately to investigate the mechanical roles of dissipative processes that are coupled with vascular growth in human PH progression. The first step of this study aimed to formulate a thermodynamic solid model that considers coupled plastic-growth-degradation dissipations for PH, to perform a model parameter study of the dissipative models, and to computationally generate in silico simulations of PH progression using the clinical features of PH, found in the morphological and mechanical data from the literature. However, because a healthy human pulmonary artery sample is generally not possible, we utilized a mechanical ex vivo test of a large animal pulmonary artery to obtain the hyperelastic material parameters. With the calibration, we present that a widely used pure hyperelastic model overestimates the pressure result compared to the experimental data when the inflation pressure is over a critical point. This presents the possibility of plastic dissipation in the artery during the inflation and the elastic-plastic model fitting shows much better results.

For the numerical analysis, this work uses a thin-walled tube simplification. Even though the plastic model and the thin-walled tube are simple, it is enough to study the possibility of plastic deformation coupled with the growth and degradation dissipations. By capturing the experimental data with discussions, this paper presents the potential of the coupled analysis for a better understanding of PH diseases. The structure of this paper is as follows: Section 2 presents the kinematics of the thermodynamics for considering coupled plastic-growth-degradation dissipations, and Sec. 3 derives the detailed constitutive equations and the artery modeling. Sections 4 and 5 present the results and discussions, respectively. The conclusion is given in Sec. 6. Finally, Appendix presents the numerical algorithm of the presented model to solve the arterial problem.

2 Thermodynamics and Modeling Considerations

Before deriving the detailed formulations, here is a brief summary of the overall modeling approach. A pulmonary artery is assumed to be a nonlinear solid; a thermodynamic inequality leads a condition for the homeostatic process for an isothermal process; two dissipative models are implemented for elastic–plastic deformation and material softening, and a growth model is used as a compensatory mechanism from the arterial damage. Based on the standard formulation of inelasticity [20], the total deformation gradient can be multiplicatively separated into elastic and inelastic parts. Moreover, in order to account for the coupled growth and plastic dissipation with a degradation effect, the inelastic part of the deformation gradient should be decomposed again into growth and plastic deformation. In this process, while arbitrariness in the selection of the intermediate and reference configurations affects the inelastic solution, this work only focuses on the coupled effect of growth, plasticity, and degradation by using commonly used orthonormal material axes. For the structure of the coupled modeling, this work proposes a coupled dissipative function that controls both the growth and plastic deformation. The role of the coupled dissipative function is to define the direction of each plastic and growth deformation while satisfying the inequality condition of the material dissipation. Because this role is very similar to the plastic potential function [29,30] in plasticity theory, this work calls this proposed function the inelastic potential function accounting for both growth and plasticity. However, this method, using a stress function to define the direction of the inelastic deformation, has not been used in the modeling of living tissues. General tissue models directly define the growth deformation gradient based on assumed paths. Recently, Lee [31] showed that the growth of living tissue also can be modeled by a potential function; however, this model also did not consider plastic deformation. In the inelastic potential modeling of this paper, for the growth modeling, a stress-driven volumetric growth model is used for the vascular adaptation, which considers an isotropic case and a simple anisotropic case. Plastic modeling uses the J₂ flow rule based on the associated flow rule, which only considers isotropic hardening, because the Bauschinger effect is mainly observed in large cyclic plastic deformation [29,30].

2.1 Kinematics.

In the theory of continuum mechanics, the total deformation gradient ($\mathbf{F}$) and the velocity gradient ($\mathbf{L}$) lead to the material time differential of the total deformation gradient given as

$$\dot{\mathbf{F}}=\mathbf{L}\mathbf{F}\hspace{1em}\text{where}\hspace{1em}\mathbf{F}=\frac{\partial \mathbf{x}}{\partial \mathbf{X}}\hspace{1em}\text{and}\hspace{1em}\mathbf{L}=\frac{\partial \mathbf{v}}{\partial \mathbf{x}}$$ (1)

Here $\mathbf{X}$ and $\mathbf{x}$ denote the position vectors in the reference (${\kappa }_R$) and deformed (${\kappa }_t$) configurations, respectively, shown in Fig. 1. $\mathbf{v}$ represents the velocity vector in the deformed configuration ($\dot{\mathbf{x}}=\mathbf{v}$). The Jacobian of $\mathbf{F}$ is denoted by $J=\det (\mathbf{F})$, and the time derivative of $J$ gives

$$\dot{J}=J\left(\mathbf{D}:\mathbf{I}\right)\hspace{1em}\text{where}\hspace{1em}\mathbf{D}=\frac{1}{2}\left(\mathbf{L}+{\mathbf{L}}^{\mathbf{T}}\right)$$ (2)

Fig. 1.

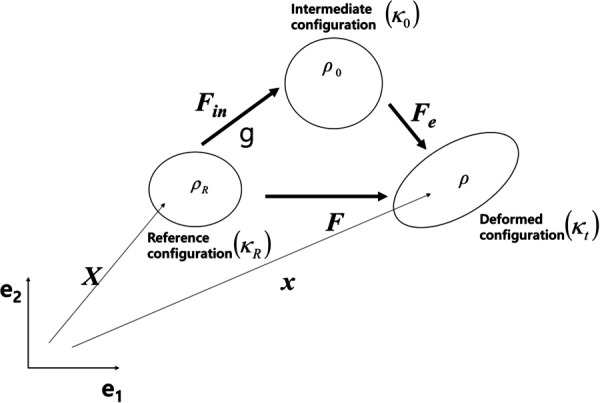
Kinematics of the material

$\mathbf{D}$ and $\mathbf{I}$ represent the rate of the deformation tensor and identity matrix, respectively. The operator “:” is an inner product between two tensors. For example, two tensors $\mathbf{A}$ and $\mathbf{B}$ result in a scalar value $c=\mathbf{A}:\mathbf{B}=A_{ij}{B}_{ij}$ following the Einstein notation. Consequently, $\mathbf{D}:\mathbf{I}={\mathit{D}}_{ij}{\delta }_{ij}={\mathit{D}}_{11}+{\mathit{D}}_{22}+{\mathit{D}}_{33}$ where ${\delta }_{ij}$ is the Kronecker delta. $\mathbf{F}$ can be multiplicatively separated into the inelastic (${\mathbf{F}}_{\text{in}}$) and elastic parts (${\mathbf{F}}_e$) as shown in Eq. (3) below:

$$\mathbf{F}={\mathbf{F}}_e{\mathbf{F}}_{\text{in}}\hspace{1em}\text{and}\hspace{1em}J=J_e{J}_{\text{in}}\hspace{1em}\text{where}\hspace{1em}{\mathbf{F}}_{\text{in}}=\frac{\partial {\mathbf{X}}_0}{\partial \mathbf{X}}$$ (3)

where $J_e=\det ({\mathbf{F}}_e)$ and $J_{\text{in}}=\det ({\mathbf{F}}_{\text{in}})$. ${\mathbf{X}}_0$ denotes the position vector in the intermediate configuration (${\kappa }_0$) between the reference and deformed configurations. The evolution of the elastic and inelastic deformation gradients is obtained by

$${\dot{\mathbf{F}}}_e=(\mathbf{L}-{\mathbf{L}}_{\text{in}}){\mathbf{F}}_e\hspace{1em}\text{where}\hspace{1em}{\dot{\mathbf{F}}}_e=\dot{\mathbf{F}}{\mathbf{F}}_{\text{in}}^{-1}+\mathbf{F}{\dot{\mathbf{F}}}_{\text{in}}^{-1}$$ (4)

$${\dot{\mathbf{F}}}_{\text{in}}={\mathbf{\Lambda }}_{\text{in}}{\mathbf{F}}_{\text{in}}\hspace{1em}\text{where}\hspace{1em}{\mathbf{L}}_{\text{in}}={\mathbf{F}}_e{\mathbf{\Lambda }}_{\text{in}}{\mathbf{F}}_e^{-1}={\Gamma }_{\text{in}}{\overline{\mathbf{L}}}_{\text{in}}$$ (5)

${\mathbf{L}}_{\text{in}}$ denotes the inelastic velocity gradient, ${\overline{\mathbf{L}}}_{\text{in}}$ means the direction of the inelastic velocity gradient, and ${\Gamma }_{\text{in}}$ is the inelastic deformation parameter to define the equivalent magnitude of the inelastic deformation. In order to obtain ${\overline{\mathbf{L}}}_{\text{in}}$ and ${\Gamma }_{\text{in}}$, inelastic constitutive equations are defined in Sec. 3. The inelastic deformation rate is then given by

$${\mathbf{D}}_{\text{in}}=\frac{1}{2}\left({\mathbf{L}}_{\text{in}}+{\mathbf{L}}_{\text{in}}^T\right)={\Gamma }_{\text{in}}{\overline{\mathbf{D}}}_{\text{in}}\hspace{1em}\text{where}\hspace{1em}{\overline{\mathbf{D}}}_{\text{in}}=\frac{1}{2}\left({\overline{\mathbf{L}}}_{\text{in}}+{\overline{\mathbf{L}}}_{\text{in}}^T\right)$$ (6)

${\overline{\mathbf{D}}}_{\text{in}}$ is the direction of the inelastic deformation rate. Next, the elastic left and right Cauchy-Green deformation tensors (${\mathbf{B}}_e$ and ${\mathbf{C}}_e$) are given by

$${\mathbf{B}}_e={\mathbf{F}}_e{\mathbf{F}}_e^{\mathit{T}},\hspace{1em}{\mathbf{C}}_e={\mathbf{F}}_e^{\mathit{T}}{\mathbf{F}}_e$$ (7)

and the deviatoric parts of the tensor are presented by

$$\begin{array}{c}{\overline{\mathbf{F}}}_e=\frac{1}{J_e^{1/3}}{\mathbf{F}}_e,\hspace{1em}{\overline{\mathbf{B}}}_e=J_e^{-2/3}{\mathbf{B}}_e={\overline{\mathbf{F}}}_e{\overline{\mathbf{F}}}_e^{\mathit{T}}\hspace{0.17em}\\ {\overline{\mathbf{C}}}_e=J_e^{-2/3}{\mathbf{C}}_e={\overline{\mathbf{F}}}_e^{\mathit{T}}{\overline{\mathbf{F}}}_e\end{array}$$ (8)

Next, using the decomposition of the time derivative of $J$ ($\dot{J}={\dot{J}}_e{J}_{\text{in}}+J_e{\dot{J}}_{\text{in}}$), the evolution of the elastic dilatation is determined by

$${\dot{J}}_e=J_e\left(\mathbf{D}:\mathbf{I}-\frac{{\dot{J}}_{\text{in}}}{J_{\text{in}}}\right)$$ (9)

During the disease progress, there is a complex process of arterial damage and growth, which induces the total mass change. With an interstitial mass change, the mass balance law gives a continuity equation

$$\frac{d\rho }{dt}+\rho \left({\mathbf{F}}^{-\mathit{T}}:\dot{\mathbf{F}}\right)=\mathrm{g}$$ (10)

where $\rho$ is the density and $\mathrm{g}$ is the rate of the interstitial production/removal (e.g., growth/atrophy). In the arterial wall model, it is typically assumed that the newly born tissue is produced with the same density as the existing tissue [24] in the reference configuration, resulting in the same density as the reference (${\rho }_R$) and intermediate configuration (${\rho }_0$): ${\rho }_R={\rho }_0=$ constant. The mass change rate $\mathrm{g}$ is caused by the pure inelastic volume change rate resulting in

$${\mathbf{D}}_{\text{in}}:\mathbf{I}=\frac{{\dot{J}}_{\text{in}}}{J_{\text{in}}},\hspace{1em}\text{where}\hspace{1em}g={\rho }_0{\mathbf{D}}_{\text{in}}:\mathbf{I}$$ (11)

By substituting the above relation, Eq. (9) can result in

$${\dot{J}}_e=J_e\left(\mathbf{D}:\mathbf{I}-\frac{\mathrm{g}}{{\rho }_0}\right)$$ (12)

Under the incompressible condition of the artery ($J_e=1$ and ${\dot{J}}_e=0$), volumetric change is caused by growth deformation. ($\mathbf{D}:\mathbf{I}=\frac{\mathrm{g}}{{\rho }_0}$). The evolution equations of ${\overline{\mathbf{F}}}_e$ and ${\overline{\mathbf{C}}}_e$ are then given by

$${\dot{\overline{\mathbf{F}}}}_e=(\overline{\mathbf{L}}-{\overline{\mathbf{L}}}_{\text{in}}){\overline{\mathbf{F}}}_e$$ (13)

$${\dot{\overline{\mathbf{C}}}}_e={\overline{\mathbf{F}}}_e^{\mathit{T}}({\overline{\mathbf{L}}}^{\mathit{T}}-{\overline{\mathbf{L}}}_{\text{in}}^{\mathit{T}}){\overline{\mathbf{F}}}_e+{\overline{\mathbf{F}}}_e^{\mathit{T}}(\overline{\mathbf{L}}-{\overline{\mathbf{L}}}_{\text{in}}){\overline{\mathbf{F}}}_e$$ (14)

where $\overline{\mathbf{L}}=\mathbf{L}-\frac{1}{3}(\mathbf{L}:\mathbf{I})\mathbf{I}$, and ${\overline{\mathbf{L}}}_{\text{in}}={\mathbf{L}}_{\text{in}}-\frac{1}{3}({\mathbf{L}}_{\text{in}}:\mathbf{I})\mathbf{I}$.

Then ${\mathbf{\Lambda }}_{\text{in}}$ (in Eq. (5)) can be defined by

$${\mathbf{\Lambda }}_{\text{in}}=\left({\mathbf{F}}_e^{-1}{\overline{\mathbf{L}}}_{\text{in}}{\mathbf{F}}_e\right){\Gamma }_{\text{in}}$$ (15)

${\Gamma }_{\text{in}}$ can be calculated by the inelastic constitutive equations formulated in Sec. 3.

2.2 Irreversible Material Dissipation.

We assume the free energy ψ (energy per mass) of the pulmonary artery to be a function of

$$\psi =\psi (J_e,{\overline{\mathbf{C}}}_e,a_d)$$ (16)

where $a_d$ is a degradation variable. In the thermodynamics, the Clausius–Duhem inequality condition for an isothermal process can be given by

$$\mathbf{T}:\mathbf{D}-\rho \dot{\psi }+S\ge 0$$ (17)

where $S$ denotes an external energy supply rate that necessitates the homeostatic process to be sustained in the biological body [23]. The time derivative of $\psi$ gives

$$\dot{\psi }=\frac{\partial \psi }{\partial J_e}{\dot{J}}_e+\frac{\partial \psi }{\partial {\overline{\mathbf{C}}}_e}:{\dot{\overline{\mathbf{C}}}}_e+\frac{\partial \psi }{\partial a_d}{\dot{a}}_d$$ (18)

With Eqs. (15)–(18), the inequality becomes

$$[\mathbf{T}-(2\rho {\overline{\mathbf{F}}}_e\frac{\partial \psi }{\partial {\overline{\mathbf{C}}}_e}{\overline{\mathbf{F}}}_e^T+\rho J_e\frac{\partial \psi }{\partial J_e}\mathbf{I})]:\mathbf{D}+(2\rho {\overline{\mathbf{F}}}_e\frac{\partial \psi }{\partial {\overline{\mathbf{C}}}_e}{\overline{\mathbf{F}}}_e^T+\rho J_e\frac{\partial \psi }{\partial J_e}\mathbf{I}):{\mathbf{D}}_{\text{in}}-\rho \frac{\partial \psi }{\partial a_d}{\dot{a}}_d+S\ge 0$$ (19)

Because the material dissipation is non-negative, the below relations can be postulated

$$\mathbf{T}=(2\rho {\overline{\mathbf{F}}}_e\frac{\partial \psi }{\partial {\overline{\mathbf{C}}}_e}{\overline{\mathbf{F}}}_e^T+\rho J_e\frac{\partial \psi }{\partial J_e}\mathbf{I})$$ (20)

$$(2\rho {\overline{\mathbf{F}}}_e\frac{\partial \psi }{\partial {\overline{\mathbf{C}}}_e}{\overline{\mathbf{F}}}_e^T+\rho J_e\frac{\partial \psi }{\partial J_e}\mathbf{I}):{\mathbf{D}}_{\text{in}}+S=\mathbf{T}:{\mathbf{D}}_{\text{in}}+S\ge 0$$ (21)

and

$$-\rho \frac{\partial \psi }{\partial a_d}{\dot{a}}_d\ge 0$$ (22)

Constitutive relations should satisfy the inequality condition of the inelastic dissipation in Eq. (21) and deterioration in Eq. (22).

3 Constitutive Equation

3.1 Free Energy Function.

The free energy function uses the model of Holzapfel et al. [32] given by

$$\begin{array}{c}\psi =\psi \left(J_e,{\overline{\mathbf{C}}}_e,a_d\right)\\ =\frac{k_0}{2}{\left(J_e-1\right)}^2+c_1\left(1-a_d\right)\left({\overline{I}}_1-3\right)+\sum _{i=1}^2\frac{k_1}{4k_2}\left\{\hspace{0.17em}\text{exp}\left[k_2{\left({\overline{I}}_4\left(i\right)-1\right)}^2\right]-1\right\}\end{array}$$ (23)

where $k_0$, $c_1$, $k_1$, and $k_2$ are the material parameters. $a_d$ is a scalar variable characterizing the damage effect in the material, where $a_d=[0,\hspace{0.17em}1]$; $a_d=0$ means no damage, and $a_d=1$ means complete damage. ${\overline{\mathit{I}}}_1=tr({\overline{\mathbf{C}}}_e)$ and ${\overline{\mathit{I}}}_4(i)$ are a variable of deviatoric elastic stretch for the ith fiber family. The direction vector ${\mathbf{N}}_i$ of the ith fiber family is defined as

$${\mathbf{N}}_i=\text{cos}\hspace{0.17em}{\alpha }_i{\mathbf{e}}_z+\text{sin}\hspace{0.17em}{\alpha }_i{\mathbf{e}}_{\theta }$$ (24)

having angle ${\alpha }_i$ with respect to the axial direction (${\mathbf{e}}_z$) in the reference configuration. Next, ${\overline{\mathit{I}}}_4\left(i\right)$ is given by

$${\overline{\mathit{I}}}_4(i)={\overline{\mathbf{C}}}_e:{\mathbf{M}}_i,\hspace{1em}\text{where}\hspace{1em}{\mathbf{M}}_i={\mathbf{N}}_i\otimes {\mathbf{N}}_i$$ (25)

${\mathbf{M}}_i$ is a second-order tensor based on ${\mathbf{N}}_i$ having angle ${\alpha }_i$ with respect to the axial direction (${\mathbf{e}}_z$) in the reference configuration. Note that Helfenstein et al. [33] showed that the invariant ${\overline{I}}_4\left(i\right)$ produces an unphysical response in models for fiber-reinforced hyperelastic materials, but the ${\overline{\mathit{I}}}_4(i)$ based free energy function in Eq. (23) is still efficient in the numerical simulation of an artery. Then, using Eq. (20), the Cauchy stress is given by

$$\begin{array}{c}\mathbf{T}=\rho J_e{k}_0(J_e-1)\mathbf{I}-\frac{2}{3}{c}_1(1-a_d)\rho {\overline{\mathit{I}}}_{\mathit{1}}\mathbf{I}+2c_1(1-a_d)\rho {\overline{\mathbf{F}}}_e\mathbf{I}{\overline{\mathbf{F}}}_e^T\\ -\frac{2}{3}\rho \sum _{i=1}^2{A}_i{\overline{I}}_4\left(i\right)\mathbf{I}+2\rho \sum _{i=1}^2{A}_i{\overline{\mathbf{F}}}_e{\mathbf{M}}_i{\overline{\mathbf{F}}}_e^T\end{array}$$ (26)

where

$$A_i=\frac{k_1}{4k_2}\left\{\hspace{0.17em}\text{exp}\left[k_2{\left({\overline{\mathit{I}}}_4\left(i\right)-1\right)}^2\right]-1\right\}2k_2\left({\overline{\mathit{I}}}_4\left(i\right)-1\right).$$

Under the incompressible condition ($J_e=1$) with an infinite value of $k_0$, $\rho J_e{k}_0(J_e-1)$ becomes indeterminate and can be replaced by a Lagrange multiplier ($p$), which is determined at the boundary condition [$-p=\rho J_e{k}_0(J_e-1)$]. Finally, the Cauchy stress is rearranged by introducing a volumetric term ($\frac{1}{3}\mathbf{I}{\sum }_{i=1}^2{A}_i$) as shown below:

$$\mathbf{T}=\frac{1}{3}tr\left(\mathbf{T}\right)\mathbf{I}+{\mathit{T}}^{\prime }$$ (27)

where $tr\left(\mathbf{T}\right)=-3p-2\rho c_1(1-a_d){\overline{\mathit{I}}}_{\mathit{1}}\mathbf{I}+2\rho \mathbf{I}{\sum }_{i=1}^2{A}_i$, and ${\mathbf{T}}^{\prime }=2\rho [c_1(1-a_d)({\overline{\mathbf{B}}}_e-\frac{1}{3}{\overline{\mathit{I}}}_{\mathit{1}})+{\sum }_{i=1}^2{A}_i({\overline{\mathbf{F}}}_e{\mathbf{M}}_i{\overline{\mathbf{F}}}_e^T-\frac{1}{3}\mathbf{I})]$.

3.2 Inelastic Potential Function.

It is assumed that the inelastic deformation of the artery wall can be separated into independent plastic and growth deformation vectors

$${\mathbf{L}}_{\text{in}}={\mathbf{L}}_p+{\mathbf{L}}_g={\Gamma }_p{\overline{\mathbf{L}}}_p+{\Gamma }_g{\overline{\mathbf{L}}}_g$$ (28)

$${\mathbf{L}}_p={\mathbf{D}}_p+{\mathbf{W}}_p\hspace{1em}\text{and}\hspace{1em}{\mathbf{L}}_g={\mathbf{D}}_g+{\mathbf{W}}_g$$ (29)

$${\mathbf{D}}_{\text{in}}={\mathbf{D}}_P+{\mathbf{D}}_g$$ (30)

where ${\mathbf{D}}_P=\frac{1}{2}({\mathbf{L}}_p+{\mathbf{L}}_p^{\mathit{T}})={\Gamma }_p{\overline{\mathbf{D}}}_P$ and ${\mathbf{D}}_g=\frac{1}{2}({\mathbf{L}}_g+{\mathbf{L}}_g^{\mathit{T}})={\Gamma }_g{\overline{\mathbf{D}}}_g$.

Note that the zero dilatancy of the plasticity leads to ${\mathbf{D}}_p:\mathbf{I}=0$. ${\Gamma }_p$ and ${\Gamma }_g$ are the plastic and growth parameters, respectively. The inelastic spin tensor is skew-symmetric and can be specified [34,35]. This work follows the assumption that the directions of the material axes are fixed during the inelastic deformation path, which makes the asymmetric inelastic spin be neglected, which is given by:

$${\mathbf{W}}_{\text{in}}={\mathbf{W}}_g+{\mathbf{W}}_p=\mathbf{0}$$ (31)

For the growth tensors, this work is restricted to two cases of volumetric growth, the isotropic and radial dominant growth cases. While the isotropic growth models have been widely used for volumetric growth [36,37], there are observations of anisotropic growth in the arterial wall [9,38–40]. Motivated by the previous anisotropic models to make the radial dominant growth, we make a simplification that the anisotropic growth occurs only in the thickness direction. Below are the two examples of isotropic and radial dominant growth given by

$${\mathbf{D}}_g={\Gamma }_g{\overline{\mathbf{D}}}_g$$ (32)

where

${\overline{\mathbf{D}}}_g=\mathbf{I}$ for the isotropic and

${\overline{\mathbf{D}}}_g=\left[\begin{array}{ccc}3& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$ for the anisotropic growth for the radial direction.

The two cases in Eq. (32) match the same magnitude of the volume change.

The inelastic dissipation in Eq. (21) is then rewritten by

$$\begin{array}{c}\left({\mathbf{T}}^{\prime }+\frac{1}{3}\text{tr}\left(\mathbf{T}\right)\mathbf{I}\right):\left({\mathbf{D}}_p+{\mathbf{D}}_g\right)+S\\ ={\mathbf{T}}^{\prime }:{\mathbf{D}}_p+\frac{1}{3}\text{tr}\left(\mathbf{T}\right)\mathbf{I}:{\mathbf{D}}_p+{\mathbf{T}}^{\prime }:{\mathbf{D}}_g+\frac{1}{3}\text{tr}\left(\mathbf{T}\right)\mathbf{I}:{\mathbf{D}}_g+S\ge 0\end{array}$$ (33)

Due to the isochoric condition of the plasticity ($\mathbf{I}:{\mathbf{D}}_p=0$), the above equation becomes

$${\mathbf{T}}^{\prime }:{\mathbf{D}}_p+\frac{1}{3}\text{tr}\left(\mathbf{T}\right)\mathbf{I}:{\mathbf{D}}_g+S\ge 0$$ (34)

The isotropic growth automatically satisfies (${\mathbf{T}}^{\prime }:{\overline{\mathbf{D}}}_g=0$), and the anisotropic case leads to that ${\mathbf{T}}^{\prime }:{\overline{\mathbf{D}}}_g$ is non-negative when atrophy is not allowed in this PH condition. The above dissipation is satisfied when

$${\mathbf{T}}^{\prime }:\hspace{0.17em}{\mathbf{D}}_{\mathrm{p}}\ge 0\hspace{1em}\text{and}\hspace{1em}\frac{1}{3}\text{tr}\hspace{0.17em}\left(\mathbf{T}\right)\hspace{0.17em}\mathbf{I}:\hspace{0.17em}{\mathbf{D}}_{\mathrm{g}}+S\ge 0$$ (35)

In order to reach the inequality of Eq. (35), this work proposes an inelastic potential function ${\phi }_{\text{in}}$, which is independent of the free energy function $\psi$, that defines the constitutive relation of ${\mathbf{D}}_p$ and ${\mathbf{D}}_g$ for satisfying the material dissipation as below:

$${\phi }_{\text{in}}({\mathbf{T}}^{\prime },\text{tr}(\mathbf{T}))={\phi }_p({\mathbf{T}}^{\prime })+{\phi }_g(\text{tr}(\mathbf{T}))$$ (36)

where ${\phi }_p$ is the plastic potential and a function of the deviatoric stress. ${\phi }_g$ denotes the growth potential and the function of $\text{tr}(\mathbf{T})$.

3.3 Plasticity.

It is assumed that the time differential of ${\phi }_p$ is the same as the hardening rate in this work given as

$${\dot{\phi }}_p\left({\mathbf{T}}^{\prime }\right)=\frac{\partial {\phi }_p}{\partial {\mathbf{T}}^{\prime }}{\dot{\mathbf{T}}}^{\prime }=H{\Gamma }_p,\hspace{1em}\text{where}\hspace{1em}{T}_Y=T_0+\int H{\Gamma }_{P}dt$$ (37)

Here, ${\mathit{T}}_Y$ is the flow stress, ${\mathit{T}}_0$ is the initial yield stress, and $H$ is the hardening slope. Next, let the partial differential of ${\phi }_p$ in the above equation define the direction of the plastic deformation rate given as

$${\overline{\mathbf{D}}}_P=\frac{\partial {\phi }_p}{\partial {\mathbf{T}}^{\prime }}\hspace{1em}\text{and}\hspace{1em}{\overline{\mathbf{D}}}_P:\mathbf{I}=0$$ (38)

which denotes the normal vector to ${\phi }_p$ at the stress state. If ${\phi }_p$ is a convex function, the normality rule guarantees ${\mathbf{T}}^{\prime }:{\overline{\mathbf{D}}}_p\ge 0$ in the material dissipation. To compete the non-negative plastic dissipation, a non-negative plastic deformation parameter ${\Gamma }_p$ should be defined. The stress change rate is

$${\dot{\mathbf{T}}}^{\prime }=\frac{\partial {\mathbf{T}}^{\prime }}{\partial J_e}{\dot{J}}_e+\frac{\partial {\mathbf{T}}^{\prime }}{\partial {\overline{\mathbf{C}}}_e}{\dot{\overline{\mathbf{C}}}}_e$$ (39)

Note that the artery is generally modeled as a cylindrical tube without a rigid body rotation. The material axes of the axial (${\mathbf{e}}_z$), circumferential (${\mathbf{e}}_{\theta }$), and radial (${\mathbf{e}}_r$) are aligned with the Cartesian coordinate system. Consequently, the evolution equations of the tensors including the Cauchy stress do not consider the rotation of the frame in this work. Substituting Eq. (39) into Eq. (37) results in

$${\Gamma }_P=\frac{\widehat{y}}{\overline{y}}\mu$$ (40)

where

$$\widehat{y}=[\frac{\partial {\phi }_p}{\partial J_e}{J}_e\mathbf{I}+2({\overline{\mathbf{F}}}_e\frac{\partial {\phi }_p}{\partial {\overline{\mathbf{C}}}_e}{\overline{\mathbf{F}}}_e^T-\frac{1}{3}\mathbf{I})]:[\mathbf{D}-{\mathbf{D}}_g]\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\overline{y}=2{\overline{\mathbf{F}}}_e\frac{\partial {\phi }_p}{\partial {\overline{\mathbf{C}}}_e}{\overline{\mathbf{F}}}_e^T:{\overline{\mathbf{D}}}_P+H.$$

The parameter $\mu$ is given by

$$\mu =0\hspace{1em}\text{when}\hspace{1em}\hspace{0.17em}{\phi }_p({\mathbf{T}}^{\prime })-{\mathit{T}}_Y<0\hspace{1em}\text{or}\hspace{1em}[{\phi }_p({\mathbf{T}}^{\prime })-{\mathit{T}}_Y=0\hspace{1em}\text{and}\hspace{1em}\widehat{y}<0]$$ (41)

and $\mu =1$ when [${\phi }_p({\mathbf{T}}^{\prime })-{\mathit{T}}_Y=0$ and [$\widehat{y}\ge 0$].

In order to define the specific form of the plastic potential, this work uses the invariant of the J₂ flow rule based function defined by

$${\phi }_p\left({\mathbf{T}}^{\prime }\right)=\sqrt{\frac{3}{2}{\mathbf{T}}^{\prime }:{\mathbf{T}}^{\prime }}.$$ (42)

Next for the yield function, this paper uses the associated flow rule with the widely used assumption that the yield function is identical to the plastic potential. Then, the plastic flow is defined perpendicular to the yield surface (31)–(33).

3.4 Growth.

A recent work [31] showed that growth is also able to be described by a potential function. But the function in that paper did not consider the separated plastic behavior from the growth. This paper proposes a new growth potential function to model the volumetric growth and at the same time, the plastic deformation as shown below:

$${\phi }_g\left(\text{tr}\left(\mathbf{T}\right)\right)=\frac{h}{2}{\left(\text{tr}\left(\mathbf{T}\right)-\text{tr}\left({\mathbf{T}}_h\right)\right)}^2$$ (43)

${\mathbf{T}}_h$ is the homeostatic stress and $h$ is a non-negative material parameter with a unit of 1/(Pa·s). Let the time differential of ${\phi }_g$ be the volumetric growth rate

$${\dot{\phi }}_g(\text{tr}(\mathbf{T}))=h(\text{tr}(\mathbf{T})-\text{tr}({\mathbf{T}}_h))={\Gamma }_g{\overline{\mathbf{D}}}_g:\mathbf{I}$$ (44)

Equation (44) is close to the growth form in Ref. [41]. Next, the mass flow in Eq. (12) is given for both the isotropic and aniostopic growth determined by

$$g={\rho }_0{\Gamma }_g{\overline{\mathbf{D}}}_g:\mathbf{I}$$ (45)

and the growth parameter ${\Gamma }_g$ is

$${\Gamma }_g=\frac{1}{3}\frac{g}{{\rho }_0}$$ (46)

The growth dissipation in Eq. (35) then becomes

$$\frac{1}{3}\text{tr}\left(\mathbf{T}\right)\frac{g}{{\rho }_0}+S\ge 0$$ (47)

Note that the effect of the external energy source $S$ is enough to satisfy the non-negative condition in the biology system [25,41].

If ${\mathbf{T}}_h={\mathbf{T}}^{\prime }$, the rate of growth can be given by

$${\phi }_g\left(\text{tr}\left(\mathbf{T}\right)\right)=h\left(\mathbf{T}-{\mathbf{T}}^{\prime }\right):\mathbf{I}=\frac{1}{3}\frac{g}{{\rho }_0}\mathbf{I}:\mathbf{I}$$ (48)

If the $h$ variable is non-negative, the external energy term $S$ can be zero, which satisfies the inequality condition as shown below:

$$\text{tr}(\mathbf{T})\mathbf{I}:{\mathbf{D}}_g=h{[\text{tr}(\mathbf{T})]}^2\ge 0$$ (49)

The final form of the inelastic potential function is consequently given by

$${\phi }_{\text{in}}\left({\mathbf{T}}^{\prime },\text{tr}\left(\mathbf{T}\right)\right)=\sqrt{\frac{3}{2}{\mathbf{T}}^{\prime }:{\mathbf{T}}^{\prime }}+\frac{h}{2}{\left(\text{tr}\left(\mathbf{T}\right)-\text{tr}\left({\mathbf{T}}_h\right)\right)}^2$$ (50)

and it controls and connects the plasticity and growth deformation.

3.5 Material Deterioration.

The enzymatic degradation variable $a_d$ in the free energy function is defined by

$$a_d={[1-\text{exp}(-C_d{\phi }_d({\psi }_{\max },{\psi }_{\min },{\psi }_{\mathrm{avr}}))]}^b$$ (51)

where $C_d$ and $b$ are material parameters and non-negative. ${\psi }_{\text{max}}$ and ${\psi }_{\text{min}}$ are free energy functions at the systolic and diastolic pressures of the cardiac cycle, respectively. Note that because this work is based on an idealized thin-walled tube assumption, ${\psi }_{\text{max}}$ and ${\psi }_{\text{min}}$ are considered maximum and minimum values of a material point. ${\psi }_{\text{avr}}$ is the average value of ${\psi }_{\text{max}}$ and ${\psi }_{\text{min}}$. This work defines ${\phi }_d({\psi }_{\text{max}},{\psi }_{\text{min}},{\psi }_{\text{avr}})$ function as below

$${\phi }_d\left({\psi }_{\text{max}},{\psi }_{\text{min}},{\psi }_{\text{avr}}\right)=\frac{1}{2}{\left[\frac{\langle {\psi }_{\text{max}}-{\psi }_{\text{min}}\rangle }{{\psi }_{\text{avr}}}\right]}^{\beta }$$ (52)

where $\langle x\rangle =\text{max}(x,0)$, which is the Macaulay bracket, and $\beta$ is a material parameter.

During the deterioration, it is usually assumed that the mass is not changed for healthy subjects. Next, the satisfaction of the deterioration dissipation is shown as

$$-\rho \frac{\partial \psi }{\partial a_d}{\dot{a}}_d=\rho c_1\left({\overline{I}}_1-3\right)\text{exp}\left[-C_d{\phi }_d\left({\psi }_{\text{max}},{\psi }_{\text{min}},{\psi }_{\text{avr}}\right)\right]C_{d}b{a}_d{\dot{\phi }}_d\ge 0$$ (53)

Consequently, the material dissipation of the thermodynamics in Eq. (17) is fully satisfied by the proposed constitutive equations.

3.6 Modeling of the Artery.

Consider an idealized cylindrical tube in terms of a cylindrical polar coordinate {$R$, $\Theta$, $Z$} for the free stress configuration, whereby the tube may not be the full circumference when the original traction-free vessel has residual stress. The reference configuration is given by a fictitious geometry without the stress or physically releasing the residual stress by a radial cut. The parameter ranges are defined by

$$R_i\le R\le R_o,\hspace{1em}\hspace{0.17em}0\le \Theta \le 2\pi -\alpha ,\hspace{1em}\hspace{0.17em}0\le Z\le L$$ (54)

where $R_i$, $R_o$, $\alpha$, and $L$ are the inner and outer radii, the opening angle and the length of the undeformed tube. Then, the deformed configuration is given as the coordinate {$r$, $\theta$, $z$}, and the parameter ranges to

$$r_i\le r\le r_o,\hspace{1em}\hspace{0.17em}0\le \theta \le 2\pi ,\hspace{1em}0\le z\le l$$ (55)

where $r_i$, $r_o$, and $l$ are the inner and outer radii and the length of the deformed tube. The arterial wall is incompressible, and $\mathbf{F}$ is given in terms of the cylindrical polar coordinates as

$$\mathbf{F}=\left[\begin{array}{ccc}{\lambda }_r& 0& 0\\ 0& {\lambda }_{\theta }& 0\\ 0& 0& {\lambda }_z\end{array}\right]=\left[\begin{array}{ccc}\frac{h_t}{H_t}& 0& 0\\ 0& \frac{r}{R}& 0\\ 0& 0& \frac{z}{Z}\end{array}\right]$$ (56)

where the angle of the twist of the tube is assumed to be negligible. $H_t$ and $h_t$ denote the initial and current thickness of the tube, respectively. In order to get ${\lambda }_r$, ${\lambda }_{\theta }$, and ${\lambda }_z$ at the nth time-step, the equilibrium equation should be solved. In this work, the inflation experiment was conducted with a fixed ${\lambda }_z$ condition, and then, the stress and external pressure equilibrium can be solved with respect to considering the coupled elastic-plastic-degradation-growth models. The nonlinear differential equations are solved by an iterative numerical method written in the matlab program, and the numerical algorithm is explained in Appendix.

3.7 Experimental Data for the Model Calibration.

The model should be calibrated by an experimental dataset from a porcine artery experiment. In the ex vivo inflation tests, pig pulmonary arterial specimens were fixed with an axial stretch of 1.1, and intramural pressure was applied inside the artery tube while measuring the diameter of the artery. Three sets of pressure-diameter data were obtained with respect to the pressure range; inflation of 0–30 mmHg pressure, 0–50 mmHg pressure, and 0–100 mmHg pressure. The details of the experimental setup are explained in Ref. [15], and we used the inflation test data from the reference to extract the hyperelastic model parameters. The parameters $c_1$, $k_1$, $k_2$, and ${\alpha }_i$ in the free energy function Eq. (23) were calibrated with the inflation data of the pressure values from 0 to 30 mmHg, assuming $a_d=0$, only for the elastic deformation range. Note that because this model is based on a two fiber family, the fiber angles ${\alpha }_{i=1,2}$ are assumed to have the same absolute value with the opposite sign. In the calibration, the nonlinear regression function was used by minimizing the error between the experimental transmural pressure and the computed pressure. Although PH has traditionally been defined by a mean pulmonary arterial pressure (mPAP) of greater than 25 mmHg, later studies have suggested a lower threshold of 20 mmHg [42]. A population-based study reported that the mPAP range was 51–60 mmHg for a moderate group of PH patients [43]. Based on this clinical data, we make the numerical setup for the first part of the parametric study and the second part of the in silico simulation, for an independent variable of mPAP, ranging from 20 to 60 mmHg. We also utilize a population-based relationship between the systolic and diastolic pulmonary arterial pressure by setting the systolic and diastolic pressure, given as a linear function of mPAP [18].

4 Results

4.1 Plastic Deformation in the Inflation Test.

The fitted parameters of the elastic pulmonary arterial wall are summarized in Table 1, and the diameter-pressure data were fitted with the hyperelastic model, presented in Fig. 2(a). Note that k₀ does not affect the computation results because of the incompressible condition. The pure elastic model calibrated by the 0–30 mmHg data also fits the 0–50 mmHg data well shown in Fig. 2(b). In Fig. 2(c), the elastic model presents the fitting of the 0–100 mmHg condition without considering any irreversible dissipation. Unlike the 0–30 and 0–50 mmHg cases, the hyperelastic model fitting leads to large over estimations compared to the experimental data after the pressure is over 50 mmHg. This means that after some stress levels, there is another dissipation phenomenon besides the growth and degradation because the specimen in the experiment cannot make the growth and long-term degradation dissipation. Even though the plastic deformation has been rarely studied for the artery, it is reasonable to infer that the ex vivo experimental test shows that plastic yielding starts near the 50 mmHg pressure. For this reason, the plastic parameters were calibrated by the inflation data for the 0–100 mmHg pressure by using the elastic parameters that fit against the 0–30 mmHg data. Figure 2(d) shows that the elastic–plastic result is fitted well with the 0–100 mmHg inflation data. The best/fit values of the yield stress and hardening variable $H$ are also summarized in Table 1. Based on Fig. 2, it can be concluded that the model calibration for elastic–plastic deformation is reasonable. However, because of the experimental limitation, the growth and degradation parameters were not calibrated by the inflation data here. A parametric study for the growth and degradation was conducted and presented in Sec. 4.2. It investigated the mechanical roles of the dissipative phenomena in the disease progress.

Table 1.

Fitted material parameters (elastic and plastic parameters)

Elastic parameters					Plastic parameters
$k_0$	$c_1$ (kPa)	$k_1$ (kPa)	$k_2$ (kPa)	${\alpha }_i$ (deg)	${\mathit{T}}_0$ (kPa)	$H$ (kPa)
N/A	13.04	30.56	3.03	$\pm$57.89	134.35	70

Fig. 2.

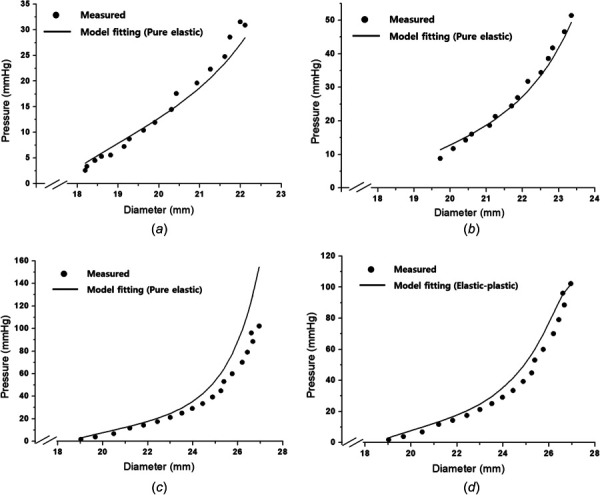
Model calibration of initial material parameters for elastic–plastic behavior with ex vivo test data: (a) elastic modeling fitting (0–30 mmHg data), (b) elastic model fitting (0–50 mmHg data), (c) elastic modeling fitting (0–100 mmHg data), and (d) elastic–plastic model fitting (0–100 mmHg data)

4.2 Parametric Study for the Growth and Degradation.

In the parametric study, the internal pressure $P_i$ is used as the input variable of mPAP in the range of 20–60 mmHg, and the axial stretch is fixed at 1.1 for all of the cases. Figure 3 shows the effect of the degradation on the disease progress. Note the other inelastic effects of the plasticity and growth were excluded in this degradation study. Figure 3(a) presents the degradation variable $a_d$ that tends to increase with increases in mPAP with respect to the internal variable $C_d$; the internal variable $C_d$ strongly affects the degradation speed and value. To consider the degradation caused by the systolic and diastolic pressures of the cardiac cycle, the systolic and diastolic pressures were assumed to be a function of mPAP where the systolic pressure $P_s$ and the diastolic pressure $P_d$ are proportionally set as $P_s$ = 1.49 mPAP and $P_d$ = 0.74 mPAP, respectively [18]. Based on the $a_d$ tendency, Figs. 3(b) and 3(c) show the diameter and thickness changes, respectively. An increase of $a_d$ clearly leads to an increase of the diameter and a decrease of the thickness. Figure 3(d) presents the linearized stiffness of the artery with respect to the internal pressure and $a_d$ parameters. The presented stiffness is the summation of the radial stiffness and thickness stiffness in the figure, and the stiffness increases with increasing $a_d$. It is well known that the stiffness increase is an important sign of disease progression.

Fig. 3.

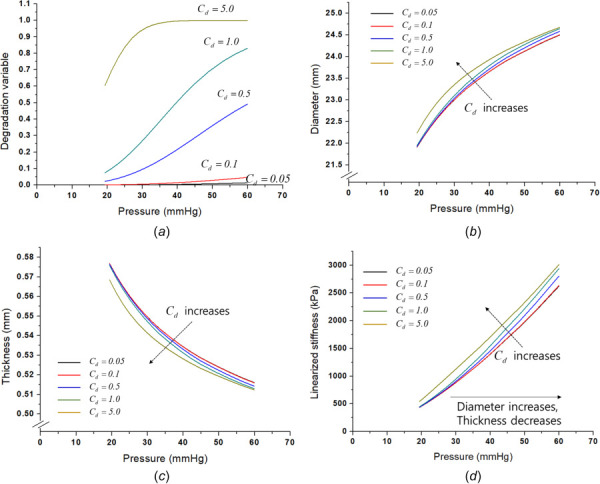
Degradation effect on the disease progress: (a) degradation variable change according to the C_d parameter, (b) degradation effect on diameter, (c) degradation effect on thickness, and (d) degradation effect on the linearized stiffness

Figure 4 presents the growth effect on the disease progress. Note that the unit time of the growth was one year, and the time increment of the growth was 0.02. Consequently, the growth continues for 40 months from 20 to 60 mmHg. The relevant time variable was set based on a clinical study in which half of the patients died within 3 years [44]. As shown in Figs. 4(a) and 4(b), as the $h$ parameter increases, the diameter and thickness both increase. If $h$ has a very large value ($h$ = 1.0), the degree of thickening is accelerated shown in Fig. 4(b). This results in a continuous diameter increase until the global equilibrium is reached, as shown in Eq. (58), without deceleration of the diameter change in the case of a large $h$. Figure 4(c) presents the effect of the growth on the linearized stiffness. Larger growth deformations with larger values of $h$ lead to accelerating the disease progress. Figures 4(d) and 4(e) compare three cases for growth with ($h$ = 0.5), growth with ($h$ = 1.0), and growth with degradation ($h$ = 1.0 and $C_d$ = 0.5) on the diameter and thickness, respectively. Note that the ($h$ = 1.0) case without degradation is an extreme case for the parametric study, and the degradation can relieve the extreme growth.

Fig. 4.

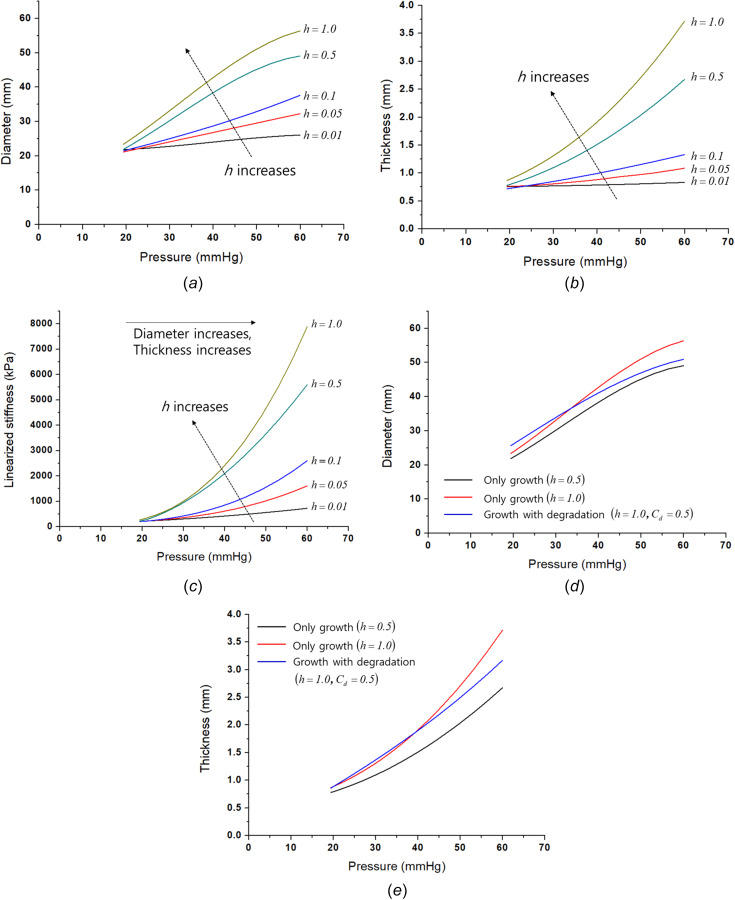
Growth effect on the disease progress: (a) growth effect on diameter, (b) growth effect on thickness, (c) growth effect on the linearized stiffness, (d) growth with degradation effect on diameter, and (e) growth with degradation effect on thickness

4.3 Disease In Silico Simulations.

Based on the calibrated results, numerical simulation of the disease progression was conducted. The growth and degradation parameters used an assumed value shown in Table 2 and the calibrated elastic–plastic parameters in Table 1. Figure 5 shows the simulation results and compares the inelastic mechanisms in the disease progress. Figure 5(a) presents the diameter change of the pressure-induced elastic, elastic–plastic, elastic-growth, elastic-degradation, and elastic-plastic-growth-degradation (full) mechanisms. The pure elastic, plastic, and degradation results have similar behaviors compared to the growth and full mechanisms; the growth and full cases lead to much larger diameter increases. Because only the growth and full simulations can make a volume change, the others should not alter the total volume. Hence, the incompressible condition ($J_e$ = 1) enables a volume change only when growth occurs based on Eqs. (12) and (13). This condition leads to a thickness decrease in the elastic, plastic, and degradation cases by isochoric deformation shown in Fig. 5(b). However, the growth and the full cases lead to a thickness increase with the diameter increasing due to the growth volume change. If the full case is compared to the growth model, the changes in the diameter and thickness are smaller than the growth because the dissipation mechanisms (growth, plastic, and degradation) can affect each other.

Table 2.

Growth and degradation parameters for the case study

Degradation parameters			Growth parameters
$C_d$	$b$	$\beta$	$\text{tr}({\mathit{T}}_h)$ (kPa)	$h$ (1/kPa· year)
1.0	2.0	2.0	4000	0.1

Fig. 5.

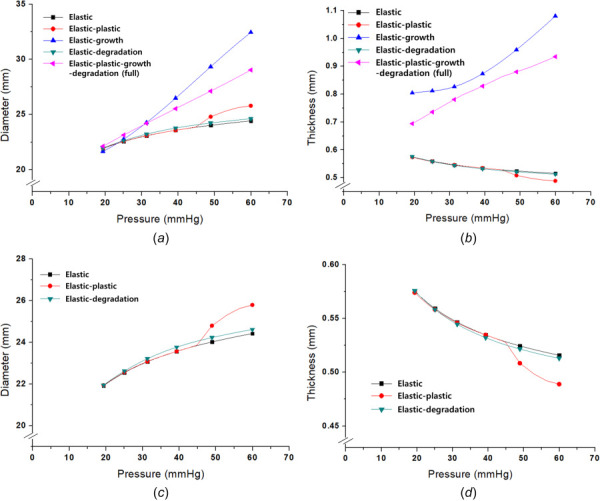
Numerical analysis of the disease progress: (a) comparison of five mechanisms for diameter change (elastic, plastic, growth, degradation, and full), (b) comparison of five mechanisms for thickness change (elastic, plastic, growth, degradation, and full), (c) pressure-diameter of three cases for diameter change (elastic, plastic, and degradation), and (d) pressure-diameter of three cases for thickness change (elastic, plastic, and degradation)

In order to clearly compare the elastic, plastic, and degradation cases, Figs. 5(c) and 5(d) present enlarged curves of the diameter and thickness changes. The elastic–plastic curves of the diameter and thickness are almost the same to the elastic results until about 50 mmHg; afterward, the elastic–plastic deformation increases the dimension changes because of the inelastic dissipation. The degradation also magnifies the changes of the diameter and thickness compared to the pure elastic behavior. Because the degradation and growth values were not fixed, additional parametric studies for the degradation and growth were conducted.

In Fig. 6, the anisotropic growth effect on the full model is discussed because some studies presented the anisotropic growth of the artery [38,40] for the thickness direction. Here, the full model with the isotropic growth and the full model with an anisotropic growth are compared. In this case, the anisotropic growth simply assumes that all of the growth is independently generated for only the thickness direction. The simulation conditions are summarized in Table 3, and the axial stretch is fixed at 1.1. Figures 6(a) and 6(b) show the anisotropic growth decreases in the diameter expansion while increasing the thickness because the growth is generated only in the thickness direction. Similarly, studies [38,40] have reported the radial direction-based anisotropic growth occurs in the measurements.

Fig. 6.

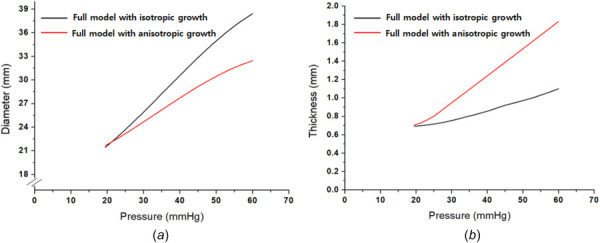
Anisotropic growth effect: (a) anisotropic growth effect on diameter and (b) anisotropic growth effect on thickness

Table 3.

Growth and degradation parameters for the case study with the anisotropic growth

Elastic parameters							Plastic parameters
$c_1$ (kPa)	$k_1$ (kPa)		$k_2$ (kPa)		${\alpha }_i$ (deg)		${\mathit{T}}_0$ (kPa)		$H$ (kPa)
13.04	30.56		3.03		$\pm$57.89		134.35		70

Degradation parameters						Growth parameters
$C_d$		$b$		$\beta$		$\text{tr}({\mathit{T}}_h)$ (kPa)		$h$ (1/kPa· year)
1.0		2.0		2.0		4000		0.15

Based on the presented results shown in Figs. 2–6, the full model with the anisotropic growth is used to generate in silico simulations (from 20 mmHg to 60 mmHg) for the arterial thickening, luminal enlargement, and arterial stiffening. However, those values from the simulations are not perfectly matched to the clinical data from the literature due to missing patient's information or conditions (e.g., mPAH, extent of severity). Instead, the generated in silico simulations compute the ratios of the arterial thickening, luminal enlargement, and arterial stiffening against the initial state (at 20 mmHg), shown in Fig. 7. Then, this study compares the changed ratios of the thickness, diameter, and stiffness between the modeling and reference data. For the reference data, the ratios are computed by the values of PH patients against those of healthy subjects obtained from the Ref. [45] for arterial thickening, Ref. [46] for luminal enlargement, and Ref. [45] for arterial stiffening. For selecting parameters for the in silico simulation, the elastic parameters ($c_1$, $k_1$, $k_2$, and ${\alpha }_i$) and plastic parameters (${\mathit{T}}_0$ and $H$) were calibrated by using the inflation experimental data shown in Fig. 2. For the growth ($\text{tr}({\mathbf{T}}_h)$ and $h$) and degradation ($C_d$, $b$, and $\beta$) parameters, the results of the parametric studies (in Figs. 3–6) were used. In Fig. 3(a), $C_d$ = 1.0 (with $b=2.0$, and $\beta =2.0$) provided a smooth increase of the degradation while the other values resulted in excessive or insufficient degradations. As a result, $C_d$ = 1.0 (with $b=2.0$ and $\beta =2.0$) was chosen for the in silico simulation. For the growth, $\text{tr}({\mathbf{T}}_h)$ used a fixed homeostatic value given with an onset value at the early disease stage. In Fig. 3(a), the isotropic growth case with $h$= 0.15 led to enough growth, and in Fig. 7, $h$ was assumed to be 0.15 slightly higher than 0.1. Based on the discussion of Fig. 6, the full model with the anisotropic growth was employed. The parameters that were used are summarized in Table 3. Note that because this model is built based on thin-wall tube modeling, the luminal enlargement is roughly calculated using the mean radius and thickness. The results of the anisotropic growth in the full model are close to the obtained value from the previous studies for human PH, whereas luminal enlargement (∼1.22 times [46]), arterial thickening (∼2.4 times [47], and arterial stiffening (∼4 times [45]) are prominent features of PH.

Fig. 7.

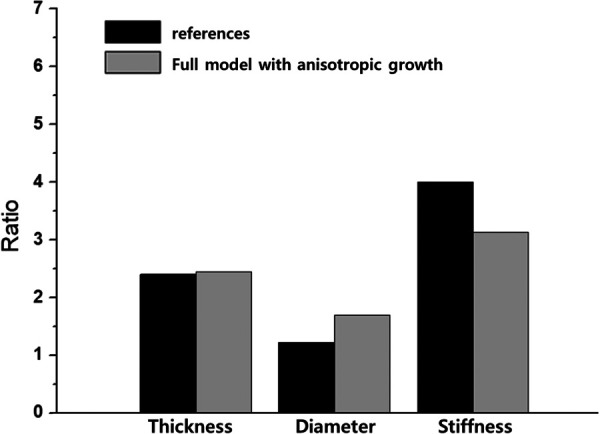
The ratios of the arterial thickening, luminal enlargement, and arterial stiffening against the initial state that are computed from the generated in silico simulations. For the reference data, the ratios are computed by the values of PH patients against those of healthy subjects obtained from the references.

The advantage of the full model is that the irreversible energy dissipations caused by several effects (growth, plasticity, and degradation) can be examined in the thermodynamically integrated energy balance. So, the integrated model can describe that the degradation irreversibility decelerates the stress-induced growth and plastic dissipations. This decelerated growth caused by the degradation effect is presented in Figs. 4(d) and 4(e). Figures 8(a) and 8(b) present the pressure-diameter and pressure-thickness curves of the plastic model according to a different value for the degradation variable $a_d$, and the figures clearly show that the $a_d$ value affects the plastic deformation in the diameter and thickness. This degradation effect on the plastic behavior is also observed in other materials [48]. Moreover, if the growth affects the stress state itself, the plastic behavior is also changed. In order to explain the coupling effect, Fig. 9 presents the J₂ deviatoric stress invariant with respect to different growth variables, $h$, for the isotropic growth. The J₂ invariant is decreased as $h$ increases meaning that growth affects the stress state itself, and the onset of plastic yielding is delayed with the increased growth effect which shows a coupling effect between growth and plasticity. In addition, as $h$ increases, the speed of the J₂ change becomes faster. Consequently, in the full model shown in Fig. 5, plastic yielding is decelerated by degradation and growth and starts near at about 60 mmHg. Even though the elastic-plastic fitting of the inflation test makes the onset of yielding near 50 mmHg. The results of the numerical study discuss the role of plastic behavior, degradation, and growth in arterial disease. It shows the potential of the coupled model considering the plastic deformation and degradation with the growth for a better understanding of PH diseases.

Fig. 8.

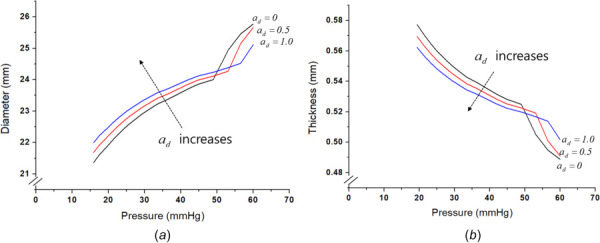
Effect of degradation on the plastic behavior: (a) pressure-diameter curves of plastic model according to the degradation variable and (b) pressure-thickness curves of plastic model according to the degradation variable

Fig. 9.

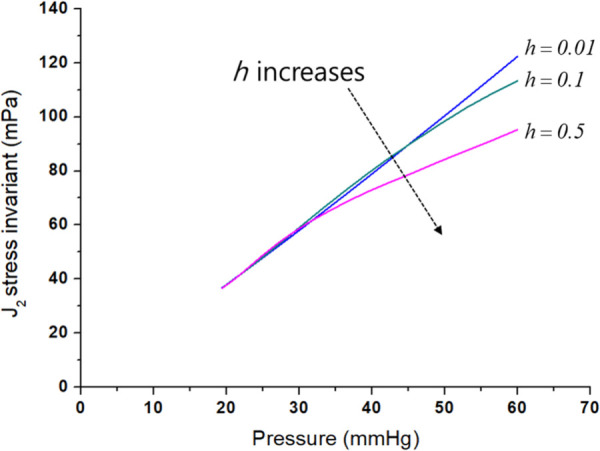
Effect of growth on J₂ deviatoric stress invariant

5 Discussions

There has been a question for a long time on PH as to why do most types of PH have no cure, while pharmacological management of systemic hypertension has been so effective for decades. Various studies using animal models showed promises of new pharmacological agents for PH intervention [49,50], but current human PH medications only delay disease progression and are not curative [51]. In order to answer the question, computational models of PH have been developed to test multiple hypotheses on the disease progression in the mechanics of the main pulmonary arteries [45,52], pulmonary circulation [53,54] and cardiac growth [55]. Recent computational studies suggest, in contrast to previous studies, that the interaction between the right ventricle and the pulmonary vasculature may be a key determinant of the clinical course of PH [56]. Nonetheless, those previous computational models were based on hyperelastic and volumetric growth, and few have investigated the role of dissipative changes, such as plasticity and degradation, of the pulmonary arterial wall in PH modeling.

This study presented the first mechanics-based modeling framework of PH that captures the inelastic and vascular remodeling behavior of the pulmonary artery in the presence of the pulsatile cardia cycle. This modeling used the small-on-large (SoL) time-scale theory approach [57], assuming that the cardiac cycle (short time scale) only leads to a small deformation within the elastic range while the accumulated cycling results in a large deformation with growth in a long time scale. The model assumed that plasticity is based on the J₂ flow caused by the elevated systolic pulmonary arterial pressure; degradation is magnified leading to isotropic damage of elastin (fragmented elastin layers) via an elevated pulse pressure, and growth is generated via stress-mediated volumetric growth. The parametric study showed that degradation enlarges the diameter and with an isochoric deformation, decreases the thickness shown in Figs. 3(a)–3(d). Stiffness is also increased as the disease progresses with degradation and growth shown in Figs. 3(d) and 4(c). The stress-mediated volumetric growth results in diameter increases and thicker walls when the mean pulmonary arterial pressure is gradually elevated shown in Fig. 4. Although the degradation ought to cause a softening of the vascular matrix, this simulation, however, found the opposite to be true. This was mainly due to a load transferring from a low-stretched state to a higher stretched state via an elevated transmural pressure during the time course of the disease progress. Furthermore, the volumetric growth renders an increased arterial stiffness during the course, both by increased intrinsic stiffening and thickening. The elevated stress directly links to the volume change; however, the growth also has an indirect, recovery mechanism by which pulmonary vascular remodeling is caused by the arterial damage, whereas smooth muscle hypertrophy and adventitial thickening are well documented in animal models of PH [58]. It is also widely accepted that arterial stiffening plays an important role both in systemic and pulmonary hypertension progression in clinics [59,60]. Nevertheless, although its parameter sensitivity study clearly illustrated that arterial damage and growth cause increased stiffness, the full simulation (combining all) reveals a key postpathological recovery process of compensating for the vessel damage by vascular adaptation and reducing the rate of vessel dilation and mediating vascular wall stress.

6 Conclusion

In conclusion, this work confirms that the thermodynamics model with the inelastic potential function of combining growth and plastic behavior is capable of calibrating within the range of clinical PH data. With more experimental data, such as pressure dependency of yielding and anisotropic behavior and microstructure dependency [61–63], this potential function can be updated to capture more complex behavior. In the future, the accumulation of more data along with the continuous improvement of the model will allow the model to serve as a tool that calibrates against patient-specific data and help in the optimal treatment for patients, such as elastase inhibitors [64].

Appendix A

A.1 Numerical Process of the Global Equilibrium.

This section presents the numerical algorithm implemented in the matlab program. The inflation experiment was conducted with a fixed ${\lambda }_z$ condition; then stress and external pressure equilibrium can be solved for a thin wall at the given diameter in the two-dimensional condition, as below:

$$E_{rr}={\mathit{T}}_{rr}+\frac{P_i}{2}=0\hspace{1em}\text{and}\hspace{1em}{E}_{\theta \theta }={\mathit{T}}_{\theta \theta }-\frac{r}{h_t}{P}_i=0$$ (A1)

where $E_{rr}$ and $E_{\theta \theta }$ are residual errors from the equilibrium in the radial and circumferential directions, $P_i$ denotes the internal wall pressure in the inflated tube. Since $r$ and $h_t$ are functions of ${\lambda }_{\theta }$ and ${\lambda }_r$, the nonlinear Eq. (A1) can be solved by the Newton–Raphson method

$$\begin{array}{c}{\left[\frac{\partial {\mathit{T}}_{rr}}{\partial {\lambda }_r}\right]}^{i-1}{\dot{\lambda }}_r^i\Delta t+{\left[\frac{\partial {\mathit{T}}_{rr}}{\partial {\lambda }_{\theta }}\right]}^{i-1}{\dot{\lambda }}_{\theta }^i\Delta t=-E_{rr}^{i-1}\hspace{0.17em}\hspace{0.17em}\text{and}\\ {\left[\frac{\partial \left({\mathit{T}}_{\theta \theta }-\frac{r}{h_t}{P}_i\right)}{\partial {\lambda }_r}\right]}^{i-1}{\dot{\lambda }}_r^i\Delta t+{\left[\frac{\partial \left({\mathit{T}}_{\theta \theta }-\frac{r}{h_t}{P}_i\right)}{\partial {\lambda }_{\theta }}\right]}^{i-1}{\dot{\lambda }}_{\theta }^i\Delta t=-E_{\theta \theta }^{i-1}\end{array}$$ (A2)

The superscript i denotes the iteration number and $\Delta t$ is the time increment. The system Eq. (A2) is solved until $\sqrt{E_{rr}^2+E_{\theta \theta }^2}$ becomes smaller than the tolerance to get ${\lambda }_{\theta }$ and ${\lambda }_r$ by

$${\lambda }_r^n={\lambda }_r^{n-1}+\sum {\dot{\lambda }}_r\Delta t\hspace{1em}\text{and}\hspace{1em}{\lambda }_{\theta }^n={\lambda }_{\theta }^{n-1}+\sum {\dot{\lambda }}_{\theta }\Delta t$$ (A3)

During the iteration, $h_t$ and $r$ should be updated by

$$r={\lambda }_{\theta }R\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}{h}_t=\frac{R}{r}{H}_t{\lambda }_{\theta }{\lambda }_r$$ (A4)

At each iteration, ${\dot{\lambda }}_r\Delta t$ and ${\dot{\lambda }}_{\theta }\Delta t$ denote the total stretch while the stress components (${\mathit{T}}_{rr}$ and ${\mathit{T}}_{\theta \theta }$) in Eq. (A2) are affected by only the elastic stretch. For this reason, the inelastic deformation should also be considered. The numerical loop of the inelastic dissipation is inside the global iteration of Eqs. (A2)–(A3), and the details of the inelastic numerical procedure is explained in Secs. A.2 and A.3. Next, the Lagrange multiplier $p$ is also updated at every iteration by using the equilibrium between the stress components given by

$$\frac{\partial {\mathit{T}}_{rr}}{\partial r}+\frac{{\mathit{T}}_{rr}-{\mathit{T}}_{\theta \theta }}{r}=0$$ (A5)

$$\frac{\partial {\mathit{T}}_{zz}}{\partial z}=0$$ (A6)

The stress components in the above equation are obtained after the inelastic loop (see Sec. A.3), and the remaining stresses for the incompressible material can be written as

$${\mathit{T}}_{rr}=-p+{\overline{\mathit{T}}}_{rr}$$ (A7)

$${\mathit{T}}_{\theta \theta }=-p+{\overline{\mathit{T}}}_{\theta \theta }$$ (A8)

$${\mathit{T}}_{zz}=-p+{\mathit{T}}_{zz}$$ (A9)

The internal pressure $P_i$ is given for the inflated tube, and ${\mathit{T}}_{rr}(r=r_i)=-P_i$ and ${\mathit{T}}_{rr}(r=r_o)=0$ where $r_i$ and $r_o$ are in and out radius for the tube. The integration of Eq. (A7) gives

$${\mathit{T}}_{rr}\left(r\right)={\int }_{r_i}^{r_o}\frac{{\overline{\mathit{T}}}_{rr}-{\overline{\mathit{T}}}_{\theta \theta }}{\xi }d\xi$$ (A10)

$F_z$ are given by integral forms as

$$p=-{\int }_{r_i}^{r_o}\frac{{\overline{\mathit{T}}}_{rr}-{\overline{\mathit{T}}}_{\theta \theta }}{r}dr$$ (A11)

$$F_z=-{\int }_{r_i}^{r_o}(-p+{\overline{\mathit{T}}}_{zz})(2\pi r)dr$$ (A12)

The Lagrange multiplier $p$ can be solved using Eqs. (A7) and (A10), then (A12) becomes

$$F_z=2\pi {\int }_{r_i}^{r_o}\left({\int }_{r_i}^{r_o}\frac{{\overline{\mathit{T}}}_{rr}-{\overline{\mathit{T}}}_{\theta \theta }}{\xi }d\xi -{\overline{\mathit{T}}}_{rr}+{\overline{\mathit{T}}}_{zz}\right)rdr$$ (A13)

Since

$${\int }_{r_i}^{r_o}r{\int }_{r_i}^{r_o}\frac{{\overline{\mathit{T}}}_{rr}-{\overline{\mathit{T}}}_{\theta \theta }}{\xi }d\xi dr=\pi r_i^2{P}_i+{\int }_{r_i}^{r_o}\frac{r}{2}\left({\overline{\mathit{T}}}_{rr}-{\overline{\mathit{T}}}_{\theta \theta }\right)dr$$ (A14)

The Eq. (A13) results in

$$F_z=2\pi {\int }_{r_i}^{r_o}\left({\overline{\mathit{T}}}_{zz}-\frac{{\overline{\mathit{T}}}_{\theta \theta }+{\overline{\mathit{T}}}_{rr}}{2}\right)rdr+\pi r_i^2{P}_i$$ (A15)

If the vessel is assumed to be a thin membrane, the integration ${\int }_{r_i}^{r_o}f(r)dr$ can be approximated by $f(r_m)/h_t$ where $r_m=(r_o+r_i)/2$ and $h_t=r_o-r_i$.

Hence

$$P_i=\frac{h\left({\overline{\mathit{T}}}_{\theta \theta }-{\overline{\mathit{T}}}_{rr}\right)}{r_m}$$ (A16)

$$F_{\mathit{z}}=2\pi r_{m}h({\overline{T}}_{zz}-{\overline{T}}_{rr})-\pi (r_m^2-r_i^2)$$ (A17)

A.2 Numerical Process of the Growth.

The inelastic loop is inside the global iteration loop in Eq. (A2). In the ith global iteration at nth time-step of numerical analysis, the total deformation and elastic dilatation are given under the pure elastic deformation assumption, as below:

$${[{\mathbf{F}}_e]}_n^t={[\mathbf{F}]}_n\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{[J_e]}_n^t={[J_e]}_{n-1}(1+\mathbf{D}:\mathbf{I})$$ (A18)

The superscript t denotes the trial value and the subscript n means the nth time-step, and $\mathbf{D}$ is given by integrating the rate of the stretch tensor component through the global iteration of Eq. (A3)

$$\mathbf{D}:\mathbf{I}=\sum ({\dot{\lambda }}_r+{\dot{\lambda }}_{\theta })$$ (A19)

The trial Cauchy stress is determined by Eq. (27), and then the inelastic potential function ${\phi }_{\text{in}}\left({\mathbf{T}}^{\prime },\text{tr}\left(\mathbf{T}\right)\right)$ defines the inelastic deformation. The increment of the growth potential can define a $g_1$ function

$$g_1={\dot{\phi }}_g(\text{tr}(\mathbf{T}))\Delta t-d{\phi }_g(\text{tr}(\mathbf{T}))=0$$ (A20)

and be solved by the Newton–Raphson scheme as below:

$$g_1^k=g_1^{k-1}+{\left[\frac{\partial {\dot{\phi }}_g}{\partial {\phi }_g}d{\phi }_g\Delta t-d{\phi }_g\right]}^k=0$$ (A21)

where k is the local iteration number in the growth loop and $\Delta t$ is the time increment. The growth deformation is determined by

$${\Gamma }_g=\frac{1}{3}\sum d{\phi }_g,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{where}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}d{\phi }_g={\left[1-{\left(\frac{\partial {\dot{\phi }}_g}{\partial {\phi }_g}\right)}^k\Delta t\right]}^{-1}{g}_1^{k-1}$$ (A22)

Then ${\mathbf{F}}_e$ is updated at each iteration as below:

$${[{\mathbf{F}}_e]}_n^k={[{\mathbf{F}}_g]}^{-1}{[\mathbf{F}]}_n^t\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{[J_e]}_n^k={[J_e]}_n^t-3{[J_e]}_{n-1}{\Gamma }_g$$ (A23)

Based on the incompressible condition, Eqs. (A21)–(A23) are repeated until reaching the condition of ${[J_e]}_n^k=1$. Following Eqs. (44) and (45), ${\mathbf{F}}_g$ is given by:

$${\mathbf{F}}_g={(3{\Gamma }_g)}^{1/3}\mathbf{I}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\text{isotropic},\hspace{0.17em}\text{and}$$ (A24)

${\mathbf{F}}_g=3{\Gamma }_g\mathbf{A}$ where $\mathbf{A}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1/3{\Gamma }_g& 0\\ 0& 0& 1/3{\Gamma }_g\end{array}\right]$ for anisotropic.

The trial stress is then updated by new ${[{\mathbf{F}}_e]}_n^t$ and ${[J_e]}_n$.

A.3 Numerical Process of the Plastic Deformation.

If ${\phi }_p({\mathbf{T}}^{\prime t})-{\mathit{T}}_Y<0$, the trial stress becomes the Cauchy stress ($\mathbf{T}={\mathbf{T}}^t$) at the ith global iterations. On the other hand, ${\phi }_p({\mathbf{T}}^{\prime t})-{\mathit{T}}_Y>0$, the plastic deformation is generated. Since the rotational and shear deformation are neglected, the plastic spin tensor is also neglected by

$$W_{p12}=W_{p13}=W_{p23}=0$$ (A25)

and the direction of the plastic deformation is calculated by neglecting the shear plastic deformation

$${\overline{\mathbf{D}}}_p^k={\overline{\mathbf{L}}}_p^k=\frac{3}{2}\frac{1}{{\phi }_p^{k-1}}{\left[{\mathbf{T}}^{\prime }\right]}^{k-1}$$ (A26)

${\Gamma }_P$ is then calculated

$${\Gamma }_P=\sum \frac{{\widehat{y}}_2^k}{{\overline{y}}_2^k}$$ (A27)

where

$${\widehat{y}}_2^k={\left[\frac{\partial {\phi }_p}{\partial J_e}{J}_e\mathbf{I}+2\left({\overline{\mathbf{F}}}_e\frac{\partial {\phi }_p}{\partial {\overline{\mathbf{C}}}_e}{\overline{\mathbf{F}}}_e^{\mathit{T}}-\frac{1}{3}\mathbf{I}\right)\right]}^{k-1}:\left[\mathbf{D}-\frac{1}{3}\frac{\mathrm{g}}{{\rho }_o}\mathbf{I}\right]\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}{\overline{y}}_2^k={\left[2{\overline{\mathbf{F}}}_e\frac{\partial {\phi }_p}{\partial {\overline{\mathbf{C}}}_e}{\overline{\mathbf{F}}}_e^{\mathit{T}}:{\overline{\mathbf{D}}}_P+H\right]}^{k-1}$$

${\Gamma }_P$ in Eq. (A27) is accumulated until $y_3={\phi }_p({\mathbf{T}}^{\prime })-{\mathit{T}}_Y$ reaches the tolerance. ${\overline{\mathbf{F}}}_e$ and ${\overline{\mathbf{C}}}_e$ can be updated by

$${\overline{\mathbf{F}}}_e^k={\overline{\mathbf{F}}}_e^t+(\overline{\mathbf{L}}-{\Gamma }_p^k{\overline{\mathbf{D}}}_p^{k-1}){\overline{\mathbf{F}}}_e^{k-1}\Delta t$$ (A28)

$${\overline{\mathbf{C}}}_e^k={({\overline{\mathbf{F}}}_e^k)}^{\mathrm{T}}{\overline{\mathbf{F}}}_e^k$$ (A29)

Finally, the Cauchy stress of ith global iteration at the nth step is determined by Eq. (27).

Funding Data

• National Research Foundation of Korea (NRF) grant funded from the Korea government (No. 2021R1C1C1007946; Funder ID: 10.13039/501100003725).

• National Institutes of Health (Grant No. U01 1HL135842; Funder ID: 10.13039/100000002).